1 Introduction

Over the past decade, there have been tremendous efforts in controlling and synchronization of nonlinear hyperchaotic system due to the ubiquity of this kind of systems with its potential applications in many disciplines such as in encryption, secure communication and aerospace engineering. Since the first introduction of chaos synchronization by Pecora and Carroll in 1990 [1], many techniques have been reported in the literatures for discovering the state trajectories of hyperchaotic systems tend asymptotically to be identical. Some of the useful control schemes have been presented for synchronization of chaos such as drive-response control, adaptive backstepping control, impulsive control, backstepping control, projective control, passive control, optimal control, and so on [2–19].

Based on the Lyapunov stability theory, many contributions deal with the control and synchronization problem of chaotic systems via sliding mode control (SMC) technique in recent years. The main feature of SMC is to switch the control law to force the states of the system from the initial states onto some predefined sliding surface. The system on the sliding surface has desired properties such as stability, disturbance rejection capability, and tracking ability. Konishi et al. [20] proposed a bang-bang type SMC method to stabilize a class of chaotic systems whose nonlinearity vanishes on a sliding surface. A higher order SMC scheme for uncertain nonlinear systems was proposed in [21]. In [22], an active SMC was proposed for synchronizing two chaos with parametric uncertainty. In [23], Yan et al. presented the synchronization of chaotic gyros with unknown parameters and external disturbance via adaptive SMC. Furthermore, anti-synchronization for a novel class of multiple chaotic systems via SMC scheme has been given [24]. Unfortunately, very few studies have investigated the synchronization problem of the non-integral order high-dimensional chaotic or hyperchaotic systems via SMC control strategy [25–27].

Although the classical differential operation from the integral-order case to the non-integral order (fractional-order) case has been expanded for more than three century, its applications to real physics and engineering are just gaining attention [28]. It is observed that many fractional-order dynamical systems behave chaotically, such as the fractional-order Chua system, the fractional-order Chen system, the fractional cellular neural network system, the fractional form of Lu and Liu system [29–32]. Afterward, various effective control methods for fractional order chaotic system synchronization were reported [33–39]. However, to our best knowledge, the synchronization of fractional-order arbitrary dimensional chaotic system especially high dimensional hyperchaotic system via fractional-order adaptive SMC has not been well discussed. In [40], based on active sliding mode approach, a controller has been proposed for fractional-order chaotic system synchronization. In [41], an intelligent robust fractional SMC method for a class of nonlinear system is studied. In addition, Lin and Tun proposed an adaptive fuzzy SMC to synchronize two different uncertain fractional order time delay chaotic systems [42]. In [43], the authors investigated the chaos control of a class of low dimensional fractional order chaotic systems via sliding mode.

Motivated by the above discussion, a class of \(n\)-dimensional fractional-order hyperchaotic system with parametric uncertainty is proposed by using fractional derivatives. By employing Lyapunov stability theorem and fractional-order stability theory, a fractional-order adaptive sliding mode controller is represented to achieve the synchronization of two identical five dimensional fractional order hyperchaotic systems with bounded disturbance and uncertainty key parameters. In our design procedure, global stability between the outputs of master and slave systems can be approved by employing a modification Lyapunov function. Moreover, numerical analysis illustrate that the proposed control approach can eliminate asymptotic synchronization between master system and slave system.

The rest of the paper is organized as follows: the problem formulation of fractional-order \(n\)-dimensional hyperchaotic system are given in Sect. 2. In Sect. 3, based on the fractional order stability theory, an modified adaptive sliding mode controller is designed to synchronize the fractional-order hyperchaotic system with unknown parameters and bounded disturbance. Results of extensive simulation studies are shown to demonstrate the effectiveness of the approach in Sect. 4. The brief comments and conclusions are drawn in Sect. 5.

2 Preliminaries for fractional-order \(n\)-dimensional hyperchaotic systems

Throughout this paper, \(\Vert \cdot \Vert \) denotes the Euclidean norm of vectors and induced norm of matrices, \([\cdot ]^\mathrm{T}\) represents the transpose of vector, \(\Gamma (\cdot )\) denots the Euler’s Gamma function, \(\mathbf {R}^{n}\) denotes the real \(n\)-dimensional space.

Consider a class of nonlinear integral-order \(n\)-dimensional hyperchaotic system composed of linear term and nonlinear term with unknown parameters:

$$\begin{aligned} \dot{x}=F_{i}(x,p), \end{aligned}$$
(1)

where \(x=[x_{1},x_{2},\ldots ,x_{n}]^\mathrm{T}\in R^{n}, 1<i\le n\) is the state vector, \(F_{i}(x_{i},p)=[F_{1}(x,p),F_{2}(x,p),\ldots ,\) \(F_{i}(x,p)]^{T}\in R^{n}, 1<i\le n\) are smooth continuous nonlinear functions, which is described as

$$\begin{aligned} F_{i}(x,p)&= C_{i}f_{i}(x)\nonumber \\&\quad +\, P_{ij}\sum ^{m}_{j=1}g_{ij}(x),~~(i=1,2,\ldots ,n), \end{aligned}$$
(2)

where \(C_{i}\in R^{n\times n}~(i=1,2,\ldots ,n)\) and \(P_{ij}\in R^{n\times m}~(i=1,2,\ldots ,n;~j=1,2,\ldots ,m)\) are unknown constant virtual coefficients, respectively; \(f_{i}(\cdot )\) and \(g_{ij}(\cdot )\) are smooth linear functions and nonlinear functions, respectively.

In order to analysis the fractional-order form of system (1), some definitions of fractional derivative and approximation approach will be given in the Section.

2.1 Fractional derivatives

In real applications, there are several original definitions of fractional derivatives have been successfully used as a model construction function to achieve system equations. The commonly used definitions for the general fractional differential integral are the Grünwald–Letnikov (GL) definition and Riemann–Liouville (RL) definition. The GL definition is expressed as

$$\begin{aligned} \frac{{\mathrm{d}^\alpha }f(t)}{\mathrm{d}t^\alpha }= \lim _{h\rightarrow 0}h^{-r}\sum ^{[\frac{t-\alpha }{h}]}_{j=0}(-1)^{j}\left( \begin{array}{c} r \\ j \\ \end{array} \right) f(t-jh), \end{aligned}$$
(3)

where \([\cdot ]\) means the integer part. The RL fractional derivative is defined as:

$$\begin{aligned} _{t}D^{\alpha }_{a}f(t)&= \frac{{\mathrm{d}^\alpha }f(t)}{\mathrm{d}t^\alpha }\nonumber \\&= \frac{1}{\Gamma (n-\alpha )}\frac{\mathrm{d}^n}{\mathrm{d}t^n}\mathop \int \limits ^{t}_{a}\frac{f(\tau )}{(t-\tau )^{\alpha -n+1}}\mathrm{d}\tau , \end{aligned}$$
(4)

where n is an integer larger than \(\alpha \), i.e., \(n-1<\alpha <n\). The gamma function is a generalization of the factorial function \(n!\) and can be written in the following form

$$\begin{aligned} \begin{aligned}&\Gamma (z) = \mathop \int \limits ^{1}_{0} \mathrm{e}^{-t}t^{z-1} \mathrm{d}t+\mathop \int \limits ^{\infty }_{1} \mathrm{e}^{-t}t^{z-1} \mathrm{d}t,~~Re(z)>0 \\&\Gamma (z+1)= z\Gamma (z). \end{aligned} \end{aligned}$$
(5)

Based on the RL definition, the fractional-order form of system (1) can be express as follows:

$$\begin{aligned} D^{\alpha _{i}}x_{i}(t)= F(x_{i},p), \end{aligned}$$
(6)

where \(\alpha _{i}=[\alpha _{1},\alpha _{2},\ldots ,\alpha _{n}]^\mathrm{T}\in (0,1]\) is the fractional-order satisfying \(x_{i}=[x_1,x_2,\ldots ,x_n]^\mathrm{T}\in R^{n}\), \(F: R^{1}\rightarrow R^{m}\) is a smooth nonlinear vector functions in the term of \(x_{i}\).

2.2 ABM approximation algorithm

Generally, a very brief overview of approximation approach which can be useful for numerical investigation of the considered generalized fractional-order nonlinear systems. The approximation design procedure based on the Adams–Bashforth–Moulton(ABM) predictor–corrector algorithm which is usually used for numerical solutions of the fractional-order corresponding systems [44]. This scheme is at least super linearly convergent and has good stability, especially it preserves the inherent attribute of fractional derivatives.

The initial value equation of system (6) can be described as follows:

$$\begin{aligned} \left\{ \begin{array}{l} D^{\alpha _{i}}_{*}x_{i}(t)= F(t,x_{i}(t))\\ x^{k}(0)= x^{(k)}_{0}, k=0,1,\ldots ,[\alpha ]-1 \end{array} \right. , \end{aligned}$$
(7)

where \(0\le t\le T,~~0<i\le n\), and \(\alpha _{i}=(\alpha _{1},\alpha _{2},\ldots ,\alpha _{n})^{T}\) is the fractional order satisfying \(\alpha \in (0,1]; x_{i}=(x_1,x_2,\ldots ,x_n)^{T}\in R^{n}\), \(F_{\cdot }: R^{1}\rightarrow R^{m}\) is a smooth nonlinear vector functions in the term of \(x_{i}\), \(0\le t\le T,~~0<i\le n\)

Lemma 1

\(D:=[0,T^*]\times [x_{0}-\delta , x_{0}+\delta ]\) with \(T^{*}>0\) and \(\delta >0\), then let the function \(F: D\rightarrow R\) be continuous. Furthermore, define \(T:=\min \Big \{{T^{*},\big (\frac{\delta \gamma (\alpha +1)}{\Vert F\Vert _{\infty }}\big )^\frac{1}{\alpha }}\Big \}\), then there exists a function \(x: [0,T]\rightarrow R\) solving the initial value form (7). Notice that \(\Vert F\Vert _{\infty }\) is the norm of function \(F\).

Note that the differential equation (7) is equivalent to the Volerra integral equation:

$$\begin{aligned} x(t)=\sum ^{[\alpha ]-1}_{k=0}\frac{t^{k}}{k!}x^{(k)}_{0} +\frac{1}{\Gamma (\alpha )}\mathop \int \limits ^{t}_{0} (t-\tau )^{\alpha -1}f(\tau ,x(\tau )) \mathrm{d}\tau ,\nonumber \\ \end{aligned}$$
(8)

set \(h=\frac{T}{N}, t_{j}=jh,~(j=0,1,\ldots ,N\in Z^{+})\), the corresponding discretization equation for (6) is defined by

$$\begin{aligned} x_{h}(t_{n+1})&= \sum ^{[\alpha ]-1}_{k=0}x^{(k)}_{0} \frac{t^{k}_{n+1}}{k!}+\frac{h^{\alpha }}{\Gamma (\alpha +2)}f\big (t_{n+1},x^{p}_{h}(t_{n+1})\big )\nonumber \\&+\frac{h^{\alpha }}{\Gamma (\alpha +2)}\sum ^{n}_{j=0}a_{j,n+1}f\big (t_j,x_{h}(t_j)\big ), \end{aligned}$$
(9)

where

$$\begin{aligned} a_{(j,n+1)}\left\{ \begin{array}{ll} n^{\alpha +1}-(n-\alpha )(n+1)^{\alpha },~~~~~~~~~~~~~ j=0\\ (n-j+2)^{\alpha +1}+(n-j)^{\alpha +1}-2 (n-j+1)^{\alpha +1},\\ \quad 1\le j\le n\\ 1, ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ j=n+1 \end{array} \right. \end{aligned}$$
(10)

the predictor \(x^{p}_{(t_{n+1})}\) is given by

$$\begin{aligned} x^{p}_{h}(t_{n+1})=\sum ^{n+1}_{k=0}\frac{t^{k}_{n+1}}{k!}x^{k}_{0}+\frac{1}{\gamma (\alpha )}\sum ^{n}_{j=0}f\big (t_{j},x_h(t_j)\big ), \end{aligned}$$
(11)

where

$$\begin{aligned} b_{(j,n+1)}=\frac{h^{\alpha }}{\alpha }\big ((n+1-j)^{\alpha } -(n-j)^{\alpha }\big ),~~0\le j\le n. \end{aligned}$$
(12)

Comparing Eqs. (7) and (8), estimation error of the approximation is

$$\begin{aligned}&e^{*}=\max _{j=0,1,\ldots ,N}|x(t_j)-x_{h}(t_j)|=O(h^{p}),\nonumber \\&\qquad \qquad p=\min (2,1+\alpha ). \end{aligned}$$
(13)

3 Modified SMC design for fractional-order hyperchaotic synchronization

In this section, we will derive a globally synchronization for \(n\)-dimensional hyperchaotic systems via adaptive SMC approach. We refer to system (6) as the master system, and the controlled slave system can be described by following differential equation:

$$\begin{aligned} D^{\alpha _{i}}y=F(y_{i},p)+d(t)+u, \end{aligned}$$
(14)

where \(y_{i}=[y_{1},y_{2},\ldots ,y_{n}]^\mathrm{T}\in R^{n}\) is the vector of states; \(F(y,p)=[F_{1}(y,p),F_{2}(y,p) ,\ldots , F_{n}(y,p)]^\mathrm{T} \in R^{n}\) are smooth continuous nonlinear functions; \(d(\cdot )\) are the unknown external time varying disturbances, and controller \(u=(u_{1},u_{2},\ldots ,u_{n})^{T}\in R^{n}\) are fed into arbitrary equation to form the controlled system.

Remark 1

Assume that disturbance \(d(t)=[d_{1}(t), d_{2}(t),\ldots ,d_{n}(t)]^\mathrm{T}\in R^{n}\) are bounded, i.e., \(\Vert d_{i}(t)\Vert \le \tilde{k}_{i}<\infty , (i=1,2,\ldots ,n), \forall t\). the values of every \(\tilde{k}_{i} (i=1,2,\ldots ,n)\) are not required to be known but can be achieved by adaptive law.

Substituting (2) into (14), we obtain

$$\begin{aligned} D^{\alpha }y&= f_{i}(y)+\sum ^{m}_{j=1}p_{ij}g_{ij}(y)+d_{i}(t)+u_{i},\nonumber \\&(i=1,2,\ldots ,n). \end{aligned}$$
(15)

Definition 1

To design an appropriate fractional-order active sliding mode controller \(u(x)\) such that the trajectory of the salve system (15) asymptotically approaches the master system (6) and finally implement synchronization, in the sense if there exists a constant \(T=T(e(0))>0\), such that

$$\begin{aligned} \lim _{t\rightarrow T}\Vert y-x\Vert =\lim _{t\rightarrow T}\Vert e(t)\Vert =0, \end{aligned}$$

where \(\Vert e(t)\Vert \equiv 0\), if \(t\ge T\), which means that asymptotic synchronization is achieved.

The tracking error vector of master system (6) and slave system (15) can be written as

$$\begin{aligned} e_{i}&= (e_{1},e_{2},\ldots ,e_{n})^{T}\nonumber \\&= (y_{1}-x_{1},y_{2}-x_{2},\ldots ,y_{n}-x_{n})^{T}. \end{aligned}$$
(16)

Substituting (2) and (4) into (6), it follows that

$$\begin{aligned} D^{\alpha _{i}}e_{i}&= f_{i}(y)-f_{i}(x)+\sum ^{m}_{j=1}p_{ij}[g_{ij}(y)-g_{ij}(x)]\nonumber \\&\quad +\,d_{i}(t)+u_{i},\quad (i=1,2,\ldots ,n). \end{aligned}$$
(17)

The control objective is to ensure that all signals of slave system are bounded while tracking the signals of master system.

In accordance to the standard SMC theory, the design procedure of modified adaptive SMC with fractional-order state contains two main steps as:

  1. (i)

    Constructing a sliding surface (sliding mode) which represents the desired system dynamics;

  2. (ii)

    Developing a switching control law to guarantee the sliding mode possible on every point in the sliding surface. Any states outside the surface are driven to reach the surface in a finite time.

For clarity and conciseness of presentation, detailed explanation of steps are described as follows.

Step 1. To ensure the asymptotical stability of the sliding mode, as a choice for the sliding surface, one has:

$$\begin{aligned} S_{i}=D^{\alpha _{i}-1}e_{i}+\mathop \int \limits ^{\tau }_{0}c_{i}e_{i}(\tau ) \mathrm{d}\tau , ~~~(i=1,2,\ldots ,n). \end{aligned}$$
(18)

To guarantee the sliding mode on the sliding surface, the surface is defined as

$$\begin{aligned} S_{i}=D^{\alpha _{i}}e_{i}+\mathop \int \limits ^{\tau }_{0}c_{i}e_{i}(\tau ) \mathrm{d}\tau =0, ~~~(i=1,2,\ldots ,n) \end{aligned}$$
(19)

and its derivative satisfy as

$$\begin{aligned} \dot{S}_{i}=D^{\alpha _{i}}e_{i}+c_{i}e_{i}(\tau )=0, ~~~(i=1,2,\ldots ,n). \end{aligned}$$
(20)

Noting (21), fractional tracking error can be expressed as

$$\begin{aligned} D^{\alpha _{i}}e_{i}=-c_{i}e_{i}(\tau ),~~~(i=1,2,\ldots ,n). \end{aligned}$$
(21)

To avoid control singularity, the continuously differentiable Lyapunov function candidate can be chosen as

$$\begin{aligned} \dot{V}_{i}=\frac{1}{2}e^{2}_{i}, ~~~(i=1,2,\ldots ,n). \end{aligned}$$
(22)

Its derivative is given by

$$\begin{aligned} \dot{V}_{i}=e_{i}\dot{e}_{i}=-c_{i}e_{i}^{2}(\tau ) ~~~(i=1,2,\ldots ,n), \end{aligned}$$
(23)

where \(c_{i}>0,~~(i=1,2,\ldots ,n)\) is a design constant, such that \(\dot{V}_{i}<0\). At the same time we can see that the controlled error system in sliding mode and the system is insensitive to external interference. In other words, the system showed strong robustness to external interference. Therefore, the closed loop system is globally asymptotically stable when the error system enters the sliding mode.

To guarantee the fractional order hyperchaotic system asymptotically stable, the Theorem 1 should be considered.

Theorem 1

For \(n\)-dimensional fractional hyperchaotic system \(D^{\alpha _{i}}x=Ax,x(0)=x_{0}\), where \(0<\alpha _{i}<1, x\in R^{n}\), \(A\in R^{n\times n}\) is the \(n\)-dimension matrix. If all eigenvalues of \(A(x)\) satisfy \(|\mathrm{arg}(\mathrm{eig}(A))|>\alpha \pi /2\), then the system is asymptotically steady at the equilibrium.

Based on the Theorem 1, the stability region of the fractional-order hyperchaotic system with order \(\alpha _{i}\) is illustrated in Fig. 1, in which \(\omega , \sigma \) refer to the real and imaginary parts of the eigenvalues, respectively. Thus, the asymptotic stability of Eq. (22) can be guaranteed by choosing \(c_{i}>0,(i=1,2,\ldots ,n)\).

Fig. 1
figure 1

Stability region of the fractional order dynamical system

Full size image

Step 2. To design the reaching mode control scheme, which drives states onto the sliding surface, the possible control structure \(u_{i}(i=1,2,\ldots ,n)\) should be chosen as:

$$\begin{aligned} u_{i}(t)=-\gamma _{i}\zeta _{i} \mathrm{sign}(S_{i}), \end{aligned}$$
(24)

where the constant \(\gamma _{i}\) satisfies \(\forall \gamma _{i}>1\); \(\mathrm{sign}(\cdot )\) denotes the sign function. The sign function of this study is defined as

$$\begin{aligned} \mathrm{sign}(S)=\left\{ \begin{array}{l@{\quad }l} +1,&{}\mathrm{if}\ S>0\\ 0,&{} \mathrm{if}\ S=0\\ -1, &{} \mathrm{if}\ S<0\\ \end{array}\right. , \end{aligned}$$
(25)

where \(\zeta _{i}\) is an adaptive parameter in the control law which can be written in a compact form as

$$\begin{aligned} \zeta _{i}&= |f_{i}(y)-f_{i}(x)+c_{i}e_{i}|\nonumber \\&\quad +\sum ^{m}_{j}\hat{p}_{ij}|g_{ij}(y)-g_{ij}(x)|+\hat{k}_{i}, \end{aligned}$$
(26)

where \(\hat{k}_{i}\) and \(\hat{p}_{ij} ~~(i=1,2,\ldots ,n; j=1,2,\ldots ,m)\) are estimate parameters of \(\zeta _{i}\), which can transform with the change of state of the error system, and the parameters update law can be chosen as

$$\begin{aligned} \dot{\hat{p}}_{ij}=|g_{ij}(y)-g_{ij}(x)||S_{i}| \end{aligned}$$
(27)

and

$$\begin{aligned} \dot{\hat{k}}_{i}=|S_{i}|. \end{aligned}$$
(28)

To avoid the reaching condition of sliding mode surface, the controller should be designed to guarantee the surface converges to zero in limited period of time.

Define \(q_{ij}\) and \(k_{i}\) as

$$\begin{aligned} q_{ij}=\hat{p}_{ij}+|p_{ij}|~~~(i=1,2,\ldots ,n; j=1,2,\ldots ,m) \end{aligned}$$

and

$$\begin{aligned} k_{i}=\hat{k}_{i}-\tilde{k}_{i}. \end{aligned}$$

Proof

Consider the following Lyapunov function candidate

$$\begin{aligned} V(t)=\frac{1}{2}\left( \sum ^{n}_{i=1}S^{2}_{i}+\sum ^{n}_{i=1}\sum ^{m}_{j=1}q^{2}_{ij}+\sum ^{n}_{i=1}k^{2}_{i}\right) . \end{aligned}$$
(29)

The time derivative of \(V(t)\) becomes

$$\begin{aligned} \dot{V}(t)&= \sum ^{n}_{i=1}S_{i}\dot{S}_{i}+\sum ^{n}_{i=1}\sum ^{m}_{j=1}q_{ij}\dot{q}_{ij}+\sum ^{n}_{i=1}k_{i}\dot{k}_{i}\nonumber \\&= \sum ^{n}_{i=1}S_{i}(D^{\alpha _{i}}e_{i}+c_{i}e_{i}) +\sum ^{n}_{i=1}\sum ^{m}_{j=1}(\hat{p}_{ij}+|p_{ij}|)\dot{\hat{p}}_{ij}\nonumber \\&\quad +\sum ^{n}_{i=1}(\hat{k}_{i}-\tilde{k}_{i})\dot{\hat{k}}_{i}. \end{aligned}$$
(30)

Substituting Eq. (18) into (31), we have

$$\begin{aligned} \dot{V}(t)&= \sum ^{n}_{i=1}\left[ (f_{i}(y)-f_{i}(y)) +\sum ^{m}_{j=1}(p_{ij}g_{ij}(y)-p_{ij}g_{ij}(x))\right. \nonumber \\&\quad \left. \quad \quad \quad +\,d_{i}(t)+u_{i}+c_{i}e_{i}\right] S_{i}\nonumber \\&+\sum ^{n}_{i=1}\sum ^{m}_{j=1}(\hat{p}_{ij}+|p_{ij}|)\dot{\hat{p}}_{ij}+\sum ^{n}_{i=1}(\hat{k}_{i}-\tilde{k}_{i})\dot{\hat{k}}_{i}. \end{aligned}$$
(31)

Furthermore, according to absolute value inequality theory, substituting Eqs. (25), (28) and (29) into Eq.(32), it follows that

$$\begin{aligned} \dot{V}(t)&\le \sum ^{n}_{i=1}|[f_{i}(y)-f_{i}(y)+c_{i}e_{i}]||S_{i}|\nonumber \\&\quad +\sum ^{n}_{i=1}\sum ^{m}_{i}|p_{ij}||g_{ij}(y)-g_{ij}(x)||S_{i}|\nonumber \\&\quad +\sum ^{n}_{i=1}|d_{i}(t)||S_{i}|-\sum ^{n}_{i=1}\gamma _{i}\zeta _{i}S_{i} \mathrm{sign}(S_{i})\nonumber \\&\quad +\sum ^{n}_{i=1}\sum ^{m}_{j=1}(\hat{p}_{ij}+|p_{ij}|)|g_{ij}(y)-g_{ij}(x)||S_{i}|\nonumber \\&\quad +\sum ^{n}_{i=1}(\hat{k}_{i}-\tilde{k}_{i})|S_{i}|. \end{aligned}$$
(32)

Noting that \(\mathrm{sign}(S_{i})S_{i}=|S_{i}|\) and \(\Vert d_{i}(t)\Vert \le \tilde{k}_{i}\), it yields inequality (33) as following

$$\begin{aligned} \dot{V}(t)&\le \sum ^{n}_{i=1}|[f_{i}(y)-f_{i}(y)+c_{i}e_{i}]||S_{i}|\nonumber \\&\quad +\sum ^{n}_{i=1}\sum ^{m}_{i}|p_{ij}||g_{ij}(y)-g_{ij}(x)||S_{i}|\nonumber \\&\quad +\sum ^{n}_{i=1}\tilde{k}_{i}|S_{i}|-\sum ^{n}_{i=1}\gamma _{i}\zeta _{i}|S_{i}|\nonumber \\&\quad +\sum ^{n}_{i=1}\sum ^{m}_{j=1}(\hat{p}_{ij}+|p_{ij}|)|g_{ij}(y)-g_{ij}(x)||S_{i}|\nonumber \\&\quad +\sum ^{n}_{i=1}(\hat{k}_{i}-\tilde{k}_{i})|S_{i}|\nonumber \\&= \sum ^{n}_{i=1}|f_{i}(y)-f_{i}(y)+c_{i}e_{i}||S_{i}|\nonumber \\&\quad +\sum ^{n}_{i=1}\sum ^{m}_{j=1}\hat{p}_{ij}|g_{ij}(y)-g_{ij}(x)||S_{i}|\nonumber \\&\quad +\sum ^{n}_{i=1}\hat{k}_{i}|S_{i}|-\sum ^{n}_{i=1}\gamma _{i}\zeta _{i}||S_{i}|\nonumber \\&= \sum ^{n}_{i=1}\left( |f_{i}(y)-f_{i}(y)+c_{i}e_{i}|\right. \nonumber \\&\quad \quad \quad \left. +\sum ^{m}_{j=1}\hat{p}_{ij}|g_{ij}(y)-g_{ij}(x)|+\hat{k}_{i}\right) |S_{i}|\nonumber \\&\quad \quad \quad -\sum ^{n}_{i=1}\gamma _{i}\zeta _{i}|S_{i}|. \end{aligned}$$
(33)

Using Eq. (27), the above inequality can be further written as

$$\begin{aligned} \dot{V}(t)&\le \sum ^{n}_{i=1}\zeta _{i}|S_{i}|-\sum ^{n}_{i}\gamma _{i}\zeta _{i}|S_{i}|\nonumber \\&= \sum ^{n}_{i=1}(1-\gamma _{i})\zeta _{i}|S_{i}|. \end{aligned}$$
(34)

Because \(\gamma _{i}>1\), thus if guarantee \(\zeta _{i}>0\), we further obtain

$$\begin{aligned} \dot{V}(t)\le \sum ^{n}_{i=1}(1-\gamma _{i})\zeta _{i}|S_{i}|\le 0. \end{aligned}$$
(35)

Remark 2

When select bounded initial conditions of \(\hat{p}_{ij}, \hat{k}_{i}~(i=1,2,\ldots ,n;j=1,2,\ldots ,m)\) as \(\hat{p}_{ij}(0)>0, \hat{k}_{i}(0)>0\), it is seen from Eqs. (28) and (29) that there exist \(\hat{p}_{ij}>0,\hat{k}_{i}>0~(i=1,2,\ldots ,n;j=1,2,\ldots ,m)\) with time \(t\) variation under this conditions; By substitution \(\hat{p}_{ij}(0)>0, \hat{k}_{i}(0)>0\) into (27), it follows that \(\zeta _{i}>0~(i=1,2,\ldots ,n)\)

Therefore, a Lyapunov function (30) has been found that satisfies the conditions of the Lyapunov theorem \((V>0; \dot{V}<0)\). The inequality (35) confirms that the fractional-order dynamical system in the presence of the sliding mode controller (25) is globally asymptotically stable.

4 Numerical simulation

In this section, to illustrate the effectiveness of the proposed control design procedure for synchronization, extensive simulations were carried out for a new fractional-order five dimensional hyperchaotic system synchronization by using (ABM) approximation algorithm.

Consider a novel five-dimensional hyperchaotic system as following

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_{1}=\beta _{1}(x_{2}-x_{1})\\ \dot{x}_{2}=\beta _{2}x_{1}-\beta _{3}x_{1}x_{3}-\beta _{4}x_{4}\\ \dot{x}_{3}=\beta _{5}x_{1}x_{2}-\beta _{6}x_{2}-\beta _{7}x_{3}\\ \dot{x}_{4}=-2x_{1}-2x_{4}\\ \dot{x}_{5}=-2x_{3}x_{4}-2x_{5} \end{array}\right. , \end{aligned}$$
(36)

where \(x_{i}(i=1,2,3,4,5)\) are the state variables, and \(\beta _{i}(i=1,2,3,4,5,6,7)\) are positive constant parameters.

Master system: Fractional-order form of dynamical equation (37) can be described as the following

$$\begin{aligned} \left\{ \begin{array}{l} D^{\alpha _{1}}x_{1}=\beta _{1}(x_{2}-x_{1})\\ D^{\alpha _{2}}x_{2}=\beta _{2}x_{1}-\beta _{3}x_{1}x_{3}-\beta _{4}x_{4}\\ D^{\alpha _{3}}x_{3}=\beta _{5}x_{1}x_{2}-\beta _{6}x_{2}-\beta _{7}x_{3}\\ D^{\alpha _{4}}x_{4}=-2x_{1}-2x_{4}\\ D^{\alpha _{5}}x_{5}=-2x_{3}x_{4}-2x_{5} \end{array}\right. , \end{aligned}$$
(37)

where \(x_{i}(i=1,2,3,4,5)\) are the state variables, \(\alpha _{i}(i=1,2,3,4,5)\) are fractional orders, and \(\beta _{i}(i=1,2,3,4,5,6,7)\) are positive constant parameters.

Slave system: With the external time varying disturbances, the controlled corresponding fractional-order form can be rewritten as

$$\begin{aligned} \left\{ \begin{array}{l} D^{\alpha _{1}}y_{1}=\beta _{1}(y_{2}-y_{1})+d_{1}(t)+u_{1}(t)\\ D^{\alpha _{2}}y_{2}=\beta _{2}y_{1}-\beta _{3}y_{1}y_{3} -\beta _{4}y_{4}+d_{2}(t) +u_{2}(t)\\ D^{\alpha _{3}}y_{3}=\beta _{5}y_{1}y_{2} -\beta _{6}y_{2}-\beta _{7}y_{3} +d_{3}(t)+u_{3}(t)\\ D^{\alpha _{4}}y_{4}=-2y_{1}-2y_{4}+d_{4}(t)+u_{4}(t)\\ D^{\alpha _{5}}y_{5}=-2y_{3}y_{4}-2y_{5}+d_{5}(t)+u_{5}(t) \end{array}\right. , \end{aligned}$$
(38)

where \(y_{i}(i=1,2,3,4,5)\) are the state variables, \(\alpha _{i}(i=1,2,3,4,5)\) are fractional orders, and \(\beta _{1}, \beta _{2}, \beta _{3}\), \(\beta _{4}, \beta _{5}, \beta _{6}, \beta _{7}\) are positive constant parameters. As the external time varying disturbance, \(d(t)=[d_{1}(t),d_{2}(t)\), \(d_{3}(t),d_{4}(t),d_{5}(t)]^\mathrm{T}\) is random noise generated by the random function. Its value is evenly distributed in the interval \([-0.1, 0.1]\). \(u=[u_{1},u_{2},u_{3}, u_{4},u_{5}]^\mathrm{T}\) represents the proper controller

According to Definition 1 and Eq. (18), the synchronization error can be expressed as

$$\begin{aligned} \left\{ \begin{array}{l} D^{\alpha _{1}}e_{1}=\beta _{1}(e_{2}-e_{1})+d_{1}(t)+u_{1}(t)\\ D^{\alpha _{2}}e_{2}=\beta _{2}e_{1}-\beta _{3}(y_{1}y_{3} -x_{1}x_{3})-\beta _{4}e_{4} +d_{2}(t)+u_{2}(t)\\ D^{\alpha _{3}}e_{3}=\beta _{5}(y_{1}y_{2} -x_{1}x_{2})-\beta _{6}e_{2} -\beta _{7}e_{3}+d_{3}(t) +u_{3}(t).\\ D^{\alpha _{4}}e_{4}=-2e_{1}-2e_{4}+d_{4}(t)+u_{4}(t)\\ D^{\alpha _{5}}e_{5}=-2(y_{3}y_{4}-x_{3}x_{4})-2e_{5}+d_{5}(t)+u_{5}(t) \end{array}\right. \end{aligned}$$
(39)

Regarding to (19), the sliding mode surface are chosen as follows

$$\begin{aligned} \left\{ \begin{array}{l} S_{1}(t)=D^{\alpha _{1}-1}e_{1}+\int \nolimits ^{\tau }_{0}c_{1}e_{1}(\tau )\mathrm{d}\tau \\ S_{2}(t)=D^{\alpha _{2}-1}e_{2}+\int \nolimits ^{\tau }_{0}c_{2}e_{2}(\tau )\mathrm{d}\tau \\ S_{3}(t)=D^{\alpha _{3}-1}e_{3}+\int \nolimits ^{\tau }_{0}c_{3}e_{3}(\tau )\mathrm{d}\tau \\ S_{4}(t)=D^{\alpha _{4}-1}e_{4}+\int \nolimits ^{\tau }_{0}c_{1}e_{1}(\tau )\mathrm{d}\tau \\ S_{5}(t)=D^{\alpha _{5}-1}e_{5}+\int \nolimits ^{\tau }_{0}c_{1}e_{1}(\tau )\mathrm{d}\tau \end{array}\right. , \end{aligned}$$
(40)

where \(c_{i}>0~(i=1,2,\ldots ,n)\) is determined by the design parameters, thus, we choose \((c_{1},c_{2},c_{3}, c_{4},c_{5})^{T}=(0.4,0.3,0.32,0.4,0.3)^{T}\).

To ensure the occurrence of the sliding motion, a proper controller is proposed as the following

$$\begin{aligned} \left\{ \begin{array}{l} u_{1}(t)=-\gamma _{1}\zeta _{1}\mathrm{sign}(S_{1})\\ u_{2}(t)=-\gamma _{2}\zeta _{2}\mathrm{sign}(S_{2})\\ u_{3}(t)=-\gamma _{3}\zeta _{3}\mathrm{sign}(S_{3})\\ u_{4}(t)=-\gamma _{4}\zeta _{4}\mathrm{sign}(S_{4})\\ u_{5}(t)=-\gamma _{5}\zeta _{5}\mathrm{sign}(S_{5}) \end{array}\right. , \end{aligned}$$
(41)

where

$$\begin{aligned} \left\{ \begin{array}{l} \zeta _{1}=|c_{1}e_{1}|+\hat{p}_{11}|y_{2}-x_{2}|+\hat{p}_{12}|x_{1}-y_{1}|+\hat{k}_{1} \\ \zeta _{2}=|x_{1}x_{3}-y_{1}y_{3} +c_{2}e_{2}|+\hat{p}_{21}|y_{1} -x_{1}|+\hat{p}_{22}|x_{4} -y_{4}|+\hat{k}_{2}\\ \zeta _{3}=|y_{1}y_{2}-x_{1}x_{2} +c_{3}e_{3}|+\hat{p}_{31}|x_{2} -y_{2}|+\hat{p}_{32}|x_{3} -y_{3}|+\hat{k}_{3}\\ \zeta _{4}=|c_{4}e_{4}|+\hat{p}_{41}|x_{1}-y_{1}|+\hat{p}_{42}|x_{4}-y_{4}|+\hat{k}_{4}\\ \zeta _{5}=|c_{5}e_{5}|+\hat{p}_{51}|x_{3}x_{4}-y_{3}y_{4}|+\hat{p}_{52}|x_{5}-y_{5}|+\hat{k}_{5} \end{array}\right. \end{aligned}$$
(42)

and \(\hat{p}_{11}, \hat{p}_{12}, \hat{p}_{21}, \hat{p}_{22}, \hat{p}_{31}, \hat{p}_{32}, \hat{p}_{41}, \hat{p}_{42}, \hat{p}_{51}, \hat{p}_{52}\) are defined as adaptive parameters, the update rule can be written as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\hat{p}}_{11}=|y_{2}-x_{2}||S_{1}|,~~~\dot{\hat{p}}_{12}=|x_{1}-y_{1}||S_{1}| \\ \dot{\hat{p}}_{21}=|y_{1}-x_{1}||S_{2}|,~~~\dot{\hat{p}}_{22}=|x_{4}-y_{4}||S_{2}|\\ \dot{\hat{p}}_{31}=|x_{2}-y_{2}||S_{3}|,~~~\dot{\hat{p}}_{32}=|x_{3}-y_{3}||S_{3}|\\ \dot{\hat{p}}_{41}=|x_{1}-y_{1}||S_{4}|,~~~\dot{\hat{p}}_{42}=|x_{4}-y_{4}||S_{4}|\\ \dot{\hat{p}}_{51}=|x_{3}x_{4}-y_{3}y_{4}||S_{5}|,~~~\dot{\hat{p}}_{52}=|x_{5}-y_{5}||S_{5}| \end{array}\right. \end{aligned}$$
(43)

and

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\hat{k}}_{1}=|S_{1}| \\ \dot{\hat{k}}_{2}=|S_{2}|\\ \dot{\hat{k}}_{3}=|S_{3}|\\ \dot{\hat{k}}_{4}=|S_{4}|\\ \dot{\hat{k}}_{5}=|S_{5}| \end{array}\right. . \end{aligned}$$
(44)

In practice, the fourth order Runge–Kutta integration with \(0.001\) step size has been employed in simulation analysis. According to (ABM) approximation algorithm, the master system should be discrete in the following form

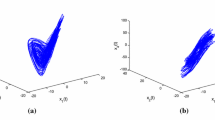
$$\begin{aligned} \left\{ \begin{array}{l} x_{1(n+1)}=x_{1(0)}+\frac{\beta _{1}h^{\alpha _{1}}}{\Gamma (q+2)}\big [x^{*}_{2(n+1)}-x^{*}_{1(n+1)}\\ ~~~~~~~~~~~~~~~~+\sum ^{n}_{j=0}\alpha _{j,n+1}\cdot (x_{2(j)}-x_{1(j)})\big ]\\ x_{2(n+1)}=x_{2(0)}+\frac{h^{\alpha _{2}}}{\Gamma (q+2)} \big [\beta _{2}x^{*}_{2(n+1)}\\ ~~~~~~~~~~~~~~~~-\beta _{3}x^{*}_{1(n+1)}x^{*}_{3(n+1)}-\beta _{4}x^{*}_{4(n+1)}\\ ~~~~~~~~~~~~~~~~+\sum ^{n}_{j=0}\alpha _{j,n+1}\cdot (\beta _{2}x_{1(j)}\\ ~~~~~~~~~~~~~~~~-\beta _{3}x_{1(j)}x_{3(j)}-\beta _{4}x_{4(j)})\big ]\\ x_{3(n+1)}=x_{3(0)}+\frac{h^{\alpha _{3}}}{\Gamma (q+2)} \big [\beta _{5}x^{*}_{1(n+1)}x^{*}_{2(n+1)}\\ ~~~~~~~~~~~~~~~~-\beta _{6}x^{*}_{2(n+1)}-\beta _{7}x^{*}_{3(n+1)}+\sum ^{n}_{j=0}\alpha _{j,n+1}\\ ~~~~~~~~~~~~~~~~\cdot (\beta _{5}x_{1(j)}x_{2(j)}-\beta _{6}x_{2(j)}-\beta _{7}x_{3(j)}) \big ]\\ x_{4(n+1)}=x_{4(0)}+\frac{-2h^{\alpha _{4}}}{\Gamma (q+2)} \big [x^{*}_{1(n+1)}+x^{*}_{4(n+1)} \\ ~~~~~~~~~~~~~~~~+\sum ^{n}_{j=0}\alpha _{j,n+1}\cdot (x_{1(j)}+x_{4(j)}) \big ] \\ x_{5(n+1)}=x_{5(0)}+\frac{-2h^{\alpha _{5}}}{\Gamma (q+2)} \big [x^{*}_{3(n+1)}x^{*}_{4(n+1)}-x^{*}_{5(n+1)}\\ ~~~~~~~~~~~~~~~~ +\sum ^{n}_{j=0}\alpha _{j,n+1}\cdot (x_{3(j)}x_{4(j)}+x_{5(j)}) \big ] \end{array}\right. \end{aligned}$$
(45)

where the fractional order of master system are chosen as: \(\alpha _{1}=0.85\), \(\alpha _{2}=0.85\), \(\alpha _{3}=0.85\), \(\alpha _{4}=0.85\), \(\alpha _{5}=0.85\), parameters are chosen as \(\beta _{1}=8\), \(\beta _{2}=40\), \(\beta _{3}=1.5\), \(\beta _{4}=1.2\), \(\beta _{5}=1.5\), \(\beta _{6}=10/3\), \(\beta _{7}=4\), the initial conditions are taken as \([x_{1}(0),x_{2}(0),x_{3}(0),x_{4}(0),x_{5}(0)]^\mathrm{T}=[0.8, 2.2, 2.0, 0, 1.5]^\mathrm{T}\). Fig. 2a–f show the observed fractional-order projections of 3-D space on different phase planes via solid line.

Fig. 2
figure 2

Phase portraits of the fractional order five-dimensional hyperchaotic attractors in 3D plane

Full size image

If the controller does not activated, we assume that the controlled fractional-order dynamical system is originally \([u_{i}=0,~(i=1,2,3,4,5)]\) in the hyperchaotic state. The asymptotically tracking performance can not be achieved, and the tracking error can not converge to the zero with \(u_{i}=0\). This means that the error system can display randomness properties within the master system and slave system under different initial conditions.

When the controller activated, the control law is determined by Eq. (25) and (42). The initial conditions of slave system are given as \((y_{1}(0),y_{2}(0),y_{3}(0), y_{4}(0),y_{5}(0))^\mathrm{T}=(3.2,1.8,2.2,3.2,2.5)^\mathrm{T}\) All other conditions being the same as the master system. Regarding (43), (44) and (45), the design parameters of controller (42) and parameter update law are chosen as \(\gamma _{1}=1.3\), \(\gamma _{2}=1.2\), \(\gamma _{3}=1.25\), \(\gamma _{4}=1.38\), \(\gamma _{5}=1.5\). \(\hat{p}_{11}(0)=0.1\), \(\hat{p}_{12}(0)=0.2\), \(\hat{p}_{21}(0)=0.1\), \(\hat{p}_{22}(0)=0.1\), \(\hat{p}_{31}(0)=0.2\), \(\hat{p}_{32}(0)=0.2\), \(\hat{p}_{41}(0)=0.1\), \(\hat{p}_{42}(0)=0.1\), \(\hat{p}_{51}(0)=0.1\), \(\hat{p}_{52}(0)=0.1\), \(\hat{k}_{1}(0)=0.02\), \(\hat{k}_{2}(0)=0.013\), \(\hat{k}_{3}(0)=0.01\), \(\hat{k}_{4}(0)=0.02\), \(\hat{5}(0)=0.01\). The state trajectories of the master system and slave system are shown in Fig. 3a–e. Furthermore, Fig. 4a–f clearly show the synchronization errors and the time responses of sliding surface, respectively. From Fig. 4 we observe that the state trajectories asymptotically converge to zero, which implies the synchronization between the fractional-order slave system and fractional-order master system is realized under the adaptive sliding mode controller.

Fig. 3
figure 3

Synchronization state trajectories of system when the controller activated

Full size image
Fig. 4
figure 4

Synchronization errors and the time response of surface

Full size image

5 Conclusion

In this paper, an effective modified adaptive SMC method for synchronizing fractional-order arbitrary dimensional hyperchaotic system has been proposed using Lyapunov stability theorem and fractional stability theorem. Based on the intuitive principle of fractional derivatives, the developed sliding mode controller can guarantee that all signals involved are ultimately bounded. Furthermore, theoretical analysis and numerical simulations have been shown to verify the results through a novel fractional-order five dimensional hyperchaotic system. The error dynamics governing the difference between the master states and the slave states are required to be globally stable while approaching zeros to ensure complete synchronization.