1 Introduction

Time-delay phenomenon and transportation lag are commonly happened in control systems. It has been shown that the delay differential equations are useful to describe many real-world problems such as metal cutting, traffic models, chemical kinetics, neuroscience, population dynamics [1, 2]. Delay systems are infinite-dimensional systems in nature, and the delay in the model of one system enriches its dynamics [3].

It has been proven that many real-world physical systems can be more precisely described by using fractional-order models. The stability analysis and controller synthesis for time-delay integer-order systems have widely been studied by using delay-dependent Lyapunov–Krasovskii function [4,5,6]. However, time-delay fractional-order systems have seldom been considered. For instance, in [7], a fractional-order PID controller is presented to stabilize the fractional-order linear systems with time-delay, in which, based on a numerical algorithm, a set of global stability regions is determined and then the biggest stability region in this set is chosen. Stability regions are described by plotting the real root boundary line, infinite root boundary line and complex root boundary curve. The presented method is effective for time-delay linear systems, but it is not a simple and straight scheme, and also the considered time-delay is constant and there is no delay in control signal. In [8], another approach based on the finite-time stability analysis is proposed for a class of linear fractional-order systems with time-invariant delay. In [8], a stability criterion for a class of linear fractional-order systems is obtained by considering the generalized Gronwall inequality. In [9], the linear time-delay fractional-order systems are studied and some sufficient conditions for the finite-time stability are derived. In [10], an analytical stability bound is derived for a class of the time-delay fractional-order differential equations by using Lambert function, in which the first-order time-delay fractional-order differential equations with constant coefficients are considered. The stability of the linear time-delay fractional differential equations with n-dimensional is investigated in [11]. In this paper, by using the Laplace transform, the characteristic equation for such systems is obtained and then based on this equation the stability criterions are derived. In [12], the intervals of stability for the time-delay fractional-order systems are investigated. In all of the mentioned works, it is assumed that the dynamics of the system is known and also the delay in constant.

Although the synchronization of the fractional-order chaotic systems without time-delay has abundantly been studied, not many contributions are available about synchronization of the time-delay fractional-order chaotic systems. This problem has been investigated in some works. For instance, in [13] the parameters of the time-delay fractional-order chaotic systems are identified by a numerical algorithm. The fractional-order neural networks with time-varying delay are studied in [14]. In [15], an active control method is proposed to synchronize time-delay fractional-order neural networks. In [16, 17], the bifurcation and stability behaviors of the delayed fractional-order systems are studied. In [18], an adaptive neural network control is presented for the synchronization of the fractional-order time-delay systems. In [18], the radial basis function neural network is used for the estimation of the unknown functions, and it is assumed that the time-delay is constant and there is no time-delay in the control signal.

In this paper, a new approach based on Lyapunov–Krasovskii stability analysis is presented to design control signal and to derive adaptation laws for the consequent parameters of the proposed RNT2SFNN. The proposed RNT2SFNN is a recurrent sequential fuzzy system which is developed based on the type-2 fuzzy neural network with non-singleton fuzzification. Unlike the most of related works, it is assumed that the dynamics of the system are unknown and are perturbed by the bounded external disturbances. Furthermore, a time-varying delay is considered in the dynamics of the system and also in the control signal. To demonstrate the effectiveness of the controller, in the other practical applications, the proposed controller is applied to synchronize the master–slave bilateral teleoperation problem with time-varying delay.

The reminder of this paper is organized as follows: The problem statement and the system description are given in Sect. 2. The proposed fuzzy system is presented in Sect. 3. Stability and robustness analysis is given in Sect. 4. Simulation results are given in Sect. 5, and the obtained main results are summarized and concluded in Sect. 6.

2 Problem statement and system description

Definition 1

The Caputo derivative and integral of fractional-order q of a function f are given as follows:

$$\begin{aligned}&D_t^q\, f(t) = \frac{1}{{\Gamma (m - q)}}\int _0^t {{{(t - \tau )}^{m - q - 1}}\frac{{{\mathrm{d}^m}}}{{\mathrm{d}{t^m}}}f(\tau )\mathrm{d}\tau } \end{aligned}$$
(1)
$$\begin{aligned}&I_t^qf(t) = \frac{1}{{\Gamma (q)}}\int _0^t {{{(t - \tau )}^{q - 1}}f(\tau )\mathrm{d}\tau } \end{aligned}$$
(2)

where \(\Gamma ( \cdot )\) is Gamma function, and m is an integer so that \(m - 1< q < m\).

In this paper, the following class of fractional-order time-delay chaotic systems is considered as the master system:

$$\begin{aligned} \hbox {Master system:}\,\left\{ {\begin{array}{*{20}{l}} {{D_t^q}{y_i} = {y_{i + 1}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,1 \le i \le n - 1}\\ \begin{array}{l} {D_t^q}{y_n} = g(\underline{y}(t) ,\underline{y} (t - {\tau _{m1}}(t)),\ldots ,\underline{y} (t - {\tau _{mr}}(t)))\\ \,\underline{y} = \left[ {{y_1},{y_2},\,\ldots ,{y_n}} \right] \in {R ^n} \end{array} \end{array}} \right. \end{aligned}$$
(3)

where \(0< q < 1\) is the fractional derivative order, and \(g(\underline{y} ,\underline{y} (t - {\tau _{m1}}(t)),\ldots ,\underline{y} (t - {\tau _{mr}}(t)))\) is unknown but bounded function. \({y_i} \in R,\,\,\,i = 1,2,\ldots ,n\) are the outputs of the master system, and \({\tau _{m1}}(t),\,\ldots ,\,{\tau _{mr}}(t)\) are the time-varying delays.

Fig. 1
figure 1

The block diagram of the proposed control

Full size image

The slave system is:

$$\begin{aligned} \hbox {Slave system}: \left\{ {\begin{array}{*{20}{l}} {{D_t^q}{x_i} = {x_{i + 1}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,1 \le i \le n - 1}\\ \begin{array}{l} {D_t^q}{x_n} = f(\underline{x}(t) ,\underline{x} (t - {\tau _{s1}}(t)),\ldots ,\underline{x} (t - {\tau _{sr}}(t)))\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\quad +\,d(t) + u(t-\tau (t))\\ \underline{x} = \left[ {{x_1},{x_2},\,\ldots ,{x_n}} \right] \in {R^n} \end{array} \end{array}} \right. \end{aligned}$$
(4)

where \(f(\underline{x} ,\underline{x} (t - {\tau _{s1}}),\ldots ,\underline{x} (t - {\tau _{sr}}))\) is unknown but bounded function, d(t) is the bounded external disturbance, u(t) is the control signal, and \(\underline{x} = {\left[ {{x_1},{x_2},\ldots ,{x_n}} \right] ^{T}}\) are the outputs of the slave system. \({\tau _{s1}}(t),{\tau _{s2}}(t),\ldots ,{\tau _{sr}}(t)\) are the time-varying delays, and \(\tau (t)\) is the variable time-delay in control signal such that \(0 \le \tau (t) \le h\) and \(\dot{\tau }(t) \le \mu \).

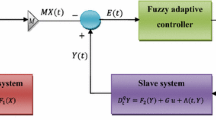
The block diagram of the proposed control is shown in Fig. 1. The control objective is to design nonlinear controller u(t), such that the slave system tracks the master system.

To begin the designing of controller, a dynamic surface is defined as follows:

$$\begin{aligned} s(t) = {\lambda _1}{e_1}(t) + \cdots + {\lambda _{n - 1}}{e_{n - 1}}(t) + {\lambda _n}{e_n}(t) \end{aligned}$$
(5)

where \({e_i}(t) = {x_i}(t) - {y_i}(t),\,\,i = 1,\ldots ,n\), and \({\lambda _i},\,\,i = 1,\ldots ,n\) are chosen such that defined surface (5) is stable. The derivative of fractional-order q of Eq. (5) gives:

$$\begin{aligned} D_t^qs(t)= & {} \sum \limits _{i = 1}^{n - 1} {{\lambda _i}{e_{i + 1}}(t)} + {\lambda _n}\left[ f(t) + d(t) \right. \nonumber \\&\left. +\,u\left( {t - \tau (t)} \right) - g(t) \right] \end{aligned}$$
(6)

where g(t) and f(t) are the unknown functions in the dynamics of master and slave systems (3, 4), respectively, and d(t) is the external disturbance.

From the fact that \(\dot{x} = {D_t^{1 - q}}{D_t^q}x\) (see the properties of the fractional derivative in [19]), Eq. (6) can be rewritten as follows:

$$\begin{aligned} \dot{s}(t) = w(t) + {\lambda _n}D_t^{1 - q}u\left( {t - \tau (t)} \right) \end{aligned}$$
(7)

where

Fig. 2
figure 2

The proposed recurrent non-singleton type-2 sequential fuzzy neural network

Full size image
$$\begin{aligned} w(t) = D_t^{1 - q}\left[ {\sum \limits _{i = 1}^{n - 1} {{\lambda _i}{e_{i + 1}}(t)} + {\lambda _n}\left( {f(t) + d(t) - g(t)} \right) } \right] \end{aligned}$$
(8)

The dynamics of s in (7) can be estimated as:

$$\begin{aligned} \dot{\hat{s}}(t) = \hat{w}\left( {\theta (t)|{u_{nn}}(t)} \right) + {\lambda _n}D_t^{1 - q}u\left( {t - \tau (t)} \right) \end{aligned}$$
(9)

where \(\hat{w}(t)\) is the estimation of w(t), which is obtained by the proposed RNT2SFNN, \(u_{nn}(t) = [{\underline{x} ^T}(t),{\underline{y} ^T}(t), D_t^{1 - q}{\underline{e} ^T}(t)]^T\) and \(\theta (t)\) is the vector of trainable parameters of RNT2SFNN. By considering (9), the control signal is proposed as:

$$\begin{aligned} u(t) = \frac{1}{{{\lambda _n}}}I_t^{1 - q}\left[ { - K\hat{s}(t) - \hat{w}\left( {\theta (t)|{u_{nn}}(t)} \right) } \right] \end{aligned}$$
(10)

where K and the adaptation laws of \(\theta (t)\) are determined based on the Lyapunov–Krasovskii stability analysis such that the dynamics of \(\hat{s}\) (11) are asymptotically stable (see Theorem 1). By replacing control signal (10) into (9), and subtracting (9) from (7), the dynamics of \(\hat{s}(t)\) and \(\tilde{s}(t) = s(t) - \hat{s}(t)\) are as follows:

$$\begin{aligned} \dot{\hat{s}}(t)= & {} - K\hat{s}\left( {t - \tau (t)} \right) + \varepsilon (t)\end{aligned}$$
(11)
$$\begin{aligned} \dot{\tilde{s}}(t)= & {} w(t) - \hat{w}\left( {\theta (t)|{u_{nn}}(t)} \right) \end{aligned}$$
(12)

where \(\varepsilon (t) = \hat{w}( {\theta (t)|{u_{nn}}(t)} ) - \hat{w}( \theta \left( {t - \tau (t)} \right) |{u_{nn}}( t - \tau (t) ) )\).

3 Proposed recurrent non-singleton type-2 sequential fuzzy neural network

In this section a recurrent non-singleton type-2 sequential fuzzy neural network is presented. The proposed structure is the development of the sequential fuzzy system, presented in [20]. The sequential fuzzy system is designed based on the functional similarity between a fuzzy system and a radial basis function neural network. The proposed structure is shown in Fig. 2, where \({u_{n{n_i}}},\,i = 1,\ldots ,{N_u}\) and \(o_{nn}\) are the inputs and the output of RNT2SFNN, respectively. In the fuzzification layer for each input \(u_{nn_j},\,j=1,\ldots ,{N_u}\), a type-2 Gaussian MF \({\tilde{B}_j}\) with center \(u_{nn_j}\), upper MF \({\bar{B}_j}\), lower MF \({\underline{B}_j}\), upper width \(\bar{\sigma } _{\tilde{B}_j}\) and lower width \(\underline{\sigma } _{\tilde{B}_j}\) is considered. \(N_u\) is the number of inputs. In membership layer for each input \(u_{nn_j}\), \({N_m}\) Gaussian type-2 MFs \(\tilde{A}^i_j, \,i=1,\ldots ,{N_m},\,j=1,\ldots ,{N_u}\), with upper MF \(\bar{A}^i_j\), lower MF \(\underline{A}^i_j\), center \(c_{\tilde{A}^i_j}\), upper width \(\bar{\sigma } _{\tilde{A}^i_j}\) and lower width \(\underline{\sigma } _{\tilde{A}^i_j}\) are considered (see Fig. 3). \(\underline{\theta }_1,\ldots ,\underline{\theta }_{N_m}\) and \(\bar{\theta }_1,\ldots ,\bar{\theta }_{N_m}\) are the lower and upper consequent parameters. The output of the proposed RNT2SFNN \(o_{nn}\) is calculated step by step as follows:

Fig. 3
figure 3

The type-2 membership function

Full size image

Step 1 Compute the upper and the lower memberships for each input. Consider ith MF for jth input \(u_{nn_j}\), and to compute the upper membership \({\bar{\mu } }_{\tilde{A}_j^i}\) and the lower membership \({\underline{\mu } }_{ \tilde{A}_j^i}\), at first, based on the non-singleton fuzzification and by using minimum inference, the input \(u_{nn_j}\) is transformed to \(\bar{u}_{nn^i_j}\) and \(\underline{u}_{nn^i_j}\) as follows:

$$\begin{aligned} \begin{array}{l} {{\bar{u}}_{n{n^i_j}}} = \displaystyle \frac{{\bar{\sigma } _{{\tilde{B}_j}}^2{c_{\tilde{A}_j^i}} + \bar{\sigma } _{\tilde{A}_j^i}^2{u_{n{n_j}}}}}{{\bar{\sigma } _{{\tilde{B}_j}}^2 + \bar{\sigma } _{\tilde{A}_j^i}^2}},\,\, {{\underline{u}}_{n{n^i_j}}} =\displaystyle \frac{{\underline{\sigma } _{{\tilde{B}_j}}^2{c_{\tilde{A}_j^i}} + \underline{\sigma } _{\tilde{A}_j^i}^2{u_{n{n_j}}}}}{{\underline{\sigma } _{{\tilde{B}_j}}^2 + \underline{\sigma } _{\tilde{A}_j^i}^2}} \end{array} \end{aligned}$$
(13)

where \(\bar{\sigma } _{{\tilde{B}_j}}\)/\(\underline{\sigma } _{{\tilde{B}_j}}\) and \(\bar{\sigma } _{\tilde{A}_j^i}\)/\(\underline{\sigma } _{\tilde{A}_j^i}\) are upper/lower width of the MFs \({{\tilde{B}_j}}\) and \({\tilde{A}_j^i}\), respectively. Then we can write:

$$\begin{aligned} {\bar{\mu } _{\tilde{A}_j^i}}= & {} \exp \left[ {\displaystyle \frac{{ - {{\left( {{{\bar{u}}_{nn_j^i}}(t) - {c_{\tilde{A}_j^i}}(t)} \right) }^2}}}{{\bar{\sigma } _{_{ \tilde{A}_j^i}}^2}}}\right] ,\nonumber \\ {\underline{\mu } _{\tilde{A}_j^i}}= & {} \exp \left[ {\displaystyle \frac{{ - {{\left( {{{\underline{u}}_{nn_j^i}}(t) - {c_{\tilde{A}_j^i}}(t)} \right) }^2}}}{{\underline{\sigma } _{_{\tilde{A}_j^i}}^2}}}\right] \end{aligned}$$
(14)

Step 2 Compute the firing degree of rules. The number of rules is equal to the number of MFs for each input (\(N_m\)). Each rule is written as follows:

$$\begin{aligned}&{R^l}:\hbox {If}\,{u_{n{n_1}}}\,\hbox {is}\,\tilde{A}_1^l\,\hbox {and}\, \ldots \,\hbox {and}\,{u_{n{n_j}}}\,\hbox {is}\,\tilde{A}_j^l\,\hbox {and}\, \ldots \,\hbox {and}\,{u_{n{n_{{N_u}}}}}\,\hbox {is}\,\tilde{A}_{n{n_{{N_u}}}}^l\nonumber \\&\quad \hbox {Then}\,{o_{nn}} \in \left[ {{{\underline{\theta }}_l},\,{{\bar{\theta } }_l}} \right] \nonumber \\&\quad l=1,\ldots ,N_m \end{aligned}$$
(15)

where \(\tilde{A}_j^l,\,j=1,\ldots ,N_u\) is the lth Gaussian type-2 MF for the jth input.

Consider the following definitions:

$$\begin{aligned}&\begin{array}{l} {{\bar{\sigma } }_{\tilde{A}_{\,1}^1}} = {{\bar{\sigma } }_{\tilde{A}_{\,2}^1}} = \cdots = {{\bar{\sigma } }_{\tilde{A}_{\,{N_u}}^1}} = {{\bar{\sigma } }_1}\\ {{\bar{\sigma } }_{\tilde{A}_{\,1}^2}} = {{\bar{\sigma } }_{\tilde{A}_{\,2}^2}} = \cdots = {{\bar{\sigma } }_{\tilde{A}_{\,{N_u}}^2}} = {{\bar{\sigma } }_2}\\ \,\,\,\,\,\,\,\,\,\, \vdots \\ {{\bar{\sigma } }_{\tilde{A}_{\,1}^{{N_m}}}} = {{\bar{\sigma } }_{\tilde{A}_{\,2}^{{N_m}}}} = \cdots = {{\bar{\sigma } }_{\tilde{A}_{\,{N_u}}^{{N_m}}}} = {{\bar{\sigma } }_{{N_m}}} \end{array} \end{aligned}$$
(16)
$$\begin{aligned}&\begin{array}{l} {{\underline{\sigma } }_{\tilde{A}_{\,1}^1}} = {{\underline{\sigma } }_{\tilde{A}_{\,2}^1}} = \cdots = {{\underline{\sigma } }_{\tilde{A}_{\,{N_u}}^1}} = {{\underline{\sigma } }_1}\\ {{\underline{\sigma }}_{\tilde{A}_{\,1}^2}} = {{\underline{\sigma } }_{\tilde{A}_{\,2}^2}} = \cdots = {{\underline{\sigma } }_{\tilde{A}_{\,{N_u}}^2}} = {{\underline{\sigma } }_2}\\ \,\,\,\,\,\,\,\,\,\, \vdots \\ {{\underline{\sigma } }_{\tilde{A}_{\,1}^{{N_m}}}} = {{\underline{\sigma } }_{\tilde{A}_{\,2}^{{N_m}}}} = \cdots = {{\underline{\sigma } }_{\tilde{A}_{\,{N_u}}^{{N_m}}}} = {{\underline{\sigma } }_{{N_m}}} \end{array} \end{aligned}$$
(17)
$$\begin{aligned}&{C_i} = {\left[ {{c_{\tilde{A}_{\,1}^i}},\,{c_{\tilde{A}_{\,2}^i}},\,\ldots ,\,{c_{\tilde{A}_{\,{N_u}}^i}}} \right] ^{T}} \end{aligned}$$
(18)
$$\begin{aligned}&{U_{nn}}_{_i} = {\left[ {{u_{nn_1^i}},\,{u_{nn_2^i}},\,\ldots ,\,{u_{nn_{{N_u}}^i}}} \right] ^{T}} \end{aligned}$$
(19)

The upper and the lower firing degrees of each rule are computed as follows:

$$\begin{aligned} \begin{array}{l} {{\bar{z}}_{{i}}(t)} =r{{\bar{z}}_{{i}}(t-1)}+ {e^ {\frac{\displaystyle { - {{\left\| {{U_{nn_i}(t)} - {C_i}(t)} \right\| }^2}}}{\displaystyle {{{\bar{\sigma } }_i^2}}}}}\\ {\underline{z}_{{i}}(t)} =r{\underline{z}_{{i}}(t-1)}+ {e^ {\frac{\displaystyle { - {{\left\| {{U_{nn_i}(t)} - {C_i}(t)} \right\| }^2}}}{\displaystyle {{{\underline{\sigma } }_i^2}}}}},\quad i = 1,\ldots ,{N_m} \end{array} \end{aligned}$$
(20)

where \({{\bar{z}}_{{i}}(t-1)}\) and \({\underline{z}_{{i}}(t-1)}\) are the upper and the lower firing degrees of ith rule, at previous sample time, respectively. r, \(\underline{\sigma }_i\), \(\bar{\sigma }_i\) and \(C_i,\,i=1,\ldots ,N_m \) are the constant designable parameters.

Step 3 Compute the output as follows:

$$\begin{aligned} {o_{nn}}(t) = \frac{{\sum \nolimits _{i = 1}^{{N_m}} {{{\bar{\theta } }_i}(t) \times {{\bar{z}}_i}(t)} + \sum \limits _{i = 1}^{{N_m}} {{{\underline{\theta } }_i}(t) \times {{\underline{z}}_i}(t)} }}{2}\nonumber \\ \end{aligned}$$
(21)

where \({\bar{\theta }}_i\) and \({\underline{\theta }}_i\) are considered as linear combination of inputs:

$$\begin{aligned} {{\bar{\theta } }_i}(t)= & {} \bar{\alpha } _i^0(t) + \bar{\alpha } _i^1(t){u_{n{n_1}}}(t) + \cdots + \bar{\alpha } _i^{{N_u}}(t){u_{n{n_{{N_u}}}}}(t)\,\nonumber \\ {\underline{\theta } _i}(t)= & {} \underline{\alpha } _i^0(t) + \underline{\alpha } _i^1(t){u_{n{n_1}}}(t) + \cdots \nonumber \\&+\,\underline{\alpha } _i^{{N_u}}(t){u_{n{n_{{N_u}}}}}(t),\,\,\,i = 1,\ldots ,{N_m} \end{aligned}$$
(22)

From (21), the output of RNT2SFNN can be written in the vector form as follows:

$$\begin{aligned} {o_{nn}}\left( {\theta (t)|{u_{nn}}(t)} \right) = {\theta ^{T}}(t)\zeta (t) \end{aligned}$$
(23)

where

$$\begin{aligned}&\begin{array}{l} \theta (t) = \left[ {\bar{\alpha } _1^0(t),\bar{\alpha } _1^1(t),\,\ldots ,\,\bar{\alpha } _1^{{N_u}}(t),\,\ldots ,\,\bar{\alpha } _{{N_m}}^0(t),\bar{\alpha } _{{N_m}}^1(t),\,\ldots ,\,\bar{\alpha } _{{N_m}}^{{N_u}}(t)} \right. \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\left. {\underline{\alpha } _1^0(t),\underline{\alpha } _1^1(t),\,\ldots ,\,\underline{\alpha } _1^{{N_u}}(t),\,\ldots ,\,\underline{\alpha } _{{N_m}}^0(t),\underline{\alpha } _{{N_m}}^1(t),\,\ldots ,\,\underline{\alpha } _{{N_m}}^{{N_u}}(t)} \right] ^{T}} \end{array} \end{aligned}$$
(24)
$$\begin{aligned}&\begin{array}{l} \zeta (t) = \frac{1}{2}\left[ {} \right. {{\bar{z}}_{{1}}}(t),\,{{\bar{z}}_{{1}}}(t){u_{n{n_1}}}(t),\,\ldots ,\,{{\bar{z}}_{{1}}}(t){u_{n{n_{{N_u}}}}}(t),\,\ldots ,\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{\bar{z}}_{{{{N_m}}}}}(t),\,{{\bar{z}}_{{{{N_m}}}}}(t){u_{n{n_1}}}(t),\,\ldots ,\,{{\bar{z}}_{{{{N_m}}}}}(t){u_{n{n_{{N_u}}}}}(t),\,\ldots ,\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\underline{z}_{{1}}}(t),\,{\underline{z} _{{1}}}(t){u_{n{n_1}}}(t),\,\ldots ,\,{\underline{z} _{{1}}}(t){u_{n{n_{{N_u}}}}}(t),\,\ldots ,\,\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\underline{z}_{{{{N_m}}}}}(t),{\underline{z} _{{{{N_m}}}}}(t){u_{n{n_1}}}(t),\,\ldots ,\,{\underline{z} _{{{{N_m}}}}}(t){u_{n{n_{{N_u}}}}}(t)\,{\left. {} \right] ^{T}} \end{array} \end{aligned}$$
(25)

Remark 1

As mentioned before the nonlinear function w(t) in (8) is estimated by RNT2SFNN \(\hat{w}\left( {\theta (t)|{u_{nn}}(t)} \right) \). The parameters \(\theta (t)\) are tuned based on the Lyapunov–Krasovskii stability analysis [see Theorem 1 and relation (28)].

4 Stability and robustness analysis

Consider the dynamics of \({\tilde{s}}(t)\) in (12), we assume that there exists the optimal \({{\theta ^*}(t)}\) such that if \(\theta (t)\) is reached to \({{\theta ^*}(t)}\), \(\hat{w}\left( {\theta (t)|{u_{nn}}(t)} \right) \) will be reached to w(t). In other words we can write:

$$\begin{aligned} w(t) = {\theta ^*}^T(t)\zeta (t) \end{aligned}$$
(26)

Then from (12), (23) and (26) we have:

$$\begin{aligned} \dot{\tilde{s}}(t) = {{\tilde{\theta } }^T}(t)\zeta (t) \end{aligned}$$
(27)

where \(\tilde{\theta } (t) = {\theta ^ * }(t) - \theta (t)\) and \(\theta (t) \) and \(\zeta (t)\) have been defined in (24) and (25), respectively.

Theorem 1

The dynamics of (11), with delay \(\tau (t)\) such that \(0 \le \tau (t) < h\) and \(\dot{\tau }(t) < \mu \), is asymptotically stable and \(\tilde{s}(t) \rightarrow 0\) [see (12)], if there exist \(K> 0\), \(Z \ge 0\) and \(N_1\) and \(N_2\), such that:

$$\begin{aligned}&\dot{\theta }(t) = \left\{ \begin{array}{ll} \gamma \tilde{s}(t)\zeta (t)&{}\quad \text {if}\,\,\underline{\theta }< \theta (t)\,< \bar{\theta } \\ &{}\quad \hbox {or}\,\,\theta (t)\, \ge \bar{\theta } \,\hbox {and}\,\gamma \tilde{s}(t)\zeta (t) < 0\\ &{}\quad \hbox {or}\,\,\theta (t)\, \le \underline{\theta }\,\hbox {and}\,\gamma \tilde{s}(t)\zeta (t) > 0\,\\ 0&{}\quad \hbox {or}\,\,\theta (t)\, \ge \bar{\theta } \,\hbox {and}\,\gamma \tilde{s}(t)\zeta (t) \ge 0\\ &{}\quad \hbox {or}\,\,\theta (t)\, \le \underline{\theta }\,\hbox {and}\,\gamma \tilde{s}(t)\zeta (t) \le 0\, \end{array} \right. \end{aligned}$$
(28)
$$\begin{aligned}&\Phi = \left[ {\begin{array}{*{20}{c}} {{\phi _{11}}}&{}{{\phi _{12}}}&{}0\\ *&{}{{\phi _{22}}}&{}{hK}\\ *&{}*&{}{ - h} \end{array}} \right] < 0 \end{aligned}$$
(29)
$$\begin{aligned}&\Xi = \left[ {\begin{array}{*{20}{l}} {{z_{11}}}&{}{{z_{12}}}&{}{{N_1}}\\ *&{}{{z_{22}}}&{}{{N_2}}\\ *&{}*&{}1 \end{array}} \right] \ge 0 \end{aligned}$$
(30)

where \(\underline{\theta }\) and \(\bar{\theta }\) are the lower and upper bound of \(\theta \), and:

$$\begin{aligned}&\begin{array}{l} {\phi _{11}} = {N_1} + \psi + 1 + h{z_{11}}\\ {\phi _{12}} = - \frac{1}{2}K - \frac{1}{2}{N_1} + \frac{1}{2}{N_2} + h{z_{12}}\\ {\phi _{22}} = -\,{N_2} + h{z_{22}} - ( {1 - \mu }) \end{array} \end{aligned}$$
(31)
$$\begin{aligned}&Z = \left[ {\begin{array}{*{20}{c}} {{z_{11}}}&{}{{z_{12}}}\\ *&{}{{z_{22}}} \end{array}} \right] \end{aligned}$$
(32)

\(\gamma \) is the adaptation rate, and \(\psi \) is a positive constant [see (37)].

Proof

Consider a Lyapunov–Krasovskii functional candidate as follows:

$$\begin{aligned} V(t)= & {} \frac{1}{2}{{\hat{s}}^2}(t) + \frac{1}{2}{{\tilde{s}}^2}(t) + \int _{t - \tau (t)}^t {{{\hat{s}}^2}(\upsilon )} \mathrm{d}\upsilon \nonumber \\&+ \int _{ - h}^0 {\int _{t + \alpha }^t {{{\dot{\hat{s}}}^2}(\upsilon )} } \mathrm{d}\upsilon \mathrm{d}\alpha + \frac{1}{{2\gamma }}{{\tilde{\theta } }^T}(t)\tilde{\theta } (t)\nonumber \\ \end{aligned}$$
(33)

Time derivative of (33) yields:

$$\begin{aligned} \begin{array}{l} \dot{V}(t) = \hat{s}(t)\dot{\hat{s}}(t) + \tilde{s}(t)\dot{\tilde{s}}(t)\\ \quad + {{\hat{s}}^2}(t) - \left( {1 - \dot{\tau }(t)} \right) {{\hat{s}}^2}\left( {t - \tau (t)} \right) \\ \quad +\,h{{\dot{\hat{s}}}^2}(t) - \int _{t - h}^t {{{\dot{\hat{s}}}^2}(\upsilon )} \mathrm{d}\upsilon - \frac{1}{\gamma }{{\tilde{\theta } }^T}(t)\dot{\theta }(t) \end{array} \end{aligned}$$
(34)

By replacing \({\dot{\hat{s}}(t)}\) and \(\dot{\tilde{s}}(t)\) from (11) and (12), into (34), and by considering the assumption that \(\dot{\tau }(t) \le \mu \), we have:

$$\begin{aligned}&\dot{V}(t) \le \hat{s}(t)\left[ { - K\hat{s}\left( {t - \tau (t)} \right) + \varepsilon (t)} \right] \nonumber \\&\quad +\,\tilde{s}(t){{\tilde{\theta } }^T}(t)\zeta (t) - \frac{1}{\gamma }{{\tilde{\theta } }^T}(t)\dot{\theta }(t)\nonumber \\&\quad +\,{{\hat{s}}^2}(t) - \left( {1 - \mu } \right) {{\hat{s}}^2}\left( {t - \tau (t)} \right) - \int _{t - h}^t {{{\dot{\hat{s}}}^2}(\upsilon )} \mathrm{d}\upsilon \nonumber \\&\quad +\,h{\left[ { - K\hat{s}\left( {t - \tau (t)} \right) + \varepsilon (t)} \right] ^2} \end{aligned}$$
(35)

From the adaptation law for \(\theta (t) \) (see 28), inequality (35) becomes:

$$\begin{aligned} \begin{array}{l} \dot{V}(t) \le -\,K\hat{s}(t)\hat{s}\left( {t - \tau (t)} \right) + h{K^2}{{\hat{s}}^2}\left( {t - \tau (t)} \right) \\ +\,\left[ {\varepsilon (t)\hat{s}(t) - \varepsilon (t)hK\hat{s}\left( {t - \tau (t)} \right) + h{\varepsilon ^2}(t)} \right] \\ +\,{{\hat{s}}^2}(t) - ( {1 - \mu }){{\hat{s}}^2}\left( {t - \tau (t)} \right) - \int _{t - h}^t {{{\dot{\hat{s}}}^2}(\upsilon )} \mathrm{d}\upsilon \end{array} \end{aligned}$$
(36)

A variable \(\psi \) is chosen such that

$$\begin{aligned}&\left[ {\varepsilon (t)\hat{s}(t) - \varepsilon (t)hK\hat{s}\left( {t - \tau (t)} \right) + h{\varepsilon ^2}(t)} \right] \nonumber \\&\quad \le \psi \left[ {{{\hat{s}}^2}(t) + {{\hat{s}}^2}\left( {t - \tau (t)} \right) } \right] \end{aligned}$$
(37)

Then we have:

$$\begin{aligned} \dot{V}(t)\le & {} - K\hat{s}(t)\hat{s}\left( {t - \tau (t)} \right) \nonumber \\&+ \left[ {h{K^2} + \psi \qquad + \mu - 1} \right] {{\hat{s}}^2}\left( {t - \tau (t)} \right) \nonumber \\&+ \left[ {1 + \psi } \right] {{\hat{s}}^2}(t) - \int _{t - h}^t {{{\dot{\hat{s}}}^2}(\upsilon )} \mathrm{d}\upsilon \end{aligned}$$
(38)

Based on Newton–Leibniz formula, for any appropriately dimensioned matrices \(N_1\) and \(N_2\) the following relation holds

$$\begin{aligned}&\left[ {{{\hat{s}}}(t){N_1} + {{\hat{s}}}\left( {t - \tau (t)} \right) {N_2}} \right] \left[ \hat{s}(t) - \int _{t - \tau (t)}^t {\dot{\hat{s}}(\upsilon )} \mathrm{d}\upsilon \right. \nonumber \\&\quad \left. - \,\hat{s}\left( {t - \tau (t)} \right) \right] = 0 \end{aligned}$$
(39)

Note that \(\int _{t - \tau (t)}^t {\dot{\hat{s}}(\upsilon )} \mathrm{d}\upsilon = \hat{s}(t) - \hat{s}\left( {t - \tau (t)} \right) \) and then \(\left[ {\hat{s}(t) - \int _{t - \tau (t)}^t {\dot{\hat{s}}(\upsilon )} \mathrm{d}\upsilon - \hat{s}\left( {t - \tau (t)} \right) } \right] = 0\). Also by considering \({\eta _1} = \left[ {{{\hat{s}}}(t),{{\hat{s}}}\left( {t - \tau (t)} \right) } \right] \) for any \(Z\ge 0\) the following inequality is true

$$\begin{aligned} h{\eta _1}^T(t)Z{\eta _1}(t) - \int _{t - \tau \left( t \right) }^t {{\eta _1}^T(t)Z{\eta _1}(t)} \mathrm{d}\upsilon \ge 0 \end{aligned}$$
(40)

Note that \(\int _{t - \tau \left( t \right) }^t {{\eta _1}^T(t)Z{\eta _1}(t)} \mathrm{d}\upsilon = {\eta _1}^T(t)Z{\eta _1}(t)\tau \left( t \right) \), then:

$$\begin{aligned}&h{\eta _1}^T(t)Z{\eta _1}(t) - \int _{t - \tau \left( t \right) }^t {{\eta _1}^T(t)Z{\eta _1}(t)} \mathrm{d}\upsilon \nonumber \\&\quad = {\eta _1}^T(t)Z{\eta _1}(t)\left[ {h - \tau \left( t \right) } \right] \end{aligned}$$
(41)

Since \({\tau \left( t \right) < h}\) and \(Z \ge 0\), inequality (40) is true. By adding (39) and (40) into right-hand side of (38) and some simple calculations, we have

$$\begin{aligned} \dot{V}(t) \le {\eta _1}^T(t)\Theta {\eta _1}(t) - \int _{t - \tau (t)}^t {{\eta _2}^T(t,\upsilon )\Xi {\eta _2}(t,\nu )} \mathrm{d}\upsilon \end{aligned}$$
(42)

where

$$\begin{aligned}&{\eta _2}(t,\nu ) = {\left[ {{{\hat{s}}}(t),{{\hat{s}}}\left( {t - \tau (t)} \right) ,{{\dot{\hat{s}}}}(\upsilon )} \right] ^T} \end{aligned}$$
(43)
$$\begin{aligned}&\Theta = \left[ {\begin{array}{*{20}{c}} {{\phi _{11}}}&{}{{\phi _{12}}}\\ * &{}{{\phi _{22}} + h{K^2}} \end{array}} \right] \end{aligned}$$
(44)

and \(\Xi \), \(\phi _{11}\), \(\phi _{12}\) and \(\phi _{22}\) have been defined in (30) and (31).

Given that:

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{\phi _{11}}}&{}{{\phi _{12}}}\\ *&{}{{\phi _{22}} + h{K^2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\phi _{11}}}&{}{{\phi _{12}}}\\ *&{}{{\phi _{22}}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} 0\\ {hK} \end{array}} \right] {h^{ - 1}}\left[ {\begin{array}{*{20}{c}} 0&{hK} \end{array}} \right] \end{aligned}$$
(45)

From (45) and based on Schur complement inequality (42) becomes:

$$\begin{aligned} \dot{V}(t) \le {\eta _1}^T(t)\Phi {\eta _1}(t) - \int _{t - \tau (t)}^t {{\eta _2}^T(t,\upsilon )\Xi {\eta _2}(t,\nu )} \mathrm{d}\upsilon \end{aligned}$$
(46)

Then if \(\Phi <0\) and \(\Xi \ge 0\), then \(\dot{V}(t) \le 0\). To derive asymptotic stability the following lemma is used:

Barbalat’s lemma: Assume that f(t) is a function of time and has a limit when \(t \rightarrow \infty \), if \(\dot{f}(t)\) is uniformly continuous (\(\ddot{f}\left( t \right) \) is bounded), then \(\dot{f}\left( t \right) \rightarrow \infty \) as \(t \rightarrow \infty \).

From \(\dot{V}(t) \le 0\) it is obtained that \(V\left( t \right) \le V\left( 0 \right) \). To verify the boundedness of \({\ddot{V}}\), it needs to show that \({\eta _1} \in {\ell ^2}\) and \({\eta _2} \in {\ell ^2}\) and also the approximation error \(\varepsilon \) must be bounded. Considering the definition of \(\varepsilon (t) = \hat{w}\left( {\theta (t)|{u_{nn}}(t)} \right) - \hat{w}\left( {\theta \left( {t - \tau (t)} \right) |{u_{nn}}\left( {t - \tau (t)} \right) } \right) \) [see (11)], and the adaptation law of \(\theta \) [see (28)], the boundedness of \(\varepsilon \) is obvious.

Table 1 The simulation parameters
Full size table
Fig. 4
figure 4

The synchronization performance in Example 1

Full size image
Fig. 5
figure 5

The synchronization errors, Example 1

Full size image
Fig. 6
figure 6

Control signal, Example 1

Full size image

To show \({\eta _1} \in {\ell ^2}\) and \({\eta _2} \in {\ell ^2}\), note that V is a non-increasing and positive definite function then:

$$\begin{aligned} - \int _0^t {\dot{V}} = V\left( 0 \right) - V\left( t \right) < \infty \end{aligned}$$
(47)

Then

$$\begin{aligned} \begin{array}{*{20}{l}} \begin{array}{l} - \int _0^t {\dot{V}\,\mathrm{d}\tau }< \infty \\ \Rightarrow \int _0^t {\left[ {{\lambda _{\min }}\left( { - \Phi } \right) {{\left\| {{\eta _1}} \right\| }^2} + {\lambda _{\min }}\left( \Xi \right) {{\left\| {{\eta _2}} \right\| }^2}} \right] } \mathrm{d}\tau< \infty \end{array}\\ { \Rightarrow \sqrt{\int _0^t {\left[ {{\lambda _{\min }}\left( { - \Phi } \right) {{\left\| {{\eta _1}} \right\| }^2} + {\lambda _{\min }}\left( \Xi \right) {{\left\| {{\eta _2}} \right\| }^2}} \right] \mathrm{d}\tau } }< \infty }\\ { \Rightarrow \sqrt{\int _0^t {{{\left\| {{\eta _1}} \right\| }^2}\mathrm{d}\tau } }< \infty {} {}\,\hbox {and}\,{} {} \sqrt{\int _0^t {{{\left\| {{\eta _2}} \right\| }^2}\mathrm{d}\tau } } < \infty } \end{array} \end{aligned}$$
(48)

where \({\lambda _{\min }}\left( { - \Phi } \right) \) and \({\lambda _{\min }}\left( \Xi \right) \) represent the minimum eigenvalues of \(- \Phi \) and \(\Xi \), respectively. From (48), it is concluded that \({\eta _1} \in {\ell ^2}\) and \({\eta _2} \in {\ell ^2}\). Then it is derived that \({\mathop {\lim }\limits _{t \rightarrow 0}} \dot{V}\left( t \right) = 0\), and by considering \(\dot{V}\left( t \right) \) in (34) the asymptotic stability is concluded. This completes the proof. \(\square \)

5 Simulation

In this section four examples are used to demonstrate the results of the proposed method.

Example 1

In this example, synchronization of two different uncertain fractional-order Duffing–Holmes time-delay chaotic systems is considered. The master system is given as follows:

$$\begin{aligned} {D_t^q}{y_1}= & {} {y_2}\nonumber \\ {D_t^q}{y_2}= & {} - \frac{1}{{{{2.5}^2}}}y_1^3 - {y_1} - 0.1{y_2} + 0.025{y_1}\left( {t - \tau _1} \right) \nonumber \\&+\,0.025y_1^2\left( {t - \tau _1} \right) + 0.01{y_2}\left( {t - \tau _1} \right) \nonumber \\&+\,62.5\cos (1.29t) \end{aligned}$$
(49)

The slave system is given as follows:

$$\begin{aligned} {D_t^q}{x_1}= & {} {x_2}\nonumber \\ {D_t^q}{x_2}= & {} - \frac{{2.2}}{{{{2.5}^2}}}x_1^3 - \frac{{2.2}}{{1.8}}{x_1} - 0.1{x_2} + 0.022{x_1}\left( {t - \tau _1} \right) \nonumber \\&+\,0.022x_1^2\left( {t - \tau _1} \right) + 0.01{x_2}\left( {t - \tau _1} \right) \nonumber \\&+\,55\cos (1.29t) + d(t) + u(t-\tau _2 (t)) \end{aligned}$$
(50)

where \(d(t) = 0.7\sin (t)\) is the external disturbance. The time-delays \(\tau _1\) and \(\tau _2 (t)\) are considered as \(\tau _1=0.001\) and \(\tau _2 (t) = 0.02 {\tanh (t)} \). Since the simulation sample time is 0.001, then maximum delay \(\tau _2 (t)\) will be 20 sample times. The initial conditions are \({y_1}(- \tau _1) = 0\), \({y_2}(- \tau _1) = 0\), \({x_1}(- \tau _1) = 1\) and \({x_2}(- \tau _1) = - 1\). The initial conditions in \(t \in \left[ { - {\tau _1},0} \right] \) are constant. The fractional derivative order is \(q = 0.98\). For each input five MFs with centers \([-1,\,-0.5,\,0,\,0.5,\,1]\), upper width 1 and lower width 0.1 are chosen [see (16)–(18)]. The upper and lower widths of the MF in the fuzzification layer are 0.05 and 0.01, respectively [see (13)]. Other parameters of the controller are given in Table 1.

The output trajectories of the slave and master systems are shown in Fig. 4. The synchronization errors and the control signal are given in Figs. 5 and 6, respectively. As it can be seen, the proposed control method gives a good performance in the synchronization of two uncertain time-delay fractional-order chaotic systems.

Example 2

Consider the synchronization of two non-identical fractional-order time-delay chaotic systems, where the dynamics of the master system are given as follows:

$$\begin{aligned} \begin{array}{l} {D_t^q}{y_1}(t) = {y_3}(t) - 3{y_1}(t) + {y_1}(t){y_2}(t -\tau (t) ) + d_1^m(t)\\ {D_t^q}{y_2}(t) = 1 - 0.1{y_2}(t) - y_1^2(t - \tau (t) ) + d_2^m(t)\\ {D_t^q}{y_3}(t) = - {y_1}(t - \tau (t) ) - {y_3}(t) + d_3^m(t) \end{array} \end{aligned}$$
(51)

where \(q = 0.92\), \(d_i^m(t),i = 1,2,3\) are the external disturbances which are taken to be as \(d_1^m(t) = 0.1\cos (10t)\), \(d_2^m(t) = 0.2\cos (20t)\) and \(d_3^m(t) = 0.1\sin (10t)\). The initial conditions are \({y_1}(- \tau ) = 0.1\) , \({y_2}(- \tau ) = 4\) (the initial conditions in \(t \in \left[ { - {\tau },0} \right] \) are constant.) and \({y_3}(- \tau ) = 0.5\). The time-varying delay \(\tau (t)\) is randomly chosen 0.01 and 0.05 s. Since the simulation sample time is 0.001, then the number of delay samples is between 10 and 50.

Fig. 7
figure 7

The synchronization performance in Example 2

Full size image
Fig. 8
figure 8

Control signals, Example 2

Full size image

The slave system is Liu fractional-order time-delay chaotic system in which its dynamics are as follows:

$$\begin{aligned} {D_t^q}{x_1}(t)= & {} 10\left( {{x_2}(t) - {x_1}(t)} \right) + d_1^s(t) + {u_1}(t-\tau _1(t))\nonumber \\ {D_t^q}{x_2}(t)= & {} 40{x_1}(t - \tau ) - {x_1}(t){x_3}(t) \nonumber \\&+\,d_2^s(t) + {u_2}(t-\tau _2(t))\nonumber \\ {D_t^q}{x_3}(t)= & {} -\,2.5{x_3}(t - \tau ) + 4x_1^2(t) \nonumber \\&+\,d_3^s(t) + {u_3}(t-\tau _3(t) ) \end{aligned}$$
(52)
Fig. 9
figure 9

Block diagram of the bilateral teleoperation problem, Example 3

Full size image

where \(q = 0.92\), \({\tau _i}(t),\,i = 1,2,3\) are the time-varying delays which are randomly changed between 0 and 20s, \(d_i^s(t),i = 1,2,3\) are the external disturbances which are taken to be as \(d_1^s(t) = 0.1\sin (20t)\), \(d_2^s(t) = -\,0.3\sin (10t)\) and \(d_3^s(t) = -\,0.5\cos (10t)\), and the initial conditions are \({x_1}(- \tau ) = 1.2\) , \({x_2}(- \tau ) = 2.4\) and \({x_3}(- \tau ) = 11\). The controller design procedure and parameters are the same as Example 1, with only difference that \(k=300\) [see (10)].

Fig. 10
figure 10

Position tracking, in the teleoperation problem, Example 3

Full size image

The synchronization performance and the control signals are shown in Figs.7 and 8, respectively. As it can be seen, the proposed controller effectively synchronizes two non-identical fractional-order time-delay chaotic systems.

Example 3

As mentioned before, the proposed controller can be used in many applications. To show this property, in this example the proposed control scheme is applied to the master–slave bilateral teleoperation system with varying communication time-delay. The subject of bilateral teleoperation is reviewed in [21]. The block diagram of the bilateral teleoperation problem is shown in Fig. 9, in which \(f_h\) and \(f_e\) are the applied forces to the master and the slave systems, by the operator and environment, and \(d_1(t)\) and \(d_2(t)\) are the time-varying delay. In this problem, the master device is manipulated by the human operator and the objective is to design a controller such that the slave manipulator executes real tasks in a remote site.

The state space representation of the slave and master systems is obtained as follows [22]:

$$\begin{aligned} {{\dot{x}}_1}(t)= & {} {x_2}(t)\nonumber \\ {{\dot{x}}_2}(t)= & {} - \frac{{{b_s}}}{{{m_s}}}{x_2}(t) + \frac{1}{{{m_s}}}u(t) \end{aligned}$$
(53)
$$\begin{aligned} {{\dot{y}}_1}(t)= & {} {y_2}(t)\nonumber \\ {{\dot{y}}_2}(t)= & {} - \frac{K}{M}{y_1}(t) - \frac{B}{M}{y_2}(t) \nonumber \\&+ \frac{1}{M}{f_h}\left( {t - {d_1}(t)} \right) - \frac{1}{M}u\left( {t - {d_1}(t) - {d_2}(t)} \right) \nonumber \\ \end{aligned}$$
(54)

where \(M = 1\) kg, \(B = 1\) Ns/m, \(K = 1\) N/m, \(m_s = 1\) kg, \(b_s = 1\) Ns/m, \(d_1(t)\) and \(d_2(t)\) are the random time-varying delays, with maximum values 0.2 s. (Sample time is 0.001; then, the maximum of delay is 200 sample times.) Other controller parameters are the same as Example 1.

The outputs of the master and the slave systems are shown in Fig. 10, and the control signal is given in Fig. 11. It must be noted that we assume the dynamics of the master and the slave systems are unknown and the controller with the same parameters in Example 1 is applied to this problem. The simulation results are shown the good performance of the proposed scheme in spite of the big time-varying delay and the unknown dynamics. This example shows that the proposed control scenario can be successfully applied to other practical applications.

Fig. 11
figure 11

Control signal, in the teleoperation problem, Example 3

Full size image
Table 2 Results of nonlinear identification problem, Example 4
Full size table

Example 4

In this example, to evaluate the performance of the proposed RNT2SFNN, the following nonlinear system identification problem is considered [20]:

$$\begin{aligned} y(t) = \frac{{y(t - 1)y(t - 2)( {y(t - 1) - 0.5})}}{{1 + {y^2}(t - 1) + {y^2}(t - 2)}} + u(t - 1) \end{aligned}$$
(55)

where the input u(t) is uniformly chosen in the range \([-1.5,\,1.5]\) and the test input u(t) is given by \(u(t) = sin(2\pi t/25)\). For testing and training 200 and 5000 input–output data pairs are produced [20]. The performance of proposed non-singleton type-2 sequential fuzzy neural network (NT2SFNN) is compared with the singleton type-2 sequential fuzzy neural network (ST2SFNN), sequential adaptive fuzzy inference system (SAFIS) [20], minimal radial basis function MRBF [23], evolving Takagi–Sugeno fuzzy system ETSFS [24]. The simulation parameters are the same as Example 1, with the exception that the recurrent weight q is considered as \(q=0\). The values of the root-mean-square error (RMSE) are given in Table 2. As it can be seen, the performance of the proposed type-2 sequential fuzzy neural network with non-singleton fuzzification is better than other structures.

6 Conclusion

Synchronization of the fractional-order chaotic systems with time-varying delay is considered in this paper. A new method based on the Lyapunov–Krasovskii stability analysis and by using a proposed recurrent non-singleton type-2 sequential fuzzy neural network (RNT2SFNN) is presented for deriving asymptotically stability performance. The proposed control method is applied to synchronize two non-identical and identical chaotic systems with time-varying delay. Also the proposed controller is applied to synchronize the master–slave bilateral teleoperation problem. The simulation results show that the proposed control scheme gives good performance in the presence of external disturbance, time-varying delay and unknown functions in the dynamics of the system and the proposed controller can be used in wide practical applications. Also the proposed non-singleton type-2 sequential fuzzy neural network is applied on a identification problem, and it is shown that the proposed structure gives better performance than other well-known neural networks.