Multi-authority attribute-based encryption access control scheme with policy hidden for cloud storage

Abstract

For realizing the flexible, scalable and fuzzy fine-grained access control, ciphertext policy attribute-based encryption (CP-ABE) scheme has been widely used in the cloud storage system. However, the access structure of CP-ABE scheme is outsourced to the cloud storage server, resulting in the disclosure of access policy privacy. In addition, there are multiple authorities that coexist and each authority is able to issue attributes independently in the cloud storage system. However, existing CP-ABE schemes cannot be directly applied to data access control for multi-authority cloud storage system, due to the inefficiency for user revocation. In this paper, to cope with these challenges, we propose a decentralized multi-authority CP-ABE access control scheme, which is more practical for supporting the user revocation. In addition, this scheme can protect the data privacy and the access policy privacy with policy hidden in the cloud storage system. Here, the access policy that is realized by employing the linear secret sharing scheme. Finally, the security and performance analyses demonstrate that our scheme has high security in terms of access policy privacy and efficiency in terms of computational cost of user revocation.

1 Introduction

Cloud computing has been widely concerned and continually developed (Yu et al. 2016; He et al. 2015; Castiglione et al. 2011), while the security of cloud computing has also put forward higher requirements. In order to enhance the security of cloud computing, the scheme of efficient ciphertext retrieval (Fu et al. 2015; Xia et al. 2016), verifiable data auditing (Wang et al. 2015; Ren et al. 2015) and identity authentication (Huang et al. 2015; Chatterjee and Sarkar 2006) has been put forward successively. Cloud storage is an important service paradigm of cloud computing. With the development of the cloud storage system, many enterprise users or individual users may outsource their huge numbers of data in the cloud storage servers. In order to protect the data confidentiality, it is imperative to employ an efficient encryption scheme to realize the fine-grained access control in the cloud storage system. CP-ABE scheme (Yang and Jia 2014b; Zhou et al. 2015b; Hu et al. 2015) is the most appropriate encryption system. In the CP-ABE scheme, the ciphertext is related to the access structure, while the user’s secret keys are related to the attribute sets. The user can decrypt a ciphertext only if his attributes set satisfies the access structure embedded in the ciphertext. CP-ABE scheme (Li et al. 2015; Wang et al. 2016b; De and Ruj 2015) can realize a flexible access control and has been widely used to implement the secure storage and flexible access control in cloud storage system. However, most proposed CP-ABE schemes may not work well for the users to share their data by outsourcing on the cloud servers. First of all, the access policy may be revealed to the public, and it will disclose sensitive information of the decryptors or encryptors. Then, a user may have attributes delegated by different authorities, while a data owner has a shared data supervised by multiple authorities in practice. Multi-authority ABE (Wang et al. 2016a) is more appropriate for access control for the cloud storage system, as users hold attributes issued by different authorities. For example, an enterprise may release a number of specific files, and these files should be reviewed only by the staff who holds the attribute of Leader generated by the authority A or the attribute of Secretary generated by the authority B. Therefore, a multi-authority attribute-based encryption access control scheme with policy hidden can provide an effective solution to protect privacy in the cloud storage system. In this paper, we mainly provide a multi-authority attribute-based encryption scheme to realize fine-grained access control in the cloud storage system and protect access policy privacy. Moreover, this scheme should be flexible, practicable, and secure.

1.1 Related work and research contributions

Since Sahai and Waters (2005) firstly proposed an attribute-based encryption(ABE) scheme, many works (Bethencourt et al. 2007; Zhou et al. 2015a; Shao et al. 2015) have been proposed for realizing more expressive, flexible and practical versions of this technique. In addition, the first CP-ABE scheme was proposed by Bethencourt et al. (2007). However, the aforementioned schemes included a single authority. Subsequently, several researchers have proposed some multi-authority ABE schemes (Yang and Jia 2014a; Jung et al. 2013; Han et al. 2015). However, these schemes were not suitable for the complicated cloud storage system, for the reason that each authority needed to work with each other; it resulted that the schemes were at high communication cost and lack of scalability. Other multi-authority CP-ABE schemes (Müller et al. 2008; Liu et al. 2011) demanded a global central authority to administrate attributes by diverse authorities, but the performance was poor in lager distributed systems, and the central authority became a security bottleneck. There was a decentralizing CP-ABE with multi authorities proposed by Lewko and Waters (2011) to remove any central authority, but user revocation wasn’t considered in the scheme. A multi-authority CP-ABE scheme with user revocation was proposed by Yang and Jia (2014a); however, the scheme included a central authority. There was a decentralized multi-authority CP-ABE scheme with user revocation proposed by Ruj et al. (2014), but the scheme needed to deliver ciphertext components to the non-revoked user, resulting in expensive communication costs of the system.

CP-ABE schemes have been widely used in the cloud storage system for supporting the flexible access control, but the access policy is revealed to the public, which will disclose sensitive information of the decryptors or encryptors. Later, Yadav and Ali (2015), Phuong et al. (2016) and Zhou et al. (2015b) proposed hidden access policy CP-ABE schemes, but these schemes were based on simple ‘AND’ gate access structure. Although Xu and Lang (2015) proposed a CP-ABE scheme with hidden access policy, which adopted tree-based access structure and made access policy more abundant, but it cannot be directly applied to multi-authority cloud storage system. In addition, Lai et al. (2012) proposed a partial hidden policy scheme which was based on LSSS matrix access structure and it was constructed on bilinear groups with a composite order. This scheme was less efficient compared to the hidden policy ABE schemes Nishide et al. (2008). Furthermore, the scheme only supported partial hidden information and did not support user revocation.

1.2 Our research contributions

In this paper, in order to address the above challenges in the cloud storage system, we propose an access control scheme based on a decentralized CP-ABE scheme with policy hidden. There are three main contributions in this paper.

• 1. In order to resolve the problem in cloud storage system, we construct a secure decentralized CP-ABE access control scheme with policy hidden. This scheme adopts more flexible LSSS matrix access structure.

• 2. We also design an efficient user revocation method for multi-authority CP-ABE scheme. This method decreases communication cost and computation cost of the revocation.

• 3. We give the security and performance analyses which demonstrate that our scheme has high security in terms of access policy privacy and efficiency in terms of computational cost of user revocation.

2 Preliminaries and problem formulation

2.1 Preliminaries

2.1.1 Bilinear map

Definition 1

Let $G_{1}$ and $G_{2}$ be two cyclic groups with prime order p, and g be a generator of $G_{1}$. A map $e:{G_1}\times {G_1}\rightarrow {G_2}$ is a bilinear map if the following properties can be satisfied:

• 1. Bilinearity. $\forall a,b\in {Z_p}$ and $u,v\in {G_1},e({u^a},{v^b}) = e{(u,v)^{ab}}$.

• 2. Non-degeneracy. $e(g,g) \ne 1$ for the generator g of $G_{1}$.

• 3. Computability. For all $u,v \in {G_1}$, there exists an efficient algorithm to compute $e\left( {u,v} \right)$.

2.1.2 Access structure

Definition 2

We suppose a set of $\left\{ {{p_1},{p_2}, \ldots ,{p_n}} \right\}$ as an attributes set. For $\forall B,C:$ if $B \in A \wedge B \subseteq C$, then $C \in A$, we can get the set $A \subseteq {2^{\left\{ {{p_1},{p_2}, \ldots ,{p_n}} \right\} }}$ is monotone. An access structure (respectively, monotone access structure) is a set A which is non-empty subsets of $\left\{ {{p_1},{p_2}, \ldots ,{p_n}} \right\}$. The sets in A are named authorized sets, and the sets not belong to A are named as unauthorized sets.

The definition of linear secret sharing scheme (LSSS) can be found in Beimel (1996). From the discussion of Beimel (1996), each LSSS scheme $\Pi$ for the access structure ${A_{l\,\times \,n}}$ can be used to linear reconstruction. Let $C \in \mathrm{A}$ be any authorized set $I \subset \left\{ {1, \ldots ,l} \right\}$ defined as $I = \left\{ {i:\!\rho (i) \in C} \right\}$. We can choose constants ${\left\{ {{\omega _i} \in {Z_N}} \right\} _{i \in I}}$ such that $\sum \nolimits _{i \in I} {{\omega _i}{\lambda _i}} = \mu$, if $\left\{ {{\lambda _i}} \right\}$ that are valid shares of any $\mu$ in $\Pi$. These $\left\{ {{\omega _i}} \right\}$ can be gained in polynomial time.

2.1.3 One-way anonymous key agreement

There was a one-way anonymous key agreement scheme (Kate et al. 2007), which can guarantee anonymity for one participant. Suppose Alice $({ ID}_A)$ and Bob $({ ID}_B)$ are users of one KGC (key generation center) whose master secret is s. Alice wants to keep anonymity with Bob. The progress of key agreement protocol is as follows:

• 1. Alice calculates ${Q_B} = H({ ID}_B)$. It randomly selects a number ${r_A} \in Z_p^ *$ to generate the pseudonym ${P_A} = Q_A^{{r_A}}$ and calculates the session key ${K_{A,B}} = e{({d_A},{Q_B})^{{r_A}}} = e{({Q_A},{Q_B})^{s{r_A}}}$. Finally, it responses its pseudonyms $P_{A}$ to Bob.

• 2. Bob calculates the session key ${K_{A,B}}=e({P_A},{d_B})=e{({Q_A},{Q_B})^{s{r_A}}}$ using his secret key $d_{B}$, where ${d_i}=H{(\textit{ID}_i)^s} \in {G_1}$is user’s private key for $i \in \left\{ {A,B} \right\}$, and $H:{\{ 0,1\} ^ * } \rightarrow {G_1}$ is a strong collision-resistant hash function.

2.2 Problem formulation

2.2.1 System model

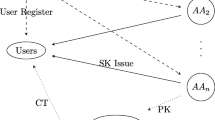
As described in Fig. 1, there are four entities in the cloud storage system: data owner, CS (cloud storage server), N attribute authorities (AAs), data user.

• 1. Data owner: Before outsourcing data on the cloud storage system, the data owner encrypts it under the access policy which is enforced on the ciphertext. The data owner is accountable for defining access policy and obfuscating the policy. Once the attributes of one user are revoked, the owner needs to update partial ciphertext components which contain all revoked attributes.

• 2. Attribute authorities: The attribute authorities are trusted and independently manage their respective attributes set. Meanwhile, authorities then generate the secret key for each legitimate user. When one user is revoked, the authorities will generate the updated key for the non-revoked users.

• 3. Cloud storage server: The cloud storage server stores shared files which belong to the data owners and provide access service for the users. We suppose that the cloud storage server is honest-but-curious. Thus, not only the data but also the access policy in the ciphertext should be hidden.

• 4. Data user: The authorities generate relevant private keys for each data user. In addition, only the users whose private keys satisfy the access control policy can gain data, while any legitimate users can download any ciphertext from the CS.

2.2.2 Security requirements

We formalize three fundamental security requirements for a decentralized CP-ABE access control scheme in cloud storage systems.

• 1. Data confidentiality: In the cloud storage system, only authorized users whose attributes satisfy the access structure can decrypt the ciphertext and gain the data. In the meantime, revoked users cannot decrypt the ciphertext.

• 2. Collusion resistance: All ABE schemes need to prevent the collusion attack. Different users can acquire no information about the access policy and the ciphertext through the combination of their own private key components.

• 3. Policy privacy: When data are outsourced to the cloud storage system , the cloud servers and unauthorized users could not get any information about the access structure embedded in the ciphertext.

Fig. 1

System model of our scheme

2.2.3 Scheme definition:

In this section, we define the decentralized CP-ABE access control scheme with policy hidden for the cloud storage system. Our scheme has the following polynomial time algorithms:

• 1. $AASetup(\lambda ) \rightarrow \left\{ {{{(PK[j],SK[j])}_{j \in [N]}}} \right\}$: The authority setup algorithm inputs the security parameter $\lambda$. It outputs the AA(Attribute Authorities)’s public/secret key pair $\left( {PK[j],SK[j]} \right)$ for each authority.

• 2. $KeyGen\left( {{I_{j,{ GID}}},SK[j]} \right) \rightarrow {K_{j,{ GID}}}$: The key generation algorithm inputs the user’s attribute sets ${I_{j,{ GID}}}$ and the secret key$SK[j]$ and then outputs a secret key ${K_{j,{ GID}}}$ for user.

• 3. $Encrypt\left( {MSG,\left( {M,\rho } \right) ,PK[j]} \right) \rightarrow CT$: The encryption algorithm inputs a monotone access structure ${\left( {M,\rho } \right) }$, the public key PK[j] and the message MSG and then outputs the ciphertext CT.

• 4. $Decrypt\left( {CT,{K_{j,{ GID}}}} \right) \rightarrow MSG$: The decryption algorithm inputs the ciphertext CT and the user’s private keys ${K_{j,{ GID}}}$ and then outputs the message MSG.

• 5. $UKeyGen\left( {{\phi _{j,{ GID}'}},SK[j]} \right) \rightarrow U{K_j}$: The update key generation algorithm inputs an attributes set ${\phi _{j,{ GID}'}}$ that contains the revoked attributes of user ${{ GID}'}$. It outputs the updated key $U{K_j}$.

• 6. $SKUpdate\left( {U{K_j},{K_{j,{ GID}}}} \right) \rightarrow {K'_{j,{ GID}}}$: The user’s secret key update algorithm inputs the updated key $U{K_j}$ and the user’s secret key ${K_{j,{ GID}}}$ and then outputs the updated secret key ${K'_{j,{ GID}}}$.

• 7. $CTUpdate\left( {CT,U{K_j}} \right) \rightarrow CT'$: The ciphertext update algorithm inputs the ciphertext CT and updated key $U{K_j}$ and then outputs the new ciphertext $CT'$.

2.2.4 Security model

Let S represents the set of authorities, and then we define a security model for the decentralized CP-ABE access control scheme which hides the access policy for the cloud storage system through the following game between an adversary $\mathbb {A}$ and a challenger $\mathbb {C}$.

$\mathbf {Setup:}$ A corrupted authorities set $S' \subseteq S$ is specified by the adversary $\mathbb {A}$. The adversary $\mathbb {A}$ submits the challenge access structure $({M^*},{\rho ^*})$ and the revoked attribute set $\phi$. For the set $S - S'$ which is non-corrupted authorities set, the challenger $\mathbb {C}$ generates public/secret key pair $\left( {PK[j],SK[j]} \right)$ by executing the AASetup algorithm. For each attribute $x \in \phi$, the challenger updates public/private key pair $\left( {PK[j],SK[j]} \right)$ and responses the public key $PK[j]$ to $\mathbb {A}$.

$\mathbf {Key\; Queries\; 1\!:}$ $\mathbb {A}$ issues a key query on the attributes set ${I_j}$ and the user GID, where $\mathbb {A}$ cannot make key queries on any attributes set ${I_j}$ which satisfies the access structure $({M^*},{\rho ^*})$ and belong to the corrupted authorities set $S'$. $\mathbb {C}$ generates the secret key by using KeyGen algorithm and the updated key $U{K_j}$ for each attribute $x \in \phi$ by using UKeyGen algorithm, and sends ${K_{j,{ GID}}}$ and $U{K_j}$ to $\mathbb {A}$.

$\mathbf {Challenge\!:}$ $\mathbb {A}$ must submit two distinct messages ${M_0}, {M_1}$ with the same length and an access structure $({M^*},{\rho ^*})$ on the condition that any attributes set ${I_j}$ cannot satisfy the access structure $({M^*},{\rho ^*})$ and belong to corrupted authorities set $S'$. $\mathbb {C}$ selects $\beta \in \left\{ {0,1} \right\}$ and runs the Encrypt algorithm on ${M_\beta }$ to get $C{T^*}$. Finally, $\mathbb {C}$ sends $C{T^*}$ to $\mathbb {A}$.

$\mathbf {Key\; Queries\; 2\!:}$ $\mathbb {A}$ continues to make key queries adaptively, and $\mathbb {C}$ returns the answer as $\mathbf {Key\; Queries\; 1}$. However, $\mathbb {A}$ cannot make key queries on any attributes set ${I_j}$ which satisfies the access structure ${M_\beta }$ and belongs to corrupt authorities $S'$.

$\mathbf {Outputs\!:}$ $\mathbb {A}$ outputs a guess bit $\beta '$ for $\beta$. The winning advantage is $Pr[\beta = \beta '] - \frac{1}{2}$.

Definition 3

A decentralized CP-ABE access control scheme with policy hidden for the cloud storage system is selective CPA-secure, if the advantages of all probably polynomial-time adversaries in the above game are negligible.

3 The proposed scheme

3.1 High-level overview

Provided there are N authorities $\left\{ {{A_1},{A_2}, \ldots ,{A_N}} \right\}$ in the scheme, and each authority ${A_j}$ monitors a set of attributes ${L_j}$ for $j = 1,2, \ldots ,N$. First, each ${A_j}$ randomly selects a number ${\beta _j} \in {Z_p}$. For each attribute $x \in {L_j}$, ${A_j}$ selects a random number ${v_x} \in {Z_p}$ for implementing the attribute revocation. Then, the public key is computed as ${g^{{\beta _j}}}$, where ${\beta _j}$ is the partial secret key of ${A_j}$. For the reason that ${g^{{\beta _j}}}$ can be used by a user to obfuscate attribute of the ciphertext, ${g^{{\beta _j}}}$ is included in the public key $PK[j]$.

In order to resist the collusion attack, when creating a secret key for a user GID and a set of attributes ${I_{j,{ GID}}}$ from the authority ${A_j}$, each ${A_j}$ computes ${g^{{\alpha _x}{v_x}}}H{({ GID})^{{y_x}}}$ by using a global user identity GID. If two users with different GID and GID’ attempt to make a collusion attack by combine their keys, then it would appear some terms in the form of $e{(g,g)^{{\mu _i}}}e(H({ GID}),{g^{{\varphi _i}}})$ and other terms in the form of $e{(g,g)^{{\mu _i}}}e(H({ GID}'),{g^{{\varphi _i}}})$ during the decryption; therefore, we can prevent the process of collusion attack.

In order to preserve policy privacy of ciphertext, the owner randomly selects a number $a \in Z_p^ *$ and computes ${s_y} = e({({g^{{\beta _j}}})^a},H({\lambda _y}))$ when encrypting the message. So it can implement the policy privacy preservation by using ${s_y}$ that replaces the attribute ${\lambda _y}$ in the access policy.

In order to solve the attribute revocation problem, each ${A_j}$ assigns a version number ${v_x}$ for each attribute x. Once there is an attribute revocation, only those components associated with the revoked attribute in secret keys and ciphertexts need to be updated by using ${g^{{\alpha _x}({v_x}^\prime - {v_x})}}$.

3.2 Construction of our scheme

Let $G_{1}$ and $G_{2}$ be two cyclic groups with prime order p, and g be a generator of $G_1$. A map $e:{G_1} \times {G_1} \rightarrow {G_2}$ is a bilinear map. Furthermore, we employ a strong collision-resistant hash function $H:{\{ 0,1\} ^ * } \rightarrow {G_1}$. Our decentralized CP-ABE access control scheme with policy hidden includes the following five procedures:

1) System initialization

Each authority ${A_j}\left( {j \in N} \right)$ which has a set of attributes ${L_j}$ runs the AASetup algorithm. The attributes set disjoint $({L_i} \cap {L_j} = \emptyset ,i \ne j)$.

• 1. The authority $A_{j}$ chooses a number ${\beta _j} \in {Z_p^ *}$ and three random numbers ${\alpha _x},{y_x},{v_x} \in {Z_p^ *}$ for each attribute $x\left( {x \in {L_j}} \right)$, where $v_{x}$ is an attribute version key. The secret key of authority ${A_j}\left( {j \in N} \right)$ is:

  $$\begin{aligned} SK[j] = ({\{ {\alpha _x},{y_x},{v_x}\} _{x \in {L_j}}},{\beta _j}) \end{aligned}$$

  (1)

• 2. The authority $A_{j}$ computes ${\{ e{(g,g)^{{\alpha _x}{v_x}}},{g^{{y_x}}}\} _{x \in {L_j}}}$ for each attribute and ${g^{{\beta _j}}}$. The public key of authority ${A_j}\left( {j \in N} \right)$ is :

  $$\begin{aligned} PK[j] = \left( {\{ {P_{1,x}} = e{(g,g)^{{\alpha _x}{v_x}}},{g^{{y_x}}}\} _{x \in {L_j}}},{g^{{\beta _j}}}\right) \end{aligned}$$

  (2)

2) Key generation

When the user GID wants to access the data, it requests the secret keys from all relevant authorities. After authenticating the user’s identity, each authority runs the KenGen algorithm. The authority ${\mathrm{A}_j}(j \in N)$ gives the attributes set ${I_{j,{ GID}}}$ and corresponding private key ${K_{j,{ GID}}}$ to the user:

$$\begin{aligned} {K_{j,{ GID}}}= & {} (\{ {D_{1,x}} = {g^{{\alpha _x}{v_x}}}H{({ GID})^{{y_x}}},\nonumber \\ {D_{2,x}}= & {} H{(x)^{{\beta _j}}}\}_{x \in {I_{j,{ GID}}}} ) \end{aligned}$$

(3)

where ${\alpha _x},{y_x},{v_x},{\beta _j} \in SK[j]$. Note that the user’s private keys are disseminated under the secure channel.

3) Encryption

The data owner outsources the data to the cloud storage system, after encrypting it with a content key $MSG \in {G_2}$ using symmetric encryption technique. Then the data owner defines an access policy T over attributes from the related AAs. Finally, the owner encrypts MSG using the Encrypt algorithm.

• 1. The owner randomly selects a number $a \in Z_p^ *$ and computes ${s_y} = e({({g^{{\beta _j}}})^a},H({\lambda _y}))$, where ${\lambda _y}(y \in Y)$ denotes one attribute of the access policy T and Y is the number of attributes in T. It is necessary to note that we can be precompute $s_{y}$ once and for all.

• 2. In order to realize the policy privacy preservation, the owner uses $s_{y}$ to replaces the attribute ${\lambda _y}$ in the access policy. Then, the access policy T is converted to LSSS access matrix $\left( {{M_{m\, \times \, h}},\rho } \right) ,{M_i}$ is the i th row of M.

• 3. The owner encrypts MSG by running the Encrypt algorithm as follows:

  • (a) Randomly selects a number $s \in Z_p^*$ and a vector $\nu = {(s,{r_2},{r_3}, \ldots ,{r_h})^\mathrm{T}}\in Z_p^h$.

  • (b) Computes ${\mu _i} = {M_i} \cdot \nu$.

  • (c) Selects a random vector $\omega = {(0,{t_2},{t_3}, \cdots ,{t_h})^\mathrm{T}} \in Z_p^h$.

  • (d) Computes ${\varphi _i} = {M_i} \cdot \omega$.

  • (e) Randomly selects a number ${\sigma _i} \in Z_p^*$ for each row $M_{i}$ of M.

  • (f) Computes the ciphertext components as follows

    $$\begin{aligned} \begin{array}{l} {C_0} = MSGe{(g,g)^s},{h_0} = {g^a}.\\ {C_{1,i}} = e{(g,g)^{{\mu _i}}}e{(g,g)^{{v_{\rho (i)}}{\alpha _{\rho (i)}}{\sigma _i}}},\forall i \in [m].\\ {C_{2,i}} = {g^{{\sigma _i}}},\forall i \in [m].\\ {C_{3,i}} = {g^{{y_{\rho (i)}}{\sigma _i}}}{g^{{\varphi _i}}},\forall i \in [m]. \end{array} \end{aligned}$$

    (4)

  • (g) The ciphertext CT are outsourced to the cloud storage system.

    $$\begin{aligned} CT = ({C_0},\{ {C_{1,i}},{C_{2,i}},{C_{3,i}}\}_{\forall i \in [m]} ,{h_0},(M,\rho ))\quad \end{aligned}$$

    (5)

4) Decryption

If the user’s attributes satisfy the access policy , it can acquire its MSG and gain the owner’s data further.

• 1. Firstly, the user computes $s' = e({h_0},H{(x)^{{\beta _j}}}) = e({g^a},H{(x)^{{\beta _j}}})$ for $\forall x \in {I_{j,u}}$ by using the component ${h_0} = {g^a}$ from the CT.

• 2. Using $s'$ to replace the attribute x, it can construct an attributes set ${I'_{{ GID}}} = \left\{ {{{I'}_{j,{ GID}}},j \in [N]} \right\}$. The user gains the access policy $\left( {M,\rho } \right)$ from CT, and computes the set $R' = \{ i:{(\rho \left( i \right) \cap {I'_{{ GID}}})_{i \in [m]}}\}$.

• 3. Finally, the user chooses constants ${c_i} \in {Z_p^ *}$ such as $\sum \nolimits _{i \in R'}\! {{c_i}{M_i}} = \left( {1,0, \ldots ,0} \right)$. The decryption process is as follows:

  • (a) For each $i \in R'$, it computes

    $$\begin{aligned} dec(i)= & {} \frac{{{C_{1,i}}e(H({ GID}),{C_{3,i}})}}{{e({K_{\rho (i),{ GID}}},{C_{2,i}})}}\nonumber \\= & {} e{(g,g)^{{\mu _i}}}e(H({ GID}),{g^{{\varphi _i}}}) \end{aligned}$$

    (6)

  • (b) It obtains the plaintext

    $$\begin{aligned} MSG = {{{C_0}} \big /{\prod \nolimits _{i \in [m]} {dec{{(i)}^{{c_i}}}} }} \end{aligned}$$

    (7)

5) User revocation

The attributes set ${\phi _{j,{ GID}'}}$ of the user ${ GID}'$ is supposed to be revoked from the authority $A_{j}$. In order to prevent revoked users from decrypting the ciphertext, all non-revoked users who have attributes set ${\phi _{j,{ GID}'}}$ change their stored data. The user revocation’s three phases are as follows:

1. Update key by AAs

When the user is revoked, the $A_{j}$ runs the UKeyGen algorithm. It firstly chooses a random version key ${v'_x} \in Z_p^*$ for each attribute $x \in {\phi _{j,{ GID}'}}$. The authority $A_{j}$ then calculates update key $U{K_j} = \{ {g^{{\alpha _x}({v_x}^\prime - {v_x})}},x \in {\phi _{j,{ GID}'}}\}$and the public key ${P'_{1,x}} = {P_{1,x}}.e{(g,g)^{{\alpha _x}({{v'}_x} - {v_x})}} = e{(g,g)^{{\alpha _x}{{v'}_x}}}$. Finally, the authority $A_{j}$ sends $UK_{j}$ to non-revoked users and data owners under the secure channel.

2. Secret key update by non-revoked users

When the user receives the update key $UK_{j}$ from the authority $A_{j}$, it will run the SKUdate algorithm to update its secret key as

$$\begin{aligned} \begin{aligned} {{K'}_{j,u}}&= (\forall x \in {\phi _{j,{ GID}'}}:{{D'}_{1,x}} = {D_{1,x}} \cdot U{K_j}\\&= {g^{{\alpha _x}{{v'}_x}}}H{({ GID})^{{y_x}}},{{D'}_{2,x}} = {D_{2,x}}\\&\qquad \forall x \notin {\phi _{j,{ GID}'}}:{{D'}_{1,x}} = {D_{1,x}},{{D'}_{2,x}} = {D_{2,x}}) \end{aligned} \end{aligned}$$

(8)

The $UK_{j}$ is associated with revoked user GID’, so the non-revoked users can be distinguished by the authority. Thus, the revoked user ${ GID}'$ cannot receive the update key $UK_{j}$.

3. Ciphertext update by the data owner

When the data owner receives the updated key $UK_{j}$ from the authority $A_{j}$, it will run the CTUpdate algorithm to update its ciphertext. Firstly, the data owner collects the ciphertext components $({C_{1,i}},{C_{2,i}})$ which contain attributes set ${\phi _{j,{ GID}}}$ in the cloud storage system. For each ciphertext component, the following steps is calculated:

$$\begin{aligned} \forall \ i= & {} 1\ \mathrm{to}\ m:if\ \rho (i) \in {\phi _{j,{ GID}}}\nonumber \\ {{C'}_{1,i}}= & {} {C_{1,i}} \cdot e({C_{2,i}},{g^{{\alpha _{\rho (i)}}({{v'}_{\rho (i)}} - {v_{\rho (i)}})}})\nonumber \\= & {} e{(g,g)^{{\mu _i}}}e{(g,g)^{{{v'}_{\rho (i)}}{\alpha _{\rho (i)}}{\sigma _i}}}\nonumber \\&\quad \mathrm{else} \ {{C'}_{1,i}} = {C_{1,i}} \end{aligned}$$

(9)

Finally, the new values of ${C'_{1,i}}\left( {i \in [1,m]} \right)$ are outsourced to the cloud storage system. For each revoked attribute, only the component $C_{1,i}$ needs to be updated in our scheme. Thus, the user revocation is more efficient.

4 Security and performance analyses

4.1 Correctness analysis

Correctness: Our scheme is correct as the following equations hold. From Eq. (6), we can get:

$$\begin{aligned}&dec(i)\nonumber \\&\quad = \frac{{{C_{1,i}}e(H({ GID}),{C_{3,i}})}}{{e({K_{\rho (i),{ GID}}},{C_{2,i}})}}\nonumber \\&\quad = \frac{{e{{(g,g)}^{{\mu _i}}}e{{(g,g)}^{{v_{\rho (i)}}{\alpha _{\rho (i)}}{\sigma _i}}}e(H({ GID}),{g^{{y_{\rho (i)}}{\sigma _i}}}{g^{{\varphi _i}}})}}{{e({g^{{\alpha _x}{v_x}}}H{{({ GID})}^{{y_x}}},{g^{{\sigma _i}}})}}\nonumber \\&\quad = \frac{{e{{(g,g)}^{{\mu _i}}}e{{(g,g)}^{{v_{\rho (i)}}{\alpha _{\rho (i)}}{\sigma _i}}}e(H({ GID}),{g^{{y_{\rho (i)}}{\sigma _i}}})e(H({ GID}),{g^{{\varphi _i}}})}}{{e({g^{{\alpha _x}{v_x}}},{g^{{\sigma _i}}})e(H{{({ GID})}^{{y_x}}},{g^{{\sigma _i}}})}}\nonumber \\&\quad = e{(g,g)^{{\mu _i}}}e(H({ GID}),{g^{{\varphi _i}}}) \end{aligned}$$

(10)

Then, evaluating the Eq. (7), we can get:

$$\begin{aligned}&{{{C_0}} \big / {\prod \nolimits _{i \in m} {dec{{(i)}^{{c_i}}}} }}\nonumber \\&\quad = {{MSGe{{(g,g)}^s}} \big /{\prod \nolimits _{i \in m} {{{(e{{(g,g)}^{{\mu _i}}}e(H({ GID}),{g^{{\varphi _i}}}))}^{{c_i}}}} }}\nonumber \\&\quad = {{MSGe{{(g,g)}^s}} \big / {e{{(g,g)}^{\sum \limits _{i \in m} {{\mu _i}{c_i}} }}e{{(H({ GID}),g)}^{\sum \limits _{i \in m} {{\omega _i}{c_i}} }}}}\nonumber \\&\quad = {{MSGe{{(g,g)}^s}} \big / {e{{(g,g)}^{\sum \limits _{i \in m} {{\mu _i}{c_i}} }}}}= MSG \end{aligned}$$

(11)

where $\sum \nolimits _{i \in [m]} {{\mu _i}{c_i}} = s,\sum \nolimits _{i \in [m]} {{\omega _i}{c_i}} = 0.$ Thus, our scheme is correct.

4.2 Security analysis

Theorem 1

If Lewko and Waters’ (2011) decentralized CP-ABE scheme is selectively CPA-secure, our scheme is also selectively CPA-secure.

Proof

This theorem is proved by the following games and lemmas. Firstly, game $Game_{0}$ is an original game of Lewko and Waters’ scheme. The second game $Game_{1}$ is the same as $Game_{0}$ except that $h_{0}$ in challenge ciphertext is generated randomly and a random number $D_{2,x}$ in $G_{1}$ is added in user’s key ${K_{j,{ GID}}}$. The first lemma is that $Game_{0}$ and $Game_{1}$are computationally indistinguishable, while the second lemma is that the advantage probability of adversary in $Game_{1}$ is negligible, and then the Theorem 1 is proved secure. $\square$

Lemma 1

If Lekwo and Waters’ (2011) decentralized CP-ABE scheme is selectively CPA-secure, $Game_0$ and $Game_1$ are computationally indistinguishable.

Proof

If a distinguisher $\mathbb {A}$ can discriminate $Game_{0}$ and $Game_{1}$, then there is an algorithm $\mathbb {B}$ which can break Lewko and Waters’ decentralized CP-ABE scheme. Suppose $\mathbb {C}$ is a simulator corresponding to $\mathbb {B}$. $\mathbb {A}$ runs $\mathbb {B}$ as follows:

$\mathbf {Setup\!:}$ $\mathbb {A}$ gives $\mathbb {B}$ its challenge access structure $({M^*},{\rho ^*})$ and the revoked attribute set $\phi$, and then $\mathbb {B}$ sends $({M^*},{\rho ^*})$ and $\phi$ to $\mathbb {C}$ as its challenge. $\mathbb {C}$ computes ${P'_{1,x}} = e{(g,g)^{{\alpha _x}{{v'}_x}}}$ for each attribute $x \notin \phi$ and computes ${P'_{1,x}} = {P'_{1,x}} .e{(g,g)^{{\alpha _x}({{v'}_x} - {{v}_x})}} = e{(g,g)^{{\alpha _x}{{v'}_x}}}$ for $x \in \phi$. $\mathbb {C}$ provides the public key $PK'[j]= (\{ {P_{1,x}} = {P'_{1,x}},{g^{{{y'}_x}}}\}_{x \in {L_j}}, g,G_1,G_2, e,H)$. $\mathbb {B}$ randomly selects ${\beta _j} \in {\mathrm{{Z}}_p^ *}$. Finally, $\mathbb {B}$ sends the master public key $PK[j] = (\{ {P_{1,x}} = {P'_{1,x}},{g^{{y_x}}}\}_{x \in {L_j}} ,{g^{{\beta _j}}})$ to $\mathbb {A}$.

$\mathbf {Key\; Queries\; 1\!:}$  When $\mathbb {A}$ issues a key query by submitting pairs $({\{ {I_j}\} _{j \in [N]}},{\textit{GID}})$, $\mathbb {B}$ sends it to $\mathbb {C}$ and obtains the key ${K'_{j,{\textit{GID}}}} = ({\{{D_{1,x}} = {g^{{\alpha _x}{v_x}}}H{({\textit{GID}}^{{y_x}}}\} _{x \in {I_{j,{\textit{GID}}}}}})$. $\mathbb {C}$ generates $U{K_j} = \{{g^{{\alpha _x}({v_x}^\prime - {v_x})}}\}$ for each attribute $x \in \phi$. $\mathbb {B}$ randomly chooses ${\beta _j} \in {Z_p^ *}$ and responses $K_{j,{ GID}} = ({D_{1,x}} = {g^{{\alpha _x}{v_x}}}H{({ GID})^{{y_x}}}, {D_{2,x}} = H{(x)^{{\beta _j}}})$ and $U{K_j} = ( {g^{{\alpha _x}({v_x}^\prime - {v_x})}})$ to $\mathbb {A}$ as the answer, where $x \in {I_{j,{ GID}}}$.

$\mathbf {Challenge\!:}$ When $\mathbb {A}$ submits two different messages $M_{0}$ and $M_{1}$ with equal length to $\mathbb {B}$ , and $\mathbb {B}$ chooses a bit $\beta \in \left\{ {0,1} \right\}$ and sends $M_{0}$ and $M_{1}$ to $\mathbb {C}$. Then, $\mathbb {C}$ selects a bit $\mu \in \left\{ {0,1} \right\}$ and encrypts ${M_\mu }$ under $PK[j]$ and $({M^*},{\rho ^*})$ using Waters’ scheme, and sends $CT' = ({C_0},{\{ {C_{1,i}},{C_{2,i}},{C_{3,i}}\} _{\forall i \in [m]}}, ({M^*},{\rho ^*}))$ to $\mathbb {B}$. $\mathbb {B}$ computes ${C'_{1,i}} = {C_{1,i}} \cdot e({C_{2,i}},{g^{{\alpha _{\rho (i)}}({{v'}_{\rho (i)}} - {v_{\rho (i)}})}}) = e{(g,g)^{{\mu _i}}}e{(g,g)^{{{v'}_{\rho (i)}}{\alpha _{\rho (i)}}{\sigma _i}}}$ for each attribute $x \in \phi$ and ${C'_{1,i}} = {C_{1,i}}$ for $x \notin \phi$. $\mathbb {B}$ randomly chooses $a \in {Z_p^ *}$ and responses $CT = ({C_0},{h_0} = {g^a},{\{ {C_{1,i}},{C_{2,i}},{C_{3,i}}\} _{\forall i \in [m]}},({M^*},{\rho ^*}))$.

$\mathbf {Key\; Queries \;2\!:}$ $\mathbb {A}$ makes key queries adaptively, and $\mathbb {B}$ response as $\mathbf {Key\; Queries\; 1}$.

$\mathbf {Outputs\!:}$ $\mathbb {A}$ outputs $\beta '$ to $\mathbb {B}$, and $\mathbb {B}$ sends it to $\mathbb {C}$ as its guess about $\mu$.

If $\beta = \mu$, then $\mathbb {C}$ has simulated $Game_{0}$. Otherwise, it has simulated $Game_{1}$. Therefore, if $\mathbb {A}$ can distinguish $Game_{0}$ and $Game_{1}$, then $\mathbb {B}$ can break Lewko and Waters’ decentralized CP-ABE scheme.

Lemma 2

If Lewko and Waters’ (2011) CP-ABE decentralized scheme is selectively CPA-secure, the probability of adversary $\partial 's$ advantage in $Game_1$ is negligible.

Proof

If an adversary $\mathbb {A}$ can win $Game_{1}$, then there is an algorithm $\mathbb {B}$ which can break Lewko and Waters’ decentralized CP-ABE scheme. Suppose $\mathbb {C}$ is a simulator corresponding to $\mathbb {B}$. $\mathbb {A}$ runs $\mathbb {B}$ as follows:

$\mathbf {Setup:}$ $\mathbb {A}$ gives $\mathbb {B}$ its challenge access structure $({M^*},{\rho ^*})$ and the revoked attribute set $\phi$, and then $\mathbb {B}$ sends $({M^*},{\rho ^*})$ and $\phi$ to $\mathbb {C}$ as its challenge. $\mathbb {C}$ computes ${P'_{1,x}} = e{(g,g)^{{\alpha _x}{{v'}_x}}}$ for each attribute $x \notin \phi$ and computes ${P'_{1,x}} = {P'_{1,x}}.e{(g,g)^{{\alpha _x}({{v'}_x} - {{v}_x})}} = e{(g,g)^{{\alpha _x}{{v'}_x}}}$ for $x \in \phi$. $\mathbb {C}$ provides the public key $PK'[j]= (\{ {P_{1,x}} = {P'_{1,x}},{g^{{{y'}_x}}}\}_{x \in {L_j}}, g,G_1,G_2,e,H)$. $\mathbb {B}$ randomly selects ${\beta _j} \in {\mathrm{{Z}}_p^ *}$. Finally, $\mathbb {B}$ sends the master public key $PK[j] = (\{ {P_{1,x}} = {P'_{1,x}},{g^{{y_x}}}\}_{x \in {L_j}} ,{g^{{\beta _j}}})$ to $\mathbb {A}$.

$\mathbf {Key\; Queries\; 1\!:}$ When $\mathbb {A}$ issues a key query by submitting pairs $({\{ {I_j}\} _{j \in [N]}},{\textit{GID}})$, $\mathbb {B}$ sends it to $\mathbb {C}$ and obtains the key ${K'_{j,{\textit{GID}}}} = ({\{ {D_{1,x}} = {g^{{\alpha _x}{v_x}}}H{({\textit{GID}})^{{y_x}}}\} _{x \in {I_{j,{\textit{GID}}}}}})$. $\mathbb {C}$ generates $U{K_j} = \{ {g^{{\alpha _x}({v_x}^\prime - {v_x})}}\}$ for each attribute $x \in \phi$. $\mathbb {B}$ randomly chooses ${\beta _j} \in {Z_p^ *}$, and responses $K_{j,{\textit{GID}}} = ({D_{1,x}} = {g^{{\alpha _x}{v_x}}}H{({\textit{GID}})^{{y_x}}}, {D_{2,x}} = H{(x)^{{\beta _j}}})$ and $U{K_j} = ( {g^{{\alpha _x}({v_x}^\prime - {v_x})}})$ to $\mathbb {A}$ as the answer, where $x \in {I_{j,{\textit{GID}}}}$.

$\mathbf {Challenge\!:}$ When $\mathbb {A}$ submits two messages $M_{0}$ and $M_{1}$ (distinct messages but with equal length) to $\mathbb {B}$ , and $\mathbb {B}$ sends $M_{0}$ and $M_{1}$ to $\mathbb {B}$. Then, $\mathbb {B}$ selects a bit $\mu \in \left\{ {0,1} \right\}$ and encrypts ${M_\mu }$ under $PK[j]$ and $({M^*},{\rho ^*})$ by using the encrypt algorithm of Waters’ scheme, and sends $CT' = ({C_0},({M^*},{\rho ^*}), {\{ {C_{1,i}},{C_{2,i}},{C_{3,i}}\} _{\forall i \in m}})$ to $\mathbb {B}$. $\mathbb {B}$ computes ${C'_{1,i}} = {C_{1,i}} \cdot e({C_{2,i}},{g^{{\alpha _{\rho (i)}}({{v'}_{\rho (i)}} - {v_{\rho (i)}})}}) = e{(g,g)^{{\mu _i}}} e{(g,g)^{{{v'}_{\rho (i)}}{\alpha _{\rho (i)}}{\sigma _i}}}$ for each attribute $x \in \phi$ and ${C'_{1,i}} = {C_{1,i}}$ for $x \notin \phi$. $\mathbb {B}$ randomly chooses ${\hat{h}_0} \in G$, and responses $CT = ({C_0}, {\{ {C_{1,i}},{C_{2,i}},{C_{3,i}}\} _{\forall i \in m}},{h_0} = {\hat{h}_0},({M^*},\rho ^* ))$.

$\mathbf {Key\; Queries \;2\!:}$ $\mathbb {A}$ makes key queries adaptively, and $\mathbb {B}$ returns the answer as $\mathbf {Key\; queries\; 1}$.

$\mathbf {Outputs\!:}$ $\mathbb {A}$ outputs $\beta '$ to $\mathbb {B}$, and $\mathbb {B}$ sends it to $\mathbb {C}$ as its guess to $\mu$.

Obviously, $\mathbb {C}$ has properly simulated $Game_{1}$. So, if $\mathbb {A}$ can win $Game_{1}$, then $\mathbb {B}$ can break Waters’ CP-ABE decentralized scheme with non-negligible advantage.

Table 1 Comparison of flexibility

Fig. 2

Comparison of encryption, decryption and ciphertext re-encryption Time. a Encryption. b Decryption. c Re-encryption

Theorem 2

Our scheme supports data confidentiality, collusion resistant and only allows non-revoked and authorized users to access data.

Proof

Suppose that the colluders include attributes set $R$, such that $\sum \nolimits _{i \in R} {{c_i}{M_i}} = \left( {1,0, \ldots ,0} \right)$. However, they need to compute the components $e{(g,g)^{{\mu _i}}}e(H({\textit{GID}}),{g^{{\varphi _i}}})$ according to Eq. (6). Even if they collude, they cannot decrypt the ciphertext because different users have different values of $e(H({\textit{GID}}),{g^{{\varphi _i}}})$. For an unauthorized user, it does not have the attribute corresponding to some rows i, so it cannot compute the vector $< {c_i} >$, such that $\sum \nolimits _{i \in R} {{c_i}{M_i}} = \left( {1,0, \ldots ,0} \right)$. Thus, it cannot calculate the component $e{(g,g)^s}$. On the other hand, the non-revoked user updates its private key by using the update key ${g^{{\alpha _x}{{v'}_x}}}H{({\textit{GID}})^{{y_x}}}$. However, the revoked user cannot receive the update key from the authority so it cannot acquire the content key MSG and gain the owner’s data further.

Theorem 3

Our scheme is policy privacy against the cloud server in the system.

Proof

When the data owner’s encrypted data are outsourced to the cloud storage system, it obfuscates each attribute x as $e({({g^{{\beta _j}}})^a},H(x))$ of the access policy embedded in the ciphertext using the one-way anonymous key agreement protocol (Kate et al. 2007) where a is a random number. Only authorized users that have the corresponding key ${D_{2,x}} = H{(x)^{{\beta _j}}}$ can compute the obfuscated value $e({({g^{{\beta _j}}})^a},H(x))$. The cloud storage server cannot guess x from the obfuscated value $e({({g^{{\beta _j}}})^a}, H(x))$ due to the value a. Further, the property of policy privacy is guaranteed by the security of the one-way anonymous key agreement protocol (Kate et al. 2007), if not knowing the corresponding $H{(x)^{{\beta _j}}}$, anyone cannot compute $e({g^a}, H{(x)^{{\beta _j}}})= e({({g^{{\beta _j}}})^a},H(x))$ to gain the attribute. In addition, users also cannot know the information of access policy when they collude, because they cannot infer the attribute x from $e({({g^{{\beta _j}}})^a},H(x))$.

4.3 Performance analysis

We make a comparison between previous ABE schemes and our scheme in Table 1 with regard to access structure, hidden access policy, user revocation, and the number of authorities. It is shown that this proposed scheme is much more abundant in Table 1.

We simulate the computation time of encryption, decryption and re-encryption in our scheme and RSN’s scheme (Ruj et al. 2014). We do the simulation on a Windows 7 system with Intel CoreTM i5-4440 CPU at 4 GB RAM and 3.10 GHz. The implementation adopts a 160-bit elliptic curve group relied on the curve ${y^2} = {x^3} + x$ which bases on Java pairing-based library (version 0.5.12). In Fig. 2a, b, supposed that the user gets 10 attributes from each AA. The results are the average values for 20 rounds in each experiment. The comparison of encryption time, decryption time on the user with different authority number is shown in Fig. 2a, b, respectively. Figure 2c indicates the comparison of ciphertext re-encryption to the revoked attributes’ number. It is shown that this proposed scheme’s required encryption time nearly equal to RSN’s schemes, while needed less time for re-encryption. It takes a little more decryption time than RSN’s schemes for adding a process to obfuscate attributes in decryption that can be precomputed once and for all before decryption. All in all, the computation efficiency of the proposed scheme is better than RSN’s scheme.

5 Conclusion

In this paper, fuzzy access control schemes for the cloud storage system are studied. Subsequently, we propose a secure decentralized CP-ABE scheme to design a access control scheme with policy hidden. Our access control scheme supports privacy preservation of data and access policy and adopts more flexible LSSS matrix access structure. It also supports efficient user revocation for multi-authority CP-ABE and decreases communication cost and computation cost of the user revocation. Then, we prove the schemes security and analyze its performance. Finally, we demonstrate the scheme is feasible through the experiment.