Decentralized, Revocable and Verifiable Attribute-Based Encryption in Hybrid Cloud System

Abstract

Cloud can provide storage space and services for data owners to host their data, where data privacy and confidentiality become critical issues. Ciphertext policy attribute-based encryption (CP-ABE) is one of the most suitable methods to protect data privacy and provide structured access control. In this paper, we propose a multi-authority CP-ABE scheme with a direct attribute revocation mechanism, cause revocation is an inevitable problem in the application process. Under our proposed revocation mechanism, the remaining users need not to update their secret keys when revocation happens. It relies on the matching of public keys’ version and ciphertext’ version. In a cloud storage model, the update of ciphertext is executed by public cloud, which cannot be fully trusted by data owners. In this case, we propose a hybrid CP-ABE cloud storage model aiming at solving the public cloud trust management problem. The data owners can authorize private cloud to verify whether their ciphertexts have been updated to the newest version. In addition, we prove our construction secure in selective-CPA model. Finally, we compare our scheme with similar multi-authority CP-ABE schemes from functionality, communication overhead and computation cost. The simulation results show that our scheme is more efficient than similar works in encryption, decryption and revocation stages.

1 Introduction

Cloud computing has become increasingly popular in recent years, and provides computing and storage resources in a pay-as-you-go manner [1]. As an important component, cloud storage service enables end-users to host their data in cloud servers, thereby bypassing the impasse of limited local storage space. Unfortunately, the public cloud server is generally considered untrustworthy to store plaintext [2]. As a public key encryption mechanism, ciphertext policy attribute-based encryption (CP-ABE) defines a user by a group of attributes, while files are encrypted against a predefined access structure. The user can decrypt a file, if and only if its attributes satisfy the structure. It emancipates data owners (DOs) from continually distributing keys and enables them to share the same encryption operations with a certain group of users through an access structure. By using this technique, files are stored as ciphertext in the cloud server for privacy consideration and can be shared with a group of data users [3].

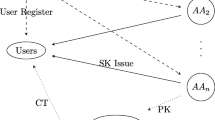
The basic cloud storage structure typically consists of Cloud Layer, Data Owner/User Layer and a Central Authority (CA) [2]. The structure is described by Fig. 1. The CA sets up the system and publishes public parameters. It is also responsible for registering users and generating secret keys for the users. A typical process of a CP-ABE cloud storage system involves (1). the data owners encrypt files against an access structure, and upload the ciphertext to cloud server; (2). users request the ciphertext from the cloud server and decrypt them with their secret keys. Note that a data owner can be the user of some other data, and vice versa.

Fig. 1

The basic CP-ABE cloud storage structure

Revocation is a key and crucial part of a CP-ABE based cloud storage system. This is due to the fact that the attributes which a user holds may change frequently in practice [2]. Attribute revocation mechanism can ensure data privacy of the attribute group and prevent illegitimate access of the removed user in the future. Generally speaking, there are two methods to implement fine-grained attribute revocation: indirect revocation and direct revocation [4]. In the indirect revocation mode, all the remaining users need to update their private keys at the change of the attribute group. This could incur heavy communication and computational overhead, leading to a bottleneck of the system. In direct revocation systems, the ciphertext is updated to a newer version, together with public information. In these systems, revocation typically relies on the cloud to update the ciphertext. However, with an increasing number of end-hosts, the computational overhead to refresh all related files can grow exponentially. The data owners may worry about their data stored on the cloud [5]. Therefore, it is important for the data owners to make sure that their files are updated honestly according to the protocol.

To solve this problem, we propose a new Decentralized, Revocable and Verifiable Attribute-Based Encryption (DRV-ABE) scheme in the hybrid cloud computing framework, which aims to balance between the efficiency and security of public cloud. We assume that the private cloud is closer to users and more trustworthy. As illustrated in Fig. 2, we introduce a Private Cloud Layer between the end-users and the public cloud to provide a more trustworthy storage service. Each server in the Private Cloud Layer helps its internal legitimate end-users to periodically audit their data stored in public cloud.

Fig. 2

The proposed DRV-ABE system structure

Besides that, all the attributes of acceptable users can be divided into m disjoint sets. Each AA is responsible for managing the attributes in its subset. To support the direct revocation mechanism, for each attribute, the corresponding AA maintains a public key, which contains the identities of users with this attribute. The revocation is realized by updating this public key and refreshing the ciphertext with this attribute. Only the ciphertext in the newest version can prevent the revoked users from accessing data any more.

1.1 Our Contribution

In this paper, we propose a secure data access control scheme for cloud storage platforms. The key idea is that we develop a DRV-ABE access control scheme to share data with a group of users, where multiple attribute authorities are developed to distribute attribute secret keys. The proposed scheme also supports direct revocation mechanism, and the attribute public keys are dependent on the end-users with this attribute. Therefore, revocations can be efficiently achieved by revoking a specific public key for the attribute group with changed memberships. Another important aspect of the proposed scheme is that we propose a private cloud layer to periodically audit the public cloud for its internal users. The proposed scheme is proved to be selective-CPA secure under the Decisional q-Papallel Bilinear Diffe-Hellman Exponent (q-PBDHE) assumption.

1.2 Related Work

Fine-grained attribute mechanisms such as [6,7,8,9,10,11,12] were proposed to achieve the revocation of a single attribute of a user. In [9], a two-factor access control was proposed for multi-authority cloud storage systems, where the recovery of outsourced data were controlled by two factors: attribute secret key and authorization key. Only the users with both of the keys were able to decrypt the ciphertext. Yang et al. proposed a multi-authority CP-ABE access control scheme for cloud storage applications in [12], where only indirect attribute revocation is supported. In other words, the remaining users have to update their secret keys frequently. Li et al. [6] implemented user revocation by introducing the concept of user group, where a user’s secret key consists of two parts. One is associated with the attributes of the user and the other is associated with the group which the user belongs to. When a user departs from the group, i.e., the user is revoked, the group manager can update the group key pair and private keys for unrevoked users.

Indirect attribute revocation schemes are always based on unrevoked users’ key updating. However, in practical, the users may miss many key update messages so that they can not keep their keys up-to-date. In [8], Hur et. al solved this problem in indirect revocation systems by introducing a stateless group key distribution mechanism. But their attribute revocation schemes are proposed relying on a trusted cloud server. In the same time, direct revocation has been widely studied. Fan et. al proposed an arbitrary-state ABE scheme with dynamic membership in [10]. In their scheme, all the attributes are maintained by a Key Generation Center (KGC), which mean that it has risk of system single-point bottleneck.

There are also a branch of ABE schemes with outsourced verifiability. But most of them focus on verifying the correctness of outsourced decryption. For example, Lai et al. [13] realized the verifiability of their scheme by generating a commitment for a random message and the actual plaintext. After the user decrypts the ciphertext, he can use the commitment to verify whether the transformation is generated correctly. Li et. al also proposed an outsourced ABE scheme, which can simultaneously check the correctness for transformed ciphertext for the authorized users and unaothorized users [14]. In their scheme, not only the authorized users, but also the unauthorized users can verify the transformed ciphertext. In [15], Ma et. al proposed general verification mechanisms to audit the cloud servers and check the correctness of outsourced computations. In [16], Wang et. al proposed an anonymous distributed fine-grained access control with verifiable outsourced decryption. The user’s identity can be protected when accessing sensitive remote data. As to the designing of decentralized multi-authority attribute-based encryption scheme, Chow et. al proposed a framework in [17] to construct a multi-authority ABE schemes with attribute-revocation and outsourced decryption. And a decentralized ABE with fast encryption, outsourced decryption and user revocation was given in [18].

Because the data owners no longer have possession of the outsourced data, the integrity protection method is also important in cloud storage model. Wang et al. [19] proposed a public auditing system to enable an external auditor to audit user’s cloud adta without learning the data content. And [20] proposed a remote data integrity checking mechanism to prove that the cloud server is actually storing a data owner’s data hoestly.

2 Preliminaries and Definitions

We define the algorithms in the proposed DRV-ABE scheme and the decisional q-parallel Bilinear Diffie-Hellman Exponent problem in this section. The notations in this paper are listed in Table 1.

Table 1 Notations

2.1 Definition of the DRV-ABE Protocol

• $CASetup(\lambda ) \rightarrow (GPP, MSK)$ The CA is a fully trusted party in our framework. It generates the public key for system and initializes the AAs by running this algorithm. Here, GPP stands for global public parameters and MSK represents master secret key.

• $AASetup(MSK) \rightarrow (PK_{aid_k}, SK_{aid_k})$ Each attribute authority generates the public keys and secret keys by running the AASetup algorithm.

• $KeyGen(SK_{aid_k}, S_u) \rightarrow SK_u$ Each AA executes the KeyGen algorithm to generate the secret keys for user u by taking their secret key $SK_{aid_k}$ and the attribute set of this user $S_u$ as the input.

• $Enc(PK, {\mathscr {M}}, {\mathscr {T}}) \rightarrow (CT, AK)$ The data owner encrypts the message ${\mathscr {M}}$ by taking the public keys and an access structure ${\mathscr {T}}$ as the input. The Enc algorithm outputs the ciphertext CT and the auditing key AK. Then it transfers the auditing key to a private cloud server.

• $Dec(PK, CT) \rightarrow {\mathscr {M}}$ User u checks the access structure, and finds a subset of its attributes that can be used to decrypt. If the access structure of the ciphertext CT can be satisfied by the attributes of u, the Dec algorithm outputs the plaintext ${\mathscr {M}}$ directly.

• $Revoke(PK, u, MSK) \rightarrow ({\widetilde{PK}}, UK)$ If the jth attribute of user u is revoked, the corresponding AA executes this algorithm to update the public key of this attribute and generates an update key UK to update the ciphertexts.

• $CTUpdate(CT, UK) \rightarrow {\widetilde{CT}}$ The public cloud server updates all the ciphertexts which contain the revoked attribute. The algorithm takes the ciphertext and the update key UK as the input and generates a new ciphertext ${\widetilde{CT}}$.

• $Auditing(CT, AK) \rightarrow ( ''0'' or ''1'')$ The private cloud periodically audits the ciphertext version stored on the public cloud by using this algorithm. It takes the ciphertext CT and the auditing key AK as the input, and outputs “0” or “1” to represent abnormal or normal, respectively.

2.2 Security Assumption of Cloud Servers

2.2.1 Public Cloud

The public cloud is responsible for providing storage services for end-users in the system. It is defined as a malicious cloud server. It is curious about the content of the ciphertext and may choose not to update the ciphertexts when revocation occurs.

2.2.2 Private Cloud

The private cloud servers are more trustworthy than the public cloud. They audit the ciphertexts for their internal end-users honestly, and are also curious about the files.

2.3 Decisional q-PBDHE Assumption [21]

Assume that there are two groups ${\mathbb {G}}$ and ${\mathbb {G}}_T$ with prime order p. Let $a, s, b_1, \ldots \, b_q \in {\mathbb {Z}}_p$ be chosen at random and g be a generator of ${\mathbb {G}}.$ If an adversary is given ${\mathbf {y}}=$

$$\begin{aligned}&g,g^s,g^a,\ldots ,g^{(a^q)}, \ ,g^{(a^{q+2})} ,\ldots ,g^{(a^{2q})}\\&\quad ~_{\forall ~~{1\le j \le q},} ~~ \ g^{s \cdot b_j},g^{a / b_j},\ldots ,g^{(a^q/b_j)}, \ ,g^{(a^{q+2}/b_j)} ,\ldots ,g^{(a^{2q}/b_j)}\\&\quad ~_{\forall ~~{1 \le j,k \le q,k\ne j},} ~~ \ g^{a \cdot s \cdot b_k/b_j} ,\ldots ,g^{(a^q \cdot s \cdot b_k/b_j )}, \end{aligned}$$

it is hard to distinguish $e(g,g)^{a^{q+1}s} \in {\mathbb {G}}_T$ from a random element in ${\mathbb {G}}_T$.

3 Decentralized, Revocable and Verifiable Attribute-Based Encryption Scheme

In this section, the detailed algorithms of the proposed DRV-ABE scheme are described. In addition, we use the Linear Secret Sharing Scheme (LSSS) structure [21] to share the secret value among attribute in the access policy.

3.1 System Initialization

3.1.1 CASetup

The CA has three main functions in the designed scheme, including publishing the system parameters, generating secret values for the AAs, and registering users. In the CASetup algorithm, it plays the first two functions as follows.

• 1. Given a security parameter $\lambda$, the TA is responsible for initializing the system by publishing the global public parameters for all the internal users and generating secret values for each attribute authority. Here, $\lambda$ can be defined as the number of bits in each element in the multiplicative groups, measuring the security level of the system, as will be articulated later. By using the celebrated bilinear mapping, the TA first sets up two multiplicative groups ${\mathbb {G}}$ and $\mathbb {G_T}$ both with the prime order p. The generator of the two groups are g and $e(g,g)^{\alpha }$ respectively. The TA also sets up a symmetric bilinear map $e:{\mathbb {G}}\times {\mathbb {G}}\rightarrow \mathbb {G_T}$ with two properties: (1). Billinearity: $e(g^a,g^b)=e(g,g)^{ab}=e(g^b,g^a)$, $a,b\in {\mathbb {Z}}_p$. (2). Non-degeneracy: $e(g,g)\ne 1$. The TA also defines a mapping function, $H(\cdot )$, which is a one-to-one mapping of the attributes to the elements of the multiplicative group ${\mathbb {G}}$. By this means, the attributes are parameterized to generate attribute-specific public and secret keys. The TA also produces a random value $c \in {\mathbb {Z}}_p$, where ${\mathbb {Z}}_p$ is an additive cyclic group, and computes $g^c$. As a result, the GPP can be defined and published as $GPP =(g,g^c,H(\cdot ))$.

• 2. The CA also generates the secret keys for each AA. Assume that there are m attribute authorities and they are denoted by $AA_{aid_1}$, $\ldots$, $AA_{aid_{m}}$. The CA chooses random values $n_{aid_1}, \ldots n_{aid_{m}} \in {\mathbb {Z}}_p$, which satisfy $\textstyle \sum _{k \in [1, m]}{n_{aid_k}}=0$. These values connect the authorities together and make sure that the only the users with legitimate secret keys from each authority can decrypt ciphertexts. The CA transmits $g^{n_{aid_k}}$ to its corresponding $AA_{aid_k}$, as the private key of the AA. The master secret key is set to be $MSK =(m, n_{aid_1}, n_{aid_2}, \ldots , n_{aid_{m}}).$

3.1.2 AASetup

After receiving $g^{n_{aid_k}}$, each AA picks random values $\alpha _{aid_k}$, $\beta _{aid_k}$, $\gamma _{aid_k}$, $\delta _{aid_k} \in {{\mathbb {Z}}_{p}}$ as its secret key and then computes $e(g,g)^{\alpha _{aid_k}}$ and $g^{c\delta _{aid_k}}$ as its public key. After that, the AA proceeds to initialize attributes in the corresponding domain.

Assume that $AA_{aid_k}$ has a set of attributes in the domain denoted by $S_{aid_k}$. For each attribute $j\in S_{aid_k}$, $AA_{aid_k}$ generates two default users $u_0$, $u_1$ and sets the user group of attribute j to $U_j =\{u_0, u_1\}$. For each user $u_i \in U_j$, $AA_{aid_k}$ chooses $v_{i,j},t_{i,j} \in {\mathbb {Z}}_p$ and computes the attribute public keys $PK_{1,j}$ and $PK_{2,j}$, as will be described under this paragraph. Moreover, the AA also publishes a set of public keys $\{{w_{i,j}}\}_{\forall i \in U_j}$ corresponding to the users in the attribute group. As a result, $AA_{aid_k}$’s secret key and public key can be written as

$$\begin{aligned} SK_{aid_k}= & {} \{g^{n_{aid_k}},\alpha _{aid_k},\beta _{aid_k},\gamma _{aid_k},\delta _{aid_k}\}; \end{aligned}$$

(1)

$$\begin{aligned} PK_{aid_k}= & {} \{ e(g,g)^{\alpha _{aid_k}}; g^{c\delta _{aid_k}}, \{PK_{1,j}; PK_{2,j}, \{{w_{i,j}}\}_{i \in U_j} \}_{j \in S_{aid_k}}\}; \end{aligned}$$

(2)

where

$$\begin{aligned} \begin{aligned} PK_{1,j}&= g^{\frac{\prod \nolimits _{i\in U_j}{v_{i,j}}}{\beta _{aid_k}}}; ~~~~~~ PK_{2,j} = H(att_j)^{\gamma _{aid_k}\delta _{aid_k}\prod \limits _{i\in U_j}{v_{i,j}}}; ~~~~~~{w_{i,j}} =t_{i,j} \textstyle \prod \limits _{k\in U_j,k\ne i} v_{k,j}^{-1}+v_{i,j}. \end{aligned} \end{aligned}$$

3.2 User Registration

The TA registers the users, generates the secret keys for them and update the PKs corresponding to their attributes. For a new user u with an attribute set $S_u$, the enrollment consists of three steps IDGen, KeyGen, and PubKeyUpdate.

3.2.1 IDGen

In our protocol, the central authority does not participate in users’ secret key generation. It only accepts the registration of all users and assigns a certificate associated with the user’s global identity. This certificate proves the user’s legal identity in the system. For example, a user u comes into the system, the CA verifies its identity and assigns a global unique identifier $ID_u$.

3.2.2 KeyGen

We assume that the attributes managed by each AA have no intersection. So we can divide the attributes set of user u to m disjoint subsets and they satisfy $S_{u,aid_1} \cup S_{u,aid_2} \cup \cdots \cup S_{u, aid_{m}} = S_u$. Then user u interacts with each AA for secret key. The user submits its identity $ID_u$ and the corresponding attribute set $S_{aid_k}$ to $AA_{aid_k}$. The attribute authority $AA_{aid_k}$ generates $K_{u, aid_k}$ and $K'_{i,aid_k}$ for legitimate user u.

$$\begin{aligned} K_{u,aid_k}=g^{\alpha _{aid_k}}g^{cID_u}g^{n_{aid_k}ID_u},~~K'_{u,aid_k}=g^{\frac{ID_u}{\delta _{aid_k}}}. \end{aligned}$$

(3)

Then $AA_{aid_k}$ generates the secret keys for each attribute $j \in S_{aid_k} \bigcap S_u$. It chooses two random values $v_{u,j},t_{u,j}\in {\mathbb {Z}}_p$ and computes the secret keys corresponding to the attribute j, i.e., $K_{1,j}, K_{2,j}, K_{3,j}, K_{4,j}$. Then the secret key of user u is computed as given by

$$\begin{aligned} SK=\, & {} \{\{K_{i,aid_k},K'_{i,aid_k}\}_{k\in S_A},~~\{K_{1,j},K_{2,j},K_{3,j},K_{4,j}\}_{j\in S_u}\};\nonumber \\ K_{1,j}=\, & {} H(att_j)^{\beta _{aid_k}(ID_u+\gamma _{aid_k})}; \nonumber \\ K_{2,j}=\, & {} H(att_j)^{\beta _{aid_k}ID_u(\gamma _{aid_k}-v_{u,j})};\nonumber \\ K_{3,j}=\, & {} H(att_j)^{-t_{u,j} v_{u,j}(ID_u+\gamma _{aid_k})};\nonumber \\ K_{4,j}=\, & {} H(att_j)^{\beta _{aid_k}\gamma _{aid_k}v_{u,j}}. \end{aligned}$$

(4)

3.2.3 PubKeyUpdate

As the attribute public keys $\small \{PK_{1,j}; PK_{2,j}, \{{w_{i,j}}\}_{\forall i \in U_j} \}$ depend on the attribute group information, the AAs update them once a new user with attribute j has been registered. For each attribute j that the user u holds, the corresponding AA sets the attribute group ${\widetilde{U}}_j=U_j\cup \{u\}$. Then for $\forall j\in S_{u,aid_k}$, $AA_{aid_k}$ updates $PK_{1,j}$, $PK_{2,j}$ and $\{\overline{v_{i,j}}\}$, and adds $\overline{v_{u,j}}$ to the public parameters.

$$\begin{aligned} {\widetilde{PK}}_{1,j}= & {} PK_{1,j}^{v_{u,j}};~~~~~~{\widetilde{PK}}_{2,j}=PK_{2,j}^{v_{u,j}}; \end{aligned}$$

(5)

$$\begin{aligned} \{\widetilde{{w_{i,j}}}= & {} ({w_{i,j}}-v_{i,j}) v_{u,j}^{-1}+v_{i,j}\}_{\forall i \in U_j};~~~~ {w_{u,j}}=t_{u,j} \textstyle \prod \limits _{k\in U_j,k\ne u} v_{k,j}^{-1}+v_{u,j}. \end{aligned}$$

(6)

3.3 Data Encryption

The LSSS access structure consists of an $L \times N$ matrix, and a function $\rho$ which maps the rows of the matrix to the attributes. $\rho$ may map different rows to the same attribute. First of all, the data owner chooses a random value $s\in {\mathbb {Z}}_p$ and computes C and $C'$ as given by

$$\begin{aligned} C={\mathscr {M}}\cdot \left( \textstyle \prod \limits _{aid_k\in I_{{\mathbf {M}}_A}} e(g,g)^{\alpha _{aid_k}}\right) ^s,~~~ C'=g^s. \end{aligned}$$

(7)

Then the data owner shares the secret s under the matrix ${\mathbf {M}}$ by choosing random values $y_2,\ldots ,y_N$, $r_1,r_2,\ldots ,r_L\in {\mathbb {Z}}_p$, and constructing a vector ${\mathbf {v}}=(s,y_2,\ldots ,y_N)\in {\mathbb {Z}}_p^N$. For $i=1$ to L, the data owner computes $\lambda _i={\mathbf {v}}\cdot {\mathbf {M}}_i$, where ${\mathbf {M}}_i$ represents the ith row of the matrix ${\mathbf {M}}$. For $\forall j\in S_{aid_k}$, the data owner computes $C_i$, $C_i'$, $D_i$, and $AK_i$ as follows.

$$\begin{aligned} \begin{aligned} C_i&= g^{c\delta _{aid_k}\lambda _i}{H(att_j)}^{-r_i\gamma _{aid_k}\delta _{aid_k} \prod \nolimits _{i\in U_j}{v_{i,j}}};\\ C_i'&= PK_{1,j} ^{r_i}=g^{\frac{r_i \prod \nolimits _{i\in U_j}{v_{i,j}}}{\beta _{aid_k}}};\\ D_i&= g^{r_i};\\ AK_i&= g^{c\delta _{aid_k}\lambda _i}. \end{aligned} \end{aligned}$$

The data owner then transmits $CT=\{C,C',(C_1,C_1',D_1, AK_1),\ldots ,(C_L,C_L',D_L, AK_L)\}$ to the public cloud server for storage and $AK = \{AK_i\}$ to the private cloud server for auditing.

Note that the public cloud can be untrustworthy, and try to intercept the ciphertext of the users. It provides storage services for users in the system and would like to learn information of encrypted contents as much as possible. In our protocol, we can ensure that the public cloud cannot retrieve the data from the ciphertext. This is because that the plaintext ${\mathscr {M}}$ is protected by $\small (\prod _{k\in I_A} e(g,g)^{\alpha _{aid_k}})^s$. The cloud is not able to remove the secret value s without the knowledge of required attributes. As will be explained in the security analysis, the encryption yields a q-PBDHE problem and therefore cannot be intercepted by the public cloud.

3.4 Data Decryption

Given the attribute set $I_{{\mathbf {M}}}$ corresponding to the access control structure ${\mathbf {M}}$, i.e., $\hbox {Att}_1$, $\hbox {Att}_2$, $\ldots$, $\hbox {Att}_L$, the user can identify an intersection I between its own attribute set $S_u$ and $S_{{\mathbf {M}}}$, i.e., $I = S_u \cap I_{{\mathbf {M}}}$. User u tries to find a set of coefficients $\{\omega _i\in {\mathbb {Z}}_p\}_{i\in I}$ such that the linear combination of the matrix can form a vertor $\mathbf {v'}=[1, 0, \ldots , 0]$, i.e., $\sum _{i\in I}{\omega _i {\mathbf {M}}_i}=\mathbf {v'}$. We say that user u can decrypt the ciphertext if such a set of $\{\omega _i\in Z_p\}_{i\in I_{\mathbf {M}}}$ exists. This is because $\sum _{i\in I}{\omega _i {\mathbf {M}}_i} = [1, 0, \ldots , 0]$ can be multiplied by ${\mathbf {v}} = [s,y_2,\ldots ,y_n]$ on both sides, and hence proved to be equivalent to $\sum _{i\in I}{\omega _i \lambda _i} = s$. Therefore, the user u decrypts as follows.

$$\begin{aligned} \begin{aligned} \textcircled {{1}}&= \textstyle \prod \limits _{aid_k\in I_{{\mathbf {M}}_A}}{e(C',K_{u,aid_k})} \\&= \textstyle \prod \limits _{aid_k\in I_{{\mathbf {M}}_A}}{e(g^s,g^{\alpha _{aid_k}}g^{cID_u}g^{n_{aid_k}ID_u})}\\&= e(g,g)^{scID_un_A}\cdot \textstyle \prod \limits _{aid_k\in I_{{\mathbf {M}}_A}} e(g^s,g^{\alpha _{aid_k}})\cdot e(g,g)^{sID_u\sum n_{aid_k}}\\&= e(g,g)^{scID_un_A}\cdot \textstyle \prod \limits _{aid_k\in I_{{\mathbf {M}}_A}} e(g^s,g^{\alpha _{aid_k}}); \\ \textcircled {{2}}&= \textstyle \prod \limits _{j \in S_u} \left( \textstyle \frac{e(C_i,\!K'_{u, aid_k})e(C_i',K_{1,j}^{{w_{u,j}}})e(C_i',\!K_{2,j})e(D_i,\!K_{3,j})}{e(C_i',\!K_{4,j})}\right) ^{\omega _i m} \\&= \textstyle \prod \limits _{j \in S_u}e(g,g)^{c\lambda _iu \omega _i m} = e(g,g)^{csum}; \\ \textcircled {{3}}&= \textstyle \frac{\textcircled {{1}} }{\textcircled {{2}}} = \textstyle \frac{e(g,g)^{scID_um}\cdot \prod \limits _{aid_k\in I_{{\mathbf {M}}_A}} e(g^s,g^{\alpha _{aid_k}})}{e(g,g)^{csID_um}} = \prod \limits _{aid_k\in I_{{\mathbf {M}}_A}} e(g^s,g^{\alpha _{aid_k}}). \end{aligned} \end{aligned}$$

At last, the user can recover the plaintext by computing $\mathscr {M} = \frac{C}{\textcircled {{3}}}$.

3.5 Revocation

As an important feature of our proposed scheme, direct revocation mechanism is based on embedding secret information $v_{u,j}$ and $t_{u,j}$ to the public key of the jth attribute, more specifically $PK_{1,j}$ and $PK_{2,j}$. The two items are also used in encryption process to generate $C_i$ and $C_i'$. By combining the public keys and ciphertext, the users who do not in the attribute group can be effectively prevented from access the data. In this case, the revocation can be divided into two steps: the Revoke algorithm and the CTUpdate algorithm.

3.5.1 Revoke

The corresponding AA maintains the information of attributes if revocation takes place. When the jth attribute of user u is revoked in this section, the corresponding AA, for example $AA_{aid_k}$ needs to update the public keys by removing the secret value $v_{u,j}$ from $PK_{1,j}$ and $PK_{2,j}$. The $AA_{aid_k}$ publishes the update key $UK =v_{u,j}^{-1}$ and sets the attribute group ${\widetilde{U}}_j=U_j \setminus \{u\}$. After that, it updates $PK_{1,j}$, $PK_{2,j}$ and $\{{w_{i,j}}\}_{i \in {\widetilde{U}}_j}$ as given by

$$\begin{aligned} {\widetilde{PK}}_{1,j}=\, & {} PK_{1,j}^{UK},~~{\widetilde{PK}}_{2,j}=PK_{2,j}^{UK}; \end{aligned}$$

(8)

$$\begin{aligned} \{\widetilde{{w_{k,j}}}=\, & {} ({w_{k,j}}-v_{k,j}) v_{u,j}+v_{k,j}\}_{\forall i \in U_j}. \end{aligned}$$

(9)

3.5.2 CTUpdate

On the receipt of update key UK from $AA_{aid_k}$, the public cloud removes the corresponding secret value $v_{u,j}$ from ciphertexts. This can be done as given by

$$\begin{aligned} \begin{aligned} \widetilde{C_i}&= (C_i)^{UK}\cdot (AK_i)^{{1-UK}}=g^{m\lambda _i\delta _{aid_k}}{\widetilde{PK}}_{2,j}^{-r_i};\\ \widetilde{C_i'}&= (C_i')^{UK}={\widetilde{PK}}_{1,j}^{r_i}. \end{aligned} \end{aligned}$$

3.6 Auditing

The private cloud in our scheme is proprietary, and is used by its internal legitimate data owners to audit the public cloud. In this stage, it is given only the Auditing Keys (AKs) to examine whether the public cloud has refreshed the ciphertext according to the protocol. The private cloud executes the following auditing algorithm for users in its domain periodically.

• 1. Check $C_i'$: The private cloud checks whether the following equation is satisfied.

  $$\begin{aligned} e(C_i',g)=e({\widetilde{PK}}_{1,j},D_i); \end{aligned}$$

  (10)

  Correctness:

  $$\begin{aligned} Left = e({\widetilde{PK}}_{1,j}^{r_i},g)=e({\widetilde{PK}}_{1,j},g^{r_i}) = Right; \end{aligned}$$

  (11)

• 2. Check $C_i$: If $C_i'$ is verified in Step 1, we can use the newest $C_i'$ to check $C_i$.

  $$\begin{aligned} e(AK_i,{\widetilde{PK}}_{1,j})=e(\widetilde{C_i'},{\widetilde{PK}}_{2,j}) \cdot e(C_i,{\widetilde{PK}}_{1,j}); \end{aligned}$$

  (12)

  Correctness:

  $$\begin{aligned} \begin{aligned} Left&= e(g^{c\delta _{aid_k}\lambda _i},{\widetilde{PK}}_{1,j}); \\ Right&= e\left( {\widetilde{PK}}_{1,j}^{r_i},H(att_j)^{\gamma _{aid_k}\delta _{aid_k}\prod \limits _{i\in U_j}{v_{i,j}}}\right) \cdot e\left( g^{c\delta _{aid_k}\lambda _i}{H(att_j)}^{-r_i\gamma _{aid_k}\delta _{aid_k} \prod \limits _{i\in U_j}{v_{i,j}}},{\widetilde{PK}}_{1,j}\right) \\&=e\left( {\widetilde{PK}}_{1,j}^{r_i},H(att_j)^{\gamma _{aid_k}\delta _{aid_k}\prod \limits _{i\in U_j}{v_{i,j}}}\right) \cdot e(g^{c\delta _{aid_k}\lambda _i}, {\widetilde{PK}}_{1,j}) \cdot e({H(att_j)}^{-r_i\gamma _{aid_k}\delta _{aid_k} \prod \limits _{i\in U_j}{v_{i,j}}} ,{\widetilde{PK}}_{1,j})\\&= e(g^{c\delta _{aid_k}\lambda _i},{\widetilde{PK}}_{1,j}) . \end{aligned} \end{aligned}$$

If both (10) and (12) are successfully verified, the private cloud returns “1” to the data owner. Otherwise, returns “0” which means that the ciphertexts have yet to be updated. An improvement is that DO can transmit the AKs to the private cloud once CT is uploaded. Then the private cloud can check the ciphertext periodically, but only return feedback to DO when anomaly is detected.

4 Security Proof

We adopte the standard q-PBDHE assumption as the underlying hard problem of our proposed scheme. We simulate the proposed scheme by using the parameters of the assumption, and prove our scheme is selective-CPA secure.

4.1 Proof

We use the main idea of proving the standard CP-ABE scheme secure for reference [21]. Firstly, we define a simulator ${\mathscr {T}}$ to simulate the behavior of the CA and AAs in Sect. 3, and an attacker ${\mathscr {A}}$, which aims at breaking our protocol. The ${\mathscr {A}}$’s ability is defined as follow:

• It can observe the outside network, including the system public keys, encrypted ciphertext and the update keys.

• It can combine with several users, i.e, it may know some users’ secret keys.

• It may capture the update keys during the transmission from attribute authorities to public cloud server. So we give ${\mathscr {A}}$ the ability to ask for the update keys if revocation happens.

The interaction between the attacker ${\mathscr {A}}$ and the simulator ${\mathscr {T}}$ can be skillfully simulated as the stages below. If the ${\mathscr {A}}$ can obtain the original information, then the ${\mathscr {T}}$ can solve the defined q-PBDHE hard problem. However, as the q-PBDHE assumption is recognized as difficult, we can indirectly state that our CP-ABE scheme is secure by contradiction.

Assume that the attacker chooses a challenge access structure $({\mathbf {M}}^*,\rho ^*)$, where ${\mathbf {M}}^*$ is an matrix with $L^*$ rows and $N^*$ columns and $L^*,N^*\leqslant q-1$. We will build a ${\mathscr {T}}$ that embedds the Decisional q-parallel Bilinear Diffie-Hellman Exponent problem into the system parameters.

4.1.1 CASetup and AASetup Simulation

The simulator $\mathscr {T}$ takes in a q-parallel BDHE challenge ${\mathbf {y}}$ as given in Sect. 2.3. Then the adversary ${\mathscr {A}}$ gives the challenge access structure (${\mathbf {M}}^*,\rho ^*$) to ${\mathscr {T}}$.

Here, the ${\mathscr {T}}$ simulates the CASetup and AASetup algorithms to initialize the public parameters. It sets $m=a$ by letting $g^m=g^a$, and $\delta _{aid_k}=\frac{\delta '_{aid_k}}{a}$ by $g^{m\delta _{aid_k}}=g^{\delta '_{aid_k}}$ with random $\delta '_{aid_k}\in Z_p$. It randomly picks $n_{aid_k}$ for each authority such that $\sum \nolimits _{k\in S_A}{n_{aid_k}}=0$. The simulator also chooses $\alpha _{aid_k}'\in Z_p$, and implicitly sets $\alpha _{aid_k}=\alpha _{aid_k}'+a^{q+1}$ by letting $e(g,g)^{\alpha _{aid_k}}=e(g^a,g^{a^q})e(g,g)^{\alpha _{aid_k}'}$. The parameters $v_{i,j}$ and $t_{i,j}$ are randomly chosen like the scheme above.

Then we describe how the ${\mathscr {T}}$ “programs” the elements $H(att_j)$, $PK_{1,j}$, $PK_{2,j}$ and other public parameters. Let $X_j$ denotes the set of indices for all i in the access structure $({\mathbf {M}}^*,\rho ^*)$ such that $\rho ^*(i)=\rho ^*(j)$, which means that i maps to the same attribute as j according to $\rho$. Let $\overline{X_j}$ denotes $X_j/j$. For each attribute $x=\rho ^*(j)$, the simulator ${\mathscr {T}}$ chooses $z_x \in {\mathbb {Z}}_p$ and sets

$$\begin{aligned} H(att_j)=g^{az_j} \textstyle \prod \limits _{i\in X_j}{g^\frac{a^2{\mathbf {M}}^*_{i,1}}{b_i}}{g^\frac{a^3{\mathbf {M}}^*_{i,2}}{b_i}}\cdots {g^\frac{a^{N^*+1}{\mathbf {M}}^*_{i,N^*}}{b_i}}. \end{aligned}$$

(13)

Then the ${\mathscr {T}}$ randomly chooses $\beta _{aid_k}$ and $\gamma _{aid_k} \in Z_p$. And computes

$$\begin{aligned} \begin{aligned} PK_{1,j}&= g^{\frac{\prod \nolimits _{i\in U_j} v_{i,j}}{\beta _{aid_k}}}; \\ PK_{2,j}&= H(att_j)^{\gamma _{aid_k}\delta _{aid_k}\prod \nolimits _{i\in U_j}{v_{i,j}}};\\&= \left( \textstyle \prod \limits _{i\in X_i}{g^\frac{a{\mathbf {M}}^*_{i,1}}{b_i}}{g^\frac{a^2{\mathbf {M}}^*_{i,2}}{b_i}}\cdots {g^\frac{a^{N^*}{\mathbf {M}}^*_{i,N^*}}{b_i}}\right) ^{\gamma _{aid_k}\delta '_{aid_k}\prod \limits _{i\in U_j} v_{i,j}} \cdot g^{z_j\gamma _{aid_k}\delta '_{aid_k}\prod \limits _{i\in U_j} v_{i,j}}. \end{aligned} \end{aligned}$$

The other parameters are computed like the scheme described in Sect. 3. Then the simulator sends the public parameters: $\{g^m=g^a$; $e(g,g)^{\alpha _{aid_k}}$; $\{PK_{1,j}; PK_{2,j}\}_{j\in S_{aid_k}}$; $\{{w_{i,j}}\}\}$ to ${\mathscr {A}}$.

4.1.2 KeyGen Simulation

In this phase, the ${\mathscr {T}}$ answers private key queries. Suppose that the adversary asks for the private key of user u with an attribute set $S_u$. If $S_u$ does not satisfy ${\mathbf {M}}^*$, then the ${\mathscr {T}}$ generates secret keys for it. Note that, the adversary can repeat this process as long as the submitted attribute set does not satisfy the challenge access structure (${\mathbf {M}}^*, \rho ^*$). For each secret key query, the ${\mathscr {T}}$ chooses a random number $r\in {\mathbb {Z}}_p^*$, and implicitly defines $u=r-\frac{a^{q+1}}{m+n_{aid_k}}$ by computing

$$\begin{aligned} \begin{aligned} K_{i,aid_k}&= g^{\alpha _{aid_k}'}\cdot g^{a^{q+1}}\cdot g^{(m+n_{aid_k})\left( r-\frac{a^{q+1}}{m+n_{aid_k}}\right) }\\&= g^{\alpha _{aid_k}'}\cdot g^{mr}\cdot g^{n_{aid_k}r}; \\ K'_{i,aid_k}&= g^\frac{u}{\delta _{aid_k}}=g^{\frac{a}{\delta _{aid_k}'}\left( r-\frac{a^{q+1}}{m+n_{aid_k}}\right) } \\&= g^{\frac{ar}{\delta _{aid_k}'}}g^\frac{a^{q+2}}{\delta _{aid_k}'(m+n_{aid_k})}. \end{aligned} \end{aligned}$$

And then for each attribute $\forall att_j \in {S_{u,aid_k}}$, the simulator chooses $v_{i,j},t_{i,j}\in {\mathbb {Z}}_p$ and computes the secret keys as given by

$$\begin{aligned} \begin{aligned} K_{1,j}&= H(att_j)^{\beta _{aid_k}\left( r- \frac{a^{q+1}}{m+n_{aid_k}}+\gamma _{aid_k}\right) } \\&= \left( g^{az_x} \textstyle \prod \limits _{i \in X_j}{g^\frac{a^2{\mathbf {M}}^*_{i,1}}{b_i}}{g^\frac{a^3{\mathbf {M}}^*_{i,2}}{b_i}}\cdots {g^\frac{a^{{N}^*+1}{\mathbf {M}}^*_{i,N^*}}{b_i}}\right) ^{\beta _{aid_k}(\gamma _{aid_k}+r)} \cdot \left( \textstyle \prod \limits _{i\in X_j}{g^\frac{a^{q+3}{\mathbf {M}}^*_{i,1}}{b_i}}{g^\frac{a^{q+4}{\mathbf {M}}^*_{i,2}}{b_i}}\cdots {g^\frac{a^{q+N^*+2}{\mathbf {M}}^*_{i,N^*}}{b_i}}\right) ^{-\frac{\beta _{aid_k}}{m+n_{aid_k}}} \\&~~~~\cdot (g^{a^{q+2}})^{-\frac{z_x\beta _{aid_k}}{m+n_{aid_k}}}; \\ K_{2,j}&= H(att_j)^{\left( r-\frac{a^{q+1}}{m+n_{aid_k}}\right) \beta _{aid_k}(\gamma _{aid_k}-v_{i,j})}\\&= \left( \textstyle \prod \limits _{i\in X_j}{g^\frac{a^2{\mathbf {M}}^*_{i,1}}{b_i}}{g^\frac{a^3{\mathbf {M}}^*_{i,2}}{b_i}}\cdots {g^\frac{a^{{N}^*+1}{\mathbf {M}}^*_{i,n^*}}{b_i}}\right) ^{r\beta _{aid_k}(\gamma _{aid_k}-v_{i,j})} \cdot g^{-\frac{a^{q+2}z_x\beta _{aid_k}(\gamma _{aid_k}-v_{i,j})}{m+n_{aid_k}}} \cdot g^{az_xr\beta _{aid_k}(\gamma _{aid_k}-v_{i,j})} \\&~~~~\cdot \left( \textstyle \prod \limits _{i\in X_j}{g^\frac{a^{q+3}{\mathbf {M}}^*_{i,1}}{b_i}}{g^\frac{a^{q+4}{\mathbf {M}}^*_{i,2}}{b_i}} \cdots {g^\frac{a^{q+N^*+2}{\mathbf {M}}^*_{i,n^*}}{b_i}}\right) ^{-\frac{\beta _{aid_k}(\gamma _{aid_k}-v_{i,j})}{m+n_{aid_k}}} ;\\ K_{3,j}&= H(att_j)^{-t_{i,j}v_{i,j}\left( r-\frac{a^{q+1}}{m+n_{aid_k}}+\gamma _{aid_k}\right) } \\&= \left( \textstyle \prod \limits _{i\in X_j}{g^\frac{a^2{\mathbf {M}}^*_{i,1}}{b_i}}{g^\frac{a^3{\mathbf {M}}^*_{i,2}}{b_i}}\cdots {g^\frac{a^{{N}^*+1}{\mathbf {M}}^*_{i,n^*}}{b_i}}\right) ^{-t_{i,j}v_{i,j}(r+\gamma _{aid_k})} \cdot \left( \textstyle \prod \limits _{i\in X_j}{g^\frac{a^{q+3}{\mathbf {M}}^*_{i,1}}{b_i}}{g^\frac{a^{q+4}{\mathbf {M}}^*_{i,2}}{b_i}}\cdots {g^\frac{a^{q+N^*+2}{\mathbf {M}}^*_{i,N^*}}{b_i}}\right) ^{\frac{t_{i,j}v_{i,j}}{m+n_{aid_k}}} \\&~~~~ \cdot g^{\frac{a^{q+2}z_xt_{i,j}v_{i,j}}{m+n_{aid_k}}} \cdot g^{-az_xt_{i,j}v_{i,j}(r+\gamma _{aid_k})} ; \\ K_{4,j}&= H(att_j)^{\beta _{aid_k}\gamma _{aid_k}v_{i,j}}=\left( g^{az_x}\textstyle \prod \limits _{i\in X_j}{g^\frac{a^2{\mathbf {M}}^*_{i,1}}{b_i}}{g^\frac{a^3{\mathbf {M}}^*_{i,2}}{b_i}}\cdots {g^\frac{a^{N^*+1}{\mathbf {M}}^*_{i,N^*}}{b_i}}\right) ^{\beta _{aid_k}\gamma _{aid_k}v_{i,j}}. \\ \end{aligned} \end{aligned}$$

4.1.3 Encryption Simulation

Finally, we build the challenge ciphertext. The ${\mathscr {A}}$ submits two messages $m_0$, $m_1$ to the simulator. Then the simulator flips a coin, chooses a random $s\in {\mathbb {Z}}_p^*$ and computes C and $C'$ as follows.

$$\begin{aligned} C=m_b\cdot \textstyle \prod \limits _{aid_k\in I_A} e(g^s,g^{\alpha _{aid_k}'})\cdot T^{n_A}, ~~~~~~C'=g^s; \end{aligned}$$

(14)

And for each attribute in the predefined LSSS matrix ${\mathbf {M}}^*$, the ${\mathscr {T}}$ chooses random $r_1,\ldots ,r_L, y_2',\ldots ,y_{N^*}' \in {\mathbb {Z}}_p$. It implicitly shares the secret s using the vector $\overrightarrow{v}=(s,a+y_2',a^2+y_3',\ldots ,a^{N^*-1}+y_{N^*}')\in {\mathbb {Z}}_p^{N^*}$ and computes $\lambda _i={\mathbf {M}}^*_i\overrightarrow{v_i}={\mathbf {M}}^*_{i,1}s+{\mathbf {M}}^*_{i,2}(a+y_2')+\cdots +{\mathbf {M}}^*_{i,N^*}(a^{N^*-1}+y_{N^*}')$ by simulating the ciphertext $C_i$, $C_i'$, $D_i$$AK_i$ as follows.

$$\begin{aligned} \begin{aligned} C_i&= g^{m\lambda _i\delta _{aid_k}}V_j^{-r_i\gamma _{aid_k}\delta _{aid_k}} \\&= g^{\delta '_{aid_k}({\mathbf {M}}^*_{i,1}s+{\mathbf {M}}^*_{i,2}(a+y_2')+\cdots +{\mathbf {M}}^*_{i,N^*}(a^{N^*-1}+y_{N^*}'))} \cdot \left( \textstyle \prod \limits _{i\in X_j}{g^\frac{a{\mathbf {M}}^*_{i,1}}{b_i}}{g^\frac{a^2{\mathbf {M}}^*_{i,2}}{b_i}}\cdots {g^\frac{a^{N^*}{\mathbf {M}}^*_{i,N^*}}{b_i}}\right) ^{-r_i\gamma _{aid_k}\delta '_{aid_k}\prod \limits _{i\in U_j} v_{i,j}} \\&~~~~ \cdot g^{-z_xr_i\gamma _{aid_k}\delta '_{aid_k}\prod \nolimits _{i\in U_j} v_{i,j}} \\ C_i'&= V_j'^{\frac{r_i}{\beta _{aid_k}}}=g^{\frac{r_i{\prod \nolimits _{i\in U_j} v_{i,j}}}{\beta _{aid_k}}}\\ D_i&= g^{r_i} \\ AK_i&= g^{m\lambda _i\delta _{aid_k}}=g^{\delta '_{aid_k}({\mathbf {M}}^*_{i,1}s+{\mathbf {M}}^*_{i,2}(a+y_2')+\cdots +{\mathbf {M}}^*_{i,n^*}(a^{N^*-1}+y_{N^*}'))}. \end{aligned} \end{aligned}$$

4.1.4 Guess

The adversary ${\mathscr {A}}$ will eventually output a guess $b'$ of b. If $b'=b$, then the ${\mathscr {T}}$ outputs 0 to guess that $T=e(g,g)^{a^{q+1}s}$; otherwise, it outputs 1 to indicate that it believes T is a random element in ${\mathbb {G}}_T$. So if the attacker can break our scheme, the simulator can solve the q-PBDHE successfully.

5 Performance Analysis

In this section, we analyze the performance of our proposed scheme by comparing with several multi-authority CP-ABE schemes due to [9, 12, 22, 23]. The comparisons in terms of access policy, revocation mechanism and computation efficiency are summarized in the Table 2 below. We can obtain from the table that [12, 22] and our proposed scheme are designed under LSSS access structure, while [23] is based on (t, n) threshold tree and [9] only supports AND gates access control. In addition, we also compare with Li’s algorithm [9] and Yang’s algorithm [12] from revocation mechanism, and the computation and communication overhead triggered by revocation.

Table 2 Comparison of several multi-authority CP-ABE schemes

Fig. 3

Performance comparison

The communication cost of CP-ABE schemes are almost the same, except the revocation stage. Note that, the revocation mode influences the communication cost of users directly. Here in, we compare the communication overhead in the revocation stage in the sixth column of Table 2. We can obtain that in [9, 12], the remaining users have to communicate with authority frequently to update secret keys. So their communication cost has a linear relationship with the number of users with the revoked attribute.

The computation overhead of attribute revocations can be simulated by exponentiation and multiplication operation in groups. We implement the operations by using the Pairing-Based Cryptography library version 0.5.14, and a ubuntu 14.4 system with an Intel Core i7-5500 at a frequency of 3.0GHz and 8GB memory. The results of each scheme are presented in Fig. 3. And all our benchmarks are the average of 20 repetitions.

The horizontal axis of Fig. 3a represents the number of users with the revoked attributes in the system, and the vertical axis is the simulation results of the average execution time of revocation. As shown in the figure, our revocation overhead is consistent, while both the algorithms developed in [9, 12] exhibit growths proportional to the increasing number of users. When the number of users is more than 10, our scheme is shown to be superior to the others in terms of efficiency.

Note that the proposed approach does not explicitly optimize the encryption method itself. But it does improve the way on how the encryption method is run. Specifically, we design multiple attribute authorities to generate secrecy keys for different attributes in parallel (as opposed to a single authority, as typically considered in the literature). By taking the advantage of parallel computing, we are able to substantially reduce the time of encryption. We implement [12], which has the same functions as our proposed scheme in terms of multi-authority and LSSS access structure, and our scheme with the same configuration described above. In addition, we use the elliptic curve “MNT224”, where the base size is 224-bit and the embedding degree is 6. The implementation of our scheme and [12] is in the Python 3.5.2 environment. The number of attributes managed by each authority is set to be 10. Figure 3b, c show the encryption and decryption time over the number of attribute authorities.

In Fig. 3b, the horizontal axis represents the number of authorities involved in the access policy and vertical is the average encryption time. With the increase of the total number of attributes, both [12] and our scheme show an overall upward trend. Especially to deserve to be mentioned, our encryption time is shorter than [12] when the number of authorities is more than 4, and the growth rate of ours is relatively slower. Figure 3c presents the decryption time of the two schemes changing with the number of authorities. From the graphs, we may safely draw the conclusion, although the decryption time of both the two schemes increase with the number of authorities, our scheme shows obvious advantages over [12].

6 Discussion and Further Plan

In this paper, the design of multiple authorities can reduce the communication overhead of the central authority. The private cloud severs enable the update of ciphertext stored on untrustworthy public cloud. This enables the implementation of dynamic attribute revocation. Although the communication and computational overhead of each authority is reduced, the total time for secret key generation can still be further improved. This will be solved by our future work.

7 Conclusion

In this paper, we constructed a multi-authority CP-ABE scheme supporting direct attribute revocation, and proved it secure in selective-CPA model under the q-PBDHE assumption. We designed an auditing algorithm for the private cloud to periodically check the ciphertext for data owners. In addition, by comparing with other revocable CP-ABE schemes, the revocation mechanism of our proposed scheme can largely reduce the system communication overhead triggered by revocation. We also compared the encryption and decryption time with another multi-authority CP-ABE scheme, and the performance results showed that our scheme has an advantage over it.