Nonlinear process monitoring based on new reduced Rank-KPCA method

Abstract

Kernel Principal Component Analysis (KPCA) is an efficient multivariate statistical technique used for nonlinear process monitoring. Nevertheless, the conventional KPCA suffers high computational complexity in dealing with large samples. In this paper, a new kernel method based on a novel reduced Rank-KPCA is developed to make up for the drawbacks of KPCA. The basic idea of the proposed novel approach consists at first to construct a reduced Rank-KPCA model that describes properly the system behavior in normal operating conditions from a large amount of training data and after that to monitor the system on-line. The principle of the proposed Reduced Rank-KPCA is to eliminate the dependencies of variables in the feature space and to retain a reduced data from the original one. The proposed monitoring method is applied to fault detection in a numerical example, Continuous Stirred Tank Reactor and air quality-monitoring network AIRLOR and is compared with conventional KPCA and Moving Window KPCA methods.

1 Introduction

The modern manufacturing industries require higher product quality and safety operations. In order to ensure the suitable functioning system and to minimize downtime in case of failure, it is important to detect process faults as early as possible (Baklouti et al. 2016). Several process monitoring-based Multivariate Statistical Process (MSP) methods were developed thanks to their efficiencies and simplicities (Botre et al. 2016; Mansouri et al. 2016). In fact, these methods are based on the analysis of process history data in order to model the relationships between variables (Chetouani 2008). Principal Components Analysis (PCA) (Tharrault et al. 2008; Jaffel et al. 2014) and Partial Least Squares (PLS) (Li et al. 2010; Taouali et al. 2015) are the two commonly used methods in the field of process fault detection and diagnosis. More recently Independent Component (ICA) (Lee et al. 2004a, b; Zhao et al. 2008) have been proposed for this purpose.

The PCA method (Harkat et al. 2006) is a statistical method widely used of analysis and dimensional reduction. It is used to identify the dependency structure between the observations in order to transform the input space into a smaller dimensional space while retaining the maximum variance of the input data. The PCA technique produces new uncorrelated variables called principal components (PC) with each component is linear combinations of original variables. However, the majority of chemical and biological processes data have nonlinear relationships. In fact, PCA only defines a linear projection of data. Hence, it is incapable to analyze and represent the data with nonlinear characteristics. This limitation and nonlinearity problem have motivated various researchers to develop nonlinear extensions, such as nonlinear PCA that combined principal curve and Neural Network (NN) (Harkat et al. 2010; Dong and McAvoy 1996) and Kernel Principal Components Analysis (KPCA) that define a nonlinear generalization of the conventional linear PCA (Schölkopf et al. 1998; Mika et al. 1998).

The KPCA method is a simple and interesting technique developed by Schölkopf to faithfully model the nonlinear relationships between process data. Using the concept of kernel tricks (Aronszajn 1950; Aizerman et al. 1964), KPCA can efficiently project the input data with linearly inseparable structure onto a higher dimensional feature space in which the data becomes linearly separable and then perform the conventional PCA in the feature space. KPCA requires only solving an eigenvalue problem without any nonlinear optimization compared to other nonlinear PCA techniques based on NN. Moreover, KPCA was applied in several applications and showed a good results in terms of analysis, modeling and fault detection accuracies: face recognition (Kim et al. 2002) speech recognition (Amaro et al. 2005) nonlinear process monitoring and fault diagnosis (Lee et al. 2004a, b; Fazai et al. 2016; Cho et al. 2005; Kazor et al. 2016; Sheriff et al. 2017).

However, it suffers from two major drawbacks. Firstly, the KPCA is not a sparse model (the computation time of projections in feature space and memory increase with the number of training data). Secondly, the conventional KPCA relies on a time invariant model thus not adapted for monitoring time-varying industrial processes. To overcome these disadvantages, in this paper we proposed a novel method to reduce the order of KPCA model and to guarantee a good fault detection.

This article is organized as follows. In Sect. 2, a brief presentation KPCA and its fault detection index. Section 3 presents the new proposed approach called Reduced Rank-KPCA and its principle. In Sect. 4, we develop two online algorithms for dealing with fault detection of nonlinear dynamic process. Section 5 demonstrates the efficiency of the proposed method compared to classical methods through three examples. Conclusions are given at the end of the paper.

2 Previews work

2.1 Review of kernel principal component analysis (KPCA) description

Kernel Principal Component Analysis (KPCA) is among the most popular dimensional reduction and analysis method (Li and Zhang 2013). It extends the linear PCA to deal with nonlinear modes. The main objective of Kernel PCA is to model process data with non-linear structure. It consists to transform the nonlinear part of input data space $E$ into a linear part in a new high dimensional feature space denoted $H$ and to perform PCA in that space. The feature space $H$ is nonlinearly transformed from the input space $E$ with a non-linear mapping function $\phi$. The mapping of sample $x \in \,E\,$ in the feature space $H$ can be written as:

$$\begin{aligned} \phi :E \subset & \,{\mathbb{R}}^{m} \to \,H \subset \,{\mathbb{R}}^{H} \\ \, & \,x\, \to \,\phi (x) \\ \end{aligned}$$

(1)

Let us consider $X = \left[ {x_{1} , \ldots ,x_{i} , \ldots ,x_{N} } \right]^{T}$ the training data matrix scaled to zero mean and unit variance. Where $x_{i} \in \,E\, \subset \,{\mathbb{R}}^{m}$ is a data vector, $N$ is the number of observation samples and $m$ is the number of process variables.

The monitoring phase based on linear PCA approach requires the selection of principal components that maximize the variance in the data set. This is done by the Eigen-decomposition of the covariance matrix. Similarly, this approach was generalized in Kernel PCA approach by scholkopf (Schölkopf et al. 1998). The covariance matrix $C_{\varPhi }$ in the feature space $H$ is given by:

$$C_{\varPhi } \, = \,\frac{1}{N}\,\sum\limits_{i = 1}^{N} {\,\phi (x_{i} )\,\phi (x_{i} )^{T} \,}$$

(2)

Let $\chi = \left[ {\phi (x_{1} ) \ldots \phi (x_{i} ) \ldots \phi (x_{N} )} \right]^{T} \in \,{\mathbb{R}}^{N \times h}$ define the data matrix in the feature space $H$, then $C_{\varPhi }$ can be expressed as:

$$C_{\varPhi } \, = \,\frac{1}{N}\chi^{T} \,\chi$$

(3)

The principal components of the mapped data $\phi (x_{1} ) \ldots \phi (x_{i} ) \ldots \phi (x_{N} )$ are computed by solving the eigenvalue decomposition of $C_{\varPhi }$ such that:

$$\lambda_{j\,} \mu_{j} \, = \,\,C_{\varPhi } \,\mu_{j} \quad \;{\text{with}}\quad j = \,1, \ldots ,\,h$$

(4)

with $\mu_{j}$ is $j$ th eigenvector and $\lambda_{j\,}$ is the associated $j$ th eigenvalue. For $\lambda_{j\,} \ne \,\,0$ there exist coefficients $\alpha_{i,j} ;\,\,i = 1 \ldots {\text{N}}$ such all eigenvectors $\mu_{j}$ can be considered as a linear combination of $\left[ {\phi (x_{1} ) \, \phi (x_{2} ) \ldots \phi (x_{N} )} \right]$ and can be expressed by:

$$\mu_{j} \, = \,\,\sum\limits_{i = 1}^{N} {\alpha_{i,j} \,\phi (x_{i} )\,}$$

(5)

However, in practice, the mapping function $\phi$ is not defined and then the covariance matrix $C_{\varPhi }$ in the feature space cannot be calculated implicitly. Thus, instead of solving eigenvalue problem directly on $C_{\varPhi }$, we apply the kernel trick used firstly for Support Vector Machine (SVM) (Vapnik 1999). The inner product given in Eq. (2) may be calculated by a kernel function ${\mathbf{k(}}\,{\mathbf{.}}\,{\mathbf{ , }}{\mathbf{. )}}$ that satisfy Mercer’s theorem (Mercer 1909) as follow:

$$\left\langle {\phi (x),\phi (x^{\prime})} \right\rangle_{H} \,\, = \,\,{\mathbf{k}}(x,x^{\prime})\quad \;\forall \,\,x,\,\,x^{\prime}\,\, \in \,\,{\mathbb{R}}^{m}$$

(6)

Let define a kernel matrix $K$ associated to a kernel function ${\mathbf{k}}$ as:

$$K\,\, = \,\,\chi \chi^{T} \, = \,\,\left[ {\begin{array}{*{20}c} {{\mathbf{k}}(x_{1} ,x_{1} )} & \cdots & {{\mathbf{k}}(x_{1} ,x_{N} )} \\ \vdots & \ddots & \vdots \\ {{\mathbf{k}}(x_{N} ,x_{1} )} & \cdots & {{\mathbf{k}}(x_{N} ,x_{N} )} \\ \end{array} } \right] \in {\mathbf{\mathbb{R}}}^{N \times N}$$

(7)

Applying the kernel matrix may reduce the problem of eigenvalue decomposition of $C_{\varPhi }$. Hence, Eigen-decomposition of the kernel matrix $K$ is equivalent to performing PCA in $\,{\mathbb{R}}^{H}$, so that:

$$N\varLambda V = KV$$

(8)

With: $\varLambda$ is the diagonal matrix of eigenvalues $\lambda_{j}$ arranged in descending order.

$$\varLambda = diag(\lambda_{1} \ldots \lambda_{j} \ldots \lambda_{N} )$$

(8.a)

And $V$ is the matrix of their corresponding eigenvectors.

$$V = \left[ {\alpha_{1} \ldots \alpha_{j} \ldots \alpha_{N} } \right]$$

(8.b)

Since the principal components are orthonormal, it is required to guarantee the normality of $\mu_{j}$in Eq. (4), such that:

$$\left\langle {\mu_{j} ,\mu_{j} } \right\rangle_{H} = 1;\quad {\text{j}}\, = \,1 \ldots n$$

(9)

With $n$ the number of the first non-zero Eigen-values.

Using Eqs. (5) and (9) leads to:

$$\begin{aligned} \left\langle {\mu_{j} ,\mu_{j} } \right\rangle_{H} \, & = \sum\limits_{i,k}^{N} {\alpha_{i,j} \alpha_{k,j} \left\langle {\phi (x_{i} ),\phi (x_{k} )} \right\rangle_{H} } \\ & = \sum\limits_{i,k}^{N} {\alpha_{i,j} \alpha_{k,j} K_{i,k} } \\ & = \left\langle {\alpha_{j} ,K\alpha_{j} } \right\rangle_{H} \\ & = \lambda_{j} \left\langle {\alpha_{j} ,\alpha_{j} } \right\rangle_{H} \\ \end{aligned}$$

(10)

where:$K_{i,k} = \,{\mathbf{k}}(x_{i} ,x_{k} )$. The corresponding eigenvectors $\alpha_{j}$ must be scaled as:

$$\left\langle {\alpha_{j} ,\alpha_{j} } \right\rangle_{H} = \left\| {\alpha_{j} } \right\|^{2} = \frac{1}{{\lambda_{j} }}\quad \quad {\text{j}} = 1 ,\ldots ,n$$

(11)

Many kernel functions have been proposed in literature i.e.:

• Laplacian kernel:

  $${\mathbf{k}}(x_{i} ,x_{j} )\, = \,\exp \left( { - \frac{{\left\| {x_{i} - x_{j} } \right\|}}{\sigma }} \right)$$

  (12)

• Gaussian kernel [Radial Basis Function (RBF)]:

  $${\mathbf{k}}(x_{i} ,x_{j} )\, = \,\exp \left( { - \frac{{\left\| {x_{i} - x_{j} } \right\|^{2} }}{{2\sigma^{2} }}} \right)$$

  (13)

• Polynomial function:

  $${\mathbf{k}}(x_{i} ,x_{j} ) = \left( { < x_{i} ,x_{j} > + 1} \right)^{d}$$

  (14)

where $d$ is a positive integer.

• Sigmoid function

  $${\mathbf{k}}(x_{i} ,x_{j} ) = \tanh \left( {\beta_{0} \left( { < x_{i} ,x_{j} > } \right) + \beta_{1} } \right)$$

  (15)

  where $\beta_{0}$ and $\beta_{1}$ are fixed by the user to satisfy Mercer’s theorem.

Finally, in Eq. (2) we have implicitly assumed that $\sum\nolimits_{i = 1}^{N} {\phi (x_{i} )} = 0$. Generally, this is not the case, this leads to the normalization of the kernel matrix, where we replacing $K$ by the Gram matrix $G$ as follows:

$$G = K - 1_{N} K - K1_{N} + 1_{N} K1_{N}$$

(16)

with:$1_{N} = \frac{1}{N}\left( {\begin{array}{*{20}c} 1 & \ldots & 1 \\ \vdots & \ddots & \vdots \\ 1 & \cdots & 1 \\ \end{array} } \right) \in {\mathbb{R}}^{N \times N}.$

2.2 Number of principal components

Determining the number of retained principal components ($\ell$) is the important step of modeling based on KPCA. The cumulative percent variance (CPV) has been proposed to compute the retain PC ($\ell$) (Zhang et al. 2012) and (Jaffel et al. 2016a, b). The cumulative percent variance (CPV) is the sum of the first $\ell$ eigenvalues divided by their total variations. It can be expressed as:

$$CPV(\ell ) = \frac{{\sum\nolimits_{j = 1}^{\ell } {\lambda_{j} } }}{{\sum\nolimits_{j = 1}^{m} {\lambda_{j} } }}100\%$$

(17)

The number $\ell$ of retained PCs is chosen if the CPV is higher to 95%.

2.3 Fault detection

Like in PCA approach, the squared prediction error (SPE) is usually used for fault detection using KPCA (Nomikos and MacGregor 1995; Lahdhiri et al. 2017). However, the conventional KPCA does not provide any approach of data reconstruction in the feature space. Thus, the computation SPE index is difficult in the KPCA method. (Lee et al. 2004a, b; Choi et al. 2005) proposed a simple expression to calculate SPE in the feature space H, which is shown as follows:

$$SPE\,\, = \,\,\left\| {\,{\mathbf{k}}(x,x) - k_{{x_{t} }}^{T} \,\hat{P}\,\hat{\varLambda }^{ - 1} \,\hat{P}^{T} \,k_{{x_{t} }} \,} \right\|$$

(18)

where, $\hat{P}\,\, = \,\,\left[ {\alpha_{1} , \ldots ,\alpha_{\ell } } \right]$ is the matrix of the first $\ell$ principal eigenvectors of $K$,$\hat{\varLambda }\, = \,diag\left[ {\lambda_{1} , \ldots \,,\,\lambda_{\ell } } \right]$ is the diagonal matrix of the first $\ell$ eigenvalues of $K$ and ${\text{k}}_{{x_{t} }} \, = \left[ {{\mathbf{k}}(x_{1} ,x_{t} ), \ldots ,{\mathbf{k}}(x_{N} ,x_{i} ), \ldots ,{\mathbf{k}}(x_{N} ,x_{t} )} \right]^{T} ;\,\,i = 1 \ldots N$.

The confidence limit for SPE index can be calculated using the $\chi^{2}$-distribution and is given by:

$$SPE_{\lim } \, \approx \,\delta_{\alpha }^{2}$$

(19)

where $\delta_{\alpha }^{2}$ is the control limit expressed by:

$$\delta_{\alpha }^{2} = g\chi_{h,\alpha }^{2}$$

(20)

with: $g = \frac{b}{2a}$ and $h = \frac{{2a^{2} }}{b}$, where $a$ is the estimated mean and $b$ is the variance of the SPE.

3 The proposed reduced Rank-KPCA approach

3.1 Principle

For fault detection based on conventional KPCA approach, we would like to identify the best KPCA monitoring model. For a given test observation $x_{t} \in \,{\mathbb{R}}^{m}$, the calculation of its projections in the feature space requires computation of kernel vector $\,k_{{x_{t} }}$ in respect of all $\,N$ training data. Therefore, the amount of training data tends to be large, which leads to computational complexity of the KPCA model. Considering this, the choice of reduced training data can be made randomly, but this does not insure that the reduced data will represent an optimal model of the system behavior. Recently, several solutions have been developed to solve this problem and to search a reduced data set that represent adequately the system (Taouali et al. 2016; Jaffel et al. 2016a, b; Honeine 2012).

This section will present a new reduced Rank-KPCA method for monitoring nonlinear dynamic system. The key idea of this proposed method is to remove the dependencies of variables in the feature space and to retain a reduced data from the original one $X_{r} = \left[ {x_{1} , \ldots ,x_{i} ,.\,.\,.\,,x_{r} } \right]^{T} \,\, \in \,\,{\mathbb{R}}^{r \times m}$, where $r$ is the number of retained observations. The procedure of this novel monitoring process includes two phases: offline reduced Rank-KPCA model identification and online fault detection procedure. The first phase is to identify the reduced reference model that describes the normal operating condition. Its principle is to retain the observations that generate independent linear combinations in the feature space and reveal the useful information. After that, the built model is performed on-line in order to monitor the system.

3.2 Reduced Rank-KPCA: model identification

In order to identify the reduced Rank-KPCA model, we save the most useful new observation in term of information about the system in a reduced training data matrix $X_{r}$. Let consider that the system operate in the normal condition during $N_{0}$ instants. At first time, the initial reduced data matrix is expressed as: $X_{r} = \,\left[ {x_{1} } \right]\, \in {\mathbb{R}}^{1 \times m} \,$.

At each instant $t$, a new observation $x_{t} \,$ is collected, its kernel vector $k_{{x_{t} }}$ is calculated and the kernel matrix is updated by adding a column and a row to the previous one, as:

$$K_{r}^{t} \,\, = \,\,\left[ {\begin{array}{ll} {K_{r}^{t - 1} } &{k_{{x_{t} }} } \\ {k_{{x_{t} }}^{T} } &{{\mathbf{k}}(x_{t} ,x_{t} )} \\ \end{array} } \right]\,\, \in \,{\mathbb{R}}^{r \times r}$$

(21)

The rank of the updated kernel matrix is calculated, its value leading to either case: the reduced data matrix is incremented by adding the new observation or it is left unchanged.

• Case 1:

  $$rank\,(K_{r}^{t} )\,\, = \,r$$

  (22)

The kernel matrix has a full rank, which describes the independencies between the projection data in the feature space. In this case, the new observation is added to the reduced data matrix.

• Case 2:

  $$rank\,(K_{r}^{t} )\,\, < \,\,r$$

  (23)

The kernel matrix has not a full rank, which describes the dependencies between the projection data in the feature space. In this case, the reduced data matrix left unchanged and we return the kernel matrix to its previous state.

Once, all the observations were evaluated, we obtain the reduced data matrix $X_{r} \, \in {\mathbb{R}}^{r \times m}$ and we construct the reduced kernel matrix $K_{r} \,\, \in \,{\mathbb{R}}^{r \times r} \,$, such that

$$K_{r} \,\,\,\, = \,\,\,\,\,\left[ {\begin{array}{*{20}c} {{\mathbf{k}}(x_{1} ,x_{1} )} & \cdots & {{\mathbf{k}}(x_{1} ,x_{r} )} \\ \vdots & \ddots & \vdots \\ {{\mathbf{k}}(x_{r} ,x_{1} )} & \cdots & {{\mathbf{k}}(x_{r} ,x_{r} )} \\ \end{array} } \right] \in {\mathbf{\mathbb{R}}}^{r \times r}$$

(24)

Then, we estimate the initial reduced Rank-KPCA model (eigenvalues and eigenvectors).

4 The proposed monitoring strategies based on reduced Rank-KPCA

The monitoring strategies based on the novel reduced Rank-KPCA, are presented by two phases: offline learning and online monitoring. The off-line phase is useful for the two proposed online monitoring processes.

4.1 Off-line learning

Consider the system in normal operating condition during $N_{0}$ instants.

Step 1 Get a new observation $x_{t} \, \in {\mathbb{R}}^{m}$, scale it and calculate its kernel vector.

Step 2 Update the kernel matrix $K_{r}$.

Step 3 Test if $K_{r}$ has a full rank, the new observation contain useful information. Then, go to step 4. Otherwise, cancel the updating of the kernel matrix and return to step 1.

Step 4 Update the reduced data matrix.

When, all the $N_{0}$ observations were evaluated, we obtain the reduced training data $X_{r} \, \in {\mathbb{R}}^{r \times m}$.

Step 5 Compute the mean and variance of the reduced training data.

Step 6 Construct the reduced kernel matrix and scale it to obtain the Gram matrix $G_{r}.$

Step 7 Solve the eigenvalue problem and determine the number $\ell$ of retained kernel principal components.

Step 8 Compute the monitoring index SPE and its confidence limit.

4.2 Online monitoring with fixed reduced Rank-KPCA model

Step 1 Obtain a new observation $x_{t + 1} \,$ and scale it with the mean and variance computed at off-line training.

Step 2 Calculate the kernel vector ${\text{ k}}_{t} { = }{\kern 1pt} {\mathbf{k}}(x_{t} ,x_{i} ) \in {\mathbb{R}}^{1 \times N}$ and scale it.

Step 3 Compute the fault detection index SPE for $x_{t + 1} \,$, if the control limit is exceeded, a fault is declared.

Step 4 Return to step 1.

4.3 Online monitoring based on reduced Rank-KPCA and moving window

The idea of this proposed monitoring process is to improve the effectiveness of the new Reduced Rank-KPCA method for dealing with fault detection of nonlinear dynamic process. Its principle is to update the built reduced model with moving window only if a new observation contains new pertinent information about the process and satisfies the condition (22) is available. A detailed algorithm steps are shown as follows:

Step 1 Obtain a new observation $x_{k + 1} \,$ and scale it with the mean and variance computed at off-line training.

Step 2 Calculate the kernel vector ${\text{ k}}_{t} { = }{\kern 1pt} {\mathbf{k}}(x_{t} ,x_{i} ) \in {\mathbb{R}}^{1 \times N}$ and scale it.

Step 3 Compute the fault detection index SPE for $x_{t + 1} \,$, if the control limit is exceeded, a fault is declared so turn to step 1, else go to step 4.

Step 4 If the condition (22) is not satisfied, it is not required to update the reduced Rank-KPCA model, so turn to step 1, else go to next step.

Step 5 Update the reduced data matrix $X_{r}$ by rejecting the oldest observation and adding the new observation.

Step 6 Actualize the reduced Rank-KPCA model (update the number of PC).

Step 7 Update the control limit of the SPE statistic.

Step 4 Return to step 1.

5 Simulation results

The utility and validity of our proposed monitoring strategies were demonstrated using the statistic SPE index. First, we applied the proposed approach to fault detection in a numerical example. Second, the well Known simulated CSTR process and the air quality monitoring network are used to test the effectiveness of the proposed technique and compare it to the classical monitoring techniques KPCA and MWKPCA (Liu et al. 2009).

5.1 Application to numerical example

5.1.1 Process description

We study the applicability of the proposed reduced Rank-KPCA approach by applying it for a simple numerical example (Kallas et al. 2014). This example contains four variables $s_{i} ,\,i = 1 \ldots 4$.

The following equations detail the nonlinear redundancy interrelationships between $s_{1} ,\,s_{2} ,\,s_{3}$ and $s_{4}$. Where $s_{1} ,\,s_{2} \in \,\left[ {0\,.\,.\,.1} \right]\,$ were uniformly distributed signals.

$${\text{ }}\left\{ \begin{gathered} s_{3} - s_{1} \,s_{2} = 0 \hfill \\ s_{4} \,\, - s_{1}^{2} \, = 0 \hfill \\ \end{gathered} \right.$$

(25)

The observation vector $x(k)$ is given by: $x(k) = \left[ {s_{1} (k)\,s_{2} (k)\,s_{3} (k)\,s_{4} (k)} \right]^{T}$.

5.1.2 Fault detection results

Thousand samples were generated from this process. The 500 first samples were used to construct the reduced model and the 500 last samples are used to test the fault detection techniques. In this study, we have used the Gaussian kernel [Radial Basis Function (RBF)]. The kernel parameter $\sigma$ is determined using the cross validation. The number of selected observations using the new reduced Rank-KPCA is equal to $r = 167$ from 500 observations. The confidence limits of the statistical SPE index are set to 95 and 99%, respectively. Next, the detection performance of developed technique is assessed and compared to the classical methods, through two types of faults:

• Fault 1: A step bias of $s_{1}$ by adding 30% than its range of variation. The fault is introduced between the samples 550 and 750.

• Fault 2: A ramp change of $s_{4}$ by adding $0.015\, \times \,(k - 699)$ was introduced between the samples 700 and 900.

The evolution of the SPE index for conventional KPCA, MWKPCA and the proposed monitoring techniques with Fault 1 and Fault 2 is shown in Figs. 1, 2, 3 and 4. It is clear that the injected faults are successfully detected in both thresholds (95 and 99%). In Table 1, we summarize the detection performances in terms of False Alarm Rate (FAR), Good Detection Rate (GDR) and the average Computation Time (CT). We notice that the evaluated GDR and FAR using KPCA, MWKPCA monitoring and Reduced Rank-KPCA methods still comparable in normal operating conditions and for both Fault1 and Fault2. However, the two developed techniques based on Reduced Rank-KPCA provide a smaller CT when compared to the KPCA and MWKPCA. We can show also from Table 1, that the developed MW Reduced Rank-KPCA provides better results when compared to the developed Reduced Rank-KPCA in terms of FAR and GDR, and both of them out performances the classical monitoring methods: KPCA and MWKPCA.

Fig. 1

Evolution of the SPE index with Fault 1 using KPCA and Reduced Rank-KPCA

Fig. 2

Evolution of the SPE index with Fault 1 using MWKPCA and MW Reduced Rank-KPCA

Fig. 3

Evolution of the SPE index with Fault 2 using KPCA and Reduced Rank-KPCA

Fig. 4

Evolution of the SPE index with Fault 2 using MWKPCA and MW Reduced Rank-KPCA

Table 1 Performances of (KPCA, Reduced Rank-KPCA, MWKPCA and MW Reduced Rank-KPCA) for online monitoring

5.2 Proposed techniques and its applications to CSTR process

5.2.1 Process description

The non-isothermal Continuous Stirred Tank Reactors (CSTR) is a dynamic nonlinear process, which has been mostly used for comparison of several process monitoring and fault detection strategies such as VMWKPCA (Fazai et al. 2016), SVD-RKPCA (Jaffel et al. 2016a, b) and RKPCA (Taouali et al. 2016).

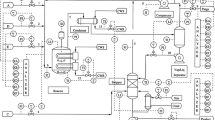
The CSTR process is composed of two feed streams that are the stream of reactant 1 and 2 which are mixed to furnish a final product. The schematic diagram of the reactor is configured in Fig. 5. The dynamic behavior of the process is described by the following equations:

$$\left\{ \begin{aligned} \frac{dh(t)}{dt} &= w_{1} (t) + w_{2} (t) - 0.2\sqrt {h(t)} \hfill \\ \frac{{dC_{b} (t)}}{dt} &= (C_{b1} (t) - C_{b} )\frac{{w_{1} }}{h(t)} + (C_{b2} (t) - C_{b} )\frac{{w_{2} }}{h(t)} - \frac{{k_{1} C_{b} (t)}}{{(1 + k_{2} C_{b} (t))^{2} }} \hfill \\ \end{aligned} \right.$$

(26)

where $h,\,C_{b}$ and $w_{0}$ are respectively the height, the concentration and the feed of reacting mixture, $C_{b1} \;and\;C_{b2}$ are the concentration of reactant 1 and reactant 2, respectively, $w_{1} \;and\;{\text{w}}_{2}$ are the flow rate of reactant 1 and reactant 2, respectively, $k_{1} \;{\text{and}}\;k_{2}$ are the reaction rates assumed to be constants ($k_{1} = k_{2} = 1$).

Fig. 5

Schematic diagram of the reactor

In this study, we considered five monitored variables $w_{1} ,\,w_{2} ,\,\,C_{b} ,\,\,C_{b1}$ and $\, C_{b2}$. The observation vector $x(k)$ defined by:

$$x(k) = \left[ {w_{1} (k) \, w_{2} (k) \, Cb(k) \, Cb_{1} (k) \, Cb_{2} (k) \, } \right]^{T}.$$

(27)

5.2.2 Simulation results

During a normal operation of the process, 1000 simulated observations are used. The first 300 observations were used as a training dataset in order to construct the initial reduced model, and the 700 last samples were used as a test dataset, to illustrate the performances of the new proposed method, three types of faults are considered (Table 2).

Table 2 Sensor Fault description

Table 3 shows a comparison of the average computation time (CT), FAR and GDR for the proposed methods and conventional ones in normal operating conditions. According to Table 3, conventional KPCA and reduced Rank-KPCA have similar performances in term of FAR and GDR but we remark that the proposed Reduced Rank-KPCA has a reduced CT. It is also noted that the proposed MW Reduced Rank-KPCA has a higher GDR and a reduced FAR at the confidence level 99% compared to MWKPCA.

Table 3 Performances of (KPCA, Reduced Rank-KPCA, MWKPCA and MW Reduced Rank-KPCA) in normal operating conditions

Figures 6, 7, 8 and 9 show the monitoring results of conventional KPCA, Reduced Rank-KPCA, MWKPCA and MW Reduced Rank-KPCA using the SPE index in the cases of Fault 1 and Fault 2. We can show that, the faults are detected at time in the both thresholds (95 and 99%). The performances of the four monitoring methods are summarized in Table 4. We note that the proposed Reduced Rank-KPCA and MW Reduced Rank-KPCA at the confidence level 99% have a higher GDR and less CT compared to conventional KPCA and MWKPCA.

Fig. 6

Evolution of the SPE index with Fault 1 using KPCA and Reduced Rank-KPCA

Fig. 7

Evolution of the SPE index with Fault 1 using MWKPCA and MW Reduced Rank-KPCA

Fig. 8

Evolution of the SPE index with Fault 2 using KPCA and Reduced Rank-KPCA

Fig. 9

Evolution of the SPE index with Fault 2 using MWKPCA and MW Reduced Rank-KPCA

Table 4 Performances of (KPCA, reduced Rank-KPCA, MWKPCA and MW reduced Rank-KPCA) for online monitoring

Figure 10 shows the monitoring results of conventional KPCA and Reduced Rank-KPCA using the SPE index in the case of Fault 3. We notice also that the conventional KPCA and the Reduced Rank-KPCA are not able to detect the fault in the threshold 99%. Figure 11 show the ability of the MWKPCA and MW Reduced Rank-KPCA to detect this fault. MW Reduced Rank-KPCA has a less computation time and a reduced false alarm rate than MWKPCA (see Table 4, Fig. 7).

Fig. 10

Evolution of the SPE index with Fault 3 using KPCA and Reduced Rank-KPCA

Fig. 11

Evolution of the SPE index with Fault 3 using MWKPCA and MW Reduced Rank-KPCA

5.3 Proposed techniques and its application to an air quality monitoring network

5.3.1 Process description

The air quality monitoring network AIRLOR, operating in Lorraine, France. The AIRLOR consists of twenty stations placed in several sites: rural, peri-rural and urban. Each station served to the acquisition of some pollutants in the air like nitrogen oxides (NO and NO₂), ozone (O₃), carbon monoxide (CO) and Sulphur dioxide (SO₂). In this study, six stations are served to the registering of the additional metrological parameters. The main objective is to detect defects of the sensors, which measure ozone concentration O₃ and nitrogen oxides NO and NO₂. The phenomenon of photochemical pollution presents a dynamic nonlinear behavior (Harkat et al. 2006).

The observation vector $x(k)$ contains 18 monitored variables $v_{1}$ to $v_{18}$, which corresponding to ozone concentration, nitrogen oxide and nitrogen dioxide, respectively, of each station.

$$x(k) = \left[ {\begin{array}{*{20}c} {\underbrace {{v_{1} (k) \, v_{2} (k) \, v_{3} (k)}}_{{O_{3} (k){\text{ NO}}(k){\text{ NO}}_{2} (k):\,station1}}} & \cdots & {\underbrace {{v_{10} (k) \, v_{11} (k) \, v_{12} (k)}}_{{O_{3} (k){\text{ NO}}(k){\text{ NO}}_{2} (k):\,station4}}} & \cdots & {\underbrace {{v_{16} (k) \, v_{17} (k) \, v_{18} (k)}}_{{O_{3} (k){\text{ NO}}(k){\text{ NO}}_{2} (k):station6}}} \\ \end{array} } \right]^{\,\,T}$$

(28)

5.3.2 Simulation results

Only 1000 simulated observations are used. The first 500 observations were used in the training phase to elaborate the reduced Rank-KPCA model and the last observations 501–1000 were used to test the proposed fault detection methods. In this part, we simulated two faults, which are presented in Table 5.

Table 5 Sensor Fault description

Table 6 summarizes the monitoring performances of the four methods when the process is operating in normal condition. We note that the proposed monitoring methods have a less computation time compared to the others.

Table 6 Performances of (KPCA, Reduced Rank-KPCA, MWKPCA and MWReduced Rank-KPCA) in normal operating condition

Figures 12 and 13 show the monitoring results of the four methods using the SPE index in the case of bias fault at the measured concentration of ${\text{NO}}_{2}$. The fault is detected at time in the both thresholds (95 and 99%), using Reduced Rank-KPCA, MWKPCA and MW Reduced Rank-KPCA. From Table 7, we show that MW Reduced Rank-KPCA has a highly GDR, reduced FAR and significantly reduced CT compared to MWKPCA.

Fig. 12

Evolution of the SPE index with Fault 1 using KPCA and Reduced Rank-KPCA

Fig. 13

Evolution of the SPE index with Fault 1 using MWKPCA and MW Reduced Rank-KPCA

Table 7 Performances of (KPCA, Reduced Rank-KPCA, MWKPCA and MW reduced Rank-KPCA) for online monitoring

The second fault is a bias, it was introduced into the measured concentration of ${\text{NO}}$. Figure 14 shows the detection index SPE for this fault. It is impossible to detect this fault using conventional KPCA. However, the proposed Reduced Rank-KPCA method provides a good detection of the simulated fault at the time in the threshold 95%. As it can be seen in Table 7, the evaluated GDR at the threshold 99% is less than 50%. Since the reduced Rank-KPCA is a monitoring method based on the use of a fixed model so it is powerless to monitoring a dynamic non-linear process. The simulation results of the two adaptive KPCA methods were shown in Fig. 15. The injected fault is clearly detected in both thresholds (95 and 99%) using the proposed MW Reduced Rank-KPCA. We notice that MWKPCA is unable to detect this fault.

Fig. 14

Evolution of the SPE index with Fault 2 using KPCA and Reduced Rank-KPCA

Fig. 15

Evolution of the SPE index with Fault 2 using MWKPCA and MW Reduced Rank-KPCA

6 Conclusion

In this paper, a new reduced Rank-KPCA method has been proposed. Firstly, we derive an algorithm for choosing the pertinent observations that describe the independence between variables in feature space and after we build the reduced Rank-KPCA model. Then, this proposed method was developed into two monitoring strategies for non-linear processes. The first one was called Reduced Rank-KPCA based on a fixed reduced model and is applied to fault detection in a numerical example, a CSTR benchmark and an air quality-monitoring network. This proposed monitoring method gives more sophisticated results and better monitoring performance compared with the conventional KPCA.

The computation time is the most important criterion when using Reduced Rank-KPCA model for process monitoring. In offline training, the CT of reduced model construction seems large in comparison to KPCA model construction. However, once the reduced model and the confidence limits of normal operating data have been calculated, the online monitoring procedure of Reduced Rank-KPCA has provided the shortest CT.

The training data set of the numerical example is assumed invariant in time. Thus, the efficiency of the proposed monitoring with fixed reduced Rank-KPCA model has been proved. Moreover, most of real industrial processes are time varying, hence the reduced Rank-model should be updated. Seeing that, a second monitoring strategy has been proposed to improve the Reduced Rank-KPCA called MW Reduced Rank-KPCA, which aims to update the reduced model using moving window. Applications to the CSTR and Air Quality Monitoring Network have demonstrated that the proposed adaptive monitoring method shows a higher performance for most faults than the MWKPCA method.