1 Introduction

Process development and continuous request for productivity led to an increasing complexity of industrial units. In order to operate a successful plant or process, continuous improvement must be made in the areas of safety, quality and reliability. Improvement in these areas will lead to cost reductions which help make the plant a viable operation in a competitive market. Central to the continuous improvement of safety, quality and reliability is the early or proactive detection of process faults. Such a tool could allow to use an on-condition maintenance policy instead of regular systematic inspections. This would decrease maintenance costs (Kinnaert et al. 2000; Chetouani 2006a). Components, sensors, and actuators in an automated process are often subject to the so-called “faults”, which are defined as unexpected changes or prohibited deviations from normal conditions. And these faults may lead to undesired reactions and damages to the plant, personnel, or the environment. These process abnormalities have significant impact, in such a way that hundreds of billion of dollars are lost by the industry due to poor abnormal situation management (Huang et al. 2000; Skogestad 2003). They show that the early detection of faults can prevent the destruction of equipment and avoid great losses. Also the availability of the process would thus increase if fitted with a suitable detection system (Chetouani 2006b).

In order to improve the process performance, reliability, and safety, many researchers have focused their attention on the issues of fault detection during the last 2 decades. Therefore, the development of effective and robust methods for fault detection has become an important field of research in numerous applications as can be found from the related survey papers (Luh et al. 2005), and books (Patton 2000) and (Gertler 1998). The fault detection techniques can be broadly classified as model-based methods or history based methods (Dash et al. 2000). Process model-based methods rely on a fundamental understanding of the process which includes qualitative methods (fault trees and signed diagrams) and quantitative methods (when mathematical relations exist to describe the process) (Venkatasubramanian 2003a; Venkatasubramanian et al. 2003b). On the other hand, process history-based methods use large amounts of process history data and can also be further subdivided into quantitative methods (statistical techniques) and qualitative methods (qualitative trend analysis and rule-based) (Venkatasubramanian 2003c; Dash et al. 2000).

In recent years, a growing interest in the application of artificial neural networks to fault detection systems has been observed (Isermann 2005; Ferentinos 2005). ANNs have been shown to be extremely suited to model highly complex and nonlinear phenomena (Subai 2005). The author used a dynamic fuzzy neural network to analyze epileptiform discharges in recorded brain waves for patient with absence seizure. Spectral analysis of the EEG signals produces information about the brain activities. He shows that the ANNs may propose a potentially superior technique of EEG signal analysis to the spectral analysis methods. In contrast to the conventional spectral analysis methods, ANNs not only model the signal, but also make a decision as to the class of signal (Subasi et al. 2005; Subasi 2005). Owing to their inherent nature to model and learn ‘complexities’, ANNs have found wide applications in various areas of chemical engineering and related fields (Sharma et al. 2004; Himmelblau 2000). Engell et al. (2003) discussed general aspects of the control of reactive separation processes. They used a semi-batch reactive distillation process. A comparison was carried out between conventional control structures and model-based predictive control by using a neural net plant model. Nanayakkara et al. (2002) presented a novel neural network to control an ammonia refrigerant evaporator. The objective is to control evaporator heat flow rate and secondary fluid outlet temperature while keeping the degree of refrigerant superheat at the evaporator outlet by manipulating refrigerant and evaporator secondary fluid flow rates. This work is motivated by developing a combination of ANNs and CUSUM algorithm for process fault detection. The most important feature of the CUSUM algorithm is its optimization property which has been proved by (Lorden 1971) and (Pollak et al. 1985); that is the mean detection delay derived by using the CUSUM algorithm is a minimum for a given false alarm rate. This study also focuses on the development, and implementation of a NARX neural model for the multi-step ahead forecasting of the process dynamics. It is based on the neural approach for modeling the process behavior in normal conditions. The performance of this stochastic model was evaluated using the performance criteria. Then we examined the abnormal behavior of a process due to faults in its control parameters. Fault detection results show that the CUSUM test is a powerful tool to detect changes in the behavior of the process dynamics. The modeling procedure, neural prediction, experimental set-up and FD results are described in the following sections.

2 Input–output modeling approach

Fault detection methods can be divided into two classes, depending on the presence or absence of an appropriate process model; techniques using the state variables and parameters from a known process model and techniques using only measurable signals (input and output signals from the process). Modeling strategies of various kinds by means of input–output measurements are commonly used in many situations in which it is not necessary to achieve a deep mathematical knowledge of the system under study, but it is sufficient to predict the system evolution (Fung et al. 2003; Mu et al. 2005). This is often the case in control applications, where satisfactory predictions of the system that are to be controlled and sufficient robustness to parameter uncertainty are the only requirements. In chemical systems, parameter variations and uncertainty play a fundamental role on the system dynamics and are very difficult to be accurately modeled (Cammarata et al. 2002). Therefore, the modeling approach based on input–output measurements can be applied.

2.1 Neural modelling

Fault detection systems for industrial plants can benefit from employing empirical models, such as statistical (Bayesian, nearest neighbours, time series), polynomial, experts systems, neural networks, evolutionary computation, fuzzy and neurofuzzy classification methods (Huang et al. 2006). The classification methods include statistical methods (Schneiderman et al. 2004; Liu 2003; Yang et al. 2001), artificial neural networks (Isermann 2005) and support vector machines (Adankon et al. 2007; Cheng et al. 2007), etc. Artificial neural networks are a type of massively parallel computer architectures based on brain-like information encoding and processing models which exhibit brain like behaviors such as learning, association, categorization, generalization, feature extraction and optimization. This approach allows bypassing both the exact determination of model parameters and of their unpredictable variations, and the achievement of deep physical knowledge of the process and of its governing equations. Neural networks are usually used as a particular type of non parametrical statistical model (Thiria et al. 1997). The most important and interesting characteristics shared by most neural networks models are nonlinear modelling capacity, generic modelling capacity, robustness to noisy data and ability to deal with high dimensional data.

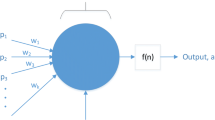
The purpose of this modeling is to establish a reliable model of the dynamic behavior of a process. This reliable model enables to reproduce the process dynamics under different operating conditions in a normal mode. In order to provide a closer approximation to the process is some situations, a NARX nonlinear model is employed (Previdi 2002; Qin et al. 1996), which is identified by means of ANNs. In this study, the NARX neural model used to describe accurately the process behavior is the classical Multi-Layer Perceptron (MLP) neural networks (Narendra et al. 1990; Chen et al. 1989) with one layer of hidden neurons (Fig. 1). The NARX nonlinear model of a finite dimensional system (Ljung 1999) with order (n y , n u ) and scalar variables y and u are defined by:

$$y(t) = \phi (y(t - 1),\ldots, y(t - n_{y}),u(t - 1),\ldots, u(t - n_{u}))$$
(1)

where y(k) is the auto-regressive (AR) variable or system output; u(k) is the eXogenous (X) variable or system input. n y and n u are the AR and X orders, respectively. φ is a nonlinear function. For engineering purposes, the neural network can be thought of as a black box model which accepts inputs, processes them and produces outputs according to some nonlinear transfer function (Zaknich 2003).

Fig. 1
figure 1

Feed-forward network for prediction

Full size image

The MLP neural networks consist in a large number of highly connected nonlinear simple neurons. Figure 1 shows typical feed-forward network architecture with one hidden layer. The term ‘feed-forward’ means that the connections between nodes only allows signals to be sent to the next layer of nodes and not to the previous (Warnes et al. 1996). We can differentiate three types of neurons; input, hidden and output neurons. The input neurons receive information to be processed. The hidden neurons which are neither input nor output neurons are used to keep an internal representation of the problem. The output neurons give the results of the neural network. The parameters associated with each of these connections are called weights. Knowledge of the network is kept in these weights. The determination of these weights for the node connections allows the ANN to learn the information about the system to be modeled. Each hidden and output unit computes its value as the weighted sum of its inputs, passed through a nonlinear function. The structure is based on a result by Cybenko (1989) who proved that a neural network with one hidden layer of sigmoid or hyperbolic tangent units and an output layer of linear units is capable of approximating any continuous function:

$$f(z) = \frac{2}{{1 + e^{{- 2 z}}}} - 1$$
(2)

where z is the sum of the weighted inputs and bias term. In this study, we used the tan-sigmoid transfer function on the hidden layer and a linear transfer function on the output layer. The input data are presented to the network via the input layer. These data are propagated through the network to the output layer to obtain the network output. The network error (generally the mean square error function) is then determined by comparing the network output with the actual output. If the error is not smaller than a desired performance, the weights are adjusted and the training data are presented to the network again to determine a new network error. The aim of this step is to find the appropriate weights which minimize the cost function. This is usually done using an iterative procedure. One of the best known learning mechanisms for neural networks is the back-propagation algorithm (BPA) (Rumelhart et al.1986). It is a simple gradient descent technique, which minimizes the cost function in weight space by modifying the weights in the opposite direction of the gradient error with respect to the weights. The BPA is often too slow for practical problems. Since 1986, a variety of improvements (Hertz et al. 1991) have been proposed (introduction of a momentum term, use of conjugate gradient techniques, use of second order information, etc.). In this study, a back-propagation training function for feed-forward networks using momentum and adaptive learning rate techniques is used (Vogl et al. 1988). This version of back-propagation learns quickly compared to classical algorithm and minimizes the chance that the network parameters will become stuck in a high error minimum. In this algorithm, as with any other gradient approach, large values of learning rate will speed up the learning process, but lead to instability, and convergence can only be expected for small values of learning rate. The momentum factor is used to damp down oscillations in the learning process. The latter is repeated until the network error reaches the desired performance. In this case the network is then said to have converged and the last set of weights are retained as the network’s parameters.

2.2 Calculation of the NN output

Though the applicability of neural networks to solve several nonlinear complex problems has been amply demonstrated, the time taken to train neural networks can be quite excessive (Fung et al. 2003). ANNs are trained off-line and then used for on-line FD. The following steps explain the calculation of the ANNs output based on the input vector.

  1. 1.

    Assign \({\hat{w}^{T} (k)}\) to the input vector x T(k) and apply it to the input units where \({\hat{w}^{T} (k)}\) is the regression vector given by the following equation:

    $$\hat{w}^{T} (t) = [y(t - 1), \ldots, y(t - n_{y}),u(t - 1), \ldots, u(t - n_{u})]$$
    (3)
  2. 2.

    Calculate the input to the hidden layer units:

    $${ne}_{j}^{h} {{(k) =}}{\sum\limits_{{{i = 1}}}^{{p}} {{W}^{h}_{ji} {(k)x}_{i} {{(k) + b}}^{{h}}_{j}}}$$
    (4)

    where p is the number of input nodes of the network, i.e., p = n y  + n u  + n b ; j is the jth hidden unit; W h ji is the connection weight between ith input unit and jth hidden unit; b h j is the bias term of the jth hidden unit.

  3. 3.

    Calculate the output from a node in the hidden layer:

    $${z}_{j} = f_{j}^{h} {(net}_{j}^{h} (k))$$
    (5)

    where f h j is the tan-sigmoid transfer function defined by the Eq. (2).

  4. 4.

    Calculate the input to the output nodes:

    $$net_{l}^{q} (k) = \sum\limits_{j = 1}^{h} {W}^{q}_{lj} (k)z_{j} (k)$$
    (6)

    where l is the lth output unit; W q lj (k) is the connection weight between jth hidden unit and lth output unit.

  5. 5.

    Calculate the outputs from the output nodes:

    $${\hat{v}}_{l} (k) = f ^{q}_{l} (net^{q}_{l} (k))$$
    (7)

    where f q l is the linear activation function defined by:

    $${f}_{l}^{q} (net_{l}^{q} (k)) = net_{l}^{q} (k)$$
    (8)

2.3 Back-propagation training algorithm

The error function E is defined as:

$$E = \frac{1}{2}{\sum\limits_{l = 1}^q {(v_{l} (k)}} - \hat{v}_{l} (k))^{2}$$
(9)

where q is the number of output units and v l (k) is the lth element of the output vector of the network. Within each time interval from k to k + 1, the back-propagation (BP) algorithm tries to minimize the error for the output value as defined by E by adjusting the weights of the network connections, i.e., W h ji and W q lj . The BP algorithm uses the following procedure (Eqs. 10–13):

$$W^{h}_{{ji}} (k + 1) = W^{h}_{{ji}} (k) + \alpha \Delta W^{h}_{{ji}} (k) - \eta \frac{{\partial E}}{{\partial W^{h}_{{ji}} (k)}}$$
(10)
$$W^{q}_{{lj}} (k + 1) = W^{q}_{{lj}} (k) + \alpha \Delta W^{q}_{{lj}} (k) - \eta \frac{{\partial E}}{{\partial W^{q}_{{lj}} (k)}}$$
(11)

where η and α are the learning rate and the momentum factor, respectively; ΔW h ji and ΔW q lj are the amounts of the previous weight changes; ∂E/∂W h ji (k) and ∂E/∂W q lj (k) are given by:

$$\frac{{\partial E}}{{\partial W^{h}_{{ji}} (k)}} = - {\left[ {z_{j} (k)(1 - z_{j} (k))x_{i} (k)} \right]}{\sum\limits_{l = 1}^q {{\left[ {(v_{l} (k) - \hat{v}_{l} (k))\hat{v}_{l} (k)W^{h}_{{lj}} (k)} \right]}}}$$
(12)
$$\frac{{\partial E}}{{\partial W^{q}_{{lj}} (k)}} = - (v_{l} (k) - \hat{v}_{l} (k))z_{j} (k)$$
(13)

The implementation of the ANN for forecasting is as follows:

  1. 1.

    Initialize the weights using small random values and set the learning rate and momentum factor for the ANN.

  2. 2.

    Apply the input vector given by Eq. 3 to the input units.

  3. 3.

    Calculate the forecast value of the error using the data available at (k−1)th sample (Eqs. 3–8).

  4. 4.

    Calculate the error between the forecast value and the measured value.

  5. 5.

    Propagate the error backwards to update the weights (Eqs. 10–13).

  6. 6.

    Go back to step 2.

For weights initialization, the Nguyen-widrow initialization method (Nguyen et al. 1990) is best suited for the use with the sigmoid/linear network which is often used for function approximation.

3 CUSUM test for detecting changes

For fault detection, important measurable variables, unmeasurable variables, or parameters which are estimated, are tracked and checked whether they are within a certain tolerance of their normal values. If the values are not within the specified tolerance, a fault has been detected (Chetouani 2006b). Abnormal situations occur when processes deviate significantly from their normal regime during on-line operation. The area of fault detection is an important aspect of process engineering. Not only is it important from a safety viewpoint but also for the maintenance of yield and quality in a process. This area has received considerable attention from industry and academia alike because of the economic and safety impacts involved (Cheng et al. 2001; Scenna et al. 2000; Wang et al. 1998). Residuals are quantities that are nominally zero but become nonzero in response to faults (Chetouani 2004). However, the presence of disturbances, noise, and modelling errors causes the residuals to become nonzero and thus interferes with the detection of faults (Fouladirad et al. 2005). This will lead to a trade-off between a false alarm rate and a missed detection rate. As a result, the residual generator needs to be designed so that it is unaffected by those unknown uncertainties. And robustness to noise and model uncertainties is the key issue in the application of model-based fault detection methods (Sharma et al. 2004; Dash et al. 2000), since modelling errors and noises in complex engineering systems are inevitable. The CUSUM test (Hinkley 1971; Basseville 1986) is founded according the optimization property and is performed as a cumulative sum test, where jumps in the mean occur at unknown time instants.

Let \({\gamma (k) = y(k) - \hat{y}(k)}\) be the sequence of the residuals, and let ɛ (k) be a white noise sequence with variance σ2.

$$\gamma (k) = \mu (k) + \varepsilon (k)$$
(14)

where μ(k) = μ0 if k ≤ r − 1 and μ(k) = μ1 if k ≥ r

The problem is to detect the change in the mean of the residual signal γ(k), to estimate the change time r and the mean values μ0 and μ1 before and after the jump. In this study, we investigate the case where only μ0 is known which is of interest in practice for the on-line fault detection. In this case, two approaches may be used (Basseville 1986). The first one consists in running two tests in parallel corresponding to an a priori chosen minimum jump magnitude δ and to two possible directions (decrease or increase in the mean). The corresponding stopping rules are as follows:

For decrease in the mean of the residual

$$ \left\{ {\begin{array}{*{20}c} {{T_{0} = 0}} \\ {{T_{n} = {\sum\limits_{k = 1}^n {{\left({\gamma (k) - \mu _{0} + \frac{\delta } {2}} \right)}} } }} \\ {{M_{n} = {\mathop {\max (T_{k})}\limits_{0 \leqslant k \leqslant n} }}} \\ {{{\rm Alarm\; when}\; M_{n} - T_{n} \succ \lambda }} \\ \end{array} } \right. $$
(15)

and for an increase in the mean of the residual

$$\left\{{\begin{array}{*{20}c} {{U_{0} = 0}} \\ {{U_{n} = {\sum\limits_{k = 1}^n {{\left({\gamma (k) - \mu _{0} - \frac{\delta}{2}} \right)}}}}} \\ {{m_{n} = {\mathop {\min (U_{k})}\limits_{0 \leqslant k \leqslant n}}}} \\ {{{\rm Alarm\;when}\; U_{n} - m_{n} \succ \lambda}} \\ \end{array}} \right.$$
(16)

The detector will set the alarm at the first time n at which \({M_{n} - T_{n} \succ \lambda}\) (Eq. 15) for detecting a decrease in the mean and at the first time n at which \({U_{n} - m_{n} \succ \lambda}\) (Eq. 16) for detecting an increase in the mean of the residual. The limit λ is determined by learning. The statistical threshold λ is selected so that it corresponds to a physical reality of the process. It must take account of the modelling errors. It is generally raised in order to avoid to false alarms. The initial value is calculated by the expression (λ = 2*h*σ/δ) where h = 2 for normal distributions and σ is the standard deviation of the residual signal (Moatar 1999; Ragot et al.1990).

4 Experimental results

4.1 Experimental device

The reactor-exchanger is a glass-jacketed reactor with a tangential input for heat transfer fluid. It is equipped with an electrical calibration heating and an input system. It is also equipped also with Pt100 temperature probes. The heating–cooling system, which uses a single heat transfer fluid, works within the temperature range of −15 and +200°C. Supervision software allows the fitting of the parameters and their instruction value. It displays and stores data during the experiment as well as for its further exploitation. The input of the reactor-exchanger u(t) represents the heat transfer fluid temperature allowing the heating–cooling of the water. y(t) represents the outlet temperature of the reactor-exchanger. The process is excited by an input signal, very rich in frequencies and amplitudes, in order to have a data set suitable for the training procedure. The sampling period is fixed to 2 s. Before starting the training of parameters, the available data is divided into two separated sets. The first subset is the training subset which is used for computing the gradient and updating the network weights. The second subset is the validation set. The first one is sufficiently informative and covering the whole spectrum. The second one contains sufficient elements to make the validation as credible as possible. All data were standardized (zero mean and unity standard deviation) (Fig. 2).

4.2 Establishment of NARX models

One of the most important features of learning systems is their ability to generalize to new situations. An early stopping procedure to stop the learning process was used for improving generalization. The error on the validation set is monitored during the training process. The validation error will normally decrease during the initial phase of training, as does the training set error. However, when the network begins to overfit the data, the error on the validation set will typically begin to rise, the training is stopped, and the weights at the minimum of validation error are returned. The verification test subset is a set of independent data used to verify the consistency of the efficiency of the model. The right number of hidden neurons cannot be achieved from a universal formula. It is determined by the user and can vary from zero to any finite number. Networks with too many parameters tend to memorize the input patterns, while those with too few hidden parameters may not be able to simulate a complex system at all. Our initial model had few parameters, we gradually added hidden neurons during learning until the optimal result is achieved in the test subset. To establish a suitable NARX model order for a particular system, neural networks of increasing model order can be trained and their performance on the training data compared using the loss function (or mean squared error), LF. This function is expressed by the following equation:

$${\rm LF} = \frac{1}{N}{\sum\limits_{i = 1}^N {\varepsilon ^{2} (t)}}$$
(17)

where \({\varepsilon (t) = y(t) - {\mathop y\limits^ \wedge}(t)}\) represents the prediction error and N is the data length. In order to select the optimal number of hidden neurons, tests were performed by varying the number of neurons between 1 and 15. The minimal number of inputs is avoided to ensure the model flexibility. Also, the maximum number of inputs is excluded to avoid the over-fitting. The training on the database gives the evolution of the loss function (Figs. 3, 4).

Fig. 2
figure 2

Experimental device: a reactor-exchanger

Full size image
Fig. 3
figure 3

Evolution of the loss function for low complexity models

Full size image
Fig. 4
figure 4

Evolution of the loss function for high complexity models

Full size image

For well-showing the minimum of the LF for each model according to the number of hidden neurons, the LF evolution is separated in two different figures. These Figs. 3 and 4 show the LF evolution according to the structure of the neural model on the same database. The model M ny.nu.nh indicates a neural model with ny outputs, nu inputs and nh hidden neurons. The M3.2.10 model exhibits the lowest LF. In fact, the optimal result of the test set is obtained for ten neurons in the hidden layer, a choice that is justified by the absence of improvement of the model beyond this value. However, this model may not be the best choice, because there is a trade-off between the model complexity (i.e., size) and accuracy. A small decrease in the LF may be rejected if it is at the expense of enlarging the model size. Thus, the decision procedure for selecting a parsimonious model using the LF consists in deciding for each increase in model order whether any reductions in the LF are worth the expense of a larger model. The difficult trade-off between model accuracy and complexity can be clarified by using model parsimony indices from linear estimation theory (Ljung 1999), such as Aikeke’s information criterion (AIC), Rissanen’s minimum description length (MDL) and Bayesian information criterion (BIC). The validation phase thus makes it possible to distinguish the model describing correctly the dynamic behavior of the process. These statistical criteria are defined as follows:

$${\rm AIC} = {\rm ln} {\left({\frac{N}{2}{\rm LF}} \right)} + \frac{{2n_{w}}}{N}$$
(18)
$${\rm MDL} = {\rm ln} {\left({\frac{N}{2}{\rm LF}} \right)} + \frac{{2n_{w} {\rm ln} (N)}}{N}$$
(19)
$${\rm BIC} = {\rm ln} {\left({\frac{N}{2}{\rm LF}} \right)} + \frac{{n_{w} {\rm ln} (N)}}{N}$$
(20)

where n w is the number of model parameters (weights in a neural network).

Hence, the AIC, MDL and BIC are weighted functions of the LF, which penalize for reductions in the prediction errors at the expense of increasing model complexity (i.e., model order and number of parameters). Strict application of these statistical criteria means that the model structure with the minimum AIC, MDL or BIC is selected as a parsimonious structure. However, in practice, engineering judgment may need to be exercised. The Fig. 5 shows the evolution of AIC, MDL and BIC criteria according the LF minimum for each model.

Fig. 5
figure 5

Evolution of the criteria for the LF minimum

Full size image

A strict application of the indices would select the models M2.2.3 and M3.2.10 because they exhibit the lowest of three indices for all the model structures compared. Based on engineering judgment, the model M2.2.3 would be preferred without significant loss of accuracy.

4.3 Residual analysis

Once the training and the test of the NARX model have been completed, it should be ready to simulate the system dynamics. Model validation tests should be performed to validate the identified model. Billings et al. (1986) proposed some correlations based model validity tests. In order to validate the identified model, it is necessary to evaluate the properties of the errors that affect the prediction of the outputs of the model, which can be defined as the differences between experimental and simulated time series. In general, the characteristics of the error are considered satisfactory when the error behaves as white noise, i.e., it has a zero mean and is not correlated (Cammarata et al. 2002; Billings et al. 1986). In fact, if both these conditions are satisfied, it means that the identified model has captured the deterministic part of the system dynamics, which is therefore accurately modeled. To this aim, it is necessary to verify that the auto-correlation function of the normalized error ɛ(t), namely φɛɛ(τ), assumes the values 1 for t=0 and 0 elsewhere; in other words, it is required that the function behaves as an impulse. This auto-correlation is defined as follows (Zhang et al. 1996; Billings et al. 1986):

$$\phi \varepsilon \varepsilon (\tau) = E(\varepsilon (t - \tau)\varepsilon (t)] = \delta (\tau) \quad \forall \tau $$
(21)

Where ɛ is the model residual. E(X) is the expected value of X, τ is the lag.

This condition is, of course, ideal and in practice it is sufficient to verify that φɛɛ(τ), remains in a confidence band usually fixed at the 95%, which means that φɛɛ(τ) must remain inside the range \({\pm \frac{{1.96}}{{{\sqrt N}}}},\) with N the number of testing data on which φɛɛ(τ) is calculated. Billings et al. also proposed tests for looking into the cross-correlation among model residuals and inputs (Billings et al. 1986). This cross-correlation is defined by the following equation:

$$\phi u\varepsilon (\tau) = E(u (t - \tau)\varepsilon (t)] = 0 \quad \forall \tau,$$
(22)

To implement these tests (21, 22), u and ɛ are normalized to give zero mean sequences of unit variance. The sampled cross-validation function between two such data sequences u(t) and ɛ(t) is then calculated as:

$$ \phi u\varepsilon (\tau) = \frac{{{\sum\limits_{ t = 1}^{ N - \tau } {u(t)} } \varepsilon (t + \tau)}} {{{\left[ { {\sum\limits_{ t = 1}^{ N} {u ^{2}_{(t)}} } {\sum\limits_{ t = 1}^N {\varepsilon ^{2}_{(t)} } }} \right]}^{{1/2}} }} $$
(23)

If the Eqs. (21, 22) are satisfied then the model residuals are a random sequence and are not predictable from inputs and, hence, the model will be considered as adequate. These correlations based tests are used here to validate the neural network model. The results are presented in Fig. 6. In these plots, the dash dot lines are the 95% confidence bands.

Fig. 6
figure 6

Results of model validation tests

Full size image

The evolution of the cross-correlation of the NARX model is inside the 95% confidence bands. In addition, the NARX cross-correlation is low. This explains the independence of the residual signal from the input one. For the auto-correlation of the NARX neural model, all points are inside the 95% confidence bands. Therefore, this model is considered a reliable one for describing the dynamic behavior of the process. This validation phase is used with the neural weights found in the training phase. There is a good agreement between the learned neural model and the experiment in the validation phase. This result is important because it shows the ability of the neural network with only one hidden layer to interpolate any nonlinear function (Cybenko 1989). Figure 7 shows the difference between the experimental output and those simulated by the neural model M2.2.3.

Fig. 7
figure 7

Prediction error of the output temperature

Full size image

After analyzing this figure, it emerges that the NARX model M2.2.3 ensures satisfactory performances as it is indeed able to correctly identify the dynamics of the reactor-exchanger. The main advantage of the proposed neural approach consists in the natural ability of neural networks in modeling nonlinear dynamics in a fast and simple way and in the possibility to address the process to be modeled as an input–output black-box, with little or no mathematical information on the system.

4.4 Fault detection results

In order to develop the fault detection system, some fault scenarios which were to be detected had to be chosen. It was decided to attempt to detect two faults:

  • Fault1: A sudden increase in the flow rate of the cooling from 1.5 kg s−1 to 3.5 kg s−1, F1

  • Fault2: A sudden decrease in the flow rate of the cooling from 1.5 kg s−1 to 0.5 kg s−1, F2.

These faults introduce deviations in comparison with the normal behavior of the process. Figure 8 shows the temperature difference (Δ (T normal−T fault)) which results from the fault’s effect. We notice that the fault F1 which occurs at 1,500 s causes a slight increase in the dynamics of the process. This slight increase should be detected by the CUSUM test because it exceeds the tolerated threshold of 1 °C regarded as a critical temperature threshold in practice. Nevertheless, the fault F2 which occurs also at 1,500 s causes a large drift which can sometimes exceed 3 °C.

Fig. 8
figure 8

Difference between the fault temperature and the normal one

Full size image

The CUSUM test (Fig. 9) consists in fixing a priori a minimum jump magnitude δ to be detected, and running two tests in parallel, because the ‘direction’ of the jump is not known a priori (increasing or decreasing mean). The statistical application of the CUSUM test gives the results schematized in Fig. 9. The statistical threshold λ allows to delimit two distinct regions; the first region is called the safety region and is where the test evolution is considered acceptable. The second region is not acceptable (fault region) and is where the test evolution exceeds the statistical threshold λ. It is noted that the fault F1 causes an increase in the mean of the residual signal exceeding the threshold \({U_{n} - m_{n} \succ \lambda}\) at 1,898 s. The time delay in detection, which is calculated as the difference between the occurrence time of the fault and the time of its detection, is 398 s. Therefore, the temperature difference between the normal mode and abnormal one is Δ (T normal−T F1) = 1.1 °C. Concerning the fault F2, the high decrease in dynamics involves a decrease of the mean \(({M_{n} - T_{n} \succ \lambda})\) which is detected at 1,706 s representing a temperature Δ (T normal−T F2) = 1.2 °C. Also, let us notice that the evolution of the detection criterion is positive in both cases of the dynamics evolution.

Fig. 9
figure 9

Evolution of the CUSUM test

Full size image

5 Conclusion

With the rising demands of product quality, effectiveness and safety in modern industries, the research on fault detection for dynamic systems has received more and more attention and has developed quickly. This research has addressed the combination of ANNs and CUSUM statistical test for robust fault detection. A black-box model-based strategy for fault detection is proposed. The experiments are performed on a process such as a reactor-exchanger set-up. Our results show that the one-Layer Perceptron network provides promising assignments to normal and faulty states of the investigated reference process. The prediction of the dynamic behavior by the neural net can be improved by using all experimental information. Then, the application of neural networks to identify abnormal states in this process has been investigated. The example of cooling breakdowns shows that a network which is trained with data of these faults and other data of the real plant will properly classify the real operating states and identify faults. The flow rate faults are detected via detection of abrupt positive jumps in the residual signal using a ANNs/CUSUM detector. The analysis of the detection test shows that the proposed fault detection method is robust against faults. In conclusion, the combination of the MLP network and CUSUM test could promptly detect fault conditions in such nonlinear processes.