An inexact joint-probabilistic programming method for risk assessment in water resources allocation

Abstract

In this study, an inexact joint probabilistic programming (IJPP) approach is developed for risk assessment and uncertainty reflection in water resources management systems. IJPP can dominate random parameters in the model’s left- and right-hand sides of constraints and interval parameters in the objective function. It can also help examine the risk of violating joint probabilistic constraints, which allows an increased robustness in controlling system risk in the optimization process. Moreover, it can facilitate analyses of various policy scenarios that are associated with different levels of economic consequences when the promised targets are violated within a multistage context. The IJPP method is then applied to a case study of planning water resources allocation within a multi-reservoir and multi-period context. Solutions of system benefit, economic penalty, water shortage, and water-allocation pattern vary with different risks of violating water-demand targets from multiple competitive users. Results also demonstrate that different users possess different water-guarantee ratios and different water-allocation priorities. The results can be used for helping water resources managers to identify desired system designs against water shortage and for risk control, and to determine which of these designs can most efficiently accomplish optimizing the system objective under uncertainty.

1 Introduction

In water resources management problems, many system parameters and their inter-relationships may appear uncertain (Li et al. 2008). For instance, the random characteristics of available water quantity assumed to follow probability distribution, that are related to a number of natural and human-induced impacts such as the flows of rivers, streams and lakes, varied precipitation, evapotranspiration, and runoff levels; the randomness of water demand associated with the rapid population increase and speedy economic development are possible sources of the uncertainties. Correspondingly, it is desired to develop a more efficient, equitable, and environmentally-benign management plan to water resources allocation among multiple competing users within a basin context under various uncertainties and complexities. Previously, many researchers employed stochastic mathematical programming (SMP) methods for planning water resources management under uncertainty (Kasiviswanathan and Sudheer 2013; Kriauciuniene et al. 2013; Li and Huang 2013; Syme 2014). SMP is an extension of mathematical programming to decision problems whose coefficients (input data) are not certainly known but could be represented as chances or probabilities (Birge 1985; Huang 1998). For example, Morgan et al. (1993) proposed a mixed integer chance-constrained programming method that considered uncertainty in all linear programming constraint coefficients and did not require a prior knowledge of the distribution in a groundwater remediation problem. Huang and Loucks (2000) developed an inexact two-stage stochastic programming model for dealing with uncertainties expressed as discrete intervals and random variables in water resources management problems. Watkins et al. (2000) proposed a multistage scenario-based stochastic programming model for planning water supplies from highland lakes, where dynamics and uncertainties of water availability (and thus water-allocation) could be taken into account through generation of multiple representative scenarios. Li et al. (2006) developed an interval-parameter multistage stochastic programming method for water resources decision making under uncertainty, which could deal with uncertainties expressed as discrete random variables and intervals through constructing a set of scenarios that are representative for the universe of possible outcomes. Tilmant et al. (2008) presented a stochastic programming approach for assessing the statistical distribution of marginal water values in multipurpose multi-reservoir systems where water managers faced complex spatial and temporal trade-offs to track site and time changes in water values across different hydrologic conditions. Andrieu et al. (2010) proposed a joint dynamic chance constraints model in the case of continuous distribution for reservoir management, where the ideas of multistage stochastic programming are adapted to the situation of chance constraints; the model was particularly useful in the presence of independent random variables but worked equally well in the case of correlated variables. Housh et al. (2013) proposed a limited multistage stochastic programming method, in which the number of decision variables at each stage remained constant; consequently, the method could utilize the optimal decisions obtained by solving a set of deterministic optimization problems to identify decision nodes and the methodology was demonstrated on a multistage water supply system operation problem.

Among these SMP methods, multistage stochastic programming (MSP) improved upon the conventional SMP methods by permitting revised decisions in each time stage based on the uncertainty realized so far (Li et al. 2006); the primary advantage of the MSP was its flexibility in modeling the decision process and defining all possible scenarios (Birge 1985). Chance-constrained programming (CCP) was effective for solving optimization problems with random variables included in constraints and sometimes in the objective function as well (Charnes and Cooper 1959). CCP could reflect the reliability of satisfying (or risk of violating) system constraints under uncertainty when the probability distributions are available without requiring the constraints are totally satisfied (Charnes and Cooper 1983). However, due to the frequently observed lack of convexity and/or smoothness, stochastic programs with joint probabilistic constraints (JPC) were considered as a hard type of chance constrained optimization problems (Zhang et al. 2002). In JPC, at least, the total set of uncertain constraints were enforced to be satisfied one probability level, which allowed more robustness in controlling system risk in optimization process (Li et al. 2009). However, when uncertainties were presented as the randomness in the left-hand-sides of the constraints, the conventional JPC method could hardly reflect such uncertainty due to the difficulty in solving the caused nonlinear forms. Sun et al. (2013) proposed an inexact joint-probabilistic left-hand-side chance-constrained programming (IJCP) method for municipal solid waste management; the IJCP integrated techniques of interval-parameter programming (IPP) and left-hand-side chance-constrained programming within a general framework, such that uncertainties expressed as interval values and left-hand-side random variables were tackled. However, the IJCP was incapable of analyzing various policy scenarios that were associated with different levels of economic penalties when the promised targets were violated, especially for large-scale problems with sequential structure.

Therefore, the objective of this study is to develop an inexact joint probabilistic programming (IJPP) approach for solving random parameters in the model’s left- and right-hand sides of constraints and interval parameters in the objective function within a multistage context. Penalties will be exercised with recourse against any infeasibility, such that the IJPP can be used for analyzing various policy scenarios that are associated with different levels of economic consequences when the promised water-allocation targets are violated. The IJPP can also help examine the risk of violating joint probabilistic constraints, which allows an increased robustness in controlling system risk in the optimization process. A case study will then be provided for demonstrating how the developed method will support the planning of water resources management within a multi-user, multi-reservoir and multi-period context.

2 Model development

For water resources management within a multi-user system, uncertainties presented in terms of joint probabilities may exist among multiple users to satisfy their water demands (i.e., a level of probability represents the admissible risk of violating the uncertain satisfactory constraints). The technique of JPC can be used for dealing with such complexities (Miller and Wager 1965; Charnes and Cooper 1983; Li et al. 2009). A general JPC formulation can be expressed as (Miller and Wager 1965):

$$ {\text{Max}}\;{\text{c}}^T x{\kern 1pt} $$

(1a)

subject to:

$$ {\text{P}}(T_{s} x \ge \varepsilon_{s} ,\quad s = 1,\;2, \ldots ,\;m_{3} ) \ge q{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} $$

(1b)

$$ Ax \ge b $$

(1c)

$$ x \ge 0{\kern 1pt} $$

(1d)

Obviously, in JPC, the entire set of uncertain constraints are enforced to be satisfied with at least a joint probability of q; thus, an increased robustness in controlling the system risk can be accomplished (Zhang et al. 2002; Lejeune and Prekopa 2005). Model (1) is generally nonlinear and possibly non-convex due to the existence of joint probabilities for multiple random variables (ε _s ). By letting the random variables take a set of individual probabilistic constraints, the JPC problem can be equivalently formulated as a linear programming model as follows (Lejeune and Prekopa 2005):

$$ {\text{Max}}{\kern 1pt} \;{\kern 1pt} {\text{c}}^{T} {x} $$

(2a)

subject to:

$$ T_{s} x \ge F_{s}^{ - 1} (q_{s} ),{\kern 1pt} \quad s = 1,\;2, \ldots ,\;m_{3} {\kern 1pt} $$

(2b)

$$ \sum\limits_{s = 1}^{{m_{s} }} {(1 - q_{s} ) \le 1 - q} {\kern 1pt} $$

(2c)

$$ Ax \ge b $$

(2d)

$$ x \ge 0 $$

(2e)

where q _s (s = 1, 2,…, m ₃ ) are individual probabilities constrained to be larger than or equal to q, and $F_{s}^{ - 1}$ refer to inverse probability distributions of the random variables (ε _s ). An improved joint-probabilistic programming (IJP) technique is proposed to reflect the randomness uncertainties in the left-hand-sides of constraints. In a linear programming problem, when the left-hand-sides (a _ij ) of constraints are expressed as random parameters with normal distributions (μ _ij is expectation and $\sigma_{ij}$ is standard variation), the related constraints are satisfied at a certain probability (1 − q _i ). Thus, an IJP model can be formulated as follows (Abdelaziz et al. 2007; Zhang et al. 2011):

$$ {\text{Max}}{\kern 1pt} \;f{\kern 1pt} = \sum\limits_{j = 1}^{n} {c_{j} x_{j} } $$

(3a)

subject to:

$$ \Pr \left\{ {\sum\limits_{j = 1}^{n} {a_{ij} \left( \omega \right)x_{j} \le b_{j} } } \right\} \ge 1 - q_{i} ,{\kern 1pt} \quad i = 1,{\kern 1pt} \;2, \ldots ,\;m $$

(3b)

$$ \sum\limits_{i = 1}^{{m_{{}} }} {q_{i} \le q} {\kern 1pt} $$

(3c)

$$ a_{ij} \left( \omega \right) \sim N\left( {u_{ij} ,\sigma_{ij}^{2} } \right) $$

(3d)

$$ x_{j} \ge 0,\quad j = 1,{\kern 1pt} \;2, \ldots ,\;m $$

(3e)

where f is a linear objective function, x _j is a real-number decision variable, b _j and c _j are real-number parameters and 1 − q is a prescribed joint probability level at which the entire set of uncertain constraints are enforced to be satisfied. In real-world water resources management problems, complexities in water allocation problems where interactive and dynamic relationships exist within a multistage context are desired to reflect. Besides, uncertain parameters may be expressed as interval values with known lower and upper bounds, but unknown membership or distribution functions (Suo et al. 2013; Xu and Qin 2013). For uncertainties in left-and right-hand sides and cost/revenue parameters in the objective function, an extended consideration is the introduction of techniques of IPP and MSP into the IJP framework. This leads to an IJPP model as follows:

$$ {\text{Max }}f^{ \pm } = \sum\limits_{t = 1}^{T} {C_{t}^{ \pm } } X_{t}^{ \pm } - \sum\limits_{t = 1}^{T} {\sum\limits_{k = 1}^{{K_{t} }} {p_{tk} D_{tk}^{ \pm } Y_{tk}^{ \pm } } } $$

(4a)

subject to:

$$ A_{rt}^{ \pm } X_{t}^{ \pm } \le B_{rt}^{ \pm } {\kern 1pt} ,{\kern 1pt} \quad r = 1,\;2, \ldots ,\;m_{1} ;\quad t = 1,{\kern 1pt} \;2, \ldots ,\;T $$

(4b)

$$ A_{it}^{ \pm } X_{t}^{ \pm } + A_{itk}^{' \pm } Y_{tk}^{ \pm } \le \tilde{w}_{itk}^{ \pm } ,\quad i = 1,\;2, \ldots ,\;m_{2} ;{\kern 1pt} \quad t = 1,\;2, \ldots ,\;T;\quad k = 1,\;2, \ldots ,\;K_{t} $$

(4c)

$$ \Pr \left\{ {\alpha_{st} \left( \omega \right)A_{st}^{ \pm } X_{t}^{ \pm } \le B_{st}^{ \pm } } \right\} \ge 1 - q_{s} ,\quad {\kern 1pt} s = 1,\;2, \ldots ,\;m_{3} ;\quad t = 1,\;2, \ldots ,\;T $$

(4d)

$$ \alpha_{st} \left( \omega \right) \sim N\left( {u_{st} ,\sigma_{st}^{2} } \right),\quad \forall s,\;t $$

(4e)

$$ \sum\limits_{s = 1}^{{m_{3} }} {q_{s} \le q} $$

(4f)

$$ x_{jt}^{ \pm } \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x_{jt}^{ \pm } \in X_{t}^{ \pm } ,\quad j = 1,\;2, \ldots ,\;n_{1} ;\;t = 1,\;2, \ldots ,\;{\kern 1pt} T $$

(4g)

$$ y_{jtk}^{ \pm } \ge 0,{\kern 1pt} \;y_{jtk}^{ \pm } \in Y_{tk}^{ \pm } ,\quad j = 1,\;2, \ldots ,\;n_{2} ;\quad t = 1,\;2, \ldots ,\;T;\quad k = 1,\;2, \ldots ,\;K_{t} $$

(4h)

where superscripts ‘−’ and ‘+’ represent lower and upper bounds of the interval parameters, respectively. Moreover, the IJPP model forms a non-linear programming one, due to the reflection of uncertainties of randomness in the left- and right-hand sides simultaneously in constraint (4d), which can hardly be solved through general arithmetic algorithms. An alternative solution for model (4) is that the constraint (4d) can be reformulated to its approximated linearization form (Sun et al. 2013). Thus, model (4) can be converted into:

$$ Max\;f^{ \pm } = \sum\limits_{t = 1}^{T} {C_{t}^{ \pm } } X_{t}^{ \pm } - \sum\limits_{t = 1}^{T} {\sum\limits_{k = 1}^{{K_{t} }} {p_{tk} D_{tk}^{ \pm } Y_{tk}^{ \pm } } } $$

(5a)

subject to:

$$ A_{rt}^{ \pm } X_{t}^{ \pm } \le B_{rt}^{ \pm } ,\quad {\kern 1pt} r = 1,\;2, \ldots ,\;m_{1} ;\quad t = 1,\;2, \ldots ,\;{\kern 1pt} T $$

(5b)

$$ A_{it}^{ \pm } X_{t}^{ \pm } + A_{itk}^{{\text{'} \pm }} Y_{tk}^{ \pm } \le \tilde{w}_{itk}^{ \pm } ,\quad i = 1,\;2, \ldots ,\;m_{2} ;{\kern 1pt} \quad t = 1,\;2, \ldots ,\;T;\quad k = 1,\;2, \ldots ,\;K_{t} $$

(5c)

$$ {\kern 1pt} A_{st}^{ \pm } X_{t}^{ \pm } \left( {u_{st} + \sigma_{st} \phi^{ - 1} \left( {1 - q_{s} } \right)} \right) \le B_{st}^{ \pm } ,\quad s = 1,\;2, \ldots ,\;m_{3} ;\quad t = 1,\;2, \ldots ,\;T $$

(5d)

$$ \sum\limits_{s = 1}^{{m_{3} }} {q_{s} \le q} $$

(5e)

$$ x_{jt}^{ \pm } \ge 0,\;{\kern 1pt} x_{jt}^{ \pm } \in X_{t}^{ \pm } ,{\kern 1pt} \quad j = 1,\;2, \ldots ,\;{\kern 1pt} n_{1} ;\quad t = 1,\;2, \ldots ,\;T $$

(5f)

$$ y_{jtk}^{ \pm } \ge 0,\;y_{jtk}^{ \pm } \in Y_{tk}^{ \pm } ,\quad {\kern 1pt} j = 1,\;2, \ldots ,\;n_{2} ;{\kern 1pt} \quad t = 1,\;2, \ldots ,\;T;\quad k = 1,\;2, \ldots ,\;K_{t} $$

(5g)

where $\phi^{ - 1}$ is the inverse cumulative distribution function of a standard normal random variable. A two-step solution method is proposed for solving the IJPP model. The sub-model corresponding to $f^{ + }$ can be formulated in the first step when the system objective is to be maximized; the other sub-model (corresponding to $f^{ - }$ ) can then be formulated based on the solution of the first sub-model. Thus, the first sub-model is (assume that $B^{ \pm } > 0$ and $f^{ \pm } > 0$):

$$ Max\;f^{ + } = \sum\limits_{t = 1}^{T} {(\sum\limits_{j = 1}^{{j_{1} }} {c_{jt}^{ + } x_{jt}^{ + } } } + \sum\limits_{{j = j_{1} + 1}}^{{n_{1} }} {c_{jt}^{ + } x_{jt}^{ - } } ) - \sum\limits_{t = 1}^{T} {\sum\limits_{k = 1}^{{K_{t} }} {p_{tk} \left(\sum\limits_{j = 1}^{{j_{2} }} {d_{jtk}^{ - } y_{jtk}^{ - } } + \sum\limits_{{j = j_{2} + 1}}^{{n_{2} }} {d_{jtk}^{ - } y_{jtk}^{ + } } \right)} } $$

(6a)

subject to:

$$ \sum\limits_{j = 1}^{{j_{1} }} {\left| {a_{rjt} } \right|^{ - } } {\text{Sign(}}a_{rjt}^{ - } )x_{jt}^{ + } + \sum\limits_{{j = j_{1} + 1}}^{{n_{1} }} {\left| {a_{rjt} } \right|^{ + } } {\text{Sign(}}a_{rjt}^{ + } )x_{jt}^{ - } \le b_{rt}^{ + } {\kern 1pt} ,\quad \forall r,\;t $$

(6b)

$$ \left[ {\sum\limits_{j = 1}^{{j_{1} }} {\left| {a_{sjt} } \right|^{ - } } {\text{Sign(}}a_{sjt}^{ - } )x_{jt}^{ + } + \sum\limits_{{j = j_{1} + 1}}^{{n_{1} }} {\left| {a_{sjt} } \right|^{ + } } {\text{Sign(}}a_{sjt}^{ + } )x_{jt}^{ - } } \right]\left( {u_{st} + \sigma_{st} \phi^{ - 1} \left( {1 - q_{s} } \right)} \right) \le b_{st}^{ + } ,\quad {\kern 1pt} \forall s,\;{\kern 1pt} t $$

(6c)

$$ \sum\limits_{j = 1}^{{j_{1} }} {\left| {a_{ijt} } \right|^{ - } } {\text{Sign(}}a_{ijt}^{ - } )x_{jt}^{ + } + \sum\limits_{{j = j_{1} + 1}}^{{n_{1} }} {\left| {a_{ijt} } \right|^{ + } } {\text{Sign(}}a_{ijt}^{ + } )x_{jt}^{ - } + \sum\limits_{j = 1}^{{j_{2} }} {\left| {a_{ijtk}^{'} } \right|^{ + } } {\text{Sign(}}a_{ijtk}^{' + } )y_{jtk}^{ - } + \sum\limits_{{j = j_{2} + 1}}^{{n_{2} }} {\left| {a_{ijtk}^{'} } \right|^{ - } } {\text{Sign(}}a_{ijt}^{' - } )y_{jtk}^{ + } \le \tilde{w}_{itk}^{ + } {\kern 1pt} ,\quad \forall i,{\kern 1pt} \;t;\quad k = 1,\;2, \ldots ,\;K_{t} $$

(6d)

$$ \sum\limits_{s = 1}^{{m_{3} }} {q_{s} \le q} $$

(6e)

$$ x_{jt}^{ + } \ge 0,{\kern 1pt} \quad \forall t;\quad j = 1,\;2, \ldots ,\;j_{1} $$

(6f)

$$ x_{jt}^{ - } \ge 0,\quad \forall t;\quad {\kern 1pt} j = j_{1} + 1,{\kern 1pt} \quad j_{1} + 2, \ldots ,\;n_{1} $$

(6g)

$$ y_{jtk}^{ - } \ge 0,{\kern 1pt} \quad \forall t;\quad j = 1,\;2, \ldots ,\;j_{2} ;{\kern 1pt} \quad k = 1,\;2, \ldots ,\;K_{t} $$

(6h)

$$ y_{jtk}^{ + } \ge 0,{\kern 1pt} \quad \forall t;{\kern 1pt} \quad j = j_{2} + 1,{\kern 1pt} \quad j_{2} + 2, \ldots ,\;n_{2} ;{\kern 1pt} \quad {\kern 1pt} k = 1,\;2, \ldots ,\;K_{t} $$

(6i)

Let $x_{jt}^{ \pm } ({\kern 1pt} {\kern 1pt} j = 1,\;2, \ldots ,\;j_{1} )$ be variables with positive coefficients in the objective function, $x_{jt}^{ \pm } ({\kern 1pt} {\kern 1pt} j = j_{1} + 1,\;j_{1} + 2, \ldots ,\;n_{1} )$ be variables with negative coefficients, $y_{jtk}^{ \pm } ({\kern 1pt} {\kern 1pt} j = 1,\;2, \ldots ,\;j_{2} {\kern 1pt}$ and ${\kern 1pt} {\kern 1pt} {\kern 1pt} k = 1,\;2, \ldots ,\;K_{t} )$ be recourse variables with positive coefficients in the objective function, and $y_{jtk}^{ \pm } ({\kern 1pt} j = j_{2} + 1,\;j_{2} + 2, \ldots ,\;n_{2}$ and ${\kern 1pt} {\kern 1pt} {\kern 1pt} k = 1,\;2, \ldots ,\;K_{t} )$ be recourse variables with negative coefficients. Solutions of $x_{{jt{\text{opt}}}}^{ + } ({\kern 1pt} {\kern 1pt} j = 1,\;2, \ldots ,\;j_{1} )$, and $x_{{jt{\text{opt}}}}^{ - } ({\kern 1pt} {\kern 1pt} j = j_{1} + 1,\quad j_{1} + 2, \ldots ,\;n_{1} )$, $y_{{jtk{\text{opt}}}}^{ - } (j = 1,\;{\kern 1pt} 2, \ldots ,\;j_{2}$ and ${\kern 1pt} {\kern 1pt} {\kern 1pt} k = 1,\;2, \ldots ,\;K_{t} )$, and $y_{{jtk{\text{opt}}}}^{ + } ({\kern 1pt} {\kern 1pt} j = j_{2} + 1,\;j_{2} + 2, \ldots ,\;n_{2} {\kern 1pt}$ and ${\kern 1pt} {\kern 1pt} {\kern 1pt} k = 1,\;2, \ldots ,\;K_{t} )$ can be obtained through solving sub-model (6). Based on the above solutions, the second sub-model corresponding to $f^{ - }$ can be formulated as follows:

$$ Max{\kern 1pt} \;f^{ - } = \sum\limits_{t = 1}^{T} {(\sum\limits_{j = 1}^{{j_{1} }} {c_{jt}^{ - } x_{jt}^{ - } } } + \sum\limits_{{j = j_{1} + 1}}^{{n_{1} }} {c_{jt}^{ - } x_{jt}^{ + } } ) - \sum\limits_{t = 1}^{T} {\sum\limits_{k = 1}^{{K_{t} }} {p_{tk} (\sum\limits_{j = 1}^{{j_{2} }} {d_{jtk}^{ + } y_{jtk}^{ + } } + \sum\limits_{{j = j_{2} + 1}}^{{n_{2} }} {d_{jtk}^{ + } y_{jtk}^{ - } } )} } $$

(7a)

subject to:

$$ \sum\limits_{j = 1}^{{j_{1} }} {\left| {a_{rjt} } \right|^{ + } } {\text{Sign(}}a_{rjt}^{ + } )x_{jt}^{ - } + \sum\limits_{{j = j_{1} + 1}}^{{n_{1} }} {\left| {a_{rjt} } \right|^{ - } } {\text{Sign(}}a_{rjt}^{ - } )x_{jt}^{ + } \le b_{rt}^{ - } ,\quad \forall r,\;t $$

(7b)

$$ \left[ {\sum\limits_{j = 1}^{{j_{1} }} {\left| {a_{sjt} } \right|^{ + } } {\text{Sign(}}a_{sjt}^{ + } )x_{jt}^{ - } + \sum\limits_{{j = j_{1} + 1}}^{{n_{1} }} {\left| {a_{sjt} } \right|^{ - } } {\text{Sign(}}a_{sjt}^{ - } )x_{jt}^{ + } } \right]\left( {u_{st} + \sigma_{st} \phi^{ - 1} \left( {1 - q_{s} } \right)} \right) \le b_{st}^{ - } {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \forall s,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} t $$

(7c)

$$ \sum\limits_{j = 1}^{{j_{1} }} {\left| {a_{ijt} } \right|^{ + } } {\text{Sign(}}a_{ijt}^{ + } )x_{jt}^{ - } + \sum\limits_{{j = j_{1} + 1}}^{{n_{1} }} {\left| {a_{ijt} } \right|^{ - } } {\text{Sign(}}a_{ijt}^{ - } )x_{jt}^{ + } + \sum\limits_{j = 1}^{{j_{2} }} {\left| {a_{ijtk}^{'} } \right|^{ - } } {\text{Sign(}}a_{ijtk}^{' - } )y_{jtk}^{ + } + \sum\limits_{{j = j_{2} + 1}}^{{n_{2} }} {\left| {a_{ijtk}^{'} } \right|^{ + } } {\text{Sign(}}a_{ijt}^{' + } )y_{jtk}^{ - } \le \tilde{w}_{itk}^{ - } {\kern 1pt} ,\quad \forall i,\;t;\quad k = 1,\;2, \ldots ,\;K_{t} $$

(7d)

$$ \sum\limits_{s = 1}^{{m_{3} }} {q_{s} \le q} $$

(7e)

$$ 0 \le x_{jt}^{ - } \le x_{jtopt}^{ + } ,\quad \forall t;\quad {\kern 1pt} j = 1,\;2, \ldots ,\;j_{1} $$

(7f)

$$ x_{jt}^{ + } \ge x_{{jt{\text{opt}}}}^{ - } ,\quad {\kern 1pt} \forall t;\quad j = j_{1} + 1,\;j_{1} + 2, \ldots ,\;n_{1} $$

(7g)

$$ y_{jtk}^{ + } \ge y_{{jtk{\text{opt}}}}^{ - } ,\quad \forall t;\quad j = 1,\;2, \ldots ,\;j_{2} ;\quad k = 1,\;2, \ldots ,\;K_{t} $$

(7h)

$$ 0 \le y_{jtk}^{ - } \le y_{{jtk{\text{opt}}}}^{ + } ,\quad \forall t;{\kern 1pt} \quad j = j_{2} + 1,\;{\kern 1pt} j_{2} + 2, \ldots ,\;n_{2} ;{\kern 1pt} \quad k = 1,\;2, \ldots ,\;K_{t} $$

(7i)

Solutions of $x_{jtopt}^{ - } ({\kern 1pt} {\kern 1pt} j = 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} .{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} .{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} .{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} j_{1} )$, $x_{{jt{\text{opt}}}}^{ + } (j = j_{1} + 1,\;j_{1} + 2, \ldots ,\;{\kern 1pt} n_{1} )$, $y_{{jtk{\text{opt}}}}^{ + } (j = 1,{\kern 1pt} \;2, \ldots ,\;j_{2}$ and ${\kern 1pt} {\kern 1pt} {\kern 1pt} k = 1,\;2, \ldots ,\;K_{t} )$, and $y_{{jtk{\text{opt}}}}^{ - } (j = j_{2} + 1,\;j_{2} + 2, \ldots ,\;n_{2} {\kern 1pt}$ and ${\kern 1pt} {\kern 1pt} {\kern 1pt} k = 1,\;2, \ldots ,\;K_{t} )$ can be obtained through solving sub-model (7). Therefore, combining solutions of sub-models (6) and (7), solution for the IJPP model can be expressed as follows:

$$ x_{{jt{\text{opt}}}}^{ \pm } = \left[ {x_{{jt{\text{opt}}}}^{ - } ,x_{{jt{\text{opt}}}}^{ + } } \right],{\kern 1pt} \quad j = 1,\;2, \ldots ,\;n_{1} ;\quad \forall t $$

(8a)

$$ y_{{jtk{\text{opt}}}}^{ \pm } = \left[ {y_{{jtk{\text{opt}}}}^{ - } ,y_{{jtk{\text{opt}}}}^{ + } } \right],\quad j = 1,{\kern 1pt} \;2,{\kern 1pt} \ldots ,\;n_{2} ;\quad k = 1,{\kern 1pt} \;2,{\kern 1pt} \ldots ,\;K_{t} ;\quad \forall t $$

(8b)

$$ f_{\text{opt}}^{ \pm } = \left[ {f_{\text{opt}}^{ - } ,f_{\text{opt}}^{ + } } \right] $$

(8c)

3 Case study

The following water resources management problem is used to demonstrate applicability of the IJPP method. Consider a case in which a manager is responsible for allocating water from two unregulated reservoirs to three users: a municipality, an industrial unit, and an agricultural sector. Owing to the extremely uneven distributions of precipitation, the available water resources present a remarkable pattern of seasonal variations (Li et al. 2006; Fayaed et al. 2013; Mahiny and Clarke 2013; Gibbs et al. 2014). In the wet seasons, high rainfall recharging into the river may result in ample available water, total water demands of users may be satisfied. While in the dry seasons, low rainfall may result in insufficient available water; there is not enough available water to satisfy all needs, leading to that the competing water users would face the water-shortage risk. Water shortage can pose a number of impacts on water-resources management, the human life and health, as well as industrial and agricultural development. Otherwise to protect water supplies against shortages, the water may be obtained from more expensive sources or the demand will be curtailed, resulting in penalties (i.e., negative consequences) to the local economy (Li and Huang 2009). Meanwhile, the effects of water shortage and the need for clean water have led to competition and political strife among competing agricultural, industrial, and municipal sectors. Moreover, with the effects of the different characters of economic data and water demand targets in these competing water users, different water consumers have characters of different guarantee ratios and different priorities from different water supply schemes. The differentiation for each user that the water user whom is more likely to engage in water scarcity conflicts and more easily convinced to engage in more shortages of water resources are existed in the water resources management. If the targeted water is delivered, revenues will be generated for each unit of water allocated; however, if the targeted water is not delivered, penalties will be generated from the shortfalls (Loucks et al. 1981; Li et al. 2006).

In the study system, the stream inflow is random variable with known probability distributions; the relevant water allocation plan would be of dynamic feature over a three-period context; and uncertainties also provided as intervals for water-allocation targets and economic data existed in water uses. Furthermore, in such a multi-user system, uncertainties presented in terms of joint probabilities are existed in terms of water availabilities among multiple competing water users (i.e., the available water may be fixed with a level of probability). Different joint probabilities represent the different admissible risk of violating the uncertain available water constraints and it can be accounted as part of risk management to control water shortage in order to avoid or mitigate the loss in decision making processes. Additionally, a tradeoff may exist between system benefit and constraint-violation risk which often needs to be made in an attempt to find an acceptable balance between reliability and vulnerability of the system. In general, since uncertainties exist in water resources management system components (provided as intervals, randomness, joint probability, as well as dynamic policy scenarios), the IJPP method can help to identify desired water-allocation plans with a maximized net benefit and a minimized water shortage risk. Thus, the study problem can be formulated as follows:

$$ {\text{Max}}\;{\kern 1pt} f^{ \pm } = \sum\limits_{i = 1}^{I} {\sum\limits_{t = 1}^{T} {(NB_{it}^{ \pm } - EX_{it}^{ \pm } )W_{it}^{ \pm } } } - \sum\limits_{i = 1}^{I} {\sum\limits_{t = 1}^{T} {\sum\limits_{k = 1}^{{K_{t} }} {p_{tk} } C_{it}^{ \pm } D_{itk}^{ \pm } } } $$

(9a)

subject to:

$$ S_{1(t + 1)k}^{ \pm } = S_{1tk}^{ \pm } + \tilde{Q}_{tk}^{ \pm } - \left[ {A_{1a} e_{1t} \left( {\frac{{S_{1t}^{ \pm } + S_{1(t + 1)}^{ \pm } }}{2}} \right) + A_{10} e_{1t} } \right] - R_{1tk}^{ \pm } ,\quad \forall t;{\kern 1pt} \quad k = 1,\;2, \cdots ,\;K_{t} $$

(9b)

$$ S_{2(t + 1)k}^{ \pm } = S_{2tk}^{ \pm } + R_{1tk}^{ \pm } - \left[ {A_{2a} e_{2t} \left( {\frac{{S_{2t}^{ \pm } + S_{2(t + 1)}^{ \pm } }}{2}} \right) + A_{20} e_{2t} } \right] - R_{2tk}^{ \pm } ,\quad \forall t;\quad k = 1,\;2, \ldots ,\;K_{t} $$

(9c)

$$ \Pr \left\{ {\sum\limits_{i = 1}^{I} {(W_{it}^{ \pm } - D_{itk}^{ \pm } )} (1 + \theta_{m} ) \le R_{2tk}^{ \pm } } \right\} \ge 1 - q_{m} ,\quad m = 1,\;2,\;3 $$

(9d)

$$ \sum\limits_{m = 1}^{M} {q_{m} \le q} $$

(9e)

$$ \theta_{m} \sim N(\mu_{m} ,\sigma_{m}^{2} ) $$

(9f)

$$ S_{ntk}^{ \pm } \le RSC_{n}^{ \pm } ,\quad \forall t;\quad n = 1,\;2 ;\quad k = 1,\;2, \ldots ,\;K_{t} $$

(9g)

$$ S_{ntk}^{ \pm } \ge RSV_{n}^{ \pm } ,\quad \forall t;\quad n = 1,\;2 ;\quad k = 1,\;2, \ldots ,\;K_{t} $$

(9h)

$$ W_{it\hbox{max} }^{ \pm } \ge W_{it}^{ \pm } \ge D_{itk}^{ \pm } \ge 0,{\kern 1pt} \quad \forall \;i,\;t,\;k $$

(9i)

where A ₀ is the storage-area coefficient; A _a is the area per unit of active storage volume above A ₀ ; PE _it is the reduction of net benefit to user i per unit of water not delivered during period t ($/m³), (PE _it  > NB _it ); EX _it is the acquisition cost, proportional to the amount of imported water to users during period t ($/m³); D _itk is the shortage by which the water-allocation target (W _it ) is not met in period t under scenario k (m³); e _t is the average evaporation rate in period t; f is the net system benefit over the planning horizon ($); i is the water user, i = 1, 2,…, I; K _t is the number of scenarios in period t; NB _it is the net benefit to user i per unit of water allocated during period t ($/m³); p _tk is the probability of occurrence for scenario k in period t, with p _tk  > 0 and $\sum\nolimits_{k = 1}^{{K_{t} }} {p_{tk} } = 1$; Q _tk is the random inflows into the river in period t under scenario k (m³); R _tk is the release flows from the river in period t under scenario k (m³); RSC is the storage capacity of the river (m3); RSV is the reserved storage level for the river (m³); S _tk is the storage level in the river in period t under scenario k (m³); t is the time period, t = 1, 2,…, T; W _it is the fixed allocation target for water that is promised to user i during period t (m³); W _itmax is the maximum demand amount for user i during period t (m³). In the expression given by constraint (9d), the related constraints are satisfied at a certain probability (1 − q _m ); q _m stands for individual probability and q stands for a pre-determined joint probability denoting the acceptable risk-level set by the decision-makers to violate the chance constraint. In the above nonlinear programming model, the water loss rates $\theta_{m}$ of the constraints are expressed as random parameters with normal distributions ($\mu_{m}$ is expectation and $\sigma_{m}$ is standard variation).

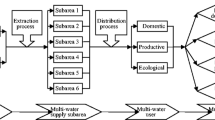
Figure 1 shows the framework of IJPP method for water-resources management. The objective is to maximize the expected net system benefit through allocating the water resources to multiple users over a multistage context. Constraints (9b) and (9c) present the mass balance for water resources in each time period (i.e., the change in storage equals inflows minus releases and evaporation losses), where the evaporation loss is assumed to be a linear function of the average storage; constraint (9d) means that the actual water allocated to the users must not exceed the amount of water released from the reservoir, and this constraint also allows the spill of extra water; constraint (9 g) specifies that the storage amount must not exceed the reservoir capacity under all scenarios; constraint (9 h) requires that the storage will not lower a reserve level under all scenarios; constraint (9i) indicates that the allocated water must not exceed the users’ maximum requirements and means that the shortage (i.e., decision variable) must be nonnegative.

Fig. 1

Framework of IJPP method for planning water resources system

Table 1 shows the target demands from municipal (including residential, tourism, and municipal services), industrial (including livestock and fisheries, industry and urban public facilities), and agricultural (including irrigation, forestry and animal husbandry) sectors. The time horizon of this study is divided into three planning periods. Table 2 shows the available water resources in the river basin and the associated probabilities of occurrence in three planning periods. Shortages in water supply will occur if insufficient water is available, such that the promised demand targets cannot be satisfied (i.e., shortage = demand target − available stream). Under such a situation, the actual water-allocation value will be the difference between the fixed demand and the probabilistic shortage (i.e., water allocation = demand target − shortage). Table 3 presents the related benefits and penalties. If the promised water is not delivered, either the water must be obtained from higher priced alternatives, or the demands must be curtailed with the costs of reduced industrial and/or agricultural productions. These would then result in a reduction of net benefit (i.e., penalty) to each user (Loucks et al. 1981; Li et al. 2006). In this case, random water availability with probability p _tk was used to construct three scenario trees for the planning horizon with a branching structure of 1–3–3–3. In detail, there are one initial node at time 0 (the present) and three succeeding ones in period 1; each node in period 1 has three succeeding nodes in period 2, and so on for each node in period 3. These result in 27 nodes (scenarios) in period 3. Besides, the initial storages in reservoirs 1 and 2 are [5.0, 40.0] and [10.0, 50.0] × 10⁶ m³, respectively; the storage capacities in reservoirs 1 and 2 are [38.0, 56.0] and [36.0, 55.0] × 10⁶ m³, respectively; the reserved storage levels in reservoirs 1 and 2 are [25.0, 28.0] and [30.0, 32.0] × 10⁶ m³. Water loss rates are N (0.05, 0.07²), N (0.04, 0.06²) and N (0.03, 0.05²) in the three periods, respectively.

Table 1 Water allocation targets

Table 2 Stream flows (10⁶ m³)

Table 3 Net benefit, penalty and acquisition cost

4 Results and discussion

4.1 Result analysis

In this study, a number of cases associated with different joint and individual probabilities (as listed in Table 4) were examined. In the IJPP model, an increased q level means a raised risk of violating joint-probabilistic constraints and, at the same time, a decreased strictness for the satisfactory level in meeting the water demand constraint, and vice versa. To demonstrate the effect of robustness on the model results, the system is optimized for violation joint probabilities ranging from 0.01 (the most conservative) to 0.20 (the most radical). Meanwhile, at each level of joint probability, two individual probabilities were considered. For example, case 1 and case 2 are under the same joint probability with different individual probabilities.

Table 4 Different probability levels

In the study area, the water resources are used to satisfy the water needs from municipal, industrial, and agricultural sectors. Deficits would occur if the available flows do not meet the user’ demands over the planning horizon. The solutions for most of the non-zero water shortages ($D_{itk}^{ \pm }$) are interval numbers under the given targets, reflecting potential system-condition variations due to uncertain inputs. Particularly, based on the modeling solutions, it can be concluded that there would be almost no water deficit for the municipal user under most possible scenarios over the planning periods. This implies that the optimized allocated water would equal the water-allocation targets for the municipality. Figures 2 and 3 present the optimized lower- and upper-bound water shortage patterns for industrial and agricultural sectors under case 3 (joint probability = 0.05) and case 9 (joint probability = 0.20). For industrial user under case 3, shortages may exist under low, medium and high flow levels in period 1, (i.e., $D_{211opt}^{ \pm } = 9 2. 2 \times 10^{ 6} {\text{m}}^{ 3}$, $D_{212opt}^{ \pm } = \left[ { 5 6. 1,{ 92}. 2} \right] \times 10^{ 6} {\text{m}}^{ 3}$, and $D_{213opt}^{ \pm } = \left[ {0,{ 62}. 3} \right] \times 10^{ 6} {\text{m}}^{ 3}$). Similarly in period 2, water shortages for the industry would be 115.2 × 10⁶, [58.7, 88.7] × 10⁶ and 0 m³, respectively, when the flow levels are low, medium and high in period 2 (following a low flow in period 1). In period 3, if the water levels are low in the previous two periods, while flows in period 3 are low, medium and high, then the water shortages would be 132.7 × 10⁶, [94.6, 132.7] × 10⁶ and [0, 70.9] × 10⁶ m³, respectively. In comparison, when the flows are high in the previous two periods, there would be no shortage for all users in period 3 even though the flow level in this period is low (i.e., $D_{1325opt}^{ \pm } = D_{2325opt}^{ \pm } = D_{3325opt}^{ \pm } = 0$). Moreover, the water shortage pattern as well as shows a significant difference between the agricultural and industrial sectors over the planning periods. For example, while flows in period 3 are low, medium and high (following a medium flow in the previous two periods), shortages for agricultural sector would be 112.6, 112.6 and [87.8, 112.6] × 10⁶ m³, respectively; correspondingly, the shortage for the industrial sector would be [97.5, 132.7], [17.0, 72.0] and [0, 14.5] × 10⁶ m³, respectively, which are different from the agricultural sector. The water-shortage patterns under other scenarios can be similarly interpreted based on the results.

Fig. 2

Solutions of water shortage under case 3 (a industry and b agriculture)

Fig. 3

Solutions of water shortage under case 9 (a industry and b agriculture)

Additionally, it can be obviously observed that with the highest risk of violating the water target demands (i.e., q = 0.20), the water-shortage patterns under case 9 (as shown in Fig. 3) are different from it under case 3 (as shown in Fig. 2). For example, in period 2 when flow levels are low, medium and high (following a medium flow in period 1), shortages for industrial user under case 9 would be 115.2, [0, 67.4] and 0 × 10⁶ m³, respectively; correspondingly, it would be 115.2, [0, 66.6] and 0 × 10⁶ m³, respectively, under case 3. Similarly in period 3 while flows are low, medium and high (following a low flow in the previous two periods), shortages for agricultural sector under case 9 would be 112.6, 112.6 and [95.0, 112.6] × 10⁶ m³, respectively; while it would be 112.6, 112.6 and [108.8, 112.6] × 10⁶ m³, respectively, under case 3.

Each allocated flow is the difference between the promised target and the probabilistic shortage under a given stream condition with an associated probability level ($A_{itopt}^{ \pm } = W_{itopt}^{ \pm } - D_{itkopt}^{ \pm }$). Figure 4 provides the optimized water allocation patterns to the municipal, industrial, and agricultural sectors over the planning horizon under q = 0.01 and q = 0.20 (i.e., case 1 and case 9). There are 117 scenarios for water allocation associated with different probabilities over the planning horizon. Under case 1 (i.e., q = 0.01), when flows are all low during the entire planning horizon (the worst condition), the total water allocated would be [106.1, 147.1] × 10⁶ m³ ($A_{opt}^{ \pm } = \left[ { 10 6. 1,{ 147}. 1} \right] \times 10^{ 6} {\text{m}}^{ 3}$), while the total water demand from the three users would be 476.7 × 10⁶ m³ ($W_{opt}^{ \pm } = 4 7 6. 7 \times 10^{ 6} {\text{m}}^{ 3}$), demonstrating a serious water shortage ($D_{opt}^{ \pm } = \left[ { 3 2 9. 6,{ 37}0. 6} \right] \times 10^{ 6} {\text{m}}^{ 3}$). Correspondingly, the shortage for municipal would be [84.3, 125.3] × 10⁶ m³ (occupying [25.6, 33.8]% of the total shortage); which is lower than 132.7 × 10⁶ m³ (occupying [35.8, 40.2]%) for industrial; and 112.6 × 10⁶ m³ (occupying [30.4, 34.1]%) for agricultural sectors, respectively. Under a medium condition (i.e., when water flows are medium during the entire planning horizon), the total water allocated would be [280.3, 328.4] × 10⁶ m³, while the total shortage would be [148.3, 196.4] × 10⁶ m³, indicating a significant shortage as well (but less serious than that under the worst condition). The shortages for municipality, industry and agriculture would be 0, [35.7, 83.8], and 112.6 × 10⁶ m³, respectively. In the case of insufficient water, allotments to the agriculture could be first decreased due to its low benefit from water allocation and low penalty for shortfall; then, the shortage would be passed to the industry, while the municipal user should be first guaranteed since it is associated with both high benefit (when target is satisfied) and high penalty (when the promised water is not delivered) with the same amount of water deficit.

Fig. 4

Optimized water-allocation patterns under a case 1 and b case 9

Variations of joint probability would result in different water use efficiencies in different cases (denoted as cases 1–10) in Fig. 5. For example, the joint probability and the water use efficiency (i.e., q = 0.20 and 87.0 %) under case 10 would both be higher than those under case 1 (i.e., q = 0.01 and 79.6 %). It can be explained that the relaxations(i.e., a higher joint probability) of system constraints would lead to raised available water amount and reduced water losses, correspondingly a higher water use efficiency; and vice versa. On the other hand, the water use efficiency would vary with individual probability (q _i ) level. For example, when a same joint probability (i.e., q = 0.05) is existed under case 3 (i.e., q ₁  = 0.008, q ₂  = 0.012 and q ₃  = 0.030) and case 4 (i.e., q ₁  = q ₂  = q ₃  = 0.0166), the water use efficiencies would be 82.9 and 83.2 % differently.

Fig. 5

Different water use efficiencies in different cases

Variations in the q level correspond to the decision makers’ preferences regarding the tradeoff among system benefit, penalty, and constraint-violation risk. Figures 6 and 7 provide the variations of system-benefit and penalty with different water use efficiencies (i.e., varying joint probability levels). Given different underlying probability levels as well as water-availabilities, the expected system benefit and the total penalty would change correspondingly between their lower and upper bound. A lower joint probability level would result in a lower system benefit and a lower constraint-violation risk; conversely, a higher joint probability would sacrifice the system safety in order to reduce the penalty. For example, the system benefit ($f_{opt}^{ \pm }$) in Fig. 6 would be $ [415.1, 6744.0] × 10⁶ under case 3, lower than $ [547.2, 6876.8] × 10⁶ under case 5, and $ [636.9, 6961.5] × 10⁶ under case 7 (i.e., when q = 0.05, 0.10 and 0.15), respectively. Solutions indicate that the system benefit would also vary with individual probability (q _i ) level.

Fig. 6

System benefits from the IJPP model under varying water use efficiencies

Fig. 7

Penalties under varying water use efficiencies

However, an opposite trend of the variations of total penalty with different water use efficiencies (i.e., varying joint probability levels) is shown in Fig. 7. For example, the total penalty would be $ [3445.5, 7003.3] × 10⁶ under case 3, which is higher than $ [3365.7, 6911.0] × 10⁶ under case 5 and $ [3308.3, 6841.7] × 10⁶ under case 7, respectively. It can be concluded that different policies in regulating the constraint-violation risks are associated with different levels of economic benefit and economic implications (e.g., losses or penalties caused by improper policies). For example, decisions with lower constraint-violation risks would be associated with a lower system benefit but increased system reliability; a desire for higher benefit could result in raised risks of violating the system constraints. However, a desire for lower total penalty would result in decreased system reliability and higher risks of violating the system constraints; which is opposite to the relationship between system benefit and system reliability.

Figure 8 provides a comparison of resulting lower- and upper-bound water shortage patterns for industrial and agricultural users under case 1 and case 9. These imply that (a) under advantageous conditions (e.g., when the available water amounts approach their upper bounds), the shortage levels may be low, and (b) under demanding conditions, the shortage levels may be raised. Meanwhile, a larger number of water shortage scenarios is existed under case 1 than under case 9. For example, under advantageous conditions under case 1, the number of scenarios subjecting to water-shortage risks w would be 60 (occupying 51.3 % of the total water-allocation scenarios; in this case, the number of total water-allocation scenarios would be 117 over the planning horizon) under case 1, that is higher than 56 (occupying 47.9 %) under case 9. However, under demanding conditions, such a number would be increased to 78 (occupying 66.7 %) under case 1 under case 1, which is also higher than 72 (occupying 61.5 %) under case 9.

Fig. 8

Solutions of water shortage under case 1 and case 9 (a industry and b agriculture)

Moreover, a larger amount of water shortage is existed under case 1 than under case 9. For example, when the flow levels are medium and high in period 3 (following a low flow in period 1 and a medium flow in period 2), water shortages for the industrial sector would be [72.3, 130.1] and [46.7, 78.7] × 10⁶ m³ under case 1, which is higher than [48.6, 111.1] and [20.9, 55.5] × 10⁶ m³ under case 9. Similarly, when the flow levels are medium and high in period 3 (following a high flow in period 1 and a medium flow in period 2), water shortages for the agricultural sector would be [111.3, 112.6] and [42.2, 112.6] × 10⁶ m³ under case 1, which is also higher than [81.7, 112.6] and [3.3, 85.2] × 10⁶ m³ under case 9. The water shortage patterns for all users would have generally decreasing trends with the increasing joint probability. It can be explained that a higher level of joint probability corresponds to a relaxed decision domain, a more reliability of sufficient water supply, which results in a higher satisfactory degree of water demands constraint and lower risk of water-shortage.

On the other hand, at the same joint probability over the planning horizon, the optimized water-shortage patterns between increasing individual probability and those at equal individual probability for each user as well show an obvious difference. Figure 9 presents the typical different water shortage patterns under case 9 and case 10. The total number of typical different water-shortage patterns is 58, which is consisted of eleven typical different water shortage scenarios for municipal, thirty scenarios for industrial and seventeen scenarios for agricultural sectors. It can be found that a higher amount of water shortage pattern is existed under case 9 than under case 10. For example, when the flow levels is low in period 1 and high in period 2, the water shortage would be [30.9, 64.6] × 10⁶ m³ under case 9, lower than [36.5, 70.3] × 10⁶ m³ under case 10. Similarly, when the flow level is medium in period 3 (following low flows in period 1 and period 2), the water shortage for the industrial sector would be [84.5, 132.7] × 10⁶ m³ under case 9, lower than [88.4, 132.7] × 10⁶ m³ under case 10. However, for all users in period 1, the relationship between the optimized water-shortage patterns at the same joint probability would be higher under the case with increasing individual probability, than the other case with equal individual probability. It is indicated that the effects of individual probability levels on the IJPP model results would vary in different periods when joint probability levels were kept as the same.

Fig. 9

Water shortage scenarios under case 9 and case 10

4.2 Comparison of IJCP with IJPP

If the uncertainty in the stream inflow is simplified from random variable into interval value, the study problem can then be formulated as an inexact joint-probabilistic left-hand-side chance-constrained programming (IJCP) model. Similarly, ten cases of IJCP model were examined based on multiple joint probabilities and individual probabilities. Each IJCP model was transformed into two submodels that corresponded to the lower and upper bounds of the objective function values. The solutions of water-allocation patterns from the IJCP model are provided in Table 5, which are significantly different from the solutions from the IJPP (as shown in Fig. 4). For example, in period 1, from the IJCP model (joint probability = 0.01), the amounts of water allocated to municipal, industrial and agricultural sectors would be 312.7 × 10⁶, [208.4, 248.6] × 10⁶ and [0, 54.3] × 10⁶ m³, respectively; in comparison, when the stream inflow is low in period 1, the amounts of water allocated to municipal, industrial and agricultural sectors would be [106.1, 134.7] × 10⁶, 0 and 0 m³, respectively; similarly, when the inflow level is medium in period 1, the amounts of water allocated to the three users would be [102.1, 134.7] × 10⁶, [0, 32.8] × 10⁶ and 0 m³, respectively; and when the stream inflow is high in period 1, the water allocated to municipal, industrial and agricultural sectors would be 134.7 × 10⁶, [26.6, 92.2] × 10⁶ and 0 m³, respectively, from the IJPP model. In period 3, there would also be only one water-allocation pattern for each water user from the IJCP; in compassion, under the same case (joint probability = 0.01), there would be totally 81 water-allocation scenarios for municipal, industrial and agricultural users from the IJPP model, with a three-period (four-stage) scenario tree that generated with a branching structure of 1-3-3-3 from IJPP model. Summarily, the IJPP could incorporate more dynamic and uncertain information within its modeling framework, for its formulation of the dynamics and uncertainties of water availability (and thus water allocation and shortage) is conceptualized into generation of a set of representative scenarios within a multistage context. In comparison, without transactions at discrete points of a complete scenario set over a multistage context, the IJCP is unable to reflect the dynamic uncertainties of inflow stream in terms of decisions for water allocation.

Table 5 Water-allocation patterns and net system benefits from the IJCP model

Table 5 also presents the solutions of system benefits from the IJCP model. The results indicate that the system benefits obtained through the IJCP model are higher than those through the IJPP model (as shown in Fig. 6) under a range of joint and individual probability levels. For example, the result of system benefit from IJCP under case 1 would be $ [3371.6, 5875.6] × 10⁶, higher than $ [98.2, 6494.6] × 10⁶ from IJPP. The corresponding mid-value (i.e., $f_{opt}^{mid} = (f_{opt}^{ - } + f_{opt}^{ + } )/2$) would be $ 4623.6 × 10⁶ from IJCP, which is also higher than it from IJPP (i.e., $ 3296.4 × 10⁶). Due to the simplification of the uncertainties, the IJCP cannot reflect economic penalties as corrective measures or recourse against any infeasibilities arising due to a particular realization of uncertainty, lead to a higher system benefit from the IJCP. In comparison, the IJPP shows a conservative attitude towards the economic benefit (i.e., a lower system benefit), and can make a decision at each stage in a real-time manner based on information about the actual realizations of the random variables as well as the earlier decisions. Generally, the IJCP is unable to support analyses for a variety of policy scenarios that are associated with different levels of economic penalties.

5 Conclusions

In this paper, an IJPP model was developed for water resource decision making under uncertainty. It integrates the technique of MSP, IJP, and IPP within a general framework. The major advantages of the developed IJPP method can be outlined as follows: firstly, it can dominate uncertainties presented as intervals in the objective function and randomness in the left- and right-hand sides of constraints. Secondly, with joint probabilistic constraints, it possesses an increased robustness in tackling the system risk in the optimization process. Thirdly, it treats the dynamics of system uncertainties via a scenario tree and the splitting variable representation of the stochastic problem has been considered. Finally, it will facilitate a risk analysis and enable decision-makers to identify effective managing strategies with tackling tradeoffs among system reliability and objectivity.

The developed IJPP method has been applied to a case study of water-resources management. Owing to the randomness uncertainty of available water, risks of water- shortage are existed when there is not enough available water to satisfy all needs. Meanwhile, in such a multi-user system, competition are existed to satisfying the competing water demands from different water users, where risk of violating the water target demands are presented as joint probabilities. The results demonstrate that different joint probabilities associated with different admissible risks of violating the uncertain available water constraints, leading to different system benefits, economic penalties, water shortage, and water-allocation patterns. For example, under a medium scenario, with the highest risk of violating the water target demands (i.e., q = 0.20), the total water shortage pattern would be [115.9, 174.6] × 10⁶ m³, lower than [129.6, 184.6] × 10⁶ m³ when the constraint-violation risk is 0.05. Similarly, the economic penalty would also be lower with a higher risk of constraint-violation (i.e., $ [3445.5, 7003.3] × 10⁶ when q = 0.05, and $ [3261.7, 6786.8] × 10⁶ when q = 0.20). In short, a desire for a lower water shortage pattern and a lower economic penalty would be associated with higher risks of violating the system constraints and decreased system reliability; and vice versa.

In comparison, an opposite variation in the system benefit and water-allocation pattern with different constraint-violation risks can be found. Decisions with a higher water-allocation pattern and a higher system benefit would result in higher constraint-violation risk; and vice versa. For example, the system benefit would be $ [708.1, 7029.7] × 10⁶ when q = 0.20, higher than $ [415.1, 6744.0] × 10⁶ when q = 0.05. Correspondingly, the water allocation pattern would be [302.1, 360.8] × 10⁶ m³ when q = 0.20, as well as higher than [292.1, 347.1] × 10⁶ m³ when q = 0.05. Therefore, there is a tradeoff between economic objective, water-shortage and water-allocation patterns and constraint-violation risk. Moreover, different water-guarantee ratios and different water-allocation priorities have been attached to different water consumers with the effects of the different characters of economic data. In general, by explicitly considering a number of different admissible risks of violating the water target demands, the application of IJPP method cannot only gain insight into the tradeoffs between economic objective, water-allocation pattern and constraint-violation risk; but can also help the water resources managers in making a range of alternatives of water allocation on how to effectively allocate water resource to meet competing demands with different water-allocation priorities under uncertainty. Although this study was the first application of the IJPP method to water resources management problems, the results suggest that this improved optimization technique is effective to make decisions based on with risk assessment in controlling the tradeoff between economic objective and constrain-violation risk, and that can be extended to other environmental problems to generate decision alternatives in handling high-variability conditions.