Spatial risk assessment of typhoon cumulated rainfall: a case study in Taipei area

Abstract

Typhoon is one of the most destructive disasters in Taiwan, which usually causes many floods and mudslides and prevents the electrical and water supply. Prior to its arrival, how to accurately forecast the path and rainfall of typhoon are important issues. In the past, a regression-based model was the most applied statistical method to evaluate the associated problems. However, it generally ignored the spatial dependence in the data, resulting in less accurate estimation and prediction, and the importance of particular explanatory variables may not be apparent. Therefore, in this paper we focus on assessing the spatial risk variations regarding the typhoon cumulated rainfall at Taipei with respect to typhoon locations by using the spatial hierarchical Bayesian model combined with the spatial conditional autoregressive model, where the model parameters are estimated by designing a family of stochastic algorithms based on a Markov chain Monte Carlo technique. The proposed method is applied to a real data set of Taiwan for illustration. Also, some important explanatory variables regarding the typhoon cumulated rainfall at Taipei are indicated as well.

1 Introduction

Taiwan is an island country and locates in the subtropical zone. Due to its special geographical position, earthquakes and typhoons both are major natural disasters. In this paper, we focus on discussing the associated problems of typhoon. In Taiwan, typhoon usually happens in summer from early May to late August and attacks us about three or four times every year. It generally brings heavy rain and strong wind, resulting in many floods and mudslides and stops the electrical and water supply. At the same time, typhoon also usually causes heavy economic loss and many people die. In recent years, weather satellites have been able to help us to gain more information about typhoon prior to its arrival, so we may go through a series of preparatory tasks to prevent possible damages; even so, typhoon is still the main cause of disaster loss in Taiwan every year. Therefore, in addition to taking necessary precautions against typhoon, how to develop an efficient statistical methodology to accurately assess the path, rainfall, or intensity of typhoon prior to its arrival is essential. As pointed out by Yeh et al. (1999), there are relatively few methods that can be applied for solving the associated problems. In the past, a regression-based model is a popular statistical method. For example, Neumann (1972) and Xu and Neumann (1985) used a regression model to forecast the path of typhoon, while DeMaria and Kaplan (1994) and Fitzpatrick (1997) also applied a regression model to forecast the intensity of typhoon. In addition, Carter et al. (1989) applied regression prediction equations to an usual weather forecast, and then the Central Weather Bureau (CWB) of Taiwan adopted the same scheme to establish a statistical forecast system to predict the daily high and low temperatures, cloud cover, and rainfalls (Chen et al. 2000). Other issues regarding the rainfall estimation have been widely studied and the readers may consult Unal et al. (2004), Xu and Tung (2009), Lee et al. (2010), and Haddad et al. (2010) for more details. For predicting the rainfall brought by typhoons, Yeh et al. (2001) and Yeh (2002) proposed the forecast models of rainfall based on a linear regression model and the empirical orthogonal function modes, respectively. In addition, Fan and Lee (2007) further combined the Bayesian technique to develop a mixture model for predicting the typhoon rainfall at Taipei. However, none of these studies accommodate the spatial dependence in the data, resulting in the estimation and prediction that may be inaccurate. Hoeting et al. (2006) also indicated that the importance of particular explanatory variables may not be significant when spatial correlation is ignored. Therefore, incorporating spatial dependence into models to assess the spatial risk variations of rainfall is essential.

Spatial statistics arises when the data are points in some Euclidean space and has been widely developed in many fields of study, such as geography, biology, and epidemiology. In the past, researchers mostly focused on modeling the spatial variations in disease risk (e.g., Kelsall and Wakefield 2002; Stern and Cressie 2002). However, how to assess the spatial risk variations for the natural disaster caused by earthquake or typhoon is also an important problem, but it has not been extensively studied in the literatures. Chen and Yang (2011) proposed a joint spatial modeling approach to assess the spatial variations in earthquake risks and obtained much useful information. To our knowledge, there does not have a suitable spatial model that can be satisfactorily applied to the problems of typhoon cumulated rainfall. It is known that most of the disasters caused by typhoons in Taiwan are due to heavy rain, and therefore we focus on assessing the spatial risk variations of typhoon cumulated rainfall at Taipei with respect to typhoon locations in this paper. Motivated from Chen and Yang (2011), we use the spatial hierarchical Bayesian model combined with the spatial conditional autoregressive (CAR) model to account for the spatial dependence among the risks, where a family of stochastic algorithms based on a Markov chain Monte Carlo (MCMC) technique is designed to estimate the model parameters. Based on the framework, some important factors influencing the typhoon cumulated rainfall at Taipei are also discussed.

The rest of this paper is organized as follows. Section 2 introduces the proposed spatial models for assessing the spatial risk variations of typhoon cumulated rainfall at Taipei with respect to typhoon locations and then displays the procedures of estimating the model parameters. Section 3 applies the proposed method to a real data set recorded by Taiwan’s CWB from 1961 to 1994. Finally, a brief discussion is given in Sect. 4.

2 Modeling

Assume that ${\mathbf{A}}\subset{\mathbb{R}}^2$ is the study region of interest. We partition ${\mathbf{A}}$ into N = n ₁ × n ₂ non-overlapping regular grids and denote them as A _i ; i = 1, 2, …, N. In this paper, we are interested in investigating the impact of typhoon locations with respect to h-hour cumulated rainfall over M (in millimeter) at some rainfall station, where h and M are pre-specified values and a data set of h-hour cumulated rainfall at some rainfall station is required for each typhoon within ${\mathbf{A}}.$ Thus, there may be several events (i.e., h-hour cumulated rainfall over M at some rainfall station) for the same typhoon. Let Y _i be a nonnegative integer random variable which counts the number of events when the locations of candidate typhoons are in grid A _i ; i = 1, 2, …, N. In addition, we define the corresponding expected number to be $E_{M}\equiv N^{-1}\sum\nolimits_{j=1}^N Y_j,$ where M is a pre-specified threshold value of typhoon cumulated rainfall. In general, the quantity r _i  = Y _i /E _M is usually used to estimate the relative risk of h-hour cumulated rainfall over M at some rainfall station when a typhoon passes through grid A _i , but it does not accommodate the spatial dependence in the data. It may result in less accurate estimation and large variation. Instead of using independent r _i , in the next section, we introduce the spatial hierarchical Bayesian model combined with the spatial CAR model to account for the spatial dependence among the risks.

2.1 Spatial statistical models

Suppose that R _i is the relative risk of h-hour cumulated rainfall over M at some rainfall station when typhoon locations are in grid A _i . We consider to model the random variables ${\user2{Y}}\equiv(Y_1,\ldots,Y_N)^{\prime}$ to be Poisson distributions as follows

$$ Y_i|R_i\sim Poi(R_iE_M);\quad i=1,2,\ldots,N, $$

(1)

where R _i E _M is the intensity rate of the Poisson process. As suggested in Besag et al. (1991), we further model the relative risks as

$$ \log(R_i)=\alpha+{\user2{X}}_i{\varvec\beta}+\delta_i;\quad i=1,2,\ldots,N, $$

(2)

where ${\user2{X}}_i=(x_{i1},\ldots,x_{ik})$ are grid-level covariates, α and ${\varvec{\beta}}=(\beta_1,\ldots,\beta_k)^{\prime}$ are regression parameters, and ${\varvec{\delta}}=(\delta_1,\ldots,\delta_N)^{\prime}$ are random effects with spatial correlations that reflect small-scale spatial variabilities. In other words, all the variations of log(R _i ), apart from the small-scale fluctuations of spatial dependence, are absorbed mostly into the mean structure $\alpha+{\user2{X}}_i{\varvec{\beta}}.$ For the spatial random component ${\varvec{\delta}},$ it is often assumed to be a stationary process and follows a multivariate normal distribution as follows

$$ {\varvec{\delta}}|\sigma^2,\phi\sim N(0, \sigma^{2}{\user2{V}}(\phi)), $$

(3)

where ${\user2{V}}(\phi)$ is an N × N correlation matrix with the unknown parameter ϕ measuring the degree of spatial dependence among ${\varvec{\delta}},$ and $\sigma^{2}$ is the variance of δ _i ; i = 1, …, N. Here, we further consider the CAR model for the process {δ _i : i = 1, …, N}, resulting in the covariance matrix $\sigma^{2}{\user2{V}}(\phi)$ of (3) that can be decomposed into $({\user2{I}}-\phi{\user2{C}})^{-1}{\user2{M}},$ where ${\user2{I}}$ is an identity matrix, ${\user2{C}}=(c_{ij})$ is a pre-specified N × N spatial association matrix with c _ii  = 0 and c _ij  = c _ji , and ${\user2{M}}=\sigma^{2}{\user2{I}}.$ Note that $({\user2{I}}-\phi{\user2{C}})$ is invertible and $({\user2{I}}-\phi{\user2{C}})^{-1}{\user2{M}}$ is symmetric and positive definite when ϕ ∈ (ϕ _min , ϕ _max ), where ϕ _min and ϕ _max are determined by the reciprocals of the smallest and the largest eigenvalues of ${\user2{C}}.$ There are many spatial correlation functions that can be considered to construct the spatial association matrix ${\user2{C}}.$ However, it would suffer a problem regarding the selection of covariance functions but is beyond the scope of this study. We will briefly discuss the problem in Sect. 4 For simplicity in this study, we defined the (i, j)th entry of ${\user2{C}}$ to be I(i ∼ j), where I(·) is an indicator function and $i \sim j$ represents that grids A _i and A _j are neighbors. The definition is typically called the rook contiguity and I(i ∼ i) ≡ 0. Thus, the conditional distribution of δ _i conditioned on ${\varvec{\delta}}_{-i}$ is given by

$$ \delta_i|\sigma^{2},\phi,{\varvec{\delta}}_{-i}\sim N\left(\phi \sum\limits_{j\in N_i}c_{ij}\delta_j,\sigma^{2}\right);\quad i=1,2,\ldots,N, $$

where ${\varvec{\delta}}_{-i}$ is a vector with the ith element deleted from ${\varvec{\delta}}$ and $N_i\equiv\{j:j \sim i\}$ is the neighborhood set of grid A _i . Obviously, the spatial dependence is found based on the information of neighbors and the degree of dependence depends on the value of ϕ. Applying the Factorization Theorem of Besag (1974) and the properties of a multivariate normal distribution (Cressie 1993, p. 413), the joint distribution of $\delta_i|\sigma^{2},\phi,{\varvec{\delta}}_{-i};\;i=1,\ldots,N$ is a multivariate normal distribution of (3). More details regarding the CAR model can refer to Besag (1974) and Cressie (1993).

2.2 Prior and posterior distributions

Under the Bayesian framework, the prior specification and derivation of posterior distribution both are required. First, some mutually independent and non-informative or conjugate priors for $\sigma^{2},\phi,\alpha,$ and ${\varvec{\beta}}$ are given as follows: (i) the usual non-informative prior is considered for α and ${\varvec{\beta}};$ (ii) an inverse gamma prior IG(a, b) is assumed for $\sigma^{2},$ where constants a and b are pre-specified values so that the prior has variance as large as possible; (iii) we assume an uniform prior U(0, ϕ _max ) for the spatial correlation parameter ϕ because a negative value for ϕ seems unlikely in most applications. Then, applying the Bayes’ theorem, the joint posterior distribution of $(\sigma^2,\phi,\alpha,{\varvec{\beta}},{\varvec{\delta}})$ conditioned on ${\user2{Y}}$ satisfies

$$ \begin{aligned} p\left(\sigma^2,\phi,\alpha,{\varvec{\beta}},{\varvec{\delta}} |{\user2{Y}}\right)&\propto\prod\limits_{i=1}^{N}p\left(Y_i|R_i\right)p \left({\varvec{\delta}}|\sigma^2,\phi\right) \pi(\sigma^2)\pi(\phi)\pi(\alpha)\pi({\varvec{\beta}})\\ &\propto\exp\left(\sum\limits_{i=1}^{N}Y_{i} (\alpha+{\user2{X}}_i{\varvec{\beta}}+\delta_{i})-E_{M}\exp (\alpha+{\user2{X}}_i{\varvec{\beta}}+\delta_{i})\right) \\ &\quad\times(\det(\sigma^2{\user2{V}}(\phi)))^{-1/2} \exp\left(-\frac{1}{2\sigma^2}{\varvec{\delta}}^{\prime} {\user2{V}}(\phi)^{-1}{\varvec{\delta}}\right) \\ &\quad\times\sigma^{-2(a+1)}\exp\left(-\frac{1}{b\sigma^2}\right), \end{aligned} $$

(4)

where π(·) represents a given prior distribution. Because the joint posterior distribution of (4) can not be summarized analytically, we design a family of stochastic algorithms based on MCMC techniques to estimate the model parameters in the next subsection.

2.3 Estimation of parameters

Due to the conjugate prior, we obtain that the conditional posterior distribution of $\sigma^2$ conditioned on all other variables follows an inverse gamma distribution as follows

$$ \sigma^{2}|\phi,{\varvec{\delta}}\sim IG\left(\frac{N}{2}+a, \left(\frac{1}{2}{\varvec{\delta}}^{\prime}({\user2{I}}- \phi{\user2{C}}){\varvec{\delta}}+\frac{1}{b}\right)^{-1}\right). $$

(5)

Therefore, we can apply the Gibbs sampler technique (e.g., Geman and Geman 1984) to generate the posterior samples of $\sigma^{2},$ where the stochastic algorithm successively samples from the conditional posterior distribution of (5) and results in a Markov chain that converges to the joint posterior distribution given in (4) under mild conditions (Tierney 1994).

For $\alpha,\;{\varvec{\beta}},$ and δ _i ; i = 1, …, N, the corresponding conditional posterior distributions are all non-standard. We summarize them as follows

$$ \begin{aligned} p\left(\alpha|\sigma^2,\phi,{\varvec{\beta}},{\varvec{\delta}}, {\user2{Y}}\right)&\propto\prod\limits_{i=1}^{N}p(Y_i|R_i)\pi(\alpha) \\ &\propto\exp\left(\sum\limits_{i=1}^{N}\alpha Y_{i} - E_{M}\exp(\alpha+{\user2{X}}_i{\varvec{\beta}}+\delta_{i})\right), \\ p\left({\varvec{\beta}}|\sigma^2,\phi,\alpha,{\varvec{\delta}}, {\user2{Y}}\right)&\propto\prod\limits_{i=1}^{N}p (Y_i|R_i)\pi({\varvec{\beta}}) \\ &\propto\exp\left(\sum\limits_{i=1}^{N}Y_{i}{\user2{X}}_i{\varvec{\beta}} -E_{M}\exp(\alpha+{\user2{X}}_i{\varvec{\beta}}+\delta_{i})\right), \\ p\left(\delta_i|\sigma^2,\phi,\alpha,{\varvec{\beta}}, {\varvec{\delta}}_{-i},{\user2{Y}}\right) &\propto p(Y_i|R_i) p(\delta_i|\sigma^2,\phi,{\varvec{\delta}}_{-i}) \\ &\propto\exp\left(Y_i\delta_i-E_M\exp(\alpha+{\user2{X}}_i {\varvec{\beta}}+\delta_i)-\frac{1}{2\sigma^2} \left(\delta_i^2-2\delta_i\phi\sum_{j\in N_i}c_{ij} \delta_j\right)\right). \end{aligned} $$

For each variable, a Metropolis–Hastings algorithm is applied to iteratively generate an ergodic Markov chain that yields the posterior samples (e.g. Metropolis et al. 1953; Hastings 1970; Chib and Greenberg 1995). In each step, an update of the current state of the chain is generated from a proposal distribution and the update is then accepted or rejected according to a certain acceptance probability. In practice, a most commonly used algorithm is Gaussian random-walk Metropolis, where the proposal distribution is Gaussian with mean being equal to the current state.

Finally, the conditional posterior distribution of the spatial dependent parameter ϕ is also non-standard but has the following proportional form

$$ \begin{aligned} p\left(\phi|\sigma^2,\alpha,{\varvec{\beta}},{\varvec{\delta}}, {\user2{Y}}\right) &\propto p({\varvec{\delta}}|\sigma^2,\phi)\pi(\phi)\\ &\propto\left(\det\left({\user2{V}}(\phi)\right)\right)^{-1/2} \exp\left(\frac{\phi}{2\sigma^2}{\varvec{\delta}}^{\prime} {\user2{C}}{\varvec{\delta}}\right). \end{aligned} $$

In this paper, a discrete method is considered to generate ϕ due to its computational simplicity, where matrix ${\user2{V}}(\phi)$ can be computed in advance on fine grid points of ϕ. For each step, the probability mass function of ϕ on find grid points can be evaluated and then the posterior sample of ϕ is generated.

3 Analysis on the typhoon cumulated rainfall

In this section, we carry out models (1)–(3) to a real data set of typhoon cumulated rainfall accompanied with some covariates for evaluating the spatial risk variations of typhoon cumulated rainfall in Taipei area with respect to typhoon locations.

3.1 Description of data

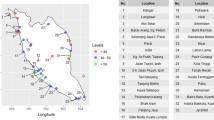
A data set of h-hour typhoon cumulated rainfall at Taipei rainfall station with respect to typhoon locations was supplied by Taiwan’s CWB from 1961 to 1994, which contains 145 typhoons and 9595 data regarding the typhoon cumulated rainfalls at Taipei rainfall station. Note that the original data were collected by Joint Typhoon Warning Center of USA based on 6-h best tracks data of typhoons, and then Taiwan’s CWB adopted the linear interpolation technique to obtain the hourly typhoon center position and relative information. As mentioned in Yeh et al. (1999, 2001), Taipei area is easier to have heavy rains when typhoons pass through ${\user2{A}}=[120^{\circ}{\hbox{E}},125^{\circ}{\hbox{E}}]\times[21.9^{\circ}{\hbox{N}},25.5^{\circ}{\hbox{N}}].$ Thus, in this paper we let ${\user2{A}}$ be our study region and we partition it into N = 15(= 5 × 3) non-overlapping regular grids according to their suggestion. It results in 68 typhoons that appear within ${\user2{A}}.$ Figure 1 shows the study region ${\user2{A}}$ and 15 non-overlapping regular grids. In this study, we use three threshold values of 24-h typhoon cumulated rainfalls, say, M = 50, 100, and 130, to respectively assess the spatial risk variations of 24-h typhoon cumulated rainfall at Taipei with respect to typhoon locations. According to the definition of Taiwan’s CWB, M = 50 and M = 130 are called heavy rain and extremely heavy rain, respectively. We summary the three cases in Table 1 and Figs. 2, 3, 4 display the paths of typhoons and the scatter plots of events with circle marks (i.e., the typhoon locations where 24-h cumulated rainfalls of Taipei rainfall station are over M) for the three cases, where Taipei rainfall station locates in A ₂ and is marked as a triangle.

Fig. 1

The study region A and 15 non-overlapping regular grids

Table 1 Three test cases

Fig. 2

The paths of 38 typhoons and the scatter plots of 486 events for M = 50, where the triangle represents Taipei rainfall station

Fig. 3

The paths of 17 typhoons and the scatter plots of 177 events for M = 100, where the triangle represents Taipei rainfall station

Fig. 4

The paths of 9 typhoons and the scatter plots of 87 events for M = 130, where the triangle represents Taipei rainfall station

In addition to the typhoon cumulated rainfall at Taipei rainfall station, 7 corresponding explanatory variables regarding the characteristics of the Taipei rainfall station and typhoons were also recorded. Note that these explanatory variables were the same as Yeh et al. (2001) and Fan and Lee (2007) who used the linear regression model and mixture models to predict typhoon cumulated rainfalls at Taipei area, respectively. We summarized 7 explanatory variables as follows:

• X ₁: Maximum wind speed of typhoon center

• X ₂: Distance between the Taipei rainfall station (x _s , y _s ) and the typhoon center (x, y)

      $X_2=\sqrt{((x-x_s)\times \cos 20^{\circ})^2+(y-y_s)^2}$

• X ₃: Moving direction angle of typhoon

      $X_3=\frac{360}{2\pi}\times\arctan\left(\frac{y_q-y_p}{x_q-x_p}\right),$ where (x _p , y _p ) and (x _q , y _q ) are locations of a typhoon at time t and time $t+\Updelta t,$ respectively, and $\arctan \left(\frac{y_q-y_p}{x_q-x_p}\right)$ is the corresponding direction radian.

• X ₄: Moving speed of typhoon

    $X_4=\sqrt{((x_q-x_p)\times\cos 20^{\circ})^2+(y_q-y_p)^2}/\Updelta t$

• X ₅: Surface pressure of Taipei rainfall station

• X ₆: Wind speed of Taipei rainfall station

• X ₇: Transformation of the Julian day

    $X_7=\sin\left((X^{\prime}_7-41)\times\frac{\pi}{364.75}\right),$ where $X^{\prime}_7$ is the Julian day of a typhoon at that time.

Note that the transformation formula of X ₇ is based on Neumann (1992) and its maximum value occurs at the Julian date $X^{\prime}_7$ within July–September. In Taiwan, typhoon usually happens in this period. Therefore, if the variable X ₇ is significant with a positive regression coefficient, it indicates that a typhoon happens in the period will bring heavy rainfalls for the Taipei area. In addition to variable X ₇, we can divide variables X ₁–X ₆ into two groups. The first group consists of variables X ₁–X ₄ which are associated with the characteristics of typhoons and another group includes X ₅ and X ₆ which show the status of the Taipei rainfall station.

3.2 Computations and results

For M = 50, 100, and 130, we apply models (1)–(3) with the spatial association matrix ${\user2{C}}$ given in Sect. 2.1 and consider ${\user2{X}}_i=(x_{i1},\ldots,x_{i7});\;i=1,\ldots,15,$ as grid-level covariates in model (2). That is, if there are n _i events within grid $A_i;\;i=1,\ldots,15,$ and each event has 7 explanatory variables, then each component of ${\user2{X}}_i$ can be obtained by taking average over the corresponding n _i values. In addition, for the settings of priors, we take $\sigma^{2}\sim IG(3,0.001),\phi\sim U(0,\phi_{max}),$ and U(−20,20) for α and $\beta_j;\;j=1,\ldots,7,$ where ϕ _max  = 0.32 is obtained by taking the reciprocal of the smallest eigenvalue of ${\user2{C}}.$

For each of M = 50, 100, and 130, we run 200,000 iterations for the posterior computations and discard the first 100,000 iterations as a burn-in. We retain every 10th set of parameter values to obtain approximately independent joint posterior samples of size 10,000, where convergence is assessed by examination of trace and autocorrelation plots. In addition, some theoretical results indicated that the proposal variances in Metropolis–Hastings steps should be tuned to achieve acceptance rates around 0.23 for random walk updates; see Roberts et al. (1997). In our study, the average acceptance rates for updating spatial random effects ${\varvec{\delta}}$ and regression parameters are near 0.22 and 0.20, respectively. Tables 2, 3, and 4 summarize the posterior inferences of model parameters for M = 50, 100, and 130, respectively. Again, parameter ϕ measures the degree of the spatial dependence among the risks. As expected, the posterior mean or median of ϕ for each case is distant from zero, it indicates that the spatial correlation exists among the risks. Therefore, it can not be ignored in analyzing the spatial risk variation of typhoon cumulated rainfalls. Based on the results of Tables 2, 3, and 4, we summarize important explanatory variables for each case in Table 5. In general, we notice that M = 50 and M = 100 have near important explanatory variables but are very different to the case of M = 130. For heavy rains (e.g., M = 50 or M = 100), the results of Table 5 indicate the following four facts (i)–(iv) correspond to variables X ₁, X ₂, X ₄, and X ₇, respectively: (i) if the wind speed of typhoon center is large, Taipei area will have a large risk to suffer the 24-h typhoon cumulated rainfall over M; (ii) when a typhoon approaches the Taipei rainfall station, Taipei area will have a large risk to suffer the 24-h typhoon cumulated rainfall over M; (iii) a typhoon with a slow moving speed will result in a large risk for the Taipei area to suffer 24-h typhoon cumulated rainfall over M; (iv) a typhoon happens within July–September will bring heavy rainfalls for the Taipei area. However, for the case of extremely heavy rain (i.e., M = 130), the results indicate that the moving direction angle of typhoons (X ₃) and the surface pressure of Taipei rainfall station (X ₅) are major reasons to cause the Taipei area to have the 24-h typhoon cumulated rainfall over 130. Importantly, it is very sensible that the moving speed of typhoon (X ₄) is always significant to influence the cumulated rainfalls for all cases. In addition, as mentioned in Sect. 2.1, all the variations among the risks, apart from the small-scale fluctuations of spatial dependence, are absorbed mostly into the mean structure. However, the estimate of $\sigma^{2}$ in model (3) is large for each case. It indicates that there may be other important explanatory variables that have not been discovered in analyzing the typhoon cumulated rainfall of Taipei area.

Table 2 Summary of posterior inferences for the model parameters when M = 50

Table 3 Summary of posterior inferences for the model parameters when M = 100

Table 4 Summary of posterior inferences for the model parameters when M = 130

Table 5 Significant explanatory variables for the three test cases, where “+” and “−” represent positive correlation and negative correlation, respectively

Finally, the estimated relative risks of Taipei area experiencing the 24-h typhoon cumulated rainfall over 50, 100, and 130 when the typhoon locations are within grid $A_i;i=1,\ldots,15,$ are shown in Figs. 5, 6, and 7, respectively. For all three cases, we notice that there are smaller relative risks for Taipei area when the path of typhoon appears within grids A ₆, A ₁₁ and A ₁₂. This is because the counterclockwise rotation of typhoon usually results in its structure being destroyed by the Central Mountain Range of Taiwan. In addition, we also notice that there is a higher relative risk for Taipei area when a typhoon is a west-forward type.

Fig. 5

Posterior means of $R_i=\exp(\alpha+{\user2{X}}_{i}{\varvec{\beta}}+\delta_i);\;i=1,\ldots,15,$ for M = 50

Fig. 6

Posterior means of $R_i=\exp(\alpha+{\user2{X}}_{i}{\varvec{\beta}}+\delta_i);\;i=1,\ldots,15,$ for M = 100

Fig. 7

Posterior means of $R_i=\exp(\alpha+{\user2{X}}_i{\varvec{\beta}}+\delta_i);\; i=1,\ldots,15,$ for M = 130

To sum up, the methodology presented here will help us in assessing the spatial risk variations of the typhoon cumulated rainfall at Taipei area with respect to typhoon locations and hence we can take necessary precautions against typhoon.

4 Discussion and conclusion

In this paper, we developed a spatial hierarchical Bayesian model combined with a spatial conditional autoregressive model to assess the spatial risk variations in the typhoon cumulated rainfalls for the Taipei area with respect to typhoon locations. The proposed method can be easily implemented through the MCMC algorithms. In this study, we focus on assessing the spatial risk variations of typhoon cumulated rainfalls for the Taipei area as the results shown in Figs. 5, 6, and 7. The risk trends of the three cases are basically the same, but we notice that there are different important variables that influence the relative risks of Taipei area experiencing heavy rains when different threshold values M are considered. These results would help the Taiwan’s CWB to forecast the typhoon cumulated rainfall of Taipei area within 24-h based on the typhoon locations and the changes of important explanatory variables. Therefore, we can take necessary precautions against typhoon.

In our study, we recommend the spatial random effects ${\varvec{\delta}}$ in the model to reflect the spatial correlations among the risks, in which parameter ϕ measures the degree of spatial dependence of ${\varvec{\delta}}.$ As demonstrated in Tables 2, 3, and 4, the estimate of ϕ is distant from zero for each case. It indicates that the spatial correlation exists among the risks and hence can not be ignored. In addition, Hoeting et al. (2006) also pointed out that the important explanatory variables may not be significant when spatial correlation is ignored in the modeling procedure. Therefore, incorporating spatial dependence into models to assess the spatial risk variations in typhoon cumulated rainfall is essential. For the spatial association matrix ${\user2{C}},$ we use a simple structure, called the rook contiguity, into our model. Although it may not be the best one, the results of data analysis indicate some useful and significant information for us. Undoubtedly, other spatial correlation functions could also be considered, but it would suffer a problem regarding the selection of covariance functions. For the problem, a fair selection criterion of covariance functions should be proposed, but it is beyond the scope of this study.

Furthermore, we could apply the same technique to analyze spatial risk variations of typhoon cumulated rainfalls for other rainfall stations of Taiwan with respect to typhoon locations. The results would provide some useful information for the prevention of possible damages from typhoons.