The impact of El Niño Southern Oscillation on space time PM₁₀ levels in Peninsular Malaysia: the hierarchical spatio-temporal autoregressive models approach

Abstract

Hierarchical spatio-temporal autoregressive models are useful to understand the impact of predictors on a spatio-temporal-dependent variable. This study aims to fit the model to monthly PM₁₀ concentration using potential predictors from 33 monitoring stations within Peninsular Malaysia from 2006 to 2015 and predict the space–time data spatially and temporally. Using Monte Carlo Markov Chain (MCMC), spatial predictions are obtained based on the posterior and predictive distributions of the model. The posterior distribution of the model that is without covariates exhibits a strong temporal correlation between successive months and also a strong spatial correlation with an effective range of 300 km. Spatio-temporal models were fitted to the data with a sine term, a cosine term, and a lagged El Niño Southern Oscillation (ENSO) index as predictors. Of the 33 monitoring sites, 8 were selected randomly for validation sets. The predictions and forecasts are validated using the root mean square error (RMSE), the mean absolute error (MAE), and the predictive model choice criteria (PMCC). The model with a sine term and a cosine term as predictors produces a reasonable RMSE, MAE, and PMCC of 7.23, 5.91, and 114.54, respectively. It is lower compared to those of the other models. The coverage percentage of the forecast 5–95 percentile range is 89.2% implying good prediction results. The results also show that none of the ENSO indices has a significant impact on the spatial distribution of the PM₁₀ concentration.

1 Introduction

Particulate matter PM is a mixture of fine particles and liquid droplets suspended in the air, consisting of some components such as reactive gases, metals, and carbon core particles (Olaguer 2017) that are related to mortality beyond certain concentration level. The particle size range 10 microns or smaller (PM₁₀) can cause damage to the upper respiratory tract (El Morabet 2019). High concentrations of PM₁₀ in the atmosphere are responsible for adverse health issues (Al-Hemoud et al. 2018; Asl et al. 2018; Feng et al. 2019; Yin et al. 2019), reduction in visibility (Jeensorn et al. 2018; Won et al. 2020), and damage to materials. Since the 2000s, researchers have paid increasing attention to the role of the geographical locations (Manga and Awang 2018), seasonality (Juneng et al. 2011), source of pollutants (Alifa et al. 2020), and meteorological or climatological conditions in modeling the PM₁₀ level in Malaysia. Due to the trend and spatial variability, the PM₁₀ concentration in some parts of Malaysia has exceeded the Recommended Malaysian Air Quality Guidelines (RMAQG) of 150 µg per cubic meter (µg/m3) for daily mean concentration. In this paper, we use the spatio-temporal modeling of the PM₁₀ concentration with global climatological predictors to understand the trend and spatial variability of PM₁₀ levels.

For the statistical modeling, we require attributes that are supposed relevant in conjunction with the atmospheric fields related to the transportation of the particles after emission from its primary origin (Wie and Moon 2017). Thus, attributes related to seasonality may play a role in modeling the PM₁₀ levels. In modelling seasonality, researchers fit the meteorological data with a harmonic seasonal model using the sine and cosine functions as predictors in the model (eg. Yunus et al. 2017; Hasan and Dunn 2012). A few studies have found an association between various global climatological variables and PM₁₀ concentration (eg. in Wie and Moon 2017; Sentian et al. 2018; Hassan et al. 2020; Kim et al. 2013; Kim et al. 2019) using well-known statistical methods such as the Pearson or Spearman’s correlation coefficient, multiple linear regression, and lead-lag correlation analysis. However, most researchers do not take account of both spatial and temporal properties simultaneously in the methods and models.

The seasonal peaks in the concentration of PM₁₀ in Malaysia occur between every June and September and coincide with the southwest monsoon season (Juneng et al. 2009; Noor et al. 2015; Yusof et al. 2009). The strength of the monsoon season depends on the local and sea thermal contrast, with preconditioning by the monsoon air temperatures over land play an important role. The El Niño Southern Oscillation (ENSO) can modulate Malaysia’s rainfall regime, with El Niño (La Niña) events corresponding to low (high) rainfall seasons (Chen et al. 2002; Singhrattna et al. 2005). The El Niño events are concurrent with rainfall deficits and dry weather in Malaysia and other countries in Southeast Asia (Sum 2018). During the period of El Niño events of 1997–1998 and 2014–2015, the transportation of dust particles emitted from massive biomass burning in Sumatra and Kalimantan has led to a sharp increase in the levels of PM₁₀ concentration in Malaysia (Sentian et al. 2018). As reported, the high levels of PM₁₀ coincide with the El Niño events in the country (Shaadan et al. 2015; Sentian et al. 2018).

To investigate the impact of global climatological variables on the level of PM₁₀ concentrations in Peninsular Malaysia, five ENSO indicators, namely NINO12, NINO3, NINO 34, NINO4, Southern Oscillation Indicator (SOI), and ENSO precipitation index (ESPI), are considered for the analysis. The NINO12, NINO3, NINO34, and NINO4 indices are the monthly mean sea surface temperature (SST) anomalies averaged over the region (0°–10° S, 90–80° W), (5° N–5° S, 150°–90° W), (5° N–5° S, 170°–120° W) and the (5° N–5° S, 160° E–150° W) in the Pacific, respectively. SOI is the normalized difference in surface pressure between Tahiti and Darwin. It represents the strength of trade winds that are associated with the flow from high- to low-pressure regions. An ENSO rainfall-based index, known as the ENSO precipitation index (ESPI), is based on rainfall anomalies average measured in two rectangular areas, one in the eastern tropical Pacific (10°N–10°S and 160°E–100°W) and the other over the Maritime Continent (10° S–10° N and 90° E–150° E). It is reported that ESPI is well correlated with sea surface temperature and pressure indices (e.g. NINO 34 and SOI) (Curtis and Adler 2000). Correlations in between NINO12, NINO3, NINO34, and NINO4 indices were reported moderate to strong (Rehman et al. 2012).

The data we are modeling is inherently both spatial and temporal in nature, consisting of PM₁₀ levels measurements taken over time at various locations within Peninsular Malaysia. An overview of spatio-temporal data and modeling of spatio-temporal data can be found in Cressie and Wikle (2011) and Banerjee et al. (2015). Some relevant and recent works in spatio-temporal modeling includes Benth and Šaltytė (2011), Nowak et al. (2018), with specific applications to PM₁₀ data given in Al-Awadhi and Al-Awadhi (2006), Cocchi et al. (2007) and Pollice and Lasinio (2009). Most current works undertaken in spatio-temporal adopt a Bayesian approach, as the hierarchical nature of the models naturally suitable to this framework. The spatio-temporal model that we use to model the PM₁₀ spatio-temporal data is the hierarchical Bayesian autoregressive model proposed by Sahu (2012) to space–time environmental data. It is known as the space–time autoregressive model under the Bayesian hierarchical setup. The model consists of the autoregressive term, the regression term, the Gaussian spatially correlated error term, and the Gaussian non-spatial error term. The model appears to fit better various space–time environmental data (Camaletti et al. 2011; Mukhopadhyay 2019; Manga and Awang 2018) than the other models such as the simple linear regression, the Bayesian linear regression, the Bayesian kriging-based model, and the Gaussian process model, that ignore both space and time simultaneously. Manga and Awang (2018) have considered regional factors for the prediction of the PM₁₀ level using the spatio-temporal model. With a different aim, we consider lagged global factors in our work.

The objective of the research in writing this paper is to quantify the impact of ENSO indicators on the space–time PM₁₀ concentration levels in Peninsular Malaysia using the hierarchical spatio-temporal model approach. The contents of this paper are structured as follows. The following section explains the data used in this study. In Sect. 3, we describe the hierarchical spatio-temporal models considered for the analysis. Section 4 gives the results of fitting models on the space–time PM₁₀ data and the diagnostic validation to evaluate how well the model fits the data. The last section presents the conclusions of this study.

2 Data

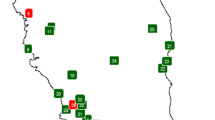
Monthly average of PM₁₀ levels from 33 stations in Peninsular Malaysia (see Fig. 1) recorded from January 2006 to December 2015 are studied (data obtained from the Department of Environmental Malaysia, available on the Malaysia Open Data Portal website https://www.data.gov.my/).

Fig. 1

Spatial distribution of the median of the monthly average of PM₁₀ levels taken over ten years for thirty-three studied stations

The distribution of average monthly PM₁₀ for the 33 stations varies across stations (see Fig. 2). The monthly average of PM₁₀ concentrations ranges from the minimum of 15.68 μg/m³ in Tanjung Malim (in the northern) to the maximum of 134.15 μg/m³ in Pelabuhan Klang (in the central region of Peninsular Malaysia). The central zone has a broader range of monthly PM₁₀ concentrations than in other places. The median of the monthly PM₁₀ levels of about 61% of the stations ranged between 40 and 50 μg/m³, 12% is above 50 μg/m³, and 27% is below 40 μg/m³ (see Fig. 1).

Fig. 2

Boxplots of monthly average PM₁₀ concentration levels for all studied stations

The annual PM₁₀ values range between 40.67 and 50.06 µg/m3 (see Fig. 3) and below the annual limit value (50 µg/m³) set by Malaysia Air Quality Guideline from 1994 to 2014, and slightly exceeds the limit for the year 2015. However, they are above the annual air quality guideline set by European and national legislation (40 µg/m³) and WHO (20 µg/m3). The variation in the monthly average concentration of PM₁₀ across time for all stations shows a cyclical pattern. Generally, the monthly PM₁₀ concentrations were higher from June to September than in the other months.

Fig. 3

Annual and monthly average PM₁₀ concentration temporal trend

The boxplots for the monthly PM₁₀ concentration distribution (Fig. 4) show the average monthly PM₁₀ levels peak from every May to September. This peak period coincides with the southwest monsoon (dry season), which is characterized by low rainfall and less cloud. Rainfall is received in most parts of Malaysia through the northeast monsoon (wet season) from every October to December. Peninsular Malaysia is experiencing lower PM₁₀ levels during the northeast monsoon across the months of the year. The ENSO can modulate Malaysia’s rainfall regime, with El Niño (La Niña) events corresponding to low (high) rainfall seasons (Chen et al. 2002; Singhrattna et al. 2005).

Fig. 4

Boxplots of the monthly average PM₁₀ concentration in all stations from January 2006 to December 2015

NINO12, NINO3, NINO34, and NINO4 indices are the average sea surface temperature (SST) anomaly in bounded regions across the Pacific. Since the region has large variability on El Niño time scales, thus is used by some authors to understand its impact on PM₁₀ levels. The monthly NINOs is available on the https://psl.noaa.gov/enso/data.html website. The ESPI is recorded based on rainfall anomalies in two rectangular areas, one in the eastern tropical Pacific (10° N–10° S and 160° E–100° W) and the other over the Maritime Continent (10° S–10° N and 90° E–150° E). The monthly ESPI data collected are obtained from http://eagle1.umd.edu/GPCP_ICDR/Data/ESPI.txt website. SOI, the standardized fluctuations in the air pressure difference between Tahiti and Darwin (Troup 1965) is associated with the strength of Pacific trade winds. Sustained negative values of SOI indicates El Niño events associated with warmer in the surface waters in the Equatorial Pacific Ocean) and positive values indicate the La Niña episodes (cooler ocean temperature in the Equatorial Pacific). The SOI data are available on https://psl.noaa.gov/gcos_wgsp/Timeseries/Data/soi.long.data website.

Lagged values of the climatological variables, the value of the climatological variables of the previous month is used to model the PM₁₀ concentration of a given month.

3 Statistical models

3.1 Hierarchical Bayesian autoregressive spatio-temporal model

The hierarchical Bayesian autoregressive spatio-temporal model will be used to analyze the PM₁₀ levels in the study region.

Let $Z\left({{\varvec{s}}}_{i},t\right)$ be the log-transformed of the monthly average of PM₁₀ values at location ${{\varvec{s}}}_{i}$ for time $t$, where the spatial reference ${{\varvec{s}}}_{i}$ is a two-dimensional vector represents the latitude–longitude pair, $i=1,\dots ,n,$ and $t=1,\dots ,T$. Here, $n$ is the total number of monitoring sites, and $T$ is the total number of months throughout the study.

The hierarchical model of the first level is given by

$$Z\left( {s_{i} ,t} \right) = O\left( {{\varvec{s}}_{i} ,t} \right) + \in \left( {{\varvec{s}}_{i} ,t} \right),$$

(1)

where $O\left({{\varvec{s}}}_{i},t\right)$ represents the true underlying spatio-temporal and $\epsilon \left({{\varvec{s}}}_{i},t\right)$ represents the error term that is normal $N(0,{\sigma }_{\epsilon }^{2})$. Here, ${\sigma }_{\epsilon }^{2}$ is the unknown pure error variance or nugget effect that describes the variation in space and $\epsilon \left({{\varvec{s}}}_{1},t\right), \epsilon \left({{\varvec{s}}}_{2},t\right),\dots ,$ $\epsilon \left({{\varvec{s}}}_{n},t\right)$ are independently and identically distributed.

For the second level of the hierarchical model, following Sahu et al. (2007), the true spatial temporal process $O\left({{\varvec{s}}}_{i},t\right)$ with autoregressive terms is specified by:

$$O\left( {s_{i} ,t} \right) = \rho O\left( {{\varvec{s}}_{i} ,t - 1} \right) + {\varvec{x}}\left( {s_{i} ,t} \right)^{\prime } {\varvec{\beta}} + \eta \left( {{\varvec{s}}_{i} ,t} \right),$$

(2)

where ${\varvec{\beta}}$ is a $p$ dimensional vector of regression terms associated with covariates ${\varvec{x}}\left( {{\varvec{s}}_{i} ,t} \right) = \left( {x_{1} \left( {{\varvec{s}}_{i} ,t} \right),x_{2} \left( {{\varvec{s}}_{i} ,t} \right), \ldots ,x_{p} \left( {{\varvec{s}}_{i} ,t} \right)} \right)^{\prime }$. The model specifies the first-order autoregressive term $\rho O\left({{\varvec{s}}}_{i},t-1\right)$ to describe dependence on past values. Temporal correlation parameter denoted by $\rho$ describes the strength of temporal dependence of PM₁₀ levels between successive months. The spatial temporal random effect is denoted by $\eta \left({{\varvec{s}}}_{i},t\right)$ and $\eta \left({{\varvec{s}}}_{i},t=1\right), \eta \left({{\varvec{s}}}_{i},t=2\right),\dots ,\eta \left({{\varvec{s}}}_{i},t=T\right)$ are independent (in time) and $\eta \left({{\varvec{s}}}_{i},t\right)$ follows a Gaussian Process (GP) assumption, thus $\eta \left({{\varvec{s}}}_{i},t\right)\sim N(0,{\sum }_{\eta }),$ where ${\sum }_{\eta }={\sigma }_{\eta }^{2}{{\varvec{S}}}_{\eta }$ for $t=\mathrm{1,2},\dots , T$. Here, ${\sigma }_{\eta }^{2}$ denotes the site invariant spatial variance and ${{\varvec{S}}}_{\eta }$ is the spatial correlation matrix.

In spatial modeling, the correlation is driven by the distance between locations. That is, two units that are located near each other are more highly correlated. The spatial correlation matrix ${{\varvec{S}}}_{\eta }$ is constructed from a positive definite function (p.d.f). A flexible and popular p.d.f. is the Matern correlation function. This function is indexed by the scale and smoothness parameters denoted by $\phi$ and $v$ (Handcock and Stein 1993), respectively. Following several authors, this study chooses the most used form of the Matern class of function which is the exponential covariance function. In the exponential case, when the degree of spatial smoothing $v=0.5$. the covariance, $\kappa$ depends on the distance between site ${{\varvec{s}}}_{i}$ and ${{\varvec{s}}}_{j}$ and $\phi$ and it is given by

$$\kappa \left( {\left\| {s_{i} - s_{j} } \right\|,\phi } \right) = \exp \left( { - \phi \left\| {s_{i} - s_{j} } \right\|} \right),$$

(3)

where $\phi$ denotes the rate of decay of the correlation as the distance $\Vert {{\varvec{s}}}_{i}-{{\varvec{s}}}_{j}\Vert$ increases. The initial condition of the autoregressive model $O({{\varvec{s}}}_{i},0)$ is ${O}_{0}\sim N(\mu , {\sigma }^{2}{{\varvec{S}}}_{0})$ where ${{\varvec{S}}}_{0}$ is the correlation matrix obtained using the Matern correlation function in Eq. (3).

Then, the specification of the model is completed by assigning proper prior distributions for all the parameters of this model denoted by ${\varvec{\theta}}=({\sigma }_{\epsilon }^{2},{\sigma }_{\eta }^{2},{\varvec{\beta}},\rho ,\phi ,v)$. The prior distribution for the parameters ${\varvec{\beta}}$ and $\rho$ is specified through normal distributions $N\left({\mathrm{0,10}}^{4}\right)$. In this study, inverse Gamma distribution $IG\sim (a,b)$ is assumed for the variance parameters ${\sigma }_{\epsilon }^{2}$ and ${\sigma }_{\eta }^{2}$ with hyper-parameters $a=2$ and $b=1$. The prior used for the spatial decay parameter $\phi$ is Gamma prior $(\mathrm{2,1})$ and random-walk Metropolis–Hastings is adopted for sampling $\phi$ from its full conditional distribution.

In the Bayesian framework, inference on model parameters is based on posterior distribution of the process and parameters given the data. The posterior distribution can be obtained by using Bayes theorem;

$$P\left( {\theta {|}Z\left( {{\varvec{s}},t} \right)} \right) \propto l\left( {\theta {|}Z\left( {{\varvec{s}},t} \right)} \right)\pi \left( \theta \right),$$

(4)

where $l\left(\theta |Z\left({\varvec{s}},t\right)\right)$ is the likelihood function and $\pi \left(\theta \right)$ denotes the prior distribution of $\theta .$

However, because of the complexity of the probability distribution, Markov Chain Monte Carlo (MCMC) techniques are usually used to approximate the posterior distribution. The technique used for this study is Gibbs sampling where the approximation of posterior distribution is done by simulating sequence of samples from the full conditional distributions of the parameters in the model. Furthermore, prediction of monthly PM₁₀ levels at any unobserved location ${{\varvec{s}}}_{0}$ and at a future time point $t^{\prime}$ can be obtained based on Sahu (2012) from the posterior predictive distribution of $Z\left({{\varvec{s}}}_{0}, \right)$ given ${\varvec{z}}$:

$$P\left( {Z\left( {{\varvec{s}}_{0} ,t^{\prime}} \right){|}{\varvec{z}}} \right) = \int {\left\{ {\begin{array}{*{20}c} {P\left( {Z\left( {{\varvec{s}}_{0} ,t^{\prime}} \right){|}O\left( {{\varvec{s}}_{0} ,t^{\prime}} \right),\sigma_{ \in }^{2} } \right)P\left( {O\left( {{\varvec{s}}_{0} ,t^{\prime}} \right){|}{\varvec{\theta}},{\varvec{O}},{\varvec{z}}^{\user2{*}} } \right) \cdot } \\ { \cdot P\left( {{\varvec{\theta}},{\varvec{O}},{\varvec{z}}^{\user2{*}} {|}{\varvec{z}}} \right)dO\left( {{\varvec{s}}_{0} ,t^{\prime}} \right)d{\varvec{O}}d{\varvec{\theta}}d{\varvec{z}}^{\user2{*}} } \\ \end{array} } \right\}} ,$$

(5)

where $Z\left({{\varvec{s}}}_{0}, \right)$ follows the normal distribution $N(O\left({{\varvec{s}}}_{0}, \right),{\sigma }_{\epsilon }^{2})$ and ${\varvec{\theta}}=({\varvec{\beta}},\rho ,{\sigma }_{\epsilon }^{2},{\sigma }_{\eta }^{2},\phi )$, ${{\varvec{z}}}^{\boldsymbol{*}}$ and ${\varvec{z}}$ denote the vectors of missing and observed data, respectively. The integral in Eq. (5) is also evaluated by MCMC method and R package spTimer (Bakar and Sahu 2015) is used to obtain the posterior density estimates and predictions.

3.2 Models for the monthly average PM₁₀ and model assessment

Many studies have shown a high correlation between any two global climatological variables. To quantify the impact of the global climatological variable on monthly average of PM₁₀ levels, we consider seven hierarchical spatio-temporal autoregressive models. The linear predictor for.

Model 1, ${\varvec{x}}{\left({{\varvec{s}}}_{i},t\right)}^{\boldsymbol{^{\prime}}}{\varvec{\beta}}={\beta }_{1}\mathrm{sin}\left(2\pi m/12\right)+{\beta }_{2}\mathrm{cos}\left(2\pi m/12\right),$

Model 2, ${\varvec{x}}{\left({{\varvec{s}}}_{i},t\right)}^{\boldsymbol{^{\prime}}}{\varvec{\beta}}={\beta }_{1}\mathrm{sin}\left(2\pi m/12\right)+{\beta }_{2}\mathrm{cos}\left(2\pi m/12\right)+{\beta }_{3}{\mathrm{NINO}12}_{t-1}$,

Model 3, ${\varvec{x}}{\left({{\varvec{s}}}_{i},t\right)}^{\boldsymbol{^{\prime}}}{\varvec{\beta}}={\beta }_{1}\mathrm{sin}\left(2\pi m/12\right)+{\beta }_{2}\mathrm{cos}\left(2\pi m/12\right)+{\beta }_{3}{\mathrm{NINO}3}_{t-1}$,

Model 4, ${\varvec{x}}{\left({{\varvec{s}}}_{i},t\right)}^{\boldsymbol{^{\prime}}}{\varvec{\beta}}={\beta }_{1}\mathrm{sin}\left(2\pi m/12\right)+{\beta }_{2}\mathrm{cos}\left(2\pi m/12\right)+{\beta }_{3}{\mathrm{NINO}34}_{t-1}$,

Model 5, ${\varvec{x}}{\left({{\varvec{s}}}_{i},t\right)}^{\boldsymbol{^{\prime}}}{\varvec{\beta}}={\beta }_{1}\mathrm{sin}\left(2\pi m/12\right)+{\beta }_{2}\mathrm{cos}\left(2\pi m/12\right)+{\beta }_{3}{\mathrm{NINO}4}_{t-1}$,

Model 6, ${\varvec{x}}{\left({{\varvec{s}}}_{i},t\right)}^{\boldsymbol{^{\prime}}}{\varvec{\beta}}={\beta }_{1}\mathrm{sin}\left(2\pi m/12\right)+{\beta }_{2}\mathrm{cos}\left(2\pi m/12\right)+{\beta }_{3}{\mathrm{SOI}}_{t-1}$,

Model 7, ${\varvec{x}}{\left({{\varvec{s}}}_{i},t\right)}^{\boldsymbol{^{\prime}}}{\varvec{\beta}}={\beta }_{1}\mathrm{sin}\left(2\pi m/12\right)+{\beta }_{2}\mathrm{cos}\left(2\pi m/12\right)+{\beta }_{3}{\mathrm{ESPI}}_{t-1}$,where $m=$ month of the year ($1=$ January, $2=$ February, …, and so on, $t=12\left(i-1\right)+m$, $i=1$ (first year of studied data), $i=2$(second year of studied data), …, so on. Model 1 is the simplest with only sine and cosine terms as predictors and is nested within the other six models. Models 2, 3, …, 7 consider the lagged values from one of the ENSO indices, respectively, in addition to harmonic sine and cosine terms.

We use the root means square error (RMSE), mean absolute error (MAE), and predictive model choice criteria (PMCC) to determine the best fitted model. The RMSE and the MAE measure the difference between the fitted spatio-temporal model at the testing sites $({{\varvec{s}}}_{1},\dots ,{{\varvec{s}}}_{{n}_{0}})$ (the posterior mean of the predictive distribution), and the observed space–time PM₁₀ concentration data at the validation sites $\left({{\varvec{s}}}_{{n}_{0}+1},\dots ,{{\varvec{s}}}_{n}\right)$. The $RMSE=\sqrt{\frac{1}{m}\sum_{j={n}_{0}+1}^{n}\sum_{t=1}^{T}{\left(Z\left({{\varvec{s}}}_{j},t\right)-\widehat{Z}\left({{\varvec{s}}}_{j},t\right)\right)}^{2}}$ and $MAE= \frac{1}{m}\sum_{j={n}_{0}+1}^{n}\sum_{t=1}^{T}\left|Z\left({{\varvec{s}}}_{j},t\right)-\widehat{Z}\left({{\varvec{s}}}_{j},t\right)\right|,$ where $m$ is the total number of observations from the validation sites and $\widehat{Z}\left({{\varvec{s}}}_{j},t\right)$ denotes the posterior mean of the predictive distribution. Smaller values of RMSE and MAE indicate a superior model.

The predictive model choice criteria (PMCC) is used to compare the prediction capability (Gelfand and Ghosh 1998) and it is given by,

$$PMCC=\sum_{i=}^{n}\sum_{l=1}^{r}\sum_{t=1}^{{T}_{l}}\left\{E{\left(Z{\left({{\varvec{s}}}_{i},t\right)}_{rep}-z({{\varvec{s}}}_{i},t)\right)}^{2}+Var(Z{\left({{\varvec{s}}}_{i},t\right)}_{rep})\right\},$$

where $Z{\left({{\varvec{s}}}_{i},t\right)}_{rep}$ is a future replicate of the data $z({{\varvec{s}}}_{i},t)$. The first term of PMCC assesses the goodness of fit while the second term is a penalty term for complexity of the model. This value is computed and estimated by sampling the posterior predictive distribution that is given in the Eq. (5). The model with the smallest value of PMCC has better prediction capability.

4 Results and discussion

Summaries of the posterior distribution displayed in Table 1 are for the model parameters associated with sine, cosine, and ENSO index. The parameter estimates were obtained just by fitting the model to the data of the testing sites in the period 2006–2015. The Gibbs sampler is run for 5000 iterations to obtain the results. The 1000 initial iterations run as burn-in and the others for making inference on the model parameters. Each of the models is run with the same set of parameters and hyper-parameters. For validation purposes, the RMSE, MAE, and PMCC are calculated to choose the superior model.

Table 1 Summaries of the posterior distributions of model parameters

Model 1 (without ENSO indices) has the smallest value of PMCC. Amongst the models with ENSO indices, Model 7 (with ESPI) has the lowest RMSE, Model 4 (with NINO34) has the lowest MAE, and Model 6 (with SOI) has the lowest PMCC. However, observing the 95% credible interval, the ENSO indices are not statistically significant in these models, while sine and cosine are significant for almost all models. From the posterior distribution of the model parameters corresponding to the predictor variables, the ENSO indices are insignificant in each model. Therefore, there is no enough evidence in concluding ENSO indices are important predictors and have a significant impact on the space–time PM₁₀ concentrations.

We observe the convergence of the model parameters using the trace-plot given in Fig. 5. The result is satisfactory. As the number of iterations increases, the results showed that the increment does not improve the convergence of the chain.

Fig. 5

MCMC trace plots of the model parameters

All regression coefficients of Model 1 are statistically significant as the 95% credible intervals do not contain zero (see Table 1). The estimate of the spatial variance parameter ${\sigma }_{\eta }^{2}$ (0.0396) is substantially higher than that of the error (non-spatial) variance parameter ${\sigma }_{\epsilon }^{2}$ (0.0057). This result shows that the ability of the model to explain the variability in the data is good. The estimate of the autoregressive temporal correlation parameter $\rho$ is 0.8536. This estimate implies a strong correlation of PM₁₀ levels between successive months. The 0.0073 posterior mean value of parameter $\phi$ shows that spatial correlation falls to zero at a distance of approximately 410 km, which is determined by the relationship $\mathrm{exp}\left(-\phi {d}_{0}\right)\approx 0.05$(Sahu 2012), where ${d}_{0}$ denotes the effective range. Thus, the spatial correlation in PM₁₀ levels between locations covering a distance of 410 km and beyond this distance, spatial correlation is negligible.

Figure 6 presents the line graph of the general temporal trend of lagged SOI, ESPI, NINO12, and PM₁₀ levels averaged over all the validating sites. The line graph shows a non-linear trend with a fluctuating pattern throughout the study period from 2006 to 2015. The predicted values of PM₁₀ generated using the predictive output of the spatio-temporal model (dotted blue line in Fig. 6) seem close to the observed values of PM₁₀ recorded at the monitoring stations (solid red line). El Niño events occurred during 2006–2007 and 2009–2010 but were weaker than 2014–2016 (CPC 2019). The figure suggests the peaks in the PM₁₀ levels curve concurrent with the El Niño episodes. The nonregular periodic pattern of ENSO indicators during the El Niño events coincides with high PM₁₀ levels. The PM₁₀ concentration levels usually maximum every May to September and coincide with the southwest monsoon winds season with a low wind scale, often below 7 m/s. However, the El Niño events of 2014–2015 prolonged the high levels of PM10 to the highest peak in October 2015.

Fig. 6

The general temporal trend of monthly PM₁₀ levels averaged over the validating sites and associated ENSO indices

We also compute the coverage percentage of the forecast 5–95 percentile range which we find to be 89.2% implying good prediction results since 89.2% of observations are covered by the predictions. The coverage percentage is the percentage of observations that the 5–95 percentile range of predicted future values contains the true outcomes. A good prediction method, say, for the 5–95 percentile range should have coverage close to 90%.

Figure 7 displays the forecast map of PM₁₀ in Peninsular Malaysia in October 2015. We perform the spatial interpolation (kriging) to estimate the PM₁₀ concentrations at the unmonitored locations. Both fields and MBA R packages (Nychka et al. 2015; Lee et al. 1997) were used in the study to obtain the forecast map. Figure 7 provides a graphical representation in visualizing PM₁₀ values in all areas for a certain period. From the spatial variation in the forecasts observed in Fig. 7, the PM₁₀ levels are lower on the north and east coasts than on the south and west coasts of Peninsular Malaysia during the El Niño event. The mean of the monthly PM₁₀ levels is above 80 $\mu g/{m}^{3}$ in the central region.

Fig. 7

Forecast map for PM₁₀ in Peninsular Malaysia on October 2015

Based on the posterior distribution of the model parameters, given in Table 1, none of the ENSO indices is significant and has an impact on the spatial distribution of the PM₁₀ concentration. Therefore, to quantify the effect of the ENSO indices, we apply the autoregressive seasonal model on the PM₁₀ concentration averaged over all the stations. By this means, we ignore the spatial effect. We consider the following models:

Model 1A, $\mathrm{log}{\mathrm{PM}10}_{t}={\beta }_{1}\mathrm{sin}\left(2\pi m/12\right)+{\beta }_{2}\mathrm{cos}\left(2\pi m/12\right)$

Model 2A, $\mathrm{log}{\mathrm{PM}10}_{t}={\beta }_{1}\mathrm{sin}\left(2\pi m/12\right)+{\beta }_{2}\mathrm{cos}\left(2\pi m/12\right)+{\beta }_{3}{\mathrm{NINO}12}_{t-1}$

Model 3A, $\mathrm{log}{\mathrm{PM}10}_{t}={\beta }_{1}\mathrm{sin}\left(2\pi m/12\right)+{\beta }_{2}\mathrm{cos}\left(2\pi m/12\right)+{\beta }_{3}{\mathrm{NINO}3}_{t-1}$

Model 4A, $\mathrm{log}{\mathrm{PM}10}_{t}={\beta }_{1}\mathrm{sin}\left(2\pi m/12\right)+{\beta }_{2}\mathrm{cos}\left(2\pi m/12\right)+{\beta }_{3}{\mathrm{NINO}34}_{t-1}$

Model 5A, $\mathrm{log}{\mathrm{PM}10}_{t}={\beta }_{1}\mathrm{sin}\left(2\pi m/12\right)+{\beta }_{2}\mathrm{cos}\left(2\pi m/12\right)+{\beta }_{3}{\mathrm{NINO}4}_{t-1}$

Model 6A, $\mathrm{log}{\mathrm{PM}10}_{t}={\beta }_{1}\mathrm{sin}\left(2\pi m/12\right)+{\beta }_{2}\mathrm{cos}\left(2\pi m/12\right)+{\beta }_{3}{\mathrm{SOI}}_{t-1}$

Model 7A, $\mathrm{log}{\mathrm{PM}10}_{t}={\beta }_{1}\mathrm{sin}\left(2\pi m/12\right)+{\beta }_{2}\mathrm{cos}\left(2\pi m/12\right)+{\beta }_{3}{\mathrm{ESPI}}_{t-1}$

We then perform a robust MM estimation procedure on the model parameters to obtain statistical results that are more reliable. Table 2 shows the summary statistics for all models. Based on the $t$-test and the Akaike Information Criteria (AIC), Model 2A is the best model compared to the other models. Thus, NINO12 is the most dominant ENSO indices that can affect the (temporal) distribution of PM₁₀ concentration in Peninsular Malaysia. The other ENSO indices that were significant at the 5% level of significance using the t test are SOI (Model 6A) and ESPI (Model 7A), and the AIC values are slightly larger than of Model 2A.

Table 2 The autoregressive models analysis of the PM₁₀ concentration data

5 Conclusion

We have studied the impact of ENSO indices on the space–time monthly PM₁₀ levels data recorded in 33 sites across Peninsular Malaysia from 2006 to 2015 using the Bayesian hierarchical autoregressive spatio-temporal statistical model. The ENSO indices that we have considered in this study are the NINO12, NINO3, NINO34, NINO4, SOI, and ESPI indices. We have fitted the space–time PM₁₀ data with several models, each with a sine term, a cosine term and one of the ENSO indices as predictors. Based on the 95% credible interval of the posterior distribution of the model parameters associated with the predictors, none of the ENSO indices is associated with the space–time PM₁₀ levels of Peninsular Malaysia in this study. We have concluded that ENSO indices has no association with the spatial distribution of the PM₁₀ concentration.

However, the sine and cosine terms are useful for predicting the PM₁₀ concentrations. Besides, based on the RMSE, MAE and PMCC obtained for the validation set, the model with sine and cosine only is preferred over the other seasonal models with ENSO indices as a predictor. Based on the autoregressive temporal correlation parameter, there is a strong temporal correlation between successive months. On the basis of the spatial correlation parameter, the PM₁₀ levels are correlated spatially as far as 410 km, and past this distance, spatial correlation is negligible. The prediction map of PM₁₀ concentration shows a reasonable prediction of the PM₁₀ levels. The central region of Peninsular Malaysia recorded the highest PM₁₀ concentration levels than in the other places in October 2015. The model with sine and cosine functions as predictors is useful to predict and forecast the PM₁₀ levels in the locations and time points where the data are not being collected. In comparison to some other regression models, we have considered both the spatial and temporal impact simultaneously using a single model. The prediction and forecasting help in the line of action to take in air quality planning, surveillance, intervention and also health funding allocation.

None of the ENSO indices has shown a significant impact on the spatial distribution of the PM₁₀ concentration. Among all the ENSO indices, NINO12, SOI and ESPI show a significant association with the temporal distribution of the PM₁₀ concentrations averaged over all stations in Malaysia. The result of this study provides a piece of valuable information on identifying suitable models, methods, and approaches to quantify the relationship between ENSO indices and PM₁₀ concentration. To study the impact of the global climatological variable on the spatial distribution of the PM₁₀ in the country seems unfeasible using the spatio-temporal model. Fitting the ordinary autoregressive model to the PM₁₀ averaged over all the stations does not take into consideration the spatial variability. To identify which ENSO indices are significant, we have to fit the model to the PM₁₀ concentrations at each location separately. By this means, each location site in the country has its model. However, an effortless analysis of data should be much more preferred using a single model.