Bayesian model averaging assessment on groundwater management under model structure uncertainty

Abstract

This study introduces Bayesian model averaging (BMA) to deal with model structure uncertainty in groundwater management decisions. A robust optimized policy should take into account model parameter uncertainty as well as uncertainty in imprecise model structure. Due to a limited amount of groundwater head data and hydraulic conductivity data, multiple simulation models are developed based on different head boundary condition values and semivariogram models of hydraulic conductivity. Instead of selecting the best simulation model, a variance-window-based BMA method is introduced to the management model to utilize all simulation models to predict chloride concentration. Given different semivariogram models, the spatially correlated hydraulic conductivity distributions are estimated by the generalized parameterization (GP) method that combines the Voronoi zones and the ordinary kriging (OK) estimates. The model weights of BMA are estimated by the Bayesian information criterion (BIC) and the variance window in the maximum likelihood estimation. The simulation models are then weighted to predict chloride concentrations within the constraints of the management model. The methodology is implemented to manage saltwater intrusion in the “1,500-foot” sand aquifer in the Baton Rouge area, Louisiana. The management model aims to obtain optimal joint operations of the hydraulic barrier system and the saltwater extraction system to mitigate saltwater intrusion. A genetic algorithm (GA) is used to obtain the optimal injection and extraction policies. Using the BMA predictions, higher injection rates and pumping rates are needed to cover more constraint violations, which do not occur if a single best model is used.

1 Introduction

Groundwater management models, e.g., hydraulic barrier and extraction systems for saltwater intrusion mitigation (Mahesha 1996; Mantoglou 2003; Reichard and Johnson 2005; Abarca et al. 2006), rely heavily on groundwater flow and contaminant transport modeling to predict contaminant dynamics in the aquifer system. Simulation–optimization models have been extensively used to find the optimal actions for groundwater resource development, aquifer remediation and aquifer protection (Gorelick 1983; Yeh 1992; Ahlfeld and Heidari 1994; Wagner 1995; Mayer et al. 2002). Deterministic management models aim to obtain the optimal operation policy by utilizing simulation models without uncertainty (Minsker and Shoemaker 1998; Park and Aral 2004; Reichard and Johnson 2005; Abarca et al. 2006; Guan et al. 2008). On the contrary, stochastic management models account for uncertain predictions of flow and transport owing to imprecise model parameters (mainly hydraulic conductivity) (Tung 1986; Wagner and Gorelick 1987; Wagner and Gorelick 1989; Wagner et al. 1992; Ranjithan et al. 1993 Morgan et al. 1993; Chan 1993; Watkins and McKinney 1997; Aly and Peralta 1999; Smalley et al. 2000; Feyen and Gorelick 2004; Singh and Minsker 2008; Ko and Lee 2009), initial condition (Baú and Mayer 2008), and boundary condition (Georgakakos and Vlatsa 1991; Oliver and Christakos 1996; Feyen and Gorelick 2004). Feyen and Gorelick (2005) employed a multiple-realization groundwater management model to assess the economic worth of data collection to reduce management uncertainty.

In the literature, we often discuss parameter (structure) identification using a single simulation model with one parameter estimation method. The statistical properties of the estimated parameters are then employed to study the stochastic management models under one simulation model. However, the remediation planning and management are extremely complex because of a lack of hydrogeological data for targeted aquifers. Model structure uncertainty always exists due to data scarcity and uncertainty, which calls for multiple simulation models. Many studies have recognized model structure uncertainty, but intentionally seek for the best single model (Carrera and Neuman 1986a, b; Russo 1988; Hyun and Lee 1998). The use of single simulation model with a single parameter estimation method intrinsically underestimates management model uncertainty and may cause unexpected failure of optimized remedial operations. To ensure the robustness of optimized operations for a management model, predictions from multiple models in light of model structure uncertainty should be considered.

The non-uniqueness of conceptual models has been extensively discussed in the hydrological modeling communities, where the generalized likelihood uncertainty estimation (GLUE) was introduced (Beven and Binley 1992; Beven and Freer 2001; Dean et al. 2009). Tolson and Shoemaker (2008) presented an efficient search algorithm to obtain multiple acceptable or behavioral model parameter sets to improve the GLUE efficiency in obtaining prediction uncertainty. Hassan et al. (2008) introduced a GLUE-based ensemble averaging approach to obtain expectation and variance of Monte Carlo simulated realizations for stochastic groundwater modeling. Prediction using multiple models has recently received great attention in the groundwater community by the advent of the Bayesian model averaging (BMA) method (Draper 1995; Hoeting et al. 1999). The BMA was introduced in the groundwater literature to deal with multiple choices of semivariogram models (Neuman 2003; Ye et al. 2004), parameterization methods in permeability/hydraulic conductivity estimation (Poeter and Anderson 2005; Foglia et al. 2007; Tsai and Li 2008a, b), and groundwater head predictions (Li and Tsai 2009).

An exhaustive study of model structure uncertainty in all model components is very difficult. This study only focuses on model structure uncertainty in the boundary condition values of the groundwater model and in the semivariograms of hydraulic conductivity, and adopts the BMA to account for those uncertainties. The boundary conditions in a groundwater flow model represent the sources and sinks of water along the boundary of the system. Selecting proper boundary conditions requires a thorough understanding of hydrologic processes at boundaries which is often difficult because of limited data. Without doubt, boundary condition values assigned to models contain huge uncertainty in practical problems. Oliver and Christakos (1996) analyzed the effect of random and deterministic boundary conditions on the flow system and concluded that boundary condition can make significant difference in the mean and variance of the hydraulic gradient. This study considers multiple groundwater flow models with a wide range of boundary condition values to incorporate boundary condition uncertainty in the management model.

Semivariogram model selection is not unique as it is often decided subjectively by fitting semivariogram models to experimental semivariograms. Semivariogram uncertainty of hydraulic conductivity was studied based on the uncertainty of measurement data by Ortiz and Deutsch (2002). Eggleston et al. (1996) studied a heavily sampled aquifer and reported that the number of data points significantly affects permeability structure models. Feyen et al. (2001) considered the data uncertainties in terms of the spatial correlation uncertainty (or semivariogram uncertainty) and uncertainty propagation to groundwater flow responses and predictions. Feyen et al. (2003) examined semivariogram uncertainty for capture zones in a Bayesian framework. Following the work of Ortiz and Deutsch (2002), Rahman et al. (2008a, b) studied the semivariogram parameter uncertainty in capture zone modeling and demonstrated the importance of semivariogram model uncertainty compared with fluctuations of a fixed geostatistical model. Similar to the works in Neuman (2003) and Ye et al. (2004), this study considers multiple semivariogram models for estimating hydraulic conductivity in the BMA framework.

The objective of this study is to introduce a variance-window-based BMA method to assist model uncertainty analysis in groundwater management problems. BMA considers the importance of each model based on the evidence of data (likelihood), which avoids over-emphasis on poor models (or poor realizations) with equal weights that could lead to significantly overdesigned optimal solutions. In this study, the groundwater management model consists of a joint operation of a hydraulic barrier system and an extraction system to reduce the chloride concentration and prevent further saltwater intrusion in the “1,500-foot” sand aquifer in the Baton Rouge area, Louisiana. The hydraulic barrier serves to intercept and dilute chloride concentration. The extraction wells pump out brackish water in the area intruded by saltwater. Uncoupled groundwater flow and mass transport models are employed to simulate saltwater intrusion in the two-dimensional “1,500-foot” sand aquifer.

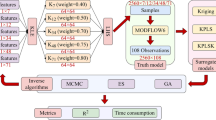
A flowchart that incorporates multiple simulation models into the groundwater management model is shown in Fig. 1. In the model calibration step, this study considers uncertainty in boundary condition values of the groundwater model, which leads to multiple saltwater intrusion simulation models M⁽ⁱ⁾ in Fig. 1. In each simulation model, multiple semivariogram models along with the generalized parameterization (GP) method (Tsai and Yeh 2004; Tsai 2006) are considered to estimate spatially correlated hydraulic conductivity. The data weighting coefficients (β) in the GP for each semivariogram model are estimated using head data measured from the “1,500-foot” sand aquifer from year 1990 to 2004 using a quasi-Newton method. In the management step, a genetic algorithm (GA) is used to optimize the selection of active injection and extraction wells for each month as well as the injection rate and extraction rate. The calibrated simulation models are embedded in GA to predict saltwater intrusion $C_{j}^{(i)}$ in Fig. 1 from year 2005 to 2019. The BMA method is employed to average salt concentrations predicted by multiple models. Moreover, BMA estimates prediction variances to represent uncertainty of salt concentration caused by the uncertainty from the boundary condition values and semivariogram models.

Fig. 1

Flowchart of using BMA in groundwater management model

2 Joint operation of hydraulic barrier and extraction systems for saltwater intrusion mitigation in “1,500-foot” sand aquifer in Baton Rouge Area, Louisiana

The Baton Rouge aquifer system located at south central Louisiana is a major source of drinking and industrial water. The aquifer has a fault running east-west located at the southern part near the coastline of the region. The fault cuts the aquifer system into two parts: the up-thrown north side and the down-thrown south side. The fault was considered to act as an impermeable barrier to groundwater movement across it. A recent study suggests the Baton Rouge Fault as a conduit-barrier fault (Bense and Person 2006). Predominantly, the region south of the aquifer contains saltwater and north of the aquifer contains fresh water. However, by 1990, the water quality data at the existing wells to the north of the fault indicated that increasing water withdrawn in the region was resulting in saltwater intrusion to the north and a decrease in water quality within the aquifer system (Tomaszewski 1996). The sources of the saltwater are nearby the St. Gabriel salt dome and Darrow salt dome (Bray and Hanor 1990).

The study area shown in Fig. 2 is the “1,500-foot” sand aquifer, where the extent of the saltwater intrusion was predicted at the beginning of year 2005. There are three major groundwater production centers in this area, which have developed a large depression cone and caused saltwater intrusion from south of the Baton Rouge fault. Recent study of groundwater modeling in this area indicated that the groundwater heads are continuously decreasing (Tsai and Li 2008a, Li and Tsai 2009), which could result in undesired chloride concentration levels at production wells in the future.

Fig. 2

The study area of the “1,500-foot” sand aquifer in the Baton Rouge area, Louisiana. The contour lines represent the saltwater concentration (%) distribution at the beginning of 2005

This study develops a management model using an injection-extraction approach to protect the production wells from saltwater intrusion. The idea has been actually implemented for hydraulic control to the West Coast Basin of coastal Los Angeles, California (Reichard and Johnson 2005) and was considered in Spain (Abarca et al. 2006). This study considers the joint operations of the hydraulic barrier system and the extraction system shown in Fig. 2 to (i) intercept the incoming saltwater plume toward the production wells and (ii) reduce brackish water north of the fault. The injection wells align to form a hydraulic barrier to reduce saltwater movement towards the production wells. The pumping wells are placed at the pathway of the brackish water in order to remove the brackish water from the aquifer and prevent northward movement of the brackish water pushed by the hydraulic barrier system. The locations of these well pumps are fixed in this study.

The objective of the management model is to minimize the total amount of injected and extracted water as follows

$$ \mathop {\min }\limits_{\begin{subarray}{l} z_{i,n}^{R} \in \{ 0,1\} ,q^{R} \\ z_{j,n}^{P} \in \{ 0,1\} ,q^{P} \end{subarray} } \quad \sum\limits_{i} {\sum\limits_{n} {z_{i,n}^{R} q^{R} \Updelta t_{n} } } + \sum\limits_{j} {\sum\limits_{n} {z_{j,n}^{P} q^{P} \Updelta t_{n} } } , $$

(1)

where q ^R and q ^P are the injection rate and the extraction rate, respectively. The superscript R refers to “recharge” for injection wells and the superscript P refers to “pumping” for extraction wells. $z_{i,n}^{R}$ and $z_{j,n}^{P}$ are the scheduling variables for spatial and temporal allocation of the pump rates. They are binary variables to select active injection and extraction wells, respectively, at injection site i, pumping site j, and time period n. If z _i,n = 1 (or z _j,n = 1), the well pump i (or j) is active with the injection rate, q ^R (or the extraction rate, q ^P) in the period t. Otherwise, the well pump is not active in the period n. Δt _n is the time interval for the period n. The objective function can consider different injection rates and extraction rates for different well pumps at different time. However, this would result in a very complicated management problem and would not be practical. In reality, operators cannot arbitrarily control the flow rate of a single-speed well pump, but can control the switch of the well pump to turn the pump on or off. To reduce the computation effort, this study searches for optimal single injection rate and extraction rate and optimal values for scheduling variables to determine the well pump activities.

The range of injection and extraction rates is constrained by

$$ \begin{array}{l} 0\,{\le}\,q^{R}\, {\le}\, q_{\max }^{R} \\ 0\, {\le}\, q^{P}\, {\le}\, q_{\max }^{P} , \\ \end{array} $$

(2)

where q ^R_max and q ^P_max the maximum injection rate and extraction rate, respectively. This study particularly focuses on the concentration at the Lula Avenue pumping center (Lula wells, see Fig. 2) because the saltwater intrusion posts a direct threat to Lula production wells due to very large groundwater withdrawals. Therefore, this study considers the concentration at Lula wells at anytime to be less than the maximum permissible level (MPL):

$$ C\left( {{\mathbf{x}} \in {\mathbf{x}}_{\text{Lula}} ,t \in \left[ {t_{0} ,t_{T} } \right];z_{i,n}^{R} ,q^{R} ,z_{j,n}^{P} ,q^{P} } \right) \le C_{\text{MPL}} , $$

(3)

where C is the predicted concentration by simulation models, C _MPL is the MPL of concentration, x _Lula is the set of Lula wells, t ₀ is the starting time of remediation horizon, and t _T is the end of the remediation horizon. Similarly, this study aims to reduce the concentration in the remediation area (see Fig. 2) below the MPL at the end of the remediation period:

$$ C\left( {{\mathbf{x}} \in \Upomega_{R} ,t = t_{T} ;z_{i,n}^{R} ,q^{R} ,z_{j,n}^{P} ,q^{P} } \right) \le C_{\text{MPL}} , $$

(4)

where Ω _R is the domain of the remediation area. It is noted that the constraint for Lula wells is applied throughout the management period, whereas the constraint for the remediation area is only applied at the end of the management period.

The joint operation optimization of hydraulic barrier and extraction systems is a mixed integer nonlinear programming (MINLP) problem, which involves the groundwater model and transport model. Solving the MINLP problem by gradient-based optimization algorithms would be very complicated because the solution needs combinatorial optimization algorithms. Genetic algorithms or evolutionary algorithms are derivative-free algorithms and have been proven to be efficient optimization approaches for groundwater remediation problems involving integer variables (McKinney and Lin 1994; Guan and Aral 1999; Park and Aral 2004; Bayer and Finkel 2004; Bayer and Finkel 2007; Singh and Minsker 2008). This study employs a GA with binary chromosomes to search for the pump rates and the binary values of the scheduling variables.

Using the GA, the two constraints are moved as the penalty terms to the objective function. Then, the multiobjective problem is formulated into a single-objective function:

$$ \mathop {\min }\limits_{\begin{subarray}{l} z_{i,n}^{R} \in \{0,1\} ,q^{R} \\ z_{j,n}^{P} \in \{ 0,1\} ,q^{P}\end{subarray} } w_{1} \left( {\sum\limits_{i} {\sum\limits_{n}{z_{i,n}^{R} q^{R} \Updelta t_{n} } } + \sum\limits_{j}{\sum\limits_{n} {z_{j,n}^{P} q^{P} \Updelta t_{n} } } } \right) +w_{2} \int\limits_{{t_{0} }}^{{t_{T} }} {\max \left[ {C\left({{\mathbf{x}} \in {\mathbf{x}}_{\rm Lula} ,t;z_{i,n}^{R} ,q^{R},z_{j,n}^{P} ,q^{P} } \right) - C_{\text{MPL}} ,0} \right]dt} +w_{3} \int\limits_{{\Upomega_{R} }} {\max \left[ {C\left({{\mathbf{x}},t = t_{T} ;z_{i,n}^{R} ,q^{R} ,z_{j,n}^{P} ,q^{P} }\right) - C_{\text{MPL}} ,0} \right]d{\mathbf{x}}},$$

(5)

where w ₁, w ₂, and w ₃ are the weights of objective functions. The weights represent the relative importance of one objective over others and reflect the priorities. The orders of magnitude of weight values should be carefully determined with the consideration of the units in different objectives. To reduce the violation on the constraints, the priorities in the following order are considered: minimizing the sum of concentration violations at the Lula wells, minimizing the sum of concentration violations in the remediation area, and minimizing the total amount of water injected and extracted.

The optimized joint operations are subject to the uncertainty of model structure that can cause large constraint violations. To assess the robustness of the optimized operations, this study considers model uncertainty and calls for multiple model structures. In what follows, a variance-window-based Bayesian model averaging method is introduced to predict concentrations in the management model in Eq. 5 to evaluate constraint violations at the Lula wells and in the remediation area.

3 Concentration prediction using Bayesian model averaging

Let ${\mathbf{M}} = \left\{ {\text{M}^{(p)} ;\quad p = 1,2, \ldots } \right\}$ be a set of saltwater intrusion simulation models based on different boundary condition values of groundwater heads. Each simulation model may have different semivariogram models to estimate hydraulic conductivity, which is denoted as ${\varvec{\uptheta}} = \left\{ {{{\theta}}_{q}^{(p)} ;\quad q = 1,2, \ldots } \right\}.$ Given data D, the probability of the prediction of chloride concentration, C, using the BMA (Hoeting et al. 1999) is

$$ \Pr \left( {{\mathbf{C}}|{\mathbf{D}}} \right) =\sum\limits_{p} {\sum\limits_{q} {\Pr \left({{\mathbf{C}}|{\text{M}}^{(p)} ,\theta_{q}^{(p)} ,{\mathbf{D}}}\right) \quad \times \Pr \left( {\theta_{q}^{(p)} |{\text{M}}^{(p)},{\mathbf{D}}} \right)\Pr \left( {{\text{M}}^{(p)} |{\mathbf{D}}}\right)}},$$

(6)

where $\Pr \left( {{\mathbf{C}}|{\text{M}}^{(p)} ,{{\theta}}_{q}^{(p)} ,{\mathbf{D}}} \right)$ is the conditional probability of chloride concentration given the data D, simulation model p, and semivariogram model q. The posterior probability of semivariogram model q used in simulation model p is given by the Bayes rule:

$$ \Pr \left( {{{\theta}}_{q}^{(p)} |{\text{M}}^{(p)} ,{\mathbf{D}}} \right) = {\frac{{\Pr \left( {{\mathbf{D}}|{\text{M}}^{(p)} ,{{\theta}}_{q}^{(p)} } \right)\Pr \left( {{{\theta}}_{q}^{(p)} |{\text{M}}^{(p)} } \right)}}{{\sum_{q} {\Pr \left( {{\mathbf{D}}|{\text{M}}^{(p)} ,{{\theta}}_{q}^{(p)} } \right)\Pr \left( {{{\theta}}_{q}^{(p)} |{\text{M}}^{(p)} } \right)} }}} , $$

(7)

where $\Pr \left( {{\mathbf{D}}|{\text{M}}^{(p)} ,{{\theta}}_{q}^{(p)} } \right)$ is the likelihood value of semivariogram model q in simulation model p. $\Pr \left( {{{\theta}}_{q}^{(p)} |{\text{M}}^{(p)} } \right)$ is the prior probability of semivariogram model q in simulation model p. According to the Bayes rule, the posterior probability of simulation model p is

$$ \Pr \left( {{\text{M}}^{(p)} |{\mathbf{D}}} \right) = {\frac{{\Pr \left( {{\mathbf{D}}|{\text{M}}^{(p)} } \right)\Pr \left( {{\text{M}}^{(p)} } \right)}}{{\sum_{p} {\Pr \left( {{\mathbf{D}}|{\text{M}}^{(p)} } \right)\Pr \left( {{\text{M}}^{(p)} } \right)} }}}, $$

(8)

where $\Pr \left( {{\mathbf{D}}|{\text{M}}^{(p)} } \right)$ is the likelihood value of simulation model p, which is

$$ \Pr \left( {{\mathbf{D}}|{\text{M}}^{(p)} } \right) = \sum\limits_{q} {\Pr \left( {{\mathbf{D}}|{\text{M}}^{(p)} ,{{\theta}}_{q}^{(p)} } \right)\Pr \left( {{{\theta}}_{q}^{(p)} |{\text{M}}^{(p)} } \right)} , $$

(9)

Pr(M^(p)) is the prior probability of simulation model p. The model weight can be represented in terms of the joint probability:

$$ \Pr \left( {{{\theta}}_{q}^{(p)} , {\text{M}}^{(p)} |{\mathbf{D}}} \right) = \Pr \left( {{{\theta}}_{q}^{(p)} |{\text{M}}^{(p)} ,{\mathbf{D}}} \right)\Pr \left( {{\text{M}}^{(p)} |{\mathbf{D}}} \right). $$

(10)

The expectation and covariance of the chloride concentration are as follows

$$ {\text{E}}\left[ {{\mathbf{C}}|{\mathbf{D}}} \right] = \sum\limits_{p} {\sum\limits_{q} {{\text{E}}\left( {{\mathbf{C}}|{\text{M}}^{(p)} , {{\theta}}_{q}^{(p)} ,{\mathbf{D}}} \right) \quad \times { \Pr }\left( {{{\theta}}_{q}^{(p)} |{\text{M}}^{ (p )} ,{\mathbf{D}}} \right){ \Pr }\left( {{\text{M}}^{ (p )} |{\mathbf{D}}} \right)}} ,$$

(11)

$$ \begin{aligned} & {\text{Cov}}\left[ {{\mathbf{C}}|{\mathbf{D}}} \right] = {\text{E}}_{\text{M}} {\text{E}}_{{{\theta}}} \left[ {{\text{Cov}}\left[ {{\mathbf{C}}|{\text{M}}^{(p)} ,{{\theta}}_{q}^{(p)} ,{\mathbf{D}}} \right]} \right] + {\text{E}}_{\text{M}} {\text{Cov}}_{{{\theta}}} \left[ {{\text{E}}\left[ {{\mathbf{C}}|{\text{M}}^{(p)} ,{{\theta}}_{q}^{(p)} ,{\mathbf{D}}} \right]} \right] \\ & \quad + {\text{Cov}}_{\text{M}} {\text{E}}_{{{\theta}}} \left[ {{\text{E}}\left[ {{\mathbf{C}}|{\text{M}}^{(p)} ,{{\theta}}_{q}^{(p)} ,{\mathbf{D}}} \right]} \right] \\ \end{aligned}, $$

(12)

where the within-model covariance of the concentration is

$$ {\text{E}}_{\text{M}} {\text{E}}_{{{\theta}}} \left[ {{\text{Cov}}\left[ {{\mathbf{C}}|{\text{M}}^{(p)} ,{{\theta}}_{q}^{(p)} ,{\mathbf{D}}} \right]} \right] = \sum\limits_{p} {\sum\limits_{q} {{\text{Cov}}\left[ {{\mathbf{C}}|{\text{M}}^{(p)} ,{{\theta}}_{q}^{(p)} ,{\mathbf{D}}} \right]\Pr \left( {{{\theta}}_{q}^{(p)} |{\text{M}}^{(p)} ,{\mathbf{D}}} \right)\Pr \left( {{\text{M}}^{(p)} |{\mathbf{D}}} \right)} }.$$

(13)

The covariance of the concentration due to different semivariogram models in individual simulation models is

$$ \begin{aligned} &{\text{E}}_{\text{M}}{\text{Cov}}_{{{\theta}}} \left[ {{\text{E}}\left[{{\mathbf{C}}|{\text{M}}^{(p)} ,{{\theta}}_{q}^{(p)},{\mathbf{D}}} \right]} \right] \\ &\quad = \sum\limits_{p}{\sum\limits_{q} {\left( {{\text{E}}\left[{{\mathbf{C}}|{\text{M}}^{(p)} ,{{\theta}}_{q}^{(p)},{\mathbf{D}}} \right] - {\text{E}}\left[{{\mathbf{C}}|{\text{M}}^{(p)} ,{\mathbf{D}}} \right]} \right)} }\times \left( {{\text{E}}\left[ {{\mathbf{C}}|{\text{M}}^{(p)},{{\theta}}_{q}^{(p)} ,{\mathbf{D}}} \right] - {\text{E}}\left[{{\mathbf{C}}|{\text{M}}^{(p)} ,{\mathbf{D}}} \right]} \right)^{T}\\ & \qquad \cdot \Pr \left( {{{\theta}}_{q}^{(p)}|{\text{M}}^{(p)} ,{\mathbf{D}}} \right)\Pr \left({{\text{M}}^{(p)} |{\mathbf{D}}} \right) \\ \end{aligned}. $$

(14)

The covariance of the concentration due to different simulation models is

$$ \begin{aligned} & {\text{Cov}}_{\text{M}} {\text{E}}_{{{\theta}}} \left[ {{\text{E}}\left[ {{\mathbf{C}}|{\text{M}}^{(p)} ,{{\theta}}_{q}^{(p)} ,{\mathbf{D}}} \right]} \right] \\ & \quad = \sum\limits_{p} {\left( {{\text{E}}\left[ {{\mathbf{C}}|{\text{M}}^{(p)} ,{\mathbf{D}}} \right] - {\text{E}}\left[ {{\mathbf{C}}|{\mathbf{D}}} \right]} \right)} \quad \times \left( {{\text{E}}\left[ {{\mathbf{C}}|{\text{M}}^{(p)} ,{\mathbf{D}}} \right] - {\text{E}}\left[ {{\mathbf{C}}|{\mathbf{D}}} \right]} \right)^{T} { \Pr }\left( {{\text{M}}^{(p)} |{\mathbf{D}}} \right) \\ \end{aligned}. $$

(15)

The expectation of $\left( {{\mathbf{C}}|{\text{M}}^{(p)} ,{\mathbf{D}}} \right)$ is

$$ {\text{E}}\left[ {{\mathbf{C}}|{\text{M}}^{(p)} ,{\mathbf{D}}} \right] = \sum\limits_{q} {{\text{E}}\left[ {{\mathbf{C}}|{\text{M}}^{(p)} ,{{\theta}}_{q}^{(p)} ,{\mathbf{D}}} \right]\Pr \left( {{{\theta}}_{q}^{(p)} |{\text{M}}^{(p)} ,{\mathbf{D}}} \right)} . $$

(16)

The likelihood value, $\Pr \left( {{\mathbf{D}}|{\text{M}}^{(p)} ,{{\theta}}_{q}^{(p)} } \right)$ is approximated using the Bayesian information criterion (BIC) (Raftery 1995; Madigan et al. 1996): $\Pr \left( {{\mathbf{D}}|{\text{M}}^{(p)} ,{{\theta}}_{q}^{(p)} } \right) \approx \exp \left( { - {\frac{1}{2}}{\text{BIC}}_{q}^{(p)} } \right),$ where the BIC is

$$ {\text{BIC}}_{q}^{(p)} = - 2\ln \Pr \left( {{\mathbf{D}}|{\text{M}}^{(p)} ,{{\theta}}_{q}^{(p)} ,{\hat{\varvec{\upbeta}}}_{q}^{(p)} } \right) + m_{q}^{(p)} \ln L. $$

(17)

${\hat{\varvec{\upbeta}}}_{q}^{(p)}$ are the maximum-likelihood estimated unknown parameters, $m_{q}^{(p)}$ is the dimension of ${\hat{\varvec{\upbeta}}}_{q}^{(p)} ,$ and L is the size of the data D.

The prior probabilities of models are subjective values depending on a relative weight of one model against other models in the analyst’s belief. This study simplifies the problem by considering equal prior probabilities for simulation models and semivariogram models. Moreover, the variance window (Tsai and Li 2008a, b) is adopted to determine a proper acceptance window size in the BMA in order to avoid underestimating posterior probabilities of good models. Then, the posterior probability of semivariogram model q in simulation model p is approximated to

$$ \Pr \left( {{{\theta}}_{q}^{(p)} |{\text{M}}^{(p)} ,{\mathbf{D}}} \right) \approx {\frac{{\exp \left( { - {\frac{1}{2}}\alpha \Updelta {\text{BIC}}_{q}^{(p)} } \right)}}{{\sum_{q} {\exp \left( { - {\frac{1}{2}}\alpha \Updelta {\text{BIC}}_{q}^{(p)} } \right)} }}}, $$

(18)

where α is the scaling factor that defines the size of the variance window and $\Updelta {\text{BIC}}_{q}^{(p)} = {\text{BIC}}_{q}^{(p)} - {\text{BIC}}_{ \min } ,$ where BIC_min is the minimum BIC value among all candidate models. The scaling factor α is a statistical parameter defined as α = s ₁/(s ₂ σ _D ), where σ _D is the standard deviation of the error chi-square distribution, s ₁ is the ΔBIC value corresponding to the significance level in Occam’s window, and s ₂ is the width of the variance window in the unit of σ _D (Tsai and Li 2008a, b). The selection of the α value depends on the analyst’s statistical preference. It is recommended that s ₂ ≤ 4 since 95% of ΔBIC is unlikely to be larger than 4σ _D . Statistical analysis normally considers 1% or 5% significance level in Occam’s window to determine s ₁ = 9.22 or s ₁ = 6, respectively. This study considers s ₁ = 6 and s ₂ = 2 for the case of the “1,500-foot” sand aquifer.

Inserting Eq. 9 into Eq. 8 and using Eq. 18, the posterior probability of simulation model p with the variance window is approximated to

$$ \Pr \left( {{\text{M}}^{(p)} |{\mathbf{D}}} \right) \approx {\frac{{\sum_{q} {\exp \left( { - {\frac{1}{2}}\alpha \Updelta {\text{BIC}}_{q}^{(p)} } \right)} }}{{\sum_{p} {\sum_{q} {\exp \left( { - {\frac{1}{2}}\alpha \Updelta {\text{BIC}}_{q}^{(p)} } \right)} } }}} $$

(19)

Using α = 1 in Eqs. 18 and 19 reflects the model weights calculated by Occam’s window.

Therefore, one can assess the constraint violations by using the BMA expectation for the concentration prediction as follows

$$ \mathop {\min }\limits_{\begin{subarray}{l} z_{i,n}^{R} \in \{0,1\} ,q^{R} \\ z_{j,n}^{P} \in \{ 0,1\} ,q^{P}\end{subarray} } w_{1} \left( {\sum\limits_{i} {\sum\limits_{n}{z_{i,n}^{R} q^{R} \Updelta t_{n} } } + \sum\limits_{j}{\sum\limits_{n} {z_{j,n}^{P} q^{P} \Updelta t_{n} } } } \right) + w_{2} \int\limits_{{t_{0} }}^{{t_{T} }} {\max\left[ {C_{\text{BMA}} \left({{\mathbf{x}} \in {\mathbf{x}}_{\rm Lula} ,t;z_{i,n}^{R} ,q^{R} ,z_{j,n}^{P} ,q^{P} } \right) -C_{\text{MPL}} ,0} \right]dt}+ w_{3} \int\limits_{{\Upomega_{R} }}{\max \left[ {C_{\text{BMA}} \left( {{\mathbf{x}},t = t_{T};z_{i,n}^{R} ,q^{R} ,z_{j,n}^{P} ,q^{P} } \right) - C_{\text{MPL}},0} \right]d{\mathbf{x}}} $$

(20)

where C _BMA is obtained by Eq. 11 using the variance window, which is

$$ C_{\rm BMA} = {\frac{{\sum_{p} {\sum_{q} {{\text{E}}\left( {C|{\text{M}}^{(p)} , {{\theta}}_{q}^{(p)} ,{\mathbf{D}}} \right)\exp \left( { - {\frac{1}{2}}\alpha \Updelta {\text{BIC}}_{q}^{(p)} } \right)} } }}{{\sum_{p} {\sum_{q} {\exp \left( { - {\frac{1}{2}}\alpha \Updelta {\text{BIC}}_{q}^{(p)} } \right)} } }}} . $$

(21)

This optimization problem is very time-consuming because it involves many simulation models and semivariogram models in the management model.

The BMA approach is different from the multi-realization method where the optimal policy has to satisfy a “stack” of realizations (Wagner and Gorelick 1989; Chan 1993). The multi-realization approach cannot avoid unrealistic realizations without judging their importance by the evidence of data and can overdesign expensive policies. Instead, the BMA prediction is made by the weighted models that are ranked by the evidence of data. Unrealistic models with zero model weights will not affect the optimal policies.

Another approach to study the overdesign issue is the risk-based probabilistic constraint formulation, e.g., the chance-constrained models (Tung 1986; Morgan et al. 1993; USEPA 1997; National Research Council 2001). The chance-constrained formulation has better flexibility than the use of a stack of realizations. The degree of overdesign is proportional to the reliability level of constraints that are not violated. The BMA formulation in this study is a special case of the chance-constrained formulation. Based on the deterministic equivalent of a chance-constrained equation (Tung 1986), Eqs. 3–4 using BMA prediction, C _BMA, implicitly refer to the consideration of a 50% risk in the chance-constrained formulation. For targeting a lower risk, both BMA prediction in Eq. 21 and BMA variance in Eq. 12 are needed along with a desired level of reliability to form the deterministic equivalent of a chance-constrained equation (e.g., formula (16) in Tung 1986). Although not within the scope of this study, the chance-constrained formulation with BMA would provide broader risk analysis.

4 Generalized parameterization for hydraulic conductivity estimation and uncertainty propagation to concentration

This study uses the GP method (Tsai and Yeh 2004; Tsai 2006) along with different semivariogram models to estimate the spatially correlated hydraulic conductivity. Let π = ln K be the natural logarithm of hydraulic conductivity. The GP method estimates π by honoring m measurements (π _j  = ln K _j , j = 1, 2,…,m) and combining the interpolation and zonation methods:

$$\begin{array}{l} \pi_{\rm GP} \left( {\mathbf{x}} \right) ={\sum\limits_{\substack{j = 1 \atop j \ne k\left( {\mathbf{x}} \right) } }^{m}} {\phi_{j} \left( {\pi_{j} - \pi_{{k\left( {\mathbf{x}} \right)}}} \right)\beta_{j}}+{\pi_{{k\left( {\mathbf{x}} \right)}}} \end{array},$$

(22)

where ϕ _j are the basis functions of an interpolation method, k(x) is the data index for the data point at x _k when the GP estimates ln K at unsampled location x, and ${{\varvec{\upbeta}}}=\{{\beta_{j}},\;j=1,2,\ldots,m\}$ are the data weighting coefficients for the m data points. The zones are predetermined by the data points, and each zone encompasses one data point. When ${{\varvec{\upbeta}}}=0$, the GP shows a zonal distribution according to the data index k(x). The values of the data weighting coefficients are bounded between 0 and 1. This study considers the ordinary kriging (OK) weights for the basis functions and uses Voronoi tessellation to determine zones.

The GP covariance for a pair of locations (x, x′) is (Tsai 2006)

$$ {\text{C}}_{\text{GP}} \left[{{\mathbf{x}},{\mathbf{x^{\prime}}}} \right]=\sum\limits_{\substack{ i = 1 \atop i \ne k\left( {\mathbf{x}}\right) } }^{m}{\sum\limits_{\substack {j = 1 \atop j \ne k\left( {{\mathbf{x^{\prime}}}} \right)}}^{m} {\beta_{i}^{{\mathbf{x}}} \beta_{j}^{{{\mathbf{x^{\prime}}}}}\phi_{i}^{{\mathbf{x}}} \phi_{j}^{{{\mathbf{x^{\prime}}}}} R\left({{\mathbf{x}}_{i} ,{\mathbf{x}}_{j} } \right)} }-\sum\limits_{\substack{ i = 1 \atop i \ne k\left( {\mathbf{x}}\right) } }^{m} {\beta_{i}^{{\mathbf{x}}} \phi_{i}^{{\mathbf{x}}} R\left( {{\mathbf{x}}_{i} ,{\mathbf{x^{\prime}}}} \right)}-\sum\limits_{\substack{ j = 1 \atop j \ne k\left({{\mathbf{x^{\prime}}}} \right) } }^{m}{\beta_{j}^{{{\mathbf{x^{\prime}}}}}\phi_{j}^{{{\mathbf{x^{\prime}}}}} R\left({{\mathbf{x}},{\mathbf{x}}_{j} } \right)} + R\left({{\mathbf{x}},{\mathbf{x^{\prime}}}} \right) $$

(23)

where, the function R in the covariance is

$$ R\left( {{\mathbf{x}}_{a} ,{\mathbf{x}}_{b} } \right) = \gamma \left( {{\mathbf{x}}_{a} ,{\mathbf{x}}_{{k\left( {{\mathbf{x^{\prime}}}} \right)}} } \right) + \gamma \left( {{\mathbf{x}}_{b} ,{\mathbf{x}}_{{k\left( {\mathbf{x}} \right)}} } \right) - \gamma \left( {{\mathbf{x}}_{a} ,{\mathbf{x}}_{b} } \right) - \gamma \left( {{\mathbf{x}}_{{k\left( {\mathbf{x}} \right)}} ,{\mathbf{x}}_{{k\left( {{\mathbf{x^{\prime}}}} \right)}} } \right) , $$

(24)

where γ is the semivariogram.

The data weighting coefficients ${{\varvec{\upbeta}}}$ in the GP method are the unknown parameters as shown in the BIC in this study. For a given semivariogram model in a saltwater intrusion model, one can use a maximum-likelihood method to estimate ${{\varvec{\upbeta}}}$ based on the groundwater head data (Tsai and Yeh 2004). The estimated ${{\varvec{\upbeta}}}$ is ${\hat{\varvec{\upbeta}}}_{q}^{(p)}$ in Eq. 17.

Based on the first-order Taylor series expansion (Dettinger and Wilson 1981; Tung 1986; Wagner and Gorelick 1987), the expectation and covariance of predicted concentration can be approximated. Using the GP method and following the approach in Li and Tsai (2009), the expectation is ${\text{E}}\left[ {{\mathbf{C}}|{\text{M}}^{(p)} ,{{\theta}}_{q}^{(p)} ,{\mathbf{D}}} \right] \approx {\mathbf{C}}\left( {{\varvec{\uppi}}_{{\rm GP},q}^{(p)} } \right)$ and the concentration covariance is ${\text{Cov}}\left[ {{\mathbf{C}}|{\text{M}}^{(p)} ,{{\theta}}_{q}^{(p)} ,{\mathbf{D}}} \right] \approx J_{\pi ,q}^{(p)} \left[ {{\text{C}}_{{\rm GP},q}^{(p)} } \right]\left[ {J_{\pi ,q}^{(p)} } \right]^{T} ,$ where ${J_{\pi ,q}^{(p)}} = {\partial {\mathbf{C}}}/\partial {\varvec{\uppi}}|_{{{\varvec{\uppi}}_{{\rm GP},q}^{(p)} }}$ is the Jacobian matrix. Therefore, one can evaluate the BMA expectation and covariance in Eqs. 11–15. Therefore, C _BMA in the management model is obtained by

$$ C_{\rm BMA} = {\frac{{\sum_{p} {\sum_{q} {C\left( {{\varvec{\uppi}}_{{\rm GP},q}^{(p)} } \right)\exp \left( { - {\frac{1}{2}}\alpha \Updelta {\text{BIC}}_{q}^{(p)} } \right)} } }}{{\sum_{p} {\sum_{q} {\exp \left( { - {\frac{1}{2}}\alpha \Updelta {\text{BIC}}_{q}^{(p)} } \right)} } }}} . $$

(25)

The total covariance of the predicted concentration can be evaluated by the following

$$ {\text{Cov}}\left[ {{\mathbf{C}}|{\mathbf{D}}} \right] = {\text{E}}_{\text{M}} {\text{E}}_{{{\theta}}} \left[ {J_{\pi ,q}^{(p)} \left[ {{\text{C}}_{{\rm GP},q}^{(p)} } \right]\left[ {J_{\pi ,q}^{(p)} } \right]^{T} } \right] + {\text{E}}_{\text{M}} {\text{Cov}}_{{{\theta}}} \left[ {C\left( {{\varvec{\uppi}}_{{\rm GP},q}^{(p)} } \right)} \right] + {\text{Cov}}_{\text{M}} {\text{E}}_{{{\theta}}} \left[ {C\left( {{\varvec{\uppi}}_{{\rm GP},q}^{(p)} } \right)} \right] . $$

(26)

5 Results and discussions

5.1 Saltwater intrusion simulation and management models

A saltwater intrusion simulation model for the “1,500-foot” sand aquifer in the Baton Rouge area is further developed from the groundwater flow model developed by Tsai and Li (2008a,b). The modeling area is shown in Fig. 2. The model incorporates the connector well, EB-1293, which recharges groundwater from the “800-foot” sand to the “1500-foot” sand. A recharge rate of 2,200 m³/day of the connector well is determined based on the flow rates reported by the Louisiana Capital Area Ground Water Conservation Commission (CAGWCC 2002). MODFLOW (Harbaugh et al. 2000) and MT3DMS (Zheng and Wang 1999) are employed, but uncoupled to simulate saltwater intrusion in the two-dimensional “1,500-foot” sand aquifer in the planar discretization. Permeability of the Baton Rouge Fault is characterized using the hydraulic characteristic (Hsieh and Freckleton 1993). The model parameters are listed in Table 1.

Table 1 Parameters in groundwater flow and transport models of the “1,500-foot” sand aquifer

The simulation model runs two consecutive stages: calibration stage and management stage. In calibration stage, the data weighting coefficients in the GP method and the BMA model weights are estimated by 706 groundwater head data of the “1,500-foot” sand of Baton Rouge Area [12115BR], obtained from the USGS Louisiana Water Science Center available at http://la.water.usgs.gov/. The horizon of the calibration stage is 15 years from January 1, 1990 to December 31, 2004 with 180 stress periods.

In the management stage, the simulation model predicts saltwater intrusion for 15 years from January 1, 2005 to December 31, 2019 with 180 stress periods. Twenty injection wells and 12 pumping wells are added into the study area. The GA uses the saltwater intrusion model in the management model to optimize the joint operations of the hydraulic barrier and extraction systems. The groundwater head distribution on December 31, 2004 is used as the head initial condition for the management stage. The groundwater head boundary condition values in the management stage were kept the same as in December 2004. The initial chloride concentration is shown in Fig. 2. Due to very limited chloride concentration data, a mass flux boundary condition of the chloride concentration with an incoming concentration C ₀ = 1.0 (or 100%), i.e., −θ D∇C + θ v C = θ v C ₀ (Zheng and Wang 1999), is assumed at the southern boundary of the modeling area, where θ is the porosity, D is the dispersion tensor, and v is the pore velocity vector. This study considers the MPL of chloride concentration to be 2.5%, i.e., C _MPL = 0.025, to determine constraint violations. The time-varied monthly pumping (production) rates in individual production wells (Lula wells and other wells for water supply) were fixed to the average pumping rates of the last 3 years (2002–2004) in the calibration stage.

The groundwater model for the “1,500-foot” sand aquifer uses the time-varied constant head boundary condition in MODFLOW. Although the boundary condition values for the groundwater model have been carefully determined, the values are not completely certain because the groundwater head data are scarce. To assess the robustness of the optimized joint operations under this uncertainty, five groundwater flow models are created, which have 0, ±10, and ±20% changes of the predetermined head boundary values over the entire boundary. It is noted that in theory, the percentage change in the head boundary values could be treated as an unknown parameter to be estimated in model calibration. However, this study takes a practical approach that is commonly used for sensitivity analysis based on different values of percentage change. This study takes advantage of this approach by creating multiple groundwater models for BMA analysis on head boundary value uncertainty. Moreover, the uncertainty in the semivariogram models for hydraulic conductivity is considered. Figure 3 shows the experimental semivariograms of the hydraulic conductivity and three semivariogram models (exponential, spherical and Gaussian models). A total of 15 simulation models are developed. The model weights are calculated below.

Fig. 3

Experimental semivariograms (filled circles) of log-hydraulic conductivity (ln K) and semivariogram models

5.2 Model calibration and BMA weights

Fifteen sets of the data weighting coefficients in the GP method are estimated for the 15 models using a quasi-Newton method (Byrd et al. 1994) that minimizes the sum of squared residuals between simulated heads and observation heads. It assumes that the errors in heads are Gaussian distributed. Then, the BIC in Eq. 17 becomes

$$ {\text{BIC}}_{q}^{(p)} = Q_{q}^{(p)} + \ln \left| {{\mathbf{V}}_{h} } \right| + L\ln 2\pi + m_{q}^{(p)} \ln L , $$

(27)

where $Q_{q}^{(p)}$ is the sum of head fitting errors:

$$ Q_{q}^{(p)} = \left( {{\mathbf{h}}^{\rm cal}{\left({\hat{\varvec{\upbeta}}}_{q}^{(p)}\right)}} -{\mathbf{h}}^{\rm obs} \right)^{T} {{\mathbf{V}}_{h}^{ - 1}}\left( {{\mathbf{h}}^{\rm cal}\left({\hat{\varvec{\upbeta}}}_{q}^{( p)}\right)} -{\mathbf{h}}^{\rm obs} \right) , $$

(28)

where h ^obs and h ^cal are the observed and calculated groundwater heads, and L is the number of the observed groundwater heads. V _h is the diagonal matrix, whose elements are the variances of head errors. The term $\ln \left| {{\mathbf{V}}_{h} } \right|$ can be eliminated in Eq. 27 by considering standard Gaussian distribution of heads that are scaled by h ^obs and head variances (Li 2008; Li and Tsai 2009). In this study, the number of unknown parameters (m ^(p) _q ) and head variances are the same for all models. Therefore, the BIC difference can be simply calculated by $\Updelta {\text{BIC}}_{q}^{(p)} = \Updelta Q_{q}^{(p)} .$

The transport model parameters were not calibrated because the chloride data size is extremely small and chloride was only sampled at few observation wells. The initial plume and the transport parameters were best guessed based on information from Tomaszewski (1996) and the chloride data at the USGS Louisiana Water Science Center.

A variance window with a 5% significance level and two times the standard deviation of the data chi-squares distribution is adopted (Tsai and Li 2008a). The scaling factor is $\alpha={2.12/{\sqrt {706}}}=0.080.$ The sum of head fitting errors, the ΔBIC values, and the BMA model weights for 15 models are shown in Table 2. The simulation models with no change in the predetermined head boundary values have the smallest head fitting errors; and a 10% reduction on the head boundary values shows small increase in the head fitting errors. Changes over 20% on the head boundary values significantly increase the fitting errors. Figure 4 shows scatter plots of calculated groundwater head values against observed head data for the best model (Gau + 0%) and the worst model (Exp + 20%). The root mean squared error (RMSE), $\sqrt {{\frac{1}{706}}\sum_{i = 1}^{706} {\left( {h_{i}^{\text{cal}} - h_{i}^{\text{obs}} } \right)^{2} } } ,$ for the best model is 1.31 m, and is 2.95 m for the worst model. The calculated heads using the best model show good agreement to the observed head data.

Table 2 Sum of squared errors of head, ΔBIC values, and BMA model weights

Fig. 4

Scatter plots of calculated groundwater head values against observed head data and the RMSE of heads for a Gau + 0% model (the best model) and b Exp + 20% model (the worst model). The groundwater head datum is sea level

The ΔBIC values are calculated based on Eq. 27, where L = 706 and $m_{q}^{(p)} = 20.$ Using Occam’s window (α = 1.0), the Gaussian model dominates other two semivariogram models in all simulation models. The simulation model with no change in head boundary values has a dominant weight (99.91%). Other simulation models with changes in head boundary values are literally discarded. As discussed in Tsai and Li (2008a), using Occam’s window may exaggerate the importance of the best model and overlook the importance of other good models. Using the variance window, shown in Table 2 the best simulation model (M⁽³⁾) has a weight of 53.31%. The second best simulation model (M⁽⁴⁾) has a weight of 32.05%. The simulation models with a 20% increase or reduction on the head boundary values can be discarded. Within the best simulation model, the best semivariogram model is the Gaussian model (θ ⁽³⁾₃ ) with a weight of 40.42%. The second best is the exponential model (θ ⁽³⁾₂ ) with a weight of 30.13%. Table 2 also shows the BMA model weights in terms of the joint probability to represent the actual importance for each model. The best model (Gau + 0%), the pair of M⁽³⁾ and ${{\theta}}_{3}^{(3)} ,$ has a model weight of 21.55%, which can be seen as important as the second best model (Exp + 0%) and the third best model (Sph + 0%). If only considering the single best model (Gau + 0%) in the management model, the optimized joint operations may not be able to achieve the management objectives due to neglecting the model structure uncertainty. In the following discussions, the variance-window-based BMA is considered. The management model only incorporates 12 simulation models with non-zero model weights (i.e., model M⁽¹⁾ is discarded), which are linked together in Eq. 25 of the BMA for saltwater intrusion management.

5.3 Joint operations and concentration prediction

5.3.1 No-action scenario

Without the hydraulic barrier and extraction systems (no-action scenario), the chloride concentration is slowly moving northward toward the Lula wells. Figure 5 shows the predicted isochlors at the end of 15 years in the management stage. The concentration distributions predicted by the best model (Gau + 0%) and the BMA are similar. Both confirm that the 2.5% isochlor does not reach the Lula wells within the management period. Figure 6 shows the variances of the predicted chloride concentrations at the end of 15 years due to different semivariogram models in simulation models (Eq. 14) and due to different simulation models (Eq. 15). Obviously, the variances of the predicted chloride concentrations due to different semivariogram models in individual simulation models are much smaller than the variances due to different simulation models. Given the similar weights of the semivariogram models in the best and second best simulation models (see Table 2), this indicates similar concentration predictions made by different semivariogram models within a simulation model. However, different simulation models due to head boundary uncertainty exhibit relatively large differences in concentration predictions.

Fig. 5

Predicted isochlors by a the best model (Gau + 0%) and b the BMA with the variance window at the end of 15 years, for the no-action scenario

Fig. 6

Variances of predicted chloride concentrations for a between semivariogram models and b between simulation models at the end of 15 years, using BMA with the variance window for the no-action scenario

5.3.2 Joint operations with well pumps active all the time

By considering the well pumps of the hydraulic barrier and extraction systems active all the time, the injection rates and extraction rates are increased systematically from the no-action scenario to illustrate the impact of the systems on the saltwater intrusion. According to the results in Fig. 5, a viable remedial action is defined for the case where the sum of violations (the second term in Eq. 5 or in Eq. 20 without w ₂) at the Lula wells is zero during the management period. Otherwise, the remedial action not acceptable. For example, the no-action scenario is a viable scenario. A viable remediation scenario represents the minimum requirement for an operation action because any actions that cause the Lula wells to be contaminated are not acceptable. Moreover, optimized operations would become very expensive if one was restricted to zero violation in the remediation area at the end of the management period. This study relaxes this restriction for practical purposes and considers a remedial action acceptable with a violation of less than 0.001 for the third term in Eq. 5 or in Eq. 20 without w ₃. The threshold for this small acceptable violation is subjective and depends on decision makers.

Figure 7 shows the matrix of scenarios without violation (open circles) and with violation (filled circles) at Lula wells, created by enumerating the combinations of different injection rates and extraction rates using the best model (Gau + 0) and the BMA. The injection and extraction rates are operated full time for 15 years. The total amount of pumped and injected water in million cubic meters (MCM) is plotted in Fig. 7, which is the potential (maximum) amount of water the systems need to deal with. For example, an injection rate of 3,250 m³/day and extraction rate of 2,750 m³/day operate a potential amount of water of 537 MCM. Figure 7 also shows the contour lines of the sum of violations in the remediation area at the end of the 15-year management period. Based on the information in Fig. 7, one can draw the following observations: (1) Actions with low injection rates and low extraction rates are unacceptable because they cannot cleanup the remediation area even though they are viable actions to the Lula wells. (2) High injection rates with low extraction rates are unacceptable because the hydraulic barrier system pushes northward and end up brackish water in the Lula wells. This can result in zero violation in the remediation area at the end of the management period. (3) Low injection rates with high extraction rates are generally not acceptable remedial actions. While no violation occurs in the Lula wells, the extraction system enlarges and deepens the depression core, induces more saltwater intrusion northward, and causes high violations in the remediation area. (4) Using higher injection rates and higher extraction rates is likely to achieve the goal of cleaning the brackish water in the remediation area without jeopardizing the Lula wells.

Fig. 7

Matrix of actions with different injection and extraction rates using a the best model and b the BMA with the variance window. Open circle represents a viable action. Filled circle represents an unacceptable action. Solid line represents the sum of violations in the remediation area. The dotted-dashed line represents the total amount water injected and pumped in MCM

5.3.3 Joint operation optimization

To reduce the complexity of the management model and increase the efficiency of searching for the optimal operation, the operation considers all injection wells and all pumping wells are active or inactive on a monthly basis for 15 years. Therefore, there are 180 scheduling variables for the injection wells and 180 scheduling variables for the pumping wells. A micro-GA solver (Carroll 1996) is used to minimize the objective function. The population in the micro-GA is five, the uniform crossover probability is 0.5, and the mutation probability is 0.02. The tournament selection strategy is used. The maximum number of generations for each GA run is 200. These GA parameters are suggested in the solver (Carroll 1996). The maximum injection rate (q ^R_max ) and extraction rate (q ^P_max ) in the GA are set to 4,000 m³/day. The injection rate and extraction rate are given the same length of 12 bits in the binary chromosomes. To prioritize the multiple objections, it sets w ₁ = 10⁻¹¹, w ₂ = 100, w ₃ = 1.0 for the objective function. The length of a binary chromosome is 384 bits. To obtain the fitness of each chromosome (one possible operation solution), the 12 simulation models are executed together to calculate the BMA concentrations (Eq. 25). The computation is extremely extensive.

Again, the author recognizes the possibility of considering individual operations of the well pumps on the monthly basis. This will reduce operation costs by increasing flexibility in well operations in the management model. However, this will result in 3,600 scheduling variables for the injection wells and 2,160 scheduling variables for the pumping wells. This complicated optimization problem is avoided in this study.

Two management models are compared to show the difference if model uncertainty is not considered. The first management model only considers the best model (Gau + 0%). The second management model uses the BMA to predict concentration based on the 12 simulation models. The optimization results are shown in Table 3. Again, for the no-action scenario, two management models show no violation at Lula wells (see row 1 and row 2 of Table 3). However, the sum of violations in the remediation area is very high. If considering the best model only in the management model, the GA obtains the optimal injection rate to be 3,217 m³/day and the optimal extraction rate to be 2,448 m³/day. No violation occurs at the Lula wells and in the remediation area at the end of the management period (see row 3 of Table 3). The total amount of water injected and pumped is 331 MCM. Comparing to the same injection and extraction rates in Fig. 7, the management model significantly reduces concentration violations and the amount of water to deal with compared to pumping all wells all 15 years. Figure 8a–c shows the chloride concentration predictions at 5-, 10-, and 15-years. However, if model uncertainty is considered, one can test if the optimal operation from the best model is acceptable by re-evaluating the sum of violations using the BMA concentrations in Eq. 25. As shown in Table 3, this optimal solution produces noticeable violation in the remediation area at the end of the management period (see row 4 of Table 3). The violation can be seen in Fig. 8(f) at the end of the 15 years based on the BMA prediction. The violation is expected because the optimal operation from the best model neglects other good models and gives a biased solution.

Table 3 Optimization results using the best model (Gau + 0%) and the variance-window-based BMA model

Fig. 8

Isochlors predicted by the best model (Gau + 0%) at a 5 years, b 10 years, and c 15 years, and by the BMA with the variance window at d 5 years, e 10 years, and f 15 years, given the optimal joint operation, injection rate = 3,217 m³/day and extraction rate = 2,448 m³/day, from the best model

Using the BMA to predict chloride concentration in the management model, the GA increases the optimal injection rate to 3,729 m³/day and increases the optimal extraction rate to 3,012 m³/day in order to reduce the violations from other models. The increased injection and extraction rates due to considering model uncertainty reflect the need of “overdesigning” the strategy to insure reliability (Wagner and Gorelick 1987). As shown in Table 3, the optimal operation using the BMA presents an acceptable solution because no violation occurs at the Lula wells and the sum of violations in the remediation area is less than 0.001 (see row 6 of Table 3). The total amount of water injected and pumped is 371 MCM. The optimal operation using BMA is also tested if it is an acceptable solution for the best model. After re-evaluating the sum of violations, as shown in Table 3, the optimal operation using the BMA also works for the best model (see row 5 of Table 3). Figure 9 shows the chloride concentration distributions at the end of 15 years using the best model and the BMA with this optimal operation. As shown in Fig. 10, the variances of chloride concentration at the end of 15 years due to different semivariogram models in individual simulation models are much smaller than the variances due to different simulation models.

Fig. 9

Isochlors predicted by a the best model (Gau + 0%) and b the BMA with the variance window at the end of 15 years, given the optimal joint operation, injection rate = 3,729 m³/day and extraction rate = 3,012 m³/day, from the BMA with the variance window

Fig. 10

Variances of predicted chloride concentrations for a between semivariogram models and b between simulation models at the end of 15 years, given the optimal joint operation, injection rate = 3,729 m³/day and extraction rate = 3,012 m³/day, from the BMA with the variance window

Using the BMA prediction in the management model does not prevent other models from violation. The violations in the remediation area for individual models at the end of the management period are listed in Table 4. An exhaustive management model can consider the constraints that include concentration predictions from individual models, but this would result in a very expensive management policy in terms of the total amount of injected and pumped water in order to satisfy all models. Moreover, this way would exaggerate the influence from insignificant models. With BMA, one can avoid this problem while considering the model uncertainty.

Table 4 The sum of violations in the remediation area at the end of the management period using BMA prediction

6 Conclusions

• 1. Groundwater management is far more difficult and complex because of model structure uncertainty. Uncertain model structure often results in multiple possible simulation models. Management plans under the consideration of a single simulation model tend to bias optimized operations. To alleviate the biasedness, a reliable groundwater management model should take into account the predictions from multiple simulations models.

• 2. Bayesian model averaging has been shown to be capable of integrating multiple models for prediction in the management model. Optimized operations based on the BMA predictions show more reliable management outcomes than those from one simulation model. However, the optimized operation is more expensive in order to reduce constraint violations elevated by considering many models.

• 3. The study has demonstrated the importance of considering the model structure uncertainty in a real-world case study. Using the best model underestimates the optimized injection rate and extraction rate for the hydraulic barrier and extraction systems. Using the BMA prediction for chloride concentration, the optimized injection and extraction rates increase in order to reduce the concentration violation in the remediation area.

• 4. The study also demonstrates the importance of using the variance window for uncertainty analysis in the management model. Using Occam’s window literally accepts only the best model and neglects model uncertainty. However, the incorporation of more simulation models in the management model, as suggested by the variance window, could result in more expensive operations in order to reduce additional constraint violations created by the additional simulation models. A further investigation should be conducted to understand the impact of the size of the variance window with respect to Occam’s window.