Performance Assessment of Model Averaging Techniques to Reduce Structural Uncertainty of Groundwater Modeling

Abstract

Accurate estimates of groundwater modeling in arid regions have a crucial role in reaching a sustainable management of groundwater sources. However, groundwater modeling has been faced with different uncertainty sources; besides our imperfect knowledge, it is difficult to derive a proper prediction that can lead to reliable planning. This study aimed to improve the groundwater numerical simulations using different Model Averaging Techniques (MATs). For this, three numerical models, such as Finite Difference (FD), Finite Element (FE), and Meshfree (Mfree), were developed and their performance was verified in a real-world case study. Then various MATs including Simple Model Average (SMA), Weighted Average Method (WAM), Multi Model Super Ensemble (MMSE), Modified MMSE (M3SE) and Bayesian Model Averaging (BMA) were employed to improve the simulated groundwater level Fluctuations (outputs of three numerical models). The findings of this study demonstrated that the numerical model uncertainty is considerable and should not be neglected in the uncertainty analysis of groundwater modeling. In terms of RMSE, the lowest value of 0.148 m was obtained by Mfree while higher values of 1.355 m and 0.287 m are calculated for FD and FE respectively. In addition, the performance assessment of MATs showed a capacity to generate a skillful simulation compared to numerical predictions. Although the MMSE and M3SE (with RMSE values of 0.088 and 0.103 m) generated a desirable prediction in the majority of piezometers, they suffer from a main deficiency, such as the multicollinearity issue. From this perspective, it was concluded that the BMA produced a more reliable and reasonable prediction than other MATs.

1 Introduction

Groundwater modeling without uncertainty analysis may lead to contradictory predictions; consequently, the unreliable options are delivered to policymakers in planning water resource management (Wu and Zeng 2013). Hence, in ground water modeling studies, it is tried to consider and fix the major influencing uncertainty sources as much as possible. There are different types of uncertainty in groundwater modeling, including conceptual model structure uncertainty (consisting of boundary conditions, hydrodynamic parameters, and aquifer recharge), mathematical uncertainty (numerical structure uncertainty and parameter uncertainty related to shape and weight functions), input data uncertainty (rainfall, evaporation and abstraction rate) and epistemic uncertainty (Rajabi et al. 2018).

So far, many studies were conducted in the context of groundwater aiming to assess different types of uncertainty, including parameters uncertainty (Jing et al. 2019; Pagnozzi et al. 2020) input data uncertainty (Xu et al. 2017; Hassanzadeh et al. 2019) model structure and boundary conditions uncertainty (Refsgaard et al. 2012; Pham and Tsai 2016; Enemark et al. 2019; Cao et al. 2019; Pan et al. 2020; Rojas et al. 2010; Person et al. 2012). The most commonly used methods in literature for quantifying the parameters and input data uncertainty is employing a numerical algorithm such as Generalized Likelihood Uncertainty Estimation (Mertens et al. 2004; Rojas et al. 2008; Hassan et al. 2008) and Monte Carlo Markov Chain-MCMC (Troldborg et al. 2007; Yoon et al. 2013 ). In addition, a number of studies employed the Kalman Filtering (KF) in estimating parameter uncertainty (Yu et al. 2020). Further, it is suggested in literature to combine the predictions of different alternative conceptual models to consider the uncertainty arising from model structure and boundary conditions (Nettasana et al. 2012; Mustafa et al. 2019). These studies perform the combination stage using different techniques among which Bayesian Model Averaging (BMA) is known as the most effective and practical ones. Additionally, there are few studies, coupling the Ensemble KF (EnKF) simulations to the BMA to quantify model structure uncertainty (Xue and Zhang 2014).

Although there are many literatures to assess the uncertainty sources of groundwater process, quantifying, and fixing all uncertainty sources is very difficult in practice due to high complexities and our defective knowledge. Hence, some studies such as Mosavi et al. (2021), Mustafa et al. (2020), Roy and Datta (2019), Zhang et al. (2018), and Rajib et al. (2017) suggested improving groundwater model outputs using Model Averaging Techniques (MATs) as post processing measurements.

The literature reveals that most relevant studies aiming to improve the total uncertainty in groundwater modeling have usually employed the BMA (Mustafa et al. 2020) and EnKF (Van Geer et al. 1991; Klise and McKenna 2007; Rajib et al. 2017; Zhang et al. 2018) techniques. For example, Rajib et al. (2017) simulated contaminant concentration through Finite Difference (FD) in a synthetic test case. After that, the numerical results were updated using different types of EnKF and were compared with analytical solutions. However, addressing the various sources of uncertainty is not possible in Kalman’s approaches (Ridler et al. 2018). Mustafa et al. (2020) have presented a comprehensive framework to quantify and improve the total uncertainty in groundwater modeling. They used the DREAM algorithm to identify the uncertainty arising from hydrodynamic parameters, boundary conditions, and input data in different conceptual models. Then they feed the different model outputs into the BMA to improve simulations. Despite considerable achievements obtained in their study, it is not without drawbacks; for example, they employed FD to simulate groundwater table through Processing Modflow for Windows (PMWIN), while there are the serious drawbacks due to irregular and non-continuous domains in its application in real case studies (Hu et al. 2020). Indeed, the mathematical model uncertainty is missing in their study.

Besides, the literature review indicates that due to more frequent use and easier access to FD-based platforms (e.g. GMS, PMWIN, and VISTA) majority of studies utilize the FD method for groundwater modeling. (Pacheco et al. 2018; Karimi et al. 2019; Aliyari et al. 2019; Gelsinari et al. 2020; Sabzzadeh and Shourian 2020). While the FD has been criticized for its structure and many researches have acknowledged that, the performance of other numerical methods such as Finite Element (FE) and Meshfree (Mfree) is much more desirable than FD (Anshuman and Eldho 2019). Further, the literature suggests that most related studies not only did not compare the performance of different numerical models, but also have ignored the uncertainty of mathematical model. However, this type of uncertainty is very important because if the conceptual model and input datasets are installed on an inappropriate mathematical framework, the model may give the invalid results. Therefore, the examination of the mathematical model uncertainty takes precedence over other uncertainty sources.

Moreover, there are some MATs, which their application has been investigated mainly in meteorological sciences and hydrology, in particular in rainfall-runoff modeling (Georgakakos et al. 2004). Ajami et al. (2006) reported that MAT methods such as Multi Model Super Ensemble (MMSE) and Modified MMSE (M3SE) have noticeable performance in hydrology science. Despite some deficiencies in estimated weights related to model ranking (Duan et al. 2007), the performance of these methods in improving groundwater modeling uncertainty has been neglected.

Hence, improving the total uncertainty of groundwater modeling in the real-world studies requires more researches which examines different numerical model at same time to consider mathematical model uncertainty. Therefore, it needs the different approaches of MAT methods employed and assessed in groundwater studies.

Accordingly, the current study aims to enrich previous works by presenting an applicable design for quantifying the uncertainty arising from different mathematical models. Furthermore, this design is capable of improving total prediction uncertainty by employing different varieties of MAT. In this plan, the simulations of FD, FE, and Mfree methods are given to different types of MATs such as Simple Model Averaging (SMA), Weighted Average Method, MMSE, and M3SE, as well as BMA to produce the skillful simulation series for groundwater modeling in a real-world case. This study implements its plan on Birjand aquifer, eastern Iran, to address the performance of the proposed framework in the actual conditions.

2 Methods

2.1 Study Area

Birjand plain is located in eastern Iran, where annual rainfall is very low (<100 mm), and is classified as an arid region based on Dumbarton climate classification (see Fig. 1). The average annual temperature and evaporation are 24.5 centigrade and 2600 mm (Jafarzadeh et al. 2021a). It is worth noting that the basic element of development was traditionally defined as the agriculture section, which is resulting in severe withdrawal of groundwater resources.

Fig. 1

Location of Birjand plain and aquifer

2.2 Conceptual Model

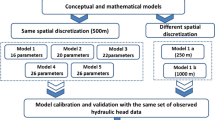
Some studies that have been previously conducted in Birjand aquifer focused on uncertainty issues. These studies employed a well-predefined conceptual model in which either parameter uncertainty has been perfectly examined (e.g., Hamraz et al. 2015; Mohtashami et al. 2017) or conceptual model was revised and enhanced in the recent studies by Sadeghi-Tabas et al. (2016) and Sadeghi-Tabas et al. (2017). According to assumption of these studies, Birjand aquifer is known as a one-layer hydrogeological model with different thickness (8 m to 255 m). Ten input and output paths were also added to aquifer domain to account for the effects subsurface recharge and depletion (see Fig. 2). Boundary conditions in these sections are considered constant values (Dirichlet conditions).In addition, the drain flows (in the southwest regions), the surface recharge arising from rainfall and the return flow of extraction wells concerning spatial and temporal variations are imposed to conceptual models. Moreover, there are about 191 extraction points (including wells, springs, and Qanat) and 11 piezometers, within the Birjand aquifer. Finally, given the geology heterogeneous and anisotropy conditions, 17 zones for hydraulic conductivity and specific yield were considered over the aquifer domain (see Fig. 3).

Fig. 2

Adopted from Hamraz et al. 2015)

Definiation of grid model in Birjand aquifer (

Fig. 3

Adopted from Sadeghi-Tabas et al. 2017)

Definition of specific yield and hydraulic conductivity zones in Birjand aquifer (

2.3 Mathematical Modelling

Numerical methods are classified into weak and strong form methods. In the strong form methods, the initial form of the governing equation is kept and numerical method approximates directly solution. For example, FD discretizes the second-order spatial derivatives through Taylor series and solves the discretized equation. While, strong numerical methods, such as FE and Mfree, convert the initial form of governing equation to secondary form by decreasing the order derivatives. The most commonly used weak form methods are subset of Weighted Residual Methods (WRMs). In the WRMs, a mathematic trick is used to force the residuals to be zero. One of the most commonly used methods is to compute a weighted average of residuals through a series of weight functions and then, minimize the integral of weighted average throughout problem domain as much as possible. For each numerical method, the weight functions are selected based on different approaches. For example, the FE method employs the Galerkin while Petrov- Galerkin is used in the Mfree method (Liu and Gu 2005). The FE method splits the global domain into triangular, square or rectangular elements, while Mfree uses local quadrature or circle domains surrounding each grid point.

2.3.1 Groundwater Flow-governing Equations

The governing equation of groundwater flow for two dimensional, isotropic and homogenous aquifers is given by (Arnold et al. 1993):

$$K.h\frac{{{\partial^2}h}}{{\partial {x^2}}} + K.h\frac{{{\partial^2}h}}{{\partial {y^2}}} + Q(i,j) = {S_y}\frac{\partial h}{{\partial t}},\,\,\,\,\,\,\left( {Q(i,j) = q + \sum\limits_{i = 1}^n {{Q_i}\delta ({x_o} - {x_i},{y_o} - {y_i})} } \right)$$

(1)

Considering following boundary and initial conditions:

$$\begin{array}{*{20}{c}} {\frac{\partial h}{{\partial \Gamma t}}\, = \frac{{q_t}}{K}\, \Rightarrow on\,\,\,\,\Gamma = \Gamma t} \\ {h(x,y,t) = \bar h\, \Rightarrow on\,\,\,\,\Gamma = \Gamma u\,} \\ {h(x,y,o) = {h_0}\,\, \Rightarrow on\,\,\,\,\,\Omega } \end{array}$$

(2)

where h, Sy, K, t are potential groundwater level (m), specific yield, hydraulic conductivity in horizontal and vertical direction (m/day), time (day). While Q, q and $\delta$ are source or sink function (m³/day), distributed rate of recharge or evapotranspiration over aquifer domain (m/day) and Dirac Delta function respectively. Also, $qt,\bar h,\,{h_0}$ are known inflow rate (m²/day), constant groundwater level (m), and initial head (m). Furthermore, $\Gamma ,\,\Gamma t,\,\Gamma u\,$ are global, essential (Dirichlet) and natural (Neuman) boundary conditions respectively, while $\Omega$ indicates aquifer domain.

Since the FD, FE, and Mfree models in groundwater modeling frequently –are applied in several literatures, as well due to a recent related publication of current research team (Jafarzadeh et al. 2021b, c), this paper did not repeat them. Interested readers are referred to Appendix where more details about the formulation of numerical models, in particular Mfree as a newer method, has been provided.

2.3.2 Numerical Modeling Process

This study performed the groundwater modeling by designing a conceptual model for Birjand aquifer. First, the various datasets including rainfall and evaporation time series, geologic information (groundwater depth, bedrock, hydraulic conductivity, and specific yield), topographic maps, extraction wells (type, location, and rate), as well as observation wells are collected and through Arc GIS converted to gridded data. Then, considering boundary conditions, the conceptual model of Birjand aquifer was constructed. Birjand aquifer domain was gridded to 34 rows and 94 columns in which horizontal and vertical distance (size of mesh) is 500 m. Also, the size of local and support domains was considered 0.8 and 3 respectively to ensure the stability and accuracy of results (Liu and Gu 2005; Mohtashami et al. 2017). Further, the parameter of radial shape function was considered 0.3. The numerical methods employed the gridded datasets to simulate the groundwater table fluctuations influenced by continued pumping during a hydrologic water year (from 23 October 2011 to 21 October 2012). In this study, monthly stress periods with daily time steps were considered and used for simulating. The groundwater table in the first stress period was simulated to verify the hydrodynamic components and boundary conditions (calibration step). This model setup was later used as initial conditions of the transient state. Since in the current field study the most rainfall occurred in winter and the early spring (from Mid-November until Mid-April), the abstraction rates of extraction wells in this period are minimum. Hence, the temporal variation of the abstraction rates and rainfall were considered in models.

Moreover, since the current study intends to present a numerical model in an open-source format coded in MATrix LABoratory (MATLAB) environment, the verification of the presented model is inevitable. This stage was carried out based on the findings of Jafarzadeh et al. (2021b, c) where the validity of numerical model was carefully examined in a synthetic case modeling. They revealed that based on the comparison of simulated groundwater levels with analytical solutions, the validity of all three proposed models was confirmed successfully. Also, their results acknowledged that the ability of Mfree is better than FE, and FD, respectively in terms of RMSE. After verification of proposed numerical models, we performed the groundwater simulation of Birjand aquifer.

2.4 Model Averaging Techniques (MATs)

The robustness of various MAT methods is examined through an ensemble of different competing numerical models. The first applications of these models have been around since 1970s when they were tested in the meteorology and economics sciences (Bates and Granger 1969; Dickinson 1973; Thompson 1977). There are two common approaches of MATs; deterministic and probabilistic. Some methods such as BMA generate a consensus probabilistic simulation from competing models outputs. In the process of probabilistic methods, the concepts such as likelihood functions and sampling methods (i.e., MCMC) play a vital role (Duan et al. 2007). While the fundamental of other techniques, including Weighted Average Method (WAM) and MMSE, is based on linear combination techniques such as Multiple Linear Regression (MLR). Though, the interested readers are referred to Zhous (2012) for more discussion about ensemble methods and their formulation, here an overview of used MATs was provided as the following.

2.4.1 SMA

The SMA is the simplest method among MATs because it presents a simple weighted average of the models’ outputs. In this method, the weight of each model is equal to one. Historical review of SMA indicates that Georgakakos et al. (2004) firstly employed this method to improve rainfall-runoff simulations. The formulation of SMA for each time step is given by the following equation:

$$D_{SMA}^t = {\bar D_{Obs}} + \sum\limits_{i = 1}^m {\frac{{D_{Sim}^{t,i} - \bar D_{Sim}^i}}{m}}$$

(3)

where $D_{SMA}^t$ is SMA output, ${\bar D_{Obs}}$ is observation values, m indicates number of individual competing models (here FD, FE, and Mfree simulations) while $D_{Sim}^{t,i}$ and $\bar D_{Sim}^i$ denote simulation and mean value simulation of ith numerical method.

2.4.2 WAM

Shamseldin et al. (1997) firstly applied this approach for hydrology research to enhance the runoff simulation output of five conceptual models. In WAM, the weight of competing models is computed based on a constrained MLR such that they have to be positive, and the sum of them must be equal to one. The following equation expresses WAM formulation:

$$D_{WAM}^t = \sum\limits_{i = 1}^m {{x_i}.D_{Sim}^{t,i}}$$

(4)

where $D_{WAM}^t$ is simulation obtained by WAM and, ${x_i}$ is weight of i th of numerical model.

2.4.3 MMSE

Krishnamurti et al. (1999) advanced previous techniques (SMA and WAM) and proposed the MMSE method. Examination of MMSE in different studies indicated its better performance than both competing models and traditional MATs (i.e., SMA and WAM) (Mayers et al. 2001; Yun et al. 2003). In the MMSE procedure, the weight of competing models is calculated based on non-constrained MLR. Indeed, weights can take any real numbers, and there is no specific limitation for their summation. The MMSE formulation can be expressed as the following:

$$D_{MMSE }^t = {\overline D_{Obs}} + \sum\limits_{i = 1}^n {{x_i}.(D_{Sim}^{t,i} - } \overline D_{Sim}^i)$$

(5)

where $D_{MMSE }^t$ is the tth output of MMSE.

2.4.4 M3SE

The M3SE technique, introduced by Ajami et al. (2006), is based on the MMSE concept, except putting a powerful bias correction method that is called frequency mapping. In the frequency mapping, the simulation values will be replaced by observations that have the same frequency. The other stages, including weight estimation and formulation, are repeated similarly to the MMSE method. Figure 4 displays the procedure of M3SE containing of bias correction, weight estimation, and formulation modules.

Fig. 4

The flowchart of M3SE method

2.4.5 BMA

BMA as an ensemble averaging method presents a consensus simulation from competing models outputs. It estimates the weights of competing models based on the probabilistic likelihood function. Let to consider observation values as $Y = [y_1^{obs},y_2^{obs},\,...\,,\,y_T^{obs}]$ and $\left\{ {{S_1},{S_2},\,...,\,{S_K}} \right\}$ as numerical simulation. In the first step, the numerical simulations are corrected using linear regression (i.e., $\left\{ {{S_i},i = 1,\,2,\,...,\,n} \right\}$ is converted to $\left\{ {{f_i},i = 1,2,...,n} \right\}$). Based on probability’s law, the probabilistic density of observation (y) can be expressed as following:

$$p(\left. y \right|{f_1},{f_2}\,...\,,\,{f_k},Y) = \sum\limits_{i = 1}^K {p(\left. {f_i} \right|Y).{p_i}\left( {\left. y \right|{f_i},Y} \right)}$$

(6)

where $p(\left. {f_i} \right|Y)$ is the posterior probability of ith competing model and it reflects the similarity of ith model relative to observation. Hence, it can be considered as the weights of competing models so that they sum to one as formula $\sum\limits_{i = 1}^K {w_i} = 1$ where,${w_i} = p(\left. {f_i} \right|Y)$. Also, ${p_i}(\left. y \right|{f_i},Y)$ denotes the conditional Probabilistic Density Function (PDF) of ith competing model. BMA represents conditional PDF by a Gaussian distribution with zero average and ${\sigma_i}$ variance. The revised version of Eq. (6) is given by:

$$p(\left. y \right|{f_1},{f_2}\,...\,,\,{f_k},Y) = \sum\limits_{i = 1}^K {p(\left. {f_i} \right|Y).{p_i}\left( {\left. y \right|{f_i},Y} \right)} = \sum\limits_{i = 1}^K {{w_i}.g(\left. y \right|{f_i},\sigma_i^2)}$$

(7)

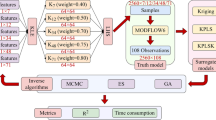
The BMA consider weights of competing models and ${\sigma_i}$ as parameters set ($\theta = \left\{ {{w_i},{\sigma_i},\,i = 1,\,...\,,\,K} \right\}$) and estimates them using a numerical algorithm. This study employed the MCMC based DiffeRential Evolution Adaptive Metropolis (DREAM) algorithm for producing the prior distribution of parameters set and the strength of each parameters set was evaluated by log likelihood function as following:

$$\ell (\theta ) = \log \left( {\sum\limits_{i = 1}^k {{w_i}.{p_i}\left( {\left. y \right|{f_i},Y} \right)} } \right)$$

(8)

For more details see Raftery et al. (2005).

2.5 Model Evaluation

To evaluate the performance of numerical methods and to examine the effects of different MATs, error estimation was quantified through Root Mean Square Error (RMSE). Since the groundwater level has generally a low dynamic, the variance-based indicators, such as Nash Sutcliff Efficiency (NSE) and Kling Gupta Efficiency (KGE), are not recommended for model ranking. In addition, the correlated-based criteria such as coefficient of determination do not consider over or under prediction, and these factors merely account for how much of the observed dispersion is explained by the prediction. Then RMSE has enough merits than other criteria in in groundwater modeling field. More discussion about performance criteria and their formulation can be found in study done by Krause et al. (2005).

3 Results and Discussion

3.1 Numerical Methods Efficiency

The evaluation of the numerical model performance through observed and simulated temporal groundwater level fluctuations was carried out in Birjand aquifer. Table 1 represents the RMSE value obtained from the Mfree, FE, and FD, for each piezometer. Moreover, the last row indicates the total RMSE for each individual numerical method, so that higher accuracy of Mfree method is displayed with bolded value equal to 0.148 m.

Table 1 The amount of calculated RMSE for different numerical methods

Figure 5 displays the visual comparison of measured and predicted groundwater level fluctuation for four observation wells (the remaining piezometers are not shown here). As shown in Fig. 5, the Mfree method has generated a skillful prediction of groundwater fluctuation at all observation wells during the simulation period. The examination of simulations reveals that the spatial variations of some influencing factors (e.g., rainfall, abstraction rate, and geology conditions) challenge the numerical models to reflect their impacts. The obtained results showed that Mfree mimics the spatial and temporal variations well, while FE, and FD can’t present a perfect and reliable prediction in some observational wells (e.g., Piez995). This issue may be related to the structure of the numerical method. As discussed in Appendix, the computation domain in the Mfree method is local and smaller than FE and FD methods.

Fig. 5

Comparison of observed and simulated groundwater level by different numerical methods

Moreover, the results demonstrate a conflicting behavior between numerical models in some piezometers. For example, the best prediction of the Mfree belongs to the Piez482 piezometer where the FE and specially FD yield the inefficient predictions. Also, in the Piez749, FE presented one of the best responses, while the Mfree produced inappropriate estimation.

Considering the simulated fluctuations of groundwater level in Piez212 and Piez749 (first and third panels in Fig. 8), it can be found that FE has superior accuracy to Mfree from 7 Feb to 4 Apr while in total simulation period and in terms of RMSE the Mfree outperformed FE in both piezometers. This pattern can verify that the accuracy of numerical models has a temporal dependency besides the spatial correlation and can vary for different sections of a groundwater level curve.

The findings of some studies conducted in the Birjand aquifer have a close agreement with the current study. Hamraz et al. (2015) and Sadeghi-Tabas et al. (2017) employed MODFLOW package to simulate the groundwater level and reported that the RMSE of FD is nearly 3.46 and 0.9 m, respectively. The explanation for the difference in results may be related to the fact that they performed simulations on a monthly scale, it leads to more accuracy and they ignored the surface recharge. Also, Mohtashami et al. (2017) reported that Mfree has a better capability than conventional numerical methods such as FD and FD.

It is noticeable that although different numerical models take advantage of an identical conceptual model, their outputs are just different (see Table 1 and Fig. 5). It is likely related to the ability of each numerical model on how to simulate the groundwater behavior (i.e., the model structure uncertainty). As shown in Table 1, the higher RMSE values of numerical models, (e.g., FD) are significant and it can be very effective in the outcomes. Also, the graphical user interfaces, including GMS, PMWIN, VISTA, and MODFLOW, are based on FD formulations. Hence, considering all strengths of FD-based models and according to current research’s findings, it can be inferred that the numerical model uncertainty in mentioned platforms is most likely, inevitable, and considerable. Therefore, for enhancing the groundwater modeling uncertainty, firstly it needs to polish the numerical model uncertainty. A recent study involved with this issue is conducted by Mustafa et al. (2020), which have disregarded this argument.

3.2 Performance Assessment of Model Averaging Techniques (MATs)

This section describes the efficiency of different MATs in improving the numerical models’ predictions. The RMSE of MATs was represented in Table 2, and the best value has been bolded. As shown, the MMSE and M3SE yield better than other MATs, as these two methods have the first and second ranks in the most piezometers. Also, From Table 2, it may be discovered that MATs have the required potential to reduce the uncertainty of numerical models predictions, since the MATs outcomes is much better than original numerical simulations for each piezometer.

Table 2 the RMSE values for MATs

Figure 6 exhibited the color map of RMSE values for MATs and numerical models in all piezometers, at the same time. It can be derived from the figure that the RMSE color of the MATs in all piezometers is lighter than FD and FE, while the Mfree yields better performance than some MATs in few piezometers (e.g., Piez340 and Piez482). For example, the Mfree in the Piez482 is outperformed the SMA prediction. Further, the RMSE color has a wide range in some piezometers (e.g., Piez482 and Piez 560), while some cells has almost stable color for others, including Piez631 and Piez13. This matter also reveals the spatial dependency of the numerical models and MTAs.

Fig. 6

The Spectral color map represented RMSE variations between different piezometers

The effect of MATs in enhancing the numerical models’ prediction was shown in Fig. 7 for some piezometers. As shown, the fluctuation of the groundwater level has been improved using MMSE and M3SE, and consequently, as the MATs predictions have a more closeness, the total uncertainty will be reduced. The same findings were obtained for other piezometers that were skipped here.

Fig. 7

Comparison of observed and simulated groundwater level by Mfree, MMSE, and M3SE

3.3 Examination of Ensemble Estimations

The results in the previous section showed that the MATs simulated different predictions, so here we focused on MTAs approaches and discussed their employed strategies for producing an ensemble averaging. As mentioned in Sect. 2.4, the MATs utilized different techniques to estimate the weights of the ensemble members (i.e., numerical models). The SMA considered the same weight for all numerical models, while The WAM evaluated them based on a constrained MLR. Also, both MMSE and M3SE used the unconstrained MLR to estimate weights, and the BMA computed them based on the probabilistic likelihood function. Furthermore, only the M3SE and BMA involved with the correction step into computations. Anyway, these assumptions affect the weights and combined outputs largely. Since the weights directly represent the importance of each numerical model in ensemble averaging, so they must be related to the performance and accuracy of each member reasonably. Table 3 represents the estimated weights of different MATs for each piezometer. As results showed, it can be discovered that the estimated weights by the MMSE and M3SE are not connected to the numerical model's ability for some piezometers. For example, in the Piez13 the MMSE and M3SE allocated the highest weight to the FD prediction, while FD has been resulted to less accuracy than FE and Mfree models (see Sect. 3.1). Furthermore, it can be understood that wherever there is a strong correlation between the predictions of the numerical models, the multicollinearity issue is problematic for the MMSE and M3SE methods (see Jafarzadeh et al. 2021c). However, the estimated weights by the BMA and WAM in all piezometers reflect completely the performance of the numerical models.

Table 3 Estimated weights of numerical models by different MATs for different piezometers

It seems that the main objective of MATs is the rational use of all capacities of members because each member has its unique strengths and weaknesses. From this perspective, there are some violations in the process of some MATs. For example, despite the SMA involved all numerical models, it does not consider their superiority because the SMA assumes similar weights for ensemble members. Also, the WAM sets the weights of the FD and FE in most piezometers to be zero to eliminate them. But, the estimated weights by BMA satisfied all mentioned issues, including multicollinearity (MMSE and M3SE), similar weights (SMA), and ensemble member elimination (WAM). Further, the BMA produces a PDF instead of a particular value for weights of numerical models; hence, no single optimum weight set can be determined. Figure 8 illustrated the obtained results of the BMA for Piez560 (other piezometers are not shown here). The posterior distribution of the numerical models’ weights is shown in the first three panels (a, b, and c), and the best values were displayed as red lines. Also, the last panel shows the 95% prediction uncertainty bounds of the BMA estimated by the DREAM algorithm (the gray area) versus the observed potential groundwater level (red line-circle). In this panel (d), the best prediction of the BMA is showed by blue dots, and the green line shows the Mfree simulation (as the best numerical model). This figure revealed that the best estimation of the BMA is associated with each numerical model skill. Also, the BMA did not set zero value as the weight of some numerical models to remove them from model averaging. Moreover, the BMA generated a distribution of different weights to supply the various combinations of the numerical models' prediction for better analysis.

Fig. 8

The BMA results about the posterior distribution of numerical models’ weights and predictions

Fig. 9

The posterior distribution of (a) FD’s weight) and (b) Mfree’s weight (b) in the different piezometers. 

Moreover, in order to provide more insight about weight identifiability, Fig. 9 illustrates the posterior distribution for the FD and Mfree models for Piez85, Piez560, Piez631, and Piez760 to compare the PDF of estimated weights. This figure revealed that the posterior distribution of the FD’s weights has a positive skew, while the PDF of the Mfree’ weight has more identifiability. In the final solution of the DREAM algorithm, the Mfree model has obtained higher weight than FD. This conclusion proves that the estimated weights by the BMA have a direct relation to numerical model ability.

4 Conclusion

In this work, we developed MATLAB program coding for three numerical models to simulate the groundwater level and compare the ability of five MATs to reduce prediction uncertainty. Afterward, the verification of proposed numerical models was implemented in a synthetic case study, and then simulation of fluctuations of groundwater level in a field study (Birjand aquifer) was performed using three verified models. Five different MATs approaches were then employed to combine three different numerical methods. Here are the major findings of this study:

First, the comparison of numerical model predictions with the observed values revealed the outstanding verification of proposed numerical models in groundwater modeling even in real and complex conditions. It was found that the Mfree model outperformed FE and FD. Also, contrary to the routine of most related researches that the uncertainty of the numerical model is mainly neglected, current work confirmed that the numerical model uncertainty is considerable and it can significantly affect the final predictions.

Second, the results of the performance assessment of the MATs discovered that the application of MATs was effective in decreasing the total prediction uncertainty of numerical models, as some MATs, including the MMSE and M3SE yield more accurate than numerical models. Therefore current study extended effectiveness and applicability domain of MATs in groundwater numerical modeling context with high complex landscape.

However, there were some defects for the MATs based on MLR (i.e., WAM, MMSE, and MMSE). Some challenging including, similar weights and member elimination (by assigning the weights close to zero) complicate the interpretation of estimated weights by mentioned MATs. Also, The SMA considers the same weight for different numerical models, so that dismisses the superiority of the ensemble members. By contrast, the BMA prediction is not only outperformed numerical models but also BMA’s weights were highly correlated with the model ability, confirming that members that are more accurate give higher weight values.

Third, the promising results of the BMA in this study provide the required incentive for further addressing this approach for groundwater modeling. For example, the BMA has many developments in recent years, especially in determining the likelihood functions. Compared to standard BMA, the main advantage of recent versions is formal likelihood functions, assessing the correlated, heterscedastic, and non‐Gaussian residual errors (Schoups and Vrugt 2010). Hence, it is worthy that, future studies in this field examine the applicability of the various formal functions to quantify the total uncertainty of groundwater modeling. Also, recently some related studies attempted to estimate the conditional PDF of the BMA through other fixed and flexible prior distributions such as Uniform, Binomial, Binomial-Beta, Benchmark, and Global Empirical Bayes (Samadi et al. 2020) and different approaches, such as Copula (Madadgar et al. 2014). Therefore, these modified versions of BMA can be tested in the groundwater modeling to present their ability. Further, the current versions of BMA allocate larger/smaller weights to more/less proficient competing models, and these estimated weights are constant during simulation. This is while a relatively weak model may simulate some part of the groundwater level curve better than a high-performance model. Therefore, here is posed a suggestion in future research to address new aspects of our research problem; the assessing the weights of the competing 006Dodels whose simulation period is divided into several periods to consider the dynamic behavior of each competing model during the simulation process.

Fourth, regarding the successful application of new numerical methods and their capability of parameterizing (e.g., Mfree), it is suggested to integrate uncertainty of mathematical modeling next to other sources of uncertainty to provide a more realistic representation of the groundwater process. Also, this study was based on limited datasets, and there were some existed limitations in research progress that can be considered and overcome in future studies. For example, in the Mfree and FE formulations, there are various and influencing weight and shape functions. It would be an interesting future scope to examine their effect in the final prediction of numerical models. Moreover, this study applied the standard code of the DREAM introduced by Vrugt et al. (2008), while some researchers such as Laloy and Vrugt (2012) rendered more advanced DREAM codes (e.g., DREAMzs) in multi-dimensional and high-nonlinear problems.

Appendix

The appendix shows the formulations and discretization of numerical models used in the current study.

1.1 A.1 FD

Taking the Taylor series approximation, the space derivatives of h in horizontal and vertical directions can be calculated for each point. The change of variable $v = {h^2}$ is imposed into to Eq. (1), to simplify computations for unconfined aquifer. Finally, using the forward difference approximation for time derivatives, the fully implicit of FD is given by:

$$\begin{gathered} v_{i,j}^{t + 1} = (\frac{1}{\omega + 1})*\left( {(\frac{{v_{i + 1,j}^{t + 1} + v_{i - 1,j}^{t + 1} + v_{i,j + 1}^{t + 1} + v_{i,j - 1}^{t + 1}}}{4}) + \left[ {\omega *v_{i,j}^t} \right] + \left[ {\frac{{{Q_{i,j}}}}{4*K}} \right]} \right) \hfill \\ where, \hfill \\ \,\omega = \frac{{{S_y}*{a^2}}}{{4*K*dt.\sqrt {v_{i,j}^t} }},a = \Delta x = \Delta y \hfill \\ \end{gathered}$$

(9)

In the last, the groundwater level is obtained by using $h = \sqrt v$.

1.2 A.2 FE

This study used triangular element due to simplify in implementation and successful performance. Therefore, the global domain of aquifer was divided to many elements and calculation was performed on each element. The First step in FE is trial solution definition:

$$\hat h(x,y) = \sum\limits_{L = 1}^n {{h_L}{N_L}(x,y)}$$

(10)

where $\hat h(x,y)$ is trial solution (m),${h_L}$: is groundwater level for Lth node, n: total number of nodes in aquifer domain and ${N_L}(x,y)$: is shape function. By substituting Eq. (10) into Eq. (1), and using fundamental assumption of WRM:

$$\int\limits_\Omega {\left( {Kh(\frac{{{\partial^2}\hat h}}{{\partial {x^2}}} + \frac{{{\partial^2}\hat h}}{{\partial {y^2}}}) + Q(i,j) - {S_y}\frac{\partial \hat h}{{\partial t}}} \right)} {W_L}.d\Omega = 0\,\,\,$$

(11)

where ${W_L}$ is weight function that in FE method is similar to shape function based on Galerkin approach. The formulation of shape function for a specific triangular element consisted of i, j, and k vertices, is given by:

$$\begin{gathered} {N_i} = \frac{1}{2A}\left[ {({x_k}{y_j} - {x_j}{y_k}) + ({y_k} - {y_j})x + ({x_j} - {x_k})y} \right] \hfill \\ {N_j} = \frac{1}{2A}\left[ {({x_k}{y_j} - {x_j}{y_k}) + ({y_k} - {y_j})x + ({x_j} - {x_k})y} \right] \hfill \\ {N_k} = \frac{1}{2A}\left[ {({x_k}{y_j} - {x_j}{y_k}) + ({y_k} - {y_j})x + ({x_j} - {x_k})y} \right] \hfill \\ \end{gathered}$$

(12)

where A: is the area of triangular element. Using the integration by part in Eq. (11), the second spatial derivatives of $\hat h$ is converted to first spatial derivatives of $\hat h$ and ${N_L}$. Regarding Eq. (12), these spatial derivatives are calculated and final matrix form of FE is obtained. Considering forward approximation, the fully implicit scheme is given by:

$$\left( {[G] + \frac{[P]}{{\Delta t}}} \right).\left\{ {{h^{t + 1}}} \right\} = \left( {\frac{[P]}{{\Delta t}}} \right).\left\{ {h^t} \right\} + \{ {B_L}\} + \left\{ {F_L} \right\}$$

(13)

where [G] is the conductance matrix, [P] is the mass matrix, {F} is the boundary flux and, {B} is the load vector.

1.3 A.3 Mfree

Mfree uses the local support domain ($\Omega s$) around each node to determine the influencing nodes surrounding the point of interest. It can have various shapes (circle and rectangle) as well as different sizes. The local support domain is calculated from $\Omega s = {r_s}.dc$ where dc is nodal distancing and ${r_s}$ is local support domain size. The effect of each point into support domain is determined by weight function. The weigh function has a very important role in Mfree, such that it influences on computation time, speed, and accuracy (He 2012). Indeed, weight function determines the weights of nodes fallen in support domain based on their distance (see Fig. 10). Each weight function should satisfy the following conditions: its magnitude for all points located into support domain is positive and it continuously reduces by increasing distance from center as it gives the maximum value in center while, the minimum values are obtained in support domain edges. The most widely used functions are exponential and spline. This study employs the quartic spline function as following:

$${W_L}(x) = \left\{ {\left. {\begin{array}{*{20}{c}} {1 - 6r_L^2 + 8r_L^3 - 3r_L^4}&{{r_L} < 1} \\ 0&{{r_L} > 1} \end{array}} \right\}\,} \right.where,\,\,\,{r_L} = \frac{{\left| {x - {x_L}} \right|}}{{r_w}}$$

(14)

where ${W_L}(x)$ is weight function of Lth node relative to interested node, and ${r_w}$ is the weight function size.

Fig. 10

Illustration of problem domain and boundaries, local quadrature domain, support domain and weight function in the Mfree method

In the Mfree, the Eqs. (10) and (11) is repeated exactly. In continue, the weight function is multiplied by each interior component of Eq. (11), and using the integration by part, the second spatial derivative is later converted to first order;

$$\begin{gathered} - \int\limits_{\Omega q} {(Kh(\frac{\partial \hat h}{{\partial x}}.\frac{{\partial {W_L}}}{\partial x} + \frac{\partial \hat h}{{\partial y}}.\frac{{\partial {W_L}}}{\partial y}))} d\Omega + \int\limits_{\Omega q} {(Q} .{W_L})d\Omega - \int\limits_{\Omega q} {({S_y}\frac{\partial \hat h}{{\partial t}}.{W_L})} d\Omega + \hfill \\ + \int\limits_{\Gamma q} {Kh(\frac{\partial \hat h}{{\partial x}}{n_x}. + \frac{\partial \hat h}{{\partial y}}{n_y}){W_L}} d\Gamma = 0\,\,\, \hfill \\ \end{gathered}$$

(15)

where $\Omega q$ and $\Gamma q$ are local domain and boundary. The local quadrature domain is taken from formula,$\Omega q = {r_q}.dc$ where ${r_q}$ is local domain size. As shown in Fig. 10, the boundary $\Gamma q$ is comprised of three parts $\Gamma qt,\,$ $\Gamma qu\,$ and $\Gamma qi$, where, $\Gamma qu\,$ and $\Gamma qt,\,$ indicate the part of local domain located on essential and natural boundaries, while $\Gamma qi$ indicates the interior boundary of local domain that has noting intersection with problem domain ($\Omega$). We set the weight function size (${r_w}$) equal with quadrature domain size (${r_q}$) to vanish the integration over the $\Gamma qi$, as recommended in previous studies (Atluri and Shen 2002; Liu 2002). Hence, the Eq. (15) can be simplified as following:

$$\begin{gathered} - \int\limits_{\Omega q} {(Kh(\frac{\partial \hat h}{{\partial x}}.\frac{{\partial {W_L}}}{\partial x} + \frac{\partial \hat h}{{\partial y}}.\frac{{\partial {W_L}}}{\partial y}))} d\Omega + \int\limits_{\Omega q} {(Q} .{W_L})d\Omega - \int\limits_{\Omega q} {({S_y}\frac{\partial \hat h}{{\partial t}}.{W_L})} d\Omega + \hfill \\ + \int\limits_{\Gamma qt} {Kh(\frac{\partial \hat h}{{\partial x}}{n_x}. + \frac{\partial \hat h}{{\partial y}}{n_y}){W_L}} d\Gamma qt + \int\limits_{\Gamma qu} {Kh(\frac{\partial \hat h}{{\partial x}}{n_x}. + \frac{\partial \hat h}{{\partial y}}{n_y}){W_L}} d\Gamma qu = 0\,\,\, \hfill \\ \end{gathered}$$

(16)

The approximation of Radial Point Interpolation Method (RPIM) was used to contrast Mfree shape function as following:

$$\begin{gathered} \hat h(x,y,t) = \sum\limits_{L = 1}^n {{h_L}{\Phi_L}(x,y)} \hfill \\ where, \hfill \\ \,{\Phi_L}(x,y) = \left\{ {R(x,y)\,P(x,y)} \right\}.{G^{ - 1}},\,\,G = \left[ {\begin{array}{*{20}{c}} {R_0}&{P_m} \\ {P_m^T}&0 \end{array}} \right] \hfill \\ \end{gathered}$$

(17)

where ${\Phi_L}(x,y)$, $R(x,y)\,$ and $P(x,y)$ are shape, radial and polynomial functions. Also, ${R_0}$ is the matrix of radial distance of points into support domain while, ${P_m}$ is a polynomial function with m monomial. In this study, the Gaussian radial function and Pascal triangle with three monomials (m=3), were employed to create shape function:

$$\begin{gathered} {R_X}({r_{X^{\prime}}}) = \exp [ - {\alpha_c}{(\frac{{{r_{x^{\prime}}}}}{dc})^2}],{r_{x^{\prime}}} = \sqrt {{{(x - x^{\prime})}^2} + {{(y - y^{\prime})}^2}} \hfill \\ P_m^T = \left[ {\begin{array}{*{20}{c}} {{P_m}({X_1})}&{{P_m}({X_2})}&{...}&{{P_m}({X_n})} \end{array}} \right],{P_3}(X) = \left\{ {\begin{array}{*{20}{c}} 1&x&y \end{array}} \right\} \hfill \\ \end{gathered}$$

(18)

where ${\alpha_c}$ is a constant parameter of radial function. Substituting Eq. (18) into back Eq. (16), leads to following equation:

$$\begin{gathered} \left( {\int\limits_{\Omega q} {(K{h^t}(\frac{\partial \Phi }{{\partial x}}.\frac{{\partial {W_L}}}{\partial x} + \frac{\partial \Phi }{{\partial y}}.\frac{{\partial {W_L}}}{\partial y}))} d\Omega - \int\limits_{\Gamma qu} {K{h^t}(\frac{\partial \Phi }{{\partial x}}{n_x}. + \frac{\partial \Phi }{{\partial y}}{n_y}){W_L}} d{\Gamma_{qu}}} \right).\left\{ h \right\} + \hfill \\ + \left( {\int\limits_{\Omega q} {{S_y}(\Phi .{W_L})} d\Omega } \right)\left\{ {\frac{\partial h}{{\partial t}}} \right\} = + \int\limits_{\Omega q} {(Q} .{W_L})d\Omega + \int\limits_{\Gamma qt} {({h^t}.qt){W_L}} d{\Gamma_{qt}} \hfill \\ \end{gathered}$$

(19)

For accurate numerical integration in Eq. (21), each local domain ($\Omega q$) should be divided into small regular partitions comprising multi Gauss quadrature points. Therefore, as shown in Fig. 10 for a point of interest there are two local domains: local quadrature domain and support domain ($\Omega s$) of Gauss quadrature point. By simplification and rearranging of Eq. (19) we have:

$$\left[ G \right].\left\{ h \right\} + \left[ P \right]\left\{ {\frac{\partial h}{{\partial t}}} \right\} = \left\{ B \right\} + \left\{ F \right\}$$

(20)

Similar to FD and FE, using forward approximation for time, the fully implicit scheme can be expressed as following:

$$\left( {\left[ G \right] + \frac{\left[ P \right]}{{\Delta t}}} \right)\left\{ {{h^{t + 1}}} \right\} = \left( {\frac{\left[ P \right]}{{\Delta t}}} \right)\left\{ {h^t} \right\} + \left\{ B \right\} + \left\{ F \right\}$$

(21)

The all components in above equation are same to Eq. (13). A detailed discussion about local Mfree method is available in Atluri and Shen (2002), Liu (2002), and Liu and Gu (2005).