Introduction

Groundwater flow models have been used in many regulatory applications such as well pumping, aquifer sustainability, and capture zone analysis. Simulated drawdown from a groundwater flow model has also been used to determine well specific capacity. Specific capacities reflect hydraulic conductivity or potential of the aquifer, which affects groundwater resource management. For example, management guidelines may stipulate that the average water level for a region should not drop below specified levels. Therefore, uncertainty in model responses leads to uncertainty in the management field.

Groundwater modeling requires hydrogeological parameters as well as other information, e.g., initial/boundary conditions and discharge/recharge fluxes, to constitute a model structure. Although mathematical problems associated with model structure account for all components in the groundwater model, hydraulic conductivity is one of the most essential aquifer parameters in the inverse problem of groundwater hydrology (McLaughlin and Townley 1996). The importance of studying hydraulic conductivity arises from its wide spatial variability (Koltermann and Gorelick 1996) and its significant influence on dispersion and mass transport (Rehfeldt et al. 1992; Neuman 1990; Poeter and Gaylord 1990).

A number of studies have attempted to evaluate and compare various techniques for estimating hydraulic conductivity fields. Ritzi et al. (1994) compared three indicator-based geostatistical methods to predict zones of higher hydraulic conductivity. Eggleston et al. (1996) compared the hydraulic conductivity field and its sensitivity by using two estimation methods (i.e., kriging and conditional mean) and two simulation methods (i.e., sequential Gaussian and simulated annealing) and found that simulation methods are better at reproducing local contrasts and large-scale features. Boman et al. (1995) studied the response of a transport model to four schemes (three deterministic and one fractal-based stochastic) to interpolate field-measured hydraulic conductivity data, concluding that kriging and fractal interpolation were not significantly better than simpler methods; this study was based on densely sampled measurements which may not be typical of groundwater studies.

In groundwater studies, measurements of hydraulic conductivity are typically sparse. Conductivity fields estimated using regionalized (univariate) models such as kriging or simulation are therefore highly uncertain, as these methods depend on data density. Eggleston et al. (1996) studied a heavily sampled aquifer and reported that the number of data points significantly affects permeability field models. Therefore, data integration from various sources is essential. Hydraulic conductivity estimation with hydrologic data (e.g., hydraulic heads) has been extensively studied through the Bayesian maximum likelihood estimation (Carrera and Neuman 1986) and geostatistics of cokriging (Kitanidis and Vomvoris 1983). Many types of geophysical data have been incorporated in hydraulic conductivity estimation due to their relatively low cost, abundant field measurements, and high correlation with hydraulic conductivity. Geophysical data integration through geostatistics improves the estimation of conductivity (Gloaguen et al. 2001).

In a hydrogeological framework, the spatial structures are constructed from field-measured data. However, field measurements are always limited. Uncertainties associated with the field measurements lead to uncertainties in the correlation structure. Kitanidis (1986) examined the effect of semivariogram model uncertainty in a Bayesian framework. Feyen et al. (2003) examined semivariogram model uncertainty for capture zones in a Bayesian framework, concluding that predictions based on fitted models do not reflect field variance.

This research focuses on a real-world case study, in the estimation of hydraulic conductivity of the Upper Chicot Aquifer, Acadia Parish, in southwestern Louisiana using hydrogeological data and geophysical data. The case study presents many challenges that are commonly encountered in regional groundwater modeling. First of all, the measured hydraulic conductivity data (primary data) from pumping tests and the borehole electrical resistivity data (secondary data) are integrated through a geostatistical approach to better estimate the hydraulic conductivity field. Borehole resistivity data correlate well with the effective porosity of a saturated formation (Archie 1942), which consequently infers the hydraulic conductivity. Second, a pseudo cross-semivariogram is introduced in the geostatistical framework to cope with the estimation challenge stemming from non-collocation of the resistivity logs and pumping test sites. This study adopts the approach suggested in Clark et al. (1989) to calculate the pseudo cross-semivariogram of these two data sets. Details of the pseudo cross-semivariogram technique are given in Myers (1991). Third, the semivariogram uncertainty due to data scarcity is quantified in terms of mean and variance of the semivariogram at each lag distance using an approach suggested by Ortiz and Deutsch (2002). Assuming lognormal distribution in auto-semivariograms and pseudo cross-semivariograms, the upper and lower limits of the semivariograms, given a confidence interval, are obtained with the requirement of positive definiteness (Goovaerts 1997). The study uses the mean, upper limit and lower limit semivariograms to examine the impact of semivariogram uncertainty on the aquifer hydraulic responses. Fourth, this study develops a groundwater flow model to examine the impact of regionalized and coregionalized hydraulic conductivity fields, semivariogram uncertainty, and simulation processes in a groundwater system. Two regionalized models (kriging and sequential Gaussian simulation) and two coregionalized models (cokriging and cosimulation) are compared. Analysis of variance (ANOVA) assesses the significance of secondary data, interpolation method, and semivariogram uncertainty on the groundwater flow behavior. The relevant methods are discussed first. Data and modeling results for the parish-scale study (25 km2) are then described. Finally, the results are interpreted statistically and implications for model choice and interpretation are presented.

Hydrogeologic interpretation of borehole electrical resistivity data

Borehole electrical resistivity readings reflect the combination of geologic formation and water ionic content with depth. In general, when fresh groundwater is present, electrical resistivity identifies the interfaces between the clay layers (low resistivity value) and sand aquifers (high resistivity value) due to high clay porosity and conductive minerals on the clay surface. Another strong influence on electrical resistivity is the presence of fluid salinity; erratic electrical resistivity readings are often found in sand aquifers when salt water is present.

Typical resistivity data for the Chicot Aquifer are shown in Fig. 1. The resistivity readings distinguish the Upper Chicot Aquifer and Lower Chicot Aquifer, separated by a thin clay layer with low resistivity around a depth of 122 m (400 ft). The erratic resistivity readings in Fig. 1b also show the salt-water intrusion in deep aquifers due to heavy pumping activity. The areas affected by salt water will not be considered in this study.

Fig. 1
figure 1

a Cross section G-G’ through southern Acadia Parish, (location also shown in Fig. 2) b geophysical log illustrating the various horizons in the Chicot Aquifer, Acadia Parish, Louisiana (well No. 078272; after Hanson et al. 2001). The wavy lines in boreholes indicate that they continue beyond the depth shown in the figure

Full size image

Borehole resistivity in the saturated sand aquifer has a high correlation to the formation porosity and water resistivity, which is often expressed as Archie’s law (Archie 1942):

$$R_0 = a\,\Phi ^{ - {\text{m}}} R_{\text{w}} $$
(1)

where R 0 is the resistivity of the saturated formation, R w is the formation water resistivity, Φ is the sand porosity. Two parameters a and m in Eq. (1) represent the pore geometry coefficient and the cementation factor, respectively. Typically, the pore geometry coefficient a varies between 0.62 and 2.45, and the value of the cementation factor m has a range between 1.08 and 2.15 depending on the formation type (Asquith and Gibson 1982). The formation water resistivity varies with local geochemical and ionic content. However, when fresh groundwater is considered, the variation is not significant. Assuming constant formation water resistivity is reasonable.

The formulas for determining hydraulic conductivity from particle-size distribution are reduced to the following generalized formula (Vukovic and Soro 1992).

$$K = \frac{{\gamma _{\text{w}} }}{{\mu _{\text{w}} }}CG\left( \Phi \right)d_{\text{e}}^{\text{2}} $$
(2)

where K is the hydraulic conductivity, γ w is the specific weight of water, μ w is the dynamic viscosity of water, C is a dimensionless parameter, G(Φ) is the function of porosity, and d e is the effective grain diameter. The term \(CG\left( \Phi \right)d_{\text{e}}^{\text{2}} \) in Eq. (2) refers to the soil permeability. In Eq. (2), the hydraulic conductivity can be evaluated with the resistivity data and Archie’s law. In this study, the Kozeny-Carman equation (Carman 1956) is adopted, where C=1/180 and \( G{\left( \Phi \right)} = \Phi ^{3} {\left( {1 - \Phi } \right)}^{{ - 2}} \). Substituting Eq. (1) into Eq. (2), the hydraulic conductivity relating to formation/water resistivity results and is denoted as K F:

$$K_{\text{F}} = \frac{{\gamma _{\text{w}} }}{{180\mu _{\text{w}} }}\frac{{\left( {{{R_0 } \mathord{\left/ {\vphantom {{R_0 } {R_{\text{w}} }}} \right. \kern-\nulldelimiterspace} {R_{\text{w}} }}} \right)^{{{{\text{ - 1}}} \mathord{\left/ {\vphantom {{{\text{ - 1}}} {\text{m}}}} \right. \kern-\nulldelimiterspace} {\text{m}}}} a^{{{\text{3}} \mathord{\left/ {\vphantom {{\text{3}} {\text{m}}}} \right. \kern-\nulldelimiterspace} {\text{m}}}} }}{{\left[ {\left( {{{R_0 } \mathord{\left/ {\vphantom {{R_0 } {R_{\text{w}} }}} \right. \kern-\nulldelimiterspace} {R_{\text{w}} }}} \right)^{{{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {\text{m}}}} \right. \kern-\nulldelimiterspace} {\text{m}}}} - a^{{{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {\text{m}}}} \right. \kern-\nulldelimiterspace} {\text{m}}}} } \right]^2 }}d_{\text{e}}^{\text{2}} $$
(3)

where the ratio R 0/R w is defined as the formation factor (Archie 1942). The formation factor obtained from borehole resistivity logs (Asquith and Gibson 1982) is a relatively common and low-cost measurement, particularly compared to pumping tests. Kelly (1977) and Kosinski and Kelly (1981) studied site-specific electrical resistivity and hydraulic conductivity and established empirical relationships between the formation factor and hydraulic conductivity. However, their studies did not investigate the theoretical basis for the correlation and the empirical relationship is not necessarily applicable to other sites. The study reported here interprets the hydraulic conductivity using the geophysical resistivity data through Archie’s law (1942) and the Kozeny-Carman equation (Carman 1956) for sand units.

Data integration and simulation via geostatistics

Data non-collocation and pseudo cross-semivariogram

Data integration of the resistivity-driven hydraulic conductivity and the measured hydraulic conductivity by pumping tests is possible through a geostatistical approach. Commonly, the measured hydraulic conductivity denoted as K y is considered as the primary data because the hydraulic conductivity is measured directly through the groundwater responses. The measured and resistivity-driven hydraulic conductivity data are considered as the random fields and are transformed to a normal distribution (the hydraulic conductivity is usually considered as a lognormal distribution) such that these two types of data are classified as second-order stationary. Let Y and F be the data transform of K Y and K F, respectively. If both Y and F have sample values at the same locations, the cross-semivariogram of Y and F can be obtained for the collocated data

$$\widehat\gamma _{{\text{YF}}} \left( h \right) = \frac{1}{{2n_{\text{c}} \left( h \right)}}\sum\limits_{{\text{i = 1}}}^{{\text{n}}_{\text{c}} \left( {\text{h}} \right)} {\left( {Y_{\text{i}} - Y_{{\text{i + h}}} } \right)\left( {F_{\text{i}} - F_{{\text{i + h}}} } \right)} $$
(4)

where \(Y_{\text{i}} = Y\left( {{\mathbf{x}}_{\text{i}} } \right)\); \(Y_{{\text{i}} + {\text{h}}} = Y\left( {{\mathbf{x}}_{\text{i}} + h} \right)\); h is the lag distance between a pair of sample data; n c is the number of pairs of Y or F at a distance h apart. However, in practice the electrical resistivity log sites rarely coincide with the pumping test sites. Equation (4) fails for non-collocated data and a cross-semivariogram between Y and F cannot be obtained. To cope with this problem, a pseudo cross-semivariogram has to be introduced to replace Eq. (4). For this study, the pseudo cross-semivariogram introduced by Clark et al. (1989) was used, where the two random functions must have the same unconditional mean and unconditional variance. The easiest way to achieve this requirement is to transform the primary and secondary data into the standard normal distribution (normal score) that has zero mean and unity variance (Deutsch and Journel 1998). In this study, the K Y and K F are transformed to the normal scores y and f, respectively, with zero means and unity variances. The pseudo cross-semivariogram is given by the expected squared difference between y and f measured at different locations,

$$\widetilde\gamma _{{\text{yf}}} \left( h \right) = \frac{1}{{2n_{{\text{yf}}} \left( h \right)}}\sum\limits_{{\text{j}} = {\text{1}}}^{{\text{n}}_{{\text{yf}}} \left( {\text{h}} \right)} {\left( {y_{\text{j}} - f_{{\text{j}} + {\text{h}}} } \right)^2 } $$
(5)

where \(\widetilde\gamma _{{\text{yf}}} \) is the pseudo cross-semivariogram; and n yf is the number of pairs of y and f at a distance h apart. It can be shown that \(\widetilde\gamma _{{\text{yf}}} \left( h \right) = \widetilde\gamma _{{\text{fy}}} \left( { - h} \right)\). The auto-semivariograms for y and f are:

$$\widehat\gamma _{{\text{yy}}} \left( h \right) = \frac{1}{{2n_{{\text{yy}}} \left( h \right)}}\sum\limits_{{\text{j}} = {\text{1}}}^{{\text{n}}_{{\text{yy}}} \left( {\text{h}} \right)} {\left( {y_{\text{j}} - y_{{\text{j}} + {\text{h}}} } \right)^2 } $$
(6)

and

$$\widehat\gamma _{{\text{ff}}} \left( h \right) = \frac{1}{{2n_{{\text{ff}}} \left( h \right)}}\sum\limits_{{\text{j}} = 1}^{{\text{n}}_{{\text{ff}}} \left( {\text{h}} \right)} {\left( {f_{\text{j}} - f_{{\text{j}} + {\text{h}}} } \right)^2 } $$
(7)

Details of the pseudo cross-semivariogram technique can be found in Myers (1991). Due to the normalization, the sills for \(\widehat\gamma _{{\text{yy}}} \), \(\widehat\gamma _{{\text{ff}}} \), and \(\widetilde\gamma _{{\text{yf}}} \) are unity as the unconditional variance. Moreover, the Cauchy-Schwarz inequality \( \widetilde{\gamma }_{{yf}} \leqslant {\sqrt {\widehat{\gamma }_{{yy}} \widehat{\gamma }_{{ff}} } } \) is required to ensure the positive definiteness in the following cokriging method. The Cauchy-Schwarz inequality will be used determine the lower and upper limits of the auto- and pseudo cross-semivariograms when semivariogram uncertainty is considered in the section Significance analysis using ANOVA.

Conditional estimation using hydrogeological data and resistivity data

The conditional estimation of the normalized hydraulic conductivity is made through a linear-weighted interpolation form, which honors the normalized primary and secondary data:

$$ \widehat{y}_{{CoK}} = {\sum\limits_{j = 1}^{n_{y} } {\lambda _{j} y_{j} } } + {\sum\limits_{{\ell } = 1}^{n_{f} } {\nu _{{\ell }} f_{{\ell }} } } $$
(8)

where \( \widehat{y} \) is the estimate of y; λ j and \( \nu _{{\ell }} \) are the weighting coefficients that need to be determined. n y is the number of primary data; and n f is the number of the secondary data. The conditional estimate of hydraulic conductivity is obtained via the back transformation of the normal score. By minimizing the variance of estimation error \( {\left[ {\widehat{y}{\left( {{\mathbf{x}}_{0} } \right)} - y{\left( {{\mathbf{x}}_{0} } \right)}} \right]} \) at an unsampled site x0, the optimal weighting coefficients λ j and \( \nu _{{\ell }} \) are obtained by the following set of linear equations,

$$ \left\{ {\begin{array}{*{20}c} {{{\sum\limits_{j = 1}^{n_{y} } {\lambda _{j} \widehat{\gamma }_{{yy}} {\left( {{\mathbf{x}}_{k} ,{\mathbf{x}}_{j} } \right)}} } + {\sum\limits_{{\ell } = 1}^{n_{f} } {\nu _{{\ell }} \widetilde{\gamma }_{{yf}} {\left( {{\mathbf{x}}_{k} ,{\mathbf{x}}_{{\ell }} } \right)}} } + \mu = \widehat{\gamma }_{{yy}} {\left( {{\mathbf{x}}_{0} ,{\mathbf{x}}_{k} } \right)},\quad k = 1,2, \cdots ,n_{y} }} \\ {{{\sum\limits_{j = 1}^{n_{y} } {\lambda _{j} \widetilde{\gamma }_{{fy}} {\left( {{\mathbf{x}}_{i} ,{\mathbf{x}}_{j} } \right)}} } + {\sum\limits_{{\ell } = 1}^{n_{f} } {\nu _{{\ell }} \widehat{\gamma }_{{ff}} {\left( {{\mathbf{x}}_{i} ,{\mathbf{x}}_{{\ell }} } \right)}} } + \mu = \widetilde{\gamma }_{{yf}} {\left( {{\mathbf{x}}_{0} ,{\mathbf{x}}_{i} } \right)},\quad i = 1,2, \cdots ,n_{f} }} \\ {{{\sum\limits_{j = 1}^{n_{y} } {\lambda _{j} + {\sum\limits_{{\ell } = 1}^{n_{f} } {\nu _{{\ell }} } } = 1} }}} \\ \end{array} } \right. $$
(9)

where μ is the Lagrange multiplier. Equation (9) involves auto-semivariograms of y and f as well as the pseudo cross-semivariogram for non-collocated data fusion.

If primary data are sparse and more densely sampled secondary data are strongly correlated to the primary variable, geostatistics of cokriging can help improve estimates of the primary variable. In this work, the secondary data (the borehole resistivity logs) are non-collocated with the pumping test sites. Therefore, a pseudo cross-semivariogram, \( \widetilde{\gamma }_{{yf}} \) has to be used to replace the cross-semivariogram. For the comparison purpose, the kriging conditional estimation, which uses only the measured hydraulic conductivity data, is also considered

$$ \widehat{y}_{{OK}} = {\sum\limits_{j = 1}^{n_{y} } {\lambda _{j} y_{j} } } $$
(10)

Therefore, Eq. (9) is reduced to the following for y,

$$ \left\{ {\begin{array}{*{20}c} {{{\sum\limits_{j = 1}^{n_{y} } {\lambda _{j} \widehat{\gamma }_{{yy}} {\left( {{\mathbf{x}}_{i} ,{\mathbf{x}}_{j} } \right)}} } + \mu = \widehat{\gamma }_{{yy}} {\left( {{\mathbf{x}}_{0} ,{\mathbf{x}}_{i} } \right)},\quad i = 1,2, \cdots ,n_{y} }} \\ {{{\sum\limits_{j = 1}^{n_{y} } {\lambda _{j} = 1} }}} \\ \end{array} } \right. $$
(11)

Conditional simulation and cosimulation of hydraulic conductivity

The conditional estimation of hydraulic conductivity obtained by the kriging and cokriging methods is a smoothed distribution over the region, which does not reveal the actual variability of the hydraulic conductivity. However, the K variability has a significant influence on the groundwater responses when a groundwater flow model is adopted (Fogg 1986). In this study, conditional simulation and conditional cosimulation will be conducted to study the K variability in relation to groundwater model responses in the real-world case study. Moreover, the significance analysis using the conditional cosimulation against conditional simulation in groundwater responses will be conducted using analysis of variance (ANOVA), and is discussed later. Conditional simulation and cosimulation techniques simulate the estimation error (kriging error) as a correlated random process using the semivariogram and cross-semivariogram. For non-collocated data, a pseudo cross-semivariogram is adopted in the cosimulation process. This section provides the information and procedure for conducting cosimulation of the measured hydraulic conductivity and the resistivity-derived hydraulic conductivity in the study. The K simulation using measured hydraulic conductivity can be inferred by reducing the cosimulation procedure for a univariate model.

A cosimulated hydraulic conductivity field is generated by using a full linear model of cross covariance. The steps followed in the cosimulation algorithm include (1) modeling \( \widehat{\gamma }_{{yy}} \), \( \widehat{\gamma }_{{ff}} \), and \( \widetilde{\gamma }_{{yf}} \) for ensuring positive definiteness; (2) obtaining a cokriged estimate of the secondary data \( \widehat{f}_{{CoK}} \) at computation grids; and (3) calculating hydraulic conductivity estimates \( \widehat{y}_{{CoK}} \) (using SGSIM_FC subroutine; C.V. Deutsch, University of Alberta, Canada, personal communication, 2003). In the study area, the number of borehole resistivity data points is approximately the same number as that of the measured hydraulic conductivity data points. Therefore, the information from the primary data (y j) for the secondary data estimation (\( \widehat{f}_{{CoK}} \)) is important. This was verified by comparing the kriged estimate against the cokriged estimate of \( \widehat{f}_{{CoK}} \). A hybrid method was used to impose joint correlation and the correct variability in the cosimulation procedure:

  1. Step 1.

    Obtain a cokriged estimation of secondary data \( \widehat{f}_{{CoK}} \) over the field.

  2. Step 2.

    Obtain a single-variable simulation of the correlated residual of the secondary variable only, using the semivariogram for the secondary data and zero at the secondary data locations.

  3. Step 3.

    Sum the simulated result in step 2 and the cokriged results in step 1.

  4. Step 4.

    Use SGSIM_FC with the normal score transform of the conductivity data and results from step 3 in place of the secondary variable simulation.

  5. Step 5.

    Back-transform from normal score values of the primary data to the hydraulic conductivity values.

The aim here is to get the primary variable structure into the secondary variable via the cokriging step, with the assumption that the mean carries most of the information; the secondary residual is approximated as uncorrelated with the primary data.

Due to scarcity of measured hydraulic conductivity data and electrical-log data, one needs to investigate the uncertainty embedded in the semivariograms \( \widehat{\gamma }_{{yy}} \), \( \widehat{\gamma }_{{ff}} \), and \( \widetilde{\gamma }_{{yf}} \). From Eq. (5), the mean or expected pseudo cross-semivariogram is given by

$${\text{E}}\left[ {\widetilde\gamma _{{\text{yf}}} \left( h \right)} \right] = \frac{1}{{2n_{{\text{yf}}} \left( h \right)}}\sum\limits_{{\text{j = 1}}}^{{\text{n}}_{{\text{yf}}} \left( {\text{h}} \right)} {{\text{E}}\left( {y_{\text{j}} - f_{{\text{j + h}}} } \right)^2 } $$
(12)

The variance of the pseudo cross-semivariogram is given by

$$ \sigma ^{2} {\left[ {\widetilde{\gamma }_{{yf}} {\left( h \right)}} \right]} = \frac{1} {{4n^{2}_{{yf}} {\left( h \right)}}}{\sum\limits_{i = 1}^{n_{{yf}} {\left( h \right)}} {{\sum\limits_{j = 1}^{n_{{yf}} {\left( h \right)}} {{\text{E}}{\left[ {{\left( {y_{i} - f_{{i + h}} } \right)}^{2} {\left( {y_{j} - f_{{j + h}} } \right)}^{2} } \right]}} }} } - {\left\{ {{\text{E}}{\left[ {\widetilde{\gamma }_{{yf}} {\left( h \right)}} \right]}} \right\}}^{2} $$
(13)

The covariance of \( {\left( {y_{i} - f_{{i + h}} } \right)}^{2} \) and \( {\left( {y_{j} - f_{{j + h}} } \right)}^{2} \) is

$$\widetilde{\text{C}}_{{\text{yf}}} \left( {{\mathbf{x}}_{\text{i}} ,{\mathbf{x}}_{\text{j}} \left| h \right.} \right){\text{ = E}}\left[ {\left( {y_{\text{i}} - f_{{\text{i + h}}} } \right)^2 \left( {y_{\text{j}} - f_{{\text{j + h}}} } \right)^2 } \right] - {\text{E}}\left[ {\left( {f_{\text{i}} - f_{{\text{i + h}}} } \right)^2 } \right]{\text{E}}\left[ {\left( {f_{\text{j}} - f_{{\text{j + h}}} } \right)^2 } \right]$$
(14)

Substituting Eq. (11) into Eq. (10), the pseudo cross-semivariogram variance is

$$ \sigma ^{2} {\left[ {\widetilde{\gamma }_{{yf}} {\left( h \right)}} \right]} = \frac{1} {{4n^{2}_{{yf}} {\left( h \right)}}}{\sum\limits_{i = 1}^{n_{{yf}} {\left( h \right)}} {{\sum\limits_{j = 1}^{n_{{yf}} {\left( h \right)}} {\widetilde{{\text{C}}}_{{yf}} {\left( {{\mathbf{x}}_{i} ,{\mathbf{x}}_{j} \left| h \right.} \right)}} }} } $$
(15)

Similarly, the auto-semivariogram variances for y and f are

$$ \sigma ^{2}_{{\gamma _{{yy}} {\left( h \right)}}} = \frac{1} {{4n^{2}_{{yy}} {\left( h \right)}}}{\sum\limits_{i = 1}^{n_{{yy}} {\left( h \right)}} {{\sum\limits_{j = 1}^{n_{{yy}} {\left( h \right)}} {\widehat{{\text{C}}}_{{yy}} {\left( {{\mathbf{x}}_{i} ,{\mathbf{x}}_{j} \left| h \right.} \right)}} }} } $$
(16)

and

$$ \sigma ^{2}_{{\gamma _{{ff}} {\left( h \right)}}} = \frac{1} {{4n^{2}_{{ff}} {\left( h \right)}}}{\sum\limits_{i = 1}^{n_{{ff}} {\left( h \right)}} {{\sum\limits_{j = 1}^{n_{{ff}} {\left( h \right)}} {\widehat{{\text{C}}}_{{ff}} {\left( {{\mathbf{x}}_{i} ,{\mathbf{x}}_{j} \left| h \right.} \right)}} }} } $$
(17)

where \( \widehat{C}_{{yy}} \) is the covariance of \( {\left( {y_{i} - y_{{i + h}} } \right)}^{2} \) and \( {\left( {y_{j} - y_{{j + h}} } \right)}^{2} \); and \( \widehat{{\text{C}}}_{{ff}} \) is the covariance of \( {\left( {f_{i} - f_{{i + h}} } \right)}^{2} \) and \( {\left( {f_{j} - f_{{j + h}} } \right)}^{2} \). Equations (16) and (17) represent the variances of the semivariograms for a given lag distance, which are the average covariances between pairs of pairs used to calculate the semivariograms. If the data in y i and f j are Gaussian distributions, \( \widetilde{{\text{C}}}_{{yf}} \), \( \widehat{{\text{C}}}_{{yy}} \) and \( \widehat{{\text{C}}}_{{ff}} \) can be evaluated by the methods described in Ortiz and Deutsch (2002).

As for the semivariogram uncertainty analysis, the specific lower-limit and upper-limit semivariograms using the semivariogram variances for the auto-semivariogram models and pseudo cross-semivariogram models will be determined according to the real data. The lower and upper limit semivariograms along with the mean semivariograms will be used for the significance analysis using ANOVA.

Significance analysis using ANOVA

A single estimate of hydraulic conductivity cannot simulate the actual heterogeneity and complexity. In order to better understand the influence of the coregionalized model, ANOVA (analysis of variance) was adopted to differentiate the statistical significance among different approaches on generating K distributions. ANOVA is able to make inferences about mean differences by comparing variances among different groups (between-group variance) to the variance within the groups (within-group variance) using F-test (Fisher 1935). Donnelly-Makoweckia and Moore (1999) used a combination of ANOVA and jackknife to test the statistical significance of differences in a hydrologic model performance using different factors. Rong (2002) used ANOVA to compare MTBE (methyl tertiary-butyl ether) concentrations in sand/gravel and fine-grained soils. Ikem et al. (2002) used ANOVA to compare upgradient and downgradient contaminant concentrations near a waste site to find the impact of the waste site on the groundwater quality.

In this study, four groups of simulations, each using an alternative hydraulic conductivity field created by kriging, cokriging, simulation, and cosimulation, were run with variogram means, upper and lower bounds. Statistics from various flow responses are calculated and the significance of the (1) process (kriging versus simulation and cokriging versus cosimulation); (2) variables (kriging versus cokriging and simulation versus cosimulation); and (3) variogram variance (mean, 95% upper and lower bounds) are tested using a multifactor ANOVA test.

Case study

Semivariogram estimation and uncertainty in the upper Chicot Aquifer

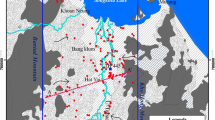
The Chicot aquifer system is the principal groundwater source for southwestern Louisiana, which underlies 15 parishes. It is also the most heavily pumped aquifer in Louisiana. Rice irrigation accounts for about 85% of the groundwater pumped from the aquifer in Acadia Parish (Sargent 2002). The Chicot system in Acadia Parish is divided into Upper and Lower Chicot units (sandy aquifers) separated by clay lenses referred to as the Upper/Lower confining zone (Fig. 1). This study focuses on the hydraulic conductivity estimation in the Upper Chicot Aquifer in Acadia Parish.

The local characterization of the Chicot Aquifer in Acadia Parish was developed using geophysical resistivity logs obtained from 74 oil and gas exploration wells. Note that not all the geophysical logs could be used; only 53 of them were used in the cokriging method as some of them did not cover the Upper Chicot Aquifer. The geology is divided into: confining clay layer, Upper Chicot Aquifer, dividing layer, Lower Chicot Aquifer. Figure 1a shows a west-east cross section of the local model.

Field K measurements

There are 42 hydraulic conductivity values (Fig. 2c) determined from specific capacity tests according to Eq. (15) (Bradbury and Rothschild 1985),

$$K_{\text{Y}} = \frac{Q}{{4\pi b\left( {s - CQ^2 } \right)}}\left[ {\ln \left( {\frac{{2.25Kt}}{{r_{\text{w}}^{\text{2}} S_{\text{s}} }}} \right) + 2\frac{{1 - {{\ell _{\text{s}} } \mathord{\left/ {\vphantom {{\ell _{\text{s}} } b}} \right. \kern-\nulldelimiterspace} b}}}{{{{\ell _{\text{s}} } \mathord{\left/ {\vphantom {{\ell _{\text{s}} } b}} \right. \kern-\nulldelimiterspace} b}}}\left( {\ln \frac{b}{{r_{\text{w}} }} - G} \right)} \right]$$
(18)

where Q is the pumping rate; s is drawdown at time t; b is the Upper Chicot Aquifer thickness; \( {\ell }_{s} \) is the length of screen interval; r w is the well radius; and S s is the specific storage. The term CQ 2 represents the well loss, where C is the well loss constant. The second term in the bracket corrects the K Y calculation due to partial penetration of the pumping well. The term G is the polynomial function of the ratio of the screen length to the aquifer thickness,

$$ G = 2.948 - 7.363{\left( {{{\ell }_{s} } \mathord{\left/ {\vphantom {{{\ell }_{s} } b}} \right. \kern-\nulldelimiterspace} b} \right)} + 11.447{\left( {{{\ell }_{s} } \mathord{\left/ {\vphantom {{{\ell }_{s} } b}} \right. \kern-\nulldelimiterspace} b} \right)}^{2} - 4.675{\left( {{{\ell }_{s} } \mathord{\left/ {\vphantom {{{\ell }_{s} } b}} \right. \kern-\nulldelimiterspace} b} \right)}^{3} $$
(19)

The technique solves Eq. (15) in an iterative fashion by taking other parameters as an input to Eq. (15). The Upper Chicot Aquifer thicknesses (b) were determined by analyzing well log data (Carlson et al. 2003).

Fig. 2
figure 2

a Study area in Louisiana State; adjacent to Texas (Tx), b Chicot Aquifer model grid with parish boundaries, c Acadia Parish model grid with location of hydraulic conductivity data points and geophysical logs

Full size image

The hydraulic conductivity values of this study were determined from specific capacity tests associated with the development of high-capacity wells usually for irrigation, public supply or industrial use. Because of the intended use of these wells, the average test discharge Q was 7,850±6,210 m3/day. The dimensions of the wells are large in response to the intended large demand for water: average radius is 9.8±3.1 cm, and average screen length is 17.4±7.1 m. The specific capacity tests lasted on average 9.8±9 h. These wells are clearly partially penetrating wells in that the average sand thickness surrounding a well screen is 45.1±15.9 m. The average specific capacity test drawdown is 7.9±5.0 m.

From previous studies, the storativity values for the Chicot Aquifer range from 1.1×10−4 to 3×10−3 with an average of 6.7×10−4. These values are a clear indicator that the Chicot is a confined aquifer (Weight and Sonderegger 2001). The confining clay layer above the Upper Chicot in Acadia Parish has an average thickness of 28.9±10.0 m as determined from examination of 2,648 well log reports.

The well loss constant value used for this study is 2.66×10−8 day2/m5, which is significantly smaller than the one listed in Bradbury and Rothschild (1985), which is 5.46×10−6 day2/m5 after unit conversion for Q. However, a smaller value of well loss constant is used to avoid well loss head exceeding drawdown for this study’s high capacity tests were the average Q is 7,850±6,210 m3/day compared to the smaller tests of Q=10 gallons per meter (54.5 m3/day) noted in Bradbury and Rothschild (1985).

The capacity test data set (42 values) shows that the measured hydraulic conductivity values vary from 5 to 700 m/day with a geometric mean \( \overline{K} _{Y} = 88\,{\text{m}}/{\text{day}} \) and a standard deviation \( \sigma _{{K_{Y} }} = 115\,{\text{m}}/{\text{day}} \).

Electrical-log data

A total of 53 oil and gas geophysical resistivity logs (Fig. 2c) were obtained from Louisiana Department of Natural Resources, Office of Conservation (OC), Well Log Library. To obtain the average R 0 for each log, the resistivity readings are divided into 3-m (10-ft) sections between the top and bottom elevation of Upper Chicot Aquifer. Again, it is reasonable to assume constant formation water resistivity because the study area is small and only freshwater is present in the Upper Chicot unit. The groundwater temperature is reported as 25°C. The formation water resistivity R w=12.7 ohm-m, water specific weight γ w=9.8 KN/m3 and dynamic viscosity \( \mu _{w} = 1 \times 10^{{ - 3}} \,{\text{N}}{\text{.s}}/{\text{m}}^{2} \) are used in this study. The variance in the sand formation resistivity factor (R 0/R w) is therefore the result of differences in sand/clay ratio and porosity. The effective saturated formation resistivity over the depth of the Upper Chicot is the average of the formation resistivity (R 0) values calculated at the 3 m (10 ft) intervals. The 53 borehole resistivity logs in the Upper Chicot Aquifer show that the formation resistivity value varies from 43 to 100 ohm-m with a mean of 75 ohm-m and a standard deviation 16 ohm-m. The average effective particle diameter d e is 0.42 mm (1.22 in phi units) calculated from US Geological Survey unpublished sieve test data files (US Geological Survey, unpublished data, 2003).

As for the pore geometry coefficient and cementation factor in the Archie’s equation, the maximization of the correlation over a short lag distance between the measured hydraulic conductivity (y i) and resistivity-driven hydraulic conductivity f j (a, m) in the normal scale was conducted to obtained the optimal values of for a and m. This is equivalent to finding the best a and m values such that the deviation between y i and f j (a, m) is minimized:

$$ {\mathop {\min }\limits_{a,m} }\,{\sum\limits_{{\left( {i,j} \right)}} {{\left[ {y_{i} - f_{j} {\left( {a,m} \right)}} \right]}^{{\text{2}}} } } $$
(20)

Eight pairs of y i and f j were selected with a lag distance less than 300 m. The bounds of a and m were 0.62≤a≤2.45 and 1.08≤m≤2.15, respectively, according to Asquith and Gibson (1982). It has been noted that the zero-lag distance should be used for collocated data. However, a subjective selection of a short lag distance (300 m) is necessary for non-collocated data. Equation (20) is solved by a gradient-based nonlinear optimization method and the optimal values of a and m are found to be 1.76 and 1.64. Figure 3 shows the cross plot for the eight pairs of y i and f j with optimal a and m values, which indicates a nugget between the measured hydraulic conductivity and resistivity-driven hydraulic conductivity data.

Fig. 3
figure 3

Cross plot between primary (y) and secondary (f) data at short distances. Both variables have normal score transformed values

Full size image

The electrical-log data set (53 values) shows that the resistivity-driven hydraulic conductivity values vary from 4 to 66 m/day with a geometric mean \( \overline{K} _{F} = 14\,{\text{m}}/{\text{day}} \) and a standard deviation \( \overline{\sigma } _{F} = 13.7\,{\text{m}}/{\text{day}} \).

Trend analysis and normal score transformation

The measured hydraulic conductivity data and resistivity-driven hydraulic conductivity data are tested for trend analysis using t-statistic from a bilinear model. The bilinear model is fit in the X-direction and Y-directions (Fig. 2c) to detect if a trend exits. With a 10% level of significance, Table 1 concludes that the conductivity data have no significant trend in the X or Y direction. Moreover, the measured hydraulic conductivity and resistivity-driven hydraulic conductivity show positive skewness, which indicates that one can assume hydraulic conductivity to be log-normally distributed (Domenico and Schwartz 1990). In this study, the data are standardized to zero mean and unit variance and transformed to normal scores (Deutsch and Journel 1998). The normal transform facilitated computation of the Archie coefficients (a and m) and the pseudo cross-semivariogram, which requires both random functions to have the same mean and variance.

Table 1 The t-test statistic on the trend detection in X- and Y-directions using the bilinear model
Full size table

Experimental semivariograms and pseudo cross-semivariogram

The 42 measured hydraulic conductivity values and 53 resistivity-driven hydraulic conductivity values are used in conditional estimation of the hydraulic conductivity field for both the regionalized model (i.e., \( \widehat{y} \) in Eq. (10)) and coregionalized model—i.e., \( \widehat{\gamma } \) in Eq. (8). Again, as none of the data in this study area are collocated, a pseudo cross-semivariogram is used instead of the cross-semivariogram. The experimental auto-semivariograms (\( \widehat{\gamma }_{{yy}} \) and \( \widehat{\gamma }_{{ff}} \)) and pseudo cross-semivariograms (\( \widetilde{\gamma }_{{yf}} \)) are computed using Eqs. (5)–(7) and shown in Fig. 4.

Fig. 4
figure 4

Experimental semivariograms and spherical semivariogram models a auto-semivariogram of y, b auto-semivariogram of f, and c pseudo cross-semivariogram of y and f

Full size image

This study adopts a spherical (Sph) semivariogram model with nugget as the following:

$$ \gamma _{{Sph}} {\left( h \right)} = c_{0} + c_{1} {\left\{ {\frac{3} {2}\frac{h} {{c_{2} }} - \frac{1} {2}{\left( {\frac{h} {{c_{2} }}} \right)}^{3} } \right\}}\quad ,h \leqslant c_{2} $$
(21)

where h is the lag distance; c 0 is the nugget; c 1 is the relative sill; (c 0 + c 1) is the total sill; and c 2 is the semivariogram range. Moreover, γ Sph(0)=0 and \( \gamma _{{Sph}} = c_{0} + c_{1} \) for h>c 2. With the spherical model, the integral scale is

$$ I = {\int_0^{c_{2} } {{\left( {1 - \frac{{\gamma _{{Sph}} {\left( h \right)} - c_{0} }} {{c_{1} }}} \right)}dh} } = \frac{3} {8}c_{2} $$
(22)

The parameters (nugget, sill, and range) embedded in the semivariograms are estimated through a weighted normalized least-squares estimation (Cressie 1985):

$$ {\mathop {\min }\limits_{c_{0} ,c_{1} ,c_{2} } }\,{\sum\limits_{k = 1}^n {n{\left( {h_{k} } \right)}{\left\{ {\frac{{\widehat{\gamma }{\left( {h_{k} } \right)}}} {{\gamma _{{Sph}} {\left( {h_{k} ;c_{0} ,c_{1} ,c_{2} } \right)}}} - 1} \right\}}^{2} } } $$
(23)

where h k is the kth lag distance; γ Sph is the spherical semivariogram model; and n(h) is number of points at each lag representing the weight for the selected lag distance. The minimization problem in Eq. (23) is subjected to the Cauchy-Schwarz inequality conditions to ensure the auto-semivariogram models and pseudo cross-semivariogram model are positive definite (Hohn 1998). The experimental semivariograms in Fig. 4 were fitted by the weighted least-squares estimation method to obtain the optimal values for c 0, c 1, and c 2. The total sill for the auto-semivariogram is equal to 1, which represents the unconditional variance of the normal score transformed data. However, the total sill for the pseudo cross-semivariogram is 0.9. Table 2 lists the optimized semivariogram parameter values and shows moderate correlation at short range (as expected when investigating hydraulic conductivity). The resulted semivariogram models are shown in Fig. 4. Especially, the pseudo cross-semivariogram in Fig. 4c shows correlation over a length of approximately 15,000 m, approximately one-half of the length of the study region, which indicates the appropriateness of using cokriging for the correlated primary and secondary data. The semivariogram models determine kriging weights and cokriging weights (see section Conditional estimation using hydrogeological data and resistivity data), which are used to obtain the conditional estimates and conditional variances. Moreover, these semivariogram models are the means in the following semivariogram uncertainty analysis. The kriged and cokriged hydraulic conductivity distributions using the mean semivariograms are shown in Fig. 5.

Fig. 5
figure 5

The conditional estimates of hydraulic conductivity by a cokriging and b kriging using mean semivariogram models. The K varies between K=5.18 m/day (black color) to K=701 m/day (white color)

Full size image
Table 2 Semivariogram model parameters
Full size table

Semivariogram uncertainty

The experimental auto-semivariograms of y and f are the mean semivariograms according to the method described in section Significance analysis using ANOVA. A FORTRAN program (C.V. Deutsch, University of Alberta, Canada, personal communication, 2003) is used to determine the semivariogram variance that allows determination of the lower and upper limits under the assumption that the semivariograms are log-normally distributed at each lag distance. The procedures to determine these limits are as follows.

First, the 90% confidence interval was used to determine the semivariogram limits for \( \widehat{\gamma }_{{yy}} \). Figure 6a show the 5% percentile, 10% percentile, and so forth for each lag distance. The upper limit semivariogram model is determined using the spherical model to best fit the 95% limits. As for the lower-limit semivariogram model, the spherical model has 5% limit at the first lag distance and gradually moved toward the sill according to Ortiz and Deutsch (2002). Figure 6a shows the lower and upper limit semivariograms, which are positive definite. The upper limit for \( \widehat{\gamma }_{{ff}} \) is also determined by the best fit of the spherical model to the 95% limit at each lag distance as shown in Fig. 6b. However the lower limit of \( \widehat{\gamma }_{{ff}} \) and the lower and upper limits of \( \widetilde{\gamma }_{{yf}} \) , as shown in Fig. 6c, are to be adjusted such that the Cauchy-Schwarz inequality condition \( \widetilde{\gamma }_{{yf}} \leqslant {\sqrt {\widehat{\gamma }_{{yy}} \widehat{\gamma }_{{ff}} } } \) is satisfied for positive definiteness. Again, these lower and upper limits are spherical models with the model parameters listed in Table 2.

Fig. 6
figure 6

Semivariograms and their confidence limits for a auto-semivariogram of y, b auto-semivariogram of f, and c pseudo cross-semivariogram of y and f. The upper hinge of the box indicates the 75th percentile of the data set, and the lower hinge indicates the 25th percentile

Full size image

The cokriged hydraulic conductivity fields using the lower and upper limits of the semivariograms in Fig. 7 show that the incorporation of the electrical log data introduces more heterogeneity which cannot be observed in the kriged hydraulic conductivity fields. However, because the cokriged field has less conditional variance, the simulated field using kriging has higher variability in hydraulic conductivity than that using cosimulation as shown in Fig. 8. The overall structure of the cokriging and cosimulation are similar, but the cosimulation has a higher variance. Moreover, the lower limit semivariogram introduces longer correlation length compared with that of the mean semivariogram. The upper limit semivariogram has higher kriging variance that that of the lower limit semivariogram.

Fig. 7
figure 7

The conditional estimates of hydraulic conductivity by cokriging (a, b) and kriging (c, d) using the upper limit semivariogram model and lower limit semivariogram model. The K varies between K=5.18 m/day (black color) to K=701 m/day (white color)

Full size image
Fig. 8
figure 8

Realizations using cosimulation (a–c) and simulation (d–f) with the mean semivariogram model, upper limit semivariogram model and lower limit semivariogram model. The K varies between K=5.18 m/day (black color) to K=701 m/day (white color)

Full size image

Significance analysis on groundwater responses

With the obtained semivariogram models and their associated semivariogram variances, this section investigates the significance of hydraulic conductivity heterogeneity to the groundwater system responses for different hydraulic conductivity distributions using the kriging method, cokriging method, simulation, and cosimulation with the mean, lower limit and upper limit semivariograms. In this section, a groundwater flow model in the study area is developed to conduct ANOVA on groundwater responses that include hydraulic head variability and mean groundwater level.

Development of groundwater flow model

A regional-scale model of the Chicot Aquifer system in southwest Louisiana was developed to better understand the groundwater flow system in the region (Hanson et al. 2001). The Chicot groundwater model underlying Acadia Parish is based on MODFLOW (Harbaugh and McDonald 1996) and has five layers and 50 rows and 50 columns, resulting in a grid size of approximately 0.83 km2. The grid is oriented 20° counter-clockwise from the geographic coordinate in order to closely align with the flow direction (Fig. 2). A local model in Acadia Parish has been developed to better understand the groundwater flow dynamics in the study area (Rahman 2005). A telescopic mesh refinement technique MODTMR (Leake and Claar 1999) was used to extract the modeling heads from the regional model (Chicot model) and assign the heads to the hydraulic head boundary conditions of the local model. Therefore, time-varied head boundary conditions are specified for all sides of the study domain. The top layer has a constant head-boundary condition; and the bottom layer is the no-flow boundary. The initial condition of the hydraulic head is created from the 1961 water level estimates. Pumping well types and locations were obtained from the Water Well GIS database of Louisiana Department of Transportation and Development (DOTD). A total of 411 water wells (26 industrial, 27 public supply and 358 irrigation wells) are included in the model. Only industrial, irrigation and public supply water wells are used in this study as these three types are responsible for more than 90% of the groundwater withdrawn from the Chicot Aquifer (Sargent 2002). Yearly pumping rates were estimated by linear interpolation from the 5-year water-use reports of US Geological Survey (Sargent 2002). The total rate was evenly distributed to the registered wells by dividing yearly pumping rate by total number of registered wells within each sector. The groundwater flow was simulated from the year of 1961 to the year of 2001 and the results at the final year are used for analyzing the head responses.

Groundwater responses

Three responses are derived from the groundwater flow model and investigated for the ANOVA test. The responses are (1) hydraulic head variability (R 1), (2) specific capacity of a pumping well (R 2), and (3) mean groundwater level (R 3). The hydraulic head variability (first response, R 1) is taken as the mean squares error of the difference between the initial hydraulic head distribution in 1961 and the calculated hydraulic head distribution in the year 2000 obtained using different hydraulic conductivity distributions over 2,500 computational nodes at the Upper Chicot Aquifer:

$$ R_{1} = \frac{1} {{n_{r} }}{\sum\limits_{r = 1}^{n_{r} } {{\sum\limits_{i = 1}^{2500} {{\left( {\phi {}_{{ini,i}} - \phi _{{r,i}} } \right)}^{2} } }} } $$
(24)

where φ ini,i is the initial groundwater head; φ r,i is the simulated groundwater head for a particular realization r; n r is the number of realizations.

The number of realizations needed depends on the uncertainty of the K field being addressed (Deutsch and Journel 1998). In this study, the number of realizations (n r) is selected based on a simple test. Model responses (R 1) for different numbers of hydraulic conductivity realizations are calculated while keeping everything else as constant. Response for 20 realizations is taken as the finest case. The error terms, \( \varepsilon _{R} = {\left| {R_{1} - R_{{finest}} } \right|} \), are plotted against the square root of number of realizations, \( {\sqrt {N_{{realizations}} } } \). Increasing the number of hydraulic conductivity realizations from 8 to 20 (finest case) only accounts for 6% of response uncertainty. Therefore, an average over 20 realizations was used in stochastic cases. When the kriged field and cokriged field are considered, the n r is equal to 1.

The specific capacity is also a key factor to assess the groundwater response. A decrease in the specific capacity indicates a decline in the productivity of the well due to the lower effective hydraulic conductivity field in the near-well area. A decrease in the specific capacity decreases the ability of the well to produce water economically. The specific capacity assesses influence of the hydraulic conductivity field on the ability of a well to produce water at a prescribed flow rate. In this study, the second response was chosen to be the specific capacity of an irrigation well (second response, R 2) located at row 31 and column 25—561235 E (easting), 3347383 N (northing) in the UTM coordinate system—with the real pumpage Q real=757 m3/day (0.2 million gallons per day). The irrigation well located near the center of the study area is chosen as the boundary conditions have least influence on it. Simulated drawdown (s) at the end of last stress period is used to evaluate the specific capacity:

$$ R_{2} = \frac{1} {{n_{r} }}{\sum\limits_{r = 1}^{n_{r} } {\frac{{Q_{{real}} }} {{s_{r} }}} } $$
(25)

where s r is the simulated drawdown for a particular realization. An average over 20 realizations was considered for the simulation process.

This study considers the average groundwater head from a 30×30-inner grid (from row 10 to row 40 and from column 10 to column 40) at the last stress period as the third response, R 3:

$$R_3 = \frac{1}{{900n_{\text{r}} }}\sum\limits_{{\text{r}} = 1}^{{\text{n}}_{\text{r}} } {\sum\limits_{{\text{i}} = 1}^{900} {\phi _{{\text{r,i}}} } } $$
(26)

The three responses are computed from the groundwater model using the alternative hydraulic conductivity fields (Table 3).

Table 3 Groundwater flow responses using different hydraulic conductivity distributions generated by the geostatistical methods and conditional simulation with semivariogram models
Full size table

Statistical analysis using ANOVA

All three responses are found insensitive to semivariogram uncertainty for the kriged and cokriged models. For the simulation and cosimulation results, increased variance in hydraulic conductivity fields (i.e., upper limit semivariogram) causes more variation in water-head variability and specific capacity. In all levels of semivariogram uncertainty, the coregionalized method has higher water levels than those in the regionalized method.

Results from the cosimulated scenario (Table 3) show that there is a 10% chance that specific capacity is less than the cokriging estimate by at least 11%, and specific capacity from the simulated scenario is less than the kriging estimate by at least 8%. However, this difference may be too small to be of practical importance.

Table 3 shows that the variance of the average water-level response using simulation is greater than the variance using cosimulation. To verify the significant difference in these two variances, the F-tests method was introduced to conduct the significance analysis at all three levels of semivariogram uncertainty. The F-test results shown in Table 4 conclude that the variances are different at the 10% significance level. This is because the cosimulation reduces uncertainty in aquifer heterogeneity and aquifer response by introducing the secondary variable in the simulation process.

Table 4 The F-test statistic to compare simulation and cosimulation in variance of groundwater level
Full size table

The t-tests in Table 5 show that the mean specific capacity using simulation and cosimulation is significantly different from conditional estimates using kriging and cokriging methods at 10% level of significance. Table 6 shows the ANOVA significance analysis results on the flow model responses in terms of the processes (i.e., kriging versus simulation; cokriging versus cosimulation), variables (i.e., kriging versus cokriging; simulation versus co-simulation); and semivariograms (i.e., lower limit, mean, and upper limit). At 10% level of significance, the ANOVA results show that semivariogram uncertainty does not have a significant effect on any of the flow model responses.

Table 5 The t-test statistic to test specific capacity (R 2) of conditional simulation to the kriging methods
Full size table
Table 6 ANOVA results on flow model responses
Full size table

However, the results in the ‘process’ class (Table 6) show that the use of simulation and cosimulation methods has a more significant impact on all of the flow model responses than the use of kriging and cokriging methods. The results in the ‘variable’ class (Table 6) also show that the use of the resistivity data does have a significant effect on the flow model responses.

Conclusions

Geophysical data such as borehole electrical resistivity have been integrated with the measured hydraulic conductivity under the cokriging framework to improve spatially distributed hydraulic conductivity estimation. A pseudo cross-semivariogram has been evaluated to cope with the non-collocated resistivity data. The improvements in the groundwater model have been investigated by comparing the head levels from different hydraulic conductivity models and the significance of either (1) processes; (2) variables; or (3) semivariograms as determined by ANOVA. The results show that the use of the coregionalized field is statistically significant in the flow-model response compared to the regionalized model. The study also shows that the simulation process can reproduce the aquifer heterogeneity and is statistically significant in the flow-model response; therefore, cosimulation should be used instead of cokriging. The semivariogram uncertainty has been studied in all models, both regionalized and coregionalized, by using the upper and lower-limit semivariograms, assuming that the sills are log-normally distributed. However, results show that the semivariogram uncertainty on the groundwater-flow model response is not significant.