On selection of kernel parametes in relevance vector machines for hydrologic applications

Abstract

Recent advances in statistical learning theory have yielded tools that are improving our capabilities for analyzing large and complex datasets. Among such tools, relevance vector machines (RVMs) are finding increasing applications in hydrology because of (1) their excellent generalization properties, and (2) the probabilistic interpretation associated with this technique that yields prediction uncertainty. RVMs combine the strengths of kernel-based methods and Bayesian theory to establish relationships between a set of input vectors and a desired output. However, a bias–variance analysis of RVM estimates revealed that a careful selection of kernel parameters is of paramount importance for achieving good performance from RVMs. In this study, several analytic methods are presented for selection of kernel parameters. These methods rely on structural properties of the data rather than expensive re-sampling approaches commonly used in RVM applications. An analytical expression for prediction risk in leave-one-out cross validation is derived. For brevity, the effectiveness of the proposed methods is assessed first by data generated from the benchmark sinc function, followed by an example involving estimation of hydraulic conductivity values over a field based on observations. It is shown that a straightforward maximization of likelihood function can lead to misleading results. The proposed methods are found to yield robust estimates of parameters for kernel functions.

1 Introduction

In recent decades, with improved information technology and remote sensing tools, our capabilities of collecting hydrological data have increased many fold. An unprecedented investment in collecting hydrologic data has resulted in large archives of hydrologic data (e.g., USGS national water information system, the global observing systems information center database, national operational hydrologic remote sensing center datasets, agricultural research service water database, etc.). A large fraction of such data tends to be high-dimensional (i.e., exhibits large variability over a wide range of space and time scales) and severely under-constrained (sparse coverage over the input space), and is often interspersed with spurious data that confound analysis. This renders many of the previous learning algorithms such as local regression, spline interpolation, and logistic regression either inefficient or inapplicable. For hydrologic applications, the challenges are (a) achieving good generalization performance in high dimensional data where curse of dimensionality stipulates exponential increase in the amount of data for good predictions; (b) representing and effectively combining the available physical knowledge of hydrological systems into data learning algorithms; (c) characterizing and quantifying uncertainty in predictions; and finally (d) making learning algorithms computationally efficient to handle voluminous data.

Kernel methods, which have been gaining popularity in machine learning, provide a radically different approach for high dimensional learning problems. Unlike traditional learning algorithms where data are represented individually, kernel methods seek pair-wise comparisons using kernel functions (Scholkopf and Smola 2002). This representation provides a simple and elegant way of capturing nonlinear relationships between input vectors and corresponding outputs using linear algorithms. Examples are support vector machines (Vapnik 1995), kernel Fisher discriminant (Mika et al. 1999), and kernel principal component analysis (Twining and Taylor 2003; Muller et al. 2001; Wu et al. 1997). These methods have demonstrated excellent generalization capabilities and good efficiency in high dimensional problems. However, most of these methods cannot provide important measures such as predictive distribution of the evidence as they are not developed with a probabilistic foundation. Thus the important issue of model uncertainty remains unsolved.

A possible way to overcome this problem is to exploit versatility of kernel methods in conjunction with Bayesian learning. Based on this idea, Tipping (2001) developed relevance vector machines (RVMs) that are kernel-based methods formulated under Bayesian construct. RVMs provide sparse solution to regression tasks by implementing Bayesian automatic relevance determination (MacKay 1994) in the transformed kernel space. RVMs have achieved excellent results for many learning problems including 3D image analysis (Agarwal and Triggs 2006), optical diagnosis of cancer cells (Majumder et al. 2005; Wei et al. 2005), prediction of chaotic time series (Quinonero-Candela and Hansen 2002) and analysis of radar data (Kovvali and Carin 2004). Recently, RVMs have found hydrologic applications in groundwater quality modeling (Khalil et al. 2005a), real time management of reservoir releases (Khalil et al. 2005b), and modeling of chaotic hydrologic time series (Khalil et al. 2006).

While RVMs are being used increasingly in hydrologic applications, there still remain some unresolved hurdles for their successful implementation. An important question that has not received the attention it deserves is the selection of kernel function parameters. It is widely acknowledged that a key factor that determines the generalization capabilities of kernel methods in general is the choice of kernel width parameter (Scholkopf and Smola 2002; Hastie et al. 2001; Vapnik 1995). The kernel function can be interpreted as a nonlinear transformation that maps the input space to a higher dimensional feature space. According to Cover’s theorem (Cover 1965) a linear function can be formulated in the higher dimensional feature space to seek a nonlinear relationship between inputs and outputs in the original input space. Thus, the problem of choosing a kernel is equivalent to finding an appropriate form of data representation for learning (Evgeniou et al. 2000). Although, there is no available general solution to this problem, several empirical and theoretical studies provide insights for specific applications (Scholkopf et al. 1999; Cherkassky and Mulier 1998; Vapnik 1999, 1998). Recently, Lanckriet et al. (2004) proposed a method for extracting kernel matrix from data using semi-definite programming for a classification problem. Wang et al. (2003) proposed a method for determining the width of a RBF kernel based on scale-space theory in computer vision for support vector machines. Cherkassky and Ma (2004) suggested that width of a radial basis function (RBF) kernel for regression problems can be reasonably estimated form the range of input data vectors.

In spite of various theoretical and empirical studies on kernel methods, there is no general consensus on appropriate choice of kernel parameters because of contradictory opinions presented by authors (Cherkassky and Ma 2004). Hence, for many applications, re-sampling from data remains the only recourse for model validation. Unfortunately learning kernel parameters via traditional re-sampling methods is not only computationally expensive but requires large amount of data for successful implementation. The objective of this work is to present techniques for practical selection of kernel function parameters, and to show the effectiveness of the proposed techniques through an example of spatial interpolation of hydrologic data.

The remainder of this paper is structured as follows: Section 2 presents the mathematical formulation of RVMs. The details of the data used for the study are presented in Sect. 3. In Sect. 4, results of bias–variance analysis of RVMs are provided to gain insights into the possible consequences of inappropriate selection of kernel function parameters. In Sect. 5.1, Tipping’s (2001) method of kernel function parameter selection by maximizing the likelihood is examined for the example datasets. In Sect. 5.2, the linearity in the formulation of RVMs is exploited to develop an analytical expression for leave-one-out cross-validation. In Sect. 5.3, the applicability of analytical model selection methods for obtaining optimum kernel function parameters is demonstrated. In Sect. 5.4, the possibility of selecting kernel parameters from data is explored. Thus, Sects. 4, 5.2, 5.3, and 5.4 constitute novel contributions of this paper. The proposed new kernel parameter selection methods are then applied to the example data sets and results obtained are discussed in Sect. 6. A set of conclusions drawn from this study and recommendations for future use are presented in Sect. 7.

2 Mathematical formulation

Consider a finite training sample of N patterns {(x _i , y _i ),i =  1, ..., N}, where x _i denotes i ^th input pattern in a d-dimensional space (i.e., x _i = [x _i1, ..., x _id ]∈ℜ^d; x = [x ₁, ..., x _N ]^T) and y _i ∈ℜ is the corresponding output. Further, let the learning machine f(x; w) be defined as a linear combination of kernel functions

$$ f{\left({{\mathbf{x}};{\varvec w}} \right)} = {\hat{\varvec y}} = {\sum\limits_{j = 0}^N {w_{j} K{\left({{\mathbf{x}},{\varvec x}_{j}} \right)}}} = {\varvec{\Phi}}{\varvec w} $$

(1)

such that

$$ {\varvec y} = f{\left({{\mathbf x};{\varvec w}} \right)} + {\varvec{\varepsilon}} $$

(2)

where, weight vector w = [w ₀, ..., w _M ]^T is an adjustable or tuning parameter, K(x, x _j ) are the kernel functions with K(x, x ₀)=1, ${{\varvec{\Phi}}_{{N \times N + 1}}}$ is the design matrix with elements Φ _ij =  K(x _i , x _j ), i =  1, ..., N ; j =  0, ..., N and ${{\varvec{\varepsilon}}}$ is the error term. There are several possibilities for the choice of kernel function, including linear, algebraic polynomials, trigonometric polynomials, RBFs, and sigmoid functions. In this study we have adapted a RBF kernel that is defined as

$$ K {\left({{\varvec x}_{i}, {\varvec x}_{j}, {\vec{\varvec{\sigma}}}_{j}} \right)} = \exp \left({- {\sum\limits_{z = 1}^d {\frac{{{\left({x_{{iz}} - x_{{jz}}} \right)}^{2}}}{{\sigma^{2}_{{_{{jz}}}}}}}}} \right) $$

(3)

where ${{\vec{\varvec{\sigma}}}_{{\varvec {j}}} = {\left[ {\sigma _{{j1}}, \ldots, \sigma _{{jd}}} \right]}}$ is the width of the RBF kernel. In practice, this is held constant for all basis functions (i.e., ${{\vec{\varvec{\sigma}}} _{\rm kernel} = {\vec{\varvec{\sigma}}}_{j}, j = 1, \ldots ,N}$) and is chosen to be radially symmetric (i.e., σ _{• 1} =  σ _{• 2} =  ... =  σ _{• d} =  σ_kernel).

The form of kernel function K (•) is fixed and known a priori based on domain knowledge. However, there are no general guidelines available for the selection of kernel parameters for hydrologic datasets. In Sect. 4, using bias–variance analysis, we argue that kernel width parameter (σ_kernel) is one of the most sensitive parameters and has an important role on the performance of the learning machine. This important aspect has received little attention, and here we suggest some techniques for practical selection of σ_kernel.

If the error term, ${{\varvec{\varepsilon}}}$ in Eq. (2) is assumed to normally distributed with zero mean and unknown variance ${\sigma^{2}_{\varepsilon},}$ and the input patterns {(x _i , y _i ), i = 1, ..., N} are generated independently, then the likelihood of the observed dataset can be written as

$$ p{\left({{\varvec y}|{\varvec w},\sigma^{2}_{\varepsilon}} \right)} = {\prod\limits_{i = 1}^N {\frac{1}{{{\sqrt {2\pi \sigma^{2}_{\varepsilon}}}}}\exp {\left\{{- \frac{1}{{2\sigma^{2}_{\varepsilon}}}{\left[ {{\left({y_{i} - f{\left({{\varvec x}_{i}, {\varvec w}} \right)}} \right)}^{2}} \right]}} \right\}}}} $$

(4)

Under a Bayesian perspective, model parameters w and ${\sigma^{2}_{\varepsilon}}$ can be estimated by first assigning prior distributions to the parameters and then estimating their posterior distribution using likelihood of the observed data. For RVM, Tipping (2001) proposed a prior conditional distribution of the form

$$ p{\left({w_{j} |\alpha _{j}} \right)} = {\sqrt {\frac{{\alpha _{j}}}{{2\pi}}}}\exp {\left({- \frac{1}{2}\alpha _{j} w^{2}_{j}} \right)} = \mathcal{N}{\left({0,\frac{1}{{\alpha^{2}_{j}}}} \right)}, j = 0, \ldots, N $$

(5)

for each of the weights, where ${\varvec{\alpha}} = {\left[ {\alpha _{0}, \ldots, \alpha _{N}} \right]}^{\rm T}$ are called a hyperparameters, and a uniform uninformative prior over logarithmic scale for ${\sigma^{2}_{\varepsilon}}$ and α _j . The choice of zero-mean-Gaussian-prior for weights expresses a preference for smaller weights, and hence a smoother estimate of the function f(x, w). Another advantage of this formulation is that during the process of learning, many of the hyperparameters α _j approach infinity, so the corresponding weights w _j tend to be delta functions centered at zero, and are thus deleted from Eq. (1) leading to sparseness. The remaining patterns corresponding to non-zero weights are only deemed to be relevant for function approximation, and hence the learning machine is known as RVM.

An analytical expression for the posterior distribution of model parameters, ${p{\left({{\varvec w},{\varvec{\alpha}},\sigma^{2}_{\varepsilon} |{\varvec y}} \right)}}$ is not available. However, it can be decomposed into two components as

$$ p{\left({{\varvec w},{\varvec{\alpha}},\sigma^{2}_{\varepsilon} |{\varvec y}} \right)} = p{\left({{\varvec w}|{\varvec y},{\varvec{\alpha}},\sigma^{2}_{\varepsilon}} \right)}p{\left({{\varvec{\alpha}},\sigma^{2}_{\varepsilon} |{\varvec y}} \right)} $$

(6)

The first term on the right hand side of Eq. (6) is the posterior probability of the weight w given σ ²_ɛ and ${{\varvec{\alpha}},}$ and is normally distributed.

$$ p{\left({{\varvec w}| {\varvec y},{\varvec{\alpha}},\varvec{\sigma}^{2}_{\varvec{\varepsilon}}} \right)} = {\mathcal{N}}{\left({{\varvec{\mu}}_{w}, \Sigma_{w}} \right)} $$

(7)

where mean and covariance are respectively

$$ {\varvec{\mu}}_{{\varvec w}} = \varvec{\sigma}^{{- 2}}_{\varvec{\varepsilon}} \Sigma _{w} {\varvec{\Phi}}^{\rm T} {\varvec y} $$

(8)

$$ \Sigma _{w} = {\left({\sigma^{{- 2}}_{\varepsilon} {\varvec{\Phi}}^{\rm T} {\varvec{\Phi}} + {\varvec {A}}} \right)}^{{- 1}} $$

(9)

with A =  diag(α₀, α₁, ..., α _N ).

The second term on the right hand side of Eq. (6) is the posterior probability of ${{\varvec{\alpha}}}$ and σ ²_ɛ . The estimation of this probability is analytically intractable, and is approximated by delta function at its mode i.e.,

$$ p{\left({{\varvec{\alpha}},\sigma^{2}_{\varepsilon}|{\varvec y}} \right)}\sim\delta\left({\varvec{\alpha}}_{\rm max}, {\sigma^{2}_{\varepsilon}}_{\rm max}\right) $$

(10)

where σ ²_{ɛ max} and ${{\varvec{\alpha}} _{\rm max}}$ are values for which ${p{\left({{\varvec{\alpha}},\sigma^{2}_{\varepsilon} |{\varvec y}} \right)}}$ reaches it maximum value. It turns out that maximizing ${p{\left({{\varvec{\alpha}},\sigma^{2}_{\varepsilon} |{\varvec y}}\right)}}$ is equivalent to maximizing the marginal likelihood ${p{\left({{\varvec y}|{\varvec{\alpha}},\sigma^{2}_{\varepsilon}} \right)}}$ which is given by

$$ \begin{aligned}\, p{\left({{\varvec y}|{\varvec{\alpha}},\varvec{\sigma}^{2}_{\varvec{\varepsilon}}} \right)} &= {\int {p{\left({{\varvec y}|{\varvec w},{\varvec{\alpha}},\varvec{\sigma}^{2}_{\varvec{\varepsilon}}} \right)}p{\left({{\varvec w}|{\varvec{\alpha}}} \right)}{\rm d}{\varvec w}}} \\ & = {\left({2\pi} \right)}^{{- N/2}} {\left| {\varvec{\sigma}^{2}_{\varvec{\varepsilon}} {\varvec {I}} + {\varvec{\Phi}}{\varvec {A}}^{{- 1}} {\varvec{\Phi}}^{\rm T}} \right|}^{{1/2}} \exp {\left\{{- \frac{1}{2}{\varvec y}^{\rm T} {\left({\varvec{\sigma}^{2}_{\varvec{\varepsilon}} {\varvec {I}} + {\varvec{\Phi}}{\varvec {A}}^{{- 1}} {\varvec{\Phi}}^{\rm T}} \right)}^{{- 1}} {\varvec y}} \right\}} \\ \end{aligned} $$

(11)

Closed form solutions of σ ²_{ɛ max} and ${{\varvec{\alpha}} _{\rm max}}$ are not available. Tipping (2001) proposed an iterative estimation method based on a type of automatic relevance determination (MacKay 1994; Neal 1996). After convergence, the learning algorithm provides hyperparameter posterior mode (σ ²_{ɛ max} and ${{\varvec{\alpha}} _{\rm max}}$) and posterior distributions of weights conditioned on σ ²_{ɛ max} and ${{\varvec{\alpha}}_{\rm max}.}$ The distribution of dependent variable y ^* at new location x ^* can be obtained by

$$ \begin{aligned} p{\left({y^{*} |{\varvec y}} \right)}& = {\int {p{\left({y^{*} |{\varvec w},{\sigma^{2}_{\varepsilon}} _{\rm max}} \right)}}}p{\left({{\varvec w}|{\varvec y},{\varvec{\alpha}} _{\rm max}, {\sigma^{2}_{\varepsilon}} _{\rm max}} \right)}{\rm d}{\varvec w} \\ &= {\mathcal{N}}{\left({\mu _{{y^{*}}}, \sigma^{2}_{{y^{*}}}} \right)}\\ \end{aligned}$$

(12)

where the mean and variance of the predicted value are, respectively,

$$ \mu _{{y^{*}}} = {\varvec{\mu}}_{{\varvec w}}^{\rm T} {\varvec{\Phi}}{\left({{\varvec x}^{*}} \right)} $$

(13)

$$ \sigma^{2}_{{y^{*}}} = {\sigma^{2}_{\varepsilon}} _{\rm max} + {\varvec{\Phi}}{\left({{\varvec x}^{*}} \right)}^{\rm T} \Sigma _{w} {\varvec{\Phi}}{\left({{\varvec x}^{*}} \right)} $$

(14)

The variance of the predicted value (Eq. (14)) is the sum of the variance associated with noise in the training data and uncertainty associated in prediction of weights.

3 Data used in this study

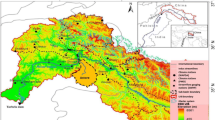
We first used synthetic data generated form sinc function for evaluation of our proposed strategies. The sinc function sinc (x) =  sin(x)/x has been a popular choice to illustrate the performance of kernel methods (Chalimourda et al. 2004; Cherkassky and Ma 2004; Vapnik 1998). In this work samples were randomly generated from the range x ∈[−10,10] and an independent Gaussian noise was added to each data point for different experiments. This was followed by a second data set of electrical conductivity measurements (surrogate for hydrologic conductivity) obtained from Zhang (1990). Surface soil samples were initially collected at 100 locations over a 1,000 by 1,000 m agricultural field near Marana, Arizona, with some additional samples collected randomly at various locations (Fig. 1). A total of 129 measurements of electrical conductivity were available for this site. One measurement was unusually large in comparison to other measurements and was not considered further in this study. The main reason of choosing a relatively small dataset is that its results are amenable to visual interpretation. Moreover, spatial interpolation of hydrologic data is often challenging due to the sparseness and presence of noisy samples in the data. Spatial interpolation of hydrologic data can be a benchmark test for statistical learning algorithms. While several other high-dimensional large data sets were also investigated, we report results from only these two data sets for clarity and brevity.

Fig. 1

Locations of electrical conductivity measurements obtained from Zhang (1990). The squares show the measurement locations, while the rhombus shows the location of outlier in the dataset

4 Bias–variance analysis

A key tool for understanding the effect of parameter selection in a machine-learning algorithm is the bias–variance decomposition of the approximation error. In recent years the use of this method for obtaining theoretical insights into machine-learning algorithms has grown rapidly (Berardi and Zhang 2003; Meyer et al. 2003; Stankovic et al. 2002; Buciu et al. 2002; Snijder et al. 1998; Twomey and Smith 1998; Geman et al. 1992) but does not appear to have been used in the context of RVMs. In bias–variance decomposition, bias measures the accuracy of the estimate given by a learning machine while variance measures the precision or specificity of the estimate. These terms are not independent but obey a form of conservation law. On one hand, a learning machine with too many degrees of freedom, will over-fit the data resulting in low bias but high variance. On the other hand, a model that contains very few degrees of freedom will not be flexible enough to approximate important features in the data resulting in high bias but low variance. The goal of learning is then to strike a right balance by identifying an appropriate tradeoff between these two terms. This tradeoff is well known in statistical literature as the bias–variance tradeoff.

For function approximation problem, the mean-square error of the learning machine can be decomposed as (Geman et al. 1992)

$$ \begin{aligned}{E}{\left[ {{\left({{\varvec y} - {\hat{\varvec y}}} \right)}^{2}} \right]} &= {E}{\left[ {{\left({{\varvec y} - {E}{\left[ {\varvec y} \right]}} \right)}^{2}} \right]} + {E}{\left[ {{\left({{\hat{\varvec y}} - {E}{\left[ {{\hat{\varvec y}}} \right]}} \right)}^{2}} \right]} + {\left({{E}{\left[ {\varvec y} \right]} - {E}{\left[ {{\hat{\varvec y}}} \right]}} \right)}^{2} \\ &= {\text{Noise}}{\left({\varvec y} \right)} + {\text{Variance}}{\left({{\hat{\varvec y}}} \right)} + {\text{Bias}}^{{\text{2}}} {\left({{\hat{\varvec y}}} \right)} \\\end{aligned} $$

(15)

The first term on the right hand side is the variance of the intrinsic noise present in the data. This term forms a lower bound on the error that can be obtained by any learning algorithm. The second term is the error in estimation due to random variation in selecting finite training samples, while the third term is the error due to mismatch between the target and approximating functions.

Although there are various advantages of studying bias–variance decomposition of a learning machine, there are certain limitations that arise when applying this method to real data sets. To be able to estimate the noise, variance, and bias for a particular problem (see Eq. (15)), we need to know the actual function being learned. This is not available for most real-world problems. To overcome this hurdle several alternatives have been suggested in the literature (Bauer and Kohavi 1999; Breiman 1998; Kohavi and Wolpert 1996). However, these approaches are marked by high computational cost and subjectivity in their design. Since the main purpose of studying bias–variance in this work is to understand the effect of kernel parameters on the performance of an RVM, we have used synthetic data (sinc dataset) to overcome this problem.

Following (Valentini and Dietterich 2004), 400 different small training sets of 50 samples each were generated from the sinc function followed by large test set of 1,000 samples. Further, to each training set a Gaussian noise with a standard deviation of 0.2 was added. The main idea behind selecting small training sets and a much larger test set is that small training sets show bias and variance more clearly, whereas a large test set gives reliable estimates of bias and variance. For each training set, RVMs were trained by varying the kernel width σ_kernel. Bias and variance decomposition of the error was then evaluated using test set as given by Eq. (15). Figure 2 depicts the estimated mean-square error, bias, and variance for different values of σ_kernel.

Fig. 2

Bias–variance decomposition of error in the estimation of sinc function by RVM as a function of kernel width σ_kernel

It is evident from the figure that the generalization capability of RVM is highly sensitive to the proper choice of σ_kernel. In particular, for high values of σ_kernel the bias is very high and so is the mean-square error. Lowering the value of σ_kernel results in sudden drop in bias, which then stabilizes for a range of σ_kernel values before beginning to increase again. Variance, on the other hand, has maximum contribution to mean-square error for smaller values of σ_kernel as expected. It generally decreases with increase in σ_kernel and stabilizes for high values of σ_kernel. Interestingly, there exists a common region in which both bias and variance take low values. This region is marked by a sudden drop in mean-square error. In summary, the bias–variance analysis demonstrates that, for RVMs, there exists a band of suitable values of σ_kernel. Outside this range, an RVM will likely have poor generalization performance. The aim of model selection should therefore be to identify this region for appropriate selection of σ_kernel.

5 Methods of kernel parameter selection

In this section, we first show that the method of estimating kernel parameters by maximizing the likelihood function (Eq. (11)) may not yield satisfactory results. Subsequently, other new methods are presented to address this issue.

5.1 Maximizing likelihood

Tipping (2001) proposed a method for estimating kernel parameters of RVM by maximizing the likelihood function (Eq. (11)). This can be achieved by taking the derivative of log-likelihood with respect to kernel parameter σ_kernel, and performing gradient-based local optimization (see Tipping (2001), p. 235 for details). This approach was adopted by Khalil et al. (2005b) for developing an adaptive RVM for real-time management of water releases.

It is to be noted that if kernel parameter σ_kernel becomes a free variable to be determined during the learning process, the learning machine (given by Eq. (1)) will become nonlinear in the unknown parameters. Estimating parameters in such a context will need a rigorous nonlinear optimization algorithm. Tipping (2001) and Quinonero-Candela and Hansen (2002) reported significant improvement in the performance of an RVM by this technique, but emphasized the difficulties in its implementation and suggested cross-validation as a better approach for practical problems.

Besides the computational costs involved with the implementation of this method, we found that for the experimental data set at the Marana site, a naïve optimization of log-likelihood may lead to severe over-fitting. In fact, Tipping (2001) cautions that maximizing the likelihood is not guaranteed to yield optimum value of kernel parameter σ_kernel in terms of model accuracy. Figure 3 shows the value of rescaled log-likelihood and number of statistically relevant vectors identified by the RVM model, as a function of σ_kernel, developed for the approximation of electrical conductivity values at the Marana site. Figure 4 illustrates the electrical conductivity surface generated by RVM for the value of σ_kernel corresponding to maximum likelihood. The generated surface is very complex with many sharp peaks and valleys. This is an example of the RVM model over-fitting the training data. Further, it may be noted that 112 out of 128 vectors were chosen as being relevant in this RVM application. Thus, a complex model has been adopted with no advantage of sparsity.

Fig. 3

Plot showing the value of rescaled log likelihood and number of vectors deemed relevant by the RVM model developed for the approximation of electrical conductivity values at the Marana site with varying kernel width σ_kernel

Fig. 4

Performance of the RVM method for the approximation of electrical conductivity values at the Marana site with kernel width σ_kernel =  20 as obtained from maximizing the likelihood function. One hundred and twelve vectors (shown as solid circles) out of a total of 128 vectors were considered statistically relevant by the RVM model

From these figures, it is seen that smaller values of σ_kernel imply that a highly complex model is needed to fit the data. Such models typically over-fit the training data resulting in higher values of likelihood function, but result in poor generalization performance. Therefore, in some cases, estimation of kernel parameter by maximizing the likelihood function alone may be undesirable.

5.2 Derivation of prediction risk by leave-one-out cross-validation

Estimation of parameters by re-sampling is by far the most popular method utilized in learning problems (Scholkopf and Smola 2002; Hastie et al. 2001; Haykin 1999; Cherkassky and Mulier 1998). The basic approach is to partition the available data into two sets; a training set and a validation set. The model is trained using the first set, and the validation error is measured using the second set. The validation error gives an estimate of the prediction risk or generalization error of the model. The parameters for which the generalization error is minimized are selected as best parameters. The main drawback of this approach is that it assumes that both training and validation sets are representative of the entire data. This holds true only for large data sets. When the number of samples is small, choice of partitions of training and validation data sets have an impact on the estimate of prediction risk.

Cross-validation provides a strategy so that estimate of prediction risk is invariant to a particular partitioning of data. This method of parameter estimation has gained wide popularity in hydrologic literature (Khalil et al. 2005a; Asefa et al. 2004). One practical approach to cross-validation is k-fold cross-validation. In this approach available data is divided into k disjoint sets of approximately equal sizes. The model is trained on all the sets except for one and validation error is measured on the set left out. The procedure is repeated for a total of k trials, each time using a different subset for validation. Average error under validation over all trials of the experiment is used to assess the generalization performance of the model. The limitation of the k-fold cross-validation method is the high computational cost and uncertainty associated in the choice of k. Leave-one-out is a special case of k-fold cross-validation, where k equals the available number of input patterns N. Luntz and Brailovsky (1969) proved that leave-one-out is an almost unbiased estimator of prediction risk. However, leave-one-out estimate of prediction risk can yield a high variance.

For linear learning machines, it is possible to compute an analytical expression for leave-one-out estimate of prediction risk (R _LOO ). This has a significant computational advantage over other re-sampling approaches in vogue in the literature for selection of parameters in RVM (Khalil et al. 2005a; Tipping 2001). The analytical expression for R _LOO is derived next for RVMs.

The RVM is linear in parameter w, once the design matrix ${{\varvec{\Phi}}}$ is fixed (Eq. (1)). Therefore, the function f(x, w) learned from RVM obeys the superposition principle. Further, Tipping (2004) shows that estimation of weights in RVM formulation is identical to penalized least square estimation. It then follows from duality in least square problems (Strang 2006) that there always exists a projection matrix P that projects the observed output y into its estimate ${{\hat{\varvec y}}}$ which in turns lies in the column space of design matrix ${{\varvec{\Phi}},}$ so that

$$ {\hat{\varvec y}} = f{\left({{\mathbf{x}};{\varvec w}} \right)} = {\varvec{\Phi}}{\varvec w} = {\varvec {Py}} $$

(16)

The projection matrix P is a N ×  N matrix often called as ‘hat matrix‘ or ‘smoothing matrix’. From Eqs. (1), (8) and (13)

$$ {\hat{\varvec y}} = {\varvec{\Phi}}{\varvec w} = {\varvec{\Phi}}{\varvec{\mu}}_{{\varvec w}} = \sigma^{{- 2}}_{\varepsilon} {\varvec{\Phi}}\Sigma _{w} {\varvec{\Phi}}^{{\text{T}}} {\varvec y} $$

(17)

Comparing Eqs. (16) and (17) the projection matrix P for RVM learning is given by

$$ {\varvec {P}}_{{N \times N}} = \sigma^{{- 2}}_{\varepsilon} {\varvec{\Phi}}\Sigma _{w} {\varvec{\Phi}}^{ \rm T} $$

(18)

Further, let the j th pattern x _j be left out of training set during leave-one-out cross-validation. Then the prediction for x _j during validation operation is given as (Cherkassky and Mulier 1998)

$$ \hat{y}_{j} = \frac{1}{{1 - {{P}}_{{jj}}}} {\sum\limits_{\begin{subarray}{l}i = 1 \\i \ne j\end{subarray}}^N {{P}}_{{ji}} y_{i}} $$

(19)

where P _ji is the j th row and i th column element of the projection matrix P. The square error in the prediction of x _j can be computed by

$$ \begin{aligned} {\left({y_{j} - \hat{y}_{j}} \right)}^{2} &= {\left({y_{j} - \frac{1}{{1 - P_{{jj}}}} {\sum\limits_{\begin{subarray}{l}i = 1 \\i \ne j\end{subarray}}^N {P_{{ji}} y_{i}}}} \right)}^{2} \\ & = {\left({\frac{{y_{j} - {\sum\limits_{i = 1}^N {P_{{ji}} y_{i}}}}}{{1 - P_{{jj}}}}} \right)}^{\rm 2} = {\left({\frac{{y_{j} - \hat{y}_{j}}}{{1 - P_{{jj}}}}} \right)}^{2} \\ \end{aligned} $$

(20)

Hence, the leave-one-out estimate of prediction risk is

$$ R_{{\rm LOO}} = \frac{1}{N}{\sum\limits_{j = 1}^N {{\left({y_{j} - \hat{y}_{j}} \right)}^{2}}} = \frac{1}{N}{\sum\limits_{j = 1}^N {{\left({\frac{{y_{j} - \hat{y}_{j}}}{{1 - P_{{jj}}}}} \right)}^{2}}} $$

(21)

Figures 5 and 6 illustrate the estimation of prediction risk by analytical leave-one-out cross-validation for sinc data and Marana site data, respectively. For sinc data (Fig. 5), leave-one-out cross-validation can successfully identify the region of sudden drop in prediction risk as obtained during bias–variance analysis. The prediction risk then remains approximately constant for a wide range of σ_kernel values before increasing again. Increase in prediction risk for smaller values of σ_kernel occurs at a slower rate when compared to the results of bias–variance analysis. For Marana site data (Fig. 6), there are some local minima in the estimate of prediction risk. These may be attributed to high variance that is associated with leave-one-out cross-validation. However, unlike log-likelihood maximization, the leave-one-out estimate does not show monotonic behavior with decrease in values of σ_kernel.

Fig. 5

Estimation of prediction risk using analytical form of leave-one-out cross-validation (labeled LOO) for the approximation of sinc function by RVM with varying kernel width σ_kernel

Fig. 6

Estimation of prediction risk using analytical form of leave-one-out cross-validation (labeled LOO) for the approximation of electrical conductivity values at the Marana site by RVM with varying kernel width σ_kernel

5.3 Analytical model selection

Under regularization framework, it is widely accepted that for a given sample size, there exists a model of optimal complexity corresponding to the smallest prediction risk (Hastie et al. 2001; Haykin 1999; Cherkassky and Mulier 1998). Analytical model selection criterion uses analytical estimates of the prediction risk as a function of training error [empirical risk (R _empirical)] and a penalty term based on some measure of model complexity. These estimates are grouped into two categories: classical estimates that are based on asymptotic analysis (as sample size N → ∞) and the structural risk minimization (SRM) method from statistical learning theory that is based on non-asymptotic analysis (Cherkassky and Mulier 1998).

5.3.1 Asymptotic analysis

In classical estimates, the forms of prediction risk vary depending on the class of approximating functions supported by the learning machine. For linear models, a number of these estimates are available such as Akakie information criterion (AIC), Bayes information criterion (BIC), minimum description length, etc. Among them, AIC and BIC are very popular in hydrologic literature (Xu and Li 2002; Gyasi-Agyei 2001; Honjo and Kashiwagi 1999; Knotters and De Gooijer 1999; Mutua 1994; Gregory et al. 1992). The general form of the classical estimate of prediction risk for a linear model can be written as

$$ {\rm prediction}\; {\rm risk} = \Psi {\left({\frac{{\rm dof}}{N}} \right)} \cdot R_{{\rm empirical}} $$

(22)

where Ψ is a monotonic increasing function of the ratio of degrees of freedom (dof) and training sample size (N). For penalized linear models, the effective degrees of freedom can be determined from the projection matrix P (Hastie et al. 2001; Cherkassky and Mulier 1998). To the best of our knowledge, this has not been investigated for RVMs. From linear algebra (Strang 2006), it is well known that the eigen values of P for a penalized linear model are in the range [0,1]. The effective degrees of freedom is given by the number of eigen values that are proximal to unity. Determining eigen values of P is computationally intensive, hence approximations are made to determine the number of large eigen values, and hence the dof. One popular approximation (Cherkassky and Ma 2003; Cherkassky and Mulier 1998; Hastie et al. 2001) is

$$ {\rm dof} \approx {\rm trace} {\left({{\varvec {PP}}^{\rm T}}\right)} $$

(23)

Thus if we know the dof, we can estimate prediction risk based on a particular choice of Ψ using Eq. (22). For demonstration, we have used BIC or Schwarz’ criteria (Schwarz 1978). BIC estimate of prediction risk is given by

$$ {\rm prediction}\; {\rm risk} = - 2 \cdot {\text{log-likelihood}} + \log(N) \cdot {\rm dof} $$

(24)

The estimated prediction risk obtained from BIC for sinc data and Marana site data are shown in Figs. 7 and 8, respectively. BIC estimate of sinc data (Fig. 7) could not only capture the region of sudden drop in prediction risk but closely follows the pattern obtained from bias–variance analysis. For Marana site data, the estimate of prediction risk (Fig. 8) shows a suitable range of σ_kernel, penalizing very simple as well as very complex models.

Fig. 7

Estimation of prediction risk using Bayes information criterion (BIC) for the approximation of sinc function by RVM with varying kernel width σ_kernel

Fig. 8

Estimation of prediction risk using Bayes information criterion (BIC) for the approximation of electrical conductivity values at the Marana site by RVM with varying kernel width σ_kernel

5.3.2 Structural risk minimization

Statistical learning theory provides a very general and conceptual framework for complexity control using SRM. Under SRM principle, a set of possible models are arranged in order of increasing complexity. Selection of an optimal model is based on computation of the Vapnik-Chervonenkis (VC) generalization bound that provides an upper bound on prediction risk. For a function approximation problem with N samples, the following VC generalization bound holds with a probability 1 − Θ (Vapnik 1998)

$$ {\rm prediction}\; {\rm risk} \leqslant R_{{\rm empirical}} \cdot {\left\{{1 - c {\sqrt {a_{1} \frac{{h{\left[ {\log {\left({\raise0.7ex\hbox{${a_{2} N}$} \!\mathord{\left/{\vphantom {{a_{2} N} h}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$h$}} \right)} + 1} \right]} - \log {\left({\raise0.7ex\hbox{$\Theta $} \!\mathord{\left/{\vphantom {\Theta 4}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$4$}} \right)}}}{N}}}} \right\}}^{{-1}}_{{+}} $$

(25)

where h is the VC dimension of the approximating function, and c is a theoretical constant that depends on the choice of loss function. The quantities a ₁ and a ₂ are constants with values in the range 0 <  a ₁ ≤  4; 0 <  a ₂ ≤  2. The values of a ₁ and a ₂ depend upon the joint distribution of the input and output variables that is usually unknown. For worst case distribution (discontinuous density function), a ₁ and a ₂ have been derived to be 4 and 2 respectively (Vapnik 1995, 1999). For a function approximation problem with square error loss function, empirical studies suggest values of a ₁ =  1, a ₂ =  1 and c =  1 (Cherkassky et al. 1999; Vapnik 1998). However Cherkassky and Mulier (1998) suggested that a ₁ and a ₂ should be altered based on data. The quantity Θ in Eq. (25) determines the confidence interval to be described shortly.

The main difficulty in applying VC bound is to estimate VC dimension (h) of the approximating function. Unfortunately, it is not possible to obtain an exact analytical estimate of h for most approximating functions including the form given by Eq. (1). To overcome this difficulty, experimental methods of determining h are available (Cherkassky and Mulier 1999; Shao et al. 2000). Most of these methods are too complex to be applied for practical problems. However for penalized linear models like RVM, h can be approximated by effective dof given by Eq. (23). This heuristic estimate of h has been successfully applied in various statistical learning problems (Cherkassky and Ma 2003; Cherkassky et al. 1999; Cherkassky and Mulier 1998) and is used in this study. The upper bound on prediction risk for RVM is therefore given by

$$ {\rm prediction}\; {\rm risk} \leqslant R_{{\rm empirical}} \cdot {\left\{{1 - {\sqrt {\frac{{{\rm dof}{\left[ {\log {\left({\raise0.7ex\hbox{$N$} \!\mathord{\left/{\vphantom {N {\rm dof}}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{${\rm dof}$}} \right)} + 1} \right]} - \log {\left({\raise0.7ex\hbox{$\Theta $} \!\mathord{\left/{\vphantom {\Theta 4}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$4$}} \right)}}}{N}}}} \right\}}^{{- 1}}_{{+}} $$

(26)

The value of confidence interval Θ should be chosen based on the number of samples. When the number of samples is small, the confidence level is set low, whereas when the number of samples is large, the confidence level is set high. Vapnik (1995) recommended the following rule for choosing the confidence interval, and was used in this study

$$ \Theta = \min {\left({\frac{4}{{{\sqrt N}}},1} \right)} $$

(27)

The upper bound on prediction risk as estimated by SRM principle for sinc data and Marana site data are shown in Figs. 9 and 10, respectively. The results from sinc data suggest that for the value of a ₁ =  1 and a ₂ =  1 as suggested in literature, the estimated prediction risk could capture the region of sudden drop, but increases only for very small values of σ_kernel. However, we found that the estimated prediction risk closely follows the results of bias–variance analysis for a ₁ =  2 and a ₂ =  1. The results from Marana site data also indicate that SRM principle can be useful in finding values of σ_kernel for which RVM model is neither very complex nor very simple. In fact, results obtained from SRM principle are very similar to those obtained from BIC estimate of prediction risk.

Fig. 9

Estimation of upper bound on prediction risk using structural risk minimization (SRM) principle for the approximation of sinc function by RVM with varying kernel width σ_kernel. The bound holds with probability 0.6

Fig. 10

Estimation of upper bound on prediction risk using structural risk minimization (SRM) principle for the approximation of electrical conductivity values at the Marana site by RVM with varying kernel width σ_kernel. The bound holds with probability 0.65

5.4 Structure of data

The kernel function, used in a model such as Eq. (1), can be visualized as mathematical formulation for the notion of similarity in input space of x (Scholkopf and Smola 2002; Vapnik 1998). In the context of Gaussian processes, kernel function is often interpreted as a covariance function that encodes our knowledge of how observations at different points of input space are related (Rasmussen and Williams 2006; Scholkopf and Smola 2002). Since RVMs also belong to the family of Gaussian processes (Tipping 2001), this interpretation can provide a way for selecting kernel width (σ_kernel). The Euclidean distance in the input space (x) beyond which the dependent variable (y) ceases to have any significant correlation can provide a reasonable estimate for the value of kernel width. This strategy has been reported to give satisfactory results in the context of SVM regression (Asefa et al. 2004).

The correlogram for sinc data and Marana site data are shown in Figs. 11 and 12, respectively. For sinc data, the correlation goes to zero at approximately 2.5 separation distance. This value is close to the optimum value as obtained from bias–variance analysis. It can be seen from Fig. 12 that for Marana site data, the estimated value of σ_kernel from correlogram and optimum RBF kernel obtained from Bayes information criterion and SRM principle are in close agreement.

Fig. 11

Plot showing correlation in the sinc data as a function of distance in input space along with Gaussian kernel obtained from bias–variance analysis (σ_kernel =  2.2)

Fig. 12

Plot showing correlation in the measurements of electrical conductivity values at the Marana site as a function of spatial distance and Gaussian kernel as obtained from BIC and SRM principle (σ_kernel = 180)

In an attempt to explain the regularization capability of kernel methods, Smola et al. (1998) argue that kernels act as a filter in frequency domain. For example an RBF kernel with a large kernel width will act as a low-pass filter in frequency domain, attenuating higher order frequencies and thus resulting in a smooth function. Alternatively, an RBF kernel with small kernel width will retain most of the higher order frequencies leading to an approximation of a complex function by the learning machine. This interpretation provides yet another way of determining kernel width. It is widely acknowledged in the field of signal processing that the frequency of optimal filter should match the frequency distribution of the signal to be constructed (Scholkopf and Smola 2002). Thus, if we know the distribution of data in frequency domain we can construct an appropriate kernel such that it filters out spurious frequencies of the data.

Power spectrum of sinc data and Marana site data along with the power spectrum of the optimal kernel as obtained from previous analyses are shown in Figs. 13 and 14, respectively. It is evident from the figure that the chosen kernels are effective in filtering out low power high frequency signals. These signals can be attributed to the noise present in data. This interpretation of kernel as filters in frequency domain can also be used for designing anisotropic kernels. Figure 14 shows the power spectra in two orthogonal directions (X and Y) for the Marana site data. The similarity in these figures suggests that the kernel function should be isotropic in this case.

Fig. 13

Plot showing the normalized power spectrum of sinc data and power spectrum of normalized Gaussian kernel obtained from bias–variance analysis (σ_kernel = 2.2)

Fig. 14

Plot showing normalized power spectrum of electrical conductivity measurements at the Marana site for two orthogonal directions (X and Y) along with power spectrum of normalized Gaussian kernel corresponding to optimal σ_kernel as obtained from BIC and SRM principle (σ_kernel =  180)

6 Results

The procedures described in Sect. 5 were tried on many datasets of different size and dimensionality, and the RVM performance was found to be qualitatively similar. For brevity, the values of σ_kernel obtained for electrical conductivity measurements at Marana site along with sinc data are presented in Table 1. It is evident from the tabulated results that there exists a range of appropriate values for RVM kernel width σ_kernel. This is in agreement with the findings of Wang et al. (2003) that the generalization performance of kernel methods (SVM in their case) remains stable within a certain range of σ_kernel values. It also corroborates the findings of bias–variance analysis discussed in Sect. 4. The results further indicate that the ranges of σ_kernel obtained from various methods generally tend to overlap. Based on many different datasets, the performance of BIC and SRM principles in selecting the value of σ_kernel appears to be promising.

Table 1 Range of Gaussian kernel width parameter σ _kernel for sinc data and electrical conductivity measurements at the Marana site data obtained from different model selection methods

Figures 15 and 16 illustrate the fitted surface obtained from developed RVM model based on the value of σ_kernel selected from above analysis. The RVM performed reasonably well in approximating sinc function (Fig. 15) and selected only 8 out of a total of 100 data points as relevant vectors. For electrical conductivity values at the Marana site, the RVM model considered only 11 vectors out of total 128 vectors as statistically relevant (Fig. 16a). The corresponding prediction variance surface shown in Fig. 16b is quite revealing. Note that the high variance estimates are associated with locations where the separation between observed values and model prediction is large, as one would expect intuitively. Similarly, the model variances tend to be larger for locations that have little or no data support. It is worth mentioning that the number of data points deemed relevant by RVM depends on the complexity of the function to be approximated. However, for the various datasets used in this study, RVM typically chose less than 10% of available data as relevant.

Fig. 15

Plot showing RVM approximation of sinc function with kernel width σ_kernel =  2.2. Eight vectors (shown as solid circles) out of a total of 100 vectors were considered statistically relevant by the RVM model

Fig. 16

Performance of the RVM method for the approximation of electrical conductivity values at the Marana site with kernel width σ_kernel =  180. a The RVM fitted surface (mesh) along with measurements in circles. Eleven vectors (shown as solid circles) out of a total of 128 vectors were considered statistically relevant by the RVM model. b The prediction variance surface of the RVM estimates

7 Concluding remarks

In this study the importance of kernel parameters in generalization performance of RVMs was established using bias–variance analysis. Following this, several techniques for practical selection of kernel parameters were suggested. The effectiveness of the proposed techniques was illustrated through application to synthetic as well as real data sets using Gaussian kernels. For clarity, the results are presented for small data sets only. However, the proposed techniques are general, and the same approach can be easily extended to other forms of kernel functions. Further the proposed techniques are applicable to both small and large hydrologic data sets.

Bias–variance analysis of RVMs suggested that there exists a region of suitable values for RBF kernel width σ_kernel over which both bias and variance have low values. Outside this region, both bias and variance increase resulting in poor generalization performance of RVMs.

Maximizing the likelihood function to estimate kernel parameters for RVMs have gained popularity in spite of the fact that its implementation requires solution of highly complex nonlinear optimization problems. Results from this study indicate that in some cases, estimation of kernel parameters by maximizing the likelihood alone may result in over-fitting. Thus, apart from maximizing the likelihood function, other methods as mentioned here should be utilized.

Linear models have been the mainstay of statistical learning for many decades. Consequently, a vast array of tools is available for parameter selection in linear models. In this work, linearity in the formulation of RVMs was used to develop an analytical expression for leave-one-out cross-validation. Further, linearity was exploited to adopt analytical model selection methods for use in RVMs. In particular BIC and Vapnik-Chervonenkis (VC) generalization bounds were demonstrated to yield satisfactory results in selection of σ_kernel.

It is widely accepted that the form of kernel function and its parameters depends on the structure of data. The results from this study reveal that the correlogram can be used to get a satisfactory range of σ_kernel in context of RVMs also. The interpretation of kernels as filters in frequency domain can not only help in understanding the regularization property of kernels, but can also be useful for designing anisotropic kernels.

Based on empirical studies with a variety of hydrologic data sets, we found that the following steps yield reasonable value of σ_kernel and are therefore recommend for practical hydrologic applications. (1) Preliminary data analysis: this includes detecting outliers and applying appropriate transformation to the data. (2) Plotting correlogram or power spectrum of the data to decide an approximate range of σ_kernel: for high dimensional data where, relative importance of input variables in estimating desired output varies, power spectrum can be more useful. (3) Training RVM for the chosen range of σ_kernel and estimating prediction risk using BIC or SRM principle. (4) Selecting σ_kernel corresponding to minimum value of prediction risk as optimal value for kernel parameter. Our experience suggests that the above steps yield satisfactory value of σ_kernel and will make RVMs more amenable to hydrologic applications.

Although RVMs are new to the field of hydrology, they provide a promising alternative to many statistical hydrologic problems because of their excellent generalization properties. Besides this they have the added advantage of probabilistic interpretation that yields prediction uncertainty. Therefore, several avenues should be explored in order to make this technique better-suited to a wide variety of hydrologic data. In particular, incorporating and representing physics of the hydrologic system into RVM learning, modifying the RVM formulation to handle flexible priors, and making the algorithm robust against outliers will make RVMs more amenable to hydrologic problems. Further studies by the authors will be directed at addressing some of these issues.