1 Introduction

The basic problem studied in this paper is point location in an arrangement of hyperplanes, in any dimension, in the linear decision tree model. In the general version of this problem we are given a set H of n hyperplanes in \({\mathbb R}^d\), where both n and d are assumed to be large, and we seek an algorithm that, given a query point \(\mathbf{x}:= (x_1, x_2, \ldots , x_d)\), computes the cell of the arrangement \(\mathcal {A}(H)\) of H that contains \(\mathbf{x}\). In many of the applications, though, it suffices to determine whether \(\mathbf{x}\) lies on some hyperplane of H. To simplify the presentation, most of the study in this paper is devoted to this special case, but we will also address the general case.

Point location problems of this kind arise in several interesting applications, such as the k-SUM problem, and the more general k-linear degeneracy testing (k-LDT) problem, as well as their looser (and harder) variants SubsetSum and Knapsack. In the k-SUM problem, we are given a set of n real numbers, represented as a point \(\mathbf{x}:= (x_1, x_2, \ldots , x_n) \in {{\mathbb R}}^n\), and want to decide whether there exist k indices \(i_1, i_2, \ldots , i_k\) such that \(x_{i_{1}} + x_{i_{2}} + \cdots + x_{i_{k}} = 0\). In the k-LDT problem, we are also given a fixed k-variate linear function \(f(y_1, \ldots , y_k) = a_0 + \sum _{i=1}^k a_i y_i\), where \(a_0, a_1, \ldots , a_k\) are real coefficients, and, for a query point \(\mathbf{x}:= (x_1, x_2, \ldots , x_n) \in {{\mathbb R}}^n\), we want to decide whether there exist k indices \(i_1, i_2, \ldots , i_k\) such that \(f(x_{i_1}, x_{i_2}, \ldots , x_{i_k}) = 0\). In the SubsetSum problem, the input consists of n integers, and the goal is to decide whether they contain a non-empty subset whose elements sum to 0. The Knapsack problem is a variant of SubsetSum where given n real numbers, we would like to determine whether there is a (non-empty) subset of them that sums to 1.

Following the approach in Cardinal et al. [3] for k-SUM (see also [2, 12]), we define H to be the collection of the \({n \atopwithdelims ()k}\) hyperplanes h in \({\mathbb R}^n\) of the form \(x_{i_1} + x_{i_2} + \cdots + x_{i_k} = 0\), over all k-tuples \(1\le i_1< i_2< \cdots < i_k\le n\). The k-SUM problem can then be reformulated as asking, for a query point \(\mathbf{x}\), whether \(\mathbf{x}\) lies on any hyperplane of H. This reduces the k-SUM problem to the special variant of point location in hyperplane arrangements, as discussed above. A similar reduction applies to the k-LDT problem, and also to the more general Knapsack or SubsetSum problems, in which the relevant hyperplanes are of the form \(x_{i_1} + \cdots + x_{i_k} = 1\) or 0, for all the \(2^n-1\) possible non-empty subsets \(\{i_1,\ldots ,i_k\}\) of \(\{1,\ldots ,n\}\).

The model in which we consider this problem is the s-linear decision tree model: Solving an instance of the problem with input \(\mathbf{x}=(x_1,\ldots ,x_d)\) is implemented as a search with \(\mathbf{x}\) in some tree T. Each internal node v of T is assigned a linear function in the d variables \(x_1,\ldots ,x_d\), with at most s non-zero coefficients. The outgoing edges from v are labeled <, >, or \(=\), indicating the branch to follow depending on the sign of the expression at v evaluated at \(\mathbf{x}\). Leaves are labeled “YES” or “NO”, where “YES” means that we have managed to locate \(\mathbf{x}\) on a hyperplane of H, and “NO” means that \(\mathbf{x}\) does not lie on any hyperplane. Each “YES” leaf has an edge labeled “\(=\)” leading to it (but not necessarily vice versa, because some of the tests may involve auxiliary hyperplanes that are not part of the input). To solve an instance of the problem, we begin at the root of T. At each node v that we visit, we test the sign at \(\mathbf{x}\) of the linear function at v, and proceed along the outgoing edge labeled by the result of the test. We conduct this search until we reach a leaf, and output its label “YES” or “NO”. At each internal node, the test (which we also refer to as a linear query) is assumed to cost one unit. All other operations are assumed (or rather required) not to depend on the specific coordinates of \(\mathbf{x}\) (although they might, and generally do, depend on discrete data that has been obtained from the preceding queries with \(\mathbf{x}\)), and incur no cost in this model. Thus the length of the search path from the root is the overall number of linear queries performed by the algorithm on the given input, and is thus our measure for its cost. In other words, the worst-case complexity of the algorithm, in this model, is the maximum depth of its corresponding tree. As in [3], when \(s=d\) (the maximum possible value for s), we refer to the model just as a “linear decision tree”. The study in this paper will only consider this unconstrained case.

We also note that, although we could in principle construct the whole tree T in a preprocessing stage, which would cost nothing in our model, the algorithm that we present only constructs, on the fly, the search path that \(\mathbf{x}\) traces in T.

To recap, solving a point location instance in this model, with a query point \(\mathbf{x}\), amounts to processing a sequence of linear queries of the form “Does \(\mathbf{x}\) lie on some hyperplane h, or else on which side of h does it lie?”. Each such query is a sign test, asking for the sign of \(h(\mathbf{x})\), where \(h(\cdot )\) is the linear expression defining h. Some of the hyperplanes h that participate in these queries will be original hyperplanes of H, but others will be auxiliary hyperplanes that the algorithm constructs. For this special variant of point location, the algorithm succeeds if at least one of the linear queries that involves an original hyperplane results in an equality, determining that \(\mathbf{x}\) does lie on a hyperplane of H.

The same model applies for the general point location problem, except that each leaf of the tree is labeled with some cell C of \(\mathcal {A}(H)\) (of any dimension), and each query that reaches that leaf lies in C. In the companion paper [14] we address several concrete issues that arise in this general version, such as a compact way to represent cells of the arrangement. However, in this paper these issues are not important for the linear decision tree model, as they are independent of the concrete coordinates of the query point.

Previous work The k-SUM, k-LDT, SubsetSum, and Knapsack problems have been studied extensively over the years. These problems are NP-complete (the first two are NP-complete when k is part of the input), which raised interest in finding polynomial-time solutions in restricted models, such as the linear decision tree model considered here. The dependence of k-SUM and k-LDT on k (say, in the standard RAM model) has not yet been fully resolved. Improved performance bounds have been obtained by Erickson [12] (see also Ailon and Chazelle [2]).

Meyer auf der Heide [29] showed an upper bound of \(O(n^{4} \log {n})\) on the number of linear queries for the n-dimensional Knapsack problem, and thus, in particular, for k-SUM.

Meiser [28] presented an efficient point-location mechanism for high-dimensional hyperplane arrangements, in the standard real RAM model. When interpreted in the linear decision tree model, and applied to the instances at hand, it yields a linear decision tree for k-SUM (as well as for the more general problem k-LDT) of depth that is only polynomial in k and n. We remark that the original analysis of Meiser was sketchy and relied on a suboptimal choice of parameters. Meiser’s analysis has been somewhat tightened by Liu [25]. A careful and meticulous study of Meiser’s algorithm, with improved performance bounds, is given in the companion paper with Har-Peled and Kaplan [14]. Cardinal et al. [3] improved this bound to \(O(k n^{3} \log ^2{n})\). Concerning lower bounds in this model of computation, Dobkin and Lipton [11] showed a lower bound of \(\Omega (n\log {n})\) on the depth of the linear decision tree for k-LDT, and, in another paper [10], a lower bound of \(\Omega (n^2)\) for the n-dimensional Knapsack problem. We mention the very recent work of Kane et al. [22], who present an almost tight bound of \(O(k n \log ^2{n})\) on the number of linear queries for k-SUM. Below we discuss this latter work in more detail and compare it to our results.

We remark that the case \(k=3\), i.e., the 3SUM-problem, is related to various geometric problems to which it can be reduced. These problems are known as 3SUM-hard. For example, the problem of testing whether there exist three collinear points in a given planar set of n points is 3SUM-hard. These problems have been introduced in the seminal work of Gajentaan and Overmars [16], who showed subquadratic reductions from 3-SUM to many of these problems. The prevailing conjecture was that any algorithm for 3-SUM requires \(\Omega (n^2)\) time, but in a recent dramatic development, this has been refuted by Grønlund and Pettie [18], who presented a (slightly) subquadratic algorithm for 3-SUM (see also [15] and the more recent works of [4, 5, 17]). Furthermore, Grønlund and Pettie showed that in the \((2k - 2)\)-linear decision tree model, only \(O(n^{k/2}\sqrt{\log {n}})\) queries are required for k odd. In particular, for 3-SUM, this bound is \(O(n^{3/2} \sqrt{\log {n}})\), and it has been slightly improved to \(O(n^{3/2})\) [17].

Our results Our main result is the following improved algorithm for point location in hyperplane arrangements, under the linear decision tree model.

Theorem 1.1

(Restricted point location) Let H be a set of n arbitrary hyperplanes in \({\mathbb R}^d\). Given a point \(\mathbf{x}\in {\mathbb R}^d\), we can determine whether \(\mathbf{x}\) lies on any hyperplane of H with \(O(d^2\log n)\) linear queries. The algorithm terminates almost surely, and can be implemented in the real RAM model, where it makes the same number of linear queries, runs in overall polynomial time, and all its other operations do not access explicitly the coordinates of \(\mathbf{x}\).

In some applications one seeks a procedure that actually returns the cell of the arrangement (of the appropriate dimension) that contains the query point \(\mathbf{x}\), for example by outputting the sign vector of \(\mathbf{x}\), which is a vector indexed by the hyperplanes of H, so that each component is \(-1,0\), or 1, if \(\mathbf{x}\) lies below, on, or above the corresponding hyperplane, respectively. A suitable extension of our technique can perform this task too; see the companion paper [14] for details.

Our analysis uses a variant of the approach in [3], inspired by the point-location mechanism of Meiser [28], where we locate the input point \(\mathbf{x}\) in \(\mathcal {A}(H)\) using a recursive algorithm that searches with \(\mathbf{x}\) through a sequence of arrangements of random samples from the input set H. While this framework is not new, a major difference between the construction of [3, 28] and ours is that the former constructions apply bottom-vertex triangulation to the cells in arrangements of suitable (random) subsets of H, which partitions each cell into simplices. In dimension d, each simplex is defined (in general) by \(\Theta (d^2)\) hyperplanes of H; see, e.g., [1, 9] and below. In contrast, in our construction we partition the cells of such an arrangement using the vertical decomposition technique [1, 7], where each cell of the arrangement is partitioned into a special kind of vertical prisms, each of which is defined by only at most 2d hyperplanes of H. In both studies, ours and those of Meiser [28] and of Cardinal et al. [3], the local construction of the cell containing \(\mathbf{x}\) (in an arrangement of some subsample of H) is carried out through d recursive steps (reducing the dimension by 1 at each step). The difference is that the algorithm in [3] needs to perform roughly quadratically many queries at each such recursive step, whereas our algorithm performs only linearly many queries. With a few additional observations about the structure of vertical decompositions (see below for a detailed discussion), this will eventually decrease the overall depth of the linear decision tree by (slightly more than) a factor of d, with respect to the bound in [3]. We note that, although the combinatorial bound on the overall complexity of (number of simplices in) bottom-vertex triangulations in hyperplane arrangements is in general smaller than the currently best known bound on the complexity of (number of prisms in) vertical decompositions (in dimensions \(d\ge 5\)), this is not an issue in the decision tree model. In other words, for the purpose of locating the cell containing \(\mathbf{x}\), in the linear decision tree model, using vertical decompositions is the decisive winning strategy.Footnote 1

We can apply this result to the k-SUM, k-LDT, Knapsack and SubsetSum problems, using the reduction described above, which maps the problem to a point-location problem in \({\mathbb R}^n\) (where n is the size of the input), with a set of \(\left( {\begin{array}{c}n\\ k\end{array}}\right) \) hyperplanes for the former two problems, or of \(2^n-1\) hyperplanes for latter two problems. We obtain:

Theorem 1.2

  1. (a)

    For any fixed k, the complexity of k-SUM and k-LDT in the (randomized) linear decision-tree model is \(O(kn^2\log n)\) with high probability. Moreover, the algorithms solving these two problems terminate almost surely.

  2. (b)

    The complexity of the n-dimensional SubsetSum and Knapsack problems in the (randomized) linear decision-tree model is \(O(n^3)\) with high probability. Moreover, the algorithms solving these two problems terminate almost surely.

On the “real” algorithmic front, we show that in the RAM model the k-SUM and k-LDT problems, for k fixed, can be solved in expected polynomial time, with the same number, namely \(O(kn^2\log n)\), of linear queries (and with all other operations independent of the actual coordinates of \(\mathbf{x}\)), as in Theorem 1.2. This is described in Sect. 4.4.

We note that while the bounds that we obtain in Theorem 1.2 are a significant improvement over the previous works [3, 28], they have been improved in a more recent work of Kane et al. [22], who present an almost tight bound of \(O(k n \log ^2{n})\) on the number of linear queries for k-SUM, a similar nearly-tight bound of \(O(k^2 n \log ^2{n})\) for k-LDT, and a bound of \(O(n^2 \log {n})\) for the Knapsack and SubsetSum problems. Their approach is considerably different from ours and from the earlier works [3, 28], and uses the concept of “inference dimension” developed in the context of active learning. Moreover, the results in [22] hold, for the k-SUM and k-LDT problems, already for the (2k)-linear decision tree model. However, as already mentioned, this groundbreaking progress requires the hyperplanes that arise in the corresponding point-location problem to have a few and small integer coefficients (the \(\ell _1\)-norm of the vector of the integer coefficients should be a small integer). This holds for k-SUM, and, after a certain reduction, also for k-LDT, and also for Knapsack and SubsetSum, but does not yield a good bound for arbitrary hyperplanes, as does our algorithm. Kane et al., in a more recent work [23], have extended their approach to apply to arbitrary hyperplanes, but the number of linear queries is larger than ours; namely, for n hyperplanes in \({\mathbb R}^d\), their algorithm requires \(O(d^4 \log {d} \log {n})\) linear queries.Footnote 2 In conclusion, our result still provides the best known bounds for the number of linear queries for performing point location in an arrangement of arbitrary hyperplanes in higher dimensions.

2 Preliminaries: Arrangements and Vertical Decomposition

Let H be a collection of n hyperplanes in \({{\mathbb R}}^d\). We emphasize that H is not necessarily in general position, and that it may contain vertical hyperplanes (as it does in the case of the k-SUM problem and its variants), as well as vertices that are incident to more than d hyperplanes. We allow degeneracies of the latter kind, but we get rid of vertical hyperplanes by performing a slight random rotation of the coordinate frame (generating a random rotation using the technique in [30]). This is made in order to simplify the presentation and is also the approach taken in the companion paper [14]. See later for a discussion of this step.

The description of vertical decomposition and its related constructs, as presented below, while being constructive, is made only to define the relevant notions, and to set the infrastructure within which our algorithm will operate and will be analyzed. The algorithm itself will not construct explicitly the entire vertical decompositions through which it searches.

The vertical decomposition\(\mathcal {V}(H)\) of the arrangement \(\mathcal {A}(H)\) is defined in the following recursive manner (see [1, 7] for the general setup, and [19, 24] for the case of hyperplanes in four dimensions). Let the coordinate system be \(x_1, x_2, \ldots , x_d\), and let C be a cell in \(\mathcal {A}(H)\). For each \((d-2)\)-face g on \({\partial }{C}\), we erect a \((d-1)\)-dimensional vertical wall passing through g and confined to C; this is the union of all the maximal \(x_d\)-vertical line-segments that have one endpoint on g and are contained in C. The walls extend downwards (resp., upwards) from faces g on the top boundary (resp., bottom boundary) of C (faces on the “equator” of C, i.e., faces that have an \(x_d\)-vertical supporting hyperplane, have no wall (within C) erected from them). This collection of walls subdivides C into convex vertical prisms, each of which is bounded by (potentially many) vertical walls, and by two hyperplanes of H, one appearing on the bottom portion and one on the top portion of \({\partial }{C}\), referred to as the floor and the ceiling of the prism, respectively; in case C is unbounded, a prism may be bounded by just a single (floor or ceiling) hyperplane of H. More formally, this step is accomplished by projecting the bottom and the top portions of \({\partial }{C}\) onto the hyperplane \(x_d=0\), and by constructing the overlay of these two convex subdivisions. Each full-dimensional (i.e., \((d-1)\)-dimensional) cell in the overlay, when lifted vertically back to \({\mathbb R}^d\) and intersected with C, becomes one of the above prisms.

Note that after this step, the two bases (or the single base, in case the prism is unbounded) of a prism may still have arbitrarily large complexity, or, more precisely, be bounded by arbitrarily many hyperplanes. It is simpler to describe the construction using the overlay interpretation given in the preceding paragraph. That is, assume that both bases exist. Then there exist a facet \(f^-\) on the lower boundary of C and a facet \(f^+\) on the upper boundary of C, such that \(f^-\) and \(f^+\) are vertically visible within C, and the common \(x_d\)-projection of the bases of (or of all of) the prism is the intersection \(C'\) of the projections of \(f^-\) and of \(f^+\). Let \(h^-\) (resp., \(h^+\)) be the hyperplane in H that contains \(f^-\) (resp., \(f^+\)). Note that \(C'\) is a convex polyhedron in \({\mathbb R}^{d-1}\), bounded by at most \(n-1\)\((d-1)\)-hyperplanes, each of which is the projection of either (i) an intersection of the form \(h^-\cap h\), for h lying below C, or (ii) an intersection of the form \(h^+\cap h\), for h lying above C, or (iii) the intersection \(h^+\cap h^-\) (in which case the corresponding \((d-1)\)-hyperplane bounding \(C'\) is the projection of an equator face of C). In what follows we refer to the prisms obtained so far as undecomposed prisms, or partially decomposed prisms, or first-stage prisms.

Before continuing, we summarize the preceding observations in the following lemma for future references.

Lemma 2.1

Let \(\tau \) be a first-stage prism, whose ceiling and floor are contained in two respective hyperplanes \(h^-,h^+\). The \(x_d\)-projection of \(\tau \) is a convex polyhedron, bounded by at most \(n-1\) hyperplanes (in \(x_d=0\)), each of which is of one of the following types (i)–(iii):

  1. (i)

    an intersection \(h^-\cap h\), for some hyperplane h that passes below C, or

  2. (ii)

    an intersection \(h^+\cap h\), for some hyperplane h that passes above C, or

  3. (iii)

    \(h^-\cap h^+\).

Remark

An important feature of the preceding argument is that it also holds when \(\tau \) is any convex vertical prism, obtained at any recursive step of the decomposition (as described shortly), and, in particular, when \(\tau \) is the vertical prism obtained at the final step. This property will be used in the complexity analysis of our point-location algorithm, to be presented in Sect. 4.

Our goal is to decimate the dependence of the complexity of the prisms on n, and to construct a decomposition of this kind so that each of its prisms is bounded by no more than 2d hyperplanes. To do so, we recurse with the construction within the \(x_d\)-projection \(C'\) of the prism, so each recursive subproblem is now \((d-1)\)-dimensional.

Specifically, after the first decomposition step described above, we project each of the first-stage prisms just obtained onto the hyperplane \(x_d = 0\), obtaining a \((d-1)\)-dimensional convex polyhedron \(C'\), which we vertically decompose using the same procedure described above, only in one lower dimension. That is, we now erect vertical walls within \(C'\) from each \((d-3)\)-face of \({\partial }{C'}\), in the \(x_{d-1}\)-direction. These walls subdivide \(C'\) into \(x_{d-1}\)-vertical (undecomposed) prisms, each of which is bounded by (at most) two facets of \(C'\), which contain its floor and ceiling (in the \(x_{d-1}\)-direction), and by some of the vertical walls.

We keep projecting these prisms onto hyperplanes of progressively lower dimensions, and produce the appropriate vertical walls. We stop the recursion as soon as we reach a one-dimensional instance, in which case all prisms projected from previous steps become line-segments (including two halflines), requiring no further decomposition.Footnote 3 We now backtrack, and lift the vertical walls (constructed in lower dimensions, over all iterations), one dimension at a time, ending up with \((d-1)\)-dimensional walls within the original cell C; that is, a \((d-i)\)-dimensional wall is “stretched” in directions \(x_{d-i+2}, \ldots , x_{d}\) (applied in that order), for every \(i=d, \ldots , 2\), where at each step it is clipped between the floor and ceiling of the corresponding dimension.

Each of the final cells is a “box-like” prism, bounded by at most 2d hyperplanes. Of these, two are original hyperplanes, two are hyperplanes supporting two \(x_d\)-vertical walls erected from some \((d-2)\)-faces, two are hyperplanes supporting two \(x_{d-1}x_d\)-vertical walls erected from some \((d-3)\)-faces (within the appropriate lower-dimensional subspaces), and so on.

We note that each final prism is defined in terms of at most 2doriginal hyperplanes of H, in a sense made precise in the ensuing description. In degenerate situations where there are vertices that are incident to more than d hyperplanes, the defining set may not be unique, however, as we show below, we can still define the final prism with at most 2d original hyperplanes. We establish this property using backward induction on the dimension of the recursive instance. Initially, we have two original hyperplanes \(h^-,h^+\), which contain the floor and ceiling of the prism, respectively, and belong to the defining set. We intersect each of the remaining hyperplanes of H with either \(h^-\) or \(h^+\), as prescribed earlier (including the intersection \(h^-\cap h^+\)), and project all these intersections onto the \((d-1)\)-hyperplane \(x_d=0\). Suppose inductively that, when we are at dimension j, we already have a set \(D_j\) of (at most) \(2(d-j)\) original defining hyperplanes (namely, all the original hyperplanes defining the walls erected so far that bound the current, still not fully decomposed, prism), and that each (lower-dimensional) hyperplane in the current collection \(H_j\) of \((j-1)\)-hyperplanes is obtained by an interleaved sequence of intersections and projections, which are expressed in terms of some subset of the at most \(2(d-j)\) defining hyperplanes and (at most) one additional original hyperplane. Clearly, all this holds trivially at the initial step \(j=d\). We now choose a new floor and a new ceiling from among the hyperplanes in \(H_j\), gaining two new defining hyperplanes: The unique ones that define the new floor and ceiling and are the ones not in \(D_j\).Footnote 4 We add them to \(D_j\) to form \(D_{j-1}\), intersect each of the other hyperplanes in \(H_j\) with either the new floor or the new ceiling, using the rule given above (see Lemma 2.1), and project all the resulting \((j-2)\)-intersections onto the \((j-1)\)-hyperplane \(x_j=0\), to obtain a new collection \(H_{j-1}\) of \((j-2)\)-hyperplanes. Clearly, the inductive properties that we assume carry over to the new sets \(D_{j-1}\) and \(H_{j-1}\), so this holds for the final setup in \(d=1\) dimensions. Since each step adds at most two new defining hyperplanes, and since no extra hyperplanes are present at \(d=1\), the claim follows.

We apply this recursive decomposition for each cell C of \(\mathcal {A}(H)\), and thereby obtain the entire vertical decomposition \(\mathcal {V}(H)\). We remark though that our algorithm does not explicitly construct \(\mathcal {V}(H)\). In fact, it does not even construct the (full discrete representation of the) prism of \(\mathcal {V}(H)\) containing the query point \(\mathbf{x}\). It will be clear shortly from the presentation what the algorithm actually constructs.

3 \({\varepsilon }\)-Cuttings and Optimistic Sampling with Vertical Decompositions

Given a finite collection H of hyperplanes in \({{\mathbb R}}^d\), by an \({\varepsilon }\)-cutting for H we mean a subdivision of space into prism-like cells, of the form just defined, that we simply refer to as prismsFootnote 5, such that every cell is crossed by (i.e., the interior of the cell is intersected by) at most \({\varepsilon }|H|\) hyperplanes of H, where \(0< {\varepsilon }< 1\) is the parameter of the cutting. \({\varepsilon }\)-cuttings are a major tool for a variety of applications; they have been established and developed in several fundamental studies more than twenty five years ago [6, 8, 26].

Roughly speaking, when d is a (small) constant, the random sampling theory of Clarkson and Shor [9] (see also Clarkson [8]) produces an \({\varepsilon }\)-cutting as follows. We use the drawing model in which, to obtain a random sample R of target size r, we make r independent random draws from H; we allow repetitions, so the actual size of R might be smaller than r. This is the model used in the \({\varepsilon }\)-net theorem of Haussler and Welzl [21] and in several related works. We refer to a sample drawn in this manner as an r-sample. We now draw an r-sample R from H, for \(r:= \frac{cd}{{\varepsilon }} \log {\frac{d}{{\varepsilon }}}\), where c is a suitably large absolute constant, and construct the arrangement \(\mathcal {A}(R)\) of R and its vertical decomposition \(\mathcal {V}(R)\). With a suitable choice of c, the random sampling technique of Clarkson and Shor [9] then guarantees, with constant (highFootnote 6) probability, that every prism of \(\mathcal {V}(R)\) is crossed by at most \({\varepsilon }|H|\) hyperplanes of H. (This also follows from the \({\varepsilon }\)-net theory of Haussler and Welzl [21], but, as it turns out, the dependence of r on d is much larger when d is large; see the companion paper [14] for more details.)

A weak aspect of \({\varepsilon }\)-cuttings is that they require that every cell of the cutting be “light” (crossed by at most \({\varepsilon }|H|\) hyperplanes of H). This is important if we are after a data structure that has to be constructed in a single preprocessing stage, and then has to cater to every possible query point. However, in the linear decision tree model, this is an overkill—all we want to ensure is that the prism containing the single query point \(\mathbf{x}\) be light. In Theorem 3.1, we consider the single-prism variant, and show that its lightness can be guaranteed (with high probability) by using a smaller-size sample; see also the companion paper [14], where this latter, single-prism approach is referred to as optimistic sampling, for further details.

3.1 The Clarkson–Shor Framework

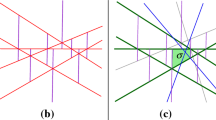
We keep denoting by H a set of n hyperplanes in \({\mathbb R}^d\). Following the definitions and notations in [20, Chap. 8], put \({\displaystyle \mathcal {T}= \mathcal {T}(H):= \bigcup \nolimits _{S \subseteq H} \mathcal {V}(S)}\); that is, \(\mathcal {T}\) is the set of all possible prisms defined by the subsets of H. For each prism \(\tau \in \mathcal {T}\), we associate with \(\tau \) its defining set\(D(\tau )\) and its conflict list\(K(\tau )\). The former is the smallest subset \(D \subseteq H\) such that \(\tau \) is a prism in \(\mathcal {V}(D)\), and the latter is the set of all hyperplanes \(h \in H\) for which \(\tau \) does not appear in \(\mathcal {V}(D \cup \{h\})\); they are precisely the hyperplanes in \(H \setminus D\) that cross \(\tau \). In degenerate situations (as those allowed in this paper), \(D(\tau )\) may not be uniquely defined; see Fig. 1 for an illustration.

Fig. 1
figure 1

(a) A degeneracy, in which a geometric prism \(\tau \) has many defining sets. The prism results from nine combinatorially distinct prisms, each with a different signature defining set, consisting of the floor, the ceiling, one of the other lines through the top-left corner, and one of the other lines through the bottom-right corner. (b) Another possible degeneracy, where a defining set is not unique. In this case the two hyperplane intersections coincide after projection. Both scenarios happen with probability 0

Full size image

To overcome this hurdle, we distinguish between the notions of a geometric prism, which is the spatial region occupied by the prism, and a combinatorially defined prism (or just a combinatorial prism for short), which comes with its own unique defining set, to which we refer as its signature; see again Fig. 1 for this distinction. That is, in degenerate scenarios different sets D may define the same geometric prism \(\tau \), but in the combinatorial sense each of these sets D defines its own distinct combinatorial prism. When two (or more) distinct sets \(D_1\) and \(D_2\) define two respective combinatorially distinct prisms \(\tau _1\) and \(\tau _2\) that give rise to the same geometric prism \(\tau \), the hyperplanes in \(D_2\setminus D_1\) are irrelevant for the prism \(\tau _1\)—they neither define it nor cross it. In what follows the unqualified term \(\tau \) always refers to the combinatorial version of the prism (and, with a bit of abuse of notation, also to its geometric counterpart). Of course, when the hyperplanes are in general position, all these fine issues are irrelevant—each geometric prism has a unique defining set.

By our discussion in Sect. 2 we have \(|D(\tau )| \le 2d\), for each \(\tau \in \mathcal {T}\). In other words, in the definition of \(\mathcal {T}\), it suffices to consider subsets \(S \subseteq H\) with \(|S| \le 2d\).

We have the following two axioms, which hold for any subset \(S\subseteq H\) (recall that, by convention, all prisms are now combinatorial):

(i):

For any \(\tau \in \mathcal {V}(S)\), we have \(D(\tau ) \subseteq S\), for the defining set (signature) \(D(\tau )\) of \(\tau \), and \(K(\tau ) \cap S = \emptyset \).

(ii):

If \(D(\tau ) \subseteq S\), for the defining set \(D(\tau )\) of \(\tau \), and \(K(\tau ) \cap S = \emptyset \), then \(\tau \in \mathcal {V}(S)\).

Theorem 3.1

Given a set H of n hyperplanes in d-space, a parameter \({\varepsilon }\in (0,1)\), and a fixed point \(\mathbf{x}\in {\mathbb R}^d\), a random sample R of \(r = \frac{cd}{{\varepsilon }} \log {\frac{1}{{\varepsilon }}}\) independent draws (with repetitions) of hyperplanes of H, where c is a sufficiently large absolute constant, satisfies, with constant (high) probability, the property that either (i) \(\mathbf{x}\) lies on a hyperplane of R, or (ii) the unique prism in the vertical decomposition \(\mathcal {V}(R)\) of \(\mathcal {A}(R)\) that contains \(\mathbf{x}\) is crossed by at most \({\varepsilon }|H|\) hyperplanes of H.

Proof

Although the proof is rather standard, the specific sampling model that we use requires some attention. We present the proof (i) for the sake of completeness, (ii) for properly handling our drawing model, and (iii) for highlighting the way in which the analysis is affected by the dependence of the “constant” of proportionality on d.

Fix a prism \(\tau \in \mathcal {T}(H)\) that contains \(\mathbf{x}\) in its interior. Let \(k:=|K(\tau )|\) denote the size of its conflict list, and assume, without loss of generality, that \(|D(\tau )|\) is exactly 2d. The probability that \(\tau \) appears in \(\mathcal {V}(R)\) is the probability that we draw all elements in \(D(\tau )\) and none of \(K(\tau )\) (once again, we emphasize that \(D(\tau )\) is the unique representative signature of \(\tau \)). To obtain such a successful event, enumerate \(D(\tau )\) as \(h_1,h_2,\ldots ,h_{2d}\). Choose a drawing index (out of the r draws) at which \(h_1\) is picked, then another index at which \(h_2\) is picked, and so on. In any of the \(r-2d\) remaining indices, choose any of the \(n-k\) hyperplanes of \(H\setminus K(\tau )\). The number of such events is at most

$$\begin{aligned} r(r-1)\cdots (r-2d+1) \cdot (n-k)^{r-2d} . \end{aligned}$$

This is an upper bound, rather than an equality, because we allow repetitions, so the same event may be counted more than once in this bound. Hence the probability that \(\tau \) appears in \(\mathcal {V}(R)\) is at most

$$\begin{aligned} \frac{ r(r-1)\cdots (r-2d+1) \cdot (n-k)^{r-2d} }{n^r}\le & {} \bigg ( \frac{r}{n}\bigg )^{2d} \bigg ( \frac{n-k}{n}\bigg )^{r-2d}\\\le & {} \bigg ( \frac{r}{n}\bigg )^{2d} e^{-k(r-2d)/n} . \end{aligned}$$

We have \(r\gg 2d\), with a suitable choice of constants, so we can write \(r-2d \ge c_0r\), for \(c_0\approx 1\). The above probability is then at most

$$\begin{aligned} \bigg ( \frac{r}{n}\bigg )^{2d} e^{-c_0kr/n} . \end{aligned}$$

In particular, if k is heavy, that is, if \(k \ge {\varepsilon }n\) then \(c_0rk/n \ge c_0r{\varepsilon }\).

Recall that we take \(r = O\bigl (\frac{d}{{\varepsilon }} \log {\frac{1}{{\varepsilon }}} \bigr )\). In this case,

$$\begin{aligned} c_0r{\varepsilon }= c_0cd \log {\frac{1}{{\varepsilon }}} , \end{aligned}$$

and the probability of \(\tau \) to appear in \(\mathcal {V}(R)\) is at most

$$\begin{aligned} \bigg (\frac{r}{n}\bigg )^{2d} e^{-c_0cd \log {\frac{1}{{\varepsilon }}}} . \end{aligned}$$

We repeat this analysis for each heavy prism \(\tau \in \mathcal {T}(H)\) that contains \(\mathbf{x}\) in its interior. The overall number of prisms that contain \(\mathbf{x}\) is estimated as follows. For any subset R of H, if \(\mathbf{x}\) does not lie on any hyperplane of R (barring degenerate situations, in which \(\mathbf{x}\) lies on a vertical wall of a prism or on one of its vertical faces of lower dimension, in which case it lies on the boundary of several prisms, an event which occurs with probability 0), then it lies in (the interior of) a unique prism in \(\mathcal {V}(R)\). Since any such prism is defined by at most 2d hyperplanes of H, it follows that the number of such prisms is

$$\begin{aligned} \left( {\begin{array}{c}n\\ 2d\end{array}}\right) \le \frac{n^{2d}}{(2d)!} = O\bigg ( \frac{n^{2d}}{d^{1/2}} \biggl ( \frac{e}{2d}\biggr )^{2d} \bigg ) . \end{aligned}$$

Hence, substituting the value of r and using the probability union bound, we conclude that the probability that the prism of \(\mathcal {V}(R)\) that contains \(\mathbf{x}\) in its interior is heavy is at most

$$\begin{aligned} O\bigg ( \frac{n^{2d}}{d^{1/2}} \biggl ( \frac{e}{2d}\biggr )^{2d} \cdot \frac{r^{2d}}{n^{2d}} e^{-c_0cd \log {\frac{1}{{\varepsilon }}}} \bigg ) = O\bigg ( \biggl ( \frac{ce}{2{\varepsilon }} \biggr )^{2d} e^{-c_0cd \log {\frac{1}{{\varepsilon }}}} \bigg ) . \end{aligned}$$

This expression will be (much) smaller than 1 if we choose c large enough to have

$$\begin{aligned} \biggl ( \frac{ce}{2{\varepsilon }} \biggr )^2 e^{-c_0c \log {\frac{1}{{\varepsilon }}}}< 1 , \quad \text {or}\quad c^2{\varepsilon }^{c'_0c} < \biggl (\frac{2{\varepsilon }}{e}\biggr )^2 , \end{aligned}$$

where \(c_0'\) is another absolute constant, which will be the case if we take c to be a sufficiently large absolute constant. This completes the proof. \(\square \)

Remark

Our construction uses vertical decomposition. Expanding upon an earlier made comment, we note that an alternative construction, for arrangements of hyperplanes, is the bottom-vertex triangulation (see [1, 27]). However, its major disadvantage for the analysis in this paper is that the typical size of a defining set of a simplex in this decomposition is \(d_0 = d(d+3)/2\), as opposed to the much smaller value \(d_0 = 2d\) for vertical decomposition; see above [1, 27], and the companion paper [14], for more details. The fact that prisms in the vertical decomposition have such a smaller bound on the size of their defining sets is what makes vertical decomposition a superior technique for the decision-tree complexity of point location in hyperplane arrangements. As a matter of fact, we show in the companion paper [14] that this superiority also holds, with suitable caveats, in the uniform RAM model.

4 The Algorithm

4.1 Algorithm Outline

The input to the algorithm is a set of n hyperplanes in \({\mathbb R}^d\), and a query point \(\mathbf{x}\). The high-level approach of our algorithm can be regarded as an optimized variant of the algorithm of Cardinal et al. [3], which is inspired by the point-location mechanism of Meiser [28]. We choose \({\varepsilon }= 1/2\), and apply the refined sampling strategy given in Theorem 3.1. The algorithm proceeds as follows.

(i):

Construct a random sample R of \(r := O\bigl (\frac{d}{{\varepsilon }} \log {\frac{1}{{\varepsilon }}}\bigr ) = O(d)\) hyperplanes of H, with a suitable absolute constant of proportionality.

(ii):

Construct the prism \(\tau =\tau _\mathbf{x}\) of \(\mathcal {V}(R)\) that contains the input point \(\mathbf{x}\). If at that step we detect an original hyperplane of H that contains \(\mathbf{x}\), we stop and return “YES”.

(iii):

Construct the conflict list \(K(\tau )\) of \(\tau \) (the subset of hyperplanes of H that cross \(\tau \)). If \(|K(\tau )| > n/2\), discard R and restart the algorithm at step (i). Otherwise, recurse on \(K(\tau )\).

(iv):

Stop as soon as \(|K(\tau )|\) is smaller than the sample size \(r = O\bigl (\frac{d}{{\varepsilon }} \log {\frac{1}{{\varepsilon }}}\bigr )\) (we use the same sample size in all recursive steps). When that happens, test \(\mathbf{x}\), in brute force, against each original hyperplane of H in \(K(\tau )\); return “YES” if one of the tests results in an equality, and “NO” otherwise.

We note that those parts of the algorithm that do not explicitly dependFootnote 7 on \(\mathbf{x}\), which are costly in the RAM model, are performed here for free. That is, our goal at this point is only to bound the number of linear queries performed by the algorithm. We also note that the construction of the prism containing \(\mathbf{x}\) (described below) is conceptually simple, mainly due to the fact that there are no vertical hyperplanes (after we apply the random rotation). The other kind of degeneracy, that is, vertices that are incident to arbitrarily many hyperplanes, is handled relatively easily, at least in the linear decision tree model—see below.

We comment that step (i) costs nothing in our model, so we do not bother with its implementation details (which are thoroughly investigated in [14]). The tests in step (iii), although being very costly in the standard real RAM model of computation, are independent of the specific coordinates of \(\mathbf{x}\), and thus cost nothing in our model. Thus only steps (ii) and (iv) need to be analyzed. We focus on the more involved step (ii); step (iv) is trivial to analyze.

Constructing the prism containing\(\mathbf{x}\) Since the overall complexity of the prism (the number of its faces of all dimensions) is exponential in the dimension d, we do not construct it explicitly. Instead we only construct explicitly its at most 2d bounding hyperplanes, consisting of a floor and a ceiling (or only one of them in case the cell \(C_{\mathbf{x}}\) in \(\mathcal {A}(R)\) containing \(\mathbf{x}\) is unbounded), and at most \(2d-2\) vertical walls (we have strictly fewer than \(2d-2\) walls in cases when either the floor of \(\tau \) intersects its ceiling (on \({\partial }\tau \)), or when this happens in any of the projections \(\tau ^{*}\) of \(\tau \) in lower dimensions, or when the current subcell becomes unbounded at any of the recursive steps). The prism \(\tau \), as defined in step (ii), is then implicitly represented as the intersection of the halfspaces bounded by these hyperplanes and containing \(\mathbf{x}\). Let \(H_{\mathbf{x}}\) denote this set of at most 2d hyperplanes. From now on we assume, to simplify the presentation but without real loss of generality, that \(C_{\mathbf{x}}\) is bounded, and that \(\tau \) has exactly \(2d-2\) vertical walls (and thus exactly 2d bounding hyperplanes).

The following recursive algorithm constructs \(H_{\mathbf{x}}\), and also detects whether \(\mathbf{x}\) lies on one of the bounding hyperplanes of \(\tau \). Let \(r = O\bigl (\frac{d}{{\varepsilon }} \log {\frac{1}{{\varepsilon }}}\bigr )\) denote the size of our sample R. Initially, we set \(H_{\mathbf{x}} := \emptyset \). We first perform r linear queries with \(\mathbf{x}\) and each of the hyperplanes of R, resulting in a sequence of r output labels “above” / “below” / “on”. At the top level of recursion (before reducing the dimension), encountering a label “on” means that \(\mathbf{x}\) lies on an original hyperplane of H, and thus there is a positive solution to our instance of the restricted variant of point location considered here, and we stop the entire procedure and output “YES”. At deeper recursive levels (in lower-dimensional spaces), the hyperplanes passed to such a recursive instance are no longer the original hyperplanes of \(R\subseteq H\). Under a random tilting of the coordinate frame, the probability of encountering any “on” output is 0. If we do encounter “on”, we have two options: We can either abort, or discard the current random tilting and apply another one. In the former approach, the algorithm may fail with probability 0, and in the latter it will never fail, but may not terminate, again only with probability 0. In what follows we opt for the second approach. (Note that when we re-tilt the coordinate frame, the coordinates of \(\mathbf{x}\) also vary accordingly.)

We thus assume, without loss of generality, that initially all labels are “above” or “below”. We next partition the set of the hyperplanes in R according to their labels, letting \(R_{1}\) denote the set of hyperplanes lying above \(\mathbf{x}\), and \(R_{2}\) the set of hyperplanes below it. We then identify the upper hyperplane \(h_1 \in R_1\) and the lower hyperplane \(h_2 \in R_2\) with shortest vertical distances from \(\mathbf{x}\). We do this by computing the minimum of these vertical distances, each of which is a linear expression in \(\mathbf{x}\), using \((|R_1|-1)+(|R_2|-1) < r\) additional comparisons. The hyperplanes \(h_1\) and \(h_2\) contain the ceiling and the floor of \(\tau \), respectively, and we thus insert them into \(H_{\mathbf{x}}\).

In order to produce the hyperplanes containing the vertical walls of \(\tau \), we recurse on the dimension d. This process somewhat imitates the one producing the entire vertical decomposition of \(C_{\mathbf{x}}\) described above. However, the challenges in the current construction are to build only the single prism containing \(\mathbf{x}\), to keep the representation implicit, and to do this efficiently.

In accordance with the preceding observations, summarized in Lemma 2.1 and the remark following it, we generate the pairwise intersections \(h_1 \cap h\), for \(h\in R_1\setminus \{h_1\}\), \(h_2 \cap h\), for \(h \in R_2\setminus \{h_2\}\), and \(h_1\cap h_2\), and project all of them onto \(x_d=0\) (note that by our assumption the number of defining hyperplanes is exactly 2d, \(h_1 \cap h_2\) is not needed for the construction, but it should be considered in the more general case where \(\tau \) has less than 2d bounding hyperplanes). We denote by \(R^{(1)}\) the resulting set of projections. By construction we have \(|R^{(1)}| \le r-1\).

We continue the construction recursively on \(R^{(1)}\) in \(d-1\) dimensions. That is, at the second iteration, we project \(\mathbf{x}\) onto the subspace \(x_d=0\); let \(\mathbf{x}^{(1)}\) be the resulting point. We first perform at most r linear tests with \(\mathbf{x}^{(1)}\) and each of the hyperplanes in \(R^{(1)}\). If we encounter “on” for some \(h^{(1)} \in R^{(1)}\) then \(\mathbf{x}\) lies on a vertical wall of \(\tau \) passing through \(h^{(1)}\), and then we re-tilt the coordinate frame, as discussed above.

The general flow of the recursive procedure is as follows. At each step i, for \(i=1,2,\ldots ,d\), we have a collection \(R^{(i-1)}\) of at most |R| (actually of at most \(|R|-i\)) hyperplanes of dimension \(d-i\), and a point \(\mathbf{x}^{(i-1)}\), in the \(x_1\cdots x_{d-i+1}\)-hyperplane (for \(i=1\) we have \(R^{(0)}=R\) and \(\mathbf{x}^{(0)}=\mathbf{x}\)). We first test whether \(\mathbf{x}^{(i-1)}\) lies on any of the hyperplanes \(h^{(i-1)}\) in \(R^{(i-1)}\). If so, we re-tilt the frame (unless \(i=1\), in which case we report “YES”), as above. Otherwise, no “on” label is produced, and we find the pair of hyperplanes \(h_1^{(i-1)},h_2^{(i-1)}\) that lie respectively above and below \(\mathbf{x}^{(i-1)}\) in the \(x_{d-i+1}\)-direction, and are closest to \(\mathbf{x}^{(i-1)}\) in that direction (they support the ceiling and floor of the recursive prism, in the \(x_{d-i+1}\)-direction). We note that in degenerate situations, when there are vertices that are incident to more than d hyperplanes, or, more generally, when there are flats of dimension j that are incident to more than \(d-j\) hyperplanes, it is possible that \(h_1^{(i-1)},h_2^{(i-1)}\) are not unique. Typically, this might happen when all the corresponding original hyperlanes that give rise to \(h_1^{(i-1)}\) or to \(h_2^{(i-1)}\) coincide after transformed and projected to the current \(x_1\cdots x_{d-i+1}\)-hyperplane, and they all touch the full-dimensional prism containing \(\mathbf{x}\) at a corresponding common \((d-i-1)\)-face; see Fig. 1 for an illustration. In this case, we can select \(h_1^{(i-1)},h_2^{(i-1)}\) arbitrarily (among the collection of candidates), which determines the pair of original hyperplanes to be added to the signature of the final prism containing \(\mathbf{x}\). Another situation that can arise, but only with probability 0, is that the point q, where the \(x_{d-i+1}\)-directed ray from \(\mathbf{x}^{(i-1)}\) meets these hyperplanes is a transversal intersection of some pair of them; see Fig. 2. In this case, which can easily be tested by an operation that costs nothing in this model, \(\mathbf{x}\) lies on the boundary of a prism, and, as before, we discard the current tilting and apply a new one. We will revisit this scenario when we discuss the algorithm in the RAM model in Sect. 4.4.

Fig. 2
figure 2

The ray from \(\mathbf{x}^{(i-1)}\) meets the current ceiling at a transversal intersection of two hyperplanes

Full size image

Having \(h_1^{(i-1)},h_2^{(i-1)}\) as above, we produce a set \(R^{(i)}\) of at most \(|R^{(i-1)}|-1\) hyperplanes of dimension \(d-i-1\) in the \(x_1\cdots x_{d-i}\)-hyperplane. We also project \(\mathbf{x}^{(i-1)}\) onto this hyperplane, thereby obtaining the next point \(\mathbf{x}^{(i)}\). The construction of \(R^{(i)}\) is performed similarly to the way it is done for \(i=1\), as described above, and Lemma 2.1 (and the discussion surrounding it) continues to apply, so as to ensure that indeed \(|R^{(i)}|\) continues to be (progressively) smaller than |R|, and that its members are easy to construct.

We stop when we reach \(i = d\), in which case we are given a set of at most |R| points on the real line, and we locate the two closest points to the final projected point \(\mathbf{x}^{(d)}\).

To complete the construction, we take each of the hyperplanes \(h_1^{(i-1)},h_2^{(i-1)}\), obtained at each of the iterations \(i = 2, \ldots , d\), and lift it “vertically” in all the remaining directions \(x_{d-i+2},\ldots ,x_d\), and add the resulting \((d-1)\)-hyperplanes in \({\mathbb R}^d\) to \(H_{\mathbf{x}}\).

Remark

The importance of Lemma 2.1 is that it controls the sizes of the sets \(R^{(i)}\), \(i \ge 1\). Without the filtering that it provides, the size of each \(R^{(i)}\) would be roughly twice the size of \(R^{(i-1)}\). This would happen if, in the above notation, for each \(h \in R \setminus \{h_1, h_2\}\), we would take the projections of both intersections \(h_1 \cap h\), \(h_2 \cap h\), and the query would then require exponentially many linear tests. This doubling effect also shows up in the original analysis of the complexity of vertical decompositions [7].

Constructing the conflict list of\(\tau \) This is step (iii) of the algorithm. As we noted above, the construction of the conflict list of \(\tau \) costs nothing in the decision tree model. This follows by noting that the discrete representation of \(\tau \) is independent of the actual coordinates of \(\mathbf{x}\). Specifically, \(\tau \) is the intersection of (at most) 2d halfspaces in \({\mathbb R}^d\), namely, those containing \(\mathbf{x}\) and bounded by the hyperplanes in \(H_{\mathbf{x}}\). Each of these hyperplanes is defined in terms of some subset of the set D of the (at most) 2d defining hyperplanes of \(\tau \) in H (see the definition of defining sets in Sect. 3), via a sequence of operations, each of which is either (i) taking the intersection of some \(h\in D\) with a previously constructed flat, or (ii) projecting some flat one dimension down, or (iii) lifting, in (one or more of) the remaining coordinate directions, a lower-dimensional flat to a hyperplane in \({\mathbb R}^d\). (Note that an operation of type (iii) is vacuous algebraically—as already mentioned, the equation of the flat within its ambient space is the equation of the lifted hyperplane in \({\mathbb R}^d\); all the added coordinate variables have zero coefficients.)

Once we have constructed \(\tau \), in this implicit manner, we take each hyperplane \(h \in H\) and test whether it intersects \(\tau \). We describe such a procedure in detail when we later discuss, in Sect. 4.4, an extension of the algorithm to the RAM model, and ignore these issues, irrelevant in our model, for now. We only note here that there is a straightforward way to preform this step via linear programming, but, for efficiency reasons, we will use a different approach in Sect. 4.4.

Implementing step (iv) This final step is trivial to implement, especially in our model, as all it needs are at most r linear tests of \(\mathbf{x}\) against each hyperplane in the final conflict list.

4.2 Algorithm Correctness

It is clear from the preceding presentation that the algorithm will never report that \(\mathbf{x}\) lies on a hyperplane of H when it does not.

Consider then the case where \(\mathbf{x}\) is contained in some hyperplane h of H. Consider a fixed step of the main recursion (on the size of H), and let \(\tau \) be the full-dimensional prism, in the vertical decomposition of the corresponding sample R, that contains \(\mathbf{x}\). (Recall our discussion of handling queries that, with probability 0, happen to lie on the boundary of a prism but not on its first-level floor or ceiling.) Clearly, h must intersect the interior or the boundary of \(\tau \). In the former case, h belongs to \(K(\tau )\), and will be passed down the recursion. (And if we are at the bottom of the recursion, h will be explicitly tested.) In the latter case, h must intersect the (first-stage) floor or ceiling of \(\tau \), and then, if \(\mathbf{x}\in h\) then \(\mathbf{x}\) also lies on the respective floor or ceiling (because there are no \(x_d\)-vertical hyperplanes in H), and the first stage of constructing \(\tau \) will detect that \(\mathbf{x}\in h\).

We also comment that at each recursive step we construct the prism \(\tau \) only with respect to the conflict list of its parent cell \(\tau _0\) (initially, \(\tau _0 = {{\mathbb R}}^d\) and \(K(\tau _0) = H\)), implying that \(\tau \) is not necessarily contained in \(\tau _0\). In other words, the sequence of cells \(\tau \) constructed in our algorithm are spatially in no particular relation to one another (except that all of them contain \(\mathbf{x}\)). Still, this does not harm the correctness of the search process, as argued above.

The termination of the algorithm We next claim that the algorithm terminates (almost surely). Indeed, at each recursive step, the sample R is drawn from the corresponding subset \(K(\tau _0)\). Applying Theorem 3.1 to \(K(\tau _0)\), we obtain that the conflict list of the next prism \(\tau \) contains (with certainty, due to the test applied at step (iii), under the assumption that this resampling process terminates) only at most \({\varepsilon }|K(\tau _0)| = \tfrac{1}{2} |K(\tau _0)|\) hyperplanes of \(K(\tau _0)\). Another source of potential non-termination is the handling of events where \(\mathbf{x}\) lies on the vertical boundary of a prism, in which case we re-tilt the frame, and risk non-convergence of this process, which however happens only with probability 0. Hence, with probability 1, after a logarithmic number of steps (see below for the concrete analysis) we will reach step (iv), and then the algorithm will correctly determine whether \(\mathbf{x}\) lies on a hyperplane of H (by the invariant that we maintain, any such hyperplane belongs to the final conflict list \(K(\tau )\)).

The termination is guaranteed only almost surely, because of the possibility of the event (that has probability 0) of repeatedly failing to choose a good sample at some recursive application of step (i), or of repeatedly finding \(\mathbf{x}\) to lie on a vertical wall of a prism.

4.3 The Query Complexity

We now analyze the query complexity, beginning with the analysis of step (ii). Consider, for simplicity, the top recursive step, in dimension d. We test each hyperplane h of R with \(\mathbf{x}\) in order to determine whether h lies above, below, or on \(\mathbf{x}\). This information also defines the cell \(C_\mathbf{x}\) in \(\mathcal {A}(R)\) containing \(\mathbf{x}\). Overall, we perform at most r linear queries at this step. Finding the ceiling and floor hyperplanes \(h_1\) and \(h_2\) that lie directly above and below \(\mathbf{x}\) takes at most r additional linear queries.

In general, we recall that at each recursive step i, we are given a corresponding set \(R^{(i-1)}\) of fewer than r hyperplanes (which is a consequence of Lemma 2.1). We test each of them with the corresponding projection \(\mathbf{x}^{(i-1)}\) of \(\mathbf{x}\), in order to determine, for each hyperplane in \(R^{(i-1)}\), whether it lies above, below (in the \(x_{d-i+1}\)-direction), or on \(\mathbf{x}^{(i-1)}\). Overall, we perform at most r linear queries at this step, and identify the new pair of floor and ceiling with r additional comparisons. We stop when we reach \(i=d\), where we obtain the interval between two consecutive points of \(R^{(d-1)}\) that contains \(\mathbf{x}^{(d-1)}\) and return it. We emphasize that backtracking through the recursion does not involve any additional cost in our model of computation.

Overall, this amounts to \(O(r) = O\bigl (\frac{d}{{\varepsilon }} \log {\frac{1}{{\varepsilon }}}\bigr ) = O(d)\) linear queries at each recursive step, for a total of \(O(d^2)\) linear queries over all d steps of the recursion (on the dimension).

As already argued, step (iii) of the algorithm does not depend on the query point \(\mathbf{x}\). Step (iv) is implemented in brute force, performing at most \(r=O(d)\) additional linear tests on \(\mathbf{x}\). The recursion is powered by Theorem 3.1, which guarantees that at each step we eliminate at least half of the hyperplanes in H, so the algorithm terminates (almost surely) within \(O(\log {|H|}) = O(\log n)\) steps. Therefore the overall number of linear queries is \(O(d^2\log n)\). This completes the proof of the restricted point location (Theorem 1.1).

Applications The technique just described can be applied to the k-SUM, k-LDT, SubsetSum and Knapsack problems, using the reduction explained in the introduction. It yields the bounds \(O(k n^2\log {n})\) for k-SUM and k-LDT, and \(O(n^3)\) for SubsetSum and Knapsack. This established Theorem 1.2. We recall that for k-LDT, the very recent work in [22] does improve these solutions, as noted earlier, although the bound of [22] for k-LDT is \(O(k^2 n\log ^2{n})\), so our bound for this problem is asymptotically smaller whenever \(k > n/\log {n}\).

4.4 A Polynomial Time Algorithm for Point Location in the RAM Model

We next discuss a polynomial-time implementation of our algorithm in the real RAM model. Steps (i), (ii), and (iv) are easy to implement in polynomial time, so that the number of (linear) tests that access the actual coordinates of the query point does not change, and so that all other operations do not access (explicitly) this data. We leave the straightforward details to the reader.

Regarding the implementation of step (iii) of the construction of the conflict list of a prism \(\tau \), we need to test for each hyperplane \(h \in H\) (not in the sample R) whether it intersects the interior of \(\tau \). We use the following simple approach. Recall that \(H_{\mathbf{x}}\) is the set of the (at most) 2d hyperplanes bounding \(\tau \). With a slight abuse of notation, let us now denote this set by \(H_{\tau }\).

We first need to rule out the possibility that in degenerate situations (where there are multiple defining sets for the same geometric representation of \(\tau \)) h does not touch \(\tau \) in a face of dimension \(d-2\) or lower. That is, in such a scenario h appears in one of the (geometric) defining sets of \(\tau \), and therefore it does not properly intersect \(\tau \) and should not be part of \(K(\tau )\). We thus slightly modify our algorithm to construct \(\tau \) so that it produces on the side the union \(\mathcal {D}\) of all (geometric) defining sets \(D_1, \ldots , D_t\) of \(\tau \), for some integer \(t \ge 1\). We proceed as follows. Recall that in the construction of \(\tau \), at any recursive step i we find the pair of hyperplanes \(h_1^{(i-1)},h_2^{(i-1)}\) that are vertically closest to the query point. In degenerate scenarios, where these hyperplanes may not be unique, instead of choosing such an arbitrary pair (as does the algorithm applied in the linear decision tree model), we report all such hyperplanes, which enables us to obtain all the corresponding original hyperplanes touching \(\tau \) in the sense described above. This forms the generalized defining set \(\mathcal {D}\). We note that since we initially have \(H_{\tau }\) at hand, this application of the modified algorithm does not involve \(\mathbf{x}\). Thus at the termination of this procedure, we obtain the generalized defining set \(\mathcal {D}\), and then we need to test whether h is in \(\mathcal {D}\). If it does, we exclude h from \(K(\tau )\).

If h is not in \(\mathcal {D}\), then either h properly crosses \(\tau \) or h is disjoint from \(\tau \). We next observe that h crosses \(\tau \) if and only if the prism \(\tau '\) in the vertical decomposition of \(\mathcal {A}(\mathcal {D}\cup \{h\})\) that contains \(\mathbf{x}\) is properly contained in the original prism \(\tau \). Moreover, this implies that \(\tau \) and \(\tau '\) have different defining sets, and, in particular, h is part of the defining set of \(\tau '\). We thus apply the modified version of our algorithm as outlined above, in order to construct the generalized defining set \(\mathcal {D}'\) of \(\tau '\). Once the construction is completed we test whether h belongs to \(\mathcal {D}'\), if so, it is added to the conflict list of \(\tau \). Repeating this for all \(h \in H\setminus R\), we obtain \(K(\tau )\).

The execution of our algorithm to construct \(\mathcal {D}\) and \(\mathcal {D}'\) takes time, which is linear in n and polynomial in d (note that each sign test costs O(d) in the RAM model), since in degenerate scenarios, the cardinality of \(\mathcal {D}\) (and \(\mathcal {D}'\)) might be as large as \(\Theta (|H|)\). This also serves as an asymptotic time bound for checking whether h is in \(\mathcal {D}\), and later, in \(\mathcal {D}'\). We once again emphasize that none of the operations performed in this step involve the query point \(\mathbf{x}\). We thus conclude that constructing the entire conflict list of \(\tau \), when processing all hyperplanes \(h \in H\), can be performed in overall \(O(n^2)\) time, where the constant of proportionality depends polynomially in d.

We thus obtain the following results.

Theorem 4.1

(Restricted point location in the RAM model) The point location problem for n hyperplanes in \({\mathbb R}^d\) can be solved in polynomial time in the RAM model, using only \(O(d^2\log n)\) linear queries on the input, so that all other operations do not explicitly access the input. The algorithm terminates almost surely.

Corollary 4.2

The k-SUM and k-LDT problems, for any fixed k, can be solved in polynomial time in the RAM model, using only \(O(kn^2\log n)\) linear queries on the input, so that all other operations do not explicitly access the input. The algorithm terminates almost surely.