Improved Subquadratic 3SUM

Abstract

In the 3SUM problem we are given three lists $\mathcal {A}$, $\mathcal {B}$, $\mathcal {C}$, of n real numbers, and are asked to find $(a,b,c)\in \mathcal {A}\times \mathcal {B}\times \mathcal {C}$ such that $a+b=c$. The longstanding 3SUM conjecture—that 3SUM could not be solved in subquadratic time—was recently refuted by Grønlund and Pettie. They presented $\hbox {O}\left( n^2(\log \log n)^{\alpha }/(\log n)^{\beta }\right)$ algorithms for 3SUM and for the related problems Convolution3SUM and ZeroTriangle, where $\alpha$ and $\beta$ are constants that depend on the problem and whether the algorithm is deterministic or randomized (and for ZeroTriangle the main factor is $n^3$ rather than $n^2$). We simplify Grønlund and Pettie’s algorithms and obtain better bounds, namely, $\alpha =\beta =1$, deterministically. For 3SUM our bound is better than both the deterministic and the randomized bounds of Grønlund and Pettie. For the other problems our bounds are better than their deterministic bounds, and match their randomized bounds.

1 Introduction

The 3SUM problem is: given three lists of n real numbers $\mathcal {A}$, $\mathcal {B}$, $\mathcal {C}$, find $(a,b,c)\in \mathcal {A}\times \mathcal {B}\times \mathcal {C}$ such that $a+b=c$. [We assume real numbers can be read, written, added, subtracted, and compared in $\hbox {O}(1)$ time.] The problem is often presented in different flavors—e.g., $a+b+c$ should be 0 or some given target number; or that the input consists of a single list from which three numbers summing to 0 should be drawn. These flavors are equivalent to each other in the sense that they are reducible to one another in linear time.

While 3SUM is something of an “interview question” it has gained a degree of prominence in the theory of algorithms as a very simple problem that admits a quadratic time algorithm but for which no subquadratic algorithm was known until recently. This suited the problem for the role of a yardstick against which other problems could be measured. The term 3SUM hard has been coined to describe a problem that 3SUM could be efficiently reduced to, so that if the 3SUM hard problem could be solved in subquadratic time then so could 3SUM. The literature is replete with 3SUM hardness. Gajentaan and Overmars [7] compiled a long list of computational geometry problems that are 3SUM hard, and others (e.g., [3, 10]) have shown this for numerous problems in other areas. Grønlund and Pettie [8] provide many references, as well as a nice summary of the state of the art on 3SUM and related problems.

Over the years, upper and lower bounds have been shown for different computational models and variants of the problem [1, 2, 6], but for the problem as defined here (real numbers, RAM) no progress has been made until recently. The breakthrough came in a paper of Grønlund and Pettie [8], which presented an o$(n^2)$ algorithm, thereby refuting the 3SUM conjecture that 3SUM could not be solved in subquadratic time. The weaker conjecture—that 3SUM cannot be solved in $\hbox {O}(n^{2-\epsilon })$ time remains impregnable.

In addition to 3SUM, Grønlund and Pettie [8] also deal with some related problems. The following list summarizes their results, as they pertain to this paper.

• 3SUM: Grønlund and Pettie describe a deterministic algorithm with $\hbox {O}\left( n^2\left( \frac{\log \log n}{\log n}\right) ^{2/3}\right)$ running time and a randomized algorithm with $\hbox {O}\left( n^2\frac{\left( \log \log n\right) ^2}{\log n}\right)$ running time.

• Integer3SUM: The problem is the same as 3SUM but the numbers are integers in some range $\{-U,\ldots ,U\}$. Grønlund and Pettie provide no results specific to this problem beyond their results for 3SUM (which carry over immediately).

• Convolution3SUM: This problem was defined by Pǎtraşcu [10] as follows: given a vector $\mathcal {A}\in \mathbb {R}^n$, find i and j such that $a_i+a_j=a_{i+j}$. Grønlund and Pettie describe a deterministic $\hbox {O}\left( n^2(\log \log n)^2/\log n\right)$ algorithm and a randomized $\hbox {O}(n^2 \log \log n/ \log n)$ algorithm.

• ZeroTriangle: The problem is: given an edge weighted graph, find a triangle whose edge weights sum to 0. Grønlund and Pettie give a deterministic $\hbox {O}\left( n^3(\log \log n)^2/\log n\right)$ algorithm and a randomized $\hbox {O}(n^3 \log \log n/ \log n)$ algorithm, where n is the number of vertices. They also obtain $\hbox {O}\left( m^{1.5}(\log \log m)^{1/2}/(\log m)^{1/4}\right)$ and $\hbox {O}\left( m^{1.5}(\log \log m/\log m)^{1/4}\right)$ deterministic and randomized, respectively, upper bounds, where m is the number of edges.

Grønlund and Pettie also derive upper bounds on the decision tree complexity (i.e., number of comparisons) of these problems (as well as k-LDT, which is the weighted version of k-SUM). In this paper we do not address this issue.

1.1 Our Contribution

We develop a 3SUM algorithm that is somewhat simpler than Grønlund and Pettie’s. We use the same ideas and techniques, but in a more straightforward manner. We are able to eliminate one of Grønlund and Pettie’s conceptual building blocks, as well as some of their reliance on previous work (Lemmata 2.1–2.3 in Ref. [8]). While the simplification is modest, it also leads to a better running time. We achieve an aesthetically pleasing deterministic bound of $\hbox {O}\big (n^2\frac{\log \log n}{\log n}\big )$, which is superior to both $\hbox {O}\left( n^2\left( \frac{\log \log n}{\log n}\right) ^{2/3}\right)$ and $\hbox {O}\left( n^2\frac{\left( \log \log n\right) ^2}{\log n}\right)$—the deterministic and randomized bounds obtained by Grønlund and Pettie [8]. For the other problems we provide deterministic bounds that match the randomized bounds obtained by Grønlund and Pettie, thus obviating them.¹ For 3SUM and Convolution3SUM our bound is $\hbox {O}\big (n^2\frac{\log \log n}{\log n}\big )$, and for ZeroTriangle we get $\hbox {O}\big (n^3\frac{\log \log n}{\log n}\big )$ and $\hbox {O}\left( m^{1.5}\left( \frac{\log \log m}{\log m}\right) ^{1/4}\right)$.

Briefly, the core of our 3SUM solution can be summarized as follows. The main technical problem we solve is to partition the sumset $\mathcal {A}+\mathcal {B}$ into $g\times g$ subarrays (for a carefully chosen value of g), and sort each sub-array. When $|\mathcal {A}|=|\mathcal {B}|=n$ and $g=\text {O}(\log n)$, we show how to do this in $\hbox {O}\left( (n/g)^2 g\log g\right)$ time, which then lets us solve 3SUM in $\hbox {O}(n^2(\log g)/g)$ time using the Grønlund-Pettie approach. The differences between the Grønlund-Pettie sorting algorithm and ours are rather subtle. Grønlund and Pettie pick special locations in the $g\times g$ “box,” then select so-called contours passing through those locations, and sort the elements in the areas between pairs of contours. The problem with their approach is that the sizes of these areas are unknown a priori, but must be $\hbox {O}(\log n)$, which is easy to guarantee in expectation by picking special locations randomly. Our algorithm fixes $s={\varTheta }(g/\log g)$ and picks contours and special locations in a different order to guarantee that the area between two contours has size precisely s. The key observation is that if all the elements in a $g\times g$ box are distinct, an element’s contour encodes its rank, and it is therefore possible to discard all contours that are not for elements with ranks $s,2s,3s,\ldots$ inside the box. In this way our algorithm never considers more than $g^2/s$ contours per box.

1.2 Organization of this Paper

As mentioned above, our algorithms build on Grønlund and Pettie’s and are thus very similar to them. Consequently, much of the material herein is repetitious of Grønlund and Pettie [8]. We provide it for the sake of completion, to furnish context, to flesh out details that were glossed over by Grønlund and Pettie, and to give another perspective on their work. In each section we point out where our algorithm departs from Grønlund and Pettie’s.

In Sect. 2 we discuss the 2SUM problem on sorted input, together with its standard linear time algorithm and the standard quadratic 3SUM algorithm derived from it. This algorithm forms the basis for our improved subquadratic algorithm, described in Sect. 3. In Sect. 4 we discuss Convolution3SUM, and in Sect. 5 we present our algorithm for ZeroTriangle.

2 Linear Time 2SUM on Sorted Input; Quadratic 3SUM

The 2SUM problem on sorted input is: given two sorted lists of numbers $\mathcal {A}$ and $\mathcal {B}$, both of length n, and given a target number c, find $a\in \mathcal {A}$ and $b\in \mathcal {B}$ such that $a+b=c$. Following is the standard linear time solution.

The running time of the algorithm is clearly $\hbox {O}(n)$, and its correctness follows from the easily proven invariant that $a_i$ cannot be part of the solution for all $i< lo$, and $b_j$ cannot be part of the solution for all $j> hi$.

Algorithm 1 can be used to solve 3SUM in quadratic time: sort $\mathcal {A}$ and $\mathcal {B}$; then, for each $c\in \mathcal {C}$, run Algorithm 1 on the sorted $\mathcal {A}$ and $\mathcal {B}$ with target c.

3 Improved 3SUM

Building on the quadratic algorithm from the previous section, we achieve subquadratic time by partitioning the data into small blocks, from which are derived even smaller chunks. These are then preprocessed so that the algorithm proper can be speeded up. The chunks are sufficiently small that their preprocessing can be done more efficiently by enumerating all possible outcomes than by computing the outcomes for each chunk separately.

Similar to Algorithm 1, correctness (for each $c\in \mathcal {C}$) follows from the invariant that no member of any block $A_p$, $p< lo$ can participate in the solution, and neither can any member of any block $B_q$, $q> hi$.

For each iteration of the outer loop, the inner loop iterates $<$ $2n/g$ times, so the time complexity of Algorithm 2, excluding the work done in Lines 3 and 8, is $\hbox {O}(n^2/g)$. [The time spent sorting the arrays is negligible, as g will be chosen to be $\hbox {O}(\log n)$, so $\hbox {O}(n\log n)=\text {o}(n^2/g)$.]

3.1 Searching Within a Pair of Blocks (Line 8)

Roughly speaking, the preprocessing step (Line 3) will have sorted $\{a+b\,|\,a\in A_{ lo }, b\in B_{ hi }\}$ into an array of size $g^2$. Line 8 performs a binary search for c in this array. Thus the total running time of the algorithm, excluding the preprocessing work, is $\hbox {O}(n^2\log g / g)$. We say “roughly speaking” because the preprocessing step does not actually create a sorted array for each block pair. Rather, it creates a more complex data structure that is functionally equivalent in that it supports random access in constant time. We now describe this data structure.

In what follows we shall denote by A an arbitrary block from the partition of $\mathcal {A}$ (i.e., $A=A_p$ for some unspecified p), and will denote by $a_i$ the ith member of A. (Recall that $\mathcal {A}$ has been sorted in Line 1 so A is ordered.) We will similarly denote B and $b_j$ with respect to $\mathcal {B}$.

Fix A and B. Define $ranking _{A,B}$ as the sequence of index pairs (i, j), where i and j are in $\{1,\ldots ,g\}$, sorted in increasing order of $a_i+b_j$ [so (i, j) comes before $(i',j')$ iff $a_i+b_j < a_{i'}+b_{j'}$]. See Fig. 1 for an example. We assume that all values $a_i+b_j$ are distinct. Section 3.4 lifts this restriction.

Fig. 1

An example of the rankings of two block pairs $(A_3,B_9)$ and $(A_8,B_5)$ (For simplicity—to keep the numbers small—we ignore the fact that the numbers in $A_8$ and $B_9$ must be greater than those in (respectively) $A_3$ and $B_5$ (since the blocks come from the sorted lists $\mathcal {A}$ and $\mathcal {B}$). The example can be made real by simply adding a sufficiently large constant to each of the numbers in $A_8$ and $B_9$.). In this example the block size is $g=6$. The grids depict some of the sums $a_i+b_j$: the horizontal axes are annotated with the $a_i$s, increasing left to right; the vertical axes are annotated with the $b_j$s, increasing bottom up; the grid entries are the corresponding sums. The first (lowest) twelve sums are shown for each block pair. Note that elements 5–8 of $ranking _{A_3,B_9}$ are identical to elements 9–12 of $ranking _{A_8,B_5}$, and similarly, elements 9–12 of $ranking _{A_3,B_9}$ are identical to elements 5–8 of $ranking _{A_8,B_5}$. This will come into play in Fig. 2

The preprocessing step partitions $ranking _{A,B}$ into $g^2/s$ chunks of size s (to be determined later) and stores each chunk in an array. However, it does not do so by actually computing $ranking _{A,B}$ and then breaking it into chunks—that would consume too much time. Instead, it manages to compute all of the chunks without explicitly constructing the ranking. In addition, it constructs a forwarding array $F_{A,B}$ of $g^2/s$ pointers to the chunks, in order. The preprocessing step computes the chunks and the forwarding array for each pair of blocks (A, B), and stores pointers to the forwarding arrays in a two-dimensional lookup table L indexed by the corresponding block indices. See Fig. 2.

Fig. 2

The data structure used to perform lookups in service of the binary searches. In this contrived example $n=60$, $g=6$, and $s=4$. The entry L[p, q] corresponding to block pair $(A_p,B_q)$ is the entry at column p (from the left), row q (from the bottom). The blocks $A_3,B_9,A_8,B_5$ are the same as in Fig. 1. The second chunk of $ranking _{A_3,B_9}$ is identical to the third chunk of $ranking _{A_8,B_5}$. Both are therefore realized by the same chunk array $CA _{T'}$. Similarly, the third chunk of $ranking _{A_3,B_9}$ and the second chunk of $ranking _{A_8,B_5}$ are both realized by the same chunk array $CA _{T''}$

Thus, to find the kth element in $ranking _{A_{ lo },B_{ hi }}$ the algorithm dereferences the pointer at $L[ lo , hi ]$ to find the forwarding array $F_{A_{ lo },B_{ hi }}$. It then dereferences the pointer at $F_{A_{ lo },B_{ hi }}[{\lceil }k/s{\rceil }]$ to find the corresponding chunk array $CA _T$ (where T denotes the information defining the chunk). Finally, it reads $CA _T\left[ ((k-1){\hbox {mod}}s) + 1\right]$.² This entry is an index pair (i, j), which the algorithm can then use to compute $a_i+b_j$ by looking up the ith and jth entries in the blocks $A_{ lo }$ and $B_{ hi }$, respectively. Thus each binary-search comparison takes constant time, as desired. In the sequel, when referring to a particular chunk array under consideration we will often denote it simply $CA$ (unindexed).

The whole point of the above triple indirection is this: while each $ranking _{A,B}$ has its own forwarding array, the chunk arrays are typically shared among multiple rankings. In other words, if two chunks belonging to two different rankings consist of the same sequence of index pairs, then both of these chunks will be realized by the same chunk array, which will be computed only once, and will be pointed to from both corresponding forwarding arrays. Figure 2 depicts this for the example described in Fig. 1. This sharing of chunk arrays is key to achieving subquadratic time for the preprocessing step.

For easy reference while reading the remainder of this section we now recap the notation just introduced.

Summary of new notation introduced so far.

• $A_p$ and $B_q$ are the pth and qth blocks in the partitions of $\mathcal {A}$ and $\mathcal {B}$, respectively.

• Unindexed A and B denote arbitrarily chosen blocks from the respective partitions.

• g is the block size.

• $a_i$ is the ith member of A; $b_j$ is the jth member of B.

• $ranking _{A,B}$ is the sequence of index pairs (i, j) ordered by $a_i + b_j$. We assume all values $a_i+b_j$ are distinct.

• $F_{A,B}$ is the forwarding array for a given A and B.

• s is the chunk size.

• L denotes the lookup table: L[p, q] points to $F_{A_p,B_q}$.

• $CA$ denotes a chunk array under consideration.

3.2 Preprocessing (Line 3)

The first step is to allocate memory for L and the forwarding arrays, and to point L’s entries to the forwarding arrays. Since there are $(n/g)^2$ block pairs, and each forwarding array is of size $g^2/s$, the total space and time complexity of this step is $\hbox {O}(n^2/s)$. This bound also covers the cost of pointing the forwarding array entries to the chunk arrays (but does not cover the cost of computing the contents of the chunk arrays).

The next step is to compute the chunks. Our (initial) approach is exhaustive enumeration. The parameters associated with a particular chunk are: the blocks A and B; the position $1\le e\le g^2/s$ of the chunk within $F_{A,B}$; the set S of index pairs that appear in the chunk; and the permutation $\pi$ defining the order of these index pairs within the chunk. Thus we have the following algorithm:

For all A and B, for all $1\le e\le g^2/s$, for every $S\subset \{1,\ldots ,g\}^2$ of size s, for every $\pi$, check (somehow) whether S ordered by $\pi$ agrees with the eth chunk of $ranking _{A,B}$. If it does, create an array $CA$, store S’s members there in order, and make $F_{A,B}[e]$ point to $CA$.

Of course this algorithm is prohibitively expensive, and does not share chunk arrays. To take advantage of chunk array sharing we reverse the nesting order of the loops:

This algorithm is still quite wasteful, as nearly all choices of $(S, \pi , e)$ can never agree with any $ranking _{A,B}$, regardless of the contents of A and B. Luckily, it is possible to avoid this excessive enumeration. Additionally, it is possible to parallelize (in a sense) the determination of which pairs (A, B) agree with a given $(S, \pi , e)$. The combination of these two optimizations allows us to achieve subquadratic preprocessing time.

3.2.1 Avoiding Excessive Enumeration

Fix A and B. Imagine $g^2$ squares formed by a $g\times g$ grid. Associate with each square (i, j) the number $a_i+b_j$, which we we shall refer to as the square’s value. To visualize the square arrangement we use a chessboard-like naming scheme: square (i, j) is the square in the ith column from the left and the jth row from the bottom.³ See Fig. 3 for an example. We identify the index pair naming a square with the square being named; we shall use the terms square and index pair interchangeably.

Fig. 3

Squares arranged in a $g\times g$ grid (for $g=5$). The solid black square is square (5, 3) and its value is $a_5+b_3$. The gray squares trace an rd-path that falls off the bottom edge. This path might be a contour, in which case its anchor must be one of the squares (1, 4), (2, 4), or (3, 2), since these are the only squares from which the path moves right

Suppose we are given a square (k, l), and wish to partition the squares into those with values greater than its value $a_k+b_l$, and those with values less than or equal to it. The motivation for this will become clear shortly. We trace the path taken by the following algorithm (which is essentially the linear-time 2SUM algorithm on sorted input, except that it does not stop when it finds a solution).

Start at the top left square and keep moving in accordance with the following rule: if the value of the current square is greater than the value of (k, l), move one square down; otherwise move one square right. Keep moving in this manner until you fall off the right edge or the bottom edge of the grid.

Clearly the algorithm makes at most $2g-1$ moves. We define the path taken by the algorithm as the sequence of right/down steps it takes rather than the sequence of squares it visits—the difference being that if the algorithm reaches the bottom right corner, the sequence of squares does not reveal whether it fell off the right edge or the bottom edge. The directions in which the algorithm moves are just as important as the squares it visits.

Definition 1

An rd-path is a sequence of at most $2g-1$ instructions over instruction set $\{\text {right, down}\}$ such that if x is the last instruction in the sequence, then x appears in the sequence precisely g times. An rd-path induces a sequence of squares in the obvious manner (by starting at the top left square and following the instructions). We say that the path visits these squares in the order defined by the sequence. We say that the path moves right (resp. down) from square (i, j) if there is some r such that square (i, j) is the rth square visited by the path, and the rth instruction is right (resp. down).

The sequence of moves made by the above algorithm defines an rd-path. Following Grønlund and Pettie [8] we define the notion of contour.

Definition 2

The contour associated with square (k, l), denoted $contour _{k,l}^{\scriptscriptstyle A,B}$, is the rd-path defined by the above algorithm’s movements on input (k, l). We say that square (k, l) anchors $contour _{k,l}^{\scriptscriptstyle A,B}$.

Note that by our assumption that all square values are distinct, and by the fact that A and B are sorted, every contour necessarily visits its anchor. See Fig. 3 for an example of an rd-path that might be a contour.

Definition 3

Square (i, j) is said to be below $contour _{k,l}^{\scriptscriptstyle A,B}$ if there exists $j'\ge j$ such that $contour _{k,l}^{\scriptscriptstyle A,B}$ moves right from $(i,j')$; otherwise the square is said to be above $contour _{k,l}^{\scriptscriptstyle A,B}$.

We remark that the term above was chosen as the opposite of below, but the true defining property of squares above the contour is that they are in fact to the right of the contour. Also note that every square, including squares visited by the contour, is defined to be either above or below the contour.

The significance of Definition 3 is brought to light by the following easy observation (which follows from the fact that A and B are sorted). It shows that the algorithm partitions the squares as desired.

Observation 1

If (i, j) is a square below $contour _{k,l}^{\scriptscriptstyle A,B}$ then its value is less than or equal to the value of square (k, l). If it is above $contour _{k,l}^{\scriptscriptstyle A,B}$ then its value is greater than the value of square (k, l).

Note that by our assumption that all square values are distinct, equality occurs only at the anchor (k, l).

Why do we care about partitioning the squares around the value of some square (k, l)? Because it allows us to figure out the position of index pair (k, l) in $ranking _{A,B}$. That position is r, where r is the number of squares below $contour _{k,l}^{\scriptscriptstyle A,B}$. Given the contour, computing r in $\hbox {O}(g)$ time is easy: just sum the indices j of the squares (i, j) from which the contour moves right. Observe that for all $1\le r\le g^2$ there exists a unique square x such that there are precisely r squares below the contour anchored by x (x is simply the rth element in $ranking _{A,B}$).

We are now in position to curtail the enumeration in Algorithm 3. For a given combination of A, B, e, and S, a necessary and sufficient condition for S to be the set of index pairs in chunk e of $ranking _{A,B}$ is the following:

Let (k, l) and $(k',l')$ be such that there are precisely $(e-1)s$ and es squares below $contour _{k,l}^{\scriptscriptstyle A,B}$ and $contour _{k',l'}^{\scriptscriptstyle A,B}$, respectively (i.e., these index pairs are the last elements in chunks $e-1$ and e, respectively). Then S consists precisely of those squares that are above $contour _{k,l}^{\scriptscriptstyle A,B}$ and below $contour _{k',l'}^{\scriptscriptstyle A,B}$. (The case $e=1$ is special, since then (k, l) does not exist. In that case the condition is that S consists precisely of those squares that are below $contour _{k',l'}^{\scriptscriptstyle A,B}$.)

The contours mentioned in this condition depend of course on the choice of A and B. However, given the contours, the condition is purely structural—it does not depend in any way on A and B. Because we do not have an A and B in the outer loop of Algorithm 3, we enumerate all possible pairs of contours. Algorithm 4 below refines Algorithm 3 by implementing this idea, but we need one last definition before presenting it.

Definition 4

An rd-path $P'$ is said to dominate another rd-path P if every square above $P'$ is also above P.

It is an easy matter to determine in $\hbox {O}(g)$ time whether $P'$ dominates P, and in another $\hbox {O}(g+s)$ time to find S. In fact, it is not difficult to tighten the enumeration so that for each e only the rd-paths with es squares below them are enumerated, and for each such $P'$, only the rd-paths which are dominated by $P'$ and which have $(e-1)s$ squares below them are enumerated.

It is also possible to conserve space in cases such as those depicted in Fig. 2, where, for example, the second chunk of $ranking _{A_3,B_9}$ is identical to the third chunk of $ranking _{A_8,B_5}$. The figure shows both chunks being stored in the same chunk array, but Algorithm 4 actually places each in a different chunk array (because the corresponding rd-path pairs are different). To ensure complete sharing we can rearrange the enumeration so that primarily the valid sets S are generated, and secondarily, for each such set, all pairs of rd-paths consistent with it are enumerated. The details of doing this efficiently (e.g., generating only valid sets) are somewhat tedious but straightforward.

3.2.2 Finding All Pairs of Blocks that Agree with a Given Chunk

For a particular choice of A and B, we need to test three conditions:

• 1. That P is $contour _{k,l}^{\scriptscriptstyle A,B}$.

• 2. That $P'$ is $contour _{k',l'}^{\scriptscriptstyle A,B}$.

• 3. That S ordered by $\pi$ is an increasing sequence in terms of the square values.

Let |P| denote the length of P. The first condition can be broken down into $|P|-1$ constituent conditions, one per square visited by P except for the anchor (k, l), as follows. If P moves right from square (i, j) then the corresponding condition is $a_i+b_j < a_k+b_l$, and if it moves down, the condition is $a_k+b_l < a_i+b_j$. These two conditions can be written equivalently as $b_j-b_l < a_k-a_i$ and $b_l-b_j < a_i-a_k$. Grønlund and Pettie [8] call this Fredman’s trick, the significance of which will become apparent shortly. Let us combine these $|P|-1$ inequalities into a single vector inequality $u^B < u^A$, where $u^A$ and $u^B$ are $|P|-1$ dimensional vectors such that in $u^B$ the rth component is the left hand side of the rth inequality above, and in $u^A$ it is the right hand side.⁴ Here, “$<$” represents pointwise less-than. A similar construction with respect to $P'$ transforms the second condition into a single vector inequality as well.

The third condition is treated in the same spirit. We break it down to $s-1$ inequalities, which we then combine into a single vector inequality. Let $(i_r,j_r)$ be the rth index pair in S ordered by $\pi$. For all $1\le r<s$, the corresponding condition is $a_{i_r}+b_{j_r}<a_{i_{r+1}}+b_{j_{r+1}}$, or equivalently, $b_{j_r}-b_{j_{r+1}}<a_{i_{r+1}}-a_{i_r}$.

Finally, we write all three conditions as a single vector inequality $v^B < v^A$, where each of $v^A$ and $v^B$ is the concatenation of the corresponding three vectors. The two vectors in the inequality are of dimension $|P|+|P'|+s-3<4g+s$.

We have thus shown how to translate the three conditions into a single vector inequality for a given pair (A, B). Our goal can be restated as that of finding all pairs (A, B) such that $v^B < v^A$. Naively, we could enumerate all $n^2$ pairs (A, B), generate the corresponding inequality for each, and test it. This of course would gain us nothing. Instead, we note that by virtue of Fredman’s trick, each $v^A$ depends only on A, and each $v^B$ depends only on B, so there are only 2n / g vectors to construct overall. Once they are constructed, our task becomes to find all pairs $(v^A,v^B)$ among them that satisfy $v^B < v^A$. This is known as the Dominance Merge problem [11, pp. 365–373], or the Bichromatic Dominance Reporting problem [8]:

Given N vectors in $\mathbb {R}^d$, each of which is either red or blue, find all pairs of vectors (u, v) such that u is blue an v is red, and $u < v$.

To find the dominance pairs $(v^B,v^A)$ satisfying $v^B < v^A$ we feed all of the $v^A$s (red) and all of the $v^B$s (blue) to the following recursive algorithm described by Preparata and Shamos [11]. The algorithm allows the vectors to have dimension greater than d but only cares about dominance in the first d dimensions, which we denote by “$<_d$”.

The correctness of this algorithm is straightforward. (Placing the red vectors before the blue ones in the equal-to-x region ensures that the dominance pairs emitted by the third recursive call—which detects dominance in the first $d-1$ dimensions—possess the desired dominance relation in the dth dimension as well.)

Emitting the dominance pairs takes O(|D|) time, where D is the set of dominance pairs emitted by the algorithm. (Of course, the output of the algorithm is made by means of pointers to vectors, not copies). The “standard” bound given by Preparata and Shamos [11] is $\hbox {O}(|D| + N\log ^dN)$, but for a certain range of d there is a tighter bound (on the same algorithm) obtained by Chan [4]:⁵ $\hbox {O}\left( |D|+c_{\epsilon }^d N^{1+\epsilon }\right)$ for any $\epsilon >0$, where $c_{\epsilon }=2^{\epsilon }/(2^{\epsilon }-1)$. We will use Chan’s bound with $\epsilon =1/2$, which implies $c_{\epsilon }<4=2^2$, so the bound will be $\hbox {O}\left( |D| + 2^{2d}N^{1.5}\right)$. In our application the number of input vectors is $N=2n/g\le n$, and the dimension is $d<4g+s$, so the bound for a single invocation of Algorithm 5 is $\hbox {O}\left( |D| + 2^{8g+2s}n^{1.5}\right)$.

The enumeration size is bounded by: [$2^{4g}$ pairs $(P,P')] \times [g^2$ choices of corresponding anchors] $\times$ [$s!\le 2^{s\log s}$ permutations] = $\hbox {O}\left( g^2 2^{4g+s\log s}\right)$, so the total running time of the preprocessing step is $\hbox {O}\left( \tilde{D} + g^2 2^{12g+2s+s\log s}n^{1.5}\right)$ where $\tilde{D}$ is the total number of dominance pairs emitted across all invocations of the dominance algorithm. These pairs are in 1:1 correspondence with the forwarding array entries, so the contribution of this term is already covered by our bound for setting up the forwarding arrays. Thus the total time charged to the chunk computation phase is $\hbox {O}\left( g^2 2^{12g+2s+s\log s}n^{1.5}\right)$. The additional work of computing $\left( P, P', (k,l), (k',l'), \pi \right)$ and setting up the input vectors is negligible relative to the cost of invoking the dominance algorithm.

3.3 The Overall Running Time

We have covered the different parts of the algorithm by three bounds: $\hbox {O}(n^2\log g/ g)$ for the binary searches; $\hbox {O}(n^2/s)$ for setting up the lookup table and the forwarding arrays; and $\hbox {O}\left( g^2 2^{12g+2s+s\log s}n^{1.5}\right)$ for computing the chunk arrays. The first two bounds decrease when g and s increase, while the third increases. From the first two bounds we see that there is no advantage to making the relation between g and s anything other that $s={\varTheta }(g/\log g)$. From the third bound we see that pushing g or $s\log s$ asymptotically above $\hbox {O}(\log n)$ will inflate the bound to an unacceptable $n^{\omega (1)}$, whereas choosing both to be ${\varTheta }(\log n)$ will yield a polynomial expression whose degree is controllable by the choice of the constant within the ${\varTheta }$ notation. Serendipitously, this will also allow us to take full advantage of the first two bounds by making $s={\varTheta }(g/\log g)$. To nail the constants let us choose $s=g/\log g$, yielding $s\le s\log s \le g$, so the third bound becomes $\hbox {O}\left( g^2 2^{15g}n^{1.5}\right)$. We further put $g=\frac{1}{31}\log n$, which turns the first two bounds into $\hbox {O}\left( n^2\frac{\log \log n}{\log n}\right)$, and the third into a negligible $\hbox {O}\left( n^{2-\frac{1}{62}}\log ^2n\right)$.

Theorem 1

The total running time of the Algorithm 2 with the binary searches and preprocessing implemented as described above is $\hbox {O}\left( n^2\frac{\log \log n}{\log n}\right)$.

3.4 Lifting the Value Distinctness Restriction

As Grønlund and Pettie show, it is easy to achieve distinctness by replacing the numbers with triplets involving both the numbers and the indices, with a suitable definition of order between triplets. This however does not explain how doing so actually ensures that the algorithm remains correct, since the algorithm is defined in terms of numbers, not triplets. We believe it is worthwhile to spend some time understanding this, as it is not some trifling technicality, but rather more fundamental.

A close examination of the algorithm reveals that the assumption that all square values are distinct was actually made just to simplify the language describing the preprocessing. Reviewing the development of the preprocessing algorithm, we see that its correctness rests on the following three properties of $ranking _{A,B}$.

• 1. The ordering respects the value order of the index pairs. In other words, if $a_i+b_j<a_{i'}+b_{j'}$ then (i, j) appears earlier in $ranking _{A,B}$ than $(i',j')$. This is the fundamental property that allows binary search to work.

• 2. The ordering is monotone in the horizontal and vertical grid directions, i.e., if $i<i'$ then (i, j) appears earlier in $ranking _{A,B}$ than $(i',j)$, and if $j<j'$ then (i, j) appears earlier than $(i,j')$. This enables the partitioning by contours.

• 3. Given distinct (i, j) and $(i',j')$, there is an easy method of comparison to determine which appears earlier in $ranking _{A,B}$, and this comparison can be “decomposed” into an A part and a B part à-la Fredman’s trick. This enables the efficient use of the dominance algorithm.

Ordering by value while making the assumption that all values are distinct served us well in securing these properties, and at the same time simplified the language. Any arguments we made (explicitly or implicitly) concerning values of squares were actually arguments in disguise about the squares’ positions in $ranking _{A,B}$.

Since the assumption does not hold true in general we need to define the ordering more carefully in order to ensure that the above requirements are met. For example, we can define that (i, j) appears earlier than $(i',j')$ iff either $a_i+b_j<a_{i'}+b_{j'}$, or $a_i+b_j=a_{i'}+b_{j'}$ and $i<i'$, or $a_i+b_j=a_{i'}+b_{j'}$ and $i=i'$ and $j<j'$. This ordering has the desired properties. The only part of the algorithm that actually compares square positions is the dominance algorithm, which does these comparisons implicitly in the form $a_i-a_{i'}>b_{j'}-b_j$. We need to pass to it the index information so that it can break ties properly in cases of value equality. (The dominance algorithm also performs comparisons between components belonging to two identically colored vectors. Ties in such comparisons can be broken arbitrarily, as it will have no effect on the outcome of the dominance algorithm.)

A more abstract way to achieve the same goal is to identify the $a_i$s and $b_j$s with elements drawn from a totally ordered universe equipped with suitably defined addition and subtraction, such that different squares always have different values, and to redefine the algorithm in terms of these elements. For example, Grønlund and Pettie map each $a_i$ onto $(a_i,i,0)$ and each $b_j$ onto $(b_j,0,j)$, with the usual vector pointwise addition and subtraction, and with lexicographic order. Thus $a_i+b_j$ maps to $(a_i+b_j, i, j)$, so different squares have different values. It is easy to see that the above three properties attach. Other mappings are also possible.

3.5 Comparison with Grønlund and Pettie

The algorithm we described is identical to Grønlund and Pettie’s, down to the level of chunks (which they call boxes). The difference is in the definition of the eth chunk (for a given choice of A and B). Whereas we define it simply as elements $e(s-1)+1$ through es in $ranking _{A,B}$, they use a more oblique definition. They need to select a set P of squares that has certain properties, and they then partition $ranking _{A,B}$ around the squares in P to obtain the chunks. Because of the freedom inherent in the definition of P they either select it by random sampling, and then prove that it has the desired properties with high probability, or define it deterministically in terms of fixed square positions in the grid, and show that the conditions on P are always met. In both cases the chunk sizes are not fixed. In contrast, our construction essentially defines P in terms of $ranking _{A,B}$ in a simple and uniform manner, yielding equal sized chunks by definition. Grønlund and Pettie’s roundabout use of P forces them to use a smaller value of g, resulting in $\hbox {O}\left( n^2(\log \log n/\log n)^{2/3}\right)$ deterministic and $\hbox {O}\left( n^2(\log \log n)^2/\log n\right)$ randomized bounds.

4 Improved Convolution3SUM

As Grønlund and Pettie [8] mention in passing, Convolution3SUM can be easily reduced to 3SUM. For the sake of completeness, here is one way to do it: replace each $a_i$ with the pair $(a_i,i)$ and use pointwise addition and lexicographic ordering. (Here we use the single-list variant of 3SUM.) In light of this linear time reduction it is immediately seen that Convolution3SUM can be solved deterministically in $\hbox {O}\left( n^2\frac{\log \log n}{\log n}\right)$ time.

In order to improve the bound for Convolution3SUM beyond that of 3SUM, Grønlund and Pettie proceed to sketch a specialized algorithm that achieves $\hbox {O}\left( n^2(\log \log n)^2/\log n\right)$ deterministic time and $\hbox {O}\left( n^2\log \log n/\log n\right)$ randomized time. The algorithm uses binary searches within sorted arrays containing elements from the diagonals of suitably defined blocks. The sorting is done in a preprocessing stage by enumerating permutations, much as in 3SUM. We remark that by further breaking each diagonal array into smaller, shared, chunks, and enumerating those instead, it is possible to bring the deterministic algorithm down to $\hbox {O}\left( n^2\frac{\log \log n}{\log n}\right)$ time. We omit the details for brevity. The main idea is the same as the one we use on ZeroTriangle in the next section.

5 Improved ZeroTriangle

Let the vertices be named $1,2,\ldots ,n$, and let W be the graph’s weighted incidence matrix, that is, $w_{i,j}$ is the weight of the edge (i, j), or $\infty$ if there is no edge there. In terms of W,  a simple search strategy for a zero triangle is: find a row i and column j such that $w_{i,j}\ne \infty$ and there is a position k such that $w_{i,k}+w_{k,j}=-w_{i,j}$. To avoid infinities let us replace $\infty$ with a constant I that is greater than twice the maximum absolute value of any actual edge weight.

We find it convenient to generalize the problem and allow the rows to come from one matrix, the columns from another, and the target values from a third. The problem becomes:

Given matrices $\mathcal {A}_{n\times n}$, $\mathcal {B}_{n\times n}$, $\mathcal {C}_{n\times n}$, find (i, j, k) such that $c_{i,j}$ is valid (i.e., $\ne -I$), and $a_{i,k}+b_{k,j}=c_{i,j}$. (We use the standard matrix notation, where $\text {[lowercase letter ]}_{i,j}$ denotes the corresponding matrix’s element at row i, column j.)

In the generalized problem we can actually impose any validity condition on $c_{i,j}$ (or no condition) as long as checking it can be done sufficiently fast, so as not to impair our bound on the algorithm’s running time.

To expedite the searches we partition the input into blocks. Let g be the block size (to be determined later). Denote by $A_{i,t}$ the tth horizontal block of row i of $\mathcal {A}$, defined as the sequence of g entries $a_{i,(t-1)g+1}, a_{i,(t-1)g+2}, \ldots , a_{i,tg}$. Similarly, denote by $B_{j,t}$ the tth vertical block of column j of $\mathcal {B}$, defined as the sequence of g entries $b_{(t-1)g+1,j}, b_{(t-1)g+2,j}, \ldots , b_{tg,j}$. Given a pair $(A_{i,t},B_{j,t})$, define the sumset $A_{i,t}+B_{j,t}$ as the sequence of the g sums of corresponding block elements: $A_{i,t}+B_{j,t}\triangleq \left\{ a_{i,(t-1)g+k}+b_{(t-1)g+k,j}\right\} _{k=1}^g$.

We can now formulate the algorithm in the language of blocks.

Note that of the $n^4/g^2$ pairs of (horizontal block, vertical block), the algorithm only ever considers $n^3/g$ pairs, namely, those pairs where both blocks have the same second index t. The algorithm’s running time, excluding Line 1, is clearly $\hbox {O}(n^3\log g/g)$.

Because the algorithm is based on binary searches within sumsets, we need to sort the sumsets—at least implicitly. Consider a pair $(A_{i,t},B_{j,t})$. define $ranking _{i,j,t}$ as the set of indices $k\in \{1,2,\ldots ,g\}$ sorted by value $a_{i,(t-1)g+k}+b_{(t-1)g+k,j}$, breaking ties by k (or, more abstractly, by mapping $a_{i,l}$ to $(a_{i,l},l)$ and $b_{l,j}$ to $(b_{l,j},l)$ with pointwise addition and subtraction, and lexicographic order).

Example 1

Suppose $g=4$, $A_{i,t}=-5,12,-20,19$, and $B_{j,t}=-5,-1,35,-29$. Then $A_{i,t}+B_{j,t}=-10,11,15,-10$, and $ranking _{i,j,t}=1,4,2,3$.

As in 3SUM, we break each ranking into chunks. Denote by $i_1,i_2,\ldots ,i_g$ the index sequence $ranking _{i,j,t}$. Then the eth chunk of $ranking _{i,j,t}$ is the subsequence $i_{(e-1)s+1}, i_{(e-1)s+2}, \ldots , i_{es}$, where s is the chunk size (to be determined later).

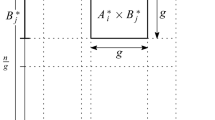
The data structure constructed in Line 1 consists of a 3-dimensional $n\times n\times n/g$ lookup table L where entry L[i, j, t] corresponds to sumset $A_{i,t}+B_{j,t}$, and contains a pointer to the corresponding forwarding array $F_{i,j,t}$. Forwarding array $F_{i,j,t}$ consists of g / s pointers to chunk arrays. The chunk array pointed to by $F_{i,j,t}[e]$ contains the eth chunk of $ranking _{i,j,t}$. Thus to look up the kth smallest sum in $A_{i,t}+B_{j,t}$ we go to L[i, j, t] and dereference it to find $F_{i,j,t}$. We then dereference $F_{i,j,t}[{\lceil }k/s{\rceil }]$ and get some chunk array $CA$. We read $CA [((k-1){\hbox {mod}}s) + 1]$ and get some index l. Finally, we extract $a_{i,(t-1)g+l}$ and $b_{(t-1)g+l, j}$ from the input matrices and add them. Thus each lookup required by the binary searches is done in $\hbox {O}(1)$ time, as desired.

To construct the data structure we first allocate L and all forwarding arrays, and make L’s entries point to the corresponding forwarding arrays. We then need to construct the chunk arrays and point the forwarding arrays to them. The key observation is the following. Given (i, j, t) and chunk number e, there is a unique quartet $(R,S,T,\pi )$ such that (R, S, T) is a partition of the index set $\{1,\ldots ,g\}$, $|R|=(e-1)s$, $|T|=(g/s-e)s$, $\pi$ is a permutation of S such that S ordered by $\pi$ is chunk e of $ranking _{i,j,t}$, all members of R appear in $ranking _{i,j,t}$ before the first member of S, and all members of T appear after the last member of S. Our chunk array algorithm is:

To find all (i, j, t) such that $ranking _{i,j,t}$ agrees with a given $(R,S,T,\pi ,e)$ we use the dominance algorithm (Sect. 3.2.2, Algorithm 5) by encoding three sets of conditions, as follows. Fix (i, j, t). Let $R'$, $S'$, and $T'$ be the sets obtained, respectively, from R, S, T by adding $t(g-1)$ to each of their members. Let $k_1,\ldots ,k_{(e-1)s}$ denote the members of $R'$ (in any order), let $k_{(e-1)s+1},\ldots ,k_{es}$ denote the members of $S'$ in order, and let $k_{es+1},\ldots ,k_{g}$ denote the members of $T'$ (in any order). The three sets of conditions are:

• 1. $a_{i,k_l}+b_{k_l,j}<a_{i,k_{(e-1)s+1}}+b_{k_{(e-1)s+1},j}$ for $1\le l\le (e-1)s$;

• 2. $a_{i,k_l}+b_{k_l,j}<a_{i,k_{l+1}}+b_{k_{l+1},j}$ for $(e-1)s+1\le l<es$;

• 3. $a_{i,k_{es}}+b_{k_{es},j}<a_{i,k_l}+b_{k_l,j}$ for $es+1\le l\le g$.

In total we have $g-1$ inequalities. We employ Fredman’s trick to get only as on the left hand sides of the inequalities and only bs on the right hand sides. We then convert the $g-1$ inequalities into a single vector inequality $u^{i,t}<v^{j,t}$, where $u^{i,t}$ corresponds to the left hand sides and $v^{j,t}$ corresponds to the right hand sides.

For each t we generate the above defined vectors $u^{i,t}$, $i=1,\ldots ,n$, and $v^{j,t}$, $j=1,\ldots ,n$, and run the dominance algorithm on these 2n vectors of dimension $g-1$. We then read off the desired (i, j)s from the dominance pairs emitted by the algorithm.

We can bound the time complexity of the preprocessing step as follows. We first note that the cost of enumerating the combinations and constructing the input vectors for the dominance algorithms is dominated by the cost of the actual algorithm invocations. Next we bound the cost of the algorithm invocations. There are less than $3^g$ valid partitions (R, S, T), and there are s! permutations. For each such such combination we run the dominance algorithm n / g times on $N=2n$ vectors of dimension $d=g-1$. So the total cost of all invocations of the algorithm, excluding the output size (|D|) terms, is $\hbox {O}\big (3^g s! (\frac{n}{g}) 2^{2(g-1)} (2n)^{1.5}\big )=\text {O}\left( 2^{4g+s\log s} n^{2.5}\right)$. Putting $g=\frac{1}{11}$ log n and $s=g/\log g$ gives O($n^{3-\frac{1}{22}})$. To this we must add $\hbox {O}(\tilde{D})$, where $\tilde{D}$ is the total number of dominance pairs emitted by the algorithm across all invocations. The dominance pairs are in 1:1 correspondence with the chunks, which implies that $\tilde{D}=n^3/s$, so $\hbox {O}(\tilde{D})=\text {O}\left( n^3\frac{\log \log n}{\log n}\right)$. It also implies that $\hbox {O}(\tilde{D})$ covers the cost of pointing the forwarding arrays to the chunk arrays. Since this bound dominates our bound for the dominance algorithm invocations, the overall bound on the preprocessing time is $O\left( n^3\frac{\log \log n}{\log n}\right)$.

Finally, substituting $g=\text {O}(\log n)$ in our bound on the running time of Algorithm 6 excluding the preprocessing gives $\hbox {O}\left( n^3\frac{\log \log n}{\log n}\right)$ as well.

Theorem 2

Our algorithm solves ZeroTriangle deterministically in $\hbox {O}(n^3\frac{\log \log n}{\log n})$ time.

Grønlund and Pettie [8] also obtain an edge-oriented deterministic bound of $\hbox {O}\left( m^{1.5}(\log \log m)^{1/2}/(\log m)^{1/4}\right)$ and a randomized one of $\hbox {O}\left( m^{1.5}(\log \log m/\log m)^{1/4}\right)$, where m is the number of edges. These bounds are better for sparse graphs. Their edge-oriented deterministic algorithm reduces the problem to a relatively dense subgraph, and then runs their vertex-oriented algorithm on it (see the proof of Theorem 1.4 in their paper). By plugging in our version of the vertex-oriented algorithm instead, we can match deterministically their randomized bound.

Theorem 3

Plugging our algorithm into Grønlund and Pettie’s deterministic edge-oriented algorithm yields a deterministic algorithm solving ZeroTriangle in $\hbox {O}\left( m^{1.5}(\log \log m/\log m)^{1/4}\right)$.

5.1 Comparison with Grønlund and Pettie

Grønlund and Pettie [8] define the problem a little more broadly—instead of searching for a single (i, j, k) they ask to find a k for every (i, j), and in fact, do not ask for k such that $a_{ik}+b_{kj}=c_{ij}$ but rather for k that minimizes the difference $a_{ik}+b_{kj}-c_{ij}$ subject to $a_{ik}+b_{kj}\ge c_{ij}$. They call this problem target-min-plus. It is easy to adapt the binary searches to find a minimizing, rather than equalizing, k, and the algorithm searches for each $c_{ij}$ anyway, so this problem can be solved at no additional cost.

The outline of our algorithm is the same as Grønlund and Pettie’s [8], except that they organize the work a little differently—they break it into n / g rounds of preprocessing and searching. However, as with their Convolution3SUM algorithms, Grønlund and Pettie neglect to partition the sorted boxes into chunks, and therefore end up with fairly complex constructions involving either random sampling within a multilevel partitioning, or a deterministic enumeration of permutations, leading to the bounds we have mentioned.