1 Introduction

Initiation and propagation of fractures and cracks in an elastic media have been challenging problems for the civil and mechanical engineers involved in designing structures and analysing structural stability. In this scientific era, fracture mechanics has become an important tool for enhancing the performance of mechanical components and attaining the structural stability of the materials. Nowadays, the study of fractures and cracks in elastic media is oriented towards the analysis of SIF, as SIF contributes in the study of strength of the structures in elastic fracture mechanics. In multiple engineering fields, quite a good amount of research has been performed corresponding to the study of SIF at the vicinity of the crack tip subjected to various loading constraints.

Crack can be found inside any elastic materials such as wood, ceramic, bones, muscles, skin, ice and rock due to cyclic loading, wedging, non-uniform temperature, mechanical impact, static overstress, residual stress and so forth. There are also many other different reasons which may causes imitation of crack inside the elastic materials. Any type of irregularity inside the material pave way for stress concentration, for instance, a sharp indentation, is more favourable for generation of crack growth. As far as present scientific advancement is concerned, composite materials are mostly used in various engineering structures. Due to their lightweight and stronger in nature, orthotropic composite materials are preferable as structural materials. Hence, it becomes imperative to quest for SIF for the crack present in orthotropic composite materials.

Numerous research exist in the literature concerning stress analysis of various structures containing crack. Mal [1] obtained SIF for a dynamic crack located inside an isotropic medium. He observed radiation phenomenon of torsional elastic waves due to the presence of the crack. Theocaris and Papadopoulo [2] investigated the behaviour of running cracks under constant velocity. Srivastava et al. [3] studied behaviour of coplanar cracks in elastic strip. Kuo [4] examined the transient analysis of SIF for the crack in anisotropic half-spaces. With the help of Jacobi polynomials and singular integral equations, he obtained dynamic SIF numerically. Kundu [5] also displayed the interaction phenomenon between two cracks in a three-layered plate. The transient response for crack subjected to dynamic loading was delineated by Chien-Ching and Ying-Chung [6]. Initiation of fracture due to asymmetric impact loading in an edge cracked plate was studied by Lee and Freund [7]. The transient behaviour of the crack subjected to dynamic loading was examined by Ma and Hou [8]. Zhang [9] studied transient phenomenon of anti-plane crack in anisotropic solid. Wei et al. [10] examined stress intensity factor analysis of interfacial crack in viscoelastic medium. Later on, Wang and Gross [11] studied the interfacial crack in multi-layered medium. Bi et al. [12] investigated finite length crack in functionally graded material. Under the plane loading condition, the propagating crack in functionally graded elastic media was studied by Ma et al. [13]. Lee [14] investigated crack propagation in functionally graded materials. The three-dimensional dynamic interface crack was studied by Guz et al. [15]. Guz [16] established the foundations of the mechanics of fracture of materials compressed along cracks. Bogdanov [17] examined spatial problems of fracture of materials loaded along crack. Nazarenko and Kipnis [18] obtained stress concentration for semi-infinite crack. Singh et al. [19] and Singh et al. [20] derived expression of SIF for the crack present at the interface of homogeneous and non-homogeneous pre-stressed poroelastic structure. A good account of work pertaining to elastic wave behaviour in distinct orthotropic structures was reported in the literature [21,22,23,24,25,26]. Lately, the dynamic behaviour of fracture and obstacle present in different structures of interest were investigated by prolific researchers [27,28,29,30,31,32]. Following the foregoing works in context to orthotropic elastic solid, it is worthy to mention that the investigation inclined towards the propagation of semi-infinite crack in dissimilar orthotropic composite strip under the influence of harmonic and non-harmonic loadings remains untraced. This motivated to look at the dynamic behaviour of crack owing to SH-wave in such a realistic engineering structure. Till date, no attempt has been made to develop a mathematical model for the moving crack caused by SH-wave propagating in orthotropic composite strip under distinct loading environment, which is being attempted here.

In the present investigation, a model has been developed mathematically to study the dynamic behaviour of rectilinear crack present at the interface of an orthotropic composite strip. The exact expression for SIF has been obtained with reference to HL along with CAL (constant amplitude loading) and SF (stress free) condition. For the case of NHL along with CL (constant loading) and SF condition, the expression for SIF has also been derived. The static solution for SIF has also been obtained as the limiting case for HL and NHL constraints on the edges of the crack.

2 Formulation and solution of the problem

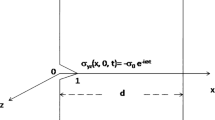
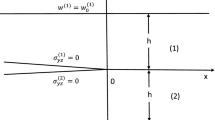
A composite strip of thickness \(2l\) containing a moving rectilinear semi-infinite crack with uniform velocity \(s\) due to SH-wave propagating in the direction of \(x_{1}\)-axis has been considered, as exhibited in Fig. 1. A Cartesian coordinate system has been assumed, wherein \(z_{1}\)-axis is pointing in vertically downward direction, and \(x_{1}\)-axis is pointing positively in the direction of SH-wave propagation in composite strip. Further, the strip is rigidly clamped by its upper surface \(\left( {z_{1} = - l_{1} } \right)\) and lower surface \(\left( {z_{1} = l_{2} } \right)\). The middle point of the strip is assumed at \(z_{1} = 0\), that involves rectilinear semi-infinite crack \(x_{1} \le 0\), moving with uniform velocity \(s\) in the direction of \(x_{1}\)-axis, which separates the strip into two different orthotropic materials. Owing to SH-wave propagating in \(x_{1}\)-direction, the displacement is caused only in \(y_{1}\)-direction. The constitutive relation for orthotropic medium with \(y_{1}\) as diagonal axis is given by

$$\left( \begin{gathered} \tau_{{x_{1} x_{1} }} \hfill \\ \tau_{{y_{1} y_{1} }} \hfill \\ \tau_{{z_{1} z_{1} }} \hfill \\ \tau_{{y_{1} z_{1} }} \hfill \\ \tau_{{x_{1} z_{1} }} \hfill \\ \tau_{{x_{1} y_{1} }} \hfill \\ \end{gathered} \right) = \left( \begin{gathered} B_{11} \,\,\,B_{12} \,\,\,B_{13} \,\,\,0\,\,\,0\,\,\,0 \hfill \\ B_{12} \,\,\,B_{22} \,\,\,B_{23} \,\,\,0\,\,\,0\,\,\,0 \hfill \\ B_{13} \,\,\,B_{23} \,\,\,B_{33} \,\,\,0\,\,\,0\,\,\,0 \hfill \\ 0\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,0\,\,\,\,M\,\,\,0\,\,\,0 \hfill \\ 0\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,0\,\,\,\,\,\,0\,\,\,L\,\,\,0 \hfill \\ 0\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,0\,\,\,\,\,\,\,0\,\,\,0\,\,\,N \hfill \\ \end{gathered} \right)\left( \begin{gathered} e_{11} \hfill \\ e_{22} \hfill \\ e_{33} \hfill \\ 2e_{23} \hfill \\ 2e_{13} \hfill \\ 2e_{12} \hfill \\ \end{gathered} \right)$$
(1)

wherein \(\tau_{i\,j}\) denotes the stress components, \(B_{i\,j} (i,\,\,j = 1,\,\,2,\,\,3)\) and \(L,\,\,M,\,\,N\) are material elastic constants, and \(e_{ij} = \frac{1}{2}\left( {u_{i,\,j} + u_{j,\,i} } \right)\) represents the strain components. As displacement is caused in \(y_{1}\)-direction only because of SH-wave propagation, hence, we may consider

$$u_{1} = u_{3} = 0,\,\,u_{2} = u_{2} \left( {x_{1} ,\,\,z_{1} ,\,\,t} \right),$$
(2)

where \(u_{i} = \left( {u_{1} ,\,\,u_{2} ,\,\,u_{3} } \right)\) denotes the displacement components in \(x_{1} ,\,\,y_{1}\) and \(z_{1}\)-directions, respectively.

Fig. 1
figure 1

Geometrical model of the problem

Full size image

Now, with the help of (2), (1) may be written as

$$\tau_{{x_{1} x_{1} }} = \tau_{{y_{1} y_{1} }} = \tau_{{z_{1} z_{1} }} = \tau_{{x_{1} z_{1} }} = 0,\,\,\tau_{{y_{1} z_{1} }} = M\frac{{\partial u_{2} }}{{\partial z_{1} }},\,\,\tau_{{y_{1} x_{1} }} = N\frac{{\partial u_{2} }}{{\partial x_{1} }}.$$
(3)

In view of (3), the only equation of motion appearing for propagating SH-wave in the composite strip without body force can be given by

$$\frac{{\partial \tau_{{y\,_{1} \,x\,_{1} }} }}{{\partial x_{1} }} + \frac{{\partial \tau_{{y\,_{1\,} z_{1} }} }}{{\partial z_{1} }} = \rho \frac{{\partial^{2} u_{2} }}{{\partial t^{2} }},$$
(4)

where \(\rho\) is density of the orthotropic material, \(t\) refers to time, together with

$$\tau_{{y_{1} x_{1} }} = N\frac{{\partial u_{2} }}{{\partial x_{1} }}\,\,{\text{and}}\,\,\tau_{{y_{1} z_{1} }} = M\frac{{\partial u_{2} }}{{\partial z_{1} }}.$$
(5)

By means of Eqs. (3) and (4), we have

$$N\left( {\frac{{\partial^{2} u_{2} }}{{\partial x_{1}^{2} }}} \right) + M\left( {\frac{{\partial^{2} u_{2} }}{{\partial z_{1}^{2} }}} \right) = \rho \frac{{\partial^{2} u_{2} }}{{\partial t^{2} }},$$
(6)

Now again, Eq. (6) may be rewritten as

$$\frac{{\partial^{2} u_{2} }}{{\partial x_{1}^{2} }} + \frac{1}{{\alpha_{0}^{2} }}\frac{{\partial^{2} u_{2} }}{{\partial z_{1}^{2} }} = \frac{1}{{S_{T}^{2} }}\frac{{\partial^{2} u_{2} }}{{\partial t^{2} }},$$
(7)

where \(\alpha_{0} = \sqrt {N/M} ,\,\,{\text{and}}\,\,S_{T}^{2} = N/\rho\) is SH-wave velocity in the composite strip.

Now, defining the both sided Fourier integral transform as

$$\left. \begin{gathered} f\left( {\alpha ,z_{1} } \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{\infty } {\tilde{f}\left( {x_{1} ,z_{1} } \right)} e^{{i\alpha x_{1} }} {\text{d}}x_{1} , \hfill \\ \tilde{f}\left( {x_{1} ,z_{1} } \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{{ - \infty + ic^{\prime}}}^{{\infty + ic^{\prime}}} {f\left( {\alpha ,z_{1} } \right)} e^{{ - i\alpha x_{1} }} {\text{d}}\alpha . \hfill \\ \end{gathered} \right\}$$
(8)

where \(\alpha\) is a complex variable and it denotes the transform parameter of the transformation. The transform parameter is chosen such that \(f\left( {\alpha ,z_{1} } \right)\) is analytic in the domain, which lies within the strip \({\hslash }_{1}<\text{Im}\left(\alpha \right)<{\hslash }_{2}; {\hslash }_{1} \text{and} {\hslash }_{2}\) being real constants.

Now, the analytic function \(f\left( {\alpha ,z_{1} } \right)\) may be decomposed as (Titchmarsh [33])

$$f\left( {\alpha ,z_{1} } \right) = f^{ - } \left( {\alpha ,z_{1} } \right) + f^{ + } \left( {\alpha ,z_{1} } \right),$$
(9)

wherein

$$\left. \begin{gathered} f^{ - } \left( {\alpha ,z_{1} } \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{0} {\tilde{f}\left( {x_{1} ,z_{1} } \right)} e^{{i\alpha x_{1} }} {\text{d}}x_{1} , \hfill \\ f^{ + } \left( {\alpha ,z_{1} } \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{0}^{\infty } {\tilde{f}\left( {x_{1} ,z_{1} } \right)} e^{{i\alpha x_{1} }} {\text{d}}x_{1} , \hfill \\ \end{gathered} \right\}$$
(10)

are analytic functions in half-planes \({\text{Im}} \left( \alpha \right) < \hbar_{2} \,\,{\text{and}}{\text{Im}} \left( \alpha \right) > \hbar_{1}\), respectively.

2.1 Mathematical model of the crack under NHL conditions

The objective here is to formulate the mathematical model for the crack \(\left( {x_{1} < 0,\,\,z_{1} = 0} \right)\) moving along \(x_{1}\)-axis subjected to NHL conditions on edges of the crack in the composite strip. The aforementioned crack is under a load represented by \(\tau_{{y_{1} z_{1} }} = \varphi \left( {x_{1} } \right).\)

In light of the undertaken problem, a convective transformation (Galilean transformation) may be defined for fixing the frame of reference as

$$x_{1} = x_{1}^{\prime } + st,\;y_{1} = y_{1}^{\prime } ,\;z_{1} = \alpha_{0} z_{1}^{\prime }$$
(11)

where \(s\) denotes the moving velocity of the system.

With the help of Eqs. (7) and (11), we have

$$c^{2} \frac{{\partial^{2} u_{2} }}{{\partial x_{1}^{\prime 2} }} + \frac{{\partial^{2} u_{2} }}{{\partial z_{1}^{\prime 2} }} = 0,\;{\text{with}}\;c = \sqrt {1 - \,\frac{{s^{2} }}{{S_{T}^{2} }}} .$$
(12)

With the help of Fourier transform (8), Eqs. (5) and (12) takes the form

$$\left. \begin{gathered} \frac{{{\text{d}}^{2} \tilde{u}_{2} (\alpha ,z_{1}^{\prime } )}}{{{\text{d}}z_{1}^{\prime 2} }} - \alpha^{2} c^{2} \tilde{u}_{2} \left( {\alpha ,z^{\prime}_{1} } \right) = 0, \hfill \\ \tilde{\tau }_{{y_{1}^{\prime } x^{\prime}_{1} }} (\alpha ,z_{1}^{\prime } ) = - iN\alpha \tilde{u}_{2} \left( {\alpha ,z^{\prime}_{1} } \right), \hfill \\ \tilde{\tau }_{{y_{1}^{\prime } z^{\prime}_{1} }} (\alpha ,z_{1}^{\prime } ) = M\frac{{{\text{d}}\tilde{u}_{2} \left( {\alpha ,z^{\prime}_{1} } \right)}}{{{\text{d}}z^{\prime}_{1} }}, \hfill \\ \end{gathered} \right\}$$
(13)

where \(\tilde{u}_{2} (\alpha ,\,\,z^{\prime}_{1} )\), \(\tilde{\tau }_{{x_{1}^{\prime } y^{\prime}_{1} }} (\alpha ,\,\,z^{\prime}_{1} ),\,\,\tilde{\tau }_{{y^{\prime}_{1} z^{\prime}_{1} }} (\alpha ,\,\,z^{\prime}_{1} )\) are Fourier transform of \(u_{2} (x^{\prime}_{1} ,\,\,z^{\prime}_{1} )\), \(\tau_{{x_{1}^{\prime } y^{\prime}_{1} }} (x^{\prime}_{1} ,\,\,z^{\prime}_{1} )\) and \(\tau_{{y^{\prime}_{1} z^{\prime}_{1} }} (x^{\prime}_{1} ,\,\,z^{\prime}_{1} )\) respectively.

The solutions of the set of Eq. (13) are given by

$$\left. \begin{gathered} \tilde{u}_{2} \left( {\alpha ,\,\,z^{\prime}_{1} } \right) = A_{1} \left( \alpha \right)\sinh \xi cz^{\prime}_{1} + A_{2} \left( \alpha \right)\cosh \alpha cz^{\prime} \hfill \\ \tilde{\tau }_{{x^{\prime}_{1} y^{\prime}_{1} }} \left( {\alpha ,\,\,z^{\prime}_{1} } \right) = - iN\alpha \left[ {A_{1} \left( \alpha \right)\sinh \alpha cz^{\prime}_{1} + A_{2} \left( \alpha \right)\cosh \alpha cz^{\prime}_{1} } \right] \hfill \\ \tilde{\tau }_{{y^{\prime}_{1} z^{\prime}_{1} }} \left( {\alpha ,\,\,z^{\prime}_{1} } \right) = M\alpha c\left[ {A_{1} \left( \alpha \right)\cosh \alpha cz^{\prime}_{1} + A_{2} \left( \alpha \right)\sinh \alpha cz^{\prime}_{1} } \right] \hfill \\ \end{gathered} \right\}$$
(14)

where \(A_{1} \left( \alpha \right)\) and \(A_{2} \left( \alpha \right)\) are constants to be determined by means of proposed geometrical (boundary) conditions of the problem.

With the help of Eq. (11), the geometrical conditions of the adopted problem are given by

$$\begin{aligned} u_{2}^{\left( 1 \right)} \left( {x^{\prime}_{1} ,z^{\prime}_{1} } \right) = & 0,\;\;{\text{for}}\;\left| {x^{\prime}_{1} } \right| < \infty ,\;z^{\prime}_{1} = - l_{1} , \\ u_{2}^{\left( 2 \right)} \left( {x^{\prime}_{1} ,z^{\prime}_{1} } \right) = & 0,\;\;{\text{for}}\;\left| {x^{\prime}_{1} } \right| < \infty ,\;z^{\prime}_{1} = l_{2} , \\ \tau_{{y^{\prime}_{1} z^{\prime}_{1} }}^{\left( 1 \right)} \left( {x^{\prime}_{1} ,z^{\prime}_{1} } \right) = & \tau_{{y^{\prime}_{1} z^{\prime}_{1} }}^{\left( 2 \right)} \left( {x^{\prime}_{1} ,z^{\prime}_{1} } \right)\, = \varphi \left( {x^{\prime}_{1} } \right),\;\;{\text{for}}\;x^{\prime}_{1} < 0,\;z^{\prime}_{1} = 0, \\ u_{2}^{\left( 1 \right)} \left( {x^{\prime}_{1} ,z^{\prime}_{1} } \right) = & u_{2}^{\left( 2 \right)} \left( {x^{\prime}_{1} ,z^{\prime}_{1} } \right),\;\;{\text{for}}\,\,x^{\prime}_{1} > 0,\;z^{\prime}_{1} = 0, \\ \tau_{{y^{\prime}_{1} z^{\prime}_{1} }}^{\left( 1 \right)} \left( {x^{\prime}_{1} ,z^{\prime}_{1} } \right) = & \tau_{{y^{\prime}_{1} z^{\prime}_{1} }}^{\left( 2 \right)} \left( {x^{\prime}_{1} ,z^{\prime}_{1} } \right),\;\;{\text{for}}\;x^{\prime}_{1} > 0,\;z^{\prime}_{1} = 0, \\ \end{aligned}$$
(15)

where \(u_{2}^{\left( i \right)}\) denotes the displacement in the upper orthotropic medium \(\left( {i = 1} \right)\) and lower orthotropic medium \(\left( {i = 2} \right)\) in the composite strip, and \(\tau^{(i)}\) represents the component of stress of the upper orthotropic medium \(\left( {i = 1} \right)\) and lower orthotropic medium \(\left( {i = 2} \right)\) in the composite strip. Now using Fourier integral transform (8) in Eq. (15), and making use of Eq. (14), the two Wiener–Hopf equations may be obtained as

$$\left. \begin{gathered} \tilde{u}_{2}^{\left( 1 \right)} (\alpha ,\,\,0) = - \frac{{\tanh \alpha c_{1} l_{1} }}{{M_{1} c_{1} \alpha }}\tilde{\tau }_{{y^{\prime}_{1} z^{\prime}_{1} }}^{\left( 1 \right)} (\alpha ,\,\,0) \hfill \\ \tilde{u}_{2}^{\left( 2 \right)} (\alpha ,\,\,0) = - \frac{{\tanh \alpha c_{2} l_{2} }}{{M_{2} c_{2} \alpha }}\tilde{\tau }_{{y^{\prime}_{1} z^{\prime}_{1} }}^{\left( 2 \right)} (\alpha ,\,\,0) \hfill \\ \end{gathered} \right\}$$
(16)

where \(c_{1,2} = \sqrt {1 - \frac{{s^{2} }}{{S_{{T_{1,2} }}^{2} }}}\);\(S_{{T_{1} }}\) and \(S_{{T_{2} }}\) signify SH-wave velocity in the upper orthotropic medium and lower orthotropic medium respectively, \(M_{1}\) and \(M_{2}\) represent elastic material constants for the upper orthotropic medium and lower orthotropic medium respectively in the composite strip.

From Eqs. (9) and (10), we have

$$\left. \begin{gathered} \tilde{u}_{2}^{\left( 1 \right) - } (\alpha ,\,\,0) - \tilde{u}_{2}^{\left( 2 \right) - } (\alpha ,\,\,0) = \tilde{u}_{2}^{ - } \left( \alpha \right), \hfill \\ \tilde{\tau }_{{y^{\prime}_{1} z^{\prime}_{1} }}^{\left( 1 \right) - } (\alpha ,\,\,0) + \tilde{\tau }_{{y^{\prime}_{1} z^{\prime}_{1} }}^{\left( 1 \right) + } (\alpha ,\,0) = \tilde{\tau }_{{y^{\prime}_{1} z^{\prime}_{1} }}^{ + } (\alpha ) + \psi \left( \alpha \right), \hfill \\ \psi \left( \alpha \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{0} {\varphi \left( {x^{\prime}_{1} } \right)} e^{{i\alpha x_{1}^{\prime } }} dx^{\prime}_{1} , \hfill \\ \end{gathered} \right\}$$
(17)

By means of the last two relations of Eq. (15), and Eq. (17), a single Wiener–Hopf equation may be written as

$$\tilde{u}_{2}^{ - } \left( \alpha \right) = - \zeta \left( \alpha \right)\left[ {\tilde{\tau }_{{y^{\prime}_{1} z^{\prime}_{1} }}^{ + } (\alpha ) + \psi \left( \alpha \right)} \right],$$
(18)
$${\text{where}}\;\;\zeta \left( \alpha \right) = \frac{1}{\alpha }\left( {\frac{{\tanh \alpha c_{1} l_{1} }}{{M_{1} c_{1} }} + \frac{{\tanh \alpha c_{2} l_{2} }}{{M_{2} c_{2} }}} \right),$$
(19)

denotes the kernel of Eq. (18).

Equation (18) has a feasible domain as

$$- \min \left( {\frac{\pi }{{2c_{1} l_{1} }},\frac{\pi }{{2c_{2} l_{2} }}} \right) < - \varepsilon < {\text{Im}} \alpha < 0.$$
(20)

Now, following the method given by Koiter [34], the kernel of Eq. (18) can be factorized as

$$\zeta \left( \alpha \right) = \zeta^{ - } \left( \alpha \right)\zeta_{1} (\alpha ),$$
(21)

where \(\zeta^{ - } \left( \alpha \right)\) has been taken such that the function \(\zeta^{ - } \left( \alpha \right) \to \infty\) when \(\left| \alpha \right| \to \infty\), and the function \(\zeta^{ - } \left( \alpha \right) \to 0\) when \(\left| \alpha \right| \to 0\), i.e. the behaviour of the functions \(\zeta^{ - } \left( \alpha \right)\) and \(\zeta \left( \alpha \right)\) is same in the considered domain. We have also assumed that the function \(\zeta_{1} \left( \alpha \right)\) is free from singularities within the domain \(\left( {\left| {{\text{Im}} \alpha } \right| < \varepsilon_{1} } \right)\), wherein

$$0 < \varepsilon \le \varepsilon_{1} < \min \left( {\frac{\pi }{{2c_{1} l_{1} }},\frac{\pi }{{2c_{2} l_{2} }}} \right).$$
(22)

According to the aforementioned consideration regarding \(\zeta^{ - } \left( \alpha \right)\), it may be assumed that

$$\zeta^{ - } \left( \alpha \right) = \frac{1 + \vartheta }{{M_{1} c_{1} }}I^{ - } \left( \alpha \right)I^{ + } \left( \alpha \right),$$
(23)

where

$$I^{ \pm } \left( \alpha \right) = \frac{1}{{\sqrt {\alpha \pm i \mathchar'26\mkern-10mu\lambda } }},\; \mathchar'26\mkern-10mu\lambda = \frac{1 + \vartheta }{{c_{1} l_{2} \left( {k + \lambda } \right)}},\;k = \frac{{l_{1} }}{{l_{2} }},\;\vartheta = \lambda \frac{{c_{1} }}{{c_{2} }},\;\lambda = \gamma \frac{{M_{1} }}{{M_{2} }},\;\gamma = \frac{{\gamma_{2} }}{{\gamma_{1} }},\;{\text{and}}\;\gamma_{i} = \frac{{M_{i} }}{{N_{i} }}.$$
(24)

With the assumption considered for \(\zeta_{1} \left( \alpha \right)\), we have \(\zeta_{1} \left( \alpha \right) \to 1\) in the strip \(\left| {{\text{Im}} \alpha } \right| < \varepsilon_{1} \,\,{\text{for }}\left| \alpha \right| \to \infty\). Now using the method of factorization following Nobel [35], the function \(\zeta_{1} \left( \alpha \right)\) can be written as

$$\zeta_{1} \left( \alpha \right) = \frac{{\zeta_{1}^{ + } \left( \alpha \right)}}{{\zeta_{1}^{ - } \left( \alpha \right)}},$$
(25)

where

$$\left. \begin{gathered} \log \zeta_{1}^{ + } \left( \alpha \right) = \frac{1}{2\pi i}\int\limits_{{ - \infty + \Lambda_{2} }}^{{\infty + \Lambda_{2} }} {\frac{\log \zeta \left( \alpha \right)}{{\Psi - \alpha }}} d\Psi , \hfill \\ \log \zeta_{1}^{ - } \left( \alpha \right) = \frac{1}{2\pi i}\int\limits_{{ - \infty + i\Lambda_{1} }}^{{\infty + i\Lambda_{1} }} {\frac{\log \zeta \left( \alpha \right)}{{\Psi - \alpha }}} d\Psi , \hfill \\ \end{gathered} \right\}$$
(26)

where \(- \varepsilon_{1} < \Lambda_{2} < \Lambda_{1} < \varepsilon_{1}\), and the value of \(\zeta_{1}^{ + } \left( \alpha \right)\) and \(\zeta_{1}^{ - } \left( \alpha \right)\) are defined in Eq. (25). It is also assumed that they are free from singularities in the half planes \({\text{Im}} \alpha > \Lambda_{2}\) and \({\text{Im}} \alpha > \Lambda_{1}\), respectively.

In view of relations \(\zeta_{1} \left( 0 \right) = \zeta_{1} \left( \infty \right) = 1,\) and \(\zeta_{1}^{ \pm } \left( 0 \right) = \zeta_{1}^{ \pm } \left( \infty \right) = 1\), and applying the method given by Entov and Salganik [36], Eq. (17) together with Eqs. (21), (22), and (24), lead to

$$\frac{{ - M_{1} c_{1} \zeta_{1}^{ - } \left( \alpha \right)}}{{\left( {1 + \vartheta } \right)I^{ - } \left( \alpha \right)}}\tilde{u}_{2}^{ - } \left( \xi \right) = I^{ + } \left( \alpha \right)\zeta_{1}^{ + } \left( \alpha \right)\tilde{\tau }_{{y^{\prime}_{1} z^{\prime}_{1} }}^{ + } (\alpha ) + R\left( \alpha \right),$$
(27)
$${\text{where}}\;R\left( \alpha \right) = I^{ + } \left( \alpha \right)\zeta_{1}^{ + } \left( \alpha \right)\psi \left( \alpha \right).$$
(28)

Now, we assume that the function \(R\left( \alpha \right)\) is analytic at least within \(- {\text{min}}\left( {\frac{\pi }{{2c_{1} l_{1} }},\frac{\pi }{{2c_{2} l_{2} }}} \right) < - \varepsilon < {\text{Im}} \alpha < 0.\) Applying the method given by Nobel [35], \(R\left( \alpha \right)\) may be represented as

$$R\left( \alpha \right) = R^{ + } \left( \alpha \right) - R^{ - } \left( \alpha \right).$$
(29)

wherein

$$\left. \begin{gathered} R^{ + } \left( \alpha \right) = \frac{1}{2\pi i}\int\limits_{{ - \infty - i\delta_{2} }}^{{\infty - i\delta_{2} }} {\frac{R\left( \xi \right)}{{\xi - \alpha }}} d\xi , \hfill \\ R^{ - } \left( \alpha \right) = \frac{1}{2\pi i}\int\limits_{{ - \infty - i\delta_{1} }}^{{\infty - i\delta_{1} }} {\frac{R\left( \xi \right)}{{\xi - \alpha }}} d\xi , \hfill \\ \end{gathered} \right\}$$
(30)

such that \(0 < \delta_{1} < \delta_{2} < \varepsilon\) and the region of analyticity of \(R^{ \pm } \left( \alpha \right)\) are the half-planes \({\text{Im}}\alpha > - \varepsilon \,\,{\text{and Im}}\alpha < 0\) respectively. Now, in view of Eqs. (27), (29) and using the generalized Liouville theorem, Eq. (18) take the form

$$\left. \begin{gathered} \tilde{u}_{2}^{ - } \left( \alpha \right) = \frac{{\left( {1 + \vartheta } \right)R^{ - } \left( \alpha \right)I^{ - } \left( \alpha \right)}}{{M_{1} c_{1} \zeta_{1}^{ - } \left( \alpha \right)}}, \hfill \\ \tilde{\tau }_{{y^{\prime}_{1} z^{\prime}_{1} }}^{ + } (\alpha ) = - \frac{{R^{ + } \left( \alpha \right)}}{{I^{ + } \left( \alpha \right)\zeta_{1}^{ + } \left( \alpha \right)}}, \hfill \\ \end{gathered} \right\}$$
(31)

where the region of analyticity of the displacement and stress function \(\tilde{u}_{2}^{ - } \left( \alpha \right)\) and \(\tilde{\tau }_{{y^{\prime}_{1} z^{\prime}_{1} }}^{ + } (\alpha )\) are \({\text{Im}}\alpha < 0\) and \({\text{Im}}\alpha > - \varepsilon\) respectively. By means of results in Eq. (30), we can determine SIF. Now, following Eqs. (24) and (30), and making use of the characteristics of \(R^{ \pm } \left( \alpha \right)\) and \(\zeta_{1}^{ \pm } \left( \alpha \right),\) the behaviour of displacement and stress functions \(\tilde{u}_{2}^{ - } \left( \alpha \right)\) and \(\tilde{\tau }_{{y^{\prime}_{1} z^{\prime}_{1} }}^{ + } (\alpha ,\,\,0)\) in Eq. (31) can be defined at \(\left| \alpha \right| \to \infty\) as

$$\tilde{u}_{2}^{ - } \left( \alpha \right) = - \frac{1 + \vartheta }{{M_{1} c_{1} }}\frac{P}{\alpha \sqrt \alpha }\;{\text{and}}\;\tilde{\tau }_{{y^{\prime}_{1} z^{\prime}_{1} }}^{ + } \left( \alpha \right) = \frac{P}{\sqrt \alpha },\;P = \frac{1}{\alpha \pi i}\int\limits_{{ - \infty - i\delta_{1} }}^{{\infty + i\delta_{1} }} {R\left( \xi \right)d\xi } ,\,\,0 < \delta_{1} < \varepsilon .$$
(32)

By means of Abel theorem, the results for displacement and stress concerned with crack along \(x^{\prime}_{1}\)-axis at \(\left| {x^{\prime}_{1} } \right| \to 0\) are given by

$$\left. \begin{gathered} u_{2}^{\left( 1 \right)} (x^{\prime}_{1} ) - u_{2}^{\left( 2 \right)} \left( {x^{\prime}_{1} } \right) = \frac{{2K\left( {1 + \vartheta } \right)}}{{M_{1} c_{1} }}\sqrt { - x^{\prime}_{1} } \,\,{\text{for}}\,x^{\prime}_{1} \to 0^{ - } , \hfill \\ \tau_{{y^{\prime}_{1} z^{\prime}_{1} }}^{\left( 1 \right)} (x^{\prime}_{1} ) - \tau_{{y^{\prime}_{1} z^{\prime}_{1} }}^{\left( 2 \right)} (x^{\prime}_{1} ) = \frac{K}{{\sqrt {x^{\prime}_{1} } }},\,for\,\,x^{\prime}_{1} \to 0^{ + } , \hfill \\ \end{gathered} \right\}$$
(33)
$${\text{with}}\;K = - \sqrt { - 2iP} .$$
(34)

Equation (34) gives the expression of SIF for the propagating crack under arbitrary NHL in non-homogeneous composite strip.

2.1.1 Case 1 rectilinear semi-infinite crack edges under CL

Here, we shall find the expression of SIF when crack edges are under CL condition in non-homogeneous composite strip. We assume that edges of crack in non-homogeneous composite strip are under a load \(\tau_{{y^{\prime}_{1} z^{\prime}_{1} }} \left( {x^{\prime}_{1} ,0} \right) = F_{c}\), and therefore, with the help Eqs. (17), (24), (32) and (34), we have

$$K = - F_{c} \sqrt {\frac{ - i}{\pi }} \frac{1}{2\pi i}\int\limits_{ - \infty - i\delta }^{\infty - i\delta } {\frac{{\zeta_{1}^{ \pm } \left( \xi \right)}}{{\xi \sqrt {\xi + i \mathchar'26\mkern-10mu\lambda } }}} {\text{d}}\xi .$$
(35)

Now on simplifying Eq. (35), and using Eqs. (23) and (24) along with the fact that \(\zeta_{1}^{ + } \left( 0 \right) = 1,\) we have

$$K = - F_{c} \sqrt {\frac{{c_{1} l_{2} \left( {k + \lambda } \right)}}{{\pi \left( {1 + \vartheta } \right)}}} .$$
(36)

Equation (36) gives the result of SIF for the propagating rectilinear semi-infinite non-centrally \(\left( {{\text{i}}{\text{.e}}{.}\,\,l_{1} \ne l_{2} } \right)\) located crack in non-homogeneous composite strip when edges of crack are subjected to CL condition.

Now, as a special case for isotropic elastic medium, i.e. when \(N_{1} = M_{1} = \mu_{1} ,\;N_{2} = M_{2} = \mu_{2} ,\) then Eq. (36) reduces to

$$K^{\prime} = - F_{c} \sqrt {\frac{{c^{\prime}_{1} l_{2} \left( {k + \lambda^{\prime}} \right)}}{{\pi \left( {1 + \vartheta^{\prime}} \right)}}} ,\,\,\vartheta^{\prime} = \lambda^{\prime}\frac{{c^{\prime}_{1} }}{{c^{\prime}_{2} }},\,\,\lambda^{\prime} = \frac{{\mu_{1} }}{{\mu_{2} }},\,\,c^{\prime}_{1} = \sqrt {1 - \frac{{s^{2} }}{{S_{{T^{\prime}_{1} }}^{2} }}} ,\,\,c^{\prime}_{2} = \sqrt {1 - \frac{{s^{2} }}{{S_{{T^{\prime}_{2} }}^{2} }}} ,\,\,S_{{T_{1}^{\prime } }}^{2} = \frac{{\mu_{1} }}{{\rho_{1} }},\,\,S_{{T_{2}^{\prime } }}^{2} = \frac{{\mu_{2} }}{{\rho_{2} }},$$

which leads to SIF for the propagating crack in non-homogeneous isotropic elastic strip when edges of crack are subjected to CL condition. This expression of SIF is in well agreement with the result established by Matczyński [37].

2.1.1.1 Subcase 1.1

When \(N_{1} = N_{2} ,\;M_{1} = M_{2} \,\,{\text{and}}\,\rho_{1} = \rho_{2} ,\) then (36)) reduces to

$$K = - F_{c} \sqrt {\frac{cl}{\pi }} ,\,\,\,\,{\text{where}}\,\,\,c = \sqrt {1 - \frac{{s^{2} }}{{S_{T}^{2} }}} ,\,\,2l = l_{1} + l_{2} .$$
(37)

Equation (37) gives the result of SIF for non-centrally \(\left( {{\text{i}}{\text{.e}}{.}\,\,l_{1} \ne l_{2} } \right)\) located crack propagating in homogeneous composite strip when crack edges are under CL condition.

2.1.1.2 Subcase 1.2

When \(N_{1} = N_{2} ,M_{1} = M_{2} ,\rho_{1} = \rho_{2} \,\,and\,\,l_{1} = l_{2} = l\), Eq. (36) transforms to

$$K = - F_{c} \sqrt {\frac{cl}{\pi }} ,\,\,{\text{where}}\,\,\,c = \sqrt {1 - \frac{{s^{2} }}{{S_{T}^{2} }}} .$$
(38)

Equation (38) gives the result for SIF for propagating rectilinear semi-infinite centrally \(\left( {{\text{i}}{\text{.e}}{.}\,\,l_{1} = l_{2} } \right)\) located crack in homogeneous composite strip when crack edges are under CL condition.

2.1.1.3 Subcase 1.3

For the limiting case of static crack, i.e. when \(s \to 0\), Eq. (36) results in

$$K_{s} = - F_{c} \sqrt {\frac{{l_{2} \left( {k + \lambda } \right)}}{{\pi \left( {1 + \lambda } \right)}}} .$$
(39)

Equation (39) gives the result for SIF for the propagation of rectilinear semi-infinite non-centrally \(\left( {{\text{i}}{\text{.e}}{.}\,\,l_{1} \ne l_{2} } \right)\) located static crack in non-homogeneous composite strip when edges of crack are subjected to CL condition.

2.1.1.4 Subcase 1.4

When \(N_{1} = N_{2} ,M_{1} = M_{2} ,\,\,\rho_{1} = \rho_{2} ,\,\,l_{1} = l_{2} = l,\,\,\,{\text{and}}\,\,\,s \to 0\), Eq. (36) imparts

$$K_{s} = - F_{c} \sqrt {\frac{l}{\pi }} .$$
(40)

Equation (40) gives the result of SIF for centrally \(\left( {{\text{i}}{\text{.e}}{.}\,\,l_{1} = l_{2} } \right)\) located static crack propagating in homogeneous composite strip when crack edges are under CL condition.

2.1.2 Case 2 rectilinear semi-infinite crack edges under SF

Here, we shall formulate the problem for moving crack caused by propagating SH-wave in non-homogeneous composite strip when crack edges are subjected to SF condition. We suppose that the constant displacement \(u_{2} = \pm u_{0}\) is prescribed over the surfaces \(z_{1} = l_{1} \,\,\,{\text{and}}\,\,z_{1} = - l_{2}\), and edges of crack in non-homogeneous composite strip are under SF conditions.

Now, using the superposition method in the determined result of SIF given by Eq. (36), we obtain the solution for SIF by adding solutions for composite strip considering \(u_{2} = \pm u_{0}\) on surfaces \(z_{1} = l_{1} \,\,\,{\text{and}}\,\,z_{1} = - l_{2}\), and composite strip containing a crack loaded by constant load \(\overline{\overline{\tau }}_{{y_{1}^{\prime } z^{\prime}_{1} }} \left( {x^{\prime}_{1} ,\,\,0} \right) = - \overline{\tau }_{{y_{1}^{\prime } z^{\prime}_{1} }} \left( {x^{\prime}_{1} ,\,\,0} \right) = \varphi_{0}\). The component of displacement function \(\overline{u}_{2} ,\) and the components of stress \(\overline{\tau }_{{x^{\prime}_{1} y^{\prime}_{1} }} \left( {x^{\prime}_{1} ,\,\,z^{\prime}_{1} } \right)\,\,{\text{and}}\,\,\overline{\tau }_{{y^{\prime}_{1} z^{\prime}_{1} }} \left( {x^{\prime}_{1} ,\,\,z^{\prime}_{1} } \right)\) may be defined as

$$\left. \begin{aligned} \overline{u}_{2} \left( {x^{\prime}_{1} ,z^{\prime}_{1} } \right) =\; & u_{0} \left[ { - 1 + \frac{{2(l_{1} - z^{\prime}_{1} )}}{{l_{2} (k + \lambda )}}} \right]\;\;{\text{for}}\;\left| {z^{\prime}_{1} } \right| < \infty ,\;0 \le z^{\prime}_{1} \le l_{1} , \\ =\; & u_{0} \left[ {1 - \frac{{2\lambda (l_{2} + z^{\prime}_{1} )}}{{l_{2} (k + \lambda )}}} \right]\;\;{\text{for}}\;\left| {z^{\prime}_{1} } \right| < \infty ,\; - l_{2} \le z^{\prime}_{1} \le 0, \\ \overline{\tau }_{{x_{1}^{\prime } y_{1}^{\prime } }} \left( {x^{\prime}_{1} ,z^{\prime}_{1} } \right) =\; & 0,\;\;{\text{for}}\;\left| {z^{\prime}_{1} } \right| < \infty ,\; - l_{2} \le z^{\prime}_{1} \le l_{1} , \\ \overline{\tau }_{{y^{\prime}_{1} z^{\prime}_{1} }} \left( {x^{\prime}_{1} ,z^{\prime}_{1} } \right) =\; & - \frac{{2M_{1} u_{0} }}{{l_{2} (k + \lambda )}},\;\;{\text{for}}\;\left| {x^{\prime}_{1} } \right| < \infty ,\; - l_{2} \le z^{\prime}_{1} \le l_{1} , \\ \end{aligned} \right\}$$
(41)

such that

$$\overline{\overline{\tau }}_{{y^{\prime}_{1} z^{\prime}_{1} }} \left( {x^{\prime}_{1} ,\,\,0} \right) = - \overline{\tau }_{{y^{\prime}_{1} z^{\prime}_{1} }} \left( {x^{\prime}_{1} ,\,\,0} \right) = \varphi_{0} = \frac{{2M_{1} u_{0} }}{{l_{2} \left( {k + \lambda } \right)}}.$$
(42)

In view of Eq. (41), the result for SIF in Eq. (36) yields

$$K = - 2M_{1} u_{0} \sqrt {\frac{{c_{1} }}{{\pi l_{2} \left( {k + \lambda } \right)\left( {1 + \vartheta } \right)}}} .$$
(43)

Equation (43) gives the result for SIF for propagating rectilinear semi-infinite non-centrally \(\left( {{\text{i}}{\text{.e}}{.}\,\,l_{1} \ne l_{2} } \right)\) located crack in non-homogeneous composite strip when crack edges in the strip are subjected to SF condition.

2.1.2.1 Subcase 2.1

When \(N_{1} = N_{2} ,\,M_{1} = M_{2} ,\,\,\rho_{1} = \rho_{2} ,\,\,{\text{and}}\,\,l_{1} = l_{2} = l\), then Eq. (43) transforms to

$$K = - M_{1} u_{0} \sqrt {\frac{c}{\pi l}} .$$
(44)

Equation (44) gives the result of SIF for centrally \(\left( {{\text{i}}{\text{.e}}{.}\,\,l_{1} = l_{2} } \right)\) located crack propagating in homogeneous composite strip when crack edges in the strip are subjected to SF condition.

2.1.2.2 Subcase 2.2

When \(s \to 0,\) Eq. (43) takes the form

$$K_{s} = - \frac{{2M_{1} u_{0} }}{{\sqrt {\pi l_{2} \left( {k + \lambda } \right)\left( {1 + \lambda } \right)} }}.$$
(45)

Equation (45) gives the result of SIF for non-centrally \(\left( {{\text{i}}{\text{.e}}{.}\,\,l_{1} \ne l_{2} } \right)\) located static crack in non-homogeneous composite strip when edges of the static crack are under SF condition.

2.1.2.3 Subcase 2.3

When \(N_{1} = N_{2} ,M_{1} = M_{2} ,\,\,\rho_{1} = \rho_{2} ,\,\,s \to 0\,\,{\text{and}}\,\,l_{1} = l_{2} = l,\) Eq. (43) yields

$$K_{s} = - \frac{{M_{1} u_{0} }}{{\sqrt {\pi l} }}.$$
(46)

Equation (46) gives the result of SIF for centrally \(\left( {{\text{i}}{\text{.e}}{.}\,\,l_{1} = l_{2} } \right)\) located static crack in homogeneous composite strip when crack edges are under SF condition.

2.1.2.4 Subcase 2.4

When \(N_{1} = N_{2} ,M_{1} = M_{2} ,\,\,\rho_{1} = \rho_{2} \,{\text{and}}\;s \to 0,\) Eq. (43) reduces to

$$K_{s} = - \frac{{M_{1} u_{0} }}{{\sqrt {\pi l} }}.$$
(47)

Equation (47) gives the result of SIF for non-centrally \(\left( {{\text{i}}{\text{.e}}{.}\,\,l_{1} \ne l_{2} } \right)\) located static crack in non-homogeneous composite strip when edges of the crack are under SF condition.

2.2 Mathematical model of the crack under HL conditions

In order to model the quasi static HL on crack edges, it is assumed that displacement and stress are time dependent harmonic function, and therefore, the following transformation has been considered, which is represented as

$$\ell \left( {x_{1} ,\,\,z_{1} ,\,\,t} \right) = \ell^{*} \left( {x_{1} ,\,\,z_{1} } \right)\exp \left( {i\omega t} \right),$$
(48)

wherein \(\omega\) is the frequency.

With the help of (48), Eq. (7) leads to

$$\frac{{\partial^{2} u_{2}^{*} }}{{\partial x_{1}^{2} }} + \frac{1}{{\alpha_{0}^{2} }}\frac{{\partial^{2} u_{2}^{*} }}{{\partial z_{1}^{2} }} + \eta^{2} u_{2}^{*} = 0,\,$$
(49)
$$\,{\text{with}}\,\,\eta = \frac{\omega }{{S_{T} }}.$$

Performing Fourier transform (8) to Eqs. (5) and (49) leads to the following equations

$$\left. \begin{gathered} \frac{{{\text{d}}^{2} \tilde{u}_{2}^{*} (\alpha ,z_{1} )}}{{dz_{1}^{2} }} - \alpha_{0}^{2} \left( {\alpha^{2} - \eta^{2} } \right)\tilde{u}_{2}^{*} \left( {\alpha ,z_{1} } \right) = 0, \hfill \\ \tilde{\tau }_{{x_{1} y_{1} }}^{*} (\alpha ,z_{1} ) = - iN\tilde{u}_{2}^{*} \left( {\alpha ,z_{1} } \right), \hfill \\ \tilde{\tau }_{{y_{1} z_{1} }}^{*} (\alpha ,z_{1} ) = M\frac{{{\text{d}}\tilde{u}_{2}^{*} \left( {\alpha ,z_{1} } \right)}}{{{\text{d}}z_{1}^{2} }}. \hfill \\ \end{gathered} \right\}$$
(50)

After solving Eq. (50), we obtain harmonic function displacement and stresses as

$$\left. \begin{aligned} \tilde{u}_{2}^{*} (\alpha ,z_{1} ) =\; & A_{3} \left( \alpha \right)\sinh z_{1} \alpha_{0} \sqrt {\alpha^{2} - \eta^{2} } + A_{4} \left( \alpha \right)\cosh z_{1} \alpha_{0} \sqrt {\alpha^{2} - \eta^{2} } , \\ \tilde{\tau }_{{x_{1} y_{1} }}^{*} (\alpha ,z_{1} ) =\; & - iN\alpha \left[ {A_{3} \left( \alpha \right)\sinh z_{1} \alpha_{0} \sqrt {\alpha^{2} - \eta^{2} } + A_{4} \left( \alpha \right)\cosh z_{1} \alpha_{0} \sqrt {\alpha^{2} - \eta^{2} } } \right], \\ \tilde{\tau }_{{y_{1} z_{1} }}^{*} (\alpha ,z_{1} ) =\; & M\alpha_{0} \sqrt {\alpha^{2} - \eta^{2} } \left[ {A_{3} \left( \alpha \right)\cosh z_{1} \alpha_{0} \sqrt {\alpha^{2} - \eta^{2} } + A_{4} \left( \alpha \right)\sinh z_{1} \alpha_{0} \sqrt {\alpha^{2} - \eta^{2} } } \right], \\ \end{aligned} \right\}$$
(51)

where \(A_{3} \left( \alpha \right)\) and \(A_{4} \left( \alpha \right)\) are unknown functions to be determined.

Now, the following form of the load may be considered to be applicable on crack edges in the composite strip

$$\tau_{{y_{1} z_{1} }} = \varphi_{0} \left( {x_{1} } \right) + \varphi \left( {x_{1} } \right)\exp \left( {i\omega t} \right).$$
(52)

With the help of Eq. (48), the geometrical constraints are transformed as

$$\left. \begin{gathered} u_{2}^{{*^{\left( 1 \right)} }} \left( {x_{1} ,\,\,z_{1} } \right) = 0,\,\,{\text{for}}\,\,\left| {x_{1} } \right| < \infty ,\,\,z_{1} = - l_{1} , \hfill \\ u_{2}^{{*^{\left( 2 \right)} }} \left( {x_{1} ,\,\,z_{1} } \right) = 0,\,\,{\text{for}}\,\,\left| {x_{1} } \right| < \infty ,\,\,z_{1} = l_{2} , \hfill \\ \tau_{{y_{1} z_{1} }}^{*\left( 1 \right)} \left( {x_{1} ,\,\,z_{1} } \right) = \tau_{{y_{1} z_{1} }}^{*\left( 2 \right)} \left( {x_{1} ,\,\,z_{1} } \right) = \varphi \left( {x_{1} } \right)\,\,{\text{for}}\,\,x_{1} < 0,\,\,z_{1} = 0, \hfill \\ u_{2}^{{*^{\left( 1 \right)} }} \left( {x_{1} ,\,\,z_{1} } \right) = u_{2}^{{*^{\left( 2 \right)} }} \left( {x_{1} ,\,\,z_{1} } \right)\,\,{\text{for}}\,\,x_{1} > 0,\,\,z_{1} = 0, \hfill \\ \tau_{{y_{1} z_{1} }}^{*\left( 1 \right)} \left( {x_{1} ,\,\,z_{1} } \right) = \tau_{{y_{1} z_{1} }}^{*\left( 2 \right)} \left( {x_{1} ,\,\,z_{1} } \right)\,\,{\text{for}}\,\,x_{1} > 0,\,\,z_{1} = 0, \hfill \\ \end{gathered} \right\}$$
(53)

where superscripts (1) and (2) correspond to upper orthotropic medium and lower orthotropic medium, respectively.

Using Fourier transform (8) and Eq. (51), Eq. (53) gives the following equations

$$\left. \begin{gathered} \tilde{u}_{2}^{*\left( 1 \right)} \left( {\alpha ,0} \right) = - \frac{{\tanh l_{1} \alpha_{0}^{\left( 1 \right)} \sqrt {\left( {\alpha^{2} - \eta_{1}^{2} } \right)} }}{{M_{1} \alpha_{0}^{\left( 1 \right)} \sqrt {\left( {\alpha^{2} - \eta_{1}^{2} } \right)} }}\tilde{\tau }_{{y_{1} z_{1} }}^{*\left( 1 \right)} (\alpha ,0), \hfill \\ \tilde{u}_{2}^{*\left( 2 \right)} \left( {\alpha ,0} \right) = \frac{{\tanh l_{2} \alpha_{o}^{\left( 2 \right)} \sqrt {\left( {\alpha^{2} - \eta_{2}^{2} } \right)} }}{{M_{2} \alpha_{0}^{\left( 2 \right)} \sqrt {\left( {\alpha^{2} - \eta_{2}^{2} } \right)} }}\tilde{\tau }_{{y_{1} z_{1} }}^{*\left( 2 \right)} (\alpha ,0), \hfill \\ \end{gathered} \right\}$$
(54)
$${\text{where}}\;\eta_{i} = \frac{\omega }{{S_{{T_{i} }} }},\;\alpha_{0}^{\left( i \right)} = \sqrt {\frac{{N_{i} }}{{M_{i} }}} ,\;i = 1,\;2.$$

In view of last two relations of Eq. (53) and Eqs. (9) and (10), we may obtain the following relations as

$$\left. \begin{gathered} \tilde{u}_{2}^{*\left( 1 \right)} \left( {\alpha ,0} \right) - \tilde{u}_{2}^{*\left( 2 \right)} \left( {\alpha ,0} \right) = \tilde{u}_{2}^{* - } \left( \alpha \right), \hfill \\ \tilde{\tau }_{{y_{1} z_{1} }}^{*\left( 1 \right)} \left( {\alpha ,0} \right) = \tilde{\tau }_{{y_{1} z_{1} }}^{* + } \left( \alpha \right) + \psi \left( \alpha \right), \hfill \\ \end{gathered} \right\}$$
(55)
$${\text{where}}\;\psi \left( \alpha \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{0} {\varphi \left( {x_{1} } \right)} e^{{i\alpha x_{1} }} {\text{d}}x_{1} .$$
(56)

Following Eq. (55), Eq. (54) can be written as

$$\tilde{u}_{2}^{* - } \left( \alpha \right) = - \zeta \left( \alpha \right)\left[ {\tilde{\tau }_{{y_{1} z_{1} }}^{* + } (\alpha ) + \psi \left( \alpha \right)} \right],$$
(57)

where

$$\zeta \left( \alpha \right) = \frac{{\tanh l_{1} \alpha_{0}^{\left( 1 \right)} \sqrt {(\alpha^{2} - \eta_{1}^{2} )} }}{{M_{1} \alpha_{0}^{\left( 1 \right)} \sqrt {(\alpha^{2} - \eta_{1}^{2} )} }} + \frac{{\tanh l_{2} \alpha_{0}^{\left( 2 \right)} \sqrt {(\alpha^{2} - \eta_{2}^{2} )} }}{{M_{2} \alpha_{0}^{\left( 2 \right)} \sqrt {(\alpha^{2} - \eta_{2}^{2} )} }}.$$
(58)

The feasible domain for Eq. (57) is given by

$${\text{ - min}}\left( {\sqrt {\frac{{\pi^{2} }}{{4l_{1}^{2} \left( {\alpha_{0}^{\left( 1 \right)} } \right)^{2} }} - \eta_{1}^{2} } ,\sqrt {\frac{{\pi^{2} }}{{4l_{2}^{2} \left( {\alpha_{0}^{\left( 2 \right)} } \right)^{2} }} - \eta_{2}^{2} } } \right) < - \varepsilon < {\text{Im}} \alpha { < 0}{\text{.}}$$
(59)

Now, following the method of Koiter [34], we can factorize \(\zeta \left( \alpha \right)\) as

$$\zeta \left( \alpha \right) = \zeta^{ - } \left( \alpha \right)\zeta_{1} \left( \alpha \right),$$
(60)

where

$$\zeta^{ - } \left( \alpha \right) = \frac{1 + \lambda }{{M_{1} }}I^{ - } \left( \alpha \right)I^{ + } \left( \alpha \right),\;I^{ \pm } \left( \alpha \right) = \frac{1}{{\sqrt {\alpha \pm iT_{1} } }},\;T_{1} = \frac{{\eta_{1} \left( {1 + \lambda } \right)}}{{\tan l_{1} \eta_{1} + r\tan l_{2} \eta_{2} }},\;r = \lambda \frac{{\eta_{1} }}{{\eta_{2} }},$$
(61)

and we assume that the function \(\zeta_{1} \left( \alpha \right)\) is analytic, and does not contain zeros and singularities in the considered domain

$$\left| {{\text{Im}}\,\alpha } \right| < \varepsilon_{1} ,\,\,0 < \varepsilon \le \varepsilon_{1} < \min \left( {\sqrt {\frac{{\pi^{2} }}{{4l_{1}^{2} \left( {\alpha_{0}^{1} } \right)^{2} }} - \eta_{1}^{2} } ,\,\,\sqrt {\frac{{\pi^{2} }}{{4l_{2}^{2} \left( {\alpha_{0}^{2} } \right)^{2} }} - \eta_{2}^{2} } } \right).$$
(62)

Applying Abel theorem [35], the results for displacement and stress concerned with quasi-static crack along \(x^{\prime}_{1}\)-axis at \(\left| {x^{\prime}_{1} } \right| \to 0\) involving HL in a non-homogeneous composite strip are given by

$$\left. \begin{gathered} u_{2}^{\left( 1 \right)} \left( {x_{1} } \right) - u_{2}^{\left( 2 \right)} \left( {x_{1} } \right) = \frac{{2\left( {1 + \lambda } \right)K_{q} }}{{M_{1} }}\sqrt { - x_{1} } \,\,{\text{for }}x_{1} \to 0^{ - } , \hfill \\ \tau_{{y_{1} z_{1} }}^{\left( 1 \right)} \left( {x_{1} } \right) = \tau_{{y_{1} z_{1} }}^{\left( 2 \right)} \left( {x_{1} } \right) = \frac{{K_{q} }}{{\sqrt {x_{1} } }},\,\,{\text{for }}x_{1} \to 0^{ + } . \hfill \\ \end{gathered} \right\}$$
(63)

The expression of SIF for the propagating crack subjected to HL in a non-homogeneous composite strip may be written as

$$K_{q} = K^{*} \left( {\varphi ,\omega } \right)\exp \left( {i\omega t} \right),$$
(64)
$${\text{wherein}}\;K^{*} \left( {\varphi ,\omega } \right) = - \frac{{\sqrt { - 2i} }}{2\pi i}\int\limits_{ - \infty - i\delta }^{\infty - i\delta } {I^{ + } \left( \alpha \right)} \zeta_{1}^{ + } \left( \alpha \right)\psi (\alpha ){\text{d}}\alpha ,$$
(65)

with \(\omega < \min \left( {{{\pi S_{{T_{1} }} } \mathord{\left/ {\vphantom {{\pi S_{{T_{1} }} } {2l_{1} }}} \right. \kern-0pt} {2l_{1} }},\;{{\pi S_{{T_{2} }} } \mathord{\left/ {\vphantom {{\pi S_{{T_{2} }} } {2l_{2} }}} \right. \kern-0pt} {2l_{2} }}} \right)\).

The SIF for static crack subjected to NHL in a non-homogeneous composite strip can be determined by substituting \(\omega = 0\) in Eqs. (64) and (65). Applying principle of superposition on the deduced results thereafter, the resulting expression of SIF can be obtained for the crack loaded by \(\tau_{{y_{1} z_{1} }} = \varphi_{0} \left( {x_{1} } \right) + \varphi \left( {x_{1} } \right)\exp \left( {i\omega t} \right)\) in a non-homogeneous composite strip, and it may be considered in the form

$$K_{q} = K^{*} \left( {\varphi_{0} ,0} \right) + K^{*} \left( {\varphi ,\omega } \right)\exp \left( {i\omega t} \right).$$
(66)

2.2.1 Case 3 rectilinear semi-infinite crack edges under CAL

Here, we shall find SIF pertaining to crack edges under HL along with CAL in non-homogeneous composite strip, i.e.

$$\tau_{{y_{1} z_{1} }} = \varphi_{0} + \varphi_{1} \cos \omega t,$$
(67)

where \(\varphi_{0} \,\,{\text{and}}\,\,\varphi_{1}\) are constants.

In view of Eqs. (56), (61) and (67), Eq. (65) yields

$$K^{*} \left( {\varphi ,\omega } \right) = - \varphi_{1} \sqrt {\frac{i}{\pi }} \frac{1}{2\pi i}\int\limits_{ - \infty - i\delta }^{\infty - i\delta } {\frac{{\zeta_{1} \left( \alpha \right)}}{{\alpha \sqrt {\alpha + iT_{1} } }}{\text{d}}\alpha } .$$
(68)

On performing integration in Eq. (68) and using the fact that \(\zeta_{1}^{ + } \left( 0 \right) = 1,\) SIF may be obtained as

$$K^{*} \left( {\varphi ,\omega } \right) = - \varphi_{1} \sqrt {\frac{{l_{2} }}{\pi }} \sqrt {\frac{{k\left( {\tan \eta_{1}^{*} - \psi \tan \delta \eta_{1}^{*} } \right)}}{{\eta_{1}^{*} \left( {1 + \lambda } \right)}}} ,$$
(69)
$${\text{where}}\;\eta_{1}^{*} = \eta_{1} l_{1} ,\;\delta = \frac{\lambda }{kr}.$$

The expression of SIF for limiting static case, when crack edges are under HL along with CAL in non-homogeneous composite strip, may be obtained by assuming \(\omega = 0\) in Eq. (69). With the help of (39), (66) and (69), the final expression of SIF may be given by

$$K = - \varphi_{0} \sqrt {\frac{{l_{2} }}{{\pi \left( {1 + \lambda } \right)}}} \left[ {\sqrt {k + \lambda } + \frac{{\varphi_{1} }}{{\varphi_{0} }}\sqrt {\frac{{k\left( {\tan \eta_{1}^{*} + r\tan \delta \eta_{1}^{*} } \right)}}{{\eta_{1}^{*} }}} \cos \omega t} \right].$$
(70)

Now, as a special case for isotropic elastic medium, i.e. when \(N_{1} = M_{1} = \mu_{1} ,\;N_{2} = M_{2} = \mu_{2} ,\) then Eq. (70) reduces to

$$\begin{aligned} K^{\prime \prime } = & - \varphi_{0} \sqrt {\frac{{l_{2} }}{{\pi \left( {1 + \lambda^{\prime } } \right)}}} \left[ {\sqrt {k + \lambda^{\prime } } + \frac{{\varphi_{1} }}{{\varphi_{0} }}\sqrt {\frac{{k\left( {\tan \eta_{1}^{\prime \prime } + r^{\prime } \tan {\updelta }^{\prime } \eta_{1}^{\prime \prime } } \right)}}{{\eta_{1}^{\prime \prime } }}} \cos \omega t} \right],\;\eta_{1}^{\prime \prime } = \eta_{1}^{\prime } l_{1} ,\;\eta_{1}^{\prime } = \frac{\omega }{{S_{{T_{1}^{\prime } }} }}, \\ \eta_{2}^{\prime } = & \frac{\omega }{{S_{{T_{2}^{\prime } }} }}\;{\updelta }^{\prime } { = }\frac{{\lambda^{\prime } }}{{kr^{\prime}}},\;r^{\prime } = \lambda^{\prime } \frac{{\eta_{1} }}{{\eta_{2} }}, \\ \end{aligned}$$

which leads to SIF for the propagating crack in non-homogeneous isotropic elastic strip when edges of crack are subjected to CAL condition. This expression of SIF concurs well with the result established by Matczyński [37].

Following Eq. (70), it is seen that when \(\omega \to \min \left( {\frac{{\pi S_{{T_{1} }} }}{{2l_{1} }},\frac{{\pi S_{{T_{2} }} }}{{2l_{2} }}} \right)\), a resonance-type phenomena occurs. Owing to the occurrence of resonance-type phenomena, arbitrary small load component \(\varphi_{1}\) results in \(K \to \infty .\) Further, the maximum value of SIF for a constant \(\omega\) can be written as

$$K_{m} = - \varphi_{0} \sqrt {\frac{{l_{2} }}{{\pi \left( {1 + \lambda } \right)}}} \left[ {\sqrt {k + \lambda } + \frac{{\varphi_{1} }}{{\varphi_{0} }}\sqrt {\frac{{k\left( {\tan \eta^{*} + r\tan {\updelta }\eta^{*} } \right)}}{{\eta^{*} }}} } \right].$$
(71)

Equation (71) imparts the result of SIF for the propagating rectilinear semi-infinite non-centrally \(\left( {{\text{i}}{\text{.e}}{.}\,\,l_{1} \ne l_{2} } \right)\) located crack in non-homogeneous composite strip when edges of crack are subjected to CAL condition.

2.2.1.1 Subcase 3.1

When \(k = \lambda = r = 1,\) Eq. (70) leads to

$$K = - \varphi_{0} \sqrt {\frac{l}{\pi }} \left[ {1 + \frac{{\varphi_{1} }}{{\varphi_{0} }}\sqrt {\frac{{\tan \eta^{*} }}{{\eta^{*} }}} \cos \omega t} \right],$$
(72)
$${\text{where}}\;\;\eta^{{*^{{}} }} = \frac{l\omega }{{S_{T} }}.$$

Equation (72) gives the result of SIF when centrally located crack edges in homogeneous composite strip are subjected to HL along with CAL.

2.2.2 Case 4 rectilinear semi-infinite crack edges under SF

Here, we shall determine the result of SIF when crack edges are stress free. We may use the assumption on the boundary surface that \(z_{1} = l_{1} \,\,{\text{and}}\,\,z_{1} = - l_{2}\) are under \(u_{2} = \pm \left( {u_{0} + u_{0}^{*} \cos \omega t} \right),\,\,\omega < \min \left( {\frac{{\pi S_{{T_{1} }} }}{{2l_{1} }},\frac{{\pi S_{{T_{2} }} }}{{2l_{2} }}} \right);\,\,u_{0} ,\,\,u_{0}^{*}\) being constants. Now, the displacement \(\left( {u_{2} } \right)\) and the stress components \(\left( {\tau_{{x_{1} y_{1} }} \,{\text{and}}\,\,\tau_{{y_{1} z_{1} }} } \right)\) take the form

$$u_{2} \left( {x_{1} ,z_{1} ,t} \right) = \left\{ \begin{gathered} - u_{0}^{*} \cos \omega t\left[ {g_{1} \left( \eta \right)\sin \eta_{1} z_{1} - g_{2} \left( \eta \right)\cos \eta_{1} z_{1} } \right]\,\,{\text{for}}\,0 \le z_{1} \le l_{1} , \hfill \\ - u_{0}^{*} \cos \omega t\left[ {\,rg_{1} \left( \eta \right)\sin \eta_{2} z_{1} - g_{2} \left( \eta \right)\cos \eta_{2} z_{1} } \right]\,\,{\text{for}} - l_{2} \le z_{1} \le 0, \hfill \\ \end{gathered} \right.$$
(73)
$$\tau_{{x_{1} y_{1} }} \left( {x_{1} ,z_{1} ,t} \right) = 0\,\,{\text{for}} - l_{2} \le z_{1} \le l_{1} ,$$
(74)
$$\tau_{{y_{1} z_{1} }} \left( {x_{1} ,z_{1} ,t} \right) = \left\{ \begin{gathered} - u_{0}^{*} M_{1} \eta_{1} \cos \omega t\left[ {g_{2} \left( \eta \right)\sin \eta_{1} z_{1} + g_{1} \left( \eta \right)\cos \eta_{1} z_{1} } \right]\,\,{\text{for}}\,\,{0} \le z_{1} \le l_{1} , \hfill \\ - u_{0}^{*} M_{2} \eta_{2} \cos \omega t\left[ {g_{2} \left( \eta \right)\sin \eta_{2} z_{1} + rg_{1} \left( \eta \right)\cos \eta_{2} z_{1} } \right]\,\,{\text{for}} - l_{2} \le z_{1} \le 0, \hfill \\ \end{gathered} \right.$$
(75)
$${\text{where}}\;\;g_{1} \left( \eta \right) = \frac{{\cos \eta_{1}^{*} + \cos {\updelta }\eta_{1}^{*} }}{{\cos \eta_{1}^{*} \cos {\updelta }\eta_{1}^{*} \left( {\tan \eta_{1}^{*} + r\tan {\updelta }\eta_{1}^{*} } \right)}},\;g_{2} \left( \eta \right) = \frac{{\sin \eta_{1}^{*} - r\sin {\updelta }\eta_{1}^{*} }}{{\cos \eta_{1}^{*} \cos {\updelta }\eta_{1}^{*} \left( {\tan \eta_{1}^{*} + r\tan {\updelta }\eta_{1}^{*} } \right)}}.$$

In view of Eqs. (41), (42), (73) and (75), we may have

$$\left. \begin{gathered} \varphi_{0} = \frac{{2M_{1} u_{0} }}{{l_{2} (k + \lambda )}}, \hfill \\ \varphi_{1} = \frac{{M_{1} u_{0} \left( {\cos \eta_{1}^{*} + \cos {\updelta }\eta_{1}^{*} } \right)}}{{\cos \eta_{1}^{*} \cos {\updelta }\eta_{1}^{*} \left( {\tan \eta_{1}^{*} + r\tan {\updelta }\eta_{1}^{*} } \right)}}. \hfill \\ \end{gathered} \right\}$$
(76)

By means of Eq. (76), Eq. (70) gives

$$K = - \frac{{2M_{1} u_{0} }}{{\sqrt {\pi l_{2} \left( {1 + \lambda } \right)} }}\left[ {\frac{1}{{\sqrt {k + \lambda } }} + \frac{{u_{0}^{*} p\left( \eta \right)}}{{u_{0} }}\cos \omega t} \right],$$
(77)
$${\text{where}}\, \, p\left( \eta \right) = \frac{{\cos \eta_{1}^{*} + \cos \delta \eta_{1}^{*} }}{{2\cos \eta_{1}^{*} \cos \delta \eta_{1}^{*} }}\sqrt {\frac{{\eta_{1}^{*} }}{{k\left( {\tan \eta_{1}^{*} + r\tan \delta \eta_{1}^{*} } \right)}}} .$$
(78)

Equation (77) establishes the result of SIF when non-centrally located crack edges are SF in non- homogeneous composite strip.

2.2.2.1 Subcase 4.1

To obtain the expression of SIF for propagating crack in limiting static case, we can assume that \(\omega \to 0\) in the Eq. (77), and in limiting static case of the propagating crack in the composite strip, \(u_{2} = \pm \left( {u_{0} + u_{0}^{*} } \right)\), and SIF is given as

$$K_{s} = - \frac{{2M_{1} u_{0} }}{{\sqrt {\pi l_{2} \left( {k + \lambda } \right)\left( {1 + \lambda } \right)} }}.$$
(79)

Equation (79) signifies the result of SIF in the limiting static case when non-centrally located crack edges are SF in non-homogeneous composite strip. It may also be noted from Eq. (77) that when \(\omega \to {\text{min}}\left( {\frac{{\pi S_{{T_{1} }} }}{{2l_{1} }},\frac{{\pi S_{{T_{2} }} }}{{2l_{2} }}} \right)\), yet again resonance-type phenomena is seen that leads to \(K \to \infty\).

Now, the maximum value of SIF for the constant \(\omega\) is determined by using Eq. (77) as

$$K_{m} = - \frac{{2M_{1} u_{0} }}{{\sqrt {\pi l_{2} \left( {1 + \lambda } \right)} }}\left[ {\frac{1}{{\sqrt {k + \lambda } }} + \frac{{u_{0}^{*} p\left( \eta \right)}}{{u_{0} }}} \right].$$
(80)
2.2.2.2 Subcase 4.2

When \(k = \lambda = r = 1,\) Eq. (77) leads to

$$K = - \frac{{M_{1} u_{0} }}{{\sqrt {\pi l} }}\left[ {1 + \frac{{u_{0}^{*} }}{{u_{0} }}\sqrt {\frac{{2\eta^{*} }}{{\sin 2\eta^{*} }}} \cos \omega t} \right],\;\;{\text{where}}\;\;\eta^{*} = \frac{\omega l}{{S_{T} }}.$$
(81)

Equation (81) imparts the result of SIF when centrally located crack edges are SF in homogeneous composite strip.

3 Numerical simulation and discussion

In order to perform numerical simulation and execute graphical demonstration of SIF, different kind of materials (Prosser and Green [38]) have been used with the following mechanical properties:

$${\text{Si}}_{3} {\text{N}}_{4} :N = 38.5 \times 10^{9} \;\left( {N/m^{2} } \right),\;M = 1.08 \times 10^{9} \;\left( {N/m^{2} } \right),\;\rho = 3200\;\left( {kg/m^{3} } \right),$$
$${\text{Zinc}}:N = 38.5 \times 10^{9} \;\left( {N/m^{2} } \right),\;M = 1.08 \times 10^{9} \;\left( {N/m^{2} } \right),\;\rho = 1740\;\left( {kg/m^{3} } \right),$$

T300/5208 graphite/epoxy material:

$$N = 14.295 \times 10^{9} \;\left( {N/m^{2} } \right),\;M = 5.27 \times 10^{9} \;\left( {N/m^{2} } \right),\;\rho = 1422\;\left( {kg/m^{3} } \right).$$

Unless otherwise specified

$$k = 0.5,\,\,1.0,\,\,2.0;\,\,k_{1} = \frac{{\varphi_{1} }}{{\varphi_{0} }} = 0.5,\,\,1.0,\,\,2.0;\,\,d = \frac{{u_{0}^{*} }}{{u_{0} }} = 0.5,\,\,1.0,\,\,2.0;\,\,\gamma { = 0}{\text{.5,}}\,\,1.0,\,\,1.5.$$

Figures 2, 4 and 6 portray the efficacy of SIF against the velocity of crack \(\left( {s/S_{{T_{1} }} } \right)\) subjected to SH-wave propagation in non-homogeneous composite strip when edges of crack are under NHL conditions. In the aforesaid figures, the curves 1, 2 and 3 are directed towards the case of NHL under CL while the curves 4, 5 and 6 are associated with crack edges under NHL and SF conditions. After minute observation of the above figures, it has been noticed that SIF for CL and SF reduces slowly with rise in velocity of crack in composite strip. It is also reported that as the velocity of crack tends to 1, SIF for both the aforesaid loading constraints falls down to zero.

Furthermore, the analysis of SIF against dimensionless crack velocity \(\left( {\eta_{1}^{*} } \right)\) under HL condition in non-homogeneous composite strip is delineated in Figs. 3, 5, 7 and 9. In the aforementioned figures, curves 1, 2 and 3 indicate the case of HL on crack edges subjected to CAL condition, whereas curves 4, 5 and 6 signify the case of SF condition. It can be traced out from these figures that the value of SIF in both the aforementioned cases associated with HL upsurge incessantly with rise in velocity of crack in composite strip.

The influence of thickness ratio parameter on SIF for CL and SF under NHL condition on crack edges has been outlined in Fig. 2. Moreover, the impact of thickness ratio parameter on SIF for both the cases (CAL and SF) in harmonic loading (HL) condition is depicted in Fig. 3. In the aforesaid figures (Figs. 2 and 3), curves 2 and 5 represent the condition when the crack is centrally located in the non-homogenous composite strip, whereas curves (1, 3, 4 and 6) describe the situation of crack which is non-centrally located in non-homogenous composite strip. The computational results of Figs. 2 and 3 manifest that thickness ratio parameter have favourable impact on SIF in the case of NHL along with CL condition and in HL with CAL condition. On the other hand, thickness ratio parameter disfavours SIF for the scenario when crack edges are subjected to SF condition for both types of HL and NHL conditions.

Fig. 2
figure 2

Variation of SIF for the case of NHL along with CL and SF conditions against dimensionless crack velocity \(\left( {s/S_{{T_{1} }} } \right)\) for various values of thickness ratio parameter \(\left( k \right)\) of non-homogenous composite strip

Full size image
Fig. 3
figure 3

Variation of SIF for the case of HL along with CAL and SF conditions against dimensionless crack velocity \(\left({\eta }_{1}^{*}\right)\) for various values of parameter \(\left(k\right)\) of non-homogenous composite strip

Full size image

The impact of inhomogeneity parameter on stress intensity factor for non-harmonic loading and harmonic loading constraints is depicted in Figs. 4 and 5. It can be observed from Figs. 4 and 5 that the increment in inhomogeneity parameter of the layers in the composite strip leads to increment in the value of SIF when crack edges are under NHL with CL conditions. However, in the case of SF condition on edges of crack subjected to NHL condition, it leads to adverse impact on SIF. Moreover, SIF for HL with CAL and SF conditions dismounts as inhomogeneity parameter surmounts.

Fig. 4
figure 4

Variation of SIF for the case of NHL along with CL and SF conditions against dimensionless crack velocity \(\left( {s/S_{{T_{1} }} } \right)\) for various values of inhomogeneity parameter \(\left( \gamma \right)\) of layered medium of non-homogenous composite strip

Full size image
Fig. 5
figure 5

Variation of SIF against crack velocity \(\left({\eta }_{1}^{*}\right)\) in non-homogeneous composite strip [upper (Zn) layer and lower (Si3N4) layer] for various values of parameter \(\left( \gamma \right)\) of layered medium for the case of HL along with CAL and SF conditions

Full size image

For the purpose of comparative analysis of SIF pertaining to non-centrally located crack in different material combinations of configured composite strip [viz. when upper layer is made up of Zn material and lower layer is made up of graphite/epoxy material (non-homogeneous strip); when upper and lower layer are made up of Zn material (homogeneous strip); and when upper layer is of Zn material, and lower layer is of Si3N4 material (non-homogeneous composite strip)], Figs. 6 and 7 have been traced out for the cases of NHL and HL conditions, respectively. It has been found that when non-homogenous composite strip becomes homogeneous, SIF is minimum for CL case, whereas it is moderate for SF case under NHL condition. It is further noticed that SIF is moderate for both the cases of CAL and SF under HL condition, when non-homogenous composite strip becomes homogeneous.

Fig. 6
figure 6

Comparison of SIF against crack velocity \(\left( {s/S_{{T_{1} }} } \right)\) for various material layers in composite strip for the case of NHL along with CL and SF conditions

Full size image
Fig. 7
figure 7

Comparison of SIF against crack velocity \(\left({\eta }_{1}^{*}\right)\) for various material layers in composite strip for the case of HL along with CAL and SF conditions

Full size image

For static crack, the impact of inhomogeneity parameter on SIF for NHL and HL conditions has been demonstrated in Fig. 8. It is reported from the Fig. 8 that when the crack is non-centrally located under NHL or HL condition, and the thickness ratio of the composite strip \(k < 1\), then the SIF increases with rise in inhomogeneity parameter, whereas when the thickness ratio of composite strip \(k > 1\), then the trend gets altered after an inversion point (\(k = 1\)). Moreover, it is also traced out that aforementioned scenario for SIF occurs when the thickness ratio of the composite strip \(k = 1\) (i.e. when crack is centrally located). Furthermore the value of SIF is same irrespective of the nature of loading (i.e. non harmonic or harmonic) when crack is centrally located. It can be pointed out that when non-homogenous composite strip becomes homogeneous, the value of SIF is moderate for both the cases of NHL and HL conditions.

Fig. 8
figure 8

Variation of SIF against parameter \(\left( k \right)\) of non-homogeneous composite strip [upper (Zn) and lower (Si3N4) layer] for various values of parameter \(\left( \gamma \right)\) for static crack in NHL as well as HL conditions

Full size image

Figure 9 exhibits the impact of stress amplitude ratio (when crack edges are under HL along with CAL condition) and effect of displacement ratio (when crack edges are subjected to HL along with SF constraint) on the SIF in the considered composite strip. It is examined from Fig. 9 that both the stress amplitude ratio as well as displacement ratio has substantial favourable impact on SIF subjected to harmonic loading in considered composite strip.

Fig. 9
figure 9

Variation of SIF against crack velocity \(\left({\eta }_{1}^{*}\right)\) subjected to SH-wave propagation in non-homogeneous composite strip [upper (Zn) layer and lower (Si3N4) layer] for various values of stress amplitude ratio \(\left( {k_{1} } \right)\) and displacement ratio \(\left( d \right)\) in the case of HL along with CAL and SF conditions

Full size image

4 Conclusions

An analytical model for the moving crack caused by propagating SH-wave in dissimilar orthotropic composite strip has been developed. Wiener–Hopf method along with complex variable transform has been applied for obtaining the analytical solution that leads to the determination of stress intensity factor. Non-harmonic and harmonic loadings on edges of crack in the considered orthotropic composite strip have been taking into account along with special cases (constant loading, constant amplitude loading and stress-free condition). Three different types of orthotropic material (Zn, Si3N4 and graphite/epoxy material) have been considered for the composite strip in view of numerical simulation. The static case has also been investigated for the crack present in the composite strip. In nutshell, the salient features of the investigated work are as follows:

  • When crack edges are under non-harmonic loading, stress intensity factor disfavours crack velocity, while, stress intensity factor favours crack velocity, when crack edges are under harmonic loading.

  • The thickness ratio parameter has favourable impact on stress intensity factor for non-harmonic loading along with constant loading condition and also for harmonic loading with constant amplitude loading condition, whereas, it disfavours stress intensity factor for crack edges under stress free condition for both harmonic and non-harmonic loadings.

  • With increase in inhomogeneity parameter, stress intensity factor increases when crack edges are under non-harmonic loading with constant loading condition, while, stress intensity factor decreases for stress free condition on crack edges subjected to non-harmonic loading. Moreover, stress intensity factor falls down with rise in inhomogeneity parameter for harmonic loading with constant amplitude loading and stress-free conditions.

  • When non-homogenous composite strip becomes homogeneous, the comparative analysis of stress intensity factor pertaining to non-centrally located crack reflects on the fact that it is minimum for constant loading case while it is moderate for stress free case under non-harmonic loading, whereas, it is moderate for both constant amplitude loading and stress free conditions under harmonic loading.

  • When static crack is centrally located, the value of stress intensity factor is same irrespective of the nature of loading.

  • When non-homogenous composite strip becomes homogeneous, the value of stress intensity factor for static crack is found to be moderate for both harmonic and non-harmonic loadings.

  • With increase in stress amplitude ratio as well as displacement ratio, stress intensity factor increases under the application of harmonic loading in the composite strip.

The consequences of present study may play significant role in the realm of strength and safety analysis of building and other engineering structures. The outcomes of this investigation may also be helpful in the earthquake resistant designing of the building structures.