Impact of inhomogeneity on SH-type wave propagation in an initially stressed composite structure

Abstract

The present analysis has been made on the influence of distinct form of inhomogeneity in a composite structure comprised of double superficial layers lying over a half-space, on the phase velocity of SH-type wave propagating through it. Propagation of SH-type wave in the said structure has been examined in four distinct cases of inhomogeneity viz. when inhomogeneity in double superficial layer is due to exponential variation in density only (Case I); when inhomogeneity in double superficial layers is due to exponential variation in rigidity only (Case II); when inhomogeneity in double superficial layer is due to exponential variation in rigidity, density and initial stress (Case III) and when inhomogeneity in double superficial layer is due to linear variation in rigidity, density and initial stress (Case IV). Closed-form expression of dispersion relation has been accomplished for all four aforementioned cases through extensive application of Debye asymptotic analysis. Deduced dispersion relations for all the cases are found in well-agreement to the classical Love-wave equation. Numerical computation has been carried out to graphically demonstrate the effect of inhomogeneity parameters, initial stress parameters as well as width ratio associated with double superficial layers in the composite structure for each of the four aforesaid cases on dispersion curve. Meticulous examination of distinct cases of inhomogeneity and initial stress in context of considered problem has been carried out with detailed analysis in a comparative approach.

Introduction

Excavation of large quantity of raw materials, such as minerals, crude oils, coal, natural gases, etc., from inside of the earth surface is to accomplish the need of mounting population as well as the demand of growing industries, which contribute a lot to the increase in the frequency of earthquake. An earthquake is rapid and transient vibrations of earth produced by the sudden release of energy stored in an elastically strained rock and send waves of elastic energy throughout the earth. The investigations concerned with seismic waves generated during an earthquake are invaluable to study the interior of the Earth as well as to understand and predict the seismic behavior at the different margin of the earth. Also, the study of behavior of surface waves in layered structures is of prime importance due to its possible applications in geophysical prospecting, mechanical engineering, civil engineering construction and many other engineering branches. A detailed discussion and contribution to surface waves in layered medium are available in Ewing et al. (1957). The investigation made by many authors concerning the behavior of surface waves in layered medium can be quoted from Bullen (1963), Achenbach (1973), Pilant (1979), Bath (1968), Carcione (1992) and Pujol (2003).

Our Earth is extensively more complicated than the models presented earlier. Therefore, a more realistic representation of the Earth as a medium is required through which seismic waves propagate. The very well-known fact is that inhomogeneity lies in most of the elastic bodies and also inside the earth where it is basically one dimensional which varies with depth. The continuous change in the material properties (rigidity and density) of the medium with the space co-ordinates (e.g. in the vertical direction of depth or thickness) contributes to inhomogeneity and it affects the waves (seismic) characteristics significantly propagating through the medium. Inhomogeneity inside earth or a body exists in various types and may be represented by distinct mathematical functions viz. linear, quadratic, exponential, trigonometric, etc. However, through the study of exponential type of inhomogeneity in a problem, effect of linear and quadratic type of heterogeneity may be realized in a problem when value of inhomogeneity parameter is very small. Also, Bullen (1940) suggested that the density varies at different rates with different layers within the Earth. The study of propagation of Love waves in a double superficial layer over heterogeneous medium by taking variation in rigidity has been studied by Sato (1952). Mal (1962) obtained the frequency equation for Love waves due to abrupt thickening of the crustal layer. Sinha (1967) investigated the propagation of love waves in a non-homogeneous layer of finite depth sandwiched between two semi-infinite isotropic media. Bhattacharya (1962, 1969) discussed the dispersion curves for Love-type wave propagation in a transversely isotropic crustal layer with an irregularity in thickness and further studied the possibility of the propagation of Love type waves in an intermediate heterogeneous layer lying between two semi-infinite isotropic homogeneous elastic layers. Chattopadhyay (1975) studied the propagation of Love-type wave considering nonhomogeneous intermediate layer lying between two semi-infinite homogeneous elastic media. Singh et al. (1976) investigated the propagation of Love waves in heterogeneous layered media. Kar (1977) studied the propagation of love type waves in a non-homogeneous internal stratum of finite thickness lying between two semi-infinite isotropic media. Sahu et al. (2014) further considered propagation of SH-waves in viscoelastic heterogeneous layer over half space with self-weight. Later on, Kumari et al. (2015) discussed influence of heterogeneity on the propagation behavior of Love-type waves in a layered isotropic media. Singh et al. (2015) considered the dispersion of shear wave propagating in vertically heterogeneous double layers overlying an initially stressed isotropic half-space. Recently, Chatterjee et al. (2016) showed that the initial stress has great influence on wave velocity; however, Kumari et al. (2016) has performed the modelling of magnetoelastic shear waves due to point source in a viscoelastic crustal layer over an inhomogeneous viscoelastic half space.

Our earth is considered to be an initially stressed medium because of a quantity of initial stress get raised due to many physical causes for example resulting from difference of temperature, process of quenching, shot peening and cold working, pressure due to over burden layer, differential external forces, gravity variations, etc. Thus it is a matter of great interest to study the propagation of waves in a medium under the influence of initial stresses. As discussed by Biot (1940) initial stress has a prominent influence on the propagation of elastic waves. Biot (1963) extended the surface instability of an elastic body under initial stress in finite strain to anisotropic elasticity. Further mechanics of incremental deformation has also been discussed (Biot 1965). Various works includes wave propagation in an initially stressed media can be cited (Dey and Addy 1978; Chattopadhyay et al. 2010; Kumari et al. 2017). Several authors have considered different forms of inhomogeneity and other geological parameter in their elasto-dynamic problems but the form of inhomogeneity in density as well as rigidity considered in the present study for its extensive mathematical analysis has not been attempted by any author till date.

In the present study an attempt has been made to highlight the impact of four different forms of inhomogeneity in a composite structure comprised of double superficial layers lying over a half-space, on the phase velocity of SH-type wave propagating through it. Four distinct cases of inhomogeneity which are taken into consideration are Case I (when inhomogeneity in double superficial layer is due to exponential variation in density only), Case II (when inhomogeneity in double superficial layers is due to exponential variation in rigidity only), Case III (when inhomogeneity in double superficial layer is due to exponential variation in rigidity, density and initial stress) and Case IV (when inhomogeneity in double superficial layer is due to linear variation in rigidity, density and initial stress). Dispersion relations for all four aforementioned cases are deduced through extensive application of Debye asymptotic analysis and are found in well-agreement to the classical Love-wave equation. Numerical computation and graphical demonstration have been carried out to unravel the effect of inhomogeneity parameters, initial stress parameters as well as width ratio associated with double superficial layers in the composite structure on dispersion curve for all four said cases. Comparative study has been carried out for the distinct cases of inhomogeneity and initial stress in context of present problem with detailed analysis.

Formulation and solution of the problem

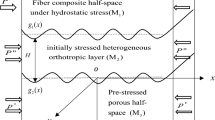
The geometry of the current study consists of two isotropic heterogeneous initially stressed elastic layers $(M_{1}$ and $M_{2}$ respectively) lying over homogeneous isotropic elastic half-space (M ₃). The two media $M_{1}$ and $M_{2}$ are of finite width $h_{1} \;\text{and} \;h_{2}$ respectively. It is assumed that superficial layers $(M_{1} )\;{\text{and}}\;(M_{2} )$ are acted upon by the horizontal initial stress $P_{1} \;\text{and} \;P_{2}$, respectively. The rectangular coordinate system is chosen in such a way that x-axis is in the direction of wave propagation and along the common interface of medium $M_{1}$ and $M_{2}$.The z-axis is pointing vertically downward, as shown in Fig. 1. Let $u_{j}$, $v_{j}$ and $w_{j}$ denote the components of displacement for medium $M_{1} ,\;M_{2} \;\text{and} \;M_{3}$ where $(j = 1,2,3)$, respectively. Now, for the SH-type wave propagating in x-direction causing displacement only in the y-direction, the displacement components may be considered as

$$ u_{j} = w_{j} = 0,\;v_{j} = v(x,z,t)\quad {\text{for}}\quad j = 1,2,3. $$

(1)

Fig. 1

Geometry of the problem

Let us consider $\mu_{j}$ $\mu_{j} \;\text{and} \;\rho_{j} (j = 1,\,2,\,3)$ as the density and rigidity of the layers and half-space $(M_{j} )(j = 1,\,2,\,3)$. Inhomogeneity is a trivial characteristic in a material body and it is found in various ways which are being represented by different sort of mathematical function, for example exponential, linear, trigonometric, etc. It is also noted that variation in rigidity and density with respect to the space variable, leading to cause inhomogeneity, is not found similar in general. Further to explore the effects of inhomogeneity on shear type wave propagation in an extensive manner, four distinct following cases have been studied.

Case I: when inhomogeneity is caused in double superficial layers due to exponential variation in density only

In this case, we intend to explore the effect of inhomogeneity caused in double superficial layer due to exponential variations (with respect to space variable pointing vertically downwards) of density only on the propagation characteristics of SH type wave. Assumed inhomogeneity in this case for the layers $(M_{1} )\;\text{and} \;(M_{2} )$ may mathematically be expressed as

$$ \mu_{j} = \mu_{j}^{(1)} ,\;\rho_{j} = \rho_{j}^{(1)} e^{{2n_{j} z}} \;(j = 1,2), $$

(2)

where $\mu_{1}^{(1)}$ and $\mu_{2}^{(1)}$ denote the constants with dimension of rigidity; $\rho_{1}^{(1)}$ and $\rho_{2}^{(1)}$ denote the constants with dimension of rigidity; $n_{1}$ and $n_{2}$ denote the inhomogeneity parameter, associated with density of layer medium $(M_{1} )\;\text{and} \;(M_{2} ),$ respectively.

In view of Eq. (1), the non-vanishing equation of motion in the absence of body forces for isotropic heterogeneous initially stressed elastic layers $M_{1} \;\text{and} \;M_{2}$ under initial stress (Biot 1940) can be, respectively given for $j = 1\;{\text{and}}\;2$ as

$$ \frac{\partial }{\partial x}\left( {\mu_{j} \frac{{\partial v_{j} }}{\partial x}} \right) + \frac{\partial }{\partial z}\left( {\mu_{j} \frac{{\partial v_{j} }}{\partial z}} \right) - \frac{{P_{j} }}{2}\frac{{\partial^{2} v_{j} }}{{\partial x^{2} }} = \rho_{j} \frac{{\partial^{2} v_{j} }}{{\partial t^{2} }}, $$

(3)

whereas the non-vanishing equation of motion in the absence of body forces for isotropic homogeneous elastic half-space $(M_{3} )$ is given by

$$ \mu_{3} \frac{{\partial^{2} v_{3} }}{{\partial x^{2} }} + \mu_{3} \frac{{\partial^{2} v_{3} }}{{\partial z^{2} }} = \rho_{3} \frac{{\partial^{2} v_{3} }}{{\partial t^{2} }}. $$

(4)

For plane wave propagating in the x-direction with common velocity $c$ and wave number $k$, we may consider the solution for Eqs. (3) and (4) in the form

$$ v_{j} (x,z,t) = V_{j} (z)e^{i\,k(x - ct)} , $$

(5)

where above solution corresponds to layers and half-space $(M_{1} ),\;(M_{2} )\;{\text{and}}\;(M_{3} )$ for $j = 1,\;2\;{\text{and}}\;3$.

In light of Eqs. (3, 5), for uppermost heterogeneous layer $(M_{1} )$(for $j = 1$) result in

$$ \frac{{{\text{d}}^{2} V_{1} }}{{{\text{d}}z^{2} }} + k^{2} \left( {\frac{{c^{2} }}{{\left( {\beta_{1}^{(1)} } \right)^{2} }}e^{{2\,n_{1} z}} - 1 + \frac{{P_{1} }}{{2\mu_{1}^{(1)} }}} \right)V_{1} = 0, $$

(6)

where $\beta_{1}^{(1)} = \sqrt {{{\mu_{1}^{(1)} } \mathord{\left/ {\vphantom {{\mu_{1}^{(1)} } {\rho_{1}^{(1)} }}} \right. \kern-0pt} {\rho_{1}^{(1)} }}} .$

Now, setting $X_{1} = e^{{\,n_{1} \,z}} ,$ Eq. (6) yields

$$ \frac{{{\text{d}}^{2} V_{1} }}{{{\text{d}}X_{1}^{2} }} + \frac{1}{{X_{1} }}\frac{{{\text{d}}V_{1} }}{{{\text{d}}X_{1} }} + k^{2} \left( {\delta_{1}^{2} - \frac{{p_{1}^{2} }}{{X_{1}^{2} }}} \right)V_{1} = 0, $$

(7)

where $\delta_{1} = {{kc} \mathord{\left/ {\vphantom {{kc} {n_{1} \beta_{1}^{(1)} }}} \right. \kern-0pt} {n_{1} \beta_{1}^{(1)} }}$, $\zeta_{1}^{(1)} = {{P_{1} } \mathord{\left/ {\vphantom {{P_{1} } {2\mu_{1}^{(1)} }}} \right. \kern-0pt} {2\mu_{1}^{(1)} }}$ and $p_{1} = {{k\sqrt {1 - \zeta_{1}^{(1)} } } \mathord{\left/ {\vphantom {{k\sqrt {1 - \zeta_{1}^{(1)} } } {n_{1} }}} \right. \kern-0pt} {n_{1} }}$.

Solution of Eq. (7) may be obtained as

$$ V_{1} = A_{1} J_{{p_{{_{1} }} }} (\delta_{1} e^{{n_{1} z}} ) + B_{1} Y_{{p_{{_{1} }} }} (\delta_{1} e^{{n_{1} z}} ), $$

(8)

where $J_{{p_{1} }}$ and $Y_{{p_{1} }}$ are the Bessel functions of the first kind and second kind, respectively, of order $p_{1}$, with $A_{1}$ and $B_{1}$ being arbitrary constants.

Therefore, the expression of non-vanishing displacement component for the uppermost heterogeneous layer $(M_{1} )$ may be written as

$$ v_{1} = \left[ {A_{1} J_{{p_{1} }} (\delta_{1} e^{{n_{1} z}} ) + B_{1} Y_{{p_{1} }} (\delta_{1} e^{{n_{1} z}} )} \right]e^{ik(x - ct)} . $$

(9)

In the similar fashion expression for non-vanishing displacement component for the intermediate heterogeneous layer $\,M_{2}$ may be obtained as

$$ v_{2} = \left[ {C_{1} J_{{p_{2} }} (\delta_{2} e^{{n_{2} z}} ) + D_{1} Y_{{p_{2} }} (\delta_{2} e^{{n_{2} z}} )} \right]e^{ik(x - ct)} , $$

(10)

where $J_{{p_{2} }} \;{\text{and}}\;Y_{{p_{2} }}$ are the Bessel functions of the first kind and second kind, respectively, of order $p_{2}$ with $C_{1} \;\text{and} \;D_{1}$ being the arbitrary constants. Some newly introduced symbols appearing in Eq. (10) are as follows:

$$ \beta_{2}^{(1)} = \sqrt {{{\mu_{2}^{(1)} } \mathord{\left/ {\vphantom {{\mu_{2}^{(1)} } {\rho_{2}^{(1)} }}} \right. \kern-0pt} {\rho_{2}^{(1)} }}} .\delta_{2} = {{kc} \mathord{\left/ {\vphantom {{kc} {n_{2} \beta_{2}^{(1)} }}} \right. \kern-0pt} {n_{2} \beta_{2}^{(1)} }},\;\zeta_{2}^{(1)} = {{P_{2} } \mathord{\left/ {\vphantom {{P_{2} } {2\mu_{2}^{(1)} }}} \right. \kern-0pt} {2\mu_{2}^{(1)} }}\quad {\text{and}}\quad p_{2} = {{k\sqrt {1 - \zeta_{2}^{(1)} } } \mathord{\left/ {\vphantom {{k\sqrt {1 - \zeta_{2}^{(1)} } } {n_{2} }}} \right. \kern-0pt} {n_{2} }}. $$

With aid of Eq. (5), Eq. (4) (for j = 3) associated with $M_{3}$ takes the form

$$ \frac{{{\text{d}}^{2} V_{3} }}{{{\text{d}}z^{2} }} - k^{2} r^{2} V_{3} = 0, $$

(11)

where $r = \sqrt {1 - ({c \mathord{\left/ {\vphantom {c {\beta_{3} }}} \right. \kern-0pt} {\beta_{3} }})^{2} }$ and $\beta_{{_{3} }} = \sqrt {{{\mu_{3} } \mathord{\left/ {\vphantom {{\mu_{3} } {\rho_{3} }}} \right. \kern-0pt} {\rho_{3} }}}$.

Now, the appropriate solution for the Eq. (11) may be written as

$$ V_{3} = Ee^{ - krz} . $$

(12)

where $E$ is an arbitrary constant.

Therefore, non-vanishing displacement component for the lower half space $M_{3}$ can be expressed as

$$ v_{3} = Ee^{ - krz} e^{ik(x - ct)} . $$

(13)

Boundary conditions

• 1. The upper surface of the uppermost heterogeneous layer $(M_{1} )$ is stress free, i.e.

  $$ \mu_{1} \frac{{\partial v_{1} }}{\partial z} = 0\quad {\text{at}}\quad z = - \,h_{1} , $$

  (14)

• 2. The stress and displacement components are continuous at the common interface of the uppermost $(M_{1} )$ and intermediate heterogeneous layers $(M_{2} )$, i.e.

  $$ \mu_{1} \frac{{\partial v_{1} }}{\partial z} = \mu_{2} \frac{{\partial v_{2} }}{\partial z}\quad {\text{at}}\quad z = 0, $$

  (15)
  $$ v_{1} = v_{2} \quad {\text{at}}\quad z = 0, $$

  (16)

• 3. The stress and displacement components are continuous at the common interface of the intermediate heterogeneous layer $(M_{1} )$ and isotropic half space $(M_{3} ) ,$ i.e.

  $$ \mu_{2} \frac{{\partial v_{2} }}{\partial z} = \mu_{3} \frac{{\partial v_{3} }}{\partial z}\quad {\text{at}}\quad z = h_{2} , $$

  (17)
  $$ v_{2} = v_{3} \quad {\text{at}}\quad z = h_{2} . $$

  (18)

Using Eqs. (9), (10) and (13) in the boundary conditions (14–18)yields

$$ A_{1} J_{{p_{1} }}^{\prime } (\delta_{1} e^{{ - n_{1} h_{1} }} ) + B_{1} Y_{{p_{1} }}^{\prime } (\delta_{1} e^{{ - n_{1} h_{1} }} ) = 0, $$

(19)

$$ \mu_{1}^{(1)} \delta_{1} n_{1} \left[ {A_{1} J_{{p_{1} }}^{\prime } (\delta_{1} ) + B_{1} Y_{{p_{1} }}^{\prime } (\delta_{1} )} \right] = \mu_{2}^{(1)} \delta_{2} n_{2} \left[ {C_{1} J_{{p_{2} }}^{\prime } (\delta_{2} ) + D_{1} Y_{{p_{2} }}^{\prime } (\delta_{2} )} \right], $$

(20)

$$ A_{1} J_{{p_{1} }} (\delta_{1} ) + B_{1} Y_{{p_{1} }} (\delta_{1} ) = C_{1} J_{{p_{2} }} (\delta_{2} ) + D_{1} Y_{{p_{2} }} (\delta_{2} ), $$

(21)

$$ \mu_{2}^{(1)} \delta_{2} n_{2} \left[ {C_{1} J_{{p_{2} }}^{\prime } (\delta_{2} e^{{\,n_{2} h_{2} }} ) + D_{1} Y_{{p_{2} }}^{\prime } (\delta_{2} e^{{n_{2} h_{2} }} )} \right] = - kr\mu_{3} Ee^{{ - krh_{2} }} , $$

(22)

$$ C_{1} J_{{p_{2} }} (\delta_{2} e^{{n_{2} h_{2} }} ) + D_{1} Y_{{p_{2} }} (\delta_{2} e^{{\,n_{2} h_{2} }} ) = Ee^{{ - krh_{2} }} . $$

(23)

Eliminating arbitrary constants $A_{1} ,\;B_{1} ,\;C_{1} ,\;D_{1} \quad {\text{and}}\quad E$ from the Eqs. (19–23) the dispersion relation is obtained as

$$ \frac{{R_{1} }}{{R_{2} }} = \frac{{\mu_{1}^{(1)} \delta_{1} n_{1} [\mu_{2}^{(1)} \delta_{2} n_{2} R_{3} + kr\mu_{3} R_{4} ]}}{{\mu_{2}^{(1)} \delta_{2} n_{2} [\mu_{2}^{(1)} \delta_{2} n_{2} R_{5} + kr\mu_{3} R_{6} ]}}, $$

(24)

where the new terms $R_{j} (j = 1,\,2 \ldots 6)$ appearing in Eq. (24) contain Bessel functions and are defined in the “Appendix I”.

Special case

When both of the superficial layers become homogeneous, i.e. inhomogeneity is absent in the two superficial layers, derived dispersion relation (24) must be further simplified for $n_{1} \to 0\quad {\text{and}}\quad n_{2} \to 0$ and will be undertaken using Debye asymptotic expansion.

Now, considering $n_{1} \to 0\quad {\text{and}}\quad n_{2} \to 0$ leads to $\delta_{1} \to \infty$ and $\delta_{2} \to \infty$. Further, it is to be noted that for large values of $\nu ,$ we have the following Debye asymptotic expansions (Watson 1958):

$$ J_{\nu } \left( {\nu \sec \theta } \right) \sim \sqrt {\frac{2}{\nu \pi \tan \theta }} \cos \left( {\nu \tan \theta - \nu \theta - \frac{\pi }{4}} \right), $$

$$ Y_{\nu } \left( {\nu \sec \theta } \right) \sim \sqrt {\frac{2}{\nu \pi \tan \theta }} \sin \left( {\nu \tan \theta - \nu \theta - \frac{\pi }{4}} \right). $$

Above asymptotic expansions can be used for the function appearing in Eq. (24) to yield the following:

$$ \left[ {J_{{p_{1} }} (\delta_{1} e^{{ - n_{1} h_{1} }} )Y_{{p_{1} }} (\delta_{1} ) - Y_{{p_{1\,} }} (\delta_{1} e^{{ - n_{1} h_{1} }} )J_{{p_{1} }} (\delta_{1} )} \right] \approx \frac{{ - 2\sin [p_{1} (\tan \phi_{1} - \tan \phi_{2} ) - p_{1} (\phi_{1} - \phi_{2} )]}}{{\pi p_{1} \sqrt {\tan \phi_{1} \tan \phi_{2} } }}, $$

$$ \left[ {J_{{p_{2} }} (\delta_{2} e^{{n_{2} h_{2} }} )Y_{{p_{2} }} (\delta_{2} ) - Y_{{p_{2} }} (\delta_{2} e^{{n_{2} h_{2} }} )J_{{p_{2} }} (\delta_{2} )} \right] \approx \frac{{ - 2\sin [p_{2} (\tan \phi_{3} - \tan \phi_{4} ) - p_{2} (\phi_{3} - \phi_{4} )]}}{{\pi p_{2} \sqrt {\tan \phi_{3} \tan \phi_{4} } }}, $$

$$ \left[ {J_{{p_{1} }} (\delta_{1} e^{{ - n_{1} h_{1} }} )Y_{{p_{1} }}^{\prime } (\delta_{1} ) - Y_{{p_{1} }} (\delta_{1} e^{{ - n_{1} h_{1} }} )J_{{p_{1} }}^{\prime } (\delta_{1} )} \right] \approx \frac{{2\sin \phi_{2} \cos [p_{1} (\tan \phi_{1} - \tan \phi_{2} ) - p_{1} (\phi_{1} - \phi_{2} )]}}{{\pi p_{1} \sqrt {\tan \phi_{1} \tan \phi_{2} } }}, $$

$$ \left[ {J_{{p_{2} }} (\delta_{2} e^{{n_{2} h_{2} }} )Y_{{p_{2} }}^{\prime } (\delta_{2} ) - Y_{{p_{2} }} (\delta_{2} e^{{n_{2} h_{2} }} )J_{{p_{2} }}^{\prime } (\delta_{2} )} \right] \approx \frac{{2\sin \phi_{4} \cos [p_{2} (\tan \phi_{3} - \tan \phi_{4} ) - p_{2} (\phi_{3} - \phi_{4} )]}}{{\pi p_{2} \sqrt {\tan \phi_{3} \tan \phi_{4} } }}, $$

$$ \left[ {J_{{p_{1} }}^{\prime } (\delta_{1} e^{{ - n_{1} h_{1} }} )Y_{{p_{1} }} (\delta_{1} ) - Y_{{p_{1} }}^{\prime } (\delta_{1} e^{{ - n_{1} h_{1} }} )J_{{p_{1} }} (\delta_{1} )} \right] \approx \frac{{ - 2\sin \phi_{1} \cos [p_{1} (\tan \phi_{1} - \tan \phi_{2} ) - p_{1} (\phi_{1} - \phi_{2} )]}}{{\pi p_{1} \sqrt {\tan \phi_{1} \tan \phi_{2} } }}, $$

$$ \left[ {J_{{p_{2} }}^{\prime } (\delta_{2} e^{{n_{2} h_{2} }} )Y_{{p_{2} }} (\delta_{2} ) - Y_{{p_{2} }}^{\prime } (\delta_{2} e^{{n_{2} h_{2} }} )J_{{p_{2} }} (\delta_{2} )} \right] \approx \frac{{ - 2\sin \phi_{3} \cos [p_{2} (\tan \phi_{3} - \tan \phi_{4} ) - p_{2} (\phi_{3} - \phi_{4} )]}}{{\pi p_{2} \sqrt {\tan \phi_{3} \tan \phi_{4} } }}, $$

$$ \left[ {J_{{p_{1} }}^{\prime } (\delta_{1} e^{{ - n_{1} h_{1} }} )Y_{{p_{1} }}^{\prime } (\delta_{1} ) - Y_{{p_{1} }}^{\prime } (\delta_{1} e^{{ - n_{1} h_{1} }} )J_{{p_{1} }}^{\prime } (\delta_{1} )} \right] \approx \frac{{ - 2\sin \phi_{1} \sin \phi_{2} \sin [p_{1} (\tan \phi_{1} - \tan \phi_{2} ) - p_{1} (\phi_{1} - \phi_{2} )]}}{{\pi p_{1} \sqrt {\tan \phi_{1} \tan \phi_{2} } }}, $$

$$ \left[ {J_{{p_{2} }}^{\prime } (\delta_{2} e^{{n_{2} h_{2} }} )Y_{{p_{2} }}^{\prime } (\delta_{2} ) - Y_{{p_{2} }}^{\prime } (\delta_{2} e^{{n_{2} h_{2} }} )J_{{p_{2} }}^{\prime } (\delta_{2} )} \right] \approx \frac{{ - 2\sin \phi_{3} \sin \phi_{4} \sin [p_{2} (\tan \phi_{3} - \tan \phi_{4} ) - p_{2} (\phi_{3} - \phi_{4} )]}}{{\pi p_{2} \sqrt {\tan \phi_{3} \tan \phi_{4} } }}, $$

where the relations for newly introduced functions appearing in above expansions are provided in “Appendix I”.

Using the above Debye asymptotic expansion, dispersion relation (24) reduces to

$$ \tan (ks_{1}^{(1)} h_{1} ) = \frac{{\mu_{2}^{(1)} \mu_{3} rs_{2}^{(1)} - (\mu_{2}^{(1)} s_{2}^{(1)} )^{2} \tan (ks_{2}^{(1)} h_{2} )}}{{\mu_{1}^{(1)} \mu_{2}^{(1)} s_{1}^{(1)} s_{2}^{(1)} + \mu_{1}^{(2)} \mu_{3} rs_{1}^{(1)} \tan (ks_{2}^{(1)} h_{2} )}}, $$

(25)

where $s_{1}^{(1)} = \sqrt {({c \mathord{\left/ {\vphantom {c {\beta_{1}^{(1)} }}} \right. \kern-0pt} {\beta_{1}^{(1)} }})^{2} - 1 + \zeta_{1}^{(1)} } \quad \text{and} \quad s_{2}^{(1)} = \sqrt {({c \mathord{\left/ {\vphantom {c {\beta_{2}^{(1)} }}} \right. \kern-0pt} {\beta_{2}^{(1)} }})^{2} - 1 + \zeta_{2}^{(1)} } .$

Equation obtained in (25) represents dispersion relation for SH-type wave propagating in homogeneous double superficial layers $(M_{1} \quad {\text{and}}\quad M_{2} )$, both under the effect of initial stress, lying over an isotropic half- space $(M_{3} )$.

Case II: when inhomogeneity is caused in double superficial layers due to exponential variation in rigidity only

In this case inhomogeneity is considered in double superficial layer due to exponential variation in rigidity only and the effect of such inhomogeneity on the propagation characteristics of SH-type wave is analyzed. Assumed inhomogeneity in this case for the layers $(M_{1} )\quad {\text{and}}\quad (M_{2} )$ may mathematically be expressed as

$$ \mu_{j} = \mu_{j}^{(2)} e^{{2l_{j} z}} ,\text{ }\quad \rho_{j} = \rho_{j}^{(2)} \quad (j = 1,\,2), $$

(26)

where $\mu_{1}^{(2)}$ and $\mu_{2}^{(2)}$ denote the constants with dimension of rigidity, $\rho_{1}^{(2)}$ and $\rho_{2}^{(2)}$ denote the constants with dimension of density; $l_{1}$ and $l_{2}$ denote the inhomogeneity parameter, associated with rigidity of layer medium $(M_{1} )\quad {\text{and}}\quad (M_{2} ) ,$ respectively.

In view of Eqs. (1) and (26), the non-vanishing equation of motion in the absence of body forces for isotropic heterogeneous initially stressed elastic layers $M_{1}$ and $M_{2}$ under initial stress (Biot 1940) can be, respectively, given for $j = 1\quad {\text{and}}\quad 2$ as

$$ \left( {\mu_{j} - \frac{{P_{j} }}{2}} \right)\frac{{\partial^{2} v_{j} }}{{\partial x^{2} }} + \mu_{j} \frac{{\partial^{2} v_{j} }}{{\partial z^{2} }} + \frac{{\partial \mu_{j} }}{\partial z}\frac{{\partial v_{j} }}{\partial z} = \rho_{j} \frac{{\partial^{2} v_{j} }}{{\partial t^{2} }}\quad j = 1,\,2, $$

(27)

and non-vanishing equation of motion in the absence of body forces for isotropic homogeneous elastic half-space $(M_{3} )$ is given by Eq. (4).

Now, we may consider the solution of Eqs. (27), as (5).

Then equation of motion (27) with the aid of Eq. (5) for the uppermost heterogeneous layer $M_{1}$ (for $j = 1$) results in

$$ \frac{{{\text{d}}^{2} V_{1} }}{{{\text{d}}z^{2} }} + 2l_{1} \frac{{{\text{d}}V_{1} }}{{{\text{d}}z}} + k^{2} \left( {\frac{{c^{2} }}{{(\beta_{1}^{(2)} )^{2} }}e^{{ - 2l_{1} z}} - 1 + \zeta_{1}^{(2)} } \right)V_{1} = 0, $$

(28)

where $\beta_{1}^{(2)} = \sqrt {{{\mu_{1}^{(2)} } \mathord{\left/ {\vphantom {{\mu_{1}^{(2)} } {\rho_{1}^{(2)} }}} \right. \kern-0pt} {\rho_{1}^{(2)} }}} \quad {\text{and}}\quad \zeta_{1}^{(2)} = {{P_{1} } \mathord{\left/ {\vphantom {{P_{1} } {2\mu_{1}^{(2)} }}} \right. \kern-0pt} {2\mu_{1}^{(2)} }}.$

On substituting $V_{1} = \sqrt \xi V_{1}^{\prime }$ with $\xi = e^{{ - s_{1} z}}$ and $s_{1} = 2l_{1} ,$ in Eq. (28), we obtain

$$ \frac{{{\text{d}}^{2} V_{1}^{\prime } }}{{{\text{d}}\xi^{2} }} + \frac{1}{\xi }\frac{{{\text{d}}V_{1}^{\prime } }}{{{\text{d}}\xi }} + \frac{{k^{2} }}{{s_{1}^{2} }}\left\{ {\frac{{c^{2} }}{{(\beta_{1}^{(2)} )^{2} }}\frac{1}{\xi } - \left( {1 - \zeta_{1}^{(2)} + \frac{{s_{1}^{2} }}{{4k^{2} }}} \right)\frac{1}{{\xi^{2} }}} \right\}V_{1}^{\prime } = 0. $$

(29)

Further, using a transformation $\xi^{\prime } = {{2kc\sqrt \xi } \mathord{\left/ {\vphantom {{2kc\sqrt \xi } {s_{1} \beta_{1}^{(2)} }}} \right. \kern-0pt} {s_{1} \beta_{1}^{(2)} }}$ in Eq. (29) following form may be instated:

$$ \frac{{d^{2} V_{1}^{\prime } }}{{d\xi^{\prime 2} }} + \frac{1}{{\xi^{\prime}}}\frac{{dV_{1}^{\prime } }}{{d\xi^{\prime}}} + \left( {1 - \frac{{q_{1}^{2} }}{{\xi^{\prime 2} }}} \right)V_{1}^{\prime } = 0, $$

(30)

where $q_{1} = \sqrt {1 + \left\{ {{{k^{2} (1 - \zeta_{1}^{(2)} )} \mathord{\left/ {\vphantom {{k^{2} (1 - \zeta_{1}^{(2)} )} {l_{1}^{2} }}} \right. \kern-0pt} {l_{1}^{2} }}} \right\}} .$

The solution of the Eq. (30) may be written as

$$ V_{1}^{\prime } = A_{2} J_{{q_{1} }} (\gamma_{1} \sqrt \xi ) + B_{2} Y_{{q_{1} }} (\gamma_{1} \sqrt \xi ), $$

where $\gamma_{1} = {{kc} \mathord{\left/ {\vphantom {{kc} {l_{1} \beta_{1}^{(2)} }}} \right. \kern-0pt} {l_{1} \beta_{1}^{(2)} }},\quad J_{{q_{1} }}$ and $Y_{{q_{1} }}$ are the Bessel functions of the first kind and second kind, respectively, of order $q_{1}$ with $A_{2}$ and $B_{2}$ being the arbitrary constants, and, therefore, non-vanishing displacement component for the uppermost heterogeneous layer $(M_{1} )$ may be written as

$$ v_{1} = e^{{ - l_{1} z}} [A_{2} J_{{q_{1} }} (\gamma_{1} e^{{ - l_{1} z}} ) + B_{2} Y_{{q_{1} }} (\gamma_{1} e^{{ - l_{1} z}} )]e^{ik(x - ct)} . $$

(31)

Adopting the similar mathematical treatment expression for non-vanishing displacement component for the intermediate heterogeneous layer $(M_{2} )$ may be obtained as

$$ v_{2} = e^{{ - l_{2} z}} [C_{2} J_{{q_{2} }} (\gamma_{2} e^{{ - l_{2} z}} ) + D_{2} Y_{{q_{2} }} (\gamma_{2} e^{{ - l_{2} z}} )]e^{{ik\left( {x - ct} \right)}} , $$

(32)

where $J_{{q_{2} }}$ and $Y_{{q_{2} }}$ are the Bessel functions of the first kind and second kind, respectively, of order $q_{2}$ with $C_{2}$ and $\,D_{2}$ being the arbitrary constants. Other new symbols appearing in Eq. (32) are as follows:

$$ \begin{aligned} \beta_{2}^{(2)} = \sqrt {{{\mu_{2}^{(2)} } \mathord{\left/ {\vphantom {{\mu_{2}^{(2)} } {\rho_{2}^{(2)} }}} \right. \kern-0pt} {\rho_{2}^{(2)} }}} ,\quad \gamma_{2} = \,{{kc} \mathord{\left/ {\vphantom {{kc} {l_{2} \beta_{2}^{(2)} }}} \right. \kern-0pt} {l_{2} \beta_{2}^{(2)} }}, \hfill \\ \zeta_{2}^{(1)} = {{P_{2} } \mathord{\left/ {\vphantom {{P_{2} } {2\mu_{2}^{(2)} }}} \right. \kern-0pt} {2\mu_{2}^{(2)} }},\quad q_{2} = \sqrt {1 + \left\{ {{{k^{2} \left( {1 - \zeta_{2}^{(2)} } \right)} \mathord{\left/ {\vphantom {{k^{2} \left( {1 - \zeta_{2}^{(2)} } \right)} {l_{2}^{2} }}} \right. \kern-0pt} {l_{2}^{2} }}} \right\}} . \hfill \\ \end{aligned} $$

For this case also the non-vanishing displacement component for the lower half space $(M_{3} )$ is given by Eq. (13).

Using Eqs. (13), (31) and (32) in the boundary conditions (14–18), following equations may be instated:

$$ \left[ {l_{1} \left\{ {A_{2} J_{{q_{1} }} (\gamma_{1} e^{{l_{1} h_{1} }} ) + B_{2} Y_{{q_{1} }} (\gamma_{1} e^{{l_{1} h_{1} }} )} \right\} + l_{1} \gamma_{1} \left\{ {A_{2} J_{{q_{1} }}^{\prime } (\gamma_{1} e^{{l_{1} h_{1} }} ) + B_{2} Y_{{q_{1} }}^{\prime } (\gamma_{1} e^{{l_{1} h_{1} }} )} \right\}} \right] = 0, $$

(33)

$$ \begin{aligned} & \mu_{1}^{(2)} \left[ {l_{1} \left\{ {A_{2} J_{{q_{1} }} (\gamma_{1} ) + B_{2} Y_{{q_{1} }} (\gamma_{1} )} \right\} + l_{1} \gamma_{1} \left\{ {A_{2} J_{{q_{1} }}^{\prime } (\gamma_{1} ) + B_{2} Y_{{q_{1} }}^{\prime } (\gamma_{1} )} \right\}} \right] \\ & \quad = \mu_{2}^{(2)} \left[ {l_{2} \left\{ {C_{2} J_{{q_{2} }} (\gamma_{2} ) + D_{2} Y_{{q_{2} }} (\gamma_{2} )} \right\} + l_{2} \gamma_{2} \left\{ {C_{2} J_{{q_{2} }}^{\prime } (\gamma_{2} ) + D_{2} Y_{{q_{2} }}^{\prime } (\gamma_{2} )} \right\}} \right], \\ \end{aligned} $$

(34)

$$ A_{2} J_{{q_{1} }} (\gamma_{1} ) + B_{2} Y_{{q_{1} }} (\gamma_{1} ) = C_{2} J_{{q_{2} }} (\gamma_{2} ) + D_{2} Y_{{q_{2} }} (\gamma_{2} ), $$

(35)

$$ \begin{aligned} & \mu_{2}^{\left( 2 \right)} e^{{l_{2} h_{2} }} \left[ {l_{2} \left\{ {C_{2} J_{{q_{2} }} (\gamma_{\,2} e^{{ - l_{2} h_{2} }} ) + D_{2} Y_{{q_{2} }} (\gamma_{2} e^{{ - l_{2} h_{2} }} )} \right\}} \right. \\ & \quad + \left. {l_{2} \gamma_{\,2} \left\{ {C_{2} J_{{q_{2} }}^{\prime } (\gamma_{\,2} e^{{ - l_{2} h_{2} }} ) + D_{2} Y_{{q_{2} }}^{\prime } (\gamma_{\,2} e^{{ - l_{2} h_{2} }} )} \right\}} \right] = \mu_{3} Ekre^{{ - krh_{2} }} , \\ \end{aligned} $$

(36)

$$ e^{{ - l_{2} h_{2} }} \left[ {C_{2} J_{{q_{2} }} (\gamma_{2} e^{{ - l_{2} h_{2} }} ) + D_{2} Y_{{q_{2} }} (\gamma_{2} e^{{ - l_{2} h_{2} }} )} \right] = Ee^{{ - krh_{2} }} . $$

(37)

Now, eliminating arbitrary constant $A_{2} ,\,B_{2} ,\,C_{2}$, $D_{2}$, $E$ from the above Eqs. (33–37), we arrive at the dispersion relation for the present case as

$$ \begin{aligned} & \frac{{\mu_{1}^{(2)} l_{1}^{2} [R_{7} + \delta_{1} (R_{8} + R_{9} ) + \delta_{1}^{2} R_{10} ]}}{{\mu_{2}^{(2)} l_{1} [R_{7} + \delta_{1} R_{8} ]}} \\ & \quad = \frac{{(\mu_{2}^{(2)} l_{2}^{2} e^{{2l_{2} h_{2} }} - \mu_{3} krl_{2} )[R_{11} + \delta_{2} R_{12} ] + \mu_{2}^{(2)} l_{2}^{2} e^{{2l_{2} h_{2} }} \delta_{2} (R_{13} + \delta_{2} R_{14} )}}{{(\mu_{2}^{(2)} e^{{2l_{2} h_{2} }} l_{2} - \mu_{3} kr)R_{11} + \mu_{2}^{(2)} e^{{2l_{2} h_{2} }} l_{2} \delta_{2} R_{13} }}. \\ \end{aligned} $$

(38)

The newly introduced terms $R_{6 + j} (j = 1,\,2, \ldots 8)$ in (38) and are provided in terms of some relation of Bessel Functions in “Appendix II”.

Special case

For the case, when both the superficial layers are homogeneous i.e. when $l_{1} \to 0\, {\text{and}}\, l_{2} \to 0.$

Now, for $l_{1} \to 0,\quad and\quad l_{2} \to 0$ we have $\gamma_{1} \to \infty$ and $\gamma_{2} \to \infty$. Also, the terms $R_{6 + j} (j = 1,\,2, \ldots 8)$ of derived dispersion relation (38) are defined in terms of some relation of Bessel functions; the corresponding Debye asymptotic approximations are provided in “Appendix II”. The employment of Debye asymptotic approximations in derived dispersion relation (38) reduces it to

$$ \tan (ks_{1}^{(2)} h_{1} ) = \frac{{Numr_{2} }}{{Den\,r_{2} }}, $$

(39)

$$ \begin{aligned} & Numr_{2} \\ & \quad = ({{ks_{1}^{(2)} } \mathord{\left/ {\vphantom {{ks_{1}^{(2)} } {l_{1} }}} \right. \kern-0pt} {l_{1} }})\left[ {\left\{ {\left( {(\mu_{2}^{(2)} l_{2}^{(2)} )^{2} e^{{2l_{2} h_{2} }} - \mu_{2}^{(2)} \mu_{3} krl_{2}^{(2)} } \right) + (\mu_{2}^{(2)} )^{2} k^{2} s_{2}^{2} e^{{2l_{2} h_{2} }} } \right\}\tan (ks_{2}^{(2)} h_{2} ) + \mu_{2}^{(2)} \mu_{3} k^{2} rs_{2}^{(2)} } \right], \\ \end{aligned} $$

$$ \begin{aligned} Den\,r_{2} & = \left( {\mu_{1}^{(2)} l_{1} + \mu_{1}^{(2)} {{(ks_{1}^{(2)} )^{2} } \mathord{\left/ {\vphantom {{(ks_{1}^{(2)} )^{2} } {l_{1} }}} \right. \kern-0pt} {l_{1} }}} \right)\left[ {\mu_{2}^{(2)} ke^{{2l_{2} h_{2} }} s_{2}^{(2)} + (\mu_{2}^{(2)} l_{2} e^{{2l_{2} h_{2} }} - \mu_{3} kr)\tan (ks_{2}^{(2)} h_{2} )} \right] \\ & \quad - \left[ {\left\{ {\left( {\left( {\mu_{2}^{(2)} l_{2} } \right)^{2} e^{{2l_{2} h_{2} }} - \mu_{2}^{(2)} \mu_{3} krl_{2} } \right)\tan (ks_{2}^{(2)} h_{2} ) + \mu_{2}^{2} k^{2} s_{2}^{2} e^{{2l_{2} h_{2} }} } \right\} + \mu_{2}^{(2)} \mu_{3} k^{2} rs_{2}^{(2)} } \right], \\ \end{aligned} $$

with $s_{1}^{(2)} = \sqrt {\left( {{c \mathord{\left/ {\vphantom {c {\beta_{1}^{(2)} }}} \right. \kern-0pt} {\beta_{1}^{(2)} }}} \right)^{2} - 1 + \zeta_{1}^{(2)} } ,\quad s_{2}^{(2)} = \sqrt {\left( {{c \mathord{\left/ {\vphantom {c {\beta_{2}^{(2)} }}} \right. \kern-0pt} {\beta_{2}^{(2)} }}} \right)^{2} - 1 + \zeta_{1}^{(2)} } .$

Since $l_{1} \to 0\quad {\text{and}}\quad l_{2} \to 0$, Eq. (39) finally becomes

$$ \tan (ks_{1}^{(2)} h_{1} ) = \frac{{\mu_{2}^{(2)} \mu_{3} rs_{2}^{(2)} - (\mu_{2}^{(2)} s_{2}^{(2)} )^{2} \tan (s_{2} kh_{2} )}}{{\mu_{1}^{(2)} \mu_{2}^{(2)} s_{1}^{(2)} s_{2}^{(2)} + \mu_{1}^{(2)} \mu_{3} rs_{1}^{(2)} \tan (s_{2}^{(2)} kh_{2} )}}, $$

(40)

Equation (40) represents dispersion relation for the propagation of SH-type wave in initially stressed homogeneous isotropic double superficial layer $(M_{1} )\quad {\text{and}}\quad (M_{2} )$ lying over an isotropic half-space $(M_{3} ).$

Case III: when inhomogeneity is caused in double superficial layer due to exponential variation in rigidity, density and initial stress

The present case discusses the exponential form of variation (with depth) of rigidity, density and initial stress associated with the uppermost and intermediate layers $M_{1} \quad {\text{and}}\quad M_{2}$ of the composite structure. To serve the purpose, the following form of inhomogeneity are assumed:

$$ \mu_{j} = \mu_{j}^{(3)} e^{{\varsigma_{j} z}} ,\quad \rho_{j} = \rho_{j}^{(3)} e^{{\sigma_{j} z}} ,\quad P_{j} = P_{j}^{(3)} e^{{\varsigma_{j} z}} ,\quad (j = 1,2), $$

(41)

where $\mu_{j}^{(3)} (j = 1,\,2)$ are the constants with dimension of rigidity, $\rho_{j}^{(3)} (j = 1,2)$ represent the constant with dimension of density, $P_{j}^{(3)} (j = 1,\,2)$ denote the constants with dimension of stress, $\varsigma_{j} (j = 1,\,2)$ represents the inhomogeneity parameters associated with rigidity and initial stress and $\sigma_{j} (j = 1,\,2)$ are the inhomogeneity parameter associated with density, of the uppermost $(M_{1} )$ and intermediate heterogeneous layer $(M_{2} )$, respectively.

In light of Eqs. (1) and (41), for $j = 1$, the non-vanishing equation of motion for the upper heterogeneous layer $(M_{1} )$ of the considered composite structure, we have,

$$ \frac{{{\text{d}}^{2} V_{1} }}{{{\text{d}}z^{2} }} + \varsigma_{1} \frac{{{\text{d}}^{2} V_{1} }}{{{\text{d}}z^{2} }} + k^{2} \left( {\left( {{c \mathord{\left/ {\vphantom {c {\beta_{1}^{(3)} }}} \right. \kern-0pt} {\beta_{1}^{(3)} }}} \right)^{2} e^{{ - 2\hbar_{1} z}} - 1 + \frac{{P_{1}^{(3)} }}{{2\mu_{1} }}} \right)V_{1} = 0, $$

(42)

with the phase velocity $\beta_{1}^{(3)} = \sqrt {{{\mu_{1}^{(3)} } \mathord{\left/ {\vphantom {{\mu_{1}^{(3)} } {\rho_{1}^{(3)} }}} \right. \kern-0pt} {\rho_{1}^{(3)} }}}$ and $2\hbar_{1} = (\varsigma_{1} - \sigma_{1} ).$

Considering $\mathchar'26\mkern-10mu\lambda_{1} = e^{{ - 2\hbar_{1} z}}$, Eq. (42) becomes

$$ \frac{{{\text{d}}^{2} V_{1} }}{{{\text{d}}\mathchar'26\mkern-10mu\lambda \mathchar'26\mkern-10mu\lambda_{1}^{2} }} + \frac{{4\hbar_{1}^{2} - 2\varsigma_{1} \hbar_{1} }}{{4\hbar_{1}^{2} }}\frac{1}{{\mathchar'26\mkern-10mu\lambda_{1} }}\frac{{{\text{d}}V_{1} }}{{{\text{d}}\mathchar'26\mkern-10mu\lambda_{1} }} + \frac{{k^{2} }}{{4\hbar_{1}^{2} }}\left[ {{{({{c^{2} } \mathord{\left/ {\vphantom {{c^{2} } {\beta_{1}^{(3)} }}} \right. \kern-0pt} {\beta_{1}^{(3)} }})^{2} } \mathord{\left/ {\vphantom {{({{c^{2} } \mathord{\left/ {\vphantom {{c^{2} } {\beta_{1}^{(3)} }}} \right. \kern-0pt} {\beta_{1}^{(3)} }})^{2} } {\mathchar'26\mkern-10mu\lambda_{1} }}} \right. \kern-0pt} {\mathchar'26\mkern-10mu\lambda_{1} }} - \frac{{1 - \zeta_{1} }}{{2\mathchar'26\mkern-10mu\lambda_{1}^{2} }}} \right]V_{1} = 0. $$

(43)

where $\zeta_{1}^{\left( 3 \right)} = {{P_{1}^{\left( 3 \right)} } \mathord{\left/ {\vphantom {{P_{1}^{\left( 3 \right)} } {2\mu_{1}^{\left( 3 \right)} }}} \right. \kern-0pt} {2\mu_{1}^{\left( 3 \right)} }}$ is the dimensionless initial stress parameter associated with the uppermost layer $(M_{1} )$

Putting $V_{1} = \mathchar'26\mkern-10mu\lambda_{1}^{{{{\varsigma_{1} } \mathord{\left/ {\vphantom {{\varsigma_{1} } {4\hbar_{1} }}} \right. \kern-0pt} {4\hbar_{1} }}}} Z_{1}$ in Eq. (43), we obtain,

$$ \frac{{{\text{d}}^{2} Z_{1} }}{{{\text{d}}\mathchar'26\mkern-10mu\lambda_{1}^{2} }} + \frac{1}{{\mathchar'26\mkern-10mu\lambda_{1} }}\frac{{{\text{d}}^{2} Z_{1} }}{{{\text{d}}\mathchar'26\mkern-10mu\lambda_{1}^{2} }} + \left[ {\left( {\frac{kc}{{\hbar_{1} \beta_{1}^{(3)} }}} \right)^{2} \frac{1}{{4\mathchar'26\mkern-10mu\lambda_{1} }} - \left( {\frac{{\varsigma_{1}^{2} }}{{4\hbar_{1}^{2} }} + k^{2} \frac{{1 - \zeta_{1}^{(3)} }}{{2\hbar_{1}^{2} }}} \right)\frac{1}{{4\mathchar'26\mkern-10mu\lambda_{1}^{2} }}} \right]Z_{1} = 0. $$

(44)

Substituting $\mathchar'26\mkern-10mu\lambda_{1}^{'} = \left( {{{kc} \mathord{\left/ {\vphantom {{kc} {\hbar \beta_{1}^{(3)} }}} \right. \kern-0pt} {\hbar \beta_{1}^{(3)} }}} \right)\sqrt {\mathchar'26\mkern-10mu\lambda_{1} }$, Eq. (44) leads to

$$ \frac{{{\text{d}}^{2} Z_{1} }}{{{\text{d}}\mathchar'26\mkern-10mu\lambda_{1}^{'2} }} + \frac{1}{{\mathchar'26\mkern-10mu\lambda_{1}^{'} }}\frac{{{\text{d}}Z_{1} }}{{{\text{d}}\mathchar'26\mkern-10mu\lambda_{1}^{'} }} + \left[ {1 - \frac{{s_{3}^{2} }}{{\mathchar'26\mkern-10mu\lambda_{1}^{'2} }}} \right]Z_{1} = 0, $$

(45)

with $s_{3} = \left[ {({{\varsigma_{1} } \mathord{\left/ {\vphantom {{\varsigma_{1} } {2\hbar_{1} }}} \right. \kern-0pt} {2\hbar_{1} }})^{2} + {{k^{2} (1 - \zeta_{1}^{(3)} )} \mathord{\left/ {\vphantom {{k^{2} (1 - \zeta_{1}^{(3)} )} {\hbar_{1}^{2} }}} \right. \kern-0pt} {\hbar_{1}^{2} }}} \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} .$

Therefore, the solution for Eq. (45) can be gained as (46)

$$ V_{1} = \mathchar'26\mkern-10mu\lambda^{{{{\varsigma_{1} } \mathord{\left/ {\vphantom {{\varsigma_{1} } {4\hbar }}} \right. \kern-0pt} {4\hbar }}}} [A_{3} J_{{s_{3} }} (\varOmega_{1} \mathchar'26\mkern-10mu\lambda^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} ) + B_{3} Y_{{s_{3} }} (\varOmega_{1} \mathchar'26\mkern-10mu\lambda^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} )], $$

(46)

where $J_{{s_{3} }} \quad {\text{and}}\quad Y_{{s_{3} }}$ denote Bessel functions of the first kind and second kind, respectively, of order $s_{3}$ with $\varOmega_{1} = {{kc} \mathord{\left/ {\vphantom {{kc} {\hbar_{1} }}} \right. \kern-0pt} {\hbar_{1} }}\beta_{1}^{(3)}$. $A_{3} \quad \text{and} \quad B_{3}$ are arbitrary constants.

Hence, the displacement components for the upper heterogeneous layer $(M_{1} )$ is as follows

$$ v_{1} = e^{{{{ - \varsigma_{1} z} \mathord{\left/ {\vphantom {{ - \varsigma_{1} z} 2}} \right. \kern-0pt} 2}}} [A_{3} J_{{s_{3} }} (\varOmega_{1} e^{{ - \hbar_{1} z}} ) + B_{3} Y_{{s_{3} }} (\varOmega_{1} e^{{ - \hbar_{1} z}} )]e^{ik(x - ct)} . $$

(47)

In order to obtain displacement component for the intermediate layer $(M_{2} )$, similar steps can be followed. Therefore, displacement components for the intermediate layer may be obtained as

$$ v_{2} = e^{{{{ - \varsigma_{2} z} \mathord{\left/ {\vphantom {{ - \varsigma_{2} z} 2}} \right. \kern-0pt} 2}}} [C_{3} J_{{s_{4} }} (\varOmega_{2} e^{{ - \hbar_{2} z}} ) + D_{3} Y_{{s_{4} }} (\varOmega_{2} e^{{ - \hbar_{2} z}} )]e^{ik(x - ct)} , $$

(48)

with $s_{4} = [({{\varsigma_{2} } \mathord{\left/ {\vphantom {{\varsigma_{2} } {2\hbar_{2} }}} \right. \kern-0pt} {2\hbar_{2} }})^{2} + {{k^{2} (1 - \zeta_{2}^{(3)} )} \mathord{\left/ {\vphantom {{k^{2} (1 - \zeta_{2}^{(3)} )} {\hbar_{2}^{2} }}} \right. \kern-0pt} {\hbar_{2}^{2} }}]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} ,\quad 2\hbar_{2} = (\varsigma_{2} - \sigma_{2} ),\quad \varOmega_{2} = {{kc} \mathord{\left/ {\vphantom {{kc} {\hbar_{2} }}} \right. \kern-0pt} {\hbar_{2} }}\beta_{2}^{(3)} ,$ dimensionless initial stress parameter $\zeta_{2}^{(3)} = {{P_{3}^{(2)} } \mathord{\left/ {\vphantom {{P_{3}^{(2)} } {2\mu_{2}^{(3)} }}} \right. \kern-0pt} {2\mu_{2}^{(3)} }},$ dimensionless phase velocity $\beta_{2}^{(3)} = \sqrt {{{\mu_{2}^{(3)} } \mathord{\left/ {\vphantom {{\mu_{2}^{(3)} } {\rho_{2}^{(3)} }}} \right. \kern-0pt} {\rho_{2}^{(3)} }}}$ associated with intermediate layer $(M_{1} )$. Also, $J_{{s_{4} }} \quad {\text{and}}\quad Y_{{s_{4} }}$ denote Bessel functions of the first kind and second kind, respectively, of order $s_{4} .$ $C_{3} \quad {\text{and}}\quad D_{3}$ are the arbitrary constants.

The displacement components for the lower isotropic half-space $(M_{3} ),$ will be same as of the two previous cases, given by Eq. (13).

Using Eqs. (13), (47) and (48) in the boundary conditions (14–18) for the present case, the following relations may be obtained as

$$ A_{3} \left\{ {\frac{{\varsigma_{1} }}{2}J_{{s_{1} }} (\varOmega_{1} e^{{\hbar_{1} h_{1} }} ) + \varOmega_{1} \hbar_{1} e^{{\hbar_{1} h_{1} }} J_{{s_{1} }}^{'} (\varOmega_{1} e^{{\hbar_{1} h_{1} }} )} \right\} + B_{3} \left\{ {\frac{{\varsigma_{1} }}{2}Y_{{s_{1} }} (\varOmega_{1} e^{{\hbar_{1} h_{1} }} ) + \varOmega_{1} \hbar_{1} e^{{\hbar_{1} h_{1} }} Y_{{s_{1} }}^{'} (\varOmega_{1} e^{{\hbar_{1} h_{1} }} )} \right\} = 0, $$

(49)

$$ \begin{aligned} & \mu_{1}^{(2)} \left[ {A_{3} \left\{ {\frac{{\varsigma_{1} }}{2}J_{{s_{1} }} (\varOmega_{1} ) + \varOmega_{1} \hbar_{1} J_{{s_{1} }}^{'} (\varOmega_{1} )} \right\} + B_{3} \left\{ {\frac{{\varsigma_{1} }}{2}Y_{{s_{1} }} (\varOmega_{1} ) + \varOmega_{1} \hbar_{1} Y_{{s_{1} }}^{'} (\varOmega_{1} )} \right\}} \right] \\ & \quad = \mu_{1}^{\left( 2 \right)} \left[ {C_{3} \left\{ {\frac{{\varsigma_{2} }}{2}J_{{s_{2} }} (\varOmega_{2} ) + \varOmega_{2} \hbar_{2} J_{{s_{2} }}^{'} (\varOmega_{2} )} \right\} + D_{3} \left\{ {\frac{{\varsigma_{2} }}{2}Y_{{s_{2} }} (\varOmega_{2} ) + \varOmega_{2} \hbar_{2} Y_{{s_{2} }}^{'} (\varOmega_{2} )} \right\}} \right]. \\ \end{aligned} $$

(50)

$$ A_{3} J_{{s_{1} }} (\varOmega_{1} ) + B_{3} Y_{{s_{1} }} (\varOmega_{1} ) = C_{3} J_{{s_{2} }} (\varOmega_{2} ) + D_{3} Y_{{s_{2} }} (\varOmega_{2} ), $$

(51)

$$ \mu_{2} e^{{ - \varsigma_{2} h_{2} /2}} \left[ {C_{3} \left\{ {\frac{{\varsigma_{2} }}{2}J_{{s_{2} }} (\varOmega_{2} e^{{ - \hbar_{2} h_{2} }} ) + \varOmega_{2} \hbar_{2} e^{{ - \hbar_{2} h_{2} }} J_{{s_{2} }}^{'} (\varOmega_{2} e^{{ - \hbar_{2} h_{2} }} )} \right\} + D_{3} \left\{ {\frac{{\varsigma_{2} }}{2}Y_{{s_{2} }} (\varOmega_{2} e^{{ - \hbar_{2} h_{2} }} ) + \varOmega_{2} \hbar_{2} e^{{ - \hbar_{2} h_{2} }} Y_{{s_{2} }}^{'} (\varOmega_{2} e^{{ - \hbar_{2} h_{2} }} )} \right\}} \right] = kr\mu_{3} Ee^{{ - krh_{\,2} }} , $$

(52)

$$ \mu_{2} e^{{{{ - \varsigma_{2} h_{2} } \mathord{\left/ {\vphantom {{ - \varsigma_{2} h_{2} } 2}} \right. \kern-0pt} 2}}} \left\{ {C_{3} J_{{s_{2} }} (\varOmega_{2} e^{{ - \hbar_{2} h_{2} }} ) + D_{3} Y_{{s_{2} }} (\varOmega_{2} e^{{ - \hbar_{2} h_{2} }} )} \right\} = Ee^{{ - krh_{2} }} . $$

(53)

The elimination of the arbitrary constants $A_{3} ,\,B_{3} ,\,C_{3} ,\,D_{3} \quad {\text{and}}\quad E$ yield the following relation:

$$ \begin{aligned} & ({{\mu_{1}^{(3)} } \mathord{\left/ {\vphantom {{\mu_{1}^{(3)} } {\mu_{2}^{(3)} }}} \right. \kern-0pt} {\mu_{2}^{(3)} }})\frac{{({{\varsigma_{1} } \mathord{\left/ {\vphantom {{\varsigma_{1} } 2}} \right. \kern-0pt} 2})^{2} R_{15} + \left\{ {{{\varOmega_{1} \hbar_{1} \varsigma_{1} (R_{16} + R_{17} )} \mathord{\left/ {\vphantom {{\varOmega_{1} \hbar_{1} \varsigma_{1} (R_{16} + R_{17} )} 2}} \right. \kern-0pt} 2}} \right\} + (\varOmega_{1} \hbar_{1} )^{2} R_{18} }}{{\left( {{{\varsigma_{1} } \mathord{\left/ {\vphantom {{\varsigma_{1} } 2}} \right. \kern-0pt} 2}} \right)R_{15} + \varOmega_{1} \hbar_{1} R_{16} }} \\ & \quad = \frac{{\mu_{2}^{(3)} ({{\varsigma_{2} } \mathord{\left/ {\vphantom {{\varsigma_{2} } 2}} \right. \kern-0pt} 2})^{2} R_{19} + \left\{ {{{\mu_{2}^{(3)} \varsigma_{2} \varOmega_{2} \hbar_{2} (R_{20} + R_{21} )} \mathord{\left/ {\vphantom {{\mu_{2}^{(3)} \varsigma_{2} \varOmega_{2} \hbar_{2} (R_{20} + R_{21} )} 2}} \right. \kern-0pt} 2}} \right\} + \mu_{2}^{(3)} (\varOmega_{2} \hbar_{2} )^{2} R_{22} + \mu_{3} kr\varOmega_{2} \hbar_{2} R_{21} }}{{\left\{ {\mu_{2}^{(3)} e^{{\hbar_{2} h_{2} }} ({{\varsigma_{2} } \mathord{\left/ {\vphantom {{\varsigma_{2} } 2}} \right. \kern-0pt} 2}) + \mu_{3} kr} \right\}R_{19} + \mu_{2}^{(3)} e^{{\hbar_{2} h_{2} }} \varOmega_{2} \hbar_{2} R_{20} }}. \\ \end{aligned} $$

(54)

Equation (54) represents dispersion relation for SH-type wave propagating double superficial layers $(M_{1} )\quad {\text{and}}\quad (M_{2} ),$ having exponential form of variation associated with each of the rigidity, density and initial stress of the two layers, lying over an isotropic half-space. The terms $R_{14 + j} \,(j = 1,\,2, \ldots 8)$ appearing in Eq. (54) are new and provided in the “Appendix III”.

Special case

When the two layers $(M_{1} )\quad {\text{and}}\quad (M_{2} )$ become homogeneous, i.e. which require $\varsigma_{1} \to 0,$ $\varsigma_{2} \to 0$ ${\text{and}}\quad \sigma_{1} \to 0,\quad \sigma_{2} \to 0$, the dispersion equation for this case can be obtained with the aid of Debye asymptotic expansions.

Now, for $\varsigma_{1} \to 0,\;\varsigma_{1} \to 0\quad and\quad \sigma_{1} \to 0,\;\sigma_{2} \to 0$, we have $\hbar_{1} \to \infty$ and $\hbar_{2} \to \infty$. The relations in terms of Bessel functions are involved in the terms $R_{14 + j} \,(j = 1,\,2, \ldots 8)$ of deduced dispersion relation (54). Further in view of Debye asymptotic expansions, stated in the “Appendix III”, the dispersion relation reduces to

$$ \tan (ks_{1}^{(4)} h_{1} ) = \frac{{Numr_{4} }}{{Den\,r_{4} }}, $$

where

$$ Numr_{4} = ks_{1}^{(4)} \left[ {\mu_{2}^{2} e^{{\hbar_{2} h_{2} }} \{ ({{\varsigma_{2}^{2} } \mathord{\left/ {\vphantom {{\varsigma_{2}^{2} } 4}} \right. \kern-0pt} 4}) + k^{2} s_{2}^{2} \} \tan ks_{2} h_{2} - \mu_{2} \mu_{3} k^{2} rs_{2} } \right], $$

$$ \begin{aligned} Den\,r_{4} = \left\{ {({{\varsigma_{1}^{2} } \mathord{\left/ {\vphantom {{\varsigma_{1}^{2} } 4}} \right. \kern-0pt} 4}) + k^{2} s_{1}^{2} } \right\}\left[ {\mu_{1} \mu_{2} e^{{\hbar_{2} h_{2} }} \left( {({{\varsigma_{2} } \mathord{\left/ {\vphantom {{\varsigma_{2} } 2}} \right. \kern-0pt} 2}) + ks_{2} } \right) - \mu_{1} \mu_{2} kr\tan ks_{2} h_{2} } \right] \hfill \\ \quad ({{\varsigma_{1} } \mathord{\left/ {\vphantom {{\varsigma_{1} } 2}} \right. \kern-0pt} 2})\left[ {\mu_{2}^{2} e^{{\hbar_{2} h_{2} }} \left\{ {({{\varsigma_{2}^{2} } \mathord{\left/ {\vphantom {{\varsigma_{2}^{2} } 4}} \right. \kern-0pt} 4}) + k^{2} s_{2}^{2} } \right\}\tan ks_{2} h_{2} - \mu_{2} \mu_{3} k^{2} rs_{2} } \right], \hfill \\ \end{aligned} $$

$$ \text{with} \quad s_{1}^{(3)} = \sqrt {({c \mathord{\left/ {\vphantom {c {\beta_{1}^{(3)} }}} \right. \kern-0pt} {\beta_{1}^{(3)} }})^{2} - 1 + \zeta_{1}^{(3)} } ,\quad s_{2}^{(3)} = \sqrt {({c \mathord{\left/ {\vphantom {c {\beta_{2}^{(3)} }}} \right. \kern-0pt} {\beta_{2}^{(3)} }})^{2} - 1 + \zeta_{2}^{(3)} } . $$

Since$\varsigma_{1} \to 0\quad {\text{and}}\quad \varsigma_{2} \to 0$ therefore, in this view, Eq. (54) becomes

$$ \tan (ks_{1}^{(3)} h_{1} ) = \frac{{\mu_{2}^{(3)} \mu_{3} rs_{2}^{(3)} - (\mu_{2}^{(3)} s_{2}^{(3)} )^{2} tan(ks_{2}^{(3)} h_{2} )}}{{\mu_{1}^{(3)} \mu_{2}^{(3)} s_{1}^{(3)} s_{2}^{(3)} + \mu_{2}^{(3)} \mu_{2}^{(3)} s_{1}^{(3)} r\tan (ks_{2}^{(3)} h_{2} )}}. $$

(55)

The above Eq. (55) constitutes the dispersion relation for the SH-type wave propagating in initially stressed homogeneous double layer $(M_{1} \quad \text{and} \quad M_{2} )$ lying over an isotropic half-space $(M_{3} )$.

Case IV: when inhomogeneity is caused in double superficial layer due to linear variation in rigidity, density and initial stress

The present study considers the linear form of variation accompanying rigidity, density, initial stress of the uppermost layer $(M_{1} )$ and intermediate layer $(M_{2} )$ and are supposed as follows:

$$ \mu_{j} = \mu_{j}^{(4)} (1 + \varepsilon_{j} z),\quad \rho_{j} = \rho_{j}^{(4)} (1 + \varepsilon_{j} z),\quad P_{j} = P_{j}^{(4)} (1 + \varepsilon_{j} z);\quad j = 1,2, $$

(56)

where $j = 1$ and $j = 2$ denotes distinct parameters corresponding to uppermost and intermediate heterogeneous layer $\left( {M_{1} } \right)\,\,\text{and} \,\,\,\left( {M_{2} } \right)$, respectively.

Assuming

$$ v_{j} = \left( {{{V_{j} (x,z,t)} \mathord{\left/ {\vphantom {{V_{j} (x,z,t)} {\sqrt {\mu_{j} } }}} \right. \kern-0pt} {\sqrt {\mu_{j} } }}} \right)e^{ik(x - ct)} ;\quad (j = 1,2). $$

(57)

Then, with the aid of Eq. (1) and (57), for $j = 1$, the reduced form of equation for the upper heterogeneous layer $(M_{1} )$ may be taken as

$$ \mu_{1} \frac{{\partial^{2} V_{1} }}{{\partial z^{2} }} + \left( {\mu_{1} - \frac{{P_{1} }}{2}} \right)\frac{{\partial^{2} V_{1} }}{{\partial x^{2} }} + \left[ {\frac{1}{{4\mu_{1} }}\left( {\frac{{{\text{d}}\mu_{1} }}{{{\text{d}}z}}} \right)^{2} - \frac{1}{2}\frac{{{\text{d}}^{2} \mu_{1} }}{{{\text{d}}z^{2} }}} \right]V_{1} = \rho_{1} \frac{{{\text{d}}^{2} \mu_{1} }}{{{\text{d}}t^{2} }}. $$

(58)

In view of (56), Eq. (58) becomes

$$ (1 + \varepsilon_{1} z)^{2} \frac{{{\text{d}}^{2} V_{1} }}{{{\text{d}}z^{2} }} + \left[ {(1 + \varepsilon_{1} z)^{2} k^{2} \left\{ {\left( {\frac{c}{{\beta_{1}^{(4)} }}} \right)^{2} - 1 + \zeta_{1}^{(4)} } \right\} + \frac{{\varepsilon_{1}^{2} }}{4}} \right]V_{1} = 0, $$

(59)

where $\beta_{1}^{(4)} = \sqrt {{{\mu_{1}^{(4)} } \mathord{\left/ {\vphantom {{\mu_{1}^{(4)} } {\rho_{1}^{(4)} }}} \right. \kern-0pt} {\rho_{1}^{(4)} }}}$ and $\zeta_{1}^{(4)} = {{P_{1}^{(4)} } \mathord{\left/ {\vphantom {{P_{1}^{(4)} } {2\mu_{1}^{(4)} }}} \right. \kern-0pt} {2\mu_{1}^{(4)} }}$ are phase velocity and dimensionless initial stress parameter of the uppermost heterogeneous layer $(M_{1} )$ of the composite structure for the present case.

Substituting $W_{1}$ in place $(1 + \varepsilon_{1} z)$ in Eq. (59), we obtain

$$ W_{1}^{2} \frac{{{\text{d}}^{2} V_{1} }}{{{\text{d}}W_{1}^{2} }} + (a + bW_{1}^{2} )V_{1} = 0, $$

(60)

with $a = {1 \mathord{\left/ {\vphantom {1 {4,\,b = }}} \right. \kern-0pt} {4,\,b = }}({{k^{2} } \mathord{\left/ {\vphantom {{k^{2} } {\varepsilon_{1}^{2} }}} \right. \kern-0pt} {\varepsilon_{1}^{2} }})[({c \mathord{\left/ {\vphantom {c {\beta_{1}^{(4)} }}} \right. \kern-0pt} {\beta_{1}^{(4)} }})^{2} - 1 + \zeta_{1}^{(4)} ].$

Further, using $V_{1} = W^{{\ell_{1} }} V_{1} '$ in Eq. (52), it gives

$$ W_{1}^{2} \frac{{{\text{d}}^{2} V_{1}^{'} }}{{{\text{d}}W_{1}^{2} }} + 2\ell_{1} W_{1} \frac{{{\text{d}}V_{1}^{'} }}{{{\text{d}}W_{1} }} + [\ell_{1} (\ell_{1} - 1) + (a + bW_{1}^{2} )]V_{1}^{'} = 0. $$

(61)

Choosing $\ell_{1} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}\quad {\text{and}}\quad \sqrt b W_{1} = i\varPhi_{1}$

$$ \varPhi_{1}^{2} \frac{{{\text{d}}^{2} V_{1}^{'} }}{{{\text{d}}^{2} \varPhi_{1}^{2} }} + \varPhi_{1} \frac{{{\text{d}}V_{1}^{'} }}{{{\text{d}}\varPhi_{1}^{{}} }} - \varPhi_{1}^{2} V_{1}^{'} = 0, $$

(62)

Thus we can find the solution of Eq. (62) as

$$ V_{1}^{'} = A_{4} I_{0} \left( {\varPhi_{1} } \right) + B_{4} K_{0} \left( {\varPhi_{1} } \right), $$

(63)

$I_{0} \quad {\text{and}}\quad K_{0}$ being the modified Bessel function of the first and third kinds, respectively, of zero order with arbitrary constants $A_{4}$ and $B_{4}$.

In view of (63), the solution for the upper heterogeneous layer $(M_{1} )$ may be obtained as

$$ v_{1} = \left( {{1 \mathord{\left/ {\vphantom {1 {\sqrt {\mu_{1}^{(4)} } }}} \right. \kern-0pt} {\sqrt {\mu_{1}^{(4)} } }}} \right)\left[ {A_{4} I_{0} \left\{ {({{t_{1} } \mathord{\left/ {\vphantom {{t_{1} } {i\varepsilon_{1} }}} \right. \kern-0pt} {i\varepsilon_{1} }})(1 + \varepsilon_{1} z)} \right\} + B_{4} K_{0} \left\{ {({{t_{1} } \mathord{\left/ {\vphantom {{t_{1} } {i\varepsilon_{1} }}} \right. \kern-0pt} {i\varepsilon_{1} }})(1 + \varepsilon_{1} z)} \right\}} \right]e^{{ik\left( {x - ct} \right)}} , $$

(64)

with $t_{1} = k\sqrt {\left( {{c \mathord{\left/ {\vphantom {c {\beta_{1}^{(4)} }}} \right. \kern-0pt} {\beta_{1}^{(4)} }}} \right)^{2} - 1 + \zeta_{1}^{(4)} }.$

Similarly, solution for the intermediate heterogeneous layer $(M_{2} )$ can be taken as

$$ v_{2} = \left( {{1 \mathord{\left/ {\vphantom {1 {\sqrt {\mu_{2}^{(4)} } }}} \right. \kern-0pt} {\sqrt {\mu_{2}^{(4)} } }}} \right)\left[ {C_{4} I_{0} \left\{ {({{t_{2} } \mathord{\left/ {\vphantom {{t_{2} } {i\varepsilon_{2} }}} \right. \kern-0pt} {i\varepsilon_{2} }})(1 + \varepsilon_{2} z)} \right\} + D_{4} K_{0} \left\{ {({{t_{2} } \mathord{\left/ {\vphantom {{t_{2} } {i\varepsilon_{2} }}} \right. \kern-0pt} {i\varepsilon_{2} }})(1 + \varepsilon_{2} z)} \right\}} \right]e^{ik(x - ct)} , $$

(65)

with $A_{4} \quad {\text{and}}\quad B_{4}$ being arbitrary constants and $t_{2} = k\sqrt {\left( {{c \mathord{\left/ {\vphantom {c {\beta_{2}^{(4)} }}} \right. \kern-0pt} {\beta_{2}^{(4)} }}} \right)^{2} - 1 + \zeta_{2}^{(4)} } .$

The terms $\beta_{2}^{(4)} = \sqrt {{{\mu_{2}^{(4)} } \mathord{\left/ {\vphantom {{\mu_{2}^{(4)} } {\rho_{2}^{(4)} }}} \right. \kern-0pt} {\rho_{2}^{(4)} }}}$ and $\zeta_{2} = {{P_{2}^{(4)} } \mathord{\left/ {\vphantom {{P_{2}^{(4)} } {2\mu_{2}^{(4)} }}} \right. \kern-0pt} {2\mu_{2}^{(4)} }}$ represent phase velocity and initial stress parameter of the intermediate heterogeneous layer $(M_{2} )$ for composite structure.

The displacement components for the lower isotropic half space $(M_{3} )$ will be given by Eq. (13).

In view of (13), (64) and (65), the boundary conditions (14–18) yielding following relations may be obtained as

$$ A_{4} I_{0}^{'} \left[ {\frac{{t_{1} }}{{i\varepsilon_{1} }}(1 - \varepsilon_{1} h_{1} )} \right] + B_{4} K_{0}^{'} \left[ {\frac{{t_{1} }}{{i\varepsilon_{1} }}(1 - \varepsilon_{1} h_{1} )} \right] = 0, $$

(66)

$$ \sqrt {\mu_{1}^{(4)} } t_{1} \left[ {A_{4} I_{0}^{'} (t_{1} /i\varepsilon_{1} ) + B_{4} K_{0}^{'} (t_{1} /i\varepsilon_{1} )} \right] = \sqrt {\mu_{2}^{(4)} } t_{2} \left[ {C_{4} I_{0}^{'} (t_{2} /i\varepsilon_{2} ) + D_{4} K_{0}^{'} (t_{2} /i\varepsilon_{2} )} \right], $$

(67)

$$ \sqrt {\mu_{2}^{(4)} } [A_{4} I_{0}^{{}} (t_{1} /i\varepsilon_{1} ) + B_{4} K_{0}^{{}} (t_{1} /i\varepsilon_{1} )] = \sqrt {\mu_{1}^{(4)} } [C_{4} I_{0}^{{}} (t_{2} /i\varepsilon_{2} ) + D_{4} K_{0}^{{}} (t_{2} /i\varepsilon_{2} )], $$

(68)

$$ \sqrt {\mu_{2}^{(4)} } (1 + \varepsilon_{2} h_{2} )t_{2} \left[ {C_{4} I_{0}^{'} \left\{ {\frac{{t_{2} }}{{i\varepsilon_{2} }}(1 + \varepsilon_{2} h_{2} )} \right\} + D_{4} K_{0}^{'} \left\{ {\frac{{t_{2} }}{{i\varepsilon_{2} }}(1 + \varepsilon_{2} h_{2} )} \right\}} \right] = - i\mu_{3} krE^{{ - krh_{2} }} , $$

(69)

$$ \sqrt {\mu_{2}^{(4)} } \left[ {C_{4} I_{0}^{{}} \left\{ {\frac{{t_{2} }}{{i\varepsilon_{2} }}(1 + \varepsilon_{2} h_{2} )} \right\} + D_{4} K_{0}^{{}} \left\{ {\frac{{t_{2} }}{{i\varepsilon_{2} }}(1 + \varepsilon_{2} h_{2} )} \right\}} \right] = E^{{ - krh_{2} }} . $$

(70)

Eliminating the arbitrary constants $A_{4} ,\,B_{4} ,\,C_{4} ,\,D_{4}$ and $E$ from the relations (66–70) gives the dispersion relation for the propagation of SH-type wave in the considered geometry (Case IV) as:

$$ \frac{{\mu_{1}^{(4)} t_{1} }}{{\mu_{2}^{(4)} t_{2} }}\frac{{R_{23} }}{{R_{24} }} = \frac{{\mu_{2}^{(4)} t_{2} (1 + \varepsilon_{2} h_{2} )R_{25} + i\mu_{3} krR_{26} }}{{\mu_{2}^{(4)} t_{2} (1 + \varepsilon_{2} h_{2} )R_{27} + i\mu_{3} krR_{28} }}, $$

(71)

where $R_{22 + j} (j = 1,2, \ldots 6)$ are provided in the “Appendix IV”.

Considering following relations

$$ I_{\upsilon } (z) = e^{{ - {1 \mathord{\left/ {\vphantom {1 {i2\pi \upsilon }}} \right. \kern-0pt} {i2\pi \upsilon }}}} J_{\upsilon } (iz),\quad K_{\upsilon } (z) = \frac{1}{2}i\pi e^{{{1 \mathord{\left/ {\vphantom {1 {i2\pi \upsilon }}} \right. \kern-0pt} {i2\pi \upsilon }}}} [J_{\upsilon } (iz) + iY_{\upsilon } (iz)]. $$

(72)

the dispersion equation in (71) can be rewritten as

$$ \frac{{\mu_{1} t_{1} }}{{\mu_{2} t_{2} }}\frac{{R_{29} }}{{R_{30} }} = \frac{{\mu_{2} t_{2} (1 + \varepsilon_{2} h_{2} )R_{31} - \mu_{3} krR_{32} }}{{\mu_{2} t_{2} (1 + \varepsilon_{2} h_{2} )R_{33} + \mu_{3} krR_{34} }}, $$

(73)

with all the new terms $R_{28 + j} (j = 1,\,2, \ldots 6)$ of Eq. (73) provided in the “Appendix IV”.

Again, using following asymptotic expansion of Bessel function, we have

$$ \begin{aligned} J_{0} (\lambda ) & \approx \frac{2}{{3\sqrt {\pi \lambda } }}\left( {\cos \lambda + \sin \lambda } \right),Y_{0} (\lambda ) \approx \frac{2}{{3\sqrt {\pi \lambda } }}\left( {\cos \lambda + \sin \lambda } \right), \\ J_{0} '(\lambda ) & \approx \frac{2}{{3\sqrt {\pi \lambda } }}\left[ {\left( {1 - \frac{1}{2\lambda }} \right)\cos \lambda + \left( {1 + \frac{1}{2\lambda }} \right)\sin \lambda } \right], \\ Y_{0} '(\lambda ) & \approx \frac{ - 2}{{3\sqrt {\pi \lambda } }}\left[ {\left( {1 - \frac{1}{2\lambda }} \right)\sin \lambda - \left( {1 + \frac{1}{2\lambda }} \right)\cos \lambda } \right]. \\ \end{aligned} $$

(74)

Using above relations mentioned in (74), we have the following results:

$$ \begin{aligned} Y_{0} '(\lambda_{2} )J_{0} '(\lambda_{1} ) - Y_{0} '(\lambda_{1} )J_{0} '(\lambda_{2} ) & \approx \frac{ - 4}{{9\pi \sqrt {\lambda_{1} \lambda_{2} } }}\left[ {2\cos (\lambda_{2} )\sin (\lambda_{1} ) - 2\cos (\lambda_{1} )\sin (\lambda_{2} )} \right], \\ Y_{0} '(\lambda_{2} )J_{0} (\lambda_{1} ) - Y_{0} (\lambda_{1} )J_{0} '(\lambda_{2} ) & \approx \frac{ - 4}{{9\pi \sqrt {\lambda_{1} \lambda_{2} } }}\left[ {2\sin (\lambda_{2} )\sin (\lambda_{1} ) - 2\cos (\lambda_{1} )\cos (\lambda_{2} )} \right], \\ \end{aligned} $$

(75)

Using results of (75), in Eq. (73), we obtain

$$ \frac{{\mu_{1}^{(4)} t_{1} }}{{\mu_{2}^{(4)} t_{2} }}\frac{{\tan (\lambda_{1} ) - \tan (\lambda_{2} )}}{{1 + \tan (\lambda_{1} )\tan (\lambda_{2} )}} = \frac{{\mu_{2}^{(4)} t_{2} (1 + \varepsilon_{2} h_{2} )\{ \tan (\lambda_{3} ) - \tan (\lambda_{4} )\} + \mu_{3} kr\{ 1 + \tan (\lambda_{3} )\tan (\lambda_{4} )\} }}{{\mu_{3} kr\{ \tan (\lambda_{3} ) - \tan (\lambda_{4} )\} - \mu_{2}^{\left( 4 \right)} t_{2} (1 + \varepsilon_{2} h_{2} )\{ 1 + \tan (\lambda_{3} )\tan (\lambda_{4} )\} }}, $$

(76)

taking $\lambda_{1} = {{t_{1} } \mathord{\left/ {\vphantom {{t_{1} } {\varepsilon_{1} ,\quad \lambda_{2} = {{t_{1} (1 - \varepsilon_{1} h_{1} )} \mathord{\left/ {\vphantom {{t_{1} (1 - \varepsilon_{1} h_{1} )} {\varepsilon_{1} }}} \right. \kern-0pt} {\varepsilon_{1} }}}}} \right. \kern-0pt} {\varepsilon_{1} ,\quad \lambda_{2} = {{t_{1} (1 - \varepsilon_{1} h_{1} )} \mathord{\left/ {\vphantom {{t_{1} (1 - \varepsilon_{1} h_{1} )} {\varepsilon_{1} }}} \right. \kern-0pt} {\varepsilon_{1} }}}},\quad \lambda_{3} = {{t_{2} (1 + \varepsilon_{2} h_{2} )} \mathord{\left/ {\vphantom {{t_{2} (1 + \varepsilon_{2} h_{2} )} {\varepsilon_{2} ,\quad \lambda_{2} = {{t_{2} } \mathord{\left/ {\vphantom {{t_{2} } {\varepsilon_{2} }}} \right. \kern-0pt} {\varepsilon_{2} }}}}} \right. \kern-0pt} {\varepsilon_{2} ,\quad \lambda_{2} = {{t_{2} } \mathord{\left/ {\vphantom {{t_{2} } {\varepsilon_{2} }}} \right. \kern-0pt} {\varepsilon_{2} }}}},$which further reduces to

$$ \tan (t_{1} h_{1} ) = \frac{{\mu_{2}^{(4)} \mu_{3} krt_{2} - (\mu_{2}^{(4)} t_{2} )^{2} (1 + \varepsilon_{2} h_{2} )\tan (t_{2} h_{2} )}}{{\mu_{1}^{(4)} \mu_{2}^{(4)} t_{1} t_{2} + \mu_{1}^{(2)} \mu_{3} krt_{1} (1 + \varepsilon_{2} h_{2} )\tan (t_{2} h_{2} )}}, $$

(77)

Special case

When both of the upper and intermediate layers becomes homogeneous, i.e. $\varepsilon_{1} \to 0,\;\varepsilon_{2} \to 0;$ then deduced dispersion relation in (77) yields

$$ \tan (t_{1} h_{1} ) = \frac{{\mu_{2}^{(4)} \mu_{3} krt_{2} - (\mu_{2}^{(4)} t_{2} )^{2} \tan (t_{2} h_{2} )}}{{\mu_{1}^{(4)} \mu_{2}^{(4)} t_{1} t_{2} + \mu_{1}^{(2)} \mu_{3} rt_{1} \tan (t_{2} h_{2} )}}. $$

(78)

Validation with the classical case

In each case, if intermediate layer of composite structure vanishes and corresponding initial stress associated with upper layer is assumed to be absent, which mathematically may be represented as $h_{2} \to 0\quad \text{and} \quad \zeta_{1}^{(1)} = 0$ in Case I, $h_{2} \to 0\quad \text{and} \quad \zeta_{1}^{(2)} = 0$ in Case II, $h_{2} \to 0\quad \text{and} \quad \zeta_{1}^{(3)} = 0$ in Case III and $h_{2} \to 0\quad \text{and} \quad \zeta_{1}^{(4)} = 0$ in Case IV. Then, dispersion relation obtained in Eqs. (25), (39), (55) and (77), for Case I, Case II, Case III and Case IV associated with each of the four distinct cases reduce to

$$ \tan \left( {kh_{1} \sqrt {\left( {{c \mathord{\left/ {\vphantom {c {\beta_{1}^{(j)} }}} \right. \kern-0pt} {\beta_{1}^{(j)} }}} \right)^{2} - 1} } \right) = \frac{{\mu_{3} \sqrt {1 - \left( {{c \mathord{\left/ {\vphantom {c {\beta_{3} }}} \right. \kern-0pt} {\beta_{3} }}} \right)^{2} } }}{{\mu_{1}^{(j)} \sqrt {\left( {{c \mathord{\left/ {\vphantom {c {\beta_{1}^{(j)} }}} \right. \kern-0pt} {\beta_{1}^{(j)} }}} \right)^{2} - 1} }}, $$

(79)

for $j = 1,\,2,\,3,\quad \text{and} \quad 4 ,$ respectively. Equation (79) represents classical Love wave equation with $\beta_{1}^{(j)} \left( { = \sqrt {\mu_{1}^{(j)} /\rho_{1} } } \right)$ being the shear wave velocity associated with uppermost layer for Case j. This validates the result accomplished in each of the four distinct cases in view of classical results.

Analysis through numerical results

For the purpose of graphical depicture of the results, numerical computation has been carried out for deduced dispersion relations (24), (38), (54) and (73) for the propagation of SH-type wave in composite structure with inhomogeneous double superficial layers with initial stress and an isotropic half-space for Cases I, II, III and IV, respectively. Each of the considered cases deals with a distinct with form of inhomogeneity viz. when inhomogeneity in double superficial layer is due to exponential variation in density only (Case I); when inhomogeneity in double superficial layers is due to exponential variation in rigidity only (Case II); when inhomogeneity in double superficial layer is due to exponential variation in rigidity, density and initial stress (Case III) and when inhomogeneity in double superficial layer is due to linear variation in rigidity, density and initial stress (Case IV). The effect of the inhomogeneity parameters, initial stress parameters and width ratio associated with the two layers in the composite structure for each of the four aforesaid cases on dispersion curve (representing the variation of dimensionless phase velocity ${c \mathord{\left/ {\vphantom {c \beta }} \right. \kern-0pt} \beta }( {c \mathord{\left/ {\vphantom {c {\beta_{1}^{(j)} ;\quad j = 1,\,2,\,3,\,4}}} \right. \kern-0pt} {\beta_{1}^{(j)} ;\, = j = 1,\,2,\,3,\,4}}),$ against wavenumber, $kh_{1}$) of SH-type wave has been analyzed and their pictorial delineation has been accomplished through Figs. 2a, b, 3a, b, 4a, b, 5a, b, 6a and b.

Fig. 2

Variation of dimensionless phase velocity $(c/\beta )$ of SH-type wave against dimensionless wave number $(kh_{1} )$ for different values of distinct heterogeneity parameter of the uppermost layer $(M_{1} )$ a for Case I $(\beta = \beta_{1}^{(1)} )$ and Case II $(\beta = \beta_{1}^{\left( 2 \right)} )$ b for Case III $(\beta = \beta_{1}^{(3)} )$ and Case IV $(\beta = \beta_{1}^{(4)} )$

For simplicity of the graphical representation, we have considered the following notations for all the figures as below:

In Figs. 2a, 3a, 4a, 5a and 6a: (1) Case I: replacing $\beta_{1}^{(1)}$ by $\beta$. (2) Case II: replacing $\beta_{1}^{(2)}$ by $\beta$.

Fig. 3

Variation of dimensionless phase velocity $(c/\beta )$ of SH-type wave against dimensionless wave number $(kh_{1} )$ for different values distinct heterogeneity parameter of the intermediate layer $(M_{2} )$ a for Case I $(\beta = \beta_{1}^{(1)} )$ and Case II $(\beta = \beta_{1}^{(2)} )$ b for Case III $(\beta = \beta_{1}^{(3)} )$ and Case IV $(\beta = \beta_{1}^{(4)} )$

Fig. 4

Variation of dimensionless phase velocity $(c/\beta )$ of SH-type wave against dimensionless wave number $(kh_{1} )$ for different values initial stress (comressive/tensile) parameter of the uppermost layer $(M_{1} )$ a for Case I $(\beta = \beta_{1}^{(1)} )$ and Case II $(\beta = \beta_{1}^{(2)} )$ b for Case III $(\beta = \beta_{1}^{(3)} )$ and Case IV $(\beta = \beta_{1}^{(4)} )$

Fig. 5

Variation of dimensionless phase velocity $(c/\beta )$ of SH-type wave against dimensionless wave number $(kh_{1} )$ for different values of initial stress (comressive/tensile) parameter of the intermediate layer $(M_{2} )$ a for Case I $(\beta = \beta_{1}^{(1)} )$ and Case II $(\beta = \beta_{1}^{(2)} )$ b for Case III $(\beta = \beta_{1}^{(3)} )$ and Case IV $(\beta = \beta_{1}^{(4)} )$

Fig. 6

Variation of dimensionless phase velocity $(c/\beta )$ of SH-type wave against dimensionless wave number $(kh_{1} )$ for different values of width ratio a for Case I $(\beta = \beta_{1}^{(1)} )$ and Case II $(\beta = \beta_{1}^{(2)} )$ b for Case III $(\beta = \beta_{1}^{(3)} )$ and Case IV $(\beta = \beta_{1}^{(4)} )$

In Figs. 2b, 3b, 4b, 5b and 6b: (1) Case III: replacing $\beta_{1}^{(3)}$ by $\beta$. (2) Case IV: replacing $\beta_{1}^{(4)}$ by $\beta$.

Following data (Gubbins 1990) have been taken into the account for numerical computation:

For the uppermost layer $(M_{1} )$:

$$ \mu_{1}^{(1)} = \mu_{1}^{(2)} = \mu_{1}^{(3)} = \mu_{1}^{(4)} = 3.23 \times 10^{10} \;{\text{N/m}}^{2} ,\quad \rho_{1}^{(1)} = \rho_{1}^{(2)} = \rho_{1}^{(3)} = \rho_{1}^{(4)} = 2802\;{\text{Kg/m}}^{3} , $$

for the intermediate layer $(M_{2} )$:

$$ \mu_{2}^{(1)} = \mu_{2}^{(2)} = \mu_{2}^{(3)} = \mu_{2}^{(4)} = 6.54 \times 10^{10} \;{\text{N/m}}^{2} ,\quad \rho_{1}^{(1)} = \rho_{1}^{(2)} = \rho_{1}^{(3)} = \rho_{1}^{(4)} = 3409\;{\text{Kg/m}}^{3} , $$

for the lowermost half-space $(M_{3} )$:

$$ \mu_{3} = 29.17 \times 10^{10} \;{\text{N/m}}^{2} ,\quad \rho_{3} = 5563\;{\text{Kg/m}}^{3} . $$

Moreover, following values (unless otherwise stated) have also been taken into consideration:

$$ n_{1} h_{1} = 0.1,\,0.2,\,0.3;\quad n_{2} h_{2} = 0.1,\,0.2,\,0.3;\quad l_{1} h_{1} = 0.1,\,0.2,\,0.3;\quad l_{2} h_{2} = 0.1,\,0.2,\,0.3;\quad \varsigma_{1} h_{1} = 0.13,\,0.15,\,0.17; $$

$$ \varsigma_{1} h_{1} = 0.13,\,0.15,\,0.17;\quad \varsigma_{2} h_{2} = 0.13,\,0.15,\,0.17;\quad \sigma_{1} h_{1} = 0.01,\,0.02,\,0.03;\quad \sigma_{2} h_{2} = 0.01,\,0.02,\,0.03; $$

$$ \sigma_{2} h_{2} = 0.01,\,0.02,\,0.03;\quad \varepsilon_{1} h_{1} = 0.13,\,0.15,\,0.17;\quad \varepsilon_{2} h_{2} = 0.13,\,0.15,\,0.17;\quad \zeta_{1}^{(1)} = \,0, \,\pm 0.2;\quad \zeta_{2}^{(1)} = 0, \pm \,0.2; $$

$$ \,\zeta_{1}^{(2)} = 0, \,\pm\, 0.2;\quad \zeta_{2}^{(2)} = \,0, \,\pm\, 0.2\,\,\zeta_{1}^{(3)} = 0, \,\pm\, 0.2;\quad \zeta_{2}^{(3)} = \,0, \,\pm\, 0.2;\,\zeta_{1}^{(4)} = 0, \,\pm\, 0.2;\quad \zeta_{2}^{(4)} = 0, \,\pm\, 0.2. $$

To unravel the effect of different form of inhomogeneity in uppermost layer due to consideration of Case I, II, III and IV, Fig. 2a, b has been portrayed. In Fig. 2a curves 1, 2 and 3 reflect the effect of exponential inhomogeneity parameter $(n_{1} h_{1} )$ of the uppermost layer associated with Case I, whereas curves 4, 5 and 6 are concerned with variation of exponential inhomogeneity parameter $(l_{1} h_{1} )$ of uppermost layer associated with Case II, on phase velocity of SH-type wave. In view of the consideration of very small value of $n_{1} h_{1} ,$ curve 1 corresponds to the situation of linear heterogeneity, in close approximation, in density and rigidity being constant in uppermost layer, whereas for small value of $l_{1} h_{1} ,$ curve 4 realizes the situation of the uppermost layer to be Gibson layer (Gibson 1967) in close approximation, as it will correspond to the existence of linear inhomogeneity in rigidity and constant density. It is examined through this figure that exponential inhomogeneity parameter associated with density $(n_{1} h_{1} )$ encourages the phase velocity; on the other hand, exponential inhomogeneity parameter associated with rigidity $(l_{1} h_{1} )$ discourages the phase velocity of SH-type wave propagating in the considered structure.

On the other hand, in Fig. 2b, curves 1, 2 and 3 manifest the effect of exponential inhomogeneity parameter $(\sigma_{1} h_{1} )$ associated with rigidity and initial stress of uppermost layer, whereas curves 4, 5 and 6 correspond to the variation of distinct exponential inhomogeneity parameter associated with the density of the uppermost layer on the phase velocity of SH-type wave for Case III. Further, curves 7, 8 and 9 represent the influence of linear inhomogeneity parameter associated with rigidity, density and initial stress on the phase velocity of SH-type wave in Case IV. It is exhibited in Fig. 2b that for Case III, exponential inhomogeneity parameter associated with rigidity and initial stress disfavors whereas distinct exponential inhomogeneity parameter associated with density favors significantly the phase velocity of SH-type with increment in their magnitude. This observed trend in phase velocity of SH-type wave with concerned inhomogeneity parameter for Case III is found to be fairly compliant with the trend found for the associated inhomogeneity parameters in Case I and Case II. However, the magnitude-wise deviation is being observed. Further, in Case IV, linear inhomogeneity $(\varepsilon_{1} h_{1} )$ parameter associated with density, rigidity and initial stress affects favorably the phase velocity of SH-type wave. Meticulous examination of curves in Fig. 2a reveals that the presence of Gibson layer as an uppermost layer in the considered composite structure supports the phase velocity of SH-type wave.

The influence of distinct form of inhomogeneity, which has been taken into consideration in Cases I, II, III and IV, for intermediate layer, is demonstrated graphically in Figs. 3a, b. The variation of inhomogeneity parameter associated with material property of intermediate layer for Case I and Case II has been manifested through Fig. 3a, whereas that for Case III and Case IV has been delineated through Fig. 3b. Again curve 1 closely represents the linear heterogeneity in density and a constant rigidity in intermediate layer as $n_{2} h_{2}$ is taken very small, whereas curve 4 accounts for Gibson intermediate layer for $l_{2} h_{2}$ being very small. More precisely, in Fig. 3a, the curves 1, 2 and 3 show the pronounced discouraging influence of exponential inhomogeneity parameter $(n_{2} h_{2} )$ associated with Case I of intermediate layer on the phase velocity of SH-type wave. On the contrary curves 4, 5 and 6 show the significant encouraging effect of exponential inhomogeneity parameter $l_{2} h_{2}$ associated with Case II of intermediate layer on the same. Again in Fig. 3b, curves 1, 2 and 3 reflect the favorable effect of exponential inhomogeneity parameter associated with rigidity and initial stress $(\sigma_{2} h_{2} )$ of intermediate layer, on the phase velocity of SH-type wave, for Case III. However, curves 4, 5 and 6 account for the discouraging effect of exponential inhomogeneity parameter associated with density of intermediate layer on the same for Case III. Besides this, the curves 7, 8 and 9 indicate the substantial increasing effect of linear inhomogeneity $(\varepsilon_{2} h_{2} )$ parameter associated with rigidity, density and initial stress for intermediate layer on the phase velocity of SH-type wave in Case IV. Subtle analysis establishes that presence of Gibson layer as intermediate layer in the considered composite structures discourages the phase velocity of SH-type wave.

To demonstrate the effect of compressive as well as tensile initial stress acting in the uppermost layer for Case I and Case II Fig. 4a is portrayed, whereas for Case III and Case IV, Fig. 4b is plotted. In Fig. 4a, b, curves 1 and 4 correspond to the presence of tensile initial stress; curves 2 and 5 correspond to the presence of no initial stress; and curves 3 and 6 indicate the presence of compressive initial stress in the uppermost layer for the Case I and II, respectively. On the other hand, in Fig. 4b, curves 1 and 4 represent the presence of tensile initial stress; curves 2 and 5 represent no initial stress; and curves 3 and 6 account for compressive initial stress, associated with the uppermost layer, of Case III and Case IV. It is established through Fig. 4a, b that initial stress acting in uppermost layer has a disfavoring influence on phase velocity of SH-type wave in all four aforementioned cases. Specifically, as compressive initial stress grows in the uppermost layer, phase velocity of SH-type wave gets decreased, whereas as tensile initial stress increases in the uppermost layer, phase velocity of SH-type wave get increased in all four cases.

Figure 5a, b manifests the impact of dimensionless initial stress parameter associated with intermediate layer of composite structure for Case I & Case II and Case III & Case IV, respectively. The association of the case with the numbering of curves in Fig. 5a, b follows the same fashion, which is followed in Fig. 4a, b but for intermediate layer. It is examined that for intermediate layer, with the growth of compressive initial stress, phase velocity of SH-type wave diminishes, whereas with the growth of tensile initial stress in the same leads to the increase in phase velocity of SH-type wave in all four considered cases. Although the same trend has been exhibited for initial stress acting in the uppermost layer and intermediate layer for all four said cases yet the effect in terms of magnitude may easily be observed.

Effect of width ratio associated with double superficial layer in the considered composite structure on the phase velocity of SH-type wave is described graphically for Case I (Curves 1, 2, 3, 4) and Case II (Curves 5, 6, 7, 8) in Fig. 6a and for Case III (Curves 1, 2, 3, 4) and Case IV (Curves 5, 6, 7, 8) in Fig. 6b. In Fig. 6a, b, curve 1 corresponds to Case I and Case III, respectively, when there exists only uppermost layer over half-space (i.e. intermediate layer is absent); curve 2 is associated with the Case I and Case III, respectively, when thickness of the uppermost layer greater than the intermediate layer; curve 3 associated with the Case I and III, respectively, when thickness of the uppermost layer is equal to the thickness of the intermediate one; curve 4 is associated with the Case I and III, respectively, when thickness of the uppermost layer is smaller than the thickness of the intermediate one; curve 5 corresponds to Case II and IV, respectively, when there intermediate layer is absent in the considered composite structure; curve 6 corresponds to Case II and IV, respectively, when thickness of the uppermost layer greater than the intermediate layer; curve 7 indicates Case II and IV, respectively, when thickness of the uppermost layer is equal to the thickness of the intermediate one and curve 8 is associated with the Case II and IV, respectively, when thickness of the uppermost layer is smaller than the thickness of the intermediate one. It is reported from these two figures that phase velocity of SH-type wave decreases with the increase in the width ratio of double superficial layers for all aforesaid cases. Subtle examination of these curves in both the figures suggest that phase velocity of SH-type is maximum, when intermediate layer is absent in the considered composite structure and minimum when thickness of uppermost layer is less than that of intermediate one among all considered cases of width ratio.

The comparative study of all the figures concludes that the phase velocity of SH-type wave is maximum when heterogeneity is considered in composite structure as per case IV and minimum when it is considered as per case III, among all four studied cases. Besides this, phase velocity is found to be more when heterogeneity is considered as per case I as compared to the situation when it is according to the case II. The meticulous examination of these figures establishes that the influence of heterogeneity parameter associated with density dominates over the effect of heterogeneity parameter associated with rigidity on the phase velocity of SH-type wave. In addition to this, it may be concluded that the linear heterogeneity in the material properties of the medium favors more to the phase velocity as compared to the exponential heterogeneity in material property of the medium. This may be cause due to the reason that extent of heterogeneity is more in case of exponential heterogeneity as compared to linear heterogeneity and as prevalence of heterogeneity is more in a medium, phase velocity is greater.

Conclusion

Analysis on the influence of different form of inhomogeneity in a composite structure comprised of double superficial layers lying over a half-space, on the phase velocity of propagating SH-type wave has been accomplished through present study using Debye asymptotic analysis. Propagation of SH-type wave in a composite structure has been examined in four distinct cases of inhomogeneity viz. when inhomogeneity in double superficial layer is due to exponential variation in density only (Case I); when inhomogeneity in double superficial layers is due to exponential variation in rigidity only (Case II); when inhomogeneity in double superficial layer is due to exponential variation in rigidity, density and initial stress (Case III) and when inhomogeneity in double superficial layer is due to linear variation in rigidity, density and initial stress (Case IV). Closed-form expression of dispersion relation has been obtained for all four aforementioned cases. Numerical computation has been carried out to graphically demonstrate the effect of inhomogeneity parameters, initial stress parameters as well as width ratio associated with double superficial layers in the composite structure for each of the four aforesaid cases on dispersion curve. Meticulous examination of distinct cases of inhomogeneity and initial stress in context of considered problem has been carried out with extensive analysis in a comparative approach. Following points may be encapsulated through the analysis undertaken in present paper:

• 1. Dispersion equations of SH-type wave have been deduced in closed-form through analytical treatment with extensive application of Debye asymptotic analysis for all four said cases and they are found in well-agreement with the classical Love-wave equation as well.

• 2. The substantial effect of wave number has been reported on phase velocity of SH-type wave in all four said cases. Phase velocity decreases significantly with the increase in wave number.

• 3. It may be stated through the comparative study of Case I and Case II that, the influence of heterogeneity parameters associated with rigidity is of opposite nature to the influence of heterogeneity parameters associated with density, accompanying either of the superficial layers $M_{1} \, \text{and} \, M_{2}$ are of the conflicting nature. More precisely, the influence of heterogeneity parameter present in the upper layer follows a completely opposite trend in contrast to that of the intermediate layer for each of Case I and Case II.

• 4. Comparative study of Case III and Case IV emphasized that linear form of inhomogeneity (Case III) assumed in both the superficial layers favors the phase velocity of SH-type wave, However, the inhomogeneity contributing to exponential variation in corresponding density of each of the two superficial layers disfavors the phase velocity of SH-type wave. On the other hand, the exponential form of inhomogeneity existing in the upper layer and intermediate layer, accompanying rigidity and that of initial stress favors and disfavors the phase velocity significantly.

• 5. It can be stated through minute contemplation of all four cases that the phase velocity of SH-type wave is maximum when heterogeneity is considered in composite structure as per case IV and minimum when it is considered as per case III, among all four studied cases. Besides this, phase velocity is found to be more when heterogeneity is considered as per case I as compared to the situation when it is according to the case II.

• 6. The meticulous examination carried out in comparative manner establishes that the influence of heterogeneity parameter associated with density dominates over the effect of heterogeneity parameter associated with rigidity on the phase velocity of SH-type wave. In addition to this, it may also be concluded that the linear heterogeneity in the material properties of the medium favors more the phase velocity as compared to the exponential heterogeneity in material property of the medium.

• 7. It is revealed that the presence of Gibson layer as an uppermost layer in the considered composite structure encourages, whereas presence of Gibson layer as an intermediate layer in the considered composite structure discourages the phase velocity of SH-type wave.

• 8. It is established that as compressive initial stress grows in the uppermost as well as intermediate layer, phase velocity of SH-type wave gets decreased, whereas as tensile initial stress increases in the uppermost as well as intermediate layer, phase velocity of SH-type wave gets increased in all four said cases.

• 9. It is reported that phase velocity of SH-type wave decreases with the increase in the width ratio of double superficial layers for all aforesaid cases. Subtle examination establishes that phase velocity of SH-type is maximum, when intermediate layer is absent in the considered composite structure and minimum when thickness of uppermost layer is less than that of intermediate one among all considered cases of width ratio.

The earth is considered to be consisting of a sequence of horizontal layers bearing different elastic properties. The study of propagation of seismic waves is done extensively to predict and understand the behavior of the earth’s interior. Therefore, the present study may find its worthy applications in the sphere of seismology, engineering geology, earthquake engineering and geophysics: specifically, in the problems affiliated to waves and vibrations through heterogeneous media.

Appendices

Appendix I

$$ \begin{aligned} R_{1} & = J_{{p_{1} }}^{\prime } (\delta_{1} e^{{ - n_{\,1} h_{\,1} }} )Y_{{p_{1} }} (\delta_{1} ) - Y_{{p_{1} }}^{\prime } (\delta_{1} e^{{ - n_{\,1} h_{\,1} }} )J_{{p_{1} }} (\delta_{1} ),R_{2} = J_{{p_{1} }}^{\prime } (\delta_{1} e^{{ - n_{\,1} h_{\,1} }} )Y_{{p_{1} }}^{\prime } \left( {\delta_{1} } \right) - Y_{{p_{1} }}^{\prime } (\delta_{1} e^{{ - n_{\,1} h_{\,1} }} )J_{{p_{1} }}^{\prime } (\delta_{1} ), \\ R_{3} & = J_{{p_{2} }}^{\prime } (\delta_{2} e^{{n_{\,2} h_{\,2} }} )Y_{{p_{2} }} (\delta_{2} ) - Y_{{p_{2} }}^{\prime } (\delta_{2} e^{{n_{\,2} h_{\,2} }} )J_{{p_{2} }} (\delta_{2} ),R_{4} = J_{{p_{2} }} (\delta_{2} e^{{n_{\,2} h_{\,2} }} )Y_{{p_{2} }} (\delta_{2} ) - Y_{{p_{2} }} (\delta_{2} e^{{n_{\,2} h_{\,2} }} )J_{{p_{2} }} (\delta_{2} ), \\ R_{5} & = J_{{p_{2} }}^{\prime } (\delta_{2} e^{{n_{2} h_{2} }} )Y_{{p_{2} }} '(\delta_{2} ) - Y_{{p_{2} }}^{\prime } (\delta_{2} e^{{n_{2} h_{2} }} )J_{{p_{2} }} '(\delta_{2} ),R_{6} = J_{{p_{2} }} (\delta_{2} e^{{n_{\,2} h_{2} }} )Y_{{p_{2} }}^{\prime } (\delta_{2} ) - Y_{{p_{2} }} (\delta_{2} e^{{n_{\,2} h_{2} }} )J_{{p_{2} }}^{\prime } (\delta_{2} ), \\ \end{aligned} $$

$$ p_{1} \sec \phi_{1} = \frac{kc}{{n_{\,1} \beta_{1}^{(1)} }}e^{{ - n_{1} h_{1} }} ,\quad p_{2} \sec \phi_{2} = \frac{kc}{{n_{\,1} \beta_{1}^{(1)} }},\quad p_{1} \tan \phi_{1} = \frac{k}{{n_{1} }}\sqrt {\frac{{c^{2} }}{{(\beta_{1}^{(1)} )^{2} }} - 1 + \zeta_{1}^{(1)} } \left[ {1 - \frac{{c^{2} n_{1} h_{1} }}{{c^{2} - (\beta_{1}^{(1)} )^{2} }}} \right], $$

$$ p_{1} \tan \phi_{2} = \frac{k}{{n_{1} }}\sqrt {\frac{{c^{2} }}{{(\beta_{1}^{(1)} )^{2} }} - 1 + \zeta_{1}^{(1)} } ,(\phi_{1} - \phi_{2} )\sim n_{1} h_{1} \frac{{\sqrt {1 - \zeta_{1}^{(1)} } }}{{\sqrt {\frac{{c^{2} }}{{(\beta_{1}^{(1)} )^{2} }} - 1 + \zeta_{1}^{(1)} } }}, $$

$$ p_{1} (\tan \phi_{1} - \tan \phi_{2} ) - p_{1} (\phi_{1} - \phi_{2} )\sim - kh_{1} \sqrt {\frac{{c^{2} }}{{(\beta_{1}^{(1)} )^{2} }} - 1 + \zeta_{1}^{(1)} } , $$

$$ \sin \phi_{1} \sim \frac{{\beta_{1}^{(1)} }}{c}\sqrt {\frac{{c^{2} }}{{(\beta_{1}^{(1)} )^{2} }} - 1 + \zeta_{1}^{(1)} } \sim \sin \phi_{2} ,\quad p_{2} \sec \phi_{3} = \frac{kc}{{n_{2} \beta_{2}^{(1)} }}e^{{n_{2} h_{2} }} ,\quad p_{2} \sec \phi_{4} = \frac{kc}{{n_{2} \beta_{2}^{(1)} }}, $$

$$ p_{2} \tan \phi_{3} = \frac{k}{{n_{2} }}\sqrt {\frac{{c^{2} }}{{(\beta_{2}^{(1)} )^{2} }} - 1 + \zeta_{2}^{(1)} } ,\quad p_{2} \tan \phi_{4} = \frac{k}{{n_{2} }}\sqrt {\frac{{c^{2} }}{{(\beta_{2}^{(1)} )^{2} }} - 1 + \zeta_{2}^{(1)} } \left[ {1 + \frac{{c^{2} n_{2} h_{2} }}{{c^{2} - (\beta_{2}^{(1)} )^{2} }}} \right], $$

$$ (\phi_{3} - \phi_{4} )\sim n_{2} h_{2} \frac{{\sqrt {1 - \zeta_{2}^{(1)} } }}{{\sqrt {\frac{{c^{2} }}{{(\beta_{2}^{(1)} )^{2} }} - 1 + \zeta_{2}^{\left( 1 \right)} } }},\quad p_{2} (\tan \phi_{3} - \tan \phi_{4} ) - p_{2} (\phi_{3} - \phi_{4} )\sim kh_{2} \sqrt {\frac{{c^{2} }}{{(\beta_{2}^{(1)} )^{2} }} - 1 + \zeta_{2}^{(1)} } , $$

$$ {\text{and}}\;\sin \phi_{3} \sim \frac{{\beta_{2}^{(1)} }}{c}\sqrt {\frac{{c^{2} }}{{\left( {\beta_{2}^{(1)} } \right)^{2} }} - 1 + \zeta_{2}^{(1)} } \sim \sin \phi_{4} . $$

Appendix II

$$ \begin{aligned} R_{7} = J_{{q_{1} }} (\delta_{1} e^{{l_{1} h_{1} }} )Y_{{q_{1} }} (\delta_{1} ) - J_{{q_{1} }} (\delta_{1} )Y_{{q_{1} }} (\delta_{1} e^{{l_{1} h_{1} }} ),\quad R_{8} = J_{{q_{1} }}^{\prime } (\delta_{1} e^{{l_{1} h_{1} }} )Y_{{q_{1} }} (\delta_{1} ) - J_{{q_{1} }} (\delta_{1} )Y_{{q_{1} }}^{\prime } (\delta_{1} e^{{l_{1} h_{1} }} ), \hfill \\ R_{9} = J_{{q_{1} }} (\delta_{1} e^{{l_{1} h_{1} }} )Y_{{q_{1} }}^{\prime } (\delta_{1} ) - J_{{q_{1} }}^{\prime } (\delta_{1} )Y_{{q_{1} }} (\delta_{1} e^{{l_{1} h_{1} }} ),\quad R_{10} = J_{{q_{1} }}^{\prime } (\delta_{1} e^{{l_{1} h_{1} }} )Y_{{q_{1} }}^{\prime } (\delta_{1} ) - J_{{q_{1} }}^{\prime } (\delta_{1} )Y_{{q_{1} }}^{\prime } (\delta_{1} e^{{l_{1} h_{1} }} ), \hfill \\ \end{aligned} $$

$$ \begin{aligned} R_{11} = J_{{q_{2} }} (\delta_{2} e^{{ - l_{2} h_{2} }} )Y_{{q_{2} }} (\delta_{2} ) - J_{{q_{2} }} (\delta_{2} )Y_{{q_{2} }} (\delta_{2} e^{{ - l_{2} h_{2} }} ),\quad R_{12} = J_{{q_{2} }} (\delta_{2} e^{{ - l_{2} h_{2} }} )Y_{{q_{2} }}^{\prime } (\delta_{2} ) - J_{{q_{2} }}^{\prime } (\delta_{2} )Y_{{q_{2} }} (\delta_{2} e^{{ - l_{2} h_{2} }} ), \hfill \\ R_{13} = J_{{q_{2} }}^{\prime } (\delta_{2} e^{{ - l_{2} h_{2} }} )Y_{{q_{2} }} (\delta_{2} ) - J_{{q_{2} }} (\delta_{2} )Y_{{q_{2} }}^{\prime } (\delta_{2} e^{{ - l_{2} h_{2} }} ),\quad R_{14} = J_{{q_{2} }}^{\prime } (\delta_{2} e^{{ - l_{2} h_{2} }} )Y_{{q_{2} }}^{\prime } (\delta_{2} ) - J_{{q_{2} }}^{\prime } (\delta_{2} )Y_{{q_{2} }}^{\prime } (\delta_{2} e^{{ - l_{2} h_{2} }} ). \hfill \\ \end{aligned} $$

$$ \left[ {J_{{q_{1} }} (\gamma_{1} e^{{l_{1} h_{1} }} )Y_{{q_{1} }} (\gamma_{1} ) - Y_{{q_{1\,} }} (\delta \gamma_{1} e^{{l_{1} h_{1} }} )J_{{q_{1} }} (\gamma_{1} )} \right] \approx \frac{{ - 2\sin [q_{1} (\tan \psi_{1} - \tan \psi_{2} ) - q_{1} (\psi_{1} - \psi_{2} )]}}{{\pi q_{1} \sqrt {\tan \psi_{1} \tan \psi_{2} } }}, $$

$$ \left[ {J_{{q_{2} }} (\gamma_{2} e^{{ - l_{2} h_{2} }} )Y_{{q_{2} }} (\delta_{2} ) - Y_{{q_{2} }} (\gamma_{2} e^{{ - l_{\,2} h_{2} }} )J_{{q_{2} }} (\gamma_{2} )} \right] \approx \frac{{ - 2\sin [q_{2} (\tan \psi_{3} - \tan \psi_{4} ) - q_{2} (\psi_{3} - \psi_{4} )]}}{{\pi q_{2} \sqrt {\tan \psi_{3} \tan \psi_{4} } }}, $$

$$ \left[ {J_{{q_{1} }} (\gamma_{1} e^{{l_{1} h_{1} }} )Y_{{q_{1} }}^{\prime } (\gamma_{1} ) - Y_{{q_{1\,} }} (\gamma_{1} e^{{l_{1} h_{1} }} )J_{{q_{1} }}^{\prime } (\gamma_{1} )} \right] \approx \frac{{2\sin \psi_{2} \cos [q_{1} (\tan \psi_{1} - \tan \psi_{2} ) - q_{1} (\psi_{1} - \psi_{2} )]}}{{\pi q_{1} \sqrt {\tan \psi_{1} \tan \psi_{2} } }}, $$

$$ \left[ {J_{{q_{2} }} (\gamma_{2} e^{{ - l_{2} h_{2} }} )Y_{{q_{2} }}^{\prime } (\gamma_{2} ) - Y_{{q_{2} }} (\gamma_{2} e^{{ - l_{2} h_{2} }} )J_{{q_{2} }}^{\prime } (\gamma_{2} )} \right] \approx \frac{{2\sin \psi_{4} \cos [q_{2} (\tan \psi_{3} - \tan \psi_{4} ) - q_{2} (\psi_{3} - \psi_{4} )]}}{{\pi q_{2} \sqrt {\tan \psi_{3} \tan \psi_{4} } }}, $$

$$ \left[ {J_{{q_{1} }}^{\prime } (\gamma_{1} e^{{l_{1} h_{1} }} )Y_{{q_{1} }} (\gamma_{1} ) - Y_{{q_{1\,} }}^{\prime } (\gamma_{1} e^{{l_{1} h_{1} }} )J_{{q_{1} }} (\gamma_{1} )} \right] \approx \frac{{ - 2sin\psi_{1} \cos [q_{1} (\tan \psi_{1} - \tan \psi_{2} ) - q_{1} (\psi_{1} - \psi_{2} )]}}{{\pi q_{1} \sqrt {\tan \psi_{1} \tan \psi_{2} } }}, $$

$$ \left[ {J_{{q_{2} }}^{\prime } (\gamma_{2} e^{{ - l_{2} h_{2} }} )Y_{{q_{2} }} (\gamma_{2} ) - Y_{{q_{2} }} '(\gamma_{2} e^{{ - l_{2} h_{2} }} )J_{{q_{2} }} (\gamma_{2} )} \right] \approx \frac{{ - 2\sin \psi_{3} \cos [q_{2} (\tan \psi_{3} - \tan \psi_{4} ) - q_{2} (\psi_{3} - \psi_{4} )]}}{{\pi q_{2} \sqrt {\tan \psi_{3} \tan \psi_{4} } }}, $$

$$ \left[ {J_{{q_{1} }}^{\prime } (\gamma_{1} e^{{l_{1} h_{1} }} )Y_{{q_{1} }}^{\prime } (\gamma_{1} ) - Y_{{q_{1\,} }}^{\prime } (\gamma_{1} e^{{l_{1} h_{1} }} )J_{{q_{1} }}^{\prime } (\gamma_{1} )} \right] \approx \frac{{ - 2\sin \psi_{1} \sin \psi_{2} \sin [q_{1} (\tan \psi_{1} - \tan \psi_{2} ) - q_{1} (\psi_{1} - \psi_{2} )]}}{{\pi q_{1} \sqrt {\tan \psi_{1} \tan \psi_{2} } }}, $$

$$ \left[ {J_{{q_{2} }}^{\prime } (\gamma_{2} e^{{ - l_{2} h_{2} }} )Y_{{q_{2} }}^{\prime } (\gamma_{2} ) - Y_{{q_{2} }}^{\prime } (\gamma_{2} e^{{\, - l_{2} \,h_{2} }} )J_{{q_{2} }}^{\prime } (\gamma_{2} )} \right] \approx \frac{{ - 2\sin \psi_{3} \sin \psi_{4} \sin [q_{2} (\tan \psi_{3} - \tan \psi_{4} ) - q_{2} (\psi_{3} - \psi_{4} )]}}{{\pi q_{2} \sqrt {\tan \psi_{3} \tan \psi_{4} } }}, $$

$$ q_{1} \sec \psi_{1} = \frac{kc}{{l_{1} \beta_{1}^{\left( 2 \right)} }}e^{{l_{1} h_{1} }} ,\quad q_{1} \sec \psi_{2} = \frac{kc}{{l_{1} \beta_{1}^{(2)} }},\quad q_{1} \tan \psi_{1} = \frac{k}{{l_{1} }}\sqrt {\frac{{c^{2} }}{{(\beta_{1}^{(2)} )^{2} }} - 1 + \zeta_{1}^{\left( 1 \right)} } \left[ {1 + \frac{{c^{2} l_{1} h_{1} }}{{c^{2} - (\beta_{1}^{(2)} )^{2} }}} \right], $$

$$ q_{1} \tan \psi_{2} = \frac{k}{{l_{1} }}\sqrt {\frac{{c^{2} }}{{\left( {\beta_{1}^{(2)} } \right)^{2} }} - 1 + \zeta_{1}^{(2)} } ,\quad \psi_{1} - \psi_{2} \sim l_{1} h_{1} \frac{{\sqrt {1 - \zeta_{1}^{(2)} } }}{{\sqrt {\frac{{c^{2} }}{{\left( {\beta_{1}^{(2)} } \right)^{2} }} - 1 + \zeta_{1}^{(2)} } }}, $$

$$ q_{1} (\tan \psi_{1} - \tan \psi_{2} ) - q_{1} (\psi_{1} - \psi_{2} )\sim kh_{1} \sqrt {\frac{{c^{2} }}{{\left( {\beta_{1}^{(2)} } \right)^{2} }} - 1 + \zeta_{1}^{(2)} } ,\quad \sin \psi_{1} \sim \frac{{\beta_{1}^{(2)} }}{c}\sqrt {\frac{{c^{2} }}{{\left( {\beta_{1}^{(2)} } \right)^{2} }} - 1 + \zeta_{1}^{(2)} } \sim \sin \psi_{2} . $$

$$ q_{2} \sec \psi_{3} = \frac{kc}{{l_{2} \beta_{2}^{(1)} }}e^{{ - l_{2} h_{2} }} ,\quad q_{2} \sec \psi_{4} = \frac{kc}{{l_{2} \beta_{2}^{(2)} }},\quad q_{2} \tan \psi_{3} = \frac{k}{{l_{2} }}\sqrt {\frac{{c^{2} }}{{(\beta_{2}^{(2)} )^{2} }} - 1 + \zeta_{2}^{(2)} } \left[ {1 - \frac{{c^{2} l_{2} h_{2} }}{{c^{2} - (\beta_{2}^{(2)} )^{2} }}} \right], $$

$$ q_{2} \tan \psi_{4} = \frac{k}{{l_{2} }}\sqrt {\frac{{c^{2} }}{{(\beta_{2}^{(2)} )^{2} }} - 1 + \zeta_{2}^{(2)} } ,\quad q_{2} (\tan \psi_{3} - \tan \psi_{4} ) - q_{2} (\psi_{3} - \psi_{4} )\sim - kh_{2} \sqrt {\frac{{c^{2} }}{{(\beta_{2}^{(2)} )^{2} }} - 1 + \zeta_{2}^{(2)} } , $$

$$ \psi_{3} - \psi_{4} \sim l_{2} h_{2} \frac{{\sqrt {1 - \zeta_{2}^{\left( 2 \right)} } }}{{\sqrt {\frac{{c^{2} }}{{\left( {\beta_{2}^{(2)} } \right)^{2} }} - 1 + \zeta_{2}^{(2)} } }}\quad {\text{and}}\quad \sin \psi_{3} \sim \frac{{\beta_{2}^{(2)} }}{c}\sqrt {\frac{{c^{2} }}{{\left( {\beta_{2}^{(2)} } \right)^{2} }} - 1 + \zeta_{2}^{(2)} } \sim \sin \psi_{4} . $$

Appendix III

$$ \begin{aligned} R_{15} = J_{{s_{3} }} (\varOmega_{1} e^{{\hbar_{1} h_{1} }} )Y_{{s_{1} }} (\varOmega_{1} ) - J_{{s_{3} }} (\varOmega_{1} )Y_{{s_{3} }} (\varOmega_{1} e^{{\hbar_{1} h_{1} }} ),\quad R_{16} = J_{{s_{3} }}^{'} (\varOmega_{1} e^{{\hbar_{1} h_{1} }} )Y_{{s_{3} }} (\varOmega_{1} ) - J_{{s_{3} }} (\varOmega_{1} )Y_{{s_{3} }}^{'} (\varOmega_{1} e^{{\hbar_{1} h_{1} }} ), \hfill \\ R_{17} = J_{{s_{3} }}^{{}} (\varOmega_{1} e^{{\hbar_{1} h_{1} }} )Y_{{s_{3} }}^{'} (\varOmega_{1} ) - J_{{s_{3} }}^{'} (\varOmega_{1} )Y_{{s_{3} }}^{{}} (\varOmega_{1} e^{{\hbar_{1} h_{1} }} ),\quad R_{18} = J_{{s_{3} }}^{'} (\varOmega_{1} e^{{\hbar_{1} h_{1} }} )Y_{{s_{3} }}^{'} (\varOmega_{1} ) - J_{{s_{3} }}^{'} (\varOmega_{1} )Y_{{s_{3} }}^{'} (\varOmega_{1} e^{{\hbar_{1} h_{1} }} ), \hfill \\ \end{aligned} $$

$$ \begin{aligned} R_{19} = J_{{s_{4} }} (\varOmega_{2} e^{{ - \hbar_{2} h_{2} }} )Y_{{s_{4} }} (\varOmega_{2} ) - J_{{s_{4} }} (\varOmega_{2} )Y_{{s_{4} }} (\varOmega_{2} e^{{ - \hbar_{2} h_{2} }} ),\quad R_{20} = J_{{s_{4} }}^{'} (\varOmega_{2} e^{{ - \hbar_{2} h_{2} }} )Y_{{s_{4} }} (\varOmega_{2} ) - J_{{s_{4} }} (\varOmega_{2} )Y_{{s_{4} }}^{'} (\varOmega_{2} e^{{ - \hbar_{2} h_{2} }} ), \hfill \\ R_{21} = J_{{s_{4} }}^{{}} (\varOmega_{2} e^{{ - \hbar_{2} h_{2} }} )Y_{{s_{4} }}^{'} (\varOmega_{2} ) - J_{{s_{4} }}^{'} (\varOmega_{2} )Y_{{s_{4} }}^{{}} (\varOmega_{2} e^{{ - \hbar_{2} h_{2} }} ),\quad R_{22} = J_{{s_{4} }}^{'} (\varOmega_{2} e^{{ - \hbar_{2} h_{2} }} )Y_{{s_{4} }}^{'} (\varOmega_{2} ) - J_{{s_{4} }}^{'} (\varOmega_{2} )Y_{{s_{4} }}^{'} (\varOmega_{2} e^{{ - \hbar_{2} h_{2} }} ), \hfill \\ \end{aligned} $$

$$ \left[ {J_{{s_{3} }} (\varOmega_{1} e^{{\hbar_{1} h_{\,1} }} )Y_{{s_{3} }} (\varOmega_{1} ) - Y_{{s_{3} }} (\varOmega_{1} e^{{\hbar_{1} h_{\,1} }} )J_{{s_{3} }} (\varOmega_{1} )} \right] \approx \frac{{ - \,2\sin [s_{3} (\tan \phi_{21} - \tan \phi_{22} ) - s_{3} (\phi_{21} - \phi_{22} )]}}{{\pi s_{3} \sqrt {\tan \phi_{21} \tan \phi_{22} } }}, $$

$$ \left[ {J_{{s_{4} }} (\varOmega_{2} e^{{ - \hbar_{2} h_{2} }} )Y_{{s_{4} }} (\varOmega_{2} ) - Y_{{s_{4} }} (\varOmega_{2} e^{{ - \hbar_{2} h_{2} }} )J_{{s_{2} }} (\varOmega_{2} )} \right] \approx \frac{{ - \,2\sin [s_{4} (\tan \phi_{23} - \tan \phi_{24} ) - s_{4} (\phi_{23} - \phi_{24} )]}}{{\pi s_{4} \sqrt {\tan \phi_{23} \tan \phi_{24} } }}, $$

$$ \left[ {J_{{s_{3} }} (\varOmega_{1} e^{{\hbar_{1} h_{\,1} }} )Y_{{s_{3} }} '(\varOmega_{1} ) - Y_{{s_{3} }} (\varOmega_{1} e^{{\hbar_{1} h_{\,1} }} )J_{{s_{3} }} '(\varOmega_{1} )} \right] \approx \frac{{2\sin \phi_{21} \sin [s_{3} (\tan \phi_{21} - \tan \phi_{22} ) - s_{3} (\phi_{21} - \phi_{22} )]}}{{\pi s_{3} \sqrt {\tan \phi_{21} \tan \phi_{22} } }}, $$

$$ \left[ {J_{{s_{4} }} (\varOmega_{2} e^{{ - \hbar_{2} h_{2} }} )Y_{{s_{4} }} '(\varOmega_{2} ) - Y_{{s_{4} }} (\varOmega_{2} e^{{ - \hbar_{2} h_{2} }} )J_{{s_{4} }} '(\varOmega_{2} )} \right] \approx \frac{{2\sin \phi_{24} \cos [s_{4} (\tan \phi_{23} - \tan \phi_{24} ) - s_{4} (\phi_{23} - \phi_{24} )]}}{{\pi s_{4} \sqrt {\tan \phi_{23} \tan \phi_{24} } }}, $$

$$ \left[ {J_{{s_{3} }} '(\varOmega_{1} e^{{\hbar_{1} h_{\,1} }} )Y_{{s_{3} }} (\varOmega_{1} ) - Y_{{s_{3} }} '(\varOmega_{1} e^{{\hbar_{1} h_{\,1} }} )J_{{s_{3} }} (\varOmega_{1} )} \right] \approx \frac{{ - \,2\sin \phi_{21} \cos [s_{3} (\tan \phi_{21} - \tan \phi_{22} ) - s_{3} (\phi_{21} - \phi_{22} )]}}{{\pi s_{3} \sqrt {\tan \phi_{21} \tan \phi_{22} } }}, $$

$$ \left[ {J_{{s_{4} }} '(\varOmega_{2} e^{{ - \hbar_{2} h_{2} }} )Y_{{s_{4} }} (\varOmega_{2} ) - Y_{{s_{4} }} '(\varOmega_{2} e^{{ - \hbar_{2} h_{2} }} )J_{{s_{4} }} (\varOmega_{2} )} \right] \approx \frac{{ - \,2\sin \phi_{23} \cos [s_{4} (\tan \phi_{23} - \tan \phi_{24} ) - s_{4} (\phi_{23} - \phi_{24} )]}}{{\pi s_{4} \sqrt {\tan \phi_{23} \tan \phi_{24} } }}, $$

$$ \left[ {J_{{s_{3} }} '(\varOmega_{1} e^{{\hbar_{1} h_{\,1} }} )Y_{{s_{3} }} '(\varOmega_{1} ) - Y_{{s_{3} }} '(\varOmega_{1} e^{{\hbar_{1} h_{\,1} }} )J_{{s_{3} }} '(\varOmega_{1} )} \right] \approx \frac{{ - \,2\sin \phi_{21} \sin \phi_{22} \sin [s_{3} (\tan \phi_{21} - \tan \phi_{22} ) - s_{3} (\phi_{21} - \phi_{22} )]}}{{\pi s_{3} \sqrt {\tan \phi_{21} \tan \phi_{22} } }}, $$

$$ \left[ {J_{{s_{4} }} '(\varOmega_{2} e^{{ - \hbar_{2} h_{2} }} )Y_{{s_{4} }} '(\varOmega_{2} ) - Y_{{s_{4} }} '(\varOmega_{2} e^{{ - \hbar_{2} h_{2} }} )J_{{s_{4} }} '(\varOmega_{2} )} \right] \approx \frac{{ - \,2\sin \phi_{23} \cos [s_{4} (\tan \phi_{23} - \tan \phi_{24} ) - s_{4} (\phi_{23} - \phi_{24} )]}}{{\pi s_{4} \sqrt {\tan \phi_{23} \tan \phi_{24} } }}, $$

$$ s_{3} \sec \varphi_{21} = \frac{kc}{{\hbar_{1} \beta_{1}^{(3)} }}e^{{\hbar_{1} h_{1} }} ,\quad s_{3} \sec \varphi_{22} = \frac{kc}{{\hbar_{1} \beta_{1}^{(3)} }},\quad s_{3} \tan \varphi_{21} = \frac{k}{{\hbar_{1} }}\sqrt {\frac{{c^{2} }}{{(\beta_{1}^{(3)} )^{2} }} - 1 + \zeta_{1}^{(3)} } \left[ {1 - \frac{{c^{2} \hbar_{1} h_{1} }}{{c^{2} - (\beta_{1}^{(3)} )^{2} }}} \right], $$

$$ s_{3} \tan \phi_{22} = \frac{k}{{\hbar_{1} }}\sqrt {\frac{{c^{2} }}{{\left( {\beta_{\,1}^{(3)} } \right)^{2} }} - 1 + \zeta_{1}^{(3)} } ,\quad \left( {\phi_{21} - \phi_{22} } \right)\sim \hbar_{1} h_{1} \frac{{\sqrt {1 - \zeta_{1}^{(3)} } }}{{\sqrt {\frac{{c^{2} }}{{\left( {\beta_{\,1}^{(3)} } \right)^{2} }} - 1 + \zeta_{1}^{(3)} } }}, $$

$$ s_{3} (\tan \phi_{21} - \tan \phi_{22} ) - s_{3} (\phi_{21} - \phi_{22} )\sim kh_{1} \sqrt {\frac{{c^{2} }}{{(\beta_{1}^{(3)} )^{2} }} - 1 + \zeta_{1}^{(3)} } , $$

$$ \sin \phi_{21} \sim \frac{{\beta_{1}^{(3)} }}{c}\sqrt {\frac{{c^{2} }}{{(\beta_{1}^{(3)} )^{2} }} - 1 + \zeta_{1}^{(3)} } \sim \sin \phi_{22} ,\quad s_{4} \sec \phi_{23} = \frac{kc}{{\hbar_{2} \beta_{2}^{(3)} }}e^{{\hbar_{2} h_{2} }} ,\quad s_{4} \sec \phi_{24} = \frac{kc}{{\hbar_{2} \beta_{2}^{(3)} }}, $$

$$ s_{4} \tan \phi_{23} = \frac{k}{{\hbar_{2} }}\sqrt {\frac{{c^{2} }}{{(\beta_{2}^{(3)} )^{2} }} - 1 + \zeta_{2}^{(3)} } ,\quad s_{4} \tan \phi_{24} = \frac{k}{{\hbar_{2} }}\sqrt {\frac{{c^{2} }}{{(\beta_{2}^{(3)} )^{2} }} - 1 + \zeta_{2}^{(3)} } \left[ {1 + \frac{{c^{2} \hbar_{2} h_{2} }}{{c^{2} - (\beta_{2}^{(3)} )^{2} }}} \right], $$

$$ \left( {\phi_{23} - \phi_{24} } \right)\sim \hbar_{2} h_{2} \frac{{\sqrt {1 - \zeta_{2}^{\left( 3 \right)} } }}{{\sqrt {\frac{{c^{2} }}{{\left( {\beta_{2}^{\left( 3 \right)} } \right)^{2} }} - 1 + \zeta_{2}^{\left( 3 \right)} } }},s_{4} \left( {tan\phi_{23} - tan\phi_{24} } \right) - s_{4} \left( {\phi_{23} - \phi_{24} } \right)\sim \hbar_{2} h_{2} \sqrt {\frac{{c^{2} }}{{\left( {\beta_{2}^{\left( 3 \right)} } \right)^{2} }} - 1 + \zeta_{2}^{\left( 3 \right)} } \,, $$

$$ {\text{and}}\;\sin \phi_{23} \sim \frac{{\beta_{2}^{(3)} }}{c}\sqrt {\frac{{c^{2} }}{{(\beta_{2}^{(3)} )^{2} }} - 1 + \zeta_{2}^{(3)} } \sim \sin \phi_{24} . $$

Appendix IV

$$ \begin{aligned} R_{23} & = I_{0}^{'} \left\{ {{{t_{1} (1 - \varepsilon_{1} h_{1} )} \mathord{\left/ {\vphantom {{t_{1} (1 - \varepsilon_{1} h_{1} )} {i\varepsilon_{1} }}} \right. \kern-0pt} {i\varepsilon_{1} }}} \right\}K_{0}^{'} ({{t_{1} } \mathord{\left/ {\vphantom {{t_{1} } {i\varepsilon_{1} }}} \right. \kern-0pt} {i\varepsilon_{1} }}) - K_{0}^{'} \left\{ {{{t_{1} (1 - \varepsilon_{1} h_{1} )} \mathord{\left/ {\vphantom {{t_{1} (1 - \varepsilon_{1} h_{1} )} {i\varepsilon_{1} }}} \right. \kern-0pt} {i\varepsilon_{1} }}} \right\}I_{0}^{'} ({{t_{1} } \mathord{\left/ {\vphantom {{t_{1} } {i\varepsilon_{1} }}} \right. \kern-0pt} {i\varepsilon_{1} }}), \\ R_{24} & = I_{0}^{'} \left\{ {{{t_{1} (1 - \varepsilon_{1} h_{1} )} \mathord{\left/ {\vphantom {{t_{1} (1 - \varepsilon_{1} h_{1} )} {i\varepsilon_{1} }}} \right. \kern-0pt} {i\varepsilon_{1} }}} \right\}K_{0}^{{}} ({{t_{1} } \mathord{\left/ {\vphantom {{t_{1} } {i\varepsilon_{1} }}} \right. \kern-0pt} {i\varepsilon_{1} }}) - K_{0}^{'} \left\{ {{{t_{1} (1 - \varepsilon_{1} h_{1} )} \mathord{\left/ {\vphantom {{t_{1} (1 - \varepsilon_{1} h_{1} )} {i\varepsilon_{1} }}} \right. \kern-0pt} {i\varepsilon_{1} }}} \right\}I_{0}^{{}} ({{t_{1} } \mathord{\left/ {\vphantom {{t_{1} } {i\varepsilon_{1} }}} \right. \kern-0pt} {i\varepsilon_{1} }}), \\ R_{25} & = I_{0}^{'} \left\{ {{{t_{2} (1 + \varepsilon_{2} h_{2} )} \mathord{\left/ {\vphantom {{t_{2} (1 + \varepsilon_{2} h_{2} )} {i\varepsilon_{2} }}} \right. \kern-0pt} {i\varepsilon_{2} }}} \right\}K_{0}^{'} ({{t_{2} } \mathord{\left/ {\vphantom {{t_{2} } {i\varepsilon_{2} }}} \right. \kern-0pt} {i\varepsilon_{2} }}) - K_{0}^{'} \left\{ {{{t_{2} (1 + \varepsilon_{2} h_{2} )} \mathord{\left/ {\vphantom {{t_{2} (1 + \varepsilon_{2} h_{2} )} {i\varepsilon_{2} }}} \right. \kern-0pt} {i\varepsilon_{2} }}} \right\}I_{0}^{'} ({{t_{2} } \mathord{\left/ {\vphantom {{t_{2} } {i\varepsilon_{2} }}} \right. \kern-0pt} {i\varepsilon_{2} }}), \\ R_{26} & = I_{0}^{{}} \left\{ {{{t_{2} (1 + \varepsilon_{2} h_{2} )} \mathord{\left/ {\vphantom {{t_{2} (1 + \varepsilon_{2} h_{2} )} {i\varepsilon_{2} }}} \right. \kern-0pt} {i\varepsilon_{2} }}} \right\}K_{0}^{'} ({{t_{2} } \mathord{\left/ {\vphantom {{t_{2} } {i\varepsilon_{2} }}} \right. \kern-0pt} {i\varepsilon_{2} }}) - K_{0}^{{}} \left\{ {{{t_{2} (1 + \varepsilon_{2} h_{2} )} \mathord{\left/ {\vphantom {{t_{2} (1 + \varepsilon_{2} h_{2} )} {i\varepsilon_{2} }}} \right. \kern-0pt} {i\varepsilon_{2} }}} \right\}I_{0}^{'} ({{t_{2} } \mathord{\left/ {\vphantom {{t_{2} } {i\varepsilon_{2} }}} \right. \kern-0pt} {i\varepsilon_{2} }}), \\ R_{27} & = I_{0}^{'} \left\{ {{{t_{2} (1 + \varepsilon_{2} h_{2} )} \mathord{\left/ {\vphantom {{t_{2} (1 + \varepsilon_{2} h_{2} )} {i\varepsilon_{2} }}} \right. \kern-0pt} {i\varepsilon_{2} }}} \right\}K_{0}^{{}} ({{t_{2} } \mathord{\left/ {\vphantom {{t_{2} } {i\varepsilon_{2} }}} \right. \kern-0pt} {i\varepsilon_{2} }}) - K_{0}^{'} \left\{ {{{t_{2} (1 + \varepsilon_{2} h_{2} )} \mathord{\left/ {\vphantom {{t_{2} (1 + \varepsilon_{2} h_{2} )} {i\varepsilon_{2} }}} \right. \kern-0pt} {i\varepsilon_{2} }}} \right\}I_{0}^{{}} ({{t_{2} } \mathord{\left/ {\vphantom {{t_{2} } {i\varepsilon_{2} }}} \right. \kern-0pt} {i\varepsilon_{2} }}), \\ R_{28} & = I_{0}^{{}} \left\{ {{{t_{2} (1 + \varepsilon_{2} h_{2} )} \mathord{\left/ {\vphantom {{t_{2} (1 + \varepsilon_{2} h_{2} )} {i\varepsilon_{2} }}} \right. \kern-0pt} {i\varepsilon_{2} }}} \right\}K_{0}^{{}} ({{t_{2} } \mathord{\left/ {\vphantom {{t_{2} } {i\varepsilon_{2} }}} \right. \kern-0pt} {i\varepsilon_{2} }}) - K_{0}^{{}} \left\{ {{{t_{2} (1 + \varepsilon_{2} h_{2} )} \mathord{\left/ {\vphantom {{t_{2} (1 + \varepsilon_{2} h_{2} )} {i\varepsilon_{2} }}} \right. \kern-0pt} {i\varepsilon_{2} }}} \right\}I_{0}^{{}} ({{t_{2} } \mathord{\left/ {\vphantom {{t_{2} } {i\varepsilon_{2} }}} \right. \kern-0pt} {i\varepsilon_{2} }}), \\ R_{29} & = J_{0}^{'} ({{t_{1} } \mathord{\left/ {\vphantom {{t_{1} } {\varepsilon_{1} }}} \right. \kern-0pt} {\varepsilon_{1} }})Y_{0}^{'} \left\{ {{{t_{1} (1 - \varepsilon_{1} h_{1} )} \mathord{\left/ {\vphantom {{t_{1} (1 - \varepsilon_{1} h_{1} )} {\varepsilon_{1} }}} \right. \kern-0pt} {\varepsilon_{1} }}} \right\} - J_{0}^{'} \left\{ {{{t_{1} (1 - \varepsilon_{1} h_{1} )} \mathord{\left/ {\vphantom {{t_{1} (1 - \varepsilon_{1} h_{1} )} {\varepsilon_{1} }}} \right. \kern-0pt} {\varepsilon_{1} }}} \right\}Y_{0}^{'} ({{t_{1} } \mathord{\left/ {\vphantom {{t_{1} } {\varepsilon_{1} }}} \right. \kern-0pt} {\varepsilon_{1} }}), \\ R_{30} & = J_{0}^{'} \left\{ {{{t_{1} (1 - \varepsilon_{1} h_{1} )} \mathord{\left/ {\vphantom {{t_{1} (1 - \varepsilon_{1} h_{1} )} {\varepsilon_{1} }}} \right. \kern-0pt} {\varepsilon_{1} }}} \right\}Y_{0}^{{}} ({{t_{1} } \mathord{\left/ {\vphantom {{t_{1} } {\varepsilon_{1} }}} \right. \kern-0pt} {\varepsilon_{1} }}) - J_{0}^{{}} ({{t_{1} } \mathord{\left/ {\vphantom {{t_{1} } {\varepsilon_{1} }}} \right. \kern-0pt} {\varepsilon_{1} }})Y_{0}^{'} \left\{ {{{t_{1} (1 - \varepsilon_{1} h_{1} )} \mathord{\left/ {\vphantom {{t_{1} (1 - \varepsilon_{1} h_{1} )} {\varepsilon_{1} }}} \right. \kern-0pt} {\varepsilon_{1} }}} \right\}, \\ R_{31} & = J_{0}^{'} ({{t_{2} } \mathord{\left/ {\vphantom {{t_{2} } {\varepsilon_{2} }}} \right. \kern-0pt} {\varepsilon_{2} }})Y_{0}^{'} \left\{ {{{t_{2} (1 + \varepsilon_{2} h_{2} )} \mathord{\left/ {\vphantom {{t_{2} (1 + \varepsilon_{2} h_{2} )} {\varepsilon_{2} }}} \right. \kern-0pt} {\varepsilon_{2} }}} \right\} - J_{0}^{'} \left\{ {{{t_{2} (1 + \varepsilon_{2} h_{2} )} \mathord{\left/ {\vphantom {{t_{2} (1 + \varepsilon_{2} h_{2} )} {\varepsilon_{2} }}} \right. \kern-0pt} {\varepsilon_{2} }}} \right\}Y_{0}^{'} ({{t_{2} } \mathord{\left/ {\vphantom {{t_{2} } {\varepsilon_{2} }}} \right. \kern-0pt} {\varepsilon_{2} }}), \\ R_{32} & = J_{0}^{{}} \left\{ {{{t_{2} (1 + \varepsilon_{2} h_{2} )} \mathord{\left/ {\vphantom {{t_{2} (1 + \varepsilon_{2} h_{2} )} {\varepsilon_{2} }}} \right. \kern-0pt} {\varepsilon_{2} }}} \right\}Y_{0}^{'} ({{t_{2} } \mathord{\left/ {\vphantom {{t_{2} } {\varepsilon_{2} }}} \right. \kern-0pt} {\varepsilon_{2} }}) - J_{0}^{'} ({{t_{2} } \mathord{\left/ {\vphantom {{t_{2} } {\varepsilon_{2} }}} \right. \kern-0pt} {\varepsilon_{2} }})Y_{0}^{{}} \left\{ {{{t_{2} (1 + \varepsilon_{2} h_{2} )} \mathord{\left/ {\vphantom {{t_{2} (1 + \varepsilon_{2} h_{2} )} {\varepsilon_{2} }}} \right. \kern-0pt} {\varepsilon_{2} }}} \right\}, \\ R_{33} & = J_{0}^{'} \left\{ {{{t_{2} (1 + \varepsilon_{2} h_{2} )} \mathord{\left/ {\vphantom {{t_{2} (1 + \varepsilon_{2} h_{2} )} {\varepsilon_{2} }}} \right. \kern-0pt} {\varepsilon_{2} }}} \right\}Y_{0}^{{}} ({{t_{2} } \mathord{\left/ {\vphantom {{t_{2} } {\varepsilon_{2} }}} \right. \kern-0pt} {\varepsilon_{2} }}) - J_{0}^{{}} ({{t_{2} } \mathord{\left/ {\vphantom {{t_{2} } {\varepsilon_{2} }}} \right. \kern-0pt} {\varepsilon_{2} }})Y_{0}^{'} \left\{ {{{t_{2} (1 + \varepsilon_{2} h_{2} )} \mathord{\left/ {\vphantom {{t_{2} (1 + \varepsilon_{2} h_{2} )} {\varepsilon_{2} }}} \right. \kern-0pt} {\varepsilon_{2} }}} \right\}, \\ R_{34} & = J_{0}^{{}} \left\{ {{{t_{2} (1 + \varepsilon_{2} h_{2} )} \mathord{\left/ {\vphantom {{t_{2} (1 + \varepsilon_{2} h_{2} )} {\varepsilon_{2} }}} \right. \kern-0pt} {\varepsilon_{2} }}} \right\}Y_{0}^{{}} ({{t_{2} } \mathord{\left/ {\vphantom {{t_{2} } {\varepsilon_{2} }}} \right. \kern-0pt} {\varepsilon_{2} }}) - J_{0}^{{}} ({{t_{2} } \mathord{\left/ {\vphantom {{t_{2} } {\varepsilon_{2} }}} \right. \kern-0pt} {\varepsilon_{2} }})Y_{0}^{{}} \left\{ {{{t_{2} (1 + \varepsilon_{2} h_{2} )} \mathord{\left/ {\vphantom {{t_{2} (1 + \varepsilon_{2} h_{2} )} {\varepsilon_{2} }}} \right. \kern-0pt} {\varepsilon_{2} }}} \right\}, \\ \end{aligned} $$