Fracture study of wood considering the effect of T-stress term based on matrix reinforcement coefficients model

Abstract

A new comprehensive criterion has been presented to assess the fracture response in cracked wood as natural orthotropic material based on the maximum strain energy release rate criterion (SER) under mixed-mode I/II loading. A general off-axis case is assumed for desired crack-fiber angle. The most important purpose of the proposed paper is to accurately predict the fracture behavior of orthotropic materials. In this article, two influencing factors on fracture assessment are discussed comprehensively. The first one is employing the accurate model of the orthotropic material named as reinforcement isotropic solid (RIS) model, and the second factor is considering the effects of the T-stress term. The SER concept is extended in combination with the reinforcement isotropic solid (RIS) model for orthotropic materials. Using RIS, a mapping between the stress fields in the isotropic and orthotropic materials is established. In this article, the reinforcement coefficients are extracted using a new method called "corresponding stresses" for the desired crack-fiber angles. These coefficients depend on the mechanical properties of the orthotropic material and crack-fiber angle. The results obtained from the curves of reinforcement coefficients indicate that as the crack-fiber angle increases, the reinforcement coefficients decrease drastically. The SER around the crack tip is extracted considering the normal and shear stress fields and the non-singular T-stress term. Using extracted results, it can be shown that the T-stress term has a serious role in predicting the crack behavior of orthotropic materials. It is practically impossible to calculate the fracture toughness of pure modes I and II when the crack is not along the fibers. Based on the proposed extended maximum strain energy release rate (EMSER) criterion, a new concept called equivalent fracture toughness (EFT) is introduced as a fracture property of orthotropic materials. To validate and evaluate the accuracy of the EMSER criterion, the fracture limit curves (FLCs) for different angles between crack and fibers are compared with available experimental data from the literature. Compared to other criteria, a prominent correlation is obtained between the theoretical results evaluated by the EMSER criterion and available test data.

1 Introduction

Composite materials are widely employed because of their special physical and mechanical properties [1,2,3]. For this reason, it is important to accurately assess the behavior of these materials under different loads [4,5,6,7,8,9,10]. Long fiber composite materials have been widely utilized due to their high load-bearing capacity in the required directions. These materials may always contain defects in various forms such as cracks during construction or operation [11,12,13,14,15,16,17,18,19,20,21,22,23,24]. Therefore, under mixed-mode I/II, the analysis of crack formation and growth during the life of composite specimens and the use of an appropriate criterion to investigate the fracture response of cracked materials is necessary [18, 25,26,27,28,29,30,31,32,33].

An efficient fracture criterion should be easily employable in complex loading conditions and must be independent of unattainable mechanical and fracture properties such as fracture toughness of mode II and provide an accurate prediction of material fracture behavior [34,35,36,37,38,39,40]. Significant studies have been performed on the extraction of orthotropic fracture properties [41,42,43,44,45,46,47,48,49].

Investigating the fracture behavior of concrete structures is important in the analysis and design of these structures [50]. In unreinforced concrete structures, in spite of creation of micro-cracks in the material there is a possibility of brittle fracture [39]. In investigating the destruction process of these materials, extracting the fracture toughness is important. In this way, extensive research has been done to extract the mode I and II fracture toughness of these materials experimentally [51].

Van der Put presented a novel theory for orthotropic materials with orthotropic–isotropic transformation [52]. According to Van der Put’s approach, a novel aspect for fracture assessment was developed defining the reinforcement isotropic solid (RIS) model [53].

Experimental and theoretical criteria are presented to investigate the fracture response in orthotropic materials under mixed-mode I/II loading. In experimental criteria, stress intensity factors are extracted based on critical loads. Then, by fitting a curve on the test data, the FLCs can be extracted. Research has been conducted to derive experimental fracture criteria of wood specimens under mixed-mode I/II [54,55,56]. Because deriving experimental mixed-mode criteria needs significant time to provide experimental data, theoretical criteria have been replaced by experimental ones.

Based on energy and stress approaches, theoretical criteria are proposed. Criteria based on maximum tangential stress (MTS) [57,58,59,60,61], minimum strain energy density (SED) [62,63,64,65,66,67,68] and maximum strain energy release rate (SER) [69,70,71,72] were presented for isotropic and orthotropic materials.

Considering the effects of FPZ in orthotropic materials, more accurate analysis of the crack behavior of can be provided [73, 74]. The first step, the damaged isotropic solid properties extract based on the stress and energy. Under the stress field of micro-cracks, Budiansky and O'connell [75] and Nemat-Nasser and Hori [76] calculated the elastic properties of a damaged solid using an energy balance method for a cracked body.

Fakoor conducted studies to provide a criterion for investigating the crack behavior by considering the effects of FPZ [77,78,79]. He was able to derive the damage coefficient using the RIS concept.

Researches have been conducted on the role of non-singular T-stress term on the crack behavior of different isotropic and orthotropic materials in mixed-mode I/II loading. Positive or negative values of this stress on the plastic zone affect the fracture response of materials [80]. Under mixed-mode I/II loading, Fakoor et al. provided SED [65], MTS [81] and the energy dissipation in the FPZ [78] for arbitrary crack-fiber angle. They concluded that the non-singular T-stress term has a significant effect on the fracture response of orthotropic materials, especially in conditions where mode II loading is dominant. Also, they investigated the effect of positive and negative values of this stress on the FLC.

Reviewing the mentioned references prove that a comprehensive criterion is needed for fracture evaluation in cracked orthotropic materials. This criterion should be able to consider the desired angle between crack and fiber and also T-stress effects.

In this paper, a new approach entitled "corresponding stresses" is proposed to calculate the reinforcement coefficients in the RIS model for the desired crack-fiber angle. In this method, the reinforcement coefficients are extracted based on the ratio between the stress field of the isotropic material to the orthotropic material. Using the corresponding stresses method, a new criterion is presented based on the maximum energy release rate concept and RIS model as an efficient material model. The effects of the T-stress term on the crack behavior of orthotropic materials are investigated. Equivalent stress intensity factor in mode I is extracted for different crack-fiber angles. Comparing FLCs with available experimental data [60] shows that this criterion assesses the fracture response with high accuracy.

2 Reinforcement isotropic solid model

For orthotropic materials, a premier material model is introduced in accordance with the physics of fracture of these materials. Based on Fig. 1, experimental observations show that cracks always initiate and propagate in isotropic parts along the fibers.

Fig. 1

Testing the wood specimen a before and b after fracture under tension [70]

This phenomenon is due to the weaker strength properties of the matrix. According to this assumption, a relationship can be established between orthotropic and isotropic stress fields. In this scheme, orthotropic material is considered to be a combination of fibers and matrix. Fibers are embedded in the matrix part to tolerate a portion of the applied load. The stress reduction coefficients correspond to the stresses in the isotropic matrix and the whole orthotropic material. Fakoor et al. extracted Van der Put’s theory in the reinforcement isotropic solid model (RIS). They extracted RIS coefficients employing suitable representative volume elements (RVE) [82]. An accurate RVE can be defined as the smallest part of the orthotropic material that shows all the properties of the material [65]. The proposed element has all the strength, elastic properties and boundary conditions of the composite material. Therefore, the mechanical behavior of the composite material can be extracted by the behavior of the aforementioned RVE. To define reinforcement coefficients, Fig. 2 shows RVEs under three independent loading patterns.

Fig. 2

RVE for deriving RIS coefficients under a tension along the fiber, b shear load, c tension perpendicular to the fiber

The ratio of the stress field of isotropic material to orthotropic material in different directions of loading is considered as follows:

$$\alpha_{1} = \frac{{\sigma_{xx}^{Iso} }}{{\sigma_{xx}^{Orth} }}$$

(1)

$$\alpha_{2} = \frac{{\sigma_{yy}^{Iso} }}{{\sigma_{yy}^{Orth} }}$$

(2)

$$\alpha_{3} = \frac{{\sigma_{xy}^{Iso} }}{{\sigma_{xy}^{Orth} }}$$

(3)

In Fig. 1c, the bearing stress by the matrix is the same as the fiber. Thus, the reinforcement coefficient is equal to “one.” To satisfy the structural and compatibility equations for isotropic matrix, $\alpha_{1}$ and $\alpha_{3}$ coefficients are defined as follows [65]:

$$\alpha_{1} = \frac{{C_{22} }}{{C_{11} }} = \frac{{E_{1} }}{{E_{2} }}$$

(4)

$$\alpha_{3} = \left( {2 - \frac{{C_{12} }}{{C_{22} }} - \frac{{C_{12} }}{{C_{11} }}} \right)\frac{{C_{22} }}{{C_{66} }} = \left( {2 + \nu_{12} + v_{21} } \right)\frac{{G_{12} }}{{E_{2} }}$$

(5)

in which $\alpha_{1}$ and $\alpha_{3}$ are stress reduction coefficients (SRC) that the mechanical properties affect these coefficients. $C_{ij}$ are compliance coefficient in elastic materials that are extracted by structural relations. These coefficients are defined as follows:

$$\varepsilon_{ij} = C_{ij} \sigma_{ij}$$

(6)

$$\left[ {\begin{array}{*{20}c} {\varepsilon_{11} } \\ {\varepsilon_{22} } \\ {\varepsilon_{33} } \\ {\begin{array}{*{20}c} {\gamma_{23} } \\ {\gamma_{31} } \\ {\gamma_{12} } \\ \end{array} } \\ \end{array} } \right] = \left( {\begin{array}{*{20}c} {\frac{1}{{E_{1} }}} & {\frac{{ - v_{21} }}{{E_{2} }}} & {\frac{{ - v_{31} }}{{E_{3} }}} & 0 & 0 & 0 \\ {\frac{{ - v_{12} }}{{E_{1} }}} & {\frac{1}{{E_{2} }}} & {\frac{{ - v_{32} }}{{E_{3} }}} & 0 & 0 & 0 \\ {\frac{{ - v_{13} }}{{E_{1} }}} & {\frac{{ - v_{23} }}{{E_{2} }}} & {\frac{1}{{E_{3} }}} & 0 & 0 & 0 \\ 0 & 0 & 0 & {\frac{1}{{G_{23} }}} & 0 & 0 \\ 0 & 0 & 0 & 0 & {\frac{1}{{G_{31} }}} & 0 \\ 0 & 0 & 0 & 0 & 0 & {\frac{1}{{G_{12} }}} \\ \end{array} } \right)\left[ {\begin{array}{*{20}c} {\sigma_{11} } \\ {\sigma_{22} } \\ {\sigma_{33} } \\ {\begin{array}{*{20}c} {\sigma_{23} } \\ {\sigma_{31} } \\ {\sigma_{12} } \\ \end{array} } \\ \end{array} } \right]$$

(7)

3 RIS coefficients for the desired crack-fiber angle

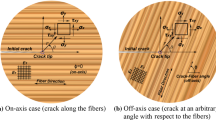
In this section, a new method for modeling the RIS coefficients for orthotropic materials in desired crack-fiber angle based on Fig. 3 is studied.

Fig. 3

Stress field around crack tip for off-axis case [83]

The effect of fiber strength is quantified by defining the RIS coefficients in the tensile and shear modes. The strength coefficients obtained from the studied method depend on the elastic properties of the material and crack-fiber angles.

Equations (4) and (5) are extracted for the crack along the fibers (on-axis state). For arbitrary crack-fiber angle (off-axis state), Eqs (4) and (5) must be generalized. At the arbitrary crack-fiber angle, since the material properties vary in different directions, the reinforcement coefficients must be a function of crack-fiber angle. In this study, fibers have a reinforcement role for the isotropic matrix and the reinforcement of fibers is quantified by these coefficients. A new method called "corresponding stresses" examines the reinforcement coefficients. The corresponding stresses method is extracted based on the reinforcement role of fibers. In this method, the singular stress field of isotropic and orthotropic materials around the crack tip is completely extracted and the reinforcement coefficients are obtained by using the ratio between these stresses. The stress field around the crack tip in orthotropic material is as follows:

$$\sigma_{xx}^{orth} = \left( {\frac{{K_{I}^{orth} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{11} (\theta )}}{{\sqrt {2\pi r_{c}^{orth} } }} + + \frac{{K_{II}^{orth} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g}_{11} (\theta )}}{{\sqrt {2\pi r_{c}^{orth} } }}} \right)$$

(8)

$$\sigma_{xy}^{orth} = \left( {\frac{{K_{I}^{orth} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{12} (\theta )}}{{\sqrt {2\pi r_{c}^{orth} } }} + \frac{{K_{II}^{orth} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g}_{12} (\theta )}}{{\sqrt {2\pi r_{c}^{orth} } }}} \right)$$

(9)

$$\sigma_{yy}^{orth} = \left( {\frac{{K_{I}^{orth} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{22} (\theta )}}{{\sqrt {2\pi r_{c}^{orth} } }} + \frac{{K_{II}^{orth} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g}_{22} (\theta )}}{{\sqrt {2\pi r_{c}^{orth} } }}} \right)$$

(10)

The stress field of isotropic materials around the crack tip is as follows:

$$\sigma_{xx}^{Iso} = \left( {\frac{{K_{I}^{Iso} f_{11} (\theta )}}{{\sqrt {2\pi r_{c}^{Iso} } }} + \frac{{K_{II}^{Iso} g_{11} (\theta )}}{{\sqrt {2\pi r_{c}^{Iso} } }}} \right)$$

(11)

$$\sigma_{xy}^{Iso} = \left( {\frac{{K_{I}^{Iso} f_{12} (\theta )}}{{\sqrt {2\pi r_{c}^{Iso} } }} + \frac{{K_{II}^{Iso} g_{12} (\theta )}}{{\sqrt {2\pi r_{c}^{Iso} } }}} \right)$$

(12)

$$\sigma_{yy}^{Iso} = \left( {\frac{{K_{I}^{Iso} f_{22} (\theta )}}{{\sqrt {2\pi r_{c}^{Iso} } }} + \frac{{K_{II}^{Iso} g_{22} (\theta )}}{{\sqrt {2\pi r_{c}^{Iso} } }}} \right)$$

(13)

The values of $f_{ij}$,$g_{ij}$,$\hat{f}_{ij}$ and $\hat{g}_{ij}$ are stated in Appendix A. Thus, the reinforcement coefficients are as follows:

$$\alpha_{1} = \sqrt {\frac{{r_{c}^{orth} }}{{r_{c}^{Iso} }}} .\frac{{(K_{I}^{Iso} f_{11} (\theta ) + K_{II}^{Iso} g_{11} (\theta ))}}{{(K_{I}^{orth} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{11} (\theta ) + K_{II}^{orth} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g}_{11} (\theta ))}}$$

(14)

$$\alpha_{2} = \sqrt {\frac{{r_{c}^{orth} }}{{r_{c}^{Iso} }}} .\frac{{(K_{I}^{Iso} f_{22} (\theta ) + K_{II}^{Iso} g_{22} (\theta ))}}{{(K_{I}^{orth} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{22} (\theta ) + K_{II}^{orth} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g}_{22} (\theta ))}}$$

(15)

$$\alpha_{3} = \sqrt {\frac{{r_{c}^{orth} }}{{r_{c}^{Iso} }}} .\frac{{(K_{I}^{Iso} f_{12} (\theta ) + K_{II}^{Iso} g_{12} (\theta ))}}{{(K_{I}^{orth} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{12} (\theta ) + K_{II}^{orth} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g}_{12} (\theta ))}}$$

(16)

Therefore, fiber reinforcement coefficients depend on the modes I and II SIFs in the isotropic matrix and orthotropic material and crack-fiber angle. The reinforcement coefficients at a certain crack-fiber angle depend only on the mechanical properties of the orthotropic material, so these coefficients must be constant under any mixed-mode I/II loading. Therefore, pure mode I and II loading conditions can be applied to these coefficients. So, $\alpha_{1}$ and $\alpha_{2}$ coefficients are extracted in pure mode I and $\alpha_{3}$ coefficient is extracted in pure mode II condition.

$$\alpha_{1} = \sqrt {\frac{{r_{c}^{orth} }}{{r_{c}^{Iso} }}} .\frac{{K_{Ic}^{Iso} f_{11} (\theta )}}{{K_{Ic}^{orth} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{11} (\theta )}}$$

(17)

$$\alpha_{2} = \sqrt {\frac{{r_{c}^{orth} }}{{r_{c}^{Iso} }}} .\frac{{K_{Ic}^{Iso} f_{22} (\theta )}}{{K_{Ic}^{orth} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{22} (\theta )}}$$

(18)

$$\alpha_{3} = \sqrt {\frac{{r_{c}^{orth} }}{{r_{c}^{Iso} }}} .\frac{{K_{IIc}^{Iso} g_{12} (\theta )}}{{K_{IIc}^{orth} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g}_{12} (\theta )}}$$

(19)

The critical distance ($r_{c}$) in the strain energy density criterion for isotropic and orthotropic materials is expressed as follows [84]:

$$r_{c}^{Iso} = \frac{{(1 + \nu_{m} )(5 - 8\nu_{m} )}}{4\pi }{.}\left( {\frac{{K_{Ic}^{Iso} }}{{\sigma_{Ic}^{Iso} }}} \right)$$

(20)

$$r_{c}^{Iso} = \frac{{(1 + \nu_{m} )(5 - 8\nu_{m} )}}{4\pi }{.}\left( {\frac{{K_{Ic}^{Iso} }}{{\sigma_{Ic}^{Iso} }}} \right)$$

(21)

The $\nu_{m}$ is related to Poisson's ratio of the matrix section. (The matrix section is made of isotropic material.) Due to the fact that crack grows in an isotropic section of orthotropic material, the critical distance is considered equal to the critical distance in orthotropic materials. Using Eqs (20) and (21), $\frac{{K_{Ic}^{orth} }}{{K_{Ic}^{Iso} }}$ ratio is extracted as follows:

$$\frac{{K_{Ic}^{orth} }}{{K_{Ic}^{Iso} }} = \frac{{\sigma_{c}^{orth} }}{{\sigma_{c}^{Iso} }}$$

(22)

$\sigma_{c}^{Iso}$ is the mechanical properties. Hankinson-type formula is used for the extraction of $\sigma_{c}^{orth}$. Using Hankinson equations, the strength of the composite material changes in different directions. Therefore, the maximum tensile strength in the direction of $\theta$ is defined as follows:

$$\sigma_{c}^{orth} = \frac{PQ}{{P\sin^{n} \theta + Q\cos^{n} \theta }}$$

(23)

${\text{P}}$ and ${\text{Q}}$ are defined the strengths along and across the fibers. $n$ is the experimental factor. Thus, $\frac{{K_{Ic}^{orth} }}{{K_{Ic}^{Iso} }}$ can be extracted as follows:

$$\frac{{K_{{{\text{Ic}}}}^{{{\text{orth}}}} }}{{K_{{{\text{Ic}}}}^{{{\text{Iso}}}} }} = \frac{PQ}{{\sigma_{c}^{Iso} .(P\sin^{n} \theta + Q\cos^{n} \theta )}}$$

(24)

Using Ref [85], the following relationship is established between the modes I and II SIFs of orthotropic and isotropic materials:

$$\frac{{K_{{{\text{IIc}}}}^{{{\text{orth}}}} }}{{K_{{{\text{IIc}}}}^{{{\text{Iso}}}} }} = \frac{{(2 + \nu_{12} + \nu_{21} ).G_{12} }}{{E_{1} }}.\frac{{K_{{{\text{Ic}}}}^{{{\text{orth}}}} }}{{K_{{{\text{Ic}}}}^{{{\text{Iso}}}} }}$$

(25)

Finally, $\frac{{K_{IIc}^{orth} }}{{K_{IIc}^{Iso} }}$ is as follows:

$$\frac{{K_{IIc}^{orth} }}{{K_{IIc}^{Iso} }} = \frac{{(2 + \nu_{12} + \nu_{21} ).G_{12} }}{{E_{1} }}.\frac{PQ}{{\sigma_{c}^{Iso} .(P\sin^{n} \theta + Q\cos^{n} \theta )}}$$

(26)

Thus, the reinforcement coefficients for desired crack-fiber angle are as follows:

$$\alpha_{1} = \frac{{f_{11} (\phi )}}{{\hat{f}_{11} (\phi )}}.\frac{{\sigma_{c}^{Iso} .(P\sin^{n} \phi + Q\cos^{n} \phi )}}{PQ}$$

(27)

$$\alpha_{2} = \frac{{f_{22} (\phi )}}{{\hat{f}_{22} (\phi )}}.\frac{{\sigma_{c}^{Iso} .(P\sin^{n} \phi + Q\cos^{n} \phi )}}{PQ}$$

(28)

$$\alpha_{3} = \frac{{g_{12} (\phi )}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g}_{12} (\phi )}}.\frac{{E_{1} }}{{(2 + \nu_{12} + \nu_{21} ).G_{12} }}.\frac{{\sigma_{c}^{Iso} .(P\sin^{n} \phi + Q\cos^{n} \phi )}}{PQ}$$

(29)

4 Derivation of extended maximum strain energy release rate (EMSER) criterion in orthotropic materials

The critical strain energy release rate $G_{C}^{orth}$ for a cracked orthotropic material in terms of crack tip parameter is expressed as follows:

$$G_{C}^{orth} (\theta ) = \frac{{(K_{I}^{orth} (\theta ))^{2} }}{{E_{I} }} + \frac{{(K_{II}^{orth} (\theta ))^{2} }}{{E_{II} }}$$

(30)

in which $K_{I}^{orth} (\theta )$ and $K_{II}^{orth} (\theta )$ are stress intensity factors. $E_{I}$ and $E_{II}$ are generalization elastic modulus and defined as follows [68]:

$$E_{I} = \left[ {\frac{{C_{11} C_{22} }}{2}\left( {\sqrt {\frac{{C_{22} }}{{C_{11} }}} + \frac{{2C_{12} + C_{66} }}{{2C_{11} }}} \right)} \right]^{{ - \frac{1}{2}}}$$

(31)

$$E_{II} = \left[ {\frac{{(C_{11} )^{2} }}{2}\left( {\sqrt {\frac{{C_{22} }}{{C_{11} }}} + \frac{{2C_{12} + C_{66} }}{{2C_{11} }}} \right)} \right]^{{ - \frac{1}{2}}}$$

(32)

$G_{C}^{orth}$ can be expressed as follows [77, 85]:

$$G_{C}^{orth} (\theta ) = 2\pi r(\frac{{\sigma_{\theta \theta }^{2} }}{{E_{I} }} + \frac{{\sigma_{r\theta }^{2} }}{{E_{II} }})^{orth}$$

(33)

In Eq. (33), the SER criterion is defined in terms of normal and shear stress fields of orthotropic material. Figure 4 illustrates the cracked orthotropic material under mixed-mode I/II loading. $\varphi$ is the angle between the crack and fibers.

Fig. 4

Cracked orthotropic material under mixed-mode I/II loading

Using the RIS model, a relationship can be established between the stress field of orthotropic material and the isotropic one. Using Eqs. (1)–(3), the strain energy release rate in terms of isotropic stress field is expressed as follows:

$$G_{C}^{orth} (\theta ) = 2\pi r\left( {\frac{{\sigma_{\theta \theta }^{2} }}{{\alpha_{1}^{2} (\varphi )E_{I} }} + \frac{{\sigma_{r\theta }^{2} }}{{\alpha_{3}^{2} (\varphi )E_{II} }}} \right)^{iso}$$

(34)

The normal and shear stress fields of isotropic material are expressed as follows by considering T-stress term for isotropic materials:

$$\sigma_{\theta \theta }^{iso} (\theta ) = \frac{1}{{\sqrt {2\pi r} }}[K_{I} A_{1} (\theta ) + K_{II} A_{2} (\theta )] + T\sin^{2} \theta$$

(35)

$$\sigma_{r\theta }^{iso} (\theta ) = \frac{1}{{\sqrt {2\pi r} }}[K_{I} A_{3} (\theta ) + K_{II} A_{4} (\theta )] - T\sin \theta \cos \theta$$

(36)

Normal and shear stress field coefficients are expressed as follows:

$$A_{1} (\theta ) = \cos \frac{\theta }{2}(1 + \cos \theta )$$

(37)

$$A_{2} (\theta ) = - 3\sin \theta \cos \frac{\theta }{2}$$

(38)

$$A_{3} (\theta ) = \sin \theta \cos \frac{\theta }{2}$$

(39)

$$A_{4} (\theta ) = (3\cos \theta - 1)\cos \frac{\theta }{2}$$

(40)

It is important to investigate the distribution of the T-stress term around the crack tip. This stress has a significant influence on the fracture response of isotropic and orthotropic materials [27]. Under mixed-mode I/II, the crack Kinks from its original orientation. With crack deviation, this stress plays an important role in the stress distribution. T-stress term creates tension or compressive stress field along crack near the crack tip. The amount and sign of the T-stress term are influenced by the geometry of the body, the mechanical characterization of the orthotropic material and the loading conditions.

For isotropic materials under pure mode I in Fig. 5, the crack will grow along the original orientation and T-stress term does not affect crack growth. Passing pure mode I and the emergence of mode II, crack kink happens and this stress along kinked crack has a component [86].

Fig. 5

Effect of T-stress term on the fracture of isotropic test specimen in a pure mode I, b mixed-mode I/II loading [83]

Due to self-similar crack propagation in orthotropic materials, for crack along fibers, this stress has no components along the crack under mixed-mode I/II. Thus, this stress does not affect the crack growth process. According to Fig. 6, for desired crack-fiber angle, crack in macroscale kinks along the fibers. Thus, this stress along crack has a component and affects the crack growth process.

Fig. 6

Cracked orthotropic material with considering the effect of T-stress term [72]

For crack perpendicular to the fibers, the T-stress term has a profound effect on the fracture behavior of orthotropic materials. The dimensionless parameter B is defined to normalize the T-stress term. Thus, the T-stress term is expressed as follows [78, 87]:

$$T = \frac{B}{{\sqrt {2\pi a} }}$$

(41)

$$\frac{{E_{I} }}{{E_{II} }} = \sqrt {\frac{{C_{11} }}{{C_{22} }}}$$

(42)

The ratio between $E_{I}$ and $E_{II}$ using Eqs. (31) and (32) is as follows:

Thus, the SER criterion is extracted as follows:

$$\begin{gathered} G_{C}^{orth} (\theta ) = \frac{1}{{E_{I} }}(\frac{1}{{\alpha_{1}^{2} (\varphi )}}.[K_{I}^{2} A_{1}^{2} (\theta ) + K_{II}^{2} A_{2}^{2} (\theta ) + 2K_{I} K_{II} A_{1} (\theta )A_{2} (\theta ) + B^{2} \sin^{4} \theta + 2B\sin^{2} \theta K_{I} A_{1} (\theta ) + 2B\sin^{2} \theta K_{II} A_{2} (\theta )] + \hfill \\ \sqrt {\frac{{C_{11} }}{{C_{22} }}} .\frac{1}{{\alpha_{3}^{2} (\varphi )}}.[K_{I}^{2} A_{3}^{2} (\theta ) + K_{II}^{2} A_{4}^{2} (\theta ) + 2K_{I} K_{II} A_{3} (\theta )A_{4} (\theta ) + B^{2} \sin^{2} \theta \cos^{2} \theta - 2BK_{I} A_{3} (\theta )\sin \theta \cos \theta - 2BK_{II} A_{4} (\theta )\sin \theta \cos \theta ]) \hfill \\ \end{gathered}$$

(43)

So, the strain energy release rate is finally as follows:

$$G_{C}^{orth} (\theta ) = \frac{1}{{E_{I} }}(K_{I}^{2} D_{1} (\theta ) + K_{II}^{2} D_{2} (\theta ) + K_{I} K_{II} D_{3} (\theta ) + D_{4} (\theta )K_{I} + D_{5} (\theta )K_{II} + D_{6} (\theta ))$$

(44)

$$D_{1} (\theta ) = \left( {\frac{{A_{1}^{2} (\theta )}}{{\alpha_{1}^{2} (\varphi )}} + \sqrt {\frac{{C_{11} }}{{C_{22} }}} \frac{{A_{3}^{2} (\theta )}}{{\alpha_{3}^{2} (\varphi )}}} \right)$$

(45)

$$D_{2} (\theta ) = \left( {\frac{{A_{2}^{2} (\theta )}}{{\alpha_{1}^{2} (\varphi )}} + \sqrt {\frac{{C_{11} }}{{C_{22} }}} \frac{{A_{4}^{2} (\theta )}}{{\alpha_{3}^{2} (\varphi )}}} \right)$$

(46)

$$D_{3} (\theta ) = \left( {2\frac{{A_{1} (\theta )A_{2} (\theta )}}{{\alpha_{1}^{2} (\varphi )}} + 2\sqrt {\frac{{C_{11} }}{{C_{22} }}} \frac{{A_{3} (\theta )A_{4} (\theta )}}{{\alpha_{3}^{2} (\varphi )}}} \right)$$

(47)

$$D_{4} (\theta ) = \left( {2\frac{{A_{1} (\theta )B\sin^{2} \theta }}{{\alpha_{1}^{2} (\varphi )}} - 2\sqrt {\frac{{C_{11} }}{{C_{22} }}} \frac{{A_{3} (\theta )B\sin \theta \cos \theta }}{{\alpha_{3}^{2} (\varphi )}}} \right)$$

(48)

$$D_{5} (\theta ) = \left( {2\frac{{A_{2} (\theta )B\sin^{2} \theta }}{{\alpha_{1}^{2} (\varphi )}} - 2\sqrt {\frac{{C_{11} }}{{C_{22} }}} \frac{{A_{4} (\theta )B\sin \theta \cos \theta }}{{\alpha_{3}^{2} (\varphi )}}} \right)$$

(49)

$$D_{6} (\theta ) = \left( {\frac{{B^{2} \sin^{4} \theta }}{{\alpha_{1}^{2} (\varphi )}} + \sqrt {\frac{{C_{11} }}{{C_{22} }}} \frac{{B^{2} \sin^{2} \theta \cos^{2} \theta }}{{\alpha_{3}^{2} (\varphi )}}} \right)$$

(50)

Thus, the extended maximum strain energy release rate (EMSER) criterion is extracted to investigate the fracture behavior of orthotropic materials under mixed-mode I/II loading.

Based on the SER criterion, the moment and direction of crack growth can be predicted as follows:

(1) According to the SER criterion, the crack when $G(\theta )$ reaches $G_{c}$ will grow. In pure mode I, regardless of the T-stress term, $G(\theta )$ considering $K_{I} = K_{IC}$ and $K_{II} = 0$ is extracted as follows:

$$G_{c} = \frac{4}{{\alpha_{1}^{2} (0)E_{I} }}K_{IC}^{2}$$

(51)

Thus, to extract the moment of crack growth, Eq. (51) is equated with Eq. (44):

$$\begin{gathered} K_{IC}^{2} = \frac{{\alpha_{1}^{2} (0)}}{4}(\frac{1}{{\alpha_{1}^{2} (\varphi )}}.[K_{I}^{2} A_{1}^{2} (\theta ) + K_{II}^{2} A_{2}^{2} (\theta ) + 2K_{I} K_{II} A_{1} (\theta )A_{2} (\theta ) + B^{2} \sin^{4} \theta + 2B\sin^{2} \theta K_{I} A_{1} (\theta ) + 2B\sin^{2} \theta K_{II} A_{2} (\theta )] + \hfill \\ \sqrt {\frac{{C_{11} }}{{C_{22} }}} .\frac{1}{{\alpha_{3}^{2} (\varphi )}}.[K_{I}^{2} A_{3}^{2} (\theta ) + K_{II}^{2} A_{4}^{2} (\theta ) + 2K_{I} K_{II} A_{3} (\theta )A_{4} (\theta ) + B^{2} \sin^{2} \theta \cos^{2} \theta - 2BK_{I} A_{3} (\theta )\sin \theta \cos \theta - 2BK_{II} A_{4} (\theta )\sin \theta \cos \theta ]) \hfill \\ \end{gathered}$$

(52)

(2) Based on the SER criterion, the crack will grow in the orientation that $G(\theta )$ reaches to the maximum value (or in mathematical expression: $\frac{\partial G(\theta )}{{\partial \theta }} = 0$ and $\frac{{\partial^{2} G(\theta )}}{{\partial \theta^{2} }} < 0$). Using Eq. (44), $\frac{\partial G(\theta )}{{\partial \theta }}$ is defined as follows:

$$\frac{\partial G(\theta )}{{\partial \theta }} = \frac{1}{{E_{I} }}(K_{I}^{2} C_{1} (\theta ) + K_{II}^{2} C_{2} (\theta ) + K_{I} K_{II} C_{3} (\theta ) + C_{4} (\theta )K_{I} + C_{5} (\theta )K_{II} + C_{6} (\theta )) = 0$$

(53)

$$C_{1} (\theta ) = \frac{{\partial D_{1} (\theta )}}{\partial \theta } = \frac{1}{{\alpha_{1}^{2} (\varphi )}}\frac{{\partial A_{1}^{2} (\theta )}}{\partial \theta } + \sqrt {\frac{{C_{11} }}{{C_{22} }}} \frac{1}{{\alpha_{3}^{2} (\varphi )}}\frac{{\partial A_{3}^{2} (\theta )}}{\partial \theta }$$

(54)

$$C_{2} (\theta ) = \frac{{\partial D_{1} (\theta )}}{\partial \theta } = \frac{1}{{\alpha_{1}^{2} (\varphi )}}\frac{{\partial A_{2}^{2} (\theta )}}{\partial \theta } + \sqrt {\frac{{C_{11} }}{{C_{22} }}} \frac{1}{{\alpha_{3}^{2} (\varphi )}}\frac{{\partial A_{4}^{2} (\theta )}}{\partial \theta }$$

(55)

$$C_{3} (\theta ) = \frac{{\partial D_{3} (\theta )}}{\partial \theta } = \frac{2}{{\alpha_{1}^{2} (\varphi )}}\frac{{\partial (A_{1} (\theta )A_{2} (\theta ))}}{\partial \theta } + 2\sqrt {\frac{{C_{11} }}{{C_{22} }}} \frac{1}{{\alpha_{3}^{2} (\varphi )}}(\frac{{\partial (A_{3} (\theta )A_{4} (\theta ))}}{\partial \theta })$$

(56)

$C_{i}$ coefficients are defined as follows:

$$C_{4} (\theta ) = \frac{{\partial D_{4} (\theta )}}{\partial \theta } = \frac{2B}{{\alpha_{1}^{2} (\varphi )}}\frac{{\partial (A_{1} (\theta )\sin^{2} \theta )}}{\partial \theta } - 2\sqrt {\frac{{C_{11} }}{{C_{22} }}} \frac{B}{{\alpha_{3}^{2} (\varphi )}}\frac{{\partial (A_{3} (\theta )\sin \theta \cos \theta )}}{\partial \theta }$$

(57)

$$C_{5} (\theta ) = \frac{{\partial D_{5} (\theta )}}{\partial \theta } = \frac{2B}{{\alpha_{1}^{2} (\varphi )}}\frac{{\partial (A_{2} (\theta )\sin^{2} \theta )}}{\partial \theta } - 2\sqrt {\frac{{C_{11} }}{{C_{22} }}} \frac{B}{{\alpha_{3}^{2} (\varphi )}}\left( {\frac{{\partial (A_{4} (\theta )\sin \theta \cos \theta )}}{\partial \theta }} \right)$$

(58)

$$C_{6} (\theta ) = \frac{{\partial D_{6} (\theta )}}{\partial \theta } = \frac{{B^{2} }}{{\alpha_{1}^{2} (\varphi )}}\frac{{\partial (\sin^{4} \theta )}}{\partial \theta } + \sqrt {\frac{{C_{11} }}{{C_{22} }}} \frac{{B^{2} }}{{\alpha_{3}^{2} (\varphi )}}\left( {\frac{{\partial (\sin^{2} \theta \cos^{2} \theta )}}{\partial \theta }} \right)$$

(59)

These equations are a function of $\theta$. Based on Fig. 7, when a load is applied to a cracked material, the crack kinks along the fibers and grows.

Fig. 7

Kink in wood specimen for arbitrary crack-fiber angle [83]

For desired crack-fiber angle, the crack propagates along the fibers in the macro-mechanical scale; thus, $\theta_{C} = \varphi$. Equation (44) is reformulated as the following equation:

$$K_{Ic}^{2} = \frac{{\alpha_{1}^{2} (0)}}{4}[K_{I}^{2} D_{1} (\varphi ) + K_{II}^{2} D_{2} (\varphi ) + K_{I} K_{II} D_{3} (\varphi ) + D_{4} (\varphi )K_{I} + D_{5} (\varphi )K_{II} + D_{6} (\varphi )]$$

(60)

Solving Eqs. (53) and (60) simultaneously, the EMSER criterion for orthotropic materials is derived and FLC based on the presented criterion is extracted.

5 Equivalent fracture toughness in mode I for orthotropic materials

Due to desired crack-fiber angle, it is impossible to establish conditions for estimating $K_{Ic}$. Thus, the new concept is expressed for arbitrary crack-fiber angle as equivalent fracture toughness in mode I $(K_{Ic} )_{eq}$. Figure 8 shows the definition of $(K_{Ic} )_{eq}$ under pure mode I in orthotropic material.

Fig.8

Concept of mode I equivalent fracture toughness

To derive equivalent fracture toughness in mode I (EFT) for an off-axis orthotropic material, pure mode I conditions (i.e., $K_{I} = K_{IC}$ and $K_{II} = 0$) are established in Eq. (52).

$$K_{Ic}^{2} = \frac{{\alpha_{1}^{2} (0)}}{4}[(K_{Ic} )^{2}_{eq} D_{1} (\varphi ) + D_{4} (\varphi )(K_{Ic} )_{eq} + D_{6} (\varphi )]$$

(61)

$(K_{Ic} )_{eq}$ is a function of crack-fiber angle ($\varphi$). The mechanical properties of the material and non-singular T-stress term affect $(K_{Ic} )_{eq}$. In this way, $(K_{Ic} )_{eq}$ is extracted as follows:

$$(K_{Ic} )_{eq} = \frac{{ - D_{4} (\varphi ) + \sqrt {D_{4}^{2} (\varphi ) - 4.D_{1} (\varphi ).(D_{6} (\varphi ) - \frac{{4K_{Ic}^{2} }}{{\alpha_{1}^{2} (0)}})} }}{{2D_{1} (\varphi )}}$$

(62)

EFT is a new parameter that expresses the strength of orthotropic material to off-axis fracture. The curve of EFT in terms of crack-fiber angle in the absence of T-stress term is shown in Fig. 9.

Fig. 9

Curve of mode I EFT in terms of crack-fiber angle

Fig. 10

Curves of reinforcement coefficients in terms of crack-fiber angle for red spruce

Fig. 11

Curves of reinforcement coefficients in terms of crack-fiber angle for Scots pine

Fig. 12

Curves of reinforcement coefficients in terms of crack-fiber angle for Norway spruce

Maximum $(K_{I} )_{eq}$ occurs in $60 < \varphi < 80$ interval. In this domain, the composite material has maximum load-bearing capacity.

6 Result and discussion

6.1 The reinforcement coefficients for desired crack-fiber angle

In this section, the results of “corresponding stresses method” for deriving the reinforcement coefficients in the RIS model are investigated. Reinforcement coefficients have been extracted for three specimens of red spruce, Scots pine and Norway spruce for the arbitrary crack-fiber angle. All specimens are assumed highly orthotropic materials. Figures 10, 11 and 12 show the curves of the reinforcement coefficients for these specimens. The reinforcement coefficients depend on the mechanical properties of material and crack-fiber angle.

According to Figs 10, 11 and 12, these curves are very close to the extracted curves in Ref [88]. Reinforcement coefficients have the highest value at $\varphi = 0$. With increasing crack-fiber angle, $\alpha_{i}$ coefficients decrease. In addition, these coefficients converge to zero at $\varphi = 75$.

The curves of $\alpha_{3}$ coefficients in these materials indicate that fibers tolerate high shear stress relative to the matrix at $\varphi = 0$ angle. As $\varphi$ angle increases, the fibers and matrix tolerate less and more stresses, respectively. Failure may occur if the matrix is ​​not strong enough.

After $\varphi = 28$ angle, $\alpha_{3}$ value is less than 1. Thus, fibers do not reinforce the matrix and the matrix bears the whole loading. Therefore, if $\varphi$ angle is more than 28 degrees, the composite material will be prone to fiber–matrix debonding due to shear stress. If the crack-fiber angle is $0 < \varphi { < }28$, the fibers will bear more load than the matrix. After $\varphi = 45$ angle, $\alpha_{1}$ coefficients are less than one. After this angle, fibers do not reinforce the matrix and matrix will tolerate the whole of tensile loading. By increasing crack-fiber angle, the matrix withstands more tensile stress than the fibers, which makes the composite material prone to matrix-cracking failure. In Ref [89], this angle is defined as the transition angle from fiber fracture mode to matrix one of orthotropic materials. The curve of the reinforcement coefficients confirms the transition angle.

6.2 Cracks along the fibers

For cracks along the fibers, the fracture response of cracked orthotropic materials is evaluated utilizing the EMSER criterion under mixed-mode I/II. The crack behavior is extracted by simultaneously solving Eqs. (53) and (60) for $\varphi = 0$. The comparison of the FLCs of Scots pine and Norway spruce with available experimental data [90] is shown in Figs. 13 and 14, respectively.

Fig. 13

Comparison of FLCs of EMSER and SER criteria with experimental data of Scots pine [90] (units are ${\text{MPa}}\sqrt m$)

Fig. 14

Comparison of FLCs of EMSER and SER criteria with experimental data of Norway spruce [90] (units are ${\text{MPa}}\sqrt m$)

Fig. 15

Comparison of FLC of EMSER criterion with experimental data of Norway spruce [60] for $\varphi = 22.5$(units are ${\text{MPa}}\sqrt m$)

Fig. 16

Comparison of FLC of EMSER criterion with experimental data of Norway spruce [60] for $\varphi = 45$(units are ${\text{MPa}}\sqrt m$)

Fig. 17

Comparison of FLC of EMSER criterion with experimental data of Norway spruce [60] for $\varphi = 67.5$(units are ${\text{MPa}}\sqrt m$)

Fig. 18

Comparison of FLC of EMSER criterion with experimental data of Norway spruce [60] for $\varphi = 90$(units are ${\text{MPa}}\sqrt m$)

In Ref [68], Jernkvist presented the SER criterion for predicting the fracture behavior of orthotropic materials under mixed-mode I/II for crack along the fibers. In Figs. 13 and 14, Jernkvist's criterion and EMSER criterion are compared with experimental data. Based on these figures, it can be seen that the EMSER criterion is closer to the experimental data and estimates the crack behavior with higher accuracy. In addition, the SER criterion is conservative.

Figures 13 and 14 depict that the EMSER criterion has acceptable adaptation with the available experimental data. The excellent correlation demonstrated the validity of this criterion in predicting crack growth for cracks along the fibers.

6.3 Desired crack-fiber angle

The fracture response in orthotropic materials is investigated employing the EMSER criterion Cracks with arbitrary direction with respect to the fibers under mixed-mode I/II. The EMSER criterion is validated by experimental data of Norway spruce wood for different crack-fiber angles [60]. FLCs for crack-fiber angles of $\varphi = 22.5,45,67.5,90$ are shown in Figs. 15, 16, 17 and 18, respectively. Predicted FLCs by EMSER criterion are evaluated with the test data.

FLCs based on the EMSER criterion in Figs. 15, 16, 17 and 18 are in accordance with experimental data. Figures 15, 16, 17 and 18 confirm that the EMSER criterion has acceptable compatibility with experimental data and is an acceptable criterion for predicting the fracture response of orthotropic materials. For $\varphi = 90$, the FLC of the EMSER criterion is very close to the FLC of Ref [90]. Thus, under mixed-mode I/II loading, the EMSER criterion presents good anticipation of the fracture response of orthotropic materials.

The presented criterion can conservatively predict the experimental data. The experimental data are scattered in the FLC due to the effects of the T-stress term. Crack along the fibers propagates in its original plane even under mixed-mode I/II loading, and the T-stress term does not affect the crack propagation direction. But in the case of arbitrary crack-fiber angles, the crack kinks and propagates along the fibers. In this condition, the T-stress term has a significant effect on fracture behavior.

7 T-stress effects on fracture limit curves

In this section, the effect of the T-stress term on the crack behavior of orthotropic materials is assessed. As stated, in the case of cracks along the fibers, the T-stress term has no effect on the fracture of orthotropic materials. As the angle between the crack and the fibers increases, the effect of the T-stress term on the fracture of orthotropic material increases. In the case of a crack perpendicular to the fibers, the effect of the T-stress term on the fracture of orthotropic materials is investigated. For crack perpendicular to the fibers, the positive or negative values of this stress affect FLCs [91]. According to Fig. 19, FLC is drawn upwards for $B < 0\,$ and downwards for $B > 0\,$. The negative values of this stress delay the fracture of the material while positive T-stress values accelerate it. Thus, this stress affects the safe zone of fracture remarkably.

Fig.19

Influence of T-stress term on FLC of orthotropic materials for $\varphi = 90$ in comparison with experimental data in Ref [90] (units are ${\text{MPa}}\sqrt m$)

As expected, the positive and negative values of the T-stress term decrease and increase SIFs in mode I and II, respectively. According to Fig. 19, the experimental data are in the range of positive and negative values of the T-stress term. So, considering the T-stress term plays an important role in predicting the fracture of orthotropic materials. To accurately predict the crack behavior of the material by considering this stress, the value of this stress must be calculated for each load, geometry and crack length.

8 Practical application of the EMSER fracture criterion

Composite materials are used extensively in various industries such as aerospace structures, automobiles, submarines, electricity, oil, gas and other industries. Also, there is a possibility of cracks and defects in these materials. Thus, it is important to provide an appropriate fracture criterion for these materials. In this article, a fracture criterion based on the maximum strain energy release rate for orthotropic materials under mixed-mode I/II loading was presented. In addition, the effect of the T-stress term on the presented criterion was investigated. Using Eqs (53) and (60) in this article, the FLC of orthotropic material was extracted. For each test specimen, the FLC can be drawn using the mechanical properties of the specimen. After placing the test specimen in the tensile test, the critical load values are estimated. Using finite element software, the test specimen is modeled and critical loads are applied to it, and the SIFs are extracted. The areas under and above the FLC are the safe and the unsafe zones, respectively. If the SIFs are below the FLC, the fracture will not occur, and if the SIFs are above the FLC, the fracture will occur. Also, if the SIFs are placed on the FLC, the test specimen is on the threshold of fracture. In this way, the fracture of different species can be investigated using the EMSER criterion.

9 Conclusion

In an attempt to understand crack growth in orthotropic materials under mixed-mode I/II loading, an extended maximum strain energy release rate (EMSER) criterion is presented for arbitrary crack-fiber angle. Using the RIS concept as a practical material model, the orthotropic material is modeled. The most important achievements of the presented article are as follows:

• (1) The significant advantage of the EMSER criterion in comparison with the other similar fracture criteria is that the orthotropic material based on RIS concept is modeled using the corresponding stresses method at the arbitrary crack-fiber angle. The fracture response is predicted for desired crack-fiber angle. Providing this method is an important step in the development of orthotropic material modeling.

• (2) In arbitrary crack-fiber angle, the results show that the T-stress term has a significant role in assessing the crack behavior of orthotropic materials.

• (3) EMSER criterion is an efficient criterion for engineering applications because employing this criterion is simply possible with only accessing the mechanical properties of the material and crack-fiber angle.

• (4) A novel approach as equivalent fracture toughness in off-axis orthotropic materials at arbitrary crack-fiber angles is presented.

• (5) Extracted results of the EMSER criterion are evaluated with available test data. Comparison of FLCs with the experimental data of orthotropic materials shows that the EMSER criterion has sufficient reliability for evaluating the fracture response.

Appendix A

$F_{ij} (\theta )$ and $g_{ij} (\theta )$ coefficients in Eqs. (11)-(13) are as follows:

$$f_{11} (\theta ) = \cos \frac{\theta }{2}\left( {1 - \sin \frac{\theta }{2}\sin \frac{3\theta }{2}} \right)$$

(A1)

$$f_{22} (\theta ) = \cos \frac{\theta }{2}\left( {1 + \sin \frac{\theta }{2}\sin \frac{3\theta }{2}} \right)$$

(A2)

$$f_{12} (\theta ) = \sin \frac{\theta }{2}\cos \frac{\theta }{2}\cos \frac{3\theta }{2}$$

(A3)

$$g_{11} (\theta ) = - \sin \frac{\theta }{2}\left( {2 + \cos \frac{\theta }{2}\cos \frac{3\theta }{2}} \right)$$

(A4)

$$g_{22} (\theta ) = \sin \frac{\theta }{2}\cos \frac{\theta }{2}\cos \frac{3\theta }{2}$$

(A5)

$$g_{12} (\theta ) = \cos \frac{\theta }{2}\left( {1 - \sin \frac{\theta }{2}\sin \frac{3\theta }{2}} \right)$$

(A6)

In addition, $\hat{f}_{ij} (\theta )$ and $\hat{g}_{ij} (\theta )$ coefficients in Eqs. (8)-(10) are expressed as follows:

$$\hat{f}_{11} (\theta ) = {\text{Re}} \left( {\frac{{(\mu_{1} \mu_{2} (\mu_{2} \nu_{2} - \mu_{1} \nu_{1} )}}{{\mu_{1} - \mu_{2} }}} \right)$$

(A7)

$$\hat{g}_{11} (\theta ) = {\text{Re}} \left( {\frac{{(\mu_{2}^{2} \nu_{2} - \mu_{1}^{2} \nu_{1} )}}{{\mu_{1} - \mu_{2} }}} \right)$$

(A8)

$$\hat{f}_{12} (\theta ) = {\text{Re}} \left( {\frac{{\mu_{1} \mu_{2} (\nu_{1} - \nu_{2} )}}{{\mu_{1} - \mu_{2} }}} \right)$$

(A9)

$$\hat{g}_{12} (\theta ) = {\text{Re}} \left( {\frac{{(\mu_{1} \nu_{1} - \mu_{2} \nu_{2} )}}{{\mu_{1} - \mu_{2} }}} \right)$$

(A10)

$$\hat{f}_{22} (\theta ) = {\text{Re}} \left( {\frac{{\mu_{1} \nu_{2} - \mu_{2} \nu_{1} )}}{{\mu_{1} - \mu_{2} }}} \right)$$

(A11)

$$\hat{g}_{22} (\theta ) = {\text{Re}} \left( {\frac{{\nu_{2} - \nu_{1} )}}{{\mu_{1} - \mu_{2} }}} \right)$$

(A12)

$\mu_{2}$ and $\mu_{1}$ coefficients are the roots of the following equation:

$$S_{11} \mu^{4} - 2S_{16} \mu^{3} + (2S_{12} + S_{66} )\mu^{2} - 2S_{26} \mu + S_{22} = 0$$

(A13)

$S_{ij}$ coefficients are the components of the compliance matrix as follows:

$$\left( {\begin{array}{*{20}c} {\varepsilon_{11} } \\ {\varepsilon_{22} } \\ {\varepsilon_{12} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {S_{11} } & {S_{12} } & {S_{16} } \\ {S_{21} } & {S_{22} } & {S_{26} } \\ {S_{61} } & {S_{62} } & {S_{66} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\sigma_{11} } \\ {\sigma_{22} } \\ {\sigma_{12} } \\ \end{array} } \right)$$

(A14)

$\nu_{1}$ and $\nu_{2}$ coefficients are defined as follows:

$$\nu_{1} = \frac{1}{{\sqrt {\cos \theta + \mu_{1} \sin \theta } }}$$

(A15)

$$\nu_{2} = \frac{1}{{\sqrt {\cos \theta + \mu_{2} \sin \theta } }}$$

(A16)