On the use of the extended finite element and incremental methods in brittle fracture assessment of key-hole notched polystyrene specimens under mixed mode I/II loading with negative mode I contributions

Abstract

The aim of the present study is to assess the suitability of the extended finite element method (XFEM) combined with the cohesive zone model (CZM) and also the incremental method together with the maximum tangential stress (MTS) criterion in predicting the fracture load and crack trajectory of key-hole notched brittle components subjected to mixed mode I/II loading with negative mode I contributions. For this purpose, a total number of 63 fracture test results, reported recently in the literature on the key-hole notched Brazilian disk (Key-BD) specimens made of the general-purpose polystyrene (GPPS) under mixed mode I/II loading with negative mode I contributions, are first collected. Then, the experimentally obtained fracture loads of the tested GPPS specimens are theoretically predicted by means of XFEM combined with CZM. Additionally, the crack trajectory in the tested Key-BD specimens is predicted by using both XFEM combined with CZM and the incremental method combined with MTS criterion. Finally, it is shown that both the fracture load and the crack trajectory could successfully be predicted by means of the two proposed methods for different notch geometries.

1 Introduction

Engineering components or machine elements which are made of brittle or quasi-brittle materials like ceramics or brittle polymers are susceptible to sudden fracture without any precaution. Hence, prevention of brittle fracture would be of more importance than that of ductile rupture, which normally occurs in a stable manner. As could widely be seen in engineering components, different shapes of notches, such as U, V and O shapes, are normally utilized in the components for various design purposes, like transferring the loads and connecting two or more components together. Beside their wide applications and usefulness, as a disadvantage notches are sources of stress concentration at their neighborhood. The concentrated stress field may cause cracking at the notch border, and if the material is brittle or quasi-brittle, the rate of crack growth will increase dramatically such that it cannot be captured with naked eye. Therefore, due to its great importance, brittle fracture in notched members is still an active research topic.

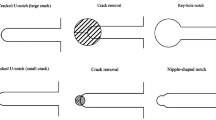
Unlike the original notch shapes (e.g., U, V or O shapes), some notch features are not present in the initial design of components, but they are resulted from applying a repairing method, such as the hole-drilling method, that removes a damage or crack emanating from the points of high stress concentration during the service life. For instance, if a small crack initiates from the tip of a U-notch, a usual repairing method is to remove the crack by drilling a hole which has a radius equal to the crack length. After the repairing process, a new notch, called the key-hole notch takes, shape (see Fig. 1). In fact, the hole-drilling method removes the crack and hence reduces significantly the stress concentration around the cracked notch border.

Fig. 1

Hole-drilling method for removing cracks emanating from a U-notch border

Due to the importance of preventing notch failure in brittle structural components, it is essential to develop appropriate fracture models for designing the notched brittle components subjected to different loading conditions. Up to now, several brittle fracture models have been suggested and utilized in the literature to predict the failure behavior of different notched components under various loading conditions. Some of them like the generalized J-integral [1,2,3,4] and the strain energy density (SED) [5,6,7,8] are energy-based criteria, and some others are stress-based criteria such as the point stress (PS) and the mean stress (MS) criteria [9,10,11,12]. The cohesive zone model (CZM) is, however, another well-known fracture model in the context of the notch fracture mechanics (NFM) [13,14,15,16].

In the 1960s, the cohesive zone model (CZM) was first proposed by Dugdale and Barenblatt [17, 18]. In the 1970s, Hillerborg et al. [19] extended CZM to explain the fracture trajectory in notched components in which no initial macroscopic crack existed at the notch border. Their research work was the starting point for applying CZM to notched problems. The CZM is closely associated with the extended finite element method (XFEM). In fact, XFEM is a numerical method that exists inside the common finite element (FE) codes, and it is usually linked to CZM for failure prediction. In recent years, XFEM has been widely utilized as an efficient numerical method for failure analysis of the cracked components, especially for predicting the fracture trajectory in cracked and notched members. Over the past decade, some new extensions of XFEM have been proposed in the literature [20,21,22,23,24,25,26,27,28,29]. For instance, Wells and Sluys [20] had investigated the fracture of concrete materials under mixed mode loading by combining XFEM with CZM and compared the predictions of the fracture trajectory with the experimental results. Moes and Belyschco [21] utilized XFEM for the crack growth problems in which a cohesive law is considered on the crack faces. Mariani and Perego [22] proposed a numerical methodology to simulate the crack propagation in quasi-brittle materials. Meschke and Dumstor [23] proposed a variational format of XFEM for prediction of cohesive cracks propagation in brittle and quasi-brittle components. An extended finite element method with analytical solution for cohesive crack modeling has been presented by Cox [24]. Giner et al. [25] had introduced an implementation of XFEM for fracture problems by using the ABAQUS finite element software. Ingraffea and co-researchers [26,27,28] had investigated the fracture trajectory for blunt V-notches in different types of gear teeth subjected to static and fatigue loading conditions. Moreover, Seidenfuss et al. [29] had studied some failure models for predicting the fracture trajectory in ductile components.

Some valuable researches have been published by Rabczuk and co-researchers in which the failure behavior of some complex cracked structures has been analyzed and predicted by some new computational methods with various mesh algorithms [30,31,32,33,34,35,36,37,38,39,40]. Some efficient FEM-based computational methods have been proposed in [30,31,32] for fracture prediction of brittle, quasi-brittle and ductile materials subjected to the basis of edge rotations. Also, a crack propagation algorithm based on the screened Poisson equations and local re-meshing techniques has been proposed for analyzing the damage behavior in some cracked components under various loading conditions [33]. Additionally, some efficient approaches based on the mesh-free and extended mesh-free methods have been proposed for modeling discrete cracks in several 2D and 3D problems subjected to static and dynamic loadings [34,35,36,37,38].

Beside the research works mentioned above, which have been performed on the specimens weakened by notches of original shapes, some investigations have also been performed dealing with brittle fracture in key-hole notched components by means of the NFM failure criteria [41,42,43,44,45,46,47,48,49]. Kullmer and Richard [50] investigated brittle fracture in key-hole notches by using the compact-tension-shear-notched (CTSN) specimens made of PMMA under mixed mode I/II loading. To predict the experimentally obtained fracture loads, they employed a stress-based fracture model [50]. Moreover, brittle fracture in key-hole notched rectangular specimens made of isostatic graphite has been studied in a valuable research by Lazzarin et al. [43]. They have tested the notched specimens under mode I and mixed mode I/II loading conditions and successfully predicted the experimental results by means of the SED criterion [43]. More recently, a few papers have been published by Torabi and co-researchers regarding brittle fracture of key-hole notched specimens under mode I [44, 45], mode II [46], and mixed mode I/II [42, 48, 49] loading conditions.

Although among the loading modes, pure mode I and mixed mode I/II loadings have attracted great interests because of their widespread practical applications, in recent years some researchers have studied the failure behavior of notched components under compression loading (the compression loading is now well known in the literature as the negative mode I loading). Berto et al. [51] had assessed brittle fracture of V-notches with end holes (VO-notches) under negative mode I loading conditions. They have reported the test results on fracture load of the double VO-notched rectangular specimens made of graphite under pure compression loading, and the experimental results have been evaluated by means of the SED criterion [51]. In a separate research, Torabi and Ayatollahi [52] haD re-predicted the experimental results reported in [51] by means of the point stress (PS) and mean stress (MS) brittle fracture criteria. Recently, two research studies have been conducted on brittle failure of blunt V-notches under pure compression. To investigate brittle fracture in V-notched components under pure compressive loading, two new test specimens, namely the flattened V-notched semi-disk (FVSD) and the V-notched stepped cottage (VSC) specimens, have been suggested and utilized in [53, 54]. The fracture loads of the specimens reported in [53, 54] have also been predicted successfully by means of the PS and MS criteria. Moreover, in a review paper, Ayatollahi et al. [55] had recently reviewed a large number of researches in which brittle fracture has been studied for engineering components containing some types of notches under different loading conditions.

A research has been more recently performed by Torabi et al. [42] on brittle fracture of key-hole notched Brazilian disk (Key-BD) specimens under mixed mode I/II loading with negative mode I contributions. In [42], the experimentally obtained fracture loads of the tested Key-BD specimens have been well predicted by using the two stress-based criteria, namely the key-hole notch maximum tangential stress (Key-MTS) and key-hole notch mean stress (Key-MS) criteria. At the best of the author’s knowledge, the latest work on this subject has been published in [41]. In [42], the present authors have re-predicted the experimental results reported in [42] by means of the two energy-based criteria, namely the averaged strain energy density (ASED) and averaged strain energy density based on the equivalent factor concept (ASED-EFC) criteria [41].

In the present research, the extended finite element method (XFEM) is utilized in conjunction with the cohesive zone model (CZM) in order to predict the fracture loads of the tested Key-BD GPPS specimens reported recently in [42]. Additionally, the crack trajectory of the tested specimens is predicted by means of two methods, namely XFEM based on the linear CZM and the incremental method on the basis of the maximum tangential stress (MTS) criterion. It is revealed that the XFEM-CZM approach could provide generally good predictions to the experimental results, including the fracture load, the fracture initiation angle (FIA) and the crack trajectory of the tested GPPS specimens. Revealed in this study is also that the incremental method supported by MTS criterion could predict the crack trajectories well, although it needs more time for predictions compared with the XFEM-CZM approach.

2 Experimental results

Torabi et al. [42] had published a research paper in which extensive fracture test results have been reported for the key-hole notched Brazilian disk (Key-BD) specimens under mixed mode I/II loading with negative mode I contributions. The material and the test specimen utilized in [42] are elaborated in the forthcoming subsections.

2.1 Material

The material studied by Torabi et al. [42] is a type of glassy polymer, namely the general-purpose polystyrene (GPPS), with the properties summarized in Table 1. It has been reported in [42] that GPPS exhibits well the brittle fracture behavior.

Table 1 Mechanical properties of the tested GPPS at room temperature [42]

2.2 Specimen

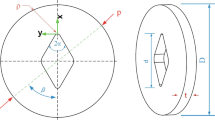
The specimen utilized by Torabi et al. [42] for fracture tests has been the Brazilian disk specimen weakened by key-hole notches (Key-BD specimen) and subjected to mixed I/II loading with negative mode I contributions. Figure 2 schematically represents the Key-BD specimen in which the parameters $\rho$, $\beta$, $L_{1}$, $L_{2}$, t and P are the notch tip radius, the loading angle (i.e., the angle between the applied load direction and the notch bisector line), the slit length, the disk diameter, the disk thickness and the remotely applied load, respectively. Moreover, the distance between the two flanks of the key-hole notch has been considered to be equal to $\rho$. The slit length $L_{1}$ has been considered to be equal to 24 and 40 mm, resulting in two different values of the relative notch length (RNL) $L_{1}/L_{2 }$ equal to 0.3 and 0.5, respectively. For the specimens with $L_{1}/L_{2}=0.3$, three notch radii of 1, 2 and 4 mm have been considered, whereas four radii of 1, 2, 4 and 6 mm have been considered for those with $L_{1}/L_{2}=0.5$. The disk thickness and diameter are equal to 7.8 and 80 mm, respectively.

Fig. 2

The Key-BD specimen

When the loading angle ($\beta$) is zero, the key-hole notch experiences only pure tensile mode I loading (i.e., the opening mode) because the tangential stress values on the notch bisector line are positive. By changing $\beta$ from zero to larger values, the loading type changes from pure tensile mode I toward pure mode II. The loading angle corresponding to pure mode II loading is called $\beta _\mathrm{II}$. If $\beta$ increases gradually from $\beta _\mathrm{II}$, the loading conditions vary from pure mode II toward mixed mode I/II loading with negative mode I contributions. Therefore, for $0^{{\circ } }< { \beta }<\beta _\mathrm{II}$, the notch is subjected to mixed mode I/II loading conditions with positive mode I contributions, while for $\beta _\mathrm{II}<\beta < 90^{\circ }$ with negative ones. Previously, the present authors have reported in [42] that four various loading conditions could exist in the Key-BD specimen as follows: (i) when the loading angle ($\beta$) is zero, the specimen experiences only pure positive mode I loading; (ii) when the angle $\beta$ gradually increases from zero to ${\beta _\mathrm{II}}$, the loading conditions change to mixed mode I/II loading with positive mode I contributions; (iii) if the loading angle reaches the specified value $\beta _\mathrm{II}$, the specimen experiences only pure mode II loading, and finally; (iv) when the loading angle gradually increases from $\beta _\mathrm{II}$ to $90^{\circ }$, the loading conditions change from pure mode II toward mixed mode I/II loading with negative mode I contributions. All of the loading conditions are schematically shown in Fig. 2.

Torabi et al. [42] had found that the values of $\beta _\mathrm{II}$ are equal to 29.5$^{^{\circ }}$ and 24.5$^{^{\circ }}$ for $\hbox {RNL} = 0.3$ and $\hbox {RNL} = 0.5$, respectively. In order to explain how to obtain the $\beta _\mathrm{II}$ values for the Key-BD specimens, some numerical finite element (FE) stress analyses are performed in this study for the notch tip radii equal to 2 mm. The variations of the tangential stress at the notch tip versus the loading angle $\beta$ for the specimen of ${\rho }= 2\,\hbox {mm}$ with $\hbox {RNL}=0.3$ and 0.5 are plotted in Fig. 3. An arbitrary constant load of 1000 N is applied to the entire FE models. Figure 3 shows that the Key-BD specimen with $\hbox {RNL}=0.3$ begins experiencing the negative mode I loading when the loading angle reaches $\beta _\mathrm{II} = 29.5{^{\circ }}$, whereas for the Key-BD specimen with $\hbox {RNL} = 0.5$, the $\beta _\mathrm{II}$ value is equal to 24.5$^{^{\circ }}$. In fact, $\beta _\mathrm{II}$ is a particular angle at which the key-hole notch experiences zero tangential stress at its tip.

Fig. 3

Variations of the tangential stress at the notch tip versus the loading angle $\beta$ in the Key-BD specimen of ${\rho } = 2\,\hbox {mm}$ and $\hbox {RNL} = 0.3$ and 0.5

By using the FE stress analyses, Torabi et al. [42] had shown that although brittle failure in the Key-BD specimens under mixed mode I/II loading with negative mode I contributions occurs from the applied load side of the notch border by local tensile stresses, the notch bisector line and the other side of the notch border sustain compressive stresses. In fact, this phenomenon explains the concept of the compressive shear loading in the Key-BD specimen. To provide mixed mode I/II loading with negative mode I contributions in the Key-BD tests, Torabi et al. [42] had examined four various loading angles $\beta$ equal to 0, 30, 50 and 70. In the experiments, the test speed has been equal to 1 mm/min, providing quasi-static loading conditions. To check the repeatability of the experimental results, they have conducted three tests for each specimen. All in all, 84 fracture tests under displacement control conditions have been performed and reported in [42].

The experimentally obtained fracture loads of the tested Key-BD GPPS specimens reported in [42] are presented in Table 2 for various geometries of the specimen. As seen in Table 2, each specimen is denoted by a specific index as, $\hbox {RNL}-{\rho }-{ \beta }$. Also, $P_{i} ({i} = 1, 2, 3)$ and $P_\mathrm{av.}$ denote the fracture loads of the three repeated tests and the average value of the three experimentally obtained fracture loads, respectively. Additionally, the experimentally obtained fracture initiation angles for the tested Key-BD specimens are summarized in Table 3 $({\vartheta _{0i}\;\hbox {values}})$. It has been reported in [42] that the load–displacement curves recorded from the fracture tests are linear up to final breakage and the fracture takes place suddenly with no effective plastic deformations around the notch border (see Fig. 4). Therefore, we are allowed to utilize any brittle fracture models in the context of the linear elastic notch fracture mechanics (LENFM) for fracture load prediction of the tested Key-BD GPPS specimens.

Table 2 Summary of the test results on the fracture load of the Key-BD GPPS specimens [42]

Table 3 Experimentally obtained fracture initiation angles for the Key-BD GPPS specimens [42]

Fig. 4

Some load–displacement curves regarding the Key-BD GPPS specimens

3 Fracture prediction models

In this section, two theoretical fracture prediction models, namely the extended finite element method (XFEM) based on the linear cohesive zone model (CZM) and the incremental method based on the maximum tangential stress (MTS) criterion, are elaborated for predicting the experimental results presented in Sect. 2.

3.1 Extended finite element method in combination with CZM

One of the well-established numerical methods to predict the crack trajectory and load-carrying capacity (LCC) of engineering components is the extended finite element method (XFEM). For the first time, Belytschko and Black [56] proposed this numerical method, and after that, it has been frequently utilized in many fracture-related researches. The basis of XFEM is that it allows the elements to create discontinuities inside them by enriching the degrees of freedom of the elements. The XFEM has several advantages in comparison with the common numerical methods. For instance, this method does not need to apply a very small mesh size at the neighborhood of the discontinuities and also this method has the ability to predict the crack trajectory of the tested notched specimens.

To apply XFEM to a theoretical brittle fracture prediction, a failure criterion in the context of LEFM should be linked to it. Hence, the failure model utilized in this research is considered to be the linear elastic cohesive zone model (CZM). Barenblatt [18] was the first one who proposed CZM for brittle fracture prediction. The CZM is based on the assumption that a fracture process zone extends before the formation of a physical crack in the defective material. In the fracture process zone, the material experiences a progressive degradation that starts from the pre-existing crack or notch tip, where the stresses are maximum, and ends at a finite distance ahead of the crack or notch tip after which the material is unscathed.

The CZM model utilized in this research has been previously proposed in [25,26,27,28], and it is presented here for predicting the fracture results of the Key-BD GPPS specimens under mixed mode I/II loading with negative mode I contributions. The CZM can be considered in a linear elastic fracture model in which the first crack initiates when the maximum principal stress attains the ultimate tensile strength of material. Also, the orientation of the initiated crack is perpendicular to the direction of the maximum principal stress. Below, the basic information of CZM is briefly described.

In the first steps of loading process, the material behaves as a linear elastic material while the maximum principal stress has not reached the ultimate tensile strength. Hence, the stress components are obtained by the following expression:

$$\begin{aligned} \sigma =D\varepsilon \end{aligned}$$

(1)

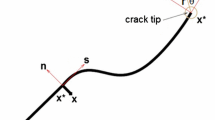
in which D, $\sigma$ and $\varepsilon$ are the fourth order of the elastic modulus tensor, the Cauchy’s stress tensor and the strain tensor, respectively. When the principal stress in an element attains the ultimate tensile strength (as a critical stress of the tested material), an initial crack forms in the element perpendicular to the direction of the maximum principal stress (n). Also, the crack opening component is characterized by the vector w, which is assumed to be a constant value along the crack trajectory. This concept is illustrated in Fig. 5.

Fig. 5

Formation of a crack inside a finite element

As shown in Fig. 5, when the crack forms in the element, it changes into two subdomains in which the lower and upper domains of the discontinuous element are called $\hbox {A}^{-}$ and $\hbox {A}^{+}$, respectively. The nodes related to the domain $\hbox {A}^{+}$ are referred to as solitary nodes. Therefore, the jump in displacement field within the element created by the crack can be written as follows:

$$\begin{aligned} u\left( x \right) = \sum _{\alpha \in A^{-}\cup A^{+}} N_\alpha \left( x \right) u_\alpha +\left[ {H\left( x \right) - \sum _{\alpha \in A^{+}} N_\alpha \left( x \right) } \right] {w} \end{aligned}$$

(2)

where $\alpha$ is the index of element node, $u_\alpha$ is the corresponding nodal displacement, and $N_\alpha \left( x \right)$ is the traditional shape function associated with the node $\alpha$. Also, $H\left( x \right)$ is the Heaviside jump function whose values for regions A$^{-}$ and A$^{+}$ are assumed to be equal to zero and one, respectively.

Figure 6 illustrates the concept of the enriched nodes in XFEM-CZM approach. According to the continuum mechanics, the strain field is evaluated by considering the symmetric part of the gradient to the displacement field proposed in Eq. (2). Hence, Eq. (3) is obtained here for strain field as follows:

$$\begin{aligned} \varepsilon ^{c}\left( x \right) =\sum _{\alpha \in A^{-}\cup A^{+}} \left[ {b_\alpha \left( x \right) \otimes u_\alpha } \right] ^{S}+\left[ {\sum _{\alpha \in A^{+}} b_\alpha \left( x \right) \otimes {w}} \right] ^{S} \end{aligned}$$

(3)

where $b_\alpha \left( X \right)$ expresses the gradient of the shape function related to node $\alpha$. Also, the symbol “$\otimes$” denotes the tensor product. Paying attention to the finite element method (FEM), it can be concluded that the first part of Eq. (3) represents the strain field the element would have if no crack exists in it. Therefore, the first term of Eq. (3) is known as apparent strain,

$$\begin{aligned} \varepsilon ^{a}\left( x \right) = \sum _{\alpha \in A^{-}\cup A^{+}} \left[ {b_\alpha \left( x \right) \otimes u_\alpha } \right] ^{S} \end{aligned}$$

(4)

Hence, Eq. (4) can be simply changed into Eq. (5) as follows:

$$\begin{aligned} \varepsilon ^{c}\left( x \right) =\varepsilon ^{a}\left( x \right) -\left[ {\sum _{\alpha \in A^{+}} b_\alpha \left( x \right) \otimes {w}} \right] ^{S} \end{aligned}$$

(5)

By substituting $b^{+}\left( x \right) =\sum _{\alpha \in A^{+}} b_\alpha \left( x \right)$ in Eq. (5), it can be rewritten as

$$\begin{aligned} \varepsilon ^{c}\left( x \right) =\varepsilon ^{a}\left( x \right) -\left[ {b^{+}\left( x \right) \otimes {w}} \right] ^{S} \end{aligned}$$

(6)

Equation (6) presents the strain field of an element containing a crack. Thus, the stress tensor can be defined by the following expression:

$$\begin{aligned} \sigma \left( x \right) =D\left[ {\varepsilon ^{a}\left( x \right) -\left[ {b^{+}\left( x \right) \otimes {w}} \right] ^{S}} \right] \end{aligned}$$

(7)

According to CZM, the stresses are governed by the softening curve and due to the fact that crack may initiate and grow in different in-plane modes, a central force model is utilized as

$$\begin{aligned} t=f\left( \tilde{\mathrm{w}}\right) \frac{{w}}{\tilde{{w}}} \end{aligned}$$

(8)

The function $f\left( \tilde{{w}}\right)$ is the softening curve, and t is the traction vector transferred along the crack. The variable w denotes the equivalent crack opening. According to Eq. (8), the relationship between the traction vector and the crack opening vector is proportional, and its modulus is obtained by the softening curve. These concepts are depicted in Fig. 7.

Note that by comparing Eqs. (7) and (8), it can be found that the traction vector in the crack is a constant value, while the stress components in the continuum are a tensorial field. Therefore, by determining the relationship between the projection in the n direction of the stress tensor and the traction vector, Eq. (9) is obtained as follows:

$$\begin{aligned} \left( {D\left[ {\varepsilon ^{a}\left( x \right) -\left[ {b^{+}\left( x \right) \otimes {w}} \right] ^{S}} \right] } \right) n=f\left( {\left| {w} \right| } \right) \frac{{w}}{\left| {w} \right| } \end{aligned}$$

(9)

As is evident in Eq. 9, the only unknown parameter is w vector, which can be determined by numerical methods.

Fig. 6

The concept of enriched nodes in the XFEM-CZM

Fig. 7

Sketch of the central force model applied to the initiated crack with the softening curve

3.2 Incremental method based on Key-MTS criterion

One of the well-known classical approaches for crack trajectory prediction in engineering components is the incremental method. According to this method, the location of the first crack emanating from the key-hole notch border is first obtained by means of the Key-MTS criterion. Then, a short crack is created at the obtained location and a new FE analysis is performed for the cracked key-hole notch in order to determine the growth direction of the first crack. The next step is to create the second short crack at the determined direction and predict its growth direction. These iterative numerical calculations should be continued until the specimen is separated into two parts (i.e., breaks). Note that the shorter embedded cracks result in more resolution of the incremental method. The incremental method of crack growth is depicted in Fig. 8. Similar to XFEM, the incremental method should also be coupled with a suitable brittle fracture criterion. Therefore, the MTS criterion is utilized herein as a well-known brittle fracture criterion for predicting the crack trajectory.

Fig. 8

Incremental crack growth process

In recent years, Torabi and co-researchers [42, 47, 49] had extended the classic MTS criterion to key-hole notched domains and proposed the Key-MTS criterion. They have successfully verified the validity of the Key-MTS criterion by means of extensive experimental results obtained from testing the Key-BD specimens. According to this criterion, brittle fracture occurs when the tangential stress $\sigma _{\theta \theta }$ at a specified critical distance $r_\mathrm{c}$ ahead of the notch border reaches the critical stress called $\sigma _\mathrm{c}$. In several references [9,10,11], it has been demonstrated that the critical stress could be assumed to be equal to the ultimate tensile strength of material $(\sigma _u)$. Additionally, the Key-MTS criterion expresses that the brittle fracture initiates from a location on the notch border at which the value of the tangential stress is maximum and propagates radially along the direction perpendicular to the notch border. The failure concept of the Key-MTS criterion is schematically depicted in Fig. 9.

Fig. 9

A key-hole notch with its brittle failure definitions related to the Key-MTS criterion

4 Numerical analysis

The numerical analyses of the two theoretical fracture prediction models proposed in Sect. 3 are elaborated in this section.

4.1 Numerical analysis of extended finite element method based on CZM approach

It is very important to note that the progressive degradation occurs when the strain in the material increases by decreasing the material strength. According to CZM, failure initiates when the cohesive traction in the material reaches the critical tensile stress which is normally considered equal to the ultimate tensile strength of material. Figure 10 schematically illustrates the basic concept of CZM. In CZM, the relationship between the cohesive traction and the crack opening displacement is as follows (see Fig. 10c):

$$\begin{aligned} {T}=f\left( \delta \right) \end{aligned}$$

(10)

In Eq. (10), T, $\delta$ and ${f}(\delta )$ are the cohesive traction, the crack opening displacement and the softening function, respectively. In fact, the softening function determines how the cohesive traction decreases as the crack opening displacement increases. Some types of softening functions utilized for XFEM based on CZM are illustrated in Fig. 10c. Two material properties, namely the tensile strength $\sigma _u$ and the specific fracture energy $G_\mathrm{f}$, have great roles in the softening function. As can be seen in Fig. 10, the specific fracture energy $G_\mathrm{f}$ is equal to the area under the softening curve.

Fig. 10

Basic concept of the Cohesive Zone Model

As mentioned in Sect. 3, an appropriate brittle fracture model should be considered to be coupled with XFEM for the theoretical failure predictions including the fracture load, crack trajectory and fracture initiation angle. Hence, the CZM is utilized herein. For applying CZM, two essential material properties, namely the ultimate tensile strength $\sigma _u$ and the specific fracture energy ${G}_\mathrm{f}$, should be given to the FE software. The commercial FE code, which is linked to the XFEM toolbox of the Dassault systems, ABAQUS 6.13 is used for the numerical calculations. All material properties utilized in the FE simulations are taken from Table 1, except for the specific fracture energy. As explained in the previous section and illustrated in Fig. 10, CZM needs the specific fracture energy. The specific fracture energy for brittle materials can be calculated through the Irwin’s equation [57] as follows:

$$\begin{aligned} G_\mathrm{f} =\frac{K_{\mathrm{Ic}^{2}}}{E/\left( {1-\upsilon ^{2}} \right) } \end{aligned}$$

(11)

Therefore, the value of ${G}_\mathrm{f}$ for the tested GPPS material is obtained from Eq. (11) to be equal to 0.559 N/mm.

Two rigid lines are considered at the top and bottom of the Key-BD specimen simulating the fixtures of the universal test machine (see Fig. 13). Therefore, the boundary conditions in the FE analyses are such that the top rigid line is constrained so that it can solely move along the loading direction and the bottom line is completely fixed during loading. Note that the surface-to-surface contact is considered between the upper half of Key-BD specimen and the top rigid line, as well as between the bottom half of the specimen and the bottom rigid line. Moreover, in order to prevent rotating the disk, the upper and bottom points of the disk, which are tangent to the top and bottom rigid lines, are fixed in the horizontal axis. The loading and boundary conditions utilized in the FE analyses agree well with the real conditions that exist in the fracture experiments. Also, 4-node bilinear plane strain quadrilateral elements are utilized in the 2D FE models.

Unlike the CZM in combination with the embedded crack approach in which the crack propagation does not have a considerable dependency on the finite element meshing algorithm, the crack propagation in the notched components is almost dependent upon the element size at the notch border in the CZM approach without any embedded crack. In both approaches, the critical distance, called the characteristic length $(l_\mathrm{ch})$, has been considered; however, application of this critical distance is different for each of them. In fact, in XFEM-CZM approach utilized in the present research, the characteristic length of material allows to apply homogeneous meshes to the notch border by setting a special region around the notch border to generate an initial crack in this area. In order to achieve representative simulations in XFEM-CZM approach, the element size at the notch border must be limited by considering the characteristic length $(l_\mathrm{ch})$ which is related to the fracture process zone (FPZ). The characteristic length can be evaluated through the following equation as previously presented in [46]:

$$\begin{aligned} l_{{\mathrm{ch}}} =\frac{{G}_\mathrm{f} E}{\left( {1-\upsilon ^{2}} \right) \sigma _{\mathrm{u}^{2}}} \end{aligned}$$

(12)

As can be seen in Eq. (12), the characteristic length depends on the material properties; hence, the value of $l_{{\mathrm{ch}}}$ for the tested GPPS material is evaluated from Eq. (12) to be equal to 2.17 mm. For this purpose, a new meshing algorithm is suggested and utilized in this research paper to determine the element size at the notch border as follows.

According to the meshing algorithm proposed herein, a circle-shaped partition whose radial size is equal to $l_{{\mathrm{ch}}}$ should firstly be created around the notch border for all of the notched specimens tested. Then, the element size around the notch border for the two notched specimens having the minimum radii (i.e., $\rho = 1$ and 2 mm) must be limited as possible to a minimum size with the main constraint that multiple cracks should not propagate within the same mesh and additionally, the element size in the fracture process zone (FPZ) should be considered in homogeneous shape by applying the bias seed edges tool. As a result, the element size at the notch border for the two notch geometries having the minimum radii is determined. After that, the element size at the notch border for the other notch geometries having larger radii can be evaluated by using a new formulation based on the mathematics principles as follows:

$$\begin{aligned} \frac{{ ES}_{\rho _{i+1} } -{ ES}_{\rho _i } }{{ ES}_{\rho _{i+2} } -{ ES}_{\rho _i } }=\frac{\rho _{i+1} -\rho _i }{\rho _{i+2} -\rho _i } \end{aligned}$$

(13)

where ES is the element size applied to the notch border in FPZ. Also, the indices $\rho _i$ and $\rho _{i+1}$ denote the notched specimens having the minimum radius and larger radius, respectively. Hence, the element size at the notch border is variously achieved for different notch tip radii. The variations of the element size versus the notch tip radius are plotted in Fig. 11.

Fig. 11

Variations of the element size at the notch border versus the notch tip radius in XFEM-CZM simulation of the Key-BD GPPS specimens

It is useful to note that by performing the iteration process (i.e., determination of the element size at the notch border with the main constraint that multiple cracks should not propagate within the same mesh) on the FE models for the two notched specimens having the minimum radii, i.e., $\hbox {RNL} = 0.5$ and $\rho = 1$ and 2 mm, the element size at the notch border for the other notch geometries having larger radii can be simply estimated by using Eq. (13). The process of evaluating the element size at the notch border is conceptually illustrated in Fig. 12. Also, a typical mesh pattern of the Key-BD specimen with $\hbox {RNL} = 0.5$ and $\rho = 4$ mm is depicted in Fig. 13.

Fig. 12

Determination of the element size at the notch border

Fig. 13

A Key-BD specimen meshed in FE software (${RNL}= 0.5$, $\rho = 4\,\hbox {mm}$

In many researches, the shape of the softening function has been deeply analyzed. Up to date, although various standard types of softening curve have been proposed for different engineering materials, like bilinear and exponential types for concrete and rectangular type for PMMA and steel, no particular method has been already proposed in the scientific literature about how to obtain the shape of softening curve for any tested material. In [13,14,15,16], researchers applied an iterative process to their numerical FE models to obtain the corrected shape of the softening curve. Therefore, the present authors decided to determine the shape of softening curve by applying an iterative method to their numerical calculations. In this way, the linear softening curve is firstly considered and applied to the numerical simulations because of its simplicity and after that, it is found that the predictions obtained from considering this softening curve are in a good agreement with the experimentally obtained fracture loads. Therefore, the linear softening function in which the specific fracture energy $G_\mathrm{f}$ is equal to the area under the softening curve is considered for polystyrene material utilized in this study (see Fig. 10c). The numerical load–displacement curves obtained from the XFEM-CZM simulations are compared with the experimental ones to verify the FE analyses performed. Figure 14 illustrates the load–displacement curves obtained from the XFEM-CZM approach and the three repeated experimentally obtained curves for the four arbitrarily selected Key-BD specimens tested under mixed mode I/II loading with negative mode I contributions.

As can be seen in Fig. 14, the trend of the curves shows that XFEM-CZM results are generally in a good consistency with the experimental results for the fracture loads (i.e., the peak points). However, for some specimens tested, such as 0.5-4-50, the peak point is satisfactorily predicted, but the load–displacement curve is not. Moreover, for some other specimens, like 0.5-6-30, neither the peak point nor the load–displacement curve is predicted well by XFEM-CZM approach. About the inconsistency of the load–displacement curves, it should be expressed that a commercial code with explicit time integration is utilized in all of the finite element (FE) models. The numerical codes utilized in this research need small integration time steps, and therefore, it is expected that the peak point (i.e., the fracture load) is reached by XFEM-CZM approach quicker than the fracture tests. As a result, it is seen that the displacement at the peak point for XFEM-CZM approach is significantly less than that for the experiment. Hence, these effects are ignored and just the peak point is recognized to be important for reporting the critical load of the tested specimens. Additionally, in some research papers published, it has been stressed that there is no necessity for coinciding the load–displacement curves obtained from the experiments and the numerical FE models [13,14,15,16]. About the specimen 0.5-6-30, however, the peak point is not also predicted very well as shown in Fig. 14. For this specific geometry, most of the mentioned criteria, including XFEM-CZM criterion, could not provide very good predictions to the experimental results (see Table 5). Although the fracture load prediction of XFEM-CZM criterion is not very well for this specific geometry, its accuracy (84%) seems satisfactory from the viewpoint of engineering.

Fig. 14

Load–displacement curves obtained from the fracture experiments in comparison with the numerical results of the XFEM-CZM for some of the tested Key-BD GPPS specimens

4.2 Numerical analysis of the incremental method based on the Key-MTS criterion

In this subsection, the numerical FE analysis performed to estimate the crack trajectory by using the incremental method combined with the MTS criterion is elaborated. The whole FE analyses in this study are performed on the Key-BD specimens with the plane strain and linear elastic assumptions. Unlike for XFEM, refined elements should be utilized at the notch vicinity for the incremental method due to the high level of stress gradient. Moreover, the boundary and loading conditions utilized in the incremental method are the same as those used in XFEM approach. For each FE model of the Key-BD specimens, a polar coordinate system is defined with the origin located on the key-hole notch bisector line at the center of curvature of the notch border. As stated in Sect. 2, the loading angles $\beta$ in Key-BD specimen which are between $\beta _\mathrm{II}$ and $90^{\circ }$ result in mixed mode I/II loading with negative mode I contributions. To understand better this concept, for instance, the tangential stress distributions around the notch border corresponding to the specimen with $\hbox {RNL} = 0.5$, $\rho = 2\,\hbox {mm}$, $\beta = 50^{\circ }$ and $P = 2637\,\hbox {N}$ are presented in Fig. 15.

Fig. 15

Tangential stress contours around the notch border corresponding to the load of 2637 N ($\hbox {RNL} = 0.5$, $\rho = 2\,\hbox {mm}$, $\beta = 50^{\circ })$

This figure indicates that the key-hole notch sustains two types of stress distributions. As seen in Fig. 15, the right half of the notch bisector line experiences tensile stresses, while the left half and the bisector line sustain compressive stresses, meaning that the key-hole notch is subjected to mixed mode I/II loading with negative mode I contributions. Torabi et al. [42] had recently shown that although the stress level at the compressive side of the notch border is higher than that at the tensile side, brittle fracture always initiates from the tensile side of the notch border.

To perform the crack trajectory estimations by means of the incremental method, first, a crack of 1 mm length is considered as an embedded crack at the notch right border where the tensile tangential stress is a maximum. The orientation of this crack is radial and perpendicular to the maximum tangential stress. After the first step of FE analysis, the next steps begin. As can be seen in Fig. 9, the orientations of the new embedded cracks are obtained by means of the MTS criterion. Erdogan and Sih [58] were the first ones who proposed the MTS criterion for predicting the fracture toughness and fracture initiation angle in brittle materials under mixed mode I/II loading. The crack growth equation of the MTS criterion is as follows:

$$\begin{aligned} K_\mathrm{I} \hbox {Sin}\theta _0 +K_\mathrm{II} \left( {\hbox {Cos}\theta _0 -1} \right) =0 \end{aligned}$$

(14)

In Eq. (14), the parameters $K_\mathrm{I}, K_\mathrm{II}$ and $\vartheta _{0}$ denote the mode I and mode II stress intensity factors (SIFs) and the fracture initiation angle, respectively. The orientation of the next embedded crack $(\vartheta _{0})$ can be obtained by first calculating the values of the SIFs (i.e., $K_\mathrm{I}$ and $K_\mathrm{II})$ for the existing crack using the FE analysis and then substituting into Eq. 14. These calculations are continued until the embedded cracks reach the outer boundary of the Key-BD specimen. Note that the size of the crack embedded at each step of the incremental method is set to be equal to 1 mm. The values of the SIFs together with those of the next crack orientation $(\theta _{0})$ obtained for the first 9 steps of the incremental method are presented in Table 5 for the Key-BD specimen with $\hbox {RNL} = 0.5$, $\rho = 2\,\hbox {mm}$ and $\beta = 30^{\circ }$. The entire values presented in Table 4 are calculated by considering the applied load equal to 2299 N. The first nine increments of the crack growth process obtained from the incremental method are illustrated in Fig. 16. It is worth noting that the crack trajectory prediction by the incremental method does not depend on the magnitude of the applied load. According to Eq. 14, it depends solely on the mode mixity ratio $K_\mathrm{II}/K_\mathrm{I}$. Hence, any arbitrary load could be applied to the Key-BD specimens for such a prediction.

Table 4 The values of $K_\mathrm{I}$ and $K_\mathrm{II}$ together with the values of the next crack orientation $(\theta _{0})$ for the first nine increments for the Key-BD specimen with $\hbox {RNL} = 0.5$, $\rho = 2\,\hbox {mm}, \beta = 30^{\circ }$, and $P = 2299\,\hbox {N}$

Fig. 16

The scheme of the first 9 increments of the crack growth in a Key-BD specimen obtained from the incremental method

5 Results and discussion

Three subsections of the theoretical predictions, including the fracture load, crack trajectory and fracture initiation angle of the tested Key-BD specimens are presented in this section.

5.1 Fracture load prediction

As mentioned previously, the experimental results presented in Sect. 2 have been recently predicted in [42] by means of the two stress-based brittle fracture criteria, namely the Key-MTS and Key-MS criteria, and also re-predicted in [41] by means of the two energy-based criteria, namely the averaged strain energy density (ASED) and averaged strain energy density based on the equivalent factor concept (ASED-EFC) criteria. Hence, six distinct predictions of the fracture load have been performed and reported in [41, 42] for the Key-BD GPPS specimens, four of which for the two stress-based criteria and the two other ones for the two energy-based criteria. In this subsection, a discussion is made on the differences between these six fracture load results and particularly on the new one obtained from XFEM-CZM approach. In other words, the results of XFEM-CZM approach in predicting the experimentally obtained fracture loads of the Key-BD GPPS specimens under mixed mode I/II loading with negative mode I contributions are compared with the other six results mentioned above and reported in [41, 42]. Thus, the variations of the fracture load of the Key-BD GPPS specimens versus the loading angle $\beta$ are plotted in Figs. 17 and 18 for the various notch tip radii and RNL ratios of 0.3 and 0.5, respectively. As seen in these figures, the experimental results are denoted by distinct circular symbols and the seven theoretical predictions by variously dashed and continuous solid lines.

Fig. 17

Variations of the theoretical and experimental fracture loads of the Key-BD GPPS specimens versus the loading angle $\beta$ for the $\hbox {RNL} = 0.3$ and various notch tip radii

Fig. 18

Variations of the theoretical and experimental fracture loads of the Key-BD GPPS specimens versus the loading angle $\beta$ for the $\hbox {RNL} = 0.5$ and various notch tip radii

Table 5 Percent discrepancies between the experimental results of the fracture load and the theoretical results

As is obvious in Figs. 17 and 18, the trends of both the experimental results and theoretical predictions indicate that the variations of the fracture load versus the loading angle $\beta$ first decrease and then increase as $\beta$ enhances from $30^{\circ }$ to $70^{\circ }$ except for the two cases of $\hbox {RNL} = 0.5$, $\rho = 1\,\hbox {mm}$ and $\hbox {RNL} = 0.5$, $\rho = 2\,\hbox {mm}$. More details about why these trends are seen in Figs. 17 and 18 have been presented in [42]. Briefly speaking, Torabi et al. [42] had conducted some FE analyses, for instance for the Key-BD specimen of $\hbox {RNL} = 0.3$, $\rho = 2\,\hbox {mm}$, by applying the constant external load of $P = 1000\,\hbox {N}$ at various loading angles $\beta$ and plotted the variations of the maximum tangential stress versus the loading angle. The plot showed that the value of the maximum tangential stress first increases and then decreases, meaning that the fracture load first decreases and then increases. This result of the FE analyses was in a good consistency with the trend of the experimental results. Therefore, it is expected that similar justifications can also be provided for the trends of the other tested Key-BD specimens.

Table 5 presents the discrepancies between the experimental results of the fracture load and the six theoretical predictions reported in [41, 42] plus the other ones obtained from XFEM-CZM approach. As seen in Table 5, the average discrepancies for the ASED and ASED-EFC criteria are almost identical and equal to 8.3 and 8.8%, respectively, while for the Key-MTS and Key-MS criteria with the theoretical critical distances, they are obtained to be equal to 12.7 and 10.7%, respectively. Also, the discrepancies of the Key-MTS and Key-MS criteria based on the experimentally obtained critical distances are resulted to be equal to 8.3 and 7.7%, respectively. A particular attention to Table 5 indicates that the average discrepancy for the newly proposed XFEM-CZM approach is 8.8%.

According to Table 5, the best criterion from the viewpoint of accuracy is the Key-MS criterion with the experimentally obtained critical distance. Although such a criterion is shown to be the most accurate fracture model, it is very important to note that Key-MS criterion has relatively heavy numerical calculations and additionally requires an experimentally obtained input for its prediction which can apparently be realized as a weak point. Meanwhile, such a weak point exists for the Key-MTS criterion with the experimentally obtained critical distance. While the accuracies of ASED and ASED-EFC criteria are very good and close to those of Key-MTS and Key-MS criteria with experimentally obtained critical distances, they have generally two advantages compared with the stress-based criteria: (i) they have better accuracies than the Key-MTS and Key-MS criteria with theoretical critical distances, and (ii) they have less calculations compared with the two stress-based criteria with the experimentally obtained critical distances. However, the authors believe that XFEM-CZM model is an excellent approach due to its high accuracy plus low calculations. Trivially, each of the mentioned models has some advantages and disadvantages. Therefore, they have been frequently applied to various experimental results (in some works to the same experimental results) in order to evaluate them and realize their strong and weak points. Consequently, existence of a suitable model for fracture predictions does not necessarily mean that other models should not be developed and evaluated.

To propose the pluralization of above-discussed points, it can be stated that in cases that designers are needed by simple calculations and additionally satisfied by relatively lower accuracies, the Key-MTS and Key-MS criteria regarding the theoretical critical distances may be preferred, while in the cases that designers need just high accuracies, the Key-MTS and Key-MS criteria with the experimentally obtained critical distances can be utilized. Additionally, it is very important to note that the ASED and ASED-EFC criteria are more appropriate for designers who need relatively simple calculations with acceptable accuracies. Among the mentioned criteria, XFEM-CZM approach is superior because it has simultaneously high accuracy and low calculations. The main strong point of XFEM-CZM approach is its ability in estimating rapidly and conveniently the crack trajectory of the brittle components containing key-hole notches, e.g., the Key-BD GPPS specimens studied in the present research. In the next subsection, the crack trajectory for some of the tested Key-BD GPPS specimens is investigated experimentally and theoretically by means of the XFEM-CZM approach and the incremental method based on the MTS criterion.

Fig. 19

Combined compressive shear crack trajectories of Key-BD specimens for the XFEM-CZM approach and incremental method together with the experimental results

Table 6 The theoretical and experimental fracture initiation angles of Key-BD specimens $(\theta _{0})$ together with the discrepancies for the Key-MTS criterion and XFEM-CZM approach

5.2 Crack trajectory prediction

Figure 19 illustrates the predicted results of the crack trajectory obtained by using the two theoretical models previously proposed in Sect. 3, namely XFEM based on the linear cohesive zone model (XFEM-CZM) and the incremental method based on MTS criterion, for some arbitrarily selected Key-BD GPPS specimens together with the experimental results. As seen in Fig. 19, both models are in good agreements with the experimental results under various compressive shear loading conditions. Although the incremental method has high accuracy and works well in predicting the crack trajectory for the tested specimens, it needs several steps and many iterations in mesh processing for the predictions that make this method rather time-consuming compared with XFEM. Therefore, XFEM-CZM model is the best approach to predict the crack trajectory of the notched brittle components from the viewpoint of real engineering applications. Also, it can be generally mentioned that both FEM-MTS (i.e., incremental method based on MTS criterion) and XFEM-CZM approaches could predict the crack trajectory of the tested specimens well with a bit less or more accuracy. However, FEM-MTS approach has much more computational time than XFEM-CZM approach. In other words, by utilizing XFEM-CZM approach, one can simply and accurately predict the crack trajectory of each notched specimen with reasonable computational time, while FEM-MTS approach with much computational time may not be preferred in real engineering applications. A computer with 1.6 GHz 4 CPUs processor, hard drive capacity of 1 TB and 4.0 GB RAM is provided to run the simulation of the notched specimens. For example, if 30 steps are considered in the incremental method based on the MTS criterion, the computational time is obtained equal to about 100 minutes, while the computational time of XFEM-CZM approach in our system is about 10 minutes. In fact, unlike XFEM-CZM approach in which the computer can perform all steps of numerical analysis in predicting the crack trajectory without any intervention of operator, for applying the incremental method to our numerical prediction, the operator should perform all steps of the numerical FE analysis. Therefore, the FEM-MTS approach is very time-consuming.

A question may be raised that if brittle fracture initiates always from the tensile side of the notch border regardless of existing negative or positive mode I contributions. What is the motivation behind studying especially crack growth in the Key-BD specimen under mixed mode I/II loading in the domain of negative mode I contributions? A detailed answer to this important question is provided in the next paragraph.

There are many cases in real engineering applications for which notched structural components sustain compressive stresses at some of the points on the notch border, including the notch tip. Although tensile mode I failure in notched members is much more serious than compressive one, the failure under compression loading should also be studied to assure the safety of the whole structure. Moreover, the key-hole notch is a kind of notch with widespread engineering applications; particularly, it is created where U-notched components and structures encounter damage at the notch border for which the damage is removed by the hole-drilling method and a key-hole notch is formed as a result of the damage removal. Hence, the authors studied the fracture load and crack trajectories of the tested key-hole notched specimens subjected to mixed mode I/II loading with negative mode I contributions by means of the two fracture models, namely the XFEM in combination with the cohesive zone model and the incremental method based on Key-MTS criterion. Finally, it is found that XFEM-CZM model is a suitable approach for predicting crack trajectory of the tested notched specimens because of its low computational time.

In the next subsection, the fracture initiation angles for all of the tested Key-BD GPPS specimens are theoretically predicted by means of XFEM-CZM approach.

5.3 Fracture initiation angle prediction

The fracture initiation angles for all of the tested Key-BD specimens are predicted herein by using XFEM-CZM approach and the corresponding values are compared with the predicted values obtained from the Key-MTS criterion [42] and with the average experimental values measured from the fracture tests. These results together with the discrepancies between the experimental and theoretical results are summarized in Table 6.

The capability of the Key-MTS criterion in predicting the fracture initiation angle of Key-BD GPPS specimens under combined compressive shear loading conditions has been recently shown by Torabi et al. [42], and in this subsection, the capability of XFEM-CZM approach is evaluated. As can be seen in Table 6, a good agreement exists between the experimental results and theoretical predictions of the XFEM-CZM approach. An average discrepancy of about 8% for the whole Key-BD GPPS specimens indicates that XFEM-CZM approach is successful in predicting the fracture initiation angle of the key-hole notches under mixed mode I/II loading with negative mode I contributions. As is obvious, both of the mentioned models (i.e., XFEM-CZM approach and the Key-MTS criterion) are able to predict very well the fracture initiation angles of the Key-BD specimens. At the end, it is worth noting that XFEM-CZM approach can be considered for designing key-hole notched members against brittle fracture and also maintenance and repair purposes in which the fracture initiation angle and crack trajectory are very important parameters. By using XFEM-CZM approach, one can predict the fracture load, fracture initiation angle and crack trajectory simultaneously, making the approach more interesting and convenient for designers and engineers, since they would not need more than one model for such predictions.

6 Conclusions

In the present research, mixed mode I/II brittle fracture with negative mode I contributions was investigated in key-hole notched specimens. The experimental results were taken from the recent literature on the Key-BD specimens made of GPPS. The experimentally obtained fracture loads and fracture initiation angles were predicted by means of the extended finite element method (XFEM) combined with the cohesive zone model (CZM). Moreover, the crack trajectory of the Key-BD specimens was predicted by means of the two theoretical models, namely the XFEM-CZM approach and the incremental method based on the MTS criterion. Although the incremental method was revealed to be successful in predicting the crack trajectory for the Key-BD specimens, it needs several iterations with several re-meshing stages to reach the full prediction. Therefore, in cases that designers are urged to perform simple and rapid calculations with good accuracy, XFEM approach may be preferred. Finally, it can be stated that the predictions of the XFEM-CZM approach are very nice for the fracture load, crack trajectory and fracture initiation angle because of its high accuracy and low amount of numerical calculations.