1 Introduction, equations of motion

In the restricted three-body problem (R3BP), the equations of motion describe the dynamics of an infinitesimal mass m under the action of gravitational forces effected by two celestial bodies of giant masses \(M_\mathrm{Sun}\) and \(m_\mathrm{planet}\) (\(m_\mathrm{planet} < M_\mathrm{Sun}\)), which are rotating around their common centre of mass on Keplerian trajectories. In the current research, we will assume that the small mass m is supposed to be moving (as first approximation) inside of restricted region of space near the Sun of mass \(M_\mathrm{Sun}\) far from so-called Hill sphere [1] of planet \(m_\mathrm{planet}\) with radius [2]:

$$\begin{aligned} r_H \,\,\,\cong \,\, a_p \cdot (1-e^{2})\cdot \left( \frac{m_{planet}}{3(M_{Sun} + m_{planet})}\right) ^\frac{1}{3} \end{aligned}$$

where \(a_p\) is semimajor axis of the planet’s orbit, e is the eccentricity of its orbit.

It is worth noting that there are a large number of previous and recent works concerning analytical development with respect to the R3BP equations which should be mentioned accordingly [3,4,5].

We should especially emphasize the theory of orbits, which was developed in profound work [5] by V. Szebehely for the case of the circular restricted problem of three bodies (CR3BP) (primaries \(M_\mathrm{Sun}\) and \(m_\mathrm{planet}\) are rotating around their common centre of mass on circular orbits) as well as the case of the elliptic restricted problem of three bodies (ER3BP), where the primaries \(M_\mathrm{Sun}\) and \(m_\mathrm{planet}\) are rotating around their common centre of mass on elliptic orbits. Special case of ER3BP (families of periodic orbits of the Sitnikov problem) was investigated in [6].

As for the complete introduction to the stability of problem under the current consideration, we recommend seminal works [7, 8], where a significant historical retrospection has been made as well as all the difficulties regarding stability of motion are considered insofar. Energy analysis in the elliptic restricted three-body problem was made in [9].

As for the purpose of the current research, we can formulate it as follows: the main aim is to point out a clear formulation of solving procedure (along with partial cases of semi-analytical or numerical solutions) to the system of equations under consideration. Namely, each exact or even semi-analytical solution can clarify the structure, intrinsic code and topology of the variety of possible solutions (from mathematical point of view); here, semi-analytical solution should be treated not only as analytical formulae in quadratures, but also as numerical algorithm for a system of ordinary differential equations with well-known code for analytical or numerical resolving to be presented in their final form.

Unlike the CR3BP, the position of the primaries is not fixed in the rotating frame as they move along elliptical orbits: their relative distance \(\rho \) is not constant in time [10]

$$\begin{aligned} \rho = \frac{a_p}{1 + e \cdot \hbox {cos} f} \end{aligned}$$

where e is the eccentricity of the two-body orbit of the primaries, f is the true anomaly (the unit of distances is chosen so that \(a_p \quad = 1\)).

According to [10, 11], in the ER3BP equations of motion of the infinitesimal mass m can be represented in the synodic co-rotating frame of a Cartesian coordinate system \({\vec {r}}=\{ x, y, z\}\) in non-dimensional form (at given initial conditions):

$$\begin{aligned} \ddot{x}- 2{\dot{y}}= & {} \frac{\partial \Omega }{\partial x}\nonumber \\ \ddot{y}+ 2{\dot{x}}= & {} \frac{\partial \Omega }{\partial y}\nonumber \\ \ddot{z}= & {} \frac{\partial \Omega }{\partial z} \end{aligned}$$
(1)

where dot indicates (d/df) in (1), \(\Omega \) is the scalar function

$$\begin{aligned} \Omega \;\;=\;\;\frac{1}{1+e\cdot \cos f}\left[ {\frac{1}{2}\,\left( {x^{2}+\,y^{2}-z^{2}\cdot e\cdot \cos f} \right) \;\,+\;\frac{(1-\mu )}{r_{1} }\;\,+\,\;\frac{\mu }{r_{2} }} \right] , \end{aligned}$$
(2)

and [10, 11]

$$\begin{aligned} \begin{array}{l} r_{1}^{2} \;=\;\;(x-\mu )^{2}\;+\;y^{2}\;+\;z^{2}\;, \\ \\ r_{2}^{2} \;=\;\;(x-\mu +1)^{2}\;+\;y^{2}\;+\;z^{2}\;, \\ \end{array} \end{aligned}$$
(3)

where \(r_i\) (\(i =\textit{1, 2}\)) are the distances of the infinitesimal mass m from the primaries \(M_\mathrm{Sun}\) and \(m_\mathrm{planet}\), respectively [11].

Now, the unit of mass is chosen in (1) so that the sum of the primary masses is equal to 1. We suppose that \(M_\mathrm{Sun} \cong {1 - }\mu \) and \(m_\mathrm{planet} = \mu \), where \(\mu \) is the ratio of the mass of the smaller primary to the total mass of the primaries and \(0 < \mu \quad \le 1/2\). The unit of time is chosen so that the gravitational constant is equal to 1 in (2).

We neglect the effect of variable masses of the primaries [12] as well as the effect of their oblateness as was considered earlier in [13]. As for the domain where the aforesaid infinitesimal mass m is supposed to be moving, let us consider the Cauchy problem in the whole space. Besides, we should note that the second terms in the left parts of Eq. (1) are associated with the components of the Coriolis acceleration.

Finally, let us additionally note that the spatial ER3BP when \(e > 0\) and \(\mu > 0\) is not conservative, and no integrals of motion are known [11].

By appropriately transforming the right parts with regard to partial derivatives with respect to the proper coordinates \(\{ x, y, z\}\) , system (1) can be represented as

$$\begin{aligned} \begin{array}{l} {\ddot{x}}\;\;-\;\;2\,{{\dot{y}}}\,\;=\frac{1}{1+e\cdot \cos f}\cdot \left[ {x\;\,-\;\frac{1}{2}\frac{2(1-\upmu )(x-\upmu )}{\left( {(x-\upmu )^{2}\;+\;y^{2}\;+\;z^{2}} \right) ^{\frac{3}{2}}}\,\;-\;\frac{1}{2}\frac{2\upmu (x-\upmu +1)}{\left( {(x-\upmu +1)^{2}\;+\;y^{2}\;+\;z^{2}} \right) ^{\,\frac{3}{2}}}} \right] \,\;, \\ \\ {\ddot{y}}\;\;+\;\;2\,{{\dot{x}}}\,\;=\,\;\;\frac{1}{1+e\cdot \cos f}\cdot \left[ {y\;\,-\;\frac{1}{2}\frac{2(1-\upmu )y}{\left( {(x-\upmu )^{2}\;+\;y^{2}\;+\;z^{2}} \right) ^{\frac{3}{2}}}\,\;-\;\frac{1}{2}\frac{2\upmu y}{\left( {(x-\upmu +1)^{2}\;+\;y^{2}\;+\;z^{2}} \right) ^{\,\frac{3}{2}}}} \right] \,\;, \\ \\ {\ddot{z}}\;\;\;=\,\;\;\frac{1}{1+e\cdot \cos f}\cdot \left[ {-z\cdot e\cdot \cos f\;\,-\;\frac{1}{2}\frac{2(1-\upmu )z}{\left( {(x-\upmu )^{2}\;+\;y^{2}\;+\;z^{2}} \right) ^{\frac{3}{2}}}\,\;-\;\frac{1}{2}\frac{2\upmu z}{\left( {(x-\upmu +1)^{2}\;+\;y^{2}\;+\;z^{2}} \right) ^{\,\frac{3}{2}}}} \right] \;\;. \\ \end{array} \end{aligned}$$
(4)

2 Approximated solutions of Eqs. (1)-(3) for the class of trapped   motions

As for the mathematical formulation of the problem under consideration, we restrict ourselves by mentioning works [10, 11] at referring to formulae (1)–(3) above, where such formulation has been given in a proper way.

Let us assume that coordinates \({\vec {r}}= \{ x, y, z\}\) of solutions of system (1) belong to the class of trapped motions of the infinitesimal mass m (in the vicinity of the common centre of masses \(M_\mathrm{Sun}\) and \(m_\mathrm{planet}\)), with additional natural restriction (*) given at the Discussion section:

$$\begin{aligned} \left| {\,{\vec {r}}\,} \right| \;\,<<\,\;a_{p} \quad \Leftrightarrow \quad \{x,\;y,\;z\}\;\rightarrow \;0 \end{aligned}$$
(5)

Thus, if we take into consideration the additional restriction (5) with respect to the components of solution in Eqs. (1)–(3), the aforesaid assumption should simplify Eq. (4) by the series of Taylor expansions (first, we exclude to zero all the terms with \(z^2\) in the right parts of equations (6) below):

$$\begin{aligned} \begin{array}{l} {\ddot{x}}\,-\,2\,{{\dot{y}}}\,\;=\frac{1}{1+e\cdot \cos f}\cdot \left[ {x\;\,-\;\frac{(1-\upmu )(x-\upmu )}{\left( {(x-\upmu )^{2}\;+\;y^{2}} \right) ^{\frac{3}{2}}}\,\;-\;\frac{\upmu (x-\upmu +1)}{\left( {(x-\upmu +1)^{2}\;+\;y^{2}} \right) ^{\,\frac{3}{2}}}} \right] \,\;, \\ \\ {\ddot{y}}\,+\,2\,{{\dot{x}}}\,\;=\,\;\;\frac{y}{1+e\cdot \cos f}\cdot \left[ {1\,-\,\frac{(1-\upmu )}{\left( {(x-\upmu )^{2}\;+\;y^{2}} \right) ^{\frac{3}{2}}}\,\;-\;\frac{\upmu }{\left( {(x-\upmu +1)^{2}\;+\;y^{2}} \right) ^{\,\frac{3}{2}}}} \right] \\ \\ {\ddot{z}}\,+\,\frac{z}{1+e\cdot \cos f}\cdot \left[ {e\cdot \cos f\;\,+\;\frac{(1-\upmu )}{\left( {(x-\upmu )^{2}\;+\;y^{2}} \right) ^{\frac{3}{2}}}\,\;+\;\frac{\upmu }{\left( {(x-\upmu +1)^{2}\;+\;y^{2}} \right) ^{\,\frac{3}{2}}}} \right] \,=\,0, \\ \end{array} \end{aligned}$$
(6)

where the third equation (for coordinate z) could be easily solved if expressions for coordinates \(\{ x, y\}\) are already obtained. So, we should first solve the following sub-system, which consists of first and second equations of system (6):

$$\begin{aligned} \begin{array}{l} {\ddot{x}}\;\;-\;\;2\,{{\dot{y}}}\,\;=\frac{1}{1+e\cdot \cos f}\cdot \left[ {x\;\,-\;\frac{(1-\mu )}{(x-\mu )^{2}}\,\;-\;\frac{\mu }{(x-\mu +1)^{2}}} \right] \,\;, \\ \\ {\ddot{y}}\;\;+\;\;2\,{{\dot{x}}}\,\;=\,\;\;\frac{y}{1+e\cdot \cos f}\cdot \left[ {1\;\,-\;\frac{(1-\mu )}{(x-\mu )^{3}}\,\;-\;\frac{\mu }{(x-\mu +1)^{3}}} \right] \,\;,\, \\ \end{array} \end{aligned}$$
(7)

(second, we exclude to zero all the terms with \(y^2\) in the right parts of Eq. (7)).

For further solving the system (7), we should transform it accordingly; first let us differentiate both parts of the first equation of system (7) with respect to the true anomaly f, this would let us linearly combine first and second equations of system (7) properly:

$$\begin{aligned} \left\{ {\begin{array}{l} \;\;\dddot{x}\;\;-\;\;2\,{\ddot{y}}\,\;=\frac{d}{d\,f}\left( {\frac{1}{1+e\cdot \cos f}\cdot \left[ {x\;\,-\;\frac{(1-\mu )}{(x-\mu )^{2}}\,\;-\;\frac{\mu }{(x-\mu +1)^{2}}} \right] } \right) \,\;, \\ \\ \;\;2{\ddot{y}}\;\;+\;\;4\,{{\dot{x}}}\,\;=\,\;\frac{2y}{1+e\cdot \cos f}\cdot \left[ {1\;\,-\;\frac{(1-\mu )}{(x-\mu )^{3}}\,\;-\;\frac{\mu }{(x-\mu +1)^{3}}} \right] \,\;,\, \\ \end{array}} \right. \quad \;\quad \Rightarrow \end{aligned}$$
(8)
$$\begin{aligned} \Rightarrow \quad \dddot{x}\;\;+\;\;4\,{{\dot{x}}}\,\;=\;\,\frac{d}{d\,f}\left( {\frac{1}{1+e\cdot \cos f}\cdot \left[ {x\;\,-\;\frac{(1-\mu )}{(x-\mu )^{2}}\,\;-\;\frac{\mu }{(x-\mu +1)^{2}}} \right] } \right) \;\;+ \nonumber \\ \;\;\quad \;\quad \quad \quad \quad \quad \quad \quad +\;\;\frac{2y}{1+e\cdot \cos f}\cdot \left[ {1\;\,-\;\frac{(1-\mu )}{(x-\mu )^{3}}\,\;-\;\frac{\mu }{(x-\mu +1)^{3}}} \right] \;,\quad \quad \quad \Rightarrow \nonumber \\ y\;\;=\;\;\frac{(1+e\cdot \cos f)}{2}\,\cdot \,\left( {\frac{\dddot{x}\;+\;4\,{{\dot{x}}}\;-\;\frac{d}{d\,f}\left( {\frac{1}{1+e\cdot \cos f}\cdot \left[ {x\;\,-\;\frac{(1-\mu )}{(x-\mu )^{2}}\,\;-\;\frac{\mu }{(x-\mu +1)^{2}}} \right] } \right) }{1\;\,-\;\frac{(1-\mu )}{(x-\mu )^{3}}\,\;-\;\frac{\mu }{(x-\mu +1)^{3}}}} \right) \end{aligned}$$
(9)

Using expression (9) for y, we could substitute it into the appropriate expression in the first equation of system (7); thus, we should obtain the nonlinear ordinary differential equation of the fourth order which could obviously be solved by numerical methods only (in the general case).

But taking into account the additional simplifying assumption (5) (\(y \quad \rightarrow 0\)) with regard to the expression (9), we should obtain from the first of equations (8) as below (\(x_0 = \textit{const}\)):

$$\begin{aligned} \begin{array}{l} \;\left( {\frac{d}{d\,f}\left( {\frac{1}{1+e\cdot \cos f}\cdot \left[ {x\;\,-\;\frac{(1-\mu )}{(x-\mu )^{2}}\,\;-\;\frac{\mu }{(x-\mu +1)^{2}}} \right] } \right) \;\,-\,\;(\,\dddot{x}\;+\;4\,{{\dot{x}}})} \right) \,\,\;\rightarrow \;\;0\quad \Rightarrow \\ \\ (8):\quad \Rightarrow \quad \dddot{x}\;-\;2\,{\ddot{y}}\,\cong \dddot{x}\;+\;4\,{{\dot{x}}}\,\;,\quad \Rightarrow \quad 2\,{\ddot{y}}\,\cong \;-\;4\,{{\dot{x}}}\,\;,\quad \Rightarrow \quad \,{{\dot{y}}}\,\cong \;-\;2\,(x-x_{0}) \end{array} \end{aligned}$$
(10)

So, we obtain from the first of equations (7):

$$\begin{aligned} {\ddot{x}}\;\;+\;\;4\,(x-x_{0} )\,=\frac{1}{1+e\cdot \cos f}\cdot \left[ {x\;\,-\;\frac{(1-\mu )}{(x-\mu )^{2}}\,\;-\;\frac{\mu }{(x-\mu +1)^{2}}} \right] \end{aligned}$$
(11)

- i.e. the nonlinear ordinary differential equation of the second order which could also be solved by numerical methods only.

Nevertheless, let us try to simplify Eq. (11) (we should exclude at last to zero all the terms with \(x^2\) in the right part of equation (11), \(\mu<< 1\)):

$$\begin{aligned} \begin{array}{l} \quad \;\quad {\ddot{x}}\;\;+\;\;4\,(x-x_{0} )\,=\frac{1}{1+e\cdot \cos f}\cdot \left[ {x\;\,-\;\frac{(1-\mu )}{\mu ^{2}-2x\mu }\,\;-\;\frac{\mu }{(1-\mu )^{2}+2x(1-\mu )}} \right] \,\quad \Rightarrow \\ \\ \quad {\ddot{x}}\;\;+\;\;4\,(x-x_{0} )\,=\frac{1}{1+e\cdot \cos f}\cdot \left[ {x\;\,-\;\frac{(1-\mu )}{\mu ^{2}}(1+2\frac{x}{\mu })\,\;-\;\frac{\mu }{(1-\mu )^{2}}(1-2\frac{x}{(1-\mu )})} \right] \quad \Rightarrow \\ \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad {\ddot{x}}\;\;+\;\;A\,(f)\,\cdot \,x\;+\;\,B(f)=0\;, \\ A\,(f)=\left[ {4\,-\frac{1}{1+e\cdot \cos f}\cdot \left( {1+2\frac{(4\mu ^{3}-6\mu ^{2}+4\mu -1)}{(1-\mu )^{3}\mu ^{3}}} \right) } \right] \;,\quad B(f)=\left( {\frac{1}{1+e\cdot \cos f}\cdot \frac{(1-3\mu +3\mu ^{2})}{\mu ^{2}(1-\mu )^{2}}\;-\,4x_{0} } \right) \\ \end{array} \end{aligned}$$
(12)

Equation (12) could be considered (as a first approximation) as the equation of forced oscillations (e.g. example 2.36 in [14]) if we consider \(\{ A, B\} \cong \) const or if we additionally assume

$$\begin{aligned} \left( {1+2\frac{(4\mu ^{3}-6\mu ^{2}+4\mu -1)}{(1-\mu )^{3}\mu ^{3}}} \right) \;\,\cong \;\,0 \end{aligned}$$
(13)

Meanwhile, by means of numerical analysis for the solution of 6-th order’s algebraic equation (13), we obtain its solution is approximately to be \(\mu \quad = 0.492195111 < 1/2\).

3 Final presentation of the solution

Let us present the solution \({\vec {r}}=\{ x, y, z\}\) (\(\{ x, y, z\} \rightarrow 0\)) for the trapped motion (5) of the infinitesimal mass m (in the vicinity of the common centre of masses \(M_\mathrm{Sun}\) and \(m_\mathrm{planet}\)) in its final form:

  • equation (12) for coordinate x

    $$\begin{aligned} \begin{array}{l} {\ddot{x}}\;\;+\;\;A\,(f)\,\cdot \,x\;+\;\,B(f)=0\;,\quad \;\\ \\ A\,(f)=\left[ {4\,-\frac{1}{1+e\cdot \cos f}\cdot \left( {1+2\frac{(4\mu ^{3}-6\mu ^{2}+4\mu -1)}{(1-\mu )^{3}\mu ^{3}}} \right) } \right] \;,\quad B(f)=\left( {\frac{1}{1+e\cdot \cos f}\cdot \frac{(1-3\mu +3\mu ^{2})}{\mu ^{2}(1-\mu )^{2}}\;-\,4x_{0} } \right) \;, \\ \end{array} \end{aligned}$$

could be considered (as a first approximation) as the equation of forced oscillations if we consider \(\{ A, B\} \cong \) const during a long-time period of quasi-oscillations for the trapped motion of the infinitesimal mass m; e.g. by means of numerical analysis for the solution of 6-th order’s algebraic equation (13) (\(\Rightarrow \quad A \quad =\) const), we obtain its solution is approximately to be \(\mu = 0.492195111 < 1/2\);

  • from Eq. (10) we obtain for coordinate y

    $$\begin{aligned} y\,\;\cong \;\;y_{0} -\;2\,\left( {\int \limits _0^f {x(f)\,df} -x_{0} \cdot f} \right) \end{aligned}$$
    (14)

  • from the third of Eq. (6) we obtain for coordinate z (\(\{ x, y, z\} \rightarrow 0\))

    $$\begin{aligned} \begin{array}{l} {\ddot{z}}\;\;\;+\,\;\;\frac{z}{1+e\cdot \cos f}\cdot \left[ {e\cdot \cos f\;\,-\;\frac{(1-\mu )}{\mu ^{3}\left( {1-\frac{x}{\mu }} \right) ^{3}}\,\;+\;\frac{\mu }{(1-\mu )^{3}\left( {1+\frac{x}{(1-\mu )}} \right) ^{3}}} \right] \;\;=\;\,0\;,\quad \quad \Rightarrow \\ \\ {\ddot{z}}\;\;\;+\,\;\;z\cdot \,\left( {\frac{e\cdot \cos f-\;3x\,\cdot \,\left( {\frac{(1-\mu )\,}{\mu ^{4}}\,\;+\;\frac{\mu \,}{(1-\mu )^{4}}} \right) \;\,-\;\frac{(1-\mu )}{\mu ^{3}}\;+\;\frac{\mu }{(1-\mu )^{3}}}{1+e\cdot \cos f}} \right) \;\;=\;\,0\;, \\ \end{array} \end{aligned}$$
    (15)

where Eq. (15) above can be reduced by change of variable \(({z}^\prime /z)\) to the classical Riccati ODE. It describes the evolution of coordinate z in its dependence on the coordinate x(f) in regard to the true anomaly f; such a Riccati ODE has no analytical solution in the general case [15,16,17,18,19].

4 Discussion

As we can see from the derivation above, equations of motion for the trapped motion \({\vec {r}}=\{ x, y, z\}\) (\(\{ x, y, z\} \rightarrow 0\)) of the infinitesimal mass m in the vicinity of the common centre of mass of \(M_\textit{Sun}\) and \(m_\textit{planet}\) are very hard to be solved analytically.

Nevertheless, at the first step we have succeeded in obtaining the Eq. (12) for coordinate x, which could be considered (as a first approximation) as the equation of forced oscillations during a long-time period of quasi-oscillations of the infinitesimal mass m in the vicinity of common centre of mass of \(M_\textit{Sun}\) and \(m_\textit{ planet}\). Namely, from the approximate solving the algebraic equation (13), we obtain the aforementioned assumption (regarding the considering (12) as the equation of forced oscillations) should be valid if only we choose \(\mu \quad = 0.492195111 < 1/2\).

Furthermore, at the second step we have obtained equation (14), which describes the evolution of coordinate y in its dependence on the coordinate x(f) and the true anomaly f. It is worth noting that condition \(y \quad \rightarrow \) 0 would be valid if we chose constants of integration \(\{x_0, y_0\} = 0\) in (14). In other cases, the infinitesimal mass m would escape from the vicinity of the common centre of mass of \(M_\mathrm{Sun}\) and \(m_\mathrm{planet}\) as soon as the true anomaly f increases.

Finally, we have obtained Eq. (15), which describes the evolution of coordinate z in its dependence on the coordinate x(f) and the true anomaly f.

Thus, we have succeeded in presenting by the series of Taylor expansions equations (4) of the problem under consideration in analytical form (with new analytical findings in a form of invariants as a result of integration) where a minimum numerical calculations should be required; then, we obtain final solution by means of the numerical calculations.

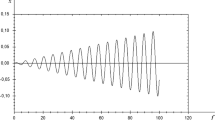
We provide below the results of numerical calculations (Fig. 1) for the proper approximated solution of equation (11) for the motion near the barycenter in “Sun-Mercury-satellite” system. We should note that we have used for calculating the data the Runge–Kutta fourth-order method with step 0.001 starting from initial values. Let us choose for numerical algorithm of modelling the motion near the barycenter in triple system “Sun-Mercury-satellite” system as follows:

\(e = 0.205, \mu = 0.165*10^{(-6)}.\)

As for the initial data, we have chosen as follows: 1) \(x_{\,0} \quad = -\, 0.1, ({{\dot{x}}})_{\,0} \quad = - 0.2\).

Let us present the results of numerical calculations for Eq. (11) in Table 1 below (a key data points from the main flow of data points have been mentioned in Table 1).

Table 1 Results of numerical calculations for Eq. (11) (for the motion near the barycenter in “Sun-Mercury-satellite” system)
Full size table

The results of numerical calculations we schematically imagine at Fig. 1.

Fig. 1
figure 1

Result of numerical calculations of the coordinate x (abscissa axis corresponds to values of the true anomaly f)

Full size image

Meanwhile, results of numerical calculations for the coordinate x in this case (Fig. 1) mean that test particle, starting its motion near the barycenter of the system “Sun-Mercury”, reveals then unpredictable and unstable dynamics: it intersects the orbit of Mercury, but not the orbit of Venus during the further oscillations. Indeed, Mercury’s orbit is inclined, or tilted, circa 7 degrees from the ecliptic of Earth’s orbit, whereas Venus’ inclination is about of 3.4 degrees (with respect to Earth’s orbit). So, test particle, which is moving in the plane of Mercury rotation on its orbit, will never intersect orbit of Venus.

Ending the discussion, let us note also that natural restriction should be valid for the trapped motion \({\vec {r}}=\{ x, y, z\}\) of the infinitesimal mass m in the vicinity of the common centre of mass of \(M_\mathrm{Sun}\) and \(m_\mathrm{planet}\):

$$\begin{aligned} \left| {\,{\vec {r}}\,} \right| \;\,>\,\;4R_{\,Sun}\quad \quad (*) \end{aligned}$$

where \(R_{\,Sun} \) is the radius of Sun with mass \(M_\mathrm{Sun}\) (the aforementioned restriction takes into account the Roche limit for fluid satellite for the reason at distance of 6-8 \(R_{\,Sun} \) even the solid satellite appears to be transformed to the fluid state during satellite’s fly-by through the hot atmosphere and corona of Sun).

Meanwhile, centre of Sun is known to be moving near the barycenter along the quasi-periodic trajectory (less than 2.19\(R_{\,Sun} \) from barycenter [20], it means that barycenter is distant from surface of Sun sometimes not less than \(R_{\,Sun} \) where \(R_{\,Sun} \sim 696\cdot 10^6\hbox { m}\)). Taking into account the restriction (*) above, it gives the maximal distance of safe approach to the surface of Sun during satellite’s fly-by at the worst scenario (in case of alignment of all the radius-vectors “barycenter vs. Sun \(+\) satellite”) is circa (\(1.19R_{\,Sun} + 2R_{\,Sun} \quad + 4R_{\,Sun} ) \quad \cong 7.19R_{\,Sun} \). So, the minimal safe distance for satellite closest approach should be not less than 8\(R_{\,Sun} \) (here electromagnetic effects have not yet been taken into consideration for this estimation).

As for the data of closest approaches of artificial satellite to the Sun during, e.g. “Parker Solar Probe”-mission in the years 2018-2025, see [21] (the closest approach during satellite’s fly-by near the Sun should be 10\(R_{\,Sun} \) from the centre of Sun). So, motion near the barycenter in “Sun-planet-satellite” system could be of practical interest (in the sense of preventing collision trajectories with the surface of Sun in future missions), indeed.

5 Conclusion

In this paper, we present a new approach for solving equations of motion for the trapped motion \({\vec {r}}=\{ x, y, z\}\) of an infinitesimal mass m in case of the elliptic restricted problem of three bodies (ER3BP) (primaries \(M_\mathrm{Sun}\) and \(m_\mathrm{planet}\) are rotating around their common centre of mass on elliptic orbits): a new type of solution is implemented here for solving equations of motion of the infinitesimal mass m in the vicinity (\(\{ x, y, z\} \rightarrow 0\)) of the barycenter of masses \(M_\mathrm{Sun}\) and \(m_\mathrm{planet}\). Meanwhile, the system of equations of motion has been successfully explored with respect to the existence of an approximated analytical solution.

As the main result, the equations of motion are reduced to the system of three nonlinear ordinary differential equations: 1) the equation for coordinate x is proved to be a kind of appropriate equation for the forced oscillations during a long-time period of quasi-oscillations (e.g. if we choose \(\mu \quad = 0.492195111 < 1/2\)), 2) the equation for coordinate y reveals that motion is not stable with respect to this coordinate and the condition \(y \quad \rightarrow \) 0 would be valid only if we choose constants of integration \(\{ x_0, y_0\} = 0\), and 3) the equation for coordinate z is proved to be a Riccati ODE of the first kind. It means that motion could not also be considered as stable with regard to the coordinate z. Thus, the infinitesimal mass m would escape from the vicinity of the common centre of mass of \(M_\mathrm{Sun}\) and \(m_\mathrm{planet}\) as soon as the true anomaly f increases (according to the dynamics (14) with respect to coordinate y) or at some definite moment of the true anomaly \(f_0\) (according to the dynamics (15) with respect to coordinate z).

The suggested approach can be used in future research for optimizing the maneuvers of spacecraft in the vicinity of the barycenter in a frame of the ER3BP. Indeed, it would be a simple algorithm for optimizing the maneuvers of spacecraft at the (x, y)-plane in the vicinity of the barycenter for the reason that coordinate x for infinitesimal mass is approximated by the solution of equation for the forced oscillations, whereas coordinate y is proved functionally dependent with respect to the expression for coordinate x (so, all these oscillations could be easily damped).

But appropriately optimizing the maneuvers of spacecraft in the vicinity of barycenter in regard to the coordinate z appears not to be so simple (the equation of motion for coordinate z is proved to be a Riccati ODE). Nevertheless, there is a modern numerical ansatz to predict when a jumping of a solution of the appropriate Riccati ODE should be [15,16,17,18]. So, in this case we also could suggest a scheme for z-optimizing for the maneuvers of spacecraft in the vicinity of the barycenter.

Also, some remarkable articles should be cited, which concern the problem under consideration, [22,23,24,25,26,27,28,29,30,31,32].