Abstract
In this paper, we present a new ansatz for solving equations of motion for the trapped orbits of the infinitesimal mass m, which is moving near the primary M3 in case of bi-elliptic restricted problem of four bodies (BiER4BP), where three primaries M1, M2, M3 are rotating around their common center of mass on elliptic orbits with hierarchical configuration M3 ≪ M2 ≪ M1. A new type of the solving procedure is implemented here to obtain the coordinates \( \vec{r} = \;\{ x,y,z\} \) of the infinitesimal mass m with its orbit located near the primary M3. Meanwhile, the system of equations of motion has been successfully explored with respect to the existence of analytical or semi-analytical (approximated) way for presentation of the solution. We obtain as follows: (1) the solution for coordinate x is described by the key nonlinear ordinary differential equation of fourth order at simplifying assumptions, (2) solution for coordinate y is given by the proper analytical expression, depending on coordinate x and true anomaly f, (3) the expression for coordinate z is given by the equation of Riccati-type—it means that coordinate z should be quasi-periodically oscillating close to the fixed plane \( \{ x,y,\,0\} \).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction, BiER4BP (bi-elliptic restricted problem of four bodies)
In the restricted three-body problem (R3BP), the equations of motion describe the dynamics of an infinitesimal mass m under the action of gravitational forces effected by two celestial bodies of giant masses M1 and M2 (M2 < M1), which are rotating around their common center of mass on Keplerian trajectories. The small mass m is supposed to be moving (as first approximation) inside of restricted region of space near the planet of mass M2 [1] (but outside the Roche-lobe’s region [2] for this planet). It is worth noting that there is a large number of previous and recent fundamental works concerning analytical development with respect to the R3BP equations which should be mentioned accordingly [1,2,3,4,5,6,7]. We should especially emphasize the theory of orbits, which was developed in profound work [3] by Szebehely for the case of the circular restricted problem of three bodies (CR3BP) (primaries are rotating around their common center of mass on circular orbits) as well as the case of the elliptic restricted problem of three bodies [4] (ER3BP, primaries are rotating around barycenter on elliptic orbits).
As the next step of the developing the topic under investigation, we should also mention the case of the circle restricted problem of four bodies (CR4BP) [5] (where particular solutions were obtained at the simplifying assumption concerning the circle orbits in case of CR4BP), and also the case of bi-elliptic restricted problem of four bodies (BiER4BP) [6, 7].
According to approach, suggested in [7], we consider in the current research the couple, consisting of two primaries of low masses {M2, M3} which are rotating around their common center of mass on elliptic orbits (with their common center of mass (M2 + M3) which is simulteneously rotating on elliptic orbit around the central giant planet or the Sun M1 on the same plane with the couple of two primaries {M2, M3} ≪ M1); additionally we mean that infinitesimal mass m is not far from the primary with mass M3, and M3 ≪ M2.
So, the motions of the primaries are coplanar (but those of infinitesimal mass is not). We assume also that distance a2 between {M2, M3} much less than distance a1 between barycenter of two primaries {M2, M3} and the central giant planet or the Sun M1
As for the natural restriction (of physical nature), we also mean that infinitesimal mass m is supposed to be moving outside the double Roche’s limit [2] for the primary with mass M3 (as first approximation, not less than 7–10 R3 where R3 is the radius of the primary with mass M3).
2 Equations of motion of BiER4BP
A non-uniformly rotating coordinate system is defined to describe the motion of the fourth particle in the elliptic planar restricted four-body problem [7]:
-
the origin O is the center of mass of all the primaries;
-
z axis is perpendicular to the plane of the mutual rotation of all the primaries and directed as the angular momentum of primaries’ orbital motion;
-
x axis is pointing from barycenter of three primaries {M1, M2, M3} to barycenter of primaries {M2, M3} (in [7] it was formulated as follows: “x axis points from primary M1 to barycenter of primaries {M2, M3}”; both assumptions coincide if {M2, M3} ≪ M1);
-
and y axis forms a right triad with x and z axes.
The dynamical equations of motion of the fourth particle in the non-uniformly rotating coordinate system can be written as in [5, 7] (we should note that Eq. (3) in [5] was obtained without assumption of finite bodies or primaries moving in circles with respect one to another with constant uniform rotation; so, all the derivation and solving procedure up to the Eq. (3) and Eq. (3) themselves coincide completely to those referred to Eq. (1) in work [7])
where U is the potential function and f denotes the true anomaly tracing the orbit of the barycenter of primaries {M2, M3} around the main barycenter of three primaries {M1, M2, M3}; let us note that for the reason that we have chosen an approximation {M2, M3} ≪ M1, the barycenter of three primaries {M1, M2, M3} is to be very close to the center of mass of central giant body M1.
It is interesting to note that in work [6] the dynamical equations of motion of the fourth particle (see Eqs. (7)–(8) in [6]) were also considered in the non-uniformly rotating coordinate system, but centered at the barycenter of primaries {M2, M3} and depending on two types of true anomalies refererred to different processes of tracing the orbits (one of the true anomalies is associated with tracing an elliptic motion of the barycenter of primaries {M2, M3} around the main barycenter of three primaries {M1, M2, M3}, another is referred to the rotating of primaries M2, M3 around their common center of mass {M2, M3}). Nevertheless, we will follow in the current research by the approach, suggested in work [7] (and applied here for investigations of the equations of motion of massless particle, moving under the action of forces considered in the plane variant of BiER4BP).
The expression [7] for U is given by
where G is the Gaussian constant of gravitation; \( R_{i} \) are distances of the infinitesimal mass m from each of the primaries Mi (i =1, 2, 3), respectively ({Xi, Yi, Zi} are the coordinates of primaries Mi).
Unlike the CR4BP [5], the positions of the primaries are not fixed in the rotating frame (in case of the elliptic restricted problem)—as they move along elliptical orbits, their relative distance ρ is not constant during a time
where e1 is the eccentricity of elliptic orbit of the rotating barycenter of primaries {M2, M3} around their common center of mass with primary M1. By setting the scaling of mass, distance and time in such a way as in [7] that
we introduce by the transformation of the previous, non-uniformly rotating coordinate system {X, Y, Z} [used in (1)], the pulsating coordinate system {x, y, z} with new scaling; so, we have with the help of (4)
Then, Eq. (1) become
where symbol ′ indicates (d/df) in (6), Ω is the scalar function
and μi = (Mi/M) (i = 1, 2, 3), r i is the dimensionless distance between the infinitesimal mass m and ith primary, respectively [7] (in [7] m1 should be associated with M3 in the denotations here, vice versa m3 instead of M1).
It is important to clarify appropriately the expressions for r i in (7) which should be used in (6) for the further calculations [taking into account expressions (2) and transformation of coordinates (4)–(5)]. According to [7], they are given by
where r denotes the distance between primaries M2, M3 whereas θ denotes the angle between radius-vector from barycenter of primaries {M2, M3} to the primary M3 and the Ox axis. The expression for r can be written as [taking into account (3)]:
where a2 is the semi-major axis of binary system {M2, M3}, M3 ≪ M2; e2 is the eccentricity of elliptic orbit of the rotating primary M3 around the barycenter of primaries {M2, M3}. The parameter θ is determined as in work [7] by
where θ0 is the initial value of θ. Meanwhile, from (9)–(10) we obtain
Let us note also that in the current research we neglect the effect of variable masses of the primaries [8]. As for the domain where the aforesaid infinitesimal mass m is supposed to be moving, let us consider the Cauchy problem in the whole space. Finally, it is worth noting that both spatial ER3BP and ER4BP are not conservative, and no complete integrals of motion are known [7, 9].
By appropriately transforming the right parts with regard to partial derivatives with respect to the proper coordinates {x, y, z}, system (6) can be represented as [taking into account (7)–(11)]
where
3 Solving procedure for the system of Eq. (12)
According to the aforesaid assumption, infinitesimal mass m is orbiting near the primary M3; it means that we can assume \( r_{3} /r_{2} \ll 1,\;r_{3} /r_{1} \ll 1 \) in Eq. (12).
The aforesaid assumptions should simplify equations of system (12) accordingly, taking into account (13):
We should take into account at transforming of (14) that we have assumed previously for the mass-parameters of primaries μ3 ≪ μ2 ⟹ (μ3 · μ2)/(μ3 + μ2) ≅ μ3 → 0 (with additional assumption (*) which means r → 0).
In this case, we obtain by the linear combining the second and third equations of (14)
where Eq. (15), which describes the dynamics of component z of the solution depending on the true anomaly f (for known components {x, y}), is known to be the ordinary differential equation of the Riccati-type [10].
Such the distinguished fact let us suggest that coordinate z belongs to the solutions \( \vec{r} = \;\{ x,y,z\} \) of system (14), associated with the class of trapped motions of the infinitesimal mass m (for which restriction z ≪ 1 is valid; it means that infinitesimal mass m is moving or oscillating near the plane \( \{ x,y\} ,\quad z \to 0 \)).
In this case, we can neglect by all the terms of order \( z^{{{\kern 1pt} 2}} \) and less in Eq. (14); the same assumption is valid for the other terms of second order and less (e.g., it concerns the factors μ3 → 0, r → 0 as well). Futhermore, we obtain directly from assumption \( r_{3} /r_{2} \ll 1 \) as shown below:
So, we have obtained 6 subclasses for the variety of partial solutions of (14), presented by (16):
where, expressions \( (x - \mu_{1} ) \) and \( (y\tan \theta ) \) should have different signs in (16.5) and, in opposite, the same signs in (16.6) for validity of assumption \( r_{3} /r_{2} \ll 1 \)(besides, \( \left| x \right| > \mu_{1} \)). Meanwhile, inequalities (16.5)–(16.6) are the most realistic cases from the aforementioned subclasses of solutions (16.1)–(16.6) [indeed, in (16.1)–(16.2) we have \( \left| y \right| \gg 1 \), whereas (16.3)–(16.4) holds inequality \( \left| {x - \mu_{1} } \right| \gg 1 \), both cases are not physically reasonable].
Thus, we obtain in case of \( (x - \mu_{1} ) \gg - y\tan \theta \) (16.6) from the first of Eq. (14) (taking into account also that \( z^{{{\kern 1pt} 2}} \to 0 \), {μ2, μ3} ≪ 1, r → 0; \( \theta \; \ne \;\pi \,(2n + 1)/2 \), n ∈ (0, 1, …)):
but from the second of Eq. (14) we should obtain in case of (16.6), taking into account additionally expression (17) \( \{ \;\left| x \right|\,\, > \,\,\mu_{{{\kern 1pt} 1}} \,\} \):
Equation (18) above is the nonlinear differential equation of 4-th order in regard to the coordinate x (with respect to the true anomaly f), which can obviously be solved by numerical methods only.
4 Final presentation of the solution
Let us present the solution \( \vec{r} = \;\{ x,y,z\} \) of system (14) for the trapped motion of the infinitesimal mass m, which is moving near the primary M3 [we suppose that restriction \( r_{\,3} \,/\,r_{\,2} \;\, < < \,\;1 \) is valid for Eq. (14)]:
-
If cos θ < 0, θ ∈ (π(2n + 1)/2, π(2n + 3)/2), n ∈ (0, 1, 2, …), the restriction \( (x - \mu_{1} ) \gg - y\tan \theta \) should be valid for the solutions (where, expressions \( (x - \mu_{1} ) \) and \( (y\tan \theta ) \) should have the same signs for validity of assumption \( r_{3} /r_{2} \ll 1 \), here \( \left| x \right| > \;\mu_{{1{\kern 1pt} }} \)); besides, the solution for coordinate \( x \) is described by the key nonlinear ordinary differential equation of fourth order (18)
$$ \begin{aligned} & \frac{{{\text{d}}\left( {\frac{{(y^{\prime\prime} + 2x^{\prime}) \cdot (1 + e_{1} \cdot \cos f)}}{{1 - \frac{{\mu_{3} }}{{(x - \mu_{1} )^{3} }}}}} \right)}}{{{\text{d}}f}} \cong \frac{{x^{\prime\prime}}}{2} - \frac{1}{{2\,(1 + e_{1} \cdot \cos f)}}\left( {x - \frac{{\mu_{3} {\kern 1pt} }}{{(x - \mu_{1} )^{2} }}} \right), \\ & \quad \left\{ {y^{\prime} \cong \frac{{x^{\prime\prime}}}{2} - \frac{1}{{2\,(1 + e_{1} \cdot \cos f)}}\left( {x - \frac{{\mu_{3} }}{{(x - \mu_{1} )^{2} }}} \right)} \right\} \\ \end{aligned} $$ -
But solution for coordinate y is described by the expression which stems from Eq. (17)
$$ y \cong \frac{{x^{\prime}}}{2} - \frac{1}{2}\int {\left( {\frac{1}{{(1 + e_{1} \cdot \cos f)}}\left( {x - \frac{{\mu_{3} }}{{(x - \mu_{1} )^{2} }}} \right)} \right){\text{d}}f} $$ -
The expression for coordinate z is given in (15) by equation of Riccati-type:
$$ z^{\prime\prime} + z \cdot \left( {1 - \left( {\frac{{y^{\prime\prime} + 2x^{\prime}}}{y}} \right)} \right){\kern 1pt} \cong 0. $$
Meanwhile, all the coordinates \( \{ x,y,z\} \) should be calculated under the optimizing natural restriction (of physical nature) so that the infinitesimal mass m is moving outside the double Roche’s limit [2] for the primary M3 (not less than 7–10 R3 where R3 is the radius of the primary).
5 Discussion
As we can see from the derivation above, equations of motion (1) even for the case of trapped motion \( \vec{r} = \;\{ x,y,z\} \) [described by appropriate approximation of equations of system (14)] of the infinitesimal mass m, which is moving near the primary M3, are proved to be very hard to solve analytically.
Nevertheless, at first step we have succeeded in obtaining from third equation of system (14) the Eq. (15) of a Riccati-type for the coordinate z (if the solutions for coordinates \( \{ x,y\} \) are already obtained)—it means that coordinate z should be quasi-periodically oscillating (close to the plane \( \{ x,y,\,0\} \)). Then we suggest a kind of reduction in a form (17)–(18) for the first and second equations of system (14), which describes the dynamics of coordinates \( \{ x,y\} \).
Meanwhile, we should note that due to the special character of the solutions of Riccati-type ODEs, there is the possibility for sudden jumping in the magnitude of the solution [11, 12] (in [12] see e.g. the solutions of Riccati-type for Abel ordinary differential equation of 1-st order). It means that any solution, which could be in principle derived from the equations of motion (1) in the form (14), are obviously not to be stable during a long the rotation of infinitesimal mass m around the primary M3 (including solutions for the libration points [6], [13,14,15]).
At the second step we have obtained the approximated solutions (17)–(18) of Eq. (14) for coordinates \( \{ x,y\} \) under simplifying assumption (16.6), where \( \;\left| x \right|\,\, > \,\,\mu_{{{\kern 1pt} 1}} \). Hereafter we have considered case with assumptions \( z^{{{\kern 1pt} 2}} {\kern 1pt} \to 0 \), {μ2, μ3} ≪ 1, r → 0; \( \theta \ne \pi (2n + 1)/2 \), n ∈ (0, 1, …) (for the sake of simplicity). The key nonlinear ODE of fourth-order in regard to the coordinate \( x(f) \) is obtained to be presented in (18). The appropriate solutions under simplifying assumption (16.5) can be obtained in the same manner.
Ending discussion, let us list below the obvious assumptions (or simplifications) which have been used at the formulation or the solution of the problem:
-
we consider in the current research two primaries of low masses {M2, M3} which are rotating on elliptic orbits (around barycenter) with their barycenter rotating on elliptic orbit around the third, giant primary M1;
-
the motions of the primaries are coplanar (but those of infinitesimal mass is not);
-
we consider the hierarchical configuration of primaries M1 ≫ M2 ≫ M3;
-
all the coordinates \( \{ x,y,z\} \) should be calculated under the natural restriction (of physical nature) so that the infinitesimal mass m is moving outside the double Roche’s limit [2] for the primary M3 (not less than 7–10 R3 where R3 is the radius of the primary). If we obtain during the solving procedure the solutions closer to the primary M3 than the double Roche’s limit, calculations should be stopped immediately at this forbidden zone;
-
distance a2 between {M2, M3} much less than distance a1 between barycenter of two primaries {M2, M3} and the giant primary M1 (a2 ≪ a1);
-
small mass m is supposed to be moving inside the restricted region of space or the so-called Hill sphere [2] of primary M3 with radius (the maximum distance from M3): \( r_{H} = a_{1} \cdot \left( {\frac{{M_{2} }}{{3M_{1} }}} \right)^{{\frac{1}{3}}} \);
-
moreover, infinitesimal mass m is orbiting near the primary M3 [in this case, we can assume \( r_{3} /r_{2} \ll 1,\;\;r_{3} /r_{1} \ll 1 \) in Eq. (12)];
-
coordinate z belongs to the class of trapped motions (i.e., infinitesimal mass m is assumed to be moving or oscillating near the plane \( \{ x,y\} ,\quad z \to 0 \));
-
in the current research we neglect the effect of variable masses of the primaries.
The last but not least, we should note that we can see from the aforementioned list of simplifications that the real conditions for orbiting of infinitesimal mass m near the primary M3 in BiER4BP are definitely very far from such the ideal formulation of the bi-elliptic restricted problem of four bodies (albeit the mathematical formulation relies heavily on simplifications based on such assumptions).
We provide the numerical calculation of the approximated solutions of first and second equations of system (14) under appropriate simplifying assumptions (see “Appendix A1”). We should note that we have used for calculating the data the Runge–Kutta fourth-order method with step 0.0001 starting from initial values. All the results of numerical calculations we schematically imagine at Figs. 1, 2 and 3.
6 Conclusion
In this paper, we present a new ansatz for solving equations of motion for the trapped orbits of the infinitesimal mass m, which is moving near the primary M3 in case of bi-elliptic restricted problem of four bodies (BiER4BP), where three primaries M1, M2, M3 are rotating around their common center of mass on elliptic orbits with hierarchical configuration M3 ≪ M2 ≪ M1.
A new type of the solving procedure is implemented here to obtain the coordinates \( \vec{r} = \;\{ x,y,z\} \) of the infinitesimal mass m with its orbit located near the primary M3. Meanwhile, the system of equations of motion has been successfully explored with respect to the existence of analytical or semi-analytical (approximated) way for presentation of the solution.
We obtain as follows: (1) the solution for coordinate x is described by the key nonlinear ordinary differential equation of fourth order at simplifying assumptions, (2) solution for coordinate y is given by the proper analytical expression, depending on coordinate x and true anomaly f, (3) the expression for coordinate z is given by the equation of Riccati-type—it means that coordinate z should be quasi-periodically oscillating close to the fixed plane \( \{ x,y,\,0\} \).
We have pointed out the optimizing procedure for the solutions \( \vec{r} = \;\{ x,y,z\} \) (the distance of the infinitesimal mass m from the primary M3 should exceed the level of minimal distances outside the double Roche-limit for the chosen primary).
The suggested approach can be used in future researches for optimizing the maneuvers of spacecraft (in space) which is moving near the smallest body M3 belonging to the triplet of massive objects which are rotating around their common center of mass on elliptic orbits with hierarchical configuration M3 ≪ M2 ≪ M1.
Also, some remarkable articles should be cited, which concern the problem under consideration, [16,17,18,19].
References
V. Arnold, Mathematical Methods of Classical Mechanics (Springer, New York, 1978)
G.N. Duboshin, Nebesnaja mehanika. Osnovnye zadachi i metody (Nauka, Moscow, 1968). (Handbook for Celestial Mechanics, in Russian)
V. Szebehely, Theory of Orbits. The Restricted Problem of Three Bodies (Yale University, Academic Press, New Haven, New-York, 1967)
F. Ferrari, M. Lavagna, Periodic motion around libration points in the elliptic restricted three-body problem. Nonlinear Dyn. 93(2), 453–462 (2018)
F.R. Moulton, On a class of particular solutions of the problem of four bodies. Trans. Am. Math. Soc. 1(1), 17–29 (1900)
A. Chakraborty, A. Narayan, Bielliptic restricted four body problem. Few-Body Syst. 60(7), 1–20 (2019)
C. Liu, S. Gong, Hill stability of the satellite in the elliptic restricted four-body problem. Astrophys. Space Sci. 363, 162 (2018)
J. Singh, O. Leke, Stability of the photogravitational restricted three-body problem with variable masses. Astrophys. Space Sci. 2010(326), 305–314 (2010)
J. Llibre, P. Conxita, On the elliptic restricted three-body problem. Celest. Mech. Dyn. Astron. 48(4), 319–345 (1990)
E. Kamke, Hand-Book for Ordinary Differential Eq (Science, Moscow, 1971)
S.V. Ershkov, Forbidden zones for circular regular orbits of the moons in solar system, R3BP. J. Astrophys. Astron. 38(1), 1–4 (2017)
S.V. Ershkov, Revolving scheme for solving a cascade of Abel equations in dynamics of planar satellite rotation. Theor. Appl. Mech. Lett. 7(3), 175–178 (2017)
J. Singh, A. Umar, On motion around the collinear libration points in the elliptic R3BP with a bigger triaxial primary. New Astron. 29, 36–41 (2014)
E.E. Zotos, Crash test for the Copenhagen problem with oblateness. Celest. Mech. Dyn. Astron. 122(1), 75–99 (2015)
E.I. Abouelmagd, M.A. Sharaf, The motion around the libration points in the restricted three-body problem with the effect of radiation and oblateness. Astrophys. Space Sci. 344(2), 321–332 (2013)
F.L. Chernousko, L.D. Akulenko, D.D. Leshchenko, Evolution of Motions of a Rigid Body About Its Center of Mass (Springer, Cham, 2017)
B.S. Kushvah, J.P. Sharma, B. Ishwar, Nonlinear Stability in the Generalised Photogravitational Restricted Three Body Problem with Poynting-Robertson Drag. Astrophys. Space Sci. 312(3–4), 279–293 (2007)
S.V. Ershkov, R.V. Shamin, The dynamics of asteroid rotation, governed by YORP effect: the kinematic ansatz. Acta Astronaut. 149, 47–54 (2018)
S.V. Ershkov, D. Leshchenko, Solving procedure for 3D motions near libration points in CR3BP. Astrophys. Space Sci. 364, 207 (2019)
Acknowledgements
Authors are thankful to unknown esteemed Reviewer with respect to the valuable efforts and advices which have improved structure of the article significantly. Sergey Ershkov is thankful to Dr. Nikolay Emelyanov for schematical graphical plot, presented at Fig. 4 (which was used previously in our working discussion regarding schematical solutions in R2BP).
Author information
Authors and Affiliations
Contributions
In this research, Dr. Sergey Ershkov is responsible for the general ansatz and the solving procedure, simple algebra manipulations, calculations, results of the article in Sects. 1–4 and also is responsible for the search of approximated solutions. Dr. Dmytro Leshchenko is responsible for theoretical investigations as well as for the deep survey in literature on the problem under consideration. Dr. Alla Rachinskaya is responsible for approximated solving the nonlinear ordinary differential equations by means of advanced numerical methods (see “Appendix A1”) as well as is responsible for numerical data of calculations and graphical plots of numerical solutions. All the authors agreed with results and conclusions of each other in Sects. 1–6.
Corresponding author
Ethics declarations
Conflict of interest
Authors declare that there is no conflict of interests regarding publication of article.
Appendix A1 (results of numerical calculations)
Appendix A1 (results of numerical calculations)
Let us provide the numerical calculation of the approximated solutions of first and second equations of system (14) (we consider approximation \( z^{{{\kern 1pt} 2}} \to 0 \))
which under appropriate simplifying assumptions such as hierarchical configuration M3 ≪ M2 ≪ M1 and (*) [it means that r → 0 in expression (11)] can be reduced as below
We should note that we have used for calculating the data the Runge–Kutta fourth-order method with step 0.0001 starting from initial values. We have chosen for our calculations (for modeling the triple system “Sun-Earth-Moon” {M1, M2, M3}) as follows:
As for the initial data, we have chosen as follows: (1) \( x_{\,0} \) = 0.001, \( (x^{\prime})_{\,0} \) = 0; (2) \( y_{\,0} \) = 0.0001, \( (y^{\prime})_{\,0} \) = 0; (3) \( z_{\,0} \) = 0, \( (z^{\prime})_{\,0} \) = 0. All the results of numerical calculations we schematically imagine at Figs. 1, 2 and 3.
Meanwhile, the numerical approximation for the dynamics of the infinitesimal mass m in this case (see Figs. 1, 2, 3) means that test particle is moving near barycenter of the system “Sun-Earth-Moon”, but the dynamics for the components of the solution is unstable. As for the example of the admissible ranges of the restrictions for the distance the infinitesimal mass m from Moon M3 for the Sun-Earth-Moon system {M1, M2, M3} we provide it as follows:
-
the double Roche’s limit [2] for the Moon M3 (not less than 7–10 R3 where R3 = 1731 km is the radius of the primary; 1 AU = 1.496 · 108 km) is at maximum circa (10·1731)/(1.496 · 108) ≅ 1.16 · 10−4;
-
the Hill sphere of the Earth M2 is circa 0.101 AU, according to the formula \( r_{\,H} \,\; = \,\;a_{{{\kern 1pt} 1}} \cdot \left( {\frac{{M_{\,2} }}{{3M_{\,1} }}} \right)^{{\,\frac{1}{3}}} \) in [2] (it seems to be obvious fact that the Hill sphere of the Earth M2 includes the Hill sphere of the Moon M3). Meanwhile, it should mean that test particle reaches the admissible range of the restriction circa at value of true anomaly f ≅ 100 (Fig. 3) or circa 16 full turns of the orbit around the Moon M3 starting from initial point.
Finally, we have schematically imagined trajectories of motion of infinitesimal particle near the Moon M3 for the Sun-Earth-Moon system {M1, M2, M3} in BiER4BP.
Let us additionally discuss and comment Figs. 1, 2, 3 and 4 (with inclusion of a more detailed analysis of these graphical plots) with the main aim to clarify what they are displaying and how they support the formulation presented:
-
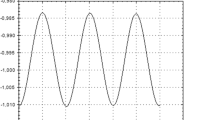
Figure 1 presents the results of numerical calculations of the coordinate x. Namely, we can see from Fig. 1 that coordinate x is oscillating in a narrow range [− 0.1; 0.1] in the pulsating coordinate system {x, y, z} (with new scaling) during a long period of changing the true anomaly f, up to the value f = 100 (which corresponds circa to the 16 full turns of orbit’s for the rotating barycenter of the primaries {M2, M3} around their common center of mass with primary M1);
-
Figure 2 presents the results of numerical calculations of the coordinate y. The same as displayed above on Fig. 1, we can see that coordinate y is oscillating in a narrow range [− 0.1; 0.1] in the pulsating coordinate system {x, y, z}, also during a long period of changing the true anomaly up to value f = 100;
-
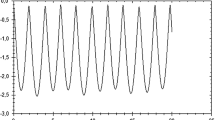
Figure 3 presents the results of numerical calculations of \( r_{\,3} \) (besides, it displays the fact that infinitesimal mass m is indeed orbiting near the primary M3), where \( r_{\,3} \) is oscillating in a narrow range [0.9; 1.1] in the pulsating coordinate system {x, y, z} (with new scaling), during a long period of changing the true anomaly up to value f = 100 as well;
-
Figure 4 schematically displays the possible trajectories of motion of infinitesimal particle near the Moon M3 for the Sun-Earth-Moon system {M1, M2, M3} in the pulsating coordinate system {x, y, z} in BiER4BP.
Rights and permissions
About this article
Cite this article
Ershkov, S., Leshchenko, D. & Rachinskaya, A. Solving procedure for the motion of infinitesimal mass in BiER4BP. Eur. Phys. J. Plus 135, 603 (2020). https://doi.org/10.1140/epjp/s13360-020-00579-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjp/s13360-020-00579-2