An efficient finite strip procedure for initial post-buckling analysis of thin-walled members

Abstract

An efficient procedure based on the semi-analytical finite strip method with invariant matrices is developed and applied to analyze the initial post-buckling of thin-walled members. Nonlinear strain–displacement equations are introduced in the manner of the von Karman assumption for the classical thin plate theory, and the formulations of the finite strip methods are deduced from the principle of the minimum potential energy. In order to improve the computational efficiency, an analytical integral of the stiffness matrix is transformed into matrix multiple calculation with introducing invariant matrices which can be integrated in advance only once. Three commonly employed benchmark problems are tested with proposed method and other state-of-the-art methods. The corresponding comparison results show that: (1) this finite strip method is proved to be a feasible and accurate tool; (2) compared with the calculation process of the conventional finite strip methods, the proposed procedure is much more efficient since it requires the integration of the stiffness matrix only once no matter how many iterations are needed; and (3) the advantage of time-saving is greatly remarkable as the number of iterations increases.

1 Introduction

In recent decades, plates and thin-walled structures have been widely used for the design of the civil engineering, due to light weight and high stiffness-to-weight ratio. Meanwhile, these light weight structures are also the eternal theme to improve the economy and operation state of aerospace equipment. Among the structural failure behaviors, the primary failure mode can be attributed to the buckling instability [1]. Thus, it is important to accurately predict the buckling and post-buckling behavior of such structures [2], which has been analyzed by experimental, analytical and numerical methodologies [3]. What is more, the analysis and computation of the initial post-buckling behavior also is useful and important, to exploit the carrying capacity of plates or thin-walled structures [4,5,6].

For the study of the initial post-buckling phenomenon of thin-walled structures, lots of finite strip methods have been developed and applied successfully [7]. The semi-analytical finite strip method (SA-FSM) based on the harmonic functions satisfied the supported boundary condition and the interpolation functions from the finite element method (FEM) was firstly developed and proved to be an efficient tool for the post-locally buckled analysis of prismatic thin-walled structures under end compression [8, 9]. For geometric nonlinear analysis of thin-walled structures, the SA-FSM has been proposed by using the moderately large displacement assumption and nonlinear strain–displacement relations, but linear curvature–displacement relations [10]. Then the SA-FSM is further developed with considering the effects of transverse shear deformation to analyze the large deflection [11], the post-local buckling problems [12] of laminated composite plates with initial geometric imperfections [13] based on linear crosswise interpolation or cubic crosswise interpolation, and the results obtained by the SA-FSM and the spline FSM have been compared and discussed [14]. For the post-buckling analysis of laminated composite plates with initial geometric imperfection subjected to progressive end-shortening, the higher-order SA-FSMs based on the higher-order shear deformation plate theory [15,16,17] and the SA-FSM for composite plates under combined compression and shear loading [18] are developed. The semi-energy SA-FSM for the post-local buckling analysis of geometrically perfect thin-walled prismatic structures [19] and composite laminates under end-shortening or normal pressure [20, 21], the semi-energy SA-FSM for post-buckling analysis of relatively thick anti-symmetric laminates [22, 23], the exact FSM for the buckling and initial post-buckling analysis of I-section struts based on the so-called full analytical method [24] and the semi-energy SA-FSM based on the concept of the first-order shear deformation theory for the post-buckling solution for thin and relatively thick functionally graded plates [25] were developed and applied efficiently.

Furthermore, in order to decrease the computational complexity, the SA-FSM using parallel cloud computing for large displacement stability analysis of orthotropic prismatic shell structures has been discussed [26]. For the buckling problems of composite laminated cylinders subjected to deformation-dependent loads, which remains normal to the shell middle surface throughout the deformation process, the SA-FSM with polynomial functions in the meridional direction and truncated Fourier series in the circumferential direction has been presented recently [27]. To take a fully nonlinear compound strip with a transverse stiffener and non-uniform characteristics in the longitudinal direction into account, a new SA-FSM has been developed for geometric nonlinear static analysis of prismatic shells recently [28]. For the elastic–plastic large-deflection thin-walled structural stability problems of the folded-plate members, the SA-FSM [29] and the semi-energy SA-FSM [30] also have been developed and applied. Up to now, the SA-FSMs have become the powerful technology for the post-buckling phenomenon of thin-walled structures.

Compare with the classical SA-FSM, the spline finite strip method (S-FSM) takes the place of the often used Fourier series by the spline function, in order to facilitate the description of local non-periodic buckles and oblique buckling modes [31,32,33,34]. Because the S-FSM requires more unknown parameters than the SA-FSM, this method can be regarded as a compromise method between the SA-FSM and the FEM [35]. For the geometric nonlinear analysis of stiffened plates with arbitrary shape, the sub-parametric mapping technology and the S-FSM have been assembled [36]. In order to deal with the geometric nonlinear problems of the perforated flat and stiffened plates [37], the material inelastic subjects [38, 39], and the inelastic buckling of the thin functionally graded material plates with cutout resting on an elastic foundation [40], the isoparametric S-FSM has been developed. Two kinds of the relationships between the elastic force (or elastic deformation energy) and the nodal line displacements can be summarized from all of above FSMs, which are global forms [17, 18, 24] and incremental formulations respectively [26, 28, 31, 34, 38, 39]. The incremental constitutive equation usually is used in the inelastic analysis [40]. For the global ones, the S-FSM often uses the numerical integration to obtain the global geometrical stiffness matrices. However, the analytical integration operator in the SA-FSM is applied even more frequently [41,42,43,44]. Generally, the reliability of the S-FSM depends on its numerical integral accuracy [34], and the analytical integration in the SA-FSM usually yields high accuracy but needs huge amount of the symbolic or manual calculation [8, 10, 18] or the hybrid method of analytical integration of the trigonometric terms and Gauss quadrature integration in other terms considering the effects of numerical integral accuracy into account can be implemented [12, 15]. In order to achieve efficient post-buckling analysis of the thin-walled structures by the FSMs above, it is important to accurately and fast evaluate the elastic force (or elastic potential energy).

Fortunately, we can find an efficacious procedure for evaluating the elastic forces and the elastic energy based on some invariant sparse matrices. The invariant sparse matrices are integrated in advance and have the property of transforming the evaluation of the elastic forces in a matrix multiplication process. With the assistance from the invariant sparse matrix, the full analytical evaluated method of the stiffness matrices and the elastic energy of the SA-FSM will be developed for the post-buckling analysis of thin-walled structures. The paper is organized as follows. In Sect. 2, the general theorem of the SA-FSM for buckling analysis of the thin-walled member is briefly described, and the control equations of the structure are discussed. The method based on the invariant matrices is then developed and discussed in Sect. 3. Numerical results calculated by the method proposed in this study and other state-of-the-art methods are presented in Sect. 4. Finally conclusions are given in Sect. 5.

2 Finite strip analysis

The plates and the thin-walled structures analyzed in this work are assumed to be simply supported along loaded edges and the classical plate theory (CPT) is applied throughout this work [45].

2.1 Degree of freedom and shape function

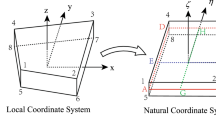
In the finite strip method two right-handed coordinate systems, i.e., the global one and the local one, are used to separate a thin plate into many strips along longitudinal direction as shown in Fig. 1. We introduce a numbering system of finite strip model in the global coordinate system. The total number of the strips is given as s. Then the total number of the nodal line is $s+1$ for the singular branched cross section member. The global coordinate system as shown in Fig. 1a is denoted as $X--Y--Z$, with the Y axis parallel to the longitudinal direction of the member. The local system is defined as $x--y--z,$ which is always associated with a strip with z-axis perpendicular to the strip as shown in Fig. 1b. Each nodal line i has two membrane Degrees Of Freedoms (DOFs), i.e., $u_i$ and $v_i$, and two bending DOFs, i.e., $w_i$ and $\theta _{i}$

Fig. 1

Coordinate systems and displacements vector

The analytical trigonometric functions of the longitudinal coordinate that satisfy the simply supported boundary condition of the loaded edges can be used to represent the strip’s deformation mode

$$\begin{aligned} S_p =\sin \frac{p\pi y}{a},\,p=1,\;2,\;3,\;\ldots ,\;m , \end{aligned}$$

(1)

where p is the axial half-wave number, m is a finite positive integer which indicates the maximum half-wave number, y is the longitudinal coordinate in the local coordinate system, a is the length of the member.

The shape function for the membrane DOFs uses a linear function matrix along transverse direction

$$\begin{aligned} {{{\varvec{h}}}}_i =\left[ {\left( 1-\frac{x}{b}\right) \,\frac{x}{b}}\right] ,\;i=1,\;2,\;\ldots ,\;m, \end{aligned}$$

(2)

and four cubic polynomials selected as the shape functions to depict the bending displacement of the strip along transverse direction

$$\begin{aligned} {\overline{{{{\varvec{h}}}}}} _i= & {} \left[ {{\begin{array}{llll} \left( {1-\frac{3x^{2}}{b^{2}}+\frac{2x^{3}}{b^{3}}} \right) &{} \left( {x-\frac{2x^{2}}{b}+\frac{x^{3}}{b^{2}}} \right) &{} \left( {\frac{3x^{2}}{b^{2}}-\frac{2x^{3}}{b^{3}}} \right) &{} \left( {\frac{x^{3}}{b^{2}}-\frac{x^{2}}{b}} \right) \\ \end{array} }} \right] ,\; \nonumber \\&\quad i=1,\;2,\; \ldots ,\;m, \end{aligned}$$

(3)

where b is the width of the strip member as shown in Fig. 1b, and x is the horizontal coordinate in local coordinate.

Then by combining with the interpolation function and the shape function, the explicit expressions in global system of two in-plane displacement vectors u, v, and one out-of-plane displacement vector w can be given as follows

$$\begin{aligned} \left[ {u,v,w} \right] =diag({{{\varvec{h}}}}_L {{{\varvec{S}}}}_u,{{{\varvec{h}}}}_L {{{\varvec{C}}}}_v ,{{{\varvec{h}}}}_w {{{\varvec{S}}}}_w){{{\varvec{d}}}}, \end{aligned}$$

(4)

where ${{\varvec{h}}}_L$ and ${{\varvec{h}}}_w$ are the shape function matrices along x direction, and ${{\varvec{S}}}_u$, ${{\varvec{C}}}_v$, and ${{\varvec{S}}}_w$ are the shape function matrices along y direction. ${{\varvec{h}}}_L$ and ${{\varvec{h}}}_w$ correspond to the in-plane displacement vectors ${{\varvec{d}}}_u$, ${{\varvec{d}}}_v$, and the out-of-plane displacement vector ${{\varvec{d}}}_w$ in the nodal lines, respectively, which can be given by applying Eqs. (2) and (3) as

$$\begin{aligned} {{{\varvec{h}}}}_L= & {} \left[ {{{\varvec{h}}}}_1 ,\;{{{\varvec{h}}}}_{2} ,\;\ldots \;{{{\varvec{h}}}}_m \right] ,\nonumber \\ {{{\varvec{h}}}}_w= & {} \left[ {\overline{{{\varvec{h}}}}}_1 ,\;{\overline{{{\varvec{h}}}}}_2 ,\;\ldots ,\;{\overline{{{\varvec{h}}}}}_m\right] . \end{aligned}$$

(5)

Meanwhile, ${{\varvec{S}}}_u$, ${{\varvec{C}}}_v$, and ${{\varvec{S}}}_w$ correspond to the displacement vectors ${{\varvec{d}}}_u$, ${{\varvec{d}}}_v$ and ${{\varvec{d}}}_w$ in the nodal lines, respectively, which can be given by applying Eq. (1) as

$$\begin{aligned} {{\varvec{S}}}_u= & {} diag(S_1 {{\varvec{I}}}_2 ,\;S_2 {{\varvec{I}}}_2 ,\;\ldots ,\;S_m {{\varvec{I}}}_2 ),\nonumber \\ {{\varvec{S}}}_w= & {} diag(S_1 {{\varvec{I}}}_4 ,\;S_2 {{\varvec{I}}}_4 ,\;\ldots ,\;S_m {{\varvec{I}}}_4 ),\nonumber \\ {{\varvec{C}}}_v= & {} diag(C_1 {{\varvec{I}}}_2 ,\;C_2 {{\varvec{I}}}_2 ,\;\ldots ,\;C_m {{\varvec{I}}}_2 ),\nonumber \\ Cp= & {} \cos \frac{p\pi y}{a},\,p=1,\,2,\,3, \ldots ,\,m, \end{aligned}$$

(6)

where ${{\varvec{I}}}_j$ is the $j\times j$ identity matrix. Finally, the displacement vector ${{\varvec{d}}}=\left[ {{\varvec{d}}}_u ^{T},{{\varvec{d}}}_v ^{T},{{\varvec{d}}}_w ^{T} \right] ^{T}$ in the nodal lines for the strip can be given as

$$\begin{aligned} {{\varvec{d}}}_u= & {} \left[ {u_i^1 ,\,u_j^1 ,\,u_i^2 ,\,u_j^2 ,\ldots ,\,u_i^m ,\,u_j^m } \right] ^{T},\nonumber \\ {{\varvec{d}}}_v= & {} \left[ {v_i^1 ,\,v_j^1 ,\,v_i^2 ,\,v_j^2 ,\ldots ,\,v_i^m ,\,v_j^m } \right] ^{T},\nonumber \\ {{\varvec{d}}}_w= & {} \left[ {w_i^1 ,\,\theta _i^1 ,\,w_j^1 ,\,\theta _j^1 ,\,w_i^2 ,\,\theta _i^2 ,\,\ldots ,\,w_j^m ,\,\theta _j^m } \right] ^{T}, \end{aligned}$$

(7)

where the subscripts i and j denote two nodal lines of one strip.

2.2 Fundamental stiffness matrix

In this section, the fundamental equations of the large-deflection plates are briefly outlined. The plates are assumed to be simply supported along all edges and the CPT is applied throughout this work [4]. With the CPT assumption, the Kirchhoff normalcy condition is incorporated into the displacement components of $u_0$, $v_0$, and $w_0$ of at a general point (x, y, z)

$$\begin{aligned} u_0 (x,y,z)= & {} u(x,y)-z\frac{\partial w(x,y)}{\partial x}, \nonumber \\ v_0 (x,y,z)= & {} v(x,y)-z\frac{\partial w(x,y)}{\partial y}, \nonumber \\ w_0 (x,y,z)= & {} w(x,y), \end{aligned}$$

(8)

where u, v and w are similar components at the middle surfaces ($z = 0$). Substituting Eq. (8) into the Green’s in-plane nonlinear strain gives rise to the following expression at a general point [6]

$$\begin{aligned} {{\varvec{\varepsilon }}}_0 =\left[ {\varepsilon _x ,\varepsilon _y ,\gamma _{xy} } \right] ^{T}={{\varvec{\varepsilon }}}+z{{\varvec{\varphi }}}, \end{aligned}$$

(9)

where ${{\varvec{\varepsilon }}}_0$ is the strain of the strip at a random point. In addition, ${{\varvec{\varepsilon }}}$ and ${{\varvec{\varphi }}}$ are the nonlinear strain–displacement relationship and the curvature variation of the middle surfaces ($z= 0$) at the strip, respectively, which can be expressed as

$$\begin{aligned} {\varvec{\varepsilon }} =\left[ {{\begin{array}{l} {\frac{\partial u}{\partial x}+\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right) ^{2}} \\ {\frac{\partial v}{\partial y}+\frac{1}{2}\left( {\frac{\partial w}{\partial y}} \right) ^{2}} \\ {\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}+\frac{\partial w}{\partial x}\frac{\partial w}{\partial y}} \\ \end{array} }} \right] ,{\varvec{\varphi }} =\left[ {{\begin{array}{l} {-\frac{\partial ^{2}w}{\partial x^{2}}} \\ {-\frac{\partial ^{2}w}{\partial y^{2}}} \\ {-2\frac{\partial ^{2}w}{\partial x\partial y}} \\ \end{array} }} \right] . \end{aligned}$$

(10)

The strain of the strip at a general point ${{\varvec{\varepsilon }}}$ can be divided into two parts, which are the linear strain ${{\varvec{\varepsilon }}}_l$ and the nonlinear strain ${{\varvec{\varepsilon }}}_{nl}$. Thus the total strain ${{\varvec{\varepsilon }}}$ can be expressed as the sum of these two strains ${{\varvec{\varepsilon }}}_l +{{\varvec{\varepsilon }}}_{nl}$ through applying Eq. (4). The linear strain ${{\varvec{\varepsilon }}}_l$ and the nonlinear strain ${{\varvec{\varepsilon }}}_{nl}$ can be denoted as

$$\begin{aligned} {{\varvec{\varepsilon }}}_l ={{\varvec{D}}}_1 {{\varvec{d}}},\;{{\varvec{\varepsilon }}}_{nl} ={{\varvec{D}}}_2 ({{\varvec{d}}}){{\varvec{d}}}. \end{aligned}$$

(11)

where ${{\varvec{D}}}_1$ defines the relationship of the linear strain–displacement expressed as

$$\begin{aligned} {{\varvec{D}}}_1= & {} \left[ {{\begin{array}{ll} {\mathop {{{{\varvec{D}}}}_{1m} }\limits _{3\times 4m} }&{} {\mathop {{{{\varvec{D}}}}_{1b} }\limits _{3\times 4m} } \\ \end{array} }} \right] , \nonumber \\ \mathop {{{\varvec{D}}}_{1m} }\limits _{3\times 4m}= & {} \left[ {{\begin{array}{ll} {\frac{\partial {{\varvec{h}}}_L }{\partial x}{{\varvec{S}}}_u }&{}\quad {\mathop {{{\varvec{O}}}}\limits _{1\times 2m} } \\ {\mathop {{\varvec{O}}}\limits _{1\times 2m} }&{}\quad {{{\varvec{h}}}_L \frac{\partial {{\varvec{C}}}_v }{\partial y}} \\ {{{\varvec{h}}}_L \frac{\partial {{\varvec{S}}}_u }{\partial y}}&{} {\frac{\partial {{\varvec{h}}}_L }{\partial x}{{\varvec{C}}}_v } \\ \end{array} }} \right] ,\mathop {{{{\varvec{D}}}}_{1b}}\limits _{3\times 4m} =-z\left[ {{\begin{array}{ll} {\frac{\partial ^{2}{{\varvec{h}}}_w }{\partial x^{2}}{{\varvec{S}}}_w } \\ {{{\varvec{h}}}_w \frac{\partial ^{2}{{\varvec{S}}}_w }{\partial y^{2}}} \\ {2\frac{\partial {{\varvec{h}}}_w }{\partial x}\frac{\partial {{\varvec{S}}}_w }{\partial y}} \\ \end{array} }} \right] , \end{aligned}$$

(12)

and ${{\varvec{D}}}_2 ({{\varvec{d}}})$ defines the relationship of the nonlinear strain–displacement expressed as

$$\begin{aligned} {{\varvec{D}}}_2 ({{\varvec{d}}})=\left[ {{\begin{array}{ll} {\mathop {{{\varvec{O}}}}\limits _{3\times 4m} }&{}\quad {\mathop {{{{\varvec{D}}}}_2^w}\limits _{3\times 4m}} \\ \end{array} }} \right] , \end{aligned}$$

(13)

and

$$\begin{aligned} \mathop {{{\varvec{D}}}_2^w }\limits _{3\times 4m} =diag({{\varvec{d}}}_w^T ,\;{{\varvec{d}}}_w^T ,{{\varvec{d}}}_w^T )\left[ {\begin{array}{l} \frac{1}{2}{{\varvec{S}}}_w^T \frac{\partial {{\varvec{h}}}_w^T }{\partial x}\frac{\partial {{\varvec{h}}}_w }{\partial x}{{\varvec{S}}}_w \\ \frac{1}{2}\frac{\partial {{\varvec{S}}}_w^T }{\partial y}{{\varvec{h}}}_w^T {{\varvec{h}}}_w \frac{\partial {{\varvec{S}}}_w }{\partial y} \\ {{\varvec{S}}}_w^T \frac{\partial {{\varvec{h}}}_w^T }{\partial x}{{\varvec{h}}}_w \frac{\partial {{\varvec{S}}}_w }{\partial y} \\ \end{array}} \right] . \end{aligned}$$

(14)

Here O denotes the zero matrix. As for the general elastic materials, the elastic deformation energy $U=\frac{1}{2}\int {{{\varvec{\varepsilon }}}_0 ^{T}{{\varvec{\sigma }}}}\,\mathrm{d}V$ can be defines through applying Eq. (11) as follow

$$\begin{aligned} U=\frac{1}{2}\int {{{\varvec{\varepsilon }}}_0 ^{T}{{{\varvec{Q}}}}{\varvec{\varepsilon }}}_0 \mathrm{d}V=\frac{1}{2}{{\varvec{d}}}^{T}{{\varvec{k}}}_e \left( {{\varvec{d}}} \right) {{\varvec{d}}}, \end{aligned}$$

(15)

where Q is elastic constant matrix, with relationship of ${{\varvec{Q}}}^{T}={{\varvec{Q}}}$, and the elastic stiffness matrix ${{\varvec{k}}}_e \left( {{\varvec{d}}} \right)$ of the strip is expressed as

$$\begin{aligned} {{\varvec{k}}}_e \left( {{\varvec{d}}} \right) =\int {\left( {{{\varvec{D}}}_1+{{\varvec{D}}}_2({{\varvec{d}}})} \right) ^{T}{{\varvec{Q}}}\left( {{{\varvec{D}}}_{1}+{{\varvec{D}}}_{2}({{\varvec{d}}})} \right) } \mathrm{d}V. \end{aligned}$$

(16)

The first item $\int {{{\varvec{D}}}_1^T {{\varvec{QD}}}_1 \mathrm{d}V}$ within the integral operator denotes the constant elastic stiffness coefficient, the second item $\int {{{\varvec{D}}}_1^T {{\varvec{QD}}}_2 ({{\varvec{d}}})} \mathrm{d}V$ and the third item $\int {{\varvec{D}}}_2^T \left( {{\varvec{d}}} \right) {{\varvec{QD}}}_{\mathrm{1}} \mathrm{d}V$ can take the first-order nonlinear stiffness with respect to the displacement vector ${{\varvec{d}}}$ into account, and the last item $\int {{{\varvec{D}}}_2^T \left( {{\varvec{d}}} \right) {{\varvec{QD}}}_2 \left( {{\varvec{d}}} \right) } \mathrm{d}V$ expresses the effect of the second-order nonlinear stiffness with respect to the displacement vector ${{\varvec{d}}}$.

As shown in Fig. 1b, if the strip is assumed to be loaded with linearly varying edge tractions, then the membrane compressive loads can be expressed as

$$\begin{aligned} T_x =T_i -\left( {T_i -T_j }\right) \frac{x}{b}, \end{aligned}$$

(17)

where $T_i$ and $T_j$ are the forces in two nodes of the strip, b is the width of the strip, x is the transverse coordinate in the local coordinate system. Similar to the deduction of the elastic stiffness matrix, the potential energy induced by the membrane compressive loads can be expressed as

$$\begin{aligned} W=\int {\frac{1}{2}T_x \left[ {\left( {\frac{\partial u}{\partial y}} \right) ^{2}+\left( {\frac{\partial v}{\partial y}} \right) ^{2}+\left( {\frac{\partial w}{\partial y}} \right) ^{2}} \right] \mathrm{d}V} =\frac{1}{2}{{\varvec{d}}}^{T}\left( {\int {T_x {{\varvec{G}}}^{T}{{\varvec{G}}}\,\mathrm{d}V} } \right) {{\varvec{d}}}, \end{aligned}$$

(18)

where G defines the relationship between the second-order strain components and the displacement vector

$$\begin{aligned} {{\varvec{G}}}=diag\left( {{\varvec{h}}}_L \frac{\partial {{\varvec{S}}}_u }{\partial y},{{\varvec{h}}}_L \frac{\partial {{\varvec{C}}}_v }{\partial y},{{\varvec{h}}}_w \frac{\partial {{\varvec{S}}}_w }{\partial y}\right) . \end{aligned}$$

(19)

Then the geometric stiffness matrix of the strip element can be expressed as

$$\begin{aligned} {{\varvec{k}}}_g =\int T_x {{\varvec{G}}}^{T}{{\varvec{G}}}\,\mathrm{d}V . \end{aligned}$$

(20)

According to the condition of the displacement continuum and the coordinate transformation, the relationship between the displacement vectors in the nodal line from the local coordinate to the global coordinate and a rotation angle $\alpha$ as shown in Fig. 2, can be determined by the following equation

$$\begin{aligned} \left[ {\begin{array}{c} u_i \\ u_j \\ v_i \\ v_j \\ w_i \\ \theta _i \\ w_j \\ \theta _j \\ \end{array}} \right] _{global}^p =\left[ {\begin{array}{cccccccc} \cos \alpha &{}\quad 0 &{}\quad 0&{}\quad 0&{}\quad -\sin \alpha &{}\quad 0 &{}\quad 0&{}\quad 0 \\ 0 &{}\quad \cos \alpha &{}\quad 0&{}\quad 0&{}\quad 0 &{}\quad 0 &{}\quad -\sin \alpha &{}\quad 0 \\ 0&{}\quad 0&{}\quad 1&{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ \sin \alpha &{}\quad 0 &{}\quad 0&{}\quad 0 &{}\quad \cos \alpha &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad \sin \alpha &{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \cos \alpha &{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1 \\ \end{array}} \right] \left[ {\begin{array}{c} u_i \\ u_j \\ v_i \\ v_j \\ w_i \\ \theta _i \\ w_j \\ \theta _j \\ \end{array}} \right] _{local}^p . \end{aligned}$$

(21)

Fig. 2

Global rotational angular of cross section of the strip

2.3 The control equation of thin-walled member

According to the virtual work principle, the global control equation of the thin-walled member can be obtained by using the elastic deformation energy in Eq. (15) and the compression potential energy in Eq. (18) and the coordinate transformation relationship Eq. (21), that is

$$\begin{aligned} ({{\varvec{K}}}_{{\varvec{e}}} ({{\varvec{D}}})-{{\varvec{K}}}_{{\varvec{g}}}){{\varvec{D}}}={{\varvec{0}}}, \end{aligned}$$

(22)

where ${{\varvec{K}}}_{{\varvec{e}}} ({{\varvec{D}}})$ and ${{\varvec{K}}}_{{\varvec{g}}}$ are the global elastic stiffness matrix and the global geometric stiffness matrix. ${{\varvec{K}}}_{{\varvec{e}}} ({{\varvec{D}}})$ and ${{\varvec{K}}}_{{\varvec{g}}}$ can be deduced from the stiffness matrix ${{\varvec{k}}}_e \left( {{\varvec{d}}} \right)$ and ${{\varvec{k}}}_g$ via coordinate transformation of the strip member, respectively, and ${{{\varvec{D}}}}$ is the global displacement vector of the thin-walled member which can be expressed as

$$\begin{aligned} {{\varvec{D}}}=[{{\varvec{D}}}_u^1 ,\;{{\varvec{D}}}_u^2 ,\;\ldots ,\;{{\varvec{D}}}_u^m ,\;{{\varvec{D}}}_v^1 ,\;{{\varvec{D}}}_v^2 ,\;\ldots ,\;{{\varvec{D}}}_v^m ,\;{{\varvec{D}}}_w^1 ,\;{{\varvec{D}}}_w^2 ,\;\ldots ,\;{{\varvec{D}}}_w^m ]^{T}. \end{aligned}$$

(23)

Here, if it is defined that $p=1,2,3,\ldots ,m$, then ${{\varvec{D}}}_u^p$ and ${{\varvec{D}}}_v^p$ are the in-plane displacement vectors of the pth axial half-wave with respect to the global coordinate X and Y, correspondingly, and ${{\varvec{D}}}_w^p$ is the out-of-plane displacement vector of the pth axial half-wave with respect to the global coordinate Z. Assuming $T_0 (x)$ is the initial axial force, the real axial force in the geometric stiffness matrix can be expressed as

$$\begin{aligned} T(x)=\lambda T_0 (x), \end{aligned}$$

(24)

where $\lambda$ is the load factor. Therefore, the geometric stiffness matrix ${{\varvec{K}}}_g$ can be rewritten as the proportionate function of the initial geometric stiffness matrix $\left. {K_g } \right| _{T_0 }$ caused by initial axial force $T_0 (x)$ and the load factor $\lambda$, that is

$$\begin{aligned} {{\varvec{K}}}_{{\varvec{g}}} =\lambda \left. {{{\varvec{K}}}_{{\varvec{g}}} } \right| _{T_0 } . \end{aligned}$$

(25)

By substituting Eq. (25) into Eq. (22), the control equation of the buckling analysis of the thin-walled member can be rewritten as

$$\begin{aligned} \left( {{{\varvec{K}}}_{{\varvec{e}}} ({{\varvec{D}}})-\lambda \left. {{{\varvec{K}}}_{{\varvec{g}}} } \right| _{T_0 } } \right) {{\varvec{D}}}={{\varvec{0}}}. \end{aligned}$$

(26)

Equation (26) gives the nonlinear relationship between the global displacement vector D and the generalized axial force described by the load factor $\lambda$ and the initial geometric stiffness matrix $\left. {{{\varvec{K}}}_g } \right| _{T_0 }$. For the initial post-buckling analysis of the thin-walled member, only the geometrical nonlinear strain–displacement relationship shown in Eq. (11) has been taken into account here.

3 Invariant matrices for stiffness computation

As for the elastic stiffness matrix of the strip element ${{\varvec{k}}}_e \left( {{\varvec{d}}} \right)$ given in Eq. (16), the unknown displacement vector ${{\varvec{d}}}$ can be contained clearly. However, it will be changed due to the integral and must be re-evaluated again in the buckling analysis of the thin-walled member for the difference configurations.

Here we deduce several invariant matrices to express the elastic stiffness matrix, and then directly avoid the huge computational consumption caused by the repeating integrations of stiffness matrix. As far as the authors known, there is no notice in currently available bibliography of the use of these invariant matrices that considerably reduce computational time in the post-buckling analysis.

3.1 Invariant matrices

In order to facilitate the analysis procedure, the elastic stiffness matrix ${{\varvec{k}}}_e \left( {{\varvec{d}}} \right)$ is divided into four parts

$$\begin{aligned} {{\varvec{k}}}_e \left( {{\varvec{d}}} \right) ={{\varvec{k}}}_{e1} +{{\varvec{k}}}_{e2} ({{\varvec{d}}})+{{\varvec{k}}}_{e3} ({{\varvec{d}}})+{{\varvec{k}}}_{e4} ({{\varvec{d}}}), \end{aligned}$$

(27)

where

$$\begin{aligned} {{\varvec{k}}}_{e1}= & {} \int {{{\varvec{D}}}_1^T {{\varvec{QD}}}_1 \mathrm{d}V} ,{{\varvec{k}}}_{e2} ({{\varvec{d}}})=\int {{{\varvec{D}}}_1^T {{\varvec{QD}}}_2 \left( {{\varvec{d}}} \right) \mathrm{d}V} , \nonumber \\ {{\varvec{k}}}_{e3} ({{\varvec{d}}})= & {} \int {{{\varvec{D}}}_2^T \left( {{\varvec{d}}} \right) {{\varvec{QD}}}_1 \mathrm{d}V} ,\;{{\varvec{k}}}_{e4} ({{\varvec{d}}})=\int {{{\varvec{D}}}_2^T \left( {{\varvec{d}}} \right) {{\varvec{QD}}}_2 \left( {{\varvec{d}}} \right) \mathrm{d}V} . \end{aligned}$$

(28)

${{\varvec{k}}}_{e1}$ is defined as a constant matrix expressed as

$$\begin{aligned} {{\varvec{k}}}_{e1} =\left[ {{\begin{array}{ll} {{{\varvec{k}}}_{e1m} }&{}\quad {\mathop {{\varvec{O}}}\limits _{4m\times 4m} } \\ {\mathop {{\varvec{O}}}\limits _{4m\times 4m} }&{}\quad {{{\varvec{k}}}_{e1b} } \\ \end{array} }} \right] , \end{aligned}$$

(29)

while ${{\varvec{k}}}_{e2} ({{\varvec{d}}})$, ${{\varvec{k}}}_{e3} ({{\varvec{d}}})$ and ${{\varvec{k}}}_{e4} ({{\varvec{d}}})$ are linear or quadratic functions of the displacements and need repeating integral calculations once the displacement vector changes.

In order to avoid the repeating operations, the unknown displacement vector d is extracted outside the integral calculation. Firstly, three $1\times 4\,m$ row matrices are defined as,

$$\begin{aligned} {{\varvec{A}}}= & {} [{{\varvec{a}}}_1 ,{{\varvec{a}}}_2 ,\ldots ,{{\varvec{a}}}_{4m} ]=\frac{1}{2}{{\varvec{S}}}_w^T \frac{\partial {{\varvec{h}}}_w^T }{\partial x}\frac{\partial {{\varvec{h}}}_w }{\partial x}{{\varvec{S}}}_w ,\nonumber \\ {{\varvec{B}}}= & {} [{{\varvec{b}}}_1 ,{{\varvec{b}}}_2 ,\ldots ,{{\varvec{b}}}_{4m} ]=\frac{1}{2}\frac{\partial {{\varvec{S}}}_w^T }{\partial y}{{\varvec{h}}}_w^T {{\varvec{h}}}_w \frac{\partial {{\varvec{S}}}_w }{\partial y}, \nonumber \\ {{\varvec{C}}}= & {} [{{\varvec{c}}}_1 ,{{\varvec{c}}}_2 ,\ldots ,{{\varvec{c}}}_{4m} ]={{\varvec{S}}}_w^T \frac{\partial {{\varvec{h}}}_w^T }{\partial x}{{\varvec{h}}}_w \frac{\partial {{\varvec{S}}}_w }{\partial y}, \end{aligned}$$

(30)

where ${{\varvec{a}}}_i ,{{\varvec{b}}}_i ,{{\varvec{c}}}_i (i=1,2,\ldots ,4\,m)$ are the column matrices. Then Eq. (14) is rewritten as

$$\begin{aligned} {{\varvec{D}}}_2^w =\left[ {{\begin{array}{lll} {\left( {{{\varvec{d}}}_w^T {{\varvec{A}}}} \right) ^{T}}&{} {\left( {{{\varvec{d}}}_w^T {{\varvec{B}}}} \right) ^{T}}&{} {\left( {{{\varvec{d}}}_w^T {{\varvec{C}}}} \right) ^{T}} \\ \end{array} }} \right] ^{T}. \end{aligned}$$

(31)

Secondly, since the transpose of the scalar quantity equals to itself, the items on the right side of Eq. (31) can be expressed as

$$\begin{aligned} {{\varvec{d}}}_w^T {{\varvec{U}}}= & {} [{{\varvec{d}}}_w^T {{\varvec{u}}}_1 ,{{\varvec{d}}}_w^T {{\varvec{u}}}_2 ,\ldots ,{{\varvec{d}}}_w^T {{\varvec{u}}}_{4m} ]=[{{\varvec{u}}}_1^T {{\varvec{d}}}_w ,{{\varvec{u}}}_2^T {{\varvec{d}}}_w ,\ldots ,{{\varvec{u}}}_{4m}^T {{\varvec{d}}}_w ], \nonumber \\&({{\varvec{U}}}={{\varvec{A}}},{{\varvec{B}}},{{\varvec{C}}};{{\varvec{u}}}={{\varvec{a}}},{{\varvec{b}}},{{\varvec{c}}}). \end{aligned}$$

(32)

Defining a $16\,m^{2}\times 4\,m$ nodal line coordinate matrix

$$\begin{aligned} \mathop {{{{\varvec{X}}}}_w }\limits _{16m^{2}\times 4m} =diag({{\varvec{d}}}_w ,{{\varvec{d}}}_{w},\ldots ,\,{{\varvec{d}}}_{w}), \end{aligned}$$

(33)

the nodal line coordinate ${{\varvec{d}}}_w$ can be then shift from the front to the back of the row matrices ${{\varvec{A}}},{{\varvec{B}}},{{\varvec{C}}}$ in Eq. (31),

$$\begin{aligned} {{\varvec{D}}}_2^w ={{\varvec{JX}}}_w , \end{aligned}$$

(34)

where the $3\times 16\,m^{2}$ spare matrix ${{\varvec{J}}}$ can be defined as

$$\begin{aligned} \mathop {{\varvec{J}}}\limits _{3\times 16m^{2}} =\left[ {{\begin{array}{lll} {\bar{{{{\varvec{A}}}}}^{T}}&{} {{\bar{{{\varvec{B}}}}}^{T}}&{} {{\bar{{{\varvec{C}}}}}^{T}} \\ \end{array} }} \right] ^{T}, \end{aligned}$$

(35)

and

$$\begin{aligned} \mathop {{\bar{{{\varvec{U}}}}}}\limits _{1\times 16m^{2}} =[{{\varvec{u}}}_1^T ,{{\varvec{u}}}_2^T ,\ldots ,{{\varvec{u}}}_{4m}^T ],({{\varvec{U}}}={{\varvec{A}}},{{\varvec{B}}},{{\varvec{C}}};{{\varvec{u}}}={{\varvec{a}}},{{\varvec{b}}},{{\varvec{c}}}). \end{aligned}$$

(36)

Thirdly Eqs. (12), (13), and (34) are cooperatively used to determine the stiffness matrix

$$\begin{aligned} {{\varvec{k}}}_{e2} ({{\varvec{d}}})=\left[ {{\begin{array}{ll} {\mathop {{\varvec{O}}}\limits _{8m\times 4m} }&{} {{{\varvec{I}}}_{\mathrm {n1}} {{\varvec{X}}}_w } \\ \end{array} }} \right] , \end{aligned}$$

(37)

where the first invariant matrix ${{\varvec{I}}}_{\mathrm {n1}}$ of the stiffness matrix can be defined as

$$\begin{aligned} {{\varvec{I}}}_{\mathrm {n1}} =\left[ {{\begin{array}{l} {{{\varvec{I}}}_{n1m} } \\ {{{\varvec{I}}}_{n1b} } \\ \end{array} }} \right] =\left[ {{\begin{array}{l} {\int {\mathop {{{\varvec{D}}}_{1m}^T }\limits _{4m\times 3} {{\varvec{QJ}}}} \mathrm{d}V} \\ {\int {\mathop {{{\varvec{D}}}_{1b}^T }\limits _{4m\times 3} {{\varvec{QJ}}}} \mathrm{d}V} \\ \end{array} }} \right] . \end{aligned}$$

(38)

Since ${{\varvec{I}}}_{\mathrm {n1}}$ independent on the displacement vector ${{\varvec{d}}}$, it requires analytical integration only once in advance for the buckling analysis of the thin-walled members. Analyzing the stiffness matrix defined by Eqs. (33), (37), and (38), we note that the integral calculation of the matrix ${{\varvec{k}}}_{e2} ({{\varvec{d}}})$ given in Eq. (37) depends on the unknown displacement vector ${{\varvec{d}}}$. However, it also can be evaluated by the multiple operator of the first invariant matrix ${{\varvec{I}}}_{\mathrm {n1}}$ and the nodal line coordinate matrix ${{\varvec{X}}}_w$. Compared with the integral calculation of the stiffness matrix of ${{\varvec{k}}}_{e2} ({{\varvec{d}}})$, the matrix multiple given in Eq. (37) can be more efficient which will be verified by the example in next section.

Since the elastic constant matrix ${{\varvec{Q}}}$ is symmetrical, the transpose of the elastic stiffness matrix ${{\varvec{k}}}_{e2} ({{\varvec{d}}})$ is ${{\varvec{k}}}_{e3} ({{\varvec{d}}})$, that is

$$\begin{aligned} {{\varvec{k}}}_{e3} ({{\varvec{d}}})={{\varvec{k}}}_{e2}^T ({{\varvec{d}}}). \end{aligned}$$

(39)

Thus the elastic stiffness matrix ${{\varvec{k}}}_{e3} ({{\varvec{d}}})$ also can be easily obtained by the matrix multiple ${{\varvec{I}}}_{\mathrm {n1}}$ and ${{\varvec{X}}}_w$ given in Eq. (37).

Substituting Eq. (13) into the stiffness matrix ${{\varvec{k}}}_{e4} ({{\varvec{d}}})$, we can get

$$\begin{aligned} {{\varvec{k}}}_{e4} ({{\varvec{d}}})=\int {\left[ {{\begin{array}{ll} {{\begin{array}{l} {\mathop {{\varvec{O}}}\limits _{4m\times 4m} } \\ {\mathop {{\varvec{O}}}\limits _{4m\times 4m} } \\ \end{array} }}&{}\quad {{\begin{array}{l} {\mathop {{\varvec{O}}}\limits _{4m\times 4m} } \\ {{{\varvec{D}}}_{2}^{wT}{{\varvec{QD}}}_2^w } \\ \end{array} }} \\ \end{array} }} \right] } \mathrm{d}V. \end{aligned}$$

(40)

The stiffness matrix ${{\varvec{k}}}_{e4} ({{\varvec{d}}})$ can be further derived by applying Eq. (34) into the following form

$$\begin{aligned} {{\varvec{k}}}_{e4} ({{\varvec{d}}})=\int {\left[ {{\begin{array}{ll} {{\begin{array}{l} {\mathop {{\varvec{O}}}\limits _{4m\times 4m} } \\ {\mathop {{\varvec{O}}}\limits _{4m\times 4m} } \\ \end{array} }}&{}\quad {{\begin{array}{l} {\mathop {{\varvec{O}}}\limits _{4m\times 4m} } \\ {{{\varvec{X}}}_w^T {{\varvec{J}}}^{T}{{\varvec{QJX}}}_w } \\ \end{array} }} \\ \end{array} }} \right] } \mathrm{d}V. \end{aligned}$$

(41)

Because the zeros matrices and the nodal line coordinate matrix ${{\varvec{X}}}_w$ are independent on the integral calculation, Eq. (41) is rewritten as

$$\begin{aligned} {{\varvec{k}}}_{e4} ({{\varvec{d}}})=\left[ {{\begin{array}{ll} {{\begin{array}{l} {\mathop {{\varvec{O}}}\limits _{4m\times 4m} } \\ {\mathop {{\varvec{O}}}\limits _{4m\times 4m} } \\ \end{array} }}&{}\quad {{\begin{array}{l} {\mathop {{\varvec{O}}}\limits _{4m\times 4m} } \\ {{{\varvec{X}}}_w^T {{\varvec{I}}}_{n2} {{\varvec{X}}}_w } \\ \end{array} }} \\ \end{array} }} \right] , \end{aligned}$$

(42)

where the second invariant matrix ${{\varvec{I}}}_{n2}$ of the stiffness matrix can be defined as

$$\begin{aligned} {{\varvec{I}}}_{n2} =\int {{{\varvec{J}}}^{T}{{\varvec{QJ}}}} \mathrm{d}V. \end{aligned}$$

(43)

Since the invariant matrix ${{\varvec{I}}}_{n2}$ is a $16\,m^{2}\times 16\,m^{2}$ constant matrix, it requires analytical calculation only once beforehand. Then the integral of the matrix ${{\varvec{k}}}_{e4} ({{\varvec{d}}})$ defined in Eq. (28) can be transformed into three matrices $\left( {{{\varvec{X}}}_w^T ,\;{{\varvec{I}}}_{n2} ,\;{{\varvec{X}}}_w } \right)$ multiples in turn.

Furthermore, substituting Eqs. (37), (39), and (42) are substituted into Eq. (27), the elastic stiffness matrix can be obtained, which is the function of the invariant matrices

$$\begin{aligned} {{\varvec{k}}}_e ({{\varvec{d}}})=\left[ {{\begin{array}{ll} {{{\varvec{k}}}_{e1m} }&{}\quad {{{\varvec{I}}}_{n1m} {{\varvec{X}}}_w } \\ {{{\varvec{X}}}_w^T {{\varvec{I}}}_{n1m}^T }&{}\quad {{{\varvec{k}}}_{e1b} +{{\varvec{I}}}_{n1b} {{\varvec{X}}}_w +{{\varvec{X}}}_w^T {{\varvec{I}}}_{n1b}^T +{{\varvec{X}}}_w^T {{\varvec{I}}}_{n2} {{\varvec{X}}}_w } \\ \end{array} }} \right] , \end{aligned}$$

(44)

and the elastic deformation energy given in Eq. (15) can be rewritten in the following form

$$\begin{aligned} U=\frac{1}{2}{{\varvec{d}}}^{T}\left[ {{\begin{array}{ll} {{{\varvec{k}}}_{e1m} }&{}\quad {{{\varvec{I}}}_{n1m} {{\varvec{X}}}_w } \\ {{{\varvec{X}}}_w^T {{\varvec{I}}}_{n1m}^T }&{}\quad {{{\varvec{k}}}_{e1b} +{{\varvec{I}}}_{n1b} {{\varvec{X}}}_w +{{\varvec{X}}}_w^T {{\varvec{I}}}_{n1b}^T +{{\varvec{X}}}_w^T {{\varvec{I}}}_{n2} {{\varvec{X}}}_w } \\ \end{array} }} \right] {{\varvec{d}}}. \end{aligned}$$

(45)

This elastic deformation energy is important for the post-buckling analysis of the thin-walled members based on the energy SA-FSMs [19, 25].

3.2 Computational process analysis

In above section, two invariant matrices ${{\varvec{I}}}_{n1}$, ${{\varvec{I}}}_{n2}$ and the nodal line coordinate matrix ${{\varvec{X}}}_w$ defined in Eqs. (38), (43), and (33), respectively, are introduced to improve the computational efficiency of the stiffness matrix in the finite strip method for the buckling analysis of the thin-walled members.

In order to clearly compare the solution processes with and without invariant matrices, two corresponding flowcharts are summarized in Fig. 3a, b, both of which can be divided into the following three stages:

In stage 1, all computational parameters of the structural system can be set firstly which include the length a and the width b of the strip, the number n of the strips, the thickness h of the strip element, initial axial force of each strip $T_0$, elastic modulus E, Poisson’s ratio $\mu$, the maximum load factor $\lambda _{max}$, and load factor increment $\Delta \lambda$. Then the linear term of elastic stiffness matrix and geometric stiffness matrix will be calculated. The initial test solution $D_0$ and the critical buckling load factor will be evaluated by the control equation of linear derivation system which neglects the stiffness items ${{\varvec{K}}}_{e2} ({{\varvec{D}}})$, ${{\varvec{K}}}_{e3} ({{\varvec{D}}})$ and ${{\varvec{K}}}_{e4} ({{\varvec{D}}})$ in Eq. (26). The two Stage 1 of both procedures described by Fig. 3a, b are the same.

Stage 2 is different for two procedures. When the proposed algorithm as shown in stage 2 in Fig. 3b is used, the invariant matrices ${{\varvec{I}}}_{\mathrm {n1}} =\int {{{\varvec{D}}}_1^T {{\varvec{QJ}}}\mathrm{d}V}$ and ${{\varvec{I}}}_{n2} =\int {{{\varvec{J}}}^{T}{{\varvec{QJ}}}} \mathrm{d}V$ can be evaluated firstly. These integration operations are required to be calculated only once and have been shifted out from the following iterations. Then set the initial load factor $\lambda$ and substitute it into the nonlinear control Eq. (26), calculate the elastic stiffness matrices ${{\varvec{k}}}_{e2} ({{\varvec{d}}})$, ${{\varvec{k}}}_{e3} ({{\varvec{d}}})$, and ${{\varvec{k}}}_{e4} ({{\varvec{d}}})$ by the matrix multiplication operations, respectively, given in Eqs. (37), (39), and (42) and assemble the elastic stiffness matrices ${{\varvec{K}}}_{e2} ({{\varvec{D}}})$, ${{\varvec{K}}}_{e3} ({{\varvec{D}}})$, and ${{\varvec{K}}}_{e4} ({{\varvec{D}}})$ in global coordinate system. As for the traditional method, the elastic stiffness matrices ${{\varvec{k}}}_{e2} ({{\varvec{d}}})$, ${{\varvec{k}}}_{e3} ({{\varvec{d}}})$, and ${{\varvec{k}}}_{e4} ({{\varvec{d}}})$ in Eq. (28) will be integrated and these integral operation must be implemented in each step of the iterative calculation for the nonlinear algebra Eq. (26). The method proposed in this study, however, transforms the integral operations into the matrix multiplication operations of the invariant matrices and the displacement vector matrices as shown in Eqs. (37), (39), and (42), which effectively avoids complex and time-consuming iterative integrations.

Fig. 3

Calculation flowcharts a with and b without invariant matrices

Stage 3 given in Fig. 3a or b is the same for two procedures. Firstly, the global stiffness matrix can be evaluated, the test solution of which can be substituted into the nonlinear control equation (Eq. 26). Then the solution $D_{new}$ of the control equations is obtained by the iterative update based on Newton’s method, through which the convergence of the iterative process is checked. If the convergence condition derived from Eq. (26)

$$\begin{aligned} lg\left[ {\left| {\left( {{{\varvec{K}}}_e ({{\varvec{D}}}_0 )-\lambda \left. {{{\varvec{K}}}_g } \right| _{T_0 } } \right) {{\varvec{D}}}_{new} } \right| } \right] \le -12 \end{aligned}$$

(46)

is satisfied, the solution $D_{new}$ can be regarded as the requested one and saved. Otherwise, the solution $D_{new}$ will be set back as the initial test solution $D_0$ into the nonlinear control equation (Eq. 26) for further iterative calculations until it satisfies the convergence condition. The obtained solution here is the displacement vector corresponding to the load factor given in stage 2. Hereafter, a new load factor $\lambda +\Delta \lambda$ is substituted into stage 2 to start the next calculation loop with $\Delta \lambda$ being as the load factor increment until the new load factor reaches the maximum load factor $\lambda _{max}$.

The comparison between two calculation flowcharts shows that the main difference with and without invariant matrices is in stage 2. The fundamental idea of the proposed procedure in this study is to transform the integral operation of ${{\varvec{k}}}_{e2} ({{\varvec{d}}})$, ${{\varvec{k}}}_{e3} ({{\varvec{d}}})$, and ${{\varvec{k}}}_{e4} ({{\varvec{d}}})$ into the matrix multiplication calculation and only half nonzero elements in ${{\varvec{k}}}_{e2} ({{\varvec{d}}})$ and a quarter of nonzero elements in ${{\varvec{k}}}_{e4} ({{\varvec{d}}})$ are required to calculated.

4 Examples and analysis

In this section, several benchmark examples are studied and the corresponding results are compared with those available in the literature or by the FEM, to demonstrate the feasibility, accuracy, and efficiency of the proposed method with MATLAB program. Firstly a classical isotropic square thin plate is analyzed, and the theoretical, the FSM’s and the experimental results are compared. Secondary, the thin-wall members of L-section and Z-section member are built by ABAQUS software, and take it as a benchmark to verify the proposed method in this study. Finally, the high efficiency of the proposed method can be approved by the comparison of calculation times generated from the two FSMs with and without invariant matrices.

4.1 Illustrations of square thin plate

A square isotropic plate with side length subjected to uniaxial uniform pressure, of a is considered. The analysis is based on the CPT condition in which all the plate edges are simply supported, recorded as “SSss”. The basic parameters are given: Elastic Modulus: $E=2\times 10^{5}$ N/mm; Poisson’s ratio: $\mu =0.326$; Shear Modulus: $G=E/2(1+\mu )$; Width: $a=500$ mm; Thickness: $h=10$ mm; Critical force: $T_0 =4\,\pi Eh^{3}/12a^{2}(1-\mu ^{2})$; Dimensionless deflection: $W=w/h$; Dimensionless load factor: $\lambda =T/T_0$. This problem was previously studied by the explicit formulation [46] and the experimental method [47]. Later a two-step perturbation method was proposed to solve von Karman equations, which give rise to the higher-order asymptotic solutions and post-buckling equilibrium paths for perfect and imperfect rectangular plates [48].

Here this benchmark example is studied by the proposed FSM and the square thin plate member is divided into 5 strips evenly along the loaded edge. Figure 4 shows the relationships between the dimensionless deflection W at the center point $O_{1}$ of the plate and the dimensionless load factor $\lambda$ calculated by the proposed FSM with five strip elements, the curves of the theoretical results [48] and the experimental results [47]. The comparison results show that the proposed FSM has good precision for the initial post-buckling analysis of plate members under the boundary condition of simply supported each edge.

Fig. 4

Comparison of initial post-buckling deflection–load curve of plate

Fig. 5

The out-of-plane deflection of the plate at section $y=a/2$ with several load factor

Figure 5 depicts the variation of out-of-plane deflection for plates at section $y=a/2$ under different load factor achieved from the FSM and the theoretical results [48]. From Fig. 5, it can be found that under the same load factor, the out-of-plane deflections of the plates obtained by the two methods have good consistency, which clearly proves that the initial post-buckling mode with the proposed FSM agrees well with the theoretical results.

4.2 Illustrations of L-section member

In this part, the L-section member with the rotation corner is taken into account to verify the reliability of the proposed method for the thin-walled structures. Assume the member is subjected to uniaxial uniform pressure, with the load edges are simply supported and the unload edge are free, namely recorded as “SSff”. The basic parameters will be given: elastic modulus: $E=2\times 10^{5}$ N/mm$^{2}$; Poisson’s ratio: $\mu =0.3$; shear modulus: $G=E/2(1+\mu )$; length: $a=400$ mm; flange width: $b_f =200$ mm; thickness: $h=10$ mm; initial axial force: $T_0 =\pi Eh^{3}/12a^{2}(1-\mu ^{2})$; dimensionless deflection: $W=w/h$; dimensionless load factor: $\lambda =T/T_0$. The finite element model is built up by software ABAQUS to verify the proposed FSM. The shell element in ABAQUS has been used. Since the ratio of width to thickness is large enough, the influence of shear strain can be neglected. Within the ABAQUS software, the linear buckling analysis is divided into two steps. The first step is a linear static analysis that determines the stress for a given reference load group. And the second step is a feature value analysis that provides results based on load factors (eigenvalues) and mode shapes (eigenvectors). Having obtained the modes from linear buckling analysis in the manner described above, they are then used as postulated imperfections in order to perform nonlinear analysis. In this analysis process, the corresponding mode shape is scaled by a small factor and the geometry of the plate is updated by using this mode shape as the new imperfection. The L-section member is evenly divided into 4 strip elements along the loaded edge, with the width of the strip at 100 mm. In order to obtain the sufficient computational precision in the FEM’s simulation the thin-wall member will be divided into 1600 square block elements with the 10 mm$\,\times 10$ mm mesh gird size.

The relationships between the deflection of the middle point $P_1$ of the flange’s lateral edge and the load factor can be obtained by the FSM and the FEM, which are shown in Fig. 6. From this figure, it should be noticed that for the given L-section member, the FSM results agree well with that achieved from the FEM. In addition, Fig. 7 depicts the out-of-plane deflections for L-section member at the location $y=a/2$ under different load factors $\lambda =0.1,\;3,\;4,\;5$ obtained by the FSM and the FEM. It shows that under the same load factor, the buckling modal obtained by FSM and FEM significantly consistent with each other. Both comparative results shown in Figs. 6 and 7 verify the feasibility and high accuracy of the proposed FSM for the initial post-buckling analysis.

Fig. 6

Comparison of initial post-buckling deflection–load curve of L-section member

Fig. 7

Comparison for the out-of-plane deflection of the L-section member at the location $y=a/2$ with several load factors

4.3 Illustrations of Z-section member

A Z-section member, as shown in Fig. 8, with the “SSff” boundary condition subjected to uniaxial uniform pressure is studied to further validate the feasibility of the proposed method. The basic parameters are given: elastic modulus: $E=2\times 10^{5}$ N/mm$^{2}$; Poisson’s ratio: $\mu =0.3$; shear modulus: $G=E/2(1+\mu )$; length: $a=500$ mm; section width: $b_c =300$ mm; flange width: $b_f =100$ mm; thickness: $h=10$ mm; initial axial force: $T_0 =\pi Eh^{3}/12a^{2}(1-\mu ^{2})$; dimensionless deflection: $W=w/h$; dimensionless load factor: $\lambda =T/T_0$. The finite element model with 2500 number of 10 mm$\,\times 10$ mm square block elements to reach the adequate precision will be built by ABAQUS software to demonstrate the feasibility, accuracy of the proposed method. The model of the FSM is divided into 5 strip elements along the loaded edge evenly, with the width of each strip at 100 mm. According to coordinate transformation in Eq. (21), the rotation angles $\alpha$ of the strips are set as $90^{\circ },\;0^{\circ },\;0^{\circ },\;0^{\circ },\;90^{\circ }$ in turn.

Figure 8 shows the relationships between the initial post-buckling deflections at the middle point $Q_1$ of the flange’s lateral edge, the groove center point $Q_2$ of the member and the load factor $\lambda$ calculated by the proposed FSM and the FEM. It indicates that for the initial post-buckling analysis the deflections at the flange and the center of the section are almost the same under the same load factor thought FSM. This phenomenon is consistent with the results of FEM modeling. Secondly, it should be noticed that the FSM results are significantly close to the FEM results with 2500 elements when the number of the strips is equal to 5. Hence we may find that the proposed FSM can achieve approximately accuracy of FEM with fewer elements for the initial post-buckling analysis of Z-section members, under the “SSff” boundary condition. Figure 9 depicts the out-of-plane deflections of the Z-section member at the location $y=a/2$ under different load factors $\lambda =0.1,\;5,\;10,\;12$ obtained by the FSM and the FEM. It reveals that even if the Z-section member itself has rotation corner, the out-of-plane deflection by these two methods still have good consistency in the global coordinate. The comparisons in Figs. 8 and 9 could confirm that the method proposed in this paper is an applicable, effective, and precise method for solving the initial post-buckling of plates and thin-walled members.

Fig. 8

Comparison of initial post-buckling deflection–load curve of Z-section member

Fig. 9

The out-of-plane deflection of the Z-section member at the location $y=a/2$ with several load factors

Fig. 10

Post-buckling modal of “SSss” plates with different ratios $\beta =0.95,\;2.1,\;3.2$

4.4 Comparative analysis

According to the comparative results of above three cases, it should be noticed that the FSM with invariant matrices possesses sufficient precision for the initial post-buckling analysis. In order to elaborated the efficiency of the FSM with invariant matrices, a thin plate member with the same materials as mentioned in Sect. 4.1, the “SSss” boundary condition and the uniaxial uniform pressure is taken into account.

In Table 1, the comparative results of CPU time by the FSM with and without invariant matrices are presented. The model of the length–width ratio of the plate $\beta =0.95\;(,\;2.1,\;3.2)$ is considered by the FSM with the number of finite strips 3 (, 4, 5). The load factor $\lambda$ changes from 0.1 to 1 (, 3 and 5) with an interval of 0.1 and the maximum half-wave number m is 1 (, 2, 3) in the case of $\beta =0.95\;(,\;2.1,\;3.2)$, respectively. If the CPU times of the FSM with and without invariant matrices is donated as $T_{with}$ and $T_{without}$, then the ratio of the CPU time $\eta$ between the FSMs without and with invariant matrices is defined as

$$\begin{aligned} \eta =\frac{T_{\mathrm{without}}}{T_{\mathrm{with}}}, \end{aligned}$$

(47)

Figure 10 depicts post-buckling modes of the three examples in Table 1. The program is implemented by MATLAB platform, and the program code is implemented in the Lenovo computer with Intel(R) Core(TM) i7- 4790CPU @ 3.60 GHz and Windows 7 system. From the first (, second and third) row datum of Table 1, it can be seen that the CPU time of the FSM without invariant matrices is $9.09 \times 10^{3}$ (, $1.74\times 10^{5}$ and $1.05\times 10^{7}$) seconds, the CPU time of the FSM with invariant matrices is $9.1 \times 10^{1}$ (,$5.92 \times 10^{3}$ and $2.14\times 10^{5}$) seconds, and the corresponding ratio of the CPU time $\eta$ without and with invariant matrices is 9.89 (, 29.39 and 49.07). It can be seen clearly that the ratio $\eta$ of consumed time with and without invariant matrices is closed to the number 10 (, 30 and 50) of load factor calculations of the first (, second and third) row datum of Table 1 because the FSM with invariant matrices can economize the CPU time for each load factor. So we can conclude that the FSM by using the invariant matrices can improve the computational efficiency obviously and as the number of calculated load factor increase this advantage of the FSM is more apparent. The tremendously boosted efficiency of FSM can be extensively used in engineering field.

Table 1 Comparison of the CPU time of the plates under several parameter types with and without invariant matrix

5 Conclusion

In order to efficiently evaluate the stiffness matrix and the elastic force in the initial post-buckling analysis of thin-walled members, two invariant matrices ${{\varvec{I}}}_{\mathrm {n1}} =\int {{{\varvec{D}}}_1^T {{\varvec{QJ}}}\,\mathrm{d}V}$ and ${{\varvec{I}}}_{n2} =\int {{{\varvec{J}}}^{T}{{\varvec{QJ}}}}\,\mathrm{d}V$ have been deduced and applied to transform the analytical integral of the stiffness matrix into the matrix multiple calculation. Three benchmark examples are studied and the results are compared with those available in the literature or by the FEM, to demonstrate the feasibility, accuracy and efficiency of the proposed method. The results determined by different methods can verify the proposed FSM with invariant matrices is an effective and efficient technology to analyze the initial post-buckling of thin-walled members.

In addition, the essential advantage of the proposed FSM with invariant matrices are summarized as: (1) The invariant matrices just need to be analytically integrated in advance only once; (2) the analytical integral of the stiffness matrix can be transformed into the matrix multiple calculation; (3) highly efficient analysis of the initial post-buckling of thin-walled members can be implemented.