A hybrid-stress formulation based reduced-order method using a solid-shell element for geometrically nonlinear buckling analysis

Abstract

The high computational efficiency of the Koiter reduced-order methods for structural buckling analysis has been extensively validated; however the high-order strain energy variations in constructing reduced-order models is still time-consuming, especially when involving the fully nonlinear kinematics. This paper presents a reduced-order method with the hybrid-stress formulation for geometrically nonlinear buckling analysis. A solid-shell element with Green-Lagrange kinematics is developed for three-dimensional analysis of thin-walled structures, in which the numerical locking is eliminated by the assumed natural strain method and the hybrid-stress formulation. The fourth-order strain energy variation is avoided using the two-field variational principle, leading to a significantly lower computational cost in construction of the reduced-order model. The numerical accuracy of the reduced-order model is not degraded, because the third-order approximation to equilibrium equations is recovered by condensing the stress. Numerical examples demonstrate that although the fourth-order strain energy variation is not involved, the advantage in path-following analysis using large step sizes is not only unaffected, but also enhanced in some cases with respect to the displacement based reduced-order method. The small computational extra-cost for the hybrid-stress formulation is largely compensated by the reduced-order analysis.

1 Introduction

Thin-walled structures are widely utilized as critical load-bearing components in aeronautical and aerospace engineering disciplines due to their favorable lightweight characteristics. Buckling has already become one of the main failure behaviors for thin-walled structures and often exhibits a severe and sudden nature, frequently leading to catastrophic accidents [1]. It is a known factor that the large out-of-plane deformation is inevitable when the structure is buckled; furthermore, a significant deflection may also occur early in the pre-buckling stage for the structures with a certain geometry and/or load condition. Therefore, geometrical nonlinearities should be fully considered to explore the load-carrying capability of thin-walled structures in the presence of buckling.

Buckling of thin-walled structures has been extensively studied by many researchers. Sadamoto et al. [2] conducted the eigenvalue buckling analysis of curvilinear shells with and without cutouts using an effective meshfree method. The buckling behavior of moderately-thick plates subjected to an in-plane biaxial compressive load was investigated by Ipek et al. [3] using the first-order shear deformation plate theory and the Galerkin method. Saoud et al. [4] adopted finite element (FE) method to investigate the buckling behavior of sandwich constructions and pointed out that buckling remains a major failure mode. Hao and Wang et al. [5,6,7] studied the significant reduction on load-carrying capacity of thin-walled cylindrical shells to the theoretical prediction and developed several novel strategies based on the finite element method to achieve a lightweight design. A modified generalized-$\alpha$ time integration scheme was combined with a geometric nonlinear isogeometric Kirchhoff-Love shell element by Guo et al. [8] to study the buckling and post-buckling behaviors of thin-shell structures. Rajanna et al. [9] applied the finite element method to study the influence of ply-orientation, nonuniform edge loads, boundary conditions, and cutout sizes on buckling characteristics of composite laminates. A novel symplectic analytic solution was developed by Li et al. [10] to study the buckling behavior of composite rectangular plates.

In recent years, the finite element method has become a primary tool for studying the buckling problems of thin-walled structures, with possibly the greatest impact among all numerical method [11]. The selected element formulations significantly impact the computational accuracy and efficiency of the finite element analysis. Shell elements are frequently employed to simulate the structures with a large span-thickness ratio; however they have some limitations compared with the solid-shell elements. Solid-shell elements can directly discretize the three-dimensional (3D) CAD structural model and utilize the 3D material constitutive relations, which cannot be realized by the shell element with a 2D geometry. Shell elements require complex operations on updating the finite rotations, while solid-shell elements with only translational degrees of freedom can avoid these issues. In addition, the solid-shell elements have a capability of dealing with the complicated contact problems by accurately capturing the through-thickness stresses. Therefore, the construction and application of solid-shell elements have been studied by many scholars. Kulikov et al. [12] established an accurate geometry solid-shell element using a sampling surfaces method and then applied it to the nonlinear 3D stress analysis in buckling and fracture problems of shell structures. An unsymmetric 8-node hexahedral solid-shell element was developed by Wu et al. [13] to be insensitive to mesh distortion. Dia et al. [14] combined the prismatic and hexahedral solid-shell elements to simulate the structures with a more complex geometric shape. Wang et al. [15] proposed two quadratic solid-shell elements for the 3D modeling of thin structures, which are implemented into the FE software ABAQUS and appropriate for problems involving large displacements and rotations as well as plasticity. An enhanced solid-shell model was established by Mellouli et al. [16] through incorporating the eight-node element with the first-order shear deformation theory.

The solid-shell element needs to overcome various locking problems that probably occur in the element with a 3D geometry, for instance, the trapezoidal, shear, membrane, thickness, and volumetric lockings [17,18,19,20,21,22,23,24]. The Assumed Natural Strain (ANS) method [25, 26], Enhanced Assumed Strain (EAS) method [27,28,29], and hybrid-stress formulation [30,31,32,33,34], are commonly applied to avoid the above locking phenomenons. The shear and membrane lockings, as well as trapezoidal locking, can be eliminated by the ANS method through interpolating the strain values at the reference points [35]. Caseiro et al.[36] extended the ANS method to NURBS-based elements within the context of a solid-shell formulation. The EAS method overcomes the volumetric and Poisson thickness lockings by additionally assuming a strain in the thickness direction [37]. The Hybrid-stress formulation can also be used to overcome the volumetric and Poisson thickness lockings by assuming a stress in the thickness direction and applying a modified generalized stiffness matrix [38]. The hybrid-stress elements developed based on a two-field (displacement and stress) variational principle, are not affected by the material compressibility and/or the span-thickness ratio, demonstrating an excellent performance compared with the standard displacement-based elements [39]. Sze [40] developed an eight-node hybrid-stress solid-shell element for the geometric nonlinear analysis of elastic shells based on the Hellinger-Reissner variational principle, which suppresses the element locking using the ANS method and a modified generalized material constitutive model. Wisniewski et al. [41] developed a mixed eight-node solid-shell elements based on the standard or partial version of the three-field Hu-Washizu functional. It has been found that the hybrid-stress element converges more readily than the selectively reduced integrated element; however the introduction of additional stress parameters requires more computing resources [42]. Although these stress parameters can be condensed when assembling the element stiffness, the extra operation is complex and the recovering of the stress still needs the matrix inversions at the element level.

As stated above, the selection of solid-shell elements has obvious advantages and potentials in finite element analysis of buckling problems of thin-walled structures. The consideration of geometrical nonlinearities requires repeated solutions of the linearized FE equations in an incremental-iterative process, leading to a significant demand on the computational resource especially for a large-scale FE system. Although the hybrid-stress formulation can overcome the locking problems when adopting the solid-shell element to achieve a 3D FE simulation for structures with a large span-thickness ratio, the additional stress parameters and the relevant extra operations further aggravate the computational burden in geometrically nonlinear analysis. Therefore, a series of reduced-order methods [43,44,45,46,47,48,49,50] has been proposed based on the Koiter’s theory[51] to decrease the scale of the nonlinear equilibrium equations required for buckling analysis. Initially, the small-scaled reduced-order model was constructed only once at the bifurcation point and a limited range of validity satisfactory up to the initial post-buckling stage can be obtained. Rahman et al. [52, 53] extended the method to consider the geometrical nonlinearities in the pre-buckling regime. Garcea and Zagari [54, 55] enhanced the range of validity of the Koiter’s solution using an asymptotic expansion based on the path tangent, buckling modes, and second-order modes. A Koiter-Newton method was proposed by Liang et al. [56, 57] to achieve a completely path-following analysis for nonlinear buckling problems, in which the Koiter asymptotic expansion is available at any equilibrium state of the structure. There is no doubt that the reduced-order model can significantly decrease the computational cost of nonlinear buckling analysis; however the Koiter’s perturbation theory requires the elemental strain energy variations up to the fourth-order with respect to the degrees of freedom (DOFs), that is two orders higher than the conventional finite element method. The complicated operations related to high-order variations bring difficulties into the FE implementation of the Koiter based reduced-order methods, and also increase the computational cost in construction of the reduced-order model.

The selection of nonlinear kinematics used for the reduced-order method is a key factor that affects the calculation of the high-order strain energy variations. The simplified Green-Lagrange kinematics were developed by Tiso [58] for Koiter reduced-order analysis. Castro and Jansen [59, 60] selected the von Kármán nonlinear kinematics and proposed a transparent correspondence to clearly present the relationships between the displacement-based formulation and the numerical achievement identified for Koiter analysis. The co-rotational and von Kármán kinematics were used to deduce the FE formulations of the Koiter-Newton method [57, 61]. Sinha et al. [62] developed an incremental updating procedure to decrease the computational cost of the Koiter-Newton analysis based on the Green-Lagrange kinematics. The mixed formulations, a combination of fully and simplified kinematics, were proposed by Liang et al. [63] to construct reduced-order models for the large deflection problem of thin-walled structures. Garcea, Magisano and Liguori et al. [64,65,66,67] developed a mixed stress-displacement formulation to simplify the finite element analysis of Koiter’s analysis using the Green-Lagrange kinematics. The reason is attributed to the fact that both displacement and stress are degrees of freedom in the strain energy functional expression, where the highest order is cubic; therefore the fourth-order variation is zero.

The main contribution of this work is to reformulate the Koiter-Newton reduced-order method using a hybrid-stress formulation, to avoid the fourth-order strain energy variation while not sacrificing the effectiveness of the reduced-order model. It can be achieved by conducting the high-order strain energy variations using a two-field variational principle and then recovering the third-order approximation to the equilibrium equations after the stress condensation. In this way, a reduced-order model is constructed by the hybrid-stress formulation at much lower cost compared with that by the displacement based formulation; whereas the asymptotic accuracy of the reduced system is not affected. A predictor-corrector strategy is developed for the proposed hybrid-stress formulation based reduced-order method to trace the nonlinear equilibrium path in a step-by-step manner. Various numerical examples demonstrate the accuracy and high-efficiency of the proposed method for geometrically nonlinear buckling analysis.

The rest of the paper is arranged as follows. A hybrid-stress solid-shell element is developed considering the geometrical nonlinearities in Sect. 2. A full-order finite element method using the hybrid-stress solid-shell element is presented in Sect. 3 for geometrically nonlinear analysis. A reduced-order method is proposed using the hybrid-stress formulation in Sect. 4 for nonlinear buckling analysis. Various numerical examples are applied to test the performance of the proposed reduced-order method in Sect. 5. We summarize the work in Sect. 6.

2 Hybrid-stress solid-shell element considering geometrical nonlinearities

Fig. 1

The diagram of the solid-shell element. (Colour figure online)

To accommodate the three-dimensional geometry of a thin-walled structure, a hybrid-stress solid-shell element is employed, comprising a total of 8 nodes that are numbered in a counterclockwise order. Within the element, a local coordinate system denoted as (x-y-z) and a natural coordinate system denoted as ($\xi$-$\eta$-$\zeta$) are established. In the local coordinate system, the z-axis is along the thickness direction. However, the structure is meshed in the global coordinate system ($x'$-$y'$-$z'$), the $z'$-axis of which probably does not align with the thickness direction of the element, because the element can be arbitrarily placed. Therefore, it is necessary to establish a relationship between the global and local coordinate systems, which can map the global coordinates $x'$, $y'$, $z'$ to the local ones x, y, z, such that the local z-axis always aligns with the thickness direction. This relationship is derived in Appendix A.

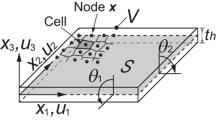
The natural coordinate system varies with the element shape, of which the coordinates $\xi$, $\eta$, and $\zeta$ are all within the range of −1 to 1. The functional values at any point within the element can be achieved through the interpolation of the nodal values. The schematic diagram of the solid-shell element is shown in Fig. 1. The shape functions within the mid-surface of the element are defined as follows,

$$\begin{aligned} \begin{gathered} N_{1}=\frac{1}{4}(1-\xi )(1-\eta ) \\ N_{2}=\frac{1}{4}(1+\xi )(1-\eta ) \\ N_{3}=\frac{1}{4}(1+\xi )(1+\eta ) \\ N_{4}=\frac{1}{4}(1-\xi )(1+\eta ) \end{gathered}. \end{aligned}$$

(1)

The coordinate $x_i$ and displacement functions $U_i$ are presented using the linear interpolations, as follows,

$$\begin{aligned} {\left\{ \begin{array}{ll} x_i(\xi ,\eta ,\zeta )=N_I(\xi ,\eta )\left[ \dfrac{1}{2}(1+\zeta )x_{iI}+\dfrac{1}{2}(1-\zeta )x_{i(I+4)}\right] \\ U_i(\xi ,\eta ,\zeta ){=}N_I(\xi ,\eta )\left[ \dfrac{1}{2}(1{+}\zeta )U_{iI}{+}\dfrac{1}{2}(1{-}\zeta )U_{i(I+4)}\right] \end{array}\right. }\nonumber \\ \text {I: from 1 to 4}, \end{aligned}$$

(2)

where the subscript i runs from 1 to 3, and the subscript I employs the Einstein summation convention.

A more concise form of Eq. (2) is obtained,

$$\begin{aligned} {\left\{ \begin{array}{ll} x_i(\xi ,\eta ,\zeta )=N_{0I}x_{iI}+\zeta N_{nI}x_{iI}\\ U_i(\xi ,\eta ,\zeta )=N_{0I}U_{iI}+\zeta N_{nI}U_{iI} \end{array}\right. } \text {I: from 1 to 8}, \end{aligned}$$

(3)

in which,

$$\begin{aligned} {\left\{ \begin{array}{ll} N_{0I}=\dfrac{1}{2}\left[ N_{1},N_{2},N_{3},N_{4},N_{1},N_{2},N_{3},N_{4}\right] \\ N_{nI}=\dfrac{1}{2}\left[ N_{1},N_{2},N_{3},N_{4},-N_{1},-N_{2},-N_{3},-N_{4}\right] \end{array}\right. }\nonumber \\ \text {I: from 1 to 8}. \end{aligned}$$

(4)

In the local coordinate system, we assume that the thickness value within the solid-shell element is kept constant and the projections of the upper and lower surfaces of the element onto the mid-surface coincide perfectly; thus the node coordinates should satisfy the following relationship,

$$\begin{aligned} {\left\{ \begin{array}{ll} x_I=x_{I+4}\\ y_I=y_{I+4}\\ z_1=z_2=z_3=z_4\\ z_5=z_6=z_7=z_8 \end{array}\right. } \text {I: from 1 to 4}, \end{aligned}$$

(5)

where the thickness direction of the solid-shell element is parallel to both the z-axis of the local coordinate system and the $\zeta$-axis of the natural coordinate system.

The Jacobian matrix describes the transformation relationship between the local and natural coordinate systems, the components $J_{ij}$ of which are given by,

$$\begin{aligned} J_{ij}=\frac{\partial x_i}{\partial \xi _j}= \begin{bmatrix} \dfrac{\partial x}{\partial \xi }&{}\dfrac{\partial x}{\partial \eta }&{}\dfrac{\partial x}{\partial \zeta }\\ \dfrac{\partial y}{\partial \xi }&{}\dfrac{\partial y}{\partial \eta }&{}\dfrac{\partial y}{\partial \zeta }\\ \dfrac{\partial z}{\partial \xi }&{}\dfrac{\partial z}{\partial \eta }&{}\dfrac{\partial z}{\partial \zeta } \end{bmatrix}. \end{aligned}$$

(6)

Substituting the coordinate interpolation functions (3) to Equation (6), we have,

$$\begin{aligned} {\left\{ \begin{array}{ll} J_{ij}=\dfrac{\partial x_i}{\partial \xi _j}=\dfrac{\partial (N_{0I}x_{iI}+\zeta N_{nI}x_{iI})}{\partial \xi _j}\\ =\dfrac{\partial N_{0I}}{\partial \xi _j}x_{iI}+\zeta \dfrac{\partial N_{nI}}{\partial \xi _j}x_{iI}&{}\text {(if }\xi _j=\xi \text { or }\eta )\\ J_{ij}=\dfrac{\partial x_i}{\partial \xi _j}=\dfrac{\partial (N_{0I}x_{iI}+\zeta N_{nI}x_{iI})}{\partial \zeta }=N_{nI}x_{iI}&{}\text {(if }\xi _j=\zeta ) \end{array}\right. }. \nonumber \\ \end{aligned}$$

(7)

According to Eqs. (4) and (5), the following relations are obtained,

$$\begin{aligned} {\left\{ \begin{array}{ll} N_{nI}x_{iI}=0&{}(x_i=x\text { or }y)\\ J_{13}=J_{23}=J_{32}=J_{31}=0 \end{array}\right. }. \end{aligned}$$

(8)

Equation (8) indicates that when transforming physical quantities between the local and natural coordinate systems, the in-plane and out-of-plane operations are uncoupled. Substituting Eq. (8) into (7), the Jacobian matrix is rewritten as,

$$\begin{aligned} J_{ij}= \begin{bmatrix} \dfrac{\partial N_{0I}}{\partial \xi }x_I&{}\dfrac{\partial N_{0I}}{\partial \eta }x_I&{}0\\ \dfrac{\partial N_{0I}}{\partial \xi }y_I&{}\dfrac{\partial N_{0I}}{\partial \eta }y_I&{}0\\ 0&{}0&{}N_{_{nI}}z_I \end{bmatrix}. \end{aligned}$$

(9)

The displacement transformation described by the Jacobian matrix between the natural and local coordinate systems is,

$$\begin{aligned} \bar{U}_j=J_{ij}U_i, \end{aligned}$$

(10)

where $\bar{U}_j$ and $U_{i}$ indicate the natural and local displacements, respectively.

The partial derivative of the displacement with respect to the coordinates is obtained by,

$$\begin{aligned}{} & {} \frac{\partial \bar{U}_{j}}{\partial \xi _{m}} = J_{ij} \frac{\partial U_{i}}{\partial \xi _{m}} = J_{ij} \frac{\partial N_{I}}{\partial \xi _{m}} U_{iI}\nonumber \\{} & {} \quad ={\left\{ \begin{array}{ll} J_{ij} \dfrac{\partial N_{0I}}{\partial \xi _{m}} U_{iI} + \zeta J_{ij} \dfrac{\partial N_{nI}}{\partial \xi _{m}} U_{iI} &{} \text {if } \xi _{m} = \xi \text { or } \eta \\ J_{ij} N_{nI} U_{iI} &{} \text {if } \xi _{m} = \zeta \end{array}\right. }. \end{aligned}$$

(11)

In the natural coordinate system, the Green-Lagrange strain is expressed by,

$$\begin{aligned} \bar{E}_{ij}=\dfrac{1}{2} \Bigg ( \dfrac{\partial \bar{U}_i}{\partial \xi _j}+\dfrac{\partial \bar{U}_j}{\partial \xi _i}+\dfrac{\partial \bar{U}_k}{\partial \xi _i}\dfrac{\partial \bar{U}_k}{\partial \xi _j} \Bigg ). \end{aligned}$$

(12)

The Green-Lagrange strain is represented to be a strain vector $\bar{\textbf{E}} = \begin{bmatrix}\bar{E}_{\xi \xi }, \bar{E}_{\eta \eta }, 2\bar{E}_{\xi \eta }, \bar{E}_{\zeta \zeta }, 2\bar{E}_{\eta \zeta }, 2\bar{E}_{\xi \zeta }\end{bmatrix}^T$, using a Voigt notation. Substituting Equation (11) into the Green-Lagrange strain, the strain–displacement relationship is written as,

$$\begin{aligned} \bar{\textbf{E}}=\bar{\textbf{B}}_{{\textrm{l}}}\textbf{q}+\frac{1}{2}\bar{\textbf{B}}_{{\textrm{nl}}}(\textbf{q})\textbf{q}, \end{aligned}$$

(13)

where $\bar{\textbf{B}}_{{\textrm{l}}}$ and $\bar{\textbf{B}}_{{\textrm{nl}}}(\textbf{q})$ are the linear and nonlinear interpolation matrices, respectively, and the vector $\textbf{q}$ collects the nodal displacements $U_{iI}$ in to a column vector.

The shear, membrane, trapezoidal, and thickness locking problems need to be overcome for the solid-shell element [34]. For the shear and trapezoidal lockings, the natural transverse normal and shear strains are redefined through the assumed natural strain (ANS) method, as follows,

$$\begin{aligned} \begin{aligned} \bar{E}_{\zeta \zeta }&= N_1 \bar{E}_{\zeta \zeta } (-1, -1, 0) + N_2 \bar{E}_{\zeta \zeta }(1, -1, 0) \\&\quad + N_3 \bar{E}_{\zeta \zeta } (1, 1, 0) + N_4 \bar{E} _{\zeta \zeta }(-1, 1, 0) \\ \bar{E}_{\eta \zeta }&= \frac{1}{2}(1-\xi )\bar{E}_{\eta \zeta }\left( -1,0,0\right) +\frac{1}{2}(1+\xi )\bar{E}_{\eta \zeta }\left( 1,0,0\right) \\ \bar{E}_{\xi \zeta }&= \frac{1}{2}(1-\eta )\bar{E}_{\xi \zeta }(0,-1,0)+\frac{1}{2}(1+\eta )\bar{E}_{\xi \zeta }(0,1,0) \end{aligned}.\nonumber \\ \end{aligned}$$

(14)

The strain transformation relationship between the natural and local coordinate systems is,

$$\begin{aligned} \textbf{E}=\textbf{T}_{\varepsilon }\bar{\textbf{E}}=\textbf{T}_{{\mathrm{\varepsilon }}}\left[ \bar{\textbf{B}}_{{\textrm{l}}}\textbf{q}+\frac{1}{2}\bar{\textbf{B}}_{{\textrm{nl}}}(\textbf{q})\textbf{q}\right] , \end{aligned}$$

(15)

where $\textbf{E}$ and $\bar{\textbf{E}}$ are the Green-Lagrange strains in the local and natural coordinate systems, respectively, $\textbf{T}_{\varepsilon }$ is a strain transformation matrix, the detailed expression of which is given by (B.1) in Appendix B.

In addition to the shear and trapezoidal lockings, the thickness and volume lockings may also occur in a solid-shell element. Sze [40] employed the hybrid-stress formulation to construct a modified constitutive relation for overcoming the locking issues. Referring to the method proposed by Pian [68], the second Piola-Kirchhoff stress S interpolation is given by,

$$\begin{aligned} {\textbf{S} =\begin{bmatrix} \textbf{S}_{{\textrm{xx}}}\\ \textbf{S}_{{\textrm{yy}}}\\ \textbf{S}_{{\textrm{xy}}}\\ \textbf{S}_{{\textrm{zz}}}\\ \textbf{S}_{{\textrm{yz}}}\\ \textbf{S}_{{\textrm{xz}}} \end{bmatrix} =\textbf{T}_{\sigma } \begin{bmatrix} \bar{\textbf{S}}_{\xi \xi }\\ \bar{\textbf{S}}_{\eta \eta }\\ \bar{\textbf{S}}_{\xi \eta }\\ \bar{\textbf{S}}_{\zeta \zeta }\\ \bar{\textbf{S}}_{\eta \zeta }\\ \bar{\textbf{S}}_{\xi \zeta } \end{bmatrix} =\textbf{T}_\sigma \bar{\textbf{P}}\varvec{\beta },} \end{aligned}$$

(16)

where $\textbf{T}_{\sigma }$ is a transformation matrix that converts the stress from the natural to local coordinate systems, $\bar{\textbf{P}}$ is a stress interpolation matrix, and $\varvec{\beta }$ is a set of 18 stress parameters. The detailed expressions for the matrices $\textbf{T}_{\sigma }$ and $\bar{\textbf{P}}$ are given by Eqs. (B.2) and (B.3) in Appendix B, respectively.

In summary, the Green-Lagrange strain $\textbf{E}$ interpolated by nodal displacements $\textbf{q}$, and the stress ${\textbf{S}}$ interpolated by independent stress parameter $\varvec{\beta }$, are obtained, as follows,

$$\begin{aligned} \textbf{E}&=\textbf{B}_{{\textrm{l}}}\textbf{q}+\frac{1}{2}\textbf{B}_{{\textrm{nl}}}(\textbf{q})\textbf{q}, \end{aligned}$$

(17)

$$\begin{aligned} {\textbf{S}}&=\mathbf {P\beta }, \end{aligned}$$

(18)

where $\textbf{P}$ is a stress interpolation matrix defined in the local coordinate system, and $\textbf{B}_{{\textrm{l}}}$ and $\textbf{B}_{{\textrm{nl}}}$ are the linear and nonlinear interpolation matrices, respectively. These matrices are obtained by $\bar{\textbf{P}}$, $\bar{\textbf{B}}_{{\textrm{l}}}$, and $\bar{\textbf{B}}_{{\textrm{nl}}}$, using the transformation matrices $\textbf{T}_\varepsilon$ and $\textbf{T}_\sigma$ from the natural to local coordinate systems.

By truncating the second-order terms of $\zeta$ in the in-plane strain $\textbf{E}_{{\textrm{p}}}$, the Green-Lagrange strain $\textbf{E}$ can be written as,

$$\begin{aligned} \textbf{E}= & {} \begin{bmatrix} \textbf{E}_{{\textrm{p}}}\\ E_{{\textrm{z}}}\\ \textbf{E}_{{\textrm{t}}} \end{bmatrix} = \begin{bmatrix} \textbf{E}_{{\textrm{m}}}+\zeta \textbf{E}_{{\textrm{b}}}\\ E_{{\textrm{z}}}\\ \textbf{E}_{{\textrm{t}}} \end{bmatrix}\nonumber \\= & {} \begin{bmatrix} \textbf{B}_{{\textrm{lm}}}+\dfrac{1}{2}\textbf{B}_{{\textrm{nlm}}}(\textbf{q})+\zeta [\textbf{B}_{{\textrm{lb}}}+\dfrac{1}{2}\textbf{B}_{{\textrm{nlb}}}(\textbf{q})]\\ \textbf{B}_{{\textrm{lz}}}+\dfrac{1}{2}\textbf{B}_{{\textrm{nlz}}}(\textbf{q})\\ \textbf{B}_{{\textrm{lt}}}+\dfrac{1}{2}\textbf{B}_{{\textrm{nlt}}}(\textbf{q}) \end{bmatrix}, \end{aligned}$$

(19)

where the components $\textbf{E}_{{\textrm{p}}}$, $E_{{\textrm{z}}}$, and $\textbf{E}_{{\textrm{t}}}$ indicate the in-plane, transverse normal, and transverse shear strain terms of the Green-Lagrange strain $\textbf{E}$, respectively.

The stress (18) with three components can be expressed as,

$$\begin{aligned} {\textbf{S} = \begin{bmatrix} \textbf{S}_{{\textrm{p}}}\\ S_{{\textrm{z}}}\\ \textbf{S}_{{\textrm{t}}} \end{bmatrix} = \begin{bmatrix} \textbf{P}_{{\textrm{p}}}\\ \textbf{P}_{{\textrm{z}}}\\ \textbf{P}_{{\textrm{t}}} \end{bmatrix} \varvec{\beta }.} \end{aligned}$$

(20)

The three-dimensional constitutive relation is,

$$\begin{aligned} {\begin{aligned}&\textbf{E}=\textbf{C}^{-1}\textbf{S}\\&\Rightarrow \begin{bmatrix} \textbf{E}_{{\textrm{p}}}\\ E_{{\textrm{z}}}\\ \textbf{E}_{{\textrm{t}}} \end{bmatrix} =\begin{bmatrix} \textbf{F}_{{\textrm{pp}}}&{}\textbf{F}_{{\textrm{pz}}}&{}\textbf{0}\\ \textbf{F}_{{\textrm{pz}}}^{{\textrm{T}}}&{}F_{{\textrm{zz}}}&{}\textbf{0}\\ \textbf{0}&{}\textbf{0}&{}\textbf{F}_{{\textrm{t}}} \end{bmatrix} \begin{bmatrix} \textbf{S}_{{\textrm{p}}}\\ S_{{\textrm{z}}}\\ \textbf{S}_{{\textrm{t}}} \end{bmatrix}, \\ \end{aligned}} \end{aligned}$$

(21)

where ${\textbf{C}^{-1}}$ is a flexibility matrix.

The locking phenomenon can be eliminated by assuming the thickness stress ${S_{{\textrm{z}}}}$ be independent of $\zeta$. Then, the constitutive relation is rewritten into two parts. The in-plane and transverse normal part of the constitutive relation is rewritten by,

$$\begin{aligned}{} & {} \begin{bmatrix} {\textbf{S} _\mathrm{{p}}}\\ E_\mathrm{{z}} \end{bmatrix} =\begin{bmatrix} \textbf{A} &{}\textbf{B}\\ -\textbf{B} ^\mathrm{{T}}&{}D \end{bmatrix} \begin{bmatrix} \textbf{E} _\mathrm{{p}}\\ {S_\mathrm{{z}}} \end{bmatrix}\nonumber \\{} & {} \quad =\begin{bmatrix} \textbf{F} _\mathrm{{pp}}^{-1}&{}- \textbf{F}_\mathrm{{pp}} ^{-1}\textbf{F}_\mathrm{{pz}}\\ \textbf{F}_\mathrm{{pz}} ^\mathrm{{T}}\textbf{F} _\mathrm{{pp}}^{-1} &{}F_\mathrm{{zz}}-\textbf{F} _\mathrm{{pz}}^\mathrm{{T}} \textbf{F}_\mathrm{{pp}} ^{-1}\textbf{F}_\mathrm{{pz}} \end{bmatrix} \begin{bmatrix} \textbf{E} _\mathrm{{p}}\\ {S_\mathrm{{z}}} \end{bmatrix}. \end{aligned}$$

(22)

The transverse shear part of the constitutive relation is presented by,

$$\begin{aligned} \textbf{E}_{{\textrm{t}}}=\textbf{F}_{{\textrm{t}}}{\textbf{S}_{{\textrm{t}}}}. \end{aligned}$$

(23)

Substituting the relation $\textbf{E}_{{\textrm{p}}}=\textbf{E}_{{\textrm{m}}}+\zeta \textbf{E}_{{\textrm{b}}}$ of Eq. (19) into the Eq. (22), and then extracting the terms related to $\zeta$, the following equations are achieved,

$$\begin{aligned} \begin{bmatrix} {\textbf{S}_{{\textrm{p}}}}\\ E_{{\textrm{z}}}\\ \zeta {\textbf{S}_{{\textrm{p}}}} \end{bmatrix} =\begin{bmatrix} \textbf{A}&{}\textbf{B}&{}\zeta \textbf{A}\\ -\textbf{B}^{{\textrm{T}}}&{}D&{}-\zeta \textbf{B}^{{\textrm{T}}}\\ \zeta \textbf{A}&{}\zeta \textbf{B}&{}\zeta ^2\textbf{A} \end{bmatrix} \begin{bmatrix} \textbf{E}_{{\textrm{m}}}\\ {S_{{\textrm{z}}}}\\ \textbf{E}_{{\textrm{b}}} \end{bmatrix}. \end{aligned}$$

(24)

Pre-integrating the above equations along the $\zeta$ direction, we have,

$$\begin{aligned} \begin{aligned}&\int _\zeta \begin{bmatrix} {\textbf{S}_{{\textrm{p}}}}\\ E_{{\textrm{z}}}\\ \zeta {\textbf{S}_{{\textrm{p}}}} \end{bmatrix}d\zeta = \int _\zeta \begin{bmatrix} \textbf{A} &{} \textbf{B} &{} \zeta \textbf{A} \\ -\textbf{B}^{{\textrm{T}}} &{} D &{} -\zeta \textbf{B}^{{\textrm{T}}} \\ \zeta \textbf{A} &{} \zeta \textbf{B} &{} \zeta ^2\textbf{A} \end{bmatrix} d\zeta \begin{bmatrix} \textbf{E}_{{\textrm{m}}}\\ {S_{{\textrm{z}}}}\\ \textbf{E}_{{\textrm{b}}} \end{bmatrix} \\&\Rightarrow \int _{\zeta } \begin{bmatrix} {\textbf{S}_{{\textrm{p}}}}\\ E_{{\textrm{z}}}\\ \zeta {\textbf{S}_{{\textrm{p}}}} \end{bmatrix}d\zeta = \begin{bmatrix} \textbf{A}_0 &{} \textbf{B}_0 &{}\textbf{A}_1 \\ -\textbf{B}_0^{{\textrm{T}}} &{} D_0 &{} -\textbf{B}_1^{{\textrm{T}}} \\ \textbf{A}_1 &{} \textbf{B}_1 &{} \textbf{A}_2 \end{bmatrix} \begin{bmatrix} \textbf{E}_{{\textrm{m}}}\\ {S_{{\textrm{z}}}}\\ \textbf{E}_{{\textrm{b}}} \end{bmatrix}. \end{aligned}\nonumber \\ \end{aligned}$$

(25)

According to Eq. (25), the modified constitutive relations are presented by,

$$\begin{aligned}{} & {} \begin{bmatrix} \int _{\zeta }{\textbf{S}_{{\textrm{p}}}}d\zeta \\ {S_{{\textrm{z}}}}\\ \int _{\zeta }\zeta {\textbf{S}_{{\textrm{p}}}}d\zeta \end{bmatrix} {=} \begin{bmatrix} \textbf{A}_0{+}\textbf{B}_0\textbf{B}_0^{{\textrm{T}}}/D_0 &{} \textbf{B}_0/D_0 &{} \textbf{A}_1{+}\textbf{B}_0\textbf{B}_1^{{\textrm{T}}}/D_0 \\ \textbf{B}_0^{{\textrm{T}}}/D_0 &{} 1/D_0 &{} \textbf{B}_1^{{\textrm{T}}}/D_0 \\ \textbf{A}_1{+}\textbf{B}_1\textbf{B}_0^{{\textrm{T}}}/D_0 &{} \textbf{B}_1/D_0 &{} \textbf{A}_2{+}\textbf{B}_1\textbf{B}_1^{{\textrm{T}}}/D_0 \end{bmatrix}\nonumber \\{} & {} \begin{bmatrix} \textbf{E}_m\\ \int _{\zeta }E_{{\textrm{z}}}d\zeta \\ \textbf{E}_b \end{bmatrix}. \end{aligned}$$

(26)

The strain energy of the hybrid-stress solid-shell element is written as,

$$\begin{aligned} {U(\textbf{S},\textbf{E})=\int _{V}\left( -\frac{1}{2}\textbf{S}^{{\textrm{T}}}\textbf{C}^{-1}\textbf{S}+\textbf{S}^{{\textrm{T}}}\textbf{E}\right) dV,} \end{aligned}$$

(27)

where the strain energy (27) can be divided into two parts. The first part of the strain energy (27) is related to the independent stress ${\textbf{S}}$ and flexibility matrix ${\textbf{C}^{-1}}$, as given by,

$$\begin{aligned} {\begin{aligned}&\int _{V}(\textbf{S}^{{\textrm{T}}}\textbf{C}^{-1}\textbf{S})dV \\&= \int _S\left\{ \begin{bmatrix} \int _\zeta \textbf{S}_{{\textrm{p}}}d\zeta&S_{z}&\int _\zeta \zeta \textbf{S}_{{\textrm{p}}}d\zeta \end{bmatrix}\right. \\&\quad \begin{bmatrix} \textbf{A}_0 + \textbf{B}_0\textbf{B}_{0}^{{\textrm{T}}}/D_0 &{}\textbf{B}_0/D_0 &{} \textbf{A}_1 + \textbf{B}_0B_{1}^{{\textrm{T}}}/D_0 \\ \textbf{B}_{0}^{{\textrm{T}}}/D_0 &{} {1}/D_0 &{} \textbf{B}_{1}^{{\textrm{T}}}/D_0 \\ \textbf{A}_1 + \textbf{B}_1B_{0}^{{\textrm{T}}}/D_0 &{} \textbf{B}_1/D_0 &{} \textbf{A} _2+ \textbf{B}_1\textbf{B}_{1}^{{\textrm{T}}}/D_0 \end{bmatrix}^{-1}\\&\quad \left. \begin{bmatrix} \int _\zeta \textbf{S}_{{\textrm{p}}}d\zeta \\ S_{{\textrm{z}}} \\ \int _\zeta \zeta \textbf{S}_{{\textrm{p}}}d\zeta \end{bmatrix} \right\} dS\\&\quad + \int _S \left\{ \int _\zeta \textbf{S}_{{\textrm{t}}}\textbf{F}_{{\textrm{t}}}\textbf{S}_{{\textrm{t}}}d\zeta \right\} dS. \end{aligned}}\nonumber \\ \end{aligned}$$

(28)

The second part of the strain energy (27) includes the independent stress ${\textbf{S}}$ and Green-Lagrange strain $\textbf{E}$, as given by,

$$\begin{aligned} {\int _{V}\textbf{S}^{{\textrm{T}}}\textbf{E}= \int _S \left\{ \begin{bmatrix} \int _{\zeta } \textbf{S}_{{\textrm{p}}} d\zeta&2S_{{\textrm{z}}}&\int _{\zeta } \zeta \textbf{S}_{{\textrm{p}}} d\zeta&2\textbf{S}_{{\textrm{t}}} \end{bmatrix} \begin{bmatrix} \textbf{E}_{{\textrm{m}}}\\ E_{{\textrm{z}}}\\ \textbf{E}_{{\textrm{b}}}\\ \textbf{E}_{{\textrm{t}}} \end{bmatrix} \right\} dS.} \nonumber \\ \end{aligned}$$

(29)

Substituting expressions (28) and (29) into (27), and then introducing relationships (17) and (18), the strain energy (27) is represented to be,

$$\begin{aligned} U=-\dfrac{1}{2}\varvec{\beta }^{{\textrm{T}}}\mathbf {H\beta }+\varvec{\beta }^{{\textrm{T}}}(\textbf{G}_{{\textrm{l}}}+\dfrac{1}{2}\textbf{G}_{{\textrm{nl}}}(\textbf{q}))\textbf{q}, \end{aligned}$$

(30)

in which,

$$\begin{aligned} \textbf{H}&= \int _{V}{\textbf{P}^{{\textrm{T}}}{\textbf{C}^{-1}}\textbf{P}dV}, \end{aligned}$$

(31)

$$\begin{aligned} \textbf{G}_{{\textrm{l}}}&= \int _{V}{\textbf{P}^{{\textrm{T}}}\textbf{B}_{{\textrm{l}}}dV}, \end{aligned}$$

(32)

$$\begin{aligned} \textbf{G}_{{\textrm{nl}}}&= \int _{V}{\textbf{P}^{{\textrm{T}}}\textbf{B}_{{\textrm{nl}}}dV}, \end{aligned}$$

(33)

where $\textbf{H}$ is derived from Eq. (28), and $\textbf{G}_{{\textrm{l}}}$ and $\textbf{G}_{{\textrm{nl}}}$ are obtained by Eq. (29). $\textbf{G}_{{\textrm{nl}}}(\textbf{q})$ represents a dot product of the three-dimensional tensor $\textbf{G}_{{\textrm{nl}}}$ and displacement vector $\textbf{q}$. The three-dimensional tensor $\textbf{G}_{{\textrm{nl}}}$ is only related to the coordinates of the element.

3 Full-order method using the hybrid-stress formulation

The total potential energy $\Pi$ of the element is,

$$\begin{aligned} \Pi =U-V, \end{aligned}$$

(34)

in which,

$$\begin{aligned} V=\textbf{q}^{{\textrm{T}}}(\lambda \textbf{f}_{{\textrm{ext}}}), \end{aligned}$$

(35)

where U is the strain energy presented by Eq. (30), V is the external potential energy, and the external load is expressed by $\textbf{f}_{{\textrm{ext}}}$ with a load multiplier $\lambda$.

Applying the two-field variational principle and minimum potential energy, the equilibrium condition is obtained,

$$\begin{aligned} \left\{ \begin{aligned} -\mathbf {H\beta }+\left[ \textbf{G}_{{\textrm{l}}}+\dfrac{1}{2}\textbf{G}_{{\textrm{nl}}}(\textbf{q})\right] \textbf{q}=&\textbf{0},\\ \left[ \textbf{G}_{{\textrm{l}}}+\textbf{G}_{{\textrm{nl}}}(\textbf{q})\right] ^{{\textrm{T}}}\varvec{\beta }=&\lambda \textbf{f}_{{\textrm{ext}}}, \end{aligned} \right. \end{aligned}$$

(36)

where the equilibrium equations include two parameters, the nodal displacement $\textbf{q}$ and stress parameter $\varvec{\beta }$.

Combining the two equations in (36) by condensing the stress parameter $\varvec{\beta }$, equilibrium equations that only relates to the displacement $\textbf{q}$ can be achieved,

$$\begin{aligned} \left[ \textbf{G}_{{\textrm{l}}}+\textbf{G}_{{\textrm{nl}}}(\textbf{q})\right] ^{{\textrm{T}}}\textbf{H}^{-1}\left[ \textbf{G}_{{\textrm{l}}}+\dfrac{1}{2}\textbf{G}_{{\textrm{nl}}}(\textbf{q})\right] \textbf{q} = \lambda \textbf{f}_{{\textrm{ext}}}. \end{aligned}$$

(37)

The Newton iteration method is applied to solve the nonlinear equilibrium equations (37), in which the tangent stiffness $\textbf{K}_{{\textrm{T}}}(\textbf{q}_0)$ at a known equilibrium configuration is required,

$$\begin{aligned} \textbf{K}_{{\textrm{T}}}(\textbf{q}_0) = \left[ \textbf{G}_{{\textrm{l}}}^{{\textrm{T}}} + \textbf{G}_{{\textrm{nl}}}^{{\textrm{T}}}(\textbf{q}_0)\right] \textbf{H}^{-1} \left[ \textbf{G}_{{\textrm{l}}} + \frac{1}{2}\textbf{G}_{{\textrm{nl}}}(\textbf{q}_0)\right] , \end{aligned}$$

(38)

where $\textbf{q}_0$ is the displacement vector at the currently known equilibrium configuration.

Note that the above derivations are conducted at the element level, the stiffness matrices of the elements still need to be assembled into a whole structure. The geometrically nonlinear response of the structure can be obtained using a path-following technique with the incremental-iterative process, in which the linear FE systems are required to be repeatedly solved. Although the additional stress parameter has been condensed and the scale of linear FE systems is the same as that for the displacement based FE method, the repeated solutions of the FE system is still computationally expensive, especially for the structure with a huge number of degrees of freedom. Therefore, the conventional finite element method is termed the full-order method in this work, which is well distinguished from the reduced-order method that will be presented in the following section.

4 Reduced-order method using the hybrid-stress formulation

Similar to the conventional finite element method that presented above, the reduced-order method traces the geometrically nonlinear response of the structure in a step-by-step manner for path-following analysis. In each path-following step, a predictor-corrector strategy is applied by using the solution of the reduced-order model as a nonlinear predictor and Newton iterations as the correctors.

4.1 Nonlinear predictor obtained by the reduced-order model

According to the two-field variational principle, the nonlinear equilibrium equations with two parameters (36) are represented using a general form,

$$\begin{aligned} \textbf{f}(\varvec{\beta },\textbf{q})=\lambda \textbf{f}_{{\textrm{ext}}}, \end{aligned}$$

(39)

where the internal force $\textbf{f}$ is functionally related to the displacement $\textbf{q}$ and the stress parameter $\varvec{\beta }$.

The reduced-order model is constructed at a known equilibrium configuration to approximate the nonlinear equilibrium Eqs. (39). Initially, the already known configuration can be directly selected to be the undeformed configuration ($\varvec{\beta }_0$, $\textbf{q}_0$, $\varvec{\lambda }_0$) and needs to be updated, if necessary, during the path-following analysis. An unknown configuration nearby the known configuration can be expressed by,

$$\begin{aligned} \varvec{\beta }&=\varvec{\beta }_0+\Delta \varvec{\beta }, \end{aligned}$$

(40)

$$\begin{aligned} \textbf{q}&=\textbf{q}_0+\Delta \textbf{q}, \end{aligned}$$

(41)

$$\begin{aligned} \lambda&= \lambda _0+\Delta \lambda , \end{aligned}$$

(42)

where $\Delta \varvec{\beta }$, $\Delta \textbf{q}$, and $\Delta \lambda$ are the increments of the three variables varying from the known to unknown configurations, respectively.

Substituting Eqs. (40), (41), and (42) into Eq. (39), the nonlinear equilibrium Eq. (39) can be expanded using Taylor’s formula, as follow,

$$\begin{aligned} \begin{aligned}&\textbf{f}(\varvec{\beta }_0+\Delta \varvec{\beta },\textbf{q}_{0}+\Delta \textbf{q}) \\&=\textbf{f}(\varvec{\beta }_0,\textbf{q}_0) + \textbf{f}^{'}(\varvec{\beta }_0,\textbf{q}_0,\Delta \varvec{\beta },\Delta \textbf{q}) \\&\quad + \textbf{f}^{(2)}(\varvec{\beta }_0,\textbf{q}_0,\Delta \varvec{\beta }^2,\Delta \textbf{q}^2) + \textbf{f}^{(3)}(\varvec{\beta }_0,\textbf{q}_0,\Delta \varvec{\beta }^3,\Delta \textbf{q}^3) \\&\quad + \textbf{O}(\varvec{\beta }_0,\textbf{q}_0,||\Delta \varvec{\beta }||^4,||\Delta \textbf{q}||^4) \\&=\lambda _0 \textbf{f}_{{\textrm{ext}}}+\Delta \lambda \textbf{f}_{{\textrm{ext}}}, \end{aligned}\nonumber \\ \end{aligned}$$

(43)

where the operators $\textbf{f}^{'}$, $\textbf{f}^{(2)}$, $\textbf{f}^{(3)}$, and $\textbf{O}$ indicate the linear, quadratic, cubic, and higher-order terms of the Taylor expansion, respectively.

Because the equilibrium condition $\textbf{f}(\mathbf {\beta } _0,\textbf{q}_0)=\lambda _0\textbf{f}_{{\textrm{ext}}}$ is naturally satisfied in the already known configuration, Equation (43) is rewritten to be,

$$\begin{aligned}{} & {} \textbf{f}^{'}(\varvec{\beta }_0,\textbf{q}_0,\Delta \varvec{\beta },\Delta \textbf{q}) + \textbf{f}^{(2)}(\varvec{\beta }_0,\textbf{q}_0,\Delta \varvec{\beta }^2,\Delta \textbf{q}^2) \nonumber \\{} & {} \qquad {+} \textbf{f}^{(3)}(\varvec{\beta }_0,\textbf{q}_0,\Delta \varvec{\beta }^3,\Delta \textbf{q}^3) {+} \textbf{O}(\varvec{\beta }_0,\textbf{q}_0,||\Delta \varvec{\beta }||^4,||\Delta \textbf{q}||^4) \nonumber \\{} & {} \quad {=}\Delta \lambda \textbf{f}_{{\textrm{ext}}}, \end{aligned}$$

(44)

where the operators $\textbf{f}^{'}$, $\textbf{f}^{(2)}$, $\textbf{f}^{(3)}$ need to be determined by the higher-order variations of the strain energy (30) with two parameters. The second-order strain energy variation related to $\textbf{f}^{'}$ is,

$$\begin{aligned} \delta ^2U = \begin{Bmatrix} \delta \varvec{\beta }^{{\textrm{T}}}&\delta \textbf{q}^{{\textrm{T}}} \end{Bmatrix} \begin{bmatrix} -\textbf{H} &{} [\textbf{G}_{{\textrm{l}}}+\textbf{G}_{{\textrm{nl}}}(\textbf{q})] \\ [\textbf{G}_{{\textrm{l}}}+\textbf{G}_{{\textrm{nl}}}(\textbf{q})]^{{\textrm{T}}} &{} \textbf{G}_{{\textrm{nl}}}^{{\textrm{T}}}\varvec{\beta } \end{bmatrix} \begin{Bmatrix} \delta \varvec{\beta } \\ \delta \textbf{q} \end{Bmatrix}. \nonumber \\ \end{aligned}$$

(45)

The third-order strain energy variation related to $\textbf{f}^{(2)}$ is,

$$\begin{aligned} \delta ^3U= \begin{Bmatrix} \delta \varvec{\beta }^{{\textrm{T}}}&\delta \textbf{q}^{{\textrm{T}}} \end{Bmatrix} \begin{bmatrix} \textbf{0}&{}\textbf{G}_{{\textrm{nl}}}\delta \textbf{q}\\ \textbf{G}_{{\textrm{nl}}}^{{\textrm{T}}}(\delta \textbf{q})&{}\textbf{G}_{{\textrm{nl}}}^{{\textrm{T}}}\delta \varvec{\beta } \end{bmatrix} \begin{Bmatrix} \delta \varvec{\beta }\\ \delta \textbf{q} \end{Bmatrix}. \end{aligned}$$

(46)

The fourth-order strain energy variation related to $\textbf{f}^{(3)}$ is,

$$\begin{aligned} \delta ^4U=0. \end{aligned}$$

(47)

Note that an interesting fact occurs on the fourth-order strain energy variation which naturally equals zero. It fundamentally distinguishes with the non-zero and extremely complicated fourth-order strain energy variation that produced by the displacement based FE formulation. The advantage of using the hybrid-stress formulation in avoiding the fourth-order variation can significantly reduce the computational cost in construction of the reduced-order model.

Substituting the high-order strain energy variations, (45), (46), and (47), into the Taylor expansion (44), the nonlinear equilibrium equations presented in a third-order form are obtained considering two independent parameters (stress and displacement),

$$\begin{aligned}&-\mathbf {H\beta }_0 + \left[ \textbf{G}_{{\textrm{l}}}+\dfrac{1}{2}\textbf{G}_{{\textrm{nl}}}(\textbf{q}_0)\right] \textbf{q}_0 + \left\{ -\textbf{H}\Delta \varvec{\beta }\right. \nonumber \\&\quad \left. +\left[ \textbf{G}_{{\textrm{l}}}+\textbf{G}_{{\textrm{nl}}}(\textbf{q}_0)\right] \Delta \textbf{q}\right\} +\dfrac{1}{2}\textbf{G}_{{\textrm{nl}}}(\Delta \textbf{q})\Delta \textbf{q}=\textbf{0}, \end{aligned}$$

(48)

$$\begin{aligned}&\left[ \textbf{G}_{{\textrm{l}}}+\textbf{G}_{{\textrm{nl}}}(\textbf{q}_0) \right] ^{{\textrm{T}}}\Delta \varvec{\beta } + \left( \textbf{G}_{{\textrm{nl}}}^{{\textrm{T}}}\varvec{\beta }_0\right) \Delta \textbf{q} \nonumber \\&\quad +\dfrac{1}{2}\left[ (\textbf{G}_{{\textrm{nl}}}^{{\textrm{T}}}\Delta \varvec{\beta })\Delta \textbf{q}+(\textbf{G}_{{\textrm{nl}}}^{{\textrm{T}}}\Delta \textbf{q})\Delta \varvec{\beta }\right] =\Delta \lambda \textbf{f}_{{\textrm{ext}}}. \end{aligned}$$

(49)

Introducing the equilibrium condition in the already known configuration into Eq. (48), the following equations can be obtained,

$$\begin{aligned} \left\{ \begin{aligned} \varvec{\beta }_0&=\textbf{H}^{-1}\left[ \textbf{G}_{{\textrm{l}}}+\frac{1}{2}\textbf{G}_{{\textrm{nl}}}(\textbf{q}_0)\right] \textbf{q}_0,\\ \Delta \varvec{\beta }&=\textbf{H}^{-1}\left\{ \left[ \textbf{G}_{{\textrm{l}}}+\textbf{G}_{{\textrm{nl}}}(\textbf{q}_0)\right] \Delta \textbf{q}+\dfrac{1}{2}\textbf{G}_{{\textrm{nl}}}(\Delta \textbf{q})\Delta \textbf{q}\right\} . \end{aligned} \right. \nonumber \\ \end{aligned}$$

(50)

Substituting Eq. (50) into (49), the nonlinear equilibrium Eqs. (48) and (49) in a third-order two-field form are rewritten to be a displacement based form by condensing the stress parameter,

$$\begin{aligned} \textbf{L}(\Delta \textbf{q})+\textbf{Q}(\Delta \textbf{q},\Delta \textbf{q})+{\textbf{C}}(\Delta \textbf{q},\Delta \textbf{q},\Delta \textbf{q})=\Delta \lambda \textbf{f}_{{\textrm{ext}}}, \end{aligned}$$

(51)

in which,

$$\begin{aligned}&\textbf{L}(\Delta \textbf{q}) = \left\{ \left[ \textbf{G}_{{\textrm{l}}}+\textbf{G}_{{\textrm{nl}}}(\textbf{q}_0)\right] ^{{\textrm{T}}}\textbf{H}^{-1}\left[ \textbf{G}_{{\textrm{l}}}+\textbf{G}_{{\textrm{nl}}}(\textbf{q}_0)\right] \right. \nonumber \\&\quad \left. +\textbf{q}_0^{{\textrm{T}}}\left[ \textbf{G}_{{\textrm{l}}}+\frac{1}{2}\textbf{G}_{{\textrm{nl}}}(\textbf{q}_0)\right] ^{{\textrm{T}}}\textbf{H}^{-1}\textbf{G}_{{\textrm{nl}}}\right\} \Delta \textbf{q}, \end{aligned}$$

(52)

$$\begin{aligned}&\quad \textbf{Q}(\Delta \textbf{q},\Delta \textbf{q}) = \frac{1}{2}\left\{ \left[ \textbf{G}_{{\textrm{l}}}+\textbf{G}_{{\textrm{nl}}}(\textbf{q}_0)\right] ^{{\textrm{T}}}\right. \nonumber \\&\quad \textbf{H}^{-1}\textbf{G}_{{\textrm{nl}}}(\Delta \textbf{q})\Delta \textbf{q}+\Delta \textbf{q}^{{\textrm{T}}}\left[ \textbf{G}_{{\textrm{l}}}\right. \nonumber \\&\quad \left. +\textbf{G}_{{\textrm{nl}}}(\textbf{q}_0)\right] ^{{\textrm{T}}}\textbf{H}^{-1}\textbf{G}_{{\textrm{nl}}}\Delta \textbf{q}+\Delta \textbf{q}^{{\textrm{T}}}\left( \textbf{G}_{{\textrm{nl}}}\right) ^{{\textrm{T}}}\nonumber \\&\quad \left. \textbf{H}^{-1}\left[ \textbf{G}_{{\textrm{l}}}+\textbf{G}_{{\textrm{nl}}}(\textbf{q}_0)\right] \Delta \textbf{q}\right\} , \end{aligned}$$

(53)

$$\begin{aligned}&\textbf{C}(\Delta \textbf{q},\Delta \textbf{q},\Delta \textbf{q}) = \dfrac{1}{4}\left[ \textbf{G}_{{\textrm{nl}}}(\Delta \textbf{q})\Delta \textbf{q}\right] ^{{\textrm{T}}}\textbf{H}^{-1}\textbf{G}_{{\textrm{nl}}}\Delta \textbf{q}\nonumber \\&\quad +\dfrac{1}{4}\left[ \textbf{G}_{{\textrm{nl}}}(\Delta \textbf{q})\right] ^{{\textrm{T}}}\textbf{H}^{-1}\textbf{G}_{{\textrm{nl}}}(\Delta \textbf{q})\Delta \textbf{q}, \end{aligned}$$

(54)

where the expression of nonlinear equilibrium equations is only related to the displacement $\textbf{q}$. Note that although the fourth-order strain energy variation is zero, the third-order approximation to equilibrium equations is again recovered by condensing the stress.

The force space of nonlinear equilibrium Eq. (51) can be represented by a linear span of a predefined set of sub-loads,

$$\begin{aligned} \Delta \lambda \textbf{f}_{{\textrm{ext}}}= \textbf{F}\varvec{\phi }, \end{aligned}$$

(55)

in which,

$$\begin{aligned} \textbf{F}&=\begin{bmatrix} \textbf{f}_1=\textbf{f}_{{\textrm{ext}}}&\textbf{f}_2&...&\textbf{f}_{m+1} \end{bmatrix},\end{aligned}$$

(56)

$$\begin{aligned} \varvec{\phi }&=\begin{bmatrix} \phi _1=\Delta \lambda&\phi _2=0&...&\phi _{m+1}=0 \end{bmatrix}, \end{aligned}$$

(57)

where $\textbf{F}$ is a load matrix formed by the sub-load vectors $\textbf{f}_{\alpha }, \alpha =1,2,...,m+1$, of which the first sub-load $\textbf{f}_1$ is the external load $\textbf{f}_{{\textrm{ext}}}$ while the others $\textbf{f}_{\alpha }, \alpha =2,3,...,m+1$ are perturbation loads. The load multiplier $\varvec{\phi }$ is designed to be a unit vector, the 1st component of which is $\Delta \lambda$ and the others are all zero. In this way, the equilibrium condition is kept constant after taking the perturbation loads into account.

To make the proposed method applicable to buckling sensitivity structures, the eigenvalue buckling analysis is required to determine the perturbation loads $\textbf{f}_{\alpha }, \alpha =2,3,... ,m+1$. The eigenvalue buckling equations constructed in the known configuration are presented by,

$$\begin{aligned} {(\textbf{K}_{{\textrm{T}}}+\lambda _i\hat{\textbf{K}}_{{\mathrm{\sigma }}})\varvec{\varphi }_i=0,} \end{aligned}$$

(58)

where $\textbf{K}_{{\textrm{T}}}$ is the tangent stiffness that requires to be updated along the nonlinear equilibrium path in the proposed method. When the eigenvalue buckling equations are constructed in the undeformed configuration, $\textbf{K}_{{\textrm{T}}}$ is exactly the same as the linear stiffness $\textbf{K}_{{\textrm{L}}}$ presented in classical eigenvalue equations [69]. $\hat{\textbf{K}}_{{\mathrm{\sigma }}}$ is the geometric or initial stress stiffness related to a linear displacement, and $\lambda _i$ and $\varvec{\varphi }_i, i=1,2,...,N$ are the buckling eigenvalues and the corresponding modes, respectively. Here, N is the total number of degrees of freedom of the structure after condensing the stress. The buckling modes with loads within 20$\%$ of the first buckling load are regarded as the closely-spaced modes and are selected to build the perturbation loads,

$$\begin{aligned} {\textbf{f}_{\alpha } = \hat{\textbf{K}}_{{\mathrm{\sigma }}}\varvec{\varphi }_{\alpha }, \alpha =1,2,...,m,} \end{aligned}$$

(59)

where $\varvec{\varphi }_{\alpha }, \alpha =1,2,...,m$ are the first m closely-spaced modes of the structure.

A new expression of equilibrium equations can be obtained by substituting Eq. (55) into the nonlinear equilibrium Eq. (51),

$$\begin{aligned} \textbf{L}(\Delta \textbf{q})+\textbf{Q}(\Delta \textbf{q},\Delta \textbf{q})+\textbf{Q}(\Delta \textbf{q},\Delta \textbf{q},\Delta \textbf{q})=\textbf{F}\varvec{\phi }. \end{aligned}$$

(60)

The load multiplier $\varvec{\phi }$ in (60) is expanded to be a third-order form with respective to the generalized displacement $\varvec{\xi }$,

$$\begin{aligned} \varvec{\phi }=\bar{\textbf{L}}(\varvec{\xi })+\bar{\textbf{Q}}(\varvec{\xi },\varvec{\xi })+\bar{\textbf{C}}(\varvec{\xi },\varvec{\xi },\varvec{\xi })+\textbf{O}(||\varvec{\xi }||^4), \end{aligned}$$

(61)

where $\bar{\textbf{L}}$, $\bar{\textbf{Q}}$, and $\bar{\textbf{C}}$, are the, still to be determined, two-dimensional, three-dimensional, and four-dimensional tensors, respectively.

In a similar way, the displacement increment $\Delta \textbf{q}$ in nonlinear equilibrium equations (60) is represented to be,

$$\begin{aligned} \Delta \textbf{q}=\textbf{u}_{{\textrm{L}}}(\varvec{\xi })+\textbf{u}_{{\textrm{Q}}}(\varvec{\xi },\varvec{\xi })+\textbf{u}_{{\textrm{C}}}(\varvec{\xi },\varvec{\xi },\varvec{\xi })+\textbf{O}(||\varvec{\xi }||^4), \end{aligned}$$

(62)

where $\textbf{u}_{{\textrm{L}}}$, $\textbf{u}_{{\textrm{Q}}}$, and $\textbf{u}_{{\textrm{C}}}$ represent the two-, three-, and four-dimensional tensors, respectively. The two-dimensional tensor $\textbf{u}_{{\textrm{L}}}$ defines a tangent plane to the equilibrium surface in the already known configuration.

The expansion of the load multiplier $\varvec{\phi }$ (61) and the displacement incremental $\Delta \textbf{q}$ (62) are introduced into both sides of the equilibrium equations (60). Assuming that the coefficients of the various powers of $\xi$ are zero, three sets of tensor equations are derived,

$$\begin{aligned} \begin{bmatrix} \textbf{L}&{}-\textbf{F}\\ -\textbf{F}^{{\textrm{T}}}&{}\textbf{0} \end{bmatrix} \begin{Bmatrix} \textbf{u}_{{\textrm{L}}}\\ \bar{\textbf{L}} \end{Bmatrix} = \begin{Bmatrix} \textbf{0}\\ -\textbf{I} \end{Bmatrix}, \end{aligned}$$

(63)

$$\begin{aligned} \begin{bmatrix} \textbf{L}&{}-\textbf{F}\\ -\textbf{F}^{{\textrm{T}}}&{}\textbf{0} \end{bmatrix} \begin{Bmatrix} \textbf{u}_{{\textrm{Q}}}\\ \bar{\textbf{Q}} \end{Bmatrix}= \begin{Bmatrix} -\textbf{Q}(\textbf{u}_{{\textrm{L}}},\textbf{u}_{{\textrm{L}}})\\ \textbf{0} \end{Bmatrix}, \end{aligned}$$

(64)

$$\begin{aligned} \bar{\textbf{C}} = -2\textbf{u}_{{\textrm{Q}}}^{{\textrm{T}}}\textbf{L}(\textbf{u}_{{\textrm{Q}}}) + \textbf{u}_{{\textrm{L}}}^{{\textrm{T}}}\textbf{C}(\textbf{u}_{{\textrm{L}}}, \textbf{u}_{{\textrm{L}}}, \textbf{u}_{{\textrm{L}}}), \end{aligned}$$

(65)

where it is worth noting that Eqs. (63) and (64) share the same coefficient matrix with a order of N+m+1. This implies that solving the systems of linear equations in (63) and (64) requires to compute the matrix inverse only once. The tensor equation (65) is composed of a series of algebraic equations which can be solved at little cost. After solving Eqs. (63), (64), and (65), the values of $\bar{\textbf{L}}$, $\bar{\textbf{Q}}$, $\bar{\textbf{C}}$ in Eq. (61) and $\textbf{u}_{{\textrm{L}}}$, $\textbf{u}_{{\textrm{Q}}}$ in Eq. (62) are obtained.

Up to this point, the reduced-order model applied to approximate the nonlinear equilibrium equations in the already known configuration is constructed as follows,

$$\begin{aligned} \bar{\textbf{L}}(\varvec{\xi })+\bar{\textbf{Q}}(\varvec{\xi },\varvec{\xi })+\bar{\textbf{C}}(\varvec{\xi },\varvec{\xi },\varvec{\xi })=\varvec{\phi }, \end{aligned}$$

(66)

where the reduced-order model is actually a nonlinear system of equations with only m+1 degrees of freedom, in which m is the number of closely-spaced buckling modes of the structure. Applying a path-following technique to solve the reduced system, the relationship ($\varvec{\xi }$ vs. $\Delta \lambda$) can be obtained. Then, the solution ($\textbf{q}$ vs. $\lambda$) is achieved by invoking the Eqs. (41), (42), and (62), which can be used as a nonlinear predictor to the geometrically nonlinear response of the structure.

4.2 Correctors based on the residual force

In contrast to the full-order method, the reduced-order model (66) possesses significantly fewer degrees of freedom. Consequently, the computational cost in path-following analysis of the geometrically nonlinear structure is markedly decreased. However, the range of validity of the reduced-order model is still limited, and its solution, that is the nonlinear predictor, is numerically accurate only in a certain region away from the already known configuration. The nonlinear predictor can be corrected using a classical Newton iteration method and based on the residual force $\textbf{f}_{{\textrm{res}}}$ that is evaluated in a full-order model,

$$\begin{aligned} \textbf{f}_{{\textrm{res}}}=\lambda \textbf{f}_{{\textrm{ext}}}-\textbf{f}(\textbf{q}), \end{aligned}$$

(67)

where $\textbf{f}(\textbf{q})$ is the internal force at the current solution point, and $\lambda \textbf{f}_{{\textrm{ext}}}$ is the corresponding external load.

Then, the range of validity of the reduced-order model can be determined through the relative deviation of the residual force with respective to external loads,

$$\begin{aligned} \frac{||\textbf{f}_{{\textrm{res}}}||}{\lambda ||\textbf{f}_{\textrm{ext}}||}<\epsilon , \end{aligned}$$

(68)

where $\epsilon$ is a predefined error threshold.

Once the predefined error threshold (68) is not satisfied, a correction process is activated to gradually reduce the deviation using the classical Newton iteration until the predefined deviation threshold is satisfied again. Each corrector is in fact a single iteration of the full-order FE system. When the error threshold $\epsilon$ in Eq. (68) is predefined to be a relatively small value ($\epsilon$ = 1$\times 10^{-3}$ in this work, for instance), there would be no numerical difficulties in the Newton iteration based correction process. Up to this point, a full path-following step with a predictor-corrector strategy is ended. The reduced-order model can be re-established in the corrected configuration, resulting in a new path-following step to trace the response curve, if necessary. In this way, the entirely geometrically nonlinear response of the structure is achieved in a step-by-step manner of the proposed reduced-order method.

Up to this point, the hybrid-stress formulation based reduced-order method using a solid-shell element is fully presented. This work distinguishes from the previous publication [66] in the following three points: (1) A more detailed and comprehensive deduction for the implementation of the two-field (displacement and stress) FE formulations into the Koiter-Newton method is presented in the present work. (2) The proposed method conducts the stress condensation much earlier than that developed in the previous work, leading to some differences in the reduced-order model. In the present work, the third-order Taylor expansion of the two-field equilibrium equations results in a rather simple form ((48) and (49)) when using the condition (47) that the fourth-order strain energy variation is zero, and then the third-order approximation with tensors $\textbf{L}$, $\textbf{Q}$, and $\textbf{C}$ to equilibrium equations (51) is completely recovered by condensing the stress immediately after applying the Taylor expansion. However, the method in the previous work holds the two-field formulations up to the calculation of the tensors ($\bar{\textbf{L}}$, $\bar{\textbf{Q}}$, and $\bar{\textbf{C}}$) in the reduced-order model. A simpler form for the tensor $\bar{\textbf{C}}$ is achieved in that work by neglecting the tensor $\textbf{C}$, when applying the condition that the fourth-order strain energy variation is zero. For the above reasons, the present method involves more terms in the tensor $\bar{\textbf{C}}$ of the reduced-order model, as listed in Eq. (65), probably resulting in an enlarged range of validity of the approximation solution. (3) Although the reduced-order method with the displacement based formulation is selected by both the work to validate the advantages of the method with the two-field FE formulations, the previous work focuses on the comparison of the number of iteration steps in the corrector phase; whereas the present work intends to demonstrate the superiority in path-following ability (the larger step size and more reliable solution, for instance) using the following numerical examples.

5 Numerical examples

In this section, five numerical examples are selected to validate the computational accuracy and efficiency of the proposed reduced-order method with the hybrid-stress formulation. Three different numerical methods, which are ABAQUS, full-order method (FOM), and reduced-order method (ROM), are involved for geometrically nonlinear buckling analysis of thin-walled structures. Actually, ABAQUS is also a type of full-order methods that adopts the displacement based finite element formulation with a 2D traditional shell element. The full-order method named in this work particularly refers to the conventional finite element method using the hybrid-stress solid-shell formulation and Newton–Raphson based incremental-iterative strategy, as presented in Sect. 3. The solution of ABAQUS is applied to validate the numerical accuracy of the full-order method. To ensure an objective evaluation on computational accuracy and efficiency of the proposed reduced-order method, the full-order method with the hybrid-stress formulation, which is also achieved by our in-house codes in MATLAB programming environment, is selected. Therefore, the full- and reduced-order methods are executed based on the identical finite element formulation, in the same programming environment and also on the same computer platform (an Intel Core i7-13700 H processor and 16GB of memory). In this way, we believe that a fair comparison can be achieved between the full and reduced-order methods.

5.1 Flat plate under in-plane compressive load

A flat plate with length $a=140\hbox { mm}$, width $b=100\hbox { mm}$, and thickness $t=0.5\hbox { mm}$ is considered, as shown in Fig. 2. The four edges of the plate are constrained to prevent the out-of-plane deformation w along the z-direction. The translations in the x and y directions are not allowed along the edge ③; whereas a uniformly distributed compressive load is applied along the edge ①. The material properties are elastic modulus $E=70000$ MPa and Poisson’s ratio $v=0.3$.

Fig. 2

The flat plate. (Colour figure online)

Fig. 3

Nonlinear response curves of the plate using ABAQUS, full-order method and reduced-order method. (Colour figure online)

First, the finite element models constructed by different methods are introduced. The flat plate is discretized by ABAQUS using a 4-node general-purpose shell element (S4R), which has a two-dimensional geometric shape and possesses three translational and three rotational degrees of freedom per node. In contrast, the full- and reduced-order methods presented in this work employ an 8-node hybrid-stress solid-shell element, which has a three-dimensional geometry with only three translational degrees of freedom per node. Due to the differences on both the geometry and degree of freedom of the two elements, $14 \times 10$ and $14 \times 10\times 2$ meshes are applied for the shell and solid-shell elements, respectively, to achieve an identical simulation on boundary conditions. We can see that the same mesh density of the shell and solid-shell elements is applied within the in-plane region of the plate, resulting in a large span-thickness ratio 40 for the solid-shell element. The shape of the first-order buckling mode with a magnitude 0.001 is introduced into the finite element model to produce the initial geometric imperfection, which is essential in the following geometrically nonlinear buckling analysis.

Then, the geometrically nonlinear response about the end-shortening u and deflection $w_A$ of the plate are depicted in Fig. 3a and b, respectively. The end-shortening is the average in-plane displacements u of edge ① and the deflection $w_A$ is the transverse displacement at the center ‘A’ of the plate. The response curves are obtained by ABAQUS, full- and reduced-order methods of our in-house codes, respectively. We notice that the typically bifurcation buckling is disturbed by the initial imperfection, leading to a uniquely determined post-buckling branch. The deformations in the initial post-buckling stage are also calculated by different methods and plotted in Fig. 3b. A maximum discrepancy of 1.3$\%$ can be observed on the response curves obtained by ABAQUS and the full-order method, which mainly arises from the differences in the element types and nonlinear kinematics used by the two methods. The reduced-order model is constructed at the undeformed configuration with two degrees of freedom, of which the first DOF indicates the primary path while the other corresponds to the first-order buckling mode. The response curve satisfactory up to the initial post-buckling stage is obtained by the reduced-order method, in which an accurate buckling point can be captured with a buckling load of 354 N. Because the reduced-order model is constructed by expanding the equilibrium equations only once at the undeformed configuration, its solution has a limited range of validity around the expansion point and up to the initial post-buckling stage. An accurate response curve in the deep post-buckling stage can be obtained if necessary, when a correction process is applied to the reduced-order solution and the reduced system is updated along the response curve.

Finally, the computational efficiency of the proposed reduced-order method is compared with that of the full-order method. Because an objective evaluation is achieved only when the two methods adopt the identical element formulation and run in the same programming environment, the full-order method that adopts the hybrid-stress formulation and executes in the MATLAB platform is selected for a fair comparison. We observe that 4.41 s are required by the reduced-order method to obtain the response curves in Fig. 3a and b; whereas the full-order method needs 109.7 s. This demonstrates that the proposed reduced-order method takes only about 4$\%$ of the computing time of the full-order method for nonlinear buckling analysis. Although the computing time of the full-order method is largely influenced by the predefined parameters of the incremental-iterative solver, a sufficient number of path-following steps is still required to obtain a smooth enough response curve; however only one path-following step is needed by the proposed reduced-order method. Note that the nonlinear predictor with a satisfactory smoothness is obtained in the path-following step, because the reduced-order model with two degrees of freedom can be solved using very small intervals at almost no cost. In addition, it is a known fact that the well-established ABAQUS has significantly superior capabilities in execution efficiency and multi-core computing within the framework of FORTRAN programs. However, we find that ABAQUS takes 13 s to achieve the response curve, which is still approximately 2 times slower than the proposed reduced-order method.

5.2 C-shaped cantilevered beam under concentrated load

The geometrically nonlinear analysis of a C-shaped cantilevered beam under a concentrated load is conducted to verify the computational accuracy and efficiency of the reduced-order method, as shown in Fig. 4. A material with elastic modulus E=$1\times 10^7$ MPa and Poisson’ ratio 0.333, is considered. The C-shaped beam is meshed by 432 solid-shell elements with only one element along the wall-thickness direction, leading to a total of 5304 degrees of freedom.

Fig. 4

The C-shaped beam. (Colour figure online)

First, ABAQUS is employed to analyze the geometrically nonlinear response of the C-shaped beam, and the result is used as a reference solution to validate the proposed method. The C-shaped beam is discretized by ABAQUS using the CSS8 element which is a three-dimensional solid-shell element with incompatible modes and assumed strain. The deflection $w_A$ at the loading point A is selected to plot the nonlinear response curve. The geometrically nonlinear response curves obtained by the full-order method with the hybrid-stress formulation and ABAQUS with the displacement based formulation are compared, as shown in Fig. 5. The deformations of the C-shaped beam in the presence of buckling, are also provided in Fig. 5. It is concluded that the solution of the full-order method matches very well with that of ABAQUS.

Fig. 5

The comparison of the geometrically nonlinear responses obtained by ABAQUS and the full-order method. (Colour figure online)

Fig. 6

Nonlinear response curve of the C-shaped beam, obtained by one path-following step of the reduced-order method. (Colour figure online)

Fig. 7

Nonlinear response curve of the C-shaped beam, obtained by two path-following steps of the reduced-order method. (Colour figure online)

Then, the geometrically nonlinear response curves obtained by the full- and reduced-order methods, are depicted in Figs. 6, 7, and 8. The C-shaped beam exhibits a typically limit-point buckling, as illustrated by the response curve solved using the full-order method. A reduced-order model with two degrees of freedom is first constructed at the undeformed configuration. The solution of the reduced-order method using only a single path-following step is plotted in Fig. 6. It can be seen that the nonlinear predictor (green curve) of the first step is numerically accurate up to a load of 70 N. Although a significant discrepancy occurs when the geometrical nonlinearity becomes serious in the pre-buckling stage, the reduced-order method with one step can roughly predict the limit-point typed behavior of the structure. As shown in Figs. 7, if the predictor of the first path-following step is corrected at the load of 70 N (circle marker ‘$\circ$’) and the second path-following step is activated by reconstructing the reduced-order model, the reduced-order method further traces the response curve satisfactory up to a load of 107 N (blue curve). The response curve obtained by the proposed method with two path-following steps is getting close to, but not successfully pass, the buckling limit-point of the C-shaped beam. Thus, after applying the correction again at the load of 107 N, the solution of the third path-following step (purple curve) successfully pass the limit point of the response curve with a buckling load of 112 N, as depicted in Fig. 8. The deformations of the C-shaped beam in the presence of buckling are also provided in Fig. 8. The solution of the proposed reduced-order method using the hybrid-stress formulation is also compared to that of the method using a mixed formulation [66]. It is observed from Fig. 9 that the proposed method requires three steps to pass the limit point of the response curve, whereas the method in literature needs four to five steps. A larger step size is obtained by the proposed method, probably because the third-order approximation to equilibrium equations is recovered by condensing the stress before the calculation of the third-order terms $\bar{\textbf{C}}$ in the reduced-order model. In this way, more terms are involved in the tensor $\bar{\textbf{C}}$ of the reduced system, resulting in an enlarged range of validity of the approximation solution.

Fig. 8

Nonlinear response curve of the C-shaped beam, obtained by three path-following steps of the reduced-order method. (Colour figure online)

Fig. 9

Comparison of the nonlinear response curves of the C-shaped beam, obtained in the literature [66] and by the present study. (Colour figure online)

Fig. 10

Nonlinear response curves of the C-shaped beam, obtained by eleven path-following steps of the reduced-order method. (Colour figure online)

Finally, the geometrically nonlinear response curve is further traced into the finite deformation range of the C-shaped beam. As presented in Fig. 10, the solution of the reduced-order method requires a total of eleven path-following steps to achieve a response curve satisfactory up to a large deflection of 4 mm. The correction point of each path-following step is marked by a black circle ‘$\circ$’. It can be observed that more steps are required by the proposed method when passing the limit point and tracing the descending segment of the response curve; however the large step size is regained immediately after the load-carrying capability of the C-shaped beam is restored. In terms of computational efficiency, the full-order method takes 841 s to trace the response curve, whereas the reduced-order method only requires 63 s. It is concluded that the reduced-order method is approximately 12.3 times faster than the full-order method. The high computational efficiency is attributed to a fairly large step size of the proposed method in path-following analysis. The reduced-order method only needs three path-following steps to pass the buckling limit-point, while much more steps are required for the full-order method to obtain the response curve with a favorable smoothness. The nonlinear predictor with a superior smoothness is obtained in each path-following step, because the reduced-order model with two degrees of freedom is solved by very small intervals at almost no cost.

5.3 L-shaped frame under uniformly horizontal load

An L-shaped frame under a uniformly horizontal load is considered, as shown in Fig. 11, which consists of two rectangular plates with a same geometric shape and perpendicularly placed to each other. The length, width, and thickness of each rectangular plate are 20 mm, 10 mm, and 0.3 mm, respectively. The three translations along the edges ① and ② of the L-shaped frame are constrained, while a uniformly load is applied horizontally on the intersection edge of the two plates. The material properties are elastic modulus $E=4.444\times 10^6$ MPa and Poisson’s ratio $v=0$. The L-shaped frame is meshed by 410 elements with a total of 2772 degrees of freedom.

Fig. 11

The L-shaped frame. (Colour figure online)

Fig. 12

Nonlinear response curves of the L-shaped frame, obtained by one path-following step of the reduced-order method. (Colour figure online)

Fig. 13

Nonlinear response curves of the L-shaped frame, obtained by seven path-following steps of the reduced-order method. (Colour figure online)

The geometrically nonlinear response curves of the L-shaped frame are achieved using the full- and reduced-order methods, as shown in Fig. 12. The average horizontal displacement u of the edge ③ and the out of plane displacement $w_A$ at the point A are selected to plot the response curves. A reduced-order model with two degrees of freedom is constructed at the undeformed configuration. The reduced-order method needs only one path-following step initiated at the undeformed configuration, to accurately trace the nonlinear response curve satisfactory up to the post-buckling regime with the horizontal displacement u of 0.2 mm and out of plane displacement $w_A$ of 1 mm. Both the nonlinear response curves and the deformations acquired by full- and reduced-order methods illustrate the accuracy of the reduced-order method. It can be observed from the response curve that the pre-buckling stage of the L-shaped frame is approximately linear and the load-carrying capability of the frame is almost completely lost in the presence of buckling. To achieve the nonlinear buckling response in Fig. 12, 255.6 and 5.1 s are taken by the full- and reduced-order methods, respectively.

The behavior of the proposed reduced-order method in a finite deformation range of the L-shaped frame is further investigated. The geometrically nonlinear responses of the L-shaped frame are traced into the deep post-buckling regime with the horizontal displacement u of 1.1 mm and out of plane displacement $w_A$ of 2.8 mm. As illustrated in Fig. 13, the proposed method adopts seven path-following steps to achieve the response curves accurately and efficiently, using a fairly large step size. The correction point of each path-following step is marked by a black circle ‘$\circ$’.

Fig. 14

The cylindrical roof. (Colour figure online)

5.4 Cylindrical roof under centralized lateral load

As shown in Fig. 14, a cylindrical roof under a centralized lateral load is chosen for geometrically nonlinear analysis. The geometric parameters of the cylindrical roof are length $l=508\hbox { mm}$, thickness $t=12.7\hbox { mm}$, central angle $\theta =0.2$ rad, and radius $R=2540\hbox { mm}$. The roof is meshed by $8 \times 8\times 2$ elements with two layers along the thickness direction to simulate a simply-supported boundary that allows a free rotation. The cylindrical roof is made of an isotropic material with elastic modulus $E=3.10275\hbox { MPa}$ and Poisson’s ratio v=0.3.

The geometrically nonlinear response curves obtained by the full- and reduced-order methods, are depicted in Figs. 15 and 16. The deflection $w_A$ at the loading point is selected to plot the response curve. The cylindrical roof exhibits a typically snap-through buckling with a load limit-point, as illustrated by the response curve solved using the full-order method. A reduced-order model with two degrees of freedom is first constructed at the undeformed configuration. The solution of the reduced-order method with only a single path-following step is plotted in Fig. 15. It is observed that the nonlinear predictor (green curve) of the first step is numerically accurate up to a load of 2.04 N. Although a significant discrepancy occurs around the buckling limit-point, the reduced-order method with one step can approximately predict the limit-point typed behavior of the structure. As shown in Fig. 16, if the predictor of the first path-following step is corrected at the load of 2.04 N (circle marker ‘$\circ$’) and the second path-following step is activated by reconstructing the reduced-order model, the reduced-order method can further traces the response curve successfully passing the buckling limit-point and satisfactory up to a post-buckling load-drop stage (black curve). Note that the second path-following step can well predict the tendency of the snap-through response. The deformations of the cylindrical roof in the presence of buckling are also plotted in Fig. 16.

Fig. 15

Nonlinear response curve of the cylindrical roof, obtained by one path-following step of the reduced-order method. (Colour figure online)

Fig. 16

Nonlinear response curve of the cylindrical roof, obtained by two path-following steps of the reduced-order method. (Colour figure online)

Fig. 17

Nonlinear response curves of the cylindrical roof, obtained using the reduced-order methods with the hybrid-stress and displacement based formulations, respectively. (Colour figure online)

To achieve the response curves in Fig. 16, the reduced-order method is 12.35 times faster, 3.7 s versus 49.4 s, than the full-order method, benefiting from the fairly large steps of the reduced-order method in path-following analysis. The reduced-order method only requires two path-following steps to pass the buckling limit-point; whereas much more steps are applied by the full-order method to obtain the response curve with a favorable smoothness. In addition, the response curve obtained by the reduced-order method with the hybrid-stress formulation is compared with that obtained using the displacement based formulation, as shown in Fig. 17. Both the two reduced-order methods adopt two path-following steps to trace the nonlinear buckling response. The green triangle symbol indicates the range of validity of the reduced-order solution. It can be observed that the reduced-order method with hybrid-stress formulation has a much larger step size in path-following analysis, resulting in a response curve satisfactory up to a deeper post-buckling stage, compared with the reduced-order method with displacement based formulation. Note that the reduced-order method with hybrid-stress formulation can approximately predict the snap-through behavior of the structure using two path-following steps; however the reduced-order method with displacement based formulation has no capability to do that.

As presented in Fig. 18, the entire snap-through behavior of the nonlinear response curve can be accurately captured by the proposed reduced-order method using three path-following steps. The correction point of each path-following step is marked by a black circle ‘$\circ$’. It is observed that all the three path-following steps have a fairly large step size to trace the snap-through response curve. This further demonstrates the high computational efficiency of the reduced-order method with hybrid-stress formulation.

5.5 Curved panel subjected to in-plane compressive load

A curved panel subjected a uniformly in-plane compressive load is selected to further test the high efficiency and accuracy of the proposed method. The geometric parameters and boundary conditions of the curved panel are illustrated in Fig. 19. The curved panel has a straight edge $l = 150\hbox { mm}$ and thickness $t = 1.68\hbox { mm}$, and the curved edge is characterized by a radius R = 80 mm and central angle $\theta = 90^\circ$. The out-of-plane displacements of the two straight edges of the panel are constrained. One of the curved edges is simply-supported, and another one is subject to a uniformly in-plane compressive load. A material with elastic modulus $E=700\hbox { MPa}$ and Poisson’s ratio $v = 0.3$ is applied. The mesh consists of $30 \times 25\times 1$ elements with only one element along the thickness direction.

Fig. 18

Nonlinear response curve of the cylindrical roof, obtained by three path-following steps of the reduced-order method. (Colour figure online)

Fig. 19

The curved panel

A linear eigenvalue buckling analysis is conducted for the curved panel. The shape of the first-order buckling mode with a magnitude 0.001 is introduced into the finite element model to produce the initial geometric imperfection. The geometrically nonlinear response curves obtained by the full- and reduced-order methods, are depicted in Figs. 20 and 21. The in-plane average compressive displacement u of the loading edge ① is selected to plot the response curve. The curved panel exhibits a typically snap-back buckling with a load limit-point, as illustrated by the response curve solved using the full-order method. A reduced-order model with three degrees of freedom is first constructed at the undeformed configuration, of which the first DOF indicates the primary path while the other two correspond to the first two closely-spaced buckling modes. The solution of the reduced-order method with only a single path-following step is plotted in Fig. 20. It can be found that the nonlinear predictor (green curve) of the first step is numerically accurate up to the limit point of the response curve with a load of 620 N, because the pre-buckling response of the panel is almost linear. Although a significant discrepancy occurs after passing the buckling limit-point, the reduced-order method with one path-following step can approximately predict the snap-back typed behavior of the structure. As shown in Fig. 21, if the predictor of the first path-following step is corrected at a load of 599 N (circle marker ‘$\circ$’) and the second path-following step is activated by reconstructing the reduced-order model, the reduced-order method can further traces the response curve satisfactory up to the initial post-buckling stage (black curve). The deformations of the curved panel in the presence of buckling are also plotted in Fig. 21.

Fig. 20

Nonlinear response curve of the curved panel, obtained by one path-following step of the reduced-order method. (Colour figure online)

Fig. 21

Nonlinear response curve of the curved panel, obtained by two path-following steps of the reduced-order method. (Colour figure online)

To achieve the response curves in Fig. 21, the reduced-order method takes 33 s, that is 10 times faster than the 375 s of the full-order method, owing to the fairly large step sizes of the reduced-order method in path-following analysis. Additionally, the reduced-order solutions of the first path-following step are plotted in Fig. 22, using the reduced-order methods with the hybrid-stress and displacement based formulations, respectively. We observe that the reduced-order method with hybrid-stress formulation can capture the buckling load and predict the initial post-buckling tendency very well; however the displacement based reduced-order method misses the limit point, overestimates the buckling load, and results in a completely wrong post-buckling behavior. This demonstrates that the reduced-order model constructed using the hybrid-stress formulation is much more numerically accurate than that using the displacement based formulation in this example.

Fig. 22

Nonlinear response curves of the curved panel, obtained using the reduced-order methods with the hybrid-stress and displacement based formulations. (Colour figure online)

Finally, the proposed reduced-order method adopts six path-following steps to trace into the deep post-buckling regime of the curved panel. As presented in Fig. 23, the entire snap-back behavior of the nonlinear response curve can be well captured when more steps are applied in the path-following analysis. The correction point of each path-following step is marked by a black circle ‘$\circ$’. This demonstrates the strong ability of the proposed method in tracing the complex snap-back response with a sharp turning point.

Fig. 23

Nonlinear response curve of the curved panel, obtained by six path-following steps of the reduced-order method. (Colour figure online)

6 Conclusions

In this work, a hybrid-stress formulation based reduced-order method is proposed for geometrically nonlinear buckling analysis. An eight-node solid-shell element with Green-Lagrange kinematics is developed and the locking problems are overcome using the EAS method and the hybrid-stress formulation. The hybrid-stress formulation is also applied to avoid the fourth-order strain energy variation of the solid-shell element while not sacrificing the effectiveness of the reduced-order model. The reason is that the high-order strain energy variations are achieved using the two-field variational principle and the third-order approximation to the equilibrium equations can be completely recovered after conducting the stress condensation. Therefore, the reduced-order model is constructed within the framework of the hybrid-stress formulation much more efficiently, compared with that using the displacement based formulation; meanwhile the numerical accuracy of the reduced system is not degraded. A predictor-corrector strategy is developed for the hybrid-stress formulation based reduced-order method to trace the nonlinear buckling response in a step-by-step manner.

Various numerical examples are applied to validate the computational accuracy and efficiency of the proposed reduced-order method with the hybrid-stress formulation. The geometrically nonlinear responses of thin-walled structures are calculated using different numerical methods. The solution of ABAQUS is used to validate the numerical accuracy of the full-order method with the hybrid-stress formulation. The proposed reduced-order method with the hybrid-stress formulation can trace the nonlinear response curve accurately up to the post-buckling stage, for the structures with bifurcation, limit-point, snap-through, and snap-back typed buckling behaviors. Compared with the full-order method using the hybrid-stress formulation, a much larger step size can be achieved in the path-following analysis using the reduced-order method with the hybrid-stress formulation, resulting in a significantly less computing time. This demonstrates that the small computational extra-cost for the hybrid-stress formulation is largely compensated in path-following analysis, by larger step sizes and reduced systems. The superior of the proposed method in computing time also exists with respect to ABAQUS that uses the displacement based formulation. Compared with the reduced-order method using the displacement based formulation, although the fourth-order strain energy variation is not involved in the reduced-order model, the path-following capability using the hybrid-stress formulation is not only unaffected, but also enhanced in some cases.

Fig. 24

Thickness identification in the global coordinate system. (Colour figure online)

Fig. 25

Transformation between global and local coordinate systems. (Colour figure online)

Appendices

Appendix A. Transformation between global and local coordinate systems

As presented in Sect. 2, a local coordinate system (x-y-z) needs to be defined for the solid-shell element, the z-axis of which must align with the thickness direction of the element. This is a significant feature that the solid-shell element distinguishes from the conventional solid element. To achieve the transformation between the global and local coordinate systems, it is essential to identify the thickness direction of the element first. The four nodes located at the upper and lower surfaces of the element are numbered in a counterclockwise order, as illustrated in Fig. 24. It can be observed that the node 1 is connected to nodes 2, 4, and 5 by three elemental edges. The thickness direction of the element aligns with the shortest edge among these three edges, and can be represent by a vector $\overrightarrow{\textbf{OA}}$.

By rotating the thickness vector $\overrightarrow{\textbf{OA}}$ to be parallel to the $z'$-direction of the global coordinate system, the transformation between the global and local coordinate systems is established. The detailed process to establish the transformation between the global and local coordinate systems is outlined in Fig. 25, and presented by the following two steps. In the first step, the thickness vector $\overrightarrow{\textbf{OA}}$ is projected onto the $y'$-o-$z'$ plane to be a new vector $\overrightarrow{\mathbf {OA'}}$ which is represented by a green line, as shown in Fig. 25a. The rotation angle $\theta$ is determined by rotating the projection vector $\overrightarrow{\mathbf {OA'}}$ until it is parallel to the $z'$ axis, as illustrated by Fig. 25b. Then, by rotating the thickness vector $\overrightarrow{\textbf{OA}}$ by $\theta$ around the $x'$-axis, it is relocated at the $x'$-o-$z'$ plane in Fig. 25c. In the second step, the thickness vector $\overrightarrow{\textbf{OA}}$ that locates at the $x'$-o-$z'$ plane is further rotated around the $y'$-axis by a angle $\varphi$ to make it parallel with the $z'$-axis.

The rotation angles $\theta$ and $\varphi$ that mentioned above are calculated by,

$$\begin{aligned} \begin{aligned}&\cos \theta ={\frac{(y',z')\cdot (0,1)}{\mid (y',z')\mid }}, \\&\sin \theta ={\frac{y'}{\mid y'\mid }}{\sqrt{1-\cos ^{2}\theta }}, \\&\cos \varphi ={\frac{(x',{\sqrt{y^{'2}+z^{'2}}})\cdot (0,1)}{\mid (x',{\sqrt{y^{'2}+z^{'2}}})\mid }}, \\&\sin \varphi ={\frac{x'}{\mid x'\mid }}{\sqrt{1-\cos ^{2}\varphi }}. \end{aligned} \end{aligned}$$

(A.1)

At this point, the rotation matrix related to the angle $\theta$ can be obtained, as given by,

$$\begin{aligned} \textbf{T}_{\theta }=\begin{bmatrix} 1&{}0&{}0\\ 0&{}\cos \theta &{}\sin \theta \\ 0&{}-\sin \theta &{}\cos \theta \end{bmatrix}. \end{aligned}$$

(A.2)

The rotation matrix related to the angle $\varphi$ is,

$$\begin{aligned} \textbf{T}_{\varphi }=\begin{bmatrix} \cos \varphi &{}0&{}\sin \varphi \\ 0&{}1&{}0\\ -\sin \varphi &{}0&{}\cos \varphi \end{bmatrix}. \end{aligned}$$

(A.3)

The product of these two rotation matrices is the required transformation matrix between the global and local coordinate systems,

$$\begin{aligned} \textbf{T}_{{\mathrm{global-local}}}=\textbf{T}_{\varphi }\textbf{T}_{\theta }. \end{aligned}$$

(A.4)

Finally, a local coordinate system, the z-axis of which aligns with the thickness direction of the element, is obtained.

Appendix B. Strain and stress transformation matrices and stress interpolation matrix

The strain transformation matrix applied in Eq. (15) is calculated by,

$$\begin{aligned} \textbf{T}_{\varepsilon }= \begin{bmatrix} j_{11}^2&{}j_{21}^2&{}j_{11}j_{21}&{}0&{}0&{}0\\ j_{12}^2&{}j_{22}^2&{}j_{12}j_{22}&{}0&{}0&{}0\\ 2j_{11}j_{12}&{}2j_{21}j_{22}&{}j_{12}j_{21}+j_{11}j_{22}&{}0&{}0&{}0\\ 0&{}0&{}0&{}j_{33}^2&{}0&{}0\\ 0&{}0&{}0&{}0&{}j_{22}j_{33}&{}j_{12}j_{33}\\ 0&{}0&{}0&{}0&{}j_{21}j_{33}&{}j_{11}j_{33} \end{bmatrix}, \nonumber \\ \end{aligned}$$

(B.1)

where $j_{mn}$ are the components of the tensor $\textbf{j}$ which is inverse of the Jacobian matrix (9).

The stress transformation matrix used in Eq. (16) is calculated by,

$$\begin{aligned} \textbf{T}_{\sigma } =\begin{bmatrix} J_{11}J_{11}&{}J_{12}J_{12}&{}2J_{11}J_{12}&{}0&{}0&{}0\\ J_{21}J_{21}&{}J_{22}J_{22}&{}2J_{21}J_{22}&{}0&{}0&{}0\\ J_{11}J_{21}&{}J_{12}J_{22}&{}J_{11}J_{22}+J_{12}J_{21}&{}0&{}0&{}0\\ 0&{}0&{}0&{}J_{33}^2&{}0&{}0\\ 0&{}0&{}0&{}0&{}J_{22}J_{33}&{}J_{21}J_{33}\\ 0&{}0&{}0&{}0&{}J_{12}J_{33}&{}J_{11}J_{33} \end{bmatrix}. \nonumber \\ \end{aligned}$$

(B.2)

The stress interpolation matrix involved in Equation (16) is given by,