1 Introduction

Functionally graded materials (FGMs) refer to the composite materials where the compositions or the microstructures are locally varied so that a certain variation of the local material properties is achieved. Determination of compositional gradient and the process of making an FGM are dependent on its intended use. There are two main types of FGMs, i.e., continuous-graded materials and discontinuous-graded materials. In the simplest FGMs, two different material ingredients change gradually from one to the other. In the second type, the material ingredients change in a discontinuous way such as the stepwise gradation. Since the concept developed in aeronautics field in 1984, FGMs are also a concern in the other fields such as industrial materials, optoelectronics, biomaterials, and energy materials. FGMs offer great promise in applications where the operating conditions are severe. Potential applications include those structural and engineering uses that require combinations of incompatible functions such as refractoriness or hardness with toughness or chemical inertness with toughness. In the design and operation of these structural components, the numerical analysis of the temperature distribution and temperature-induced stresses performed an outline of mathematical models that do not take into consideration the current temperature dependences of the thermal and mechanical characteristics of layers and do not meet the necessities of latest engineering system. Hence, the analysis of thermosensitivity is essential for the identification of the thermally stressed state of cylindrical structures made from functionally graded materials.

Noda [1] described the current state of thermoelastic problems in materials with temperature-dependent properties for analytical treatments. Popovych [2] derived a method for the solution of stationary problems for the heat conductivity of thermoelastic bodies. Lizarev [3] obtained an exact solution of the problem of displacements and stresses in a polar-orthotropic annular plate of variable thickness. Popovych and Makhorkin [4] illustrated the methods of constructing analytic numerical solutions of nonsteady heat-conduction problems for thermosensitive bodies under convective heat transfer. Awaji et al. [5] presented a numerical technique for analyzing one-dimensional transient temperature and stress distributions in a functionally graded ceramic–metal-based materials (FGMs). Tanigawa et al. [6] obtained solution for thermoelastic problems in nonhomogeneous solids. Kushnir and Popovych [7] obtained the solutions for the cases of load-free circular washer, infinite plate with circular hole, circular disk, and infinite plate, by reducing the problem of thermoelasticity for a thin thermosensitive plate placed in a central symmetric temperature field by perturbation method to a recurrent sequence of boundary-value problems for differential equations with constant coefficients. Popovych et al. [8] constructed solution of the nonstationary problem of heat conduction for a thermosensitive hollow sphere in the process of convective–radiant heat exchange. Kushnir and Popovych [9] briefly analyzed heat conduction problems of different solids with thermally sensitive material properties under complex heat exchange. Lamba et al. [10] studied the thermoelastic behavior of a hollow cylinder under heating and cooling process. Hadi et al. [11] investigated the bending of rectangular plate made of FGM by using three-dimensional elasticity theory. Popovych [12] examined the thermoelastic state of thermally sensitive solids under convective heat transfer. Manthena et al. [13] studied the effects of stress resultants and plane stress, plane strain fields of a FG rectangular plate with temperature-dependent material properties.

Ganczarski and Szubartowski [14] demonstrated the plane stress state of FGM thick plate under thermal loading. Manthena et al. [15] determined the temperature distribution, displacement, and thermal stresses of a rectangular plate with nonhomogeneous material properties by assuming the properties to vary in y coordinate by simple power law. Mahapatra et al. [16] discussed the geometrically nonlinear thermomechanical transverse deflection responses of the functionally graded curved structure under the influence of nonlinear thermal field. Eisenberger and Elishakoff [17] presented a general methodology for solving buckling problems for inhomogeneous columns. Kumar et al. [18] considered a thick circular plate with axisymmetric heat supply and determined displacement components, stresses, conductive temperature, and temperature change. Nikolić [19] studied the free vibrations of the nonuniform axially functionally graded cantilever beam with a tip body. Rizov [20] studied delamination fracture in multilayered functionally graded, split cantilever beams by taking into account the nonlinear behavior of the material. Manthena and Kedar [21] discussed the thermal stresses of thermosensitive functionally graded thick hollow cylinder under unsteady distribution of temperature. Manthena et al. [22, 23] obtained the temperature profile and thermoelastic profile of a rectangular plate due to nonhomogeneous material properties.

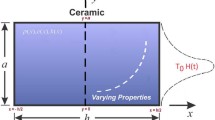
In this paper, the plane stress and plane strain field behavior of a functionally graded thermosensitive rectangular plate occupying the space defined by \(0\le x\le a, 0\le y\le b\) has been studied. All the material properties except density are assumed to be isotropic and temperature and spatial variable dependent. The transient heat conduction equation is solved by integral transform method. For theoretical treatment, all physical and mechanical quantities are taken as dimensional, whereas for numerical computations, nondimensional parameters have been considered.

2 Statement of the problem

2.1 Heat conduction equation

The unsteady state heat conduction equation with initial and boundary conditions in a rectangular plate is given by

$$\begin{aligned}&\frac{\partial }{\partial x}\left( {k(x,T)\frac{\partial T}{\partial x}} \right) +\frac{\partial }{\partial y}\left( {k(x,T)\frac{\partial T}{\partial y}} \right) =\rho C(x,T) \frac{\partial T}{\partial t} \end{aligned}$$
(1)
$$\begin{aligned}&\begin{array}{ll} T=T_0 , &{}\quad \hbox {at } t = 0 \\ k(x,T)\frac{\partial T}{\partial x}-\varepsilon _1 (T-T_0 )=f(y,t),&{}\quad \hbox {at } x = 0 \\ k(x,T)\frac{\partial T}{\partial x}+\varepsilon _2 (T-T_0 )=f(y,t), &{}\quad \hbox {at } x = a \\ k(x,T)\frac{\partial T}{\partial y}-\varepsilon _1 (T-T_0 )=0,&{} \quad \hbox {at } y = 0 \\ k(x,T)\frac{\partial T}{\partial y}+\varepsilon _2 (T-T_0 )=0, &{}\quad \hbox {at } y = b \end{array} \end{aligned}$$
(2)

where k(x, T) and C(x, T) are, respectively, thermal conductivity and calorific capacity of the material and \(\rho \) is the density which is a constant. \(T_0 \) is the temperature of the surrounding medium, and \(\varepsilon _1 , \varepsilon _2 \) are the heat transfer coefficients.

2.2 Thermoelastic equations

Let \(u_x \) and \(u_y \) be the displacement components in the in-plane directions of x and y. The strain–displacement components, equilibrium equations of the forces and stress–strain components disregarding the body forces are given by [6]

$$\begin{aligned}&\varepsilon _{xx} = \frac{\partial u_x }{\partial x}, \quad \varepsilon _{yy} =\frac{\partial u_y }{\partial y},\quad \varepsilon _{xy} =\frac{1}{2} \left( {\frac{\partial u_x }{\partial y}+ \frac{\partial u_y }{\partial x}} \right) \end{aligned}$$
(3)
$$\begin{aligned}&\frac{\partial \sigma _{xx} }{\partial x}+ \frac{\partial \sigma _{yx} }{\partial y} = 0 , \quad \frac{\partial \sigma _{xy} }{\partial x}+ \frac{\partial \sigma _{yy} }{\partial y} = 0 \end{aligned}$$
(4)
$$\begin{aligned}&\sigma _{xx} = \frac{ 2 }{1-\nu (x,T)}G(x,T)[\varepsilon _{xx} +\nu (x,T) \varepsilon _{yy} -(1+\nu (x,T)) \alpha (x,T) T] , \nonumber \\&\begin{array}{l}\sigma _{yy} = \frac{ 2 }{1-\nu (x,T)}G(x,T)[\nu (x,T) \varepsilon _{xx} +\varepsilon _{yy} -(1+\nu (x,T)) \alpha (x,T) T], \\ \sigma _{xy} = 2 G(x,T) \varepsilon _{xy}\end{array} \quad \mathbf{plane stress field } \end{aligned}$$
(5)
$$\begin{aligned}&\left. {\begin{array}{l} \sigma _{xx} = \frac{ 2 }{1-2\nu (x,T)}G(x,T)[(1-\nu (x,T))\varepsilon _{xx} +\nu (x,T) \varepsilon _{yy} \\ \qquad \qquad -(1+\nu (x,T)) \alpha (x,T) T] , \\ \sigma _{yy} = \frac{ 2 }{1-2\nu (x,T)}G(x,T)[\nu (x,T)\varepsilon _{xx} +(1-\nu (x,T))\varepsilon _{yy} \\ \qquad \qquad -(1+\nu (x,T)) \alpha (x,T) T], \\ \sigma _{xy} = 2 G(x,T) \varepsilon _{xy} \\ \end{array}} \right\} \quad \mathbf{plane~strain~field } \end{aligned}$$
(6)

where \(G(x,T), \alpha (x,T), \nu (x,T)\) are the shear modulus of elasticity, coefficient of linear thermal expansion and Poisson’s ratio, respectively.

2.3 Plane stress field

Using Eqs. (3) and (5) in (4), the displacement equations of equilibrium in x and y directions are obtained as

$$\begin{aligned}&\frac{2G(x,T)}{1 - \nu (x,T)} \left[ {\begin{array}{l} \frac{\partial ^{2}u_x }{\partial x^{2}}+\nu (x,T)\frac{\partial ^{2}u_y }{\partial x \partial y}+\frac{\partial u_y }{\partial y}\frac{\partial }{\partial x}(\nu (x,T))-(1 + \nu (x,T))\frac{\partial }{\partial x}(\alpha (x,T) T) \\ -\alpha (x,T) T\frac{\partial }{\partial x}(\nu (x,T)) \end{array}} \right] \nonumber \\&\quad +\,\frac{\partial }{\partial x}\left[ {\frac{2G(x,T)}{1 - \nu (x,T)}} \right] \left[ {\frac{\partial u_x }{\partial x} + \nu (x,T)\frac{\partial u_y }{\partial y}-(1 + \nu (x,T)) \alpha (x,T) T} \right] \nonumber \\&\quad +\,\frac{\partial }{\partial y}(G (x,T) )\left( {\frac{\partial u_x }{\partial y} + \frac{\partial u_y }{\partial x}} \right) +G(x,T) \left( {\frac{\partial ^{2}u_x }{\partial y^{2}} + \frac{\partial ^{2}u_y }{\partial x \partial y}} \right) = 0, \nonumber \\&\frac{2G(x,T)}{1 - \nu (x,T)} \left[ {\begin{array}{l} \nu (x,T)\frac{\partial ^{2}u_x }{\partial x \partial y}+\frac{\partial u_x }{\partial x}\frac{\partial }{\partial y}(\nu (x,T))+\frac{\partial ^{2}u_y }{\partial y^{2}}+-(1 + \nu (x,T))\frac{\partial }{\partial y}(\alpha (x,T) T) \\ -\alpha (x,T) T\frac{\partial }{\partial y}(\nu (x,T)) \\ \end{array}} \right] \nonumber \\&\quad +\,\frac{\partial }{\partial y}\left[ {\frac{2G(x,T)}{1 - \nu (x,T)}} \right] \left[ {\nu (x,T)\frac{\partial u_x }{\partial x} + \frac{\partial u_y }{\partial y}-(1 + \nu (x,T)) \alpha (x,T) T} \right] \nonumber \\&\quad +\,\frac{\partial }{\partial x}(G (x,T) )\left( {\frac{\partial u_x }{\partial y} + \frac{\partial u_y }{\partial x}} \right) +G(x,T) \left( {\frac{\partial ^{2}u_x }{\partial x \partial y} + \frac{\partial ^{2}u_y }{\partial x^{2}}} \right) = 0 \end{aligned}$$
(7)

2.4 Plane strain field

Similarly, the equilibrium equations in terms of displacement components are obtained by using Eqs. (3) and (6) into (4) as

$$\begin{aligned}&\frac{2G(x,T)}{1 - 2\nu (x,T)} \left[ {\begin{array}{l} \frac{\partial }{\partial x}\left[ {(1-\nu (x,T))\frac{\partial u_x }{\partial x}} \right] +\nu (x,T)\frac{\partial ^{2}u_y }{\partial x \partial y}+\frac{\partial u_y }{\partial y}\frac{\partial }{\partial x}(\nu (x,T)) \\ -(1 + \nu (x,T))\frac{\partial }{\partial x}(\alpha (x,T) T)-\alpha (x,T) T\frac{\partial }{\partial x}(\nu (x,T)) \end{array}} \right] \nonumber \\&\quad +\,\frac{\partial }{\partial x}\left[ {\frac{2G(x,T)}{1 - 2\nu (x,T)}} \right] \left[ {\frac{\partial u_x }{\partial x} + \nu (x,T)\frac{\partial u_y }{\partial y}-(1 + \nu (x,T)) \alpha (x,T) T} \right] \nonumber \\&\quad +\,\frac{\partial }{\partial y}(G (x,T) )\left( {\frac{\partial u_x }{\partial y} + \frac{\partial u_y }{\partial x}} \right) +G(x,T) \left( {\frac{\partial ^{2}u_x }{\partial y^{2}} + \frac{\partial ^{2}u_y }{\partial x \partial y}} \right) = 0, \nonumber \\&\frac{2G(x,T)}{1 - 2\nu (x,T)} \left[ {\begin{array}{l} \nu (x,T)\frac{\partial ^{2}u_x }{\partial x \partial y}+\frac{\partial u_x }{\partial x}\frac{\partial }{\partial y}(\nu (x,T))+\frac{\partial }{\partial y}\left[ {(1-\nu (x,T))\frac{\partial u_y }{\partial y}} \right] \\ -(1 + \nu (x,T))\frac{\partial }{\partial y}(\alpha (x,T) T)-\alpha (x,T) T\frac{\partial }{\partial y}(\nu (x,T)) \end{array}} \right] \nonumber \\&\quad +\,\frac{\partial }{\partial y}\left[ {\frac{2G(x,T)}{1 - 2\nu (x,T)}} \right] \left[ {\nu (x,T)\frac{\partial u_x }{\partial x} + \frac{\partial u_y }{\partial y}-(1 + \nu (x,T)) \alpha (x,T) T} \right] \nonumber \\&\quad +\,\frac{\partial }{\partial x}(G (x,T) )\left( {\frac{\partial u_x }{\partial y} + \frac{\partial u_y }{\partial x}} \right) +G(x,T) \left( {\frac{\partial ^{2}u_x }{\partial x \partial y} + \frac{\partial ^{2}u_y }{\partial x^{2}}} \right) = 0 \end{aligned}$$
(8)

The solution of Eqs. (7) and (8) without body forces can be expressed by the Goodier’s thermoelastic displacement potential \(\phi \) and the Boussinesq harmonic functions \(\varphi \) and \(\psi \) as

$$\begin{aligned} u_x= & {} \frac{\partial \phi }{\partial x}+ \frac{\partial \varphi }{\partial x}+2\frac{\partial \psi }{\partial y} \end{aligned}$$
(9)
$$\begin{aligned} u_y= & {} \frac{\partial \phi }{\partial y}+ \frac{\partial \varphi }{\partial y}-2\frac{\partial \psi }{\partial x} \end{aligned}$$
(10)

in which the three functions must satisfy the conditions

$$\begin{aligned} \nabla ^{2}\phi =K(x,T) \tau , \quad \nabla ^{2}\varphi =0\hbox { and } \nabla ^{2}\psi =0 \end{aligned}$$
(11)

where \( \nabla ^{2} = \frac{\partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}} ,K(x,T)=\frac{(1+\nu (x,T))}{(1-\nu (x,T))}\alpha (x,T)\) is the restraint coefficient and \(\tau =T-T_0 \).

By using Eqs. (9) and (10) in Eqs. (5) and (6), the results for corresponding stress functions are obtained as follows.

For plane stress field

$$\begin{aligned} \sigma _{xx}= & {} \frac{ 2G(x,T) }{1-\nu (x,T)}\left\{ {\begin{array}{l} \left( {\frac{\partial ^{2}\phi }{\partial x^{2}}+\nu (x,T)\frac{\partial ^{2}\phi }{\partial y^{2}}} \right) +\left( {\frac{\partial ^{2}\varphi }{\partial x^{2}}+\nu (x,T)\frac{\partial ^{2}\varphi }{\partial y^{2}}} \right) \\ +2\frac{\partial ^{2}\psi }{\partial x \partial y} (1-\nu (x,T))-(1+\nu (x,T)) \alpha (x,T) T \end{array}} \right\} , \nonumber \\ \sigma _{yy}= & {} \frac{ 2G(x,T) }{1-\nu (x,T)}\left\{ {\begin{array}{l} \left( {\nu (x,T)\frac{\partial ^{2}\phi }{\partial x^{2}}+\frac{\partial ^{2}\phi }{\partial y^{2}}} \right) +\left( {\nu (x,T)\frac{\partial ^{2}\varphi }{\partial x^{2}}+\frac{\partial ^{2}\varphi }{\partial y^{2}}} \right) \\ -2\frac{\partial ^{2}\psi }{\partial x \partial y} (1-\nu (x,T))-(1+\nu (x,T)) \alpha (x,T) T \end{array}} \right\} , \nonumber \\ \sigma _{xy}= & {} 2 G(x,T) \left\{ {\frac{\partial ^{2}\phi }{\partial x \partial y}+\frac{\partial ^{2}\varphi }{\partial x \partial y}+\frac{\partial ^{2}\psi }{\partial y^{2}}-\frac{\partial ^{2}\psi }{\partial x^{2}}} \right\} \end{aligned}$$
(12)

For plane strain field

$$\begin{aligned} \sigma _{xx}= & {} \frac{ 2G(x,T) }{1-2 \nu (x,T)}\left\{ {\begin{array}{l} \left( {(1-\nu (x,T))\frac{\partial ^{2}\phi }{\partial x^{2}}+\nu (x,T)\frac{\partial ^{2}\phi }{\partial y^{2}}} \right) +\left( {(1-\nu (x,T))\frac{\partial ^{2}\varphi }{\partial x^{2}}+\nu (x,T)\frac{\partial ^{2}\varphi }{\partial y^{2}}} \right) \nonumber \\ +2\frac{\partial ^{2}\psi }{\partial x \partial y} (1-2 \nu (x,T))-(1+\nu (x,T)) \alpha (x,T) T \end{array}} \right\} , \nonumber \\ \sigma _{yy}= & {} \frac{ 2G(x,T) }{1-2 \nu (x,T)}\left\{ {\begin{array}{l} \left( {\nu (x,T)\frac{\partial ^{2}\phi }{\partial x^{2}}+(1-\nu (x,T))\frac{\partial ^{2}\phi }{\partial y^{2}}} \right) +\left( {\nu (x,T)\frac{\partial ^{2}\varphi }{\partial x^{2}}+(1-\nu (x,T))\frac{\partial ^{2}\varphi }{\partial y^{2}}} \right) \nonumber \\ -2\frac{\partial ^{2}\psi }{\partial x \partial y} (1-2 \nu (x,T))-(1+\nu (x,T)) \alpha (x,T) T \end{array}} \right\} , \nonumber \\ \sigma _{xy}= & {} 2 G(x,T) \left\{ {\frac{\partial ^{2}\phi }{\partial x \partial y}+\frac{\partial ^{2}\varphi }{\partial x \partial y}+\frac{\partial ^{2}\psi }{\partial y^{2}}-\frac{\partial ^{2}\psi }{\partial x^{2}}} \right\} \end{aligned}$$
(13)

The boundary condition on the traction-free surface stress functions is

$$\begin{aligned} \left. {\sigma _{xx} } \right| _{x=0} = \left. { \sigma _{xx} } \right| _{x=a} =\left. { \sigma _{yy} } \right| _{y=0} =\left. { \sigma _{yy} } \right| _{y=b} =0 \end{aligned}$$
(14)

3 Solution of the problem

3.1 Heat conduction equation

Introducing Kirchhoff’s variable transformation following [2,3,4, 7, 9, 12]

$$\begin{aligned} \theta (T)= \int _{_{T_0 } }^{T } {k(x,T)} \mathrm{d} T \end{aligned}$$
(15)

and taking into account that the material with simple thermal nonlinearity is considered, we obtain Eq. (1) with variable \(\theta \) as

$$\begin{aligned} \frac{\partial ^{2}\theta }{\partial x^{2}}+\frac{\partial ^{2}\theta }{\partial y^{2}}= \frac{1}{\kappa } \frac{\partial \theta }{\partial t} \end{aligned}$$
(16)

The initial and boundary conditions (2) become

$$\begin{aligned} \begin{array}{ll} \theta =0, &{}\quad \hbox {at } t = 0 \\ \frac{\partial \theta }{\partial x}-\varepsilon _1 \theta =f(y,t), &{}\quad \hbox {at } x = 0 \\ \frac{\partial \theta }{\partial x}+\varepsilon _2 \theta =f(y,t), &{}\quad \hbox {at } x = a \\ \frac{\partial \theta }{\partial y}-\varepsilon _1 \theta =0, &{}\quad \hbox {at } y = 0 \\ \frac{\partial \theta }{\partial y}+\varepsilon _2 \theta =0, &{}\quad \hbox {at } y = b \\ \end{array} \end{aligned}$$
(17)

Here, \(\kappa =k_0 /(C_0\, \rho _0 )\), in which \(k_0 , C_0, \hbox { and } \rho _0 \) are the reference values of thermal conductivity, calorific capacity, and density, respectively.

For the sake of brevity, we consider \(f(y,t) = Q_1 \delta (y-y_0 ) \sin \,h (\omega t)\)

This represents a hyperbolically varying impulsive point heat of strength \(Q_1 \) at the points \((x=0,y=y_0 )\) and \((x=a,y=y_0 ).\)

Applying the transform defined in Eq. (A1—Appendix A) on Eq. (16) over the variable x, we obtain

$$\begin{aligned} -\beta _n^2 \bar{{\theta }}+A_3 \bar{{f}}(y,t)+\frac{\partial \bar{{\theta }}}{\partial y}= \frac{1}{\kappa } \frac{\partial \bar{{\theta }}}{\partial t} \end{aligned}$$
(18)

The initial and boundary conditions (17) become

$$\begin{aligned} \begin{array}{ll} \bar{{\theta }}=0, &{}\quad \hbox {at } t = 0 \\ \frac{\partial \bar{{\theta }}}{\partial y}-\varepsilon _1 \bar{{\theta }}=0,&{} \quad \hbox {at } y = 0 \\ \frac{\partial \bar{{\theta }}}{\partial y}+\varepsilon _2 \bar{{\theta }}=0, &{}\quad \hbox {at } y = b \\ \end{array} \end{aligned}$$
(19)

where \(A_3 =A_1 \beta _n +A_1 (\beta _n \cos \beta _n a+\varepsilon _1 \sin \beta _n a)\).

Again applying the transform defined in Eq. (A6—Appendix A) on Eq. (18) over the variable y, we obtain

$$\begin{aligned} \frac{\partial \bar{{\bar{{\theta }}}}}{\partial t}+A_4 \bar{{\bar{{\theta }}}}= A_5 \sin \,h (\omega t) \end{aligned}$$
(20)

Subject to the initial condition

$$\begin{aligned} \bar{{\theta }}=0, \quad \hbox {at } t = 0 \end{aligned}$$
(21)

where \(A_4 =\kappa (\beta _n^2 +\alpha _m^2 ) , A_5 =A_2 A_3 Q_1 y_0 \kappa (\alpha _m \cos \alpha _m y_0 +\varepsilon _1 \sin \alpha _m y_0 ).\)

Applying Laplace transform and its inverse on Eq. (20) using the initial condition (21), we obtain

$$\begin{aligned} \bar{{\bar{{\theta }}}}(\beta _n ,\alpha _m ,t)=E_1 \exp (-\omega t)+E_2 \exp (\omega t)+E_3 \exp (-A_2 t) \end{aligned}$$
(22)

where \(E_1 =A_5 /(2\omega -2A_4 ), E_2 =A_5 /(2\omega +2A_4 ), E_3 =A_5 \omega /(A_4^2 -\omega ^{_2 }).\)

Applying the inverse formula defined in Eq. (A7—Appendix A) on Eq. (22), we obtain

$$\begin{aligned} \bar{{\theta }}(\beta _n , y,t) = \sum _{m=1}^\infty S(\alpha _m , y) [E_1 \exp (-\omega t)+E_2 \exp (\omega t)+E_3 \exp (-A_2 t)] \end{aligned}$$
(23)

Applying inverse formula defined in Eq. (A2—Appendix A) on Eq. (23), we obtain

$$\begin{aligned} \theta (x,y, t) =\sum _{m=1}^\infty \sum _{n=1}^\infty \{S(\beta _n , x) S(\alpha _m , y) [E_1 \exp (-\omega t)+E_2 \exp (\omega t)+E_3 \exp (-A_2 t)]\} \end{aligned}$$
(24)

Applying variable inverse transformation from \(\theta \) to T (Appendix B), the temperature distribution in Eq. (24) becomes

$$\begin{aligned} T(x, y, t)\cong & {} T_0 +\sum _{m=1}^\infty \sum _{n=1}^\infty \{\{1/[u (x)\exp (\varpi _1 T_0 )]\}S(\beta _n , x) S(\alpha _m , y) \nonumber \\&\times \, [E_1 \exp (-\omega t)+E_2 \exp (\omega t)+E_3 \exp (-A_2 t)]\} \end{aligned}$$
(25)

where

$$\begin{aligned} u(x)=[f_m (x)(k_{m_0 } -k_{c_0 } ) + k_{c_0 } ], \quad f_m (x)=1-x^{\gamma } \hbox { for } \gamma \ge 0. \end{aligned}$$

3.2 Thermoelastic equations

Using Eq. (25), we obtain the solution for Goodier’s thermoelastic displacement potential \(\phi \) from Eq. (11) as

$$\begin{aligned} \phi= & {} \sum \limits _{m=1}^\infty \sum \limits _{n=1}^\infty \{\{K(x,T)g_1 (x,y)/[g_2 (x,y)(u (x))^{3}\exp (\varpi _1 T_0 )]\}S(\beta _n , x) S(\alpha _m , y) \nonumber \\&\times \, [E_1 \exp (-\omega t)+E_2 \exp (\omega t)+E_3 \exp (-A_2 t)]\} \end{aligned}$$
(26)

where

$$\begin{aligned} g_1 (x,y)= & {} S(\beta _n , x) \times S(\alpha _m , y) , \\ g_2 (x,y)= & {} S(\alpha _m , y)[u(x){g_3{^{\prime }}}(x)-2g_3 (x){u}'(x)]+S(\beta _n , x) {S}''(\alpha _m , y)(u (x))^{2}, \\ g_3 (x)= & {} u(x) {S}'(\beta _n , x)-{u}'(x)S(\beta _n , x). \\ \end{aligned}$$

For the sake of brevity, we assume the Boussinesq harmonic functions \(\varphi \) and \(\psi \) so as to satisfy Eq. (11) as

$$\begin{aligned} \varphi= & {} \psi = \sum \limits _{m=1}^\infty \sum \limits _{n=1}^\infty \{\sin \,h (p_1 t)[B_n \sin (\beta _n x) + D_n \cos (\beta _n x)] \nonumber \\&\times \, [\sin (\alpha _m y) + \cos (\alpha _m y)]\} \end{aligned}$$
(27)

where \(B_n , D_n \) are constants.

Substituting the values of \(\phi , \varphi , \psi \) from Eqs. (26) and (27) in Eqs. (9) and (10), we obtain

$$\begin{aligned} u_x= & {} \sum \limits _{m=1}^\infty \sum _{n=1}^\infty \{\phi _{,x} +\sin \,h (p_1 t)\beta _n [B_n \cos (\beta _n x) - D_n \sin (\beta _n x)][\sin (\alpha _m y) + \cos (\alpha _m y)] \nonumber \\&+\,2 \alpha _m \sin \,h (p_1 t)[B_n \sin (\beta _n x) + D_n \cos (\beta _n x)][\cos (\alpha _m y)-\sin (\alpha _m y)]\} \nonumber \\ u_y= & {} \sum \limits _{m=1}^\infty \sum _{n=1}^\infty \{\phi _{,y} +\alpha _m \sin \,h (p_1 t)[B_n \sin (\beta _n x) + D_n \cos (\beta _n x)][\cos (\alpha _m y)-\sin (\alpha _m y)] \nonumber \\&-\,2\sin \,h (p_1 t)\beta _n [B_n \cos (\beta _n x) - D_n \sin (\beta _n x)][\sin (\alpha _m y) + \cos (\alpha _m y)]\} \end{aligned}$$
(28)

where a comma denotes differentiation with respect to the following variable.

The shear modulus of elasticity (SME) G, coefficient of linear thermal expansion (CLTE) \(\alpha \), and Poisson’s ratio (PR) \(\nu \) of the FGM dependent on x are expressed using the SME, CLTE, and PR of metals \(G_m , \alpha _m , \nu _m \) and of ceramics \(G_c , \alpha _c , \nu _c \) with the volume fractions of metals \(f_m (x)\), and ceramics, \(1-f_m (x)\) as [5]

$$\begin{aligned} G(x,T)= & {} G_m (T)f_m (x)+G_c (T)(1-f_m (x)), \nonumber \\ \alpha (x,T)= & {} \alpha _m (T)f_m (x)+\alpha _c (T)(1-f_m (x)), \nonumber \\ \nu (x,T)= & {} \nu _m (T)f_m (x)+\nu _c (T)(1-f_m (x)) \end{aligned}$$
(29)

Following Noda [1], we assume \(G(T), \alpha (T), \nu (T)\) as per exponential law as follows:

$$\begin{aligned} G_j (T)= & {} G_{j0} \exp (\varpi _1 T) , \quad \alpha _j (T)=\alpha _{j0} \exp (\varpi _2 T), \quad \nu _j (T)=\nu _{j0} \exp (\varpi _2 T), \nonumber \\ j= & {} m, c ; \varpi _1 \le 0, \varpi _2 \ge 0 \end{aligned}$$
(30)

Here, \(G_{j0} \), \(\alpha _{j0}\), and \(\nu _{j0} \) are the reference values of SME, CLTE, and PR, respectively.

By using Eqs. (26), (27), (29), and (30) in Eqs. (12) and (13), the resulting components of stresses in plane stress field and plane strain field may be obtained.

By using the traction-free conditions given by Eq. (14) in the equation of stresses (12) and (13), the constants \(B_n \) and \(D_n \) may be obtained. The stresses and the constants \(B_n \) and \(D_n \) are obtained using Mathematica software.

4 Numerical results and discussion

Following Awaji et al. [5], we consider a model of a ceramic–metal-based FGM, in which alumina is selected as ceramic and nickel as metal (Table 1).

Table 1 Thermomechanical properties of alumina and nickel at room temperature
Full size table

For numerical computations, we introduce the following nondimensional parameters:

$$\begin{aligned}&\bar{{T}} = \frac{T}{T_0 } , \quad \bar{{X}} = \frac{x}{b} , \quad \bar{{Y}} = \frac{y}{b} , \quad \Gamma = \frac{\kappa t}{b^{2}} , \quad (\bar{{u}}_x ,\quad \bar{{u}}_y ) = \frac{(u_x , u_y ) }{K_0 T_o b} , \\&(\bar{{\sigma }}_{xx} ,\bar{{\sigma }}_{yy} ,\bar{{\sigma }}_{xy} ) = \frac{(\sigma _{xx} ,\sigma _{yy} ,\sigma _{xy} )}{EG_0 T_0 } , K_0 = \frac{1+\nu }{1-\nu } \alpha _0 . \\ \end{aligned}$$

with parameters \(a = 4\, \hbox {cm} , b = 2 \,\hbox {cm} , t=2\,\hbox {s} \), surrounding temperature \(T_0 = 320^{\circ }\hbox {K}\).

Figures 1, 2, 3, 4, 5, 6, 7, 8, and 9 show the variations of dimensionless temperature and thermal stresses. The figures on the left are plotted for the homogeneous case (i.e., taking \(\varpi _1 =\varpi _2 =0\), so that the material properties become independent of temperature and spatial variable), whereas those on the right are plotted for the nonhomogeneous case (i.e., taking \(\varpi _1 \ne 0, \varpi _2 \ne 0\), so that the material properties become dependent of temperature and spatial variable).

Fig. 1
figure 1

Variation of dimensionless temperature along x-axis

Full size image
Fig. 2
figure 2

Variation of dimensionless temperature along y-axis

Full size image
Fig. 3
figure 3

Variation of dimensionless stresses (plane stress field) along x-axis

Full size image
Fig. 4
figure 4

Variation of dimensionless stresses (plane stress field) along y-axis

Full size image
Fig. 5
figure 5

Variation of dimensionless stresses (plane strain field) along x-axis

Full size image
Fig. 6
figure 6

Variation of dimensionless stresses (plane strain field) along y-axis

Full size image
Fig. 7
figure 7

Variation of dimensionless temperature with time

Full size image
Fig. 8
figure 8

Variation of dimensionless stresses (plane stress field) with time

Full size image
Fig. 9
figure 9

Variation of dimensionless stresses (plane strain field) with time

Full size image

Figure 1 shows the variation of temperature along x-axis for different values of \(\bar{{Y}}=0.3, 0.7\). In the homogeneous case, the temperature is positive at the outer part of the plate which is decreasing to negative till \(\bar{{X}}=1.2,\) and suddenly increasing thereafter toward the origin. In the nonhomogeneous case, the magnitude of temperature is decreasing from higher to lower which nearly converges to zero at \(\bar{{X}}=1.2\) and monotonically increases toward the other end of the rectangular plate.

Figure 2 shows the variation of temperature along y-axis for different values of \(\bar{{X}}=0.5, 2\). In both the homogeneous and nonhomogeneous cases, it is observed that the temperature is slowly and steadily increasing till the middle part and suddenly decreasing toward the upper end of the rectangular plate.

Figure 3 shows the variation of stresses in the plane stress field along x-axis. In the homogeneous case, the stress components \(\bar{{\sigma }}_{xx} , \bar{{\sigma }}_{yy} \) are tensile throughout the plate, while \(\bar{{\sigma }}_{xy} \) is compressive in the region \(1.2<\bar{{X}}<2\) and tensile toward the origin. In the nonhomogeneous case, the stresses \(\bar{{\sigma }}_{xx} , \bar{{\sigma }}_{yy} \) are compressive throughout the plate except for \(\bar{{\sigma }}_{yy} \) near the origin where it is seen to be tensile. The stress component \(\bar{{\sigma }}_{xy} \) is tensile throughout the plate, except near the origin where it is compressive.

Figure 4 shows the variation of stresses in the plane stress field along y-axis. In both the cases, all the stress components are seen to be tensile.

Figure 5 shows the variation of stresses in the plane strain field along x-axis. In the homogeneous case, all the stress components are tensile throughout the plate. In the nonhomogeneous case, the stress component \(\bar{{\sigma }}_{xx} \) is compressive near the outer and middle parts of the plate, while tensile in the remaining region. The stress component \(\bar{{\sigma }}_{yy} \) is tensile at the outer region, while compressive toward the origin.

Figure 6 shows the variation of stresses in the plane strain field along y-axis. In both the cases, all the stress components are tensile throughout the plate.

Figure 7 shows the variation of temperature with time for different values of \(\bar{{X}}=0.5, 2\). In both the cases, the temperature is slowly and steadily increasing with the increase in time.

Figure 8 shows the variation of stresses in the plane stress field with time. In the homogeneous case, the stress components \(\bar{{\sigma }}_{xx} , \bar{{\sigma }}_{yy} \) are tensile throughout the plate with the increase in time, while \(\bar{{\sigma }}_{xy} \) is compressive with the increase in time. In the nonhomogeneous case, all the stress components are compressive with increase in time.

Figure 9 shows the variation of stresses in the plane strain field with time. In the homogenous case, the stress components \(\bar{{\sigma }}_{xx} , \bar{{\sigma }}_{yy} \) are tensile and their magnitude is increasing with increase in time. In the nonhomogeneous case, the stresses are compressive till \(\Gamma =1\), while tensile afterward.

5 Conclusion

The research work in the field of thermoelastic problems of thermosensitivity with convective heat exchange in functionally graded materials is unfortunately limited due to the mathematical complexity of equations in the stress and strain field. In most of the research work, the solutions of field equations are obtained by considering homogeneous material properties. The technique utilized as a part of this work is very effective in managing problems with nonhomogeneous materials. The proposed integral transform technique for analyzing the temperature distribution in the FGM rectangular plate gives exact solution of the heat conduction equation. The broadest articulations for temperature and stress parts have been inferred and exhibited graphically.

It is observed that temperature assumes a fundamental part in characterizing the nonlinearity of the material. To a greater extent, an impact on the temperature distribution is exercised by the thermosensitivity of the material. Numerical calculations indicate that its consideration drastically leads to a decrease in temperature. The plane stress profile is found to be compressive as well as tensile in the homogeneous case and nonhomogeneous cases. The plane strain profile is found to be tensile in both the cases. The plane stress field becomes tensile over a period of time (as time increases) in the homogeneous case while it is tensile in the nonhomogeneous case.

The pattern of curves shows the properties of thermoelastic conduct of the medium and fulfills the requisite conditions of the problem. The obtained stress components give novel data prompting to understand the deformation mechanism in auxiliary materials. The outcomes acquired can shape a reason for choosing regime parameters in the examination process of heat conduction in heatproof auxiliary components and defense for considering the changeability of the thermally sensitive coefficients in dealing with heat and mass exchange problems.