Nonlinear vibration and dynamic stability analysis of rotor-blade system with nonlinear supports

Abstract

A dynamic model of a rotor-blade system is established considering the effect of nonlinear supports at both ends. In the proposed model, the shaft is modeled as a rotating beam where the gyroscopic effect is considered, while the shear deformation is ignored. The blades are modeled as Euler–Bernoulli beams where the centrifugal stiffening effect is considered. The equations of motion of the system are derived by Hamilton principle, and then, Coleman and complex transformations are adopted to obtain the reduced-order system. The nonlinear vibration and stability of the system are studied by multiple scales method. The influences of the normal rubbing force, friction coefficient, damping and support stiffness on the response of the rotor-blade system are investigated. The results show that the original hardening type of nonlinearity may be enhanced or transformed into softening type due to the positive or negative nonlinear stiffness terms of the bearing. Compared with the system with higher support stiffness, the damping of the bearing has a more powerful effect on the system stability under lower support stiffness. With the increase in rubbing force and support stiffness, the jump-down frequency, resonant peak and the frequency range in which the system has unstable responses increase.

1 Introduction

Rotating systems including shaft, blade and bearing assembly are usually used in many engineering machineries, such as compressors, turbines and aero-engines . As they become more flexible, high-amplitude vibration or even unstable dynamic behavior may happen. So, the investigation on dynamic characteristics and stability of rotor-blade system is necessary. Considering the geometrical nonlinearity, Khadem et al. [1] adopted multiple scales method to study the free and forced vibrations of the simply supported rotating shaft under the conditions of primary resonances. They also investigated the resonances of a simply supported spinning shaft modeled as an in-extensional rotating beam with large amplitudes and discussed the influences of mass eccentricity and external damping on the steady-state response of the shaft based on harmonic balance method [2]. Shahgholi and Khadem [3] investigated the main and parametric resonances of an asymmetric rotating shaft with speed fluctuations.

Obviously, not only the dynamics of the rotating shaft, but also the vibration responses of the rotor-blade system should be investigated to consider the coupling effects of the blades or the bladed disk and shaft. The shaft–bladed disk model, where the bearing is assumed to be rigid or a linear spring model with viscous damping, is widely used to study the coupling vibration of the blades and rotor [4,5,6,7,8,9,10,11,12,13,14]. Chiu and Chen [4] investigated the influence of shaft-torsion and blade-bending vibrations on the coupling nonlinear vibrations of a multi-disk rotor system. By analyzing the natural frequencies and the mode shapes of the system, they revealed that the natural frequencies were affected by disk distance and that the instability depended on the number of disks. Chiu and Huang [5] studied the coupling vibrations among the shaft-torsion, disk-transverse and blade bending of a rotor system with a mistuned blade. Considering the centrifugal stiffening and spin softening effects of the blades, the lateral-torsional vibrations and gyroscopic effect of the shaft, Ma et al. [6] proposed a mathematical model of rotor-blade systems. Genta et al. [7] developed annular finite elements to compute the second- and higher-order harmonics modes of rotating bladed disks. Considering the effects of mass eccentricity, Diken and Alnefair [8] discussed the vibration responses of a rotor-blade system. The results showed that rotor acceleration can excite the blade’s vibration with rotor’s natural frequency at critical speed and the modal behaviors of the blades were different at the subcritical, supercritical and critical speeds of the rotor. Using Lagrange equation, Wang et al. [9] established a time-dependent nonlinear model of a flexible blade-rotor-bearing system and addressed the nonlinear behavior of the rotor-bearing system with the interaction between the blades and the rotor. Assuming the blades as Euler–Bernoulli beams, Santos et al. [10] contributed to the investigation of rotor-blades dynamic interaction, theoretically and experimentally. They carried out experiments of the rotor system at different angular velocities and verified the theoretical results. Using nonlinear bearings and a Jeffcott rotor with a number of planar blades, Najafi et al. [11,12,13] studied the nonlinear behavior of blade disk systems and discussed the damping effects on the bifurcation phenomenon of the system. Based on Floquet theory, Sanches et al. [14] predicted the bifurcation positions of the bladed rotor used in helicopters and described the instability zones under different conditions. Considering the rigid body displacement and the flexible displacement of the casing, Parent and Thouverez [15] studied the dynamic stability of a turbofan engine bearing the light contacts between fan blades and casing by reasonably simplifying an aero-engine. Considering Duffing type of nonlinear supports in rotor systems, the vibration response and bifurcation characteristics were analyzed in [16, 17].

Damping is a non-negligible factor which can influence the stability and bifurcation of the rotor and it can be divided into two types: external damping and internal damping. External damping, i.e., bearing damping, is not responsible for the instability of rotor-blade systems [18]. Internal damping, i.e., rotating damping, is caused by the friction between the rotating parts and couplings [19] and the structural damping of the blade and shaft [20]. The influences of damping on the instability of the system were discussed in Ref. [21]. Sorge et al. [22] investigated the influence of internal damping on the whirling motion of the rotor at supercritical range. Samantaray et al. [23] studied the stability of the rotor using polynomial nonlinear internal damping. Using a simple bladed-rotor model, Genta [24] pointed out that the structural damping of blades could not trigger any instability at supercritical ranges. Adopting Euler–Bernoulli beam theory to model the shaft and blade, Bab et al. [25] investigated the main resonances of a coupled flexible rotor with a disk and a set of flexible/rigid blades. The influences of mass eccentricity and damping on the steady response of the system were studied based on multiple scales method.

Rubbing has a great influence on the stability of the system. With respect to point or partial rubbing, the rubbing forces were regarded as periodic impulse loading. Petrov [26, 27] adopted nonlinear multi-harmonic rubbing force to study the response of the rotor. Sinha [28, 29] presented some mathematical expressions for the pulse force, like half-sine wave pulse, rectangular pulse and so on. Turner et al. [30, 31] also adopted half-sine wave pulse force to analyze the blade-casing rubbing. To simulate blade-casing rubbing, two kinds of pulse load functions were adopted by Kou and Yuan [32]: sine pulse function and continuous sine function. Ma et al. [33] focused on determining the maximal normal rubbing force under blade-elastic-casing rubbing. Rubbing caused by blade off was studied in Refs. [34,35,36].

The studies listed above show that in some references, the shaft was commonly assumed as a simply supported rotating beam without considering the stiffness or the damping of the bearing [1,2,3, 25]. In practice, the stiffness and the damping of the bearing change with the rotating speed, and they have a significant influence on the instability region of the system. This paper mainly focuses on the following aspects:

• (1) The Duffing type of nonlinear support [11, 16, 17] is introduced to describe the effect of the bearing on the mode shapes and critical speeds of the rotor. Furthermore, the nonlinearity type, response amplitudes and jump-down frequencies of the system under different support stiffness and Duffing term coefficients are obtained. In addition, the influence of the damping of the bearing and rotor on the stability of the system under different support stiffness is discussed.

• (2) The local intermittent blade-casing rubbing is considered; especially, the influences of normal rubbing force and friction coefficient on the response amplitudes and the instability regions are discussed. The analytical solution is also verified by the numerical solution obtained from Runge–Kutta method.

2 Equations of motion

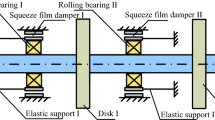
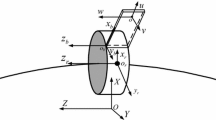
A rotor-blade system including a slender spinning shaft, a rigid disk located at $x=x_{\mathrm{d}}$ position of the shaft and a set of blades with stagger angle $\gamma$ is taken as the research object, as shown in Fig. 1. The following coordinate systems are adopted to analyze the dynamics of the rotor-blade system:

• (1) The frame $X-Y-Z$ is a fixed inertial coordinate system, where X axis is along the direction of the neutral axis of the undeformed shaft.

• (2) The frame $x-y-z$ is a dynamic local coordinate system corresponding to the principle axes of the cross section of the deformed shaft.

• (3) The frame $x_{\mathrm{b}}-y_{\mathrm{b}}-z_{\mathrm{b}}$ is a dynamic local coordinate system of blades, in which $x_{\mathrm{b}}$, $y_{\mathrm{b}}$ and $z_{\mathrm{b}}$ are along the chordwise, flapwise and radial directions, respectively.

The bearings are regarded as the nonlinear supports in Y and Z directions, and the displacement in X direction at the left end of the shaft is constrained, so is the torsional displacement, which means $k_{\phi }=\infty$. There is no constraint at the right end in X direction. For simplicity, let $c_{\mathrm{b}z1}= c_{\mathrm{b}z2}= c_{\mathrm{b}y1}= c_{\mathrm{b}y2}= c_{\mathrm{bearing}}$.

2.1 The energies of the spinning shaft

The displacements at arbitrary location of the shaft along the X, Y and Z axes are denoted by variables u(x, t), v(x, t) and w(x, t), respectively. The transformation from inertial coordinate system $X-Y-Z$ to the local coordinate system $x-y-z$ is expressed by three Euler angles $\psi (x,t)$, $\theta (x,t)$ and ${\beta }(x,t)$, as shown in Fig. 2 [1,2,3]. Firstly, the inertial coordinate system $X-Y-Z$ rotates around Y axis at the angle of $\theta$, reaching the position of $X_{1}-Y_{1}-Z_{1}$. After that, the frame $X_{1}-Y_{1}-Z_{1}$ rotates around $X_{1}$ axis at the angle of $\beta$, reaching the position of $X_{2}-Y_{2}-Z_{2}$. Finally, the frame $X_{2}-Y_{2}-Z_{2}$ rotates around $Z_{2}$ axis at the angle of $\psi$, reaching the position of $x-y-z.$ It should be noted that $\psi (x,t)$ and $\theta (x,t)$ are corresponding to the bending deformation of the shaft, while $\beta (x,t)$ is the summation of torsional deformation $\phi (x,t)$ and the rigid body rotation displacement of the shaft $\varOmega {t}$, i.e.,

$$\begin{aligned} \beta (x,t)=\varOmega t+\phi (x,t) \end{aligned}$$

(1)

where $\varOmega$ denotes the rotating speed of the shaft.

Therefore, the curvatures $k_{1}$, $k_{2}$, $k_{3}$ and the angular speeds around X, Y and Z axes $\omega _{1}$ , $\omega _{2}$, $\omega _{3}$ of the spinning shaft can be calculated as [3]:

$$\begin{aligned} k_1= & {} {\phi }'-{\psi }'\sin \theta ,k_2 ={\psi }'\cos \theta \sin \beta +{\theta }'\cos \beta ,k_3 ={\psi }'\cos \theta \cos \beta -{\theta }'\sin \beta \end{aligned}$$

(2)

$$\begin{aligned} \omega _1= & {} \dot{\beta }-{\dot{\psi }}\sin \theta ,\omega _2 ={\dot{\psi }}\cos \theta \sin \beta +{\dot{\theta }}\cos \beta ,\omega _3 ={\dot{\psi }}\cos \theta \cos \beta -{\dot{\theta }}\sin \beta \end{aligned}$$

(3)

where dot and prime denote derivative with respect to t and x, respectively.

Fig. 1

Schematic of the rotor-blade system

Fig. 2

Coordinates transformation using Euler angles

Consequently, the kinetic and potential energies of the spinning shaft can be determined as follows:

$$\begin{aligned} T_{\mathrm {shaft}}= & {} \frac{1}{2}\int _0^l {\left( {m\left( {\dot{u}^{2}+{\dot{v}}^{2}+{\dot{w}}^{2}} \right) +I_1 \omega _1^2 +I_2 \omega _2^2 +I_3 \omega _3^2 } \right) } \hbox { d}x \end{aligned}$$

(4)

$$\begin{aligned} V_{\mathrm {shaft}}= & {} \frac{1}{2}\int _0^l {\left( {N_{11} \alpha ^{2}+D_{11} k_1^2 +D_{22} k_2^2 +D_{33} k_3^2 } \right) } \hbox { d}x \end{aligned}$$

(5)

where l, m, $I_{1}$, $I_{2}$, $I_{3}$, $N_{11}$, $\alpha$, $D_{11}$, $D_{22}$ and $D_{33}$ are the length of the shaft, the mass per unit length, the polar mass moment of inertia, the mass moment of inertia around y axis, the mass moment of inertia around z axis, the longitudinal stiffness, the strain along the neutral axis of the shaft, torsional stiffness, the flexural stiffness about y axis, the flexural stiffness about z axis, respectively, which can be calculated as:

$$\begin{aligned} I_1= & {} \int _A {\left( {y^{2}+z^{2}} \right) } \hbox { d}m,I_2 =\int _A {z^{2}} \hbox {d}m,I_3 =\int _A {y^{2}} \hbox {d}m,D_{11}\nonumber \\= & {} \int _A {G\left( {y^{2}+z^{2}} \right) } \hbox { d}A,D_{22} =\int _A {Ez^{2}} \hbox {d}A,D_{33} =\int _A {Ey^{2}} \hbox {d}A \nonumber \\ N_{11}= & {} \int _A E \hbox {d}A,\alpha =\sqrt{\left( {1+{u}'} \right) ^{2}+{v}'^{2}+{w}'^{2}}-1 \end{aligned}$$

(6)

where A, E and G are cross-sectional area, Young’s modulus and shear modulus of the shaft.

The elastic potential energy stored in the bearings can be expressed as:

$$\begin{aligned} V_{\mathrm {bearing}} =\int \limits _0^{\left| z \right| } {f(z)\hbox {d}z} {\delta }(x)+\int \limits _0^{\left| z \right| } {f(z)\hbox {d}z} {\delta }(x-l) \end{aligned}$$

(7)

where f(z) is the nonlinear restoring force of the bearings and $z=v+\hbox {j}w (\hbox {j}^{2}=-1)$; $\delta (x)$ is Dirac delta function. If f(z) is expanded using Taylor series method and truncated at the cubic nonlinear term, then $f (z)={kz}+{\vartheta z}{\vert }\hbox {z}{\vert }^{2}$, where k and $\vartheta$ are the linear support stiffness and the Duffing term coefficient.

2.2 The kinetic energy of the disk with mass eccentricity

The disk is supposed to be rigid and fixed at the position $x=x_{\mathrm{d}}$ of the shaft; therefore, its potential energy is zero. With mass eccentricity in y and z directions denoted by $e_{y}$ and ${e}_{z}$, the kinetic energy is described as:

$$\begin{aligned} T_{\mathrm {disk}} =\frac{1}{2}\left( {\begin{array}{l} m_{\mathrm {disk}} \left( {\begin{array}{l} {\dot{u}}^{2}+{\dot{v}}^{2}+{\dot{w}}^{2}+\left( {\varOmega +{\dot{\phi }}} \right) ^{2}\left( {e_y^2 +e_z^2 } \right) -2\left( {\varOmega +\dot{\phi }} \right) \\ \left[ {\left( {e_z {\dot{v}}+e_y {\dot{w}}} \right) \sin \beta +\left( {e_y {\dot{v}}-e_z {\dot{w}}} \right) \cos \beta } \right] \\ \end{array}} \right) \\ +\,J_{\mathrm {disk}} \omega _1^2 +I_{\mathrm {disk}} \left( {\omega _2^2 +\omega _3^2 } \right) \\ \end{array}} \right) {\delta }(x-x_{\mathrm{d}} ) \end{aligned}$$

(8)

where $m_{\mathrm{disk}}$, $I_{\mathrm{disk}}$ and $J_{\mathrm{disk}}$ are the mass, the diametral mass moment of inertia, the polar mass moment of inertia of the disk, respectively.

2.3 The energies of the blades

At any time, the angular position of the blade depends on not only the Euler angles, but also the azimuth of the blade on the disk. Therefore, a new variable $\phi _{i}$ is defined to describe the specific angular position of the ith blade, given by:

$$\begin{aligned} \phi _i =\beta \left( {x_{\mathrm{d}} ,t} \right) +\vartheta _i =\varOmega t+\phi \left( {x_{\mathrm{d}} ,t} \right) +\vartheta _i , \quad i=1,{\ldots },N_{\mathrm{b}} \end{aligned}$$

(9)

where $N_{\mathrm{b}}$ is the number of blades, and $\vartheta _{i}$ is the azimuth angle of the ith blade on the disk, which is expressed as:

$$\begin{aligned} \vartheta _i =(i-1)\frac{2{\uppi }}{N_{\mathrm{b}} }, \quad i=1,{\ldots },N_{\mathrm{b}} \end{aligned}$$

(10)

The position vector of any point on the ith blade in the inertial coordinate system $X-Y-Z$ is expressed as [37]:

$$\begin{aligned} \mathbf{R}_i= & {} \left[ {\begin{array}{l} x_{\mathrm{d}} +u\left( {x_{\mathrm{d}} ,t} \right) \\ v\left( {x_{\mathrm{d}} ,t} \right) \\ w\left( {x_{\mathrm{d}} ,t} \right) \\ \end{array}} \right] +\left[ {{\begin{array}{l@{\quad }l@{\quad }l} {\cos \phi _i }&{} {-\sin \phi _i }&{} 0 \\ {\sin \phi _i }&{} {\cos \phi _i }&{} 0 \\ 0&{} 0&{} 1 \\ \end{array} }} \right] \left[ {{\begin{array}{l@{\quad }l@{\quad }l} 1&{} 0&{} {\theta \left( {x_{\mathrm{d}} ,t} \right) } \nonumber \\ 0&{} 1&{} 0 \\ {-\theta \left( {x_{\mathrm{d}} ,t} \right) }&{} 0&{} 1 \\ \end{array} }} \right] \nonumber \\&\left[ {{\begin{array}{l@{\quad }l@{\quad }l} 1&{} 0&{} 0 \\ 0&{} 1&{} {-\psi \left( {x_{\mathrm{d}} ,t} \right) } \\ 0&{} {\psi \left( {x_{\mathrm{d}} ,t} \right) }&{} 1 \\ \end{array} }} \right] \left[ {{\begin{array}{l@{\quad }l@{\quad }l} {\cos \gamma }&{} {-\sin \gamma }&{} 0 \\ {\sin \gamma }&{} {\cos \gamma }&{} 0 \\ 0&{} 0&{} \hbox {1} \\ \end{array} }} \right] \left\{ {\begin{array}{l} x_{\mathrm{b}} \\ \varLambda _i \left( {\varsigma ,t} \right) +y_{\mathrm{b}} \\ R_{\mathrm{d}} +\varsigma \\ \end{array}} \right\} \end{aligned}$$

(11)

where $x_{\mathrm{b}}$, $\varLambda _{\mathrm{i}}$, $y_{\mathrm{b}}$, $R_{\mathrm{d}}$ and $\zeta$ are the location of the point along the flapwise direction, the vibration amplitude, the location of the point along the chordwise direction, the disk radius, the distance of the point from the blade root, respectively. The mass density, the length of the blade and the moment of cross section area about $x_{\mathrm{b}}$ axis are denoted as $m'$, L and $I'_{11}$. Thus, the kinetic energy of the blade is described as:

$$\begin{aligned} T_{{\mathrm {(blade)}}_{i}}= & {} \frac{1}{2}{m}'\int _{0}^{L} {\int _{{A}'} {{\dot{\mathbf{R}}}_i \cdot {\dot{\mathbf{R}}}_i \hbox {d}{A}'\hbox {d}\varsigma } } =\frac{{m}'{A}'L}{2}\left( {{\dot{u}}^{2}+{\dot{v}}^{2}+{\dot{w}}^{2}} \right) +\frac{{m}'{A}'}{2}\int _0^L {{\dot{\varLambda }}_i^2 } \hbox {d}\varsigma \nonumber \\&\quad +\,\frac{{m}'{A}'}{2}\left( {\varOmega +{\dot{\phi }}} \right) ^{2}\cos ^{2}\gamma \int _0^L {{\dot{\varLambda }}_i^2 } \hbox {d}\varsigma +\frac{{m}'{I}'_{11} L}{2}\cos ^{2}\gamma \left( {\varOmega +{\dot{\phi }}} \right) ^{2}+\frac{{m}'{A}'\varGamma _3 }{2}\left( {\varOmega +{\dot{\phi }}} \right) ^{2} \nonumber \\&\quad +\,{m}'{A}'\varGamma _3 \left( {{\dot{\psi }}\left( {\varOmega +\dot{\phi }} \right) \theta } \right) +{m}'{A}'\left( {\varOmega +\dot{\phi }} \right) \int _0^L {\left( {R_{\mathrm{d}} +\varsigma } \right) \cos \gamma {\dot{\varLambda }}_i } \hbox {d}\varsigma \nonumber \\&\quad +\,{m}'{A}'\varGamma _2 \sin \phi _i \left( {-{\dot{w}}\left( {\varOmega +{\dot{\phi }}} \right) +{\dot{w}}{\dot{\psi }}+{\dot{u}}\left( {\varOmega +{\dot{\phi }}} \right) \theta } \right) \nonumber \\&\quad +\,{m}'{A}'\sin \phi _i \left( {-{\dot{w}}\cos \gamma \int _0^L {{\dot{\varLambda }}_i } \hbox {d}\varsigma -\left( {\varOmega +\dot{\phi }} \right) {\dot{v}}\cos \gamma \int _0^L {\varLambda _i } \hbox {d}\varsigma } \right) \nonumber \\&\quad +\,{m}'{A}'\sin \phi _i \sin \gamma \int _0^L {\left( {R_{\mathrm{d}} +\varsigma } \right) {\dot{\varLambda }}_i } {\dot{\psi }}\hbox {d}\varsigma +\,{m}'{A}'\sin \phi _i \sin \gamma \int _0^L {\left( {R_{\mathrm{d}} +\varsigma } \right) \theta {\dot{\varLambda }}_i } \left( {\varOmega +{\dot{\phi }}} \right) \hbox {d}\varsigma \nonumber \\&\quad +\,{m}'{A}'\varGamma _2 \cos \phi _i \left( {{\dot{v}}\left( {\varOmega +{\dot{\phi }}} \right) +{\dot{u}}\left( {\varOmega +{\dot{\phi }}} \right) \psi -\dot{u}{\dot{\theta }}} \right) \nonumber \\&\quad +\,{m}'{A}'\cos \phi _i \left( {{\dot{v}}\cos \gamma \int _0^L {{\dot{\varLambda }}_i } \hbox {d}\varsigma -\left( {\varOmega +\dot{\phi }} \right) {\dot{w}}\cos \gamma \int _0^L {\varLambda _i } \hbox {d}\varsigma } \right) \nonumber \\&\quad -\,{m}'{A}'\cos \phi _i \sin \gamma \int _0^L {\left( {R_{\mathrm{d}} +\varsigma } \right) {\dot{\varLambda }}_i } {\dot{\theta }}\hbox {d}\varsigma \nonumber \\&\quad +\,{m}'{A}'\cos \phi _i \sin \gamma \int _0^L {\left( {R_{\mathrm{d}} +\varsigma } \right) \psi {\dot{\varLambda }}_i } \left( {\varOmega +{\dot{\phi }}} \right) \hbox {d}\varsigma +\frac{{m}'{A}'\varGamma _3 }{2}\left( {{\dot{\theta }}\cos \phi _i -{\dot{\psi }}\sin \phi _i } \right) ^{2} \end{aligned}$$

(12)

where $\varGamma _{2}$ and $\varGamma _{3}$ in Eq. (12) are given by:

$$\begin{aligned} \varGamma _2 =\int _0^L {\left( {R_{\mathrm{d}} +\varsigma } \right) } \hbox {d}\varsigma ,\quad \varGamma _3 =\int _0^L {\left( {R_{\mathrm{d}} +\varsigma } \right) ^{2}} \hbox {d}\varsigma \end{aligned}$$

(13)

Considering centrifugal stiffening, the potential energy of the blade is:

$$\begin{aligned} V_{{\mathrm {(blade)}}_{i}} =\frac{1}{2}\int _0^L {E{I}'_{11} \left( {\frac{\partial ^{2}\varLambda _i \left( {\varsigma ,t} \right) }{\partial \varsigma ^{2}}} \right) }^{2}\mathrm{d}\varsigma +\frac{1}{4}{m}'{A}'\varOmega ^{2}\int _0^L {\left( {L^{2}+2R_{\mathrm{d}} L-2R_{\mathrm{d}} \varsigma -\varsigma ^{2}} \right) \left( {\frac{\partial \varLambda _i \left( {\varsigma ,t} \right) }{\partial \varsigma }} \right) }^{2}\mathrm{d}\varsigma \nonumber \\ \end{aligned}$$

(14)

Thus, the total kinetic and potential energies of all the blades are:

$$\begin{aligned} T_{\mathrm {blades}} =\sum _{i= 1}^{N_\mathrm{b} } {T_{{\mathrm {(blade)}}_{i}}} ,V_{\mathrm {blades}} =\sum _{i= 1}^{N_\mathrm{b} } {V_{{\mathrm {(blade)}}_{i}}} \end{aligned}$$

(15)

2.4 Work done by rubbing force

This study assumes that the rubbing between the blade tip and the casing results from the misalignment between the rotor and the casing (see Fig. 3). In the figure, $O_{1}$, $O_{2}$, $O'_{2}$, $R_{0}$, $\beta _{\mathrm{c}}$, $u_{\mathrm{c}}$ and $r_{\mathrm{g}}$ are the center of rotating blade, the center of static casing, the center of rubbed casing, the radius of the casing, the contact angle, the displacement of the casing and the radius of the blade tip orbit, respectively. Under the influence of centrifugal force and rotor whirl, the trajectory of blade tip denoted by red dotted line overlaps the static casing position denoted by blue dotted line. At this moment, the partial rubbing between the blade tip and the casing occurs. The casing position after rubbing is denoted by black solid line. According to Refs. [33, 38], the normal rubbing force can be expressed as follows:

$$\begin{aligned} F_{\mathrm{n}} =\left\{ {\begin{array}{ll} 0 &{} 0\le t\le t_0 ,t_\mathrm{c} +t_0 \le t \le t_\mathrm{p} \\ -F_{\mathrm {n}\max } \sin \left( {\frac{\uppi }{t_\mathrm{c} }\left( {t-t_0 } \right) } \right) &{} t_0 \le t\le t_\mathrm{c} +t_0 \\ \end{array}} \right. \end{aligned}$$

(16)

where $F_{\mathrm{nmax}}$, $t_{\mathrm{c}}$, $t_{\mathrm{p}}$, $t_{0}$ are the amplitude of normal rubbing force, the contact time, the rotating period and the start time of the rubbing; $t_{\mathrm{c}}$ and $\beta _{\mathrm{c}}$ are expressed as follows:

$$\begin{aligned} t_\mathrm{c} =\frac{60\beta _\mathrm{c} }{2{\uppi }\varOmega },\beta _\mathrm{c} =2\cos ^{-1}\left( {\frac{R_0^2 +\left( {R_0 +\delta -r_\mathrm{g} } \right) ^{2}-r_\mathrm{g}^2 }{2R_0 \left( {R_0 +\delta -r_\mathrm{g} } \right) }} \right) \end{aligned}$$

(17)

Fig. 3

Schematic of rubbing between rotor and casing

The information on the calculation of normal rubbing force is introduced in detail in Ref. [33]. The tangential rubbing force at ith blade tip is denoted by $F_{\mathrm{t}i}$ and $F_{\mathrm{t}i} = \mu {F}_{\mathrm{n}i}$, where $\mu$ is the friction coefficient. The normal and tangential rubbing forces applied to the system are shown in Fig. 4a. Furthermore, similar to Fig. 7 of Ref. [37], $F_{\mathrm{t}i}$ can be decomposed along $x_{\mathrm{b}}$ and $y_{\mathrm{b}}$ directions, i.e., $F_{\mathrm{t}yi}=F_{\mathrm{t}i}\hbox {cos}\gamma$, $F_\mathrm{t}xi=F_{\mathrm{t}i}\hbox {sin}\gamma$ (see Fig. 4b). Here, $\gamma$ is the stagger angle of the blade. The work done by the rubbing force is expressed as:

$$\begin{aligned}&W_{F_{\mathrm {n}i} } =\mu F_{\mathrm {n}i} \varLambda _i (L,t)\cos \gamma -\mu F_{\mathrm {n}i} \left( {R_{\mathrm{d}} +L} \right) \phi _i {\delta }\left( {x-x_{\mathrm{d}} } \right) \nonumber \\&\quad + F_{\mathrm {n}i} \left( {\left( {-\cos \phi _i +\mu \sin \phi _i } \right) v+\left( {-\sin \phi _i -\mu \cos \phi _i } \right) w} \right) {\delta }\left( {x-x_{\mathrm{d}} } \right) \end{aligned}$$

(18)

Fig. 4

Schematic of forces on the rotor-blade system: a normal and tangential rubbing forces, b decomposition of tangential rubbing force

2.5 Equations of motion

One of the supports (right support) is movable along the longitudinal axis (see Fig. 1). As a result, the rotating shaft is in-extensional and the strain along the neutral axis of the shaft can be ignored. Therefore, one may obtain

$$\begin{aligned} {u}'=\sqrt{1-{v}'^{2}-{w}'^{2}}-1=-\frac{1}{2}\left( {{v}'^{2}+{w}'^{2}} \right) +\cdots \end{aligned}$$

(19)

The angles $\psi$, $\theta$ and $\phi$ can be calculated as follows [1,2,3, 25]:

$$\begin{aligned} \psi= & {} \sin ^{-1}\frac{{v}'}{\sqrt{\left( {1+{u}'} \right) ^{2}+{v}'^{2}}},\theta =\sin ^{-1}\frac{-{w}'}{\sqrt{\left( {1+{u}'} \right) ^{2}+{v}'^{2}+{w}'^{2}}} \end{aligned}$$

(20)

$$\begin{aligned} \phi= & {} -\int _0^x {{v}''{w}'\hbox {d}x+\cdots } \end{aligned}$$

(21)

To obtain the nonlinear equations of motion, Hamilton principle is introduced:

$$\begin{aligned} {\delta }\int _0^t {\left( {T-V+W} \right) \hbox {d}t=0} \end{aligned}$$

(22)

where T, V, W, t and $\delta$ are the total kinetic energy, total potential energy of rotor-blade system, the work done by rubbing force, the time and variational operator, respectively. The expressions are as follows:

$$\begin{aligned} T=T_{\mathrm {shaft}} +T_{\mathrm {blades}} +T_{\mathrm {disk}} ,V=V_{\mathrm {shaft}} +V_{\mathrm {blades}} +V_{\mathrm {bearing}} ,W=\sum _{i=1}^{N_\mathrm{b} } {W_{F_{ni} } } \end{aligned}$$

(23)

Substituting Eq. (23) into Eq. (22), the equations of motion are obtained as:

$$\begin{aligned}&\left[ {{m}'{A}'\ddot{\varLambda }_i +c_{\mathrm {blade}} \dot{\varLambda }_i +E{I}'_{11} \frac{\partial ^{4}\varLambda _i }{\partial \varsigma ^{4}}} \right] +\left[ {{m}'{A}'\left( {R_{\mathrm{d}} +\varsigma } \right) \left( {\varOmega +{\dot{\phi }}} \right) ^{2}\frac{\partial \varLambda _i }{\partial \varsigma }} \right. -{m}'{A}'\left( {\varOmega +{\dot{\phi }}} \right) ^{2}\cos ^{2}\gamma \varLambda _i \nonumber \\&\quad + {m}'{A}'\left( {R_{\mathrm{d}} +\varsigma } \right) \ddot{\phi }\left. {-\frac{{m}'{A}'}{2}\left( {\varOmega +{\dot{\phi }}} \right) ^{2}\left( {\left( {R_{\mathrm{d}} +L} \right) ^{2}-\left( {R_{\mathrm{d}} +\varsigma } \right) ^{2}} \right) \frac{\partial ^{2}\varLambda _i }{\partial \varsigma ^{2}}} \right] +\left[ {-\mu F_{\mathrm {n}i} \cos \gamma {\delta }\left( {\varsigma -L} \right) } \right] \nonumber \\&\quad + {\delta }\left( {x-x_{\mathrm{d}} } \right) \left[ {{m}'{A}'\ddot{v}\cos \phi _i \cos \gamma -{m}'{A}'\ddot{w}\sin \phi _i \cos \gamma } \right] =0 \end{aligned}$$

(24)

$$\begin{aligned}&\left[ {\begin{array}{l} m\left( {\ddot{v}+\frac{{v}'}{2}\int _0^x {\left( {{\dot{v}}'^{2}+{\ddot{v}}'{v}'+{{\dot{w}}}'^{2}+{\ddot{w}}'{w}'} \right) \hbox {d}x+\frac{{v}''}{2}\int _l^x {\int _0^x {\left( {{\dot{v}}'^{2}+{\ddot{v}}'{v}'+{{\dot{w}}}'^{2}+{\ddot{w}}'{w}'} \right) \hbox {d}x\hbox {d}x} } } } \right) +c{\dot{v}} \\ -I_1 \varOmega {{\dot{w}}}''-I_2 {\ddot{v}}''+D_{22} \left( {{v}'^{2}v^{\left( {IV} \right) }+{v}'w^{\left( {IV} \right) }{w}'+3{w}'''{w}''{w}'+{v}''{w}''^{2}+{v}''^{3}+{w}'''{v}''{w}'+4{v}'{v}''{v}'''} \right) \\ \end{array}} \right] \nonumber \\&\quad +\left[ {\begin{array}{l} m_{\mathrm {disk}} {\delta }\left( {x-x_{\mathrm{d}} } \right) \left( {\ddot{v}+\frac{{v}'}{2}\int _0^{x_{\mathrm{d}} } {\left( {{\dot{v}}'^{2}+{\ddot{v}}'{v}'+{{\dot{w}}}'^{2}+{\ddot{w}}'{w}'} \right) \hbox {d}x+\frac{{v}''}{2}\int _l^{x_{\mathrm{d}} } {\int _0^{x_{\mathrm{d}} } {\left( {{{\dot{v}}}'^{2}+{\ddot{v}}'{v}'+{{\dot{w}}}'^{2}+{\ddot{w}}'{w}'} \right) \hbox {d}x\hbox {d}x} } } } \right) \\ -J_{\mathrm {disk}} \varOmega {{\dot{w}}}''{\delta }\left( {x-x_{\mathrm{d}} } \right) -I_{\mathrm {disk}} {\ddot{v}}''{\delta }\left( {x-x_{\mathrm{d}} } \right) -m_{\mathrm {disk}} {\delta }\left( {x-x_{\mathrm{d}} } \right) \varOmega ^{2}\left( {e_z \cos \varOmega t-e_y \sin \varOmega t} \right) \\ \end{array}} \right] \nonumber \\&\quad +\left[ {{\delta }\left( {x-x_{\mathrm{d}} } \right) \sum _{i=1}^{N_\mathrm{b} } {\left( {\begin{array}{l} {m}'{A}'L\ddot{v}+{m}'{A}'\varGamma _3 \left( {\left( {\varOmega +\dot{\phi }} \right) {w}'} \right) ^{\prime }-{m}'{A}'\sin \phi _i \left( {\ddot{\phi }\int _0^L {\varLambda _i \hbox {d}\varsigma +2\left( {\varOmega +{\dot{\phi }}} \right) \int _0^L {{\dot{\varLambda }}_i \hbox {d}\varsigma } } } \right) \\ + {m}'{A}'\varGamma _3 {\ddot{v}}''\sin ^{2}\phi _i -{m}'{A}'\cos \phi _i \left( {-\int _0^L {\ddot{\varLambda }_i \hbox {d}\varsigma +\left( {\varOmega +{\dot{\phi }}} \right) ^{2}\int _0^L {\varLambda _i \hbox {d}\varsigma } } } \right) \\ \end{array}} \right) } } \right] \nonumber \\&\quad +\left[ {\left( {kv+\vartheta v(v^{2}+w^{2})} \right) \left( {{\delta }x+{\delta }(x-L)} \right) +c_{\mathrm {bearing}} {\dot{v}}{\delta }x+c_{\mathrm {bearing}} {\dot{v}}{\delta }(x-L)} \right] \nonumber \\&\quad -\left[ {\left( {\sum _{i=1}^{N_\mathrm{b} } {F_{\mathrm {n}i} \left( {-\cos \phi _i +\mu \sin \phi _i } \right) } +\sum _{i=1}^{N_\mathrm{b} } {\mu F_{\mathrm {n}i} \left( {R_d +L} \right) } \int _0^{x_\mathrm{d} } {{w}'''\hbox {d}x} } \right) {\delta }\left( {x-x_{\mathrm{d}} } \right) } \right] =0 \end{aligned}$$

(25)

$$\begin{aligned}&\left[ {\begin{array}{l} m\left( {\ddot{w}+\frac{{w}'}{2}\int _0^x {\left( {{\dot{v}}'^{2}+ {\ddot{v}}'{v}'+{{\dot{w}}}'^{2}+{\ddot{w}}'{w}'} \right) \hbox {d}x+\frac{{w}''}{2}\int _l^x {\int _0^x {\left( {{\dot{v}}'^{2}+{\ddot{v}}'{v}'+{{\dot{w}}}'^{2}+{\ddot{w}}'{w}'} \right) \hbox {d}x\hbox {d}x} } } } \right) +c{\dot{w}} \\ +I_1 \varOmega {{\dot{v}}}''-I_2 {\ddot{w}}''+D_{22} \left( {{w}''{v}''^{2}+w^{\left( {IV} \right) }+{v}'{v}'''{w}''+3{w}'{v}''{v}'''+{w}'{v}'v^{\left( {IV} \right) }+{w}'^{2}w^{\left( {IV} \right) }+{w}''^{3}+4{w}'{w}''{w}'''} \right) \end{array}} \right] \nonumber \\&\quad + \left[ {\begin{array}{l} m_{\mathrm {disk}} {\delta }\left( {x-x_{\mathrm{d}} } \right) \left( {\ddot{w}+\frac{{w}'}{2}\int _0^{x_{\mathrm{d}} } {\left( {{\dot{v}}'^{2}+{\ddot{v}}'{v}'+{{\dot{w}}}'^{2}+{\ddot{w}}'{w}'} \right) \hbox {d}x+\frac{{w}''}{2}\int _l^{x_{\mathrm{d}} } {\int _0^{x_{\mathrm{d}} } {\left( {{{\dot{v}}}'^{2}+{\ddot{v}}'{v}'+{{\dot{w}}}'^{2}+{\ddot{w}}'{w}'} \right) \hbox {d}x\hbox {d}x} } } } \right) \\ + J_{\mathrm {disk}} \varOmega {{\dot{v}}}''{\delta }\left( {x-x_{\mathrm{d}} } \right) -I_{\mathrm {disk}} {\ddot{w}}''{\delta }\left( {x-x_{\mathrm{d}} } \right) -m_{\mathrm {disk}} {\delta }\left( {x-x_{\mathrm{d}} } \right) \varOmega ^{2}\left( {e_z \sin \varOmega t+e_y \cos \varOmega t} \right) \\ \end{array}} \right] \nonumber \\&\quad + \left[ {\sum _{i=1}^{N_\mathrm{b} } {\left( {\begin{array}{l} {m}'{A}'L\ddot{w}-{m}'{A}'\varGamma _3 \left( {\left( {\varOmega +\dot{\phi }} \right) {{\dot{v}}}'} \right) ^{\prime }+{m}'{A}'\sin \phi _i \left( {-\int _0^L {\ddot{\varLambda }_i \hbox {d}\varsigma +\left( {\varOmega + {\dot{\phi }}} \right) ^{2}\int _0^L {\varLambda _i \hbox {d}\varsigma } } } \right) \\ + {m}'{A}'\varGamma _3 {\ddot{w}}''\cos ^{2}\phi _i +{m}'{A}'\cos \phi _i \left( {-\ddot{\phi }\int _0^L {\varLambda _i \hbox {d}\varsigma -2\left( {\varOmega +{\dot{\phi }}} \right) \int _0^L {{\dot{\varLambda }}_i \hbox {d}\varsigma } } } \right) \\ \end{array}} \right) } {\delta }\left( {x-x_{\mathrm{d}} } \right) } \right] \nonumber \\&\quad + \left[ {\left( {kw+\vartheta w(v^{2}+w^{2})} \right) \left( {{\delta }x+{\delta }(x-L)} \right) +c_{\mathrm {bearing}} {\dot{v}}{\delta }x+c_{\mathrm {bearing}} {\dot{v}}{\delta }(x-L)} \right] \nonumber \\&\quad - \left[ {\left( {\sum _{i=1}^{N_\mathrm{b} } {F_{\mathrm {n}i} \left( {-\sin \phi _i -\mu \cos \phi _i } \right) } -\sum _{i=1}^{N_\mathrm{b} } {\mu F_{\mathrm {n}i} \left( {R_{\mathrm{d}} +L} \right) } \int _0^{x_\mathrm{d}} {{v}'''\hbox {d}x} } \right) {\delta }\left( {x-x_{\mathrm{d}} } \right) } \right] =0 \end{aligned}$$

(26)

It should be noted that Eq. (24) expresses the equation of motion of the ith blade, while Eqs. (25)–(26) describe the equations of motion of the shaft in Y and Z directions. In order to facilitate the understanding for readers, the terms are classified into some groups marked by brackets based on their characteristics. For Eq. (24), the terms are divided into four groups which are corresponding to the blade structure, the influence of rotor torsional displacement, the impact of rubbing force and the effect of rotor translational displacement on the ith blade’s vibration, respectively. For Eqs. (25)–(26), the terms are divided into five groups that are corresponding to the rotor structure, the influence of the mass, the mass moment of inertia and mass eccentricity of the disk, the effect of the vibration of blades, the effect of the bearings at both ends of the shaft and the impact of rubbing force on the lateral vibration of the rotor, respectively.

In addition, the damping forces $c_{\mathrm {blade}} {\dot{\varLambda }}_i$, $c{\dot{v}}$, $c{\dot{w}}$, $c_{\mathrm {bearing}} {\dot{v}}$ and $c_{\mathrm {bearing}} {\dot{w}}$ are attached to Eqs. (24)–(26), where $c_{\mathrm{blade}}$ and c are damping coefficients of the blade and shaft.

3 Transformations and non-dimensionalization

It is quite sophisticated and even impossible adopting analytical method to solve the large number of coupled equations. With the aim of reducing the number of equations of motion, the Coleman transformation is adopted in which two parameters $\xi$ and $\eta$ are brought in as [14]:

$$\begin{aligned} \xi =-\frac{2}{N_\mathrm{b}}\sum _{i=1}^{N_\mathrm{b} } {\varLambda _i (\varsigma ,t)\cos \phi _i ,\eta =} -\frac{2}{N_\mathrm{b} }\sum _{i=1}^{N_\mathrm{b} } {\varLambda _i (\varsigma ,t)\sin \phi _i } \end{aligned}$$

(27)

In order to make further efforts for dimensional reduction, the equations are transformed to complex plane by the following parameters:

$$\begin{aligned} p=\xi -\hbox {j}\eta ,z=v+\hbox {j}w,\bar{{p}}=\xi +\hbox {j}\eta ,\bar{{z}}=v-\hbox {j}w \end{aligned}$$

(28)

Through these transformations, the system with $2+N_{\mathrm{b}}$ degrees of freedom is switched to that with two degrees of freedom. The equations of motion are given by:

$$\begin{aligned}&\left[ {{m}'{A}'\ddot{p}+c_{\mathrm {blade}} {\dot{p}}+E{I}'_{11} \frac{\partial ^{4}p}{\partial \varsigma ^{4}}} \right] +\left[ {{m}'{A}'\left( {R_{\mathrm{d}} +\varsigma } \right) \left( {\varOmega +{\dot{\phi }}} \right) ^{2}\frac{\partial \varLambda _i }{\partial \varsigma }} \right. +{m}'{A}'\left( {\varOmega +{\dot{\phi }}} \right) ^{2}p\sin ^{2}\gamma \nonumber \\&\quad + 2{m}'{A}'\hbox {j}\left( {\varOmega +{\dot{\phi }}} \right) {\dot{p}}+c_{\mathrm {blade}} \left( {\varOmega +{\dot{\phi }}} \right) \hbox {j}{\dot{p}}+{m}'{A}'\ddot{\phi }\left. {\hbox {j}p-\frac{{m}'{A}'}{2}\left( {\varOmega +{\dot{\phi }}} \right) ^{2}\left( {\left( {R_{\mathrm{d}} +L} \right) ^{2}-\left( {R_{\mathrm{d}} +\varsigma } \right) ^{2}} \right) \frac{\partial ^{2}p}{\partial \varsigma ^{2}}} \right] \nonumber \\&\quad +\left[ {\frac{2}{N_{\mathrm{b}} }\mu \cos \gamma {\delta }\left( {\varsigma -L} \right) \sum _{i=1}^{N_\mathrm{b} } {F_{\mathrm {n}i} } e^{-\hbox {j}\phi _i }} \right] +{\delta }\left( {x-x_{\mathrm{d}} } \right) \left[ {{m}'{A}'\ddot{z}\cos \gamma } \right] =0 \nonumber \\ \end{aligned}$$

(29)

$$\begin{aligned}&\left[ {\begin{array}{l} m\left( {\ddot{z}+\frac{{z'}}{2}\int _0^x {\left( {2{{\dot{z}}}'{\dot{\bar{{z}}}}'+{\ddot{z}}'{\bar{{z}}}'+{\ddot{\bar{{z}}}}'{z'}} \right) \hbox {d}x+\frac{{z''}}{2}\int _l^x {\int _0^x {\left( {2{{\dot{z}}}'{\dot{\bar{{z}}}}'+{\ddot{z}}'{\bar{{z}}}'+{\ddot{\bar{{z}}}}'{z'}} \right) \hbox {d}x\hbox {d}x} } } } \right) +c{\dot{z}}+\hbox {j}I_1 \varOmega {{\dot{z}}}''-I_2 {\ddot{z}}'' \\ +D_{22} \left( {z^{\left( {IV} \right) }+2{z''}{z'}{\bar{{z}}}'''+\frac{1}{2}{z''}{\bar{{z}}}'{z''}'+\frac{3}{2}{\bar{{z}}}''{z'}{z''}'+{\bar{{z}}}''{z''}^{2}+\frac{1}{2}z^{\left( {IV} \right) }{\bar{{z}}}'{z'}+\frac{1}{2}z^{\left( {IV} \right) }{z'}^{2}} \right) \end{array}} \right] \nonumber \\&\quad + {\delta }\left( {x-x_{\mathrm{d}} } \right) \left[ {\begin{array}{l} \left( {m_{\mathrm {disk}} +{m}'{A}'LN_\mathrm{b} } \right) \left( {\ddot{z}+\frac{{z'}}{2}\int _0^{x_{\mathrm{d}} } {\left( {2{{\dot{z}}}'{\dot{\bar{{z}}}}'+{\ddot{z}}'{\bar{{z}}}'+{\ddot{\bar{{z}}}}'{z'}} \right) \hbox {d}x+\frac{{z''}}{2}\int _l^{x_{\mathrm{d}} } {\int _0^{x_{\mathrm{d}} } {\left( {2{{\dot{z}}}'{\dot{\bar{{z}}}}'+{\ddot{z}}'{\bar{{z}}}'+{\ddot{\bar{{z}}}}'{z'}} \right) \hbox {d}x\hbox {d}x} } } } \right) \\ +\hbox {j}\varOmega \left( {J_{\mathrm {disk}} +{m}'{A}'N_\mathrm{b} \varGamma _3 } \right) {{\dot{z}}}''-\left( {I_{\mathrm {disk}} +\frac{{m}'{A}'N_\mathrm{b} \varGamma _3 }{2}} \right) {\ddot{z}}''-m_{\mathrm {disk}} \varOmega ^{2}\left( {\hbox {j}e_z +e_y } \right) e^{\mathrm {j}\varOmega t} \end{array}} \right] \nonumber \\&\quad +\left[ {\frac{{m}'{A}'N_\mathrm{b} \cos \gamma \delta \left( {x-x_\mathrm{d} } \right) }{2}\int _0^L {\ddot{p}\hbox {d}\varsigma } } \right] +\left[ {\left( {kz+\vartheta z\left| z \right| ^{2}} \right) \left( {{\delta }x+{\delta }(x-L)} \right) +c_{\mathrm {bearing}} {\dot{z}}{\delta }x+c_{\mathrm {bearing}} {\dot{z}}{\delta }(x-L)} \right] \nonumber \\&\quad +\left[ {\sum _{i=1}^{N_\mathrm{b} } {F_{\mathrm {n}i} \left( {1+\hbox {j}\mu } \right) } e^{\mathrm {j}\phi _i }{\delta }\left( {x-x_{\mathrm{d}} } \right) +\hbox {j}\sum _{i=1}^{N_\mathrm{b} } {F_{\mathrm {n}i} \mu \left( {R_d +L} \right) } \int _0^{x_\mathrm{d} } {{z''}'} \hbox {d}x{\delta }\left( {x-x_{\mathrm{d}} } \right) } \right] =0 \end{aligned}$$

(30)

The solution of small parameter domain is obtained from multiple scales method. By non-dimensionalization, the numerical differences of the response amplitudes at different scales are greatly reduced and the morbid problem in computing can be avoided. In order to improve the calculation accuracy, the following dimensionless parameters are employed:

$$\begin{aligned}&z^{*}=\frac{z}{l},e_y^{*} =\frac{e_y }{l},e_z^{*} =\frac{e_z }{l},x^{*}=\frac{x}{l},x_{\mathrm{d}}^{{*}} =\frac{x_{\mathrm{d}} }{l},I_1^{*} =\frac{I_1 }{ml^{2}},I_2^{*} =\frac{I_2 }{ml^{2}},\varOmega ^{*}=\sqrt{\frac{ml^{4}}{D}}\varOmega ,t^{*}\nonumber \\&\quad =\sqrt{\frac{D}{ml^{4}}}t,k^{*}=\frac{kl^{3}}{D} \nonumber \\&c_{\mathrm {blade}}^{{*}} =\frac{c_{\mathrm {blade}} }{{m}'{A}'}\sqrt{\frac{ml^{4}}{D}},c^{*}=\frac{cl^{2}}{\sqrt{mD}},r^{*}=\frac{ml^{2}}{{m}'{A}'L^{2}}, \varsigma ^{*}=\frac{\varsigma }{L},R_{\mathrm{d}}^{{*}} =\frac{R_{\mathrm{d}}}{L},\varLambda _i^{*} =\frac{\varLambda _{i}}{L},{I}'_{{11}^{*}}\nonumber \\&\quad =\frac{E{I}'_{11} ml^{4}}{{m}'{A}'DL^{4}},m_{\mathrm {disk}}^{{*}} =\frac{m_{\mathrm {disk}} }{ml} \nonumber \\&m_{\mathrm{r}} =\frac{m_{\mathrm {disk}} +{m}'{A}'LN_\mathrm{b} }{ml},J_{\mathrm{r}} =\frac{J_{\mathrm {disk}} +{m}'{A}'N_\mathrm{b} \varGamma _3 }{ml^{3}},I_{\mathrm{r}} =\frac{I_{\mathrm {disk}} +\frac{{m}'{A}'N_\mathrm{b} \varGamma _3 }{2}}{ml^{3}},F_{\mathrm {n}i}^{*} =\frac{l^{2}F_{\mathrm {n}i} }{D},m_{r2} =\frac{{m}'{A}'N_\mathrm{b} }{2ml} \nonumber \\&\quad l^{*}=\frac{l}{L},L^{*}=\frac{L}{l},c_{\mathrm {bearing}}^{{*}} =\frac{c_{\mathrm {bearing}} l^{2}}{\sqrt{mD}},\vartheta ^{*}=\frac{\vartheta l^{5}}{D} \end{aligned}$$

(31)

It should be noted that $e_y^{*}$, $e_z^{*}$ and $F_{\mathrm {n}i}^{*}$ are of order $\varepsilon ^{3}$, and $c_{\mathrm {blade}}^{{*}}$, $c^{*}$ and $c_{\mathrm {bearing}}^{{*}}$ are of order $\varepsilon ^{2}$ where $\varepsilon$ is a small dimensionless parameter. Substituting Eq. (31) into Eqs. (24)–(26), the dimensionless equations of motion are expressed as:

$$\begin{aligned}&\left[ {\ddot{p}^{*}+c_{\mathrm {blade}}^{{*}} \varepsilon ^{2}{\dot{p}}^{*}+{{I}'_{11}}^{*} \frac{\partial ^{4}p^{*}}{\partial \varsigma ^{*4}}} \right] +\left[ {\left( {R_{\mathrm{d}}^{{*}} +\varsigma ^{*}} \right) \left( {\varOmega ^{*}+{\dot{\phi }}^{*}} \right) ^{2}\frac{\partial p^{*}}{\partial \varsigma ^{*}}} \right. +\left( {\varOmega ^{*}+{\dot{\phi }}^{*}} \right) ^{2}p^{*}\sin ^{2}\gamma \nonumber \\&\quad +2\left( {\varOmega ^{*}+{\dot{\phi }}^{*}} \right) \hbox {j}{\dot{p}}^{*}+c_{{\mathrm {blade}}}^{{*}} \varepsilon ^{2}\left( {\varOmega ^{*}+{\dot{\phi }}^{*}} \right) \hbox {j}p^{*}+\hbox {j}\ddot{\phi }p^{*}\left. {-\frac{\left( {\varOmega ^{*}+{\dot{\phi }}^{*}} \right) ^{2}}{2}\left( {\left( {R_{\mathrm{d}}^{{*}} +1} \right) ^{2}-\left( {R_{\mathrm{d}}^{{*}} +\varsigma ^{*}} \right) ^{2}} \right) \frac{\partial ^{2}p^{*}}{\partial \varsigma ^{*2}}} \right] \nonumber \\&\quad +\left[ {\frac{2\varepsilon ^{3}}{N_{\mathrm{b}} }\mu \cos \gamma {\delta }\left( {\varsigma ^{*}-1} \right) \sum _{i=1}^{N_\mathrm{b} } {F_{\mathrm {n}i}^{*} } r^{*}e^{-\hbox {j}\phi _i }} \right] +\ddot{z}^{*}\cos \gamma {\delta }\left( {x^{*}-x_{\mathrm{d}}^{\mathrm{*}} } \right) =0 \end{aligned}$$

(32)

$$\begin{aligned}&\left[ \begin{array}{l} \left( \ddot{z}^{*}+\frac{{z'}^{*}}{2}\int _{0}^{x^{{*}}} \left( {2{{\dot{z}}}'^{*}{\dot{\bar{{z}}}}'^{*}+{\ddot{z}}'^{*}{\bar{{z}}}'^{*}+{\ddot{\bar{{z}}}}'^{*}{z'}^{*}} \right) \hbox {d}x^{*}+\frac{{z''}}{2}\int _{1}^{{x^{*}}} {\int _{0}^{{x^{*}}} {\left( {2{{\dot{z}}}'^{*}{\dot{\bar{{z}}}}'^{*}+{\ddot{z}}'^{*}{\bar{{z}}}'^{*}+{\ddot{\bar{{z}}}}'^{*}{z'}^{*}} \right) \hbox {d}x^{*}\hbox {d}x^{*}}} \right) \\ + \varepsilon ^{2}c^{{*}}{\dot{z}}^{*}+\hbox {j}I_1^{*} \varOmega ^{*}{{\dot{z}}}''^{*}-I_2^{*} {\ddot{z}}''^{*} \\ +\left( {z}^{{{(IV)}^{*}}}+2{{z}{''^{*}}}{{z'}^{*}}{\bar{z}{'''^{*}}} +{1\over 2}{{z''}^{*}}{\bar{z}{'^{*}}}{z{'''^{*}}}+{3\over 2}{\bar{z}{{''^{*}}}} {z{'^{*}}}{z{'''^{*}}}+{\bar{z}{{''^{*}}}}{z{{{''^{*}}}^{2}}} +{1\over 2}{z^{{*^{(IV)}}}}{\bar{z}{'^{*}}}{z{{'^{*}}}}+{1\over 2} {z^{(IV)^{*}}}{z{'}^{*2}} \right) \end{array}\right] \nonumber \\&\quad + \left( z^{{(IV)}^{*}}+2{z''}^{*}{z'}^{*}{\bar{z}}'''^{*} +\frac{1}{2}{z''}^{*}{\bar{{z}}}'^{*}{z''}'^{*} +\frac{3}{2}{\bar{{z}}}''^{*}{z'}^{*}{z''}'^{*} +{\bar{{z}}}''^{*}{z''}^{{*}^{2}} +\frac{1}{2}z^{{*}{({IV})}}{\bar{{z}}}'^{*}{z'}^{*} +\frac{1}{2}z^{{({IV})}^{{{*}}}}{z'}^{{*}^{2}}\right) \nonumber \\&\quad + \left[ {\begin{array}{l} m_{\mathrm{r}} {\delta }\left( {x^{*}-x_{\mathrm{d}}^{{*}} } \right) \left( {\ddot{z}^{*}+\frac{{z'}^{*}}{2}\int _0^{x_{\mathrm{d}}^{*} } {\left( {2{{\dot{z}}}'^{*}{\dot{\bar{{z}}}}'^{*}+{\ddot{z}}'^{*}{\bar{{z}}}'^{*}+{\ddot{\bar{{z}}}}'^{*}{z'}^{*}} \right) \hbox {d}x^{*}+\frac{{z''}}{2}\int _{1}^{{x_{\mathrm{d}}^{{*}} }} {\int _{0}^{{x_{\mathrm{d}}^{{*}}}} {\left( {2{{\dot{z}}}'^{*}{\dot{\bar{{z}}}}'^{*}+{\ddot{z}}'^{*}{\bar{{z}}}'^{*}+{\ddot{\bar{{z}}}}'^{*}{z'}^{*}} \right) \hbox {d}x^{*}\hbox {d}x^{*}} } } } \right) \nonumber \\ + \hbox {j}\varOmega ^{*}J_{\mathrm{r}} {\delta }\left( {x^{*}-x_{\mathrm{d}}^{{*}} } \right) {{\dot{z}}}''^{*}-I_{\mathrm{r}} {\delta }\left( {x^{*}-x_{\mathrm{d}}^{{*}} } \right) {\ddot{z}}''^{*}-m_{\mathrm {disk}}^{{*}} \varOmega ^{{*}^{2}}\varepsilon ^{3}\left( \hbox {j}e_{z}^{*} +e_{y}^{*} \right) e^{{\mathrm {j}{\varOmega ^{*}}{t^{*}}}}{\delta } \left( x^{*}-x_{\mathrm{d}}^{{*}} \right) \\ \end{array}} \right] \nonumber \\&\quad + \left[ {m_{r2} \cos \gamma {\delta }\left( {x^{*}-x_{\mathrm{d}}^{{*}}} \right) \int _0^1 {\ddot{p}\hbox {d}\varsigma } } \right] +\left[ {\left( {k^{*}z^{*}+\vartheta ^{*}z^{*}\left| {z^{*}} \right| ^{2}} \right) \left( {{\delta }x^{*}+{\delta }(x^{*}-1)} \right) +c_{\mathrm {bearing}}^{{*}} \varepsilon ^{2}{\dot{z}}^{*}\delta x^{*}+c_{\mathrm {bearing}}^{\mathrm{*}} \varepsilon ^{2}{\dot{z}}^{*}{\delta }(x^{*}-1)} \right] \nonumber \\&\quad + \left[ {\sum _{i=1}^{N_{\mathrm{b}} } {F_{\mathrm {n}i}^{*} \varepsilon ^{3}\left( {1+\hbox {j}\mu } \right) } e^{\mathrm {j}\phi _i }{\delta }(x^{*}-x_{\mathrm{d}}^{{*}} )+\hbox {j}\sum _{i=1}^{N_\mathrm{b} } {F_{\mathrm {n}i}^{*} \varepsilon ^{3}L^{*}\mu \left( {R_d^{*} +1} \right) } \int _0^{x_\mathrm{d}^{*} } {{z''}'^{*}} \hbox {d}x^{*}{\delta }\left( {x^{*}-x_{\mathrm{d}}^{{*}} } \right) } \right] =0 \end{aligned}$$

(33)

4 Solution methodology

To solve the nonlinear equations of motion, the perturbation techniques are widely used, especially the multiple scales method, which is applied to solve the equations of motion in the following sections.

4.1 Linear mode shapes of the shaft with nonlinear supports

The support stiffness and the bladed disk clamped on the shaft have some influences on the linear mode shapes and critical speeds of the shaft, but they have been ignored by many researchers. Considering the parameters of the bladed disk and the supports at both ends, the mode shapes of rotating shaft at different speeds are solved. In this section, the bladed disk is regarded as a lumped point with mass $m_{\mathrm{D}}$, the polar mass moment of inertia $J_{\mathrm{p}}$ and the diametral mass moment of inertia $J_{\mathrm{d}}$. It is obvious that $m_{\mathrm{D}}= m_{\mathrm{disk}}+N_{\mathrm{b}}m'A'L$, $J_{\mathrm{p}}=J_{\mathrm{disk}}+ N_{\mathrm{b}} m'A'\varGamma _{3}$ and $J_{\mathrm{d}}= J_{\mathrm{p}}/2$. The shaft is regarded as a Timoshenko beam with nonlinear supports at both ends (see Fig. 5), and $l_{1}$, $l_{2}$ are the distances of the disk to the left and right end, $l_{1}=x_{\mathrm{d}}$ and $l_{2}=l-x_{\mathrm{d}}$. The angular displacements around Y and Z axes are denoted by $\theta _{yi}$ and $\theta _{zi}$, and $\theta _{i}=\theta _{yi} +\hbox {j}\theta _{zi} (i=1, 2)$. The differential equation of the shaft’s free vibration at rotating speed $\varOmega$ is [39]:

$$\begin{aligned} \frac{\partial ^{4}z_i }{\partial x^{4}}-\frac{\rho }{E}\left( {1+\frac{E}{\kappa G}} \right) \frac{\partial ^{4}z_i }{\partial x^{2}\partial t^{2}}+\frac{2\hbox {j}\varOmega \rho }{E}\frac{\partial ^{3}z_i }{\partial x^{2}\partial t}+\frac{\rho A}{EI_\mathrm{s} }\frac{\partial ^{2}z_i }{\partial t^{2}}-\frac{2\hbox {j}\varOmega \rho ^{2}}{E\kappa G}\frac{\partial ^{3}z_i }{\partial t^{3}}+\frac{\rho ^{2}}{E\kappa G}\frac{\partial ^{4}z_i }{\partial t^{4}}=0 \end{aligned}$$

(34)

where $i=1, 2; x_{i}\in [0, l_{i}]$; $\rho$, $\kappa$ and $I_\mathrm{s}$ denote density, the section shearing coefficient and the sectional moment of inertia of the shaft, respectively. Setting $\phi _{ni}(x)$ as piecewise mode shapes at the nth-order critical speeds $(n=1,2,{\ldots }), z_{i}$ can be expressed as $z_{i} =\phi _{ni}(x)\hbox {e}^{\mathrm{j}\omega t}$ under main resonances, where $\omega$ is the frequency of harmonic motion, then $\phi _{ni}(x)$ should satisfy:

$$\begin{aligned} \frac{\mathrm{d}^{4}\phi _{ni} }{\mathrm{d}x_i^4 }+\frac{2r_i }{l_i^2 }\frac{\mathrm{d}^{2}\phi _{ni} }{\mathrm{d}x_i^2 }-\frac{\lambda _i^4 }{l_i^4 }\phi _{ni} =0 \end{aligned}$$

(35)

Fig. 5

Shaft with nonlinear supports and bladed disk

where

$$\begin{aligned}&\frac{2r_i }{l_i^2 }=\frac{\rho }{E}\left( {1+\frac{E}{\kappa G}} \right) \omega ^{2}-\frac{2\varOmega \rho \omega }{E}\nonumber \\&\frac{\lambda _i^4 }{l_i^4 }=\frac{\rho A}{EI_\mathrm{s} }\omega ^{2}+\frac{2\varOmega \rho ^{2}\omega ^{3}}{E\kappa G}-\frac{\rho ^{2}\omega ^{4}}{E\kappa G} \end{aligned}$$

(36)

The general solution of Eq. (35) is given by:

$$\begin{aligned} \phi _{ni} (x)=c_{1i} \sin \alpha _{ni} x+c_{2i} \cos \alpha _{ni} x+c_{3i} \sinh \beta _{ni} x+c_{4i} \cosh \beta _{ni} x \end{aligned}$$

(37)

where $c_{1i}$,$c_{2i}$,$c_{3i}$,$c_{4i }$ are the coefficients to be solved, and $\alpha _{ni}$ and $\beta _{ni}$ should satisfy:

$$\begin{aligned} \alpha _{ni}^{2}=\frac{r_i +\sqrt{r_i^2 +\lambda _i^4 }}{l_i^2 },\beta _{ni}^{2}=\frac{-r_i +\sqrt{r_i^2 +\lambda _i^4 }}{l_i^2 } \end{aligned}$$

(38)

Setting $\varTheta _{ni}(x)$ as the piecewise nth-order mode shapes of $\theta _{i}$, it should satisfy:

$$\begin{aligned} \varTheta _{ni} =\frac{\left( {\kappa GA+EI_\mathrm{s} \frac{\rho \omega ^{2}}{\kappa G}} \right) {\phi }'_{ni} +EI_\mathrm{s} {\phi }'''_{ni} }{\kappa GA-\rho I_\mathrm{s} \omega ^{2}+2\rho I_\mathrm{s} \varOmega \omega } \end{aligned}$$

(39)

The boundary conditions of nonlinear supports at both ends can be given by:

$$\begin{aligned}&\frac{\partial \varTheta _{n1} }{\partial x_1 }\left| {_{x_1 =0} } \right. =0,\hbox { }-\kappa GA\left( {\varTheta _{n1} -{\phi }'_{n1} } \right) \left| {_{x_1 =0} } \right. =\left( {k\phi _{n1} +\vartheta \phi _{n1}^3 } \right) \left| {_{x_1 =0} } \right. \nonumber \\&\frac{\partial \varTheta _{n2} }{\partial x_2 }\left| {_{x_2 =l_2 } } \right. =0,\hbox { }\kappa GA\left( {\varTheta _{n2} -{\phi }'_{n2} } \right) \left| {_{x_2 =l_2 } } \right. =\left( {k\phi _{n2} +\vartheta \phi _{n2}^3 } \right) \left| {_{x_2 =l_2 } } \right. \end{aligned}$$

(40)

The abutment conditions at $x_{\mathrm{d}}$ position can be expressed as:

$$\begin{aligned}&\phi _{n1} \left| {_{x_1 =l_1 } } \right. =\phi _{n2} \left| {_{x_2 =0} } \right. ,\hbox { }\varTheta _1 \left| {_{x_1 =l_1 } } \right. =\varTheta _2 \left| {_{x_2 =0} } \right. \nonumber \\&\quad \kappa GA\left( {\varTheta _{n2} -{\phi }'_{n2} } \right) \left| {_{x_2 =0} } \right. -\kappa GA\left( {\varTheta _{n1} -{\phi }'_{n1} } \right) \left| {_{x_1 =l_1 } } \right. =m_\mathrm{D} \omega ^{2}\phi _{n2} \left| {_{x_2 =0} } \right. \nonumber \\&\quad EI_\mathrm{s} {\varTheta }'_{n1} \left| {_{x_1 =l_1 } } \right. -EI_\mathrm{s} {\varTheta }'_{n2} \left| {_{x_2 =0} } \right. =\left( {J_d \omega ^{2}\varTheta _{n2} -J_\mathrm{p} \varOmega \omega \varTheta _{n2} } \right) \left| {_{x_2 =0} } \right. \end{aligned}$$

(41)

Under the main resonance, it can be decided that $\varOmega = \omega$. Substituting Eq. (37) into Eqs. (40)–(41), the subsection mode shapes and critical speeds of the shaft-disk-blade system can be obtained. According to the continuity condition, the integral nth-order mode shape of the shaft is

$$\begin{aligned} \phi _n (x)=\left\{ {\begin{array}{ll} \phi _{n1} (x) &{} 0\le x\le l_1 \\ \phi _{n2} (x-l_1 ) &{}l_1 <x\le l \\ \end{array}} \right. \end{aligned}$$

(42)

Under the following parameters $l=0.5952\hbox { m}$, $A=3.14 \times 10^{-4 }\hbox {m}^{2}$, $I_\mathrm{s} = 7.85\times 10^{-9 }\hbox {m}^{4}$, $E=2\times 10^{11 }\hbox {Pa}$, $\rho =7800\hbox { kg}/\hbox {m}^{3}$, $x_{\mathrm{d}}=0.4077\hbox { m}$, $m_\mathrm{D}=0.735\hbox { kg}$, $J_{\mathrm{p}}=6.25 \times 10^{-4 }\hbox {kg}\cdot \hbox {m}^{2}$ and $\vartheta ^{*}=0$; the first two vibration mode shapes at corresponding critical speeds are shown in Fig. 6$(k=2\times 10^{8}\hbox { N/m})$ and Fig. 7$(k=2\times 10^{6}\hbox { N/m})$. In order to verify the proposed method, the finite element (FE) model of the rotor-blade system is established in Nastran software, and the mode shapes and the critical speeds are computed. The critical speeds under different boundary conditions are shown in Table 1, where $f_\mathrm{f}$ and $f_\mathrm{b}$ denote forward and backward whirl mode frequencies. When the linear support stiffness is $2\times 10^{8}\hbox { N/m}$ (see Fig. 6), the natural frequencies and the mode shapes under spring supported condition are similar to those under simply supported conditions, but when the stiffness is $2\times 10^{6}\hbox { N/m}$, they are quite different (see Fig. 7). Furthermore, in the high-order vibrations, the amplitude of the section where the disk is located is smaller. When $\vartheta ^{*}\ne 0$, the mode shapes and the backward whirl mode frequencies determined by initial conditions and excitation amplitudes are difficult to obtain using FE method, so the validation is ignored.

Fig. 6

Mode shapes of the shaft ($k=2\times 10^{8}\hbox { N/m}$, $\vartheta ^{*}=0$): first-order bending mode using proposed method (a) and FE method (b), second-order bending mode using proposed method (c) and FE method (d)

Fig. 7

Mode shapes of the shaft ($k=2\times 10^{6}\hbox { N/m}$, $\vartheta ^{*}=0$): first-order bending mode using proposed method (a) and FE method (b), second-order bending mode using proposed method (c) and FE method (d)

Table 1 Critical speeds under different boundary conditions $(\vartheta ^{*}=0)$

4.2 The multiple scales solution

$p^{*}(\varsigma ^{*},t)$ and $z^{*}(x^{*},t)$ can be expanded as [2]:

$$\begin{aligned}&p^{*}(\varsigma ^{*},t)=\varepsilon p_1 \left( {\varsigma ^{*},T_0 ,T_2 } \right) +\varepsilon ^{3}p_3 \left( {\varsigma ^{*},T_0 ,T_2 } \right) +\cdots \nonumber \\&z^{*}(x^{*},t)=\varepsilon z_1 \left( {x^{*},T_0 ,T_2 } \right) +\varepsilon ^{3}z_3 \left( {x^{*},T_0 ,T_2 } \right) +\cdots \end{aligned}$$

(43)

where $T_{0}=t$ and $T_{2}=\varepsilon ^{2}t$. Using the chain rule, the derivatives with respect to t are transformed to partial derivatives with respect to $T_{0}$ and $T_{2}$ as:

$$\begin{aligned}&\frac{\partial }{\partial t}=D_0 +\varepsilon ^{2}D_2 +\cdots \nonumber \\&\frac{\partial ^{2}}{\partial t^{2}}=D_0^2 +2\varepsilon ^{2}D_2 D_0 +\cdots \end{aligned}$$

(44)

where $D_{0}=\partial /\partial T_{0}$ and $D_{2}=\partial /\partial T_{2}$. Substituting Eqs. (43) and (44) into Eqs. (32) and (33) and equating the coefficients of like powers of $\varepsilon$ on both sides, the corresponding equations of the first and third hierarchies are obtained and presented in “Appendix A.” Galerkin method is adopted to separate variables. The solutions of Eq. (A.1) can be considered as [25]:

$$\begin{aligned}&z_1 \left( {x^{*},T_0 ,T_2 } \right) =\phi _f \left( {x^{*}} \right) A_1 \left( {T_2 } \right) e^{\mathrm{j}\beta _\mathrm{f} T_0 }+\phi _b \left( {x^{*}} \right) A_2 \left( {T_2 } \right) e^{\mathrm{j}\beta _\mathrm{b} T_0 } \nonumber \\&p_1 \left( {\varsigma ^{*},T_0 ,T_2 } \right) =\varTheta _f \psi _\mathrm{f} \left( {\varsigma ^{*}} \right) A_1 \left( {T_2 } \right) e^{\mathrm{j}\beta _\mathrm{f} T_0 }+\varTheta _b \psi _\mathrm{b} \left( {\varsigma ^{*}} \right) A_2 \left( {T_2 } \right) e^{\mathrm{j}\beta _\mathrm{b} T_0 } \end{aligned}$$

(45)

where $A_{1}(T_{2})$ and $A_{2}(T_{2})$ are the complex functions to be solved, $\phi _{f} (x^{*})$, $\phi _{b}(x^{*})$, $\beta _{f}$, $\beta _{b}$ are the forward and backward whirl mode shapes of the shaft, dimensionless forward and backward whirl mode frequencies, respectively. $\Theta _{f}$ and $\Theta _{b}$ are forward and backward mode shape coefficients for the blades, used to denote the relationship between the vibration amplitudes of the blades and the shaft; $\psi _{f} (\varsigma ^{*})$ and $\psi _{b}(\varsigma ^{ *})$ are forward and backward mode shapes of the rotating blades. It should be noted that both forward and backward whirl modes are considered in Eq. (45). According to the discussion in Section 4.1, the mode shapes of the shaft are given by:

$$\begin{aligned} \phi _f \left( {x^{*}} \right) =\phi _b \left( {x^{*}} \right) =\phi _n \left( {x^{*}} \right) , \quad n=1, 2 , {\ldots } , 0\le \, x^{*}\le 1 \end{aligned}$$

(46)

Furthermore, the blades are modeled as cantilever beams and the mode shapes are expressed as:

$$\begin{aligned} \psi _i \left( {\varsigma ^{*}} \right)= & {} \left( {\sin \left( {\beta _i L\varsigma ^{*}} \right) -\sinh \left( {\beta _i L\varsigma ^{*}} \right) } \right) -\frac{\sin \left( {\beta _i L} \right) +\sinh \left( {\beta _i L} \right) }{\cos \left( {\beta _i L} \right) -\cosh \left( {\beta _i L} \right) }\left( {\cos \left( {\beta _i L\varsigma ^{*}} \right) -\cosh \left( {\beta _i L\varsigma ^{*}} \right) } \right) \nonumber \\ \beta _1 L= & {} 1.8751,\beta _2 L=4.6941\cdots 0\le \varsigma ^{*}\le 1 \end{aligned}$$

(47)

Detuning parameter $\sigma =O(1)$ is introduced to describe the proximity of $\varOmega ^{*}$ to $\beta _{f}$:

$$\begin{aligned} \varOmega ^{*}=\beta _{f} +\varepsilon ^{2}\sigma \end{aligned}$$

(48)

Substituting Eqs. (45)–(48) into Eqs. (A.3) and (A.4) yields:

$$\begin{aligned}&D_{0}^{2} z_{3}^{*} +m_{\mathrm{r}} \delta \left( {x^{*}-x_{\mathrm{d}}^{{*}}} \right) D_{0}^{2} z_{3}^{*} +\hbox {j}\Omega {I}_{1}^{*} D_{0} {z''}_{3}^{*} +\hbox {j}\Omega ^{*}J_{\mathrm{r}} {\delta }\left( x^{*}-x_{\mathrm{d}}^{*} \right) D_{0} {z''}_{3}^{*} \nonumber \\&\quad -I_{2}^{*} D_{0}^{2} {z''}_{3}^{*} -I_{\mathrm{r}} D_{0}^{2} {z''}_{3}^{*} {\delta } \left( x^{*}-x_{\mathrm{d}}^{{*}} \right) +z_{3}^{{IV}^{*}} \nonumber \\&\quad +kz_{3}^{*} {\delta }\left( {x^{*}} \right) +kz_{3}^{*} {\delta }\left( {x^{*}-1} \right) =H_{z,f} (x^{*},T_2 )\hbox {e}^{\mathrm {j}\beta _\mathrm{f} T_0 }+H_{z,b} (x^{*},T_2 )\hbox {e}^{\mathrm {j}\beta _\mathrm{b} T_0 }+\hbox {N.S.T} \end{aligned}$$

(49)

$$\begin{aligned}&D_{0}^{2} p_{3}^{*} +{I'}_{11}^{*}\frac{\partial ^{4}p_{3}^{*} }{\partial \varsigma ^{{*}{4}}}+\varOmega ^{{*}^{2}}\sin ^{2}\gamma p_{3}^{*} +2\hbox {j}\varOmega ^{*}D_{0} p_{3}^{*} +\left( {R_{\mathrm{d}}^{{*}} +\varsigma ^{*}} \right) \varOmega ^{{*}^{2}}\frac{\partial p_{3}^{*} }{\partial \varsigma ^{*}}\nonumber \\&\quad -\frac{\varOmega ^{{*}^{2}}}{2}\left( {\left( {R_{\mathrm{d}}^{{*}} +1} \right) ^{2}-\left( {R_{\mathrm{d}}^{{*}} +\varsigma ^{*}} \right) ^{2}} \right) \frac{\partial ^{2}p_{3}^{*} }{\partial \varsigma ^{*}{2}} \nonumber \\&\quad +D_{0}^{2} z_{3}^{*} {\delta }\left( {x^{*}-x_{\mathrm{d}}^{{*}} } \right) \cos \gamma =H_{p,f} (\varsigma ^{*},T_2 )\hbox {e}^{\mathrm {j}\beta _{f} T_{0} }+H_{p,b} (\varsigma ^{*},T_2 )\hbox {e}^{\mathrm {j}\beta _{b} T_{0} }+\hbox {N.S.T} \end{aligned}$$

(50)

where N.S.T stands for non-secular terms. Four secular terms are listed in “Appendix B.” It should be noted that $H_{z,f }(x^{*}$, $T_{2})$ and $H_{p,f }(\varsigma ^{*}$,$T_{2})$ include time-dependent impulse function term $F_{\mathrm{n}i}^{*}$. Integrating Eqs. (B.1) and (B.3) for a full-cycle period at steady state with respect to $T_{0}$, $F_{ni}^{*}$is converted into a stationary function about $F_{\mathrm {nmax} i}^{{*}}$,which is the maximum rubbing force on the ith blade. Equations (49)–(50) would have nontrivial solutions if and only if the solvability conditions are satisfied:

$$\begin{aligned}&\left| {{\begin{array}{l@{\quad }l} {\displaystyle \int \limits _0^{1} {\phi _f \left( {x^{*}} \right) \eta _{\mathrm{1}} \hbox {d}x^{*}} }&{} {\displaystyle \int \limits _0^1 {\phi _f \left( {x^{*}} \right) H_{z,f} (x^{*},T_2 )\hbox {d}x^{*}} } \\ {\displaystyle \int \limits _0^{1} {\psi _\mathrm{f} \left( {\varsigma ^{*}} \right) \eta _{\mathrm{2}} \hbox {d}\varsigma ^{*}} }&{} {\displaystyle \int \limits _0^1 {\psi _\mathrm{f} \left( {\varsigma ^{*}} \right) H_{p,f} (\varsigma ^{*},T_2 )\hbox {d}\varsigma ^{*}} } \\ \end{array} }} \right| =0 \nonumber \\&\left| {{\begin{array}{l@{\quad }l} {\displaystyle \int \limits _0^1 {\phi _b \left( {x^{*}} \right) \eta _{\mathrm{3}} \hbox {d}x^{*}} }&{} {\displaystyle \int \limits _0^1 {\phi _f \left( {x^{*}} \right) H_{z,b} (x^{*},T_2 )\hbox {d}x^{*}} } \\ {\displaystyle \int \limits _0^1 {\psi _\mathrm{b} \left( {\varsigma ^{*}} \right) \eta _{\mathrm{4}} \hbox {d}\varsigma ^{*}} }&{} {\displaystyle \int \limits _0^1 {\psi _\mathrm{f} \left( {\varsigma ^{*}} \right) H_{p,b} (\varsigma ^{*},T_2 )\hbox {d}\varsigma ^{*}} } \\ \end{array} }} \right| =0 \end{aligned}$$

(51)

where

$$\begin{aligned}&\eta _{1} =-m_{r2} \cos \gamma \beta _{f}^{2} {\delta }\left( {x^{*}-x_{\mathrm{d}}^{{*}} } \right) \int _{0}^{1} {\psi _{f} } (\varsigma ^{*})\hbox {d}\varsigma ^{*} \nonumber \\&\quad \eta _{2} =\psi _{f} \left( {\varsigma ^{*}} \right) \left( -\beta _{f}^{2}+\sin ^{2}\gamma \Omega ^{{*}^{2}}+2\Omega ^{*}\beta _\mathrm{f} \right) +{I'}_{11}^{*} \frac{\hbox {d}^{4}\psi _\mathrm{f} \left( {\varsigma ^{*}} \right) }{\hbox {d}\varsigma ^{*}{4}}+\Omega ^{{*}^{2}}\left( {R_{\mathrm{d}}^{{*}} +\varsigma ^{*}} \right) \frac{\hbox {d}\psi _\mathrm{f} \left( {\varsigma ^{*}} \right) }{\hbox {d}\varsigma ^{*}} \nonumber \\&\quad -\frac{\Omega ^{{*}^{2}}}{2}\left( {\left( {R_{\mathrm{d}}^{{*}} +1} \right) ^{2}-\left( {R_{\mathrm{d}}^{{*}} +\varsigma ^{*}} \right) ^{2}} \right) \frac{\hbox {d}^{2}\psi _\mathrm{f} \left( {\varsigma ^{*}} \right) }{\hbox {d}\varsigma ^{*2}} \nonumber \\&\quad \eta _3 =-m_{r2} \cos \gamma \beta _\mathrm{b}^2 {\delta }\left( {x^{*}-x_{\mathrm{d}}^{{*}} } \right) \int _0^1 {\psi _\mathrm{b} } (\varsigma ^{*})\hbox {d}\varsigma ^{*} \nonumber \\&\quad \eta _4 =\psi _\mathrm{b} \left( {\varsigma ^{*}} \right) \left( {-\beta _\mathrm{b}^2 +\sin ^{2}\gamma \Omega ^{{*}^{2}}+2\Omega ^{*}\beta _{b} } \right) +{I'}_{11}^{*} \frac{\hbox {d}^{4}\psi _\mathrm{b} \left( {\varsigma ^{*}} \right) }{\hbox {d}\varsigma ^{*4}}+\Omega ^{{*}^{2}}\left( {R_{\mathrm{d}}^{{*}} +\varsigma ^{*}} \right) \frac{\hbox {d}\psi _\mathrm{b} \left( {\varsigma ^{*}} \right) }{\hbox {d}\varsigma ^{*}} \nonumber \\&\quad -\frac{\Omega ^{{*}^{2}}}{2}\left( {\left( {R_{\mathrm{d}}^{{*}} +1} \right) ^{2}-\left( {R_{\mathrm{d}}^{{*}} +\varsigma ^{*}} \right) ^{2}} \right) \frac{\hbox {d}^{2}\psi _\mathrm{b} \left( {\varsigma ^{*}} \right) }{\hbox {d}\varsigma ^{*2}} \end{aligned}$$

(52)

Separating the real and imaginary parts, Eq. (51) is transformed to:

$$\begin{aligned}&\hbox {Re}\left[ \left( {\int \limits _0^1 {\phi _f \left( {x^{*}} \right) \eta _{\mathrm{1}} \hbox {d}x^{*}} } \right) \left( {\int \limits _0^1 {\psi _\mathrm{f} \left( {\varsigma ^{*}} \right) H_{p,b} (\varsigma ^{*},T_2 )\hbox {d}\varsigma ^{*}} } \right) \right. \nonumber \\&\left. \quad -\left( {\int \limits _0^1 {\psi _\mathrm{f} \left( {\varsigma ^{*}} \right) \eta _{\mathrm{2}} \hbox {d}\varsigma ^{*}} } \right) \left( {\int \limits _0^1 {\phi _f \left( {x^{*}} \right) H_{z,f} (x^{*},T_2 )\hbox {d}x^{*}} } \right) \right] =0 \nonumber \\&\hbox {Im}\left[ \left( {\int \limits _0^1 {\phi _f \left( {x^{*}} \right) \eta _{\mathrm{1}} \hbox {d}x^{*}} } \right) \left( {\int \limits _0^1 {\psi _\mathrm{f} \left( {\varsigma ^{*}} \right) H_{p,b} (\varsigma ^{*},T_2 )\hbox {d}\varsigma ^{*}} } \right) \right. \nonumber \\&\left. \quad -\left( {\int \limits _0^1 {\psi _\mathrm{f} \left( {\varsigma ^{*}} \right) \eta _{\mathrm{2}} \hbox {d}\varsigma ^{*}} } \right) \left( {\int \limits _0^1 {\phi _f \left( {x^{*}} \right) H_{z,f} (x^{*},T_2 )\hbox {d}x^{*}} } \right) \right] =0 \nonumber \\&\hbox {Re}\left[ \left( {\int \limits _0^1 {\phi _b \left( {x^{*}} \right) \eta _{\mathrm{3}} \hbox {d}x^{*}} } \right) \left( {\int \limits _0^1 {\psi _\mathrm{f} \left( {\varsigma ^{*}} \right) H_{p,b} (\varsigma ^{*},T_2 )\hbox {d}\varsigma ^{*}} } \right) \right. \nonumber \\&\left. \quad -\left( {\int \limits _0^1 {\psi _\mathrm{b} \left( {\varsigma ^{*}} \right) \eta _{\mathrm{4}} \hbox {d}\varsigma ^{*}} } \right) \left( {\int \limits _0^1 {\phi _f \left( {x^{*}} \right) H_{z,b} (x^{*},T_2 )\hbox {d}x^{*}} } \right) \right] =0 \nonumber \\&\hbox {Im}\left[ \left( {\int \limits _0^1 {\phi _b \left( {x^{*}} \right) \eta _{\mathrm{3}} \hbox {d}x^{*}} } \right) \left( {\int \limits _0^1 {\psi _\mathrm{f} \left( {\varsigma ^{*}} \right) H_{p,b} (\varsigma ^{*},T_2 )\hbox {d}\varsigma ^{*}} } \right) \right. \nonumber \\&\left. \quad -\left( {\int \limits _0^1 {\psi _\mathrm{b} \left( {\varsigma ^{*}} \right) \eta _{\mathrm{4}} \hbox {d}\varsigma ^{*}} } \right) \left( {\int \limits _0^1 {\phi _f \left( {x^{*}} \right) H_{z,b} (x^{*},T_2 )\hbox {d}x^{*}} } \right) \right] =0 \end{aligned}$$

(53)

Through discussing the eigenvalues of the Jacobian matrix of the left hand of Eq. (53), the stability of the rotor-blade system is determined. The real parts of the eigenvalues give stability information: The solution is unstable if it has more than one (including one) positive real parts [15].

Using Galerkin method to separate the variables, Eqs. (32) and (33) are converted to ordinary differential equations which can be solved by Runge–Kutta numerical method. The results are used to verify the accuracy of the multiple scales perturbation solutions.

5 Numerical simulation

Numerical simulation is performed to analyze the nonlinear vibration and the stability of the rotor-blade system which is composed of a flexible rotating shaft with two nonlinear supports, a rigid disk clamped on the shaft and eight identical blades cantilevered on the disk(see Fig. 8a). The blade numbering is shown in Fig. 8c. The blue curves depict the low-order natural frequencies of the rotor-blade system at different rotating speeds, among which the first-order forward whirl mode frequency is so close to the backward whirl mode frequency that they seem to be on one curve. The red line ($\mathrm{ra}=1$) indicates that the excitation frequency is equal to the rotating frequency on this line. The frequency corresponding to the intersection point of the red line and the frequency curves is the main resonance frequency (see Fig. 8b). From Campbell diagram ($k^{*}=26860$ and $\vartheta ^{*}=0$, see Fig. 8b), it can be seen that only the first-order primary resonance may occur. The black dotted line represents the tip of the blade, and the blue double dot dash line represents the inner wall of the casing in Fig. 8c. The overlapping of the two lines represents the occurrence of rubbing.

Fig. 8

Schematic of rotor-blade system: a physical dimension, b Campbell diagram, c rubbing between blade tip and casing

Due to the assembling misalignment, the gaps among the blade tips and the casing are not circularly symmetric. The values of misalignment along Y and Z directions are denoted by $E_{{y}}$ and $E_{{z}}$. Based on the preconditions that $e_y^{*} =e_z^{*}$ and $E_{y}=E_{z}$ , it is obvious that the rubbing force reaches the maximum value at the tip of the blade $2^{\# }$ (see Fig. 8c). According to our time-domain simulation results, only blade $2^{\#}$ rubs with the casing at steady state and $t_{\mathrm{c}}\approx 0.07t_{\mathrm{p}}$. For simplicity, $F_{\mathrm {nmax2}}^{{*}}$ is denoted by $F_{\mathrm{n}}^{{*}}$ in the following section.

5.1 Effects of support stiffness parameters

Figure 9 illustrates the frequency response curves of the rotor-blade system under different Duffing term coefficients. When $\vartheta ^{*}=-2.5\times 10^{7}$, the original hardening-type nonlinearity is transformed into softening type because of negative nonlinear Duffing term. However, the hardening-type nonlinearity is enhanced by a wide margin due to positive nonlinear Duffing term, so is the jump-down frequency.

Fig. 9

Frequency response curves under different Duffing term coefficients ($e_y^{*} =e_z^{*} =0.001$, $c_{\mathrm {blade}}^{{*}}= c^{*} = c_{\mathrm {bearing}}^{{*}} =0.2$, $\mu =0.1$, $F_{\mathrm{n}}^{{*}} =0.225$, $k^{*}=26860$)

Generally, the multiple solutions are related to the initial conditions. For example, when $\vartheta ^{*}=0$, at the region around $\sigma =0.4$, there are three possible solutions, one of which is unstable and the other two are stable, as are denoted by blue curves in Fig. 9. The trends of solutions under various initial conditions are shown in Fig. 10, where $P_{1}$ and $P_{3}$ are stable focal points, while $P_{2}$ is a saddle point. These three points are marked by solid blue dots in Fig. 9. All the initial conditions in the shaded region will lead to the stable solution $P_{1}$ on the lower resonant branch, while all the initial conditions in the non-shaded region will lead to the stable solution $P_{3}$ on the upper resonant branch. The arrows indicate the directions of movements; thus, the shaded area constitutes the attraction region of point $P_{1}$, while non-shaded area constitutes the attraction region of point $P_{3}$. As an unstable solution, point $P_{2}$ is on the border of two attraction regions and it may move toward either $P_{1}$ or $P_{3}$ after being disturbed.

Fig. 10

Attraction regions of different solutions ($e_y^{*} =e_z^{*} =0.001$, $c_{\mathrm {blade}}^{{*}} =c^{*}=c_{\mathrm {bearing}}^{{*}} =0.2$, $\mu =0.1$, $F_{\mathrm{n}}^{{*}} =0.225$, $k^{*}=26860$, $\vartheta ^{*}=0$)

Figures 11 and 12 depict the phase diagram of the rotor-blade system in the absence or presence of nonlinear terms for $\sigma =0.1$ and $\vartheta ^{*}=-2.5 \times 10^{7}$. Although the solutions are all stable, the trajectories of the simulation results without nonlinear terms are smooth and regular, while those with nonlinear terms are undulant.

Fig. 11

Phase diagram in the Y-plane ($e_y^{*} =e_z^{*} =0.001$, $c_{\mathrm {blade}}^{{*}} =c^{*}=c_{\mathrm {bearing}}^{{*}} =0.2$, $\mu =0.1$, $F_{\mathrm{n}}^{{*}} =0.225$, $k^{*} =26860$, $\sigma =0.1$)

Fig. 12

Phase diagram in the Z-plane ($e_y^{*} =e_z^{*} =0.001$, $c_{\mathrm {blade}}^{{*}} =c^{*}=c_{\mathrm {bearing}}^{{*}} =0.2$, $\mu =0.1$, $F_{\mathrm{n}}^{{*}} =0.225$, $k^{*}=26860$, $\sigma =0.1$)

Figure 13 describes the frequency response curves of the system under different support stiffness. For $\sigma <-0.2$ and $\vartheta ^{*}=0$, the response amplitudes of the system under different support stiffness are very close, and for the range of $-0.2< \sigma <0.533$ and $\vartheta ^{*}=0$, the amplitudes of upper branch of the system under lower support stiffness are higher than those under higher support stiffness. With a lower jump-down frequency, it is more quick for the responses of the system to reach the resonance peak under lower support stiffness. In addition, for the system with higher support stiffness, the resonance peak and jump-down frequency are higher and the unstable range is broader.

Fig. 13

Frequency response curves under different support stiffness ($e_y^{*} =e_z^{*} =0.001$, $c_{\mathrm {blade}}^{{*}} =c^{*}=c_{\mathrm {bearing}}^{{*}} =0.2$, $\mu =0.1$, $F_{\mathrm{n}}^{{*}} =0.225$)

5.2 Effects of loading parameters

Figure 14 depicts the frequency response curves of rotor-blade system under different normal rubbing forces. The nonlinearity is of a hardening type without Duffing term. When the normal rubbing force is zero, the system has only one stable solution. With the slight increase in the normal rubbing force, the resonance peak and the corresponding frequency rise slightly, but the solution keeps stable. As the force approaches the value of 0.225, the bifurcation occurs, and for some values of detuning parameter, there are three solutions; one of them is unstable and marked with blue dotted line. The figure shows that the rubbing forces will reinforce the hardening nonlinearity, raise the formants and resonant frequencies, bring out the bifurcation and extend the unstable frequency range.

Fig. 14

Frequency response curves of rotor-blade system under different normal rubbing forces ($e_y^{*} =e_z^{*} =0.001$, $c_{\mathrm {blade}}^{{*}} =c^{*}=c_{\mathrm {bearing}}^{{*}} =0.2$, $\mu =0.1,k^{*}=26860$, $\vartheta ^{*}=0$)

Figure 15 illustrates the effect of friction coefficient on the frequency response of the system. In the range of AB, before the system approaches the jump-down frequency, the response amplitude of the system with a higher friction coefficient is slightly higher than that with lower friction coefficient, while actually they are very close. However, with a lower jump-down frequency, the amplitude of the system with lower friction coefficient no longer increases after B points. Through the BC area, the amplitude of the system with a higher friction coefficient reaches a higher resonance peak with a broader range of upper resonant branch.

Fig. 15

Frequency response curves under different friction coefficients ($e_y^{*} =e_z^{*} =0.001$, $c_{\mathrm {blade}}^{{*}} =c^{*}=c_{\mathrm {bearing}}^{{*}} =0.2$, $F_{\mathrm{n}}^{{*}} =0.225$, $\vartheta ^{*}=0$)

Figure 16 illustrates the response curves of rotor-blade system under different normal rubbing forces. Because of the characteristic of hardening-type nonlinearity, jump phenomenon does not occur when $\sigma =0$, and the amplitude increases with the increase in rubbing forces. When $\sigma =0.4$ and $\sigma =0.8\,(\vartheta ^{*}=0)$ under some values of normal rubbing force, there are three possible solutions with two stable and one unstable. When $0.099<F_{\mathrm{n}}^{{*}} <0.155$, as is highlighted with light blue in Fig. 16, there are three possible solutions under $\sigma =0.4$, with two stable, but there is only one stable solution under $\sigma =0.8$. When $0.3319<F_{\mathrm{n}}^{{*}} <0.9956$, as is highlighted with pale yellow in Fig. 16, there are three possible solutions under $\sigma =0.8$, but there is only one stable solution under $\sigma =0.4$. Therefore, the detuning parameter corresponding to the second bifurcation point is 0.8 for $F_{\mathrm{n}}^{{*}} =0.155$, while it is 0.4 for $F_{\mathrm{n}}^{{*}} =0.099$. Similarly, the detuning parameter corresponding to the first bifurcation point is 0.4 for $F_{\mathrm{n}}^{{*}} =0.3319$, while it is 0.8 for $F_{\mathrm{n}}^{{*}} =0.9956$. It is clear that the frequencies of the first and the second bifurcation points increase with the increase in normal rubbing force. For $\vartheta ^{*}=-2.5\times 10^{7}$, the system can reach the same bifurcation frequencies under a smaller rubbing force.

Fig. 16

Response curves of the rotor-blade system under different normal rubbing forces ($e_y^{*} =e_z^{*} =0.001$, $c_{\mathrm {blade}}^{{*}} =c^{*}=c_{\mathrm {bearing}}^{{*}} =0.2$, $\mu =0.1$, $k^{*}=26860$)

Figure 17 depicts the steady-state responses of the rotor-blade system with different support stiffness under normal rubbing forces assuming that $c_{\mathrm {blade}}^{{*}} =c^{*}=c_{\mathrm {bearing}}^{{*}}=0.2$ and $\sigma =0.4$. When Duffing term coefficient $\vartheta ^{*}=0$, the system with lower support stiffness will be unstable under larger normal rubbing forces, compared with the system with higher support stiffness. Therefore, the system with lower support stiffness becomes totally stable under larger normal rubbing force. When Duffing term coefficient $\vartheta ^{*}=2.5\times 10^{7}$, jump phenomenon does not occur for both systems.

Fig. 17

Response curves with different support stiffness under normal rubbing forces ($e_y^{*} =e_z^{*} =0.001$, $c_{\mathrm {blade}}^{{*}} =c^{*}=c_{\mathrm {bearing}}^{{*}} =0.2$, $\mu =0.1$, $\sigma =0.4$)

5.3 Effects of damping parameters

Figure 18 depicts the response curves of the rotor-blade system with different support stiffness under different damping coefficients of the shaft. It can be seen that the system with higher support stiffness needs a larger damping coefficient to reach a complete stable state than that with lower support stiffness. However, the response amplitude of the system with smaller support stiffness is larger than that with higher support stiffness for the same damping coefficient. As the detuning parameter increases, the response amplitudes increase, but the system needs a smaller damping coefficient to reach a stable state under both conditions. In addition, small damping coefficients of the shaft may lead to unstable responses regardless of the values of support stiffness.

Fig. 18

Response curves under different damping coefficients of the shaft ($e_y^{*} =e_z^{*} =0.001$, $F_{\mathrm{n}}^{{*}} =0$, $c_{\mathrm {blade}}^{{*}} =0.01$, $c_{\mathrm {bearing}}^{{*}} =0.02$, $\vartheta ^{*}=0$)

Figure 19 depicts the response curves of the rotor-blade system with different support stiffness under different damping coefficients of the bearing. When $c_{\mathrm {bearing}}^{{*}} \ge 0.1675$, the response of the system with smaller support stiffness is completely stable. However, the response amplitude of the system with larger support stiffness almost remains unchanged as the damping of bearing increases. It is obvious that the damping of bearing has a more powerful effect when the system is under smaller support stiffness.

Fig. 19

Response curves under different damping coefficients of the bearing ($e_y^{*} =e_z^{*} =0.001$, $F_{\mathrm{n}}^{{*}} =0$, $c_{\mathrm {blade}}^{{*}} =c^{*}=0.01$, $\sigma =0.2$, $\vartheta ^{*}=0$)

Figure 20 shows the trajectories of the bifurcation points of the rotor-blade system with different support stiffness under different damping coefficients of the shaft. As the damping coefficient increases, the detuning parameters corresponding to the first and second bifurcation points both decrease. Obviously, the decreasing velocity of the second bifurcation point is faster than that of the first bifurcation point. Finally, the two tracks meet in one point, and the real damping equal to or greater than this value will guarantee the stability of the system. It can be seen that the lower damping may lead to unstable response under both conditions. In addition, the Duffing term of support stiffness makes bifurcation frequencies higher, and the system with the larger support stiffness needs a larger damping to reach a stable state compared with that with smaller support stiffness.

Fig. 20

Trajectories of bifurcation points ($F_{\mathrm{n}}^{{*}} =0$, $e_y^{*} =e_z^{*} =0.001$, $c_{\mathrm {bearing}}^{{*}} =0.2$, $c_{\mathrm {blade}}^{{*}} =0.01$)

6 Conclusions

In this paper, the main resonances of a coupled rotor-blade system with nonlinear supports are investigated. The influences of normal rubbing force, friction coefficient, damping, support stiffness and mass eccentricity on the system responses are discussed. Some detailed conclusions are summarized as follows:

• (1) The nonlinearity of the system is of hardening type without nonlinear stiffness terms of the bearing. The original hardening type of nonlinearity may be enhanced or transformed into softening type due to the positive or negative nonlinear stiffness terms of the bearing. The increase in the normal rubbing force or the mass eccentricity destabilizes the system and reinforces the nonlinearity.

• (2) The mode shapes and critical speeds of the shaft with bladed disk are different from those without bladed disk. The decreasing support stiffness weakens the nonlinearity of the system. Lower support stiffness results in a lower jump-down frequency and a smaller resonance peak. However, the system response amplitude under lower support stiffness is larger than that under higher support stiffness before its jump-down frequency.

• (3) Before reaching the jump-down frequency, the amplitude of the system with a higher friction coefficient is slightly larger than that with a lower friction coefficient. By increasing the friction coefficient, the jump-down frequency is enhanced, which leads to the increase in the response amplitude.

• (4) Low damping of the shaft may lead to unstable response of the rotor-blade systems. Furthermore, the system with larger support stiffness needs a larger damping coefficient to reach the stable state. In addition, the damping of bearing has a more powerful effect on the system vibration responses under smaller support stiffness.

Appendices

Appendix A: The first- and third-order equations extracted from multiple scales method

$$\begin{aligned}&O(\varepsilon ): \nonumber \\&\quad D_0^2 z_1^{*} +m_{\mathrm{r}} {\delta }\left( {x^{*}-x_{\mathrm{d}}^{*} } \right) D_0^2 z_1^{*} +\hbox {j}\Omega I_1^{*} D_0 {z''}_1^{*} +\hbox {j}\Omega ^{*}J_{\mathrm{r}} \delta \left( {x^{*}-x_\mathrm{d}^{*} } \right) D_0 {z}_1{''^{*}}\nonumber \\&\qquad -I_2^{*} D_0^2 {z''}_1^{*} -I_{\mathrm{r}} D_0^{2} {z''}_1^{*} {\delta }\left( x^{*}-x_{\mathrm{d}}^{*} \right) +z_1^{{IV}^{*}} \nonumber \\&\qquad +kz_1^{*} {\delta }\left( {x^{*}} \right) +kz_1^{*} {\delta }\left( {x^{*}-1} \right) +m_{\mathrm {r}2} {\delta }\left( {x^{*}-x_{\mathrm{d}}^{*} } \right) \cos \gamma \int _{0}^{1} {D_0^{2} p_{1}^{*} } \hbox {d}\varsigma ^{*}=0 \end{aligned}$$

(A.1)

$$\begin{aligned}&D_{0}^{2} p_{1}^{*} +{I'}_{11}^{*}\frac{\partial ^{4}p_{1}^{*}}{\partial \varsigma ^{*}{4}}+\Omega ^{{*}^{2}}\sin ^{2}\gamma p_{1}^{*} +\left( {R_{\mathrm{d}}^{{*}} +\varsigma ^{*}} \right) \Omega ^{{*}^{2}}\frac{\partial p_{1}^{*} }{\partial \varsigma ^{*}}-\frac{\Omega ^{{*}^{2}}}{2}\left( {\left( {R_{\mathrm{d}}^{{*}} +1} \right) ^{2}-\left( {R_{\mathrm{d}}^{{*}} +\varsigma ^{*}} \right) ^{2}} \right) \frac{\partial ^{2}p_{1}^{*} }{\partial \varsigma ^{*}{2}} \nonumber \\&\quad +2\hbox {j}\Omega ^{*}D_{0} p_{1}^{*} -l^{*}D_{0}^{2} z_{1}^{*} {\delta }\left( {x^{*}-x_{\mathrm{d}}^{{*}} } \right) \cos \gamma =0 \end{aligned}$$

(A.2)

$$\begin{aligned}&O(\varepsilon ^{3}):\nonumber \\&\quad D_0^2 z_3^{*} +m_{\mathrm{r}} {\delta }\left( {x^{*}-x_{\mathrm{d}}^{{*}} } \right) D_0^2 z_3^{*} +\hbox {j}\Omega I_1^{*} D_0 {z''}_3^{*} +\hbox {j}\Omega ^{*}J_{\mathrm{r}} {\delta }\left( {x^{*}-x_{\mathrm{d}}^{{*}} } \right) D_0 {z''}_3^{*}\nonumber \\&\qquad -I_2^{*} D_0^2 {z''}_3^{*} -I_{\mathrm{r}} D_0^2 {z''}_3^{*} {\delta }\left( {x^{*}-x_{\mathrm{d}}^{{*}} } \right) +z_3^{{IV}^{*}} \nonumber \\&\qquad +kz_{3}^{*} {\delta }\left( {x^{*}} \right) +kz_{3}^{*} {\delta }\left( {x^{*}-1} \right) =-2D_2 D_0 z_1^{*} -2m_{\mathrm{r}} {\delta }\left( {x^{*}-x_{\mathrm{d}}^{{*}} } \right) D_2 D_0 z_1^{*} \nonumber \\&\qquad -\hbox {j}\Omega I_1^{*} D_2 {z''}_1^{*} -\hbox {j}\Omega ^{*}J_{\mathrm{r}} {\delta }\left( {x^{*}-x_{\mathrm{d}}^{{*}} } \right) D_0 {z''}_1^{*} \nonumber \\&\qquad +2I_{2}^{*} D_{2} D_{0} {z''}_{1}^{*} +2I_{\mathrm{r}} D_{2} D_{0} {z''}_{1}^{*} {\delta }\left( x^{*}-x_{\mathrm{d}}^{{*}} \right) -c^{{*}} D_{0} z_{1}^{*} -c_{\mathrm {bearing}}^{{*}} D_{0} z_{1}^{*} {\delta }\left( {x^{*}}\right) \nonumber \\&\qquad -c_{\mathrm {bearing}}^{{*}} D_0 z_1^{*} {\delta }\left( {x^{*}-1} \right) -\vartheta z_{1}^{*} \left| {z_{1}^{*}} \right| ^{2}\left( {{\delta }\left( {x^{*}} \right) +{\delta }\left( {x^{*}-1} \right) } \right) \nonumber \\&\qquad +\left( {m_{\mathrm {disk}}^{{*}} \left( {\hbox {j}e_z +e_y } \right) \varOmega ^{{*}^{2}}e^{\mathrm {j}\varOmega ^{*}T_0 }-\sum _{i=1}^{N_{\mathrm{b}} } {F_{\mathrm {n}i} } (1+\hbox {j}\mu )e^{\mathrm {j}\phi _i }} \right) {\delta }\left( {x^{*}-x_{\mathrm{d}}^{{*}} } \right) -m_{\mathrm {r}2} {\delta }\left( {x^{*}-x_{\mathrm{d}}^{{*}} } \right) \cos \gamma \nonumber \\&\qquad \int _0^{1} {2D_{2} D_{0} p_{1}^{*}} \hbox {d}\varsigma ^{*} \nonumber \\&\qquad -\frac{{z'}_1^{*}}{2}\int _0^{{x^{*}}} {\left( {2D_0 {z'}_1^{*}D_0 {\dot{\bar{z}}}_1{'^{*}}+D_0^{2} {z'}_1 ^{*}{{\bar{z}}_1{'^{*}}}+D_0^{2} {\bar{z}}_1{'^{*}}{z'}_1 ^{*}} \right) \hbox {d}x^{*}} \nonumber \\&\qquad -\frac{{z''}_1 ^{*}}{2}\int _1^{{x^{*}}} {\int _0^{{x^{*}}} {\left( {2D_0 {z'}_1 ^{*}D_0 {\dot{\bar{z}}}_1{'^{*}}+D_0^2 {z'}_1 ^{*}{\bar{z'}}_1^{*}+D_0^2 {\bar{z}}_1{'^{*}}{z'}_1 ^{*}} \right) \hbox {d}x^{*}\hbox {d}x^{*}} } \nonumber \\&\qquad -m_{\mathrm{r}} {\delta }\left( {x^{*}-x_{\mathrm{d}}^{{*}} } \right) \left( \int _0^{x_{\mathrm{d}}^{\mathrm {*}}} {\left( {2D_0 {z'}_1^{*}D_0 {\dot{\bar{z}'}}_1^{*}+D_0^2 {z'}_1^{*}{\bar{z}}_1{'^{*}}+D_0^2 {\bar{z'}}_1^{*}{{z}_1}{'^{*}}} \right) \hbox {d}x^{*}} \right. \nonumber \\&\left. \qquad + \frac{{{z''}_1}^{*}}{2}\int _1^{{x_{\mathrm{d}}^{{*}} }} {\int _0^{x_{\mathrm{d}}^{{*}} } {\left( {2D_0 {z'}_1^{*}D_0 {\dot{\bar{z}}}_1{'^{*}}+ D_0^2 {z}_1{'^{*}}{\bar{z'}}_1 ^{*}+D_0^2 {\bar{z}}_1{'^{*}}{z}_1{'^{*}}} \right) \hbox {d}x^{*}\hbox {d}x^{*}} } \right) \nonumber \\&\qquad -2{z}_1{''^{*}}{z'}_1^{*}{\bar{z}}{'''^{*}}_1 -\frac{1}{2}{z}_1{''^{*}}{{\bar{z}}_1}{'^{*}}{z}_1{'''^{*}}-\frac{3}{2}{\bar{z}}_1{''^{*}}{{z'}_1}^{*}{z}_1{'''^{*}}-{{\bar{z}}_1}{''^{*}}{{{z''}_1}^{*}}^{2}-\frac{1}{2}{z_1 ^{\left( {IV} \right) }}^{*}{{\bar{z}}_1}{'^{*}}{{z'}_1}^{*} -\frac{1}{2} {\bar{z}_{1}^{(IV)*}} {{{z'}_1}^{*}}^{2} \end{aligned}$$

(A.3)

$$\begin{aligned}&D_0^{2} p_{3}^{*} +{I}{'^{*}}_{11}\frac{\partial ^{4}p_3^{*} }{\partial \varsigma ^{*}{4}}+{\Omega ^{*}}^{2}\sin ^{2}\gamma p_3^{*} +2\hbox {j}\Omega ^{*}D_0 p_3^{*} +\left( {R_{\mathrm{d}}^{{*}} +\varsigma ^{*}} \right) {\Omega ^{*}}^{2}\frac{\partial p_{3}^{*} }{\partial \varsigma ^{*}}\nonumber \\&\quad -\frac{{\Omega ^{*}}^{2}}{2}\left( {\left( {R_{\mathrm{d}}^{{*}} +1} \right) ^{2}-\left( {R_{\mathrm{d}}^{{*}} +\varsigma ^{*}} \right) ^{2}} \right) \frac{\partial ^{2}p_3^{*} }{\partial \varsigma ^{*2}} \nonumber \\&\quad +D_0^2 z_3^{*} {\delta }\left( {x^{*}-x_\mathrm{d}^{*} } \right) \cos \gamma =-2D_2 D_0 p_1^{*} -c_{\mathrm {blade}}^{{*}} D_0 p_1^{*} -2\hbox {j}\Omega ^{*}D_2 p_1^{*} -2D_2 D_0 z_1^{*} {\delta }\left( {x^{*}-x_{\mathrm{d}}^{{*}} } \right) \cos \gamma \nonumber \\&\quad -\hbox {j}c_{\mathrm {blade}}^{{*}} \Omega ^{*}p_1^{*} -\frac{2}{N_{\mathrm{b}} }\mu \cos \gamma {\delta }\left( {\varsigma ^{*}-1} \right) \sum _{i=1}^{N_{\mathrm{b}} } {F_{\mathrm {n}i}^{*} r^{*}} e^{-\hbox {j}\phi _i } \end{aligned}$$

(A.4)

Appendix B: The coefficients of $\hbox {e}^{\mathrm{j}{\beta _{f}}{T}_{0}}$ and $\hbox {e}^{\mathrm{j}{\beta _{b}}{T}_{0}}$

$$\begin{aligned}&{H_{z,f}}\left( {{x^*},{T_2}} \right) = \left[ {2{\mathrm{j}}{{{{\mathrm{d}}^2}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}^2}}{\beta _\mathrm{f}}I_2^*} \right. - 2{\mathrm{j}}{\beta _f}{\phi _f}({x^*}) - 2{\mathrm{j}}{m_{\mathrm{{r}}}}{{ \delta }}\left( {{x^*} - x_{\mathrm{{d}}}^{\mathrm{{*}}}} \right) {\beta _f}{\phi _f}({x^*}) - {\mathrm{j}}{\Omega ^*}I_1^*{{{{\mathrm{d}}^2}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}^2}} \nonumber \\&\quad - 2{\mathrm{j}}{m_{{\mathrm{r}}2}}\cos \gamma {\beta _f}{{ \delta }}\left( {{x^*} - x_{\mathrm{{d}}}^{\mathrm{{*}}}} \right) {\varTheta _f}\int _0^1 {{\psi _\mathrm{f}}} ({\varsigma ^*}){\mathrm{d}}{\varsigma ^*} - {\mathrm{j}}{\Omega ^*}{J_{\mathrm{{r}}}}{{ \delta }}\left( {{x^*} - x_{\mathrm{{d}}}^{\mathrm{{*}}}} \right) {{{{\mathrm{d}}^2}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}^2}} \nonumber \\&\quad \left. { + 2{I_{\mathrm{{r}}}}{\beta _\mathrm{f}}{{ \delta }}\left( {{x^*} - x_{\mathrm{{d}}}^{\mathrm{{*}}}} \right) {{{{\mathrm{d}}^2}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}^2}}} \right] {{{\mathrm{d}}{A_1}({T_2})} \over {\hbox {d}{T_2}}} + \left[ {{{{{\left( {{\beta _\mathrm{f}} - {\beta _\mathrm{b}}} \right) }^2}} \over 2}{{{\mathrm{d}}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}}}} \right. \left( {\int _0^{{x^*}} {{{{\mathrm{d}}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}}}{{{\mathrm{d}}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}}}{\mathrm{d}}{x^*}} } \right) \nonumber \\ \end{aligned}$$

(B.1)

$$\begin{aligned}&\quad + {{{{\left( {{\beta _\mathrm{f}} - {\beta _\mathrm{b}}} \right) }^2}} \over 2}{{{\mathrm{d}}{\phi ^2}_b({x^*})} \over {{\mathrm{d}}{x^*}^2}}\left( {\int _1^{{x^*}} {\int _0^{{x^*}} {{{{\mathrm{d}}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}}}{{{\mathrm{d}}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}}}{\mathrm{d}}{x^*}{\mathrm{d}}{x^*}} } } \right) \\&\quad + {{{m_{\mathrm{{r}}}}{{ \delta }}\left( {{x^*} - x_{\mathrm{{d}}}^{\mathrm{{*}}}} \right) {{\left( {{\beta _\mathrm{f}} - {\beta _\mathrm{b}}} \right) }^2}} \over 2}{{{\mathrm{d}}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}}}\left( {\int _0^{x_{\mathrm{{d}}}^{\mathrm{{*}}}} {{{{\mathrm{d}}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}}}{{{\mathrm{d}}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}}}{\mathrm{d}}{x^*}} } \right) \\&\quad + {{{m_{\mathrm{{r}}}}{{ \delta }}\left( {{x^*} - x_{\mathrm{{d}}}^{\mathrm{{*}}}} \right) {{\left( {{\beta _\mathrm{f}} - {\beta _\mathrm{b}}} \right) }^2}} \over 2}{{{\mathrm{d}}{\phi ^2}_b({x^*})} \over {{\mathrm{d}}{x^*}^2}}\left( {\int _1^{x_{\mathrm{{d}}}^{\mathrm{{*}}}} {\int _0^{x_{\mathrm{{d}}}^{\mathrm{{*}}}} {{{{\mathrm{d}}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}}}{{{\mathrm{d}}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}}}{\mathrm{d}}{x^*}{\mathrm{d}}{x^*}} } } \right) \\&\quad - {5 \over 2}{{{{\mathrm{d}}^2}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}^2}}{{{\mathrm{d}}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}}}{{{{\mathrm{d}}^3}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}^3}} - {7 \over 2}{{{{\mathrm{d}}^2}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}^2}}{{{\mathrm{d}}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}}}{{{{\mathrm{d}}^3}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}^3}} \\&\quad - 2{{{{\mathrm{d}}^2}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}^2}}{{{\mathrm{d}}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}}}{{{{\mathrm{d}}^3}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}^3}} - {1 \over 2}{{{{\mathrm{d}}^4}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}^4}}{{{\mathrm{d}}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}}}{{{\mathrm{d}}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}}} \\&\quad - 2{\left( {{{{{\mathrm{d}}^2}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}^2}}} \right) ^2}{{{{\mathrm{d}}^2}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}^2}}\left. { - {1 \over 2}{{{{\mathrm{d}}^4}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}^4}}{{\left( {{{{\mathrm{d}}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}}}} \right) }^2}} \right] {A_1}({T_2}){A_2}({T_2}){{{{\bar{A}}}}_2}({T_2}) \\&\quad + \left[ { - 4{{{{\mathrm{d}}^2}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}^2}}{{{\mathrm{d}}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}}}{{{{\mathrm{d}}^3}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}^3}} - {\vartheta ^*}{{\left( {{\phi _f}({x^*})} \right) }^3}\left( {{{ \delta }}\left( {{x^*}} \right) + {{ \delta }}\left( {{x^*} - 1} \right) } \right) } \right. \\&\quad \left. { - {{\left( {{{{{\mathrm{d}}^2}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}^2}}} \right) }^3} - {1 \over 2}{{{{\mathrm{d}}^4}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}^4}}{{\left( {{{{\mathrm{d}}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}}}} \right) }^2}} \right] A_1^2({T_2}){{{{\bar{A}}}}_1}({T_2}) \\&\quad - {\mathrm{j}}{c^*}{\phi _f}({x^*}){\beta _\mathrm{f}}{A_1}({T_2}) + m_{{\mathrm{disk}}}^{\mathrm{{*}}}{\Omega ^*}^2\left( {{\mathrm{j}}{e_z} + {e_y}} \right) {{ \delta }}\left( {{x^*} - x_{\mathrm{{d}}}^{\mathrm{{*}}}} \right) {e^{{\mathrm{j}}\sigma {T_2}}} - {{ \delta }}\left( {{x^*} - x_{\mathrm{{d}}}^{\mathrm{{*}}}} \right) \sum \limits _{i = 1}^{{N_{\mathrm{{b}}}}} {F_{{\mathrm{n}}i}^*} (1 + {\mathrm{j}}\mu ){e^{{\mathrm{j}}\sigma {T_2} + {\mathrm{j}}{\vartheta _i}}} \\&\quad - {\mathrm{j}}c_{{\mathrm{bearing}}}^{\mathrm{{*}}}{\phi _f}({x^*}){\beta _\mathrm{f}}{A_1}({T_2}){{ \delta }}\left( {{x^*}} \right) - {\mathrm{j}}c_{{\mathrm{bearing}}}^{\mathrm{{*}}}{\phi _f}({x^*}){\beta _f}{A_1}({T_2}){{ \delta }}\left( {{x^*} - 1} \right) = 0 \end{aligned}$$

$$\begin{aligned}&{H_{z,b}}\left( {{x^*},{T_2}} \right) = \left[ {2{\mathrm{j}}{{{{\mathrm{d}}^2}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}^2}}{\beta _\mathrm{b}}I_2^*} \right. - 2{\mathrm{j}}{\beta _b}{\phi _b}({x^*}) - 2{\mathrm{j}}{m_{\mathrm{r}}}{{ \delta }}\left( {{x^*} - x_{\mathrm{d}}^{*}} \right) {\beta _\mathrm{b}}{\phi _b}({x^*}) - {\mathrm{j}}{\Omega ^*}I_1^*{{{{\mathrm{d}}^2}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}^2}} \nonumber \\&\quad - 2{\mathrm{j}}{m_{{\mathrm{r}}2}}\cos \gamma {\beta _b}{{ \delta }}\left( {{x^*} - x_{\mathrm{d}}^{*}} \right) {\varTheta _b}\int _0^1 {{\psi _\mathrm{b}}} ({\varsigma ^*}){\mathrm{d}}{\varsigma ^*} - {\mathrm{j}}{\Omega ^*}{J_{\mathrm{r}}}{{ \delta }}\left( {{x^*} - x_{\mathrm{d}}^{*}} \right) {{{{\mathrm{d}}^2}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}^2}} \nonumber \\&\quad \left. { + 2{I_{\mathrm{r}}}{\beta _\mathrm{b}}{{ \delta }}\left( {{x^*} - x_{\mathrm{d}}^{*}} \right) {{{{\mathrm{d}}^2}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}^2}}} \right] {{{\mathrm{d}}{A_2}({T_2})} \over {\hbox {d}{T_2}}} + \left[ {{{{{\left( {{\beta _\mathrm{f}} - {\beta _\mathrm{b}}} \right) }^2}} \over 2}{{{\mathrm{d}}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}}}} \right. \left( {\int _0^{{x^*}} {{{{\mathrm{d}}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}}}{{{\mathrm{d}}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}}}{\mathrm{d}}{x^*}} } \right) \nonumber \\&\quad + {{{{\left( {{\beta _\mathrm{f}} - {\beta _\mathrm{b}}} \right) }^2}} \over 2}{{{\mathrm{d}}{\phi ^2}_f({x^*})} \over {{\mathrm{d}}{x^*}^2}}\left( {\int _1^{{x^*}} {\int _0^{{x^*}} {{{{\mathrm{d}}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}}}{{{\mathrm{d}}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}}}{\mathrm{d}}{x^*}{\mathrm{d}}{x^*}} } } \right) \nonumber \\&\quad + {{{m_{\mathrm{r}}}{{ \delta }}\left( {{x^*} - x_{\mathrm{d}}^{*}} \right) {{\left( {{\beta _\mathrm{f}} - {\beta _\mathrm{b}}} \right) }^2}} \over 2}{{{\mathrm{d}}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}}}\left( {\int _0^{x_{\mathrm{d}}^{*}} {{{{\mathrm{d}}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}}}{{{\mathrm{d}}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}}}{\mathrm{d}}{x^*}} } \right) \nonumber \\&\quad + {{{m_{\mathrm{r}}}{{ \delta }}\left( {{x^*} - x_{\mathrm{d}}^{*}} \right) {{\left( {{\beta _\mathrm{f}} - {\beta _\mathrm{b}}} \right) }^2}} \over 2}{{{\mathrm{d}}{\phi ^2}_f({x^*})} \over {{\mathrm{d}}{x^*}^2}}\left( {\int _1^{x_{\mathrm{d}}^{*}} {\int _0^{x_{\mathrm{d}}^{*}} {{{{\mathrm{d}}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}}}{{{\mathrm{d}}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}}}{\mathrm{d}}{x^*}{\mathrm{d}}{x^*}} } } \right) \nonumber \\&\quad - {5 \over 2}{{{{\mathrm{d}}^2}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}^2}}{{{\mathrm{d}}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}}}{{{{\mathrm{d}}^3}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}^3}} - {7 \over 2}{{{{\mathrm{d}}^2}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}^2}}{{{\mathrm{d}}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}}}{{{{\mathrm{d}}^3}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}^3}} \nonumber \\&\quad - 2{{{{\mathrm{d}}^2}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}^2}}{{{\mathrm{d}}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}}}{{{{\mathrm{d}}^3}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}^3}} - {1 \over 2}{{{{\mathrm{d}}^4}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}^4}}{{{\mathrm{d}}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}}}{{{\mathrm{d}}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}}} \nonumber \\&\quad - 2{\left( {{{{{\mathrm{d}}^2}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}^2}}} \right) ^2}{{{{\mathrm{d}}^2}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}^2}}\left. { - {1 \over 2}{{{{\mathrm{d}}^4}{\phi _b}({x^*})} \over {{\mathrm{d}}{x^*}^4}}{{\left( {{{{\mathrm{d}}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}}}} \right) }^2}} \right] {A_1}({T_2}){A_2}({T_2}){{{\bar{A}}}_1}({T_2}) \nonumber \\&\quad + \left[ { - 4{{{{\mathrm{d}}^2}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}^2}}{{{\mathrm{d}}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}}}{{{{\mathrm{d}}^3}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}^3}} - {\vartheta ^*}{{\left( {{\phi _f}({x^*})} \right) }^3}\left( {{{ \delta }}\left( {{x^*}} \right) + {{\delta }}\left( {{x^*} - 1} \right) } \right) } \right. \nonumber \\&\quad \left. { - {{\left( {{{{{\mathrm{d}}^2}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}^2}}} \right) }^3} - {1 \over 2}{{{{\mathrm{d}}^4}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}^4}}{{\left( {{{{\mathrm{d}}{\phi _f}({x^*})} \over {{\mathrm{d}}{x^*}}}} \right) }^2}} \right] A_2^2({T_2}){{\bar{A}}_2}({T_2}) \nonumber \\&\quad - {\mathrm{j}}{c^*}{\phi _b}({x^*}){\beta _\mathrm{b}}{A_2}({T_2}) - {\mathrm{j}}c_{{\mathrm{bearing}}}^{*}{\phi _b}(0){\beta _b}{A_2}({T_2}) - {\mathrm{j}}c_{{\mathrm{bearing}}}^{*}{\phi _b}(1){\beta _\mathrm{b}}{A_2}({T_2}) = 0 \end{aligned}$$

(B.2)

$$\begin{aligned}&H_{p,f} \left( {\varsigma ^{*},T_2 } \right) =-2\hbox {j}\Theta _f \beta _\mathrm{f} \psi _\mathrm{f} \left( {\varsigma ^{*}} \right) \frac{\hbox {d}A_1 (T_2 )}{\hbox {d}T_2 }-\hbox {j}c_{\mathrm {blade}}^{{*}} \Theta _f \beta _\mathrm{f} \psi _\mathrm{f} \left( {\varsigma ^{*}} \right) A_1 (T_2 )-2\hbox {j}\Omega ^{*}\Theta _f \psi _\mathrm{f} \left( {\varsigma ^{*}} \right) \frac{\hbox {d}A_1 (T_2 )}{\hbox {d}T_2 } \nonumber \\&\quad -\hbox {j}c_{\mathrm {blade}}^{{*}} \Theta _f \Omega ^{*}\psi _\mathrm{f} \left( {\varsigma ^{*}} \right) A_1 (T_2 )-2\hbox {j}\beta _\mathrm{f} \phi _f (x_\mathrm{d} )\frac{\hbox {d}A_1 (T_2 )}{\hbox {d}T_2 }\cos \gamma -\frac{2}{N_{\mathrm{b}} }\mu \cos \gamma \sum _{i=1}^{N_\mathrm{b} } {F_{\mathrm {n}i}^{*} } r^{*}e^{\mathrm {j}\sigma T_2 +\hbox {j}^\vartheta _{i}} \end{aligned}$$

(B.3)

$$\begin{aligned}&H_{p,b} \left( {\varsigma ^{*},T_2 } \right) =-2\hbox {j}\Theta _b \beta _\mathrm{b} \psi _\mathrm{b} \left( {\varsigma ^{*}} \right) \frac{\hbox {d}A_2 (T_2 )}{\hbox {d}T_2 }-\hbox {j}c_{\mathrm {blade}}^{{*}} \Theta _b \beta _\mathrm{b} \psi _\mathrm{b} \left( {\varsigma ^{*}} \right) A_2 (T_2 )-2\hbox {j}\Omega ^{*}\Theta _b \psi _\mathrm{b} \left( {\varsigma ^{*}} \right) \frac{\hbox {d}A_2 (T_2 )}{\hbox {d}T_2 } \nonumber \\&\quad -\hbox {j}c_{\mathrm {blade}}^{{*}} \Theta _b \Omega ^{*}\psi _\mathrm{b} \left( {\varsigma ^{*}} \right) A_2 (T_2 )-2\hbox {j}\beta _\mathrm{b} \phi _b (x_\mathrm{d} )\frac{\hbox {d}A_2 (T_2 )}{\hbox {d}T_2 }\cos \gamma \end{aligned}$$

(B.4)