1 Introduction

In recent years, as the large-capacity high-parameter unit is put into use, the study of the dynamic response of rotor system has become an important subject in modern rotor dynamics. In the study of rotor dynamics, one of the most important content is the stability problem. The instability of blade–rotor–bearing system will result in strong vibration and even disastrous accident of rotating machinery. In the rotor system supported on oil film bearings, the instability of rotor system caused by oil film forces is particularly prominent. When a rotor reaches a certain speed, the oil whip is easy to occur, the harmfulness is equal to the rotor speed at critical speed when produce intense resonance. That equal or more violent oscillation, which not only can lead high-speed rotating machinery to have serious fault, sometimes may bring a serious hazard to machines. Therefore, irrespective of the safety or destructiveness, the research on the nonlinear dynamic behavior of oil film force is significant.

In the early study of oil film failure, the rotor–bearing model takes the nonlinear oil film force into consideration and the flexible blades are neglected. And many papers researched the rotor–bearing system by the experimental method. And the dynamic behavior of a direct coupled rotor–bearing system is researched, implemented the experimental vibration analyses in the vertical direction [1]. Santos et al. [2] made a theoretical and experimental contribution to the problem of rotor–blades dynamic interaction and carried out a validation procedure of mathematical models with the help of a simple test rig, built by a mass–spring system attached to four flexible rotating blades. Shen et al. [3] investigated the nonlinear dynamics and stability of the rotor–bearing–seal system both the theoretically and experimentally.

Due to the complexity of nonlinear systems, many numerical methods are used to analyze the rotor–bearing system. Yan et al. [4] studied the motions of a flexible rotor in short journal bearings with nonlinear damping suspension. Qin et al. [5, 6] developed an analytical model for bending stiffness of the bolted disk–drum joints and then investigated the time-varying stiffness at the joint interface with bolt loosening by means of three-dimensional (3D) nonlinear finite element (FE) models. Castro et al. [7] made an analysis about the whirl and whip instabilities taking into account the dynamic behavior of a rotating system. Chang-Jian et al. [8] presented numerical work investigating the dynamic responses of a flexible rotor supported by porous journal bearings with the fourth-order Runge–Kutta method. Laha et al. [9] carried out the nonlinear dynamic analysis of a flexible rotor with a rigid disk under unbalance excitation mounted on porous oil journal bearings at the two ends with the method of Wilson-\(\theta \). Yang et al. [10] predicted the nonlinear dynamic stiffness and damping coefficients of finite-long journal bearings with the partial derivative method.

The dynamic response of rotor system can be influenced greatly by nonlinearities. Some works have revealed the nonlinear dynamic behaviors of the rotor-bearing system. Jing et al. [11, 12] analyzed the nonlinear dynamic behavior of a rotor–bearing system based on a continuum model. Meybodi et al. [13] presented the effect of rotor mass nonlinear dynamic behavior of rigid rotor–bearing system excited by mass unbalance. The dynamic characteristics of a novel nonlinear model of rotor/bearing/seal system were studied based on the Hamilton principle [14]. Cheng et al. [15] investigated the nonlinear dynamic behaviors of a rotor–bearing–seal coupled system, analyzing the influence of parameters by state trajectory. They all investigated various nonlinear phenomena compressing periodic, quasi-periodic motion and chaotic motion. Phadatare et al. [16] described a step forward in calculating the nonlinear frequencies and resultant dynamic behavior of high-speed rotor–bearing system with mass unbalance.

These researches concluded that it is important to investigate the nonlinear dynamics of rotor–bearing system. Although the oil film forces are the leading nonlinear exciting source which results in fatal accidents, rub-impact is also one of the common nonlinear faults in rotor system. In modern industry, the rub-impact force may be neglected. But with the improvement of science and technology, the faults of rotating machines are also becoming complicated. As a result, multiple or coupled faults often occur at the same time [17, 18]. So, many scholars studied the dynamic behaviors of the rotor–bearing system considering rub-impact and oil film force. The nonlinear dynamic analysis of the rotor–bearing system is studied in this paper and is supported by oil film short bearings with nonlinear suspension [19]. Chu et al. [20] investigated the vibration characteristics of a rub-impact rotor system supported on oil film bearings. Chang-Jian et al. [21] presented a dynamic analysis of a rub-impact rotor supported by two turbulent model journal bearings with two suspensions to study the dynamics of the rotor center and bearing center. Wan et al. [22] performed a dynamic analysis of the rub-impact rotor supported by two couple stress fluid film journal bearings. And the study presented and coupled together the strong nonlinear couple stress fluid film force, nonlinear rub-impact force and nonlinear suspension. LI et al. [23] investigated an elastic rub-impact rotor system based on modern nonlinear dynamics and rotor dynamics theory. In order to make the analysis of rotor–bearing system more precise, the rub-impact between rotor and stator was also proposed in this paper.

As the improvement of engineering and materials sciences, the rotating machinery is becoming faster and more lightweight. A rotor–bearing model may not meet the need of research in engineering. In this case, many scholars began to consider the influence of flexible blade on the rotor–bearing system, and the blade–rotor–bearing coupling system was established. Han et al. [24] presented a coupled bending and torsion model of blade–rotor–bearing with nonlinear oil film force and analyzed dynamic characteristics of the coupled system. Some researches [25,26,27] addressed the nonlinear dynamic behavior of a rotor–bearing system with interaction between blades and rotor. In these papers, a time-dependent nonlinear model of a flexible blade–rotor–bearing system is established, and the dynamic behavior of system was analyzed.

As can be seen from the previous references, the most present studies simplify rotor and blade as lumped mass points. The influence of shaft’s bending and shear and the flexibility are usually ignored. In order to reflect the continuous distribution of model’s mass and damping, in this paper, the continuum model of the rotor–blades coupling system is adopted. Since this paper considers the shaft as the continuous Timoshenko beam, considering the influence of shaft’s bending and shear, and the nonlinear dynamic model of blade–rotor–bearing coupling system is presented. Then, the dynamic model is employed to study the nonlinear characteristic of rotor system and blade under the nonlinear oil film force. A detailed study is performed on the influence of the blade upon the nonlinear dynamic behavior of rotor system, which offers theoretical basis for the design of rotating machinery.

2 The establishment of dynamic model

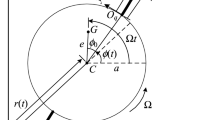
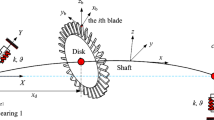
A rotor system composed of shaft, rigid disk and blades is shown in Fig. 1. The flexible disk is simplified as cantilever Timoshenko beam clamped on the rigid disk. And in Fig. 1, OXY denotes the global coordinate, \(o_\mathrm{r}\)—\(x_\mathrm{r}y_\mathrm{r}z_\mathrm{r}\) is the rotating coordinate with rotational speed of \(\varOmega \), and \(o_\mathrm{b}\)—\(x_\mathrm{b} y_\mathrm{b} z_\mathrm{b}\) represents the local blade coordinate system.

Fig. 1
figure 1

Schematic diagram of rotor–blades system

Full size image

Figure 2 shows a blade–disk configuration. \({ ox}_\mathrm{s}y_\mathrm{s}\) is the coordinate axes attached to the disk at the geometric center. The angle indicates the position of the blade with respect to the \({ ox}_\mathrm{r}y_\mathrm{r}\). r is the whirl radius of the disk center S, \(m_\mathrm{d}\) is the disk mass located at the mass center G, and R is the disk radius.

Fig. 2
figure 2

Coordinate sets and deformation of a rotating blade

Full size image

2.1 The establishment of energy equation of rotor system

2.1.1 The establishment of the energy equation of flexible rotor model

According to the relevant knowledge of elastic mechanics, the kinetic energy of the shaft can be expressed as

$$\begin{aligned} T_{\mathrm{shaft}}= & {} \frac{1}{2}\int _0^{L_\mathrm{s} } \rho _\mathrm{s} A_\mathrm{s} \left( {\dot{x}^{2}{+}\dot{y}^{2}} \right) {+}\frac{1}{2}J_\mathrm{p} \Omega \left( {\dot{\theta }_x \theta _y -\dot{\theta }_y \theta _x } \right) \nonumber \\&+\frac{1}{2}J_\mathrm{d} \left( {\dot{\theta }_x^2 +\dot{\theta }_y^2 } \right) \hbox {d}z+\frac{1}{2}J_\mathrm{p} \Omega ^{2} \end{aligned}$$
(1)

where \(J_\mathrm{d}\) and \(J_\mathrm{p}\) are cross-sectional moment of inertia (transverse moment of inertia) and polar moment of inertia, respectively.

Regarding the disk as a mass point and ignoring the influence of the disk on the vibration mode of beam, the kinetic energy of disk can be represented in the following form:

$$\begin{aligned} T_{\mathrm{disk}}= & {} \frac{1}{2}m_\mathrm{d} \dot{x}_\mathrm{d}^2 +\frac{1}{2}m_\mathrm{d} \dot{y}_\mathrm{d}^2 +\frac{1}{2}J_\mathrm{dz} \dot{\theta }_x ^{2}+\frac{1}{2}J_\mathrm{dz} \dot{\theta }_y ^{2}\nonumber \\&+\frac{1}{2}J_\mathrm{z} \Omega (\dot{\theta }_x \theta _y -\dot{\theta }_y \theta _x )+\frac{1}{2}J_\mathrm{z} \Omega ^{2} \end{aligned}$$
(2)

where \(J_{z}\) is the polar moment of inertia of the disk; \(J_\mathrm{dz}\) is the cross-sectional moment of inertia of disk; \(m_\mathrm{d}\) is the mass of disk; \(z_\mathrm{d}\) is the distance between the position of disk and left end point of shaft.

The displacements of the disk’s mass center and centroid can be described as follows:

$$\begin{aligned} \left\{ {\begin{array}{l} x_\mathrm{d} =x_\mathrm{s} +e\cos \left( \theta \right) \\ y_\mathrm{d} =y_\mathrm{s} +e\sin \left( \theta \right) \\ \end{array}} \right. \end{aligned}$$
(2a)

where e is the eccentricity; \(x_\mathrm{d}\) and \(y_\mathrm{d}\) are the displacements of the disk’s mass center in the horizontal and vertical directions, respectively; \(x_\mathrm{s}\) and \(y_\mathrm{s}\) are the displacements of disk’s centroid in the horizontal and vertical directions, respectively(see Fig. 2); \(\theta \) is the rotational angle of disk’s mass center.

The total kinetic energy of rotor system can be obtained as following

$$\begin{aligned} T_{\mathrm{rotor}} =T_{\mathrm{shaft}} +T_{\mathrm{disk}} \end{aligned}$$
(3)

According to elasticity theory, considering the torsion, bending and shearing of shaft, the total potential energy of shaft can be given as follows:

$$\begin{aligned} U_{\mathrm{shaft}}= & {} \frac{1}{2}\int _0^{L_\mathrm{s} } {E_\mathrm{s} I_\mathrm{s} \left[ {\left( {\frac{\partial x}{\partial z}} \right) ^{2}+\left( {\frac{\partial y}{\partial z}} \right) ^{2}} \right] }\nonumber \\&+\kappa _\mathrm{s} G_\mathrm{s} A_\mathrm{s} \left[ {\left( {\frac{\partial x}{\partial z}-\theta _x } \right) ^{2}+\left( {\frac{\partial y}{\partial z}-\theta _y } \right) ^{2}} \right] \hbox {d}z\nonumber \\ \end{aligned}$$
(4)

where \(G_{\mathrm{s}}\), \(E_{\mathrm{s}}\), \(I_{\mathrm{s}}\), \(\kappa _{\mathrm{s}}\) and \(A_{\mathrm{s}}\) denote the shaft’s shear elastic modulus, Young’s modulus, cross-sectional area moment of inertia, shear coefficient and cross-sectional area, respectively.

So, the total potential energy of rotor system can be described as

$$\begin{aligned} U_{\mathrm{rotor}} =U_{\mathrm{shaft}} \end{aligned}$$
(5)

2.1.2 Discretization of the energy equation rotor system

Vibration model functions of the direction of x, y and shaft torsion are \(X_i (z)\), \(Y_i (z)\) and \(\varPhi _i\), respectively. Introducing regular coordinates \(\eta _i \left( t \right) ,\xi _i \left( t \right) \) and \(q_\theta \left( t \right) \). The assumed mode method is adopted to discretize the continuous system, i.e.,

$$\begin{aligned} \left\{ {\begin{array}{l} x(z,t)=\sum \limits _{i=1}^\infty {X_i (z)\eta _i (t)} ={{\varvec{X}}}(z){\varvec{\eta }} (t) \\ y(z,t)=\sum \limits _{i=1}^\infty {Y_i (z)\xi _i (t)} ={{\varvec{Y}}}(z) {\varvec{\xi }} (t) \\ \theta _{\mathrm{T}} (z,t)=\sum \limits _{i=1}^\infty {\Phi _i (z)q_{\theta i} (t)} ={\varvec{\varPhi }} (z){{\varvec{q}}}_{\varvec{\theta }} (t) \\ \end{array}} \right. \end{aligned}$$
(6)

Assuming that the shear force Q is constant, the bending angle can be expressed as following

$$\begin{aligned} \left\{ {\begin{array}{l} \theta _x (z,t)={x}^{\prime }+\frac{E_\mathrm{s} I_\mathrm{s} }{\kappa A_\mathrm{s} G_\mathrm{s} }{x}^{\prime \prime \prime }= {{\varvec{X}}}^{\prime }(z){\varvec{\eta }}(t)+\frac{E_\mathrm{s} I_\mathrm{s} }{\kappa A_\mathrm{s} G_\mathrm{s} }{{\varvec{X}}}^{\prime \prime \prime }(z){\varvec{\eta }}(t) \\ \theta _y (z,t)={y}^{\prime }+\frac{EI}{\kappa A_\mathrm{s} G_\mathrm{s} }{y}^{\prime \prime \prime }={{\varvec{Y}}}^{\prime }(z){\varvec{\xi }}(t)+\frac{E_\mathrm{s} I_\mathrm{s} }{\kappa A_\mathrm{s} G_\mathrm{s} }{{\varvec{Y}}}^{\prime \prime \prime }(z){\varvec{\xi }}(t) \\ \end{array}} \right. \end{aligned}$$
(7)

Substitution of Eqs. (6–7) into Eq. (3), the discrete kinetic energy of shaft is written as follows

$$\begin{aligned}&T_{\mathrm{rotor}} =T_{\mathrm{shaft}} +T_{\mathrm{disk}} \nonumber \\&\quad =\frac{1}{2}\left[ {{\begin{array}{l} {\dot{{\varvec{\eta }}}(t)} \\ {\dot{{\varvec{\xi }}}(t)} \\ {\dot{{{\varvec{q}}}}_{\varvec{\theta }} } \\ \end{array} }} \right] ^{\mathrm{T}}\left[ {{\begin{array}{lll} {{{\varvec{M}}}_{\mathrm{s}1} +{{\varvec{M}}}_{\mathrm{d}1} }&{} \mathbf{0}&{} \mathbf{0} \\ \mathbf{0}&{} {{{\varvec{M}}}_{\mathrm{s}2} +{{\varvec{M}}}_{\mathrm{d}2}}&{} \mathbf{0} \\ \mathbf{0}&{} \mathbf{0}&{} {{{\varvec{M}}}_{{\uptheta }} } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\dot{{\varvec{\eta }}}(t)} \\ {\dot{{\varvec{\xi }}}(t)} \\ {\dot{{{\varvec{q}}}}_{\varvec{\theta }} } \\ \end{array} }} \right] \nonumber \\&\quad \quad +\frac{1}{2}\left[ {{\begin{array}{l} {\dot{{\varvec{\eta }}}(t)} \\ {\dot{{\varvec{\xi }}}(t)} \\ {\dot{{{\varvec{q}}}}_{\varvec{\theta }} } \\ \end{array} }} \right] ^{\mathrm{T}}\dot{\phi }\left[ {{\begin{array}{lll} \mathbf{0}&{} {{{\varvec{G}}}_{\mathrm{s}1} +{{\varvec{G}}}_{\mathrm{d}1} }&{} \mathbf{0} \\ {{{\varvec{G}}}_{\mathrm{s}2} +{{\varvec{G}}}_{\mathrm{d}2} }&{} \mathbf{0}&{} \mathbf{0} \\ \mathbf{0}&{} \mathbf{0}&{} \mathbf{0} \\ \end{array} }} \right] \left[ {{\begin{array}{l} {{\varvec{\eta }}(t)} \\ {{\varvec{\xi }}(t)} \\ {{{\varvec{q}}}_{\varvec{\theta }} } \\ \end{array} }} \right] \end{aligned}$$
(8)

And the specific expressions of matrices are given in “Appendix 1”.

In the same way, the discrete potential energy of shaft can be obtained as follows

$$\begin{aligned} U_{\mathrm{rotor}}= & {} \frac{1}{2}\int _0^l {\left\{ {\begin{array}{l} {{\varvec{q}}}_{\varvec{\theta }}^T G_\mathrm{s} J_\mathrm{s} {\Phi }^{{'}^{T}}{\Phi }^{'}{{\varvec{q}}}_\theta +{\varvec{\eta }}^{\mathrm{T}}(t)EI{{\varvec{X}}}^{{''}^{\mathrm{T}}}(z){{\varvec{X}}}^{''}(z){\varvec{\eta }}(t)+{\varvec{\xi }}^{\mathrm{T}}(t)EI{{\varvec{Y}}}^{{''}^{\mathrm{T}}}(z){{\varvec{Y}}}^{''}(z){\varvec{\xi }}(t)\\ \qquad +{\varvec{\eta }}^{\mathrm{T}}(t)\frac{(EI)^{2}}{\kappa AG}{{\varvec{X}}}^{{'''}^{\mathrm{T}}}(z){{\varvec{X}}}^{'''}(z){\varvec{\eta }}(t)+{\varvec{\xi }}^{\mathrm{T}}(t)\frac{(EI)^{2}}{\kappa AG}{{\varvec{Y}}}^{{'''}^{\mathrm{T}}}(z){{\varvec{Y}}}^{'''}(z){\varvec{\xi }}(t) \\ \end{array}} \right\} } \hbox {d}z \nonumber \\= & {} \frac{1}{2}\left[ {{\begin{array}{l} {{\varvec{\eta }}(t)} \\ {{\varvec{\xi }}(t)} \\ {{{\varvec{q}}}_{\varvec{\theta }} } \\ \end{array} }} \right] ^{\mathrm{T}}\left[ {{\begin{array}{ccc} {{{\varvec{K}}}_{\mathrm{s}1} }&{} \mathbf{0}&{} \mathbf{0} \\ \mathbf{0}&{} {{{\varvec{K}}}_{\mathrm{s}2} }&{} \mathbf{0} \\ \mathbf{0}&{} \mathbf{0}&{} {{{\varvec{K}}}_{{\uptheta }} } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {{\varvec{\eta }}(t)} \\ {{\varvec{\xi }}(t)} \\ {{{\varvec{q}}}_{\varvec{\theta }} } \\ \end{array} }} \right] \end{aligned}$$
(9)

And the specific expressions of matrices are given in “Appendix 1”.

Substituting the kinetic energy Eq. (8) and potential energy Eq. (9) into the Lagrange equation, the generalized Lagrange equation, as follows:

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}\left( {\frac{\partial L_{\mathrm{rotor}} }{\partial \dot{{{\varvec{q}}}}}} \right) -\frac{\partial T_{\mathrm{rotor}} }{\partial {{\varvec{q}}}}=-\frac{\partial D_{\mathrm{rotor}} }{\partial \dot{{{\varvec{q}}}}}+{{\varvec{F}}}_{\mathrm{rotor}} \end{aligned}$$
(10)

where \({{\varvec{L}}}_{\mathbf{rotor}} ={{\varvec{T}}}_{\mathbf{rotor}} - {{\varvec{U}}}_{\mathbf{rotor}}\) is the Lagrange function, \({{\varvec{F}}}_{\mathbf{rotor}}\) is the generalized force consisting of the gravity, the unbalance force at the disk and the oil film forces at the bearing; \({{\varvec{q}}},\dot{{{\varvec{q}}}}\) denote the generalized coordinate and its derivative including the displacement \({\varvec{\eta }}(t),{\varvec{\xi }}(t),{{\varvec{q}}}_{\varvec{\uptheta }}\).

The discretized equations of motion in matrix notation can be given as

$$\begin{aligned} {{\varvec{M}}}_{\mathrm{r}} \ddot{{{\varvec{q}}}}_{\mathrm{r}} +\left( {{{\varvec{C}}}_{\mathrm{s}} +{{\varvec{G}}}_{\mathrm{r}} } \right) \dot{{{\varvec{q}}}}_{\mathrm{r}} +{{\varvec{K}}}_{\mathrm{r}} {{\varvec{q}}}_{\mathrm{r}} ={{\varvec{F}}}_{\mathrm{rotor}} \end{aligned}$$
(11)

where matrix \({{\varvec{M}}}_{\mathrm{r}}\), \({{\varvec{C}}}_{\mathrm{r}}\), \({{\varvec{G}}}_{\mathrm{r}}\) and \({{\varvec{K}}}_{\mathrm{r}}\) are mass, damping, gyroscopic and stiffness matrices of the rotor system, and the meaning of specific expressions is shown in “Appendix 1”.

2.2 The establishment of energy equation of rotating blade

Assume that there are \(N_{\mathrm{b}}\) blades evenly distributed on the rigid disk, so the disk–blade system is a circular symmetric structure. As shown in Fig. 2, when the deformation of ith blade is considered, the displacement of arbitrary point Q on the blade in the fixed coordinate system can be written as

$$\begin{aligned} {{\varvec{r}}}_Q =\left[ {{\begin{array}{lll} {x_\mathrm{s} }&{} {y_\mathrm{s} }&{} {z_\mathrm{s} } \\ \end{array} }} \right] ^{\mathrm{T}}+ {{\varvec{A}}}_0 {{\varvec{A}}}_1 \left[ {{\begin{array}{lll} {\left( {R+x+u} \right) }&{} v&{} w \\ \end{array} }} \right] ^{\mathrm{T}} \end{aligned}$$
(12)

where \(x_\mathrm{s}\), \(y_\mathrm{s}\) and \(z_\mathrm{s}\)are the displacements of X, Y, and Z direction of the disk in the global coordinate system. \({{\varvec{A}}}_{0}\) and \({{\varvec{A}}}_{1}\) are the transformation matrices from local coordinate system to the rotational coordinate system of the blade. The specific expression is given in the “Appendix 2”.

When \(N_{\mathrm{b}} >3\), the circular symmetric structure has good geometrical and mechanical properties. Without taking into account the axial motion of rotor, the kinetic energy of the ith blade is:

$$\begin{aligned} T_{\mathrm{blade}} =\frac{1}{2}\rho _{\mathrm{b}} A_{\mathrm{b}} \int _0^{L_{\mathrm{b}} } {\dot{{{\varvec{r}}}}_Q^2 \hbox {d}x} \end{aligned}$$
(13)

Specific expression can be written as:

$$\begin{aligned}&T_{\mathrm{blade}} =\frac{1}{2}\rho _\mathrm{b} A_\mathrm{b} \int _0^{L_\mathrm{b} } {\left\{ {\begin{array}{l} \dot{x}_\mathrm{s}^2 +\dot{y}_\mathrm{s}^2 +\dot{u}^{2}+\dot{v}^{2}+\dot{w}^{2}+\dot{\psi }^{2}\left( {R+x+u} \right) ^{2}+\dot{\psi }^{2}\left( {v\cos \beta +w\sin \beta } \right) \\ \quad -2\dot{\psi }\dot{u}\left( {v\cos \beta +w\sin \beta } \right) +2\dot{\psi }\left( {R+x+u} \right) \left( {\dot{v}\cos \beta +\dot{w}\sin \beta } \right) \\ \quad +2\dot{\vartheta }_i \left[ {\left( {R+x+u} \right) \left( {\dot{v}\cos \beta +\dot{w}\sin \beta } \right) -\dot{u}\left( {v\cos \beta +w\sin \beta } \right) } \right] \\ \quad +2\dot{\vartheta }_i \dot{\psi }\left[ {\left( {R+x+u} \right) ^{2}+\left( {v\cos \beta +w\sin \beta } \right) ^{2}} \right] \\ \quad +\dot{\vartheta }_i^2 \left[ {\left( {R+x+u} \right) ^{2}+\left( {v\cos \beta +w\sin \beta } \right) ^{2}} \right] \\ \end{array}} \right\} \hbox {d}x} \nonumber \\&\quad \hbox { cos}\vartheta _i \int _0^{L_\mathrm{b} } {\rho _\mathrm{b} A_\mathrm{b} \left\{ {\begin{array}{l} \dot{x}_\mathrm{s} \dot{u}-\dot{\psi }\psi \dot{x}_\mathrm{s} \left( {R+x+u} \right) -\psi \dot{x}_\mathrm{s} \left( {\dot{v}\cos \beta +\dot{w}\sin \beta } \right) \\ \quad -\dot{\psi }\dot{x}_\mathrm{s} \left( {v\cos \beta +w\sin \beta } \right) +\psi \dot{y}_\mathrm{s} \dot{u}+\dot{\psi }\dot{y}_\mathrm{s} \left( {R+x+u} \right) \\ \quad +\dot{y}_\mathrm{s} \left( {\dot{v}\cos \beta +\dot{w}\sin \beta } \right) -\dot{\psi }\psi \dot{y}_\mathrm{s} \left( {v\cos \beta +w\sin \beta } \right) \\ \quad -\dot{\vartheta }_i \left[ {\begin{array}{l} \psi \dot{x}_\mathrm{s} \left( {R+x+u} \right) +\dot{x}_\mathrm{s} \left( {v\cos \beta +w\sin \beta } \right) \\ \quad -\dot{y}_\mathrm{s} \left( {R+x+u} \right) +\psi \dot{y}_\mathrm{s} \left( {v\cos \beta +w\sin \beta } \right) \\ \end{array}} \right] \\ \end{array}} \right\} } \hbox {d}x \nonumber \\&\quad \sin \vartheta _i \int _0^{L_\mathrm{b} } {\rho _\mathrm{b} A_\mathrm{b} \left\{ {\begin{array}{l} -\psi \dot{x}_\mathrm{s} \dot{u}-\dot{\psi }\dot{x}_\mathrm{s} \left( {R+x+u} \right) -\dot{x}_\mathrm{s} \left( {\dot{v}\cos \beta +\dot{w}\sin \beta } \right) \\ \quad +\psi \dot{\psi }\dot{x}_\mathrm{s} \left( {v\cos \beta +w\sin \beta } \right) +\dot{y}_\mathrm{s} \dot{u}-\psi \dot{\psi }\dot{y}_\mathrm{s} \left( {R+x+u} \right) \\ \quad -\psi \dot{y}_\mathrm{s} \left( {\dot{v}\cos \beta +\dot{w}\sin \beta } \right) -\dot{\psi }\dot{y}_\mathrm{s} \left( {v\cos \beta +w\sin \beta } \right) \\ \quad -\dot{\vartheta }_i \left[ {\begin{array}{l} \dot{x}_\mathrm{s} \left( {R+x+u} \right) -\psi \dot{x}_\mathrm{s} \left( {v\cos \beta +w\sin \beta } \right) \\ \quad +\psi \dot{y}_\mathrm{s} \left( {R+x+u} \right) +\dot{y}_\mathrm{s} \left( {v\cos \beta +w\sin \beta } \right) \\ \end{array}} \right] \\ \end{array}} \right\} } \hbox {d}x \end{aligned}$$
(14)

where \(\rho _{\mathrm{b}}\), \(A_{\mathrm{b}}\) and \(L_\mathrm{b}\) are density, cross-sectional area and length of the blade, respectively; R is radius of disk; \(\vartheta _i =\Omega t+\left( {i-1} \right) {2\pi }\big /{N_{\mathrm{b}}}\); and \(\psi \) is the twist angle at disk hub.

Considering the effects of bending, circumferential compression, centrifugal and normal-force-generating potential energy of blade, total potential energy of \(i^{\mathrm{th}}\) blade can be expressed as

$$\begin{aligned} U_{\mathrm{blade}}= & {} \frac{1}{2}E_{\mathrm{b}} A_{\mathrm{b}} \int _0^{L_{\mathrm{b}} } {\left( {\frac{\partial u}{\partial x}} \right) } ^{2}\hbox {d}x\nonumber \\&+\frac{1}{2}E_{\mathrm{b}} I_{\mathrm{b}} \int _0^{L_{\mathrm{b}} } {\left( {\frac{\partial ^{2}v}{\partial x^{2}}} \right) ^{2}\hbox {d}x} \nonumber \\&+\frac{1}{4}\rho _{\mathrm{b}} A_{\mathrm{b}} \left( {\dot{\vartheta }_i +\dot{\psi }} \right) ^{2}\int _0^{L_{\mathrm{b}} } \left[ L_{\mathrm{b}}^{2} -x^{2}\right. \nonumber \\&\left. +2R\left( {L_{\mathrm{b}} -x} \right) \right] \left( {\frac{\partial v}{\partial x}} \right) ^{2}\hbox {d}x \end{aligned}$$
(15)

where \(E_{\mathrm{b}}\) and \(I_{\mathrm{b}}\) are Young’s modulus and cross-sectional area moment of inertia of blade.

As the movement of end of the rigid disk and the blade is consistent, the modal function of cantilever beam is chosen for the blade:

$$\begin{aligned} \phi _i \left( x \right)= & {} V_i \left( x \right) =\cosh \frac{\lambda _i }{l}x-\cos \frac{\lambda _i }{l}x\nonumber \\&-\frac{\cosh \lambda _i +\cos \lambda _i }{\sinh \lambda _i +\sin \lambda _i }\left( {\sinh \frac{\lambda _i }{l}x-\sin \frac{\lambda _i }{l}x} \right) \nonumber \\ \end{aligned}$$
(16)

Vibration model functions of the displacement of blade u and v are \(\phi _i \left( x \right) \) and \(V_i \left( x \right) \). The assumed mode method is adopted to discretize the continuous system, i.e.,

$$\begin{aligned} u=\sum \limits _{i=1}^n {\phi _i \left( x \right) } q_{ui} ={\varvec{\varPhi }} {{\varvec{q}}}_{{{\varvec{u}}}} ;\; v=\sum \limits _{i=1}^n {V_i \left( x \right) } q_{vi} ={{\varvec{V}}}{{\varvec{q}}}_{{{\varvec{v}}}}\nonumber \\ \end{aligned}$$
(17)

In the same way, the discretized kinetic energy and potential energy of blade are shown in “Appendix 2”.

Substituting Eq. (17) into (14) and (15), the discrete kinetic energy of ith blade is shown in the “Appendix 2”.

Fig. 3
figure 3

Schematic diagram of assembly of matrices of the rotor–blade coupling system. a Mass matrix, b gyroscopic matrix, c stiffness matrix, d damping matrix

Full size image

Substituting the discrete kinetic energy of blades into simplified Lagrange equation, the differential equation of vibration of ith blade is obtained as following

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}\left( {\frac{\partial L_{\mathrm{blade}} }{\partial \dot{{{\varvec{q}}}}}} \right) -\frac{\partial T_{\mathrm{blade}} }{\partial {{\varvec{q}}}}=-\frac{\partial D_{\mathrm{blade}} }{\partial \dot{{{\varvec{q}}}}}+{{\varvec{F}}}_{\mathrm{blade}} \end{aligned}$$
(18)

where \(L_{\mathrm{blade}} =T_{\mathrm{blade}} -U_{\mathrm{blade}}\) is the Lagrange function; \({{\varvec{F}}}_{\mathrm{blade}}\) is the generalized force of external excitation; and \({{\varvec{q}}},\dot{{{\varvec{q}}}}\) denote the generalized coordinate and its derivative including the displacement u(t), v(t).

Substituting kinetic energy and potential energy into simplified Lagrange equation, the differential equation of vibration of ith blade is obtained as following

$$\begin{aligned} {{\varvec{M}}}_{\mathrm{b}i} \ddot{{{\varvec{q}}}}+({{\varvec{C}}}_{\mathrm{b}i} +{{\varvec{G}}}_{\mathrm{b}i} )\dot{{{\varvec{q}}}}+{{\varvec{K}}}_{\mathrm{b}i} {{\varvec{q}}}={{\varvec{F}}}_{\mathrm{b}i\_{\mathrm{total}}} \end{aligned}$$
(19)

where \({{\varvec{M}}}_{bi}\), \({{\varvec{C}}}_{bi}\), \({{\varvec{G}}}_{bi}\) and \({{\varvec{K}}}_{bi}\) are mass, damping, gyroscopic and stiffness matrices of the blade. \({{\varvec{F}}}_{\mathrm{b}i\_{\mathrm{total}}}\) is the generalized force the blade suffered. \({{\varvec{q}}}\,\dot{{{\varvec{q}}}}\,\ddot{{{\varvec{q}}}}\) denote the generalized coordinate. (\({{\varvec{M}}}_{\mathrm{b}i}\), \({{\varvec{C}}}_{\mathrm{b}i}\), \({{\varvec{G}}}_{\mathrm{b}i}\), \({{\varvec{K}}}_{\mathrm{b}i}\) are shown in “Appendix 2”)

2.3 Matrices assembly of the rotor–blade coupling system

Because each blade has a corresponding mass matrix M, damping matrix C, gyroscopic matrix G and stiffness matrices K and blade–disk system is cyclic symmetric structure, the matrices of each blade and rotor system can be assembled to form the global matrix of rotor–blade coupling system. As shown in Fig. 3, the schematic of the matrix for the rotor–blade system can be expressed as following

Assembled differential equation of motion of a rotor–blade coupling system is written as

$$\begin{aligned} {{\varvec{M}}}_{\mathrm{rb}} \ddot{{{\varvec{q}}}}_{\mathrm{rb}} +{{\varvec{C}}}_{\mathrm{rb}} \dot{{{\varvec{q}}}}_{\mathrm{rb}} +{{\varvec{K}}}_{\mathrm{rb}} {{\varvec{q}}}_{\mathrm{rb}} ={{\varvec{F}}}_{\mathrm{total}} \end{aligned}$$
(20)

The details of these matrices in the formula can be found in “Appendix 3”.

The total force of the rotor–blade system can be given as

$$\begin{aligned} {{\varvec{F}}}_{\mathbf{total}} ={{\varvec{F}}}_{\mathbf{oil}} +{{\varvec{Q}}}+{{\varvec{f}}}\left( {{\varvec{t}}} \right) \end{aligned}$$
(21)

where \({{\varvec{F}}}_{\mathbf{oil}}\) is the oil film force; \({{\varvec{Q}}}\) is the gravitational force; \({{\varvec{f}}}\left( {{\varvec{t}}} \right) \) is the unbalance force on the disk.

2.4 Model of oil film forces

It is assumed that laminar and isothermal lubrication occurs in short journal bearings. According to bearing theory, the dimensionless nonlinear oil film force can be expressed as [5, 6].

$$\begin{aligned}&\left\{ {\begin{array}{l} f_x \\ f_y \\ \end{array}} \right\} =-\frac{[(x-2{y}^{\prime })^{2}+(y+2{x}^{\prime })^{2}]^{1/2}}{1-x^{2}-y^{2}}\nonumber \\&\quad \left\{ {\begin{array}{l} 3xV(x,y,\alpha )-\sin \alpha G(x,y,\alpha )-2\cos \alpha S(x,y,\alpha ) \\ 3yV(x,y,\alpha )+\cos \alpha G(x,y,\alpha )-2\sin \alpha S(x,y,\alpha ) \\ \end{array}} \right\} \nonumber \\ \end{aligned}$$
(22)

where x, y are dimensionless displacement in the respective direction.

$$\begin{aligned}&V(x,y,\alpha )=\frac{2+(y\cos \alpha -x\sin \alpha )G(x,y,\alpha )}{1-x^{2}-y^{2}},\\&S(x,y,\alpha )=\frac{x\cos \alpha +y\sin \alpha }{1-(x\cos \alpha +y\sin \alpha )^{2}},\\&G(x,y,\alpha )=\frac{2}{(1-x^{2}-y^{2})^{1/2}}\nonumber \\&\quad \left[ {\frac{\pi }{2}+\hbox {arctg}\frac{y\cos \alpha -x\sin \alpha }{(1-x^{2}-y^{2})^{1/2}}} \right] ,\\&\alpha =\hbox {arctg}\frac{y+2{x}^{\prime }}{x-2{y}^{\prime }}-\frac{{\pi }}{{2}}\hbox {sgn}\left( {\frac{y+2{x}^{\prime }}{x-2{y}^{\prime }}} \right) \\&\quad -\frac{{\pi }}{{2}}\hbox {sgn}(y+2{x}^{\prime }) \end{aligned}$$

The dimensional oil film force can be obtained from \(F_x =\sigma \hbox {P}f_x\) and \(F_y =\sigma \hbox {P}f_y\) where \(\sigma \) is the modified Sommerfeld number,

$$\begin{aligned} \sigma =\frac{\mu \omega RL}{P}\left( {\frac{R}{c}} \right) ^{2}\left( {\frac{L}{\hbox {2}R}} \right) ^{2} \end{aligned}$$

P is half weight of the rotor, \(\mu \) is the absolute viscosity of lubricant, c is the dimensional thickness of the lubrication film, R is the effective radius of oil-lubricated short journal bearing and L is the effective length of oil-lubricated short journal bearing.

2.5 The model of external excitation

The corresponding vibration mode functions in the x and y directions are \(X_i (z)\) and \(Y_i (z)\), introducing regular coordinates \(\eta _i (t)\), \(\xi _i (t)\); the assumed mode method is adopted to discretize the continuous, i.e.,

$$\begin{aligned} x(z,t)= & {} \sum \limits _{i=1}^\infty {X_i (z)\eta _i (t)} ={{\varvec{X}}}(z){\varvec{\eta }}(t) \end{aligned}$$
(23)
$$\begin{aligned} y(z,t)= & {} \sum \limits _{i=1}^\infty {Y_i (z)\xi _i (t)} ={{\varvec{Y}}}(z){\varvec{\xi }}(t) \end{aligned}$$
(24)

The oil film force of the system can be expressed as:

$$\begin{aligned} W_Y= & {} \int _0^l {[x(z,t)F_x \delta (z)+x(z,t)F_x } \delta (z-l)]\hbox {d}z\nonumber \\&+\int _0^l {[y(z,t)F_y \delta (z)+y(z,t)F_y } \delta (z-l)]\hbox {d}z\nonumber \\ \end{aligned}$$
(25)

where \(F_x\) is the oil film force in vertical direction, \(F_y\) is the oil film force in horizontal direction and \(\delta (z)\) is the Dirac function.

Substitution of Eqs. (23) and (24) to Eq. (25) yields the oil film force in a vector form

$$\begin{aligned}&W_Y =\left[ {{\begin{array}{l} {{\varvec{\eta }}(t)} \\ {{\varvec{\xi }}(t)} \\ \end{array} }} \right] ^{\mathrm{T}}\nonumber \\&\quad \left[ {{\begin{array}{l} {\int _0^l {[{{\varvec{X}}}^{\mathrm{T}}(z)F_x \delta (z)+{{\varvec{X}}}^{\mathrm{T}}(z)F_x } \delta (z-l)]\hbox {d}z} \\ {\int _0^l {[{{\varvec{Y}}}^{\mathrm{T}}(z)F_y \delta (z)+{{\varvec{Y}}}^{\mathrm{T}}(z)F_y } \delta (z-l)]\hbox {d}z} \\ \end{array} }} \right] \end{aligned}$$
(26)

Dirac function has the following property

$$\begin{aligned} \int _a^b {f(x)\delta (x-c)} \hbox {d}x=f(c),\quad a<c<b \end{aligned}$$
(27)

The oil film force vector can be converted to the following form

$$\begin{aligned} {{\varvec{F}}}=\left[ {{\begin{array}{l} {{{\varvec{X}}}^{\mathrm{T}}(\textit{0})F_{x\textit{1}} +{{\varvec{X}}}^{\mathrm{T}}(l)F_{x\textit{2}} } \\ {{{\varvec{Y}}}^{\mathrm{T}}(\textit{0})F_{y\textit{1}} +{{\varvec{Y}}}^{\mathrm{T}}(l)F_{y\textit{2}}} \\ \end{array} }} \right] \end{aligned}$$
(28)

The gravity vector can be represented as

$$\begin{aligned} W_Q= & {} \int _0^l {x(z,t)\rho A} \hbox {d}z + x({l}^{\prime },t)(m_D +N_\mathrm{b} m_\mathrm{b})g \nonumber \\= & {} \int _0^l {{\varvec{\eta }}^{\mathrm{T}}(t){{\varvec{X}}}^{\mathrm{T}}(z)\rho A} \hbox {d}z+{\varvec{\eta }}^{\mathrm{T}}(t)\nonumber \\&{{\varvec{X}}}^{\mathrm{T}}({l}^{\prime })(m_D +N_\mathrm{b} m_\mathrm{b} )g \end{aligned}$$
(29)

Transformed to a matrix form:

$$\begin{aligned}&W_Q =\left[ {{\begin{array}{ll} {{\varvec{\eta }}(t)} {{\varvec{\xi }}(t)} \\ \end{array} }} \right] \nonumber \\&\left[ \int _0^l {{{\varvec{X}}}^{\mathrm{T}}(z)\rho A} \hbox {d}z+{{\varvec{X}}}^{\mathrm{T}}({l}^{\prime })(m_D +N_\mathrm{b} m_\mathrm{b} )g\quad \mathbf{0} \right] ^{\mathrm{T}} \end{aligned}$$
(30)

The gravity vector can be written as

$$\begin{aligned} {{\varvec{Q}}}=\left[ {\int _0^l {{{\varvec{X}}}^{\mathrm{T}}(z)\rho A} \hbox {d}z+{{\varvec{X}}}^{\mathrm{T}}({l}^{\prime })(m_D +N_\mathrm{b} m_\mathrm{b} )g}\quad \mathbf{0} \right] ^{\mathrm{T}} \end{aligned}$$
Table 1 Geometric and material properties of blade–rotor system
Full size table

As the oil film force vector derived, the unbalance force vector at the disk position can be directly represented as:

$$\begin{aligned} {\varvec{f}}(t)=\left[ {{\begin{array}{l} {{{\varvec{X}}}^{\mathrm{T}}(\xi )f_x } \\ {{{\varvec{Y}}}^{\mathrm{T}}(\xi )f_y } \\ \end{array} }} \right] \end{aligned}$$
(31)

where \(f_x\) is the unbalance force in the horizontal direction under the natural coordinate system; \(f_y\) is the unbalance force in the vertical direction under the natural coordinate system.

The dynamic equation of coupling system can be written as following form

$$\begin{aligned} {{\varvec{M}}}\ddot{{{\varvec{q}}}}+({{\varvec{C}}}_f +{{\varvec{G}}})\dot{{{\varvec{q}}}}+{{\varvec{Kq}}}={{\varvec{F}}}+{{\varvec{f}}}(t)-{{\varvec{Q}}} \end{aligned}$$
(32)

where \({{\varvec{M}}}\) is the mass matrix; \({{\varvec{C}}}_f\) is the proportional matrix; \({{\varvec{G}}}\) is the gyroscopic matrix; \({{\varvec{K}}}\) is the stiffness matrix; \({{\varvec{F}}}\left( {x,y,\dot{x},\dot{y}} \right) \) is the oil film force array; \({{\varvec{Q}}}\) is the gravity array; and \(\ddot{{{\varvec{q}}}}\), \(\dot{{{\varvec{q}}}}\), \({{\varvec{q}}}\) is the acceleration vector, velocity vector and displacement vector, respectively.

3 The nonlinear dynamic characteristic of rotor with/without blades

Because of the influence of the nonlinear oil film force and gravity, the motion equation is nonlinear differential equation. This paper mainly uses the direct integral method; the equation is integrated directly by the numerical integral method in the time domain under the circumstance of keeping the equation of overall form invariable. The Newmark-\(\upbeta \) method used in this paper is implicit integration, the results of the method irrespective of the step size. Besides, when selecting suitable parameters, the algorithm is unconditionally stable. Newmark-\(\upbeta \) method is considered to be the optimal algorithm in the commonly used method of linear acceleration. And the system parameters are used in Table 1. The bifurcation diagrams, system time series, shaft orbit, Poincare maps and frequency spectrum are obtained by numerical integration.

Fig. 4
figure 4

Bifurcation diagram and three-dimensional spectrum of rotor at the left bearing in the rotor–bearing system. a Bifurcation diagram, b three-dimensional spectrum plot

Full size image

3.1 The nonlinear dynamic characteristics of rotor without blades

In order to consider the gyroscopic effect, the disk is located at a distance \(2/5L_\mathrm{s}\) from the left bearing. The blades are simplified to the centroid of disk to analyze the effect of blade vibration on the nonlinear dynamics of rotor–bearing system, and the dynamic model of rotor–bearing system is established. The bifurcation diagrams and three-dimensional spectrum plots of the disk center in the horizontal direction and bearing centers are shown in Figs. 4, 5 and 6. In the bifurcation diagrams and three-dimensional spectrums, the rotational speed varies in the range from 300 to 1200 rad/s. As the bifurcation diagrams show, the dynamic responses at the bearing centers are very similar to that of disk. Therefore, the dynamic behavior of disk will be regarded as an example in the following.

Fig. 5
figure 5

Bifurcation diagram and three-dimensional spectrum of rotor at the right bearing in the rotor–bearing system. a Bifurcation diagram, b three-dimensional spectrum plot

Full size image
Fig. 6
figure 6

Bifurcation diagram and three-dimensional spectrum of rotor at the disk center in the rotor–bearing system. a Bifurcation diagram, b three-dimensional spectrum plot

Full size image

The results show that when the rotational speed is lower than 347 rad/s, there is only the fundamental frequency in three-dimensional spectrum, which means that it is the synchronous response. When the rotational speed reaches 347 rad/s, the rotor system undergoes a period-doubling bifurcation. In the three-dimensional spectrum, in additional to the fundamental frequency, the 1/2 subharmonic frequency starts to emerge in the three-dimensional spectrum, indicating that rotor system occur 2T-periodic motion, and the response of rotor begins to emerge oil whirl. With the increase in rotational speed, rotor system enters the periodic motion. After the periodic motion, rotor response evolves to quasi-periodic motion.

In order to discuss the nonlinear dynamic behavior of rotor system, the time waveform, whirl orbit, Poincare map and spectrum plot with certain rotational speeds are obtained to study the nonlinear dynamic behavior of rotor response. The time waveform, whirl orbit, Poincare map and spectrum plot with certain rotational speeds are shown in Figs. 7, 8 and 9.

Fig. 7
figure 7

Kinetic characteristic curve under the condition of \(\omega =300\,\hbox {rad}/\hbox {s}\). a Time waveform, b whirl orbit, c Poincaré map, d spectrum plot

Full size image
Fig. 8
figure 8

Kinetic characteristic curve under the condition of \(\omega =355\,\hbox {rad}/\hbox {s}\). a Time waveform, b whirl orbit, c Poincaré map, d spectrum plot

Full size image
Fig. 9
figure 9

Kinetic characteristic curve under the condition of \(\omega =495\,\hbox {rad}/\hbox {s}\). a Time waveform, b whirl orbit, c Poincaré map, d Spectrum plot

Full size image

The dynamic behavior evolution process of rotor system is complicated in the rotational speed range \(470\,\hbox {rad}/\hbox {s}\le \varOmega \le 560\,\hbox {rad}/\hbox {s}\). In order to understand more about the evolution process of dynamic behavior, local bifurcation diagrams are shown in Fig. 10 to show the dynamic behavior evolution process of rotor system clearly. From the results, we can see that the evolution process of nonlinear dynamic behavior of rotor is as following: 5T-periodic motion—55T-periodic motion—quasi-periodic motion—23T-periodic motion—quasi-periodic motion—41T-periodic motion—17T-periodic motion—quasi-periodic motion—2T-periodic motion.

Fig. 10
figure 10

Bifurcation diagram of rotor response at the disk center. a \(470\,\hbox {rad}/\hbox {s}\le \varOmega \le 550\,\hbox {rad}/\hbox {s}\), b \(545\,\hbox {rad}/\hbox {s}\le \varOmega \le 551\,\hbox {rad}/\hbox {s}\)

Full size image

When the rotational speed increases to 507 rad/s, as shown in Fig. 11, response of rotor system is a bifurcation phenomenon, evolving to 5T-periodic motion. And Fig. 9 shows the time waveform, whirl orbit, Poincare map and spectrum plot at 535 rad/s. The Poincare map consists of five isolated points, which means that the response is 5T-periodic motion.

Fig. 11
figure 11

Kinetic characteristic curve under the condition of \(\omega =535\,\hbox {rad}/\hbox {s}\). a Time waveform, b whirl orbit c Poincaré map, d spectrum plot

Full size image
Fig. 12
figure 12

Kinetic characteristic curve under the condition of \(\omega =770\,\hbox {rad}/\hbox {s}\). a Time waveform, b whirl orbit, c Poincaré map, d spectrum plot

Full size image
Fig. 13
figure 13

Kinetic characteristic curve under the condition of \(\omega =1000\,\hbox {rad}/\hbox {s}\). a Time waveform, b whirl orbit, c Poincaré map, d spectrum plot

Full size image

It can be observed from Fig. 6 that the 2T-periodic motion appears at 551 rad/s. When rotational speed increases to \(\varOmega \ge 560\,\hbox {rad}/\hbox {s}\), the dynamic behavior of rotor evolves to quasi-periodic motion, which indicates that the oil whip occurs. And Fig. 12 shows the time waveform, whirl orbit, Poincare map and Spectrum plot at 770 rad/s. Figure 13 exhibits the time waveform, whirl orbit, Poincare map and spectrum plot at 1000 rad/s. There are a large number of points lying on a closed circle, and the oil whip frequency is the main frequency components, and the amplitude of 1\(\times \) is very small, indicating that rotor response is quasi-periodic motion.

3.2 The nonlinear dynamic characteristic of rotor with blades

In order to investigate the influence of blade on rotor–bearing system, the dynamic model of blades–rotor–bearing system is established. Figure 14 shows the bifurcation diagram and three-dimensional spectrum plot of the disk center in the horizontal direction. In the bifurcation diagram and three-dimensional spectrum, the rotational speed varies in the range 300–\(1200\,\hbox {rad}/\hbox {s}\). The nonlinear dynamic behavior of the disk in the vertical direction is discussed as an example in the following study.

Fig. 14
figure 14

Bifurcation diagram and three-dimensional spectrum of rotor at the disk in the blade–rotor–bearing coupling system. a Bifurcation diagram, b three-dimensional spectrum

Full size image
Fig. 15
figure 15

Kinetic characteristic curve under the condition of \(\omega =300\,\hbox {rad}/\hbox {s}\). a Time waveform, b whirl orbit, c Poincaré map, d spectrum plot

Full size image

As shown in Figs. 4 and 14, after simplifying the blades to the disk’s mass center, the overall trend of dynamic behavior evolution process of rotor system is fundamentally identical to that of blade–rotor–bearings coupling system. The evolution process has much difference, especially, in the sensitive interval of the rotational speed, and it becomes more complex.

The results in Fig. 14 show that when the rotational speed is lower than 349 rad/s, there is only the fundamental frequency in three-dimensional spectrum, which means that it is a synchronous response. When the rotational speed reaches 349 rad/s, the rotor system undergoes a period-doubling bifurcation. In the three-dimensional spectrum, in additional to the fundamental frequency, the 1/2 subharmonic frequency starts to emerge in the three-dimensional spectrum; this phenomenon indicates that oil whirl occurs in rotor system, namely “half frequency whirl.” The influence of nonlinear characteristic caused by oil film force begins to increase gradually.

Figure 15 shows the time waveform, whirl orbit, Poincare map and spectrum plot of rotor at the disk at 300 rad/s. The response curve of rotor system in Fig. 15a is regular. The spectrum plot shows that the frequency components are the fundamental frequency and second harmonic frequency, which means fundamental frequency vibration occurs in rotor system. The whirl orbit in Fig. 15b is a regular closed curve; no oil whirl and oil whip have occurred in the rotor system. From the Poincare map, we can see that system undergoes periodic motion.

Fig. 16
figure 16

Kinetic characteristic curve under the condition of \(\omega =355\,\hbox {rad}/\hbox {s}\). a Time waveform, b whirl orbit, c Poincaré map, d spectrum plot

Full size image

As shown in Fig. 16a, the high and low harmonic components are obvious. In the plectrum plot, in addition to the multiple frequency components, the 1/2 subharmonic frequency emerges in the spectrum plot, indicating that rotor system has entered the phase of “half frequency whirl,” and oil film whirl occurs in the rotor system. The 2 isolated points in the Poincare map confirm that the response of system is indeed 2T-periodic motion, the 1/2 subharmonic frequency plays a leading role in the response at 355 rad/s.

Fig. 17
figure 17

Kinetic characteristic curve under the condition of \(\omega =535\,\hbox {rad}/\hbox {s}\). a Time waveform, b whirl orbit, c Poincaré map, d spectrum plot

Full size image

When the rotational speed reaches 466 rad/s, there is only one point in the bifurcation diagram, which indicates that it is a synchronous response. After synchronous vibration, the response of rotor system changes from periodic motion to quasi-periodic motion, which means the system enters the oil whip motion. And in the three-dimensional spectrum plot, complex frequency components start to emerge, as a consequence of the onset of oil whip. Figure 17 shows the nonlinear dynamic behavior of quasi-period motion at rotational speed 535 rad/s. The low-frequency components exist obviously in the time waveform, and whirl orbit is not irregular; the Poincare map consists of a large number of points lying on a closed curve, and continuous spectrum emerges in the spectrum plot; all of these show that the response of rotor is typical quasi-period motion.

When rotational speed reaches 550.5 rad/s, 8T-periodic motion occurs in the rotor system. In order to discuss the dynamic behavior of the system more clearly, Fig. 18 shows the local bifurcation diagram of rotor system in the range \(549.5 \le \varOmega \le 553\,\hbox {rad}/\hbox {s}\), and Fig. 19 shows the dynamic characteristics of 8T-periodic motion at speed 551 rad/s by time waveform, whirl orbit, Poincare map and spectrum plot. The main characteristic is the isolated eight points in Poincare map.

Fig. 18
figure 18

Local bifurcation diagram of rotor system at the position of disk

Full size image
Fig. 19
figure 19

Kinetic characteristic curve under the condition of \(\omega =551\,\hbox {rad}/\hbox {s}\). a Time waveform, b whirl orbit, c Poincaré map, d spectrum plot

Full size image

After a brief 8T-periodic motion, rotor system starts to enter quasi-periodic motion again at 552.5 rad/s. The 2T-periodic motion is maintained at the rotational speed of 558 rad/s; it lasts a wide speed range. The 2 isolated points mean that rotor response is 2T-periodic motion. With the increase in rotational speed, the 2T-periodic motion of rotor system evolves to quasi-periodic motion at 897.5 rad/s. Figure 21 exhibits the time waveform, whirl orbits, Poincare map and spectrum of rotor response at rotational speed 910 rad/s. The numerical results show that there is low-frequency component in whirl orbit, and large number of points lies on a smooth closed curve in the Poincare map; this indicates that the response of rotor has evolved to quasi-period motion (Fig. 20).

Fig. 20
figure 20

Kinetic characteristic curve under the condition of \(\omega =770\,\hbox {rad}/\hbox {s}\). a Time waveform, b whirl orbit, c Poincaré map, d spectrum plot

Full size image
Fig. 21
figure 21

Kinetic characteristic curve under the condition of \(\omega =910\,\hbox {rad}/\hbox {s}\). a Time waveform, b whirl orbit, c Poincaré map, d spectrum plot

Full size image

Comparing the nonlinear dynamic behavior of blade–rotor–bearing system with the behavior of rotor–bearing system, we can find that:

  1. (1)

    The overall trend of dynamic behavior evolution process of rotor system is not influenced by the blades.

  2. (2)

    In the sensitive range of rotational speed, blade vibration has severe effect on the dynamic behavior evolution process of rotor, which can be proved by Wang [22]. After considering blade vibration, the evolution process of rotor response changes from 5T-periodic motion to 8T-periodic motion. The rotational speed range of periodic motion decreases considerably, and the corresponding speed range of quasi-periodic motion increases significantly. Besides, due to the influence of the blade vibration, the quick and complex process of dynamic behavior evolution disappears completely, and rotor response evolves to quasi-periodic motion from 8T-periodic motion. So the effect of blade vibration on the nonlinear characteristics of rotor system should be considered.

  3. (3)

    Before entering the sensitive rotational speed range, the influence of blade vibration on the dynamic behavior evolution process of rotor system is not obvious. This is mainly because the vibration of blade is weak when the rotational speed is low, so the nonlinear dynamic behavior evolution of rotor system can be influenced slightly by the blade vibration. After going through the sensitive interval of rotational speed, although the blade vibration is strong, the dynamic characteristics of rotor system are mainly affected by the centrifugal force and nonlinear oil film force. Compared with the centrifugal force and nonlinear oil film force, the influence of the blade vibration on the nonlinear behavior evolution of rotor system is relatively weak. So it is difficult to reflect the influence of the blade vibration on the nonlinear behavior evolution process of rotor system.

  4. (4)

    Although the blade has no effect on the process of the dynamic behavior evolution process under high rotational speed, the influence of blade on the threshold speed of behavior evolution is significant. When the blade vibration is considered, the threshold speed that rotor response evolves from 2T-periodic motion to quasi-periodic motion is 897.5 rad/s. However, when the blades are simplified to the center of mass of disk, the threshold speed is 971 rad/s. As the results show, blade vibration accelerates the emergence of quasi-periodic motion.

Fig. 22
figure 22

Blade’s bifurcation diagram and three-dimensional spectrum in the blades–rotor–bearing coupling system. a Bifurcation diagram, b three-dimensional spectrum

Full size image

4 The nonlinear dynamic characteristic of blades in the blade–rotor–bearing coupling system

4.1 The nonlinear response of blades in the coupling system

The bifurcation diagram of blade in the blade–rotor–bearing coupling system under the oil film force is shown in Fig. 22. As shown in bifurcation diagram, the nonlinear dynamic phenomenon is demonstrated in blade response, such as the 2T-periodic motion, multi-periodic motion and quasi-periodic motion. When the speed is lower than 349 rad/s, blade response is a stable periodic motion, and there is only one point in bifurcation diagram. In the dimensional spectrum, the blade is mainly characterized with fundamental frequency. At this time, the stable periodic motion is presented under the action of the unbalance force of the blade. When the speed increases to 349 rad/s, the response is a period-doubling bifurcation, and the 1/2 subharmonic frequency starts to emerge in the three-dimensional spectrum plot, which indicates the oil whirl occurs. And the system starts to lose stability, indicating that the effect of nonlinear oil film force on blade begins to increase gradually. When the speed increases to 466 rad/s, the response re-enters the periodic motion. When the rotational speed reaches 494 rad/s, blades response enters the phase of oil whip after a brief periodic motion, the dynamic behavior of the blade evolves to quasi-periodic motion and the oil whip frequency emerges in the three-dimensional spectrum. When the speed reaches 550.5 rad/s, the blades response is a brief 8T-periodic motion. And the blades re-enter the quasi-periodic motion. The blades evolve to 2T-periodic motion at the speed 558 rad/s. And the quasi-periodic motion that appears in the blade response at the speed 897.5 rad/s is shown in Fig. 22a. From the global bifurcation diagram, we can find that the nonlinear behavior process of blade is as following: Periodic motion—2T-periodic motion—Periodic motion—Quasi-periodic motion—8T-periodic motion—Quasi-periodic motion—2T-periodic motion—Quasi-periodic motion.

In order to discuss the nonlinear dynamic characteristic of blade, the time waveform, phase diagram and spectrum plot of blade with certain rotational speed are shown in Figs. 23, 24, 25, 26, 27 and 28. And the time waveform, phase diagram and spectrum plot at speed 300 rad/s are shown in Fig. 23. The steady response curve of blade is cosine curve; phase is a closed ellipse; and 1\(\times \) frequency is the main frequency component in the spectrum plot. Therefore, the steady response of the blade exhibits stable periodic motion at this speed.

Fig. 23
figure 23

Blade’s kinetic characteristic curve under the condition of \(\omega =300\,\hbox {rad}/\hbox {s}\). a Time waveform, b phase diagram, c spectrum plot

Full size image

Figure 24 shows the time waveform, phase diagram and spectrum plot of blade response at 400 rad/s. The numerical results show that the steady response of the blade consists of six discrete frequency components; the amplitude of these frequency components is invariable. It can be found that the spectrum plot mainly contains four frequency components, such as the first-order frequency of oil whip, 1/2\(\times \) frequency, 3/2\(\times \) frequency, and 2\(\times \) frequency, and the amplitude of 1\(\times \) frequency is relatively large. Besides, the phase diagram of the blade is two overlapping circles; this is due to the emergence of the oil film whirl, but severe oil film whip has not yet occurred. All these mean that the response of blade is 2T-periodic motion.

Fig. 24
figure 24

Blade’s kinetic characteristic curve under the condition of \(\omega =355\,\hbox {rad}/\hbox {s}\). a Time waveform, b phase diagram, c spectrum plot

Full size image

It can be observed from Figs. 25 and 26 that the periodic motion of the blade response has evolved to the quasi-periodic motion at 494 rad/s and then 8T-periodic motion at 550.4 rad/s. In Fig. 25, there is complex elliptic in the phase diagram, and continuous spectrum appears in the spectrum plot; these indicate that the oil whip occurs and the response of blade is the quasi-periodic motion. In Fig. 26b, there are eight circles, which means that the response of blade has evolved to quasi-periodic motion.

Fig. 25
figure 25

Blade’s kinetic characteristic curve under the condition of \(\omega =510\,\hbox {rad}/\hbox {s}\). a Time waveform, b phase diagram, c spectrum plot

Full size image
Fig. 26
figure 26

Blade’s kinetic characteristic curve under the condition of \(\omega =551\,\hbox {rad}/\hbox {s}\). a Time waveform, b phase diagram, c spectrum plot

Full size image

After a brief 8T-periodic motion, the dynamic behavior of blade is a quasi-periodic motion, and then, the 2T-periodic motion appears at 558 rad/s. Figure 27 shows the steady motion characteristics of blade at 770 rad/s. In the time waveform, there is obvious low-frequency component. The oil whip frequency and 1x frequency with large amplitude appear in the spectrum plot. All these mean that blade response has evolved from quasi-periodic motion to 2T-periodic motion. With the increase in rotational speed, the quasi-periodic motion appears at 897.5 rad/s. Figure 28 exhibits the time waveform, phase diagram and spectrum plot of blade response at 910 rad/s, indicating that blade is undergoing quasi-periodic motion.

Fig. 27
figure 27

Blade’s kinetic characteristic curve under the condition of \(\omega =770\,\hbox {rad}/\hbox {s}\). a Time waveform, b phase diagram, c spectrum plot

Full size image
Fig. 28
figure 28

Blade’s kinetic characteristic curve under the condition of \(\omega =910\,\hbox {rad}/\hbox {s}\). a Time waveform, b phase diagram, c spectrum plot

Full size image

4.2 The influence of the different blade damping

It can be found that the effect of blade on rotor system is significant. Therefore, it is very necessary to study the influence of blade parameters on the nonlinear characteristics of rotor system. The damping is a very important parameter of blade, so this section will mainly study the influence of blade damping on the dynamic behavior of rotor system, and the other parameters are taken from Table 1.

Bifurcation diagrams of rotor system under the influence of blade vibration with different damping coefficients are shown in Fig. 29. According to the theory of vibration, when the damping coefficient is very small, blade vibration will be very close to the state of non-damping vibration. Thus, from Fig. 29a, we can find that the evolution process of rotor system has changed greatly at this time. And with the increase in blade damping, the behavior of rotor system is basically stable, and the effect of blade damping is mainly reflected in the speed threshold of behavior evolution.

Fig. 29
figure 29

Bifurcation diagram of rotor system for various damping of blades. a C = 0.75, b C = 2.5, c C = 75, d C = 300

Full size image

The speed thresholds of the dynamic behavior of rotor system under different damping coefficients are given in Table 2. The results show that blade damping coefficient has no influence on the threshold of the rotor response from the fundamental frequency vibration to oil whirl. It can be seen that when rotor system is under periodic motion, the damping coefficient of blade has little influence on nonlinear behavior of rotor system. With the increase of rotational speed, the effect of blade damping coefficient on rotor system behavior begins to increase. Besides, the increase in damping coefficient causes a brief 8T-periodic motion, thereby reducing the speed range of quasi-periodic motion. However, when damping coefficient increases to a certain extent, 8T-periodic motion is disappear. It can be seen that appropriate damping coefficient can shorten the speed range of quasi-periodic motion. What’s more, the increase in damping coefficient decreases the speed threshold of rotor system from 2T-periodic motion to quasi-periodic motion, which makes rotor response enter quasi-periodic motion earlier.

Table 2 Speed threshold of behavior evolution of rotor system under different damping coefficient
Full size table

Thus it can be seen that, when blade damping coefficient is very small, blade damping has a significant impact on the evolution process of dynamic behavior of rotor system. But when damping coefficient increases to a certain extent, the influence of blade damping begins to weaken, evolution process of dynamic behavior is maintained in a stable state and the influence of blade damping coefficients is mainly manifested in the speed threshold of behavior evolution; the appropriate damping coefficient of blade can make period-double motion appear in the rotor system, which can restrain the range interval of oil film instability; however, when rotational speed is high, the larger damping coefficient makes the rotor system enter quasi-periodic motion earlier. Therefore, it is necessary to make an optimal analysis of damping coefficient in order to ensure the stable operation of the system.

4.3 The influence of the different length of blade

Blade length has a great influence on the inherent characteristics of the blade, so the research on the influence of blade length on the dynamic behavior of rotor is very significant for engineering, and this section will mainly study the influence of the blade length on rotor system. Figure 30 shows the bifurcation diagrams of rotor system under different blade length.

Fig. 30
figure 30

Bifurcation diagram of rotor system for various length of blades. a \(L=0.1\hbox { m}\), b \(L=0.2\hbox { m}\), c \(L=0.25\hbox { m}\), d \(L=0.3\hbox { m}\)

Full size image

The results of bifurcation diagrams show that the length of blade has little influence on the overall trend of evolution process of nonlinear dynamic behavior. When rotational speed is low, blade length has little effect on the speed threshold and evolution process. With the increase in rotational speed, the influence of blade length on the nonlinear dynamic behavior of rotor system began to enhance. The influence is mainly manifested in speed threshold of nonlinear behavior evolution. And with the increase in blade length, the response of rotor evolves from 5T-periodic motion to 8T-periodic motion, and the speed range increases with the blade length. This is due to the increase in blade length, the blade vibration is constantly enhanced. In the high speed range, the increase in the blade length makes the rotating speed range of 2T-periodic motion significantly shorter, and the corresponding threshold of quasi-periodic motion is continuously reduced, which means that longer blade makes rotor system evolve into quasi-periodic motion earlier.

5 Conclusion

A blade–rotor coupling system is addressed to investigate the nonlinear dynamic behavior supported by oil film journal bearings. Considering the nonlinear oil film force, the mathematical model of coupling system is studied by dynamic method.

The numerical results show that the coupling system exhibited rich nonlinear phenomenon, such as the period-doubling bifurcation, the multi-period and quasi-period motions. The dynamics of the blade exhibited nonlinearity which is uniform with the rotor.

Besides, the comparison of the dynamic behavior of the blade–rotor–bearing model with that of the rotor–bearing model reveals that overall trend of the dynamic evolution process of rotor system is not under the influence of blade. However, in the sensitive range of the rotational speed, the effect of blades vibration on nonlinear dynamic behavior evolution of rotor is extremely obvious. What’s more, the influence of blade on the threshold of behavior evolution is significant, and blade vibration reduces the rotational speed threshold of quasi-periodic motion.

At last, the influence of blade damping coefficient and the length of blade is mainly manifested in the speed threshold of behavior evolution; and the damping coefficient and length of blade can make rotor system enter quasi-periodic motion earlier.