Magnetostriction effect in soft magnetic elastomers

Abstract

We discuss the magnetostriction effect in soft magnetic elastomers: stretching/shrinking of a sample under the action of uniform magnetic field in the absence of mechanical loads. Qualitative analysis shows that the field has a twofold effect on the medium; one of those mechanisms works at the macroscopic scale whereas the other one stems from the mesoscopic processes. Essentially, the latter one is defined by the “architecture” of short-range spatial order existing in the ferromagnet particle assembly. This conclusion is illustrated with the aid of numerical modeling. First, it is done on a 2D elastic array filled with linearly magnetizable particles. It is shown that it is indeed the presence of clusters that controls both the sign and magnitude of magnetostriction in the composite. In other words, two composites with the same matrix/filler content may behave very differently depending on their mesoscale structure. Further on, to get a more realistic description, the modeling is extended to a 3D array of spherical particles randomly distributed in an elastic matrix. Although the general conclusions hold, the quantitative results differ substantially.

1 The origin of magnetostriction in magnetic elastomers

Functional materials obtained by embedding finely dispersed ferromagnets in polymers are well known. Employing various ferromagnets (magnetically soft or highly coercive) and using rubbers (elasticity modulus $G\sim$10–100 MPa) as binding agents, one may produce the cores for induction coils or electromagnetic radiation absorbing shields [1, 2, 7, 22] as well as permanent magnets [23, 26] which sustain much higher extents of deformation without destruction than their metal or ceramic prototypes [23, 26].

The systems where the ferromagnet microparticles are admixed to a very soft ($G\sim$1–100 kPa) polymer under the particle content just two-three times lower than the maximal packing density, have attracted scientific and applicational interest much later [17, 18, 24, 35]. Now those composites make a special family of smart materials termed magnetorheological polymers or soft magnetic elastomers (SMEs). The well-known examples of the matrices for SMEs are dense polymer gels (gelatine and polyvinyl alcohol) [21, 24, 35] or weakly linked caoutchoucs (plasticized silicone rubbers) [8,9,10, 27, 33]. As the fillers, micro- or nanopowders of iron or ferrites (e.g., magnetite or maghemite) are used. The main distinction between SMEs and conventional magnetic rubbers is the scale of their deformational response to an applied magnetic field. This could be easily proven with the aid of a few simple estimates. Let the magnetic field that is in our disposal be $H\sim 1$ kOe; or—in a nonuniform case—the jump of the same field $\nabla H\sim H/l$ at a distance $l\sim 1$ cm. We note that both conditions are easily available at a laboratory. We assume that the magnetization of a SME under those fields is $M\sim 10^2$ G, in reality it might be two-three times greater. The strain $\varDelta l/l\equiv \varepsilon$—conventionally termed the magnetostriction effect [10]—that is induced in a SME by a uniform field results from the balance between the magnetic and elastic contributions to the energy density of the sample that is by the order of magnitude $M^2 \varepsilon \sim G \varepsilon ^2$. Taking the shear modulus of a SME as $G \sim 10$ kPa, one finds $\varepsilon \sim 10$%. For a magnetic rubber the same deformation would be $10^3$–$10^4$ times lower and yet less for any solid ferromagnet. In a nonuniform field, the SME deforms under the action of volumic magnetic forces. Setting their work spent on a displacement of a small element by distance $\varDelta l$ equal to the increment of elastic energy induced by that displacement, one finds $\varepsilon \sim MH/G_m$; substitution of the above-mentioned numerical values yields $\varepsilon \sim 100$%. Thus, one sees that even a moderate field is able to produce macroscopically notable shape changes in SMEs.

Fig. 1

To the discussion of the origin of magnetostriction effect in SMEs: a continual viewpoint (black arrows show the surface pressure distribution); b mesoscopic viewpoint (color arrows show the particle magnetic moments) (Color online)

The presented estimates are based on the viewpoint that a SME is an isotropic medium (continuum), where each element possesses the same unchangeable ability to magnetize. The first and most known example of using such a model is the problem of field-induced deformation of a SME sphere [11, 28,29,30,31]. Such a theory enables one to easily point out the sign of the effect, see Fig. 1a. As the internal magnetic field is uniform, the magnetization $\mathbf {M}$ of the SME is uniform as well, and is directed along the applied field $\mathbf {H}_0$. In this case, the only result of magnetizing is the occurrence of surface tension proportional to $M_n^2$, i.e., squared projection of the magnetization on the local normal. Apparently, this quantity is maximal at the “poles” that is in the points where vector $\mathbf {H}_0$ that passes through the center of the sphere, crosses its surface. This entails unambiguous conclusion that, under magnetizing, a SME sphere must stretch along the direction of the field.

Let us consider the same problem taking into account the internal structure of the composite material. This is quite a justified approach as any SME is a heterogeneous system. Figure 1b schematically shows the internal arrangement of the particles inside the same sphere as in Fig. 1a. It looks like a “watermelon with seeds”: inside a rather soft matrix a large number of small solid magnetizable particles is distributed. If the metal or ferrite has low coercivity, as, for example, carbonyl iron or magnetite do, the micron size of the particles ensures that they are multi-domain. This makes them magnetically soft that means that they have zero magnetization in zero field. It is worth noting that magnetic softness has nothing to do with the mechanical one: the Young’s modulus of the particles are many orders of magnitude greater than that of the matrix. Under the fields of moderate strength, the magnetization of such particles varies linearly as $\mathbf {M}=\chi \mathbf {H}$, where coefficient $\chi$ is called magnetic susceptibility; for simplicity, we assume here that $\chi$ is isotropic. Note that some magnetic susceptibility $\chi _m$ is inherent to the polymer matrix of the SME as well. However, the difference between $\chi$ and $\chi _m$ is at least five orders of magnitude that enables one to completely neglect the magnetic response of the matrix under moderate $\sim 1$ kOe fields.

Therefore, the magnetic field exerted on a SME sample, producing no effect on the matrix, magnetizes the particles, i.e., imparts to each of them a magnetic moment $\mathbf {m}$ in the direction of $\mathbf {H}$ (for simplicity we neglect here the inter-particles fields). In result, each of the particles becomes a source of its own nonuniform magnetic field and comes into ponderomotive interaction with all the other ones. If to assume that magnetization is uniform inside the particles, then the interparticle pair potential could be taken in the dipole approximation:

$$\begin{aligned} U_{ij}^{(dd)} = \frac{\mathbf {m}_i\!\cdot \! \mathbf {m}_j}{r_{ij}^5} - \frac{ 3(\mathbf {m}_i\!\cdot \!\mathbf {r}_{ij})(\mathbf {m}_j\!\cdot \!\mathbf {r}_{ij})}{r_{ij}^5}. \end{aligned}$$

(1)

where $\mathbf {r}_{ij}$ is center-to-center vector between i-th and j-th particles.

The anisotropy of this potential is well known. In particular, each particle in Fig. 1b is attracted to its nearest neighbors along the direction of the field (“head-to-tail” configuration) and is repelled by its neighbors in the plane transverse to $\mathbf {H}$ (“side-by-side” configuration). Given that adhesion of the particles to the matrix is sufficiently strong, those interparticle forces are transferred to the matrix and, as their actions add, make the sphere to shrink along the direction of the field.

The occurring antagonism of the predictions does not mean, however, that one of the interpretations—continual or discrete—is completely wrong. However, this contradiction definitely points out oversimplifications in considering the problem. As it is shown below, a correct approach should take into account the twofold nature of magnetizing effect on SMEs. Meanwhile, each of Fig. 1a and b is made to intentionally emphasize just one of the aspects.

The source of the first mechanism of deformation is the macroscopic magnetization $\mathbf {M}$ that induces inside and outside of the sample the field $\mathbf {H}_d$, which inside the body is called the demagnetizing field. The interaction between $\mathbf {M}$ and $\mathbf {H}_d$ defines the part of magnetostatic energy that depends on the shape of the sample. The tendency of this contribution to acquire minimum makes the body to elongate along the direction of the field¹. For small strains, the spherical problem has exact analytical solution [29, 30] whereas the case of finite field-induced strains requires numerical calculations [31].

As it follows from the afore-presented considerations, the discussed mechanism of striction emerges only in the samples whose size along the field direction is finite, i.e., they have borders which are not parallel to the applied field. With allowance for that, the considered mechanism of deformation might be termed shape magnetostriction. Since the field $\mathbf {H}_d$ acts at the macroscopic scale and but weakly depends on the details of spatial distributions of the particles in the matrix, the shape striction could be quite accurately described with the continuum model. A direct theoretical proof for that is given in [15] where the authors, starting from the sample composed of a finite number of discrete magnetic elements, have performed transition to the continual limit by unbounded diminution of the element size under simultaneous enhancement of their number to infinity.

In this connection, we remind that in solid ferromagnets and ferrites (either crystalline or amorphous) the strains caused by the shape striction are very small. Therefore, the large magnitude of shape magnetostriction in SMEs is a specific essential property of these soft magnetic materials.

The other mechanism of magnetically induced deformation—we term it structure striction—is due, as mentioned, to the particle interaction at the mesoscopic scale $\sim \left( N/V\right) ^{-1/3}$, where N is the number of particles in the sample and V its volume. This contribution to the magnetostatic energy is virtually independent of the sample shape and does not tend to zero in an infinite body. On the other hand, because of the anisotropy of dipolar interaction (1), this energy strongly depends on the short-range spatial order in the particle assembly, i.e., on the character of the magnetic phase density distribution. This implies that, contrary to the shape effect that is always positive (inducing elongation) in compact bodies, the structure magnetostriction may have any sign and vary substantially in its magnitude. In this context, one should consider Fig. 1b (a regular lattice of particles) where the structure striction is negative, just as an illustrative example.

The important role of interparticle interactions is discussed in a number of papers [3, 5, 16, 19, 25]. However, in the modern literature on ferrogels and SMEs the shape and structure contributions to the magnetostriction effect are not distinguished clearly. Indeed, even in fundamental experimental [10, 34, 35] and theoretical [4, 6] works on SMEs, any field-induced shape changes are termed and treated as a single magnetostriction effect. This is not a surprise though, since in any experiment it is quite feasible to measure the macroscopic magnetization and strain of a sample, but it is a sophisticated problem to “pre-program” the spatial distribution of the particles before polymerization and to make a detailed morphological analysis of the material in the course and after measurement.

2 Modeling of the magnetostriction effects

We consider the magnetostriction problem with the aid of numerical experiment where a SME sample is presented as a dispersion of particles of a magnetically soft ferromagnet in an isotropically elastic matrix. The number concentration of the particles—they are assumed to be identical spheres—is taken to be 20–30 vol.%, as that in the real materials which are most attractive for practical applications. Due to limited computer resources, the amount of particles cannot be taken too large, and we set this number about 100. Although such modeling might be insufficient for quantitative accuracy, it is instructive in the fundamental qualitative aspect.

The principal questions to be answered are: (i) to what extent would the sample change its shape in response to magnetizing, and (ii) what would be the orientation of the main axes of the emerging stretching/shrinking with respect to the direction of the applied field. As it has been inferred, the most relevant part belongs to the short-range details of the internal structure. In other words, we look for the causes due to which two samples identical in their initial shape and overall magnetic phase content would display different field-induced responses.

Fundamentally, this is due to the anisotropy of magnetodipole interaction. As formula (1) shows, the force that couples a pair of magnetic dipoles (induced by and co-aligned with the field $\mathbf {H}_0$) changes from attraction to repulsion under rotation of their center-to-center vector $\mathbf {r}$ from orientation $\mathbf {r}\parallel \mathbf {H}_0$ to $\mathbf {r}\perp \mathbf {H}_0$. As this force goes down with the distance rather fast, the nearest particle neighborhood is what that mostly matters. Depending on their arrangement, the particles would either group in chains or move away from one another. Each particle in its displacement entrains the region of the matrix attached to it, and in SMEs with a high filling fraction a simultaneous number of such moves is large. Evidently, if in a composite some prevailing type of the short-range arrangement has been formed, the occurring mesoscopic changes should manifest themselves in the overall behavior of the sample.

As mentioned, the shape effect in the magnetodeformational response registered in experiment is of purely macroscopic origin. Therefore, the sample shape and overall magnetic phase content practically determine its shape magnetostriction. The structure effect stems from mesoscopy, and to detect it one needs to vary the short-range order without changing the magnetic phase fraction.

A hypothetical direct way to prepare such test samples is high-resolution 3D printing of metal-polymer composites; unfortunately, such manufacturing procedure is unavailable whatsoever. The case of SMEs, however, is an example of a situation where the absence of precisely made samples is not a fatal obstacle for progressing. An advantageous circumstance is that the reference ranges of the SME material parameters fall within the scope where a numerical experiment has good chances for providing reliable results. To justify this inference, we remark the following. The range of spatial scales that is mesoscopic for SMEs (1–10 $\mu$m) is at the same time indubitably macroscopic with respect to the atomic scale (1–10 nm). The occurring three orders of magnitude difference implies that, first, the particles may be treated as massive ferromagnets and, thus, may be described with the aid of well-developed phenomenology. Second, at the same mesoscopic scale the SME matrix may be for granted considered as a continuum with high-elasticity properties and, thus, described in terms of conventional theoretical mechanics of elastomers.

This enables one to treat a SME as a two-phase material under condition of full adhesion of the particles to the matrix. The moduli of the phases differ by several orders of magnitude; in the presence of a magnetic field the solid phase behaves as a typical magnetically soft multi-domain ferromagnet. Given that, the problem of mesomechanics of a SME is in a clear way reformulated in terms of a coupled magnetoelastic problem quite suitable for computer simulation. Evidently, the transition from mesoscopic to real macroscopic scale would require averaging of the results over a large number of realizations of the SME sample.

3 Solution of a 2D problem

The model sample is a plane square, see Fig. 2, of isotropically elastic material containing 160 identical magnetically soft particles glued to the matrix; the particle radius a is 1/50 of the side of the square. A uniform field $\mathbf {H}_0$ is exerted along axis Oy; the particle magnetization grows linearly with the field. The magnetic (ponderomotive) force on a given particle is calculated as a sum of pairwise interactions with all the other particles of the assembly under assumption that their magnetic moments are point dipoles located in their centers; the occurring strains are assumed to be small.

As there are no reliable data on the morphology of real SMEs, the initial spatial distribution of the particles is taken to be random. An example of the initial configuration is shown in Fig. 2. The statistical averaging is done over 30 computer realizations of the initial state.

Fig. 2

An example of random distribution of 160 particles in a square sample, the particle radius is $a=0.02$; at two adjacent sides of the square ($x=1$ and $y=0$), normal displacements are forbidden, see conditions (5). Color shows the result of cluster analysis: empty circles are solitary (isolated) particles, colored are the particles united in clusters (Color online)

3.1 Elastic problem

As the particle–matrix interfaces in our model are unbreakable (no delamination), the SME sample is treated as a continuum with piecewise-constant properties, elastic and magnetic. Namely, we consider a limited in two directions polymer sample with N circular holes. Each hole has diameter 2a and is fully filled with a solid magnetic material (particle) and, thus, is practically undeformable; the polymer phase obeys the Hook law. Then the equation of the sample equilibrium and pertinent incompressibility condition is

$$\begin{aligned} \nabla \!\cdot \!{{\mathsf {S}}}+\mathbf {f}_\mathrm{{mag}}=0, \quad \mathrm{Tr}({\mathsf {E}})=0; \end{aligned}$$

(2)

here ${\mathsf {S}}$ is the Cauchy stress tensor, $\mathrm{Tr}({\mathsf {E}})$ the first invariant of small-strain tensor ${\mathsf {E}}$, and $\mathbf {f}_\mathrm{{mag}}$ the density of magnetic forces.

The Hook law for an incompressible medium has the form

$$\begin{aligned} {\mathsf {S}}=-p{\mathsf {g}}+2G(\mathbf {r})\,{\mathsf {E}}, \end{aligned}$$

(3)

where p is hydrostatic pressure, ${\mathsf {g}}$ unit tensor, and $G(\mathbf {r})$ shear modulus. As mentioned in above, G here is a coordinate-dependent piecewise-constant function; for the polymer matrix it is denoted as $G_m$, for the particle substance we take $G_p\sim 10^5G_m$ to virtually eliminate deformation of the particles. Introducing indicator function $I_i(\mathbf {r})$ that equals unity if radius-vector $\mathbf {r}$ ends in i-th particle and is zero otherwise, one gets for the modulus a coordinate-dependent representation

$$\begin{aligned} G(\mathbf {r})=\sum \limits _i \left\{ G_p I_i(\mathbf {r})+G_m\left[ 1-I_i(\mathbf {r})\right] \right\} . \end{aligned}$$

(4)

For the strain tensor, a standard kinematic relation is adopted:

$$\begin{aligned} {\mathsf {E}} = {\scriptstyle \frac{1}{2}}\left( \nabla \mathbf {u}+\nabla \mathbf {u}^\mathrm{T}\right) , \end{aligned}$$

(5)

that expresses it via gradients of the displacement vector $\mathbf {u}$; index T denotes matrix transposition. At two adjacent sides of the square ($x=1$ and $y=0$), an unbreakable contact of the SME with the boundary is imposed:

$$\begin{aligned} \left. u_x \right| _{x=1}=0, \quad \left. u_y \right| _{y=0} = 0; \end{aligned}$$

(6)

it prevents delamination but does not impede sliding of the sample along those boundaries. Two other sides of the sample allow for free displacements in xOy plane:

$$\begin{aligned} \left. \mathbf {n}\!\cdot \!{\mathsf {S}}\right| _{x=0}=0, \quad \left. \mathbf {n}\!\cdot \!{\mathsf {S}}\right| _{y=1}=0, \end{aligned}$$

(7)

here $\mathbf {n}$ is the vector of outer normal.

3.2 Magnetic forces

In small-strain approximation, the elastic and magnetic parts of the problem split. First, assuming that the field-induced magnetic moments of the particles may be treated as point-like ones, we evaluate the interparticle pair magnetodipole forces in the initial configuration. This is done in the following way.

As the particles are assumed to be spherical and there is no mutual magnetization, each particle has the same field-induced magnetic moment:

$$\begin{aligned} \mathbf {m}_i=\frac{3v\mathbf {H}_0}{3\chi ^{-1}+4\pi }; \end{aligned}$$

(8)

where v is the particle volume and $\chi$ volumic magnetic susceptibility of the particle substance. For strongly magnetizable materials (e.g., iron with $\chi \gtrsim 10^3$) formula (8) reduces to a well-known limiting expression $\mathbf {m}=3v\mathbf {H}_0/4\pi$ that for a spherical particle yields $\mathbf {m}=a^3\mathbf {H}_0$.

The force exerted on i-th particle is evaluated as the gradient of its dipolar energy:

$$\begin{aligned} \mathbf {F}_i= & {} - \sum \limits _{j=1\atop j\ne i}^N \nabla U^{(dd)}_{ij}=\mathbf {m}_{i}\!\cdot \!\sum \limits _{j=1\atop j\ne i}^N \nabla \left[ -\frac{\mathbf {m}_{j}}{r_{ij}^3}+\frac{3\left( \mathbf {m}_{j}\!\cdot \!\mathbf {r}_{ij}\right) \mathbf {r}_{ij}}{r_{ij}^5}\right] \\= & {} \sum \limits _{j=1\atop j\ne i}^N\left\{ \frac{3}{r_{ij}^5}\left[ \left( \mathbf {m}_{i}\!\cdot \!\mathbf {m}_{j}\right) \mathbf {r}_{ij}+\left( \mathbf {m}_{i}\!\cdot \!\mathbf {r}_{ij}\right) \mathbf {m}_{j} + \left( \mathbf {m}_{j}\!\cdot \!\mathbf {r}_{ij}\right) \mathbf {m}_{i}\right] \right. \\&\left. -\frac{15}{r_{ij}^7}\left( \mathbf {m}_{i}\!\cdot \!\mathbf {r}_{ij}\right) \left( \mathbf {m}_{i}\!\cdot \!\mathbf {r}_{ij}\right) \mathbf {r}_{ij}\right\} \end{aligned}$$

and is uniformly “smeared” over the volume of the particle that is very convenient for numerical calculations. Therefore, the force distribution in the sample is shaped up as a piecewise-constant function

$$\begin{aligned} \mathbf {f}_\mathrm{{mag}}=(\pi a^2)^{-1}\sum \limits _i\mathbf {F}_i I_i(\mathbf {r}). \end{aligned}$$

(9)

3.3 Magnetostriction deformation

After evaluation of magnetic forces, the elastic theory equations are solved by finite-element method with the aid of programme package FreeFEM$^{++}$ [14]. For that, general variational problem is written in the form

$$\begin{aligned} \int \limits _V {\left[ {\mathsf {S}}\!\cdot \!\cdot \delta {{\mathsf {E}}}+\mathrm{Tr}({\mathsf {E}})\,\delta p\right] \,dV}=\int \limits _V\mathbf {f}_\mathrm{{mag}}\!\cdot \!\delta \mathbf {u}\,dV. \end{aligned}$$

(10)

By substitution of the Hook law (3) and kinematic relation (5), functional (10) is transformed to

$$\begin{aligned}&\int \limits _V\left[ -p\nabla \delta \mathbf {u}+\frac{1}{2}G\left( \nabla \mathbf {u}+\nabla ^T\mathbf {u}\right) \!\cdot \!\cdot \!\left( \nabla \delta \mathbf {u}+\nabla ^T\delta \mathbf {u}\right) + \mathrm{Tr}({\mathsf {E}})\delta p\right] \,dV \nonumber \\&\quad =\int \limits _V\mathbf {f}_\mathrm{{mag}}\!\cdot \!\delta \mathbf {u}\,dV, \end{aligned}$$

(11)

where the elasticity modulus and magnetic force are given by piecewise-constant functions (4) and (9), respectively.

Minimization of functional (11) is performed on a sufficiently dense triangle mesh that covers all the sample and particles altogether. In result, with the given magnetic forces $\mathbf {f}_\mathrm{mag}$ one finds the displacement and pressure distributions: $\mathbf {u}$ and p. To measure elongation/shrinking of the sample, we use the average displacement of its upper boundary (the lower boundary in immovable):

$$\begin{aligned} \varepsilon =\int \limits _0^1\left. u_y \right| _{y=1}\,{\hbox {d}}x; \end{aligned}$$

(12)

in the linear problem under solution this quantity is the equivalent of strain. Since in the calculation the nondimensional magnetic field is set to unity $\left( H_0^2/G_m\right) =1$ with $G_m$ being the shear modulus of the matrix, parameter $\varepsilon$ renders the nondimensional initial “magnetostriction susceptibility” $G_m\left( d\varepsilon /dH_0^2\right) _{H_0=0}$ of the sample.

4 Results of 2D modeling

As it follows from the qualitative analysis present in Sect. 1, the deformation induced in the model sample in response to an applied uniform field comprises contributions from the shape effect and the structure striction. A direct attempt to find which of the parts prevails in the square sample with the given particle concentration ( 20% with respect to the occupied area) fails. The obtained distribution of $\varepsilon$ (30 realizations) does not provide a definite answer: the probabilities to encounter stretching or shrinking turn out to be close, see Fig. 3a. In other words, in a given sample the value of magnetostriction strongly fluctuates. The main uncertainty stems, of course, from the structure magnetostriction, once again pointing out the importance of short-range order of the particles.

To clarify the issue, we have to get back to the qualitative analysis of the structure magnetostriction. Let us assume, first, that spatial distribution of the particles is highly uniform, i.e., almost all the particles are isolated and are positioned from one another at the distances about the mean statistical value $r\sim \left( N/V\right) ^{-1/3}$. The structure magnetostriction in this case should not differ much from that of a lattice system (Fig. 1b) and, according to the above-given consideration, be negative.

Let now the magnetic filler be intentionally embedded in the matrix in the form of linear chain clusters each comprising $\nu$ particles. Such a magnetic “$\nu$-mer” responds to the applied field as a single object (a rod) and strives to set its major axis along $\mathbf {H}_0$. If the initial angle of this axis is nonzero, the turn of the chain should provoke local stretching of the matrix in the $\pm \mathbf {H}_0$ direction, and by that induce positive magnetostriction. The longer the chain the stronger the effect under a given filed strength.

These conclusions were verified with the same set of 30 realizations of the square sample in the following way. Each randomly generated configuration of the particle assembly had been analyzed for the presence of clusters. A particle was considered as belonging to a cluster, if it had at least one neighbor with the center positioned inside a surrounding sphere of radius $2a(1+\delta _*)$ with $\delta _*=0.04$. By that, all the particles in the sample were marked as either solitary (isolated) or clustered.

After the cluster analysis, each configuration was transformed in one of two ways. In the first variant, the solitary particles were left intact whereas the clustered particles were deprived of magnetic susceptibility. In the second variant, only the clustered particles were considered magnetizable. Evidently, in zero field the mechanical properties of the samples of both types are the same, the difference in deformation should manifest itself under magnetization.

For both variants of the particle “magnetic selection”, the problem of the field-induced deformational response was solved numerically for 30 realizations of the initial state, and the strain was evaluated according to formula (12). The results are presented by histograms in Fig. 3b, c.

Fig. 3

Strain histograms of the model SME; vertical axis renders the number of realizations; a all the particles are magnetically susceptible; b only solitary particles are magnetic; c only clustered particles are magnetic (Color online)

As mentioned, the difference between Fig. 3b, c is due solely to the absence/presence of elongated clusters emerged during generation of the initial state. Consider Fig. 3b characterizing the samples where only solitary particles have magnetic moments. The statistical spread notwithstanding, in this histogram there are no positive values of $\varepsilon$. This means that a square SME sample comprising no magnetic clusters always shrinks along the direction of the field. To the contrary, the samples where magnetic particles are grouped always do stretch under magnetization, see Fig. 3c. These facts enable one to easily interpret the histogram of Fig. 3a that renders the result for a sample where both the solitary and clustered particles are magnetic and contribute to the deformation. Expectably, such a sample has the most wide spread of occurring strains centered at zero.

One comment on the above-discussed model is necessary. Note the simplified expression for the particle magnetic moment (8): it is defined by the external field $\mathbf {H}_0$ and not by the local field that takes in the contributions of all the particles in the assembly. This means that the demagnetizing effect is always fixed to its value inherent to a sphere and does not depend on the geometry of the sample. In other words, the shape part of the magnetostriction is ignored, and the focus is only on the structure contribution.

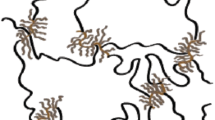
Although the results of the 2D model cannot be taken as an ultimate proof, they strongly support the conclusion that mesoscopic short-range order is crucially important for the macroscopic magnetomechanical properties of SMEs [32]. As a direct experimental confirmation (qualitative, as well) for the above-given considerations we remark Ref. [12], where measurements of magnetostriction effect are reported on an isotropic SME with silicone rubber base and carbonyl iron filler with volume fraction about 15% and mean particle diameter 6 $\mu$m. The cylinder sample of diameter 20 mm and height 10 mm was fixed by its end-wall on a solid substrate, whereas the other end-wall was free; a uniform field of 600 Oe was applied along the cylinder axis. The normal displacements of the free surface were registered with optical interferometry technique. Typical optical patterns obtained on four samples of the same material under the same conditions are shown in Fig. 4 taken from [12]. Comparison against the color scale shows that the revealed “landscape” is nonuniform being a mixture of positive (elevations) and negative (depressions) of the SME surface.

Fig. 4

Interferograms of the end-wall surface of SME cylinders in normal field 600 Oe; the color scale (at the top) graduates elevations and depressions of the surface with respect to the unperturbed level (at $H_0=0$); panes a–d correspond to four different samples; taken from Ref. [12] (Color online)

To interpret the images, we remind that observation always renders the joint action of the shape and structure magnetostriction. The tested sample is a short cylinder (height greater than diameter), and due to that the demagnetizing (shape) effect is relatively small [30, 36]. So, the more pronounced is the structure effect that makes isolated particles to group and the particle clusters to rotate. The former induce surface depressions and the latter—elevations. In an isotropic SME, there are the regions of both types and, if for just structure magnetostriction (no shape contribution), the number of those regions would have been about the same. This explains well-mixed coloration between red and blue in the images of Fig. 4.

5 Framework for 3D modeling

5.1 General remarks

The above-presented 2D modeling yields important facts for qualitative conclusions and helps to build a correct general viewpoint on the magnetomechanics of SMEs with magnetically soft fillers. However, it is essentially insufficient for even semi-quantitative consideration of the problem. The fundamental cause for that is that both the magnetostatic and elastic interactions, which “rule the game”, are long-range. For that kind of interactions, the passage from 2D to 3D usually entails very important quantitative differences. In general sense, this is due to a large change of the number of close neighbors for the particles as well as for the elements of the matrix.

The tensor form of the 3D elastic problem does not differ much from that of the 2D case and is written in following way. The SME sample occupies a 3D space region $\varOmega$ and contains N spherical particles. The i-th particle occupies the space $\varOmega _i^{(p)}$, so that the matrix region is $\varOmega ^{(m)}=\varOmega \backslash \varOmega _1^{(p)} \backslash \varOmega _2^{(p)}... \backslash \varOmega _N^{(p)}$. The outer surface $\varGamma$ of region $\varOmega$ comprises three parts. To the part $\varGamma _f$ a distributed external force $\mathbf {F}^{(b)}$ is applied, at the part $\varGamma _u$ the normal to the surface displacements are forbidden, the part $\varGamma _0$ is stress-free. Definitions (4) for the indicator function and piecewise-constant modulus remain the same and so is the kinematic relation (5). It is worth of noting that the above-given description covers not only the 3D magnetostriction problem as itself but the situations where external mechanical loads $\mathbf {F}^{(b)}$ might be exerted on a SME sample as well. Therefore, the general scheme presented in Sect. 5.2 (below) is applicable to a broad range of problems. For example, one would need the extended formulation for evaluation of the elastic moduli and forced deformations of SMEs. In what follows, we, first, specify the general problem statement and outline the way to its solution; then we focus just on magnetostriction setting $\mathbf {F}^{(b)}=0$ so that the surfaces $\varGamma _f$ and $\varGamma _0$ merge.

5.2 Elastic energy

Each particle experiences the force $\mathbf {F}_i^{(p)}$ that is applied to its center of mass; here for a time being the origin of the force is irrelevant. The equations for the stress tensor virtually coincide with (2) and (3):

$$\begin{aligned} \nabla \!\cdot \!{\mathsf {S}}+\mathbf {f}=0, \quad \mathbf {f}=\sum \limits _i^N I_i(\mathbf {r})\mathbf {F}_i^{(p)}/V_i, \end{aligned}$$

(13)

with $V_i$ being the particle volume. The boundary conditions are

$$\begin{aligned} \left. \mathbf {n}\!\cdot \!{\mathsf {S}}\right| _{\varGamma _f} = \mathbf {F}^{(b)}/S_f, \quad \left. \mathbf {n}\!\cdot \!\mathbf {u}\right| _{\varGamma _u}=0, \quad \left. \mathbf {n}\!\cdot \!{\mathsf {S}}\right| _{\varGamma _0}=0, \end{aligned}$$

(14)

where $S_f$ is the area of $\varGamma _f$.

The boundary $\varGamma _f$ moves under the action of internal forces $\mathbf {F}_i^{(p)}$ and external force $\mathbf {F}_i^{(b)}$. The mean values of displacements of the particles and the boundary $\varGamma _f$ are evaluated according to

$$\begin{aligned} \mathbf {u}_i^{(p)}=\frac{1}{V_i}\int \limits _{\varOmega _i^{(p)}}\mathbf {u}\,dV, \quad \mathbf {u}^{(b)}=\frac{1}{S_f}\int \limits _{\varGamma _f}\mathbf {u}\,dS; \end{aligned}$$

(15)

here $S_f$ is the area of the stress-free surface of the sample.

Defining generalized forces and displacements as

$$\begin{aligned} \mathbf {F}=\left\{ \mathbf {F}_1^{(p)},\,\mathbf {F}_2^{(p)},\, ...\,\mathbf {F}_N^{(p)},\,\mathbf {F}^{(b)}\right\} , \quad \mathbf {U}=\left\{ \mathbf {u}_1^{(p)},\,\mathbf {u}_2^{(p)},\, ...\,\mathbf {u}_N^{(p)},\,\mathbf {u}^{(b)} \right\} , \end{aligned}$$

(16)

we introduce the linear response matrix ${\mathsf {C}}$ that relates the displacements $\mathbf {u}_i^{(p)}$ and $\mathbf {u}^{(b)}$ with the forces $\mathbf {F}_i^{(p)}$ and $\mathbf {F}^{(b)}$:

$$\begin{aligned} \mathbf {U}={\mathsf {C}}\!\cdot \!\mathbf {F}. \end{aligned}$$

(17)

To find ${\mathsf {C}}$, one has to solve the elastic problem (13) $3(N+1)$ times. At i-th step, the generalized force vector is given by condition $\mathrm{F}_k =0$ if $k\ne i$, and $\mathbf {F}_i^{(p)}=1$ if $k=i$. Then, by solving equation (13), the sequence of values that makes i-th line of matrix ${\mathsf {C}}$ is found. For further use, it is convenient to introduce the inverse matrix ${\mathsf {L}}={\mathsf {C}}^{-1}$ so that

$$\begin{aligned} \mathbf {F}={\mathsf {L}}\!\cdot \!\mathbf {U}. \end{aligned}$$

(18)

Let us evaluate the portion of work spent by the forces $\mathbf {F}_i^{(p)}$ and $\mathbf {F}^{(b)}$ when producing displacements $\mathbf {u}_i^{(p)}$ and $\mathbf {u}^{(p)}$:

$$\begin{aligned} dA=\mathbf {F}\!\cdot \! d\mathbf {U}=\mathbf {U}\!\cdot \!{\mathsf {L}}\!\cdot \! d\mathbf {U}. \end{aligned}$$

(19)

This work is equal to the increment of accumulated elastic energy for which integration yields

$$\begin{aligned} U_{el}=\int \,dW={\scriptstyle \frac{1}{2}}\mathbf {U}\!\cdot \!{\mathsf {L}}\!\cdot \!\mathbf {U}. \end{aligned}$$

(20)

5.3 Magnetic energy

As the magnetoelastic problem is solved by minimization of the energy functional, there is no need to derive explicit formulas for magnetic forces. Unlike 2D case, here we take into account mutual magnetization of the particles. In this approach, the particle magnetic moments are induced by the local magnetic field that consists of two parts: external magnetic field and the field from all the other particles of the sample except for the given one:

$$\begin{aligned} \mathbf {m}_i=\frac{V_i}{\chi ^{-1}+4\pi /3}\left[ \mathbf {H}_0(\mathbf {r}_{i})+ \sum \limits _{j=1\atop j\ne i}^N \left( -\frac{\mathbf {m}_j}{r_{ij}^3} + 3\frac{\mathbf {m}_j}{r_{ij}^5}\left( \mathbf {m}_j\!\cdot \!\mathbf {r}_{ij}\right) \right) \right] . \end{aligned}$$

(21)

The center-to-center vector $\mathbf {r}_{ij}=\mathbf {r}_i^{(0)}-\mathbf {r}_j^{(0)}+\mathbf {u}_i^{(p)}-\mathbf {u}_j^{(p)}$ is defined with allowance for the probing displacements of the particles: $\mathbf {r}_i=\mathbf {r}_i^{(0)}+\mathbf {u}_i^{(p)}$ and $\mathbf {r}_j=\mathbf {r}_j^{(0)} + \mathbf {u}_j^{(p)}$ where the radii with index 0 denote the initial position of i-th and j-th particles: Presenting the interparticle field in explicit form and regrouping the resulting expression, one gets

$$\begin{aligned} \sum \limits _j^N \left[ (1-\delta _{ij})\left( \frac{{\mathsf {g}}}{r_{ij}^3}-\frac{3\mathbf {r}_{ij}\otimes \mathbf {r}_{ij}}{r_{ij}^5}\right) +{\mathsf {g}}\delta _{ij}\frac{\chi ^{-1}+ 4\pi /3}{V_i}\right] \!\cdot \!\mathbf {m}_j=\mathbf {H}_{0i}, \end{aligned}$$

(22)

here notation $\mathbf {H}_{0i}=\mathbf {H}_{0}(\mathbf {r}_i)$ means that the right-hand side, equal $\mathbf {H}_{0}$ (external uniform field), is present in each line of the obtained set of 3N linear equations that determines the magnitudes and directions of all the magnetic moments in the sample.

After introducing coefficients

$$\begin{aligned} {\mathsf {A}}^{ij}(\mathbf {U})=\left\{ \begin{array}{ll} {\mathsf {g}}/r_{ij}^3-3\mathbf {r}_{ij}\otimes \mathbf {r}_{ij}/r_{ij}^5 &{}\quad \mathrm{for\;} i \ne j;\\ {\mathsf {g}}\left( \chi ^{-1}+4\pi /3\right) /V_i &{}\quad \mathrm{for\;} i=j; \end{array} \right. \end{aligned}$$

(23)

the set (22) writes as

$$\begin{aligned} \sum \limits _{j = 1}^N {{\mathsf {A}}}^{ij}\!\cdot \!\mathbf {m}_j=\mathbf {H}_{0i}. \end{aligned}$$

(24)

Presenting the set of coefficients $\mathrm{{A}}^{ij}$ in block form, one gets

$$\begin{aligned} \left( {\begin{array}{lll} {\left[ {\mathrm{{A}}_{xx}^{ij}} \right] }&{}{\left[ {\mathrm{{A}}_{xy}^{ij}} \right] }&{}{\left[ {\mathrm{{A}}_{xz}^{ij}} \right] }\\ {\left[ {\mathrm{{A}}_{yx}^{ij}} \right] }&{}{\left[ {\mathrm{{A}}_{yy}^{ij}} \right] }&{}{\left[ {\mathrm{{A}}_{yz}^{ij}} \right] }\\ {\left[ {\mathrm{{A}}_{zx}^{ij}} \right] }&{}{\left[ {\mathrm{{A}}_{zy}^{ij}} \right] }&{}{\left[ {\mathrm{{A}}_{zz}^{ij}} \right] } \end{array}} \right) \left( {\begin{array}{l} {\left[ {{{({m_x})}_j}} \right] }\\ {\left[ {{{({m_y})}_j}} \right] }\\ {\left[ {{{({m_z})}_j}} \right] } \end{array}} \right) = \left( {\begin{array}{l} {\left[ {{{({H_{0x}})}_j}} \right] }\\ {\left[ {{{({H_{0y}})}_j}} \right] }\\ {\left[ {{{({H_{0z}})}_j}} \right] } \end{array}} \right) , \end{aligned}$$

(25)

or, in compact notations

$$\begin{aligned} \overline{{\mathsf {A}}}\!\cdot \!\overline{\mathbf {m}}=\overline{\mathbf {H}}_0. \end{aligned}$$

(26)

Finally, the expression for the magnetostatic energy takes the form

$$\begin{aligned} U_{mag}=-\frac{1}{2}\sum \limits _i^N \mathbf {m}_i \!\cdot \! \mathbf {H}_0=-{\scriptstyle \frac{1}{2}}\overline{\mathbf {H}}_0\!\cdot \!\overline{{\mathsf {A}}^{-1}}(\mathbf {U})\!\cdot \!\overline{\mathbf {H}}_0 \end{aligned}$$

(27)

6 Results of 3D modeling

Contributions (20) and (23) together render the magnetomechanical energy of the model SME sample to be studied numerically:

$$\begin{aligned} U=U_{el}+U_{mag}={\scriptstyle \frac{1}{2}}\mathbf {U}\!\cdot \!{\mathsf {L}}\!\cdot \!\mathbf {U}-{\scriptstyle \frac{1}{2}}\overline{\mathbf {H}}_0\!\cdot \!\overline{{\mathsf {A}}^{-1}}(\mathbf {U})\!\cdot \! \overline{\mathbf {H}} _0. \end{aligned}$$

(28)

The equilibrium configuration and structure of the SME is found by minimizing of functional (28) under constraints $\mathbf {r}_i-\mathbf {r}_j+\mathbf {u}_i-\mathbf {u}_j>a_i+a_j$ where $a_i$ and $a_j$ are the respective particle radii.

The developed approach is applied to a cube sample with the side of length l; the cube is filled with 64 randomly positioned identical magnetically polarizable particles. There is no external force ($\mathbf {F}^{(b)}=0$), and a constant magnetic field $\mathbf {H}_0$ is directed along Oz axis. The boundary conditions at the cube faces are: $u_x|_{x=0}=0$, $u_y|_{y=0}=0$, $u_z|_{z=0}=0$, see the coordinate frames in Figs. 5a, 6 and 7a. That is, three cube faces: $x=0$, $y=0$, and $z=0$ may slide without tangential resistance along the respective planes but cannot deform in normal direction; all the other faces are free.

Fig. 5

Field-induced structuring of a SME cube with volume content 0.15 at zero field (a) and $H_0^2/G_m=200$ (b). Pane c shows the field dependence of strain for five different realizations of the sample (colors), thick black lines are eye-guides obtained by averaging of the symbol series in the intervals to the left and right of $H_0^2/G_m=70$ (Color online)

Fig. 6

Same as in Fig. 5 but for volume content 0.2 (Color online)

Fig. 7

Field-induced structuring of a SME cube with volume content 0.26 at zero field (a) and $H_0^2/G_m=200$ (b). Pane c shows the field dependence of strain for five different realizations of the sample (colors), thick black lines are eye-guides obtained by averaging of the symbol series in the intervals to the left and right of $H_0^2/G_m=70$ (Color online)

Figures 5, 6 and 7 present the snapshots of the samples differing in the particle volume content: with three concentrations: 0.15 (Fig. 5), 0.2 (Fig. 6) and 0.26 (Fig. 7). Panes a in these figures show the initial configurations (at $\mathbf {H}_0=0$) and panes b render the structures occurring under the field $H_0^2/G_m=200$ that for the matrix with shear modulus about 5 kPa corresponds to the field strength about 2 kOe.

Panes c of Figs. 5, 6 and 7 show the field dependencies of the strain $u^{(b)}/l$ averaged over the upper surface of the cube, see equation (15). In simulations, for each value of the particle content, five sample realizations were generated, the field dependencies of strain obtained in particular calculations are shown by series of symbols. Solid black lines are eye-guides resulting form averaging the particular results in two regions: to the left and to the right of the point $H_0^2/G_m\approx 70$.

Due to a limited number of particles in the sample and a small number of realizations of the system, the results fluctuate substantially. However, the tendencies are sufficiently clear, and the analysis made on 2D models helps to explain them.

The initial system is generated by random positioning of the particles in the cube. The lower the concentration the more particles are solitary, i.e., non-clustered. When the field is just turned on, the dominating mode of the SME response is closing-in of the particles which reside near one another given their center-to-center vectors fall inside the space angle where the magnetodipole interaction is attractive. Thus, at this stage the degree of clusterizing enhances, although the field is not yet strong enough to notably rotate the clusters. The resulting overall magnetostriction effect is very low: function $\varepsilon (H_0^2)$ is nearly zero, see the symbols and solid lines in panes c of Figs. 5, 6 and 7 at $H_0^2/G_m<70$. With regard to the results of 2D modeling, we infer that here the negative structure striction (due to the particle mutual approaches) and positive shape striction (caused by the action of demagnetizing field) are comparable in magnitude and oppose each other. Depending on the particular configuration of the particle assembly, one or another tendency prevails slightly, see swings around zero of the symbol lines in Figs. 5c, 6 and 7c. We note that the simulated aggregation patterns very much resemble those obtained in direct X-ray observations performed on real silicone rubber-based SMEs filled with carbonyl iron [13]. As reported there, at enhanced concentrations ($\sim 10$ vol.% and higher) the particles form rather 3D loose structures than well separated chains. Indeed, all the simulated field-induced structures presented in Figs. 5, 6 and 7 resemble arrangements of that type.

This low-field process, independently of the model, should evolve proportionally to $H_0^2$, and the average low-slope lines in Figs. 5c, 6 and 7c confirm that.

After the majority of the initially solitary particles unite in clusters, the structuring effect of the applied field reduces mostly to rotation of the emerged line aggregates and their straightening. Besides that, the straightened chains which lie at short distances to one another, begin aggregate laterally. This mechanism is worth of a special comment. As it is known, see Ref. [20], for example, straight linear chains of permanent dipoles at close distances do attract each other laterally if they are configured in “zipper” way: the equator of a spherical particle of one chain is positioned opposite to the interparticle gap in another one. This pattern of aggregation—it is valid as well for the field-induced point dipoles that is the case here—becomes visible if to expand (not shown here) the transition between, for example, Fig. 6a, b in a series of snapshots.

At this stage, both the structure and shape strictions work mostly to the same effect, and the rate of strain growth increases. It is clearly seen from the change of slope of the $\varepsilon (H_0^2)$ dependence for any particular assembly as well as from their average. Notably, this process requires that there is some room for changing the cluster conformations. Whereas for concentrations 0.15 and 0.2 the dependencies $\varepsilon (H_0^2)$ look very much alike, see Figs. 5c and 6c, the most dense sample (Fig. 7c) elongates with more difficulty: the value $\varepsilon (H_0^2)$ attained at the maximum field is smaller, cf. Figs. 5c and 6c. We attribute that to the fact that at that concentration the particles hinder each other displacements.

7 Conclusions

Theoretical discussion on the origin and magnitude of the magnetostriction effect in soft magnetic elastomers (SMEs) filled with low-coercive ferromagnetic microparticles is presented. The 2D model, despite its evident roughness and naivety, enables one to understand that the striction effect comprises two main contributions—the shape and structure ones—which work on different scales. The shape striction stems from overall macroscopic properties of a SME whereas the structure contribution is essentially mesoscopic and crucially dependent on the short-range arrangement of the particle mutual positions in the matrix.

3D modeling, which brings the consideration much closer to reality, extends this understanding. It reveals that at low fields the nature of striction is mostly due to clustering of solitary particles. In this process, the shape and structure strictions work against one another, and the resulting deformation of a sample is relatively small. Upon emerging of clusters, the processes of their rotation to and straightening along the field become the dominating ones. Here both strictions work to the same effect. In result, the overall striction becomes definitely positive (elongation along the field) and enhances its rate with respect to the field strength. At this stage, a too large concentration of the particles is an impeding factor as the particles sterically hinder each other displacements. From that, it follows that for a SME with given material parameters of the particles and matrix there should exist an interval of concentrations where the striction effect is maximal.

Several features of the presented model might be considered as its drawbacks. Those are: (i) assumption of perfect sphericity and identical size of the particles; (ii) employment of isotropic linear magnetization of the ferromagnet instead of imposing a dependence with saturation; (iii) taking a simple Hook law instead of a more realistic one (Mooney-Rivlin or Gent) for describing the elastic matrix. In this connection, we remark that the goal of the paper is not to achieve a perfect agreement with experiments (besides, the presently available data are not at all coherent) but rather to advance a conceptual insight in the magnetostriction effect in SMEs. Note, however, that by order of magnitude the strain attained under maximum field in the 3D model (Figs. 5c, 6 and 7c) fully agrees with the quantitative estimates given in Sect. 1.