Mesoscopic characterization of magnetoelastic hybrid materials: magnetic gels and elastomers, their particle-scale description, and scale-bridging links

Abstract

Magnetic hybrid materials in the form of magnetic gels and elastomers, that is, magnetic or magnetizable colloidal particles embedded in an elastic polymer matrix, are fascinating substances. By addressing and adjusting the magnetic interactions between the particles through external magnetic fields, their overall material properties can be tuned reversibly while in operation. A central goal is to understand how these features can be optimized and which structural properties of the materials determine their overall behavior and its tunability. Mesoscopic theories and modeling are necessary for these purposes, resolving the arrangement of the embedded particles and linking it to the macroscopic scale of the overall material behavior. Here, we overview such recent developments of mesoscopic approaches. Particularly, we address coarse-grained but efficient dipole-spring models, explicit analytical calculations using linear elasticity theory, numerical approaches that allow to characterize nonlinear effects, or density functional theory. In this way, various properties and types of behavior of these materials are revealed, for instance, their reversible tunability of static and dynamic mechanical moduli by magnetic fields, elastic interactions between the embedded particles mediated through the polymeric matrix, or a pronounced and reversibly tunable nonlinear stress–strain behavior. Links from the mesoscopic to the micro- and macroscopic level are outlined. We mention combined efforts of theoretical descriptions, modeling, numerical simulations, and experimental investigations. It becomes evident from our treatment that an integrated approach of theory, simulations, and experiments will significantly increase our further understanding of these materials in the future and will draw possible applications into sight.

1 Introduction

The materials that we consider in this overview consist of magnetic or magnetizable particles embedded in an elastic polymeric matrix. These particles are predominantly assumed of colloidal size, i.e., of diameters ranging from several nanometers to several micrometers. Moreover, the polymeric environment that they are embedded in is considered to be permanently chemically crosslinked so that it is reversibly elastically deformable. There is no terminal flow behavior. The elastic matrix may be swollen by a solvent, forming a soft elastic gel. We consider the particles to be large enough so that they cannot move through the elastic matrix. Their positions are locked relatively to the surrounding environment.

Depending on the size and type of the embedded colloidal particles, on the kind of application one may have in mind, on the degree of swelling, and on further properties, different names for these materials have entered the terminology, e.g., ferrogels, magnetosensitive elastomers, or magnetorheological elastomers. Here, we will summarize them under the term magnetic gels and elastomers. In many cases, the detailed properties are not of particular relevance concerning the coarse but effective types of modeling of the materials introduced and overviewed below.

Several recent reviews are available on these types of hybrid materials [30, 60, 64, 79, 110]. They outline the fascinating properties of magnetic gels and elastomers. Particularly interesting from an application point of view is their tunability by external magnetic fields. These fields can alter the magnetic interactions between the particles. Due to the magnetoelastic coupling in the materials, this can affect the overall mechanical material properties. For instance, the static and dynamic elastic moduli of the materials can be tuned and switched reversibly in this way, while the materials are in operation [13, 28, 48, 95, 98, 108]. Such features allow, for instance, to construct reversibly switchable damping devices [59, 75]. Moreover, the substances may be used as soft actuators. Shape changes are triggered, for example, using magnetic fields or field gradients [94, 116].

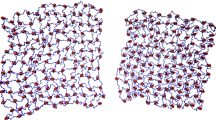
In this overview, details on the ways of synthesis and manufacturing procedures are not included. However, we mention one outstanding structural modification that can be achieved during production. One way of generating the materials is to disperse the magnetic or magnetizable particles in a crosslinkable polymer solution and then to perform the crosslinking. Such an approach, in an idealized situation, leads to rather isotropic particle distributions. In contrast to that, an external magnetic field may be applied during the process. In the presence of the field, the magnetic particles in the still not crosslinked environment and depending on their size and properties form anisotropic structures or chain-like aggregates [19, 34, 35, 40, 107] to minimize the magnetic interaction energy [53, 54]. If the crosslinking is performed in such a state, the anisotropic structures are locked in because the particles cannot move through the crosslinked matrix any longer. Consequently, permanently anisotropic samples are generated. Figure 1 shows examples of the two qualitatively different cases of isotropic and anisotropic particle arrangements that were visualized by means of X-ray microcomputed tomography [34]. From now on, we consider the materials after production, in their completed and final crosslinked elastic state.

Fig. 1

Reproduced from Ref. [34]. © IOP Publishing. Reproduced with permission. All rights reserved. (Color figure online)

Two qualitatively different structural arrangements of magnetic particles in magnetic elastomers, see Ref. [34]. The particles (yellow) are visualized via X-ray microcomputed tomography. a In the isotropic sample, the particle arrangement does not show a particular preferred direction. b In contrast to that, the anisotropic sample generated in the presence of an external magnetic field features chain-like embedded structures.

Fig. 2

Illustration of three different levels of theoretical characterization of magnetic gels and elastomers. a On the microscopic level, all components are explicitly resolved. This includes the individual polymer chains (bright, yellow), the colloidal magnetic particles (darker, green), and their magnetic moments (arrow). b Mesoscopic approaches still resolve the presence of the individual particles in a discrete way. However, the polymeric environment is treated as a continuous elastic background. It may be represented by effective elastic interactions between the particles. c In macroscopic theories, all components are described by continuum fields. Instead of a discretized account of the magnetic particles, a continuous magnetization field is included as indicated by the arrow. (Color figure online)

In terms of modeling and theoretically characterizing the behavior of magnetic gels and elastomers, we here distinguish between three different levels of description that are illustrated in Fig. 2. We use the term “microscopic” to refer to studies that explicitly resolve both the magnetic particles and individual polymer chains in a discretized way; see Fig. 2a. This may be realized in a coarse-grained manner, i.e., only a small fraction of the polymer chains is taken into account and they may be treated by coarse-grained bead-spring models. Such descriptions have been performed, for example, using molecular dynamics simulations [111, 112]. In contrast to that, we categorize theoretical approaches as “mesoscopic,” see Fig. 2b, if they still treat the individual magnetic particles explicitly; yet, they do not resolve the discrete nature of the elastic background in terms of individual polymer chains. Instead, the polymeric environment is considered as a continuous elastic medium embedding the individual particles, or it is represented by effective elastic interactions between the particles. Most of the approaches overviewed below fall into this category. We mention that genuinely mesoscopic continuum descriptions and theories exist that describe the presence of the particles by appropriate continuum fields and in this way still resolve them individually. Examples are certain types of finite-element simulation approaches [36, 51, 73] or the density functional theory mentioned below [20]. Finally, hydrodynamic-like symmetry-based theories are “macroscopic” [12, 46], like other continuum approaches [5]; see Fig. 2c. These continuum approaches do not resolve the discrete nature of any of the individual components. The presence of the embedded particles may enter through a concentration field, while their magnetic effects are included by a magnetization field. Below, we will also briefly consider links that have been worked out between these different levels.

We proceed in the following way. First, we overview in Sect. 2 simplified discretized dipole-spring models that were introduced to describe the coupling between magnetic and elastic interactions in this type of materials in terms of an effective minimal approach [4, 80,81,82, 102]. Accordingly, the changes in static and dynamic mechanical moduli under changes in the magnetic interactions can be modeled efficiently. The same is true for a hardening of the magnetic substances when chain-like aggregates of nearly touching magnetic particles form under the influence of strong external magnetic fields. Moreover, these approaches stress the importance of allowing for nonaffine, i.e., spatially inhomogeneous deformations to characterize such composite materials correctly. A first attempt of connecting the mesoscopic dipole-spring models to the statistics of particle configurations obtained from microscopic simulation results has been performed [83], while more extensive approaches of this kind should be envisaged in the future.

Going beyond the simplified representation of the polymeric matrix using elastic model springs, linearly elastic continuum environments and linear regimes of their deformations were treated by corresponding theoretical descriptions; see the overview in Sect. 3. Then, the interactions between the embedded magnetic or magnetizable particles due to their deformation of the elastic matrix can be determined explicitly and analytically. Such calculations were first performed inside bulk materials [89, 91], before they were extended to include boundary effects [67]. Both forces and torques acting on the particles were taken into account.

While these analytical calculations predominantly addressed the regime of linear elasticity, we next turn to nonlinear elastic behavior in Sect. 4. As quasistatic numerical simulation results demonstrate, the interplay between magnetic interactions and elasticity can lead to pronounced nonlinear stress–strain behavior in anisotropic materials containing chain-like aggregates of magnetic particles [21, 22]. This stress–strain behavior was termed “superelastic.”

Most of these investigations do not explicitly consider thermal fluctuations of the positions of the magnetic particles. To include them into the models, the possibility of constructing a corresponding density functional theory was outlined [20], see Sect. 5. So far, it has been used to characterize one-dimensional dipole-spring systems and chain-like aggregates embedded in an elastic matrix.

Finally, we summarize other related studies in Sect. 6. This comprises a simplified description of the buckling of chain-like aggregates in soft elastic matrices under perpendicularly applied magnetic fields [40], a simplified scale-bridging from the mesoscopic particle-scale description to a macroscopic continuum theory allowing for the calculation of explicit expressions of macroscopic material parameters [63], long-ranged thermophoretic effects in soft elastic gels upon heating of the embedded particles [92], or the spiral-like trajectories of self-propelled dipole-spring magnetic colloidal microswimmers beyond a critical threshold of their active drive [6]. Some further recent developments are summarized, before we conclude in Sect. 7.

2 Dipole-spring approaches describing nonaffine deformations, reversible elastic hardening, tunable static and dynamic mechanical moduli

The type of mesoscopic model that one may use to describe a certain effect depends on the type of behavior one is interested in. It might come as a bit of a surprise, but simplified dipole-spring models [4, 40, 80,81,82,83, 102] turned out to be very well suited for many purposes as detailed below.

The term “dipole-spring model” suggests already the background of this approach. Depending on the situation at hand, the particles are treated as discretized objects, possibly including effective steric interactions between them so that they do not collapse into each other when they come close under strong magnetic attraction [4, 81, 82]. The magnetization of each magnetic or magnetized particle is discretized in terms of a magnetic dipole, the mutual interactions between which are readily calculated [45]. To mimic the elastic interactions between the particles mediated by the polymeric matrix as well as the overall elasticity, elastic springs are set between the centers of the particles; see Fig. 3a. It is the configuration of the particles that determines how the springs need to be arranged and how many of them need to be included. Additional interstitial points that do not carry any magnetic moment were introduced to obtain a finer mesh when particle arrangements extracted from real experimental samples were used to construct the dipole-spring network [82].

Fig. 3

Simplified dipole-spring models for magnetic gels and elastomers [4, 40, 80,81,82,83, 102], here illustrated in two spatial dimensions. a Each magnetic particle carries a magnetic dipole moment (black arrows). The elastic interactions between the particles mediated by the polymeric environment are mimicked by elastic springs set between the particles. Additional interstitial points may be introduced to refine the elastic mesh [82]. b Depending on the system under consideration, it may be appropriate to introduce additional energetic penalties for rotations of the particles together with their magnetic moments relatively to their environment [4, 83, 102]. The arcuate (red) clamps illustrate energetic penalties for rotations in the plane containing each connecting spring. Moreover, rotations in the plane perpendicular to each spring can be taken into account to energetically penalize relative twisting rotations between neighboring particles [4, 83, 102]. (Color figure online)

The appealing simplicity of this approach results from the fact that the complex role of the elastic environment is reduced to the pairwise spring-like interactions between the particles, see Fig. 3a. Since the magnetic and elastic interactions are then readily evaluated, arrangements of high numbers of particles can be investigated, which allows to extract the overall behavior from sufficiently large systems. Moreover, the discretization of the material into a many-particle system enables the use of efficient semianalytical strategies to evaluate their properties [81, 82, 102].

In addition to their displacements, one may consider the effect of rotations of the particles together with their magnetic moments. There are different possibilities to achieve this goal. Figure 3b illustrates by the clamps introduced between the dipoles and the connecting vectors between the particles how rotations relatively to these connecting vectors can be energetically penalized [4, 83, 102]. In addition to that, relative rotations between the particles in the plane perpendicular to the connecting vectors may be penalized by an energetic cost for twisting-type deformations along the connecting vectors [4, 83, 102].

Fig. 4

Reproduced from Ref. [83]. © IOP Publishing. Reproduced with permission. All rights reserved. (Color figure online)

Basic microscopic minimal model to link microscopic and mesoscopic scales [83]. Two mesoscopic particles (spheres) are connected by a polymer chain. In the simulations, the latter is discretized into a chain of beads linked by harmonic springs. Extensive statistics for the relative positions and orientations of the particles was collected during molecular dynamics simulations of this system at finite temperature. The suitability of simplified mesoscopic model energies to characterize the behavior of the system only in terms of the degrees of freedom of the mesoscopic particles was tested. As a result, numerical values of the mesoscopic model parameters were extracted from the microscopic simulation in a basic scale-bridging approach [83].

By construction, the dipole-spring models represent a quite severe reduction of realistic systems. To check whether such an approach is appropriate, the model was tested against a simple microscopic minimal model system as depicted in Fig. 4. Two magnetic particles are connected by one polymer chain. In fact, such systems of polymer chains directly chemically attached to magnetic colloidal particles have been synthesized before [41, 72]. The basic system in Fig. 4 was numerically evaluated under finite temperature using molecular dynamics simulations [83]. For this purpose, the polymer chain was coarse-grained into a chain of small beads connected by elastic springs. Extensive statistics for the mutual orientations and the distance between the two particles were collected. From these statistics and from fitting to them expressions for a corresponding free energy of the effective two-particle mesoscopic system that does not explicitly resolve the polymer chain any longer, the validity of mesoscopic model energies can be tested [38, 83]. In this simplified case, the mesoscopic model energies used in the dipole-spring approaches [4, 40, 80,81,82,83, 102] describe the system suitably. While harmonic springs are sufficient to address small deviations from the average particle separation, nonlinear springs, e.g., of the FENE type [109], are more appropriate for larger stretching of the basic two-particle system [83]. Apart from that, the approach provides numerical values for the mesoscopic model parameters resulting from the microscopic setup. It therefore corresponds to a basic example of scale-bridging from the microscopic to the mesoscopic level. Further analysis of the statistics also suggests how to additionally improve the mesoscopic model to include, e.g., couplings between positional and rotational degrees of freedom [83]. In fact, the effect of wrapping of the polymer chain around the particles during their rotation played a notable role in the analysis of the system in Fig. 4; see Ref. [83] for further details.

In summary, elastic dipole-spring systems are introduced that include magnetic interactions and can be reversibly deformed. Particularly, the changes in the elastic properties under varying magnetic interactions are readily evaluated, taking into account the discrete arrangement of the mesoscopic particles in the system. The internal degrees of freedom are considered to a certain extent in terms of the degrees of freedom of the individual network nodes, which may play an even qualitative role for the obtained results [80].

2.1 Tunable static and dynamic mechanical moduli

As motivated in Sect. 1, one particularly interesting feature of magnetic gels and elastomers is that their overall static and dynamic moduli become tunable by external magnetic fields. These moduli can be regarded as genuine scale-bridging quantities, as elucidated in the following.

For instance, we consider the geometry depicted in Fig. 5. The material there is confined between two parallel plates, see Fig. 5a. Then, normal forces are applied to the plates, which drives the plates towards each other by a small amount. Consequently, the material between the plates is deformed.

Fig. 5

Reproduced from Ref. [81], with the permission of AIP Publishing. (Color figure online)

Static and dynamic mechanical moduli can be viewed as genuine scale-bridging quantities. a On the macroscopic side, they set for a given geometry the amount of stress that is necessary to achieve a deformation of a given amplitude. In the present case, the sample is confined between two parallel plates that are driven towards each other by external forces applied normal to the plates. In principle, a different modulus is associated with each type of deformation, and also with different orientations of an external magnetic field inducing different orientations of the magnetic moments $\mathbf {m}$ within the system. b However, the magnitude of each modulus is determined by the internal properties of the system. For magnetic gels and elastomers, especially the spatial arrangement of the embedded colloidal particles plays a central role [43, 44, 80,81,82, 114]. It determines the response to each given force distribution on this mesoscopic level, the forces indicated by the black arrows.

Here, the overall macroscopic mechanical stress can be defined as the force applied per area onto each plate along the normal axis. The overall macroscopic mechanical strain can be defined as the resulting change in distance between the plates divided by the distance between the plates, which leads to a measure of the distortion within the system. Finally, the corresponding mechanical modulus tells us, how strong the applied stress needs to be to achieve a certain degree of strain,

$$\begin{aligned} \mathrm {stress} = \mathrm {modulus} \times \mathrm {strain}. \end{aligned}$$

In the described geometry, this quantity is called Young modulus. In principle, any strain geometry is quantified by a corresponding modulus. For instance, in the case of shear deformations the plates are not displaced along their normal but along an in-plane surface direction. In our situation, additional cases result when different directions relatively to an external magnetic field are probed. Moreover, stresses oscillating with a certain frequency may be applied instead of static ones. Then, dynamic mechanical moduli are probed that contain a storage part, associated with the reversible part of the mechanical response, i.e., stored elastic deformation energy; and a loss part, quantifying dissipative effects, e.g., losses in mechanical energy due to internal friction generating heat.

Figure 5 indicates the scale-bridging nature of these quantities. They quantify the macroscopic mechanical deformation; see Fig. 5a. However, their magnitude is determined by the internal structure of the materials and the associated mesoscopic properties, particularly the arrangement of the embedded magnetic or magnetizable particles; see Fig. 5b. Since the magnetic interactions between these particles can be modified by external magnetic fields, also the overall response of the system to imposed deformations changes. Consequently, this affects the overall mechanical moduli. Also dynamic variations of the applied forces play a role. It is illustratively clear that high frequencies of the applied forces that vary too fast to allow internal relaxation will lead to different results than low frequencies that enable basically complete internal relaxation. Dipole-spring models are a highly suited means to study all these effects [80,81,82]. Here, we confine ourselves in Fig. 5 to imposed deformations of small amplitude, that is, we remain in the regime of linear imposed distortions. Linearly elastic Hookean springs were used in the addressed works [80,81,82]. Yet, there is no principal conceptual problem in switching to nonlinear elastic springs [40, 109].

In a simplified dipole-spring approach, it was assumed that all the magnetic moments of the embedded particles are of identical magnitude and direction. This situation approximately results for identical particles when the interactions with a homogeneous external magnetic field significantly exceed the mutual magnetic interactions between the magnetic dipole moments. Numerically, the dipole-spring system can be clamped on two faces that are then displaced by a small amount. Depending on the requested type of analysis, the particles in the clamped regions may still be able to adjust their positions, for instance, in the directions perpendicular to the displacements of the clamps under overall compression or elongation [80]. After relaxation under this enforced deformation, from the measured change in the overall energy of the system, the elastic moduli can be calculated [80]. It is found that whether under increasing magnetic interaction an elastic modulus increases or decreases strongly depends on the particle arrangement and the orientation of the magnetic moments. As an illustrative example depicted in Fig. 6, a regular two-dimensional hexagonal particle arrangement shows increasing or decreasing static Young modulus with increasing magnetization, depending on the orientation of the magnetic moments. For further analysis, see Ref. [80]. Moreover, a boundary effect was observed in this type of investigations for smaller system sizes. Yet, it was confirmed that with increasing system size, for which the number of bulk particles grows more strongly than the number of boundary particles, the determined values of the elastic moduli converge [80].

Fig. 6

Reproduced from Ref. [80], with the permission of AIP Publishing. (Color figure online)

Changes of static elastic Young moduli E with increasing magnetic interactions for two-dimensional hexagonal dipole-spring example systems. All particles carry dipoles of identical magnitude m and of identical orientation as indicated by the arrows on the insets. The insets further indicate the axes of mechanical stretching by the double arrows marked by $\varepsilon$. The actual systems were much larger than the fractions indicated by the insets. k sets the spring constant and $m_0$ sets the unit of the magnetic moments. Remarkably, an in-plane rotation of the particle structure by $90^{\circ }$ relatively to the stretching and magnetization directions reverses the change of the elastic modulus with growing m from increasing to decreasing and from decreasing to increasing [80].

As indicated above, also the dynamics of the system gets modified under changed internal magnetic interactions. On the mesoscale, so far mainly the overdamped relaxation dynamics has been investigated [81, 82, 102]. For systems of long polymer chains and gel-like materials such an overdamped nature is conceivable [25]. Then, a decomposition of the dynamics into normal relaxation modes is possible in order to study how the system reacts to changes of external mechanical stresses or induced changes in the magnetic interactions [81, 82, 102].

Particularly, following a type of linear response theory [56], the dynamic moduli for the different types of deformation can be calculated from the structure of the corresponding mesoscopic system [81, 82]. As a crucial step for this purpose, the mesoscopic force field acting on the individual degrees of freedom during a specific type of overall deformation needs to be constructed, see the black arrows in Fig. 5b [81, 82]. In the end, the storage and loss parts of the dynamic moduli can be calculated as a function of frequency [81, 82]. Their changes under modified magnetic interactions were evaluated [81, 82].

In the dynamic case, the changes in the moduli with increasing magnetic interactions can be nonmonotonous as a function of frequency. For example, at lower frequencies an increase may be observed and at higher frequencies a decrease, or vice versa [81, 82]. Different frequencies address different modes. For instance, extended, more global modes of deformation that span the whole system typically need longer time to relax than very localized modes that only involve a small number of degrees of freedom. Thus, different modes may become dominant in the overall response at different frequencies. Moreover, different modes may respond differently to changes in the magnetic interactions [82, 102].

The procedure was first tested for artificial regular dipole-spring systems [81]. Afterward, more irregular particle distributions were evaluated that had been extracted from real samples using X-ray microcomputed tomography [34, 82, 95]. In the latter case, the magnetic dipole moments differed in magnitude according to the different particle volumes extracted from the experimental samples. Moreover, it was found that additional interstitial network nodes between the particles should be added for such more irregular particle arrangements to achieve a reasonable representation of the overall elasticity [82].

2.2 Chain formation and reversible elastic hardening

Already in an initial one-dimensional system of a straight dipole-spring chain the crucial role of the formation of compact chain-like aggregates on the overall mechanical behavior was analyzed [4]. When the magnetic attraction between particles increases, they more and more approach each other. Since in this setup linearly elastic harmonic springs were used, an approach up to virtual contact between the particles is possible. This becomes obvious as the magnetic interaction more strongly increases with decreasing distance between the particles than the elastic interaction by the linear springs. At contact, hard steric repulsion between the particles sets in and balances the magnetic attraction. The mutual approach of the particles is continuous for smaller initial particle separation. For larger initial mutual distances, it becomes discontinuous, meaning that the particles snap together at a critical threshold strength of the magnetic attraction. At vanishing temperature and for an infinitely extended, initially homogeneous chain, the whole scenario can be interpreted as a phase transition [4]. In this context, also the role of an orientational memory of the magnetic moments of the particles was addressed; see Fig. 3b [4]. The elastic modulus of compressing or elongating the chain strongly increases when the particles come into contact. Therefore, the corresponding transition was termed “hardening transition” [4]. Later, the dynamics of transforming to the compact aggregates under magnetic attraction was analyzed on a straight dipole-spring chain of finite length [33].

The formation of compact chain-like aggregates induced by magnetic interactions was addressed in three-dimensional dipole-spring systems as well. Particularly, for more irregular initial particle arrangements, the numerical evaluation of corresponding dipole-spring systems demonstrated the development of such structures [81, 82]. Around the strength of the magnetic interaction at which the chain formation approximately starts, it was found that the static mechanical moduli begin to significantly increase [81, 82]. Figure 7 shows a corresponding example for different Young moduli measured on randomized fcc systems. A reversible increase in the moduli by a factor of approximately 7 is observed for the strength of the magnetic interactions investigated there. Similar behavior is found for the corresponding shear moduli [81].

Fig. 7

Reproduced from Ref. [81], with the permission of AIP Publishing. (Color figure online)

Static Young elastic modulus as a function of increasing magnetic interactions between the particles in randomized fcc dipole-spring systems. All magnetic moments point into the same direction and are of identical magnitude m. The Young moduli for stretching or compressing the system along the direction of the magnetic moments ($E_{zz}$) and perpendicular to it ($E_{xx}$, $E_{yy}$) were evaluated. These results show averages over 80 different randomizations of the systems. $m_0$ sets the unit of the magnetic moments, k is the spring constant, and $l_0$ is the initial length of the springs in the original fcc system. At the point, at which the formation of compact chain-like aggregates starts in the system ($m\approx 0.06m_0$), the Young moduli strongly increase [81]. The same is true for the elastic shear moduli (not shown here) [81].

Naturally, an exciting first question is whether such compact chain-like aggregates can also form in real samples. There, the particles have to move against the three-dimensional, often nearly incompressible elastic polymer matrix between them. If so, the second immediate question is whether such an effect is reversible, or whether it would destroy the surrounding matrix.

If observable, this effect would be of high practical relevance. In magnetic fluids the reversible formation of chain-like aggregates of suspended colloidal magnetic particles, induced by external magnetic fields, can lead to a pronounced increase in the overall viscosity. Similarly to this “magnetoviscous” effect [42, 62, 78], in the present case an externally induced formation of compact chain-like aggregates should lead to a pronounced reversible tunability of the elastic moduli.

In fact, the formation of chain-like aggregates under the influence of external magnetic fields has recently been identified and analyzed statistically in magnetic elastomers using X-ray microcomputed tomography [34]. Moreover, in a selected example system, the repeated reversible approach until virtual touching of two basically spherical paramagnetic particles in a swollen elastic polymer matrix under increasing magnetic attraction has been observed experimentally and analyzed numerically as well as by theoretical calculation [90]. The experimental results were fit well when assuming an approximately incompressible elastic matrix, despite the virtual touching of the magnetic particles. How thick the remaining polymer layer in a possible thin gap between the two particles still was in the compact state could not be identified so far within the experimental resolution. Nevertheless, the experimental observations indicate that the reversible and repeated formation of compact aggregates is possible despite the presence of the embedding polymer matrix.

Using the experimental data from X-ray microcomputed tomography of two different real samples [34, 95] as an input to dipole-spring calculations, likewise the formation of chain-like aggregates was identified; see Fig. 8a, b, and Ref. [82] for further analysis. Corresponding elastic moduli may show an interesting nonmonotonous behavior as depicted in Fig. 8c. First, they decrease with increasing particle magnetization due to the initial rearrangements of the particles when they start to become magnetic. However, when chain formation becomes dominant at higher magnetization, the moduli significantly grow.

Fig. 8

Reproduced from Ref. [82]. © IOP Publishing. Reproduced with permission. All rights reserved. (Color figure online)

Formation of chain-like aggregates together with the resulting effect of mechanical hardening under increasing magnetization in three-dimensional dipole-spring systems [82] that use input data extracted from real samples via X-ray microcomputed tomography [95]. The magnetization $\mathbf {M}$ is set identical in magnitude M and direction for all particles. $l_0$ is a typical length scale set by the particle sizes and $M_0$ is the unit of magnetization. a Initial distribution of the particles (thick, blue points) and additional interstitial network points (thin, gray points) in one numerical realization of the dipole-spring system projected onto one plane for vanishing particle magnetization. b The same for $M=7M_0$, which corresponds to a realistic experimental value. The formation of compact chain-like aggregates oriented along $\mathbf {M}$ can be inferred. c Elastic Young modulus $E_{zz}$ for stretching or compressing along the magnetization direction and elastic shear modulus $G_{zy}$ for macroscopic shear displacements perpendicular to the magnetization $\mathbf {M}$ but with $\mathbf {M}$ contained in the shear plane, both for increasing magnetization [82]. First, the particle rearrangements due to increasing magnetic interactions lead to slight mechanical softening, i.e., decreasing elastic moduli. However, with increasingly pronounced chain formation, the elastic moduli start to significantly increase, reflecting the mechanical hardening [82].

We remark that, when the particles have collapsed to the chain-like aggregates [82] or to other states of virtual touching [10, 11, 90], a characterization in terms of linearly elastic springs and magnetic dipoles located at the particle centers cannot provide a quantitatively reliable framework any longer. A corresponding comparison was performed with experiments and simulations that take into account nonlinear elasticity and spatially resolved magnetization across the particles [90]. Good quantitative agreement was demonstrated for two mutually magnetically attracting spherical particles of initial surface-to-surface separation of about 1.5 particle radii for particle displacements of up to about 15$\%$ of the initial center-to-center distance. Also the point of collapse to a virtually touching state under increased magnetic attraction was determined with good quantitative agreement [90]. However, the transition from the virtually touching state back to a separated state under decreasing magnetic attraction was predicted to occur too early by the linearly elastic description based on magnetic dipoles, with a deviation of about 25$\%$ [90]. A first step beyond the basic dipole picture is to include higher-order magnetic moments in a corresponding multipole expansion [10]. Yet, this represents an economic procedure predominantly in the regime of validity of linear magnetization laws [11]. In practice, magnetic saturation effects were observed to become important in the regions of virtual touching of collapsed magnetized particles [90].

Finally, we note that the elastic hardening was recently observed in experiments together with the chain formation [95]. Reversible increase in the elastic moduli by factors of 6–7 was found [95]. These achievements stress the prospective significance of the materials for practical usage.

2.3 The importance of nonaffine deformations

Already before the mentioned dipole-spring approaches, several different theoretical studies on magnetic gels and elastomers focused on the involved changes in the elastic moduli under homogeneous external magnetic fields [43, 44, 114]. Due to the complexity of the systems, other simplifying assumptions have often been applied in this context. One of them is the assumption of affine (homogeneous) deformations. This means that the overall deformation ratio of a given system is mapped to any distance in the inside of the system. All distances on all scales are changed by the same overall ratio. An illustrative one-dimensional example is given on the left-hand side of Fig. 9.

Fig. 9

Top: a straight arrangement of magnetic particles connected by elastic springs is compressed longitudinally as indicated by the light horizontal arrows. The particles carry magnetic moments that here are vertically oriented and all point into the same direction, leading to mutual repulsion. Bottom left: an affine (homogeneous) deformation due to the compressive forces dictates that all distances within the system, that is, also all mutual particle distances, change by the same ratio, e.g., by approximately $25\%$ in the present case. Bottom right: however, in reality, the system will deform in a nonaffine (inhomogeneous) way. Since the nearby particles in the center are closer to each other, the magnetic repulsion between them is stronger and their mutual approach under the overall deformation will be less than between the outer particles. Thus the internal degrees of freedom can play an important role. (Color figure online)

However, such an approach neglects the role of the internal degrees of freedom. To minimize the overall energy of the system, such internal degrees of freedom relax as well, for instance, under imposed macroscopic deformations. In our case, as soon as the distribution of the magnetic particles is not very regular, the relaxation of these internal degrees of freedom can lead to nonaffine (inhomogeneous) deformations; see the simple illustrative example on the right-hand side of Fig. 9.

Dipole-spring models allow the independent displacement of the particles and the network nodes to minimize the overall elastic and magnetic energy of the system. In this sense, they represent a significant improvement by including additional internal degrees of freedom, yet being simple enough to allow an efficient straightforward evaluation. This can become increasingly important for increasing disorder in the arrangements of the magnetic particles [80].

It was found that the assumption of affine deformations can even lead to qualitatively different predictions [80]. Figure 10 shows a corresponding example. There, an irregular two-dimensional particle arrangement was studied for illustration. The particles were placed at the positions at which the chain-like aggregates in a real anisotropic sample [35], similar to the one depicted in Fig. 1b, cut a cross-sectional plane. Following a Delaunay triangulation [23], springs were placed between nearby particles, see Fig. 10a. Magnetic moments of identical magnitude where assigned to the particles, pointing into one identical direction perpendicular to the plane. The elastic Young modulus E describing the stress necessary to uniaxially stretch by a small given amount a quadratic piece of the interior of this system, see the inset of Fig. 10b, was determined. This modulus is plotted as a function of the amplitude of the magnetic moments m of the particles in Fig. 10b. Obviously, the assumption of affine deformations leads to a trend with increasing m opposite to the one predicted when allowing for nonaffine deformations. This highlights the role of the internal degrees of freedom and suggests that the assumption of affine deformations needs to be handled with special care.

Fig. 10

Reproduced from Ref. [80], with the permission of AIP Publishing. (Color figure online)

Illustration of the importance of nonaffine deformations. a Using X-ray microcomputed tomography, chain-like aggregates similar to the ones in Fig. 1b were identified in a real anisotropic sample [35]. To obtain a simple two-dimensional example system, magnetic particles were placed at those positions at which the chains cut one selected cross-sectional plane. Elastic springs were set along edges between nearby particles identified via Delaunay triangulation [23, 80], see the (blue) lines. Magnetic moments of identical magnitude m, with $m_0$ setting the corresponding unit, were assigned to the particles, pointing into one common direction perpendicular to the plane [80]. b The elastic Young modulus E here describes the stress necessary to achieve a uniaxial elongation or compression of a quadratic piece cut from the interior of the system, see the inset, in the linearly elastic regime. Plotting E for increasing magnitude of the magnetic moments m shows that the assumption of affine deformations leads to the opposite trend when compared to the nonaffine dipole-spring model [80].

Another illustrative example situation, in which nonaffine deformations around rigid inclusions in an elastic matrix arise, are the rotations of magnetically anisotropic particles [91, 100], elongated magnetic particles [9], or magnetic particle clusters [99] when a homogeneous external magnetic field is applied. In particular, if the initial orientations of these inclusions are not ordered, the induced different rotations lead to an overall spatially inhomogeneous distortion of the surrounding elastic matrix. For the rotations of rigid spherical particles of no-slip surface conditions, resulting linearly elastic distortions in a continuous elastic matrix can be calculated analytically [91], see below.

3 Explicit analytical calculation of matrix-mediated interactions between the embedded particles

In a further elaborated treatment on the mesoscopic level, the elastic matrix is not discretized into a spring network. Instead, it is described as an elastic continuum. In principle, such a procedure corresponds to taking into account an infinite amount of internal degrees of freedom. Accordingly, the equations of continuum elasticity theory need to be solved in the presence of the embedded virtually rigid magnetic or magnetizable particles.

The situation of predominant interest in the context of magnetic gels and elastomers is the following. Magnetic interactions between the particles are induced or altered by external magnetic fields. Corresponding mutual magnetic forces between the particles result [45]. Additional net forces may be introduced, for instance, if the particles are subject to an external magnetic field gradient [45]. Apart from that, magnetically anisotropic particles also experience a net torque, if their axis of anisotropy is not aligned with the direction of the magnetic field [9, 93, 100].

Since the embedded particles cannot move through the surrounding matrix, they push against the elastic environment and distort it until the restoring elastic forces balance the induced magnetic ones. The same applies to induced torques and rotations of the particles, if slipping of the polymer matrix along the particle surfaces is hindered.

The induced distortions of the elastic matrix are long-ranged. Consequently, they affect all other particles embedded in the matrix. These other particles are displaced and rotated according to the distortion of the matrix surrounding them. Moreover, they resist their own deformation due to their mechanical rigidity. Altogether, this significantly couples the displacements and rotations of all particles in the elastic matrix resulting from the induced forces and torques. The problem was solved explicitly and analytically to a given order within the framework of linear elasticity theory [67, 89, 91].

3.1 Description of the formalism

We here illustrate the effects summarized above. For the explicit formulae and the path of calculation, we refer the reader to Refs. [89, 91].

For simplicity, we consider an infinitely extended, homogeneous, and isotropic elastic matrix. Its deformations are described by linear elasticity theory [58]. The displacement of any volume element of this matrix, located at position $\mathbf {r}$, is then quantified by the displacement field $\mathbf {u}(\mathbf {r})$. Linear elasticity theory dictates the following equation that needs to be satisfied within the elastic matrix [76]:

$$\begin{aligned} \nabla ^2\mathbf {u}(\mathbf {r}) + \frac{1}{1-2\nu }\nabla \nabla \cdot \mathbf {u}(\mathbf {r}) ={} -\frac{1}{\mu }\mathbf {f}_b(\mathbf {r}). \end{aligned}$$

(1)

In this equation, $\nabla$ denotes the gradient operator, $\nu$ is the Poisson ratio connected to the compressibility of the matrix, $\mu$ is the elastic shear modulus, and $\mathbf {f}_b(\mathbf {r})$ is the bulk force density applied to the polymeric matrix.

Specifically, we consider the situation of the surrounding elastic polymeric matrix persistently anchored to the surfaces of the embedded particles. The matrix may not slip along or detach from the particle surfaces. Such a situation arises, for instance, if the polymer molecules show a strong tendency to adsorb to the particle surfaces [40], or if they are covalently bound to the particle surfaces [41, 72]. Moreover, for simplicity, we only consider rigid spherical embedded particles of identical size. Then, the stick surface conditions take a relatively simple mathematical form. For a sphere with its center positioned at $\mathbf {r}_0$, we find for the displacements of the points $\mathbf {r}$ on its surface $\partial V$

$$\begin{aligned} \mathbf {U} + \varvec{\varOmega }\times (\mathbf {r}-\mathbf {r}_0) \,=\, \mathbf {u}(\mathbf {r}) + \int _{\partial V} \underline{\mathbf {G}}(\mathbf {r}-\mathbf {r}^\prime )\cdot \mathbf {f}(\mathbf {r}^\prime ) \,\mathrm {d}S^\prime . \end{aligned}$$

(2)

Here, the left-hand side describes the displacements of all the surface points of the sphere. It results from the translation $\mathbf {U}$ and the rigid rotation $\varvec{\varOmega }$ of the sphere, with $\varvec{\varOmega }$ the rotation vector. Due to the stick surface conditions, these displacements need to be identical to the displacements of the matrix elements anchored to the particle surfaces, given by the right-hand side. There, $\mathbf {u}(\mathbf {r})$ denotes the displacement field imposed onto the matrix, e.g., by an externally imposed overall deformation or by the action of the other embedded particles. Yet, also the sphere under present consideration may exert a set of forces onto the matrix across its surface, quantified by a surface force density $\mathbf {f}(\mathbf {r}')$ with $\mathbf {r}'\in \partial V$. Since an explicit expression for the corresponding Green’s function $\underline{\mathbf {G}}(\mathbf {r})$ is available [103], the resulting matrix displacements can be calculated explicitly as given by the integral expression.

Equations (1) and (2) together with the explicit expression of the Green’s function $\underline{\mathbf {G}}(\mathbf {r})$ [103] form the basis of all further evaluations. From them, the distortion of the surrounding matrix can be calculated when individual embedded spherical particles exert forces or torques on the surrounding matrix [85, 89, 91]. Moreover, the so-called Faxén laws can be derived that describe how individual embedded spherical particles are displaced and rotated in a given distortion of the matrix [52, 77, 89, 91]. For the explicit calculations, see Refs. [89, 91].

Qualitatively, the following scenarios may arise. A force on a first particle pushes it against the surrounding matrix, leading to a particle displacement and a distortion of the elastic environment, see Fig. 11a. Unless another particle embedded in the displaced matrix environment is held fixed by some external force, it is displaced together with the surrounding matrix as induced by the displacement of the first particle. This situation is referred to as translation–translation coupling between the particles. Moreover, the matrix distortion induced by the first particle decays with increasing distance from the first particle. This leads to an additional rotation of the second particle in a rotation–translation coupling, see Fig. 11b.

Fig. 11

Illustration of the matrix-mediated coupling between the translations and rotations of rigid spherical particles embedded under no-slip surface conditions in an elastic matrix [89, 91]. a Exerting a force $\mathbf {F}_{\mathrm {ext}}$ on a first particle pushes it against the surrounding matrix. This leads to a displacement of the particle and an associated distortion of the surrounding matrix, quantified by a displacement field $\mathbf {u}(\mathbf {r})$, indicated by the light bold curved arrows. As a consequence, a nearby particle, which is likewise embedded in the matrix, is displaced together with the enclosing matrix by a displacement vector $\mathbf {U}$ (translation–translation coupling). b The induced displacement field $\mathbf {u}(\mathbf {r})$ decays with the distance from the first particle. It is thus a bit stronger on that side of the second particle which is closer to the first particle. Thus, an additional rotation of the second particle results, given by the rotation vector $\varvec{\varOmega }$ (rotation–translation coupling). c Similar situations arise when the first particle is rotated by an external torque $\mathbf {T}_{\mathrm {ext}}$, leading to an associated displacement field $\mathbf {u}(\mathbf {r})$ of the matrix. Then, likewise, a nearby particle may be displaced (translation–rotation coupling), and d be rotated (rotation–rotation coupling). For the described formalism, the displacements and rotations need to be small enough to allow a characterization within the framework of linear elasticity theory. (Color figure online)

In analogy to that, under the given stick surface conditions, torques acting on the first particle induce corresponding distortions of the elastic matrix as well. The resulting matrix deformations likewise imply displacements and rotations of other embedded particles under corresponding translation–rotation and rotation–rotation couplings; see, respectively, Fig. 11c and d.

There is even more to this mutual matrix-mediated coupling between the embedded particles. Each particle is of finite size and rigid. Due to their rigidity, the particles themselves do not deform. Instead, they resist the deformation that the surrounding matrix would dictate. The resistance to deformations imposes additional stresses onto the matrix. These additional stresses lead to additional distortions that again affect all other particles, and so forth. In the end, a highly coupled situation arises.

Nevertheless, the problem can be solved explicitly and analytically by an iterative procedure that corresponds to an expansion in the inverse separation distance between the particles [89, 91]. The analytical solution has the following structure. It presumes that in a given, known particle configuration also all the forces and torques on all the particles are known. From the given particle configuration, so-called displaceability and rotateability matrices [89, 91] are calculated and multiplied to the vector of all forces and torques,

$$\begin{aligned} \left( \!\begin{array}{c} \mathrm {particle\;displacements}\\ \mathrm {particle\;rotations} \end{array}\!\right) = \left( \!\begin{array}{c} \mathrm {displaceability\; and}\\ \mathrm {rotateability\; matrices} \end{array}\!\right) \cdot \left( \!\begin{array}{c} \mathrm {forces\;on\;the\;particles}\\ \mathrm {torques\;on\;the\;particles} \end{array}\!\right) . \end{aligned}$$

(3)

The induced coupled displacements and rotations of all embedded particles on the left-hand side of this equation are the immediate result of this multiplication.

In Refs. [89, 91], the explicit analytical expressions for the displaceability and rotateability matrices were derived to quartic order in the inverse separation distance between the particle centers. These expressions represent the actual analytical solution of Eq. (1) to the set order. Then, Eq. (1) does not need to be solved numerically, e.g., by finite-element simulations, any longer. Moreover, the solution may be used to gauge related numerical approaches, or to speed them up by providing an initialization, even if the solution to a nonlinear problem, for nonspherical particle shapes, or for small distances between the particles is looked for. It should be stressed that the linearity of Eq. (1) plays a central role for the described analytical solution and for its form according to Eq. (3). A similar strategy had been pursued before in low-Reynolds-number hydrodynamics in solving the corresponding linearized limit given by the Stokes equation [24].

We add two remarks. First, the described formalism is not restricted to magnetic particles. Any types of forces and/or torques imposed on the embedded inclusions can be inserted on the right-hand side of Eq. (3), for instance, gravitational forces or those induced by external electric fields [1]. Second, the inverse situation, in which the displacements and rotations of the embedded particles are prescribed and the necessary forces and torques are calculated, had been addressed as well [86].

3.2 Comparison with experimental results

To confirm the benefit of the theory, its predictions were compared to results obtained from actual experiments. For this purpose, paramagnetic nickel particles featuring a low magnetic remanence were embedded far from any boundaries into a soft swollen polymeric gel matrix [89]. Figure 12a shows a top view of a planar arrangement of three such particles. Next, a homogeneous external magnetic field was applied to the system. Experimental details are given in Ref. [40]. The external field induced mutual magnetic interactions between the particles. To vary the magnetic interactions and to test several different configurations using the same sample, the magnetic field was rotated in the plane of the particle arrangement. In the situation depicted in Fig. 12a, a clockwise rotation was performed, starting from the direction indicated by the black arrow. Care was taken to select particles of virtually spherical shape, which allowed to concentrate on the influence of induced forces.

Fig. 12

Reprinted figure with permission from [89]. Copyright 2016 by the American Physical Society. (Color figure online)

Comparison between theoretical predictions obtained from analytical calculations and experimental results for the changes in distances between magnetically interacting particles in a soft elastic matrix [89]. a Paramagnetic nickel particles of low magnetic remanence and of diameter $208.5\pm 2.3$ $\upmu$m are embedded in a soft swollen polymeric gel matrix. Magnetic interactions between the particles are induced by applying a homogeneous external magnetic field. To tune the magnetic interactions, the field is rotated clockwise in the plane of the particle arrangement, starting from the direction of the black arrow. b–d Experimental data points obtained for the resulting changes in particle distances are given by the (blue) squares, while theoretical predictions are shown by the solid (red) lines. Uncertainties are indicated by the bars and shaded areas, respectively. There is one simultaneous overall fit parameter for all three curves, which is the local mechanical shear modulus of the matrix. In this type of micromechanical approach, it was determined as $\mu =76.3\pm 11.7$ Pa.

Fig. 13

Reproduced from Ref. [67], with permission from the Royal Society of Chemistry. (Color figure online)

Example situation, in which the influence of a nearby rigid bounding wall (hatched) can have a qualitative effect on the behavior of magnetizable particles (black spheres) in an elastic matrix [67]. The magnet below the rigid surface induces magnetic moments $\mathbf {m}$ on the particles. Consequently, they attract each other. However, the external magnetic field is inhomogeneous, simultaneously exerting gradient forces $\mathbf {F}_{\nabla }$ on the particles that pull them against the boundary. As a result, an overall net outward displacement $\mathbf {U}_{\nabla }^{\mathrm {out}}$ may result for the particles. The reason is given by the compression of the matrix between each particle and the surface, which makes the matrix escape to the sides and take the particles along.

Using a microscope, the changes in the three mutual distances between the three particles were recorded when applying and rotating the external magnetic field, see Ref. [89] for further details. The data points in Fig. 12b–d show the corresponding experimental results. In addition to that, the solid lines reflect the theoretical prediction using the experimental system parameters as an input. To calculate the curves, a dipole approximation was used to evaluate the magnetic interactions [89]. Yet, the change in the strength of the magnetic interaction with varying particle distances was taken into account [89]. In this way, the experimental data points in Fig. 12b–d can be reproduced. The different shapes of the curves result because the arrangement in Fig. 12a slightly deviates from that of a perfect equilateral triangle.

In calculating the theoretical curves, the Poisson ratio was set to $\nu =1/2$, implying an incompressible elastic matrix. There is only one simultaneous overall fit parameter, which is the local shear modulus of the surrounding matrix. Due to the softness of the gel, its magnitude could not be determined to the required accuracy in a macroscopic shear experiment. Yet, from our combined approach of theory and experiment, it can be determined in a type of micromechanical measurement. The procedure was confirmed by analyzing additional samples of two and four particles as well [89].

3.3 Influence of rigid boundaries

All the above considerations, in principle, concern particles embedded in an infinitely extended elastic matrix, or, at least, particle configurations sufficiently distanced from any boundary, see the experiments in Ref. [89]. It turns out that the presence of a nearby boundary can significantly alter the response, even qualitatively.

The influence of a flat rigid bounding wall was analyzed in the formalism illustrated above to lower order [67]. Two different surface conditions were addressed on this flat bounding wall: first, a free-slip surface that allows slipping of the elastic matrix along the wall but no penetration into or detachment from it; and second, a no-slip surface on which the elastic matrix is rigidly anchored and cannot displace at all.

Basically, the same formalism can be developed as described in Sect. 3.1. However, an explicit expression for the corresponding Green’s function is necessary [67, 84]. In Ref. [67], such an expression was calculated explicitly for a no-slip surface condition using methods of Fourier transformation.

An example situation, in which the rigid boundary has a qualitative effect, is illustrated in Fig. 13 [67]. There, a magnet acts on two magnetizable particles embedded in an elastic matrix close to a rigid surface. The induced magnetic moments in the illustrated configuration would lead to an attraction between the two particles. However, the simultaneous gradient forces of the magnetic field may draw the particles towards the rigid surface. As a consequence, the distance between the mutually attracting particles does not necessarily decrease, as might be expected at first glance, but may increase. Namely, the matrix when pushed by the particles towards the surface escapes to the sides and takes the particles along. Both free-slip and no-slip surfaces allow this type of behavior. It should be possible to observe the effect in corresponding experiments.

4 Tunable, nonlinear, superelastic stress–strain behavior of anisotropic systems

In the previous sections we were mainly confining ourselves to relatively small-scale imposed deformations in which the materials are appropriately described by linear elasticity theory. This is different in the following when we address the nonlinear stress–strain behavior. Particularly, we study the behavior of anisotropic systems that contain chain-like aggregates [19, 34, 35, 40, 107] of magnetic particles.

To achieve this goal, numerical investigations were performed [21, 22]. A typical numerical system is illustrated in Fig. 14. The magnetic particles are represented by rigid spheres of finite size, each of which carrying a permanent magnetic dipole moment of identical magnitude. They are arranged in straight and parallel particle chains of identical particle separation within the chains in the undeformed state, longitudinally shifted relatively to each other. The polymeric matrix is discretized into a mesh of tetrahedra as indicated in the figure. Each tetrahedron may deform in an affine way only, while different tetrahedra may deform in different ways. Accordingly, globally inhomogeneous, nonaffine deformations of the matrix are described. Neighboring tetrahedra are connected to each other at their vertices. The mechanical forces resulting from the affinely deformed state of each tetrahedron on its vertices can be calculated directly. A nonlinear elastic energy density in terms of a nearly incompressible Neo-Hookean model [105] was used in Refs. [21, 22] to this end. The spheres were embedded in the matrix by no-slip surface conditions.

Fig. 14

Reproduced from Ref. [21], with the permission of AIP Publishing. (Color figure online)

Numerical realizations of anisotropic systems containing rigid spherical particles of finite size arranged in chain-like aggregates [21, 22]. Each particle carries a permanent magnetic dipole moment of identical magnitude, here indicated by the bar magnets. The elastic matrix is discretized into a mesh of tetrahedra that are connected to each other at their vertices. No-slip boundary conditions apply for the vertices on the surfaces of the spheres. To determine the stress–strain behavior, the system is numerically clamped on the faces at which the chains start and end. Then, the forces necessary to achieve a certain elongation are recorded.

To analyze the features of the corresponding nonlinear stress–strain behavior, the systems were numerically clamped on their faces at which the chain-like aggregates start and end. Then, the distance between the clamps was increased in small steps. After each step, the system was given time to relax under the modified distance between its clamped faces. The forces on the clamps were determined after each relaxation as a function of the achieved elongation. In the same quasistatic manner, the clamps were afterward driven back to their initial states.

Two different types of magnetic particles were investigated. On the one hand, the magnetic moments could freely reorient within the particles, relatively to the particle frame, in order to minimize the overall magnetic interaction energy [21, 22]. On the other hand, the orientations of the magnetic moments were anchored in the particles, i.e., locked to the particle frame [22].

4.1 Freely reorientable magnetic moments

We first consider the situation of magnetic moments that may freely reorient relatively to the frames of the carrying particles to minimize the overall magnetic energy. Resulting stress–strain curves (more precisely force-strain curves) obtained numerically as described above for systems as depicted in Fig. 14 are displayed in Fig. 15. These curves are obtained by averaging over twenty different realizations of the numerical system. Solid lines mark the curves for stretching the sample, dotted lines for releasing the strain afterward. Obviously, hysteretic behavior occurs.

Fig. 15

Reproduced from Ref. [21], with the permission of AIP Publishing. (Color figure online)

Magnetically tunable nonlinear stress–strain behavior of anisotropic magnetic systems. Each curve represents an average over twenty different numerical realizations of systems as the one in Fig. 14. Solid lines represent the loading process of elongation, dotted curves refer to unloading. The black solid lines reveal pronounced nonlinear stress–strain behavior with a steep initial increase, a subsequent plateau-like regime, followed by a dip, and then a relatively regular appearance. a External magnetic fields perpendicular to the stretching axis can shift the plateau and finally switch it off completely. b In contrast to that, a magnetic field applied parallel to the stretching axis leaves the plateau intact but removes the dip from the curves.

We first concentrate on the black solid line for vanishing external magnetic field. It first shows a very steep increase. Then, a plateau-like behavior follows over a broad strain regime. Apparently, applying a small additional amount of stress in this pre-stretched region, a large additional stretching can be achieved. In analogy to the terminology used in the context of shape-memory alloys, where qualitatively similar behavior was identified, this regime was termed “superelastic.” A dip occurs at the end of this region, before a relatively regular increase in stress follows beyond this pronouncedly nonlinear interval. All deformations are reversible, as indicated by the black dotted line.

Remarkably, this nonlinear behavior can be tuned from outside by an external magnetic field, as indicated by the colored lines in Fig. 15. As Fig. 15a demonstrates, a field perpendicular to the chain and stretching axes can shift the plateau on the stress–strain curve, or even switch it off completely for high field magnitudes; see the brightest (gray) curve. In contrast to that, an external magnetic field parallel to the chain and stretching axes, see Fig. 15b, maintains the plateau, but removes the dip at its end.

All these properties can be understood in a very illustrative way [21, 22]. To comprehend the behavior in Fig. 15a, it is sufficient to concentrate for the moment on the single chain-like aggregates in Fig. 14. Starting to stretch the system, one pulls on the compact chains. Since the magnetic particles are in close vicinity to each other along each chain, the magnetic attraction between them is quite strong (the magnetic dipole–dipole interaction diverges with the cube of the inverse distance between the dipoles [45]). Pulling against this attraction leads to the steep initial increase in Fig. 15. However, if a certain threshold of applied stress is reached, the strong magnetic attraction is overcome at the weakest link of the weakest chain under the given strain. Then, the corresponding part is detached from the rest of the chain. With this increasing distance between the detached parts, the initially strong mutual magnetic attraction drops, allowing for an even further increase in distance. Along these lines, more and more parts are detached from the chains throughout the system with increasing overall strain. Each such event of detachment corresponds to a small drop along the stress–strain curve in Fig. 15 in this strain-controlled analysis, which in total with increasing overall strain leads to the pronounced plateau. After all the particles have been separated from each other, the magnetic attraction becomes comparatively weak, and the stress–strain curve crosses into a regular behavior beyond the plateau. It is then also clear why a perpendicular magnetic field can switch off the plateau. The field rotates the freely reorientable magnetic moments into a perpendicular direction, so that the underlying effect of magnetic attraction along the chains is lost. A more exhaustive illustration of these processes including corresponding figures is found in Ref. [21].

Considering the process of separating the embedded particles from each other along the horizontal stretching axis in Fig. 14, together with the disintegration of the chains as described above, also allows us to understand the dip at the end of the plateau. Due to the approximate overall volume conservation, the elongation of the system along the chain and stretching axes implies a contraction from the sides. At a certain degree of deformation, the distance between particles along the stretching axis therefore becomes comparable to distances along rather transversal axes. At this point, magnetic moments can reorient or “flip” away from the stretching axis to minimize the overall magnetic energy. When such “flipping” events occur, the magnetic moments switch from an attractive into a repulsive configuration along the stretching axis. Moreover, they mutually attract each other along a transversal direction. Due to the approximate overall incompressibility, this further adds to driving the particles apart and thus to elongate the system along the stretching axis. The process is illustrated on a more regular cuboid system in Ref. [21], including corresponding figures. In total, the dip at the end of the plateau appears in our strain-controlled analysis because “flipping” of the magnetic moments leads to a reduced stretching force necessary to maintain a given strain. Consequently, it also becomes clear why the parallel magnetic field can switch off this dip. It keeps the magnetic moments oriented along the stretching axis.

Fig. 16

Reproduced from Ref. [22], with permission from the PCCP Owner Societies. (Color figure online)

Nonlinear stress–strain behavior of mesoscopic systems as in Fig. 14, but with two central differences [22]: Each magnetic moment is rigidly anchored to the frame of its carrying particle and all chains show identical orientation of their magnetization. a As a result, the dip on the stress–strain curve is absent (compare to Fig. 15) and the system hardens at large strains for magnetic fields parallel to the initial magnetization direction. b Stretching by $100\%$ leads to rotations of particles due to the elastic inhomogeneities resulting from the particle rigidity in contrast to the softness of the elastic matrix. c However, the strongest magnetic field considered in a suppresses these reorientations.

We remark that these nonlinear stress–strain properties show significant similarities to the nonlinear stress–strain behavior of nematic liquid-crystalline monodomain elastomers [57, 70, 71, 106]. Such materials contain rod-like molecules that are on average oriented along a global preferred axis. If stretched perpendicular to this axis, likewise a type of plateau-like region can be observed, together with a reorientation of the averaged molecular orientations towards the stretching axis.

4.2 Locking the orientations of the magnetic moments

Apart from that, the consequences of rigidly locking the orientations of the permanent magnetic moments to the corresponding particle frames have been analyzed in detail [22]. Due to the no-slip surface conditions of the surrounding matrix on the particle surfaces, the magnetic moments can then only rotate by dragging the attached elastic matrix along. Thus magnetic reorientations are directly linked to distortions of the elastic matrix or global rotations of the system. The latter are suppressed by clamping the systems on their longitudinal faces as described above.

Two qualitatively different extreme cases of such systems are conceivable. First, if one generates such anisotropic materials in reality by applying external magnetic fields during fabrication as described in Sect. 1, not only the chains form. Also all the magnetic moments along all chains point into the same direction, in contrast to the situation of Fig. 14, in which different chains can show opposite orientations of the magnetic moments for overall minimization of the magnetic energy. Then, a net magnetization of the whole system arises [19].

We consider the nonlinear stress–strain curve of the latter system in Fig. 16a. The first qualitative difference when comparing to the case of freely reorientable magnetic moments in Fig. 15 is that the dip at the end of the plateau-like regime is absent. Since this dip was a consequence of the possible “flipping” of the nonanchored magnetic moments, it is illustratively clear that it is absent when locking the magnetic moments. Moreover, under an increasing magnetic field parallel to the overall magnetization direction, we now observe an elastic hardening at high strains in Fig. 16a. It can be explained as follows. Since the magnetic particles are much more rigid than the elastic matrix, strain inhomogeneities arise in the system under stretching. These lead to local shear deformations as a channel to minimize the overall elastic deformation energy. Such local shears are reflected by rotations of the magnetic particles, which become visible in Fig. 16b by the reoriented magnetic moments. However, if strong external magnetic fields block these reorientations, see Fig. 16c, also the particle rotations are hindered. Consequently, local relaxations of deformation energy involving particle rotations are blocked. Thus, the overall deformational energy is higher, reflected by an elevated stress–strain curve at higher strains in Fig. 16a. Again, this effect demonstrates the qualitative role that nonaffine deformations can play.

Yet, since the chains are still present in the system, the detachment mechanism described in Sect. 4.1 is still at work. Thus we again observe the plateau-like regime in Fig. 16a. If strong perpendicular magnetic fields can reorient the magnetic moments despite their anchoring to the particle frames, the plateau can still be altered or switched off. However, here this involves significant shear-like distortions of the system as the attached elastic matrix needs to rotate together with the particles; see the further illustration in Ref. [22].

A second, qualitatively different situation mixes the two previous cases. It contains blocked magnetic moments locked to the particle frames as just described, but opposite magnetization directions of different magnetic chains as shown in Fig. 14. In reality, it may be possible to generate such systems by not using magnetic fields to align the magnetic particles during fabrication. Potentially, external electric fields may serve the purpose [31].

In this case, the stress–strain curve in the absence of magnetic fields is qualitatively very similar to the one just described, compare the black curves in Figs. 16a and 17a. However, strong external magnetic fields applied along the magnetization direction of one randomly selected embedded particle chain can now switch off the plateau. This behavior can be understood by recalling that now about half of the magnetic moments are aligned approximately oppositely to the external magnetic field. Strong magnetic fields thus tend to reorient them. Due to their locking to the particle frames, also the corresponding particles are rotated, together with the attached elastic matrix. This strongly distorts the system; see Fig. 17b for an example. As a consequence, the chain-like aggregates are disintegrated to a significant degree. Then the detachment mechanism is disabled together with the plateau-like appearance of the stress–strain curve.

Fig. 17

Reproduced from Ref. [22], with permission from the PCCP Owner Societies. (Color figure online)

Nonlinear stress–strain behavior of mesoscopic systems as in Fig. 14, now with the only central difference [22] that each magnetic moment is rigidly locked to the frame of its carrying particle. a Then, the dip on the stress–strain curve is still absent (compare to Figs. 15 and 16a). However, an external magnetic field applied along the magnetization direction of one randomly chosen embedded chain can now switch off the plateau. b This is because the induced rotations of the misaligned magnetic moments strongly and inhomogeneously distort the system. Consequently, the chain-like structures are disintegrated, and the detachment mechanism is suspended (snapshot for intermediate magnetic field strength and $30\%$ of stretching).

Likewise, strong perpendicular magnetic fields can again reorient the magnetic moments and alter or switch off the plateau. In this case, all particles are involved in the reorientation, yet with opposite senses of rotation for the initially oppositely oriented magnetic moments [22].

A detailed analysis of all these effects together with a more profound illustration, amended by corresponding stress–strain curves for magnetic fields applied perpendicular to the stretching axis, is found in Ref. [22]. There, also the strain-induced variations in the orientational ordering of the magnetic moments has been analyzed and quantified for the different mesoscopic example systems [22]. The same applies for the strain-induced structural reorganization of the embedded magnetic particles [22].

5 Density functional theory

All the different approaches described above have one feature in common. They include the elasticity of the polymeric matrix and in this way indirectly take into account temperature effects (elasticity of polymeric networks is to a big extent due to entropy [101]). However, thermal motion of the embedded magnetic particles is not considered explicitly. For many practical purposes, this is justified for semiquantitative modeling because the particle positions are locked by the elastic network and only fluctuate around their average. Yet, if such temperature fluctuations are to be explicitly considered, statistical approaches become necessary.

As one first step in this direction, a corresponding density functional theory has been developed [20]. Density functional theory (DFT) was initially derived to describe the properties of liquids of identical particles [29, 37, 61, 97]. A key component of such systems is that the particle positions are not fixed. Since the particles continuously change their locations due to thermal motion, they become indistinguishable. This is very different from the case of the embedded magnetic particles in magnetic gels and elastomers. In this latter case, the particle positions are locked in the elastic matrix, which renders the particles distinguishable. Likewise, for instance, in dipole-spring models, see Sect. 2, the particles are distinguishable. They can be identified by their relative position within the spring network, permanently linking them to a specific set of other particles.

This problem was addressed in the following way in Ref. [20]. In the theory, the particles are treated as indistinguishable as in a liquid. However, effective pair potentials are introduced that confine their relative motion and virtually lock their relative positions [20]. To test this procedure, the results were compared to molecular dynamics simulations. Only one-dimensional particle arrangements have been considered in this initial conceptual approach.

5.1 One-dimensional dipole-spring system

First, a finite straight arrangement of magnetizable particles linked by linear elastic springs was investigated, see Fig. 18a. Only magnetic moments of the particles pointing along the chain axis are considered. Figure 18b shows corresponding statistical density profiles for more than thirty particles linked to a straight dipole-spring chain, here in the absence of magnetic effects but including the role of thermal fluctuations. The density profiles are related to the probability to find a chained particle at a certain position. This probability is higher at the locations of the density peaks. Since under thermal fluctuations the particles are in persistent motion, the peaks are not sharp. Instead, they show a finite thickness.

Fig. 18

Reproduced from Ref. [20]. © IOP Publishing. Reproduced with permission. All rights reserved. (Color figure online)

Density functional theory for one-dimensional straight dipole-spring arrangements [20]. a A finite number of identical particles (here four) is linked by harmonic elastic springs (spring constant k) between nearest neighbors. All springs in the undeformed state have identical length (here l). The particles are of finite size (diameter d) and cannot penetrate through each other. Those particles at the ends (separated by a fixed distance L from each other) form the system boundaries. If magnetized, the magnetic moments (identical magnitude m) are confined to the system axis. b Density profiles $\rho (x)$ for a chain of more than thirty nonmagnetic particles confined to a straight configuration along the x axis. To derive the theory, the springs are replaced by effective pairwise potentials between the particles (pseudo-springs). Monte Carlo simulations (“MC”) demonstrate that this replacement works well. Deviations between the theory (“DFT”) and the simulations stem from the pronounced influence of thermal fluctuations in one-dimensional systems: While simulations correctly predict a fluid-like state, the theory due to the involved mean-field approximation shows artificial crystalline appearance.

Initially, this dipole-spring system was evaluated using discrete Monte Carlo simulations (MC) at finite temperature [20]. Sampling averages lead to the density profiles. In these simulations, the systems as in Fig. 18a were evaluated directly without further approximations. The corresponding results, labeled by “MC real springs” in Fig. 18b, thus provide a benchmark to test the validity of the theory and further approximations. Next, the discrete elastic springs were replaced by effective pair potentials as described above, basically acting between nearest neighbors along the chain. As corresponding MC simulations demonstrate, this approximation works very well, see the virtually indistinguishable density profile “MC pseudo-springs” in Fig. 18b.

However, considering the results from the DFT in Fig. 18b, significant discrepancies become obvious [20]. While the simulations reveal an increasingly liquid-like state of the particles with growing distance from the boundaries, the DFT predicts a rather crystal-like arrangement. This is an artifact of the theory, which involves a mean-field approximation. It is well known that in one dimension thermal fluctuations, in the absence of sufficiently long-ranged interactions, hinder crystalline order [18]. The mean-field approximation in the DFT suppresses these fluctuations. Yet, this effect is most pronounced in one dimension. It is less dominant in higher dimensions, particularly for three-dimensional systems. Therefore, this discrepancy should not be too discouraging, if one thinks of the characterization of real samples.

5.2 Chain-like aggregate in an elastic matrix

As one step towards the description of real systems, instead of characterizing a free-standing dipole-spring chain, a regular straight arrangement of particles embedded in a three-dimensional elastic matrix was addressed [20]. The behavior of colloidal particles exposed to additional forces or torques and embedded in an isotropic linearly elastic matrix has been analyzed at length in Refs. [67, 89, 91], see also Sect. 3. Transferring the situation of an embedding three-dimensional elastic matrix to a dipole-spring picture as in Fig. 18a, there are mainly two qualitative amendments.

First, the particles are anchored to their positions by the matrix. Any motion away from these locations induces restoring forces due to the resulting matrix deformation. Thus, only thermally induced fluctuations around their average positions occur. This effect is modeled by additional springs in Fig. 18a that attach the particles to their average locations [20]. The spring constant involved in this anchoring was related to the properties of the elastic matrix, using as an input the methods described in Refs. [89, 91]. In the DFT, this contribution was represented by a corresponding external potential anchoring the particles to given positions [20].

Second, matrix distortions induced in the elastic environment by individual particles are long-ranged and thus affect all other particles. This is likewise represented by additional springs in Fig. 18a. Any two particles are now linked by one spring, the spring constant of which decaying with the distance between the particles in the undeformed state [20]. Again, these spring constants were related to the matrix properties using the approach in Refs. [89, 91]. To include these interactions in the DFT, the pair potential acting between the particles and mentioned above was supplemented by corresponding long-ranged parts [20].

Figure 19 demonstrates the quality of this procedure. First, as before, the MC simulations with and without the springs replaced by according external and pairwise potentials show very good agreement. Second, in this embedded system, now also the density profiles obtained by DFT show very good agreement with the benchmark set by the MC simulations [20]. This is encouraging in view of possible future characterizations of real systems by appropriate statistical theories.

Fig. 19

Reproduced from Ref. [20]. © IOP Publishing. Reproduced with permission. All rights reserved. (Color figure online)

Similar system as in Fig. 18, but now for a chain-like aggregate of particles embedded in a three-dimensional elastic matrix [20]. Here, additional springs were included that anchor the particles in Fig. 18a to their average positions. Moreover, additional long-ranged springs were added between all particles in Fig. 18a with a spring constant that decays with the length of the undeformed spring. To construct a density functional theory (DFT), the springs were then replaced by an external and an amended pairwise potential, respectively. The density profiles obtained from direct Monte Carlo simulations (“MC real springs”) and from MC simulations using the effective potentials (“MC pseudo-springs”) show very good agreement and confirm the procedure. In this system, also the results from the theory (“DFT”) are well consistent with the benchmark set by the MC simulations [20].

As an important point concerning more practical questions, the approach now allows to evaluate the elastic moduli with thermal contributions included. In the present case, the principal elastic modulus characterizes compressive and dilative deformations of the chain-like aggregate. It was calculated for varying magnetic interactions between the particles, taking into account finite-temperature effects [20]. For the future, an interesting topic will be to analyze in more detail the role of thermal fluctuations in these materials and how they can be controlled via the inclusions by external magnetic fields.

6 Related studies

Finally, we briefly summarize several further studies in the field that relate to or supplement the works overviewed above.

6.1 Buckling of magnetic chains in soft gels under perpendicular magnetic fields

As described in Sect. 1, anisotropic magnetic gels and elastomers can be generated by applying a homogeneous external magnetic field during the production process. In the extreme case, this leads to the formation of chain-like aggregates permanently locked into the surrounding elastic polymer matrix [19, 34, 35, 40, 107]. To study in detail the behavior of the individual magnetic particle chains, especially the interplay between the magnetic and elastic properties, soft elastic gels of well-separated embedded chains composed of colloidal superparamagnetic particles were generated [40].

Under a perpendicular magnetic field, short chains of this kind were observed to rotate into the field direction. However, as the surrounding elastic matrix counteracts these reorientations, longer chains could not perform full rotations. Instead, they showed buckling morphologies of relatively constant wavelength. Consequently, the number of buckles per chain increases with the chain length. A more detailed account of this phenomenology is given in Ref. [40].

This behavior was further analyzed by a theoretical minimal approach [40]. The induced mutual magnetic interactions between the particles drive the buckling instability, which was accounted for by magnetic dipole–dipole interactions. It turned out that the chain-like aggregates themselves feature an additional bending stiffness, possibly by an increased adsorption of polymer molecules on the particle surfaces. Not including this bending contribution, rupture of the chains is expected instead of the observed smooth buckling, which has been confirmed by corresponding simulations [40]. Finally, it was shown that the appearance of multiple buckles per chain results from the role of the surrounding elastic matrix. In comparison with full rotations, local buckling of longer chains involves lower absolute displacements of the particles against the embedding matrix, especially at the ends of the chain. Still, locally and during buckling, segments of the chain can rotate into the external field direction to reduce the overall magnetic energy. A related reasoning was developed in the case of elastic filaments longitudinally compressed in an elastic environment, where, instead of the classical Euler buckling of one buckle along the whole filament, multiple buckles occur [15, 16].

6.2 Scale-bridging to the macroscale and the importance of relative rotations in anisotropic systems

In the previous sections, several different approaches of connecting different scales in the theoretical description of magnetic gels and elastomers have been mentioned. Additionally, for anisotropic systems containing chain-like particle arrangements, a direct connection between an idealized mesoscopic minimal model and the static part of a macroscopic hydrodynamic-like continuum theory has been worked out, see Ref. [63]. The mesoscopic model system, indicated in Fig. 20a, assumes infinitely extended chains of equally distanced point-like magnetic particles. All particles carry the same magnetic dipole moment. Magnetic interactions between different chains are neglected, and for simplicity only nearest-neighbor magnetic interactions within the chains were taken into account. Moreover, only affine deformations of the system were considered.

Fig. 20

Reproduced from Ref. [63], with the permission of AIP Publishing. (Color figure online)

Bridging from a mesoscopic minimal model for anisotropic magnetic gels and elastomers to a macroscopic hydrodynamic-like continuum description. a The mesoscopic model considers point-like magnetic particles, all of identical magnetic dipole moment $\mathbf {m}$, arranged by equal mutual distances $l_0$ in regular, infinitely extended chain-like aggregates [63]. Only affine, homogeneous deformations and rotations are considered and mutual interactions between different chains are neglected. b The macroscopic theory [12] effectively considers the overall system as composed of two coupled components, characterized by the orientation $\tilde{\mathbf {m}}$ of the macroscopic magnetization field on the one hand and the elastic background, here indicated by the gray network, on the other hand. If $\tilde{\mathbf {m}}$ is rotated by an amount $\delta \tilde{\mathbf {m}}$ that differs from the rotation $\varvec{\varOmega }^{\bot }$ of the elastic background, a relative rotation $\tilde{\varvec{\varOmega }}=\delta \tilde{\mathbf {m}}-\varvec{\varOmega }^{\bot }$ occurs between the two components. As simple scale-bridging between the two levels a and b, i.e., meso- and macroscopic scale, demonstrates, these relative rotations play a central role for the consistency of the macroscopic theory [63].

The macroscopic continuum theory [12] extends linear elasticity theory for uniaxial solids [58] to the present materials. For this purpose, it adds the macroscopic variables of relative rotations $\tilde{\varvec{\varOmega }}$, which are likewise familiar from the description of liquid-crystalline elastomers [14, 32, 68, 69]. In the present context, these variables quantify the relative rotations between the major two components that magnetic gels and elastomers consist of. On the one hand, this is the magnetic component, characterized by the macroscopic magnetization; on the other hand, it is the elastic background given by the polymer matrix; see Fig. 20b. Symmetry arguments then lead to two additional energetic contributions. The first one involves an additional material parameter $D_1$, which states that relative rotations cost energy. The second one, associated with a material parameter $D_2$, couples the relative rotations $\varvec{\tilde{\varOmega }}$ to the strain tensor.

From Fig. 20a, it is readily inferred from the mesoscopic model system that relative rotations indeed cost energy and the $D_1$ term is important. If, in the depicted situation, everything is held fixed but the magnetic moments are collectively rotated out of their aligned state, for instance, by a magnetic field, the magnetic dipole–dipole energy increases as a consequence of this relative rotation between the magnetic moments and the elastic background. The reason is the energetic minimum in the head-to-tail alignment of the magnetic dipole moments [45]. In contrast to that, the significance of the $D_2$ coupling term is less obvious. However, it turns out that this term plays a crucial role as shown in detail in Ref. [63]. In fact, based on the mesoscopic minimal model, it is readily demonstrated that this contribution is necessary to render linear elasticity theory consistent in describing the present anisotropic composite materials; see Ref. [63] for the explicit analysis.

Here, we can only indicate the underlying issue, see Fig. 21. As illustrated in Fig. 21a and b, horizontal and vertical shear, respectively, have a very different effect on vertically oriented chain-like aggregates on the mesoscopic level. The horizontal shear reorients the chains, while the vertical shear leaves the overall chain orientation basically unchanged. Macroscopic linear elasticity theory [58], however, even for uniaxial systems, does not distinguish between these two situations. In both cases, it maps the shear deformation to the same elastic strain tensor; see Fig. 21c. The macroscopic linearly elastic description is based on this identical strain tensor [58]. As comparison between the mesoscopic and macroscopic energies in Ref. [63] shows, the additional macroscopic $D_2$ coupling term heals this deficiency and is therefore of central importance, together with the variables of relative rotations themselves. The details are given in Ref. [63], together with explicit expressions for the macroscopic coefficients of anisotropic elasticity and the additional macroscopic material parameters $D_1$ and $D_2$ in terms of the mesoscopic model parameters. For anisotropic magnetic gels and elastomers, this is the first time that explicit expressions are provided for the parameters $D_1$ and $D_2$.

Fig. 21

Reproduced from Ref. [63], with the permission of AIP Publishing. (Color figure online)

A deficiency of conventional linear elasticity theory for uniaxial systems arises in characterizing anisotropic magnetic gels and elastomers that contain chain-like aggregates, as can be inferred from the mesoscopic minimal model in Fig. 20a. For this purpose, a horizontal and b vertical shear deformations are considered, where states before and during distortion are indicated in gray and black, respectively. a Under horizontal shear ($\gamma$), vertical chains are reoriented. b In contrast to that, the chains remain unaffected under vertical shear ($\eta$). c However, conventional linear elasticity theory for uniaxial systems [58] cannot reproduce this difference. Both situations are projected onto the same strain tensor $\varvec{\epsilon }$ that loses the information on the orientation of the shear displacements relatively to the mesoscopic chain axis. As comparison between the mesoscopic and macroscopic approaches demonstrates, a coupling term involving the relative rotations $\varvec{\tilde{\varOmega }}$, see Fig. 20b, cures this deficiency, see Ref. [63]. This comparison also leads to explicit expressions for the macroscopic material parameters in terms of the mesoscopic model parameters [63].

6.3 Thermophoretic effects when externally heating colloidal particles in elastic polymeric gel matrices

In view of possible applications of magnetic gels and elastomers as soft actuators [30, 94, 116], inducing and altering forces and torques on or between the embedded magnetic particles by external magnetic fields appears as a promising strategy to achieve mechanical distortions. A different route would be to locally generate heat around the embedded colloidal particles through hysteretic losses during persistent remagnetization. Then, for instance, resulting phase transitions in surrounding liquid-crystalline elastomer matrices can lead to significant overall distortions [50]. A related topic is hyperthermic cancer treatment [49]. For that purpose, colloidal particles embedded in soft cancer tissue are persistently remagnetized to kill cancer cells by the generated heat.

In all these situations, temperature gradients are generated around the particles. If the surrounding matrix represents a combination of a polymeric elastic component and a fluid solvent, in principle, thermophoretic effects may become important. Thermophoresis or the Soret effect describe the displacement of different components in a two- or multicomponent system relatively to each other along a temperature gradient [113]. In this way, some components are shifted up the temperature gradient, while others are pushed downward. The same behavior should emerge in an elastic polymeric matrix swollen by a solvent to form a soft gel around heated embedded colloidal particles.

To study this scenario in reality in an extreme situation, metallic colloidal particles embedded in a swollen polymeric gel matrix were heated by laser light [92, 96]. In fact, in the investigated case, the polymeric matrix was pushed down the temperature gradient. That is, a radial displacement of the polymer outward and away from the heat center was observed, see the schematic illustration in Fig. 22a.

Fig. 22

Reproduced from Ref. [92], with the permission of AIP Publishing. (Color figure online)

Heating a colloidal particle embedded in an elastic polymeric matrix swollen by a solvent induces thermophoretic effects. In our context, heating may be achieved by hysteretic losses during persistent remagnetization. a A more direct procedure relies on the irradiation of laser light [92]. Analyzing a hydrodynamic two-fluid theory [87] for this geometry predicts a radial outward displacement of the polymer, relatively to the solvent, that to leading order does not decay in magnitude, no matter how far away from the heat center it is measured [92]. b Yet, the presence of confining heat-conducting boundaries leads to a linear decrease in the magnitude of the outward displacement [92] with increasing distance from the heat center, in qualitative agreement with corresponding experiments as shown for different powers of irradiation [92].

The experiments indicated a quite long-ranged outward displacement field. In fact, a corresponding theoretical analysis confirmed this picture, see Ref. [92]. For this purpose, a hydrodynamic two-fluid theory [87] was reduced to a corresponding spherically symmetric stationary geometry and evaluated for a point-like heat center [92]. Indeed, in this idealized situation and for an infinitely extended matrix, from the theory a radial outward displacement of the polymer is predicted that to leading order does not decay in magnitude. More precisely, $\mathbf {u}(\mathbf {r})=u(\mathbf {r})\hat{\mathbf {r}}=(u_0+u_{-2}/r^2)\hat{\mathbf {r}}$ in Fig. 22a, with constants $u_0$ and $u_{-2}$. Instead, when a heat-conducting confinement is added to the system, a linear decay in the outward displacement is predicted, in qualitative agreement with the experiment [92]; see Fig 22b.

6.4 Self-propelled magnetic dipole-spring microswimmer

A rather different recently emerging field of complex systems showing qualitatively new types of behavior is represented by active materials, self-propelled particles, and self-driven microswimmers [8, 27, 64]. The latter type of objects is given by micrometer-sized agents suspended in a fluid and equipped with an individual propulsion mechanism. Nature provides us with corresponding realizations in the form of self-propelled bacteria [74] and alga cells [88]. Also various synthetic realizations exist, given, for instance, by self-propelled droplets [115]. Even more frequently studied synthetic examples are self-propelled colloidal Janus particles that on one half of their body catalyze a chemical reaction in the surrounding fluid [39], heat the suspending liquid [47], or demix a binary mixture [17]. The driving of the swimmers then results from the gradients in concentration or temperature along their body.

Different magnetic variants of such colloidal microswimmers have been generated [7], and also magnetic self-propelled bacteria have been studied [55]. Moreover, magnetic colloidal particles can be permanently linked to each other to form chains, using, for instance, fragments of DNA as connectors [26]. Therefore, combining these aspects, the dynamics of self-propelled magnetic colloidal microswimmers that are permanently linked to each other by elastic bonds has been investigated [6].

The dipole-spring models developed in the context of characterizing magnetic gels and elastomers [4, 80,81,82,83, 102] were transferred and extended to study the dynamics of such active magnetic colloidal “microswimmer molecules.” An example consisting of three linked self-propelled spherical beads, each carrying a permanent magnetic dipole moment anchored to the particle frame, is illustrated in Fig. 23 [6]. An interesting competition arises. The magnetic interactions between the individual beads try to align them in a straight configuration. However, to propel itself, each swimmer (bead) sets the surrounding fluid into motion. The resulting self-induced flow fields affect all other swimmers (beads) and destabilize the straight arrangement. A threshold of the active drive was identified, beyond which a straight alignment of the swimmer configuration becomes unstable. Then, a corkscrew-like motion of the “microswimmer molecule” can be observed as illustrated in Fig. 23.

Fig. 23

Reproduced with permission from Ref. [6]. (Color figure online)

Illustration of the corkscrew-like trajectory of a magnetic “microswimmer molecule” [6]. The three spheres represent self-propelled colloidal beads that are suspended in a surrounding fluid. Each such microswimmer (bead) carries a permanent magnetic dipole moment that is anchored to the particle frame, indicated by the (yellow) arrows. The individual microswimmers are linked to each other by elastic bonds (green). Above a critical threshold of the active drive, a straight configuration of the arrangement becomes unstable due to destabilizing flow fields in the surrounding viscous fluid resulting from the self-propulsion mechanism, which leads to the indicated corkscrew-like motion. “com” abbreviates “center of mass”. The situation is described by a variant of the dipole-spring models introduced in the context of the mesoscopic modeling of magnetic gels and elastomers [4, 80,81,82,83, 102].

6.5 Further recent developments

Besides the strong focus on the characterization of magnetic gels and elastomers, the presented works induced several further studies reaching out into related contexts and fields. For one thing, the efficient dipole-spring modeling can also be used to describe the overall behavior of electrorheological elastomers [1, 2]. There, by external electric fields, electric dipole moments may be induced on rigid inclusions in an elastic polymer matrix. Again, the overall distortion of the material and changes in the elastic behavior may be calculated. The investigation of these materials is important, for instance, in view of energy storage devices [2].

Apart from that, the reaction of magnetic bilayered cubes to homogeneous external magnetic fields oriented along the layer normals was analyzed using a more macroscopic description [3]. Although the individual layers by themselves would extend along the field direction, the bilayered cube geometry can reverse this situation and in some cases can lead to a contraction of the overall composite along the external magnetic field.

Moreover, the stochastic motion of individual colloidal particles in a complex environment was investigated under the influence of an external net force imposed, for instance, by a magnetic field gradient [65]. Both the velocity and displacement statistics of the particles were analyzed. Related situations become important, for example, in the context of improved cancer treatment. There, magnetic or magnetizable colloidal particles loaded by appropriate drugs may be directed to and concentrated in requested areas of the body using strong external magnetic field gradients [104].

Finally, in view of a further adjusted macroscopic hydrodynamic-like continuum theory for magnetic composite materials, the consideration of variables of relative strains has been suggested [66]. This direction needs additional investigation in the future.

7 Conclusions

Above, we summarized several recent developments in the mesoscopic characterization of magnetic gels and elastomers, together with the fascinating behavior revealed for these materials. Their properties arise from their intrinsic coupling of magnetic and elastic features. Particularly, we mentioned the significance of dipole-spring approaches, explicit analytical calculations of the interactions between embedded particles via a surrounding elastic matrix, numerical approaches to address nonlinear properties, as well as the need for statistical descriptions that allow to include effects of thermal fluctuations in an efficient way. Following these procedures, systems of sizes that permit to estimate the overall macroscopic behavior can be addressed, reversible hardening of the materials by forming chain-like aggregates in magnetic fields is described, the magnetic tunability of static and dynamic mechanical moduli is characterized, matrix-mediated interactions between the particles due to induced forces and torques are addressed, and the tunable nonlinear stress–strain behavior of anisotropic systems is revealed. Moreover, links to the microscopic scale that justify the mesoscopic approaches and guide the way for improvements are outlined and connections to the macroscale to derive explicit expressions of the macroscopic material parameters in terms of the mesoscopic properties and parameters become possible.

Besides illustrating the importance of the mesoscopic approaches in various respects, our overview particularly stresses the significance and benefits of combined efforts. Due to the complexity of the materials, a description over many scales is necessary to capture the overall behavior correctly in terms of the properties of the individual constituents. First, the crosslinked polymer chains providing the elasticity introduce molecular dimensions. Next, the colloidal particles embedded in the polymer mesh set an intermediate, mesoscopic length scale. And finally, for application purposes, one is typically interested in macroscopic properties of an overall piece of material. Altogether, besides the necessary bridging between these scales and an associated coarse-graining in a bottom-up approach, a close connection between various disciplines is required. Microscopic details in these complex systems can hardly be described without large-scale computer simulations. Mesoscopic models are important to describe efficiently the structural properties and their impact on more macroscopic scales. Yet, they need to be tested and verified against explicit results from microscopic simulations and from experiments to check their validity and to enable possible improvement. And finally, a coarse-grained macroscopic description is necessary to provide the input, e.g., for finite-element simulations, if an actual practically used component is to be simulated in operation. Upon further integration of the various approaches and a combined effort of the different disciplines, such a scope at present appears feasible. It will facilitate the sought-for bottom-up optimization of the properties of the materials for tailored realizations in view of practical usage.