Introduction

The electrokinetic transport phenomena involves the electrostatic interactions between the solid and ionized liquid phases. When a charged surface is in contact with an ionized liquid, a region possessing non-zero charge density formed in the close vicinity of the surface, which is referred as the electric double layer (EDL). Under the influence of an externally applied electric field tangential to the surface, the fluid within the mobile part of the EDL experiences a non-zero electric force, which in turn causes a bulk fluid motion, termed as the electroosmotic flow (EOF). In recent years, several attempts are made on the modulation of EOF through micro/nanofludic devices. One of the important techniques to modulate the EOF through such devices is to functionalize the rigid walls by grafting with charged polymer layer (polyelectrolyte layer, PEL, [6, 17, 23, 31]). In literature, the soft channel is referred to a tiny channel in which the rigid walls are covered with PEL or soft layer. It has been recognized that the PEL bears immobile charges due to the dissociation of ionizable functional groups present in the PEL, which in turn creates a net volumetric charge entrapped within the PEL. The rigid plate that supports the PEL may also bear surface charge density. Due to the presence of the immobile charges within the PEL, a significant flow modulation can be achieved.

One of the commonly used continuum model to describe the electrostatic potential distribution as well as distribution of mobile ions is the Poisson-Boltzmann (PB) model. In PB model, the EDL-induced electric field is governed by the Poisson equation and the distribution of ionic species are described by the Boltzmann distribution. Most of the studies on EOF through soft nanochannel dealing with uniform (step-like) as well as nonuniform PEL are based on linearized PB model under the Debye-H\(\ddot {u}\)ckel limit ([3, 4, 7, 9, 20]). The PB model is based on the equilibrium distribution of ions in which the convective transport of ions and electromigration due to the applied electric field are neglected. In addition, the Debye-H\(\ddot {u}\)ckel approximation is valid for low-charge-density case. Thus, the PB model may not provide a correct analysis for the case of overlapped EDL and/or higher ranges of PEL charge density for which ion convection is non-negligible. For such cases, the ion transport can be described by the Poisson-Nernst-Planck (PNP) equations. However, the nonlinear PNP equations cannot be solved analytically even for a simple flow configuration.

Constructing nanofluidic systems to regulate the electroosmotic flow and ion selectivity has drawn interest because of its important practical relevance such as separation of biomolecules ([12, 15]), desalination of seawater ([14]), artificial cells, and drug delivery ([28]). The ion selectivity in microfluidic devices is based on the principle of creating a stronger attraction of one ionic species and depletion of other ionic species within the channel. For a nonochannel with overlapping Debye layer, the channel conductance and, hence, the ion current can be modulated by varying the wall charge. The transport selectivity of ionic species in nanopore or nanochannel by coating the walls with PEL has been demonstrated both theoretically and experimentally by several authors ([1, 2, 27, 29]). A fully “abiotic” nanochannel which displays switching behavior of ionic current, typically observed in biological channels, has been demonstrated by Yameen et al. [27] through manipulation of the surface charges of the channel walls via the protonation of the pH-regulated polyelectrolyte brush layer. Ali et al. [2] conducted theoretical and experimental analysis to create ion-selective nanopores which are functionalized with layer-by-layer assemblies of polyelectrolytes. Yeh et al. [29] have studied theoretically the ion transport behavior in a polyelectrolyte-modified nanopore.

All the foregoing studies considered a step-like PEL in which polymer segments have a constant permeability and a step change in charge density is considered. In this article, we have considered the EOF in a nanochannel where the walls are coated with diffuse PEL [8]. The diffuse PEL, in contrast to the step-like PEL, consider a inhomogeneous distribution of polymer segments where the interfacial properties asymptotically approaches to that of the bulk electrolyte phase. Use of such a description of soft layer is found to be more realistic compared to a step-like PEL [10]. The diffuse description of the soft layer is also advantageous as it does not requires any interfacial matching boundary conditions. Duval et al. [10] studied the electrokinetics of diffuse soft layers supported by a charged rigid surface of constant surface potential by considering the Boltzmann distribution of ions.

The model, as adopted here, is based on the diffusion-electromigration-convection mechanisms (e.g., Nernst-Planck equation) for the distribution of ionic species. The PEL is considered to be a Brinkman porous medium. We employ numerical tools to solve the governing equations in a coupled manner. Following Matin and Ohshima [20], we have derived analytic solutions, for the case of a step-like PEL under the Debye-H\(\ddot {u}\)ckel conditions, valid for a low-charge-density condition. The present study includes several interesting key features of the EOF including flow reversal, zero average flow by regulating the PEL charge, and the surface charge residing along the channel wall. In addition, we have also studied the tuning effect of PEL charge on the manipulation of current density through the soft nanochannel.

Mathematical model

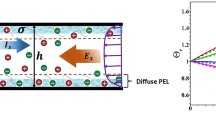
We have considered the EOF through the soft nanochannel (Fig. 1). The PEL are considered to be diffuse in nature and is supported by a rigid wall bearing a uniform surface charge density σ (Fig. 1). The characteristic volumetric immobile charge density of the PEL is given by \(\rho ^{0}_{\text {fix}}~{=}~zFN\), where z, F, and N are respectively, the valence, Faraday constant, and molar concentration of fixed charges residing in PEL. We assume univalent acidic or basic functional group residing in diffuse PEL with valence z = − 1 or 1, respectively.

Fig. 1
figure 1

a Schematic representation of the problem and b spatial distribution of polymer segments

Full size image

The distribution of the polymer segment inside the diffuse PEL is given by ([10])

$$ f(y)=\omega \left[1- \tanh\left( \frac{y-d}{\alpha} \right) \right], $$
(1)

where α is the characteristic decay length. The nominal thickness of PEL (for α → 0) is taken to be d and the channel height is h. It may be noted that for non-zero values of α, the thickness of the PEL extends beyond the nominal thickness (d) and an estimate for the diffuse PEL length is given by \(\bar {d}=d + 2.3 \alpha \). The parameter ω arises in Eq. 1 ensures the fixed amount of polymer segment within the soft layer while varying the decay length and its value is given by ([10])

$$ \omega=\frac{d}{\alpha \log\left( 1+e^{\frac{2d}{\alpha}}\right)} $$
(2)

The flow behavior within the soft nanochannel is determined on the basis of Darcy-Brinkman equation as

$$ \rho\left[\frac{\partial \mathbf{u}}{\partial t}+(\mathbf{u}\cdot\nabla) \mathbf{u}\right] +\nabla p -\eta\nabla^{2}\mathbf{u} +\rho_{e} \nabla {\Phi} +\eta \lambda^{2} \mathbf{u}= 0 $$
(3)

along with the continuity equation for an incompressible fluid, i.e., ∇.u = 0, where u = (u, v) is the velocity field. Here, η is the fluid viscosity, p is the pressure, and ρ e = eΣ i z i n i is the net charge density due to the mobile ions, where e is the elementary charge and z i and n i (i = 1,2) are the valence and ionic concentration of the mobile ions, respectively. In our current study, we consider the electrolyte solution consists of fully dissociated binary symmetric salt with z1,2 = ± 1. For diffuse soft PEL, the softness parameter λ(y) of the PEL can be expressed as

$$ \lambda(y)= \lambda_{0} \left[f(y) \right]^{\frac{1}{2}}, $$
(4)

where f(y) is given in Eq. 1. Here, \(\lambda _{0}^{-1}\) is the screening length for homogeneous distribution of polymer segment, i.e., for α → 0.

The electric potential Φ consists of the potential due to the electrical double layer ϕ and the external potential ϕext = − E0x, where E0 is the applied electric field strength. The potential due to EDL-induced effect can be obtained from Poisson equation, given as

$$ -\varepsilon_{e}\nabla^{2}\phi=\rho_{e} +\rho_{\text{fix}}^{0} f(y), $$
(5)

where ε e is the permittivity of the composite region (the diffuse PEL and the electrolyte medium). It is reasonable to consider an equal value of the permittivity of the PEL and electrolyte medium for a PEL with sufficiently high water content [8]. The concentration distribution of the mobile ions can be obtained from Nernst-Planck equation as

$$ \frac{\partial n_i}{\partial t} + \nabla.\left[ -D_{i}\nabla - z_{i}\frac{D_{i} e}{k_{B}T}\nabla {\Phi} + \mathbf{u} \right]n_{i} $$
(6)

where D i is the diffusivity of the mobile ions, which is considered to be same for both the species, i.e., D1 = D2 = D (say). Here, kB and T are the Boltzmann constant and absolute temperature, respectively.

We introduce the dimensional quantities h (channel height), n0 (bulk ionic concentration), U0(= ε e E0ϕ0/η), p0(= ηU0/h), ϕ0(= k B T/e) as the scale for length, ionic concentration, velocity, pressure, and potential, respectively. Using these scales, the governing equations can be written in nondimensional form as

$$ Re\left[\frac{\partial \mathbf{u}}{\partial t}+(\mathbf{u}\cdot\nabla) \mathbf{u}\right] +\nabla p -\nabla^{2}\mathbf{u} + \beta^{2} g(y)\mathbf{u} + \frac{(\kappa h)^{2}}{2 {\Lambda}} {\Sigma} z_{i}n_{i}\nabla {\Phi}= 0 $$
(7)
$$ \nabla. \mathbf{u}= 0 $$
(8)
$$ \nabla^{2}\phi + \frac{(\kappa h)^{2}}{2} {\Sigma}_{i} z_{i}n_{i} + z\frac{(\kappa_{s} h)^{2}}{2}.g(y)= 0 $$
(9)
$$ Pe\left[\frac{\partial n_{i}}{\partial t} + \mathbf{u}.\nabla n_{i} \right] - \nabla^{2} n_{i} - z_{i}\nabla.(n_{i}\nabla{\Phi})= 0, $$
(10)

where β = λ0h is the PEL softness parameter and Λ = E0h/ϕ0 is scaled applied electric field. The nondimensional parameter Pe (Peclet number) is given by Pe = U0h/D. The EDL thickness is defined as \(\kappa ^{-1}=\sqrt {\varepsilon _{e} \phi _{0}/2FC}\) with FC = en0, where C is the bulk molar concentration of the electrolyte. The equivalent EDL thickness inside the PEL due to additional immobile charges is given by \(\kappa _{s}^{-1}=\sqrt {\varepsilon _{e} \phi _{0}/2FN}\) [20]. The distribution of the polymer segment inside the PEL can be written with the nondimensional variables as

$$ g(y)=\frac{d_{1}}{\alpha_{1} \log\left( 1+e^{\frac{2d_{1}}{\alpha_{1}}}\right)} \left[1- \tanh\left( \frac{y-d_{1}}{\alpha_{1}} \right) \right], $$
(11)

where the scaled PEL thickness and scaled decay length are defined as d1 = d/h and α1 = α/h, respectively. In this article, we consider the channel height (h) to width (w) ratio h/w ≫ 1, which it allow us to consider a two-dimensional EOF in the soft channel. In addition, we consider no overlap of the adjacent PELs, i.e., \(h>2\bar {d}\).

Along the upstream and downstream of the channel we impose the symmetry conditions. The rigid surface is considered to be no-slip and ion-impenetrable. We have considered surface charge density (σ) distributed along the channel wall as depicted in Fig. 1. The PEL is diffuse in nature and the PEL properties gradually approach to electrolyte solution; hence, there is no need to consider any interfacial boundary conditions along the PEL-electrolyte interface. The nondimensional form of the boundary condition along the channel wall is as follows:

$$ u = 0,~~~~ v = 0,~~~~ (\nabla n_{i}+z_{i} n_{i}\nabla\phi).\mathbf{n}= 0,~~~~ \frac{d\phi }{d\mathbf{n}}=-\sigma^{*}. $$
(12)

Here, n is normal on the channel surface directing towards the fluid side. Here, σ∗ = σh/ε e ϕ0 is the scaled surface charge density.

Numerical methods

We solve the governing nonlinear equations (7–11) in its nondimensional form through the finite volume method (FVM) on a staggered grid arrangement [11]. The governing equations are integrated over each cell through the FVM. Different control volumes are used to integrate the equations. In the staggered grid system, the scalar quantities are stored at each cell center while the velocity components are evaluated at the midpoint of the cell sides in which they are normal. The variables at the interface are determined by a linear interpolation between the values of the variables at two neighboring cells. A first-order implicit scheme is used to discretize the time derivative. We employ the central difference scheme for elliptic terms, while upwind scheme [16] are used to discretize the hyperbolic terms.

At every iteration we first solve the Poisson equation (9) for induced potential using the previous iteration step solutions for the concentration of ionic species. With the updated value of the induced potential and previous iteration step solution for the velocity field, the Nernst-Planck equation (10) is solved to obtain the concentration distribution. A pressure correction-based iterative algorithm SIMPLE (Semi-Implicit Method for Pressure Linked Equations, Patankar [21]) is used for computing the velocity components. A time dependent numerical solution is achieved by advancing the variables through a sequence of short time steps. We started the time evolution from an initial stationary condition and achieve a steady-state after a certain number of time steps for which the variables become independent of time.

A theoretical analysis based on the Boltzmann distribution of ions is also made by considering a uniform distribution of monomers in PEL (step-like PEL). A detailed discussion on the linear model is presented in Appendix. The channel height (h) is considered to be 100 nm and the nominal thickness of the diffuse PEL is d = 10 nm. The strength of the externally applied electric field is taken to be E0 = 104 V/m. The surface charge density σ is chosen in the range of the experimentally estimated surface charge for silica nanochannels, i.e., σ is varied − 0.1 to − 10 mC/m2 ([13, 24, 30] and [22]). The scaled surface charge density (σ∗) varies from − 0.5472 to − 54.72. The bulk ionic concentration is varied from 0.01 to 100 mM so that the Debye-H\(\ddot {u}\)ckel parameter (κh) ranges from 1.027 to 102.7. The range of the decay length (α) of the diffuse PEL is considered to vary between 0 to 10 nm [10] so that α/d ranges from 0 to 1 (i.e., α/h ranges from 0 to 0.1). The hydrodynamic penetration length (\(\lambda _{0}^{-1}\)) of the PEL is considered to vary between 5 to 100 nm ([10]) and hence, the scaled softness parameter β can ranges from 1 to 20. The PEL charge considered to be positive as well as negative with z = ± 1 and molar concentration (N) of the PEL ion ranges from low (0.1 mM) to high (10 mM).

Results and discussions

We first consider a soft nanochannel with step-like PEL (“Nanochannel with step-like PEL: comparisons with linear model” section) and compared the present model with the corresponding linearized model to highlight the significance of the nonlinearities. The closed form solution under a low potential limit is presented in the Appendix. In “Effect of diffuse PEL” section, the effect of the soft layer properties on the flow modulation and the combination of the pertinent parameters to achieve a zero average flow is illustrated. In “Current density and ion selectivity” section, we have provided the selectivity of mobile ions for the EOF through diffuse soft nanochannel.

Nanochannel with step-like PEL: comparisons with linear model

A comparison of the numerical solution for the average EOF in a soft channel based on the present PNP model, with the closed form analytic solution (Eq. A.6) is shown in Fig. 2a–c for different values of the electrolyte concentration. We have considered the surface charge density of the channel wall as σ = − 1 mC/m2 and the PEL is consider to be either negatively charged, uncharged, or positively charged. The computed solution differs from the analytical solution at a thicker Debye layer, i.e., κh ∼ O(1) when the PEL is either uncharged or the charge of the PEL and walls have same sign, while for the case of the oppositely charged PEL and walls, analytic solution differs from the numerical solution when Debye layer is thinner, i.e., κh >> 1. The maximum difference between the analytic solution and the present numerical results are 34.6% for negatively charged PEL, 20.5% for an uncharged PEL when C = 0.01 mM and β = 20 and 7.6% for positively charged PEL when C = 100 mM and β = 20. From the results presented in Fig. 2a,b, it is clear that the average velocity decreases with the increases of electrolyte concentration and approaches a constant value at higher range of electrolyte concentration. As the thickness of the double layer reduces (increase in C), the surface potential reduces and the EOF is governed by the PEL charge density. When PEL and walls are charged similarly, the counterions (positive ions in the present case) creates a flow along the direction of the applied electric field and the flow is higher than the EOF corresponding to an uncoated channel (d1 = 0). With the increase of the bulk ionic concentration of the electrolyte, the surface potential of the walls as well as the effective charge density of the PEL reduces, which creates a reduction in EOF with the increase of C. Enhanced electroosmotic transport compared to a channel without the polymer brushes has been reported by Chen and Das [5]. When the charges of the PEL is of opposite sign to that of the walls, the counterions in the wall induced Debye layer repelled by the PEL immobile charges and the EOF is dominated by the PEL charge density for Debye length thinner than the PEL thickness, i.e., κ− 1 < d for C > 1 mM. In this case, the imbalanced negative ions attracted by the positive charges of the PEL creates an EOF opposite to the direction of the applied electric filed. The average EOF is reduced when PEL and walls are oppositely charged. The flow rate reduces with the increase of the softness parameter of the PEL, i.e., increase of β. As the PEL becomes more dense, the hydrodynamic friction increases and the neutralization of PEL charges due to the counterion condensation also rises. These together results in a reduction in uavg. Figure 2c shows that the uavg may change sign depending on the choice of PEL and wall charges, softness parameter, and electrolyte concentration. We have discussed the flow reversal in a great details later in this section.

Fig. 2
figure 2

Variation of scaled average velocity with electrolyte concentration C for a N = 1 mM and z = − 1, b uncharged PEL, and c N = 1 mM and z = 1 for different values of β = 1, 5, 10, and 20 with PELnominal thickness d1 0.1, α = 0 (step-like coating) and negatively charged wall with σ = − 1 mC/m2

Full size image

Effect of diffuse PEL

In Fig. 3a, we present the average EOF as a function of the softness parameter β. The results are presented here for three different values of the decay length for the thick EDL case (C = 0.1 mM, i.e., κh = 3.25) with fixed N = 0.1 mM, z = − 1. An increase in α elongates the PEL keeping the number of monomer segments and the net charge entrapped within the PEL invariant. Thus, an increase in α increases the effective permeability of the PEL, but it engender an increment in the local frictional force as well as charge density in the region beyond y ≥ d1 compared to a step-like PEL, i.e., α = 0. When PEL charge is relatively small (Fig. 3a), the enhanced electric force due to the PEL elongation is not sufficient to overwhelm the increased frictional force, which leads to a reduction in the average flow rate with the increase of the decay length (α). A similar phenomena has been reported by Duval [7] to study the electrokinetics of diffuse soft interfaces where the supporting rigid plates are uncharged. From the results presented in Fig. 3a, it is clear that the effect of α becomes more prominent at higher values of β where the frictional force becomes significant compared to the electrical driving force and leads to a overall flow reduction.

Fig. 3
figure 3

Variation of the scaled average velocity a with β for fixed C = 0.1 mM and b with C for fixed β = 1 and 20. Here, N = 0.1 mM, z = − 1, d1 = 0.1, α/h = 0, 0.05, and 0.1 and σ = − 1 mC/m2. In b, dashed dot (green) line corresponds to no soft layer (uncoated nanochannel) with σ = − 1 mC/m2

Full size image

In Fig. 3b, we have shown the effect of electrolyte concentration on the average flow rate. The results are shown here for low value of PEL charge (N = 0.1 mM). We have also included the corresponding results due to a uncoated nanochannel (d1 = 0). It is clear from Fig. 3b that the net flow rate decreases with the increase of electrolyte concentration irrespective of the channel type, i.e., soft or uncoated nanochannel. For lower values of electrolyte concentration, the PEL is engulfed by the thick EDL and the EOF is governed by the surface charge density. When the PEL charges are of same sign to the wall charges, a larger electrolyte concentration (thinner Debye length) creates a stronger shielding effect of the PEL immobile charges, which leads to a decrease in electrical driving force and results a decrement in the average flow rate. The impact of the decay length α is strong for low permeable PEL as the hydrodynamic friction increases due to the PEL elongation. This impact is profound for the lower range of ionic concentration where shielding effect is low. It is clear from Fig. 3 that the net average flow rate decreases with the increase of β, i.e., increase of hydrodynamic screening length \(\lambda _{0}^{-1}\) at a fixed channel height. As the PEL becomes more dense (larger β) the counterion condensation effect enhances, which leads to a decrease in the net effective charge enclosed within the diffuse PEL.

The average velocity as a function of the PEL charge density at a fixed σ is presented in Fig. 4a. We have varied the PEL charge density from negative to positive values at different decay length for two different values of the PEL permeability. The variation of the average flow rate with the increase of PEL charge density shows a flow reversal. At a fixed value of the PEL charge density, the dependence of the average flow rate on the decay length varies with the permeability of the PEL. For high permeable PEL at low β(= 1), the diffusion dominated counterion condensation of PEL charge density diminishes which results in an increment in the effective charge density of the PEL compared to a low permeable case. In addition, the increase in decay length increases the effective permeability of the diffuse PEL. As a result at low β(= 1), the electrical driving force increases sufficiently to compensate the hydrodynamical frictional force compared to the step-like PEL. On the other hand, at a sufficiently large β(= 20), strong counterion condensation effect leads to a reduction in the effective charge density entrapped within the PEL. In this case, the electrical driving force is not enough to compensate the increased local frictional force in the PEL. For that, an increase in the decay length results in reduction in the net flow rate for a low permeable PEL. This trend becomes reverse when the PEL and the walls are oppositely charged. The counterions (which are coins for the PEL) are repelled by the PEL ions. Figure 4a shows that a flow reversal can be achieved by increasing the fixed charge density of the oppositely charged PEL. It is expected that the amount of PEL charge density to create a flow reversal at a fixed σ also depend on the EDL thickness along with β and α. A detailed discussion on net-zero flow is discussed subsequently.

Fig. 4
figure 4

Variation of a scaled average velocity with N for C = 0.1 mM; α/h = 0, 0.05, and 0.1; and σ = − 1 mC/m2, and b critical PEL charge (N with z = 1) and negative wall charge density to achieve a zero velocity for different values of bulk electrolyte concentration (C = 0.1, 1, 10, and 100 mM) and α/h = 0.1. Here, β = 1, 20 and d1 = 0.1

Full size image

The flow reversal in the soft channel may occur when the PEL and channel walls are oppositely charged. In Fig. 4b, we present the critical values of the charge density of the PEL and walls at different choice of the ionic concentration of the electrolyte to obtain a zero average EOF in the nanochannel. The impact of the wall charge density on EOF depends on the Debye length. For a low ionic concentration (thick EDL), the impact of PEL charge density is weak, whereas the PEL charges dominate in driving the EOF when Debye length is thinner (higher ionic concentration). For this, we find that at a fixed σ a higher value of PEL charge density is required for dilute electrolyte to achieve a flow reversal and hence a net-zero EOF. This critical values depend also on the PEL permeability and decay length. The average EOF reduces as the PEL become less permeable, for this the critical PEL charge density for net-zero flow also reduces with the increase of β. Zuo et al. [32] have demonstrated through the molecular dynamics simulations the occurrence of EOF suppression in a nanochannel grafted with polyelectrolyte brushes.

Current density and ion selectivity

In this subsection, we analyze the ion selectivity of the soft nanochannel. The nondimensional form of the electric current (i i ) of mobile ions (i = 1,2) can be expressed as

$$ i_{i}=-\frac{1}{Pe} z_{i}\nabla n_{i} -\frac{1}{Pe} {z_{i}^{2}}n_{i}\nabla {\Phi} + \mathbf{u} z_{i}n_{i}, $$
(13)

where the scale for the current density is considered to be I0(= Fn0U0). The first two terms of the r.h.s. of Eq. 13 correspond to the conduction current and last term of Eq. 13 is due to the convection current. The cross-sectional averaged current density for the ith ionic species is defined by I i (i = 1, 2). The net cross-sectional averaged current density I = I1 + I2, where I1 and I2 corresponds to the current density due to cations and anions, respectively. The ion selectivity of the channel is determined through the parameters ([25, 26]) which are the ratio of the difference in currents due to counterions and co-ions with the total current

$$ S=\frac{\mid I_{1} \mid-\mid I_{2} \mid}{\mid I_{1} \mid+\mid I_{2}\mid} $$
(14)

The value of S can ranges from − 1 to 1 where S = − 1 stands for anion-selective, S = 1 stands for cation-selective, and S = 0 corresponds to a non-selective nanochannel.

The scaled average current density (I) as well as the cationic (I1) and anionic (I2) current density are presented in Fig. 5a–c as a function of the electrolyte concentration when the PEL is diffuse in nature. The immobile charges of PEL and wall are considered to be either of equal sign or opposite sign. We have also included the case in which the PEL is uncharged. It is clear form Fig. 5 that with the increase of electrolyte concentration, the average current density approaches a constant value. This constant current density at a higher range of electrolyte concentration (thinner κh) is equal to the current density in the uncoated channel. The current density of the soft channel is higher than the corresponding uncoated channel when electrolyte concentration is low. When the charges of PEL and walls are of same sign, more number of mobile counterions accumulates in the soft channel and a higher current density compared to the uncoated channel results. In this case, the convective transport of ions is also enhanced as the EOF becomes stronger. However, the current density in the soft channel is reduced when the walls and PEL are oppositely charged as the counterions for the wall induced EDL is repelled by the PEL immobile charges being of same sign. This reduces the ion concentration gradient as well as convective transport of ions. As the bulk ionic concentration of the electrolyte is increased (decreasing the EDL thickness), the transport of ions are dominated by the electromigration. Results show that the soft channel with charged PEL exhibit ion selectivity even at a thin Debye length. This is due to the fact that the transport of ions at a thin Debye length is governed by the immobile charge of the PEL.

Fig. 5
figure 5

Variation of electric current density with electrolyte concentration C for N = 5 mM and z = − 1; uncharged PEL (N = 0); and N = 5 mM and z = 1 for β = 1, d1 = 0.1, α/h = 0.1 and σ = − 1 mC/m2

Full size image

An ion selectivity of a slit channel may occur when Debye length is in the order of the channel height. In order to quantify the ion selectivity of the soft channel, the parameter S is obtained as a function of the PEL charge density at different values of the electrolyte concentration when the walls of the channel are kept at a fixed charge density (Fig. 6a–c). It is evident from the results that for an uncharged PEL (N = 0), the value of S is positive (cation-selective). For the uncharged PEL, the transport mechanism is driven by the negative wall charges and hence, the cationic current dominates and leads to a positive value of S. However, at a thinner Debye length with N = 0, the bulk fluid is electrically neutral and the channel behaves as non-selective to ions (S ∼ 0). The ion transport characteristics of a soft channel gets modified due to the presence of PEL charges. If the PEL bears negative immobile charge (z = − 1), it leads to a stronger cationic current. As a result, the value of S remains positive. In this case, the value of S increases for increasing negative PEL charge and the soft channel becomes a perfect cation selective (S = 1) at a larger value of PEL volume charge density. On the other hand, for increasing value of positive PEL charge, the anionic current dominates and as a result, the channel becomes anion-selective. It is evident from the results that for overlapping EDL (low ionic concentration) the soft channel behaves as perfect permselective for larger values of PEL charge density. Figure 6 shows that the ion selectivity of the soft channel can be tuned by the PEL immobile charges at a fixed ionic concentration and wall charge density. For lower values of electrolyte concentration both the PEL and wall charge plays significant role on the EOF characteristics and hence, a small negative zN can makes the channel a perfectly cation-selective. However, a relatively larger positive zN is required to convert the negatively charged channel to a anion-selective and the required value of zN is low for higher C, in which the EOF is dominated by the PEL charges. At a higher range of electrolyte concentration, the EOF is dominated by the PEL charge density.

Fig. 6
figure 6

Variation of ion selectivity parameter (S) with PEL charge (N) for different values of bulk electrolyte concentration (C = 0.1, 1, 10, and 100 mM) when β = 1, d1 = 0.1, and α/h = 0.1 when aσ = − 0.1 mC/m2, bσ = − 1 mC/m2, and c σ = − 10 mC/m2

Full size image

From Fig. 6, it is clear that a oppositely charged walls and PEL may lead to a zero value of S, i.e., a non-selective channel. The critical value of PEL concentration and wall surface charge density for which S = 0 occurs at different values of the electrolyte concentration and softness parameter is depicted in Fig. 7. As the concentration of the electrolyte increases (decrease of Debye length), the impact of the PEL immobile charges on EOF grows. For this, we find that the critical value of N for achieving S = 0 at a fixed σ decreases as C increases. An increase in the negative wall charge density will lead to a strong cationic current while, an enhancement in the positive PEL charge density will increase the anionic current. For this, the critical value of the PEL charge density increases with the increase of the wall charge density for a non-selective nanochannel. An increment in the critical PEL charge with the decrease of the PEL permeability at a fixed charge density of the wall is evident from the results. For a dense PEL, the effect of counterion condensation becomes strong due to the occurrence of low electroosmotic flow and stronger diffusion of ions, which leads to the requirement of high PEL charge to make the soft channel to become non-selective.

Fig. 7
figure 7

The variation of critical PEL charge (N with z = 1) and wall charge density (σ) to achieve a zero ion selectivity (non-selectivity) for different values of bulk electrolyte concentration (C = 0.1, 1, 10, and 100 mM) when β = 1, 20, d1 = 0.1, and α/h = 0.1

Full size image

Conclusions

In the present article, we have studied the form of EOF and current transport in a soft nanochannel in which the walls are coated with PEL. A diffuse distribution of monomers and charge density across the PEL is considered. A numerical study is made based on the Poisson-Nernst-Planck equations. A simplified model based on the Boltzmann distribution of ions for a step-like PEL is also derived. The PNP model and the simplified Poisson-Boltzmann model are compared and found a significant difference for lower range of electrolyte concentration. A difference between the two models is found even at higher value of the ionic concentration when the PEL and the walls are oppositely charged. The present study shows that the flow reversal and suppression of EOF is possible by regulating the charges entrapped within the PEL as well as wall charge density. The current density in the soft channel can be controlled and a cation-selective or anion-selective characteristics of the soft channel can be achieved by suitably tuning the walls and PEL charges.