INTRODUCTION

The electroosmotic flow (EOF) through the micro-/nanofluidic devices finds their potential applications in various areas, including LOC devices to transport of small amounts of fluid through nanopore, separation and mixing, etc. [1, 2]. When the walls of the micro-devices come in contact with the electrolyte solution, the walls become charged due to various physicochemical processes [3]. As a result the counterions experience an attracting force and the coions repel from the charged surface. It is noteworthy to mention the mobile ions have their own thermal energy. Due to combined effect of Coulombic attraction/repelling force and thermal energy of the mobile electrolyte ions, a distribution of mobile electrolyte ions occurs near the charged surface, which in turn form a layer of ions near to the charged surface. Such a layer, which is often termed as electric double layer (EDL), carries non-zero net mobile charge. Under the application of electric field, the EDL experiences a net non-zero electric driving force and results in the flow of ionized fluid across the channel. Such a fluid flow is often termed as electroosmotic flow (EOF).

There are various studies considering the flow modulation across the micro-/nanofluidic devices [4−16]. Besides the work on EOF through micro-/nanochannel in which the walls are made of rigid material, there are growing research interests to study the flow modulation through micro-/nanochannel for which the channel walls are grafted with soft polymeric materials. It is noteworthy to mention that, the grafted polymers may entrap the additional immobile charges due to the presence of functional group within it. On the other hand, the monomers present in the grafted polymeric material offers resistance to the fluid flowing through it. Such a channel for which the walls are grafted with polymeric material is often termed as soft channel and the polymeric layer are often termed as poly-electrolyte layer (PEL) [17]. The electrokinetic transport of ionized liquid through soft nanochannel finds its potential applications in controlled drug delivery [18], electrochemomechanical energy conversion systems [19], to name a few. The earliest work on the transport of ionized liquid through soft nanochannel is studied by Donath and Voigt [17]. Subsequently, several researchers studied the EOF through soft nanochannel considering several electrohydrodynamic conditions. Ohshima and Kondo [20] studied the motion of ionized fluid under the applied electric field as well as applied pressure gradient. Later, several other researchers [21−28] below made a significant contribution to the flow of ionized liquid through the soft nanochannel with step-like/diffuse PEL under the applied electric field/pressure gradient/concentration gradient.

In all these works mentioned above on flow through soft nanochannel, the dielectric permittivity of the PEL is considered to be the same as that of the electrolyte solution. However, the dielectric permittivity of the PEL is in general lower than the bulk aqueous medium. As a result, the penetration of mobile electrolyte ions within the PEL is no longer continuous. In fact, the penetration occurs in a discontinuous manner due to difference in Born energies of both the phases [29]. Such an effect is termed as ion partitioning effect. The generation of streaming potential across soft nanochannel considering the significant impact of ion partitioning effect is studied by Poddar et al. [30].

In all these studies discussed earlier, the fluidic medium is taken to be Newtonian in nature, for which the stress is directly proportional to the rate of strain. However, such a linear relation no longer valid for bio-fluids (e.g., blood, DNA solutions etc.), or liquid with suspended colloidal particles. These kinds of fluids are often termed as non-Newtonian fluid. The EOF of non-Newtonian fluid across the soft nanochannel is certainly interesting due to its applications in bio-microfluidic devices and pharmaceutical applications. Gaikwad et al. [31] studied the EOF of non-Newtonian fluid based on the power-law model. Later, Barman et al. [32] studied extensively the modulation of EOF of non-Newtonian fluid across the soft nanochannel, considering pH-dependent charge properties of the PEL. Note that the power-law model to describe the non-Newtonian behavior of the bio-fluids or liquid with suspended colloidal particles, is an acceptable model and widely used by several earlier researchers [33−35]. It is important to note that, till date there is no article available on the EOF of non-Newtonian fluid across the soft nanochannel considering the significant impact of ion partitioning effect.

Based on the knowledge gap delineated above, in this article we made a systematic study on the EOF of non-Newtonian fluid across the soft nanochannel. The dielectric permittivity of the PEL is considered to be lower than that of the bulk fluidic medium, leading to significant partitioning effect. The fluidic medium is described by the power-law model. Going beyond the widely used simplified Debye−Hückel approximation, we have solved the non-linear governing equations describing the undertaken problem. We have further illustrated graphically that the dependence of pertinent parameters describing the flow modulation. Besides, we have also studied the selectivity of mobile electrolyte ions across such a soft nanochannel. Note that transport of ions across such a soft nanochannel have potential applications in targeted drug delivery, separation of biomacromolecules etc. [36].

MATHEMATICAL MODEL

We have studied the EOF of non-Newtonian fluid through soft nanochannel under applied electric field of strength \(\mathbf{E}\) (Fig. 1). The background solution is taken to be binary \({{z}_{1}}:{{z}_{2}}\) electrolyte solution with bulk molar concentration \({{n}_{0}}\) (in mM). The net volumetric PEL charge is given by \({{\rho }_{{{\text{fix}}}}} = zFN\), where \(z\) and \(N\) are the valency and molar concentration of immobile ion, respectively and \(F\) is Faraday constant. The dielectric permittivity of the electrolyte medium \(\left( {{{\varepsilon }_{e}}} \right)\) is in general higher than the PEL medium \(\left( {{{\varepsilon }_{{{\text{pel}}}}}} \right),\) which results in a significant ion partitioning effect [30,37,38]. The net charge density due to mobile ions is defined as [37,39]

$${{\rho }_{e}} = ~F\mathop \sum \limits_{n = 1}^2 {{z}_{i}}{{n}_{i}}{{f}_{i}}.$$
(1)

Here \({{z}_{{1~}}} = + z~\) and \({{z}_{2}} = - z\) are the valency of cations and anions, respectively. The terms \({{f}_{i}}\) refers the partitioning coefficients of the ith ions and is defined by

$${{f}_{i}} = ~{\text{exp}}\left. {\left( { - \frac{{\Delta {{W}_{i}}}}{{{{k}_{B}}T}}} \right.} \right),$$

where \({{k}_{B}}\) and \(T\) are Boltzmann constant and absolute temperature, respectively. The difference in Born energy, which is the difference of electrostatic free energy \(\Delta {{W}_{i}}\) of ions in PEL as well as electrolyte medium are specified by [30]

$$\Delta {{W}_{i}} = \frac{{{{{\left( {{{z}_{{i~}}}e} \right)}}^{2}}}}{{8\pi ~{{r}_{i}}}}\left\{ {\frac{1}{{{{\varepsilon }_{{{\text{pel}}}}}}} - \frac{1}{{{{\varepsilon }_{{\text{e}}}}}}} \right\}.$$
(2)

Here \({{z}_{i}}e\) is the charge of ions whose radius are \({{r}_{i}}~\left( {i = 1,2} \right)\). The impact of ion partitioning effect reduces with the increasing value of PEL permittivity and allow more accumulation of excess of mobile ions within the PEL. It has been seen that when the PEL have more water content, then dielectric permittivities \({{\varepsilon }_{{{\text{pel}}}}}\) and \({{\varepsilon }_{{\text{e}}}}\) have almost same value and hence, value of \({{f}_{i}}\left( {i = 1,~2} \right)\) becomes unity [40]. The potential field for this system is provided by the Poisson equation, which relates the electric potential \(\psi \left( y \right)\) and charge density within and outside the PEL, and is given as

$$\left. {\begin{array}{*{20}{c}} { - {{\varepsilon }_{{{\text{pel}}}}}\frac{{{{d}^{2}}\psi }}{{d{{y}^{2}}}} = ~~F\mathop \sum \limits_{n = 1}^2 {{z}_{i}}{{n}_{i}}{{f}_{i}} + {{\rho }_{{{\text{fix}}}}};~}&{ - ~h \leqslant y \leqslant - h + \delta } \\ { - {{\varepsilon }_{e}}\frac{{{{d}^{2}}\psi }}{{d{{y}^{2}}}} = ~~F\mathop \sum \limits_{n = 1}^2 {{z}_{i}}{{n}_{i}};}&{ - ~h + \delta \leqslant y~ \leqslant 0} \end{array}} \right\}.$$
(3)

The mobile electrolyte ions within electrolyte as well as PEL region obey Boltzmann distribution and thus

$${{n}_{i}}\left( y \right) = ~~{{n}_{0}}{\kern 1pt} \exp \left. {\left( { - \frac{{{{z}_{i}}e\psi }}{{{{k}_{B}}T}}} \right.} \right).{{\;}}$$
(4)

The scaled form of the potential equations may be written as

$$\left. \begin{gathered} \frac{{{{d}^{2}}\bar {\psi }}}{{d{{{\bar {y}}}^{2}}}} = {{\left( {\kappa h} \right)}^{2}}\xi \left\{ {{\text{sinh}}{\kern 1pt} \bar {\psi }~{\text{exp}}\left( {\Delta \overline {{{W}_{i}}} } \right) - \frac{{zN}}{{2{{n}_{0}}}}} \right\},\,\,\,\, - ~1 \leqslant \bar {y} \leqslant - 1 + \bar {\delta }~ \hfill \\ \frac{{{{d}^{2}}\bar {\psi }}}{{d{{{\bar {y}}}^{2}}}} = {{\left( {\kappa h} \right)}^{2}}{\text{sinh}}{\kern 1pt} \bar {\psi },\,\,\,\, - ~1 + \bar {\delta } \leqslant \bar {y} \leqslant ~0~ \hfill \\ \end{gathered} \right\}.$$
(5)

The scaled parameter appeared in the above equation is \(\kappa h,\) termed as Debye−Hückel parameter, where \({{\kappa }^{{ - 1}}}\) is the EDL thickness and is defined by \({{\kappa }^{{ - 1}}} = \sqrt {{{\varepsilon }_{e}}{{\varphi }_{0}}{\text{/}}2F{{n}_{0}}} \). The parameter \(\xi \), the ion-partition parameter defined by \(\xi = {{\varepsilon }_{{{\text{pel}}}}}{\text{/}}{{\epsilon }_{e}}~\)which is the ratio of the relative dielectric permittivity of the PEL to the bulk electrolyte solutions. The several other scaled parameters introduced in equation (5) are given as \(\bar {y} = y{\text{/}}h\), \(\bar {\delta } = \delta {\text{/}}h\) and \(\bar {\psi } = {{z}_{i}}e\psi {\text{/}}{{k}_{B}}T\), \(\Delta \overline {{{W}_{i}}} = \Delta {{W}_{i}}{\text{/}}{{k}_{B}}T\) and φ0 = RT/F. The Potential equation (5) is solved considering the boundary conditions, summarized below

$$\left. \begin{matrix} {{\left. \frac{d\bar{\psi }}{d\bar{y}} \right|}_{\bar{y}=-1}}=0~~~~~~~~~~~~~~ \\ \bar{\psi }{{}_{\bar{y}=\left( -1+\bar{\delta } \right)-}}=\bar{\psi }{{}_{\bar{y}=\left( -1+\bar{\delta } \right)+}}~ \\ {{\left. \frac{d\bar{\psi }}{d\bar{y}} \right|}_{\bar{y}=\left( -1+\bar{\delta } \right)-}}~=\xi {{\left. \frac{d\bar{\psi }}{d\bar{y}} \right|}_{\bar{y}=\left( -1+\bar{\delta } \right)+}} \\ {{\left. \frac{d\bar{\psi }}{d\bar{y}} \right|}_{\bar{y}=0}}~=0.~~~~~~~~~~~~~~ \\ \end{matrix} \right\}.~$$
(6)

The flow velocity field within electrolyte solution is governed by Cauchy momentum equation. Besides, there must be an additional term in the flow equation within the PEL which is due to frictional forces acting within the PEL due to presence of monomers and such a term is often termed as Darcy term [41, 42]. Thus, the fluid flow equation along with the continuity equation is given below

$$\left. \begin{gathered} \rho \frac{{dq}}{{dt}} = \nabla \cdot \tau + {{\rho }_{e}}E - \frac{{\mu {\kern 1pt}^{ *}}}{{K{\kern 1pt}^{ *}}}q{{\left| q \right|}^{{n - 1}}},\,\, - h \leqslant y \leqslant - h + \delta \hfill \\ \rho \frac{{dq}}{{dt}} = \nabla \cdot \tau + {{\rho }_{e}}E,\,\, - h + \delta \leqslant y \leqslant 0 \hfill \\ \end{gathered} \right\},$$
(7)

and

$$\nabla \cdot \mathbf{q} = 0,$$
(8)

where \(\mathbf{q}\) is the velocity vector and \(\tau \) denotes the stress tensor. The modified flow consistency index is given by \(\mu {\kern 1pt}^{ *} = m{{\epsilon }^{n}},\) where \(\epsilon \) is the porosity of PEL. The modified permeability due to Christopher and Middleman [43] is given by

$$K{\kern 1pt}^{ *} = \frac{6}{{25}}{{\left\{ {\frac{{n\epsilon }}{{3n + 1}}} \right\}}^{n}}{{\left\{ {\frac{{\epsilon {{d}_{{\text{s}}}}}}{{3\left( {1 - \epsilon } \right)}}} \right\}}^{{n + 1}}},$$

where \({{d}_{{\text{s}}}}\) is the diameter of the polymer segments. For fully developed EOF through soft nanochannel, the shear term is given by

$$\tau = \mu \frac{{du}}{{dy}},$$

and the dynamic viscosity of the power-law fluid can be written as

$$\mu = ~~m{{\left| {\frac{{du}}{{dy}}} \right|}^{{n - 1}}}.$$
(9)

Here, the coefficients \(m\) and \(n\) are flow consistency and flow behavior index, respectively. We have considered the steady state fully developed flow through the undertaken channel. The axial velocity component is governed by

$$\frac{d}{{dy}}\left( {\mu \frac{{du}}{{dy}}} \right) = \left\{ \begin{gathered} - {{\rho }_{e}}{\kern 1pt} \exp \left( { - \frac{{\Delta {{W}_{i}}}}{{{{k}_{B}}T}}} \right){{E}_{0}} + \frac{{\mu {\kern 1pt}^{ *}}}{{K{\kern 1pt}^{ *}}}u{{\left| u \right|}^{{n - 1}}};\,\,\,\,~ - h \leqslant y \leqslant - h + \delta ~ \hfill \\ - {{\rho }_{e}}{{E}_{0}};\,\,\,\, - h + \delta \leqslant y \leqslant 0 \hfill \\ \end{gathered} \right..~$$
(10)

We scaled the velocity field by the reference velocity which is considered as the generalized Helmholtz–Smoluchowski electroosmotic velocity, given as \(U_{{HS}}^{N} = n{{\kappa }^{{\frac{{1 - n}}{n}}}}{{\left( {{{\varepsilon }_{e}}~{{E}_{0}}{{\phi }_{{0/m}}}} \right)}^{{\frac{1}{n}}}}.\) Note that in case of Newtonian fluid \(n = 1,\) \({{U}_{{HS}}} = {{\varepsilon }_{e}}{{E}_{0}}{{\phi }_{0}}{\text{/}}m.\) The scaled form of the fluid flow equations is given by

$$\frac{d}{{d\bar {y}}}\left( {\frac{{d\bar {u}}}{{d\bar {y}}}{{{\left| {\frac{{d\bar {u}}}{{d\bar {y}}}} \right|}}^{{n - 1}}}} \right) = \left\{ \begin{gathered} \frac{{{{{\left( {\kappa h} \right)}}^{{n + 1}}}}}{{{{n}^{n}}}}\sinh \left( {\bar {\psi }} \right)\exp \left( { - \Delta ~\overline {{{W}_{i}}} } \right) + {{\beta }^{2}}\bar {u}{{\left| {\bar {u}} \right|}^{{n - 1}}},\,\,\,\,1 \leqslant \bar {y} \leqslant - 1 + \bar {\delta } \hfill \\ \frac{{{{{\left( {\kappa h} \right)}}^{{n + 1}}}}}{{{{n}^{n}}}}\sinh \left( {\bar {\psi }} \right),\,\,\,\, - 1 + \bar {\delta } \leqslant \bar {y} \leqslant 0 \hfill \\ \end{gathered} \right..~$$
(11)

Now, the solution to equation (11) is obtained by using the following boundary conditions given below

$$\left. \begin{matrix} {{\left. {\bar{u}} \right|}_{\bar{y}=-1}}=0 \\ \bar{u}{{}_{\bar{y}=\left( -1+\bar{\delta } \right)-}}=\bar{u}{{}_{\bar{y}=\left( -1+\bar{\delta } \right)+}} \\ {{\left. \frac{d\bar{u}}{d\bar{y}} \right|}_{\bar{y}=\left( -1+\bar{\delta } \right)-}}={{\left. \frac{d\bar{u}}{d\bar{y}} \right|}_{\bar{y}=\left( -1+\bar{\delta } \right)+}} \\ {{\left. \frac{d\bar{u}}{d\bar{y}} \right|}_{\bar{y}=0}}=0 \\ \end{matrix} \right\}.\text{ }\!\!~\!\!\text{ }$$
(12)

NUMERICAL METHOD

The non-linear governing equations are solved using finite difference based numerical scheme. We discretized the equations using the finite difference method and the resulting algebraic system of equations is further solved by using tridiagonal matrix algorithm (TDMA). First the potential equation is solved with some guessed potential (i.e., zero potential) and continue the iteration until the absolute difference in the electrostatic potential in successive iteration is smaller than the tolerance limit \({{10}^{{ - 6}}}\). Once the potential field is known, the velocity equation is solved by applying similar iteration technique with known potential. The computed solutions of EDL potential and axial velocity field are compared with the corresponding analytical solutions obtained under the Debye−Hückel approximation. Note that the analytical results are further a new finding of this present study. In Appendix, we present the code validation and the related results are also explained.

RESULTS AND DISCUSSION

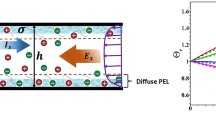
In this section, we have discussed the impact of various electrohydrodynamic parameters describing the potential distribution and the velocity field in a soft nanochannel. The parameter dictating the ion partition effect is denoted by \(\xi \) (PEL-to-electrolyte permittivity ratio); Debye−Hückel parameter \(\kappa h\), which is directly related to the concentration of electrolyte solution and softness parameters \(\beta \) which defines the impact of monomers present with in the PEL on the flow physics. The shear thinning and shear thickening nature of fluid is described by power-law index \(n\). In this study, we consider the channel height as \(h = 100\,\,~{\text{nm}}\) and PEL thickness as \(\delta = 0.1h\). For this study, the background electrolyte considered as KCl, the Debye−Hückel parameter varies from 1 to 100, as the bulk electrolyte concentration varies from \({{10}^{{ - 2}}}\)  to \({{10}^{2}}\) mM. The softness parameter \(\beta \) is taken from 1 to 10 and is expected that it has strong impact on flow modulation. The dielectric permittivity of the PEL is varied in such a manner the ion-partitioning parameter lies in the range from 0.1 to 1.

Fig. 1.
figure 1

Schematic representation of EOF through polymer-grafted nanochannel.

Full size image

In Fig. 2 we have shown the results for EDL potential for different choices of \(\kappa h~(1,\,\,~10,~\,\,{\text{and}}\) 100). The results are presented here considering various values of \(\xi \). The readers are further referred to the figure caption for other model parameters. Note that the smaller values of \(\kappa h\) refers to the electrolyte with low concentration for which the EDL is thick. However, an increase in \(\kappa h\) for fixed channel height is possible by increasing the concentration of background electrolyte medium. At a smaller value in \(\kappa h\), the neutralization of PEL charge is low compared to moderate to high value of \(\kappa h\). It is reasonable, since, an increase in \(\kappa h\) increases the neutralization of PEL due to accumulation of moderate to large number of counterions. Thus, the magnitude in electrostatic EDL potential reduces with the rise in \(\kappa h\). The accumulation of counterions across the PEL further increases with the rise in \(\xi ,\) defining ion partitioning coefficient. With the rise in \(\xi \), the difference in Born energies in PEL and electrolyte solution reduces, and hence electrostatic softness of the PEL reduces, which in turn enhances the penetration of counterions across the PEL. Thus, the neutralization of PEL occurs more rapidly with the rise in \(\xi \), which reduces the magnitude in EDL potential.

Fig. 2.
figure 2

The potential distribution across the polymer-grafted soft nanochannel is shown for \(\left( {\text{a}} \right)~\,\,\kappa h = 1\), (b) \(\kappa h = 10,\) and (c) \(\kappa h = 100\) with various values of \(\xi = 0.1,\,\,0.2,\,\,0.3,\,\,0.4,\,\,~0.5,\,\,0.6,~\,\,0.7,\) 0.8,0.9, and 1. Other model parameters are \(z = - 1,\,\,~N = 1~~{\text{mM}}~\) and \(\beta = 1.\)

Full size image

Next, we have shown the impact fluid rheological behavior on the flow modulation through soft nanochannel. In Figs. 3–5, we have shown the results for power-law index \(n = 1~\) (Newtonian fluid), \(n < 1\) (pseudo-plastic fluid), and \(n > 1\) (dilatant fluid), respectively. The other model parameters are same as considered in Fig. 2. In order to make a comparison, the dimensional value of velocity profile along the axial is shown. From Figs. 3–5, it is clear that the ion partitioning effect plays a prominent role on the flow modulation across the channel. At a given value of flow behavior index parameter, the magnitude in EDL potential reduces with the rise in \(\xi \), which results in a decrease in overall flow across the channel. Note that the impact of \(\xi \) (or in other words, the impact of ion partitioning effect) is more prominent when the effective PEL charge is high, which is certainly possible when the EDL is thick. It is reasonable, since for electrolytes with low concentration, the neutralisation PEL charge due to counterion accumulation is low compared to moderate and high concentration. Besides, at large \(\kappa h\), the axial component of flow velocity shows plug-like profile, which is certainly the key signature of EOF through microdevices. However, at a lower value of \(\kappa h,\) the flow velocity shows a parabolic profile and is reasonable due to overlap of the EDLs formed along the lower and upper walls of the channel. We observe that the magnitude in axial velocity reduces with the rise in power-law index (\(n\)). Rise in value of \(n\) enhances the effective viscosity of the ionized fluidic medium and hence reduces the magnitude in axial velocity.

Fig. 3.
figure 3

The axial velocity distribution across the polymer-grafted soft nanochannel of Newtonian fluid for (n = 1) are for \(\left( {\text{a}} \right)~\,\,\kappa h = 1\), (b) \(\kappa h = 10,\) and (c) \(\kappa h = 100\) with various values of \(\xi = 0.1,\,\,0.2,\,\,0.3,\,\,0.4,\) 0.5, 0.6, 0.7, 0.8, 0.9, and 1. The value of \(\xi \) increases along the arrow direction. Other model parameters are \(z = - 1,~\,\,N = 1~~{\text{mM}}~\) and \(\beta = 1.\)

Full size image
Fig. 4.
figure 4

Similar results as in Fig. 3, except for n = 0.8.

Full size image

In order to make a comparative study we have presented the dimensional values of the flow rate in Figs. 6–7. In Fig. 6 we have shown the results for average flow rate as a function of \(\kappa h\) for various choices of \(\xi \), defining the ion partitioning effect. In Figs. 6a–6c we have shown the results for \(n = 0.8,1,~\) and 1.2. With the rise in \(\kappa h\), the average flow reduces due to reduction in net PEL charge. Besides, the impact of partitioning is prominent for the lower range of \(\kappa h\). We observe that the flow rate also reduces with the rise \(\xi \). This is reasonable, since the penetration of counterion across the PEL-to-electrolyte interface increases, which leads to a reduction in magnitude in EDL potential and thereby the net flow rate across the undertaken channel. Besides, the impact of flow behavior index has a prominent role on the overall flow rate. The enhanced viscosity of fluid with the rise in \(n\) reduces the net throughout of the ionized liquid across the soft nanochannel. In Fig. 7 we have presented the average flow rate as a function of PEL charge. We have presented the results varying the molar concentration of the PEL-charge. A change in sign in the average flow rate is possible changing the valence of PEL-immobile ions. With the rise in \(N\), an enhanced EDL potential leads to an enhanced electromotive force to drive the fluid across the undertaken soft nanochannel. Thus, the magnitude in flow rate increases with the rise in \(N\). The reduction in average flow rate with the rise in \(\xi \) and \(n\) is already discussed to justify the findings presented in Fig. 6.

Fig. 5.
figure 5

Similar results as in Fig. 3, except for n = 1.2.

Full size image
Fig. 6.
figure 6

The average velocity distribution across the polymer-grafted soft nanochannel is shown. The results are shown for (a) \(n = 0.8\) (b) \(n = 1.0\) and (c) \(n = 1.2\) with fixed \(\kappa h = 10\) and \(\xi = 0.1,\,\,0.2,\,\,0.3,\,\,0.4,\,\,0.5,\,\,0.6,\,\,0.7,\) 0.8, 0.9, and 1. The value of \(\xi \) increases along the arrow direction. Other model parameters are \(z = - 1,~\,\,N = 1\,\,~{\text{mM}}\) and \(\beta = 1\).

Full size image
Fig. 7.
figure 7

The average velocity distribution across the polymer-grafted soft nanochannel for (a) \(n = 0.8\), (b) \(n = 1\), and (c) \(n = 1.2\) at fixed \(\beta = 1,~~\kappa h = 10\) and various value for \(\xi = 0.1,\,\,0.2,\,\,0.3,\,\,0.4,\,\,0.5,\,\,0.6,\,\,0.7,\,\,0.8,\) \(0.9~\), and 1. The value of \(\xi \) increases along the arrow direction.

Full size image

Next in Figs. 8–9, we have shown the impact of pertinent parameters on the selectivity of mobile electrolyte ions across the undertaken soft nanochannel filled ionized fluid. The selectivity of mobile ions is defined as

$$S = \frac{{\left| {{{I}_{c}}} \right| - \left| {{{I}_{a}}} \right|}}{{\left| {{{I}_{c}}} \right| + \left| {{{I}_{a}}} \right|}},$$

where \({{I}_{j}}\) represents the average current density for the jth (j = c, a) ionic species across the channel. A detailed discussion of calculation of average current densities of cations and anions is already provided in our previous study [32]. The background electrolyte is considered to be KCl and the diffusion coefficients for the anions and cations of \({{D}_{a}} = 2.047 \times \,\,{{10}^{9}}{\text{ }}{{{\text{m}}}^{{\text{2}}}}{{\;}}{{{\text{s}}}^{{ - 1}}}\) and \({{D}_{c}} = 1.943\,\, \times \,\,\,{{10}^{{ - 9}}}{\text{ }}{{{\text{m}}}^{{\text{2}}}}{\text{ }}{{{\text{s}}}^{{ - 1}}},\) respectively. Thus, the ion Peclet numbers are \(P{{e}_{a}} = 8.945\,\, \times \,\,{{10}^{{ - 3}}}\) and \(P{{e}_{c}} = 9.424\,\, \times \,\,{{10}^{{ - 3}}}\), respectively. We observe that the selectivity \(S\) for \(n = 0.8\) is higher compared to that for \(n = 1\) and 1.2. In fact, we can arrange the magnitude of S as \(\left| {S\left( {n = 0.8} \right)} \right| > \left| {~S\left( {n = 1} \right)} \right| > \,\,|~S\left( {n = 1.2} \right).\) Such a pattern in \(S\) is reasonable since the convective current is higher for \(n < 1\) compared to \(n \geqslant 1.\) For all the cases (i.e, \(0.8 \leqslant n \leqslant 1.2\)), the ionic current due to electromigration is the same. Thus, we can achieve a higher magnitude in \(S\) when \(n < 0.8~\) (Fig. 9). The magnitude in ion selectivity parameter \(S\) reduces with the rise in electrolyte concentration due to significant neutralization of PEL charge, which in term reduces the convective as well as electromigration current. In Fig. 9 we have shown the results for ion selectivity \(S\) as a function of molar concentration of the PEL-immobile charge. The net current due to anions (cations) dominates for positively (negatively) charged PEL and leads to negative value of \(S\). Note that the magnitude of PEL charge, and hence the ionic current reduces with the rise in \(\xi \) (i.e, decrease in ion partitioning effect). Thus, a smaller magnitude of \(S\) is possible with the rise in \(\xi \). The impact of fluid rheological behavior on the ion selectivity parameter is already discussed earlier.

Fig. 8.
figure 8

The selectivity distribution across the polymer-grafted soft nanochannel for different value of power-law fluid \(n = 0.8,~\,\,1,~\) and 1.2 as function of \(\kappa h\) are shown. The other model parameters are \(\xi = 0.5,~~z = 1,\,\,{\text{and}}\,\,N = 1\,\,{\text{mM}},~~\beta = 1.\)

Full size image
Fig. 9.
figure 9

The selectivity distribution across the polymer-grafted soft nanochannel. The results are shown for \(\left( {\text{a}} \right)~n = 0.8,\,\,~\left( {\text{b}} \right){{\;}}n = 1.0,~\) and \(\left( {\text{c}} \right){{\;}}\,\,n = 1.2\) with fixed value of \(\beta = 1,~~\kappa h = 10\) and \(\xi = 0.1,\,\,0.2,\,\,0.3,\,\,0.4,\) \(0.5,\,\,0.6,\,\,0.7,\,\,0.8,\,\,0.9,\) and 1. The value of \(\xi \) increases along the arrow direction.

Full size image

CONCLUSIONS

In the present article we deal with the electroosmotic flow and ion selectivity across the soft nanochannel. The background non-Newtonian fluid is modelled by using a widely employed power-law model. The impact of ion partitioning effect stemming from significant difference in dielectric permittivity of the PEL and electrolyte medium is discussed. The numerically obtained results are validated with the analytical results derived under weakly charged PEL. We observed a significant impact of ion partitioning effect on the overall flow modulation and selectivity of mobile electrolyte ions. Impact of ion partitioning is prominent when the flow behavior index \(n\) is lower than 1 and lower range of Debye−Hückel parameters. Note that for the electrolyte with low concentration for which EDL is thick, the effective PEL charge is high. In addition, for \(n \leqslant 1,\) the impact of EOF across the PEL is high enough to reduce the neutralization of PEL charge. Hence for such cases, the impact of ion partitioning effect on the flow modulation and selective nature of the soft nanochannel is prominent, which however reduces for dense PEL, large \(\kappa h\) and \(n~\,\, > \,\,~1\). The cation selective as well as anion selective nature can be achieved by regulating properly the charge properties of the PEL.