Electrokinetic Transport of Non-Newtonian Fluid through Soft Nanochannel with pH-Responsive and Partially Ion-Penetrable Polymer Layer

Abstract

The present article deals with the comprehensive parametric study on electroosmotic flow and transportation of ions through polymer grafted soft nanochannel containing non-Newtonian fluid. We consider the fully developed flow in a slit rectangular channel. The charged poly-electrolyte layer (PEL) carries a monovalent acidic ionizable group attached to a rigid wall. The ion partitioning effect is considered in our study, which arises from the difference in relative permittivity of the polyelectrolyte region and the bulk electrolyte. The non-linear Poisson−Boltzmann equation and the modified Cauchy momentum equation, which are coupled, are used to describe the mathematical model. The main objective of this analysis is to demonstrate the impact of bulk pH on the charge regulation of mono-ionic functional groups residing in PEL, the impact of flow behavior index and different electrohydrodynamic parameters, including EDL thickness, ion-partitioning parameter, the Debye−Hückel parameter, and softness parameters etc, on the overall flow modulation and selectivity parameter. This study is expected to constitute a significant step forward in the real-world continuum mathematical modelling of interfacial flow physics in the scenario of electrohydrodynamics in soft nanochannels.

1 INTRODUCTION

In recent years the electroosmotic flow (EOF) through nanochannels finds its widespread applications in designing lab-on-a-chip devices, which are often used in biological analysis, chemical analysis as well as industrial research and development [1–4]. When a charged surface is exposed in an electrolyte solution, a layer of immobile ions form just next to the surface and its thickness close to the diameter of ions (few angstroms). Such a layer is known as Stern layer. Besides, for the channel with charged walls attracts the counterions and repels coions. Besides the mobile electrolyte ions have their own thermal energy. Due to the combined effects of these two, a layer of mobile charge forms next to the Stern layer. These two layers are combinedly termed as electric double layer (EDL). Under the applied potential gradient, the net charge with the EDL experiences a driving force to generate the fluid flow. Such a fluid flow is termed as EOF. Several research works on the modulation of EOF through micro/nanochannels are available in recent days [3, 5–14]. Besides, Vinogradova and co-researchers [15–17] made a significant contribution of ions transport of hydrophobic nanopore.

The aforementioned articles deal with the electrokinetics transport of Newtonian fluids through narrow confinements. However, there are various fluids, for which the relation between stress and rate of strain is no longer linear in nature. Such a wide class of fluids are often termed as non-Newtonian for which the stress and rate of strain ceases to be linear. It can be seen that the polymeric solutions, colloidal solutions, biofluids etc. do not exhibit Newtonian properties. There are various models including power-law model, Herschel-Bulkley (HB) model, Casson model, Bingham model, and Carreau model etc., which are used to study the fluid rheological behavior of non-Newtonian fluids [18]. The power-law model is however the most popular for its ability and simplicity to describe a wide range of non-Newtonian fluids. Zhao et al. [19] examined the mathematical model to describe the electroosmotic power-law flow of liquids in a slit microchannel. They derived the analytical solution of the velocity distribution for several specific values of the flow behavior index. Das and Chakraborty [20] proposed a mathematical model for the EOF of non-Newtonian fluid in a microchannel and obtained the analytical solutions for the distribution of temperature, velocity, and dissolved concentration under the Debye−Hückel approximation. Besides, a number of research articles are available on the EOF of non-Newtonian fluids across narrow confinements [20–26]. In all these studies the charged properties of the channel walls are taken to be independent of the choice of bulk pH. However, several researchers have shown the pH-responsive charge properties on the modulation of EOF through microchannels. Sadeghi et al. [27] studied EOF and ionic conductivity through a pH regulated rectangular nanochannel. Yang et al. [28] studied the time periodic EOF through pH-regulated nanochannel. In a combined experimental and theoretical study, Kimani et al. [29] investigated the effect of pH on membrane charge ionization and reverse osmosis. Tseng et al. [30] studied the modulation of EOF through a pH-regulated cylindrical nanochannel. Besides, Schoch et al. [31] studied the impact of pH-controlled diffusion of proteins across the nanochannel. In all the aforementioned studies the modulation of EOF through micro/nanochannel, the walls are taken to be rigid in nature. However, there are several physical situations where the channel walls are grafted with a layer of polymeric material. A nanochannel for which the walls are grafted with such a polymer layer is often termed as soft nanochannel. The polymer layer, which is often termed a polyelectrolyte layer (PEL) allows the penetration of mobile ions as well as background fluidic medium. The penetration of ions is controlled by the dielectric-mediated ion partitioning effect [32–34]. Note that for PEL, the dielectric permittivity is in general lower than that of the bulk aqueous medium, which leads to a difference in electrostatic self-energy of the ions [35] or Born energy of both the phases [36]. As a result, the penetration of ions within the PEL occurs in a discontinuous manner for the partially ion-penetrable PELs which are subjected to a significant ion partitioning effect. On the other hand, the penetration and fluid flow are determined by the Brinkmann screening length of the PEL [37]. The higher the penetration length, a strong fluid flow within the PEL is possible. Note that the PEL bears the functional group, which leads to a net non-zero volume charge with the PEL. Such a volume charge, however, depends strongly on the pH of the bulk aqueous medium [38].

A series of research works are available on the flow modulation of Newtonian fluid across the soft nanochannel [25, 39–50]. However, a little attention is paid on the EOF through soft nanochannel filled with non-Newtonian fluid. Gaikwad et al. [51] studied the modulation of EOF through soft nanochannel filled with power-law fluid. Li et al. [52] studied the flow of Jeffrey fluid across the soft nanochannel under AC electric field. Patel et al. [53] studied the rotating EOF of a power-law fluid though soft nanochannel. In these studies, the PEL-charge is considered to be independent of the pH of the background electrolyte and PEL is fully ion penetrable neglecting the ion partitioning effect. Later, Barman et al. [54] studied the impact of pH-regulated charge properties of the soft layer on the flow modulation of power law fluid across soft nanochannel. However, in their study they have neglected the dielectric-gradient ion partitioning effect. Note that for partially ion penetrable PEL, the ion partitioning effect has a substantial role. Higher the ion partitioning effect, the EDL potential with PEL is higher, which causes a significant flow modulation across the soft nanochannel.

Based on the existing knowledge gap indicated above, we have considered the EOF modulation through soft nanochannel filled with non-Newtonian fluid considering the combined impacts of ion size effect and pH-regulated charged properties. The power-law fluid flow model is invoked to describe non-Newtonian rheology of the background fluidic medium. The fluid flow across the PEL and electrolyte medium is governed by modified Cauchy momentum equation. The spatial distribution of mobile ions follows the Boltzmann distribution and the EDL potential is described using non-linear Poisson−Boltzmann equation. Going beyond the widely employed Debye−Hückel approximation, we present the results for wide range of pertinent parameters. In addition, the flow modulation, we further illustrated the impact of pertinent parameters on the selectivity of mobile electrolyte ions.

2 FORMULATION OF MATHEMATICAL MODEL

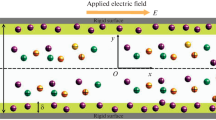
We consider the modulation of EOF through slit soft nanochannel of height $h.$ The width of the channel is considered to be much larger than that of the channel height. The thickness of the grafted PEL along the channel walls is denoted by $\delta$. The electric field of strength ${{E}_{0}}$ is applied along the axis of the channel. Figure 1 further illustrates the undertaken problem configuration. The background solution is the binary symmetric electrolyte solution with valences ${{z}_{{\left( {i = 1,2} \right)}}} = \pm 1$ and bulk concentrations ${{n}_{0}}$ (in mM). The step-like PEL bears additional fixed charge density due to presence of acidic functional group, which in turn results in a non-zero volume charge density ${{\rho }_{{{\text{fix}}}}}$ (in mM) and is given below [54, 55]

$${{\rho }_{{{\text{fix}}}}} = \frac{{{{z}_{A}}F{{N}_{A}}}}{{1 + {{{10}}^{{{\text{p}}{{{\text{K}}}_{{\text{a}}}} - ~{\text{pH}}}}}{\text{exp }}\left( { - \frac{{e\psi \left( y \right)}}{{{{k}_{B}}~T~}}} \right)~}},$$

(1)

where $e,~F,~{{z}_{A}}$ and ${{N}_{A}}$ are elementary charge, Faraday constant, valence and concentration (in mM) of acidic immobile ion entrapped within the PEL, respectively. Here, $\psi \left( y \right)$ refers the EDL electrostatic potential at location $y$. Note that when ${\text{pH}} \ll {\text{p}}{{{\text{K}}}_{{\text{a}}}}$ the PEL-charge density (${{\rho }_{{{\text{fix}}}}}$) approaches to zero and for ${\text{pH}} \gg {\text{p}}{{{\text{K}}}_{{\text{a}}}}$, ${{\rho }_{{{\text{fix}}}}}$ approaches to its maximum value ${{z}_{A}}F{{N}_{A}}.$ The dielectric permittivity ${{\varepsilon }_{{{\text{pel}}}}}$ of the PEL is in general smaller than that of the bulk aqueous medium (${{\varepsilon }_{f}}$), which in turn causes the ion partitioning effect. Note that the parameters $\xi$ refers the ion-partition parameter and is defined as $\xi = {{\varepsilon }_{{{\text{pel}}}}}{\text{/}}{{\varepsilon }_{f}}$. The difference in Born energy in both the phases is defined as

$$\Delta ~{{W}_{i}} = \frac{{{{{\left( {{{z}_{i}}e} \right)}}^{2}}}}{{8\pi {{r}_{i}}}}\left( {\frac{1}{{{{\varepsilon }_{{{\text{pel}}}}}}} - \frac{1}{{{{\varepsilon }_{f}}}}} \right).$$

Here ${{r}_{i}}$ denotes the radius of the hydrated ion, which is taken to be same for both electrolyte ions [32]. The Poisson−Boltzmann equation yields the electric potential $\psi \left( y \right)$ [54] and is given by

$$\left. {\begin{array}{*{20}{c}} { - {{\varepsilon }_{{{\text{pel}}}}}\frac{{{{d}^{2}}\psi }}{{d{{y}^{2}}}} = {{\rho }_{{{\text{pel}}}}},~}&{ - h \leqslant ~y \leqslant - h + \delta } \\ { - {{\varepsilon }_{e}}\frac{{{{d}^{2}}\psi }}{{d{{y}^{2}}}} = {{\rho }_{e}},~~~~~}&{ - h + \delta \leqslant y \leqslant ~0\} } \end{array}} \right\}$$

(2)

with

$${{\rho }_{e}} = {{z}_{A}}F\left\{ {{{n}_{ + }}\left( x \right) - {{n}_{ - }}\left( x \right)} \right\},$$

(3)

and

$${{\rho }_{{{\text{pel}}}}} = {{\rho }_{e}}~{{f}_{i}} + {{\rho }_{{{\text{fix}}}}},$$

where

$${{f}_{i}} = \exp \left( { - \frac{{\Delta {{W}_{i}}}}{{{{k}_{B}}T}}} \right).$$

Fig. 1.

The schematic signifies EOF though the polymer-grafted nanochannel.

The spatial distribution of ionic species is governed by Boltzmann distribution and is given by

$${{n}_{ \pm }}\left( y \right) = {{n}_{0}}{\kern 1pt} {\text{exp}}\left( { \mp \frac{{e\psi \left( y \right)}}{{{{k}_{B}}T}}} \right).$$

In order to scale the potential equations, we consider ${{\psi }_{0}} = {{k}_{B}}T{\text{/}}e~$ as the potential scale and half height of the channel is considered for the scale for $y$ coordinate. Thus, the non-dimensional form of the electric potential equations (2) may be written as

$$\begin{gathered} \frac{{{{d}^{2}}\bar {\psi }}}{{d{{{\bar {y}}}^{2}}}} = \frac{{{{{\left( {\kappa h} \right)}}^{2}}}}{\xi }\left\{ {\sinh {\kern 1pt} \bar {\psi }\exp \left( { - \Delta \overline {{{W}_{i}}} } \right) - \left( {\frac{{{{z}_{A}}{{N}_{A}}}}{{2{{n}_{0}}}}} \right)} \right. \\ \left. { \times \,\,\frac{1}{{1 + {{{10}}^{{{\text{p}}{{{\text{K}}}_{{\text{a}}}} - ~{\text{pH}}}}}~{\kern 1pt} \exp \left( { - \bar {\psi }} \right)}}} \right\},\,\,\,\, - ~1 \leqslant \bar {y} \leqslant - 1 + \bar {\delta }, \\ \frac{{{{d}^{2}}\bar {\psi }}}{{d{{{\bar {y}}}^{2}}}} = {{\left( {\kappa h} \right)}^{2}}~\sinh {\kern 1pt} \bar {\psi },\,\,\,\, - 1 + \bar {\delta } \leqslant \bar {y} \leqslant 0. \\ \end{gathered} $$

(4)

The non-dimensional parameter $\kappa h$ refers the Debye−Hückel parameter and is defined as $\kappa = {{\left( {\frac{{2{{F}^{2}}{{n}_{0}}}}{{{{\varepsilon }_{e}}{{\psi }_{0}}}}} \right)}^{{1/2}}}.~$ The scaled parameters are given as $\bar {y}~ = y{\text{/}}h,\,\,~\bar {\delta } = \delta {\text{/}}h~$ and $\bar {\psi } = e\psi {\text{/}}{{k}_{B}}T,\,\,~\Delta \overline {{{W}_{i}}} = \Delta {{W}_{i}}{\text{/}}{{k}_{B}}T.$ The following are the boundary conditions associated to the EDL potential $\psi \left( y \right)$

$$\left. \begin{matrix} {{\left. \frac{d\bar{\psi }}{d\bar{y}} \right|}_{\bar{y}=-1}}=0~~~~~~~~~~~~~~~ \\ \bar{\psi }{{}_{\bar{y}=\left( -1+\bar{\delta } \right)-}}=\bar{\psi }{{}_{\bar{y}=\left( -1+\bar{\delta } \right)+}}~ \\ {{\left. \frac{d\bar{\psi }}{d\bar{y}} \right|}_{\bar{y}=\left( -1+\bar{\delta } \right)+}}~=\xi {{\left. \frac{d\bar{\psi }}{d\bar{y}} \right|}_{\bar{y}=\left( -1+\bar{\delta } \right)-}} \\ {{\left. \frac{d\bar{\psi }}{d\bar{y}} \right|}_{\bar{y}=0}}~=0.~~~~~~~~~~~~~~ \\ \end{matrix}~ \right\}.$$

(5)

The flow velocity field across the electrolyte solution is given by the Cauchy momentum equation. In addition, the flow filed across the PEL, we need to consider the modified Cauchy momentum equations with the Darcy term, which refers the frictional force term acted on the PEL due to existing polymer segments [56, 57]. Beside we also considered the continuity equation for incompressible fluid. Thus, the fluid flow equations within PEL and electrolyte solutions are given by

$$\left. {\begin{array}{*{20}{c}} {\rho \frac{{Dq}}{{Dt}} = - \nabla p + \nabla \,\cdot\,\tau + {{\rho }_{{{\text{pel}}}}}E - \frac{{\mu {\kern 1pt}^{ *}}}{{K{\kern 1pt} ^{ *}}}q{{{\left| q \right|}}^{{n - 1}}},~}&{ - h \leqslant y \leqslant - h + \delta } \\ {\rho \frac{{Dq}}{{Dt}} = - \nabla p + \nabla \,\cdot\,\tau + {{\rho }_{e}}E,~~~~~~~~~~~~~~~~~~~~~~~~}&{ - h + \delta \leqslant y \leqslant 0} \end{array}} \right\}$$

(6)

and

$$\nabla \cdot q = {\text{0 }}{\text{.}}$$

(7)

Here $\mu {\kern 1pt}^{ *} = m{{\varepsilon }^{n}},\,\,\tau$ and $q$ are modified consistency index of the power-law fluid within soft polymeric PEL [56, 57], stress tensor and velocity vector, respectively. The modified permeability $K{\kern 1pt}^{ *}$ is given by (Christopher and Middleman) [54, 58]

$$~K{\kern 1pt}^{ *} = \frac{6}{{25}}{{\left\{ {\frac{{n\epsilon }}{{3n + 1}}} \right\}}^{n}}{{\left\{ {\frac{{\epsilon {{d}_{{\text{s}}}}}}{{3\left( {1 - \epsilon } \right)}}} \right\}}^{{n + 1}}}.$$

Here $\epsilon$ determines PEL’s porosity, ${{d}_{{\text{s}}}}$ is the polymer segment diameter. The component of the velocity distribution along the axial direction is $u = u\left( y \right)$ and in the transverse directions reduces to $v = 0$ for a fully developed EOF under steady state conditions at a negligible pressure. The shear stress can be calculated as $\tau = \mu ~\left( {\frac{{du}}{{dy}}} \right)$, where the fluid viscosity based on the power-law model may be given as

$$\mu = m{{\left| {\frac{{du}}{{dy}}} \right|}^{{n - 1}}},$$

(8)

where $m$ refers consistency index of the power-law fluid outside of PEL and $n$ indicate the flow characteristic index [22, 54]. The axial velocity component of momentum equation is thus governed by [22, 57]

$$\frac{d}{{dy}}\left( {\mu \frac{{du}}{{dy}}} \right) = \left\{ {\begin{array}{*{20}{c}} {\left( {{{\varepsilon }_{{{\text{pel}}}}}\frac{{{{d}^{2}}\psi }}{{d{{y}^{2}}}}} \right){{E}_{0}} + \frac{{\mu {\kern 1pt}^{ *}}}{{K{\kern 1pt}^{ *}}}u{{{\left| u \right|}}^{{n - 1}}};}&{~ - h \leqslant y \leqslant - h + \delta ~} \\ {\left( {{{\varepsilon }_{f}}\frac{{{{d}^{2}}\psi }}{{d{{y}^{2}}}}} \right){{E}_{0}};~~~~~~~~~~~~~~~~~~~~~~~}&{ - h + \delta \leqslant y \leqslant 0} \end{array}.} \right.$$

(9)

For fluid velocity, the reference velocity is considered as the generalized Helmholtz–Smoluchowski electroosmotic velocity, defined as $U_{{{\text{HS}}}}^{N} = n{{\kappa }^{{\frac{{1 - n}}{n}}}}{{\left( {{{\varepsilon }_{f}}~{{E}_{0}}{{\psi }_{0}}{\text{/}}m} \right)}^{{\frac{1}{n}}}}$ where ${{U}_{{{\text{HS}}}}} = \left( {{{\varepsilon }_{f}}{{E}_{0}}{{\psi }_{0}}{\text{/}}m} \right)$ refers the HS velocity scale for Newtonian fluid ($n = 1$). Hence, the reduced scaled form of the fluid velocity equation (9) under fully developed steady state condition with low Reynolds number flow may be given as

$$\begin{gathered} \frac{d}{{d\bar {y}}}\left( {\frac{{d\bar {u}}}{{d\bar {y}}}{{{\left| {\frac{{d\bar {u}}}{{d\bar {y}}}} \right|}}^{{n - 1}}}} \right) \\ = \left\{ {\begin{array}{*{20}{c}} {\xi \frac{{{{{\left( {\kappa h} \right)}}^{{n - 1}}}}}{{{{n}^{n}}}}\frac{{{{d}^{2}}\bar {\psi }}}{{d{{{\bar {y}}}^{2}}}} + {{\beta }^{2}}\bar {u}{{{\left| {\bar {u}} \right|}}^{{n - 1}}},~~}&{ - 1 \leqslant \bar {y} \leqslant - 1 + \bar {\delta }} \\ {\frac{{{{{\left( {\kappa h} \right)}}^{{n - 1}}}}}{{{{n}^{n}}}}\frac{{{{d}^{2}}\bar {\psi }}}{{d{{{\bar {y}}}^{2}}}},~~~~~~~~~~~~~~~~~~~~~}&{~ - 1 + \bar {\delta } \leqslant \bar {y} \leqslant 0} \end{array},} \right. \\ \end{gathered} $$

(10)

where the softness parameter $\beta = 1{\text{/}}\sqrt {Da}$ characterizes the importance of the additional resistive force within the PEL and the parameter $Da = K{\kern 1pt}^{ *}{\kern 1pt} {\text{/}}{{\varepsilon }^{n}}{{h}^{{n + 1}}}$ refers the Darcy term [32, 54]. Note that an increase in $\beta$ reduces the net flow throughout across the PEL. The boundary conditions associated to axial velocity are given as

$$\left. \begin{matrix} {{\left. {\bar{u}} \right|}_{\bar{y}=-1}}=0~~~~~~~~~~~ \\ \bar{u}{{}_{\bar{y}=\left( -1+\bar{\delta } \right)-}}=\bar{u}{{}_{\bar{y}=\left( -1+\bar{\delta } \right)+}} \\ {{\left. \frac{d\bar{u}}{d\bar{y}} \right|}_{\bar{y}=\left( -1+\bar{\delta } \right)-}}={{\left. \frac{d\bar{u}}{d\bar{y}} \right|}_{\bar{y}=\left( -1+\bar{\delta } \right)+}} \\ {{\left. \frac{d\bar{u}}{d\bar{y}} \right|}_{\bar{y}=0}}=0~~~~~~~~~~~ \\ \end{matrix}~ \right\}.$$

(11)

We employed a finite difference based iterative scheme to solve the coupled set of governing equations given in Eqs. (4) and (10) associated to the boundary conditions given in Eqs. (5) and (11). With the guess value of potential, we first solve Eq. (4). Once a converged results is obtained, we calculate the velocity equations. We continue the same process until the absolute difference between two subsequent iterations is lower than the tolerance limit of ${{10}^{{ - 6}}}$. In order to validate the numerical scheme, we further compare the numerical results with the theoretical results for flow field and EDL potential derived under Debye−Hückel limit. In the Appendix-A, the code validation and associated investigations are represented.

3 RESULTS AND DISCUSSION

In this study, we examine the effects of various electrohydrodynamic parameters to illustrate the potential distribution and velocity field across the soft nanochannel. The impact of pH-regulated monovalent ionizable functional groups within PEL, $\xi$ (PEL-to-electrolyte permittivity ratio) regulating the ion partition effect, $\kappa h$ (Debye−Hückel parameter relating the concentration of electrolyte solution) and the influence of monomers distribution in the PEL affecting the flow physics determined by the softness parameters $\beta$. In addition, we further indicate the impact of fluid’s shear thinning and thickening properties on the overall flow modulation, which is regulated via the power-law index $n$. We consider the channel height as $h~\,\, = ~\,\,100$ nm and $\delta = 0.1h$ for PEL thickness throughout this investigation. Here, KCl is considered as the background electrolyte. The effect of pH on ionizable monovalent functional groups ranges from 2 to 12 with ${\text{p}}{{{\text{K}}}_{{\text{a}}}} = 4$ $\left[ {55} \right]$ (carboxylic acid groups), the Debye−Hückel parameter generally ranges from 1 to 100, depending on the electrolyte concentration and is ranges from ${{10}^{{ - 2}}}$ to ${{10}^{2}}$ mM. It is known that the softness parameter $\beta$ usually lies between 1 and 10, and it has a significant impact on the flow modulation. The dielectric constant of the PEL is modified in such a way that the ion distribution parameter is between 0.1 to 1.

In Figs. 2a–2c we present electrostatic EDL distribution for a variety of physicochemical parameters, namely $\kappa h$, pH, and $\xi$, respectively. In Fig. 2a, the results are presented for various values of $\kappa h$ with fixed values of other parameters. The readers are further referred to the figure caption for other model parameters. In addition, for the low values of $\kappa h$ implies the electrolyte with low concentration and it refers the thick EDL and vice versa. In comparison to moderate to high $\kappa h$ values, the neutralization of the PEL charge is minimal for smaller $\kappa h$ values. Higher the values of $\kappa h$ amplifies the neutralization of PEL charge due to increase in counter ions and thus the magnitude in EDL electrostatic potential decreases as $\kappa h$ increases. In Fig. 2b, we present the electrostatic potential for various choices of bulk pH. We observe that the magnitude in EDL potential increases with the rise in pH. It is reasonable as the functional group reside in PEL is acidic in nature and thus, the net amount of PEL charge increases with the rise in pH. However, the impact of pH is insignificant when pH $\geqslant 8.$ Note that at this critical pH, the PEL-charge reaches to its maximum value and thus, further increase in pH leads no further change in electrostatic potential. In Fig. 2c, we present the results for various values in $\xi$. The difference in Born energies in PEL and electrolyte solution decreases as $\xi$ increases, which reduces the electrostatic softness of the PEL and therefore enhances counterion penetration across the PEL. As a result, the neutralization of PEL happens more rapidly as $\xi$ rises, and hence it reduces the magnitude of EDL potential.

Fig. 2.

The potential distribution across the soft polymer-grafted nanochannel is shown for (a)$~\kappa h$ = 3, 5, 7, 10, and 100 and other parameters are $\xi = 1$ and pH 7 (b) $\kappa h = 10$ with different values of pH 2, 3, 4, 5, and 12, $\xi = 1$ and (c) $\kappa h = 10$, with different values of $\xi$ = 0.1, 0.2, 0.3, 0.4, and 1, and pH 7. The other parameters of the model are $z~ = ~ - 1,~\,\,{{N}_{A}} = 1~\,\,{\text{mM}},$ and $\beta = 1$.

Next, the significance of fluid rheological behavior on flow modulation through soft nanochannels has been demonstrated. In Figs. 3a–3c, 4a–4c and 5a–5c, we have presented the average velocity for the power law index $n < 1$ (pseudo-plastic fluid), $n = 1$ (Newtonian fluid) or $n > 1$ (dilatant fluid). In order to make a comparison, the dimensional values average velocity profile are shown. In Figs. 3a–3c, the results for the mean flow rate as a function of $\kappa h$ are shown for various choices of bulk pH. The pH-regulation effect on PEL charge comprised of monovalent ionizable functional groups (carboxylic acid groups) [55], has a significant role in the flow modulation. The magnitude of the EDL potential increases as pH increases for a given value of the power-law index parameter, resulting in an increase in the total flux through the channel. It is seen that the rise in value of pH a growth in velocity can be seen but at ${\text{pH}} \geqslant 8$ the change in velocity is insignificant for various choices of pH. The average flow decreases when $\kappa h$ rises due to a decrease in net PEL charge. In Figs. 4a–4c we have shown the results for the average yield as a function of pH for different choices of $\xi$. We can see that when $\xi$ rises, the flow rate decreases as well. This is logical because as counterion penetration throughout the PEL-to-electrolyte interface grows, the magnitude in EDL potential and hence the net flow rate through the undertaken channel decreases. In Figs. 5a–5c, we have shown average flow rate as a function of pH and the results are presented for various choices of softness parameter. We observe that as $\beta$ increases, the flow also decreases. This is reasonable because as counterion penetration increases across the PEL-electrolyte interface, the amount of EDL potential, and hence the net flow rate through the channel passed, decreases. In addition, the influence of the flow behavior index on the total flow rate is also significant. With an increase of $n,$ the viscosity of the liquid increases, thus decreasing the net flux of the ionized liquid through the soft nanochannel.

Fig. 3.

The distribution of the mean axial velocity is shown as a function of the Debye−Hückel parameter in the soft polymer-grafted nanochannel for (a) $n = 0.8$, (b) $n = 1$, and (c) $n = 1.2$, with different values of pH 2, 3, 4, 5, and 12. The value of pH increases in the direction of the arrow. The other model parameters are $z = - 1,~\xi = 1,~{{N}_{A}} = 1$ mM, and $\beta = 1.$

Fig. 4.

The mean axial velocity distribution as a function of pH is shown for the soft polymer-grafted nanochannel for (a) $n = 0.8$, (b) $n = 1$, and (c) $n = 1.2$, with different values of $\xi ~\,\, = ~\,\,0.1,~\,\,0.2,~\,\,0.3,\,\,~0.4,~$and 1. The value of $\xi$ increases in the direction of the arrow. The other model parameters are $z = - 1,{{\;}}~{{N}_{A}} = 1\,\,{\text{mM}},$ and $\beta = 1$.

Fig. 5.

The mean axial velocity distribution as a function of pH is shown for the soft polymer-grafted nanochannel for (a) $n = 0.8$, (b) $n = 1$, and (c) $n = 1.2$, with different values of $~\beta = 1,3,5$, and 10. The value of $\beta$ increases in the direction of the arrow. The other model parameters are $z = - 1,{{\;}}~{{N}_{A}} = 1\,\,{\text{mM}},$ and $\xi = 1.$

3.1 Mobile Ion Selectivity

The selectivity of mobile ions is defined as

$$S = \frac{{\left| {{{I}_{c}}} \right| - \left| {{{I}_{a}}} \right|}}{{\left| {{{I}_{c}}} \right| + \left| {{{I}_{a}}} \right|}},$$

where ${{I}_{j}}$ represents the average current density for the ${{j}^{{th}}}\left( {j = c,a} \right)$ ionic species across the channel. The ${{j}^{{th}}}~$component of the ionic current density for cation and anion $\left( {j = c,a} \right)$ is

$${{I}_{j}} = ~{{z}_{j}}F{{M}_{j}},$$

the flux ${{M}_{j}}~$is stated as

$${{M}_{j}} = ~ - {{D}_{j}}\nabla {{n}_{j}} + \left( {{{\mu }_{j}}E + q} \right){{n}_{j}}.$$

Here, $q$ is velocity field, ${{\mu }_{j}}\left( { = {{z}_{j}}{{D}_{j}}F{\text{/}}RT} \right)$ is electrophoretic mobility and $~{{D}_{j}}$ is diffusion coefficient.

The axial component as

$${{M}_{{j,x}}} = ~ - {{D}_{j}}\frac{{\partial {{n}_{j}}}}{{\partial x}} + \left[ {{{\mu }_{j}}{{E}_{0}} + u\left( y \right)} \right]{{n}_{j}}~$$

and hence, the scaled axial ionic current ${{I}_{{j,x}}}$ is

$${{\bar {I}}_{{j,x}}} = - \frac{{{{z}_{j}}}}{{P{{e}_{j}}}}\frac{{\partial {{{\bar {n}}}_{j}}}}{{\partial x}} + {{\Lambda }}\frac{{z_{j}^{2}{{{\bar {n}}}_{j}}}}{{P{{e}_{j}}}} + {{z}_{j}}{{\bar {n}}_{j}}\bar {u}$$

the scale for ionic current is ${{I}_{0}} = F{{n}_{0}}{{U}_{{{\text{HS}}}}}$. The scaled velocity ${{U}_{{{\text{HS}}}}}$ used here is known as Helmholtz−Smoluchowski (HS) and $P{{e}_{j}}~\left( { = {{U}_{{{\text{HS}}}}}h~{\text{/}}{{D}_{j}}~} \right)$ is the Peclet number for Newton’s fluid. The number ${{\Lambda }}\left( { = {{E}_{0}}h{\text{/}}{{\psi }_{0}}} \right)$ gives the scaled value of the intensity of the applied electric field. In our present study, we consider flow modulation through infinitely long slit soft nanochannel. Thus, the contribution of diffusion current along the axial direction is negligible [48]. Thus, neglecting the same, Eq. (15) reduces to

$${{\bar {I}}_{{j,x}}} = \frac{{{{\Lambda }}z_{j}^{2}{{{\bar {n}}}_{j}}}}{{P{{e}_{j}}}} + {{z}_{j}}{{\bar {n}}_{j}}\bar {u}.$$

Over the entire polymer-grafted nanochannel, the average axial current density per ${{j}^{{th}}}~\left( {j = c,~a} \right)$ ionic species is given as

$${{I}_{j}} = \int\limits_0^1 {{{{\bar {I}}}_{{j,x}}}~d\bar {y}} $$

In Figs. 6a–6c we have highlighted the results for selectivity parameter as a function of $\kappa h$. The results are presented here for n = 0.8, 1, and 1.2. The pH-regulation effect on PEL with monovalent ionizable functional groups (carboxylic acid groups), have a significant role in the flow modulation throughout the channel. The magnitude of EDL potential increases as pH increases for a given value of the flow behavior index parameter, resulting in a rise in total selectivity through the channel. It is seen that the rise in value of pH a growth in selectivity can be seen but at ${\text{pH}} \geqslant 8$ the selectivity overlapping. The selectivity distribution decreases with increasing $\kappa h$ due to a decrease in net PEL charge. The main observation is that $\left| {S\left( n \right)} \right| < 1$ for all $n = 0.8,\,\,1~$ and $~1.2$ and for less than $n < 1$ the selectivity profile appears frequently.

Fig. 6.

The selectivity distribution as a function of the Debye−Hückel parameter is shown by the polymer-grafted soft nanochannel for (a) $n = 0.8,$ (b) $n = 1,$ and (c) $n = 1.2$, with different values of pH 2, 3, 4, 5, and 12, where pH increases in the direction of the arrow. The other model parameters are $z = - 1$, $\xi = 1$, ${{N}_{A}} = 1~$ mM and $\beta = 1.$

4 CONCLUSION

In this work, we investigated modulation of EOF and ion selectivity in a soft nanochannel. The well-known power-law model is invoked to simulate the non-Newtonian fluid in the channel. The mathematical model is based on non-linear Poisson–Boltzmann equation of EDL potential and Cauchy momentum equation for fluid flow across and outside the PEL. We employ the finite difference based numerical scheme to obtain the flow velocity and other unknown quantities for wide span of pertinent parameters. Besides, we further derive the analytical results for flow velocity and EDL potential under weak charge condition. We observe that dielectric gradient-mediated ion partitioning effect has a substantial impact on the flow modulation and thereby the ion selectivity parameter. The impact of ion partitioning effect further augmented for increasing values of bulk pH. However, when ${\text{pH}} \geqslant 8$, its impact gradually reaches to a saturation. The impact of ion partitioning effect has prominent role when the EDL is thick at which the neutralization of PEL-charge is less compared to the thin EDL. We further highlight the impact of fluid rheological behavior and softness parameter of the PEL on the flow modulation and the selectivity of mobile electrolyte ions.

APPENDIX A

1.1 ANALYTICAL RESULT FOR EDL POTENTIAL AND AXIAL VELOCITY UNDER WEAK POTENTIAL LIMIT

We have derived the closed solution of the coupled set of electrostatic potential and axial velocity for the Newtonian fluid (i.e., flow behavior index $n = 1$) in the case where the PEL-charge is low so that the potential EDL is less than the thermal potential. Under this assumption the EDL-potential equation can be linearized and is given below

$$\left. {\begin{array}{*{20}{c}} {\frac{{{{d}^{2}}\bar {\psi }}}{{d{{{\bar {y}}}^{2}}}} = P_{1}^{2}\bar {\psi } - {{Q}_{A}},~~ - 1 \leqslant \bar {y} \leqslant - 1\,\,~ + \,\,\bar {\delta }} \\ {\frac{{{{d}^{2}}\bar {\psi }}}{{d{{y}^{2}}}} = {{{\left( {\kappa h} \right)}}^{2}}\bar {\psi },~~~~ - 1 + \bar {\delta } \leqslant \bar {y} \leqslant ~0~~~} \end{array}} \right\}.$$

(18)

Using the linearized Poisson−Boltzmann equation, we may further deduce the linearized form of the fluid flow equation and is given below

$$\left. {\begin{array}{*{20}{c}} {\frac{{{{d}^{2}}\bar {u}}}{{d{{{\bar {y}}}^{2}}}}~ - {{\beta }^{2}}\bar {u} = {{b}_{1}}\bar {\psi },\,\,\,\,~ - 1 \leqslant \bar {y} \leqslant - 1 + \bar {\delta }} \\ {\frac{{{{d}^{2}}\bar {u}}}{{d{{{\bar {y}}}^{2}}}} = {{b}_{2}}\bar {\psi },~~~~~~~~~~~~ - 1\,\,~ + \,\,\bar {\delta } \leqslant \bar {y} \leqslant 0~~~} \end{array}} \right\},$$

(19)

where ${{b}_{1}}$ and ${{b}_{2}}$ are defined as ${{b}_{1}} = {{\left( {\kappa h} \right)}^{2}}{\text{exp}}\left( { - \Delta \overline {{{W}_{i}}} } \right)~$ and ${{b}_{2}} = {{\left( {\kappa h} \right)}^{2}}.$

We derive the EDL potential by solving equation (18) associated with the boundary condition (5) and is given below

$$\bar {\psi } = \left\{ {\begin{array}{*{20}{c}} {{{C}_{{11}}}\exp \left\{ {{{P}_{1}}\bar {y}} \right\} + {{C}_{{12}}}\exp \left\{ { - {{P}_{1}}\bar {y}} \right\} + \frac{{{{Q}_{A}}}}{{P_{1}^{2}}},\,\,\,\, - 1 \leqslant \bar {y} \leqslant - 1 + \bar {\delta }} \\ {{{C}_{{13}}}\exp \left\{ {\left( {\kappa h} \right)\bar {y}} \right\} + {{C}_{{14}}}\exp \left\{ { - \left( {\kappa h} \right)\bar {y}} \right\},~~~~~~ - 1 + \bar {\delta } \leqslant \bar {y} \leqslant 0} \end{array}} \right.$$

(20)

where

$$\begin{gathered} P_{1}^{2} = \frac{{{{{\left( {\kappa h} \right)}}^{2}}}}{\xi }\exp \left( { - \Delta \overline {{{W}_{i}}} } \right); \\ ~{{Q}_{A}} = \frac{{{{{\left( {\kappa h} \right)}}^{2}}}}{\xi }\left( {\frac{{{{z}_{A}}{{N}_{A}}}}{{2{{n}_{0}}}}} \right)\frac{1}{{1 + {{{10}}^{{{\text{p}}{{{\text{K}}}_{{\text{a}}}} - {\text{pH}}}}}}}; \\ {{C}_{{11}}} = {{C}_{{12}}}{\kern 1pt} \exp \left( {2{{P}_{1}}} \right);\,\,\,\,~{{C}_{{12}}} = - \frac{{{{A}_{{11}}}{{B}_{{13}}}}}{{{{A}_{{12}}}{{B}_{{13}}} - {{A}_{{13}}}{{B}_{{12}}}}}; \\ {{C}_{{13}}} = {{C}_{{14}}} = \frac{{{{A}_{{11}}}{{B}_{{12}}}}}{{{{A}_{{12}}}{{B}_{{13}}} - {{A}_{{13}}}{{B}_{{12}}}}}; \\ {{A}_{{11}}} = \frac{{{{Q}_{A}}}}{{P_{1}^{2}}};~\,\,\,\,{{A}_{{12}}} = 2{\kern 1pt} \exp ({{P}_{1}})\cosh \left( {{{P}_{1}}\bar {\delta }} \right)~; \\ {{A}_{{13}}} = - 2{\kern 1pt} \cosh \left( {\kappa h\left( { - 1~\,\, + \,\,\bar {\delta }} \right)} \right) \\ {{B}_{{12}}} = 2\left( {\frac{{{{P}_{1}}\xi }}{{\kappa h}}} \right)\exp \left( {{{P}_{1}}} \right)\sinh \left( {{{P}_{1}}\bar {\delta }} \right); \\ {{B}_{{13}}} = - 2{\kern 1pt} \sinh \left( {\kappa h\left( { - 1 + \bar {\delta }} \right)} \right). \\ \end{gathered} $$

(21)

Solving the equation (19) subject to the boundary conditions (12) we may derive the axial velocity component for Newtonian fluid, as follows

$$\bar {u} = \left\{ {\begin{array}{*{20}{c}} {{{d}_{{11}}}{\kern 1pt} \exp \left( {\beta \bar {y}} \right) + {{d}_{{12}}}{\kern 1pt} \exp \left( { - \beta \bar {y}} \right) + S\left( {\bar {y}} \right); - 1 \leqslant \bar {y} \leqslant - 1 + \bar {\delta }} \\ {{{d}_{{13}}} + {{d}_{{14}}}\bar {y} + T\left( {\bar {y}} \right);~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 1 + \bar {\delta } \leqslant ~\bar {y} \leqslant ~0} \end{array}} \right.$$

(22)

$$\begin{gathered} S\left( {\bar {y}} \right) = \frac{{{{b}_{1}}}}{{P_{1}^{2} - {{\beta }^{2}}}}\left( {{{C}_{{11}}}{\kern 1pt} \exp \left( {{{P}_{1}}\bar {y}} \right) + {{C}_{{12}}}{\kern 1pt} \exp \left( { - {{P}_{1}}\bar {y}} \right)} \right) \\ - \,\,\left( {\frac{{{{b}_{1}}{{Q}_{A}}}}{{P_{1}^{2}{{\beta }^{2}}}}} \right) + \frac{{{{b}_{2}}}}{{{{\beta }^{2}}}} \\ T\left( {\bar {y}} \right) = \left( {{{C}_{{13}}}{\kern 1pt} \exp \left( {\left( {\kappa h} \right)\bar {y}} \right) + {{C}_{{14}}}{\kern 1pt} \exp \left( { - \left( {\kappa h} \right)\bar {y}} \right)} \right) \\ {{d}_{{11}}} = - {{d}_{{12}}}{\kern 1pt} \exp \left( {2\beta } \right) - S\left( { - 1} \right)\exp \left( \beta \right);~ \\ {{d}_{{12}}} = \frac{1}{{2\beta {\kern 1pt} \exp \left( \beta \right)\cosh \left( {\beta \bar {\delta }} \right)}}\left( { - S\left( { - 1} \right)\beta {\kern 1pt} \exp \left( {\beta \bar {\delta }} \right)} \right. \\ \left. { + \,\,T{\kern 1pt} '\left( 0 \right) - T{\kern 1pt} '\left( { - 1 + \bar {\delta }} \right) + S{\kern 1pt} '\left( { - 1 + \bar {\delta }} \right)} \right); \\ {{d}_{{13}}} = - 2{{d}_{{14}}}{\kern 1pt} \exp \left( \beta \right)\sinh \left( {\beta \bar {\delta }} \right) - T\left( { - 1 + \bar {\delta }} \right) \\ - \,\,S\left( { - 1} \right)\exp \left( {\beta \bar {\delta }} \right) + \left( { - 1 + \bar {\delta }} \right)T{\kern 1pt} '\left( 0 \right) + S\left( { - 1 + \bar {\delta }} \right);~ \\ {{d}_{{14}}} = - T{\kern 1pt} '\left( 0 \right). \\ \end{gathered} $$

(23)

Fig. A1.

Code validation with theoretical and computational results for (a) potential distribution and (b) velocity distribution in the polymer-grafted soft nanochannel is illustrated using the Debye−Hückel approximation for $\kappa h = 3$ for Newton fluid $\left( {n = 1} \right)$ with different values of pH 2,3,4,11, and 12. The Model parameters are $z = - 1,~{{N}_{A}} = 1$ mM and $\beta = 1$. The dotted lines represent the calculation results, while the left triangle represents the theoretical results for the same value of pH.

In Fig. A1 the validity of the numerically calculated electrostatic potential and axial velocity has been confirmed. The model parameters used are shown in the figure captions. According to Fig. A1, for the weakly charged PEL, the numerical results agree well with the theoretical results. When there is a significant pH effect and partitioning effect, the EDL potential can exceed the Debye−Hückel limit, so it is necessary to use a non-linear model to study the problem, and a deviation is detected. These results show that the present numerical scheme is capable of accurately capturing the electrokinetic transport phenomena in a soft nanochannel.