Total Dominator Colorings and Total Domination in Graphs

Abstract

A total dominator coloring of a graph $G$ is a proper coloring of the vertices of $G$ in which each vertex of the graph is adjacent to every vertex of some color class. The total dominator chromatic number $\chi _d^t(G)$ of $G$ is the minimum number of colors among all total dominator coloring of $G$. A total dominating set of $G$ is a set $S$ of vertices such that every vertex in $G$ is adjacent to at least one vertex in $S$. The total domination number $\gamma _t(G)$ of $G$ is the minimum cardinality of a total dominating set of $G$. We establish lower and upper bounds on the total dominator chromatic number of a graph in terms of its total domination number. In particular, we show that every graph $G$ with no isolated vertex satisfies $\gamma _t(G) \le \chi _d^t(G) \le \gamma _t(G) + \chi (G)$, where $\chi (G)$ denotes the chromatic number of $G$. We establish properties of total dominator colorings in trees. We characterize the trees $T$ for which $\gamma _t(T) = \chi _d^t(T)$. We prove that if $T$ is a tree of $n \ge 2$ vertices, then $\chi _d^t(T) \le 2(n+1)/3$ and we characterize the trees achieving equality in this bound.

1 Introduction

A proper vertex coloring of a graph $G$ is an assignment of colors (elements of some set) to the vertices of $G$, one color to each vertex, so that adjacent vertices are assigned distinct colors. If $k$ colors are used, then the coloring is referred to as a $k$-coloring. In a given coloring of $G$, a color class of the coloring is a set consisting of all those vertices assigned the same color. The vertex chromatic number $\chi (G)$ of $G$ is the minimum integer $k$ such that $G$ is $k$-colorable. In this paper, we simply call a proper vertex coloring a proper coloring and we refer to the vertex chromatic number as the chromatic number. The concept of a graph coloring is very well-studied in graph theory. Indeed, the chromatic number is perhaps the most studied of all graph theoretic parameters.

A dominator coloring of a graph $G$ is a proper coloring of $G$ in which every vertex dominates every vertex of at least one color class; that is, every vertex in $V(G)$ is adjacent to all other vertices in its own color class or is adjacent to all vertices from at least one (other) color class. The dominator chromatic number $\chi _d(G)$ of $G$ is the minimum number of color classes in a dominator coloring of $G$. Since every dominator coloring of $G$ is a coloring of $G$, we observe that $\chi (G) \le \chi _d(G)$. The concept of a dominator coloring in a graph was introduced and studied by Gera et al. [5] and studied further, for example, by Gera [3, 4] and Chellali and Maffray [1].

The dominator chromatic number of a graph is related to its domination number. A dominating set of a graph $G$ is a set $S\subseteq V(G)$ such that every vertex in $V(G){\setminus } S$ is adjacent to at least one vertex in $S$. The domination number of $G$, denoted by $\gamma (G)$, is the minimum cardinality of a dominating set of $G$. The literature on the subject of domination parameters in graphs up to the year 1997 has been surveyed and detailed in the two books [6, 7]. Gera [3, 4] established the following upper and lower bounds on the dominator chromatic number of an arbitrary graph in terms of its domination number and chromatic number.

Theorem 1

([3, 4]) Every graph $G$ satisfies

$$\begin{aligned} \max \{ \gamma (G), \chi (G) \} \le \chi _d(G) \le \gamma (G) + \chi (G). \end{aligned}$$

Recently, Kazemi [10] studied the new concept of a total dominator coloring in a graph. A total dominator coloring, abbreviated TD-coloring, of a graph $G$ with no isolated vertex is a proper coloring of $G$ in which each vertex of the graph is adjacent to every vertex of some (other) color class. The total dominator chromatic number $\chi _d^t(G)$ of $G$ is the minimum number of color classes in a TD-coloring of $G$. A $\chi _d^t(G)$-coloring of $G$ is any total dominator coloring with $\chi _d^t(G)$ colors. A color class $C$ in a given TD-coloring $\mathcal {C}$ of $G$ is free if each vertex of $G$ is adjacent to every vertex of some color class different from $C$.

The total dominator chromatic number of a graph is related to its total domination number. A total dominating set, abbreviated TD-set, of $G$ is a set $S \subseteq V(G)$ such that every vertex in $V(G)$ is adjacent to at least one vertex in $S$. The total domination number of $G$, denoted by $\gamma _t(G)$, is the minimum cardinality of a TD-set of $G$. A TD-set of $G$ of cardinality $\gamma _t(G)$ is called a $\gamma _t(G)$-set. Total domination is now well studied in graph theory. The literature on the subject on total domination in graphs has been surveyed and detailed in the recent book [9]. A survey of total domination in graphs can also be found in [8].

Consider an arbitrary $\chi _d^t(G)$-coloring of $G$, and let $S$ be a set consisting of one vertex from each of the $\chi _d^t(G)$ color classes. Since every vertex in $G$ is adjacent to every vertex of some color class (different from its own color class), the set $S$ is a TD-set in $G$, implying that $\gamma _t(G) \le |S| = \chi _d^t(G)$. Hence we have the following result, first observed by Kazemi [10].

Observation 2

([10]) For every graph $G$ with no isolated vertex, $\gamma _t(G) \le \chi _d^t(G)$.

In this paper, we continue the study of total dominator colorings in graphs. We show that the total dominator chromatic number of a graph is bounded above by the sum of its chromatic number and total domination number. In particular, if $G$ is a bipartite graph, we show that $\gamma _t(G) \le \chi _d^t(G) \le \gamma _t(G) + 2$. For each $t \in \{0,1,2\}$, we construct an infinite family $\mathcal {G}_t$ of (bipartite) graphs such that each graph $G \in \mathcal {G}_t$ satisfies $\chi _d^t(G) = \gamma _t(G) + t$. We study properties of TD-colorings in a tree. We characterize trees $T$ satisfying $\gamma _t(T) = \chi _d^t(T)$. We also establish a tight upper bound on the total dominator chromatic number of a tree in terms of its order and we characterize the trees with maximum possible total dominator chromatic number.

1.1 Notation and Terminology

All graphs considered here are finite, undirected and simple. For standard graph theory terminology not given here we refer to [9]. Let $G = (V, E)$ be a graph with vertex set $V=V(G)$ of order $n = |V|$ and edge set $E=E(G)$ of size $m = |E|$, and let $v$ be a vertex in $V$. The graph $G$ is nontrivial if $n \ge 2$. The open neighborhood of $v$ is $N_G(v) = \{u \in V \, | \, uv \in E\}$ and the closed neighborhood of $v$ is $N_G[v] = \{v\} \cup N_G(v)$. For a set $S \subseteq V$, its open neighborhood is the set $N_G(S) = \bigcup _{v \in S} N(v)$ and its closed neighborhood is the set $N_G[S] = N_G(S) \cup S$. The degree of a vertex $v$ in $G$ is $d_G(v) = |N_G(v)|$. The neighborhood of an edge $e = uv$ is the set $N_G[e] = N_G[u] \cup N_G[v]$. If the graph $G$ is clear from the context, we simply write $d(v)$, $N(v)$, $N[v]$, $N[e]$, $N(S)$ and $N[S]$ rather than $d_G(v)$, $N_G(v)$, $N_G[v]$, $N_G[e]$, $N_G(S)$ and $N_G[S]$, respectively.

A cycle on $n$ vertices is denoted by $C_n$ and a path on $n$ vertices by $P_n$. A complete graph on $n$ vertices is denoted by $K_n$. A star is the tree $K_{1,n-1}$ of order $n \ge 2$. We call a vertex of degree one a leaf, its adjacent vertex a support vertex and its incident edge a pendant edge. The set of support vertices in a graph $G$ we denote by $S(G)$. A strong support vertex is a support vertex with at least two leaf-neighbors. A double star is a tree with exactly two non-leaves. A graph is isolate-free if it contains no isolated vertex (of degree 0).

For any subset $S \subset V(G)$, we let $G-S$ denote the graph obtained from $G$ by removing $S$ and all edges incident with vertices in $S$. We denote the subgraph induced by $S$ in $G$ by $G[S]$.

A rooted tree distinguishes one vertex $r$ called the root. For each vertex $v \ne r$ of $T$, the parent of $v$ is the neighbor of $v$ on the unique $(r,v)$-path, while a child of $v$ is any other neighbor of $v$. A descendant of $v$ is a vertex $u$ such that the unique $(r,u)$-path contains $v$. Thus, every child of $v$ is a descendant of $v$. The maximal subtree at $v$ is the subtree of $T$ induced by $v$ and its descendants, and is denoted by $T_v$.

Let $H$ be a graph. The corona $H \circ K_1$ of $H$, also denoted $\hbox {cor}(H)$ in the literature, is the graph obtained from $H$ by adding a pendant edge to each vertex of $H$. The $2$-corona $H \circ P_2$ of $H$ is the graph of order $3|V(H)|$ obtained from $H$ by attaching a path of length $2$ to each vertex of $H$ so that the resulting paths are vertex-disjoint.

A subset $S$ of vertices in a graph $G$ is a packing (respectively, an open packing) if the closed (respectively, open) neighborhoods of vertices in $S$ are pairwise disjoint. Further the set $S$ is a perfect packing (respectively, a perfect open packing) if every vertex belongs to at exactly one of the closed (respectively, open) neighborhoods of vertices in $S$. The open packing number $\rho ^o(G)$ is the maximum cardinality of an open packing in $G$.

1.2 Known Results and Observations

The total domination number of a cycle or path is easy to compute.

Observation 3

For $n \ge 3$, $\gamma _t(P_n) = \gamma _t(C_n) = \lfloor n/2 \rfloor + \lceil n/4 \rceil - \lfloor n/4 \rfloor$.

The following bound on the total domination number of a connected graph in terms of the order of the graph is due to Cockayne et al. [2].

Theorem 4

([2]) If $G$ is a connected graph of order $n \ge 3$, then $\gamma _t(G) \le 2n/3$.

Since any TD-set in a graph $G$ must have a nonempty intersection with every open neighborhood, we observe that if $G$ is a graph with no isolated vertex, then $\rho ^o(G) \le \gamma _t(G)$. We state this formally.

Observation 5

Every isolate-free graph $G$ satisfies $\rho ^o(G) \le \gamma _t(G)$.

2 General Bounds

In this section, we establish bounds on the total dominator chromatic number of a graph. As an immediate consequence of Observation 2 and Observation 5, we see that every graph $G$ with no isolated vertex satisfies $\rho ^o(G) \le \chi _d^t(G)$. One can say slightly more. First we present the following observation.

Observation 6

If $v$ is an arbitrary vertex in an isolate-free graph $G$, then in every TD-coloring of $G$ the neighborhood $N(v)$ of $v$ contains a color class.

Theorem 7

Let $G$ be a graph with no isolated vertex. Then, $\rho ^o(G) \le \chi _d^t(G)$, with strict inequality if there is no perfect open packing in $G$.

Proof

As an immediate consequence of Observation 6, we see that if $S$ is an open packing in $G$, then the open neighborhoods of vertices in $S$ contain at least $|S|$ color classes, and so $\chi _d^t(G) \ge |S|$. Choosing $S$ to be a maximum open packing, we see that $\chi _d^t(G) \ge \rho ^o(G)$. Further, if $G$ does not have a perfect open packing, then at least one additional color class is needed to contain the vertices that do not belong to the open neighborhood of any vertex of $S$, and so $\chi _d^t(G) \ge \rho ^o(G) + 1$. $\square$

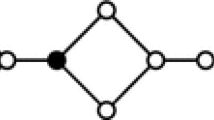
If $H$ is any connected graph of order $k \ge 1$, then the $2$-corona $G = H \circ P_2$ satisfies $\rho ^o(G) = 2k= \chi _d^t(G)$, illustrating that there do exist graphs that contain a perfect open packing and satisfy $\rho ^o(G) = \chi _d^t(G)$. The graph $C_4 \circ P_2$, for example, is shown in Fig. 1 (here, $H = C_4$).

Fig. 1

The graph $C_4 \circ P_2$

However we remark that if a graph $G$ contains a perfect open packing, then it is not necessary true that $\rho ^o(G) = \chi _d^t(G)$. The simplest example illustrating this is a path $G = P_4$, with $\rho ^o(G) = 2$ and $\chi _d^t(G) = 3$. More generally, if $G = P_n$ where $n \equiv 0 \, (\mathrm{mod}\, 4)$ and $n \ge 4$, then $G$ has a perfect open packing and $\rho ^o(G) = \gamma _t(G)$. However, by Observation 19 and Proposition 20, we have $\gamma _t(G) < \chi _d^t(G)$.

We next present an upper bound on the total dominator chromatic number. For a given graph $G$, let $\mathcal {A}_t(G)$ denote the set of all $\gamma _t(G)$-sets in $G$.

Theorem 8

Let $G$ be a connected graph of order at least $3$. Then,

$$\begin{aligned} \chi _d^t(G) \le \gamma _t(G) + \min _{S \in \mathcal {A}_t(G)} \{ \chi (G - S) \}. \end{aligned}$$

Further this bound is tight.

Proof

Let $S$ be an arbitrary $\gamma _t(G)$-set and let $\mathcal {C}$ be a proper coloring of the graph $G - S$ using $\chi (G-S)$ colors. We now extend the coloring $\mathcal {C}$ to a coloring of the vertices of $G$ by assigning to each vertex in $S$ a new and distinct color. Let $\mathcal {C}'$ denote the resulting coloring of $G$ and note that $\mathcal {C}'$ uses $\gamma _t(G) + \chi (G-S)$ colors. Since $S$ is a TD-set of $G$, every vertex in $G$ is adjacent to at least one vertex of $S$. Since the color class of $\mathcal {C}'$ containing a given vertex of $S$ consists only of that vertex, each vertex in $G$ is therefore adjacent to every vertex of some (other) color class in the coloring $\mathcal {C}'$. Hence, $\mathcal {C}'$ is a TD-coloring of $G$ using $\gamma _t(G) + \chi (G-S)$ colors. This is true for every $\gamma _t(G)$-set $S$. The desired result now follows by choosing $S$ to be a $\gamma _t(G)$-set that minimizes $\chi (G - S)$.

That the bound is tight may be seen as follows. Let $G$ be obtained from a connected graph $H$ of order $k \ge 1$ as follows: For each vertex $v \in V(H)$ add a path $P_7$ and identify the vertex $v$ with a vertex on this path at distance $2$ from a leaf. When $H = P_4$ (and so, $k = |V(H)| = 4$), for example, the graph $G$ is illustrated in Fig. 2, where the darkened vertices form a $\gamma _t(G)$-set. Then, $\gamma _t(G) = 4k$. Let $T$ be the set of all support vertices in $G$ together with a non-leaf neighbor of each support vertex. Then, $T$ is a $\gamma _t(G)$-set. Further, $G - T$ consists of isolated vertices, and so $\chi (G - T) = 1$. Hence,

$$\begin{aligned} \gamma _t(G) + \min _{S \in \mathcal {A}_t(G)} \{ \chi (G - S)\} = 4k + 1. \end{aligned}$$

As a consequence of our upper bound on $\chi _d^t(G)$, we therefore have that $\chi _d^t(G) \le 4k+1$. It remains for us to show that $\chi _d^t(G) \ge 4k+1$. Let $\mathcal {C}$ be a $\chi _d^t(G)$-coloring. By Observation 6, each support vertex in $G$ forms a color class that consists only of that vertex. Further, for each support vertex $v$ in $G$, the two neighbors of $v$ form a color class or there is a color class consisting of exactly one neighbor of $v$ and no other vertex. Since the support vertices of $G$ are at distance at least $3$ apart, and since there are $2k$ support vertices in $G$, this implies that there are at least $4k$ color classes in $\mathcal {C}$. Further the set of $k$ vertices of $G$ that do not belong to the closed neighborhood of any support vertex must be assigned at least one new color, implying that $\mathcal {C}$ contains at least $4k+1$ color classes. Hence, $\chi _d^t(G) \ge 4k+1$, as desired. Consequently,

$$\begin{aligned} \chi _d^t(G) = 4k+1 = \gamma _t(G) + \min _{S \in \mathcal {A}_t(G)} \{ \chi (G - S) \}. \end{aligned}$$

This completes the proof of Theorem 8. $\square$

Fig. 2

A graph $G$ with $\chi _d^t(G) = \gamma _t(G) + 1$

We observe that $\chi (G - S) \le \chi (G)$ for every proper subset $S \subset V(G)$. We also observe that every total dominator coloring of $G$ is a dominator coloring of $G$, and so $\chi (G) \le \chi _d(G) \le \chi _d^t(G)$. Hence as a consequence of Observation 2, we have the following analogous result to Theorem 1, thereby establishing upper and lower bounds on the total dominator chromatic number of an arbitrary graph in terms of its total domination number and chromatic number.

Theorem 9

Every isolate-free graph $G$ satisfies

$$\begin{aligned} \max \{ \gamma _t(G), \chi (G) \} \le \chi _d^t(G) \le \gamma _t(G) + \chi (G). \end{aligned}$$

As an immediate consequence of Theorem 9, we have the following result.

Corollary 10

If $G$ is a bipartite isolate-free graph, then $\gamma _t(G) \le \chi _d^t(G) \le \gamma _t(G) + 2$.

For each $t \in \{0,1,2\}$, we construct an infinite family $\mathcal {G}_t$ of (bipartite) graphs such that each graph $G \in \mathcal {G}_t$ satisfies $\chi _d^t(G) = \gamma _t(G) + t$.

Let $\mathcal {G}_0$ be the family of isolate free-graphs $G$ that contain a TD-set $S$ that is a perfect open packing in $G$ and such that the neighborhood of each edge $e$ in $G[S]$ induces a complete bipartite graph in $G$. Let $G \in \mathcal {G}_0$. We note that every edge in $G[S]$ is an isolated edge in $G[S]$. Further if $e = uv$ is an edge in $G[S]$, then the subgraph of $G$ induced by the neighborhood, $N[e]$, of $e$ is a complete bipartite graph $K_{n_1,n_2}$ where $d(u) = n_1$ and $d(v) = n_2$. For example, if $H$ is an arbitrary graph, then the graph $G = H \circ P_2$ belongs to the family $\mathcal {G}_0$ since the set $S = V(G) {\setminus } V(H)$ is a TD-set that is a perfect open packing in $G$ and the neighborhood of each edge $e$ in $G[S]$ induces a complete bipartite graph $K_{1,2}$ in $G$.

Proposition 11

If $G \in \mathcal {G}_0$, then $\chi _d^t(G) = \gamma _t(G)$.

Proof

Let $G \in \mathcal {G}_0$. Let $S$ be a TD-set in $G$ that is a perfect open packing and such that the neighborhood of each edge $e$ in $G[S]$ induces a complete bipartite graph. Then, $\gamma _t(G) \le |S| = \rho ^o(G)$, implying by Observation 5 that $\gamma _t(G) = \rho ^o(G)$. We now color the vertices of $G$ with $\gamma _t(G)$ colors, one color to the open neighborhood of each vertex in $S$, and let $\mathcal {C}$ denote the resulting coloring. Since $N(v)$ is an independent set for each vertex $v \in S$, we note that the coloring $\mathcal {C}$ is a proper coloring of $G$. Let $w \in V(G)$ and let $v$ be the (unique) vertex in $S$ adjacent to $w$. Further, let $u$ be the (unique) neighbor of $v$ in $S$ (possibly $u = w$). Since the neighborhood of the edge $uv$ induces a complete bipartite graph with partite sets $N(u)$ and $N(v)$, the vertex $w$ is adjacent to every vertex in the color class $N(u)$. Since $w$ is an arbitrary vertex in $G$, every vertex in $G$ is therefore adjacent to every vertex of some color class. The coloring $\mathcal {C}$ is therefore a TD-coloring of $G$, and so $\chi _d^t(G) \le \gamma _t(G)$. By Observation 2, $\chi _d^t(G) \ge \gamma _t(G)$. Consequently, $\chi _d^t(G) = \gamma _t(G)$. $\square$

Let $\mathcal {G}_1$ be the family of graphs that can be obtained from an isolate-free graph $H$ by attaching any number of pendant edges, but at least one, to each vertex of $H$. For example, if $H$ is an arbitrary isolate-free graph, then the corona $G = H \circ P_1$ of $H$ belongs to the family $\mathcal {G}_1$.

Proposition 12

If $G \in \mathcal {G}_1$, then $\chi _d^t(G) = \gamma _t(G) + 1$.

Proof

Let $G \in \mathcal {G}_1$. Then, $G$ can be obtained from an isolate-free graph $H$ by attaching any number of pendant edges, but at least one, to each vertex of $H$. Let $\mathcal {C}$ be a TD-coloring in $G$. By construction, the set $V(H)$ is the set of support vertices in $G$, while each vertex not in $H$ is a leaf in $G$. By Observation 6, each vertex in $V(H)$ therefore forms a color class of $\mathcal {C}$ that consists only of that vertex. At least one additional color class is needed to color the leaves in $G$, and so $\chi _d^t(G) \ge |V(H)| + 1$. However, assigning a distinct color to each vertex of $H$ and assigning an additional color to the leaves of $G$ produces a TD-coloring of $G$, implying that $\chi _d^t(G) \le |V(H)| + 1$. Consequently, $\chi _d^t(G) = |V(H)| + 1$. Since $\gamma _t(G) = |V(H)|$ (the set $V(H)$ forms the unique $\gamma _t(G)$-set), we therefore have that $\chi _d^t(G) = \gamma _t(G) + 1$. $\square$

Letting $\mathcal {G}_2$ be the family of all paths $P_n$ and cycles $C_n$, where $n \equiv 0 \, (\mathrm{mod}\, 4)$ and $n \ge 8$, we have the following result (see Observation 19, Proposition 20 and Observation 21).

Proposition 13

If $G \in \mathcal {G}_2$, then $\chi _d^t(G) = \gamma _t(G) + 2$.

3 Trees

In this section, we consider total dominator colorings in trees. By Corollary 10, if $T$ is a tree of order $n \ge 2$, then $\gamma _t(T) \le \chi _d^t(T) \le \gamma _t(T) + 2$. We have four aims in this section. First to characterize trees $T$ satisfying $\gamma _t(T) = \chi _d^t(T)$. Secondly, to establish properties of $\chi _d^t(T)$-colorings in a tree $T$. Thirdly, to establish a tight upper bound on the total dominator chromatic number of a tree in terms of its order and to characterize the trees with maximum possible total dominator chromatic number. Fourthly, to determine the total dominator chromatic number of a path.

3.1 Trees $T$ Satisfying $\gamma _t(T) = \chi _d^t(T)$

The first aim in this section is to characterize trees $T$ satisfying $\gamma _t(T) = \chi _d^t(T)$. For this purpose, let $\mathcal {T}$ be the family of trees constructed as follows. Let $\mathcal {T}$ consist of the tree $P_2$ and all trees that can be obtained from a disjoint union of $k \ge 1$ stars each of order at least $3$ by adding $k-1$ edges joining leaf vertices in such a way that the resulting graph is connected and the center of each of the original $k$ stars remains a support vertex. If $T \in \mathcal {T}$ and $T \ne P_2$, then we call each of the original $k$ stars used to construct the tree $T$ an underlying star of $T$. We remark that $\mathcal {T}$ is precisely the subfamily of $\mathcal {G}_0$ consisting of all trees; that is, $\mathcal {T}= \{T :T \in \mathcal {G}_0$ and $T$ is a tree $\}$. We proceed further with the following property of trees in the family $\mathcal {T}$.

Lemma 14

If $T \in \mathcal {T}$, then $\gamma _t(T) = \chi _d^t(T)$. Further, the color classes of a $\chi _d^t(T)$-coloring are unique, and consist of the support vertices of $T$ and the open neighborhoods of support vertices of $T$.

Proof

Let $T \in \mathcal {T}$. If $T = P_2$, then the result is immediate. Hence we may assume that $T$ has order at least $3$. Thus, $T$ can be obtained from a disjoint union of $k \ge 1$ stars each of order at least $3$ by adding $k-1$ edges joining leaf vertices in such a way that the resulting graph is connected and the center of each of the original $k$ stars remains a support vertex. We note that the set of support vertices, $S(T)$, of $T$ is precisely the set of central vertices of the underlying stars of $T$. In particular, $|S(T)| = k$. Further, the set $S(T)$ forms a perfect packing in $T$. Moreover, the set $S(T)$, together with one leaf-neighbor of each support vertex, forms a perfect open packing in $T$, implying that $\gamma _t(T) = 2k$. By Proposition 11, $\chi _d^t(T) = \gamma _t(T) = 2k$.

Let $\mathcal {C}$ be a $\chi _d^t(T)$-coloring of the tree $T$. By Observation 6, each support vertex in $T$ forms a color class that consists only of that vertex. Further, for each support vertex $v$ in $T$, the neighborhood $N(v)$ of $v$ forms a color class or contains a color class as a proper subset (in order for the vertex $v$ to be adjacent to every vertex in some color class). Hence, $\mathcal {C}$ contains at least $2k$ color class. Further if a neighborhood $N(v)$ for some vertex $v \in S(T)$ does not form a color class in $\mathcal {C}$, then an additional color class is needed, contradicting the fact that $\chi _d^t(T) = 2k$ and $\mathcal {C}$ is a $\chi _d^t(T)$-coloring. Hence the color classes in $\mathcal {C}$ are uniquely determined, and consist of the support vertices of $T$ and the open neighborhoods of support vertices of $T$. $\square$

Theorem 15

Let $T$ be a nontrivial tree. Then, $\gamma _t(T) = \chi _d^t(T)$ if and only if $T \in \mathcal {T}$.

Proof

The sufficiency follows from Lemma 14. To prove the necessity, we proceed by induction on the order $n \ge 2$ of a tree $T$ that satisfies $\gamma _t(T) = \chi _d^t(T)$. If $n \in \{2,3\}$, then $T$ is a star and $T \in \mathcal {T}$, as desired. This establishes the base case. Suppose, then, that $n \ge 4$ and that if $T'$ is a tree of order $n'$, where $2 \le n' < n$, satisfying $\gamma _t(T') = \chi _d^t(T')$, then $T' \in \mathcal {T}$. Let $T$ be a tree of order $n$ that satisfies $\gamma _t(T) = \chi _d^t(T)$. If $T$ is a star, then $T \in \mathcal {T}$, as desired. Hence we may assume that $\mathrm{diam}(T) \ge 3$. If $\mathrm{diam}(T) = 3$, then $T$ is a double star. But then $\gamma _t(T) = 2$ and $\chi _d^t(T) = 3$, a contradiction. Hence, $\mathrm{diam}(T) \ge 4$. Let $\mathcal {C}$ be a $\chi _d^t(T)$-coloring in $T$.

We proceed further with the following series of claims that we may assume are satisfied by the tree $T$. More precisely, we show in the proof of each claim that if $T$ does not satisfy the statement of the claim, then $T \in \mathcal {T}$ and the desired result follows. Hence we may assume that $T$ does indeed satisfy the statement of each claim, for otherwise there is nothing left to prove.

Claim A We may assume that the tree $T$ has no strong support vertex.

Proof

Suppose that $T$ has a strong support vertex $v$ that is adjacent to at least two leaves, $u$ and $w$. Let $T' = T - u$ and let $\mathcal {C}'$ be the restriction of the coloring $\mathcal {C}$ to the vertices in $T'$. Suppose that $\mathcal {C}'$ is not a TD-coloring of $T'$. Then since $\mathcal {C}$ is a TD-coloring of $T$, the only vertex in $T'$ that is not adjacent to every vertex of some color class in $\mathcal {C}'$ is the vertex $v$, implying that in the coloring $\mathcal {C}$ the vertex $u$ has a unique color. But then considering the tree $T' = T - w$, we see that the restriction of the coloring $\mathcal {C}$ to the vertices in $T'$ is a TD-coloring of $T'$. Hence by renaming the vertices $u$ and $w$, if necessary, we may assume that $\mathcal {C}'$ is a TD-coloring of $T'$. Since the number of color classes in $\mathcal {C}'$ is at most the number of color classes in $\mathcal {C}$, and since $\mathcal {C}$ has $\chi _d^t(T)$ color classes and is a TD-coloring of $T'$, this implies that $\chi _d^t(T') \le \chi _d^t(T)$. Further, since every TD-set of a graph contains every support vertex in the graph, every TD-set of $T'$ contains the vertex $v$ and is therefore a TD-set of $T$, implying that $\gamma _t(T) \le \gamma _t(T')$. Therefore, by Corollary 10, we see that

$$\begin{aligned} \chi _d^t(T) = \gamma _t(T) \le \gamma _t(T') \le \chi _d^t(T') \le \chi _d^t(T). \end{aligned}$$

Consequently, we must have equality throughout this inequality chain. In particular, $\gamma _t(T') = \chi _d^t(T')$. Applying the inductive hypothesis to the tree $T'$, we see that $T' \in \mathcal {T}$. Thus, $T'$ can be obtained from a disjoint union of $k \ge 2$ stars each of order at least $3$ by adding $k-1$ edges joining leaf vertices in such a way that the resulting graph is connected and the center of each of the original $k$ stars remains a support vertex. Since the vertex $v$ is a support vertex in $T'$ with $w$ as a leaf-neighbor, the vertex $v$ is the center vertex of one of the underlying stars of $T'$. Thus adding the deleted vertex $u$ back to the tree, we see that $T \in \mathcal {T}$ (where the underlying star containing $v$ is extended to contain the leaf $u$). Hence we may assume that $T$ has no strong support vertex, for otherwise $T \in \mathcal {T}$ and the desired result follows. $\square$

Let $r$ and $u$ be two vertices at maximum distance apart in $T$ and root the tree at the vertex $r$. Recall that $\mathrm{diam}(T) \ge 4$. Let $v$ be the parent of $u$, let $w$ be the parent of $v$ and let $x$ be the parent of $w$. As an immediate consequence of Claim A, we see that $d_T(v) = 2$.

Claim B $d_T(w) = 2$.

Proof

Suppose that $d_T(w) \ge 3$. Suppose that $w$ has a child, $v'$, distinct from $v$, that is not a leaf. Analogously as with the vertex $v$, we see that $d_T(v') = 2$. Let $u'$ be the leaf-neighbor of $v'$ and consider the tree $T' = T - \{u',v'\}$. We note that in the coloring $\mathcal {C}$, both (support vertices) $v$ and $v'$ are assigned unique colors. The restriction, $\mathcal {C}'$, of the coloring $\mathcal {C}$ to the vertices of $T'$ is therefore a TD-coloring, implying that $\chi _d^t(T') \le \chi _d^t(T) - 1$. Let $D'$ be a $\gamma _t(T')$-set. Then, $v \in D'$. If $u' \in D'$, then we can simply replace the vertex $u'$ in $D'$ with the vertex $w$. Hence we may choose $D'$ so that $w \in D'$. But then $D' \cup \{v'\}$ is a TD-set of $T$, implying that $\gamma _t(T) \le |D'| + 1 = \gamma _t(T') + 1$. Therefore, by Corollary 10, we see that $\chi _d^t(T) = \gamma _t(T) \le \gamma _t(T') + 1 \le \chi _d^t(T') + 1 \le \chi _d^t(T)$. Consequently, we must have equality throughout this inequality chain. In particular, $\gamma _t(T') = \chi _d^t(T')$. Further, $\chi _d^t(T') = \chi _d^t(T) - 1$, implying that $\mathcal {C}'$ is a $\chi _d^t(T')$-coloring. Applying the inductive hypothesis to the tree $T'$, we see that $T' \in \mathcal {T}$. Since the vertex $v$ is a support vertex in $T'$ with $u$ as a leaf-neighbor, the vertex $v$ is the center vertex of one of the underlying stars of $T'$. By Lemma 14, the color classes of a $\chi _d^t(T)$-coloring are unique and consist of the support vertices of $T$ and the open neighborhoods of support vertices of $T$. In particular, $N(v) = \{u,w\}$ is a color class in $\mathcal {C}'$. In order for the vertex $v'$ to be adjacent to every vertex in some color class in the coloring $\mathcal {C}$, this implies that $u'$ is assigned a unique color in $\mathcal {C}$. But then the TD-coloring $\mathcal {C}'$ of $T'$ contains two fewer color classes than does $\mathcal {C}$, implying that $\chi _d^t(T') \le \chi _d^t(T) - 2$, a contradiction. Therefore, since $T$ has no strong support vertex, we see that $d_T(w) = 3$ and the child, $v'$, of $w$ distinct from $v$ is a leaf.

In the coloring $\mathcal {C}$, the two support vertices $v$ and $w$ are assigned unique colors. We now consider the tree $T' = T - v'$ and let $\mathcal {C}'$ be the restriction of the coloring $\mathcal {C}$ to the vertices of $T'$. We note that $\mathcal {C}'$ is a TD-coloring, implying that $\chi _d^t(T') \le \chi _d^t(T)$. Further, $\gamma _t(T) \le \gamma _t(T')$ since as before we can choose a $\gamma _t(T')$-set to contain the vertex $w$. Therefore, by Corollary 10, we see that $\chi _d^t(T) = \gamma _t(T) \le \gamma _t(T') \le \chi _d^t(T') \le \chi _d^t(T)$, implying that $\gamma _t(T') = \chi _d^t(T')$, $\chi _d^t(T') = \chi _d^t(T)$, and that $\mathcal {C}'$ is a $\chi _d^t(T')$-coloring. As before, we see that $T' \in \mathcal {T}$ and that $N(v) = \{u,w\}$ is a color class in $\mathcal {C}'$. But then in the coloring $\mathcal {C}$ the vertex $v'$ is not adjacent to every vertex in some color class, a contradiction. Therefore, $d_T(w) =2$. $\square$

By Claims A and B, we see that $d_T(v) = d_T(w) = 2$. We consider the tree $T' = T - \{u,v,w\}$. Recall that $\mathcal {C}$ is defined earlier to be a $\chi _d^t(T)$-coloring in $T$.

Claim C Both sets $\{v\}$ and $N(v) = \{u,w\}$ form a color class in $\mathcal {C}$.

Proof

Since $\mathcal {C}$ is a TD-coloring in $T$, every set consisting of exactly one, but an arbitrary, vertex from each color class of $\mathcal {C}$ is a TD-set of $T$. Since $\gamma _t(T) = \chi _d^t(T)$, such a TD-set is in fact a $\gamma _t(T)$-set. Suppose that all three vertices $u$, $v$ and $w$ are assigned different colors. In this case, we choose a set $D$ to consist of $u$, $v$ and $w$, and one vertex from every color class that does not contain $u$, $v$ or $w$. The resulting set $D$ contains one vertex from each color class of $\mathcal {C}$ and is therefore a $\gamma _t(T)$-set. However, $D {\setminus } \{u\}$ is a TD-set of $T$, contradicting the minimality of the set $D$. Hence, at most two colors are used to color the vertices $u$, $v$ and $w$. Since $\mathcal {C}$ is a TD-coloring of $T$, the support vertex $v$ is assigned a unique color. Therefore, the vertices $u$ and $w$ are assigned the same color. In order for the vertex $v$ to be adjacent to every vertex of some color, the neighborhood $N(v) = \{u,w\}$ of $v$ forms a color class. Thus the set $\{v\}$ and the set $\{u,w\}$ both form a color class in $\mathcal {C}$. $\square$

Claim D $\gamma _t(T) = \gamma _t(T') + 2$ and $\gamma _t(T') = \chi _d^t(T')$.

Proof

Let $\mathcal {C}'$ be the restriction of the coloring $\mathcal {C}$ to the vertices in $T'$. By Claim C, the set $\{v\}$ and the set $\{u,w\}$ both form a color class in the coloring $\mathcal {C}$. Thus the coloring $\mathcal {C}'$ has two fewer color classes than does the coloring $\mathcal {C}$. The only possible vertex in $T'$ that is not adjacent to every vertex of some color class in $\mathcal {C}'$ is the vertex $x$. However this would imply that in the coloring $\mathcal {C}$ the vertex $w$ has a unique color, contradicting our earlier observation that $\{u,w\}$ is a color class in $\mathcal {C}$. Therefore, $\mathcal {C}'$ is a TD-coloring of $T'$, implying that $\chi _d^t(T') \le \chi _d^t(T) - 2$. Every TD-set in $T'$ can be extended to a TD-set in $T$ by adding to it the vertices $v$ and $w$, implying that $\gamma _t(T) \le \gamma _t(T') + 2$. Therefore, by Corollary 10, we see that $\chi _d^t(T) = \gamma _t(T) \le \gamma _t(T') + 2 \le \chi _d^t(T') + 2 \le \chi _d^t(T)$. Consequently, we must have equality throughout this inequality chain. In particular, $\gamma _t(T) = \gamma _t(T') + 2$ and $\gamma _t(T') = \chi _d^t(T')$. $\square$

We now return to the proof of Theorem 15. By Claim D, $\gamma _t(T') = \chi _d^t(T')$. Since $\gamma _t(T) = \chi _d^t(T)$, we note that $T \ne P_5$, and so $T'$ has order at least $3$. Applying the inductive hypothesis to the tree $T'$, we see that $T' \in \mathcal {T}$. Thus, $T'$ can be obtained from a disjoint union of $k \ge 1$ stars each of order at least $3$ by adding $k-1$ edges joining leaf vertices in such a way that the resulting graph is connected and the center of each of the original $k$ stars remains a support vertex. We note that $\gamma _t(T') = 2k$. Further, every $\gamma _t(T')$-set contains the $k$ support vertices of $T'$ and an arbitrary leaf-neighbor of every support vertex. Let $S_x$ be the underlying star of the tree $T'$ that contains the vertex $x$.

Claim E The following holds.

• (a) The vertex $x$ is a leaf in the star $S_x$.

• (b) The star $S_x$ contains a vertex that is a leaf in $T$.

Proof

• (a) Suppose to the contrary that $x$ is the center vertex of $S_x$. Let $R$ be a $\gamma _t(T')$-set. As observed earlier, the set $R$ contains the $k$ support vertices of $T'$ and one leaf-neighbor of every support vertex. In particular, $x \in R$. Let $x'$ be a leaf-neighbor of $x$ that belongs to the set $R$. Then the set $(R {\setminus } \{x'\}) \cup \{v,w\}$ is a TD-set of $T$, implying that $\gamma _t(T) \le |R| + 1 = 2k+1 = \gamma _t(T') + 1$, contradicting Claim D.

• (b) Suppose to the contrary that the star $S_x$ contains no leaf of $T$. Let $R$ be a $\gamma _t(T')$-set. Let $y$ be the center of $S_x$, and let $y_1, \ldots , y_b$ be the leaves of $S_x$ different from $x$. For each $i = 1,\ldots ,b$, let $z_i$ be a neighbor of $y_i$ different from $y$ and note that each vertex $z_i$ is a leaf in some underlying star of the tree $T'$. Further we note that in the underlying star of $T'$ containing the vertex $z_i$, we can clearly choose the set $R$ so that $z_i \in R$ (for otherwise, we simply replace the leaf in the underlying star that belongs to $R$ with the vertex $z_i$). Further we can choose the set $R$ so that $x$ is the leaf in the star $S_x$ that belongs to $R$. But then the set $(R {\setminus } \{y\}) \cup \{v,w\}$ is a TD-set of $T$, implying that $\gamma _t(T) \le |R| + 1 = 2k+1 = \gamma _t(T') + 1$, once again contradicting Claim D. $\square$

By Claim E, the vertex $x$ is a leaf of the star $S_x$. Further, the star $S_x$ contains a vertex that is leaf in $T$. This implies that $T \in \mathcal {T}$, where the underlying stars in the tree $T$ consist of the star induced by $\{u,v,w\}$ and the $k$ stars of the tree $T'$. This completes the proof of Theorem 15. $\square$

3.2 Properties of $\chi _d^t(T)$-Colorings in a Tree $T$

Our second aim in this section is to establish properties of $\chi _d^t(T)$-colorings in a tree $T$. Recall that a color class $C$ in a given TD-coloring of a graph $G$ is free if each vertex of $G$ is adjacent to every vertex of some color class different from $C$. Recall further by Corollary 10, that if $T$ is a nontrivial tree, then $\gamma _t(T) \le \chi _d^t(T) \le \gamma _t(T) + 2$. We establish next the following property of $\chi _d^t(T)$-colorings in a tree $T$.

Lemma 16

Let $T$ be a nontrivial tree. Then the following holds.

• (a) If $\gamma _t(T) = \chi _d^t(T)$, then no $\chi _d^t(T)$-coloring contains a free color class.

• (b) If $\chi _d^t(T) = \gamma _t(T) + 1$, then there exists a $\chi _d^t(T)$-coloring that contains a free color class.

• (c) If $\chi _d^t(T) = \gamma _t(T) + 2$, then there exists a $\chi _d^t(T)$-coloring that contains two free color class.

Proof

Part (a) is an immediate consequence of Lemmma 14 and Theorem 15.

To prove Part (c), suppose that $\chi _d^t(T) = \gamma _t(T) + 2$ and let $S$ be a $\gamma _t(T)$-set. If $V {\setminus } S$ is an independent set, then assigning to each vertex of $S$ a unique color and assigning to the vertices in $V {\setminus } S$ an additional color, produces a TD-coloring in $T$ with $\gamma _t(T) + 1$ color classes, implying that $\chi _d^t(T) \le \gamma _t(T) + 1$, a contradiction. Hence, $V {\setminus } S$ is not an independent set. We now $2$-color the vertices in the forest $T[V {\setminus } S]$ and we color each vertex of $S$ with a unique color. The resulting coloring is a TD-coloring of $T$ with $\chi _d^t(T) = \gamma _t(T) + 2$ color classes. However both color classes used to color the vertices in $V {\setminus } S$ are free color classes. This proves Part (c).

It remains for us to prove Part (b). We proceed by induction on the order $n$ of a nontrivial tree satisfying $\chi _d^t(T) = \gamma _t(T) + 1$. The smallest such tree is a path $T = P_4$, for which the desired result holds. This establishes the base case. Suppose, then, that $n \ge 5$ and that if $T'$ is a nontrivial tree of order less than $n$ satisfying $\chi _d^t(T') = \gamma _t(T') + 1$, then there exists a $\chi _d^t(T')$-coloring that contains a free color class. Let $T$ be a tree of order $n$ satisfying $\chi _d^t(T) = \gamma _t(T) + 1$. Let $\mathcal {C}$ be a $\chi _d^t(T)$-coloring.

If $T$ is a star, then $\chi _d^t(T) = \gamma _t(T)$, a contradiction. Hence, $\mathrm{diam}(T) \ge 3$. Suppose $\mathrm{diam}(T) = 3$. Then, $T$ is a double star and $\chi _d^t(T) = \gamma _t(T) + 1$ = 3. In this case, assigning a unique color to both central vertices of $T$ and a third color to the leaves of $T$ produces a $\chi _d^t(T)$-coloring that contains a free color class, as desired. Hence we may assume that $\mathrm{diam}(T) \ge 4$.

We proceed further with the following series of claims that we may assume are satisfied by the tree $T$.

Claim I We may assume that the tree $T$ has no strong support vertex.

Proof

Suppose that $T$ has a strong support vertex $w$ and let $u$ and $v$ be two leaf-neighbors of $w$. Then, $\chi _d^t(T-v) = \chi _d^t(T)$ and $\gamma _t(T-v) = \gamma _t(T)$, implying that $\chi _d^t(T-v) = \gamma _t(T-v) + 1$. Applying the inductive hypothesis to the tree $T - v$, there exists a $\chi _d^t(T-v)$-coloring $\mathcal {C}'$ that contains a free color class, $C$ say. Assigning to the leaf $v$ the same color as used to color the leaf $u$ in $\mathcal {C}'$ extends this coloring to a $\chi _d^t(T)$-coloring $\mathcal {C}^*$. On the one hand, if the vertex $v$ was not added to the color class $C$, then the color class $C$ remains a free color class in $\mathcal {C}^*$. On the other hand, if $v$ was added to the color class $C$, then this new color class is a free color class in $\mathcal {C}^*$. In both cases, we produce a $\chi _d^t(T)$-coloring that contains a free color class. Hence we may assume that $T$ has no strong support vertex, for otherwise the desired result follows. $\square$

Let $r$ and $u$ be two vertices at maximum distance apart in $T$ and root the tree at the vertex $r$. Let $v$ be the parent of $u$, let $w$ be the parent of $v$ and let $x$ be the parent of $w$. By Claim I, the tree $T$ has no strong support vertex. Hence, $d_T(v) = 2$. We note that $v$ is assigned a unique coloring in $\mathcal {C}$.

Claim II We may assume that $d_T(w) = 2$.

Proof

Suppose that $d_T(w) \ge 3$. Let $v'$ be a child of $w$ different from $v$. If $v'$ is a leaf, then $w$ is a support vertex and is assigned a unique color in the coloring $\mathcal {C}$. But then the color class containing the vertex $u$ is free. Hence we may assume that $v'$ is not a leaf, implying that $d_T(v') = 2$. Let $u'$ be the leaf-neighbor of $v'$. We note that $v'$ is assigned a unique coloring in $\mathcal {C}$.

Suppose that $u$ and $w$ are colored with the same color. Then, $\{u,w\}$ is the unique color class contained in $N(v)$. Further, the color class containing the vertex $u'$ is unique; that is, $\{u'\}$ is the unique color class which is contained in $N(v')$. Renaming the colors, if necessary, we may assume that $u$ and $w$ are colored with color $1$ and the vertex $u'$ is colored with color $2$. But then recoloring the vertex $u$ with color $2$, produces a new $\chi _d^t(T)$-coloring in which the color class $\{u,u'\}$ is free. Hence we may assume that $u$ and $w$ belong to different color classes. Analogously, we may assume that $u'$ and $w$ belong to different color classes.

If $w$ is assigned a unique color, then the color class containing the vertex $u$ is free. Hence we may assume that $w$ is not assigned a unique color. This implies that both vertices $u$ and $u'$ are assigned a unique color. Renaming the colors, if necessary, we may assume that $u$, $u'$ and $w$ are colored with colors $1$, $2$ and $3$, respectively. But then recoloring the vertex $u'$ with color $1$ and recoloring the vertex $w$ with color $2$, produces a new $\chi _d^t(T)$-coloring in which the color class $\{u,u'\}$ is free. Therefore, we may assume that $d_T(w) = 2$, for otherwise the desired result follows. $\square$

We now consider the tree $T' = T - \{u,v,w\}$. Let $\mathcal {C}'$ be the restriction of the coloring $\mathcal {C}$ to the tree $T'$.

Claim III We may assume that $\mathcal {C}'$ is a TD-coloring of $T'$.

Proof

Suppose that $\mathcal {C}'$ is not a TD-coloring of $T'$. This implies that the vertex $w$ has a unique color. This in turn implies that the color class of $\mathcal {C}$ that contains the vertex $u$ is free. Hence we may assume that $\mathcal {C}'$ is a TD-coloring of $T'$, for otherwise the desired result follows. $\square$

Claim IV $\chi _d^t(T') \le \chi _d^t(T) - 2$ and $\gamma _t(T) \le \gamma _t(T') + 2$.

Proof

By Claim III, the restriction, $\mathcal {C}'$, of the coloring $\mathcal {C}$ to the tree $T'$ is a TD-coloring of $T'$. Since $\mathcal {C}'$ contains at least two fewer color class than does $\mathcal {C}$, we see that $\chi _d^t(T') \le \chi _d^t(T) - 2$. Every $\gamma _t(T')$-set can be extended to a TD-set of $T'$ by adding to it the vertices $v$ and $w$, and so $\gamma _t(T) \le \gamma _t(T') + 2$. $\square$

By assumption, $\chi _d^t(T) = \gamma _t(T) + 1$. By Corollary 10, we see that $\chi _d^t(T') = \gamma _t(T') + \ell$ for some $\ell \in \{0,1,2\}$. If $\chi _d^t(T') = \gamma _t(T') + 2$, then by Claim IV, $\gamma _t(T) \le \gamma _t(T') + 2 = \chi _d^t(T') \le \chi _d^t(T) - 2 = \gamma _t(T) - 1$, which is impossible. Hence, $\chi _d^t(T') = \gamma _t(T')$ or $\chi _d^t(T') = \gamma _t(T') + 1$.

Claim V We may assume that $\chi _d^t(T') = \gamma _t(T')$.

Proof

Suppose that $\chi _d^t(T') = \gamma _t(T') + 1$. Then, by Claim IV, we see that $\gamma _t(T) \le \gamma _t(T') + 2 = \chi _d^t(T') + 1 \le \chi _d^t(T) - 1 = \gamma _t(T)$. Hence we must have equality throughout this inequality chain. In particular, $\chi _d^t(T') = \chi _d^t(T) - 2$. Applying the inductive hypothesis to the tree $T'$, there exists a $\chi _d^t(T')$-coloring, $\mathcal {D}'$, that contains a free color class, $C$ say. The coloring $\mathcal {D}'$ can be extended to a $\chi _d^t(T)$-coloring $\mathcal {D}^*$ by adding to it two new color classes, namely $\{v\}$ and $\{u,w\}$. The free color class, $C$, of $\mathcal {D}'$ is a free color class in $\mathcal {D}^*$. Hence we may assume that $\chi _d^t(T') = \gamma _t(T')$, for otherwise the desired result follows. $\square$

By Claim V, $\chi _d^t(T') = \gamma _t(T')$. By Theorem 15, $T' \in \mathcal {T}$. Recall that $x$ is the parent of $w$ in $T$ and $r$ is the root of $T$.

Claim VI We may assume that $T' \ne P_2$.

Proof

Suppose $T' = P_2$. Then, $T = P_5$ and $T$ is the path $uvwxr$. In this case, $\gamma _t(T) = 3$ and $\chi _d^t(T) = 4$. Coloring $u$ and $r$ with the color $1$, and coloring $v$, $w$ and $x$ with the colors $2$, $3$ and $4$, respectively, produces a $\chi _d^t(T)$-coloring that contains a free color class, namely the color class $\{u,r\}$. Hence we may assume that $T' \ne P_2$, for otherwise the desired result follows. $\square$

By Claim VI, $T' \ne P_2$. Hence by definition of the family $\mathcal {T}$, the tree $T'$ can be obtained from a disjoint union of $k \ge 1$ stars each of order at least $3$ by adding $k-1$ edges joining leaf vertices in such a way that the resulting graph is connected and the center of each of the original $k$ stars remains a support vertex.

Let $\mathcal {D}'$ be a $\chi _d^t(T')$-coloring. By Lemma 14, the color classes of $\mathcal {D}'$ are unique, and consist of the $k$ support vertices of $T'$ (namely, the centers of the $k$ original stars used to construct $T'$) and the open neighborhoods of these support vertices in $T'$. In particular, we note that $\chi _d^t(T') = 2k = \gamma _t(T')$. Let $S_x$ be the original star used to construct $T'$ that contains $x$. Let $x'$ be the center of the star $S_x$. (Possibly, $x = x'$.) If $T \in \mathcal {T}$, then $\chi _d^t(T) = \gamma _t(T)$, a contradiction. Hence, $T \notin \mathcal {T}$, implying that either $x = x'$ or $x$ is a leaf of $S_x$ and every leaf of $S_x$ different from $x$ has degree at least $2$ in $T'$.

Claim VI We may assume that $x = x'$.

Proof

Suppose that $x$ is not the central vertex in $S_x$; that is, $x \ne x'$. Then, $x$ is a leaf of $S_x$ and every leaf of $S_x$ different from $x$ has degree at least $2$ in $T'$. Let $R$ be the set of all vertices in $V(T') {\setminus } V(S_x)$ that are adjacent in $T'$ to a vertex in $V(S_x)$. We note that each vertex in $R$ is a leaf from one of the underlying stars of $T'$. Further, each underlying star of $T'$ contains at most one vertex from $R$. Hence we can choose a $\gamma _t(T')$-set, $D'$, to contain the $k$ support vertices of $T'$ and one neighbor of each of these support vertices in such a way that $R \subset D'$. Further, we may choose $D'$ so that $x \in D'$. With this choice of $D'$ we see that $(D' {\setminus } \{x'\}) \cup \{v,w\}$ is a TD-set of $T$, and so $\gamma _t(T) \le |D'| + 1 = 2k + 1$. However, $\gamma _t(T) \ge \rho ^o(T) \ge 2k + 1$. Consequently, $\gamma _t(T) = 2k+1$ and $\chi _d^t(T) = 2k + 2$. We may assume that the center, $x'$, of the star $S_x$ is colored with the color $1$ in $\mathcal {D}'$. We now modify the coloring $\mathcal {D}'$ as follows. Let $L$ be the set of vertices of $T'$ that belong to an underlying star of $T'$ that contains a vertex of $R$ and are leaves in that underlying star not in $R$. Since $T'$ is a tree, the set $L$ is an independent set in $T'$. We now recolor all the vertices that belong to $L$ with the color $1$ (and note that the color of vertices in $R$ remains unchanged). Let $\mathcal {D}^*$ denote the resulting modified coloring of $T'$. We now extend the coloring $\mathcal {D}^*$ to a $\chi _d^t(T)$-coloring by coloring $u$ with the color $1$ and coloring $v$ and $w$ with two new colors. In the resulting $\chi _d^t(T)$-coloring the color class consisting of vertices colored $1$ is free. Hence we may assume that $x$ is the central vertex in $S_x$, for otherwise the desired result follows. $\square$

By Claim VII, $x$ is the central vertex in $S_x$. Then, $\gamma _t(T) = 2k+1$ and $\chi _d^t(T) = 2k + 2$. We now extend the coloring $\mathcal {D}'$ to a $\chi _d^t(T)$-coloring by adding $u$ to the color class, $N_{T'}(x)$, that consists of the neighbors of $x$ in $T'$, and coloring $v$ and $w$ with two new colors. In the resulting $\chi _d^t(T)$-coloring the color class $N_{T'}(x) \cup \{u\}$ is free. This completes the proof of Part (b) and therefore of Lemma 16. $\square$

3.3 Trees with Large Total Dominator Chromatic Number

Our third aim in this section is to establish a tight upper bound on the total dominator chromatic number of a tree in terms of its order and to characterize the trees with maximum possible total dominator chromatic number. By Theorem 4 and Corollary 10, we see that if $T$ is a tree of order $n \ge 3$, then $\chi _d^t(T) \le 2n/3 + 2$. We show next that this bound can be improved slightly. For this purpose, let $\mathcal {F}$ be the family of all trees $T$ that can be obtained from a tree $H$ of order at least $2$ by selecting an arbitrary edge $e = uv$ in $H$ and attaching a path of length $2$ to each vertex of $V(H) {\setminus } \{u,v\}$ so that the resulting paths are vertex-disjoint. We call $H$ the underlying tree of $T$. A tree in the family $\mathcal {F}$ with underlying tree $H = P_5$, for example, is illustrated in Fig. 3 (here the darkened vertices form the vertices of $H$).

Fig. 3

A tree in the family $\mathcal {F}$

We remark that the smallest trees in the family $\mathcal {F}$ are the trees $P_2$ and $P_5$. We observe that if the underlying tree $H$ used to construct a tree $T \in \mathcal {F}$ has order $k \ge 3$, then $T$ has order $n = 3k-4$. Further, if $x \in V(H) {\setminus } \{u,v\}$ and $xyz$ is the path added to $x$ when constructing $T$, then in every TD-coloring of $T$ the set $\{x,y,z\}$ contains at least two color classes. Further the adjacent vertices $u$ and $v$ are assigned two distinct colors, implying that there are at least $2k - 2$ color classes, and so $\chi _d^t(T) \ge 2k - 2$. Renaming the vertices $u$ and $v$, if necessary, we may assume that $d_H(v) \ge d_H(u)$. Assigning the same color to the vertex $u$ and to each of the added $k - 2$ leaves, and assigning a unique color to each remaining vertex of $T$, produces a TD-coloring of $T$ with $2k - 2$ color classes, and so $\chi _d^t(T) \le 2k - 2$. Consequently, $\chi _d^t(T) = 2k - 2 = 2(n+1)/3$. We state this formally as follows.

Observation 17

If $T \in \mathcal {F}$ has order $n$, then $\chi _d^t(T) = 2(n+1)/3$.

We are now in a position to present a tight upper bound on the total dominator chromatic number of a tree in terms of its order and to characterize the extremal trees.

Theorem 18

Let $T$ be a tree of order $n \ge 2$. Then, $\chi _d^t(T) \le 2(n+1)/3$ with equality if and only if $T \in \mathcal {F}$.

Proof

We proceed by induction on the order $n \ge 2$ of a tree $T$. If $n = 2$, then $T = P_2 \in \mathcal {F}$ and $\chi _d^t(T) = 2 = 2(n+1)/3$. This establishes the base case. Suppose that $n \ge 3$ and that for every tree $T'$ of order $n'$, where $2 \le n' < n$, we have $\chi _d^t(T') \le 2(n'+1)/3$, with equality if and only if $T' \in \mathcal {F}$. Let $T$ be a tree of order $n \ge 3$. If $T$ is a star, then $\chi _d^t(T) = 2 < 2(n+1)/3$. If $T$ is a double-star, then $n \ge 4$ and $\chi _d^t(T) = 3 < 2(n+1)/3$. Hence we may assume that $\mathrm{diam}(T) \ge 4$, for otherwise the desired result follows.

If $T$ has a strong support vertex $v$ and if $u$ is a leaf-neighbor of $v$, then $\chi _d^t(T) = \chi _d^t(T-u)$. Applying the inductive hypothesis to the tree $T-u$ of order $n-1$, we see that $\chi _d^t(T-u) \le 2n/3$, and so $\chi _d^t(T) < 2(n+1)/3$. Hence we may assume that $T$ has no strong support vertex, for otherwise the desired result holds.

Let $r$ and $u$ be two vertices at maximum distance apart in $T$ and root the tree at the vertex $r$. Let $v$ be the parent of $u$, let $w$ be the parent of $v$ and let $x$ be the parent of $w$. Since $T$ has no strong support vertex, we see that $d_T(v) = 2$. Let $T'$ be the tree obtained from $T$ by deleting the vertex $w$ and all its descendants; that is, $T' = T - V(T_w)$, where recall that $T_w$ denotes the maximal subtree of $T$ at $w$. Let $T'$ have order $n'$. Since $\mathrm{diam}(T) \ge 4$, we note that $n' \ge 2$. We proceed further with the following series of claims.

Claim 1

If $n' = 2$ and $T \ne P_5$, then $\chi _d^t(T) < 2(n+1)/3$.

Proof

Suppose that $n' = 2$ and $T \ne P_5$. Then, $T$ can be obtained from a star $K_{1,k}$, where $k \ge 3$, by subdividing at least $k-1$ edges exactly once. If exactly $k-1$ edges are subdivided, then $n = 2k$ and $\chi _d^t(T) = k + 1 < 2(n+1)/3$. If exactly $k$ edges are subdivided, then $n = 2k + 1$ and $\chi _d^t(T) = k + 2 < 2(n+1)/3$. $\square$

Suppose that $n' = 2$. By Claim 1, if $T \ne P_5$, then $\chi _d^t(T) < 2(n+1)/3$. If $T = P_5$, then $T \in \mathcal {F}$ and $\chi _d^t(T) = 4 = 2(n+1)/3$. Hence we may assume that $n' \ge 3$.

Claim 2

If no $\chi _d^t(T')$-coloring contains a free color class, then $\chi _d^t(T) \le 2(n+1)/3$. Further if $\chi _d^t(T) = 2(n+1)/3$, then $T \in \mathcal {F}$.

Proof

Suppose that no $\chi _d^t(T')$-coloring contains a free color class. Then, since $n' \ge 3$, we have by Lemma 16 that $\gamma _t(T') = \chi _d^t(T')$. Thus, by Theorem 15, we see that $T' \in \mathcal {T}$, implying that $\chi _d^t(T') \le 2n'/3$.

If $d_T(w) = 2$, then $n' = n - 3$ and every $\chi _d^t(T')$-coloring can be extended to a TD-coloring of $T$ by adding two new color classes, namely the color classes $\{v\}$ and $\{u,w\}$, implying that $\chi _d^t(T) \le \chi _d^t(T') + 2 \le 2(n-3)/3 + 2 = 2n/3$.

Suppose that $d_T(w) \ge 3$. Then, $T_w$ can be obtained from a star $K_{1,k}$, where $k \ge 2$, by subdividing at least $k-1$ edges exactly once. Suppose that exactly $k-1$ edges are subdivided in order to construct $T_w$. Then, $n' = n - 2k$ and every $\chi _d^t(T')$-coloring can be extended to a TD-coloring of $T$ by coloring each of the $k$ support vertices in $T_w$ with a unique color and adding one additional color to color the $k$ leaves of $T$. Therefore, in this case, $\chi _d^t(T) \le \chi _d^t(T') + k + 1 \le 2(n-2k)/3 + k + 1 = (2n-k+3)/3 \le (2n+1)/3$.

Suppose that exactly $k$ edges are subdivided in order to construct $T_w$. Then, $n' = n - 2k - 1$ and every $\chi _d^t(T')$-coloring can be extended to a TD-coloring of $T$ by coloring each of the $k$ support vertices in $T_w$ with a unique color, coloring the vertex $w$ with a unique color, and adding one additional color to color the $k$ leaves of $T$. Therefore, in this case,

$$\begin{aligned} \begin{array}{lll} \chi _d^t(T) &{} \le &{} \chi _d^t(T') + k + 2 \\ &{} \le &{} 2n'/3 + k + 2 \\ &{} = &{} 2(n-2k-1)/3 + k + 2 \\ &{} = &{} (2n-k+4)/3 \\ &{} \le &{} 2(n+1)/3. \end{array} \end{aligned}$$

Suppose, further, that $\chi _d^t(T) = 2(n+1)/3$. Then we must have equality throughout the previous inequality chain. In particular, $\chi _d^t(T') = 2n'/3$ and $k=2$. Thus, $T_w = P_5$ and $T'$ can be obtained from a disjoint union of $\ell \ge 1$ copies of $P_3$ by adding $\ell -1$ edges joining leaf vertices in such a way that the resulting graph is connected and the center of each of the original $\ell$ copies of $P_3$ remains a support vertex. Thus, $T'$ is the $2$-corona $T' = H' \circ P_2$ of a tree $H'$ of order $\ell$. Further, the support vertices of $T'$ are the central vertices of the copies of $P_3$ used to construct the tree $T'$. Let $uvwv'u'$ be the path $T_w$, and so $v'$ is the child of $w$ different from $v$, and $u'$ is the child of $v'$. There are two cases to consider.

Suppose that $x$ is a support vertex of $T'$. Then, $d_T(x) = 3$. We now color the $\ell$ support vertices of $T'$ with a unique color, and we color each of $v$, $v'$ and $w$ with a unique color. For each support vertex $x'$ of $T'$ different from $x$ we color both neighbors of $x'$ with the same, but unique, color. Finally we color the two neighbors of $x$ in $T'$ and the two leaves $u$ and $u'$ all with the same, but unique, color. The resulting coloring is a TD-coloring of $T$ with $2\ell +3$ color classes. Since $n = 3\ell +5$, we therefore have that $\chi _d^t(T) \le 2\ell + 3 < 2(n+1)/3$, a contradiction. Hence, $x$ is not a support vertex of $T'$. Let $y$ be the support vertex of $T'$ that is adjacent to $x$ and let $z$ denote the remaining neighbor of $y$ in $T'$. We note that either $x$ is a leaf in $T'$ or $x \in V(H')$.

Suppose that $\ell = 1$. Then, $T' = P_3$ and $T$ is obtained from a star $K_{1,3}$ by subdividing two edges once and the remaining edge twice. In this case, $T \in \mathcal {F}$ (for example, take the underlying tree in $T \in \mathcal {F}$ to be the path $uvwx$).

Suppose that $\ell \ge 2$. Suppose that $x$ is a leaf in $T'$. Then, $z \in V(H')$. In this case, we color each support vertex of $T'$, different from $y$, with a unique color. Further we color each vertex of $H'$, different from $z$, with a unique color and we color both $x$ and $z$ with the same, but unique, color. Finally, we color each of $v$, $v'$ and $w$ with a unique color, and we color all remaining vertices (namely, the vertices $u$, $u'$, $y$ and all leaves of $T'$ different from $x$) with the same, but unique, color. The resulting coloring is a TD-coloring of $T$ with $2\ell +3$ color classes. Since $n = 3\ell +5$, we therefore have that $\chi _d^t(T) \le 2\ell + 3 < 2(n+1)/3$, a contradiction. Hence, $z$ must be a leaf in $T'$, implying that $x \in V(H')$. But then $T \in \mathcal {F}$ (take, for example, the underlying tree in $T \in \mathcal {F}$ to be the tree induced by the vertices $V(H') \cup \{u,v,w\}$). $\square$

By Claim 2, we may assume that there exists a $\chi _d^t(T')$-coloring that contains a free color class, for otherwise the desired result follows. Applying the inductive hypothesis to the tree $T'$, we see that $\chi _d^t(T') \le 2(n'+1)/3$, with equality if and only of $T' \in \mathcal {F}$.

Claim 3

If $d_T(w) \ge 3$, then $\chi _d^t(T) < 2(n+1)/3$.

Proof

Suppose that $d_T(w) \ge 3$. Then, $T_w$ can be obtained from a star $K_{1,k}$, where $k \ge 2$, by subdividing at least $k-1$ edges exactly once. Let $\mathcal {C}'$ be a $\chi _d^t(T')$-coloring that contains a free color class, $C$. Renaming colors, if necessary, we may assume that the vertices in $C$ are colored with the color $1$.

If exactly $k-1$ edges are subdivided when constructing $T_w$, then $n' = n - 2k$ and the coloring $\mathcal {C}'$ can be extended to a TD-coloring of $T$ by coloring each of the $k$ support vertices in $T_w$ with a unique color and coloring each of the $k$ leaves in $T_w$ with the color $1$ used to color the vertices in the color class $C$ of $\mathcal {C}'$. Therefore, in this case, $\chi _d^t(T) \le \chi _d^t(T') \,+\, k \le 2(n'\,+\,1)/3 \,+\, k = 2(n-2k+1)/3 \,+\, k = (2n-k\,+\,2)/3 \le 2n/3$.

If exactly $k$ edges are subdivided, then $n' = n - 2k - 1$ and the coloring $\mathcal {C}'$ can be extended to a TD-coloring of $T$ by coloring each of the $k$ support vertices in $T_w$ with a unique color, coloring the vertex $w$ with a unique color, and coloring each of the $k$ leaves in $T_w$ with the color $1$ (and adding them to the color class $C$). Therefore, in this case, $\chi _d^t(T) \le \chi _d^t(T') + k + 1 \le 2(n'+1)/3 + k + 1 = 2(n-2k)/3 + k + 1 = (2n-k+3)/3 \le (2n+1)/3$.

In both cases, we see that $\chi _d^t(T) < 2(n+1)/3$. $\square$

By Claim 3, we may assume that $d_T(w) = 2$, for otherwise $\chi _d^t(T) < 2(n+1)/3$. Thus, $T_w$ consists of the path $wvu$. Hence, $n' = n - 3$. Every TD-coloring in $T'$ can be extended to a TD-coloring of $T$ by coloring $v$ with a unique color and coloring both $u$ and $w$ with the same, but unique, color, implying that

$$\begin{aligned} \begin{array}{lll} \chi _d^t(T) &{} \le &{} \chi _d^t(T') + 2\\ &{} \le &{} 2(n'+1)/3 + 2 \\ &{} = &{} 2(n-2)/3 + 2\\ &{} = &{} 2(n+1)/3. \end{array} \end{aligned}$$

This establishes the desired upper bound. Suppose, further, that $\chi _d^t(T) = 2(n+1)/3$. Then we must have equality throughout the previous inequality chain. In particular, $\chi _d^t(T) = \chi _d^t(T') + 2$ and $\chi _d^t(T') = 2(n'+1)/3$. Applying the inductive hypothesis to the tree $T'$, we see that $T' \in \mathcal {F}$. Let $H'$ be the underlying tree of $T'$. Further, let $u'$ and $v'$ be the two adjacent vertices in $H'$ whose degrees are unchanged when constructing the tree $T'$. Renaming the vertices $u'$ and $v'$, if necessary, we may assume that $d_{H'}(v') \ge d_{H'}(u')$. Since $n' \ge 3$, we note that $d_{H'}(v') \ge 2$. Let $\mathcal {C}'$ be the $\chi _d^t(T')$-coloring of $T'$ that colors the leaves of $T'$ and the vertex $u'$ with the color $1$, and colors all remaining vertices of $T'$ with a unique color.

Claim 4

If $x$ is a support vertex of $T'$ and $x \notin V(H')$, then $T \in \mathcal {F}$.

Proof

Suppose that $x \notin V(H')$ and that $x$ is a support vertex of $T'$. Let $y_1$ and $y_2$ be the two neighbors of $x$ in $T'$, where $y_1 \in V(H')$.

Suppose that $v'$ is adjacent to a vertex in $H'$ different from $u'$ and $y_1$. In this case, let $\mathcal {C}$ be the coloring obtained from $\mathcal {C}'$ by recoloring the vertex $y_1$ with the color $1$, coloring the vertex $u$ with the color $1$, and coloring both $v$ and $w$ with a unique color. Then, $\mathcal {C}$ is a TD-coloring of $T$ with one more color class than the coloring $\mathcal {C}'$, implying that $\chi _d^t(T) \le \chi _d^t(T') + 1$, contradicting our earlier observation that $\chi _d^t(T) = \chi _d^t(T') + 2$. Therefore, $d_{H'}(v') = 2$, and so $N_T(v') = \{u',y_1\}$.

Suppose that $u'$ has degree at least $2$ in $H'$. In this case, let $\mathcal {C}$ be the coloring obtained from $\mathcal {C}'$ by recoloring the vertex $u'$ with the same color used to color $y_1$, recoloring the vertex $v'$ with the color $1$, coloring the vertex $u$ with the color $1$, and coloring both $v$ and $w$ with a unique color. Then, $\mathcal {C}$ is a TD-coloring of $T$ with one more color class than the coloring $\mathcal {C}'$, a contradiction. Therefore, $u'$ is a leaf in $H'$ (and hence in $T$).

Since $u'$ is a leaf in $T$ and $N_T(v') = \{u',y_1\}$, we see that $T \in \mathcal {F}$, where the underlying tree, $H^*$, of $T$ has vertex set $(V(H') {\setminus } \{u',v'\}) \cup \{w,x,y_2\}$ and where $x$ and $y_2$ are the two adjacent vertices in $H^*$ whose degrees are unchanged when constructing the tree $T$. This completes the proof of Claim 4. $\square$

Claim 5

If $x$ is a leaf of $T'$ and $x \notin V(H')$, then $T \in \mathcal {F}$.

Proof

Suppose that $x \notin V(H')$ and that $x$ is a leaf of $T'$. Let $y$ be the neighbor of $x$ in $T'$ and let $z$ be the neighbor of $y$ different from $x$ in $T'$. (We note that in the rooted tree $T$, the vertex $y$ is the parent of $x$ and the vertex $z$ is the parent of $y$).

Suppose that $v'$ is adjacent to a vertex in $H'$ different from $u'$ and $z$. In this case, let $\mathcal {C}$ be the coloring obtained from $\mathcal {C}'$ by recoloring both vertices $x$ and $z$ with the color assigned to $y$ in $\mathcal {C}'$, recoloring the vertex $y$ with the color $1$, coloring the vertex $u$ with the color $1$, and coloring both $v$ and $w$ with a unique color. Then, $\mathcal {C}$ is a TD-coloring of $T$ with one more color class than the coloring $\mathcal {C}'$, implying that $\chi _d^t(T) \le \chi _d^t(T') + 1$, contradicting our earlier observation that $\chi _d^t(T) = \chi _d^t(T') + 2$. Therefore, $d_{H'}(v') = 2$, and so $N_T(v') = \{u',z\}$. Recall that by assumption, $d_{H'}(u') \le d_{H'}(v')$.

Suppose that $d_{H'}(u') = 2$. Let $a$ be a vertex in $H'$, different from $v'$, that is adjacent to the vertex $u'$ in $H'$. Let $abc$ be the path of length $2$ attached to $a$ when constructing the tree $T'$. Let $\mathcal {C}$ be the coloring obtained from $\mathcal {C}'$ by recoloring the vertex $v'$ with the same color used to color $y$, coloring the vertex $u$ with the color $1$, and coloring both $v$ and $w$ with a unique color. Then, $\mathcal {C}$ is a TD-coloring of $T$ with one more color class than the coloring $\mathcal {C}'$, a contradiction. Therefore, $u'$ is a leaf in $H'$ (and hence in $T$).

Since $u'$ is a leaf in $T$ and $N_T(v') = \{u',z\}$, we see that $T \in \mathcal {F}$, where the underlying tree, $H^*$, of $T$ has vertex set $(V(H') {\setminus } \{u',v'\}) \cup \{w,x,y\}$ and where $x$ and $y$ are the two adjacent vertices in $H^*$ whose degrees are unchanged when constructing the tree $T$. This completes the proof of Claim 5. $\square$

We now return to the proof of Theorem 18 one final time. By Claim 4 and Claim 5, we may assume that $x \in V(H')$. But then $T \in \mathcal {F}$, where the underlying tree $H$ of $T$ is obtained from $H'$ by adding to it the vertex $w$ and the edge $xw$. This completes the proof of Theorem 18. $\square$

3.4 Paths

Recall from Observation 3, that for $n \ge 3$ if $G \in \{P_n,C_n\}$, then $\gamma _t(G) = n/2$ if $n \equiv 0 \, (\mathrm{mod}\, 4)$, $\gamma _t(G) = (n+1)/2$ if $n \equiv 1,3 \, (\mathrm{mod}\, 4)$, and $\gamma _t(G) = n/2 + 1$ if $n \equiv 2 \, (\mathrm{mod}\, 4)$. For small values of $n \ge 2$, the total dominator chromatic number of a path $P_n$ on $n$ vertices is easy to compute (or can be checked by computer).

Observation 19

For $2 \le n \le 15$, we have

$$\begin{aligned} \chi _d^t(P_n) = \left\{ \begin{array}{l@{\quad }l} \gamma _t(P_n) &{} \hbox {for}\, n \in \{2,3,6\} \\ \gamma _t(P_n) + 1 &{} \hbox {for} \,n \in \{4,5,7,9,10,11,14\} \\ \gamma _t(P_n) + 2 &{} \hbox {for}\, n \in \{8,12,13,15\} \end{array} \right. \end{aligned}$$

For example, coloring the vertices of $P_{11}$ with the sequence of colors $1,2,3,1,4,5, 4,1,6,7,1$ produces a $\chi _d^t(P_{11})$-coloring, while coloring the vertices of $P_{14}$ with the sequence of colors $1,2,3,1,4,5,4,6,7,6,1,8,9,1$ produces a $\chi _d^t(P_{14})$-coloring. We determine next the total dominator chromatic number of a path $P_n$ for $n \ge 16$.

Proposition 20

For $n \ge 16$, $\chi _d^t(P_n) = \gamma _t(P_n) + 2$.

Proof

We proceed by induction on $n \ge 16$. The base cases when $n \in \{16,17,18,19\}$ are easy to verify (or can be checked by computer) and a $\chi _d^t(P_{n})$-coloring is shown in Fig. 4. Suppose, then, that $n \ge 20$ and that for all $n'$ where $16 \le n' < n$, we have $\chi _d^t(P_{n'}) = \gamma _t(P_{n'}) + 2$. Let $G$ be the path $v_1v_2 \ldots v_n$ and let $\mathcal {C}$ be a TD-coloring of $G$. Let $G' = G - \{v_1,v_2,v_3,v_4\}$ and let $\mathcal {C}'$ be the restriction of the coloring $\mathcal {C}$ to the vertices in $G'$. We note that the vertex $v_2$ is assigned a unique color in $\mathcal {C}$. Further, the neighborhood $N(v_2) = \{v_1,v_3\}$ of $v_2$ contains a color class of $\mathcal {C}$. Therefore, the coloring $\mathcal {C}$ contains at least two more color classes than does the coloring $\mathcal {C}'$.

Suppose that $\mathcal {C}'$ is a TD-coloring of $G'$. Applying the inductive hypothesis to $G'$ we see that $\mathcal {C}'$ has at least $\chi _d^t(G') = \gamma _t(G') + 2 = \gamma _t(P_{n-4}) + 2 = \gamma _t(P_n) = \gamma _t(G)$ color classes, implying that the TD-coloring $\mathcal {C}$ has at least $\gamma _t(G) + 2$ color classes.

Suppose that $\mathcal {C}'$ is not a TD-coloring of $G'$. Then since $\mathcal {C}$ is a TD-coloring of $G$, the only vertex in $G'$ that is not adjacent to every vertex of some color class in $\mathcal {C}'$ is the vertex $v_5$. However, $v_6$ is the only neighbor of $v_5$ in $G'$, implying that in the coloring $\mathcal {C}$ the vertex $v_4$ has a unique color while the color class containing the vertex $v_6$ contains at least two vertices. In this case, we let $\mathcal {C}''$ be obtained from the coloring $\mathcal {C}'$ by recoloring the vertex $v_6$ with the color assigned to the vertex $v_4$ in the coloring $\mathcal {C}$. Then, $\mathcal {C}''$ is a TD-coloring of $G'$. Since at least two color classes in the TD-coloring $\mathcal {C}$ are contained in the set $\{v_1,v_2,v_3\}$, the coloring $\mathcal {C}$ contains at least two more color classes than does the coloring $\mathcal {C}''$. Applying the inductive hypothesis to $G'$ we see that the TD-coloring $\mathcal {C}''$ has at least $\chi _d^t(G') = \gamma _t(G') + 2 = \gamma _t(P_{n-4}) + 2 = \gamma _t(P_n) = \gamma _t(G)$ color classes, implying that the TD-coloring $\mathcal {C}$ has at least $\gamma _t(G) + 2$ color classes.

In both cases, the TD-coloring $\mathcal {C}$ has at least $\gamma _t(G) + 2$ color classes. Since $\mathcal {C}$ is an arbitrary TD-coloring of $G$, this implies that $\chi _d^t(G) \ge \gamma _t(G) + 2$. By Corollary 10, $\chi _d^t(G) \le \gamma _t(G) + 2$. Consequently, $\chi _d^t(G) = \gamma _t(G) + 2$. $\square$

For $n \ge 16$, we define next a $\chi _d^t(P_n)$-coloring, $\mathcal {C}_n^*$, of a path $P_n$ as follows. Let $G$ be the path $v_1v_2 \ldots v_n$, where $n \ge 16$. For each vertex $v_i$ where $i \equiv 2,3 \, (\mathrm{mod}\, 4)$, assign a unique color. For each vertex $v_i$ where $i \equiv 0 \, (\mathrm{mod}\, 4)$, assign a new additional color, say $b$. For each vertex $v_i$ where $i \equiv 1 \, (\mathrm{mod}\, 4)$, assign a further additional color, say $a$. Let $\mathcal {C}_n$ denote the resulting coloring. We now define a coloring $\mathcal {C}_n^*$ as follows. If $n \equiv 0,3 \, (\mathrm{mod}\, 4)$, let $\mathcal {C}_n^* = \mathcal {C}_n$. If $n \equiv 1 \, (\mathrm{mod}\, 4)$, then recolor the vertex $v_{n-1}$ (currently colored with color $b$) with a new distinct color and let $\mathcal {C}_n^*$ denote the resulting modified coloring. If $n \equiv 2 \, (\mathrm{mod}\, 4)$, then recolor the vertex $v_{n-1}$ (currently colored with color $a$) with a new distinct color and let $\mathcal {C}_n^*$ denote the resulting modified coloring. The coloring $\mathcal {C}_n^*$ when $n \in \{16,17,18,19\}$, for example, is illustrated in Fig. 4. The darkened vertices in this coloring of $\mathcal {C}_n^*$ in Fig. 4 form a $\gamma _t(P_n)$-set.

Fig. 4

A coloring $\mathcal {C}_{n}^*$ of a path $P_n$ for $n \in \{16,17,18,19\}$

We note that $\mathcal {C}_n^*$ is a proper coloring of the vertices of $G$. Let $S$ be the set of vertices in $G$ that are not colored with the color $a$ or $b$. By the way in which colors in $\mathcal {C}_n^*$ are assigned, each vertex in $S$ is assigned a unique color. Thus since $S$ is a TD-set in $G$, every vertex in $G$ is adjacent to every vertex of some color class. Thus, $\mathcal {C}_n^*$ is a TD-coloring of $G$. Further, the set $S$ is a (minimum) TD-set in $G$ and $|S| = \lfloor n/2 \rfloor + \lceil n/4 \rceil - \lfloor n/4 \rfloor = \gamma _t(P_n)$. Thus, $\mathcal {C}_n^*$ has $|S| + 2 = \gamma _t(P_n) + 2$ color classes. Thus by Proposition 20, we see that the coloring $\mathcal {C}_n^*$ is a $\chi _d^t(P_n)$-coloring for $n \ge 16$.

We remark that analogously to the argument for a path, one can readily determine the total dominator chromatic number of a cycle $C_n$, $n \ge 3$. We omit the routine details.

Observation 21

$\chi _d^t(C_3) = 3$, $\chi _d^t(C_4) = 2$, and $\chi _d^t(C_{11}) = 8$. For all other values of $n \ge 5$, we have $\chi _d^t(C_n) = \chi _d^t(P_n)$.

4 Open Problems

We close with three open problems that we have yet to settle. The first open problem is to establish whether the converse of Proposition 11 is true. We state this formally as follows.

Problem 1

Prove or disprove: if $G$ is an isolate-free graph satisfying $\chi _d^t(G) = \gamma _t(G)$, then $G \in \mathcal {G}_0$.

We remark that Problem 1 is true in the case when $G$ is a tree as proven by Theorem 15. Recall that by Corollary 10, if $T$ is a nontrivial tree, then $\gamma _t(T) \le \chi _d^t(T) \le \gamma _t(T) + 2$. The infinite family of trees $T$ satisfying $\gamma _t(T) = \chi _d^t(T)$ are characterized in Theorem 15. We close with the following two open problems.

Problem 2

Characterize the trees $T$ satisfying $\gamma _t(T) = \chi _d^t(T) + 1$.

Problem 3

Characterize the trees $T$ satisfying $\gamma _t(T) = \chi _d^t(T) + 2$.