1 Introduction

Non-Uniform Rational B-Splines (NURBS) were first introduced in 1975 by Versprille [1] via rational extension of B-splines. The primary motivation for introducing NURBS was to represent conical shapes precisely. This is the critical advantage of NURBS over other polynomial-based classes of splines, and one of the main reasons for its prevalence. Due to this crucial ability, NURBS are still the prevalent technology for curve and surface modelling in Computer-Aided Design/Computer-Aided Manufacturing (CAD/CAM), and an integral part of most existing CAD/CAM commercial software.

The applications of this rational form, however, is not limited to precise representation of conics. Other applications of NURBS can also be found in CAD where the weights have been employed as additional degrees of freedom for improved flexibility. A thorough review of these applications has been reported by the authors in [2]. Moreover, in addition to CAD/CAM, NURBS have also been extensively used in many other areas of applications such as isogeometric analysis (IGA) [3], NURBS-augmented finite element analysis [4], shape optimization [5, 6], topology optimization [7, 8], material modeling [9, 10], reverse engineering [11], G-code generation [12] etc.

Despite being a powerful tool in engineering design, NURBS have multiple shortcomings which restricts its capability in certain applications [13]. A thorough review of the advantages and limitations of NURBS is provided in [13]. A major shortcoming of NURBS which has received significant attention is their inability to allow for local refinement. Due to the rigid tensor-product structure of NURBS, knot-insertion is a global operation and cannot be performed locally. This was soon known as a fundamental limitation of NURBS, since local knot-insertion is critical in many applications and is considered a common and efficient way for achieving desirable accuracy in approximating sharp features [14] or scattered data of highly varying density [15]. For instance, Leal et al. [14] mention that “Despite the advantages of fitting with NURBS, it is still necessary to improve the representation of sharp features like high curvatures, edges and corners with this fitting method”.

In order to remove this fundamental limitation, various generalizations of NURBS have been proposed so far. The concept of hierarchical B-spline constructions which considers multilevel B-spline extensions where the tensor-product structure is preserved at any level was originally proposed by Forsey and Bartels in 1988 [16]. The application of hierarchical splines for adaptive scattered data fitting has recently been investigated by Bracco et al. [15]. To efficiently deal with non-trivial data configurations, they describe the local solutions in terms of (variable-degree) polynomial approximations according not only to the number of data points locally available, but also to the smallest singular value of the local collocation matrices. These local approximations are subsequently combined without the need of additional computations with the construction of hierarchical quasi-interpolants described in terms of truncated hierarchical B-splines.

Generalized Hierarchical NURBS (H-NURBS) were introduced in 2008 by Chen et al. [17] by extending the idea of hierarchical B-splines to NURBS. Another popular technology are T-splines [18, 19] which constitute a superset of NURBS, and provide the local refinement properties by allowing for unstructured-ness. Recent variations of T-splines which are mainly devised for the application in IGA include analysis-suitable unstructured T-splines [20, 21] and Truncated T-splines [22]. Other variations of splines and subdivision surfaces, such as Tuned Hybrid Non-Uniform Subdivision Surfaces [23], Blended B-Spline as well as Truncated Hierarchical Tricubic C0 Spline Constructions on Unstructured Quadrilateral or Hexahedral Meshes [24, 25] have also been recently developed and successfully implemented in IGA. Most recent class of splines which removes the limitations of T-splines are Unstructured-splines (U-splines) that have been developed by Thomas [26].

In addition to the above technologies, an alternative strategy for addressing the same issue has also been adopted by some researchers. The basic idea of these studies is to preserve the tensor-product structure of NURBS, and instead include the weights of control points as additional degrees of freedom. This idea has also shown promising results for the approximation of scattered data of highly varying local density [27] as well as for the representation of sharp geometric features [14]. For instance, Leal et al. [14] present a new method for improving NURBS surface sharp feature representation that first subdivides the fitting data in clusters, by using Self Organizing Map (SOM), also known as Kohonen network; then, in each cluster, they use an evolutionary strategy to obtain the optimal weights of the NURBS such that the fitting error is minimized and the representation of sharp features is improved. While including the weights as additional degrees of freedom in data approximation with NURBS usually results in non-linear algorithms, Ma [11, 28] proposes a two-step linear algorithm which yields the optimal coordinates of control points as well as their optimal weights by solving two separate linear systems of equations.

As discussed in [2], in spite of being an effective technique for improving the performance of NURBS, there is a wide range of applications where treating the weights as extra design variables is either impossible or can be problematic. For instance, Dimas and Briassoulis [13] point out that a bad choice of weights in approximation can lead to poor curve/surface parameterization. Piegl [29] states that “improper application of the weights can result in a very bad parameterization, which can destroy subsequent surface constructions”. Further, there are many applications where treating the weights as additional design variables is essentially impossible. These limitations inspired introducing the concept of Generalized NURBS (GNURBS) which is thoroughly discussed for parametric curves in [2] by the authors. Further, the extension of this mathematical model was introduced in [30] as a means for improved solution of boundary value problems using the isogeometric analysis method.

The focus of this paper is to comprehensively study various types of GNURBS surfaces, investigate their theoretical properties, and explore their applications in the context of CAGD. In particular, we will investigate a common application of these generalizations for improved surface approximation. It will be shown that, despite simply being disguised forms of classic NURBS, these generalizations provide significantly better approximation abilities compared to classic NURBS.

The remainder of this paper is organized as follows: in Sects. 2 and 3, we introduce different generalizations of NURBS, and develop their theoretical properties. We explore the application of GNURBS for improved approximation of surfaces in Sect. 4 where least-square approximation algorithms are developed. A series of numerical examples are presented in Sect. 5 where the performance of GNURBS compared to NURBS for the approximation of different class of surfaces is studied. Further potential areas of applications and extensions of GNURBS are discussed in Sect. 6. An interactive MATLAB toolbox for GNURBS surfaces is introduced in Sect. 7, and finally conclusions are drawn in Sect. 8.

2 Generalized NURBS surfaces: non-isoparametric form via explicit decoupling of the weights

We recall that the equation of a NURBS surface is defined in the following parametric form [29]

$${\mathbf{S}}\begin{array}{*{20}c} {\left( {\xi ,\eta } \right) = \mathop \sum \limits_{i = 0}^{{n_{1} }} \mathop \sum \limits_{j = 0}^{{n_{2} }} R_{ij}^{p,q} \left( {\xi ,\eta } \right){\mathbf{P}}_{ij} } & {\begin{array}{*{20}c} {a \le \xi \le b} \\ {c \le \eta \le d} \\ \end{array} } \\ \end{array}$$
(1)

where \({\mathbf{P}}_{ij} = \left[ {x_{ij} ,y_{ij} ,z_{ij} } \right]^{T}\) is a set of \((n_{1} + 1) \times (n_{2} + 1)\) control points and \(R_{ij}^{p,q} \left( {\xi ,\eta } \right)\) are the corresponding rational basis functions associated with (i, j)th control point defined as

$$R_{ij}^{p,q} \left( {\xi ,n} \right) = \frac{{N_{ij}^{p,q} \left( {\xi ,n} \right)w_{ij} }}{{\sum\nolimits_{k = 0}^{{n_{1} }} {\sum\nolimits_{l = 0}^{{n_{2} }} {N_{kl}^{p,q} \left( {\xi ,n} \right)w_{kl} } } }}$$
(2)

where \(w_{ij}\) are the weights associated with control points, and \(N_{ij}^{p,q} \left( {\xi ,\eta } \right) = N_{i,p} (\xi )N_{j,q} \left( \eta \right)\) are bivariate B-spline basis functions. \(N_{i,p} (\xi )\) and \(N_{j,q} \left( \eta \right)\) are the univariate B-spline basis functions of degree p and q defined on sets of non-decreasing real numbers \({{\varvec{\Xi}}} = \{ \xi_{0} ,\,\xi_{1} ,\;...,\;\xi_{{n_{1} + p}} \}\) and \({\mathbf{\rm H}} = \{ \eta_{0} ,\,\eta_{1} ,\;...,\;\eta_{{n_{2} + q}} \}\), respectively, called knot vectors.

According to Eq. (1), NURBS surfaces are isoparametric representations where all the physical coordinates are constructed by linear combination of the same set of scalar basis functions in parametric space. This is the case for all the other popular CAGD representations such as different types of splines; and ensures critical properties such as affine invariance and convex hull which are of interest in geometric modelling [2].

We extend here the concept of Generalized Non-Uniform Rational B-Splines (GNURBS) [2] to surfaces by modifying Eq. (1) as follows

$${\mathbf{S}}\begin{array}{*{20}c} {\left( {\xi ,\eta } \right) = \mathop \sum \limits_{i = 0}^{{n_{1} }} \mathop \sum \limits_{j = 0}^{{n_{2} }} {\mathbf{R}}_{ij}^{p,q} \left( {\xi ,\eta } \right) \odot {\mathbf{P}}_{ij} } & {\begin{array}{*{20}c} {a_{1} \le \xi \le a_{2} } \\ {b_{1} \le \eta \le b_{2} } \\ \end{array} } \\ \end{array}$$
(3)

where \(\odot\) denotes Hadamard (entry-wise) product of two vector variables, \({\mathbf{R}}_{ij} \left( {\xi ,\eta } \right) = \left[ {R_{ij}^{x} \left( {\xi ,\eta } \right),\,\,R_{ij}^{y} \left( {\xi ,\eta } \right),\,\,R_{ij}^{z} \left( {\xi ,\eta } \right)} \right]^{T}\) is now a vector set of basis functions, and \(a_{1} ,a_{2} ,b_{1} \,{\text{and}}\,b_{2}\) are real numbers. Note that superscripts \(p,q\) have been omitted for brevity. Denoting an arbitrary coordinate in physical space by \(d \in \left\{ {x,y,z} \right\}\), the corresponding basis function in direction d can be written as

$$R_{ij}^{d} \left( {\xi ,\eta } \right) = \frac{{N_{ij}^{p,q} \left( {\xi ,\eta } \right)w_{ij}^{d} }}{{\mathop \sum \nolimits_{k = 0}^{{n_{1} }} \mathop \sum \nolimits_{l = 0}^{{n_{2} }} N_{kl}^{p,q} \left( {\xi ,\eta } \right)w_{kl}^{d} }}.$$
(4)

In the above equation, \(\left( {w_{ij}^{x} ,w_{ij}^{y} ,w_{ij}^{z} } \right)\) represent the set of coordinate-dependent weights associated with (i, j)th control point. Comparison of the above equation with that of classic NURBS in Eq. (1) shows that the main difference of the proposed generalized form is assigning independent weights to different physical coordinates of control points. As can be seen, the above leads to a non-isoparametric representation. This representation demonstrates different geometric properties compared to NURBS which are discussed in detail in the following section.

2.1 Theory and properties

It can be shown that due to coordinate-dependence of basis functions, a GNURBS surface (in its original form) need not satisfy properties such as strong convex hull and affine invariance. We demonstrate here that most of the theoretical properties which were discussed for GNURBS curves in [2] can be extended for GNURBS surfaces.

2.1.1 Local modification effectFootnote 1

Similar to NURBS, one can show that, in GNURBS, if a control point \({\mathbf{P}}_{ij}\) is moved, or if any of the weights \(w_{ij}^{d} (d = x,y,z)\) is changed, it affects the surface shape only over the rectangle \([\xi_{i} ,\xi_{i + p + 1} ) \times [\eta_{j} ,\eta_{j + q + 1} )\). However, unlike NURBS, changing the weights will only affect the parameterization of the surface along the corresponding physical coordinate \(d\), while the surface parameterization in the other directions will be preserved. This is, in fact, the key difference between GNURBS and NURBS which provides additional flexibility. In particular, assuming \((\xi ,\eta ) \in [\xi_{i} ,\xi_{i + p + 1} ) \times [\eta_{j} ,\eta_{j + q + 1} )\), if \(w_{i}^{d}\) is increased (decreased), the surface will move closer to (farther from) \({\mathbf{P}}_{ij}\). Further, for a fixed \((\xi ,\eta )\), a point on \({\mathbf{S}}(\xi ,\eta )\) moves along a straight line along d towards \({\mathbf{P}}_{ij}\) as a weight \(w_{ij}^{d}\) is modified. This can be directly concluded from Eq. (3) and the properties of classic NURBS.

For better insight, we provide here a graphical representation of how this property differs in GNURBS compared to NURBS. For this purpose, we first generate a B-spline surface with linear in-plane parameterization using a net of \(7 \times 7\) control points and quadratic basis functions in both parametric directions constructed over the knot vectors \({{\varvec{\Xi}}} = {\mathbf{\rm H}} = \left\{ {0,0,0,0.2,0.4,0.6,0.8,1,1,1} \right\}\). The employed net of control points is illustrated in Fig. 1. As the figure shows, the heights of all control points are set to zero except for \(z_{44}\) which is raised to 1.

Fig. 1
figure 1

Employed control net for construction of different NURBS surfaces

Full size image

The B-spline surface obtained by using this control net is depicted in Fig. 2.

Fig. 2
figure 2

The B-spline surface in physical space

Full size image

Next, we increase \(w_{44}\) to 4 and plot the resulting NURBS surface in the physical space in Fig. 3.

Fig. 3
figure 3

The NURBS surface with w44 = 4 in physical space

Full size image

Finally, using Eq. (3), we construct a GNURBS surface by only setting \(w_{44}^{z}\) to 4, and maintaining all other weights at 1. The resulting surface is shown in Fig. 4.

Fig. 4
figure 4

The GNURBS surface with wz44 = 4 in physical space

Full size image

Note that the depicted GNURBS surface in Fig. 4 is obtained by using two different sets of basis functions. The in-plane coordinates are obtained using the B-spline basis functions, while the out of plane coordinate is constructed using rational basis functions.

Comparing Figs. 3, 4, one can clearly observe that modifying a weight in classic NURBS alters the parameterization of the surface in all physical directions, while in the case of GNURBS, the parameterization of the surface only changes in the direction of the varied directional weight (z-direction in Fig. 4). It will be seen later that this property is critical for treating the weights as additional degrees of freedom in certain applications.

2.1.2 Axis-aligned bounding box (AABB):

Every GNURBS knot-element lies within the axis-aligned bounding box of its corresponding control points. That is, if \(\left( {\xi ,\eta } \right) \in \left[ {\xi_{i} ,\xi_{i + 1} } \right) \times \left[ {\eta_{j} ,\eta_{j + 1} } \right)\), then \({\mathbf{S}}(\xi ,\eta )\) lies within the bounding box of the control points \({\mathbf{P}}_{kl}\), \(i - p \le k \le i\) and \(j - q \le l \le j\).

Note that Eq. (3) can be easily re-written in the following form:

$$\left\{ \begin{gathered} x\left( {\xi ,\eta } \right) \hfill \\ y\left( {\xi ,\eta } \right) \hfill \\ z\left( {\xi ,\eta } \right) \hfill \\ \end{gathered} \right\} = \mathop \sum \limits_{i = 0}^{{n_{1} }} \sum\limits_{j = 0}^{{n_{2} }} {R_{{_{ij} }}^{x} \left( {\xi ,\eta } \right)\left\{ \begin{gathered} x_{ij} \hfill \\ \,0 \hfill \\ \,0 \hfill \\ \end{gathered} \right\}} \, + \mathop \sum \limits_{i = 0}^{{n_{1} }} \sum\limits_{j = 0}^{{n_{2} }} {R_{{_{ij} }}^{y} \left( {\xi ,\eta } \right)\left\{ \begin{gathered} \,0 \hfill \\ y_{ij} \hfill \\ \,0 \hfill \\ \end{gathered} \right\}} + \mathop \sum \limits_{i = 0}^{{n_{1} }} \sum\limits_{j = 0}^{{n_{2} }} {R_{{_{ij} }}^{z} \left( {\xi ,\eta } \right)\left\{ \begin{gathered} \,0 \hfill \\ \,0 \hfill \\ \,z_{ij} \hfill \\ \end{gathered} \right\}}$$
(5)

Accordingly, Eq. (5) could be written as

$${\mathbf{S}}\left( {\xi ,\eta } \right) = {\mathbf{S}}_{x} \left( {\xi ,\eta } \right) + {\mathbf{S}}_{y} \left( {\xi ,\eta } \right) + {\mathbf{S}}_{z} \left( {\xi ,\eta } \right)\,,\,\quad \left\{ \begin{gathered} a_{1} \le \xi \le a_{2} \hfill \\ b_{1} \le \eta \le b_{2} \hfill \\ \end{gathered} \right.$$
(6)

where \({\mathbf{S}}_{x} \left( {\xi ,\eta } \right)\), \({\mathbf{S}}_{y} \left( {\xi ,\eta } \right)\) and \({\mathbf{S}}_{z} \left( {\xi ,\eta } \right)\) are simply classic NURBS surfaces. From a geometric standpoint, each of these surfaces is the projection of the original non-isoparametric surface onto the corresponding physical axes.

The following figure shows a graphical representation of the above equations for a quadratic × cubic GNURBS surface constructed over the knot vectors \({{\varvec{\Xi}}} = \left\{ {0,0,0,{\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 3$}},{\raise0.5ex\hbox{$\scriptstyle 2$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 3$}},1,1,1} \right\}\) and \({\rm H} = \left\{ {0,0,0,0,{\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 3$}},{\raise0.5ex\hbox{$\scriptstyle 2$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 3$}},1,1,1,1} \right\}\). Random weights in z-direction have been assigned to the control points and the control points are plotted proportional to these weights in size for better insight.

Since each of these projected surfaces is a classic NURBS surface, they satisfy the convex hull property. Therefore, the middle knot-element of the surface which is marked in Fig. 5, must lie within the convex hulls of its corresponding control points on all three projected surfaces. That is, if \(\left( {\xi ,\eta } \right) \in \left[ {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}},{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}} \right) \times \left[ {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}},{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}} \right)\), then \({\mathbf{S}}_{x} \left( {\xi ,\eta } \right)\) lies within the convex hull of the control points \(\left( {x_{kl} ,0,0} \right)\), \(1 \le k \le 3\) and \(1 \le l \le 4\) which is the space between the two planes parallel to yz-plane. Similarly, \({\mathbf{S}}_{y} \left( {\xi ,\eta } \right)\) lies within the convex hull of the control points \(\left( {0,y_{kl} ,0} \right)\), \(1 \le k \le 3\) and \(1 \le l \le 4\) which is the area between the two planes parallel to xz-plane, and \({\mathbf{S}}_{z} \left( {\xi ,\eta } \right)\) lies within the convex hull of the control points \(\left( {0,0,z_{kl} } \right)\), \(1 \le k \le 3\) and \(1 \le l \le 4\) which is the area between the two planes parallel to xy-plane. Consequently, \({\mathbf{S}}\left( {\xi ,\eta } \right)\) is contained in the intersection of these six planes, which is the highlighted box area shown in Fig. 5, referred to as the axis-aligned bounding box of \({\mathbf{P}}_{kl}\), \(1 \le k \le 3\) and \(1 \le l \le 4\). It is obvious that this property is less strict than the strong convex-hull property of classic NURBS surfaces.

Fig. 5
figure 5

Geometric representation of the bounding box property for a GNURBS surface

Full size image

2.2 Special case with partial decoupling of the weights

A more practical variation of GNURBS, which will be the emphasis for the rest of this paper, is obtained by partial decoupling of the weights. In particular, for 3D surfaces, one can use the same set of in-plane weights along x and y directions, denoted by \(w^{xy}\), and a different set of out-of-plane weights in z direction \(w^{z}\). Accordingly, Eq. (3) could be re-written in the following expanded form

$$\left\{ {\begin{array}{*{20}c} {x\left( {\xi ,\eta } \right)} \\ {y\left( {\xi ,\eta } \right)} \\ {z\left( {\xi ,\eta } \right)} \\ \end{array} } \right\} = \begin{array}{*{20}c} {\mathop \sum \limits_{i = 0}^{{n_{1} }} \mathop \sum \limits_{j = 0}^{{n_{2} }} \left\{ \begin{gathered} R_{ij}^{xy} \left( {\xi ,\eta } \right)x_{ij} \hfill \\ R_{ij}^{xy} \left( {\xi ,\eta } \right)y_{ij} \hfill \\ R_{ij}^{z} \left( {\xi ,\eta } \right)\,\,z_{ij} \hfill \\ \end{gathered} \right\}} & {\begin{array}{*{20}c} {a_{1} \le \xi \le a_{2} } \\ {b_{1} \le \eta \le b_{2} } \\ \end{array} } \\ \end{array}$$
(7)

where

$$R_{ij}^{xy} \left( {\xi ,\eta } \right) = \frac{{N_{ij}^{p,q} \left( {\xi ,\eta } \right)w_{ij}^{xy} }}{{\mathop \sum \nolimits_{k = 0}^{{n_{1} }} \mathop \sum \nolimits_{l = 0}^{{n_{2} }} N_{kl}^{p,q} \left( {\xi ,\eta } \right)w_{kl}^{xy} }}$$
(8)

Observe that owing to this decoupling of the in-plane and out-of-plane weights, unlike in classic NURBS, one can now freely manipulate the weights along z direction, for instance, without perturbing the geometry or parameterization of the underlying planer surface in x–y plane.

2.3 Equivalence with NURBS

Despite losing some properties of NURBS which might be of interest in certain applications, we recall here a theorem [30] which establishes that GNURBS are nothing but disguised forms of higher-order classic NURBS. Therefore, all the properties of NURBS can be recovered through a suitable transformation and a strong theoretical foundation will be ensured. We express the theorem here for the special case with partial decoupling of the weights in above section, but it could be easily extended to the generic form in Eq. (3).

Theorem 1

A 3D GNURBS surface of degree \(\left( {p,q} \right)\) with partially decoupled set of weights \((w^{xy} ,w^{z} )\), can be exactly transformed into a higher order NURBS surface of degree \(\left( {2p,\,2q} \right)\) in the following form:

$$\left\{ \begin{gathered} x\left( {\xi ,\eta } \right) \hfill \\ y\left( {\xi ,\eta } \right) \hfill \\ z(\xi ,\eta ) \hfill \\ \end{gathered} \right\} = \sum\limits_{i = 0}^{{\hat{n}_{1} }} {\sum\limits_{i = 0}^{{\hat{n}_{2} }} {\widehat{R}_{ij}^{2p,2q} \left( {\xi ,\eta } \right)} \left\{ \begin{gathered} X_{i} \hfill \\ \,Y_{i} \hfill \\ \,Z_{i} \hfill \\ \end{gathered} \right\}}$$
(9)

where

$$\widehat{R}_{ij}^{2p,2q} \left( {\xi ,\eta } \right)\; = \;\frac{{\,N_{ij}^{2p,2q} \left( {\xi ,\eta } \right)W_{ij} }}{{\sum\limits_{k = 0}^{{\hat{n}_{1} }} {\mathop \sum \limits_{l = 0}^{{\hat{n}_{2} }} N_{kl}^{2p,2q} \left( {\xi ,\eta } \right)W_{kl} } }}$$
(10)

in which \((X_{ij} ,Y_{ij} ,Z_{ij} ,W_{ij} )\) are the coordinates and weights of the \((\hat{n}_{1} + 1) \times (\hat{n}_{2} + 1)\) control points of the equivalent higher order NURBS surface. The proof of this theorem has been provided in [30].

As discussed in [30], in the special case of Rational Bézier (R-Bézier) surfaces, the following straightforward analytical expressions can be obtained for the coefficients of the equivalent higher order R-Bézier surface:

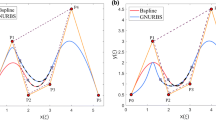
$$\begin{gathered} W_{ij} = \sum\limits_{k = \max (0,i - p)}^{\min (p,i)} {\,\sum\limits_{l = \max (0,j - q)}^{\min (q,j)} {\lambda_{ik}^{p} \,\lambda_{jl}^{q} \,w_{i - k,j - l}^{xy} \,w_{kl}^{z} } } \hfill \\ X_{ij} = \frac{1}{{W_{ij} }}\sum\limits_{k = \max (0,i - p)}^{\min (p,i)} {\,\sum\limits_{l = \max (0,j - q)}^{\min (q,j)} {\lambda_{ik}^{p} \,\lambda_{jl}^{q} \,w_{kl}^{xy} x_{kl} w_{i - k,j - l}^{z} } } \hfill \\ Y_{ij} = \frac{1}{{W_{ij} }}\sum\limits_{k = \max (0,i - p)}^{\min (p,i)} {\,\sum\limits_{l = \max (0,j - q)}^{\min (q,j)} {\lambda_{ik}^{p} \,\lambda_{jl}^{q} \,w_{kl}^{xy} y_{kl} w_{i - k,j - l}^{z} } } \hfill \\ Z_{ij} = \frac{1}{{W_{ij} }}\sum\limits_{k = \max (0,i - p)}^{\min (p,i)} {\,\sum\limits_{l = \max (0,j - q)}^{\min (q,j)} {\lambda_{ik}^{p} \,\lambda_{jl}^{q} \,w_{i - k,j - l}^{xy} \,z_{kl} w_{kl}^{z} } } \hfill \\ \end{gathered}$$
(11)

where \(\lambda_{ij}^{n} = \frac{{\left( {\begin{array}{*{20}c} n \\ j \\ \end{array} } \right)\left( {\begin{array}{*{20}c} n \\ {i - j} \\ \end{array} } \right)}}{{\left( {\begin{array}{*{20}c} {2n} \\ i \\ \end{array} } \right)}}\).Figure 6a shows an example of a degree (2, 3)th GNURBS surface with random directional weights assigned in z-direction. Its equivalent higher order NURBS surface obtained using the above theorem is depicted in Fig. 6b. Note that the size of control points in these figures are plotted proportional to their weights for better insight.

Fig. 6
figure 6

a A degree (2, 3)th GNURBS surface with random weights assigned in z-direction, and b its equivalent (isoparametric) NURBS surface of degree (4,6)

Full size image

3 Generalized NURBS surfaces: isoparametric form via implicit decoupling of the weights

It is interesting to note that the equivalent higher order NURBS representation in Eq. (9) itself provides another variation of NURBS which can be directly employed as another alternative to NURBS with better flexibility in many applications.

In order to clarify how this equation provides additional flexibility than classic NURBS, we first derive a more generic form of this equation via an alternative approach using an extension of order elevation technique. In this case, we limit our study to rational Bézier surfaces for simplicity.

Fig. 7
figure 7

Configuration of the quarter annulus

Full size image
Fig. 8
figure 8

Exact representation of the quarter annulus with normal parameterization using a (p, q) = (2, 1) rational Bézier surface

Full size image

3.1 Theory and formulation

Assume a 2D R-Bézier surface of degree (p, q) is given as follows

$$\left\{ \begin{gathered} x\left( {\xi ,\eta } \right) \hfill \\ y\left( {\xi ,\eta } \right) \hfill \\ \end{gathered} \right\} = \mathop \sum \limits_{i = 0}^{p} \sum\limits_{j = 0}^{q} {\frac{{\,B_{ij}^{p,q} \left( {\xi ,\eta } \right)w_{ij}^{xy} }}{{w^{xy} (\xi ,\eta )}}\left\{ \begin{gathered} x_{ij} \hfill \\ y_{ij} \hfill \\ \end{gathered} \right\}}$$
(12)

where \(B_{ij}^{p,q} \left( {\xi ,\eta } \right) = B_{i,p} (\xi )B_{j,q} \left( \eta \right)\) are bivariate Bézier basis functions of degree \((p,q)\). In order to elevate the degree of this surface by (r, s), we can simply multiply both numerator and denominator of this equation by any arbitrary expression in the following form

$$w^{z} (\xi ,\eta ) = \mathop \sum \limits_{i = 0}^{r} \sum\limits_{j = 0}^{s} {B_{ij}^{r,s} \left( {\xi ,\eta } \right)w_{ij}^{z} }$$
(13)

Recalling Theorem 1, we can obtain the higher order R-Bézier surface with (r, s) degree elevations as

$$\left\{ \begin{gathered} x\left( {\xi ,\eta } \right) \hfill \\ y\left( {\xi ,\eta } \right) \hfill \\ \end{gathered} \right\} = \sum\limits_{i = 0}^{{\hat{p}}} {\sum\limits_{j = 0}^{{\hat{q}}} {\widehat{R}_{ij}^{{\hat{p},\hat{q}}} \left\{ \begin{gathered} X_{ij} \hfill \\ \,Y_{ij} \hfill \\ \end{gathered} \right\}} }$$
(14)

where

$$\widehat{R}_{ij}^{{\hat{p},\hat{q}}} \left( {\xi ,\eta } \right) = \frac{{\,B_{ij}^{{\hat{p},\hat{q}}} \left( {\xi ,\eta } \right)W_{ij} }}{{\sum\limits_{k = 0}^{{\hat{p}}} {\mathop \sum \limits_{l = 0}^{{\hat{q}}} B_{kl}^{{\hat{p},\hat{q}}} \left( {\xi ,\eta } \right)W_{kl} } }}$$
(15)

in which \(\hat{p} = p + r,\,\hat{q} = q + s\) and \(\left( {X_{ij} ,Y_{ij} ,W_{ij} } \right)\) can be obtained using the following relations

$$\begin{gathered} W_{ij} = \sum\limits_{k = \max (0,i - r)}^{\min (p,i)} {\,\sum\limits_{l = \max (0,j - s)}^{\min (q,j)} {\lambda_{ik}^{p,r} \,\lambda_{jl}^{q,s} \,w_{kl}^{xy} \,w_{i - k,j - l}^{z} } } \hfill \\ X_{ij} = \frac{1}{{W_{ij} }}\sum\limits_{k = \max (0,i - r)}^{\min (p,i)} {\,\sum\limits_{l = \max (0,j - s)}^{\min (q,j)} {\lambda_{ik}^{p,r} \,\lambda_{jl}^{q,s} \,w_{kl}^{xy} x_{kl} w_{i - k,j - l}^{z} } } \hfill \\ Y_{ij} = \frac{1}{{W_{ij} }}\sum\limits_{k = \max (0,i - r)}^{\min (p,i)} {\,\sum\limits_{l = \max (0,j - s)}^{\min (q,j)} {\lambda_{ik}^{p,r} \,\lambda_{jl}^{q,s} \,w_{kl}^{xy} y_{kl} w_{i - k,j - l}^{z} } } \hfill \\ \end{gathered}$$
(16)

where \(\lambda_{ij}^{\alpha ,\beta } = \frac{{\left( {\begin{array}{*{20}c} \alpha \\ j \\ \end{array} } \right)\left( {\begin{array}{*{20}c} \beta \\ {i - j} \\ \end{array} } \right)}}{{\left( {\begin{array}{*{20}c} {\alpha + \beta } \\ i \\ \end{array} } \right)}}\).

Observe that this procedure can be seen as a natural extension of the classic order elevation techniques in the literature [31, 32]. In fact, one can simply recover the common order elevation algorithm by assigning \(w_{ij}^{z} = 1,\,\forall (i,j)\) in Eq. (13). We will refer to this procedure as generalized order elevation hereafter. Now assume we intend to add another dimension to the degree-elevated representation in Eq. (14) in an isoparametric manner. For this purpose, we extend this equation as

$$\left\{ \begin{gathered} x\left( {\xi ,\eta } \right) \hfill \\ y\left( {\xi ,\eta } \right) \hfill \\ z\left( {\xi ,\eta } \right) \hfill \\ \end{gathered} \right\} = \sum\limits_{i = 0}^{{\hat{p}}} {\sum\limits_{j = 0}^{{\hat{q}}} {\widehat{R}_{ij}^{{\hat{p},\hat{q}}} \left( {\xi ,\eta } \right)\left\{ \begin{gathered} X_{ij} \hfill \\ \,Y_{ij} \hfill \\ \,Z_{ij} \hfill \\ \end{gathered} \right\}} }$$
(17)

It is interesting to notice that, although Eq. (17) apparently seems to be a classic R-Bézier surface, it provides additional flexibility. Observe that in the above procedure,\(w_{ij}^{z}\) are arbitrary variables which can be freely chosen without perturbing the geometry or parameterization of the underlying surface in x–y plane. For better insight, we perform degree elevation on a circular annulus using the above procedure with different selections of \(w_{ij}^{z}\) and discuss how it differs from classic degree elevation technique.

For this purpose, we generate a 3D \((\hat{p},\hat{q}) = (3,2)\) isoparametric GR-Bézier surface by performing the above degree-elevation processes with \(\left( {r,s} \right) = \left( {1,1} \right)\) on an initial quarter annulus, shown in Fig. 7, which is modelled by a \((p,q) = (2,1)\) R-Bézier surface as depicted in Fig. 8 and specifying the heights of control points of the degree-elevated surface as shown in Table 1.

Table 1 Assigned heights (zij) to the control points of the resulting degree-elevated isoparametric GR-Bézier surface
Full size table

The obtained results for classic order elevation, that is, assuming unit values for all isoparametric control weights as in the following equation:

$$\left[ {\begin{array}{*{20}c} {w_{11}^{z} } & {w_{12}^{z} } \\ {w_{21}^{z} } & {w_{22}^{z} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {1.0} & {1.0} \\ {1.0} & {1.0} \\ \end{array} } \right]$$
(18)

are shown in Fig. 9.

Fig. 9
figure 9

Classic degree-elevated R-Bézier representation of the quarter annulus with control variables of Table 1: a top view, b 3D view

Full size image

Moreover, the obtained results for generalized order elevation by assuming the following values for isoparametric control weights:

$$\left[ {\begin{array}{*{20}c} {w_{11}^{z} } & {w_{12}^{z} } \\ {w_{21}^{z} } & {w_{22}^{z} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {3.0} & {1.0} \\ {1.0} & {0.5} \\ \end{array} } \right]$$
(19)

are depicted in Fig. 10.

Fig. 10
figure 10

Generalized degree-elevated R-Bézier representation of the quarter annulus with control variables of Table 1: a top view, b 3D view

Full size image

As can be clearly seen in these figures, in both cases, the in-plane representation of the annular ring as well as its parameterization has remained unchanged. However, the out of plane deformation of the annular ring in the two cases are not identical.

While this variation of NURBS, which will be referred to as isoparametric GNURBS hereafter, similarly provides the same important possibility of treating the out of plane weights as additional degrees of freedom, it provides different advantages elaborated in the following section.

The above algorithm can also be extended to NURBS in a straightforward manner using a similar three step algorithm elaborated above. That is, Eq. (17) also holds true for NURBS:

$$\left\{ \begin{gathered} x\left( {\xi ,\eta } \right) \hfill \\ y\left( {\xi ,\eta } \right) \hfill \\ z\left( {\xi ,\eta } \right) \hfill \\ \end{gathered} \right\} = \sum\limits_{i = 0}^{{\hat{n}_{1} }} {\sum\limits_{j = 0}^{{\hat{n}_{2} }} {\widehat{R}_{ij}^{{\hat{p},\hat{q}}} \left( {\xi ,\eta } \right)\left\{ \begin{gathered} X_{ij} \hfill \\ \,Y_{ij} \hfill \\ \,Z_{ij} \hfill \\ \end{gathered} \right\}} }$$
(20)

with the rational basis functions defined as

$$\widehat{R}_{ij}^{{\hat{p},\hat{q}}} \left( {\xi ,\eta } \right) = \frac{{\,N_{ij}^{{\hat{p},\hat{q}}} \left( {\xi ,\eta } \right)W_{ij} }}{{\sum\limits_{k = 0}^{{\hat{n}_{1} }} {\mathop \sum \limits_{l = 0}^{{\hat{n}_{2} }} N_{kl}^{{\hat{p},\hat{q}}} \left( {\xi ,\eta } \right)W_{kl} } }}$$
(21)

The proposed generalizations of NURBS in Eqs. (7) and (20) can effectively improve the performance of NURBS in a wide area of applications. Exploring all these applications, however, is beyond the scope of this study. We limit our study here to a few classic examples in geometric modelling, that is the approximation of certain class of surfaces such as helical, revolved or minimal surfaces using GNURBS; and concisely point out some of their potential broader areas of applications. Finally, hereafter, we will persistently refer to Eq. (7) as the first generalization of NURBS or non-isoparametric GNURBS, while we will refer to Eq. (20) as the second generalization of NURBS or isoparametric GNURBS.

3.2 Analogy with non-isoparametric GNURBS

As discussed earlier, the primary motivation for introducing GNURBS is to provide the possibility of treating the weights as additional degrees of freedom in a wider range of applications than classic NURBS. While both proposed variations allow for this additional flexibility, they differ in various aspects making them suitable for different applications.

A major difference is regarding the physical meaning of the control weights in the two variations. In the first variation, the geometric effect of manipulating the directional weights on the behavior of the surface is tangible; hence, making it suitable for free-form geometric modelling with additional flexibility than classic NURBS. On the other hand, due to the loss of the local support of control weights in the isoparametric form, the physical effect of manipulating these directional weights can be unpredictable, making the second variation impractical for geometric modelling.

Despite losing this merit, unlike the first variation, the isoparametric form allows for introducing customized rationality for approximation, i.e., the number of unknown coefficients to be considered as design variables in the denominator can be controlled. This property can help better control the approximation process.

Finally, if affine invariance and other properties of NURBS are of interest, the result of approximation using the second (isoparametric) variation directly lies in the NURBS space; hence, satisfying all the properties of NURBS, without the need for any additional post-processing. However, in the case of the first (non-isoparametric) variation, an additional transformation step as discussed in Theorem 1 is required for recovering the properties of NURBS.

4 Least-square surface approximation using NURBS versus GNURBS

In this section, we demonstrate that the proposed generalizations of NURBS are able to provide superior approximation for certain class of surfaces compared to classic NURBS. We assume here that a planar geometry with precise representation using NURBS, such as the annular ring in Fig. 8, is given as:

$${\mathbf{S}}_{xy} (\xi ,\eta ) = \left\{ \begin{gathered} x(\xi ,\eta ) \hfill \\ y(\xi ,\eta ) \hfill \\ \end{gathered} \right\},\,\,\,\,\,\begin{array}{*{20}c} {0 \le \xi \le 1} \\ {0 \le \eta \le 1} \\ \end{array}$$
(22)

Next, we assume that an analytical height function \(z(\xi ,\eta )\) is given and needs to be approximated with minimal error over the given planar surface. The problem can be posed as a least square approximation problem which leads to optimal accuracy in L2-norm. Considering \(\left\{ {\left( {\xi_{s} ,\eta_{s} } \right) \to \left( {x_{s} ,y_{s} ,z_{s} } \right):s \in {\mathcal{S}}} \right\}\) as a set of \(n_{c}\) chosen collocation points, the error function \(f\) to be minimized is defined as

$$f = \frac{1}{2}\sum\limits_{{s \in {\mathcal{S}\ominus }}} {\left\| {\hat{z}(\xi_{s} ,\eta_{s} ) - \overline{z}_{s} } \right\|^{2} } = \frac{1}{2}\sum\limits_{{s \in {\mathcal{S}\ominus }}} {\left\| {\sum\limits_{{L \in {\mathcal{L}}\,^{s} }} {R_{L} (\xi_{s} ,\eta_{s} )z_{L} - \overline{z}_{s} } } \right\|}^{2}$$
(23)

where \(\hat{z}(\xi ,\eta )\) is the approximated NURBS function, \(\mathcal{L}^{\,s}\) is the set of indices of non-zero basis functions at \(\left( {\xi_{s} ,\eta_{s} } \right)\), \(\overline{z}_{s} = z(\xi_{s} ,\eta_{s} )\), and \(z_{L}\) are the unknown control variables. For simplicity, the global index L is used for numbering which is defined as \(L = j(n_{1} + 1) + i + 1\) for the basis \((i,j)\). In the following, we provide the detailed formulation of this problem using NURBS as well as its different proposed generalizations.

4.1 Linear least-square approximation using NURBS

In the case of NURBS, the only unknowns to consider are control variables \(z_{L}\). Taking the partial derivatives of \(f\) with respect to the unknowns \(z_{L}\), and setting them to zero yields

$$\frac{\partial f}{{\partial z_{k} }} = 0,\quad k = 1,...,n_{T}$$
(24)
$$\sum\limits_{{s \in \mathcal{S}}} {\sum\limits_{{L \in \mathcal{L}\,^{s} }} {R_{k} (\xi_{s} ,\eta_{s} )} } R_{L} (\xi_{s} ,\eta_{s} )z_{L} = \sum\limits_{{s \in \mathcal{S}}} {\overline{z}_{s} } R_{k} (\xi_{s} ,\eta_{s} ),\quad k = 1,...,n_{T}$$
(25)

where \(n_{T} = \left( {n_{1} + 1} \right) \times \left( {n_{2} + 1} \right)\) denotes the total number of control points. Eq. (25) could be written in the matrix form

$$\sum\limits_{{s \in \mathcal{S}}} {\left( {\begin{array}{*{20}c} {R_{1} (\xi_{s} ,\eta_{s} )R_{1} (\xi_{s} ,\eta_{s} )} & \cdots & {R_{1} (\xi_{s} ,\eta_{s} )R_{{n_{T} }} (\xi_{s} ,\eta_{s} )} \\ \vdots & \ddots & \vdots \\ {R_{{n_{T} }} (\xi_{s} ,\eta_{s} )R_{1} (\xi_{s} ,\eta_{s} )} & \cdots & {R_{{n_{T} }} (\xi_{s} ,\eta_{s} )R_{{n_{T} }} (\xi_{s} ,\eta_{s} )} \\ \end{array} } \right)} \left( {\begin{array}{*{20}c} {z_{1} } \\ \vdots \\ {z_{{n_{T} }} } \\ \end{array} } \right) = \sum\limits_{{s \in \mathcal{S}}} {\overline{z}_{s} \,\left( {\begin{array}{*{20}c} {R_{1} (\xi_{s} ,\eta_{s} )} \\ \vdots \\ {R_{{n_{T} }} (\xi_{s} ,\eta_{s} )} \\ \end{array} } \right)}$$
(26)

which represents a classic linear least square problem and can be easily solved for the \(n_{T}\) unknowns \({{\varvec{\uplambda}}} = \left\{ {z_{1} ,...,z_{{n_{T} }} } \right\}\) by proper choice of collocation points.

4.2 Non-linear least-square approximation using non-isoparametric GNURBS

In order to improve the accuracy of the above discussed NURBS-based approximation, we develop a non-linear least-square minimization algorithm using 1st GNURBS. Invoking the non-isoparametric GNURBS surface with partial decoupling of the weights in Sect. 2.2, we can treat the out of plane weights \(w_{L}^{z}\) as extra design variables without perturbing the geometry or parameterization of the underlying precise planar surface \({\mathbf{S}}_{xy} (\xi ,\eta )\). We may refer to these variables as control weights hereafter.

The objective function to be minimized could still be written as (23). However, the vector of design variables now changes to \({\mathbf{\lambda^{\prime}}} = \left\{ {z_{1} ,...,z_{{n_{T} }} ,w_{1}^{z} ,...,w_{{n_{T} }}^{z} } \right\}\). Moreover, the following bounding constraints on control weights are often desired to be satisfied for numerical stability.

$$w_{k}^{z} > 0,\quad k = 1,...,n_{T}$$
(27)

Equation (23) with the new vector of design variables \({\mathbf{\lambda^{\prime}}}\) establishes a non-linear least-square optimization problem which could be solved using different existing algorithms. Some of these algorithms, such as Levenberg–Marquardt, do not allow for the imposition of bounding constraints on design variables. In this case, one can easily apply an exponential transformation to control weights to ensure their positivity without the imposition of bounding constraints as in [27]. We will use here the trust-region-reflective algorithm which is available in MATLAB and allows for the imposition of bounding constraints on design variables.

In order to solve the established problem, the Jacobian matrix is required. The Jacobian matrix \({\mathbf{J}}\) is composed of two parts

$${\mathbf{J}} = [{\mathbf{J}}_{z} \,\,{\mathbf{J}}_{w} ]\,$$
(28)

where \({\mathbf{J}}_{z}\) contains the partial derivatives of \(f\) with respect to \(z_{k}\), while \({\mathbf{J}}_{w}\) includes the partial derivatives of \(f\) with respect to \(w_{k}^{z}\). Differentiating with respect to \(z_{k}\), \({\mathbf{J}}_{z}\) will be easily derived as

$${\mathbf{J}}_{z} = \left[ {\begin{array}{*{20}c} {R_{1} (\xi_{1} ,\eta_{1} )} & {R_{2} (\xi_{1} ,\eta_{1} )} & \cdots & {R_{{n_{T} }} (\xi_{1} ,\eta_{1} )} \\ {R_{1} (\xi_{2} ,\eta_{2} )} & {R_{2} (\xi_{2} ,\eta_{2} )} & \cdots & {R_{{n_{T} }} (\xi_{2} ,\eta_{2} )} \\ \vdots & \vdots & \ddots & \vdots \\ {R_{1} (\xi_{{n_{c} }} ,\eta_{{n_{c} }} )} & {R_{2} (\xi_{{n_{c} }} ,\eta_{{n_{c} }} )} & \cdots & {R_{{n_{T} }} (\xi_{{n_{c} }} ,\eta_{{n_{c} }} )} \\ \end{array} } \right]$$
(29)

The other component of the Jacobian matrix can be obtained as

$$J_{w} = \left[ {\begin{array}{*{20}c} {\frac{{\partial \hat{z}\left( {\xi_{1} ,\eta_{1} } \right)}}{{\partial w_{1}^{z} }}} & \cdots & {\frac{{\partial \hat{z}\left( {\xi_{1} ,\eta_{1} } \right)}}{{\partial w_{{n_{T} }}^{z} }}} \\ \vdots & \ddots & \vdots \\ {\frac{{\partial \hat{z}\left( {\xi_{{n_{c} }} ,\eta_{{n_{c} }} } \right)}}{{\partial w_{1}^{z} }}} & \cdots & {\frac{{\partial \hat{z}\left( {\xi_{{n_{c} }} ,\eta_{{n_{c} }} } \right)}}{{\partial w_{{n_{T} }}^{z} }}} \\ \end{array} } \right]$$
(30)

In order to evaluate the partial derivatives with respect to weight design variables, we rewrite \(\hat{z}\left( {\xi ,\eta } \right)\) as

$$\hat{z}\left( {\xi ,\eta } \right) = \frac{{\mathcal{Z}(\xi ,\eta )}}{{\mathcal{W}(\xi ,\eta )}}$$
(31)

where \(\mathcal{Z}(\xi ,\eta )\) and \(\mathcal{W}(\xi ,\eta )\) are

$$\mathcal{Z}(\xi ,\eta ) = \mathop \sum \limits_{L = 1}^{{n_{T} }} N_{L} \left( {\xi ,\eta } \right)w_{L}^{z} z_{L}$$
(32)
$$\mathcal{W}(\xi ,\eta ) = \sum\limits_{L = 1}^{{n_{T} }} {N_{L} \left( {\xi ,\eta } \right)w_{L}^{z} }$$
(33)

Using these definitions, we can obtain

$$\frac{{\partial \hat{z}\left( {\xi ,\eta } \right)}}{{\partial w_{k}^{z} }} = \frac{{N_{k} (\xi ,\eta )}}{{{\mathcal{W}}(\xi ,\eta )}}\left[ {z_{k} - \hat{z}\left( {\xi ,\eta } \right)} \right],\quad \,k = 1,...,n_{T}$$
(34)

Having the analytical Jacobian matrix components in Eqs. (29) and (30), we can now solve the established non-linear least-square optimization problem efficiently. We impose the initial conditions by setting all the control variables to zero and all the control weights to 1, i.e.

$${\mathbf{\lambda^{\prime}}}_{0} = \left\{ {\underbrace {0,0,...,0}_{{n_{T} }},\underbrace {1,1,...,1}_{{n_{T} }}} \right\}$$
(35)

4.3 Non-linear least-square approximation using isoparametric GNURBS

Since the derivation of analytical Jacobian matrix with this generalization becomes complicated in case of having internal knots, we limit our derivation here to GR-Bézier. Invoking the isoparametric GR-Bézier representation in Eq. (17), we can again establish the approximation problem as a non-linear least square problem with the objective function defined in Eq. (23) but with the new set of design variables \({\mathbf{\lambda^{\prime\prime}}} = \left\{ {Z_{1} ,...,Z_{{n_{T} }} ,w_{1}^{z} ,...,w_{{n_{d} }}^{z} } \right\}\) where \(n_{d} = \left( {r + 1} \right) \times \left( {s + 1} \right)\) is the total number of isoparametric control weights, and \(n_{T} = \left( {\hat{p} + 1} \right) \times \left( {\hat{q} + 1} \right)\) is the total number of control points. The Jacobian matrix \({\mathbf{J}}\) can again be divided into two components where \({\mathbf{J}}_{z}\) contains the partial derivatives of \(f\) with respect to \(Z_{k}\), while \({\mathbf{J}}_{w}\) includes the partial derivatives of \(f\) with respect to \(w_{l}^{z}\). Differentiating with respect to \(Z_{k}\), \({\mathbf{J}}_{z}\) will be easily derived as

$${\mathbf{J}}_{z} = \left[ {\begin{array}{*{20}c} {\widehat{R}_{1} (\xi_{1} ,\eta_{1} )} & {\widehat{R}_{2} (\xi_{1} ,\eta_{1} )} & \cdots & {\widehat{R}_{{n_{T} }} (\xi_{1} ,\eta_{1} )} \\ {\widehat{R}_{1} (\xi_{2} ,\eta_{2} )} & {\widehat{R}_{2} (\xi_{2} ,\eta_{2} )} & \cdots & {\widehat{R}_{{n_{T} }} (\xi_{2} ,\eta_{2} )} \\ \vdots & \vdots & \ddots & \vdots \\ {\widehat{R}_{1} (\xi_{{n_{c} }} ,\eta_{{n_{c} }} )} & {\widehat{R}_{2} (\xi_{{n_{c} }} ,\eta_{{n_{c} }} )} & \cdots & {\widehat{R}_{{n_{T} }} (\xi_{{n_{c} }} ,\eta_{{n_{c} }} )} \\ \end{array} } \right]$$
(36)

Also, \({\mathbf{J}}_{w}\) can be obtained as

$${\mathbf{J}}_{w} = \left[ {\begin{array}{*{20}c} {\frac{{\partial \hat{z}\left( {\xi_{1} ,\eta_{1} } \right)}}{{\partial w_{1}^{z} }}} & \cdots & {\frac{{\partial \hat{z}\left( {\xi_{1} ,\eta_{1} } \right)}}{{\partial w_{{n_{d} }}^{z} }}} \\ \vdots & \ddots & \vdots \\ {\frac{{\partial \hat{z}\left( {\xi_{{n_{c} }} ,\eta_{{n_{c} }} } \right)}}{{\partial w_{1}^{z} }}} & \cdots & {\frac{{\partial \hat{z}\left( {\xi_{{n_{c} }} ,\eta_{{n_{c} }} } \right)}}{{\partial w_{{n_{d} }}^{z} }}} \\ \end{array} } \right]$$
(37)

In order to evaluate the partial derivatives of \(\hat{z}(\xi )\) with respect to isoparametric control weights \(w_{l}^{z}\), we rewrite \(\hat{z}\left( \xi \right)\) as

$$\hat{z}\left( \xi \right) = \frac{{\mathcal{Z}(\xi )}}{{\mathcal{W}(\xi )}}$$
(38)

where \(\mathcal{Z}(\xi )\) and \(\mathcal{W}(\xi )\) are

$$\mathcal{Z}(\xi ) = \mathop \sum \limits_{L = 1}^{{n_{T} }} B_{L} \left( {\xi ,\eta } \right)W_{L} \,Z_{L}$$
(39)
$$\mathcal{W}(\xi ) = \sum\limits_{L = 1}^{{n_{T} }} {B_{L} \left( {\xi ,\eta } \right)W_{L} }$$
(40)

With these definitions, we can obtain the required derivatives as

$$\frac{{\partial \hat{z}\left( {\xi ,\eta } \right)}}{{\partial w_{l}^{z} }} = \frac{1}{{\mathcal{W}\left( {\xi ,\eta } \right)}}\left[ {\frac{{\partial \mathcal{Z}\left( {\xi ,\eta } \right)}}{{\partial w_{l}^{z} }} - \hat{z}\left( {\xi ,\eta } \right)\frac{{\partial \mathcal{W}\left( {\xi ,\eta } \right)}}{{\partial w_{l}^{z} }}} \right],\quad l = 1,...,n_{d}$$
(41)

The derivatives in above equation can be evaluated using the following expressions

$$\frac{{\partial \mathcal{Z}(\xi ,\eta )}}{{\partial w_{l}^{z} }} = \sum\limits_{L = 1}^{{n_{T} }} {B_{L} (\xi ,\eta )\frac{{\partial W_{L} }}{{\partial w_{l}^{z} }}} \,Z_{L}$$
(42)
$$\frac{{\partial \mathcal{W}(\xi ,\eta )}}{{\partial w_{l}^{z} }} = \sum\limits_{L = 1}^{{n_{T} }} {B_{L} (\xi ,\eta )\frac{{\partial W_{L} }}{{\partial w_{l}^{z} }}}$$
(43)

where

$$\frac{{\partial W_{L} }}{{\partial w_{l}^{z} }} = \frac{{\partial W_{ij} }}{{\partial w_{mn}^{z} }} = \left\{ \begin{gathered} \lambda_{i,i - m}^{p,r} \,\lambda_{j,j - n}^{q,s} \,w_{i - m,j - n}^{xy} \,,\,\,\,\,\,\,\,\,\,if\,\,(i - p) \le m \le i\,\,\& \,\,(j - q) \le n \le j \hfill \\ 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,otherwise \hfill \\ \end{gathered} \right.$$
(44)

in which

\(\lambda_{i,i - m}^{p,r} = \frac{{\left( {\begin{array}{*{20}c} p \\ {i - m} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} r \\ m \\ \end{array} } \right)}}{{\left( {\begin{array}{*{20}c} {p + r} \\ i \\ \end{array} } \right)}}\), \(\lambda_{j,j - n}^{q,s} = \frac{{\left( {\begin{array}{*{20}c} q \\ {j - n} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} s \\ n \\ \end{array} } \right)}}{{\left( {\begin{array}{*{20}c} {q + s} \\ j \\ \end{array} } \right)}}\).

Similar to previous case, we specify the initial conditions as follows

$${\mathbf{\lambda^{\prime\prime}}}_{0} = \left\{ {\underbrace {0,0,...,0}_{{n_{T} }},\underbrace {1,1,...,1}_{{n_{d} }}} \right\}$$
(45)

As previously discussed, by changing \(w_{l}^{z}\) during the optimization process, the in-plane coordinates of control points also vary at each iteration. However, since the in-plane geometry and parameterization are always fixed, one may only re-evaluate and update these coordinates after the termination of the optimization process according to the obtained optimal set of isoparametric basis functions. It is important to note that this algorithm yields the combination of optimal weights and the corresponding arrangement of control points which result in the best approximation for a given in-plane parameterization. To our knowledge, no such investigation has been reported in the literature thus far.

5 Numerical examples

In this section, we present a few numerical examples of approximating various types of surfaces using the proposed generalizations of NURBS and compare the obtained results with those of classic NURBS. In all cases, the relative L2-norm of error is calculated using the following relation

$${\text{error}} = \frac{{\left( {\int_{\Omega } {\left( {\hat{z}(\xi ,\eta ) - z(\xi ,\eta )} \right)^{2} d\Omega } } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }}{{\int_{\Omega } {z(\xi ,\eta )d\Omega } }}$$
(46)

where all integrations are calculated using Gaussian quadrature.

5.1 Test case 1: helicoid modelling

As the first numerical example, we consider the approximation of a partial helical surface with the following equation:

$${\mathbf{S}}(\xi ,\eta ) = \left( {\left( {\eta + 1} \right)\cos (\xi ),\,\left( {\eta + 1} \right)\sin (\xi ),\,\xi } \right),\,\,\,\,\,\,\,\begin{array}{*{20}c} {0 \le \xi \le {\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}} \\ {0 \le \eta \le 1\,\,\,\,\,} \\ \end{array}$$
(47)

which is depicted in Fig. 11. As observed, the in-plane parameterization of this surface is a quarter annulus with the configuration already shown in Fig. 7. Since this is a geometric modelling problem where preserving the properties of NURBS are of interest, it is an ideal candidate for employing isoparametric GNURBS. Accordingly, following the procedure discussed above in Sect. 4.3, we try to approximate the given height function in Eq. (47) and compare the obtained results with classic NURBS. The obtained results for different degrees of basis functions are presented in Table 2.

Table 2 Error of approximating the height function of helical surface in Eq. (47) using R-Bézier versus isoparametric GR-Bézier in relative L2-norm
Full size table
Fig. 11
figure 11

The helical surface in Eq. (47)

Full size image

According to this table, by including larger numbers of control weights, better improvement of accuracy is achieved. This reveals superior approximation of rational functions especially when higher degrees of basis functions are employed, at the expense of increased computational time. It is clear that the proposed method offers a trade-off between the and computational cost. This trade-off depends on multiple factors including the employed degrees of basis functions, number of control points and control weights as well as the nature of the target height function, which need to be considered when the computational cost is of concern. According to this table, the increase in computational cost raises by including more control weights. However, it is important to notice that GNURBS always yields higher accuracy by making use of the same number of control points. The results, however, show no improvement in accuracy for the first level of degree elevation, i.e. \((r,s) = (1,1)\). This implies that the optimal values of control weights for this particular level of degree elevation are unity. In other words, classic order elevation results in optimal accuracy for the approximation of helical height function using this particular degree of basis functions.

5.2 Test case 2: Scherk minimal surface

As the second numerical experiment, we consider the construction of a minimal surface model referred to as Scherk minimal surface over a square domain. This example has been addressed by Pan et al. [33] using isogeometric analysis of minimal surfaces based on extended loop subdivision scheme. The equation of this minimal surface is given as

$${\mathbf{S}}(\xi ,\eta ) = \left( {\xi ,\,\eta ,\,\ln \left( {\frac{\cos (\eta )}{{\cos (\xi )}}} \right)} \right),\,\,\,\,\,\,\,\begin{array}{*{20}c} { - 1.5 \le \xi \le 1.5} \\ { - 1.5 \le \eta \le 1.5} \\ \end{array}$$
(48)

which is depicted in Fig. 12.

Fig. 12
figure 12

Scherk minimal surface

Full size image

As the figure shows, the surface features steep gradients near the boundaries. In this example, for simplicity, we use non-isoparametric GNURBS and compare its approximation properties with classic NURBS. The obtained results using various employed degrees of basis functions are shown in Table 3.

Table 3 Error of approximating the Scherk minimal surface in Eq. (48) using NURBS versus 1st GNURBS in relative L2-norm
Full size table

As observed, the accuracy of approximation using 1st GNURBS in all cases is better than that of classic NURBS. Further, the improvement in accuracy almost always increases when larger degrees of basis functions are used. According to Table 2, the only exception is in the bi-cubic case. This could be justified considering the fact that, besides the degree of basis functions, the number of control points and control weights, the accuracy of approximation also depends on additional factors such as the behavior of the height function, in particular. Further, as previously observed in Table 2, there was a similar exception for the previous test case when elevating the degree from (2, 1) to (3, 2). Finally, a similar trend in the computational times is observed when the number of employed control weights is increased.

Finally, for the case of quadratic basis functions, we also perform a convergence study where we persistently refine the knot sequence and compare the obtained accuracy of NURBS versus GNURBS. The obtained results are plotted in Fig. 13. As the figure shows, the convergence rate of GNURBS is more than one order faster than classic NURBS, resulting in substantial improvement of accuracy especially when larger numbers of control points are used.

Fig. 13
figure 13

Convergence rate of quadratic NURBS versus GNURBS for the approximation of Scherk minimal surface

Full size image

5.3 Test case 3: surface of revolution

As the final numerical study, we consider the problem of the approximation of a surface of revolution defined using Eq., which is depicted in Fig. 14.

$${\mathbf{S}}(\xi ,\eta ) = \left( {\left( {\eta + 1} \right)\cos (\xi ),\,\left( {\eta + 1} \right)\sin (\xi ),\,\mathop e\nolimits^{{\eta^{2} }} } \right),\,\,\,\,\,\,\,\begin{array}{*{20}c} {0 \le \xi \le 2\pi } \\ {0 \le \eta \le 1\,\,\,\,\,} \\ \end{array}$$
(49)
Fig. 14
figure 14

The surface of revolution in Eq. (49)

Full size image

As observed, the surface has an exponential behavior along the radial direction. In this example, we demonstrate how employing the second proposed variation of NURBS could be useful for improved approximation of these type of surfaces using the same number of control points. For simplicity, we only consider modelling a quarter of the surface, i.e. \((0 \le \xi \le {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4})\). Similar to the first numerical example, we start with the initial model of degree \((p,q) = (2,1)\) in Fig. 8. Since the height function here only varies along the radial direction, we only elevate the degree along this direction \((\eta )\) and compare the obtained approximation results using Bézier (classic order elevation) with those of isoparametric GR-Bézier (optimal order elevation). The obtained results for \((r,s) = (0,0)\) up to \((r,s) = (0,3)\) are presented in Table 4.

Table 4 Error of approximating the height function of the surface of revolution in Eq. (49) using R-Bézier versus isoparametric GR-Bézier in relative L2-norm
Full size table

According to this table, the accuracy of approximation by using isoparametric GR-Bézier is significantly higher than that of classic Bézier, especially when higher order elevations are applied. However, as can be seen, similar to previous test cases there is an exception in the case of \((r,s) = (0,2)\) which could be due to certain behavior of the assumed height function. These results clearly show the superiority of rational functions for the approximation of this class of surfaces.

Finally, the corresponding arrangements of control points for cases 3 to 8 are represented in Fig. 15. As observed, the arrangements of control points in all cases only differ along the radial direction. This was expected to be the case, since in this example, order elevation has only been performed along the radial direction.

Fig. 15
figure 15

The resulting control net for the approximation of the surface of revolution in Eq. (49): a Case 3, b Case 4, c Case 5, d Case 6, e Case 7, and f Case 8

Full size image

6 Extensions and further applications

While, in this paper, we limited our study to applying the proposed generalizations to NURBS, due to fundamental similarities between different variations of splines, similar generalizations seem plausible to other rational forms of splines such as T-spline surfaces, Tri-angular Bézier surfaces etc.

In addition to the discussed applications of GNURBS in CAGD, other applications of NURBS in this area can be found where employing the weights as additional design variables for better flexibility can be problematic or sometimes impossible. For instance, GNURBS may also help circumventing the difficulties of considering the weights as degrees of freedom in general surface fitting problems with arbitrary parameterization. As previously studied in [13, 29], employing the weights as additional degrees of freedom in data approximation can deteriorate the surface parameterization, and lead to undesirable results, especially when approximating rapidly varying data. On the other hand, employing GNURBS, by including the control weights as design variables, one can create a good surface parameterization and preserve it during fitting without imposing any restrictions on the magnitude of variations of the weights.

Furthermore, NURBS have been extensively used in other disciplines such as computational mechanics for the optimization of different fields of interest over a given computational domain. Considering these studies, we can find out that in this class of applications, the parameterization of the design domain needs to remain fixed throughout the optimization process; see [8, 34,35,36,37,38,39,40,41], for instance. Hence, they are only able to treat the out-of-plane coordinates of control points as design variables, as the variation of weights alters the underlying parameterization which is disallowed. However, owing to the proposed GNURBS representations with decoupled weights, one can now treat the control weights as additional design variables while setting up the optimization problem and still preserve the underlying geometry as well as its parameterization. As elaborated in this research, this can lead to significant improvement in the obtained accuracy in both cases of smooth as well as rapidly varying fields. Exploring some of these applications is the subject of our future studies.

7 MATLAB toolbox: GNURBS3D-Lab

In order to facilitate understanding the behavior of GNURBS surfaces and the additional abilities they serve, a comprehensive and fully interactive MATLAB toolbox, named GNURBS3D-Lab, has been developed. This toolbox is developed via the extension of GNURBS Lab, a similar interactive MATLAB toolbox already developed for GNURBS curves [2]. Snapshots of different available windows in GNURBS3D-Lab are shown in Fig. 16, which demonstrate the environment of the toolbox and numerous features that the software provides.

Fig. 16
figure 16

Snapshots of different windows of GNURBS3D-Lab: a Main window, b 3D surface plot window, c in-plane equivalent NURBS window, and d 3D equivalent NURBS window

Full size image

The figure shows an example of designing a 3D surface with an in-plane shape of a quarter annulus and a free-form out of plane shape using GR-Bézier. As demonstrated in Fig. 16, the toolbox is enabled to evaluate the equivalent higher-order rational Bézier representations with the designed surface in 2D and 3D interactively. Employing the provided wide range of tools shown in Fig. 16a, one can easily manipulate any defining parameter of the surface, including the locations of control points, or a variety of weight components, and observe the changes interactively in all four windows shown in Fig. 16, simultaneously.

The open-source toolbox is available at http://www.ersl.wisc.edu/software/GNURBS3D-Lab.zip. Detailed instructions for using this toolbox are also provided in an additional document GNURBS3D_Manual.pdf accessible via the same link.

8 Conclusion

We introduced two generalizations of NURBS surfaces, referred to as GNURBS, by decoupling of the weights associated with the control points along different physical coordinates. These generalizations were obtained via either explicit or implicit decoupling of the weights leading to non-isoparametric and isoparametric representations, respectively. As demonstrated, both these variations improve the flexibility of NURBS and circumvent its deficiencies by providing the possibility of treating the weights as additional design variables in special applications. It was proved that these representations are only variations of classic NURBS and do not constitute a new superset of NURBS. Superior approximation abilities of these variations for both smooth and rapidly varying functions were shown via simple examples in surface modelling. It was shown that GNURBS can be effectively used for improved construction of various types of surfaces such as helicoids, minimal surfaces as well as surfaces of revolution using the same number of control points. A comprehensive MATLAB toolbox, named GNURBS3D-Lab, was developed and introduced to better demonstrate the behavior of different types of GNURBS surfaces in a fully interactive manner. In summary, GNURBS were shown to serve as a new effective technology in surface modelling with superior accuracy while merely being disguised forms of classic NURBS.