A particle swarm optimization and coupled generalized differential quadrature element methods with genetic algorithm for stability analysis of the laminated microsystems

Abstract

In this paper, an attempt is made to extend a linear two-dimensional model for stability analysis of the laminated annular microplate subject to external excitation. A new approach called hybrid optimization is introduced to solve optimization problems with a high sensitive objective function to decline computational costs and increase the predicted optimum results accuracy. Regarding this issue, generalized differential quadrature element method (GDQEM), particle swarm optimization (PSO), as well as genetic algorithm (GA) methods are coupled to improve the dynamic stability of the annular microsystems via finding an optimum frequency and fiber angle of layers simultaneously. Higher-order shear deformation theory (HSDT) and Hamilton’s principle are taken into consideration for the exact derivation of the general linear governing equations and boundary conditions of the axisymmetric laminated annular plate. Also, modified couple stress theory (MCST) is presented for presenting the size-dependency of the current microsystem. The GDQEM is used to solve the governing equations of the microsystem via its boundary domains. To enhance the genetic algorithms’ performance for solving equations, the optimizer approach of particle swarm has been employed as a GA’s operator. Precise convergence and practicality of the suggested mixed-method have been disclosed. Moreover, we would have proven that for achieving the convergence PSO’s and GA’s outcomes, we have to apply higher than fifteen iterations.

1 Introduction

A broad range of engineering designers has been considerably considering laminated composites since decades ago, for instance, in mechanical and civil engineering. composites are mainly employed as the elements of heavy-load light-weight systems regarding their specific characteristics such as stiffness, high strength, and other functionalities. This kind of material can be used in various systems [1,2,3,4]. For this matter, researchers have been attending to consider laminated composites since a few decades ago. Multifarious structure types, including beams, plates, and shells, have been considered to be vibrationally analyzed by Mikhasev et al. [5]. They disclosed that shear's influence has a prominent contribution in the laminated structures’ free vibrations, and for exploring future researches, they have to be taken into consideration. Ref. [6] analyzed the frequency analysis of a laminated micro-sized beam employing the modified couple stress (MCS) approach. In that reported paper, impacts of physical/geometrically factors had been considered on the mentioned system’s stability. Their presented material can be used in many applications such as [7,8,9,10]. Sinha [11] reported the laminated plate’s frequency investigation applying numerical and empirical techniques. They, however, revealed that their achieved outcomes from the computational approach are in a decent agreement with those empirically conducted. spinning Conical FG-CNTRC shell’s vibrational behaviors have been analyzed by Ref. [12]. Then, the complicated equations have been solved employing the Kp-Ritz approach. The nonlinear vibration of a laminated plate has been scrutinized by Ref. [13]. They disclosed that for characterizing a laminated plate, number of layers and the ply directions have to be carefully considered, at the same time. It was illustrated that annular plates could be applied in a wide range of industrial and engineering practical applications [14]. The presented approach in the previous reference can be a good tool for the analysis of complex systems [15,16,17,18,19]. Employing nano-scaled reinforcements for enhancing the structures’ mechanical properties have been analyzed since decades ago [20,21,22,23,24,25,26,27,28]. In the dynamic area of the annular plate, Civalek et al. [29] applied a first-order-shear-deformation (FOSD) approach and a semi computational technique for analyzing the sector annular plate’s frequency has been investigated with assuming FG material. The mentioned solution procedure as a strong solver can be used in many systems such as [30,31,32,33]. Mohammadimehr et al. [34] reported a study on the dynamics and statics characteristics of a thin FG disk subject to primary pressure and lied in a viscoelastic condition. Their problem’s formulation has been extracted by a classical approach and GDQ technique has been used as an equation solver. Arshid et al. [35] studied the FG smart disk frequency response subjected to three types of physical loads through applying semi computational technique and thick model. They made a formulation regarding electro-magneto-elastic material for their study and assumed that the smart disk would be located in a thermal area. Their outcome discloses that by raising the field of the magnet, the system would be stiffer so it would be a reason for enhancing the system’s frequency. Also, this kind of analysis can be used in many systems [36,37,38,39]. Employing an FE analysis, Vinyas [40] reported research on the electro-magneto-elastic annular and circular FG plate’s dynamics through applying a higher-order-shear-deformation approach and there was an analysis regarding the influences of imperfection on the mode shape and the highest deflection. Due to new demand in technology composite structures can be used as the main materials in the future [41,42,43]. Safarpour et al. [44] made a formulation on the characterizing the GPLs filled an FG annular plate, cylindrical and conical shell employing a 3D-elasticity method for presenting dynamic and static behavior of the system. they selected the GDQ solver approach and they claimed that the GPLs’ geometric properties have a vital contribution to the structures’ frequency and bending behaviors. Also, owing to the new demand in technology [45,46,47,48], the previous solution procedure is a strong tool for solving various complex structures. Dai et al. [49] analyzed a dynamics of a spinning CNTs filled annular structure by taking into account the influences of hygro-thermal condition, natural imperfection in the material, and aggregation phenomenon. They selected the GDQ approach as a solver and they presented that moisture and spinning velocity would contribute significantly to the disk’s frequency. The used method of the previous reference can be a good tool for solving complex problems such as [50,51,52,53,54]. Eshraghi and Dag [55] employed the boundary element approach as a practical technique for analyzing the FG disk’s forced vibration. Khouzestani and Khorshidvand [56] scrutinized the frequency and bending of the axisymmetric imperfected disk by using the basic shear deformation method and variational approach. Their outcomes disclosed that as the imperfection raises, the stress field and frequency would be reduced. Javani et al. [57] studied thermal buckling investigation of a sector GPLs filled FG disk by applying a first-order model and a semi computational approach. Moreover, they used configurational nonlinearity employing von Kármán theory. As they revealed, GPLs would boost the critical temperature and buckling load of the imperfect disk. Heshmati et al. [58] extracted the equations of a sandwich disk considering imperfections as porosities in its material and analyzed the natural frequencies by applying the FOSD model and Chebyshev theory. They finally asserted that porosity’s density in the sandwich disk’s core would indirectly affect the structure’s frequency. Since nano science has been developed in multifarious industries. Specifically, in the area of NEMS and MEMS, size effect consideration to estimate the thermomechanical characteristics of the nano-scaled structures has become a vital issue [59,60,61,62,63,64,65,66,67,68,69]. Due to the aforementioned fact, Bidgoli et al. [70] by applying nonlocal modified strain gradient analyzed the vibration characteristics of a micro-scaled plate which is supposed that the material of the system is FG. They, however, revealed that their formulated relation has been solved through applying an analytical approach. The presented approach in the previous reference can be a good tool for the analysis of complex systems [71,72,73,74]. Mahinzare et al. [75] presented a complete study on the electrically FG disk’s dynamics in a thermal condition through using the FOSD model and nonlocal-strain-gradient approach. Moreover, they revealed the influences of the nonlocal-strain-gradient model and Eringen on the smart structure’s frequency. they selected the GDQ approach as a solver for illustrating their outcomes. This kind of analysis can be used in many structures and systems such as [76,77,78,79,80]. Arshid et al. [81] applied modified-strain-gradient, and FOSD models for analyzing stability and frequency behavior of a GPLs filled annular micro-scaled system. Their extended equations were finally solved through using the GDQ technique and they demonstrated that the viscoelastic substrate and thermal condition would be able to considerably affect the mechanics of the small-sized disk. Pal and Das [82] formulated the boundary conditions and motion equations of a spinning annular FG micro-scaled system by employing modified couple stress, Kirchhoff models, and variational methods. They assumed that the system lies in a thermal condition and they reported the disk’s shape mode in multifarious conditions. Employing Kirchhoff and nonlocal-strain-gradient models, Huang et al. [83] scrutinized the dynamic characteristics of an annular electrical micro-scaled system. They presented the influences of strain gradient on the vibration and bending behavior by extracting the equations with the lowest potential energy technique. Alinaghizadeh and Shariati [84] investigated nonlinear micro-sized sector plate’s mechanics by applying MCST. They combined that the system with a viscoelastic substrate and the strain–stress equations have been extracted by employing the classical approach. They disclosed that size dependency and nonlinearity would have the most considerable influences on the annular plate’s bending. The presented approach in the previous reference can be a good tool for the analysis of medical problems [85,86,87,88,89,90]. Mohammadimehr et al. [91] presented a complete analysis on the electro-mechanical annular sandwich micro-sized structure’s buckling in which CNTs have been employed as fillers. They assumed the size dependency applying the modified-strain-gradient model and achieved the BCs and governing equations through employing lowest energy approach. They revealed that the nonlocal and electric potential impacts would contribute significantly to the smart disk’s stability prediction. Alipour et al. [92] analyzed one of their study for studying the nano/micro annular sandwich system’s statics applying a new nonlocal technique called the zigzag approach. the annular isotropic rotary micro-sized system’s motion equation through multifarious continuum models has been presented by Bagheri et al. [93]. They disclosed that the crucial angular velocity raises with each raise in the nonlocal factor. Recently, using various methods for solving the dynamics of various structures has got a lot of attention among the researchers [94, 95]. Regarding this issue, stability analysis of various structures is investigated by many researchers [96,97,98,99,100,101,102,103]. According to the aforementioned literature review, definitely there is no published paper amongst researchers’ publications for analyzing the dynamic stability of the annular micro systems via finding optimum frequency, and fiber angle of layers via GDQE, PSO, and GA methods. Thus, in the presented scrutinization, frequency characteristics of an annular micro-scaled plate are analyzed by detail. For this matter, PSO, FSE, and GA approaches are combined for studying the frequency of an annular microplate via finding optimum frequency value. The HOSD model has been employed to make the formulation of the stress–strain equations. By applying the variational approach, the structure’s governing equations are extracted. Then, to analyze the impacts of configurational elements of the laminated system and mechanics influence on the annular plate’s frequency, aparametric study is conducted.

2 Mathematical modeling

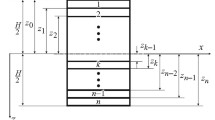
A laminated annular system is shown in Fig. 1. The inner, and outer radius of the microsystem is shown with R_i and R_o, respectively. Also, $\stackrel{-}{\theta }$ is fiber angle of the laminated material.

Fig. 1

A schematic view of laminated annular microsystem

In the current research, the displacement fields can be given as follows [104]

$$ \alpha ^{\eta } = \alpha _{0}^{\eta } + z\chi _{R}^{\eta } - C_{1} z^{3} \left( {\chi _{R}^{\eta } + \partial _{R} \left( {\gamma _{0}^{\eta } } \right)} \right) $$

(1)

$$ \beta ^{\eta } = \beta _{0}^{\eta } + z\chi _{\theta }^{\eta } - C_{1} z^{3} \left( {\chi _{\theta }^{\eta } + R^{{ - 1}} \partial _{\theta } \left( {\gamma _{0}^{\eta } } \right)} \right) $$

$$ \gamma ^{\eta } = \gamma _{0}^{\eta } $$

According to the HSDT, C₁ is 4/3h². The stress–strain relations for the laminated system are as below:

$$ \left\{ \begin{gathered} \begin{array}{*{20}c} {\sigma _{{RR}}^{{}} } \\ {\sigma _{{\theta \theta }}^{{}} } \\ \begin{gathered} \tau _{{R\theta }}^{{}} \hfill \\ \tau _{{Rz}}^{{}} \hfill \\ \end{gathered} \\ \end{array} \hfill \\ \tau _{{\theta z}}^{{}} \hfill \\ \end{gathered} \right\} = \left[ {\begin{array}{*{20}c} {\hat{\bar{Q}}_{{11}} } & {\hat{\bar{Q}}_{{12}} } & 0 & 0 & {\hat{\bar{Q}}_{{16}} } \\ {\hat{\bar{Q}}_{{21}} } & {\hat{\bar{Q}}_{{22}} } & 0 & 0 & {\hat{\bar{Q}}_{{26}} } \\ 0 & 0 & {\hat{\bar{Q}}_{{44}} } & {\hat{\bar{Q}}_{{45}} } & 0 \\ 0 & 0 & {\hat{\bar{Q}}_{{45}} } & {\hat{\bar{Q}}_{{55}} } & 0 \\ {\hat{\bar{Q}}_{{16}} } & {\hat{\bar{Q}}_{{26}} } & 0 & 0 & {\hat{\bar{Q}}_{{66}} } \\ \end{array} } \right]\left\{ \begin{gathered} \begin{array}{*{20}c} {\varepsilon _{{RR}}^{{}} } \\ {\varepsilon _{{\theta \theta }}^{{}} } \\ \begin{gathered} \gamma _{{R\theta }}^{{}} \hfill \\ \gamma _{{Rz}}^{{}} \hfill \\ \end{gathered} \\ \end{array} \hfill \\ \gamma _{{\theta z}}^{{}} \hfill \\ \end{gathered} \right\} $$

(2)

here the factors of the ${}_{ij}$ matrix, pertained to the orthotropic material associated to Lth lamina, would be explained as:

$$ \hat{\bar{Q}}^{{}} _{{11}} = \cos ^{4} \bar{\theta }\tilde{Q}^{{}} _{{11}} + 2\sin ^{2} \bar{\theta }\cos ^{2} \bar{\theta }\,\left( {\tilde{Q}^{{}} _{{12}} + 2\tilde{Q}^{{}} _{{66}} } \right) + \sin ^{4} \bar{\theta }\tilde{Q}^{{}} _{{22}} $$

(3a)

$$ \hat{\bar{Q}}^{{}} _{{12}} = \sin ^{2} \bar{\theta }\cos ^{2} \bar{\theta }\left( {\tilde{Q}^{{}} _{{11}} + \tilde{Q}^{{}} _{{22}} - 4\tilde{Q}^{{}} _{{66}} } \right)\, + \left( {\sin ^{4} \bar{\theta } + \cos ^{4} \bar{\theta }} \right)\tilde{Q}^{{}} _{{12}} $$

(3b)

$$ \hat{\bar{Q}}^{{}} _{{16}} = \cos ^{3} \bar{\theta }\sin \bar{\theta }\left( {2\tilde{Q}^{{}} _{{11}} - 2\tilde{Q}^{{}} _{{12}} - \tilde{Q}^{{}} _{{66}} } \right) + \cos \bar{\theta }\sin ^{3} \bar{\theta }\left( {\tilde{Q}^{{}} _{{66}} + 2\tilde{Q}^{{}} _{{12}} - 2\tilde{Q}^{{}} _{{22}} } \right) $$

(3c)

$$ \hat{\bar{Q}}^{{}} _{{22}} = \sin ^{4} \bar{\theta }\tilde{Q}^{{}} _{{11}} + 2\sin ^{2} \bar{\theta }\cos ^{2} \bar{\theta }\tilde{Q}^{{}} _{{12}} + \cos ^{4} \bar{\theta }\tilde{Q}^{{}} _{{22}} + 2\sin ^{2} \bar{\theta }\cos ^{2} \bar{\theta }\left( {\tilde{Q}^{{}} _{{12}} + 2\tilde{Q}^{{}} _{{66}} } \right) $$

(3d)

$$ \hat{\bar{Q}}^{{}} _{{26}} = \cos ^{3} \bar{\theta }\sin \bar{\theta }\,\left( {2\tilde{Q}^{{}} _{{12}} - 2\tilde{Q}^{{}} _{{22}} + \tilde{Q}^{{}} _{{66}} } \right) + \cos \bar{\theta }\sin ^{3} \bar{\theta }\left( {2\tilde{Q}^{{}} _{{11}} - 2\tilde{Q}^{{}} _{{12}} - \tilde{Q}^{{}} _{{66}} } \right) $$

(3e)

$$ \hat{\bar{Q}}^{{}} _{{44}} = \cos ^{2} \bar{\theta }\tilde{Q}^{{}} _{{44}} + \sin ^{2} \bar{\theta }\tilde{Q}^{{}} _{{55}} $$

(3f)

$$ \hat{\bar{Q}}^{{}} _{{45}} = \cos \bar{\theta }\sin \bar{\theta }\left( {\tilde{Q}^{{}} _{{55}} - \tilde{Q}^{{}} _{{44}} } \right) $$

(3g)

$$ \hat{\bar{Q}}^{{}} _{{55}} = \cos ^{2} \bar{\theta }\tilde{Q}^{{}} _{{55}} + \sin ^{2} \bar{\theta }\tilde{Q}^{{}} _{{44}} $$

(3h)

$$ \hat{\bar{Q}}^{{}} _{{66}} = \tilde{Q}^{{}} _{{66}} \left( {\cos ^{2} \bar{\theta } - \sin ^{2} \bar{\theta }} \right)^{2} \, + 4\sin ^{2} \bar{\theta }\cos ^{2} \bar{\theta }\left( {\tilde{Q}^{{}} _{{11}} + \tilde{Q}^{{}} _{{22}} - 2\tilde{Q}^{{}} _{{12}} } \right) $$

(3i)

As it is already mentioned, the equations written by Eq. (3) would be stress–strain constitutive equations for the Lth orthotropic lamina, which could be referred to as material in x,$y$, and z directions. In Eq. (3), $\stackrel{-}{\theta }$ would be fiber orientation angle and ${Q}_{ij}$ would be written as [105, 106]:

$$ \begin{gathered} \tilde{Q}_{{11}} = \frac{{E_{1} }}{{1 - \nu _{{12}} \nu _{{21}} }},\begin{array}{*{20}c} {} & {} \\ \end{array} \tilde{Q}_{{12}} = \frac{{\nu _{{12}} E_{2} }}{{1 - \nu _{{12}} \nu _{{21}} }},\begin{array}{*{20}c} {} & {} \\ \end{array} \tilde{Q}_{{22}} = \frac{{E_{2} }}{{1 - \nu _{{12}} \nu _{{21}} }} \hfill \\ \tilde{Q}_{{66}} = G_{{12}} ,\begin{array}{*{20}c} {} & {} \\ \end{array} \,\,\,\,\,\,\,\,\,\,\,\,\,\tilde{Q}_{{44}} = G_{{23}} ,\begin{array}{*{20}c} {} & {} \\ \end{array} \,\,\,\,\,\,\,\,\,\,\,\,\,\tilde{Q}_{{55}} = G_{{13}} \hfill \\ \end{gathered} $$

(4)

So, the strain components of the laminated layers can be given by:

$$ \varepsilon _{{RR}}^{c} = \partial _{R} \alpha _{0}^{c} + z\partial _{R} \chi _{R}^{c} - C_{1} z^{3} \left( {\partial _{R} \chi _{R}^{c} + \partial _{R}^{2} \gamma _{0}^{c} } \right) $$

(5a)

$$ \begin{gathered} \varepsilon _{{\theta \theta }}^{c} = R^{{ - 1}} \alpha _{0}^{c} + R^{{ - 1}} \partial _{\theta } \beta _{0}^{c} + zR^{{ - 1}} \left( {\chi _{R}^{c} + \partial _{\theta } \chi _{\theta }^{c} } \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\, - C_{1} z^{3} R^{{ - 1}} \left( {\left( {\chi _{R}^{c} + \partial _{R} \gamma _{0}^{c} } \right) + \left( {\partial _{\theta } \chi _{\theta }^{c} + R^{{ - 1}} \partial _{\theta }^{2} \gamma _{0}^{c} } \right)} \right) \hfill \\ \end{gathered} $$

(5b)

$$ \begin{gathered} \gamma _{{R\theta }}^{c} = R^{{ - 1}} \partial _{\theta } \alpha _{0}^{c} + \partial _{R} \beta _{0}^{c} - R^{{ - 1}} \beta _{0}^{c} + z\left( {R^{{ - 1}} \partial _{\theta } \chi _{R}^{c} + \partial _{R} \chi _{\theta }^{c} - R^{{ - 1}} \chi _{\theta }^{c} } \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\, - z^{3} C_{1} \left( {R^{{ - 1}} \left( {\partial _{\theta } \chi _{R}^{c} + \partial _{{R\theta }}^{2} \gamma _{0}^{c} } \right) + \left( {\partial _{R} \chi _{\theta }^{c} + R^{{ - 1}} \partial _{{R\theta }}^{2} \gamma _{0}^{c} } \right) - R^{{ - 1}} \left( {\chi _{\theta }^{c} + R^{{ - 1}} \partial _{\theta } \gamma _{0}^{c} } \right)} \right) \hfill \\ \end{gathered} $$

(5c)

$$ \gamma _{{Rz}}^{c} = \chi _{R}^{c} + \partial _{R} \gamma _{0}^{c} - 3C_{1} z^{2} \left( {\chi _{R}^{c} + \partial _{R} \gamma _{0}^{c} } \right) $$

(5d)

$$ \gamma _{{\theta z}}^{c} = \chi _{\theta }^{c} + R^{{ - 1}} \partial _{\theta } \gamma _{0}^{c} - 3C_{1} z^{2} \left( {\chi _{\theta }^{c} + R^{{ - 1}} \partial _{\theta } \gamma _{0}^{c} } \right) $$

(5e)

2.1 Hamilton’s principle

For obtaining the nonlinear governing equations and general boundary equations of the system, we used Hamilton’s principle as follows [107, 108]:

$$ \int_{{t_{1} }}^{{t_{2} }} {\left( {\delta T - \delta U + \delta V_{1} + \delta V_{2} + \delta V_{3} } \right)^{\eta } dt = 0} $$

(6)

The strain formulations of the current system can be given as below [109,110,111,112]:

$$ \begin{gathered} \delta U^{c} = \int\limits_{V} {\sigma _{{ij}}^{c} } \delta \varepsilon _{{ij}}^{c} dV = \hfill \\ \int\limits_{{R_{1} }}^{{R_{2} }} {\int\limits_{0}^{\theta } {\left( \begin{gathered} \left\{ {\partial _{R} N_{{RR}} + R^{{ - 1}} \partial _{\theta } N_{{R\theta }} - R^{{ - 1}} N_{{\theta \theta }} } \right\}\delta \alpha _{0} + \left\{ {R^{{ - 1}} \partial _{\theta } N_{{\theta \theta }} + \partial _{\theta } N_{{R\theta }} + R^{{ - 1}} N_{{R\theta }} } \right\}\delta \beta _{0} \hfill \\ \left\{ \begin{gathered} C_{1} \partial _{R}^{2} P_{{RR}} - R^{{ - 1}} C_{1} \partial _{R} P_{{\theta \theta }} + R^{{ - 2}} C_{1} \partial _{\theta }^{2} P_{{\theta \theta }} + 2C_{1} R^{{ - 1}} \partial _{{R\theta }}^{2} P_{{R\theta }} \hfill \\ + C_{1} R^{{ - 2}} \partial _{\theta } P_{{R\theta }} + \partial _{R} S_{{RZ}} - 3C_{1} \partial _{R} Q_{{RZ}} + R^{{ - 1}} \partial _{\theta } S_{{\theta Z}} - 3C_{1} R^{{ - 1}} \partial _{\theta } Q_{{\theta Z}} \hfill \\ \end{gathered} \right\}\delta \gamma _{0} \hfill \\ + \left\{ \begin{gathered} \partial _{R} M_{{RR}} - C_{1} \partial _{R} P_{{RR}} - R^{{ - 1}} M_{{\theta \theta }} + C_{1} R^{{ - 1}} P_{{\theta \theta }} \hfill \\ + R^{{ - 1}} \partial _{\theta } M_{{R\theta }} - C_{1} R^{{ - 1}} \partial _{\theta } P_{{R\theta }} - \left( {S_{{RZ}} + 3c_{1} Q_{{RZ}} } \right) \hfill \\ \end{gathered} \right\}\delta \chi _{R} \hfill \\ + \left\{ \begin{gathered} R^{{ - 1}} \partial _{\theta } M_{{\theta \theta }} - R^{{ - 1}} C_{1} \partial _{\theta } P_{{\theta \theta }} + \partial _{R} M_{{R\theta }} - C_{1} \partial _{R} P_{{R\theta }} \hfill \\ + R^{{ - 1}} M_{{R\theta }} - R^{{ - 1}} C_{1} P_{{R\theta }} + R^{{ - 1}} M_{{R\theta }} - R^{{ - 1}} C_{1} \partial _{\theta } P_{{R\theta }} - S_{{\theta Z}} + 3c_{1} Q_{{\theta Z}} \hfill \\ \end{gathered} \right\}\delta \chi _{\theta } \hfill \\ \end{gathered} \right)RdRd\theta } } \hfill \\ \end{gathered} $$

(7)

where:

$$ \left\{ {N_{{RR}} ,M_{{RR}} ,P_{{RR}} } \right\} = \int_{z} {\sigma _{{RR}}^{{}} \left\{ {1,z,z^{3} } \right\}} dz $$

(8a)

$$ \left\{ {N_{{\theta \theta }} ,M_{{\theta \theta }} ,P_{{\theta \theta }} } \right\} = \int_{z} {\sigma _{{\theta \theta }}^{{}} \left\{ {1,z,z^{3} } \right\}} dz $$

(8b)

$$ \left\{ {N_{{R\theta }} ,M_{{R\theta }} ,P_{{R\theta }} } \right\} = \int_{z} {\sigma _{{R\theta }}^{{}} \left\{ {1,z,z^{3} } \right\}} dz $$

(8c)

$$ \left\{ {Q_{{RZ}} ,S_{{RZ}} } \right\} = \int_{z} {\sigma _{{RZ}}^{{}} \left\{ {z^{2} ,1} \right\}} dz $$

(8d)

$$ \left\{ {Q_{{\theta Z}} ,S_{{\theta Z}} } \right\} = \int_{z} {\sigma _{{\theta Z}}^{{}} \left\{ {z^{2} ,1} \right\}} dz $$

(8e)

The variation of the work done can be given as below:

$$ \delta V_{2}^{\eta } = \int\limits_{A} {q_{{dynamic}} } \delta w^{\eta } dA $$

(9)

where q can be given as below:

$$ q_{{dynamic}} = F \times \cos \left( {\Omega \,t} \right) $$

(10)

The kinetic energy’s first variation would be given as:

$$ T = \frac{1}{2}\int\limits_{V} {\rho \left[ {\left( {\partial _{t} \alpha } \right)^{2} + \left( {\partial _{t} \beta } \right)^{2} + \left( {\partial _{t} \gamma } \right)^{2} } \right]dV} $$

(11)

$$ \delta T = \int\limits_{{R_{1} }}^{{R_{2} }} {\int\limits_{0}^{\theta } {\left[ \begin{gathered} \left\{ { - I_{0} \partial _{t}^{2} \alpha _{0} - I_{1} \partial _{t}^{2} \chi _{R} + I_{3} c_{1} \left( {\partial _{t}^{2} \chi _{R} + \partial _{{Rtt}}^{3} \gamma _{0} } \right)} \right\}\delta \alpha _{0} \hfill \\ + \left\{ { - I_{1} \partial _{t}^{2} \beta _{0} - I_{2} \partial _{t}^{2} \chi _{\theta } + I_{3} c_{1} \left( {\partial _{t}^{2} \chi _{\theta } + R^{{ - 1}} \partial _{{\theta tt}}^{3} \gamma _{0} } \right)} \right\}\delta \beta _{0} \hfill \\ + \left\{ { - c_{1} I_{3} \partial _{{Rtt}}^{3} \alpha _{0} - c_{1} I_{4} \partial _{{Rtt}}^{3} \chi _{R} + I_{6} c_{1}^{2} \left( {\partial _{{Rtt}}^{3} \chi _{R} + \partial _{{RRtt}}^{4} \gamma _{0} } \right)} \right\}\delta \gamma _{0} \hfill \\ + \left\{ \begin{gathered} - C_{1} I_{3} R^{{ - 1}} \partial _{{\theta tt}}^{3} \beta _{0} - C_{1} I_{4} R^{{ - 1}} \partial _{{\theta tt}}^{3} \chi _{\theta } \hfill \\ + I_{6} c_{1}^{2} R^{{ - 1}} \left( {\partial _{{\theta tt}}^{3} \chi _{\theta } + R^{{ - 1}} \partial _{{\theta \theta tt}}^{4} \gamma _{0} } \right) \hfill \\ \end{gathered} \right\}\delta \gamma _{0} + \left\{ { - I_{0} \partial _{t}^{2} \gamma _{0} } \right\}\delta \gamma _{0} \hfill \\ + \left\{ {c_{1} I_{3} \partial _{t}^{2} \alpha _{0} + c_{1} I_{4} \partial _{t}^{2} \chi _{R} - I_{6} c_{1}^{2} \left( {\partial _{t}^{2} \chi _{R} + \partial _{{Rtt}}^{3} \gamma _{0} } \right)} \right\}\delta \chi _{R} \hfill \\ + \left\{ { - I_{1} \partial _{t}^{2} \alpha _{0} - I_{2} \partial _{t}^{2} \chi _{R} + I_{4} c_{1} \left( {\partial _{t}^{2} \chi _{R} + \partial _{{Rtt}}^{3} \gamma _{0} } \right)} \right\}\delta \chi _{R} \hfill \\ + \left\{ { - I_{1} \partial _{t}^{2} \beta _{0} - I_{2} \partial _{t}^{2} \chi _{\theta } + I_{4} c_{1} \left( {\partial _{t}^{2} \chi _{\theta } + R^{{ - 1}} \partial _{{\theta tt}}^{3} \gamma _{0} } \right)} \right\}\delta \chi _{\theta } \hfill \\ + \left\{ {c_{1} I_{3} \partial _{t}^{2} \beta _{0} + c_{1} I_{4} \partial _{t}^{2} \chi _{\theta } - I_{6} c_{1}^{2} \left( {\partial _{t}^{2} \chi _{\theta } + R^{{ - 1}} \partial _{{\theta tt}}^{3} \gamma _{0} } \right)} \right\}\delta \chi _{\theta } \hfill \\ \end{gathered} \right]^{C} RdRd\theta } } $$

(12)

where $\left\{ {I_{i} } \right\} = \int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left\{ {z^{k} } \right\} \times \rho ^{{NCM}} \times dz} ,\,\,\,k = 1:6$. Now by replacing Eqs. (12), (10), (9), and (7) into Eq. (6) the motion equations of the current system can be given as follows:

$$ \delta \alpha _{0}^{{}} :\partial _{R} N_{{RR}}^{{}} + R^{{ - 1}} \partial _{\theta } N_{{R\theta }}^{{}} - R^{{ - 1}} N_{{\theta \theta }}^{{}} = I_{0} \partial _{t}^{2} \alpha _{0}^{{}} + I_{1} \partial _{t}^{2} \chi _{R}^{{}} - I_{3} c_{1} \left( {\partial _{t}^{2} \phi _{R} + \partial _{{Rtt}}^{3} \gamma _{0} } \right) $$

(13a)

$$ \delta \beta _{0}^{{}} :R^{{ - 1}} \partial _{\theta } N_{{\theta \theta }}^{{}} + \partial _{\theta } N_{{R\theta }}^{{}} + R^{{ - 1}} N_{{R\theta }}^{{}} = I_{1} \partial _{t}^{2} \beta _{0}^{{}} + I_{2} \partial _{t}^{2} \chi _{\theta }^{{}} - I_{3} c_{1} \left( {\partial _{t}^{2} \phi _{\theta } + R^{{ - 1}} \partial _{{\theta t}}^{2} \gamma _{0} } \right) $$

(13b)

$$ \begin{gathered} \delta \gamma _{0}^{{}} :C_{1} \partial _{R}^{2} P_{{RR}}^{{}} - C_{1} R^{{ - 1}} \partial _{R} P_{{\theta \theta }}^{{}} + C_{1} R^{{ - 2}} \partial _{\theta }^{2} P_{{\theta \theta }}^{\eta } \hfill \\ \,\,\,\,\,\,\,\,\,\,\, + 2C_{1} R^{{ - 1}} \partial _{{R\theta }}^{2} P_{{R\theta }}^{{}} + C_{1} R^{{ - 2}} \partial _{\theta } P_{{R\theta }}^{{}} \, \hfill \\ \,\,\,\,\,\,\,\,\,\, + \partial _{R} S_{{RZ}}^{{}} - 3C_{1} \partial _{R} Q_{{RZ}}^{{}} + R^{{ - 1}} \partial _{\theta } S_{{\theta Z}}^{{}} - 3C_{1} R^{{ - 1}} \partial _{\theta } Q_{{\theta Z}}^{{}} - q^{{}} \hfill \\ \,\,\,\,\,\,\,\,\,\, = \,c_{1} I_{3} \partial _{{Rtt}}^{3} \alpha _{0} ^{{}} + c_{1} I_{4} \partial _{{Rtt}}^{3} \chi _{R}^{{}} - I_{6} C_{1}^{2} \left( {\partial _{{Rtt}}^{3} \chi _{R} + \partial _{{RRtt}}^{4} \gamma _{0} } \right)\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\, + C_{1} I_{3} R^{{ - 1}} \partial _{{\theta tt}}^{3} \beta _{0} + C_{1} I_{4} R^{{ - 1}} \partial _{{\theta tt}}^{3} \chi _{\theta }^{{}} \,\, \hfill \\ \,\,\,\,\,\,\,\,\,\, - I_{6} C_{1}^{2} R^{{ - 1}} \left( {\partial _{{\theta tt}}^{3} \chi _{\theta } + R^{{ - 1}} \partial _{{\theta \theta tt}}^{4} \gamma _{0} } \right) + I_{0} \partial _{t}^{2} \gamma _{0} \hfill \\ \end{gathered} $$

(13c)

$$ \begin{gathered} \delta \chi _{R}^{{}} :\partial _{R} M_{{RR}}^{{}} - C_{1} \partial _{R} P_{{RR}}^{{}} - R^{{ - 1}} M_{{\theta \theta }}^{{}} + C_{1} R^{{ - 1}} P_{{\theta \theta }}^{{}} + R^{{ - 1}} \partial _{\theta } M_{{R\theta }}^{{}} - R^{{ - 1}} C_{1} \partial _{\theta } P_{{R\theta }}^{{}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\, - \left( {S_{{RZ}} + 3c_{1} Q_{{RZ}} } \right) = - c_{1} I_{3} \partial _{t}^{2} \alpha _{0} - c_{1} I_{4} \partial _{t}^{2} \chi _{R}^{{}} + I_{6} c_{1}^{2} \left( {\partial _{t}^{2} \chi _{R} + \partial _{{Rtt}}^{3} \gamma _{0} } \right) \hfill \\ \,\,\,\,\,\,\,\,\, + I_{1} \partial _{t}^{2} \alpha _{0} + I_{2} \partial _{t}^{2} \chi _{R}^{{}} - I_{4} c_{1} \left( {\partial _{t}^{2} \chi _{R} + \partial _{{Rtt}}^{2} \gamma _{0} } \right) \hfill \\ \end{gathered} $$

(13d)

$$ \begin{gathered} \delta \chi _{\theta }^{{}} :R^{{ - 1}} \partial _{\theta } M_{{\theta \theta }}^{{}} - C_{1} R^{{ - 1}} \partial _{\theta } P_{{\theta \theta }}^{{}} + \partial _{R} M_{{R\theta }}^{{}} - C_{1} \partial _{R} P_{{R\theta }}^{{}} + R^{{ - 1}} M_{{R\theta }}^{{}} - C_{1} R^{{ - 1}} P_{{R\theta }}^{{}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\, + R^{{ - 1}} M_{{R\theta }}^{{}} - C_{1} R^{{ - 1}} \partial _{\theta } P_{{R\theta }}^{{}} - S_{{\theta Z}}^{{}} + 3c_{1} Q_{{\theta Z}}^{{}} = I_{1} \partial _{t}^{2} \beta _{0} + I_{2} \partial _{t}^{2} \chi _{\theta }^{{}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\, - I_{4} c_{1} \left( {\partial _{t}^{2} \chi _{\theta } + R^{{ - 1}} \partial _{{\theta tt}}^{2} \gamma _{0} } \right) - c_{1} I_{3} \partial _{t}^{2} \beta _{0} - c_{1} I_{4} \partial _{t}^{2} \chi _{\theta }^{{}} + I_{6} c_{1}^{2} \left( {\partial _{t}^{2} \chi _{\theta } + R^{{ - 1}} \partial _{{\theta tt}}^{2} \gamma _{0} } \right) \hfill \\ \end{gathered} $$

(13e)

For general boundary conditions have:

$$ \delta \alpha _{0} = 0{\text{ or N}}_{{RR}}^{{}} \hat{n}_{R} + R^{{ - 1}} {\text{N}}_{{R\theta }}^{{}} \hat{n}_{\theta } = 0\,\,\, $$

(14a)

$$ \delta \beta _{0} = 0{\text{ or N}}_{{R\theta }}^{{}} \hat{n}_{R} + R^{{ - 1}} {\text{N}}_{{\theta \theta }}^{{}} \hat{n}_{\theta } = 0{\text{ }}\, $$

(14b)

$$ \begin{gathered} \delta \gamma _{0} = 0{\text{ or }}\left[ \begin{gathered} C_{1} \partial _{R} P_{{RR}} + {\text{N}}_{{RR}} \partial _{R} w - C_{1} R^{{ - 1}} P_{{\theta \theta }} + C_{1} R^{{ - 1}} \partial _{\theta } P_{{R\theta }} \hfill \\ + \left( {S_{{RZ}} - 3C_{1} Q_{{RZ}} } \right) \hfill \\ \end{gathered} \right]\hat{n}_{R} + \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left[ \begin{gathered} C_{1} R^{{ - 2}} \partial _{\theta } P_{{\theta \theta }} + C_{1} R^{{ - 1}} \partial _{R} P_{{R\theta }} + C_{1} R^{{ - 2}} P_{{R\theta }} \hfill \\ + R^{{ - 1}} \left( {S_{{\theta Z}} - 3C_{1} Q_{{\theta Z}} } \right) \hfill \\ \end{gathered} \right]\hat{n}_{\theta } = 0 \hfill \\ \end{gathered} $$

(14c)

$$ \delta \chi _{R}^{{}} = 0{\text{ or }}\left[ {{\text{M}}_{{RR}} - C_{1} {\text{P}}_{{RR}} } \right]\hat{n}_{R} + \left[ {R^{{ - 1}} {\text{M}}_{{R\theta }} - R^{{ - 1}} C_{1} {\text{P}}_{{R\theta }} } \right]\hat{n}_{\theta } = 0 $$

(14d)

2.2 Modified couple stress theory

For considering the size-dependency, MCST with one length scale parameter is presented. As studied in Ref. [113] for considering the MCST, the strain energy can be expressed as follows:

$$ \delta U_{2} = \iiint\limits_{V} {(m_{{ij}}^{s} \delta \chi _{{ij}}^{s} )r\,drd\theta dz} $$

(15)

The parameters that are introduced in Eq. (15) presented in Ref. [113]. Besides, $\chi_{\mathrm{i}\mathrm{j}}^{\mathrm{s}}$ and ${\mathrm{m}}_{\mathrm{i}\mathrm{j}}$ parameters can be given by:

$$ \begin{gathered} \chi _{{ij}}^{s} = \frac{1}{2}(\varphi _{{i,j}} + \varphi _{{j,i}} )\,\,\,\,\,\, \hfill \\ m_{{ij}}^{s} = 2l^{2} \mu \chi _{{ij}}^{s} \hfill \\ \end{gathered} $$

(16)

In Eq. (16), l represents the length scale parameter of the current microstructure. Finally, by combining the Eq. (15) into motion equations of the classical plate, the motion equations and boundary conditions of the annular microplate can be obtained.

2.3 Procedure to obtain the solution

GDQEM would be one of the most reliable computational approaches which is known for its convergence and accuracy. GDQE approach can be used for solving many systems such as [114,115,116,117]. The first assumption in this is as follows [118]:

$$ \,\left. {\frac{{\partial f}}{{\partial r}}} \right|_{{r = r_{i} ,\,\theta = \theta _{j} }} = \sum\limits_{{m = 1}}^{{N_{r} }} {\sum\limits_{{n = 1}}^{{N_{\theta } }} {A_{{im}}^{r} } } I_{{jn}}^{\theta } f_{{mn}} $$

(17a)

$$ \,\left. {\frac{{\partial f}}{{\partial \theta }}} \right|_{{r = r_{i} ,\,\theta = \theta _{j} }} = \sum\limits_{{m = 1}}^{{N_{r} }} {\sum\limits_{{n = 1}}^{{N_{\theta } }} {I_{{im}}^{r} } } A_{{jn}}^{\theta } f_{{mn}} $$

(17b)

$$ \frac{\partial }{{\partial r}}\,\left( {\left. {\frac{{\partial f}}{{\partial \theta }}} \right|_{{r = r_{i} ,\,\theta = \theta _{j} }} } \right) = \sum\limits_{{m = 1}}^{{N_{r} }} {\sum\limits_{{n = 1}}^{{N_{\theta } }} {A_{{im}}^{r} } } A_{{jn}}^{\theta } f_{{mn}} $$

(17c)

$$ \,\left. {\frac{{\partial ^{2} f}}{{\partial r^{2} }}} \right|_{{r = r_{i} ,\,\theta = \theta _{j} }} = \sum\limits_{{m = 1}}^{{N_{r} }} {\sum\limits_{{n = 1}}^{{N_{\theta } }} {B_{{im}}^{r} } } I_{{jn}}^{\theta } f_{{mn}} $$

(17d)

$$ \,\left. {\frac{{\partial ^{2} f}}{{\partial \theta ^{2} }}} \right|_{{r = r_{i} ,\,\theta = \theta _{j} }} = \sum\limits_{{m = 1}}^{{N_{r} }} {\sum\limits_{{n = 1}}^{{N_{\theta } }} {I_{{im}}^{r} } } B_{{jn}}^{\theta } f_{{mn}} $$

(17e)

Also, $I_{{im}}^{r}$ and $I_{{jn}}^{\theta }$ are equal to one when i = m and j = n, otherwise, are equal to zero. Also, $A_{{im}}^{r}$, $A_{{jn}}^{\theta }$, $B_{{im}}^{r}$ and $B_{{jn}}^{\theta }$ are first and second-order derivatives weighting coefficients through r and θ orientations, respectively, and can be given as.

$$ A_{{im}}^{r} = \left\{ {\begin{array}{*{20}l} {\frac{{\xi \left( {r_{i} } \right)}}{{\left( {r_{i} - r_{m} } \right)\xi \left( {r_{m} } \right)}}\,\,\,\,\,\,when\,\,\,\,i \ne m} \hfill \\ { - \sum\limits_{{k = 1,k \ne i}}^{{N_{r} }} {A_{{ik}} \,\,\,\,\,\,\,\,\,\,\,\,\,when\,\,\,\,i = m} } \hfill \\ \end{array} } \right.\,\,\,\,\,\,\,\,\,i,m = 1,2,...,N_{r} $$

(18a)

$$ A_{{jn}}^{\theta } = \left\{ {\begin{array}{*{20}l} {\frac{{\xi \left( {\theta _{j} } \right)}}{{\left( {\theta _{j} - \theta _{n} } \right)\xi \left( {\theta _{n} } \right)}}\,\,\,\,\,\,when\,\,\,\,j \ne n} \hfill \\ { - \sum\limits_{{k = 1,k \ne j}}^{{N_{\theta } }} {A_{{jk}} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,when\,\,\,\,j = n} } \hfill \\ \end{array} } \right.\,\,\,\,\,\,\,\,\,j,n = 1,2,...,N_{\theta } $$

(18b)

in which.

$$ \xi \left( {r_{i} } \right) = \prod\limits_{{k = 1,k \ne i}}^{{N_{r} }} {\left( {r_{i} - r_{k} } \right)} $$

(19a)

$$ \xi \left( {\theta _{j} } \right) = \prod\limits_{{k = 1,k \ne j}}^{{N_{\theta } }} {\left( {\theta _{j} - \theta _{k} } \right)} $$

(19b)

And.

$$ B_{{im}}^{r} = 2\left( {A_{{ii}}^{r} A_{{im}}^{r} - \frac{{A_{{im}}^{r} }}{{\left( {r_{i} - r_{m} } \right)}}} \right)\,\,\,\,\,i,m = 1,2,...,N_{r} \,\,,\,\,i \ne m $$

(20a)

$$ B_{{jn}}^{\theta } = 2\left( {A_{{jj}}^{\theta } A_{{jn}}^{\theta } - \frac{{A_{{jn}}^{\theta } }}{{\left( {\theta _{j} - \theta _{n} } \right)}}} \right)\,\,\,\,\,j,n = 1,2,...,N_{\theta } \,\,,\,\,j \ne n $$

(20b)

$$ B_{{ii}}^{r} = - \sum\limits_{{k = 1,k \ne i}}^{{N_{r} }} {B_{{ik}}^{r} \,\,\,\,,\,i = 1,2,...,N_{r} } ,\,\,i = m $$

(20c)

$$ B_{{jj}}^{\theta } = - \sum\limits_{{k = 1,k \ne j}}^{{N_{\theta } }} {B_{{jk}}^{\theta } \,\,\,\,,\,j = 1,2,...,N_{j} } ,\,\,j = n $$

(20d)

In the present study, a non-uniform set of seeds is selected through r and $\theta$ orientations as follows [119]:

$$ r_{i} = \frac{{R_{0} - R_{i} }}{{2 \times (el)_{R} }}\left( {1 - \cos \left( {\frac{{\left( {i - 1} \right)}}{{\left( {N_{r} - 1} \right)}}\pi } \right)} \right) + R_{i} \,\,\,\,\,\,i = 1,2,3,\,\,...\,\,,N_{r} $$

(21a)

$$ \theta _{j} = \frac{\chi }{{2 \times (el)_{\theta } }}\left( {1 - \cos \left( {\frac{{\left( {j - 1} \right)}}{{\left( {N_{\theta } - 1} \right)}}\pi } \right)} \right) \quad j = 1,2,3,\ldots,N_{\theta } $$

(21b)

In which $(el)_{R}$, and $(el)_{\theta }$ refer to the number of elements along with radius and angle directions, respectively. To solve the nonlinear governing equations, we divided the time-displacement fields of these equations to time, and displacement fields, separately, so:

$$ \alpha _{0}^{\eta } \left( {R,\theta ,t} \right) = \alpha _{0}^{\eta } \left( {R,\theta } \right)e^{{i\omega t}} $$

(22a)

$$ \beta _{0}^{\eta } \left( {R,\theta ,t} \right) = \beta _{0}^{\eta } \left( {R,\theta } \right)e^{{i\omega t}} $$

(22b)

$$ \gamma _{0}^{\eta } \left( {R,\theta ,t} \right) = \gamma _{0}^{\eta } \left( {R,\theta } \right)e^{{i\omega t}} $$

(22c)

$$ \chi _{R}^{\eta } \left( {R,\theta ,t} \right) = \chi _{R}^{\eta } \left( {R,\theta } \right)e^{{i\omega t}} $$

(22d)

$$ \chi _{\theta }^{\eta } \left( {R,\theta ,t} \right) = \chi _{\theta }^{\eta } \left( {R,\theta } \right)e^{{i\omega t}} $$

(22e)

After applying the GDQEM, have:

$$ \left\{ {\left[ {\begin{array}{*{20}c} {\left[ {M_{{dd}} } \right]} & {\left[ {M_{{db}} } \right]} \\ {\left[ {M_{{bd}} } \right]} & {\left[ {M_{{bb}} } \right]} \\ \end{array} } \right]\omega _{n}^{2} + \left[ {\begin{array}{*{20}c} {\left[ {K_{{dd}} } \right]} & {\left[ {K_{{db}} } \right]} \\ {\left[ {K_{{bd}} } \right]} & {\left[ {K_{{bb}} } \right]} \\ \end{array} } \right]} \right\}\left\{ \begin{gathered} \delta _{d} \hfill \\ \delta _{b} \hfill \\ \end{gathered} \right\} = 0 $$

(23)

here, b and d are, respectively, the boundary and domain nodes. Ultimately, displacement fields, and frequency characteristics of the system would be achieved by using GDQEM and solving the following equation,

$$ K^{*} + M^{*} \omega _{n}^{2} = 0 $$

(24)

where

$$ K^{*} = \left[ {K_{{bd}} } \right] - \left[ {K_{{bb}} } \right]\left[ {K_{{db}} } \right]^{{ - 1}} \left[ {K_{{dd}} } \right] $$

(25a)

$$ M^{*} = \left[ {M_{{bd}} } \right] - \left[ {M_{{bb}} } \right]\left[ {K_{{db}} } \right]^{{ - 1}} \left[ {K_{{dd}} } \right] $$

(25b)

3 Results and discussion

To reveal the global annular laminated plate’s highest frequency, particle swarm optimization (PSO)[120] and combined genetic algorithms (GAs) approaches [121] are applied. This combined approach is modified to overcome the disadvantages of the classical optimization approach and to enhance the genetic algorithms optimizer [121]. Some researchers used computer modeling for the analysis of various systems [122,123,124,125,126,127]. The introduced hybrid technique’s solution process to maximize the crucial angular speed of the system is reported as Fig. 2.

Fig. 2

Flowchart of iteration process

More information in the PSO and GAs approaches may be found in Ref. [121].

In Fig. 3, the convergence of the combined introduced optimizer with multifarious keeping, percent has been shown. Using an optimization algorithm can solve complex equations [128,129,130,131]. The population number is assumed 65 in this diagram and the optimizers. According to the mentioned figure it would be quite proven that just after a few iterations numbers, the method has been converged and optimum outcomes have been achieved. Then, it is clear that by raising the population keeping percent more swift solution convergency would be likely to be obtained. In other words, the PSO approach has revised the GAs solution process. Moreover, the current optimization’s flowchart would be reported as Fig. 4. From Fig. 4 can be found that a computer simulation is a strong tool for modeling a structure [132,133,134,135,136]. As well as this, genetic algorithm is a strong tool for simulating a structure [137,138,139,140,141]. In Table 1 effects of a/b ratio and angle-ply of layers to maximize phase speed of nano-scaled plate are studied. As may be seen, the optimum amount of angle-ply in the laminated layers would be $\boldsymbol{\theta }={37.5}^{^\circ }$. This would be due to the amount of phase speed in this angle-ply would be close to the highest amount of this factor in $\boldsymbol{\theta }={45}^{^\circ }$. It should be note that, the optimization algorithm method can be a good tool for solving the complex structures and systems [142,143,144,145,146]. According to the mentioned table, it would be clear that by raising R_o/R_i ratio the optimum phase speed of the system would be declined.

Fig. 3

Convergency of the current hybrid technique for phase speed of a sandwich plate for multifarious keeping percent

Fig. 4

The flowchart of optimization approach

Table 1 Optimum fibers orientations (Degree) and frequency (MHz) of annular microplate with different angle-ply of layers and R_o/R_i

4 Parametric results

In the presented section, a complete analysis has been conducted to illustrate the influences of different factors on the annular laminated micro-sized plate’s frequency. The material characteristics of the laminated system have been illustrated in Table 2.

Table 2 Material properties of unidirectional glass fiber in a polyester resin matrix

5 Validation study

The accuracy of the current results with the outcomes of published articles for different mode numbers, boundary conditions, and radius ratios are tabulated in Tables 3, 4, 5, and 6. As can be observed, the outputs of these tables show a good agreement between the outcomes of current research and Refs. [147,148,149,150] that the discrepancy is less than 2 percent. As well as the accuracy of the linear mode, for the correctness of the nonlinear frequency of the clamped annular plate made of isotropic material, Table 6 is presented. As can be seen, there is excellent accordance between the results of current research and mentioned References.

Table 3 Comparison of the first five dimensionless frequencies of an isotropic circular plate with clamped boundary condition and convergence and accuracy of DQ method is shown respect to the number of grid points. Dimensionless frequency ω* = ωr² $\sqrt{\rho h/D}$ where D is flexural rigidity D = Eh³/12(1 − ν²)

Table 4 Comparison of non-dimensional natural frequency of the annular plate for different axisymmetric vibration mode number, and inner radius to outer radius ratio for simply-simply boundary condition. (h/R_i = 0.001)

Table 5 Comparison of non-dimensional natural frequency of the annular plate for different axisymmetric vibration mode number, and inner radius to outer radius ratio for clamped-simply boundary condition. (h/Ri = 0.001)

Table 6 Comparison of non-dimensional natural frequency of the annular plate for different axisymmetric vibration mode number, and inner radius to outer radius ratio for clamped–clamped boundary condition. (h/Ri = 0.001)

6 Results and discussion

The influences of elasticity modulus ratio (${E}_{1}/{E}_{2}$) and material length scale factor ($l/h$) on the frequency of the laminated structure are reported in Fig. 5. According to Fig. 5 as the Young's modulus ratio increases the frequency of the current structure improves, exponentially and the mentioned impact is more considerable at the higher value of the material length scale parameter. In addition, it is true that the material length scale parameter has a positive impact on the dynamic responses of the structure but this impact is negligible when the Young's modulus ratio parameter is small. In addition, for a higher value of Young's modulus ratio the impact of material length scale parameter on the frequency of the current structure is much more remarkable than in the lower value of the ${E}_{1}/{E}_{2}$ parameter.

Fig. 5

Frequency of the current system versus ${E}_{1}/{E}_{2}$ value for various $l/h$ parameter

Frequency response of the current structure versus applied external load ($F$) is presented in Fig. 6 for various material length scale parameter. By having attention to Fig. 6 we can report that as the applied external load increases the frequency of the system decreases and the mentioned issue will continue till the buckling load appears. Also, increasing material length scale parameter is a reason for improving dynamic and static behavior or frequency and buckling load of the structure.

Fig. 6

Frequency of the current system versus $F$ value for various $l/h$ parameter

One of the aims of this study is displayed in Fig. 7 for investigation of the influences of radial mode number ($n$) on the frequency of the current structure. As Fig. 7 points out that it is true that increasing material length scale parameter has a positive impact on the dynamic information of the structure, but this impact can be bolded in the bigger radial mode numbers. Also, as the radial mode number increases, the frequency of the current structure improves.

Fig. 7

Frequency of the current system versus radial mode number for various $l/h$

The impacts of radius ratio (${r}_{o}/{r}_{i}$) and material length scale parameters on the frequency of the current structure are reported in Fig. 8. According to Fig. 8 as the radius ratio increases, the frequency of the current structure decreases exponentially. In addition, in the lower value of the radius ratio, the material length scale parameter has a positive impact on the frequency of the structure, but in the higher value of the radius ratio, we can ignore the impact of $l/h$ on the frequency of the current system.

Fig. 8

The impacts of ${r}_{o}/{r}_{i}$ and $l/h$ parameters on the frequency of the current system

In Fig. 9, influences of layers’ angle-ply to maximize displacement of annular micro-scaled plates have been analyzed in detail. As it would be seen, the optimum amount of angle-ply in the laminated layers would be $\boldsymbol{\theta }={37.5}^{^\circ }$. This would be due to the amount of displacement in this angle-ply would be close to minimizing the amount of this factor in $\boldsymbol{\theta }={45}^{^\circ }$. According to the mentioned table, it would be clear that by raising the angle-ply, the structure’s displacement would be smoother than less amount of it. Furthermore, as the mode number rises, the displacement field would be declined.

Fig. 9

Effects of different laminated patterns and angle ply on the deflection and deformation of the annular microplate

7 Conclusion

A general formulation was carried out to model linear vibrations of the laminated annular plate via higher order shear deformation theory in the current research. Also, characteristics of the frequency of an annular microplate made of laminated composite layers in the framework of MCST were investigated. The GDQE approach is employed to solve the governing equations of the micro-scaled structure through its boundary domains. For raising the performance of genetic algorithms to solve the problem, the particle swarm optimizer had been added as a GA’s operator. The proposed mixed approach’s convergency, accuracy, and applicability have been illustrated. Moreover, we demonstrate that for achieving the convergence outcome of the GA, PSO, and, we must assume higher than 23 iterations. Then, the most highlighted outcomes of this study would be as:

• for the higher value of elasticity modulus ratio, the impact of material length scale parameter on the frequency of the annular microplate is much more remarkable than in the less amount of the ${E}_{1}/{E}_{2}$ parameter

• as the radial mode number increases, the frequency of the current structure improves

• in the lower value of the radius ratio, the material length scale parameter has a positive impact on the frequency of the structure, but in the higher value of the radius ratio, we can ignore the impact of $l/h$ on the frequency of the current system.

• the influence of the types of layering has to be assumed more than the influence of the number of layers on the annular laminate micro-scaled plate’s amplitude

• as the mode number raises, the displacement field would be declined