On the nonlinear dynamics of the multi-scale hybrid nanocomposite-reinforced annular plate under hygro-thermal environment

Abstract

In this article, the nonlinear free and forced vibration analysis of multi-scale hybrid nano-composites (multi-scale HNC) annular plate (multi-scale HNCAP) under hygro-thermal environment and subjected to mechanical loading is presented. The material of matrix composite is enhanced by either carbon fibers (CF) or carbon nanotubes (CNTs) at the small or macro-scale. The multi-scale laminated annular plate’s displacement fields are determined using third-order shear deformation theory (third-order SDT) and nonlinearity of vibration behavior of this structure is taken into account considering Von Karman nonlinear shell model. Energy method known as Hamilton principle is applied to create the motion equations governed to the multi-scale HNCAP, while they are solved using generalized differential quadrature method (GDQM) as well as multiple scale method. The results created from finite-element simulation illustrates a close agreement with the semi-numerical method results. Ultimately, the research’s outcomes reveal that increasing value of the moisture change ($\Delta H$) and orientation angle parameter ($\theta$), and the rigidity of the boundary conditions lead to an increase in the structure’s frequency. Besides, whenever the values of the nonlinear parameter ($\gamma$) are positive or negative, the dynamic behavior of the plate tends to have hardening or softening behaviors, respectively. Also, there are not any effects from $\gamma$ parameter on the maximum amplitudes of resonant vibration of the multi-scale HNCAP. Last but not least, by decreasing the structure’s flexibility, the plate can be susceptible to have unstable responses.

1 Introduction

To achieve desired thermo-mechanical properties, carbon and its derivatives are accounted as the best choices to reinforce engineering structures. Choosing the scale of reinforcement widely depends on the purpose of the engineer. Some composites are consisted of a matrix and macro-scale reinforcement such as carbon fibers (CF) oriented in specific directions to enrich the mechanical performance of the structure. The reinforcement scale highly depends on the aim of the structure which is to be used. Recently, it is revealed that composites enriched by multi-scale HNC are much more beneficial in real engineering applications. Thereby, the dynamics of the composites enhanced by multi-scale HNC is a significant area of research. Chakrapani et al. [1] developed a nonlinear forced vibration model for fiber-reinforced composites with varying fiber orientations and laminated sequences. Furthermore, they conducted experimental research to confirm the numerical results’ accuracy. In another investigation, buckling along with the post-buckling behavior of the fiber-reinforced beam located in a hygro-thermal environment has been scrutinized via Reddy’s model by Emam and Eltaher [2].

On the other hand, enhancing composite properties using nano-scaled fibers instead of macro-sized ones reveals considerable boosting in the mechanics of structures. However, many scientists are focusing on the CNT-reinforced structures. For instance, an FE model is applied by Maghamika and Jam [3] to analyze CNTR circular and annular plate’s buckling relied on third-order SDT. They claimed that, in their method, the critical buckling load is less than those calculated based on the classical method, owing to the result of taking into consideration shear strain terms. Vibration study of continuously graded thick CNTR annular plate relying on an elastic foundation utilizing elasticity model is conducted by Tahouneh and Yas [4]. For solving the governing equations, they used a solution method known as differential quadrature method (DQM) in their research paper. As another study, Tahouneh and Jam [5] investigated natural frequencies of continuously graded CNTR annular plate relying on an elastic medium which CNTs are changed along with the plate’s thickness. In both papers reported above, to estimate the composite annular plate’s elastic properties, Eshelby–Mori–Tanaka micro-scaled mechanics is applied. Using variational DQM to solve the equations governed to this problem, which is extended based on the first-order shear deformation theory (FSDT), Ansari et al. [6] conducted buckling and vibration characteristics of functionally graded CNT-reinforced annular sector plate covered by an elastic foundation under thermal loading.

In the field of the nonlinear statics as well as dynamics of a circular annular plate, Keleshteri et al. [7] analyzed major bending responses of an functionally graded (FG) annular plate which is enhanced through employing CNTs and surrounded by an elastic foundation. They believed that in their mathematical approach, the applied von Karman and shear deformation models result in better accuracy. Furthermore, to solve equations obtained via energy methods, they employed the GDQM along with Newton–Raphson algorithm. Their emphasized outcome is that thickness and the value fraction of CNT may play a prominent role when it comes to annular disk’s nonlinear frequency. Ansari and Torabi [8] analyzed nonlinear forced and free dynamics of an FG disk using the von Kármán method as well as thin SDT. They emphasized mainly on the modified GDQ model to solve the FG disk’s governing equation and reported a structure’s large-amplitude vibration. Keleshteri et al. [9, 10] conducted a study on the post-buckling of the FG-CNT-reinforced circular sector plate with consideration of a piezoelectric layer utilizing GDQM, Von Karman nonlinearity, and FSDT. By taking into account the same process, Keleshtary et al. [11] investigated the FG-CNT-reinforced circular plate’s significant amplitude performance covered by piezoelectric layer and placed on an elastic medium. Torabi and Ansari [12] reported large-amplitude analysis of the FG-CNT-reinforced circular plate. Ansari et al. [13] reported a mathematical model for the investigation of the nonlinear dynamic responses of the compositional disk, which is rested on an elastic medium. The composite disk which they modeled is a CNT-reinforced FG annular plate. They employed the thick von Karman model and SDT for considering the nonlinearity. Gholami et al. [14] presented the nonlinear static behavior of a graphene platelet-reinforced annular plate under a dynamically load and the structure is covered with the Winkler–Pasternak media. They applied Newton–Raphson algorithm and a modified GDQ method to access the nonlinear bending behavior of the graphene reinforced disk.

Recently, in the field of stability analysis of the structures, in Ref [15] is presented the stability of a micro-sized beam with the aid of generalized thermoelasticity theory. Shaterzadeh et al. [16] studied nonlinear thermal buckling stability of imperfect FG shells. This structure was covered by a nonlinear elastic medium. Moreover, nonlinear forced vibrations of a micro-scaled beam employing analytical and numerical models were scrutinized by Ref. [17]. Besides, Truong-Thi et al. [18] studied stability analyses of CNT-reinforced plates with the aid of cell-based smoothed discrete shear gap method. In this work, they found that boundary condition, nanotube volume fraction, different distribution of carbon nanotubes, and plates’ width-to-thickness ratio have an important role in the buckling and vibrational characteristics of a CNT-reinforced plate.

According to the best scientific reports, large-amplitude behavior of the multi-scale HNCAP exposed to the hygro-thermal loadings is not explored, yet. In our work, the properties of multi-size levels of HNCAP are calculated upon the Halpin–Tsai model integrated with a micromechanical model. The motion equations are created using third-order SDT and geometrical Von-Karman nonlinearity. Based on PM and GDQM, the equations of motion are solved. The results created from finite-element simulation illustrates a close agreement with our semi-numerical method results. Ultimately, the outcomes demonstrate that some prominent physical and geometrical elements play a vital influence on the nonlinear dynamics of the multi-scale HNCAP.

2 Formulations and models

2.1 The problem

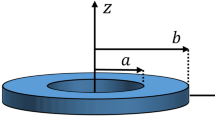
Figure 1 illustrates an HNCAP with a thickness of h, the outer radius b, and the inner radius a. on what has already been mentioned in this paper, CFs and CNTs are employed as macro-scale and nano-scale reinforcement, respectively. 3D coordinates of annular plate are presented as, R, $\theta$, and Z that show the radial, circumferential, and thickness directions, respectively.

Fig. 1

Schematic view of the multi-scale HNCAP under hygro-thermal loading, related parameters, and coordination

2.2 The homogenization procedure of multi-scale HNCAP

Two key stages are involved in the homogenization method according to the micromechanical theory as well as the Halpin–Tsai method. At the first stage, composite’s effective has to be calculated, that is [19, 20]

$$E_{11} = V_{F} E_{11}^{F} + V_{\text{NCM}} E^{\text{NCM}}$$

(1a)

$$\begin{aligned} \frac{1}{{E_{22} }} &= \frac{1}{{E_{22}^{F} }} + \frac{{V_{\text{NCM}} }}{{E^{\text{NCM}} }} - V_{F} V_{\text{NCM}}\hfill \\ &\quad- \frac{{\frac{{(\nu^{F} )^{2} E^{\text{NCM}} }}{{E_{22}^{F} }} + \frac{{(\nu^{\text{NCM}} )^{2} E_{22}^{F} }}{{E^{M} }} - 2\nu^{F} \nu^{\text{NCM}} }}{{V_{F} E_{22}^{F} + V_{\text{NCM}} E^{\text{NCM}} }}\end{aligned}$$

(1b)

$$\frac{1}{{G_{12} }} = \frac{{V_{F} }}{{G_{12}^{F} }} + \frac{{V_{\text{NCM}} }}{{G^{\text{NCM}} }}$$

(1c)

$$\rho = V_{F} \rho^{F} + V_{\text{NCM}} \rho^{\text{NCM}}$$

(1d)

$$\nu_{12} = V_{F} \nu^{F} + V_{\text{NCM}} \nu^{\text{NCM}}$$

(1e)

The adding result of the carbon fiber’s volume fraction indicated by V_F and the nanocomposite matrix’s volume fraction shown by V_NCM is should be equal to 1 [20], namely:

$$V_{F} + V_{\text{NCM}} = 1$$

(2)

At the second stage, nanocomposite’s effective properties can be calculated employing the developed Halpin–Tsai micromechanics model demonstrated as below [20]:

$$E^{\text{NCM}} = E^{M} \left[ {\frac{5}{8}\left( {\frac{{1 + 2\beta_{dd} V_{\text{CNT}} }}{{1 - \beta_{dd} V_{\text{CNT}} }}} \right) + \frac{3}{8}\left( {\frac{{1 + 2(l^{\text{CNT}} /d^{\text{CNT}} )\beta_{dl} V_{\text{CNT}} }}{{1 - \beta_{dl} V_{\text{CNT}} }}} \right)} \right]$$

(3)

in which β_dd and β_dl are given by [20]:

$$\begin{aligned} \beta_{dl} = \frac{{(E_{11}^{\text{CNT}} /E^{M} ) - (d^{\text{CNT}} /4t^{\text{CNT}} )}}{{(E_{11}^{\text{CNT}} /E^{M} ) + (l^{\text{CNT}} /2t^{\text{CNT}} )}}, \, \hfill \\ \beta_{dd} = \frac{{(E_{11}^{\text{CNT}} /E^{M} ) - (d^{\text{CNT}} /4t^{\text{CNT}} )}}{{(E_{11}^{\text{CNT}} /E^{M} ) + (d^{\text{CNT}} /2t^{\text{CNT}} )}}. \hfill \\ \end{aligned}$$

(4)

The CNTs’ volume fraction may be computed due to its weight fraction (W_CNT) written as follows [20]:

$$V_{\text{CNT}}^{ * } = \frac{{W_{\text{CNT}} }}{{W_{\text{CNT}} + \left( {\frac{{\rho^{\text{CNT}} }}{{\rho^{M} }}} \right)(1 - W_{\text{CNT}} )}},$$

(5)

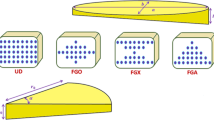
where one pattern distributed uniformly along with three FG models has been taken into account based in Fig. 2 and subsequent relations. In the mentioned models, CNTs are distributed along the multi-scale HNCAP’s thickness. FG-UD is an isotropic homogeneous plate that CNTs are regularly distributed. FG-X shows that CNTs weight fraction changes from layer to layer along the thickness. As shown in FG-X weight fraction in the midplane is the lowest and increases from the mid layer to the top and bottom layers. FG-A shows an asymmetrical CNTs in which weight fraction increases from top surface to the bottom surface. In contrast to FG-A, according to FG-V, weight fraction of CNT decreases from top surface to the bottom surface. The function of distribution can be written as below [21]:

$$\begin{aligned} V_{\text{CNT}} &= 4V_{\text{CNT}}^{*} \frac{{\left| {\xi_{j} } \right|}}{h}{\text{ FG - X}} \hfill \\ V_{\text{CNT}} &= V_{\text{CNT}}^{*} \left( {1 + \frac{{2\xi_{j} }}{h}} \right){\text{ FG - V}} \hfill \\ V_{\text{CNT}} &= V_{\text{CNT}}^{*} \left( {1 - \frac{{2\xi_{j} }}{h}} \right){\text{ FG - A}} \hfill \\ V_{\text{CNT}} &= V_{\text{CNT}}^{*} {\text{ FG - UD,}} \hfill \\ \end{aligned}$$

(6)

where $\xi_{j} = \left( {\frac{1}{2} + \frac{1}{{2N_{t} }} - \frac{j}{{N_{t} }}} \right)h{\text{ j = 1,2,}}...{,}N_{t}$. Based on the previously mentioned note, the total adding results of V_M and V_CNT as the two nanocomposite matrix’s components should be equal to 1 [20]:

$$V_{\text{CNT}} + V_{M} = 1$$

(7)

Fig. 2

Meshed FE annular plate model

The corresponding nanocomposite matrix’s shear modules, mass density, and Poisson’s ratio may be obtained using the following relations [20]:

$$G^{\text{NCM}} = \frac{{E^{\text{NCM}} }}{{2\left( {1 + \nu^{\text{NCM}} } \right)}}$$

(8a)

$$\rho^{\text{NCM}} = V_{\text{CNT}} \rho^{\text{CNT}} + V_{M} \rho^{M}$$

(8b)

$$\nu^{\text{NCM}} = \nu^{M}$$

(8c)

Furthermore, the expansion factors of the multi-scale HNC are obtained by employing a couple of equations as below [22]:

$$\alpha_{11} = \frac{{V_{f} E_{11}^{f} \alpha_{11}^{f} + V_{\text{NCM}} E^{\text{NCM}} \alpha^{\text{NCM}} }}{{E_{11}^{f} V_{f} + E^{\text{NCM}} V_{\text{NCM}} }}$$

(9a)

$$\alpha_{22} = (1 + V_{f} )V_{f} \alpha_{22}^{f} + (1 + V_{\text{NCM}} )V_{\text{NCM}} \alpha_{\text{NCM}} - \nu_{12} \alpha_{11}$$

(9b)

where $\alpha^{\text{NCM}}$ represents the nanocomposite matrix’s thermal expansion factor which can be calculated based on equation written as below [23]:

$$\begin{aligned} \alpha_{\text{NCM}} &= \frac{1}{2}\left( {\frac{{V_{\text{CNT}} E_{11}^{\text{CNT}} \alpha_{11}^{\text{CNT}} + V_{m} E_{m} \alpha_{m} }}{{V_{\text{CNT}} E_{11}^{\text{CNT}} + V_{m} E_{m} }}} \right)(1 - \nu^{\text{NCM}} ) \hfill \\ &\quad + (1 + \nu_{m} )\alpha_{m} V_{m} + (1 + \nu^{\text{CNT}} )\alpha^{\text{CNT}} V_{\text{CNT}} . \hfill \\ \end{aligned}$$

(10)

Since all water contents can be absorbed by the matrix due to its absorption property, it is fully revealed that the moisture impact on the composites’ fiber or CNTs is neglectable. Thereby, the composite’s moisture factors can be calculated as [19]:

$$\begin{aligned} \beta_{11} &= \frac{{E^{\text{NCM}} \beta^{M} V_{\text{NCM}} +_{f} E_{11}^{f} V}}{{V_{f} E_{11}^{f} + E^{\text{NCM}} V_{\text{NCM}} }}\hfill \\ \beta_{22} &= (1 + \nu_{\text{NCM}} )V_{\text{NCM}} \beta^{M} - \nu_{12} \beta_{11} \hfill \\ \end{aligned}$$

(11)

2.3 Kinematic relations

The classical plate theory and first-order shear deformation theory (FSDT) are the simplest equivalent single layer theories [24]. The third-order SDT represents the kinematics more realistically and does not require to correction factor that the FSDT requires. The third-order SDT is based on a displacement field that includes the cubic term in the thickness coordinate (z); hence, the transverse shear strain and hence stress are represented as quadratic through the plate thickness and also satisfy the stress-free conditions on the bounding planes (top and bottom surfaces) of the plate. In spite of relatively more complex algebraic equations and computational effort compared to the classical and FSDT theories, the third-order SDT yields results that are close to 3D elasticity solutions. There are some articles that incorporate the third-order plate theory to obtain more accurate results [25]. Due to the third-order SDT, the fields of displacement can be reported as [7]:

$$U\left( {R,z,t} \right) = u\left( {R,t} \right) + \left( {\phi \left( {R,t} \right) + \frac{{\partial w\left( {R,t} \right)}}{\partial R}} \right)\left( {z - c_{1} z^{3} } \right) - z\frac{{\partial w\left( {R,t} \right)}}{\partial R}$$

(12)

$$V\left( {R,z,t} \right) = 0$$

$$W\left( {R,z,t} \right) = w\left( {R,t} \right)$$

where U, V, and W are the total displacements in the (R, z) coordinates. In Eq. (12), u, v, and w are displacements of a point on the midplane. Also, ${u}_{1}$ and ${v}_{1}$ are rotations of transverse normal on the midplane. Also, $c_{1} = \frac{4}{{3h^{2} }}$. In this research, the cylindrical coordinate system ($R, \theta , z$) and axial symmetry in loading and geometry are taken into account. Also, it is assumed that the structure is an ideal annular plate that does not have any imperfection. Therefore, the geometrical nonlinearity of von Karman model and the corresponding strain components including${ \varepsilon }_{RR}$, ${\varepsilon }_{\theta \theta }$, and ${\gamma }_{RZ}$ may be shown as:

$$\left\{ {\begin{array}{*{20}c} {\varepsilon_{RR} } \\ {\varepsilon_{\theta \theta } } \\ {\gamma_{RZ} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{RR}^{0} } \\ {\varepsilon_{\theta \theta }^{0} } \\ {\gamma_{RZ}^{0} } \\ \end{array} } \right\} + z\left\{ {\begin{array}{*{20}c} {\kappa_{RR} } \\ {\kappa_{\theta \theta } } \\ {\kappa_{RZ} } \\ \end{array} } \right\} + z^{2} \left\{ {\begin{array}{*{20}c} {\kappa_{RR}^{*} } \\ {\kappa_{\theta \theta }^{*} } \\ {\kappa_{RZ}^{*} } \\ \end{array} } \right\} + z^{3} \left\{ {\begin{array}{*{20}c} {\kappa_{RR}^{**} } \\ {\kappa_{\theta \theta }^{**} } \\ {\kappa_{RZ}^{**} } \\ \end{array} } \right\}$$

(13)

where Eq. (13) is shown as:

$$\begin{aligned} &\left\{ {\begin{array}{*{20}c} {\varepsilon_{RR}^{0} } \\ {\varepsilon_{\theta \theta }^{0} } \\ {\gamma_{RZ}^{0} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{\partial u}{{\partial R}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial R}}} \right)^{2} } \\ \frac{u}{R} \\ {\frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial R}}} \\ \end{array} } \right\}, \, \left\{ {\begin{array}{*{20}c} {\kappa_{RR} } \\ {\kappa_{\theta \theta } } \\ {\kappa_{RZ} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{\partial \phi }{{\partial R}}} \\ {\frac{1}{R}\phi } \\ {\frac{\partial \phi }{{\partial z}}} \\ \end{array} } \right\}{, } \hfill \\ & \left\{ {\begin{array}{*{20}c} {\kappa_{RR}^{*} } \\ {\kappa_{\theta \theta }^{*} } \\ {\kappa_{RZ}^{*} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ { - 3c_{1} \left( {\frac{\partial w}{{\partial R}} + \phi } \right)} \\ \end{array} } \right\},\,\,\,\,\,\,\left\{ {\begin{array}{*{20}c} {\kappa_{RR}^{**} } \\ {\kappa_{\theta \theta }^{**} } \\ {\kappa_{RZ}^{**} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} { - c_{1} \left( {\frac{{\partial^{2} w}}{{\partial R^{2} }} + \frac{\partial \phi }{{\partial R}}} \right)} \\ { - \frac{{c_{1} }}{R}\left( {\frac{\partial w}{{\partial R}} + \phi } \right)} \\ { - c_{1} \left( {\frac{{\partial^{2} w}}{\partial z\partial R} + \frac{\partial \phi }{{\partial z}}} \right)} \\ \end{array} } \right\}. \hfill \\ \end{aligned}$$

(14)

2.4 Obtaining the governing equations using energy methods

The presented research extracts the governing equations employing the energy method know as Hamilton’s principle:

$$\int_{{t_{1} }}^{{t_{2} }} {\left( {\delta T - \delta U + \delta W_{1} + \delta W_{2} + \delta \dot{D}} \right){\text{d}}t = 0} .$$

(15)

The equation shown below reveals the elements involved in the procedure of extracting the aforementioned annular plate’s strain energy:

$$\delta U = \frac{1}{2}\int\limits_{V} {\sigma_{ij} } \delta \varepsilon_{ij} {\rm d}V = \int\limits_{{R_{1} }}^{{R_{2} }} {\left[ \begin{aligned} &\left\{ {\frac{{\partial N_{RR} }}{\partial R} - \frac{{N_{\theta \theta } }}{R}} \right\}\delta u \hfill \\ &+ \left\{ \begin{aligned} \frac{{\partial M_{RR} }}{\partial R} - \frac{{M_{\theta \theta } }}{R} - c_{1} \frac{{\partial P_{RR} }}{\partial R} + \frac{{c_{1} }}{R}P_{\theta \theta } \hfill \\ &- \left( {Q_{RZ} - 3c_{1} S_{RZ} } \right) \hfill \\ \end{aligned} \right\}\delta \phi \hfill \\ &+ \left\{ \begin{aligned} c_{1} \frac{{\partial^{2} P_{RR} }}{{\partial R^{2} }} - \frac{{c_{1} }}{R}\frac{{\partial P_{\theta \theta } }}{\partial R} + \left( {\frac{{\partial Q_{RZ} }}{\partial R} - 3c_{1} \frac{{\partial S_{RZ} }}{\partial R}} \right) \hfill \\ &+ \frac{\partial }{\partial R}\left( {N_{RR} \frac{\partial w}{{\partial R}}} \right) \hfill \\ \end{aligned} \right\}\delta w \hfill \\ \end{aligned} \right]} \,dR$$

(16)

The moment and the force can be obtained as:

$$\left\{ {N_{RR} ,M_{RR} ,P_{RR} } \right\} = \int_{z} {\sigma_{RR} \left\{ {1,z,z^{3} } \right\}} {\rm d}z$$

(17a)

$$\left\{ {N_{\theta \theta } ,M_{\theta \theta } ,P_{\theta \theta } } \right\} = \int_{z} {\sigma_{\theta \theta } \left\{ {1,z,z^{3} } \right\}} {\rm d}z$$

(17b)

$$\left\{ {Q_{Rz} ,S_{Rz} } \right\} = \int_{z} {\sigma_{Rz} \left\{ {1,z^{2} } \right\}} {\rm d}z$$

(17c)

Since, in this study, we have work induced by the external energy, the former can be calculated as [19]:

$$\delta W_{1} = \int\limits_{{R_{1} }}^{{R_{2} }} {\left[ {\frac{\partial \delta w}{{\partial x}}\frac{\partial w}{{\partial x}}N^{hyg} } \right]} {\rm d}R\,$$

(18)

where $N^{hyg}$ are written as [19]:

$$N^{hyg} = N^{T} + N^{H}$$

(19)

N^T and N^H are written as [19]:

$$N^{T} = \int_{ - h/2}^{h/2} {(\overline{Q}_{11} \alpha_{11} + \overline{Q}_{12} \alpha_{22} )\,(T\left( z \right) - T_{0} ){\rm d}z}$$

(20a)

$$N^{H} = \int_{ - h/2}^{h/2} {(\overline{Q}_{11} \beta_{11} + \overline{Q}_{12} \beta_{22} )\,(H\left( z \right) - H_{0} ){\rm d}z}$$

(20b)

It can be mentioned that three various patterns are taken into consideration for the moisture and temperature changes along the thickness, namely, sinusoidal temperature rise (STR), linear one (LTR), and uniform one (UTR), which can be described as follows [22]:

$${\text{UTR: }}\left\{ {\begin{array}{*{20}c} {T\left( z \right)} \\ {H\left( z \right)} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {T_{0} } \\ {H_{0} } \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {\Delta T} \\ {\Delta H} \\ \end{array} } \right\},$$

(21a)

$${\text{LTR: }}\left\{ {\begin{array}{*{20}c} {T\left( z \right)} \\ {H\left( z \right)} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\Delta T\left( {\frac{1}{2} + \frac{z}{h}} \right) + T_{0} } \\ {\Delta H\left( {\frac{1}{2} + \frac{z}{h}} \right) + H_{0} } \\ \end{array} } \right\},$$

(21b)

$${\text{STR: }}\left\{ {\begin{array}{*{20}c} {T\left( z \right)} \\ {H\left( z \right)} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\Delta T\left( {1 - \cos \frac{\pi }{2}\left( {\frac{1}{2} + \frac{z}{h}} \right)} \right) + T_{0} } \\ {\Delta H\left( {1 - \cos \frac{\pi }{2}\left( {\frac{1}{2} + \frac{z}{h}} \right)} \right) + H_{0} } \\ \end{array} } \right\}.$$

(21c)

The work variation induced by the external loads should be obtained as:

$$\delta W_{2} = \int\limits_{{R_{1} }}^{{R_{2} }} {q_{{{\text{dynamic}}}} } \delta w{\text{d}}R,$$

(22a)

where $q_{{{\text{dynamic}}}}$ can be defined as follows:

$$q_{{{\text{dynamic}}}} = F\cos \left( {\Omega t} \right).$$

(22b)

The applied work due to the damping can be presented as below:

$$\delta \dot{D} = \int\limits_{a}^{b} {C\frac{\partial \,w}{{\partial \,t}}\delta w} \,{\text{d}}R,$$

(23)

where C presents damping coefficient. Since the dynamics of the structure is analyzed, we have kinetic energy which can be obtained using Eq. (24a). Moreover, its variation can be obtained using Eq. (24b):

$$T = \int\limits_{A} \frac{1}{2} \rho \left[ {\left( {\frac{\partial U}{{\partial t}}} \right)^{2} + \left( {\frac{\partial W}{{\partial t}}} \right)^{2} + \left( {\frac{\partial V}{{\partial t}}} \right)^{2} } \right]dR{\text{dZ}}$$

(24a)

$$\delta T = \int_{a}^{b} {\rho \left[ {\frac{\partial U}{{\partial t}}\frac{\partial \delta U}{{\partial t}} + \frac{\partial V}{{\partial t}}\frac{\partial V}{{\partial t}} + \frac{\partial W}{{\partial t}}\frac{\partial \delta W}{{\partial t}}} \right]} {\rm d}R$$

(24b)

$$\delta T = \int\limits_{a}^{b} {\left[ \begin{aligned} \left\{ { - I_{O} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{1} \frac{{\partial^{2} \phi }}{{\partial t^{2} }} + I_{3} c_{1} \left( {\frac{{\partial^{2} \phi }}{{\partial t^{2} }} + \frac{{\partial^{3} w}}{{\partial R\partial t^{2} }}} \right)} \right\}\delta u + \left\{ { - I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{2} \frac{{\partial^{2} \phi }}{{\partial t^{2} }} + I_{4} c_{1} \left( {\frac{{\partial^{3} w}}{{\partial t^{2} \partial R}} + \frac{{\partial^{2} \phi }}{{\partial t^{2} }}} \right)} \right\}\delta \phi \hfill \\ + \left\{ \begin{aligned} c_{1} I_{3} \frac{{\partial^{2} u}}{{\partial t^{2} }} + c_{1} I_{4} \frac{{\partial^{2} \phi }}{{\partial t^{2} }} - \hfill \\ I_{6} c_{1}^{2} \left( {\frac{{\partial^{3} \phi }}{{\partial R\partial t^{2} }} + \frac{{\partial^{3} w}}{{\partial R\partial t^{2} }}} \right) \hfill \\ \end{aligned} \right\}\delta \phi + \left\{ \begin{aligned} - c_{1} I_{3} \frac{{\partial^{3} u}}{{\partial R\partial t^{2} }} - c_{1} I_{4} \frac{{\partial^{3} \phi }}{{\partial R\partial t^{2} }} \hfill \\ + I_{6} c_{1}^{2} \left( {\frac{{\partial^{3} \phi }}{{\partial R\partial t^{2} }} + \frac{{\partial^{4} w}}{{\partial R^{2} \partial t^{2} }}} \right) \hfill \\ \end{aligned} \right\}\delta w + \left\{ { - I_{O} \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right\}\delta w \hfill \\ \end{aligned} \right]} \,dR$$

(24c)

where $\left\{ {I_{i} } \right\} = \int\nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\rho^{\text{NCM}} \left\{ {z^{i} } \right\}{\rm d}z} ,\,\,\,i = \, 0,1,...,6$ represent inertias of the mass. Substituting Eqs. (24c), (23), (22a), (18), and (16) into Eq. (15), the Euler–Lagrange relations of multi-scale HNCAP can be defined as below:

$$\delta u{:}\frac{{\partial N_{RR} }}{\partial R} - \frac{{N_{\theta \theta } }}{R} = I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \phi }}{{\partial t^{2} }} - c_{1} I_{3} \left( {\frac{{\partial^{3} w}}{{\partial R\partial t^{2} }} + \frac{{\partial^{2} \phi }}{{\partial t^{2} }}} \right),$$

(25a)

$$\begin{aligned} \delta w{:}c_{1} \frac{{\partial^{2} P_{RR} }}{{\partial R^{2} }} - \frac{{c_{1} }}{R}\frac{{\partial P_{\theta \theta } }}{\partial R} + \frac{{\partial Q_{Rz} }}{\partial R} - 3c_{1} \frac{{\partial S_{Rz} }}{\partial R} + \frac{\partial }{\partial R}\left( {N_{RR} \frac{\partial w}{{\partial R}}} \right) \hfill \\ \, - q_{{{\text{dynamic}}}} {\text{ + C}}\frac{\partial w}{{\partial t}} - (N^{T} + N^{H} )\frac{{\partial^{2} w}}{{\partial R^{2} }} = c_{1} I_{3} \frac{{\partial^{3} u}}{{\partial R\partial t^{2} }} \hfill \\ \, + c_{1} I_{4} \frac{{\partial^{3} \phi }}{{\partial R\partial t^{2} }} - c_{1}^{2} I_{6} \left( {\frac{{\partial^{3} \phi }}{{\partial R\partial t^{2} }} + \frac{{\partial^{4} w}}{{\partial R^{2} \partial t^{2} }}} \right) + I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }}, \hfill \\ \end{aligned}$$

(25b)

$$\begin{aligned} \delta \phi {:}\frac{{\partial M_{RR} }}{\partial R} - c_{1} \frac{{\partial P_{RR} }}{\partial R} - \frac{{M_{\theta \theta } }}{R} + \frac{{c_{1} }}{R}P_{\theta \theta } - Q_{Rz} + 3c_{1} S_{Rz} \hfill \\ \, = I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \phi }}{{\partial t^{2} }} - c_{1} I_{4} \left( {\frac{{\partial^{3} w}}{{\partial t^{2} \partial R}} + \frac{{\partial^{2} \phi }}{{\partial t^{2} }}} \right) \hfill \\ \, - c_{1} I_{3} \frac{{\partial^{2} u}}{{\partial t^{2} }} - c_{1} I_{4} \frac{{\partial^{2} \phi }}{{\partial t^{2} }} + c_{1}^{2} I_{6} \left( {\frac{{\partial^{2} \phi }}{{\partial t^{2} }} + \frac{{\partial^{3} w}}{{\partial R\partial t^{2} }}} \right). \hfill \\ \end{aligned}$$

(25c)

The BCs extracted from energy methods can be indicated as:

$$\begin{aligned} \delta u &= 0{\text{ or }}N_{RR} n_{R} = 0 \hfill \\ \delta w &= 0{\text{ or }}\left[ \begin{aligned} c_{1} \frac{{\partial P_{RR} }}{\partial R} - c_{1} \frac{{P_{\theta \theta } }}{R} + Q_{RZ} - 3c_{1} S_{RZ} \hfill \\ + N_{RR} \frac{\partial w}{{\partial R}} + q\frac{\partial w}{{\partial R}} - K_{P} \frac{\partial w}{{\partial R}} + N^{T} \frac{\partial w}{{\partial R}} \hfill \\ \end{aligned} \right]n_{R} = 0. \hfill \\ \delta \phi &= 0{\text{ or }}\left[ {{\text{M}}_{RR} - c_{1} {\text{P}}_{RR} } \right]n_{R} = 0 \hfill \\ \end{aligned}$$

(26)

2.5 Governing equations

The corresponding stress–strain equation of the orthotropic composites would be shown as [26]:

$$\left\{ {\begin{array}{*{20}c} {\sigma_{RR} } \\ {\sigma_{\theta \theta } } \\ {\tau_{RZ} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\overline{Q}_{11} } & {\overline{Q}_{12} } & 0 \\ {\overline{Q}_{12} } & {\overline{Q}_{22} } & 0 \\ 0 & 0 & {\overline{Q}_{55} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{RR} } \\ {\varepsilon_{\theta \theta } } \\ {\gamma_{RZ} } \\ \end{array} } \right\},$$

(27)

with

$$\begin{aligned} \overline{Q}_{11} &= Q_{11} \cos^{4} \theta + 2Q_{12} \cos^{2} \theta \sin^{2} \theta + Q_{22} \sin^{4} \theta \hfill \\ \overline{Q}_{12} &&= Q_{12} \left( {\cos^{4} \theta + \sin^{4} \theta } \right) + \left( {Q_{22} + Q_{11} } \right)\cos^{2} \theta \sin^{2} \theta \hfill \\ \overline{Q}_{22} &= Q_{22} \cos^{4} \theta + 2Q_{12} \cos^{2} \theta \sin^{2} \theta + Q_{11} \sin^{4} \theta \hfill \\ \overline{Q}_{55} &= Q_{55} \cos^{2} \theta , \hfill \\ \end{aligned}$$

(28)

where $\theta$ is the orientation angle and [26, 27]:

$$Q_{11} = \frac{{E_{11} }}{{1 - \nu_{21} \nu_{12} }}, \, Q_{12} = \frac{{\nu_{12} E_{22} }}{{1 - \nu_{21} \nu_{12} }}, \, Q_{22} = \frac{{E_{22} }}{{1 - \nu_{12} \nu_{21} }}, \, Q_{55} = G_{12} .$$

(29)

Finally, inserting Eq. (27) in Eqs. (17a–17c) and pasting it in Eqs. 25a–25c, and governing equations of multi-scale HNCAP can be obtained using the following standard equations:

$$\begin{aligned} &\delta u:\left\{ {A_{11} \frac{{\partial^{2} u}}{{\partial R^{2} }} + B_{11} \frac{{\partial^{2} \phi }}{{\partial R^{2} }} - D_{11} c_{1} \left( {\frac{{\partial^{2} \phi }}{{\partial R^{2} }} + \frac{{\partial^{3} w}}{{\partial R^{3} }}} \right) + A_{11} \frac{{\partial^{2} w}}{{\partial R^{2} }}\frac{\partial w}{{\partial R}}} \right\} \hfill \\ \,&\quad + \left\{ {\frac{{A_{12} }}{R}\frac{\partial u}{{\partial R}} + \frac{{B_{12} }}{R}\frac{\partial \phi }{{\partial R}} - \frac{{D_{12} c_{1} }}{R}\left( {\frac{\partial \phi }{{\partial R}} + \frac{{\partial^{2} w}}{{\partial R^{2} }}} \right)} \right\} \hfill \\ \, &\quad- \left\{ {\frac{{A_{12} }}{R}\frac{\partial u}{{\partial R}} + \frac{{B_{12} }}{R}\frac{\partial \phi }{{\partial R}} - \frac{{D_{12} c_{1} }}{R}\left( {\frac{\partial \phi }{{\partial R}} + \frac{{\partial^{2} w}}{{\partial R^{2} }}} \right) + \frac{{A_{12} }}{2R}\left( {\frac{\partial w}{{\partial R}}} \right)^{2} } \right\} \hfill \\ \,&\quad - \left\{ {\frac{{A_{22} }}{{R^{2} }}u + \frac{{B_{22} }}{{R^{2} }}\phi - \frac{{D_{22} c_{1} }}{R}\left( {\frac{\phi }{R} + \frac{1}{R}\frac{\partial w}{{\partial R}}} \right)} \right\} \hfill \\ \, &\quad= I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \phi }}{{\partial t^{2} }} - I_{3} c_{1} \left( {\frac{{\partial^{2} \phi }}{{\partial t^{2} }} + \frac{{\partial^{3} w}}{{\partial R\partial t^{2} }}} \right) \hfill \\ \end{aligned}$$

(30a)

$$\begin{aligned} &\delta w:c_{1} \left\{ \begin{aligned} D_{11} \frac{{\partial^{3} u}}{{\partial R^{3} }} + E_{11} \frac{{\partial^{3} \phi }}{{\partial R^{3} }} - G_{11} c_{1} \left( {\frac{{\partial^{3} \phi }}{{\partial R^{3} }} + \frac{{\partial^{4} w}}{{\partial R^{4} }}} \right) \hfill \\ &\quad+ D_{11} \frac{{\partial^{3} w}}{{\partial R^{3} }}\frac{\partial w}{{\partial R}} + D_{11} \left( {\frac{{\partial^{2} w}}{{\partial R^{2} }}} \right)^{2} \hfill \\ \end{aligned} \right\} \hfill \\ \,&\quad + c_{1} \left\{ {\frac{{D_{12} }}{R}\frac{{\partial^{2} u}}{{\partial R^{2} }} + \frac{{E_{12} }}{R}\frac{{\partial^{2} \phi }}{{\partial R^{2} }} - \frac{{G_{12} c_{1} }}{R}\left( {\frac{{\partial^{2} \phi }}{{\partial R^{2} }} + \frac{{\partial^{3} w}}{{\partial R^{3} }}} \right)} \right\} \hfill \\ &\quad- \frac{{c_{1} }}{R}\left\{ {D_{12} \frac{{\partial^{2} u}}{{\partial R^{2} }} + E_{12} \frac{{\partial^{2} \phi }}{{\partial R^{2} }} - G_{12} c_{1} \left( {\frac{{\partial^{2} \phi }}{{\partial R^{2} }} + \frac{{\partial^{3} w}}{{\partial R^{3} }}} \right) + D_{12} \frac{{\partial^{2} w}}{{\partial R^{2} }}\frac{\partial w}{{\partial R}}} \right\} \hfill \\ \,&\quad - \frac{{c_{1} }}{R}\left\{ {\frac{{D_{22} }}{R}\frac{\partial u}{{\partial R}} + \frac{{E_{22} }}{R}\frac{\partial \phi }{{\partial R}} - \frac{{G_{22} c_{1} }}{R}\left( {\frac{\partial \phi }{{\partial R}} + \frac{{\partial^{2} w}}{{\partial R^{2} }}} \right)} \right\} \hfill \\ &\quad+ \left( {A_{55} - 3c_{1} C_{55} } \right)\left( {\frac{\partial \phi }{{\partial R}} + \frac{{\partial^{2} w}}{{\partial R^{2} }}} \right) - 3c_{1} \left( {C_{55} - 3c_{1} E_{55} } \right) \hfill \\ &\quad \left( {\frac{\partial \phi }{{\partial R}} + \frac{{\partial^{2} w}}{{\partial R^{2} }}} \right){\text{ + A}}_{11} \frac{{\partial^{2} u}}{{\partial R^{2} }}\frac{\partial w}{{\partial R}}{\text{ + A}}_{11} \frac{\partial u}{{\partial R}}\frac{{\partial^{2} w}}{{\partial R^{2} }} + \hfill \\ &\quad {\text{B}}_{11} \frac{{\partial^{2} \phi }}{{\partial R^{2} }}\frac{\partial w}{{\partial R}}{\text{ + A}}_{11} \frac{\partial \phi }{{\partial R}}\frac{{\partial^{2} w}}{{\partial R^{2} }} - D_{11} c_{1} \left( \begin{aligned} \frac{\partial w}{{\partial R}}\frac{{\partial^{2} \phi }}{{\partial R^{2} }}{ + }\frac{\partial \phi }{{\partial R}}\frac{{\partial^{2} w}}{{\partial R^{2} }} \hfill \\&\quad + \frac{{\partial^{3} w}}{{\partial R^{3} }}\frac{\partial w}{{\partial R}}{ + }\left( {\frac{{\partial^{2} w}}{{\partial R^{2} }}} \right)^{2} \hfill \\ \end{aligned} \right) \hfill \\ &\quad+ {\text{A}}_{11} \frac{{\partial^{2} w}}{{\partial R^{2} }}\left( {\frac{\partial w}{{\partial R}}} \right)^{2} + {\text{A}}_{11} \left( {\frac{\partial w}{{\partial R}}} \right)^{2} \frac{{\partial^{2} w}}{{\partial R^{2} }}{ + }\frac{{{\text{A}}_{12} }}{R}\frac{\partial u}{{\partial R}}\frac{\partial w}{{\partial R}} \hfill \\ &\quad +\frac{{{\text{A}}_{12} }}{R}u\frac{{\partial^{2} w}}{{\partial R^{2} }}{ + }\frac{{{\text{B}}_{12} }}{R}\frac{\partial \phi }{{\partial R}}\frac{\partial w}{{\partial R}} + \frac{{{\text{B}}_{12} }}{R}\phi \frac{{\partial^{2} w}}{{\partial R^{2} }} \hfill \\ &\quad-\frac{{D_{12} c_{1} }}{R}\left( {\frac{\partial \phi }{{\partial R}}\frac{\partial w}{{\partial R}}{ + }\phi \frac{{\partial^{2} w}}{{\partial R^{2} }} + 2\frac{\partial w}{{\partial R}}\frac{{\partial^{2} w}}{{\partial R^{2} }}} \right) - q_{{{\text{dynamic}}}} {\text{ + C}}\frac{\partial w}{{\partial t}} - (N^{T} + N^{H} )\frac{{\partial^{2} w}}{{\partial R^{2} }} \hfill \\ &\quad= c_{1} I_{3} \frac{{\partial^{3} u}}{{\partial R\partial t^{2} }} + c_{1} I_{4} \frac{{\partial^{3} \phi }}{{\partial R\partial t^{2} }} - c_{1}^{2} I_{6} \left( {\frac{{\partial^{3} \phi }}{{\partial R\partial t^{2} }} + \frac{{\partial^{4} w}}{{\partial R^{2} \partial t^{2} }}} \right) + I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} \hfill \\ \end{aligned}$$

(30b)

$$\begin{aligned} &\delta \phi :\left\{ {B_{11} \frac{{\partial^{2} u}}{{\partial R^{2} }} + C_{11} \frac{{\partial^{2} \phi }}{{\partial R^{2} }} - E_{11} c_{1} \left( {\frac{{\partial^{2} \phi }}{{\partial R^{2} }} + \frac{{\partial^{3} w}}{{\partial R^{3} }}} \right) + B_{11} \frac{{\partial^{2} w}}{{\partial R^{2} }}\frac{\partial w}{{\partial R}}} \right\} \hfill \\ &\quad\, + \left\{ {\frac{{B_{12} }}{R}\frac{\partial u}{{\partial R}} + \frac{{C_{12} }}{R}\frac{\partial \phi }{{\partial R}} - \frac{{E_{12} }}{R}c_{1} \left( {\frac{\partial \phi }{{\partial R}} + \frac{{\partial^{2} w}}{{\partial R^{2} }}} \right)} \right\} \hfill \\ &\quad\, - c_{1} \left\{ {E_{11} \frac{{\partial^{2} \phi }}{{\partial R^{2} }} + D_{11} \frac{{\partial^{2} u}}{{\partial R^{2} }} - G_{11} c_{1} \left( {\frac{{\partial^{2} \phi }}{{\partial R^{2} }} + \frac{{\partial^{3} w}}{{\partial R^{3} }}} \right) + D_{11} \frac{\partial w}{{\partial R}}\frac{{\partial^{2} w}}{{\partial R^{2} }}} \right\} \hfill \\ &\quad\, - c_{1} \left\{ {\frac{{D_{12} }}{R}\frac{\partial u}{{\partial R}} + \frac{{E_{12} }}{R}\frac{\partial \phi }{{\partial R}} - \frac{{G_{12} }}{R}c_{1} \left( {\frac{\partial \phi }{{\partial R}} + \frac{{\partial^{2} w}}{{\partial R^{2} }}} \right)} \right\} \hfill \\ &\quad\, - \frac{1}{R}\left\{ {B_{12} \frac{\partial u}{{\partial R}} + C_{12} \frac{\partial \phi }{{\partial R}} - E_{12} c_{1} \left( {\frac{\partial \phi }{{\partial R}} + \frac{{\partial^{2} w}}{{\partial R^{2} }}} \right) + \frac{{B_{12} }}{2}\left( {\frac{\partial w}{{\partial R}}} \right)^{2} } \right\} \hfill \\ &\quad\, - \frac{1}{R}\left\{ {B_{22} \frac{u}{R} + C_{22} \frac{\phi }{R} - E_{22} c_{1} \left( {\frac{\phi }{R} + \frac{1}{R}\frac{\partial w}{{\partial R}}} \right)} \right\} \hfill \\ &\quad\, + \frac{{c_{1} }}{R}\left\{ {D_{12} \frac{\partial u}{{\partial R}} + E_{12} \frac{\partial \phi }{{\partial R}} - G_{12} c_{1} \left( {\frac{\partial \phi }{{\partial R}} + \frac{{\partial^{2} w}}{{\partial R^{2} }}} \right) + \frac{{D_{12} }}{2}\left( {\frac{\partial w}{{\partial R}}} \right)^{2} } \right\} \hfill \\ &\quad\, + \frac{{c_{1} }}{R}\left\{ {D_{22} \frac{u}{R} + E_{22} \frac{\phi }{R} - G_{22} c_{1} \left( {\frac{\phi }{R} + \frac{1}{R}\frac{\partial w}{{\partial R}}} \right)} \right\} \hfill \\ &\quad\, - \left( {A_{55} - c_{1} 3C_{55} } \right)\left( {\phi + \frac{\partial w}{{\partial R}}} \right) + 3c_{1} \left( { - c_{1} 3E_{55} + C_{55} } \right)\left( {\phi + \frac{\partial w}{{\partial R}}} \right) \hfill \\ &\quad = I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \phi }}{{\partial t^{2} }} - I_{4} c_{1} \left( {\frac{{\partial^{2} \phi }}{{\partial t^{2} }} + \frac{{\partial^{3} w}}{{\partial R\partial t^{2} }}} \right) \hfill \\&\quad - I_{3} c_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{4} c_{1} \frac{{\partial^{2} \phi }}{{\partial t^{2} }} + I_{6} \left( {\frac{{\partial^{3} w}}{{\partial t^{2} \partial R}} + \frac{{\partial^{2} \phi }}{{\partial t^{2} }}} \right)c_{1}^{2} . \hfill \\ \end{aligned}$$

(30c)

The terms that are introduced in Eqs. (30a–30c) can be presented as follows:

$$\left\{ {G_{ij} ,F_{ij} ,E_{ij} ,D_{ij} ,C_{ij} ,B_{ij} ,A_{ij} } \right\} = \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\left\{ {z^{6} ,z^{5} ,z^{4} ,z^{3} ,z^{2} ,z^{1} ,1} \right\}} \overline{Q}_{ij} {\text{d}}z.$$

(30d)

As a result, Eqs. (30a–30c) can be formulated as follows (for details see ‘Appendix’):

$$L_{11} u\left( t \right) + L_{12} w\left( t \right) + L_{13} \phi \left( t \right) = M_{11} \ddot{u}\left( t \right) + M_{12} \ddot{w}\left( t \right) + M_{13} \ddot{\phi }\left( t \right)$$

(31a)

$$\begin{aligned} L_{21} u\left( t \right) + L_{22} w\left( t \right) + L_{23} \dot{w}\left( t \right) + L_{24} w^{3} \left( t \right) + L_{25} \phi \left( t \right) = \hfill \\ M_{21} \ddot{u}\left( t \right) + M_{22} \ddot{w}\left( t \right) + M_{23} \ddot{\phi }\left( t \right) + F\cos \left( {\Omega t} \right) \hfill \\ \end{aligned}$$

(31b)

$$L_{31} u\left( t \right) + L_{32} w\left( t \right) + L_{33} \phi \left( t \right) = M_{31} \ddot{u}\left( t \right) + M_{32} \ddot{w}\left( t \right) + M_{33} \ddot{\phi }\left( t \right).$$

(31c)

3 Solution procedure

3.1 GDQM

A range of numerical methods has been presented for solving the differential equations including FEM [23], Ritz method [28], deep collocation method [29], etc. In the current paper, we used the differential quadrature method (DQM), which has been presented by Bellman et al. [30, 31], and Grid points’ numbers are involved in this solution approach. The importance of choosing the most proper grid-points’ numbers is revealed in scholars’ research papers. For instance, Shu [32] has reported an effective method for obtaining the weighting factors for a grid-points’ infinite number called generalized differential quadrature method (GDQM). The domain decomposition model has been utilized by Shu and Richards [33] to be implemented in multi-domain equations. Estimation of the rth derivative of f(x) can be expressed as [34, 35]:

$$\left. {\frac{{\partial^{r} f(x)}}{{\partial R^{r} }}} \right|_{{x = x_{p} }} = \sum\limits_{j = 1}^{n} {g_{ij}^{(r)} f(R_{i} )} ,$$

(32)

where ${g}_{ij}$ can be formulated as follows [36]:

$$\begin{aligned} g_{ij}^{\left( 1 \right)} &= \frac{{M\left( {R_{i} } \right)}}{{\left( {R_{i} - R_{j} } \right)M\left( {R_{j} } \right)}}\,\,\,\,\,j \ne \,i\,{\text{and}}\,\,\,j,i = 1,2,...,n \hfill \\ g_{ij}^{\left( 1 \right)} &= - \sum\limits_{i \ne j,j = 1}^{n} {C_{ij}^{\left( 1 \right)} } & & & j = i \hfill \\ \end{aligned}$$

(33)

with

$$M\left( {R_{i} } \right) = \prod\limits_{j \ne i,j = 1}^{n} {\left( {R_{i} - R_{j} } \right)} .$$

(34)

The weighting factors are obtained via relations explained below when it comes to higher order derivatives:

$$\begin{aligned} g_{ij}^{\left( r \right)} = r\left[ {g_{ij}^{{\left( {r - 1} \right)}} g_{ij}^{\left( 1 \right)} - \frac{{g_{ij}^{{\left( {r - 1} \right)}} }}{{\left( {R_{i} - R_{j} } \right)}}} \right] & 2 \le r \le n - 1,j \ne i\,\,\,{\text{and}}\,\,\,j,i = 1,2,...,n \hfill \\ g_{ii}^{\left( r \right)} = - \sum\limits_{i \ne j,j = 1}^{n} {g_{ij}^{\left( r \right)} } & \,\,1 \le r \le n - 1\,{\text{and}}\,\,\,j,i = 1,2,...,n. \hfill \\ \end{aligned}$$

(35)

This study, however, chooses a grid-points’ non-uniform set which is written as below:

$$R_{j} = \frac{b - a}{2}\left( {1 - \cos \left( {\frac{{\left( {j - 1} \right)}}{{\left( {N_{j} - 1} \right)}}\pi } \right)} \right) + a \quad j = 1,2,3,\,\,\ldots\,\,,N_{j} .$$

(36)

3.2 Multiple scales method

To determine the dynamic response of the system via multiple scales method, before solving the governing equation, displacement components are presented in the following standard form to separate time and space variables:

$$u\left( {R,t} \right) = u\left( R \right){\text{e}}^{{i\omega_{mn} t}} ,\,\,\,\,\,\,w\left( {R,t} \right) = w\left( R \right){\text{e}}^{{i\omega_{mn} t}} ,\,\,\,\,\,\,\,\phi_{x} \left( {R,t} \right) = \phi_{x} \left( R \right){\text{e}}^{{i\omega_{mn} t}} .$$

(37)

Now, by substituting Eq. (37) into Eqs. (30a–30c) and using Eq. (32) for solving the unknown functions u(t), and $\phi_{x} (t)$ in terms of w(t), the nonlinear differential equation of annular plate can be extracted as:

$$\ddot{w}\left( t \right) + C\dot{w}\left( t \right) + P_{1} w\left( t \right) + P_{2} w^{2} \left( t \right) + \gamma w^{3} \left( t \right) = F\left( t \right)\cos \left( {\Omega t} \right),$$

(38)

where:

$$\gamma = - \frac{{M_{21} + M_{22} + M_{23} }}{{L_{24} }}.$$

(39)

Subsequently, the linear annular plate oscillation can be defined as:

$$\omega_{\text{L}} = \sqrt {P_{1} } ,$$

(40)

and $\overline{\omega }_{\text{L}} = \omega_{\text{L}} b^{2} \sqrt {\frac{{\rho_{m} }}{{E_{m} }}}$, where the initial boundary conditions can be identified as:

$$W\left( 0 \right) = \frac{w}{h}, \, \left. {\frac{{{\text{d}}w\left( t \right)}}{{{\text{d}}t}}} \right|_{t = 0} = 0.$$

(41)

By replacing w(t) in Eq. (38) with g(t), and by considering F(t) and C equal to zero, one has the following equation:

$$\frac{{{\text{d}}^{2} g\left( t \right)}}{{{\text{d}}t^{2} }} + P_{1} \left\{ {g\left( t \right) + \zeta g^{3} \left( t \right)} \right\} = 0,$$

(42)

in which

$$\zeta = \frac{\gamma }{{P_{1} }}$$

(43)

By implementing the homotopy perturbation method, the solution for Eq. (42) can be given as:

$$\frac{{{\text{d}}^{2} g\left( t \right)}}{{{\text{d}}t^{2} }} + \omega_{{{\text{NL}}}}^{2} g\left( t \right) + \xi \left\{ {\left( {P_{1} - \omega_{{{\text{NL}}}}^{2} } \right)g\left( t \right) + P_{1} \zeta g^{3} \left( t \right)} \right\} = 0,$$

(44)

where $\xi \in \left[ {0,1} \right]$ is an integrated variable. When $\xi = 0$, Eq. (44) will be representing linear differential relation which is shown as:

$$\frac{{{\text{d}}^{2} g\left( t \right)}}{{{\text{d}}t^{2} }} + \omega_{{{\text{NL}}}}^{2} g\left( t \right) = 0.$$

(45)

Above

$$g\left( t \right) = g_{0} \left( t \right) + \xi g_{1} \left( t \right) + \xi^{2} g_{2} \left( t \right) + \cdots .$$

(46)

It should be the following.

Substituting Eq. (45) into Eq. (46), we get:

$$\xi^{0} :\frac{{{\text{d}}^{2} g_{0} \left( t \right)}}{{{\text{d}}t^{2} }} + \omega_{{{\text{NL}}}}^{2} g_{0} \left( t \right) = 0, \, \left. {g_{0} } \right|_{t = 0} = \frac{w}{h}, \, \left. {\frac{{{\text{d}}g_{0} \left( t \right)}}{{{\text{d}}t}}} \right|_{t = 0} = 0,$$

(47a)

$$\begin{aligned} \xi^{1} :\frac{{{\text{d}}^{2} g_{1} \left( t \right)}}{{{\text{d}}t^{2} }} + \omega_{{{\text{NL}}}}^{2} g_{1} \left( t \right) + \left\{ {\left( {P_{1} - \omega_{\text{NL}}^{2} } \right)g_{0} \left( t \right) + P_{1} g_{0}^{3} \left( t \right)} \right\} = 0 \hfill \\ , \, \left. {g_{1} } \right|_{t = 0} = \frac{w}{h}, \, \left. {\frac{{{\text{d}}g_{1} \left( t \right)}}{{{\text{d}}t}}} \right|_{t = 0} = 0. \hfill \\ \end{aligned}$$

(47b)

Hence, computing Eq. (47a) results in:

$$g_{0} \left( t \right) = \frac{w}{h}\cos \left( {\omega_{{{\text{NL}}}} t} \right), \, a{ = }\frac{w}{h}.$$

(48)

Utilizing Eqs. (47b) and (48), the following expression can be achieved as shown below:

$$\begin{aligned} \frac{{{\text{d}}^{2} g_{1} \left( t \right)}}{{{\text{d}}t^{2} }} &+ P_{1} g_{1} \left( t \right) + \left( {P_{1} - \omega_{{{\text{NL}}}}^{2} + \frac{3}{4}a^{2} \zeta P_{1} } \right)a\cos \left( {\omega_{{{\text{NL}}}} t} \right) \hfill \\ &+ \frac{1}{4}P_{1} a^{3} \zeta \cos \left( {3\omega_{{{\text{NL}}}} t} \right) = 0. \hfill \\ \end{aligned}$$

(49)

Hence, elimination of g₀(t) yields the equation:

$$P_{1} - \omega_{{{\text{NL}}}}^{2} + \frac{3}{4}a^{2} \zeta P_{1} = 0,$$

(50)

in which the nonlinear form of the frequency of the multi-scale HNCAP can be formulated as:

$$\omega_{\text{NL}} = \left( {\sqrt {1 + \frac{3}{4}a^{2} \zeta } } \right)\omega_{\text{L}} ,$$

(51)

where $A^{*} = \frac{w}{{h^{2} }}$

$$\omega_{{{\text{NL}}}} = \omega_{{\text{L}}} \sqrt {1 + \frac{3}{4}h^{2} \zeta A^{*2} } .$$

(52)

3.3 Primary resonance

In the presented case, it is guessed that ${\omega }_{\text{L}}$ is near to $\Omega$. Therefore, an element of σ is presented for demonstrating the closeness of $\Omega$ to ${\omega }_{0}$ as:

$$\Omega = \omega_{0} + \sigma \varepsilon .$$

(53)

To study the oscillations and bifurcations of the nonlinear plate, the multi-scale method is presented to investigate the nonlinear vibration characteristics of the nanocomposite circular plate. The estimated solutions of Eq. (38) are determined as:

$$w = w_{0} \left( {T_{0} ,T_{1} ,T_{2} , \ldots } \right) + \varepsilon w_{1} \left( {T_{0} ,T_{1} ,T_{2} , \ldots } \right) + \varepsilon^{2} w_{2} \left( {T_{0} ,T_{1} ,T_{2} , \ldots } \right),$$

(54)

where T₀ = t and T₁ = εt. The excitation in variations of ${T}_{0}$ and ${T}_{1}$ is explained as:

$$F\left( t \right) = \varepsilon \overline{q}\cos \left( {\omega_{0} T_{0} + \sigma T_{1} } \right).$$

(55)

Then, the derivatives can be obtained using t as a parameter:

$$\frac{{\text{d}}}{{{\text{d}}t}} = D_{0} + \varepsilon D_{1} ,$$

(56a)

$$\frac{{{\text{d}}^{2} }}{{{\text{d}}t^{2} }} = D_{0}^{2} + 2\varepsilon D_{0} D_{1} + \varepsilon^{2} \left( {D_{1}^{2} + 2D_{0} D_{1} } \right),$$

(56b)

where $D_{0} = \frac{\partial }{{\partial T_{0} }},\,\,\,D_{1} = \frac{\partial }{{\partial T_{1} }},\,\,\,and\,\,D_{0} D_{1} = \frac{{\partial^{2} }}{{\partial T_{0} \partial T}}$. Substituting Eqs. (54–56a) into Eq. (38) and equating the factors of ε equal to 0 yields the following differential relations:

$$\varepsilon^{0} :D_{0}^{2} w_{0} + p_{1} w_{0} = 0$$

(57a)

$$\varepsilon^{1} :D_{0}^{2} w_{1} + p_{1} w_{1} = - 2D_{0} D_{1} w_{0} - 2CD_{0} w_{0} - \gamma w_{0}^{3} - \overline{q}\cos \left( {\omega_{0} T_{0} + \sigma T_{1} } \right),$$

(57b)

The solution of Eq. (57a) may be suggested as:

$$w_{0} \left( {T_{0} ,T_{1} ,T_{2} , \ldots } \right) = A\left( {T_{1} } \right)\exp \left( {iT_{0} } \right) + \overline{A}\left( {T_{1} } \right)\exp \left( { - iT_{0} } \right).$$

(58)

The governing equations for A are gained by demanding ${w}_{1}$ in the periodic form in ${T}_{0}$ and deriving secular parameters which are factors of ${\mathrm{e}}^{\pm i{\upomega }_{0}{T}_{0}}$ the equation can be obtained as:

$$2i\omega_{0} \left( {A + CA} \right) + 3\gamma A^{2} \overline{A} - \frac{1}{2}\overline{q}\exp \left( { - i\sigma T_{1} } \right) = 0,$$

(59)

where

$$A = \frac{1}{2}\alpha \exp \left( {i\beta } \right).$$

(60)

Inserting Eq. (60) to Eq. (59) and separating imaginary and real parts enable us to have the following relations:

$$\alpha^{\prime} = - C\alpha + \frac{1}{2}\frac{{\overline{q}}}{{\omega_{0} }}\sin \left( \theta \right)$$

(61a)

$$\alpha \beta^{\prime} = \frac{3}{8}\frac{\gamma }{{\omega_{0} }}\alpha^{3} + \frac{1}{2}\frac{{\overline{q}}}{{\omega_{0} }}\cos \left( \theta \right).$$

(61b)

In the above equation, $\theta =\sigma {T}_{1}-\beta$. Now, by considering steady-state condition (${a}^{{{\prime}}}=0,$ and ${\theta }^{{{\prime}}}=0$) and squaring, then combining the above relations, one can result in determining frequency relation as follows [37]:

$$\left[ {\left( {\sigma - \frac{3}{8}\frac{\gamma }{{\omega_{0} }}\alpha^{2} } \right)^{2} + C^{2} } \right]\alpha^{2} = \frac{{\overline{q}^{2} }}{{4\omega_{0}^{2} }}.$$

(62)

Substituting Eqs. (61a–61b) for steady-state condition to Eq. (62) and inserting it to Eq. (60) and substituting this result into Eqs. (58) and (54), one may obtain the first approximation:

$$w = \alpha \cos \left( {\omega_{0} t + \varepsilon \sigma t - \theta } \right) + O\left( \varepsilon \right).$$

(63)

For obtaining the stability/instability responses of the system and using Eq. (62), we present magnification factor that can be expressed as:

$$M = \frac{\alpha }{{\left| {\overline{q}} \right|}} = \frac{1}{{2\omega_{0} \sqrt {\left( {\sigma - \frac{3}{8}\frac{\gamma }{{\omega_{0} }}\alpha^{2} } \right) + C^{2} } }}$$

(64a)

$$\frac{{{\text{d}}M}}{{{\text{d}}\Omega }} = 0, \, \frac{{{\text{d}}^{2} M}}{{{\text{d}}\Omega^{2} }} < 0.$$

(64b)

According to Eq. (53), $\sigma$ can be achieved. By substituting $\sigma$ in Eq. (64a), the maximum value of the magnification factor could be found using Eq. (64b), so:

$$\frac{1}{32}\alpha \left( {3\gamma \alpha^{2} - 8\Omega + 8\omega_{0} } \right)\left( {3\alpha \gamma \frac{{{\text{d}}\alpha }}{{{\text{d}}\Omega }} - 4} \right) + \left( {C^{2} + \left( {\Omega - \omega_{0} - 3\gamma \alpha^{2} } \right)^{2} } \right)\frac{{{\text{d}}\alpha }}{{{\text{d}}\Omega }} = 0.$$

(65)

The above relation can be solved for $\frac{\mathrm{d}\alpha }{\mathrm{d}\Omega }$ as:

$$\frac{{{\text{d}}\alpha }}{{{\text{d}}\Omega }} = \frac{{8a\left( {3\gamma \alpha^{2} - 8\Omega + 8\omega_{0} } \right)}}{{27\gamma^{2} \alpha^{4} - 96\left( {\Omega - \omega_{0} } \right)\gamma \alpha^{2} + 64\left( {C^{2} + \left( {\Omega - \omega_{0} } \right)^{2} } \right)}}.$$

(66)

This derivative vanishes (and so does $\frac{\mathrm{d}M}{\mathrm{d}\Omega }$) when:

$$\left( {3\gamma \alpha^{2} - 8\Omega + 8\omega_{0} } \right) = 0 \Rightarrow \alpha_{{\text{p}}} = \sqrt {\frac{{8\left( {\Omega - \omega_{0} } \right)}}{3\gamma }} .$$

(67)

By considering $\frac{\mathrm{d}\Omega }{\mathrm{d}M}=0$, the values of the critical points ${\Omega }_{1}$ and ${\Omega }_{2}$ can be obtained [38]. By considering the denominator of Eq. (66) equal to zero, the instability responses of the system (${\Omega }_{1}$ and ${\Omega }_{2}$) can be achieved. Therefore:

$$27\gamma^{2} \alpha^{4} - 96\left( {\Omega - \omega_{0} } \right)\gamma \alpha^{2} + 64\left( {C^{2} + \left( {\Omega - \omega_{0} } \right)^{2} } \right) = 0.$$

(68)

And finally have:

$$\Omega_{1,2} = \frac{1}{8}\left( {8\omega_{0} + 6\gamma \alpha^{2} - \sqrt {9\gamma^{2} \alpha^{4} - 64C^{2} } } \right).$$

(69)

4 Numerical results and discussion

In this research, famous reinforcement called multi-scale HNC is employed to enhance the annular plate dynamics. The thermo-mechanical properties of epoxy and a reinforcement are shown in Table 1 [22].

Table 1 Material properties of the current structure [1]

4.1 Validation

To evaluate the reliability of the proposed method, the circular plate’s dimensionless natural frequency acquired in this paper is compared with results provided by Ref. [39] in Table 2. As can be seen in a broad range of CNT distribution pattern, and W_CNT, there is a good agreement between the results. Regarding the table, this research anticipates the vibration characteristics of the circular plate very similar and close to the results given in Ref. [39]. It should be mentioned that the model described in Ref. [39] is a linear model, but the current research is a nonlinear model of Ref. [39] as well as considering viscoelastic foundation. As can be seen, the discrepancy between the two results is less than 1.5% that is acceptable for verification. Also, in Ref. [39], the influences of hygro-thermal loading, viscoelastic, and c₁ parameters are ignored.

Table 2 Comparison of non-dimensional natural frequency ($\overline{\omega }^{2} = \omega b^{2} \sqrt {\rho /E}$) of the multi-scale HNCAP versus CNT pattern with b/a = 4, h/b = 0.2, $\theta$=$\pi /4$, and c = 0

For another verification for this work, according to Table 3, it is revealed that the proposed modeling can provide good agreement with Ref. [13] where the influences of thermal loading and viscoelastic parameters are ignored.

Table 3 Comparison of fundamental natural frequencies (Hz) of an isotropic annular plate based on the HSDT ($\rho =7800 \mathrm{kg}/{\mathrm{m}}^{3}$, E = $2.1\times {10}^{11} \mathrm{Pa}$, $\nu =0.3$, b = 3 m, a = 1 m, and h = a/10)

4.2 Finite-element modeling

For further validation and shape mode analysis of the multi-scale HNCAP, finite-element analyses have been presented with the aid of ABAQUS, where solid element C3D8R with 8-node, reduced integration, and hourglass control is employed to create the mesh for the shell model. Besides, the perfect bonding between neighboring layers has been considered. Figure 2 presents the model after meshing. In addition, boundary conditions are applied to the nodes at the inner and outer edges of the multi-scale HNCAP. It is well known that if we want to have an accurate FE model, we should pay attention to the mesh convergence [40]. For this reason, the number of elements is increased as long as the natural frequency of the structure does not have any noticeable change and the optimum number of elements is selected. According to Fig. 3, such a convergence criterion is met when there are more than 40,000 elements in the mesh. A validation study between our numerical results and finite-element outcomes is presented in Table 4. As it can be seen, the maximum relative discrepancies between our numerical results and the FEM results are less than 4%. In addition, with respect to Table 4, one can see that the best pattern in the frequency issue of the structure is pattern 2, and the more rigid the structure is, the more boosted the frequency of the multi-scale HNC annular plate. Also, with the aid of the FE model, the first four mode shapes of a multi-scale HNCAP for b/a = 5 are shown in Fig. 4.

Fig. 3

Convergence study for the FE multi-scale HNCAP model for the first and second modes

Table 4 Validation of numerical results with finite-element outcomes

Fig. 4

The first four mode shapes for multi-scale HNCAP with h = a/10, ϴ = π/4, W_CNT = 0.02, V_F = 0.2, FG-X, and = $\Delta T$₀

4.3 Parametric results

The impacts of various factors (including CNT’s distribution patterns, the plate’s geometrical ratios, the CNT’s weight fraction, carbon fibers’ volume fraction, viscoelasticity factor, and gradient of temperature) on the multi-sized HNCAP’s frequency characteristics are investigated.

Figure 5 provides a relevant result where, for the method of GDQ, an adequate grid points’ number is essential to achieve precise outcomes.

Fig. 5

Convergence of the current structure for various boundary conditions with b/a = 4, h/b = 0.1, FG-X, T_i = 273 [K], T_o = 300 [K], WCNT = 0, V_F = 0, ϴ = π/4, UTR, and β = 1

For diverse boundary conditions and a range of materials, the convergence analysis is carried out. As a generalized result, it is obvious that the structure with clamped-free (CF) BCs is more flexible than the structure with clamped–clamped (CC) BCs, resulting in a lower nonlinear frequency. Besides, in accordance with Fig. 5, the grid points’ optimum number for the structure with clamped-free (CF) BCs is obtained as 12, while, for an annular plate with clamped–clamped, clamped–simply, and simply–simply BCs, this number is six. By having detailed attention to Fig. 5, it is clear that a decrease of the rigidity of the circular plate leads to the limitation of an increase in grid points number so as to retain convergence in the GDQ method.

As it can be seen in Fig. 6, the highest and lowest values of the nonlinear frequency correspond to the structures which are made by FG-A and FG-X. Generally, each increase in amplitude ratio (A*) will be a reason for boosting the nonlinear reinforced annular plate’s frequency and this is a fact for all FG patterns.

Fig. 6

The impact of CNT distribution on the nonlinear non-dimensional frequency of the simply supported multi-scale HNCAP with b/a = 4, h/b = 0.3, T_i = 273 [K], T_o = 300 [K], ϴ = π/4, W_CNT = 0.02, V_F = 0.2, and β = 1

The main reflection from Fig. 7 is that by encountering the composite annular plate with the sinusoidal and uniform temperature patterns, we can see the highest and the lowest nonlinear frequency, respectively.

Fig. 7

The impact of temperature change pattern on the nonlinear non-dimensional frequency of the simply supported multi-scale HNCAP with b/a = 4, h/b = 0.1, FG-X, T_i = 273 [K], T_o = 300 [K], ϴ = π/4, W_CNT = 0.02, V_F = 0.2, and β = 1

Figure 8 gives an investigation about the impact of changes in moisture ($\Delta H$) on the frequency ratio of the circular annular plate for C–S, S–S, C-F, and C–C boundary conditions. For each BCs and all amounts of the A^* element, a direct relationship exists between the frequency ratio of the annular plate and $\Delta H$, which means that raising the amount of the $\Delta H$ element results in improving the frequency ratio of the multi-scale HNCAP-reinforced annular plate. By having an exact glance at Fig. 8, one may find an applicable outcome which is that the impact of $\Delta H$ factor on the structure’s nonlinear dynamics for simple–simple (S–S) BCs is by far more significant than for the cases of other BCs. Another interesting result is that $\Delta H$ parameter does not affect the frequency ratio when the clamped–simply boundary conditions are considered.

Fig. 8

The impact of different moisture on the non-dimensional natural frequency ratio of the multi-scale HNCAP for various boundary conditions with b/a = 4, h/b = 0.3, T_i = 273 [K], T_o = 300 [K], FG-X, STR, ϴ = π/4, and β = 1

Figure 9 illustrates the impacts of varying fibers’ orientation angle ($\theta \mathrm{parameter}$) on the nonlinear frequency characteristics of the circular plate for boundary conditions of C-F, C–C, S–S, and C–S. The prominent result which is coming up from this fig is that for each value of A^* factor and all BCs, through rising the $\theta$ parameter, the annular plate’s nonlinear frequency declines and this matter is more substantial at higher values of the deflection and for C-F BCs. It is not remarkable by maintaining that at the larger amount of the A^* factor one can observe the influence of $\theta$ factor on the structure’s nonlinear dynamics, particularly in the case of clamped-free (CF) BCs. The other obtained result is that by changes in the condition of the annular plate from C-F to C–C, structure’s frequency raises owing to a decrease in the structure’s flexibility.

Fig. 9

The impact of different orientation angle on the non-dimensional natural frequency ratio of the system for various boundary conditions with b/a = 4, h/b = 0.3, T_i = 273 [K], T_o = 300 [K], FG-X, ϴ = π/4, W_CNT = 0.02, V_F = 0.2, and β = 1

Comprehensive research is reported in Fig. 10 for investigation of the impacts of conditions at the edges and increasing temperature of the environment on the nonlinear dynamics of the nanocomposite-reinforced annular plate. If one pays attention to Fig. 10, one can see that boosting the temperature makes a decrease in the annular plate’s nonlinear frequency and this matter is true for each A^*. It is also true that temperature of the thermal environment negatively affects the frequency of the plate, but we should consider that this impact is more remarkable in a structure with the simply–simply boundary conditions.

Fig. 10

The impact of boundary condition and applied temperature of the top surface on the nonlinear non-dimensional natural frequency of the system for various boundary conditions with b/a = 4, FG-X, h/b = 0.3, ϴ = π/4, W_CNT = 0.02, V_F = 0.2, and β = 1

Figures 11, 12, 13, and 14 are consistent with the literature which shows influences of nonlinear parameter ($\gamma$) and increasing value of excitation frequency on the nonlinear amplitude responses of the multi-scale HNC-reinforced annular plate for various boundary conditions. Based on Figs. 11, 12, 13, and 14, it may be observed that for all BCs, when the value of the $\gamma$ parameter is positive or negative, the dynamic behavior of the plate tends to have a hardening or softening behaviors, respectively. It is well known that the $\gamma$ is the parameter of the cubic nonlinearity; when this parameter is zero, there is not hardening or softening behavior for the plate, because this behavior appears in the nonlinear plates. Moreover, by rising the positive or negative amounts of the $\gamma$ parameter, the hardening or softening behaviors of the multi-scale HNC-reinforced annular plate are intensified. According to Figs. 11 and 12, for C–C along with C–S boundary conditions, no effects from $\gamma$ parameter on the maximum amplitudes of resonant vibration of the multi-scale HNC-reinforced annular plate. In contrast, by having detailed attention to Figs. 13 and 14, one can find that for S–S and C-F boundary conditions, there is an impressive influence of the nonlinearity parameter on the backbone curve, and especially on the frequency–amplitude responses of the multi-scale HNC-reinforced annular plate could be seen. By comparing Figs. 11 and 12 with Figs. 13 and 14, one can find an applicable result, which is that when the structure’s rigidity decreases by shifting the boundary conditions from C–C to C-F ones, the effect of $\gamma$ parameter on the hardening or softening behaviors of the plate is intensified. In addition to the results mentioned above, as the main point which comes from Figs. 11, 12, 13, and 14, one can see that for C–C and C–S boundary conditions, the unstable responses appear in the backbone curve of the nonlinear model; however, in the cases of S–S and C-F boundary conditions, the backbone curve of the plate corresponds to stable conditions. Another important result is that for C–C and C–S boundary conditions, by increasing the value of the nonlinearity parameter, the unstable range at the backbone curve of the plate increases. It can be concluded from these figures that by decreasing the structure’s flexibility, the plate can be susceptible to having unstable responses.

Fig. 11

Variation of the amplitude response with respect to the excitation frequency for different values of the $\gamma$ of multi-scale HNCAP and clamped–clamped boundary conditions with b/a = 4, h/b = 0.3, T_i = 273 [K], T_o = 300 [K], STR, ϴ = π/4, W_CNT = 0.02, V_F = 0.2, β = 1, and $\stackrel{-}{q}=0.3$

Fig. 12

Variation of the amplitude response with respect to the excitation frequency for different values of the $\gamma$ of multi-scale HNCAP and clamped–simply boundary conditions with b/a = 4, h/b = 0.3, T_i = 273 [K], T_o = 300 [K], STR, ϴ = π/4, W_CNT = 0.02, V_F = 0.2, β = 1, and $\stackrel{-}{q}=0.3$

Fig. 13

Variation of the amplitude response with respect to the excitation frequency for different values of the $\gamma$ of multi-scale HNCAP and simply–simply boundary conditions with b/a = 4, h/b = 0.3, T_i = 273 [K], T_o = 300 [K], STR, ϴ = π/4, W_CNT = 0.02, V_F = 0.2, β = 1, and $\stackrel{-}{q}=0.3$

Fig. 14

Variation of the amplitude response with respect to the excitation frequency for different values of the $\gamma$ of multi-scale HNCAP and clamped-free boundary conditions with b/a = 4, h/b = 0.3, T_i = 273 [K], T_o = 300 [K], STR, ϴ = π/4, W_CNT = 0.02, V_F = 0.2, β = 1, and $\stackrel{-}{q}=0.3$

Figures 15, 16, 17, and 18 present the impact of eternal force ($\stackrel{-}{q}$ parameter) and increasing the value of excitation frequency on the nonlinear amplitude responses of the multi-scale HNC-reinforced annular plate for C–C, C–S, S–S, and C-F boundary conditions.

Fig. 15

Variation of the amplitude response with respect to the excitation frequency for different values of the external force and clamped–clamped boundary conditions with b/a = 4, h/b = 0.3, T_i = 273 [K], T_o = 300 [K], STR, ϴ = π/4, W_CNT = 0.02, V_F = 0.2, β = 1, and $\gamma =0.5$

Fig. 16

Variation of the amplitude response with respect to the excitation frequency for different values of the external force and clamped–simply boundary conditions with b/a = 4, h/b = 0.3, T_i = 273 [K], T_o = 300 [K], STR, ϴ = π/4, W_CNT = 0.02, V_F = 0.2, β = 1, and $\gamma =0.5$

Fig. 17

Variation of the amplitude response with respect to the excitation frequency for different values of the external force and simply–simply boundary conditions with b/a = 4, h/b = 0.3, T_i = 273 [K], T_o = 300 [K], STR, ϴ = π/4, W_CNT = 0.02, V_F = 0.2, β = 1, and $\gamma =0.5$

Fig. 18

Variation of the amplitude response with respect to the excitation frequency for different values of the external force for clamped-free boundary conditions with b/a = 4, h/b = 0.3, T_i = 273 [K], T_o = 300 [K], STR, ϴ = π/4, W_CNT = 0.02, V_F = 0.2, β = 1, and $\gamma =0.5$

Taking a brief glance at Figs. 15, 16, 17, and 18, it is obvious that increasing the $\stackrel{-}{q}$ parameter gives rise to getting better hardening behavior and boosts the pick amplitudes at the backbone curves of the nonlinear plate. In other words, when the external force increases, the frequency of the backbone curve shifts to the side of the larger value of the extension frequency. With respect to Figs. 15 and 16, an increase of the number of external forces results in widening the insatiable area at the backbone curves of the nonlinear disks.

5 Conclusion

In this paper, we studied the nonlinear free and forced vibrational characteristics of the multi-scale HNCAP under the hygro-thermal environment. Also, a modified Halpin–Tsai model was presented to predict the effective properties of the multi-scale HNCAP. The strain–displacement relation of the current system was obtained via the third-order SDT and with the aid of Von Karman nonlinear shell theory. The minimum potential energy method was employed to establish the governing equations of motion, which were solved with the aid of GDQM and PM. The results created from finite-element simulation illustrate a close agreement with our semi-numerical method results. The numerical results revealed that:

• The best FG distribution for obtaining the highest nonlinear dynamic response of a multi-scale HNC reinforced annular plat was FG-A.

• The effect of T_t parameter on the nonlinear frequency of the structure with the S–S boundary conditions was much more significant than of other BCs. The lowest effect of T_t parameter was seen for the structure with C-F boundary conditions.

• Increasing value of the $\Delta H$ parameter leads to improvement in the frequency ratio of the multi-scale HNCAP-reinforced annular plate.

• $\Delta H$ parameter has no effect on the frequency ratio when the clamped–simply boundary conditions are considered.

• When the rigidity of the structure decreases by changing the boundary conditions from C–C to C-F ones, the effect of $\gamma$ parameter on the hardening or softening behaviors of the plate is intensified.

Appendix

In Eqs. (31a–31c), L_ij and M_ij are expressed as follows:

$$\begin{aligned} &\delta u_{o} : \hfill \\ &\quad L_{11} = A_{11} \frac{{\partial^{2} u}}{{\partial R^{2} }} - \frac{{A_{22} }}{{R^{2} }}u, \hfill \\ &\quad L_{12} = - D_{11} c_{1} \frac{{\partial^{3} w}}{{\partial R^{3} }} + \frac{{D_{22} c_{1} }}{{R^{2} }}\frac{\partial w}{{\partial R}} \hfill \\ &\quad L_{13} = B_{11} \frac{{\partial^{2} \phi }}{{\partial R^{2} }} - D_{11} c_{1} \frac{{\partial^{2} \phi }}{{\partial R^{2} }} - \frac{{B_{22} }}{{R^{2} }}\phi + \frac{{D_{22} c_{1} }}{{R^{2} }}\phi \hfill \\& \quad M_{11} = I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }},\,\,M_{12} = - I_{3} c_{1} \frac{{\partial^{3} w}}{{\partial R\partial t^{2} }},\,\,\,M_{13} = \left( {I_{1} - I_{3} c_{1} } \right)\frac{{\partial^{2} \phi }}{{\partial t^{2} }} \hfill \\ \end{aligned}$$

(70)

$$\begin{aligned}& \delta w_{0} : \hfill \\ &\quad L_{21} = c_{1} D_{11} \frac{{\partial^{3} u}}{{\partial R^{3} }} - \frac{{c_{1} D_{22} }}{{R^{2} }}\frac{\partial u}{{\partial R}}, \hfill \\ &\quad L_{22} = - G_{11} c_{1}^{2} \frac{{\partial^{4} w}}{{\partial R^{4} }} + \frac{{G_{22} c_{1}^{2} }}{{R^{2} }}\frac{{\partial^{2} w}}{{\partial R^{2} }} + \left( {A_{55} - 3C_{55} c_{1} } \right)\frac{{\partial^{2} w}}{{\partial R^{2} }} \hfill \\ &\quad - 3c_{1} \left( {C_{55} - 3E_{55} c_{1} } \right)\frac{{\partial^{2} w}}{{\partial R^{2} }} - q \, - (N^{T} + N^{H} )\frac{{\partial^{2} w}}{{\partial R^{2} }} \hfill \\&\quad L_{23} = {\text{C}}\frac{\partial w}{{\partial t}},\,\,\,\,\,\,\,\,L_{24} = \frac{3}{2}{\text{A}}_{11} \frac{{\partial^{2} w}}{{\partial R^{2} }}\left( {\frac{\partial w}{{\partial R}}} \right)^{2} \hfill \\&\quad L_{25} = c_{1} E_{11} \frac{{\partial^{3} \phi }}{{\partial R^{3} }} - G_{11} c_{1}^{2} \frac{{\partial^{3} \phi }}{{\partial R^{3} }} - \frac{{c_{1} }}{R}\frac{{E_{22} \partial \phi }}{R\partial R} - \frac{{c_{1} }}{R}\frac{{G_{22} c_{1} }}{R}\frac{\partial \phi }{{\partial R}} \hfill \\&\quad + \left( {A_{55} - 3C_{55} c_{1} } \right)\frac{\partial \phi }{{\partial R}} - 3c_{1} \left( {C_{55} - 3E_{55} c_{1} } \right)\frac{\partial \phi }{{\partial R}} \hfill \\&\quad M_{21} = c_{1} I_{3} \frac{{\partial^{3} u}}{{\partial R\partial t^{2} }},\,\,M_{22} = I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} - c_{1}^{2} I_{6} \frac{{\partial^{4} w}}{{\partial R^{2} \partial t^{2} }}, \hfill \\&\quad M_{23} = \left( {c_{1} I_{4} - c_{1}^{2} I_{6} } \right)\frac{{\partial^{3} \phi }}{{\partial R\partial t^{2} }}, \hfill \\ \, \hfill \\ \end{aligned}$$

(71)

$$\begin{aligned} &\delta \phi : \hfill \\&\quad L_{31} = B_{11} \frac{{\partial^{2} u}}{{\partial R^{2} }} - c_{1} D_{11} \frac{{\partial^{2} u}}{{\partial R^{2} }} - \frac{{B_{22} }}{{R^{2} }}u + \frac{{D_{22} }}{{R^{2} }}u, \hfill \\&\quad L_{32} = - E_{11} c_{1} \frac{{\partial^{3} w}}{{\partial R^{3} }} + G_{11} c_{1}^{2} \frac{{\partial^{3} w}}{{\partial R^{3} }} + \frac{{E_{22} c_{1} }}{{R^{2} }}\frac{\partial w}{{\partial R}} + \frac{{G_{22} c_{1}^{2} }}{{R^{2} }}\frac{\partial w}{{\partial R}} \hfill \\&\quad - \frac{\partial w}{{\partial R}}\left( {A_{55} - 3c_{1} C_{55} } \right) + 3\frac{\partial w}{{\partial R}}\left( {C_{55} - 3c_{1} E_{55} } \right)c_{1} \hfill \\&\quad L_{33} = C_{11} \frac{{\partial^{2} \phi }}{{\partial R^{2} }} - E_{11} c_{1} \frac{{\partial^{2} \phi }}{{\partial R^{2} }} - c_{1} E_{11} \frac{{\partial^{2} \phi }}{{\partial R^{2} }} + G_{11} c_{1}^{2} \frac{{\partial^{2} \phi }}{{\partial R^{2} }} \hfill \\&\quad - \frac{1}{{R^{2} }}\left\{ {C_{22} - E_{22} c_{1} } \right\}\phi + \frac{{c_{1} }}{{R^{2} }}\left\{ {E_{22} - G_{22} c_{1} } \right\}\phi \hfill \\ &\quad - \left( {A_{55} - 3c_{1} C_{55} } \right)\phi + 3c_{1} \left( {C_{55} - 3c_{1} E_{55} } \right)\phi \hfill \\&\quad M_{31} = \left( {I_{1} - c_{1} I_{3} } \right)\frac{{\partial^{2} u}}{{\partial t^{2} }},\,\,\,M_{32} = \left( {I_{6} c_{1}^{2} - I_{4} c_{1} } \right)\frac{{\partial^{3} w}}{{\partial R\partial t^{2} }}, \hfill \\&\quad M_{33} = \left( {I_{6} c_{1}^{2} - 2c_{1} I_{4} + I_{2} } \right)\frac{{\partial^{2} \phi }}{{\partial t^{2} }}. \hfill \\ \end{aligned}$$

(72)