1 Introduction

Functionally graded materials (FGMs) are the new kinds of composites that are made from a composition from ceramics and metals. These kinds of heterogeneous materials have variable mechanical properties in one or more directions. The usages of FGMs have been enhanced quickly in all of the engineering branches, such as mechanical engineering, due to their phenomenal mechanical properties. Therefore, to have a comprehensive investigation about their features, many researchers examined the mechanical responses of the FGMs with variable mechanical properties in one or more directions [1,2,3,4,5,6,7,8,9,10,11,12].

Kazemirad et. al [13] examined the nonlinear dynamic investigation of a buckled axially moving beam. Ghayesh et. al [14] examined the vibration investigation of a simply supported spring-mass-beam system considering the thermal efficacy. Ghayesh et. al [15] presented an approximate analytical solution technique for phase-shift prediction along the length of the measuring tube of a Coriolis mass-flowmeter. Ghayesh and Amabili [16] examined the nonlinear stability of an axially moving beam in the thermal environment. Daikh et. al [17] examined the vibration investigation of the FG sandwich nanoplates in the thermal environment based on third-order shear deformation theory (TSDT). Nonlocal elasticity theory is utilized to consider nonlocality. Hosseini et. al [18] studied the free vibration investigation of the nanoplates subjected to thermal efficacy using FSDT. To ponder the thermal efficacy, linear thermal relation is utilized. Daikh et. al [19] examined the buckling and free vibration investigation of the reinforced composite nanoplates reinforced by carbon nanotubes in the thermal environment based on TSDT. Nonlocal strain gradient theory is utilized to ponder the nonlocality. Singh and Azam [20] examined the buckling and free vibration investigation of the FG nanoplates in the thermal environment based on nonlocal elasticity theory. Dastjerdi et. al [21] examined the bending investigation of the thick porous FG nanoplates in a hygro-thermal environment based on nonlocal elasticity theory. Chen et. al [22] studied the vibration examination of the nanoplates subjected to thermal loading based on fourth-order strain gradient theory. Fang et. al [23] examined the buckling investigation of the FG composite skew nanoplates with various boundary conditions. Kolahdouzan et. al [24] studied the vibration and buckling investigation of the FG-CNTRC sandwich annular nanoplates based on nonlocal elasticity theory. Dindarloo and Zenkour [25] studied the bending responses of the FG spherical nanoshells in the thermal environment. Linear relations are utilized to ponder the thermal efficacy based on nonlocal strain gradient theory. Mashat et. al [26] examined the bending responses of the FG plates under the hygro-thermo-mechanical loading based on a quasi-3D higher-order plate theory. Lal and Saini [27] examined the vibration investigation of the FG circular plates with nonlinear temperature distribution in the thickness direction. Thang et. al [28] examined the free vibration investigation of the FG nanoplates reinforced with carbon nanotubes based on nonlocal strain gradient theory. Arshid et. al [29] studied the free vibration and buckling investigation of the FG porous sandwich curved microbeams in the thermal environment based on modified couple stress theory. Esen et. al [30] examined the vibrational behavior of the FG cracked microbeam rested on an elastic foundation subjected to the thermal and magnetic fields.

Pursuant to the above review, the free vibration investigation of the 2D-FG nanoplate subjected to hygro-thermo loading based on a novel HSDT is examined for the first time. The size-dependent nonlocal higher-order theory is dedicated to pondering the nonlocality. The novelty of the current research is to present a new HSDT, which is an amalgamation of exponential, polynomial and trigonometric functions. Thickness stretching influence is considered according to higher-order shear and normal deformation theory. The transverse component of displacement is composed of bending and shear parts. We ponder the nonlinear relations for temperature and moisture fields to investigate the impacts of the thermal and moisture efficacy on the vibration characteristics of the 2D-FG nanoplates. Hamilton’s axiom is dedicated to achieving the governing equations of motion. Then, Navier solution technique is dedicated to deriving the natural frequency of the nanoplates with S–S boundary conditions. The effects of the various parameters are examined on the vibration characteristics of the 2D-FG nanoplates.

2 Size-dependent analysis of the 2D-FG nanoplates

In the current research, we use the two-directional (2D) functionally graded materials (FGMs) to investigate the vibration characteristics of the nanoplates subjected to hygro-thermo conditions. Assume the materials’ properties of the plate including density (\(\rho\)), Young’s modulus (\(E\)) and thermal and moisture parameters vary continuously with an arbitrary function in two directions as below.

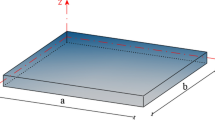
$$\begin{aligned} E\left( {x,z} \right) & = e^{{\frac{{n_{1} x}}{a}}} \left[ {E_{{\text{c}}} \left( {\frac{{2z + h}}{{2h}}} \right)^{{n_{2} }} + E_{{\text{m}}} \left( {\frac{{2z + h}}{{2h}}} \right)^{{n_{2} }} } \right] \\ \rho \left( {x,z} \right) & = e^{{\frac{{m_{1} x}}{a}}} \left[ {\rho _{{\text{c}}} \left( {\frac{{2z + h}}{{2h}}} \right)^{{m_{2} }} + \rho _{{\text{m}}} \left( {\frac{{2z + h}}{{2h}}} \right)^{{m_{2} }} } \right] \\ \alpha \left( {x,z} \right) & = e^{{\frac{{n_{3} x}}{a}}} \left[ {\alpha _{{\text{c}}} \left( {\frac{{2z + h}}{{2h}}} \right)^{{n_{4} }} + \alpha _{{\text{m}}} \left( {\frac{{2z + h}}{{2h}}} \right)^{{n_{4} }} } \right] \\ \beta \left( {x,z} \right) & = e^{{\frac{{m_{3} x}}{a}}} \left[ {\beta _{{\text{c}}} \left( {\frac{{2z + h}}{{2h}}} \right)^{{m_{4} }} + \beta _{{\text{m}}} \left( {\frac{{2z + h}}{{2h}}} \right)^{{m_{4} }} } \right], \\ \end{aligned}$$
(1)

where \(n_{i} ,m_{j} \left( {i,j = 1,...,4} \right)\) are the FG indexes; \(\alpha\) and \(\beta\) are the thermal and moisture parameters, respectively. In the current research, we consider a rectangular nanoplate with length \(a\), width \(b\) and thickness \(h\) (Fig. 1). In the present model, thickness stretching influence is considered according to higher-order shear and normal deformation theory. To study the vibration characteristics of the 2D-FG nanoplates based on a new HSDT, the displacement field is reported as below [31]:

$$\begin{aligned} u_{x} \left( {x,y,z,t} \right) & = u\left( {x,y,t} \right) - z\frac{{\partial w_{{\text{b}}} \left( {x,y,t} \right)}}{{\partial x}} - f\left( z \right)\frac{{\partial w_{{\text{s}}} \left( {x,y,t} \right)}}{{\partial x}} \\ u_{y} \left( {x,y,z,t} \right) & = v\left( {x,y,t} \right) - z\frac{{\partial w_{{\text{b}}} \left( {x,y,t} \right)}}{{\partial y}} - f\left( z \right)\frac{{\partial w_{{\text{s}}} \left( {x,y,t} \right)}}{{\partial y}} \\ u_{z} \left( {x,y,z,t} \right) & = w_{{\text{b}}} \left( {x,y,t} \right) + w_{{\text{s}}} \left( {x,y,t} \right) + g\left( z \right)w_{z} \left( {x,y,t} \right), \\ \end{aligned}$$
(2)

where \(u_{x}\), \(u_{y}\) and \(u_{z}\) are three parts of the displacement along with the \(x\), \(y\) and \(z\) directions, respectively; The transverse deflection is divided to shear (\(w_{{\text{s}}}\)) and bending (\(w_{{\text{b}}}\)) parts; \(w_{z}\) is the thickness stretching parameter.

Fig. 1
figure 1

Geometry of a rectangular FG nanoplate

Full size image

The main novelty of the present research is to render a new HSDT without including the shear correction coefficient. The new shear strain shape function \(f\left( z \right)\) presented in this research is an amalgamation of exponential, polynomial and trigonometric functions. According to this HSDT, we can investigate the mechanical responses of the composite structures, including FG plates and shells, accurately. To compare the present theory with the other theories, the variations of \(f\left( z \right)\) and \(\frac{{{\text{d}}f\left( z \right)}}{{{\text{d}}z}}\) is presented along with the thickness direction in Fig. 2.

$$f\left( z \right) = h\tan ^{{ - 1}} \left( {\frac{z}{h}} \right) + \frac{{4z^{3} }}{{15h^{2} }} + \frac{h}{\pi }\sin \left( {\frac{{\pi z}}{h}} \right) - z.$$
(3)
Fig. 2
figure 2

Variation of \(f\left( z \right)\) and \(\frac{{{\text{d}}f}}{{{\text{d}}z}}\) in several theories

Full size image

With considering the displacement field, the strain parts are reported as:

$$\begin{aligned} \varepsilon _{1} & = \frac{{\partial u_{x} }}{{\partial x}} = \frac{{\partial u}}{{\partial x}} - z\frac{{\partial ^{2} w_{{\text{b}}} }}{{\partial x^{2} }} - f\left( z \right)\frac{{\partial ^{2} w_{{\text{s}}} }}{{\partial x^{2} }} \\ \varepsilon _{2} & = \frac{{\partial u_{y} }}{{\partial y}} = \frac{{\partial v}}{{\partial y}} - z\frac{{\partial ^{2} w_{{\text{b}}} }}{{\partial y^{2} }} - f\left( z \right)\frac{{\partial ^{2} w_{{\text{s}}} }}{{\partial y^{2} }} \\ \varepsilon _{3} & = \frac{{\partial u_{z} }}{{\partial z}} = \frac{{{\text{d}}g}}{{{\text{d}}z}}w_{z} \\ \varepsilon _{6} & = \frac{{\partial u_{x} }}{{\partial y}} + \frac{{\partial u_{y} }}{{\partial x}} = \frac{{\partial u_{{}} }}{{\partial y}} + \frac{{\partial v_{{}} }}{{\partial x}} - 2z\frac{{\partial ^{2} w_{{\text{b}}} }}{{\partial x\partial y}} - 2f\left( z \right)\frac{{\partial ^{2} w_{{\text{s}}} }}{{\partial x\partial y}} \\ \varepsilon _{4} & = \frac{{\partial u_{x} }}{{\partial z}} + \frac{{\partial u_{z} }}{{\partial x}} = \left( {1 - \frac{{{\text{d}}f}}{{{\text{d}}z}}} \right)\frac{{\partial w_{{\text{s}}} }}{{\partial x}} + g\left( z \right)\frac{{\partial w_{z} }}{{\partial x}} \\ \varepsilon _{5} & = \frac{{\partial u_{y} }}{{\partial z}} + \frac{{\partial u_{z} }}{{\partial y}} = \left( {1 - \frac{{{\text{d}}f}}{{{\text{d}}z}}} \right)\frac{{\partial w_{{\text{s}}} }}{{\partial y}} + g\left( z \right)\frac{{\partial w_{z} }}{{\partial y}}. \\ \end{aligned}$$
(4)

In this paper, to ponder the nonlocality, the size-dependent nonlocal elasticity theory is dedicated. The relations between the stress and strain components with considering the thermal and moisture impacts are:

$$\left( {1 - \mu ^{2} \nabla ^{2} } \right)\left\{ \begin{gathered} \sigma _{1} \hfill \\ \sigma _{2} \hfill \\ \sigma _{3} \hfill \\ \sigma _{6} \hfill \\ \sigma _{4} \hfill \\ \sigma _{5} \hfill \\ \end{gathered} \right\} = \left[ {\begin{array}{*{20}c} {C_{{11}}^{{}} } & {C_{{12}}^{{}} } & {C_{{13}}^{{}} } & 0 & 0 & 0 \\ {C_{{12}} } & {C_{{22}} } & {C_{{23}} } & 0 & 0 & 0 \\ {C_{{13}} } & {C_{{23}} } & {C_{{33}} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {C_{{66}}^{{}} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {C_{{44}}^{{}} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {C_{{55}}^{{}} } \\ \end{array} } \right]\left\{ \begin{gathered} \varepsilon _{1} - \alpha _{{11}} \Delta T - \beta _{{11}} \Delta C \hfill \\ \varepsilon _{2} - \alpha _{{22}} \Delta T - \beta _{{33}} \Delta C \hfill \\ \varepsilon _{3} - \alpha _{{22}} \Delta T - \beta _{{33}} \Delta C \hfill \\ \varepsilon _{6} \hfill \\ \varepsilon _{4} \hfill \\ \varepsilon _{5} \hfill \\ \end{gathered} \right\},$$
(5)

where \(C_{{ij}}^{{}}\) are the stiffness parameters:

$$\begin{aligned} C_{{ii}} \left( {x,y,T} \right) & = \frac{{E\left( {x,y,T} \right)\left( {1 - \upsilon } \right)}}{{\left( {1 + \upsilon } \right)\left( {1 - 2\upsilon } \right)}},\;i = 1,2,3 \\ C_{{ii}} \left( {x,y,T} \right) & = \frac{{E\left( {x,y,T} \right)}}{{2\left( {1 + \upsilon } \right)}},\;i = 4,5,6 \\ C_{{12}} \left( {x,y,T} \right) & = C_{{23}} \left( {x,y,T} \right) = C_{{13}} \left( {x,y,T} \right) = \frac{{E\left( {x,y,T} \right)\upsilon }}{{\left( {1 + \upsilon } \right)\left( {1 - 2\upsilon } \right)}}. \\ \end{aligned}$$
(6)

To study the effects of the thermal and moisture effects on the vibration characteristics of the 2D-FG nanoplates accurately, we ponder the nonlinear relations for temperature and moisture fields as following:

$$\left\{ \begin{gathered} T\left( {x,y,z} \right) \hfill \\ C\left( {x,y,z} \right) \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} T_{1} \left( {x,y} \right) \hfill \\ C_{1} \left( {x,y} \right) \hfill \\ \end{gathered} \right\} + \frac{z}{h}\left\{ \begin{gathered} T_{2} \left( {x,y} \right) \hfill \\ C_{2} \left( {x_{{}} ,y} \right) \hfill \\ \end{gathered} \right\} + \frac{{f\left( z \right)}}{h}\left\{ \begin{gathered} T_{3} \left( {x,y} \right) \hfill \\ C_{3} \left( {x,y} \right) \hfill \\ \end{gathered} \right\},$$
(7)

where \(T_{i}\) and \(C_{i}\) are thermal and moisture loads.

Based on the nonlocal elasticity theory, the stress tensor parts in terms of displacement ingredients with considering the thermal and moisture effects are reported as below:

$$\begin{aligned} \left( {1 - \mu ^{2} \nabla ^{2} } \right)\sigma _{1} & = C_{{11}} \left( {\frac{{\partial u_{{}} }}{{\partial x}} - z\frac{{\partial ^{2} w_{{\text{b}}} }}{{\partial x^{2} }} - f\left( z \right)\frac{{\partial ^{2} w_{s} }}{{\partial x^{2} }}} \right) + C_{{12}} \left( {\frac{{\partial v_{{}} }}{{\partial y}} - z\frac{{\partial ^{2} w_{{\text{b}}} }}{{\partial y^{2} }} - f\left( z \right)\frac{{\partial ^{2} w_{{\text{s}}} }}{{\partial y^{2} }}} \right) \\ & + C_{{13}} \frac{{{\text{d}}g}}{{{\text{d}}z}}w_{z} - C_{{11}} \left( {\alpha _{{11}} \Delta T + \beta _{{11}} \Delta C} \right) - C_{{12}} \left( {\alpha _{{22}} \Delta T + \beta _{{22}} \Delta C} \right) - C_{{13}} \left( {\alpha _{{33}} \Delta T + \beta _{{33}} \Delta C} \right) \\ \left( {1 - \mu ^{2} \nabla ^{2} } \right)\sigma _{2} & = C_{{12}} \left( {\frac{{\partial u_{{}} }}{{\partial x}} - z\frac{{\partial ^{2} w_{{\text{b}}} }}{{\partial x^{2} }} - f\left( z \right)\frac{{\partial ^{2} w_{{\text{s}}} }}{{\partial x^{2} }}} \right) + C_{{22}} \left( {\frac{{\partial v_{{}} }}{{\partial y}} - z\frac{{\partial ^{2} w_{{\text{b}}} }}{{\partial y^{2} }} - f\left( z \right)\frac{{\partial ^{2} w_{{\text{s}}} }}{{\partial y^{2} }}} \right) \\ & + C_{{23}} \frac{{{\text{d}}g}}{{{\text{d}}z}}w_{z} - C_{{12}} \left( {\alpha _{{11}} \Delta T + \beta _{{11}} \Delta C} \right) - C_{{22}} \left( {\alpha _{{22}} \Delta T + \beta _{{22}} \Delta C} \right) - C_{{23}} \left( {\alpha _{{33}} \Delta T + \beta _{{33}} \Delta C} \right) \\ \left( {1 - \mu ^{2} \nabla ^{2} } \right)\sigma _{3} & = C_{{13}} \left( {\frac{{\partial u_{{}} }}{{\partial x}} - z\frac{{\partial ^{2} w_{{\text{b}}} }}{{\partial x^{2} }} - f\left( z \right)\frac{{\partial ^{2} w_{{\text{s}}} }}{{\partial x^{2} }}} \right) + C_{{23}} \left( {\frac{{\partial v_{{}} }}{{\partial y}} - z\frac{{\partial ^{2} w_{{\text{b}}} }}{{\partial y^{2} }} - f\left( z \right)\frac{{\partial ^{2} w_{{\text{s}}} }}{{\partial y^{2} }}} \right) \\ & + C_{{33}} \frac{{{\text{d}}g}}{{{\text{d}}z}}w_{z} - C_{{13}} \left( {\alpha _{{11}} \Delta T + \beta _{{11}} \Delta C} \right) - C_{{23}} \left( {\alpha _{{22}} \Delta T + \beta _{{22}} \Delta C} \right) - C_{{33}} \left( {\alpha _{{33}} \Delta T + \beta _{{33}} \Delta C} \right) \\ \left( {1 - \mu ^{2} \nabla ^{2} } \right)\sigma _{6} & = C_{{66}} \left( {\frac{{\partial u_{{}} }}{{\partial y}} + \frac{{\partial v_{{}} }}{{\partial x}} - 2z\frac{{\partial ^{2} w_{b} }}{{\partial x\partial y}} - 2f\left( z \right)\frac{{\partial ^{2} w_{s} }}{{\partial x\partial y}}} \right) \\ \left( {1 - \mu ^{2} \nabla ^{2} } \right)\sigma _{4} & = C_{{44}} \left( {\left( {1 - \frac{{{\text{d}}f}}{{{\text{d}}z}}} \right)\frac{{\partial w_{s} }}{{\partial x}} + g\left( z \right)\frac{{\partial w_{z} }}{{\partial x}}} \right) \\ \left( {1 - \mu ^{2} \nabla ^{2} } \right)\sigma _{5} & = C_{{55}} \left( {\left( {1 - \frac{{{\text{d}}f}}{{{\text{d}}z}}} \right)\frac{{\partial w_{s} }}{{\partial y}} + g\left( z \right)\frac{{\partial w_{z} }}{{\partial y}}} \right). \\ \end{aligned}$$
(8)

Considering the strain potential energy (\(U_{{\text{S}}}\)) and kinetic energy (\(U_{{\text{T}}}\)) and according to Hamilton’s principle, we have:

$$\begin{aligned} \int_{{t_{1} }}^{{t_{2} }} {\left( {\delta U_{{\text{T}}} - \delta U_{{\text{S}}} + \delta U_{{\text{W}}} } \right)} {\text{d}}t & = 0 \Rightarrow \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{a} {\int_{0}^{b} {\int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left( {\sigma _{1} \delta \varepsilon _{1} + \sigma _{2} \delta \varepsilon _{2} + \sigma _{3} \delta \varepsilon _{3} + \sigma _{4} \delta \varepsilon _{4} + \sigma _{5} \delta \varepsilon _{5} + \sigma _{6} \delta \varepsilon _{6} } \right){\text{d}}x{\text{d}}y{\text{d}}z{\text{d}}t} } } } \\ & - \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{a} {\int_{0}^{b} {\delta \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\rho \left( {\dot{u}_{x} ^{2} + \dot{u}_{y} ^{2} + \dot{u}_{x} ^{2} } \right){\text{d}}x{\text{d}}y{\text{d}}z{\text{d}}t = 0} } } } . \\ \end{aligned}$$
(9)

Implementing Eqs. (2) and (8) into Eq. (9), the governing equation of motion is reported as

$$\begin{gathered} \delta u_{x} :\frac{{\partial N_{1} }}{{\partial x}} + \frac{{\partial N_{6} }}{{\partial y}} = - I_{3} \frac{{\partial \ddot{w}_{s} }}{{\partial x}} - I_{1} \frac{{\partial \ddot{w}_{b} }}{{\partial x}} + I_{0} \ddot{u}_{{}} + q_{1} \hfill \\ \delta u_{y} :\frac{{\partial N_{2} }}{{\partial y}} + \frac{{\partial N_{6} }}{{\partial x}} = - I_{3} \frac{{\partial \ddot{w}_{s} }}{{\partial y}} + I_{0} \ddot{v}_{{}} - I_{1} \frac{{\partial \ddot{w}_{b} }}{{\partial y}} + q_{2} \hfill \\ \delta w_{b} :\frac{{\partial ^{2} M_{1} }}{{\partial x^{2} }} + \frac{{\partial ^{2} M_{2} }}{{\partial y^{2} }} + 2\frac{{\partial ^{2} M_{6} }}{{\partial x\partial y}} = - I_{4} \frac{{\partial ^{2} \ddot{w}_{s} }}{{\partial y^{2} }} + I_{0} \left( {\ddot{w}_{b} + \ddot{w}_{s} } \right) + I_{6} \ddot{w}_{z} \hfill \\ - I_{2} \frac{{\partial ^{2} \ddot{w}_{b} }}{{\partial x^{2} }} + I_{1} \frac{{\partial \ddot{u}_{{}} }}{{\partial x}} + I_{1} \frac{{\partial \ddot{v}}}{{\partial y}} - I_{4} \frac{{\partial ^{2} \ddot{w}_{s} }}{{\partial x^{2} }} - I_{2} \frac{{\partial ^{2} \ddot{w}_{b} }}{{\partial y^{2} }} + q_{3} \hfill \\ \delta w_{s} :\frac{{\partial ^{2} P_{1} }}{{\partial x^{2} }} + \frac{{\partial ^{2} P_{2} }}{{\partial y^{2} }} + 2\frac{{\partial ^{2} P_{6} }}{{\partial x\partial y}} + \frac{{\partial Q_{4} }}{{\partial x}} + \frac{{\partial Q_{5} }}{{\partial y}} = - I_{5} \frac{{\partial ^{2} \ddot{w}_{s} }}{{\partial y^{2} }} - I_{4} \frac{{\partial ^{2} \ddot{w}_{b} }}{{\partial y^{2} }} \hfill \\ + I_{0} \ddot{w}_{b} + I_{0} \ddot{w}_{s} - I_{4} \frac{{\partial ^{2} \ddot{w}_{b} }}{{\partial x^{2} }} + I_{3} \frac{{\partial \ddot{u}_{{}} }}{{\partial x}} + I_{3} \frac{{\partial \ddot{v}_{{}} }}{{\partial y}} - I_{5} \frac{{\partial ^{2} \ddot{w}_{s} }}{{\partial x^{2} }} + I_{6} \ddot{w}_{z} + q_{4} \hfill \\ \delta w_{z} :\frac{{\partial Q_{4} }}{{\partial x}} + \frac{{\partial Q_{5} }}{{\partial y}} - P_{3} = I_{6} \ddot{w}_{b} + I_{6} \ddot{w}_{s} + I_{7} \ddot{w}_{z} + q_{5} . \hfill \\ \end{gathered}$$
(10)

The unknown components of Eq. (10) including the thermal loads and moments due to the hygro-thermo conditions are reported as:

$$\begin{gathered} \left( {I_{0} ,I_{1} ,I_{2} ,I_{3} ,I_{4} ,I_{5} ,I_{6} ,I_{7} } \right) = \int_{{ - \frac{{h_{e} }}{2}}}^{{\frac{{h_{e} }}{2}}} {\rho \left( {x,y,z} \right)\left( {1,z,z^{2} ,f,fz,fz^{2} ,g,g^{2} } \right)} {\text{d}}z \hfill \\ \left( {N_{i} ,M_{i} ,P_{i} } \right) = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\sigma _{i}^{{}} \left( {1,z,f} \right)} {\text{d}}z\begin{array}{*{20}c} {} & {\left( {i = 1,2,6} \right)} \\ \end{array} \hfill \\ \left( {N_{{ii}}^{T} ,M_{{ii}}^{T} ,P_{{ii}}^{T} } \right) = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left( {C_{{i1}} + C_{{i2}} + C_{{i3}} } \right)\left( {\alpha \Delta T + \beta \Delta C} \right)\left( {1,z,f} \right)} {\text{d}}z\begin{array}{*{20}c} {} & {\left( {i = 1,2,6} \right)} \\ \end{array} \hfill \\ \left( {N_{{12}}^{T} ,M_{{12}}^{T} ,P_{{12}}^{T} } \right) = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left( {C_{{66}} } \right)\left( {\alpha \Delta T + \beta \Delta C} \right)\left( {1,z,f} \right)} {\text{d}}z \hfill \\ N_{{33}}^{T} = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left( {C_{{13}} + C_{{23}} + C_{{33}} } \right)\left( {\alpha \Delta T + \beta \Delta C} \right)\frac{{{\text{d}}g}}{{{\text{d}}z}}} {\text{d}}z \hfill \\ Q_{i} = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\sigma _{i}^{{}} g} {\text{d}}z\begin{array}{*{20}c} {} & {\left( {i = 4,5} \right)} \\ \end{array} \hfill \\ Q_{3} = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\frac{{{\text{d}}g}}{{{\text{d}}z}}\sigma _{z}^{{}} } {\text{d}}z \hfill \\ q_{1} = \frac{{\partial N_{{11}}^{T} }}{{\partial x}} + \frac{{\partial N_{{12}}^{T} }}{{\partial y}} \hfill \\ q_{2} = \frac{{\partial N_{{12}}^{T} }}{{\partial x}} + \frac{{\partial ^{2} M_{{22}}^{T} }}{{\partial y}} \hfill \\ q_{3} = - q + \frac{{\partial ^{2} M_{{11}}^{T} }}{{\partial x^{2} }} + 2\frac{{\partial ^{2} M_{{12}}^{T} }}{{\partial x\partial y}} + \frac{{\partial ^{2} M_{{22}}^{T} }}{{\partial y^{2} }} \hfill \\ q_{4} = - q + \frac{{\partial ^{2} P_{{11}}^{T} }}{{\partial x^{2} }} + 2\frac{{\partial ^{2} P_{{12}}^{T} }}{{\partial x\partial y}} + \frac{{\partial ^{2} P_{{22}}^{T} }}{{\partial y^{2} }} \hfill \\ q_{5} = N_{{33}}^{T} . \hfill \\ \end{gathered}$$
(11)

To achieve the equations of motion in terms of displacement ingredients, it is essential to substitute Eqs. (8) and (11) into Eq. (10) as below:

$$\begin{gathered} A_{{11}} \frac{{\partial ^{2} u_{{}} }}{{\partial x^{2} }} - B_{{11}} \frac{{\partial ^{3} w_{{\text{b}}} }}{{\partial x^{3} }} - D_{{11}} \frac{{\partial ^{3} w_{{\text{s}}} }}{{\partial x^{3} }} + A_{{12}} \frac{{\partial ^{2} v_{{}} }}{{\partial x\partial y}} - B_{{12}} \frac{{\partial ^{3} w_{{\text{b}}} }}{{\partial x\partial y^{2} }} - D_{{12}} \frac{{\partial ^{3} w_{{\text{s}}} }}{{\partial x\partial y^{2} }} + E_{{13}}^{'} \frac{{\partial w_{z} }}{{\partial x}} \hfill \\ + \frac{{\partial A_{{11}} }}{{\partial x}}\frac{{\partial u_{{}} }}{{\partial x}} - \frac{{\partial B_{{11}} }}{{\partial x}}\frac{{\partial ^{2} w_{{\text{b}}} }}{{\partial x^{2} }} - \frac{{\partial D_{{11}} }}{{\partial x}}\frac{{\partial ^{2} w_{{\text{s}}} }}{{\partial x^{2} }} + \frac{{\partial A_{{12}} }}{{\partial x}}\frac{{\partial v_{{}} }}{{\partial y}} - \frac{{\partial B_{{12}} }}{{\partial x}}\frac{{\partial ^{2} w_{{\text{b}}} }}{{\partial y^{2} }} - \frac{{\partial D_{{12}} }}{{\partial x}}\frac{{\partial ^{2} w_{{\text{s}}} }}{{\partial y^{2} }} + \frac{{\partial E_{{13}}^{'} }}{{\partial x}}w_{z} \hfill \\ + A_{{66}} \frac{{\partial ^{2} u_{{}} }}{{\partial y^{2} }} + A_{{66}} \frac{{\partial ^{2} v_{{}} }}{{\partial x\partial y}} - 2B_{{66}} \frac{{\partial ^{3} w_{{\text{b}}} }}{{\partial x\partial y^{2} }} - 2D_{{66}} \frac{{\partial ^{3} w_{{\text{s}}} }}{{\partial x\partial y^{2} }} = \left( {1 - \mu ^{2} \nabla ^{2} } \right)\left( {I_{0} \ddot{u}_{{}} - I_{1} \frac{{\partial \ddot{w}_{{\text{b}}} }}{{\partial x}} - I_{3} \frac{{\partial \ddot{w}_{{\text{s}}} }}{{\partial x}} + q_{1} } \right) \hfill \\ \end{gathered}$$
(12a)
$$\begin{gathered} A_{{12}} \frac{{\partial ^{2} u_{{}} }}{{\partial x\partial y}} - B_{{12}} \frac{{\partial ^{3} w_{{\text{b}}} }}{{\partial x^{2} \partial y}} - D_{{12}} \frac{{\partial ^{3} w_{{\text{s}}} }}{{\partial x^{2} \partial y}} + A_{{22}} \frac{{\partial ^{2} v_{{}} }}{{\partial y^{2} }} - B_{{22}} \frac{{\partial ^{3} w_{{\text{b}}} }}{{\partial y^{3} }} - D_{{22}} \frac{{\partial ^{3} w_{{\text{s}}} }}{{\partial y^{3} }} + E_{{23}}^{'} \frac{{\partial w_{z} }}{{\partial y}} \hfill \\ + A_{{66}} \frac{{\partial ^{2} u_{{}} }}{{\partial x\partial y}} + A_{{66}} \frac{{\partial ^{2} v_{{}} }}{{\partial x^{2} }} - 2B_{{66}} \frac{{\partial ^{3} w_{{\text{b}}} }}{{\partial x^{2} \partial y}} - 2D_{{66}} \frac{{\partial ^{3} w_{{\text{s}}} }}{{\partial x^{2} \partial y}} + \frac{{\partial A_{{66}} }}{{\partial x}}\frac{{\partial u_{{}} }}{{\partial y}} + \frac{{\partial A_{{66}} }}{{\partial x}}\frac{{\partial v_{{}} }}{{\partial x}} - 2\frac{{\partial B_{{66}} }}{{\partial x}}\frac{{\partial ^{2} w_{{\text{b}}} }}{{\partial x\partial y}} - 2\frac{{\partial D_{{66}} }}{{\partial x}}\frac{{\partial ^{2} w_{{\text{s}}} }}{{\partial x\partial y}} \hfill \\ = \left( {1 - \mu ^{2} \nabla ^{2} } \right)\left( {I_{0} \ddot{v}_{{}} - I_{1} \frac{{\partial \ddot{w}_{{\text{b}}} }}{{\partial y}} - I_{3} \frac{{\partial \ddot{w}_{{\text{s}}} }}{{\partial y}} + q_{2} } \right) \hfill \\ \end{gathered}$$
(12b)
$$\begin{gathered} B_{{11}} \frac{{\partial ^{3} u_{{}} }}{{\partial x^{3} }} - E_{{11}} \frac{{\partial ^{4} w_{{\text{b}}} }}{{\partial x^{4} }} - F_{{11}} \frac{{\partial ^{4} w_{{\text{s}}} }}{{\partial x^{4} }} + B_{{12}} \frac{{\partial ^{3} v_{{}} }}{{\partial x^{2} \partial y}} - E_{{12}} \frac{{\partial ^{4} w_{{\text{b}}} }}{{\partial x^{2} \partial y^{2} }} - F_{{12}} \frac{{\partial ^{4} w_{{\text{s}}} }}{{\partial x^{2} \partial y^{2} }} + E_{{13}}^{{''}} \frac{{\partial ^{2} w_{z} }}{{\partial x^{2} }} \hfill \\ + 2\frac{{\partial ^{{}} B_{{11}} }}{{\partial x^{{}} }}\frac{{\partial ^{2} u_{{}} }}{{\partial x^{2} }} - 2\frac{{\partial ^{{}} E_{{11}} }}{{\partial x^{{}} }}\frac{{\partial ^{3} w_{{\text{b}}} }}{{\partial x^{3} }} - 2\frac{{\partial ^{{}} F_{{11}} }}{{\partial x^{{}} }}\frac{{\partial ^{3} w_{{\text{s}}} }}{{\partial x^{3} }} + 2\frac{{\partial ^{{}} B_{{12}} }}{{\partial x^{{}} }}\frac{{\partial ^{2} v_{{}} }}{{\partial x\partial y}} - 2\frac{{\partial ^{{}} E_{{12}} }}{{\partial x^{{}} }}\frac{{\partial ^{3} w_{{\text{b}}} }}{{\partial x\partial y^{2} }} \hfill \\ - 2\frac{{\partial ^{{}} F_{{12}} }}{{\partial x^{{}} }}\frac{{\partial ^{3} w_{s} }}{{\partial x\partial y^{2} }} + 2\frac{{\partial ^{{}} E_{{13}}^{{''}} }}{{\partial x^{{}} }}\frac{{\partial ^{{}} w_{z} }}{{\partial x^{{}} }} + \frac{{\partial ^{2} B_{{11}} }}{{\partial x^{2} }}\frac{{\partial u_{{}} }}{{\partial x}} - \frac{{\partial ^{2} E_{{11}} }}{{\partial x^{2} }}\frac{{\partial ^{2} w_{{\text{b}}} }}{{\partial x^{2} }} - \frac{{\partial ^{2} F_{{11}} }}{{\partial x^{2} }}\frac{{\partial ^{2} w_{{\text{s}}} }}{{\partial x^{2} }} + \frac{{\partial ^{2} B_{{12}} }}{{\partial x^{2} }}\frac{{\partial v_{{}} }}{{\partial y}} \hfill \\ - \frac{{\partial ^{2} E_{{12}} }}{{\partial x^{2} }}\frac{{\partial ^{2} w_{{\text{b}}} }}{{\partial y^{2} }} - \frac{{\partial ^{2} F_{{12}} }}{{\partial x^{2} }}\frac{{\partial ^{2} w_{{\text{s}}} }}{{\partial y^{2} }} + \frac{{\partial ^{2} E_{{13}}^{{''}} }}{{\partial x^{2} }}w_{z} + B_{{12}} \frac{{\partial ^{3} u_{{}} }}{{\partial x\partial y^{2} }} - E_{{12}} \frac{{\partial ^{4} w_{{\text{b}}} }}{{\partial x^{2} \partial y^{2} }} - F_{{12}} \frac{{\partial ^{4} w_{{\text{s}}} }}{{\partial x^{2} \partial y^{2} }} + B_{{22}} \frac{{\partial ^{3} v_{{}} }}{{\partial y^{3} }} \hfill \\ - E_{{22}} \frac{{\partial ^{4} w_{{\text{b}}} }}{{\partial y^{4} }} - F_{{22}} \frac{{\partial ^{4} w_{{\text{s}}} }}{{\partial y^{4} }} + E_{{23}}^{{''}} \frac{{\partial ^{2} w_{z} }}{{\partial y^{2} }} + 2B_{{66}} \frac{{\partial ^{3} u_{{}} }}{{\partial x\partial y^{2} }} + 2B_{{66}} \frac{{\partial ^{3} v_{{}} }}{{\partial x^{2} \partial y}} - 4E_{{66}} \frac{{\partial ^{4} w_{{\text{b}}} }}{{\partial x^{2} \partial y^{2} }} - 4F_{{66}} \frac{{\partial ^{4} w_{{\text{s}}} }}{{\partial x^{2} \partial y^{2} }} \hfill \\ + 2\frac{{\partial B_{{66}} }}{{\partial x}}\frac{{\partial ^{2} u_{{}} }}{{\partial y^{2} }} + 2\frac{{\partial B_{{66}} }}{{\partial x}}\frac{{\partial ^{2} v_{{}} }}{{\partial x\partial y}} - 4\frac{{\partial E_{{66}} }}{{\partial x}}\frac{{\partial ^{3} w_{{\text{b}}} }}{{\partial x\partial y^{2} }} - 4\frac{{\partial F_{{66}} }}{{\partial x}}\frac{{\partial ^{3} w_{{\text{s}}} }}{{\partial x\partial y^{2} }} \hfill \\ = \left( {1 - \mu ^{2} \nabla ^{2} } \right)\left( {I_{1} \frac{{\partial \dot{u}_{{}} }}{{\partial x}} + I_{1} \frac{{\partial \dot{v}}}{{\partial y}} + I_{0} \ddot{w}_{{\text{b}}} + I_{0} \ddot{w}_{{\text{s}}} + I_{6} \ddot{w}_{z} - I_{2} \frac{{\partial ^{2} \ddot{w}_{{\text{b}}} }}{{\partial x^{2} }} - I_{4} \frac{{\partial ^{2} \ddot{w}_{{\text{s}}} }}{{\partial x^{2} }} - I_{2} \frac{{\partial ^{2} \ddot{w}_{{\text{b}}} }}{{\partial y^{2} }} - I_{4} \frac{{\partial ^{2} \ddot{w}_{{\text{s}}} }}{{\partial y^{2} }} + q_{3} } \right) \hfill \\ \end{gathered}$$
(12c)
$$\begin{gathered} D_{{11}} \frac{{\partial ^{3} u_{{}} }}{{\partial x^{3} }} - F_{{11}} \frac{{\partial ^{4} w_{{\text{b}}} }}{{\partial x^{4} }} - H_{{11}} \frac{{\partial ^{4} w_{s} }}{{\partial x^{4} }} + D_{{12}} \frac{{\partial ^{3} v_{{}} }}{{\partial x^{2} \partial y}} - F_{{12}} \frac{{\partial ^{4} w_{{\text{b}}} }}{{\partial x^{2} \partial y^{2} }} - H_{{12}} \frac{{\partial ^{4} w_{{\text{s}}} }}{{\partial x^{2} \partial y^{2} }} + E_{{13}}^{{'''}} \frac{{\partial ^{2} w_{z} }}{{\partial x^{2} }} \hfill \\ + 2\frac{{\partial ^{{}} D_{{11}} }}{{\partial x^{{}} }}\frac{{\partial ^{2} u_{{}} }}{{\partial x^{2} }} - 2\frac{{\partial ^{{}} F_{{11}} }}{{\partial x^{{}} }}\frac{{\partial ^{3} w_{{\text{b}}} }}{{\partial x^{3} }} - 2\frac{{\partial ^{{}} H_{{11}} }}{{\partial x^{{}} }}\frac{{\partial ^{3} w_{{\text{s}}} }}{{\partial x^{3} }} + 2\frac{{\partial ^{{}} D_{{12}} }}{{\partial x^{{}} }}\frac{{\partial ^{2} v_{{}} }}{{\partial x\partial y}} - 2\frac{{\partial ^{{}} F_{{12}} }}{{\partial x^{{}} }}\frac{{\partial ^{3} w_{{\text{b}}} }}{{\partial x\partial y^{2} }} \hfill \\ - 2\frac{{\partial ^{{}} H_{{12}} }}{{\partial x^{{}} }}\frac{{\partial ^{3} w_{{\text{s}}} }}{{\partial x\partial y^{2} }} + 2\frac{{\partial ^{{}} E_{{13}}^{{'''}} }}{{\partial x^{{}} }}\frac{{\partial ^{{}} w_{z} }}{{\partial x^{{}} }} + \frac{{\partial ^{2} D_{{11}} }}{{\partial x^{2} }}\frac{{\partial u_{{}} }}{{\partial x}} - \frac{{\partial ^{2} F_{{11}} }}{{\partial x^{2} }}\frac{{\partial ^{2} w_{{\text{b}}} }}{{\partial x^{2} }} - \frac{{\partial ^{2} H_{{11}} }}{{\partial x^{2} }}\frac{{\partial ^{2} w_{{\text{s}}} }}{{\partial x^{2} }} + \frac{{\partial ^{2} D_{{12}} }}{{\partial x^{2} }}\frac{{\partial v_{{}} }}{{\partial y}} \hfill \\ - \frac{{\partial ^{2} F_{{12}} }}{{\partial x^{2} }}\frac{{\partial ^{2} w_{{\text{b}}} }}{{\partial y^{2} }} - \frac{{\partial ^{2} H_{{12}} }}{{\partial x^{2} }}\frac{{\partial ^{2} w_{{\text{s}}} }}{{\partial y^{2} }} + \frac{{\partial ^{2} E_{{13}}^{{'''}} }}{{\partial x^{2} }}w_{z} + D_{{12}} \frac{{\partial ^{3} u_{{}} }}{{\partial x\partial y^{2} }} - F_{{12}} \frac{{\partial ^{4} w_{{\text{b}}} }}{{\partial x^{2} \partial y^{2} }} - H_{{12}} \frac{{\partial ^{4} w_{{\text{s}}} }}{{\partial x^{2} \partial y^{2} }} \hfill \\ + D_{{22}} \frac{{\partial ^{3} v_{{}} }}{{\partial y^{3} }} - F_{{22}} \frac{{\partial ^{4} w_{{\text{b}}} }}{{\partial y^{4} }} - H_{{22}} \frac{{\partial ^{4} w_{s} }}{{\partial y^{4} }} + E_{{23}}^{{'''}} \frac{{\partial ^{2} w_{z} }}{{\partial y^{2} }} + 2D_{{66}} \frac{{\partial ^{3} u_{{}} }}{{\partial x\partial y^{2} }} + 2D_{{66}} \frac{{\partial ^{3} v_{{}} }}{{\partial x^{2} \partial y}} - 4F_{{66}} \frac{{\partial ^{4} w_{{\text{b}}} }}{{\partial x^{2} \partial y^{2} }} \hfill \\ - 4H_{{66}} \frac{{\partial ^{4} w_{{\text{s}}} }}{{\partial x^{2} \partial y^{2} }} + 2\frac{{\partial D_{{66}} }}{{\partial x}}\frac{{\partial ^{2} u_{{}} }}{{\partial y^{2} }} + 2\frac{{\partial D_{{66}} }}{{\partial x}}\frac{{\partial ^{2} v_{{}} }}{{\partial x\partial y}} - 4\frac{{\partial F_{{66}} }}{{\partial x}}\frac{{\partial ^{3} w_{{\text{b}}} }}{{\partial x\partial y^{2} }} - 4\frac{{\partial H_{{66}} }}{{\partial x}}\frac{{\partial ^{3} w_{{\text{s}}} }}{{\partial x\partial y^{2} }} \hfill \\ + J_{{44}} \frac{{\partial ^{2} w_{{\text{s}}} }}{{\partial x^{2} }} + J_{{44}} \frac{{\partial ^{2} w_{z} }}{{\partial x^{2} }} + \frac{{\partial J_{{44}} }}{{\partial x}}\frac{{\partial ^{{}} w_{{\text{s}}} }}{{\partial x^{{}} }} + \frac{{\partial J_{{44}} }}{{\partial x}}\frac{{\partial ^{{}} w_{z} }}{{\partial x^{{}} }} + J_{{55}} \frac{{\partial ^{2} w_{{\text{s}}} }}{{\partial y^{2} }} + J_{{55}} \frac{{\partial ^{2} w_{z} }}{{\partial y^{2} }} \hfill \\ = \left( {1 - \mu ^{2} \nabla ^{2} } \right)\left( {I_{3} \frac{{\partial \dot{u}_{{}} }}{{\partial x}} + I_{3} \frac{{\partial \dot{v}_{{}} }}{{\partial y}} + I_{0} \ddot{w}_{{\text{b}}} + I_{0} \ddot{w}_{{\text{s}}} - I_{4} \frac{{\partial ^{2} \ddot{w}_{{\text{b}}} }}{{\partial x^{2} }} - I_{5} \frac{{\partial ^{2} \ddot{w}_{{\text{s}}} }}{{\partial x^{2} }} - I_{5} \frac{{\partial ^{2} \ddot{w}_{{\text{s}}} }}{{\partial y^{2} }} - I_{4} \frac{{\partial ^{2} \ddot{w}_{{\text{b}}} }}{{\partial y^{2} }} + I_{6} \ddot{w}_{z} + q_{4} } \right) \hfill \\ \end{gathered}$$
(12d)
$$\begin{gathered} J_{{44}} \frac{{\partial ^{2} w_{{\text{s}}} }}{{\partial x^{2} }} + J_{{44}} \frac{{\partial ^{2} w_{z} }}{{\partial x^{2} }} + \frac{{\partial J_{{44}} }}{{\partial x}}\frac{{\partial ^{{}} w_{{\text{s}}} }}{{\partial x^{{}} }} + \frac{{\partial J_{{44}} }}{{\partial x}}\frac{{\partial ^{{}} w_{z} }}{{\partial x^{{}} }} + J_{{55}} \frac{{\partial ^{2} w_{{\text{s}}} }}{{\partial y^{2} }} + J_{{55}} \frac{{\partial ^{2} w_{z} }}{{\partial y^{2} }} \hfill \\ - E_{{13}}^{'} \frac{{\partial u_{{}} }}{{\partial x}} + E_{{23}}^{{''}} \frac{{\partial ^{2} w_{{\text{b}}} }}{{\partial x^{2} }} + E_{{23}}^{{'''}} \frac{{\partial ^{2} w_{{\text{s}}} }}{{\partial x^{2} }} - E_{{23}}^{'} \frac{{\partial v_{{}} }}{{\partial y}} + E_{{23}}^{{''}} \frac{{\partial ^{2} w_{{\text{b}}} }}{{\partial y^{2} }} + E^{\prime\prime\prime}\frac{{\partial ^{2} w_{{\text{s}}} }}{{\partial y^{2} }} - w_{z} E_{{23}}^{{''''}} \hfill \\ = \left( {1 - \mu ^{2} \nabla ^{2} } \right)\left( {I_{6} \ddot{w}_{{\text{s}}} + I_{6} \ddot{w}_{{\text{b}}} + I_{7} \ddot{w}_{z} + q_{5} } \right). \hfill \\ \end{gathered}$$
(12e)

The unknown coefficients of Eqs. (12a-e) are reported as following:

$$\begin{gathered} \left( {A_{{ij}} ,B_{{ij}} ,E_{{ij}} ,D_{{ij}} ,F_{{ij}} ,H_{{ij}} } \right) = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {C_{{ij}} \left( {1,z,z^{2} ,f,fz,f^{2} } \right){\text{d}}z} ,\left( {i,j = 1,2,6} \right) \hfill \\ \left( {E^{\prime}_{{ij}} ,E^{\prime\prime}_{{ij}} ,E^{\prime\prime\prime}_{{ij}} ,E^{\prime\prime}_{{ij}} } \right) = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {C_{{ij}} \left( {\frac{{{\text{d}}g}}{{{\text{d}}z}},z\frac{{{\text{d}}g}}{{{\text{d}}z}},f\frac{{{\text{d}}g}}{{{\text{d}}z}},\left( {\frac{{{\text{d}}g}}{{{\text{d}}z}}} \right)^{2} } \right){\text{d}}z} \hfill \\ J_{{ij}} = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {C_{{ij}} g^{2} {\text{d}}z} \hfill \\ \end{gathered}$$
(13)

3 Navier solution method

In the current research, the Navier solution procedure is utilized to achieve the vibration characteristics of the 2D-FG nanoplates with simply supported boundary conditions. Therefore, the relations of the boundary conditions are reported as below:

$$\begin{gathered} u\left( {x,0} \right) = u\left( {x,b} \right) = v\left( {0,y} \right) = v\left( {a,y} \right) = 0 \hfill \\ w_{b} \left( {x,0} \right) = w_{b} \left( {x,b} \right) = w_{b} \left( {0,y} \right) = w_{b} \left( {a,y} \right) = 0 \hfill \\ w_{s} \left( {x,0} \right) = w_{s} \left( {x,b} \right) = w_{s} \left( {0,y} \right) = w_{s} \left( {a,y} \right) = 0 \hfill \\ w_{z} \left( {x,0} \right) = w_{z} \left( {x,b} \right) = w_{z} \left( {0,y} \right) = w_{z} \left( {a,y} \right) = 0 \hfill \\ \end{gathered}$$
(14)

According to Navier solution procedure, the components of the displacement using double Fourier series are:

$$\begin{gathered} u\left( {x,y;t} \right) = \sum\limits_{{r = 1}}^{\infty } {\sum\limits_{{s = 1}}^{\infty } {} U_{{rs}} } \cos \left( {\alpha x} \right)_{r} \sin \left( {\beta y} \right)_{s} e^{{i\omega t}} \hfill \\ v\left( {x,y;t} \right) = \sum\limits_{{r = 1}}^{\infty } {\sum\limits_{{s = 1}}^{\infty } {} V_{{rs}} } \sin \left( {\alpha x} \right)_{r} \cos \left( {\beta y} \right)_{s} e^{{i\omega t}} \hfill \\ w_{{\text{b}}} \left( {x,y;t} \right) = \sum\limits_{{r = 1}}^{\infty } {\sum\limits_{{s = 1}}^{\infty } {} W_{{rs}}^{b} } \sin \left( {\alpha x} \right)_{r} \sin \left( {\beta y} \right)_{s} e^{{i\omega t}} \hfill \\ w_{{\text{s}}} \left( {x,y;t} \right) = \sum\limits_{{r = 1}}^{\infty } {\sum\limits_{{s = 1}}^{\infty } {} W_{{rs}}^{s} } \sin \left( {\alpha x} \right)_{r} \sin \left( {\beta y} \right)_{s} e^{{i\omega t}} \hfill \\ w_{z} \left( {x,y;t} \right) = \sum\limits_{{r = 1}}^{\infty } {\sum\limits_{{s = 1}}^{\infty } {} W_{{rs}}^{z} } \sin \left( {\alpha x} \right)_{r} \sin \left( {\beta y} \right)_{s} e^{{i\omega t}} . \hfill \\ \end{gathered}$$
(15)

In which \(\omega\) is the frequency of the nanoplate; \(U_{{rs}}\), \(V_{{rs}}\), \(W_{{rs}}^{b}\),\(W_{{rs}}^{s}\) and \(W_{{rs}}^{z}\) are the unknown factors, \(\alpha = \frac{{r\pi }}{a}\),\(\beta = \frac{{s\pi }}{b}\). To report the equations of motion in terms of ingredients of displacement, it is essential to substitute Eq. (15) into Eqs. (12a-e) as below:

$$\begin{gathered} \left[ {M_{{ij}} } \right]\left\{ \begin{gathered} \ddot{U}_{{rs}} \hfill \\ \ddot{V}_{{rs}} \hfill \\ \ddot{W}_{{rs}}^{b} \hfill \\ \ddot{W}_{{rs}}^{s} \hfill \\ \ddot{W}_{{rs}}^{z} \hfill \\ \end{gathered} \right\} + \left[ {K_{{ij}} } \right]\left\{ \begin{gathered} U_{{rs}} \hfill \\ V_{{rs}} \hfill \\ W_{{rs}}^{b} \hfill \\ W_{{rs}}^{s} \hfill \\ W_{{rs}}^{z} \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} 0 \hfill \\ 0 \hfill \\ Q_{{rs}} \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{gathered} \right\} \hfill \\ \Rightarrow \left( {\left[ {K_{{ij}} } \right] - \omega ^{2} \left[ {M_{{ij}} } \right]} \right)\left\{ \Delta \right\} = 0 \Rightarrow \det \left( {\left[ {K_{{ij}} } \right] - \omega ^{2} \left[ {M_{{ij}} } \right]} \right) = 0 \Rightarrow \omega = \left( {{\text{eig}}\left( {\left[ M \right]^{{ - 1}} \left[ K \right]} \right)} \right)^{{0.5}} . \hfill \\ \end{gathered}$$
(16)

4 Numerical results

In the current research, the vibration investigation of the 2D-FG nanoplates pondering nonlocality subjected to hygro-thermo conditions according to a novel HSDT is examined for the first time. The dimensionless forms of the natural frequency parameters are presented as:

$$\begin{gathered} \varpi = \omega h\sqrt {\frac{\rho }{E}} \hfill \\ \varpi = \frac{{\omega a^{2} }}{h}\sqrt {\frac{{\rho _{{\text{m}}} }}{{E_{{\text{m}}} }}} . \hfill \\ \end{gathered}$$
(17)

The material features of the 2D-FG nanoplate are reported as \(E_{{\text{m}}} = 70\;{\text{GPa,}}\;E_{{\text{c}}} = 200\,{\text{GPa}}\),\(v_{{\text{m}}} = v_{{\text{c}}} = 0.34\), \(\rho _{{\text{m}}} = 2702\frac{{{\text{kg}}}}{{{\text{m}}^{3} }}\) and \(\rho _{{\text{c}}} = 5700\frac{{{\text{kg}}}}{{{\text{m}}^{3} }}\).

4.1 Verification of the results

To investigate the accuracy of the current research, first, the outcomes are verified. To verify the outcomes accurately, it is assumed that the material features of the plate vary based on Voigt’s rule of mixtures as following:

$$\begin{aligned} E\left( z \right) & = \left( {E_{{\text{c}}} - E_{{\text{m}}} } \right)\left( {\frac{z}{h} + 0.5} \right)^{k} + E_{{\text{m}}} \\ \rho \left( z \right) & = \left( {\rho _{{\text{c}}} - \rho _{{\text{m}}} } \right)\left( {\frac{z}{h} + 0.5} \right)^{k} + \rho _{{\text{m}}} . \\ \end{aligned}$$
(18)

where \(k\) is the FG index.

In Table 1, the natural frequency of the FG plate for various values of the FG index and \(\frac{a}{h}\)(side-to-thickness) ratio with assumption \(\Delta T = 0,\Delta C = 0,\mu = 0\) has been examined. The results of Refs [36,37,38,39,40] are dedicated to investigate the accuracy of the current model. With investigating the outcomes in Table 1, it can be deduced that the achieving data of the current research are in perfect agreement with similar researches.

Table 1 Natural frequency of the functionally-graded plates for several FG index
Full size table

In Table 2, the natural frequency of the homogeneous nanoplate for various values of the nonlocality index and \(\frac{b}{a}\)(length -to-side) ratio with assumption \(\Delta T = 0,\Delta C = 0\) has been examined. The results of Refs [41, 42] are dedicated to investigate the accuracy of the current model. With investigating the outcomes in Table 2, it can be deduced that the achieving data of the current research are in perfect agreement with the similar researches.

Table 2 The efficacy of the nonlocality on the natural frequency of the homogeneous nanoplate
Full size table

4.2 Effects of the nonlocality on the frequency of the nanoplate

In Table 3, the efficacies of the geometrical parameters and nonlocality index are reported on the vibration characteristics of the nanoplates. The results are provided for both thick (\(\frac{a}{h} = 5\)) and moderately thick (\(\frac{a}{h} = 10\)) nanoplate. We can declare that the frequency of the nanoplate reduces with growth in \(\frac{a}{h}\) and \(\frac{b}{a}\) ratios. In addition, we can report that with enhancing the value of the nonlocality index, the frequency of the structure reduces. Also, with enhancing the small size parameter, its efficacy on the frequency of the nanosize structure will reduce. Also, we can report that with increasing the small size parameter, the efficacy of the thickness stretching on the frequency of the nanoplate reduces. Therefore, we can render that with enhancing the stiffness of the structure (i.e., with reducing the nonlocality index), the thickness stretching has essential impacts on the responses of the nanosize systems.

Table 3 The efficacy of the nonlocality and geometrical parameters on the natural frequency of the nanoplate ( \(T_{i} = C_{i} = 0,\,\;n_{i} = m_{i} = 0\))
Full size table

In Fig. 3, the efficacies of the nonlocality index and \(\frac{a}{h}\) ratio on the vibration characteristics of the nanoplate are examined. The results are provided for thick (\(\frac{a}{h} = 5\)), moderately thick (\(\frac{a}{h} = 10\)) and thin (\(\frac{a}{h} = 30\)) nanoplates. We can declare that the natural frequency of the nanoplate reduces with growth in \(\frac{a}{h}\) ratio. Also, we can report that with enhancing/reducing the side/thickness of the nanoplate, its efficacy on the frequency of the nanoplate will reduce. Moreover, with enhancing the nonlocality index, the efficacy of the thickness stretching on the frequency of the nanoplate reduces. Also, in thick nanoplates (\(\frac{a}{h} = 5\)), nonlocality index has essential role on the mechanical responses of the system. However, in thin nanoplates (\(\frac{a}{h} = 30\)), nonlocality index has minor role on the mechanical responses of the system. Therefore, it is noticeable that in thin nanoplates, the efficacy of the nonlocality is neglectable.

Fig. 3
figure 3

The efficacy of the nonlocality and \(\frac{a}{h}\) ratio on the natural frequency of the nanoplate (\(T_{i} = C_{i} = 0,n_{i} = m_{i} = 0\))

Full size image

In Fig. 4, the efficacies of the nonlocality index and FG parameters on the frequency of the nanoplate are reported. We can declare that with enhancing the value of \(n_{1}\), the frequency of the nanoplate decreases. This is because with enhancing the FG index, the value of the components of the mass matrix of the system increase. Also, with reducing/increasing the value of \(n_{1}\), its efficacy on the frequency of the nanoplate reduces/enhances. Also, with enhancing/reducing the value of \(n_{1}\), the efficacy of the nonlocality index on the frequency of the nanoplate reduces/enhances. Moreover, when we ponder the nonlocality, FG indexes have important role on the dynamic responses of the FG nanoplate.

Fig. 4
figure 4

The efficacy of the FG parameter on the natural frequency of the nanoplate for several small size impact (\(T_{i} = C_{i} = 0,n_{i} = m_{i} ,n_{2} = m_{2} = 1\))

Full size image

In Fig. 5, the efficacies of the size effect parameter and FG indexes on the frequency of the nanoplate are reported. We can declare that with enhancing the value of \(n_{2}\), the frequency of the nanoplate reduces. This is because with enhancing the FG indexes, the value of the components of the mass matrix of the system increase. Also, with increasing/reducing the nonlocality index, its efficacy on the vibration characteristics of the nanoplate will reduce/enhance.

Fig. 5
figure 5

The efficacy of the FG parameter on the natural frequency of the nanoplate for several small size impact (\(T_{i} = C_{i} = 0,n_{2} = m_{2} ,n_{1} = m_{1} = n_{3} = m_{3} = 1\))

Full size image

4.3 Effects of the hygro-thermo conditions on the frequency of the nanoplate

In this part, the natural frequency investigation of the 2D-FG nanoplates in the hygro-thermo conditions is reported.

In Fig. 6, the variation of the non-dimensional frequency of the 2D-FG nanoplate against temperature variation for various Passion’s ratio is presented. We can express that with increasing the Passion’s ratio, the natural frequency of the 2D-FG nanoplate enhances. Also, with increasing the temperature variation, the natural frequency of the 2D-FG nanoplate rises linearly. In addition, with enhancing the temperature variation, the frequency chart behaves similarly for various values of Passion’s ratio.

Fig. 6
figure 6

The efficacy of the thermal conditions on the frequency of the nanoplate for several Passion’s ratio (\(T_{2} = T_{3} = C_{2} = 0,\mu = 1,n_{i} = m_{i} = 0\left( {i = 1,2, \ldots ,4} \right)\))

Full size image

In Fig. 7, the variation of the non-dimensional frequency of the 2D-FG nanoplate against temperature variation for various nonlocal size effect is presented. We can express that with increasing the nonlocal size effect, the natural frequency of the 2D-FG nanoplate decreases. Also, with increasing the temperature variation, the natural frequency of the 2D-FG nanoplate increases linearly. In addition, with enhancing the size effect parameter, its impact on the natural frequency of the plate reduces. Moreover, with enhancing/reducing the nonlocality index, the impacts of the temperature variation on the natural frequency of the 2D-FG nanoplate will reduce/increase. Therefore, we can conclude that with increasing the size effect parameter, the slope of the chart will reduce when the variation of the temperature rises.

Fig. 7
figure 7

The variation of the non-dimensional frequency of nanoplate against temperature variation for various nonolocal index (\(\frac{b}{a} = 1,n_{2} = m_{2} = 1,T_{2} = T_{3} = C_{1} = 0\))

Full size image

In Table 4, the variation of the non-dimensional frequency of the 2D-FG nanoplate against temperature variation for various FG parameters is presented. We can express that with increasing the temperature variation, the natural frequency of the 2D-FG nanoplate increases. Also, with increasing the FG parameters \(\left( {n_{1} ,n_{2} } \right)\), the natural frequency of the nanoplate decreases. This is because when the FG parameters increase, the stiffness of the system increases, however; the components of the mass matrix of the system increase more than components of the stiffness matrix (For more detail, please refer to Eqs. (12a–e). Therefore, with increasing the FG parameters, the natural frequency of the nanoplate will decrease. In addition, with increasing the value of \(n_{1}\) parameter, its impact on the natural frequency of the 2D-FG nanoplate will increase when the temperature variation grows. Also, with increasing the values of \(n_{2}\) parameter, its effects on the natural frequency of the 2D-FG nanoplate will enhance when the temperature variation increases.

Table 4 The efficacy of the temperature variation and FG parameters on the natural frequency of the FG nanoplate (\(\frac{b}{a} = 1,n_{2} = m_{2} = 1,T_{2} = T_{3} = C_{1} = 0,\mu = 0.5\))
Full size table

In Fig. 8, the variation of the non-dimensional frequency of the 2D-FG nanoplate against temperature variation for several values of \(n_{1}\) parameter is presented. We can express that with increasing/decreasing the temperature variation, the impacts of the \(n_{1}\) parameter on the frequency of the plate will decrease/rise. Also, with growing/decreasing the values of the \(n_{1}\) parameter, the impacts of the temperature variation on the natural frequency of the plate will rise/decrease.

Fig. 8
figure 8

The variation of the non-dimensional frequency of nanoplate against temperature variation for various values of \(n_{1}\) parameter (\(\frac{b}{a} = 1,n_{2} = m_{2} = 1,T_{2} = T_{3} = C_{1} = 0,\mu = 0.5\))

Full size image

In Fig. 9, the variation of the non-dimensional frequency of the 2D-FG nanoplate against temperature variation for various values of \(n_{2}\) parameter is presented. We can express that with enhancing the temperature variation, the frequency chart behaves similarly for several values of \(n_{2}\) parameter. Moreover, with enhancing the temperature variation, the intensity of the increase in frequencies are the same for various values of \(n_{2}\) parameter.

Fig. 9
figure 9

The variation of the non-dimensional frequency of nanoplate against temperature variation for various values of \(n_{2}\) parameter (\(\frac{b}{a} = 1,n_{2} = m_{2} = 1,T_{2} = T_{3} = C_{1} = 0,\mu = 0.5\))

Full size image

5 Conclusions

In the current research, a novel nonlocal higher-order theory is presented to inquire about the free vibration analysis of the 2D-FG nanoplate subjected to hygro-thermo loading. The novelty of the current research is to present a new HSDT, which is an amalgamation of exponential, polynomial and trigonometric functions. Thickness stretching influence is considered according to higher-order shear and normal deformation theory. Size-dependent nonlocal elasticity theory is dedicated to pondering the nonlocality. The transverse component of displacement is divided into bending and shear components. To ponder the effects of the thermal and moisture conditions on the vibration characteristics of the 2D-FG nanoplate, we ponder the nonlinear relations for temperature and moisture fields. Hamilton’s axiom is dedicated to achieving the governing equations of motion. Then, the Navier solution technique is dedicated to derive the natural frequency of the nanoplate with S–S boundary conditions. The achieved results of the current research are:

  • The frequency of the nanoplate reduces with growth in \(\frac{a}{h}\) and \(\frac{b}{a}\) ratios.

  • With enhancing the value of the nonlocality index, the frequency of the structure reduces.

  • With enhancing the nonlocality index, its efficacy on the frequency of the nanosize structure will reduce.

  • In thick nanoplates, nonlocality index has vital role in the mechanical responses of the nanoplates. However, in thin nanoplates, nonlocality index has a minor role in the mechanical responses of the nanoplates.

  • With enhancing the value of FG indexes, the frequency of the nanoplate decreases.

  • With increasing/decreasing the size effect parameter, the impacts of the temperature variation on the natural frequency of the 2D-FG nanoplate will reduce/increase.

  • With increasing/decreasing the temperature variation, the impacts of the \(n_{1}\) parameter on the frequency of the plate will decrease/increase.

  • With enhancing the temperature variation, the frequency chart behaves similarly for various values of \(n_{2}\) parameter.

  • With enhancing the temperature variation, the frequency chart increases similarly for various values of Passion’s ratio.

  • With increasing the values of FG indexes, their impacts on the natural frequency of the 2D-FG nanoplate will increase when the temperature variation rises.