Analytical treatment on the nonlocal strain gradient vibrational response of postbuckled functionally graded porous micro-/nanoplates reinforced with GPL

Abstract

Through production of porous materials with remarkable complexity in geometry, functionally graded porous materials (FGPMs) have gained considerable attention for use in additive manufacturing in biomedical applications. In the current study, the size-dependent linear and nonlinear vibrational characteristics of axially loaded micro-/nanoplates made of FGPM reinforced with graphene platelets (GPLs) is investigated within both the prebuckling and postbuckling regimes. To this end, the nonlocal strain gradient continuum elasticity in conjunction with geometrical nonlinearity is implemented into the refined exponential shear deformation plate theory. On the basis of the closed-cell Gaussian random field scheme as well as the Halpin–Tsai micromechanical modeling, the mechanical properties of the FGPM reinforced with GPLs are achieved corresponding to the uniform and three different patterns of porosity dispersion. Via the variational approach, the differential equations of motion related to the nonlinear problem are constructed in the presence of nonlocality and strain gradient size dependency. Finally, with the aid of an improved perturbation technique together with the Galerkin method, analytical expressions in explicit form for the size-dependent linear frequency–load and deflection–nonlinear frequency responses of the FGPM micro-/nanoplates within stability and instability domains are obtained. It is displayed that within the prebuckling regime, the nonlocality causes reduction of the linear frequency of the micro-/nanoplate, while the strain gradient size dependency leads to increasing it. But within the postbuckling domain, these patterns are vice versa. Also, it is found that for a specific value of plate deflection, increasing the value of the porosity coefficient leads to increase in the frequency ratio of ω_NL/ω_L within both the prebuckling and postbuckling regimes.

1 Introduction

With the aid of advancements in material science, a large number of inorganic porous materials have been manufactured in recent years to be utilized in various applications such as insulation, biomedication, impact protection and membranes. The characteristics of a porous material vary depending on the size, arrangement and shape of the pores. However, through addition of nanofillers, it is possible to improve the mechanical properties of porous materials. Pop et al. [1] fabricated monolithic porous carbon nanotube-reinforced metals and ceramics by non-catalytic chemical vapor deposition using a double templating approach. Jun et al. [2] reported the mechanical properties of carbon nanotube-reinforced porous CuSn oil bearings using the powder metallurgy method. Hai et al. [3] produced a novel binary conductive porous alumina including carbon nanotubes. Chen et al. [4] studied the influence of the inclusion of thermal-responsive nano-hydroxyapatite and the porous structure of polylactide composites. Xu and Li [5] examined the effect of carbon nanofiber reinforcements on the mechanical properties of porous magnesium-matrix composites. Chen et al. [6] predicted the nonlinear vibration response of multilayer functionally graded porous nanocomposite beams reinforced by graphene platelets (GPLs). Hajmohammad et al. [7] performed a numerical analysis on the dynamic response of cylindrical shells reinforced with carbon nanotubes and submerged in an incompressible fluid under earthquake, thermal and moisture loads. Hosseini and Kolahchi [8] suggested a mathematical model for the seismic response of submerged carbon nanotube-reinforced cylindrical shells subjected to hygrothermal load.

Several unconventional continuum theories of elasticity have been proposed and employed taking different size dependencies into consideration [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57]. Based on reviewing the historical background, it can be concluded that the size effect from the stress nonlocality leads to softening–stiffness influence, but the strain gradient small-scale effect results in a hardening–stiffness effect. It means that no one of these non-classical continuum theories could perfectly cover the small-scale features at nanoscale. Therefore, Lim et al. [58] developed a new size-dependent elasticity theory, namely a nonlocal strain gradient theory which includes simultaneously both the softening and stiffening influences to describe the small-scale effects more efficiently.

After that, some investigations have been carried out using the nonlocal strain gradient elasticity theory to describe the size-dependent mechanical behaviors. For instance, Li and Hu [59] reported the small-sale effects on the nonlinear bending and free vibration behavior of functionally graded nanobeams on the basis of the nonlocal strain gradient theory. Simsek [60] used nonlocal strain gradient theory to capture the size effects on the nonlinear natural frequencies of functionally graded Euler–Bernoulli nanobeams. Tang et al. [61] analyzed the viscoelastic wave propagation in carbon nanotubes based upon the nonlocal strain gradient elasticity theory. Lu et al. [62] proposed higher-order nonlocal strain gradient beam models within the frameworks of Euler–Bernoulli and Timoshenko beam theories for bending and buckling analysis of nanobeams. Shahsavari et al. [63] used the theory of nonlocal strain gradient elasticity to examine the size dependency in shear buckling of nanoplates in hygrothermal environment. Sahmani and Aghdam [64, 65] predicted the linear and nonlinear vibrational responses of lipid supramolecular micro-/nanotubules with the prebuckling and postbuckling domains including nonlocality and strain gradient size effects. Radic [66] presented the buckling behavior of porous double-layered functionally graded nanoplates in hygrothermal environment via the nonlocal strain gradient first-order shear deformation plate model. Li et al. [67] utilized the nonlocal strain gradient elasticity theory within the framework of the Euler–Bernoulli beam theory to explore bending, buckling and free vibration of axially functionally graded nanobeams. Sahmani et al. [68,69,70] anticipated the nonlinear mechanical behaviors of porous micro-/nanostructures reinforced with graphene platelets based on the nonlocal strain gradient elasticity. Zeighampour et al. [71] employed the nonlocal strain gradient theory of elasticity to investigate the wave propagation in viscoelastic single-walled carbon nanotubes. Imani and Biglari [72] introduced a nonlocal strain gradient Timoshenko beam model to capture the size effects on the buckling and vibration responses of microtubules in axons. Sahmani and Safaei [73] studied the nonlinear free vibration response of bidirectional functionally graded micro-/nanobeams on the basis of the nonlocal strain gradient theory of elasticity.

The objective of the current investigation is to develop an analytical model for size-dependent linear and nonlinear vibration responses of axially loaded micro-/nanoplates made of functionally graded porous material (FGPM) reinforced with GPLs corresponding to both the prebuckling and postbuckling regimes. To accomplish this purpose, the nonlocal strain gradient theory of elasticity together with van Karman geometric nonlinearity is applied to a refined exponential shear deformation plate theory to construct an efficient non-classical plate model taking different features of size effect. Analytical explicit expressions are proposed for the size-dependent linear frequency–load and deflection–nonlinear frequency responses of FGPM micro-/nanoplates reinforced with GPLs.

2 Material properties of FGPM composites reinforced with GPLs

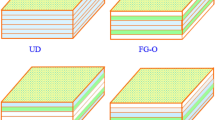
As it can be seen in Fig. 1, in addition to the uniform porous material (Pattern A), three different functionally graded patterns for FGPM, namely Patterns B, C, and D are taken into consideration for the composite micro-/nanoplate. As a result, the associated Young’s modulus (E), shear modulus (G) and mass density (ρ) can be extracted relevant to each pattern of porosity distribution as follows:

Fig. 1

Schematic representation of a FGPM micro-/nanoplate with different porosity dispersion patterns

$$\begin{aligned} & E\left( z \right) = \tilde{E}\left[ {1 - \varGamma_{p} s\left( z \right)} \right], \\ & G\left( z \right) = \frac{E\left( z \right)}{{\left( {2\left[ {1 - \nu \left( z \right)} \right]} \right)}}, \\ & \rho \left( z \right) = \tilde{\rho }\left[ {1 - \varGamma_{m} s\left( z \right)} \right] \\ \end{aligned}$$

(1)

where

$$s\left( z \right) = \left\{ {\begin{array}{*{20}l} {s_{0} } \hfill & {{\text{for}}\,{\text{pattern}}\,{\text{A}}} \hfill \\ {\cos \left( {\frac{\pi z}{2h} + \frac{\pi }{4}} \right)} \hfill & {{\text{for}}\,{\text{pattern}}\,{\text{B}}} \hfill \\ {\cos \left( {\frac{\pi z}{h}} \right)} \hfill & {{\text{for}}\,{\text{pattern}}\,{\text{C}}} \hfill \\ {1 - \cos \left( {\frac{\pi z}{h}} \right)} \hfill & {{\text{for}}\,{\text{pattern}}\,{\text{D}}} \hfill \\ \end{array} } \right.,$$

(2)

in which $\tilde{E}$ and $\tilde{\rho }$ stand for, respectively, the maximum Young’s modulus and maximum mass density of the FGPM reinforced with GPLs. It is assumed that for all porosity dispersion patterns, GPLs as the reinforcement phase are supposed to be distributed uniformly across the plate thickness. Consequently, the Halpin–Tsai micromechanical scheme [74] yields:

$$\tilde{E} = \left( {\frac{3}{8}\frac{{1 + \lambda_{L} \eta_{L} V_{\text{GPL}} }}{{1 - \eta_{L} V_{\text{GPL}} }} + \frac{5}{8}\frac{{1 + \lambda_{T} \eta_{T} V_{\text{GPL}} }}{{1 - \eta_{T} V_{\text{GPL}} }}} \right)E_{m},$$

(3)

where E_m represents the Young’s modulus of the metallic foam, and

$$\begin{aligned} & \eta_{L} = {{\left( {\frac{{E_{\text{GPL}} }}{{E_{m} }} - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{E_{\text{GPL}} }}{{E_{m} }} - 1} \right)} {\left( {\frac{{E_{\text{GPL}} }}{{E_{m} }} + \lambda_{L} } \right)}}} \right. \kern-0pt} {\left( {\frac{{E_{\text{GPL}} }}{{E_{m} }} + \lambda_{L} } \right)}},\quad \eta_{T} = {{\left( {\frac{{E_{\text{GPL}} }}{{E_{m} }} - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{E_{\text{GPL}} }}{{E_{m} }} - 1} \right)} {\left( {\frac{{E_{\text{GPL}} }}{{E_{m} }} + \lambda_{T} } \right)}}} \right. \kern-0pt} {\left( {\frac{{E_{\text{GPL}} }}{{E_{m} }} + \lambda_{T} } \right)}} \\ & \lambda_{L} = 2L_{\text{GPL}} /h_{\text{GPL}} ,\quad \lambda_{T} = 2b_{\text{GPL}} /h_{\text{GPL}} ,\\ \end{aligned}$$

(4)

in which $E_{\text{GPL}} , L_{\text{GPL}} , b_{\text{GPL}} , h_{\text{GPL}}$ in order are the Young’s modulus, length, width and thickness of the GPL reinforcements.

Furthermore, $V_{\text{GPL}}$ represents the volume fraction of the GPLs which can be evaluated as a function of weight fraction $W_{\text{GPL}}$ as follows:

$$V_{\text{GPL}} = {{W_{\text{GPL}} } \mathord{\left/ {\vphantom {{W_{\text{GPL}} } {\left[ {W_{\text{GPL}} + \left( {\frac{{\rho_{\text{GPL}} }}{{\rho_{m} }}} \right)\left( {1 - W_{\text{GPL}} } \right)} \right]}}} \right. \kern-0pt} {\left[ {W_{\text{GPL}} + \left( {\frac{{\rho_{\text{GPL}} }}{{\rho_{m} }}} \right)\left( {1 - W_{\text{GPL}} } \right)} \right]}},$$

(5)

where $\rho_{\text{GPL}}$ and ρ_m in order are the mass densities of the GPLs and the metallic foam of the reinforced porous micro-/nanoplate.

In addition, on the basis of the rule of mixture [75], the mass density ($\tilde{\rho }$) and Poisson’s ratio ($\tilde{\nu }$) of the FGPM micro-/nanoplate reinforced with GPLs can be obtained as

$$\begin{aligned} \tilde{\nu } & = \nu_{m} \left( {1 - V_{\text{GPL}} } \right) + \nu_{\text{GPL}} V_{\text{GPL}} , \\ \tilde{\rho } & = \rho_{m} \left( {1 - V_{\text{GPL}} } \right) + \rho_{\text{GPL}} V_{\text{GPL}}, \\ \end{aligned}$$

(6)

in which ν_m and ν_GPL in order denote the Poisson’s ratios of the metallic foam and GPL nanofillers.

In accordance with the Gaussian random field scheme [76], based on which all finite dimensional distributions are assumed to be multivariate normal distributions for any number of coordinates, the mass density coefficient (Γ_m) can be introduced in terms of the porosity coefficient (Γ_p) as follows:

$$\varGamma_{m} = 1.121\left[ {1 - \left( {1 - \varGamma_{p} s\left( z \right)} \right)^{1/2.3} } \right]/s\left( z \right).$$

(7)

In a similar way based upon the closed-cell Gaussian random field scheme [76], the Poisson’s ratio of the FGPM micro-/nanoplate relevant to the various porosity dispersion patterns can be extracted as:

$$\nu \left( z \right) = 0.221\left( {1 - \frac{\rho \left( z \right)}{{\tilde{\rho }}}} \right) + \tilde{\nu }\left[ {1 + 0.342\left( {1 - \frac{\rho \left( z \right)}{{\tilde{\rho }}}} \right)^{2} - 1.21\left( {1 - \frac{\rho \left( z \right)}{{\tilde{\rho }}}} \right)} \right].$$

(8)

To have an equal mass density for the FGPM micro-/nanoplate with different patterns of porosity dispersion, the correct value of s₀ can be defined as:

$$s_{0} = \frac{1}{{\varGamma_{p} }}\left[ {1 - \left( {\frac{{\frac{1}{h}\mathop \smallint \nolimits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \frac{\rho \left( z \right)}{{\tilde{\rho }}}{\text{d}}z + 0.121}}{1.121}} \right)^{2.3} } \right]$$

(9)

3 Nonlocal strain gradient refined plate model

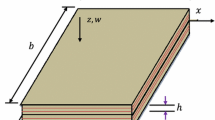
To capture the influence of shear deformation in a more efficient way, the refined plate theory with exponential distribution of the shear deformation is considered based on which there is no need to utilize a shear correction factor, and with the same number of independent variables, the bending components do not contribute toward the shear components and vice versa. Thereafter, the displacement components of an FGPM micro-/nanoplate can be expressed as:

$$u_{x} \left( {x,y,z,t} \right) = u\left( {x,y,t} \right) - z\frac{{\partial w\left( {x,y,t} \right)}}{\partial x} + ze^{{ - \frac{{2z^{2} }}{{h^{2} }}}} \psi_{x} \left( {x,y,t} \right) ,$$

(10a)

$$u_{y} \left( {x,y,z,t} \right) = v\left( {x,y,t} \right) - z\frac{{\partial w\left( {x,y,t} \right)}}{\partial y} + ze^{{ - \frac{{2z^{2} }}{{h^{2} }}}} \psi_{y} \left( {x,y,t} \right) ,$$

(10b)

$$u_{z} \left( {x,y,z,t} \right) = w\left( {x,y,t} \right) ,$$

(10c)

where u, v and w represent the associated displacements of the FGPM micro-/nanoplate reinforced with GPLs along the x-, y- and z-axis, respectively. Also, ψ_x and ψ_y in order are the rotations of the plate cross section at neutral plane normal about the y- and x-axis.

As a result, in accordance with the von Karman geometrical nonlinearity, the strain components can be written as:

$$\varepsilon_{xx} = \varepsilon_{xx}^{0} + z\kappa_{xx}^{\left( 1 \right)} + ze^{{ - \frac{{2z^{2} }}{{h^{2} }}}} \kappa_{xx}^{\left( 2 \right)} = \frac{\partial u}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} - z\frac{{\partial^{2} w}}{{\partial x^{2} }} + ze^{{ - \frac{{2z^{2} }}{{h^{2} }}}} \frac{{\partial \psi_{x} }}{\partial x},$$

(11a)

$$\varepsilon_{yy} = \varepsilon_{yy}^{0} + z\kappa_{yy}^{\left( 1 \right)} + ze^{{ - \frac{{2z^{2} }}{{h^{2} }}}} \kappa_{yy}^{\left( 2 \right)} = \frac{\partial v}{\partial y} + \frac{1}{2}\left( {\frac{\partial w}{\partial y}} \right)^{2} - z\frac{{\partial^{2} w}}{{\partial y^{2} }} + ze^{{ - \frac{{2z^{2} }}{{h^{2} }}}} \frac{{\partial \psi_{y} }}{\partial y} ,$$

(11b)

$$\gamma_{xy} = \gamma_{xy}^{0} + z\kappa_{xy}^{\left( 1 \right)} + ze^{{ - \frac{{2z^{2} }}{{h^{2} }}}} \kappa_{xy}^{\left( 2 \right)} = \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} + \frac{\partial w}{\partial x}\frac{\partial w}{\partial y} - 2z\frac{{\partial^{2} w}}{\partial x\partial y} + ze^{{ - \frac{{2z^{2} }}{{h^{2} }}}} \left( {\frac{{\partial \psi_{x} }}{\partial y} + \frac{{\partial \psi_{y} }}{\partial x}} \right) ,$$

(11c)

$$\gamma_{xz} = \left( {1 - \frac{{4z^{2} }}{{h^{2} }}} \right)e^{{ - \frac{{2z^{2} }}{{h^{2} }}}} \psi_{x} ,$$

(11d)

$$\gamma_{yz} = \left( {1 - \frac{{4z^{2} }}{{h^{2} }}} \right)e^{{ - \frac{{2z^{2} }}{{h^{2} }}}} \psi_{y} ,$$

(11e)

in which ɛ ⁰_ij , κ ⁽¹⁾_ij , κ ⁽²⁾_ij (i, j = x, y) are, respectively, the midplane strain components and the first- and higher-order curvature components.

Based upon the nonlocal strain gradient elasticity theory developed by Lim et al. [58], the coupling physical influences of the nonlocal and strain gradient size effects can be taken into account including different features of size effect. Therefore, the total nonlocal strain gradient stress tensor Λ for a FGPM micro-/nanoplate takes the following form:

$$\left( {1 - \mu^{2} \nabla^{2} } \right)\varLambda_{ij} = C_{ijkl} \varepsilon_{kl} - l^{2} C_{ijkl} \nabla^{2} \varepsilon_{kl},$$

(12)

in which μ denotes the nonlocal parameter, l is the internal material length scale parameter, C represents the elastic matrix and ∇² is the Laplacian operator. So, the nonlocal strain gradient constitutive relations for the FGPM micro-/nanoplate reinforced with GPLs can be introduced as:

$$\begin{aligned} & \left\{ {\begin{array}{*{20}c} {\varLambda_{xx} - \mu^{2} \left( {\frac{{\partial^{2} \varLambda_{xx} }}{{\partial x^{2} }} + \frac{{\partial^{2} \varLambda_{xx} }}{{\partial y^{2} }}} \right)} \\ {\varLambda_{yy} - \mu^{2} \left( {\frac{{\partial^{2} \varLambda_{yy} }}{{\partial x^{2} }} + \frac{{\partial^{2} \varLambda_{yy} }}{{\partial y^{2} }}} \right)} \\ {\varLambda_{xz} - \mu^{2} \left( {\frac{{\partial^{2} \varLambda_{xz} }}{{\partial x^{2} }} + \frac{{\partial^{2} \varLambda_{xz} }}{{\partial y^{2} }}} \right)} \\ {\varLambda_{yz} - \mu^{2} \left( {\frac{{\partial^{2} \varLambda_{yz} }}{{\partial x^{2} }} + \frac{{\partial^{2} \varLambda_{yz} }}{{\partial y^{2} }}} \right)} \\ {\varLambda_{xy} - \mu^{2} \left( {\frac{{\partial^{2} \varLambda_{xy} }}{{\partial x^{2} }} + \frac{{\partial^{2} \varLambda_{xy} }}{{\partial y^{2} }}} \right)} \\ \end{array} } \right\}, \\ & \quad = \left[ {\begin{array}{*{20}c} {Q_{11} \left( z \right)} & {Q_{12} \left( z \right)} & 0 & 0 & 0 \\ {Q_{12} \left( z \right)} & {Q_{22} \left( z \right)} & 0 & 0 & 0 \\ 0 & 0 & {Q_{44} \left( z \right)} & 0 & 0 \\ 0 & 0 & 0 & {Q_{55} \left( z \right)} & 0 \\ 0 & 0 & 0 & 0 & {Q_{66} \left( z \right)} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} - l^{2} \left( {\frac{{\partial^{2} \varepsilon_{xx} }}{{\partial x^{2} }} + \frac{{\partial^{2} \varepsilon_{xx} }}{{\partial y^{2} }}} \right)} \\ {\varepsilon_{yy} - l^{2} \left( {\frac{{\partial^{2} \varepsilon_{yy} }}{{\partial x^{2} }} + \frac{{\partial^{2} \varepsilon_{yy} }}{{\partial y^{2} }}} \right)} \\ {\gamma_{xz} - l^{2} \left( {\frac{{\partial^{2} \gamma_{xz} }}{{\partial x^{2} }} + \frac{{\partial^{2} \gamma_{xz} }}{{\partial y^{2} }}} \right)} \\ {\gamma_{yz} - l^{2} \left( {\frac{{\partial^{2} \gamma_{yz} }}{{\partial x^{2} }} + \frac{{\partial^{2} \gamma_{yz} }}{{\partial y^{2} }}} \right)} \\ {\gamma_{xy} - l^{2} \left( {\frac{{\partial^{2} \gamma_{xy} }}{{\partial x^{2} }} + \frac{{\partial^{2} \gamma_{xy} }}{{\partial y^{2} }}} \right)} \\ \end{array} } \right\} \\ \end{aligned},$$

(13)

where

$$\begin{aligned} & Q_{11} \left( z \right) = Q_{22} \left( z \right) = \frac{E\left( z \right)}{{1 - \nu \left( z \right)^{2} }},\quad Q_{12} \left( z \right) = \frac{\nu \left( z \right)E\left( z \right)}{{1 - \nu \left( z \right)^{2} }} \\ & Q_{44} \left( z \right) = Q_{55} \left( z \right) = Q_{66} \left( z \right) = \frac{E\left( z \right)}{{2\left( {1 + \nu \left( z \right)} \right)}}. \\ \end{aligned}$$

(14)

Thereafter, within the framework of the nonlocal strain gradient exponential shear deformable plate model, the total strain energy of the FGPM micro-/nanoplate reinforced with GPLs can be written as:

$$\begin{aligned} \varPi_{s} & = \frac{1}{2}\mathop \smallint \limits_{S}^{ } \mathop \smallint \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2} }} \left\{ {\sigma_{ij} \varepsilon_{ij} + \sigma_{ij}^{*} \nabla \varepsilon_{ij} } \right\}{\text{d}}z{\text{d}}S \\ & = \frac{1}{2}\mathop \smallint \limits_{S}^{ } \left\{ {N_{xx} \varepsilon_{xx}^{0} + N_{yy} \varepsilon_{yy}^{0} + N_{xy} \gamma_{xy}^{0} + M_{xx} \kappa_{xx}^{\left( 1 \right)} + M_{yy} \kappa_{yy}^{\left( 1 \right)} + M_{xy} \kappa_{xy}^{\left( 1 \right)} + R_{xx} \kappa_{xx}^{\left( 2 \right)} + R_{yy} \kappa_{yy}^{\left( 2 \right)} + R_{xy} \kappa_{xy}^{\left( 2 \right)} + Q_{x} \gamma_{xz} + Q_{y} \gamma_{yz} } \right\}{\text{d}}S, \\ \end{aligned}$$

(15)

where

$$\begin{aligned} & \left\{ {\begin{array}{*{20}c} {N_{xx} } \\ {N_{yy} } \\ {N_{xy} } \\ \end{array} } \right\} = \mathop \smallint \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \left\{ {\begin{array}{*{20}c} {\varLambda_{xx} } \\ {\varLambda_{yy} } \\ {\varLambda_{xy} } \\ \end{array} } \right\}{\text{d}}z,\quad \left\{ {\begin{array}{*{20}c} {M_{xx} } \\ {M_{yy} } \\ {M_{xy} } \\ \end{array} } \right\} = \mathop \smallint \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \left\{ {\begin{array}{*{20}c} {\varLambda_{xx} } \\ {\varLambda_{yy} } \\ {\varLambda_{xy} } \\ \end{array} } \right\}z{\text{d}}z \\ & \left\{ {\begin{array}{*{20}c} {R_{xx} } \\ {R_{yy} } \\ {R_{xy} } \\ \end{array} } \right\} = \mathop \smallint \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \left\{ {\begin{array}{*{20}c} {\varLambda_{xx} } \\ {\varLambda_{yy} } \\ {\varLambda_{xy} } \\ \end{array} } \right\}ze^{{ - \frac{{2z^{2} }}{{h^{2} }}}} {\text{d}}z,\quad \left\{ {\begin{array}{*{20}c} {Q_{x} } \\ {Q_{y} } \\ \end{array} } \right\} = \mathop \smallint \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \left\{ {\begin{array}{*{20}c} {\varLambda_{xz} } \\ {\varLambda_{yz} } \\ \end{array} } \right\}\left( {1 - \frac{{4z^{2} }}{{h^{2} }}} \right)e^{{ - \frac{{2z^{2} }}{{h^{2} }}}} dz ,\\ \end{aligned}$$

(16)

which results in the equivalent stress resultants given in “Appendix 1”. Also, the related stiffness parameters can be presented as:

$$\begin{aligned} & \left\{ {\begin{array}{*{20}c} {A_{11}^{*} ,B_{11}^{*} ,D_{11}^{*} ,F_{11}^{*} ,G_{11}^{*} ,H_{11}^{*} } \\ {A_{22}^{*} ,B_{22}^{*} ,D_{22}^{*} ,F_{22}^{*} ,G_{22}^{*} ,H_{22}^{*} } \\ {A_{12}^{*} ,B_{12}^{*} ,D_{12}^{*} ,F_{12}^{*} ,G_{12}^{*} ,H_{12}^{*} } \\ {A_{66}^{*} ,B_{66}^{*} ,D_{66}^{*} ,F_{66}^{*} ,G_{66}^{*} ,H_{66}^{*} } \\ \end{array} } \right\} \\ & \quad = \mathop \smallint \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \left\{ {\begin{array}{*{20}c} {Q_{11} \left( z \right)} \\ {Q_{22} \left( z \right)} \\ {Q_{12} \left( z \right)} \\ {Q_{66} \left( z \right)} \\ \end{array} } \right\}\left\{ {1,z,z^{2} ,ze^{{ - \frac{{2z^{2} }}{{h^{2} }}}} ,z^{2} e^{{ - \frac{{2z^{2} }}{{h^{2} }}}} ,z^{2} e^{{ - \frac{{4z^{2} }}{{h^{2} }}}} } \right\}{\text{d}}z ,\\ \end{aligned}$$

$$\left\{ {\begin{array}{*{20}c} {A_{44}^{*} } \\ {A_{55}^{*} } \\ \end{array} } \right\} = \mathop \smallint \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \left\{ {\begin{array}{*{20}c} {Q_{44} \left( z \right)} \\ {Q_{55} \left( z \right)} \\ \end{array} } \right\}\left( {1 - \frac{{4z^{2} }}{{h^{2} }}} \right)e^{{ - \frac{{2z^{2} }}{{h^{2} }}}} {\text{d}}z.$$

(17)

Moreover, the kinetic energy of the FGPM micro-/nanoplate reinforced with GPLs based upon the nonlocal strain gradient exponential shear deformable plate model can be given as:

$$\begin{aligned} \varPi_{T} = \frac{1}{2}\mathop \smallint \limits_{S}^{ } \mathop \smallint \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2} }} \rho \left( z \right)\left\{ {\left( {\frac{\partial u}{\partial t} - z\frac{{\partial^{2} w}}{\partial x\partial t} + ze^{{ - \frac{{2z^{2} }}{{h^{2} }}}} \frac{{\partial \psi_{x} }}{\partial t}} \right)^{2} + \left( {\frac{\partial v}{\partial t} - z\frac{{\partial^{2} w}}{\partial y\partial t} + ze^{{ - \frac{{2z^{2} }}{{h^{2} }}}} \frac{{\partial \psi_{y} }}{\partial t}} \right)^{2} + \left( {\frac{\partial w}{\partial t}} \right)^{2} } \right\}{\text{d}}z{\text{d}}S \hfill \\ = \frac{1}{2}\int_{S} {\left\{ {I_{0} \left( {\frac{\partial u}{\partial t}} \right)^{2} - 2I_{1} \frac{\partial u}{\partial t}\frac{{\partial^{2} w}}{\partial x\partial t} + 2I_{3} \frac{\partial u}{\partial t}\frac{{\partial \psi_{x} }}{\partial t} + I_{2} \left( {\frac{{\partial^{2} w}}{\partial x\partial t}} \right)^{2} - 2I_{4} \frac{{\partial^{2} w}}{\partial x\partial t}\frac{{\partial \psi_{x} }}{\partial t}} \right.} \hfill \\ + I_{5} \left( {\frac{{\partial \psi_{x} }}{\partial t}} \right)^{2} + I_{0} \left( {\frac{\partial v}{\partial t}} \right)^{2} - 2I_{1} \frac{\partial v}{\partial t}\frac{{\partial^{2} w}}{\partial y\partial t} + 2I_{3} \frac{\partial v}{\partial t}\frac{{\partial \psi_{y} }}{\partial t} + I_{2} \left( {\frac{{\partial^{2} w}}{\partial y\partial t}} \right)^{2} - 2I_{4} \frac{{\partial^{2} w}}{\partial y\partial t}\frac{{\partial \psi_{y} }}{\partial t} \hfill \\ \left. { + I_{5} \left( {\frac{{\partial \psi_{y} }}{\partial t}} \right)^{2} + I_{0} \left( {\frac{\partial w}{\partial t}} \right)^{2} } \right\}{\text{d}}S \hfill ,\\ \end{aligned}$$

(18)

where

$$\left\{ {I_{0} ,I_{1} ,I_{2} ,I_{3} ,I_{4} ,I_{5} } \right\} = \mathop \smallint \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \rho \left( z \right)\left\{ {1,z,z^{2} ,ze^{{ - \frac{{2z^{2} }}{{h^{2} }}}} ,z^{2} e^{{ - \frac{{2z^{2} }}{{h^{2} }}}} ,z^{2} e^{{ - \frac{{4z^{2} }}{{h^{2} }}}} } \right\}{\text{d}}z.$$

(19)

Also, an external uniform distributed load of $\fancyscript{q}\left( {x, y} \right)$ yields the following external work as:

$$\varPi_{W} = \mathop \smallint \limits_{S}^{ } \fancyscript{q}\left( {x,y} \right)w{\text{d}}S.$$

(20)

By applying the Hamilton’s principle to Eqs. (15), (18) and (20), the size-dependent governing differential equations of motion in terms of the stress resultants are derived as:

$$\frac{{\partial N_{xx} }}{\partial x} + \frac{{\partial N_{xy} }}{\partial y} = I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{1} \frac{{\partial^{3} w}}{{\partial x\partial t^{2} }} + I_{3} \frac{{\partial^{2} \psi_{x} }}{{\partial t^{2} }},$$

(21a)

$$\frac{{\partial N_{xy} }}{\partial x} + \frac{{\partial N_{yy} }}{\partial y} = I_{0} \frac{{\partial^{2} v}}{{\partial t^{2} }} - I_{1} \frac{{\partial^{3} w}}{{\partial y\partial t^{2} }} + I_{3} \frac{{\partial^{2} \psi_{y} }}{{\partial t^{2} }},$$

(21b)

$$\begin{aligned} & \frac{{\partial^{2} M_{xx} }}{{\partial x^{2} }} + 2\frac{{\partial^{2} M_{xy} }}{\partial x\partial y} + \frac{{\partial^{2} M_{yy} }}{{\partial y^{2} }} + N_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }} + 2N_{xy} \frac{{\partial^{2} w}}{\partial x\partial y} + N_{yy} \frac{{\partial^{2} w}}{{\partial y^{2} }} \\ & \quad = - I_{1} \left( {\frac{{\partial^{3} u}}{{\partial x\partial t^{2} }} + \frac{{\partial^{3} v}}{{\partial y\partial t^{2} }}} \right) + I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} - I_{2} \left( {\frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }} + \frac{{\partial^{4} w}}{{\partial y^{2} \partial t^{2} }}} \right) - I_{4} \left( {\frac{{\partial^{3} \psi_{x} }}{{\partial x\partial t^{2} }} + \frac{{\partial^{3} \psi_{y} }}{{\partial y\partial t^{2} }}} \right) \\ \end{aligned},$$

(21c)

$$\frac{{\partial R_{xx} }}{\partial x} + \frac{{\partial R_{xy} }}{\partial y} - Q_{x} = I_{3} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{4} \frac{{\partial^{3} w}}{{\partial x\partial t^{2} }} + I_{5} \frac{{\partial^{2} \psi_{x} }}{{\partial t^{2} }},$$

(21d)

$$\frac{{\partial R_{xy} }}{\partial x} + \frac{{\partial R_{yy} }}{\partial y} - Q_{y} = I_{3} \frac{{\partial^{2} v}}{{\partial t^{2} }} - I_{4} \frac{{\partial^{3} w}}{{\partial y\partial t^{2} }} + I_{5} \frac{{\partial^{2} \psi_{y} }}{{\partial t^{2} }}.$$

(21e)

By using the Airy stress function f(x, y), one will have

$$N_{xx} = \frac{{\partial f\left( {x,y} \right)}}{{\partial y^{2} }},\quad N_{yy} = \frac{{\partial f\left( {x,y} \right)}}{{\partial x^{2} }},\quad N_{xy} = - \frac{{\partial f\left( {x,y} \right)}}{\partial x\partial y}.$$

(22)

On the other hand, for a perfect FGPM micro-/nanoplate reinforced with GPLs, the compatibility equation relevant to the midplane strain components gives the following equation:

$$\frac{{\partial^{2} \varepsilon_{xx}^{0} }}{{\partial x^{2} }} + \frac{{\partial^{2} \varepsilon_{yy}^{0} }}{{\partial y^{2} }} - \frac{{\partial^{2} \gamma_{xy}^{0} }}{\partial x\partial y} = \left( {\frac{{\partial^{2} w}}{\partial x\partial y}} \right)^{2} - \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{2} w}}{{\partial y^{2} }}.$$

(23)

Now, by inserting the equivalent stress resultants in Eq. (21), the size-dependent governing differential equations of motion can be expressed in terms of the displacement components as follows:

$$\begin{aligned} & \varphi_{1} \frac{{\partial^{4} f}}{{\partial x^{4} }} + \left( {\varphi_{2} - 2\varphi_{3} } \right)\frac{{\partial^{4} f}}{{\partial x^{2} \partial y^{2} }} + \varphi_{4} \frac{{\partial^{4} f}}{{\partial y^{4} }} + \varphi_{5} \frac{{\partial^{4} w}}{{\partial x^{4} }} + \left( {\varphi_{6} + \varphi_{7} - 2\varphi_{8} } \right)\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + \varphi_{9} \frac{{\partial^{4} w}}{{\partial y^{4} }} \\ & \quad - \varphi_{10} \frac{{\partial^{3} \psi_{x} }}{{\partial x^{3} }} - \left( {\varphi_{11} - \varphi_{12} } \right)\frac{{\partial^{3} \psi_{x} }}{{\partial x\partial y^{2} }} - \varphi_{13} \frac{{\partial^{3} \psi_{y} }}{{\partial y^{3} }} - \left( {\varphi_{14} - \varphi_{12} } \right)\frac{{\partial^{3} \psi_{y} }}{{\partial x^{2} \partial y}} \\ & \quad = \left( {\frac{{\partial^{2} w}}{\partial x\partial y}} \right)^{2} - \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{2} w}}{{\partial y^{2} }} \\ \end{aligned},$$

(24a)

$$\begin{aligned} & \varphi_{15} \frac{{\partial^{4} w}}{{\partial x^{4} }} - \varphi_{15} l^{2} \left( {\frac{{\partial^{6} w}}{{\partial x^{6} }} + \frac{{\partial^{6} w}}{{\partial x^{4} \partial y^{2} }}} \right) + \varphi_{16} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} - \varphi_{16} l^{2} \left( {\frac{{\partial^{6} w}}{{\partial x^{4} \partial y^{2} }} + \frac{{\partial^{6} w}}{{\partial x^{2} \partial y^{4} }}} \right) + \varphi_{17} \frac{{\partial^{4} w}}{{\partial y^{4} }} \\ & \quad - \varphi_{17} l^{2} \left( {\frac{{\partial^{6} w}}{{\partial x^{2} \partial y^{4} }} + \frac{{\partial^{6} w}}{{\partial y^{6} }}} \right) + \varphi_{18} \frac{{\partial^{3} \psi_{x} }}{{\partial x^{3} }} - \varphi_{18} l^{2} \left( {\frac{{\partial^{5} \psi_{x} }}{{\partial x^{5} }} + \frac{{\partial^{5} \psi_{x} }}{{\partial x^{3} \partial y^{2} }}} \right) + \varphi_{19} \frac{{\partial^{3} \psi_{x} }}{{\partial x\partial y^{2} }} \\ & \quad - \varphi_{19} l^{2} \left( {\frac{{\partial^{5} \psi_{x} }}{{\partial x^{3} \partial y^{2} }} + \frac{{\partial^{5} \psi_{x} }}{{\partial x\partial y^{4} }}} \right) + \varphi_{20} \frac{{\partial^{3} \psi_{y} }}{{\partial y^{3} }} - \varphi_{20} l^{2} \left( {\frac{{\partial^{5} \psi_{y} }}{{\partial x^{2} \partial y^{3} }} + \frac{{\partial^{5} \psi_{y} }}{{\partial y^{5} }}} \right) + \varphi_{21} \frac{{\partial^{3} \psi_{y} }}{{\partial x^{2} \partial y}} \\ & \quad - \varphi_{21} l^{2} \left( {\frac{{\partial^{5} \psi_{y} }}{{\partial x^{4} \partial y}} + \frac{{\partial^{5} \psi_{y} }}{{\partial x^{2} \partial y^{3} }}} \right) \\ & \quad = \left( {1 - \mu^{2} \nabla^{2} } \right)\left[ {\frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{2} f}}{{\partial y^{2} }} - 2\frac{{\partial^{2} w}}{\partial x\partial y}\frac{{\partial^{2} f}}{\partial x\partial y} + \frac{{\partial^{2} w}}{{\partial y^{2} }}\frac{{\partial^{2} f}}{{\partial x^{2} }} - I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} + \left( {I_{2} - \frac{{I_{1} I_{3} }}{{I_{0} }}} \right)\left( {\frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }} + \frac{{\partial^{4} w}}{{\partial y^{2} \partial t^{2} }}} \right) + \left( {I_{4} - \frac{{I_{1} I_{3} }}{{I_{0} }}} \right)\left( {\frac{{\partial^{3} \psi_{x} }}{{\partial x\partial t^{2} }} + \frac{{\partial^{3} \psi_{y} }}{{\partial y\partial t^{2} }}} \right) + \fancyscript{q}} \right] \\ \end{aligned},$$

(24b)

$$\begin{aligned} & \varphi_{10} \frac{{\partial^{3} f}}{{\partial x^{3} }} + \left( {\varphi_{11} - \vartheta_{12} } \right)\frac{{\partial^{3} f}}{{\partial x\partial y^{2} }} + \varphi_{22} \frac{{\partial^{3} w}}{{\partial x^{3} }} + \varphi_{23} \frac{{\partial^{3} w}}{{\partial x\partial y^{2} }} + \varphi_{24} \frac{{\partial^{2} \psi_{x} }}{{\partial x^{2} }} + \varphi_{25} \frac{{\partial^{2} \psi_{x} }}{{\partial y^{2} }} + \varphi_{26} \frac{{\partial^{2} \psi_{y} }}{\partial x\partial y} \\ & \quad - A_{44}^{*} \psi_{x} = \left( {\frac{{I_{3}^{2} }}{{I_{0} }} - I_{4} } \right)\frac{{\partial^{3} w}}{{\partial x\partial t^{2} }} + \left( {I_{5} - \frac{{I_{3}^{2} }}{{I_{0} }}} \right)\frac{{\partial^{2} \psi_{x} }}{{\partial t^{2} }} \\ \end{aligned},$$

(24c)

$$\begin{aligned} & \varphi_{13} \frac{{\partial^{3} f}}{{\partial y^{3} }} + \left( {\varphi_{14} - \vartheta_{12} } \right)\frac{{\partial^{3} f}}{{\partial x^{2} \partial y}} + \varphi_{27} \frac{{\partial^{3} w}}{{\partial y^{3} }} + \varphi_{28} \frac{{\partial^{3} w}}{{\partial x^{2} \partial y}} + \varphi_{29} \frac{{\partial^{2} \psi_{y} }}{{\partial y^{2} }} + \varphi_{25} \frac{{\partial^{2} \psi_{y} }}{{\partial x^{2} }} + \varphi_{30} \frac{{\partial^{2} \psi_{x} }}{\partial x\partial y} \\ & \quad - A_{55}^{*} \psi_{y} = \left( {\frac{{I_{3}^{2} }}{{I_{0} }} - I_{4} } \right)\frac{{\partial^{3} w}}{{\partial y\partial t^{2} }} + \left( {I_{5} - \frac{{I_{3}^{2} }}{{I_{0} }}} \right)\frac{{\partial^{2} \psi_{y} }}{{\partial t^{2} }} \\ \end{aligned},$$

(24d)

in which $\varphi_{i} \left( {i = 1,2, \ldots ,30} \right)$ are defined in “Appendix 2”.

Additionally, the simply supported boundary conditions are applied for all four moveable edges of the FGPM micro-/nanoplate reinforced with GPLs. Thereby, the equilibrium of applied loads in the direction of x-axis can be given as:

$$\mathop \smallint \limits_{0}^{{L_{2} }} N_{xx} dy + L_{2} h\sigma_{xx} = 0.$$

(25)

4 Analytical solving process for asymptotic solutions

The following dimensionless parameters are taken into consideration to capture the asymptotic solutions for the size-dependent problem:

$$X = \frac{\pi x}{{L_{1} }},\quad Y = \frac{\pi y}{{L_{2} }},\quad \beta = \frac{{L_{1} }}{{L_{2} }} ,\quad \eta = \frac{{L_{1}^{2} }}{{\pi^{2} h^{2} }},\quad \tau = \frac{\pi h}{{L_{1} }}\sqrt {\frac{{A_{00} }}{{I_{00} }}} ,$$

$$\left\{ {\begin{array}{*{20}c} {a_{11}^{*} ,a_{22}^{*} ,a_{12}^{*} ,a_{44}^{*} ,a_{55}^{*} ,a_{66}^{*} } \\ {h_{11}^{*} ,h_{22}^{*} ,h_{12}^{*} ,h_{66}^{*} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{{A_{11}^{*} }}{{A_{00} }},\frac{{A_{22}^{*} }}{{A_{00} }},\frac{{A_{12}^{*} }}{{A_{00} }},\frac{{A_{44}^{*} }}{{A_{00} }},\frac{{A_{55}^{*} }}{{A_{00} }},\frac{{A_{66}^{*} }}{{A_{00} }}} \\ {\frac{{H_{11}^{*} }}{{A_{00} h^{2} }},\frac{{H_{22}^{*} }}{{A_{00} h^{2} }},\frac{{H_{12}^{*} }}{{A_{00} h^{2} }},\frac{{H_{66}^{*} }}{{A_{00} h^{2} }}} \\ \end{array} } \right\},$$

(26)

$$\begin{aligned} & \left\{ {\begin{array}{*{20}c} {b_{11}^{*} ,b_{22}^{*} ,b_{12}^{*} ,b_{66}^{*} ,f_{11}^{*} ,f_{22}^{*} ,f_{12}^{*} ,f_{66}^{*} } \\ {d_{11}^{*} ,d_{22}^{*} ,d_{12}^{*} ,d_{66}^{*} ,g_{11}^{*} ,g_{22}^{*} ,g_{12}^{*} ,g_{66}^{*} } \\ \end{array} } \right\} \\ & \quad = \left\{ {\begin{array}{*{20}c} {\frac{{B_{11}^{*} }}{{A_{00} h}},} & {\frac{{B_{22}^{*} }}{{A_{00} h}},} & {\frac{{B_{12}^{*} }}{{A_{00} h}},} & {\frac{{B_{66}^{*} }}{{A_{00} h}},} & {\frac{{F_{11}^{*} }}{{A_{00} h}},} & {\frac{{F_{22}^{*} }}{{A_{00} h}},} & {\frac{{F_{12}^{*} }}{{A_{00} h}},} & {\frac{{F_{66}^{*} }}{{A_{00} h}}} \\ {\frac{{D_{11}^{*} }}{{A_{00} h^{2} }},} & {\frac{{D_{22}^{*} }}{{A_{00} h^{2} }},} & {\frac{{D_{12}^{*} }}{{A_{00} h^{2} }},} & {\frac{{D_{66}^{*} }}{{A_{00} h^{2} }},} & {\frac{{G_{11}^{*} }}{{A_{00} h^{2} }},} & {\frac{{G_{22}^{*} }}{{A_{00} h^{2} }},} & {\frac{{G_{12}^{*} }}{{A_{00} h^{2} }},} & {\frac{{G_{66}^{*} }}{{A_{00} h^{2} }}} \\ \end{array} } \right\} \\ \end{aligned},$$

$$\left\{ {I_{0}^{*} ,I_{1}^{*} ,I_{2}^{*} ,I_{3}^{*} ,I_{4}^{*} ,I_{5}^{*} } \right\} = \left\{ {\frac{{L_{1}^{2} I_{0} }}{{\pi^{2} h^{2} I_{00} }},\frac{{L_{1} I_{1} }}{{\pi hI_{00} }},\frac{{I_{2} }}{{h^{2} I_{00} }},\frac{{L_{1} I_{3} }}{{\pi hI_{00} }},\frac{{I_{4} }}{{h^{2} I_{00} }},\frac{{I_{5} }}{{h^{2} I_{00} }}} \right\},$$

$$W = \frac{w}{h} ,\quad F = \frac{f}{{A_{00} h^{2} }},\quad \left\{ {\varPsi_{X} , \varPsi_{Y} } \right\} = \frac{{L_{1} }}{\pi h}\left\{ {\psi_{x} , \psi_{y} } \right\},$$

$${\mathcal{P}}_{q} = \frac{{\fancyscript{q}L_{1}^{4} }}{{\pi^{4} A_{00} h^{3} }},\quad {\mathcal{G}}_{1} = \frac{\mu }{{L_{1} }},\quad {\mathcal{G}}_{2} = \frac{l}{{L_{1} }},$$

in which $A_{00} = E_{m} h$ and $I_{00} = \rho_{m} h$. Thereafter, the nonlinear nonlocal strain gradient governing differential equations of motion for the exponential shear deformable FGPM micro-/nanoplate reinforced with GPLs can be rewritten in dimensionless form as:

$$\begin{aligned} & \vartheta_{1} \frac{{\partial^{4} F}}{{\partial X^{4} }} + \left( {\vartheta_{2} - 2\vartheta_{3} } \right)\beta^{2} \frac{{\partial^{4} F}}{{\partial X^{2} \partial Y^{2} }} + \vartheta_{4} \beta^{4} \frac{{\partial^{4} F}}{{\partial Y^{4} }} + \vartheta_{5} \frac{{\partial^{4} W}}{{\partial X^{4} }} + \left( {\vartheta_{6} + \vartheta_{7} - 2\vartheta_{8} } \right)\beta^{2} \frac{{\partial^{4} W}}{{\partial X^{2} \partial Y^{2} }} \\ & \quad + \vartheta_{9} \beta^{4} \frac{{\partial^{4} W}}{{\partial Y^{4} }} - \vartheta_{10} \frac{{\partial^{3} \varPsi_{X} }}{{\partial X^{3} }} - \left( {\vartheta_{11} - \vartheta_{12} } \right)\beta^{2} \frac{{\partial^{3} \varPsi_{X} }}{{\partial X\partial Y^{2} }} - \vartheta_{13} \beta^{3} \frac{{\partial^{3} \varPsi_{Y} }}{{\partial Y^{3} }} \\ & \quad - \left( {\vartheta_{14} - \vartheta_{12} } \right)\beta \frac{{\partial^{3} \varPsi_{Y} }}{{\partial X^{2} \partial Y}} = \beta^{2} \left( {\frac{{\partial^{2} W}}{\partial X\partial Y}} \right)^{2} - \beta^{2} \frac{{\partial^{2} W}}{{\partial X^{2} }}\frac{{\partial^{2} W}}{{\partial Y^{2} }} \\ \end{aligned},$$

(27a)

$$\begin{aligned} & \vartheta_{15} \frac{{\partial^{4} W}}{{\partial X^{4} }} - \pi^{2} {\mathcal{G}}_{2}^{2} \vartheta_{15} \left( {\frac{{\partial^{6} W}}{{\partial X^{6} }} + \beta^{2} \frac{{\partial^{6} W}}{{\partial X^{4} \partial Y^{2} }}} \right) + \vartheta_{16} \beta^{2} \frac{{\partial^{4} W}}{{\partial X^{2} \partial Y^{2} }} \\ & \quad - \pi^{2} {\mathcal{G}}_{2}^{2} \vartheta_{15} \beta^{2} \left( {\frac{{\partial^{6} W}}{{\partial X^{4} \partial Y^{2} }} + \beta^{2} \frac{{\partial^{6} W}}{{\partial X^{2} \partial Y^{4} }}} \right) + \vartheta_{17} \beta^{4} \frac{{\partial^{4} W}}{{\partial Y^{4} }} \\ & \quad - \pi^{2} {\mathcal{G}}_{2}^{2} \vartheta_{17} \beta^{4} \left( {\frac{{\partial^{6} W}}{{\partial X^{2} \partial Y^{4} }} + \beta^{2} \frac{{\partial^{6} W}}{{\partial Y^{6} }}} \right) + \vartheta_{18} \frac{{\partial^{3} \varPsi_{X} }}{{\partial X^{3} }} - \pi^{2} {\mathcal{G}}_{2}^{2} \vartheta_{18} \left( {\frac{{\partial^{5} \varPsi_{X} }}{{\partial X^{5} }} + \beta^{2} \frac{{\partial^{5} \varPsi_{X} }}{{\partial X^{3} \partial Y^{2} }}} \right) \\ & \quad + \vartheta_{19} \beta \frac{{\partial^{3} \varPsi_{X} }}{{\partial X^{2} \partial Y}} - \pi^{2} {\mathcal{G}}_{2}^{2} \vartheta_{19} \beta \left( {\frac{{\partial^{5} \varPsi_{X} }}{{\partial X^{4} \partial Y}} + \beta^{2} \frac{{\partial^{5} \varPsi_{X} }}{{\partial X^{2} \partial Y^{3} }}} \right) + \vartheta_{20} \beta^{3} \frac{{\partial^{3} \varPsi_{Y} }}{{\partial Y^{3} }} \\ & \quad - \pi^{2} {\mathcal{G}}_{2}^{2} \vartheta_{20} \beta^{3} \left( {\frac{{\partial^{5} \varPsi_{Y} }}{{\partial X^{2} \partial Y^{3} }} + \beta^{2} \frac{{\partial^{5} \varPsi_{Y} }}{{\partial Y^{5} }}} \right) + \vartheta_{21} \beta^{2} \frac{{\partial^{3} \varPsi_{Y} }}{{\partial X\partial Y^{2} }} \\ & \quad - \pi^{2} {\mathcal{G}}_{2}^{2} \vartheta_{21} \beta^{2} \left( {\frac{{\partial^{5} \varPsi_{Y} }}{{\partial X^{3} \partial Y^{2} }} + \beta^{2} \frac{{\partial^{5} \varPsi_{Y} }}{{\partial X\partial Y^{4} }}} \right) \\ & \quad = \left( {1 - \pi^{2} {\mathcal{G}}_{1}^{2} \nabla^{2} } \right)\left[ {\beta^{2} \frac{{\partial^{2} W}}{{\partial X^{2} }}\frac{{\partial^{2} F}}{{\partial Y^{2} }} + 2\beta^{2} \frac{{\partial^{2} W}}{\partial X\partial Y}\frac{{\partial^{2} F}}{\partial X\partial Y} + \beta^{2} \frac{{\partial^{2} W}}{{\partial Y^{2} }}\frac{{\partial^{2} F}}{{\partial X^{2} }} - I_{0}^{*} \frac{{\partial^{2} W}}{{\partial \tau^{2} }}} \right. \\ & \quad \left. { + \left( {I_{2}^{*} - \frac{{I_{1}^{*} I_{3}^{*} }}{{I_{0}^{*} }}} \right)\left( {\frac{{\partial^{4} W}}{{\partial X^{2} \partial \tau^{2} }} + \beta^{2} \frac{{\partial^{4} W}}{{\partial Y^{2} \partial \tau^{2} }}} \right) + \left( {I_{4}^{*} - \frac{{I_{1}^{*} I_{3}^{*} }}{{I_{0}^{*} }}} \right)\left( {\frac{{\partial^{3} \varPsi_{x} }}{{\partial X\partial \tau^{2} }} + \beta \frac{{\partial^{3} \varPsi_{y} }}{{\partial Y\partial \tau^{2} }}} \right) + {\mathcal{P}}_{q} } \right] \\ \end{aligned} ,$$

(27b)

$$\begin{aligned} & \vartheta_{10} \frac{{\partial^{3} F}}{{\partial X^{3} }} + \left( {\vartheta_{11} - \vartheta_{12} } \right)\beta^{2} \frac{{\partial^{3} F}}{{\partial X\partial Y^{2} }} + \vartheta_{22} \frac{{\partial^{3} W}}{{\partial X^{3} }} + \vartheta_{23} \beta^{2} \frac{{\partial^{3} W}}{{\partial X\partial Y^{2} }} + \vartheta_{24} \frac{{\partial^{2} \varPsi_{X} }}{{\partial X^{2} }} + \vartheta_{25} \beta^{2} \frac{{\partial^{2} \varPsi_{X} }}{{\partial Y^{2} }} \\ & \quad + \vartheta_{26} \beta \frac{{\partial^{2} \varPsi_{Y} }}{\partial X\partial Y} - a_{44}^{*} \eta^{2} \varPsi_{X} = \left( {\frac{{I_{3}^{*2} }}{{I_{0}^{*} }} - I_{4}^{*} } \right)\frac{{\partial^{3} W}}{{\partial X\partial \tau^{2} }} + \left( {I_{5}^{*} - \frac{{I_{3}^{*2} }}{{I_{0}^{*} }}} \right)\frac{{\partial^{2} \varPsi_{x} }}{{\partial \tau^{2} }} \\ \end{aligned},$$

(27c)

$$\begin{aligned} & \vartheta_{13} \beta^{3} \frac{{\partial^{3} F}}{{\partial Y^{3} }} + \left( {\vartheta_{14} - \vartheta_{12} } \right)\beta \frac{{\partial^{3} F}}{{\partial X^{2} \partial Y}} + \vartheta_{27} \beta^{3} \frac{{\partial^{3} W}}{{\partial Y^{3} }} + \vartheta_{28} \beta \frac{{\partial^{3} W}}{{\partial X^{2} \partial Y}} + \vartheta_{29} \beta^{2} \frac{{\partial^{2} \varPsi_{Y} }}{{\partial Y^{2} }} + \vartheta_{25} \frac{{\partial^{2} \varPsi_{Y} }}{{\partial X^{2} }} \\ & \quad + \vartheta_{30} \beta \frac{{\partial^{2} \varPsi_{X} }}{\partial X\partial Y} - a_{55}^{*} \eta^{2} \varPsi_{Y} = \left( {\frac{{I_{3}^{*2} }}{{I_{0}^{*} }} - I_{4}^{*} } \right)\beta \frac{{\partial^{3} W}}{{\partial Y\partial \tau^{2} }} + \left( {I_{5}^{*} - \frac{{I_{3}^{*2} }}{{I_{0}^{*} }}} \right)\frac{{\partial^{2} \varPsi_{y} }}{{\partial \tau^{2} }} \\ \end{aligned},$$

(27d)

where $\vartheta_{i} \left( {i = 1,2, \ldots ,30} \right)$ are the dimensionless form of $\varphi_{i} \left( {i = 1,2, \ldots ,30} \right).$.

In a similar way, the axial loading condition along the x-axis can be expressed in dimensionless form as follows:

$$\frac{1}{\pi }\mathop \smallint \limits_{0}^{\pi } \beta^{2} \frac{{\partial^{2} F}}{{\partial Y^{2} }}{\text{d}}Y + 4\beta^{2} {\mathcal{P}}_{x} = 0.$$

(28)

The following initial conditions are taken into account:

$$\left. W \right|_{\tau = 0} = \left. {\frac{\partial W}{\partial \tau }} \right|_{\tau = 0} ,\quad \left. {\varPsi_{X} } \right|_{\tau = 0} = \left. {\frac{{\partial \varPsi_{X} }}{\partial \tau }} \right|_{\tau = 0} ,\quad \left. {\varPsi_{Y} } \right|_{\tau = 0} = \left. {\frac{{\partial \varPsi_{Y} }}{\partial \tau }} \right|_{\tau = 0}.$$

(29)

To continue the solution methodology, an improved perturbation technique [77,78,79,80,81,82,83,84,85] is employed, based on which the independent variables are defined as the summations of the solutions with different orders of the first perturbation parameter $\epsilon$.

At first, the critical buckling load of the FGPM micro-/nanoplates reinforced with GPLs is calculated. To this end, the independent variables of the problem are defined as the summations of the solutions with various orders of the first perturbation parameter, $\epsilon$, as follows:

$$\begin{aligned} & W\left( {X,Y,\epsilon } \right) = \mathop \sum \limits_{i = 0} \epsilon^{i/2} W_{i/2} \left( {X,Y} \right),\quad F\left( {X,Y,\epsilon } \right) = \mathop \sum \limits_{i = 0} \epsilon^{i/2} F_{i/2} \left( {X,Y} \right), \\ & \varPsi_{X} \left( {X,Y,\epsilon } \right) = \mathop \sum \limits_{i = 1} \epsilon^{i/2} \varPsi_{X\,i/2} \left( {X,Y} \right),\quad \varPsi_{Y} \left( {X,Y,\epsilon } \right) = \mathop \sum \limits_{i = 1} \epsilon^{i/2} \varPsi_{Y\,i/2} \left( {X,Y} \right). \\ \end{aligned}$$

(30)

By substitution of Eq. (30) in the nonlocal strain gradient governing differential equation of motion (Eq. 27), and then collecting the expressions with similar order of $\epsilon$, the sets of perturbation equations can be derived. Thereafter, through solving them via step by step mathematical calculations, the fourth-order asymptotic solution associated with each independent variable of the problem can be achieved in the following forms:

$$\begin{aligned} & W\left( {X,Y,\epsilon } \right) = \epsilon \left[ {{\mathcal{A}}_{11}^{\left( 1 \right)} \sin \left( {mX} \right)\sin \left( {nY} \right)} \right] + \epsilon^{3} \left[ {{\mathcal{A}}_{13}^{\left( 3 \right)} \sin \left( {mX} \right)\sin \left( {3nY} \right) + {\mathcal{A}}_{31}^{\left( 3 \right)} \sin \left( {3mX} \right)\sin \left( {nY} \right)} \right] \\ & \quad + \epsilon^{4} \left[ {{\mathcal{A}}_{22}^{\left( 4 \right)} \sin \left( {2mX} \right)\sin \left( {2nY} \right) + {\mathcal{A}}_{24}^{\left( 4 \right)} \sin \left( {2mX} \right)\sin \left( {4nY} \right)} \right. \\ & \quad \left. { + {\mathcal{A}}_{42}^{\left( 4 \right)} \sin \left( {4mX} \right)\sin \left( {2nY} \right)} \right] + O\left( {\epsilon^{5} } \right) \\ \end{aligned}.$$

(31a)

$$\begin{aligned} & F\left( {X,Y,\epsilon } \right) = - B_{00}^{\left( 0 \right)} \frac{{Y^{2} }}{2} + \epsilon^{2} \left[ { - B_{00}^{\left( 2 \right)} \frac{{Y^{2} }}{2} + B_{20}^{\left( 2 \right)} \cos \left( {2mX} \right) + B_{02}^{\left( 2 \right)} \cos \left( {2nY} \right)} \right] \\ & \quad + \epsilon^{4} \left[ { - B_{00}^{\left( 4 \right)} \frac{{Y^{2} }}{2} + B_{20}^{\left( 4 \right)} \cos \left( {2mX} \right) + B_{02}^{\left( 4 \right)} \cos \left( {2nY} \right) + B_{22}^{\left( 4 \right)} \cos \left( {2mX} \right)\cos \left( {2nY} \right)} \right. \\ & \quad + B_{40}^{\left( 4 \right)} \cos \left( {4mX} \right) + B_{02}^{\left( 4 \right)} \cos \left( {4nY} \right) + B_{24}^{\left( 4 \right)} \cos \left( {2mX} \right)\cos \left( {4nY} \right) \\ & \quad \left. { + B_{42}^{\left( 4 \right)} \cos \left( {4mX} \right)\cos \left( {2nY} \right)} \right] + O\left( {\epsilon^{5} } \right) \\ \end{aligned}.$$

(31b)

$$\begin{aligned} & \varPsi_{X} \left( {X,Y,\epsilon } \right) = \epsilon \left[ {{\mathcal{C}}_{11}^{\left( 1 \right)} \cos \left( {mX} \right)\sin \left( {nY} \right)} \right] + \epsilon^{3} \left[ {{\mathcal{C}}_{31}^{\left( 3 \right)} \cos \left( {3mX} \right)\sin \left( {nY} \right) + {\mathcal{C}}_{13}^{\left( 3 \right)} \cos \left( {mX} \right)\sin \left( {3nY} \right)} \right] \\ & \quad + \epsilon^{4} \left[ {{\mathcal{C}}_{02}^{\left( 4 \right)} \sin \left( {2nY} \right) + {\mathcal{C}}_{04}^{\left( 4 \right)} \sin \left( {4nY} \right) + {\mathcal{C}}_{22}^{\left( 4 \right)} \cos \left( {2mX} \right)\sin \left( {2nY} \right)} \right. \\ & \quad \left. { + {\mathcal{C}}_{24}^{\left( 4 \right)} \cos \left( {2mX} \right)\sin \left( {4nY} \right) + {\mathcal{C}}_{42}^{\left( 4 \right)} \cos \left( {4mX} \right)\sin \left( {2nY} \right)} \right] + O\left( {\epsilon^{5} } \right) \\ \end{aligned}.$$

(31c)

$$\begin{aligned} & \varPsi_{Y} \left( {X,Y,\epsilon } \right) = \epsilon \left[ {{\mathcal{D}}_{11}^{\left( 1 \right)} \sin \left( {mX} \right)\cos \left( {nY} \right)} \right] + \epsilon^{3} \left[ {{\mathcal{D}}_{31}^{\left( 1 \right)} \sin \left( {3mX} \right)\cos \left( {nY} \right) + {\mathcal{D}}_{13}^{\left( 1 \right)} \sin \left( {mX} \right)\cos \left( {3nY} \right)} \right] \\ & \quad + \epsilon^{4} \left[ {{\mathcal{D}}_{20}^{\left( 4 \right)} \sin \left( {2mX} \right) + {\mathcal{D}}_{40}^{\left( 4 \right)} \sin \left( {4mX} \right) + {\mathcal{D}}_{22}^{\left( 4 \right)} \sin \left( {2mX} \right){ \cos }\left( {2nY} \right)} \right. \\ & \quad \left. { + {\mathcal{D}}_{24}^{\left( 4 \right)} \sin \left( {2mX} \right){ \cos }\left( {4nY} \right) + {\mathcal{D}}_{42}^{\left( 4 \right)} \sin \left( {4mX} \right){ \cos }\left( {2nY} \right)} \right] + O\left( {\epsilon^{5} } \right) \\ \end{aligned}.$$

(31d)

With the aid of Eq. (28), and after some mathematical calculations, the explicit expression for the nonlocal strain gradient load–deflection response of FGPM micro-/nanoplates is obtained as:

$${\mathcal{P}}_{x} = {\mathcal{P}}_{x}^{\left( 0 \right)} + {\mathcal{P}}_{x}^{\left( 2 \right)} \left( {{\mathcal{W}}_{m} } \right)^{2} + {\mathcal{P}}_{x}^{\left( 4 \right)} \left( {{\mathcal{W}}_{m} } \right)^{4} + \cdots,$$

(32)

in which ${\mathcal{W}}_{m}$ represents the dimensionless maximum deflection of the FGPM micro-/nanoplate reinforced with GPLs. ${\mathcal{P}}_{x}^{\left( 0 \right)} , {\mathcal{P}}_{x}^{\left( 2 \right)}$ and ${\mathcal{P}}_{x}^{\left( 4 \right)}$ are the weighting coefficients in terms of the geometric and material parameters.

Thereafter, the solving process is fulfilled for the vibration analysis of FGPM micro-/nanoplates within both the prebuckling and postbuckling domains. For this purpose, to improve the solving process, it is assumed that $\hat{\tau } = \epsilon \tau$. Consequently, one will have

$$\begin{aligned} & \tilde{W}\left( {X,Y,\hat{\tau },\epsilon } \right) = \mathop \sum \limits_{i = 1} \epsilon^{i} \tilde{W}_{i} \left( {X,Y,\hat{\tau }} \right),\quad \tilde{F}\left( {X,Y,\hat{\tau },\epsilon } \right) = \mathop \sum \limits_{i = 1} \epsilon^{i} \tilde{F}_{i} \left( {X,Y,\hat{\tau }} \right) \\ & \tilde{\varPsi }_{X} \left( {X,Y,\hat{\tau },\epsilon } \right) = \mathop \sum \limits_{i = 1} \epsilon^{i} \tilde{\varPsi }_{Xi} \left( {X,Y,\hat{\tau }} \right) ,\quad \tilde{\varPsi }_{Y} \left( {X,Y,\hat{\tau },\epsilon } \right) = \mathop \sum \limits_{i = 1} \epsilon^{i} \tilde{\varPsi }_{Yi} \left( {X,Y,\hat{\tau }} \right) \\ & {\tilde{\mathcal{P}}}_{q} \left( {X,Y,\hat{\tau },\epsilon } \right) = \mathop \sum \limits_{i = 1} \epsilon^{i} {\tilde{\mathcal{P}}}_{qi} \left( {X,Y,\hat{\tau }} \right) \\ \end{aligned}.$$

(33)

By inserting Eq. (33) in the nonlocal strain gradient governing differential equation of motion (Eq. 27), and then collecting the expressions with similar order of $\epsilon$, the fourth-order asymptotic solution associated with each independent variable of the problem can be given as:

$$\begin{aligned} & \tilde{W}\left( {X,Y,\tau } \right) = \epsilon \left[ {{\mathcal{A}}_{11}^{\left( 1 \right)} \left( \tau \right)\sin \left( {mX} \right)\sin \left( {nY} \right)} \right] \\ & \quad + \epsilon^{3} \left[ {{\mathcal{A}}_{13}^{\left( 3 \right)} \sin \left( {mX} \right)\sin \left( {3nY} \right) + {\mathcal{A}}_{31}^{\left( 3 \right)} \sin \left( {3mX} \right)\sin \left( {nY} \right)} \right] + O\left( {\epsilon^{4} } \right) \\ \end{aligned},$$

(34)

$$\begin{aligned} & \tilde{F}\left( {X,Y,\tau } \right) = - {\mathcal{B}}_{00}^{\left( 0 \right)} \frac{{Y^{2} }}{2} + \epsilon \left[ {\left( {{\mathcal{B}}_{11}^{\left( 1 \right)} \left( \tau \right) + {\ddot{\mathcal{B}}}_{11}^{\left( 3 \right)} \left( \tau \right)} \right)\sin \left( {mX} \right)\sin \left( {nY} \right)} \right] \\ & \quad + \epsilon^{2} \left[ { - {\mathcal{B}}_{00}^{\left( 2 \right)} \frac{{Y^{2} }}{2} + {\mathcal{B}}_{02}^{\left( 2 \right)} \left( \tau \right)\cos \left( {2nY} \right) + {\mathcal{B}}_{20}^{\left( 2 \right)} \left( \tau \right)\cos \left( {2mX} \right)} \right] \\ & \quad + \epsilon^{3} \left[ {{\mathcal{B}}_{13}^{\left( 3 \right)} \sin \left( {mX} \right)\sin \left( {3nY} \right) + {\mathcal{B}}_{31}^{\left( 3 \right)} \sin \left( {3mX} \right)\sin \left( {nY} \right)} \right] + O\left( {\epsilon^{4} } \right) \\ \end{aligned},$$

(35)

$$\begin{aligned} & \tilde{\varPsi }_{X} \left( {X,Y,\tau } \right) = \epsilon \left[ {\left( {{\mathcal{C}}_{11}^{\left( 1 \right)} \left( \tau \right) + {\ddot{\mathcal{C}}}_{11}^{\left( 3 \right)} \left( \tau \right)} \right)\cos \left( {mX} \right)\sin \left( {nY} \right)} \right] + \epsilon^{2} \left[ {{\mathcal{C}}_{20}^{\left( 2 \right)} \left( \tau \right)\sin \left( {2mX} \right)} \right] \\ & \quad + \epsilon^{3} \left[ {{\mathcal{C}}_{13}^{\left( 3 \right)} \cos \left( {mX} \right)\sin \left( {3nY} \right) + {\mathcal{C}}_{31}^{\left( 3 \right)} \cos \left( {3mX} \right)\sin \left( {nY} \right)} \right] + O\left( {\epsilon^{4} } \right) \\ \end{aligned},$$

(36)

$$\begin{aligned} & \tilde{\varPsi }_{Y} \left( {X,Y,\tau } \right) = \epsilon \left[ {\left( {{\mathcal{D}}_{11}^{\left( 1 \right)} \left( \tau \right) + {\ddot{\mathcal{D}}}_{11}^{\left( 3 \right)} \left( \tau \right)} \right)\sin \left( {mX} \right)\cos \left( {nY} \right)} \right] + \epsilon^{2} \left[ {{\mathcal{D}}_{02}^{\left( 2 \right)} \left( \tau \right)\sin \left( {2nY} \right)} \right] \\ & \quad + \epsilon^{3} \left[ {{\mathcal{D}}_{13}^{\left( 3 \right)} \sin \left( {mX} \right)\cos \left( {3nY} \right) + {\mathcal{D}}_{31}^{\left( 3 \right)} \sin \left( {3mX} \right)\cos \left( {nY} \right)} \right] + O\left( {\epsilon^{4} } \right) \\ \end{aligned},$$

(37)

$$\begin{aligned} & {\mathcal{P}}_{q} \left( {X,Y,\tau } \right) = \epsilon \left[ {{\mathcal{Q}}_{11}^{\left( 1 \right)} \left( \tau \right)\sin \left( {mX} \right)\sin \left( {nY} \right) + {\ddot{\mathcal{Q}}}_{11}^{\left( 1 \right)} \left( \tau \right)\sin \left( {mX} \right)\sin \left( {nY} \right)} \right] \\ & \quad + \epsilon^{3} \left[ {{\mathcal{Q}}_{11}^{\left( 3 \right)} \left( \tau \right)\sin \left( {mX} \right)\sin \left( {nY} \right) + {\ddot{\mathcal{Q}}}_{13}^{\left( 3 \right)} \left( \tau \right)\sin \left( {mX} \right)\sin \left( {3nY} \right) + {\ddot{\mathcal{Q}}}_{31}^{\left( 3 \right)} \left( \tau \right)\sin \left( {3mX} \right)\sin \left( {nY} \right)} \right] + O\left( {\epsilon^{4} } \right) \\ \end{aligned}.$$

(38)

For the free vibrational response, one will have ${\mathcal{P}}_{q} \left( {X,Y,\tau } \right) = 0$. Therefore, with the aid of the Galerkin technique, it yields:

$$\begin{aligned} & \int_{0}^{\pi } {\int_{0}^{\pi } {\left\{ {K_{0} \frac{{\partial^{2} \left( {{\mathcal{A}}_{11}^{\left( 1 \right)} \left( \tau \right)\epsilon } \right)}}{{\partial \tau^{2} }}{ \sin }\left( {mX} \right){ \sin }\left( {nY} \right) + \left( {K_{1} - \left( {m^{2} + n^{2} \beta^{2} } \right){\mathcal{P}}_{x} } \right)\left( {{\mathcal{A}}_{11}^{\left( 1 \right)} \left( \tau \right)\epsilon } \right){ \sin }\left( {mX} \right){ \sin }\left( {nY} \right)} \right.} } \\ & \quad + K_{2} \left( {{\mathcal{A}}_{11}^{\left( 1 \right)} \left( \tau \right)\epsilon } \right)^{2} { \sin }\left( {mX} \right){ \sin }\left( {nY} \right) \\ & \quad \left. { + K_{3} \left( {A_{11}^{\left( 1 \right)} \left( \tau \right)\epsilon } \right)^{3} { \sin }\left( {mX} \right){ \sin }\left( {nY} \right)} \right\}\sin \left( {mX} \right)\sin \left( {nY} \right){\text{d}}X{\text{d}}Y = 0 \\ \end{aligned},$$

(39)

where $K_{i} \left( {i = 0,1,2,3} \right)$ can be obtained as dimensionless size-dependent weighting functions in terms of the introduced parameters in Eq. (27). The analytical solution of Eq. (39) leads to the dimensionless nonlocal strain gradient nonlinear frequency of the axially loaded FGPM micro-/nanoplate reinforced with GPLs which can be written explicitly as follows:

$$\omega_{NL} = \omega_{L} \sqrt {1 + \frac{{9K_{1} K_{3} - 10K_{2}^{2} }}{{12\left( {K_{1} - \left( {m^{2} + n^{2} \beta^{2} } \right){\mathcal{P}}_{x} } \right)^{2} }}\left( {{\mathcal{W}}_{m} } \right)^{2} },$$

(40)

in which $\omega_{L} = \sqrt {\left( {K_{1} - \left( {m^{2} + n^{2} \beta^{2} } \right){\mathcal{P}}_{x} } \right)/K_{0} }.$

5 Results and discussion

In this section, the selected numerical results are shown for the nonlocal strain gradient linear and nonlinear vibration responses of axially loaded FGPM micro-/nanoplates reinforced with GPLs within the prebuckling and postbuckling domains. The matrix material is supposed to be made of titanium with $E_{m} = 116\,{\text{GPa}},\,\nu_{m} = 0.33$, and $\rho_{m} = 4506\,{\text{Kg}}/{\text{m}}^{3}$ [86]. In addition, for the reinforcement phase of GPL, it is assumed that $E_{\text{GPL}} = 1.01\,{\text{TPa}},\, \nu_{\text{GPL}} = 0.186,\,\rho_{\text{GPL}} = 1062.5\,{\text{Kg}}/{\text{m}}^{3} ,\,h_{GPL} = 0.3\,{\text{nm}}$, $L_{\text{GPL}} = 5\,{\text{nm}}$, and $b_{\text{GPL}} = 2.5\,{\text{nm}}$. The values of the geometric parameters for the FGPM micro-/nanoplates are considered as $h = 10\,{\text{nm}}$ and $L_{1} = L_{2} = 200\,{\text{nm}}$.

Firstly, the validity and accuracy of the present solving process are checked. For this purpose, by ignoring the terms related to the nonlocality and strain gradient size dependency, the frequency ratio ($\omega_{NL} /\omega_{L}$) of a square isotropic plate is calculated corresponding to different vibration amplitudes and compared with those reported by Han and Petyt [87] using the hierarchical finite element method. It can be seen from Table 1 that there is an excellent agreement between the results of two methods which confirms the validity as well as the accuracy of the current solution methodology.

Table 1 Comparison of the frequency ratio (ω_NL/ω_L) for a square isotropic plate corresponding to different vibration amplitudes ($L_{1} = L_{2} = 0.5\,{\text{m}}$ and $h = 2\,{\text{mm}}$)

Figure 2 illustrates the nonlocal strain gradient linear frequency–load responses of the FGPM micro-/nanoplate having uniform porosity dispersion (Pattern A) reinforced with GPLs corresponding to different values of small-scale parameters. It can be found that within the prebuckling regime, the nonlocality causes a reduction in the linear frequency of the micro-/nanoplate, while the strain gradient size dependency leads to increasing it. But within the postbuckling domain, these patterns are vice versa. Also, it is seen that on approaching the critical axial buckling load, the significance of both the types of size effect on the linear frequency increases.

Fig. 2

Size-dependent linear frequency–load response of an axially loaded FGPM micro-/nanoplate reinforced with GPLs corresponding to different small-scale parameters (Pattern A, $\varGamma_{p} = 0.6,\,V_{\text{GPL}} = 0.1$): a $\mu = 0\,{\text{nm}}$, b $l = 0\,{\text{nm}}$

In Fig. 3, the nonlocal strain gradient deflection–nonlinear frequency responses of the FGPM micro-/nanoplate having uniform porosity dispersion (Pattern A) reinforced with GPLs are displayed corresponding to different values of small-scale parameters. It can be observed that within both the prebuckling and postbuckling regimes, for a specific value of deflection, the nonlocality leads to increase in the frequency ratio (ω_NL/ω_L), but the strain gradient size dependency causes a decrease in it. Also, in the prebuckling domain, by increasing the plate deflection, the significance of both the types of size effect on the value of frequency ratio enhances and the gap between the plots increases. However, in the postbuckling domain, the plate deflection plays an opposite role.

Fig. 3

Size-dependent deflection–nonlinear frequency response of an axially loaded FGPM micro-/nanoplate reinforced with GPLs corresponding to different small-scale parameters (Pattern A, $\varGamma_{p} = 0.6, V_{\text{GPL}} = 0.1$): a $\mu = 0\,{\text{nm}}$, b $l = 0\,{\text{nm}}$

Figure 4 depicts the influence of the porosity dispersion pattern on the nonlocal strain gradient linear frequency–load response of FGPM micro-/nanoplates reinforced with GPLs corresponding to different values of porosity coefficient. It is revealed that within the prebuckling regime, the FGPM micro-/nanoplates with porosity dispersion Patterns C and D have, respectively, the maximum and minimum linear frequency. However, within the postbuckling regime, these observations are vice versa. Moreover, it is found that by increasing the value of the porosity coefficient, the influence of the porosity dispersion pattern on the linear frequency–load response of the FGPM micro-nanoplates becomes more considerable.

Fig. 4

Influence of the porosity dispersion pattern on the nonlocal strain gradient linear frequency–load response of an axially loaded FGPM micro-/nanoplate reinforced with GPLs ($V_{\text{GPL}} = 0.1,\,\mu = 20\,{\text{nm}}, l = 20\,{\text{nm}}$): a Γ_p = 0.2, b Γ_p = 0.8

In Fig. 5, the influence of the porosity dispersion pattern on the nonlocal strain gradient deflection–nonlinear frequency response of FGPM micro-/nanoplates reinforced with GPLs is shown corresponding to different values of porosity coefficient. It can be seen that in both the prebuckling and postbuckling domains and for a specific value of plate deflection, the nonlinear frequency associated with the FGPM micro-/nanoplates with porosity dispersion Patterns A and C is in order minimum and maximum. It is observed that by increasing the value of the porosity coefficient, the influence of the porosity dispersion pattern on the deflection–nonlinear frequency response of FGPM micro-nanoplates becomes more significant.

Fig. 5

Influence of the porosity dispersion pattern on the nonlocal strain gradient deflection–nonlinear frequency response of an axially loaded FGPM micro-/nanoplate reinforced with GPLs ($V_{\text{GPL}} = 0.1,\,\mu = 20\,{\text{nm}},\,l = 20\,{\text{nm}}$): a Γ_p = 0.2, b Γ_p = 0.8

Figure 6 displays the influence of the porosity coefficient on the nonlocal strain gradient linear frequency–load response of FGPM micro-/nanoplates reinforced with GPLs corresponding to various porosity dispersion patterns. It is indicated that within the prebuckling and postbuckling regimes, higher value of the porosity coefficient makes, respectively, a reduction and increment in the linear frequency of the FGPM micro-/nanoplates. Furthermore, it can be found that among different patterns of the porosity dispersion, in the FGPM micro-/nanoplates with Patterns C and D, the influence of the porosity coefficient on the linear frequency–load response of FGPM micro-nanoplates is minimum and maximum, respectively.

Fig. 6

Influence of the porosity coefficient on the nonlocal strain gradient linear frequency–load response of an axially loaded FGPM micro-/nanoplate reinforced with GPLs ($V_{\text{GPL}} = 0.1,\,\mu = 20\,{\text{nm}},\,l = 20\,{\text{nm}}, \varGamma_{p} = 0.6$): a Pattern A, b Pattern B, c Pattern C, d Pattern D

The plot in Fig. 7 represents the influence of the porosity coefficient on the nonlocal strain gradient deflection–nonlinear frequency response of the FGPM micro-/nanoplates reinforced with GPLs corresponding to various porosity dispersion patterns. It is indicated that for a specific value of the plate deflection, increasing the value of porosity coefficient leads to increase in the frequency ratio of ω_NL/ω_L within both the prebuckling and postbuckling domains. This observation is more prominent for the FGPM micro-/nanoplate with porosity dispersion pattern of D.

Fig. 7

Influence of the porosity coefficient on the nonlocal strain gradient deflection–nonlinear frequency response of an axially loaded FGPM micro-/nanoplate reinforced with GPLs ($V_{\text{GPL}} = 0.1,\,\mu = 20\,{\text{nm}},\,l = 20\,{\text{nm}},\,\varGamma_{p} = 0.6$): a Pattern A, b Pattern B, c Pattern C, d Pattern D

In Fig. 8, the influence of the GPL volume fraction on the nonlocal strain gradient linear frequency–load response of a reinforced FGPM micro-/nanoplate with uniform porosity dispersion pattern (Pattern A) is demonstrated corresponding to various values of the small-scale parameters. It is found that on approaching the critical axial buckling load, the influence of GPL volume fraction on the linear frequency of FGPM micro-/nanoplate increases. This prediction is more significant within the postbuckling domain. Additionally, it can be seen that by taking the nonlocality into account, the influence of the GPL volume fraction reduces, so the gap between the linear frequency–load curves decreases. However, the strain gradient size dependency plays an opposite role and causes an increase in the influence of the GPL volume fraction.

Fig. 8

Influence of the GPL volume fraction on the nonlocal strain gradient linear frequency–load response of an axially loaded FGPM micro-/nanoplate reinforced with GPLs (Pattern A, Γ_p = 0.6): a $\mu = 0\,{\text{nm}},\,l = 0\,{\text{nm}}$, b $\mu = 25\,{\text{nm}},\,l = 0\,{\text{nm}}$, c $\mu = 0\,{\text{nm}},\,l = 25\,{\text{nm}}$

Figure 9 shows the influence of the GPL volume fraction on the nonlocal strain gradient deflection–nonlinear frequency response of a reinforced FGPM micro-/nanoplate with uniform porosity dispersion pattern (Pattern A) is demonstrated corresponding to various values of the small-scale parameters. It is observed that within the prebuckling domain, by increasing the plate deflection, the GPL volume fraction plays a more important role in the value of frequency ratio (ω_NL/ω_L). However, within the postbuckling regime, the GPL volume fraction plays an opposite role. In addition, it is revealed that by taking the nonlocality into consideration, the influence of the GPL volume fraction enhances, so the gap between the linear frequency–load curves increases. However, the strain gradient size dependency plays an opposite role and causes a decrease in the influence of the GPL volume fraction.

Fig. 9

Influence of the GPL volume fraction on the nonlocal strain gradient deflection–nonlinear frequency response of an axially loaded FGPM micro-/nanoplate reinforced with GPLs (Pattern A, Γ_p = 0.6): a $\mu = 0\,{\text{nm}},\,l = 0\,{\text{nm}}$, b $\mu = 25\,{\text{nm}},\,l = 0\,{\text{nm}}$, c $\mu = 0\,{\text{nm}},\,l = 25\,{\text{nm}}$

6 Concluding remarks

The main aim of the this investigation was to analyze the size dependencies in the linear and nonlinear vibration responses of axially loaded FGPM micro-/nanoplates reinforced with GPLs within both the prebuckling and postbuckling domains. To perform this, the nonlocal strain gradient theory of elasticity is implemented into the refined exponential shear deformable plate model. Via an analytical solving process, explicit expressions for the size-dependent linear frequency–load and deflection–nonlinear frequency responses of FGPM micro-/nanoplates reinforced with GPLs were achieved.

It was observed that within the prebuckling regime, the nonlocality causes a reduction in the linear frequency of the micro-/nanoplate, while the strain gradient size dependency leads to an increase. But within the postbuckling domain, these patterns are vice versa. Moreover, within the prebuckling regime, the nonlocality causes a reduction in the linear frequency of the micro-/nanoplate, while the strain gradient size dependency leads to an increase. But within the postbuckling domain, these patterns are vice versa. Also, it was found that within the prebuckling regime, the FGPM micro-/nanoplates with porosity dispersion Patterns C and D have, respectively, the maximum and minimum linear frequency. It was seen that for a specific value of the plate deflection, increasing the value of porosity coefficient leads to an increase in the frequency ratio of ω_NL/ω_L within both the prebuckling and postbuckling domains. Furthermore, it was revealed that on approaching the critical axial buckling load, the influence of GPL volume fraction on the linear frequency of FGPM micro-/nanoplate increases. It was demonstrated that by taking the nonlocality into account, the influence of the GPL volume fraction reduces, so the gap between the linear frequency–load curves decreases. However, the strain gradient size dependency plays an opposite role and causes an increase in the influence of the GPL volume fraction.

Appendices

Appendix 1

The nonlocal strain gradient stress resultants can be expressed as:

$$\begin{aligned} & \left\{ {\begin{array}{*{20}c} {N_{xx} - \mu^{2} \left( {\frac{{\partial^{2} N_{xx} }}{{\partial x^{2} }} + \frac{{\partial^{2} N_{xx} }}{{\partial y^{2} }}} \right)} \\ {N_{yy} - \mu^{2} \left( {\frac{{\partial^{2} N_{yy} }}{{\partial x^{2} }} + \frac{{\partial^{2} N_{yy} }}{{\partial y^{2} }}} \right)} \\ {N_{xy} - \mu^{2} \left( {\frac{{\partial^{2} N_{xy} }}{{\partial x^{2} }} + \frac{{\partial^{2} N_{xy} }}{{\partial y^{2} }}} \right)} \\ \end{array} } \right\} \\ & \quad = \left[ {\begin{array}{*{20}c} {A_{11}^{*} } & {A_{12}^{*} } & 0 \\ {A_{12}^{*} } & {A_{22}^{*} } & 0 \\ 0 & 0 & {A_{66}^{*} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx}^{0} - l^{2} \left( {\frac{{\partial^{2} \varepsilon_{xx}^{0} }}{{\partial x^{2} }} + \frac{{\partial^{2} \varepsilon_{xx}^{0} }}{{\partial y^{2} }}} \right)} \\ {\varepsilon_{yy}^{0} - l^{2} \left( {\frac{{\partial^{2} \varepsilon_{yy}^{0} }}{{\partial x^{2} }} + \frac{{\partial^{2} \varepsilon_{yy}^{0} }}{{\partial y^{2} }}} \right)} \\ {\gamma_{xy}^{0} - l^{2} \left( {\frac{{\partial^{2} \gamma_{xy}^{0} }}{{\partial x^{2} }} + \frac{{\partial^{2} \gamma_{xy}^{0} }}{{\partial y^{2} }}} \right)} \\ \end{array} } \right\} \\ & \quad + \left[ {\begin{array}{*{20}c} {B_{11}^{*} } & {B_{12}^{*} } & 0 \\ {B_{12}^{*} } & {B_{22}^{*} } & 0 \\ 0 & 0 & {B_{66}^{*} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\kappa_{xx}^{\left( 1 \right)} - l^{2} \left( {\frac{{\partial^{2} \kappa_{xx}^{\left( 1 \right)} }}{{\partial x^{2} }} + \frac{{\partial^{2} \kappa_{xx}^{\left( 1 \right)} }}{{\partial y^{2} }}} \right)} \\ {\kappa_{yy}^{\left( 1 \right)} - l^{2} \left( {\frac{{\partial^{2} \kappa_{yy}^{\left( 1 \right)} }}{{\partial x^{2} }} + \frac{{\partial^{2} \kappa_{yy}^{\left( 1 \right)} }}{{\partial y^{2} }}} \right)} \\ {\kappa_{xy}^{\left( 1 \right)} - l^{2} \left( {\frac{{\partial^{2} \kappa_{xy}^{\left( 1 \right)} }}{{\partial x^{2} }} + \frac{{\partial^{2} \kappa_{xy}^{\left( 1 \right)} }}{{\partial y^{2} }}} \right)} \\ \end{array} } \right\} \\ & \quad + \left[ {\begin{array}{*{20}c} {F_{11}^{*} } & {F_{12}^{*} } & 0 \\ {F_{12}^{*} } & {F_{22}^{*} } & 0 \\ 0 & 0 & {F_{66}^{*} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\kappa_{xx}^{\left( 2 \right)} - l^{2} \left( {\frac{{\partial^{2} \kappa_{xx}^{\left( 2 \right)} }}{{\partial x^{2} }} + \frac{{\partial^{2} \kappa_{xx}^{\left( 2 \right)} }}{{\partial y^{2} }}} \right)} \\ {\kappa_{yy}^{\left( 2 \right)} - l^{2} \left( {\frac{{\partial^{2} \kappa_{yy}^{\left( 2 \right)} }}{{\partial x^{2} }} + \frac{{\partial^{2} \kappa_{yy}^{\left( 2 \right)} }}{{\partial y^{2} }}} \right)} \\ {\kappa_{xy}^{\left( 2 \right)} - l^{2} \left( {\frac{{\partial^{2} \kappa_{xy}^{\left( 2 \right)} }}{{\partial x^{2} }} + \frac{{\partial^{2} \kappa_{xy}^{\left( 2 \right)} }}{{\partial y^{2} }}} \right)} \\ \end{array} } \right\} \\ \end{aligned},$$

$$\begin{aligned} & \left\{ {\begin{array}{*{20}c} {M_{xx} - \mu^{2} \left( {\frac{{\partial^{2} M_{xx} }}{{\partial x^{2} }} + \frac{{\partial^{2} M_{xx} }}{{\partial y^{2} }}} \right)} \\ {M_{yy} - \mu^{2} \left( {\frac{{\partial^{2} M_{yy} }}{{\partial x^{2} }} + \frac{{\partial^{2} M_{yy} }}{{\partial y^{2} }}} \right)} \\ {M_{xy} - \mu^{2} \left( {\frac{{\partial^{2} M_{xy} }}{{\partial x^{2} }} + \frac{{\partial^{2} M_{xy} }}{{\partial y^{2} }}} \right)} \\ \end{array} } \right\} \\ & \quad = \left[ {\begin{array}{*{20}c} {B_{11}^{*} } & {B_{12}^{*} } & 0 \\ {B_{12}^{*} } & {B_{11}^{*} } & 0 \\ 0 & 0 & {B_{66}^{*} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx}^{0} - l^{2} \left( {\frac{{\partial^{2} \varepsilon_{xx}^{0} }}{{\partial x^{2} }} + \frac{{\partial^{2} \varepsilon_{xx}^{0} }}{{\partial y^{2} }}} \right)} \\ {\varepsilon_{yy}^{0} - l^{2} \left( {\frac{{\partial^{2} \varepsilon_{yy}^{0} }}{{\partial x^{2} }} + \frac{{\partial^{2} \varepsilon_{yy}^{0} }}{{\partial y^{2} }}} \right)} \\ {\gamma_{xy}^{0} - l^{2} \left( {\frac{{\partial^{2} \gamma_{xy}^{0} }}{{\partial x^{2} }} + \frac{{\partial^{2} \gamma_{xy}^{0} }}{{\partial y^{2} }}} \right)} \\ \end{array} } \right\} \\ & \quad + \left[ {\begin{array}{*{20}c} {D_{11}^{*} } & {D_{12}^{*} } & 0 \\ {D_{12}^{*} } & {D_{11}^{*} } & 0 \\ 0 & 0 & {D_{66}^{*} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\kappa_{xx}^{\left( 1 \right)} - l^{2} \left( {\frac{{\partial^{2} \kappa_{xx}^{\left( 1 \right)} }}{{\partial x^{2} }} + \frac{{\partial^{2} \kappa_{xx}^{\left( 1 \right)} }}{{\partial y^{2} }}} \right)} \\ {\kappa_{yy}^{\left( 1 \right)} - l^{2} \left( {\frac{{\partial^{2} \kappa_{yy}^{\left( 1 \right)} }}{{\partial x^{2} }} + \frac{{\partial^{2} \kappa_{yy}^{\left( 1 \right)} }}{{\partial y^{2} }}} \right)} \\ {\kappa_{xy}^{\left( 1 \right)} - l^{2} \left( {\frac{{\partial^{2} \kappa_{xy}^{\left( 1 \right)} }}{{\partial x^{2} }} + \frac{{\partial^{2} \kappa_{xy}^{\left( 1 \right)} }}{{\partial y^{2} }}} \right)} \\ \end{array} } \right\} \\ & \quad + \left[ {\begin{array}{*{20}c} {G_{11}^{*} } & {G_{12}^{*} } & 0 \\ {G_{12}^{*} } & {G_{22}^{*} } & 0 \\ 0 & 0 & {G_{66}^{**} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\kappa_{xx}^{\left( 2 \right)} - l^{2} \left( {\frac{{\partial^{2} \kappa_{xx}^{\left( 2 \right)} }}{{\partial x^{2} }} + \frac{{\partial^{2} \kappa_{xx}^{\left( 2 \right)} }}{{\partial y^{2} }}} \right)} \\ {\kappa_{yy}^{\left( 2 \right)} - l^{2} \left( {\frac{{\partial^{2} \kappa_{yy}^{\left( 2 \right)} }}{{\partial x^{2} }} + \frac{{\partial^{2} \kappa_{yy}^{\left( 2 \right)} }}{{\partial y^{2} }}} \right)} \\ {\kappa_{xy}^{\left( 2 \right)} - l^{2} \left( {\frac{{\partial^{2} \kappa_{xy}^{\left( 2 \right)} }}{{\partial x^{2} }} + \frac{{\partial^{2} \kappa_{xy}^{\left( 2 \right)} }}{{\partial y^{2} }}} \right)} \\ \end{array} } \right\} \\ \end{aligned},$$

$$\begin{aligned} & \left\{ {\begin{array}{*{20}c} {R_{xx} - \mu^{2} \left( {\frac{{\partial^{2} R_{xx} }}{{\partial x^{2} }} + \frac{{\partial^{2} R_{xx} }}{{\partial y^{2} }}} \right)} \\ {R_{yy} - \mu^{2} \left( {\frac{{\partial^{2} R_{yy} }}{{\partial x^{2} }} + \frac{{\partial^{2} R_{yy} }}{{\partial y^{2} }}} \right)} \\ {R_{xy} - \mu^{2} \left( {\frac{{\partial^{2} R_{xy} }}{{\partial x^{2} }} + \frac{{\partial^{2} R_{xy} }}{{\partial y^{2} }}} \right)} \\ \end{array} } \right\} \\ & \quad = \left[ {\begin{array}{*{20}c} {F_{11}^{*} } & {F_{12}^{*} } & 0 \\ {F_{12}^{*} } & {F_{22}^{*} } & 0 \\ 0 & 0 & {F_{66}^{*} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx}^{0} - l^{2} \left( {\frac{{\partial^{2} \varepsilon_{xx}^{0} }}{{\partial x^{2} }} + \frac{{\partial^{2} \varepsilon_{xx}^{0} }}{{\partial y^{2} }}} \right)} \\ {\varepsilon_{yy}^{0} - l^{2} \left( {\frac{{\partial^{2} \varepsilon_{yy}^{0} }}{{\partial x^{2} }} + \frac{{\partial^{2} \varepsilon_{yy}^{0} }}{{\partial y^{2} }}} \right)} \\ {\gamma_{xy}^{0} - l^{2} \left( {\frac{{\partial^{2} \gamma_{xy}^{0} }}{{\partial x^{2} }} + \frac{{\partial^{2} \gamma_{xy}^{0} }}{{\partial y^{2} }}} \right)} \\ \end{array} } \right\} \\ & \quad + \left[ {\begin{array}{*{20}c} {G_{11}^{*} } & {G_{12}^{*} } & 0 \\ {G_{12}^{*} } & {G_{22}^{*} } & 0 \\ 0 & 0 & {G_{66}^{**} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\kappa_{xx}^{\left( 1 \right)} - l^{2} \left( {\frac{{\partial^{2} \kappa_{xx}^{\left( 1 \right)} }}{{\partial x^{2} }} + \frac{{\partial^{2} \kappa_{xx}^{\left( 1 \right)} }}{{\partial y^{2} }}} \right)} \\ {\kappa_{yy}^{\left( 1 \right)} - l^{2} \left( {\frac{{\partial^{2} \kappa_{yy}^{\left( 1 \right)} }}{{\partial x^{2} }} + \frac{{\partial^{2} \kappa_{yy}^{\left( 1 \right)} }}{{\partial y^{2} }}} \right)} \\ {\kappa_{xy}^{\left( 1 \right)} - l^{2} \left( {\frac{{\partial^{2} \kappa_{xy}^{\left( 1 \right)} }}{{\partial x^{2} }} + \frac{{\partial^{2} \kappa_{xy}^{\left( 1 \right)} }}{{\partial y^{2} }}} \right)} \\ \end{array} } \right\} \\ & \quad + \left[ {\begin{array}{*{20}c} {H_{11}^{*} } & {H_{12}^{*} } & 0 \\ {H_{12}^{*} } & {H_{22}^{*} } & 0 \\ 0 & 0 & {H_{66}^{*} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\kappa_{xx}^{\left( 2 \right)} - l^{2} \left( {\frac{{\partial^{2} \kappa_{xx}^{\left( 2 \right)} }}{{\partial x^{2} }} + \frac{{\partial^{2} \kappa_{xx}^{\left( 2 \right)} }}{{\partial y^{2} }}} \right)} \\ {\kappa_{yy}^{\left( 2 \right)} - l^{2} \left( {\frac{{\partial^{2} \kappa_{yy}^{\left( 2 \right)} }}{{\partial x^{2} }} + \frac{{\partial^{2} \kappa_{yy}^{\left( 2 \right)} }}{{\partial y^{2} }}} \right)} \\ {\kappa_{xy}^{\left( 2 \right)} - l^{2} \left( {\frac{{\partial^{2} \kappa_{xy}^{\left( 2 \right)} }}{{\partial x^{2} }} + \frac{{\partial^{2} \kappa_{xy}^{\left( 2 \right)} }}{{\partial y^{2} }}} \right)} \\ \end{array} } \right\} \\ \end{aligned},$$

$$\left\{ {\begin{array}{*{20}c} {Q_{x} - \mu^{2} \left( {\frac{{\partial^{2} Q_{x} }}{{\partial x^{2} }} + \frac{{\partial^{2} Q_{x} }}{{\partial y^{2} }}} \right)} \\ {Q_{y} - \mu^{2} \left( {\frac{{\partial^{2} Q_{y} }}{{\partial x^{2} }} + \frac{{\partial^{2} Q_{y} }}{{\partial y^{2} }}} \right)} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {A_{44}^{*} } & 0 \\ 0 & {A_{55}^{*} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\psi_{x} - l^{2} \left( {\frac{{\partial^{2} \psi_{x} }}{{\partial x^{2} }} + \frac{{\partial^{2} \psi_{x} }}{{\partial y^{2} }}} \right)} \\ {\psi_{y} - l^{2} \left( {\frac{{\partial^{2} \psi_{y} }}{{\partial x^{2} }} + \frac{{\partial^{2} \psi_{y} }}{{\partial y^{2} }}} \right)} \\ \end{array} } \right\}.$$

Appendix 2

$$\varphi_{1} = \frac{{A_{11}^{*} }}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }},\quad \varphi_{2} = \frac{1}{{A_{66}^{*} }},\quad \varphi_{3} = \frac{{A_{12}^{*} }}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }},\quad \varphi_{4} = \frac{{A_{22}^{*} }}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }},$$

$$\varphi_{5} = \frac{{A_{11}^{*} B_{12}^{*} - A_{12}^{*} B_{11}^{*} }}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }},\quad \varphi_{6} = \frac{{A_{11}^{*} B_{11}^{*} - A_{12}^{*} B_{12}^{*} }}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }},\quad \varphi_{7} = \frac{{A_{22}^{*} B_{22}^{*} - A_{12}^{*} B_{12}^{*} }}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }},\quad \varphi_{8} = \frac{{B_{66}^{*} }}{{A_{66}^{*} }},$$

$$\varphi_{9} = \frac{{A_{22}^{*} B_{12}^{*} - A_{12}^{*} B_{22}^{*} }}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }},\quad \varphi_{10} = \frac{{A_{11}^{*} F_{12}^{*} - A_{12}^{*} F_{11}^{*} }}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }},\quad \varphi_{11} = \frac{{A_{11}^{*} F_{11}^{*} - A_{12}^{*} F_{12}^{*} }}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }},\quad \varphi_{12} = \frac{{F_{66}^{*} }}{{A_{66}^{*} }},$$

$$\varphi_{13} = \frac{{A_{22}^{*} F_{12}^{*} - A_{12}^{*} F_{22}^{*} }}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }},\quad \varphi_{14} = \frac{{A_{22}^{*} F_{22}^{*} - A_{12}^{*} F_{12}^{*} }}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }},\quad \varphi_{15} = D_{11}^{*} - \frac{{A_{11}^{*} \left( {\left( {B_{11}^{*} } \right)^{2} + \left( {B_{12}^{*} } \right)^{2} } \right)}}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }},$$

$$\varphi_{16} = 2\left( {D_{12}^{*} + 2D_{66}^{*} } \right) - \frac{{A_{11}^{*} \left( {\left( {B_{11}^{*} } \right)^{2} + \left( {B_{12}^{*} } \right)^{2} } \right) + A_{22}^{*} \left( {\left( {B_{22}^{*} } \right)^{2} + \left( {B_{12}^{*} } \right)^{2} } \right)}}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }} - 4\frac{{\left( {B_{66}^{*} } \right)^{2} }}{{A_{66}^{*} }},$$

$$\varphi_{17} = D_{22}^{*} - \frac{{A_{22}^{*} \left( {\left( {B_{22}^{*} } \right)^{2} + \left( {B_{12}^{*} } \right)^{2} } \right)}}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }} ,\quad \varphi_{18} = \frac{{A_{11}^{*} \left( {\left( {F_{11}^{*} } \right)^{2} + \left( {F_{12}^{*} } \right)^{2} } \right)}}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }} - G_{11}^{*},$$

$$\varphi_{19} = \frac{{2A_{11}^{*} F_{11}^{*} F_{12}^{*} - A_{12}^{*} \left( {\left( {F_{11}^{*} } \right)^{2} + \left( {F_{12}^{*} } \right)^{2} } \right)}}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }} + 2\frac{{\left( {B_{66}^{**} } \right)^{2} }}{{A_{66}^{*} }} - \left( {G_{12}^{*} + 2G_{66}^{*} } \right),$$

$$\varphi_{20} = \frac{{A_{22}^{*} \left( {\left( {F_{22}^{*} } \right)^{2} + \left( {F_{12}^{*} } \right)^{2} } \right)}}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }} - G_{22}^{*},$$

$$\varphi_{21} = \frac{{2A_{22}^{*} F_{22}^{*} F_{12}^{*} - A_{12}^{*} \left( {\left( {F_{22}^{*} } \right)^{2} + \left( {F_{12}^{*} } \right)^{2} } \right)}}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }} + 2\frac{{\left( {B_{66}^{**} } \right)^{2} }}{{A_{66}^{*} }} - \left( {G_{12}^{*} + 2G_{66}^{*} } \right),$$

$$\varphi_{22} = \frac{{A_{11}^{*} \left( {B_{11}^{*} F_{11}^{*} + B_{12}^{*} F_{12}^{*} } \right) - A_{12}^{*} \left( {B_{12}^{*} F_{11}^{*} + B_{11}^{*} F_{12}^{*} } \right)}}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }} - G_{11}^{*} ,$$

$$\varphi_{23} = \frac{{A_{11}^{*} \left( {B_{11}^{*} F_{12}^{*} + B_{12}^{*} F_{11}^{*} } \right) - A_{12}^{*} \left( {B_{12}^{*} F_{12}^{*} + B_{11}^{*} F_{11}^{*} } \right)}}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }} + 2\frac{{B_{66}^{*} F_{66}^{*} }}{{A_{66}^{*} }} - \left( {G_{12}^{*} + 2G_{66}^{*} } \right),$$

$$\varphi_{24} = H_{11}^{*} - \frac{{A_{11}^{*} \left( {\left( {F_{11}^{*} } \right)^{2} + \left( {F_{12}^{*} } \right)^{2} } \right)}}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }} ,\quad \varphi_{25} = H_{66}^{*} - \frac{{\left( {F_{66}^{*} } \right)^{2} }}{{A_{66}^{*} }},$$

$$\varphi_{26} = H_{12}^{*} + H_{66}^{*} + \frac{{A_{12}^{*} \left( {\left( {F_{11}^{*} } \right)^{2} + \left( {F_{12}^{*} } \right)^{2} } \right)}}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }} - \frac{{\left( {F_{66}^{*} } \right)^{2} }}{{A_{66}^{*} }},$$

$$\varphi_{27} = \frac{{A_{22}^{*} \left( {B_{22}^{*} F_{22}^{*} + B_{12}^{*} F_{12}^{*} } \right) - A_{12}^{*} \left( {B_{12}^{*} F_{22}^{*} + B_{22}^{*} B_{12}^{*} } \right)}}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }} - G_{22}^{*},$$

$$\varphi_{28} = \frac{{A_{22}^{*} \left( {B_{22}^{*} F_{12}^{*} + B_{12}^{*} F_{22}^{*} } \right) - A_{12}^{*} \left( {B_{12}^{*} F_{12}^{*} + B_{22}^{*} F_{22}^{*} } \right)}}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }} + 2\frac{{B_{66}^{*} F_{66}^{*} }}{{A_{66}^{*} }} - \left( {G_{12}^{*} + 2G_{66}^{*} } \right),$$

$$\varphi_{29} = H_{22}^{*} - \frac{{A_{22}^{*} \left( {\left( {F_{22}^{*} } \right)^{2} + \left( {F_{12}^{*} } \right)^{2} } \right)}}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }},\quad \varphi_{30} = H_{12}^{*} + H_{66}^{*} + \frac{{A_{12}^{*} \left( {\left( {F_{22}^{*} } \right)^{2} + \left( {F_{12}^{*} } \right)^{2} } \right)}}{{A_{11}^{*} A_{22}^{*} - \left( {A_{12}^{*} } \right)^{2} }} - \frac{{\left( {F_{66}^{*} } \right)^{2} }}{{A_{66}^{*} }}.$$