1 Introduction

There are many complicated problems, such as crack propagation and large deformation, in science and engineering fields must be solved with numerical methods. The boundary element method and the finite element method are the major numerical methods which based on meshes or elements.

In recent years, the meshless method has made great progress [1, 2]. When meshless method is used to solve a problem, only discrete nodes are distributed on the problem domain and its boundary without meshing. Without domain discretization, this method uses a node-based approximation to construct the approximation function or interpolation function. This fully ensures the calculation accuracy and efficiency. Moreover, the approach leads to a flexible choice of nodes in the domain for the specific characteristics. It is shown that the method has good adaptability and calculation accuracy. Therefore, as a new and efficient method in scientific and engineering computing, the meshless method has gradually become a research hotspot.

Currently, the element-free Galerkin method (EFG) [3] and the reproducing kernel particle method (RKPM) [4, 5] are major meshless methods. Based on the moving least-squares (MLS) approximation [6], the EFG method has high calculation accuracy, because the MLS approximation is obtained from the ordinary least squares method with the best approximation [7,8,9,10]. Because of the complicated shape function of the MLS approximation, the computational efficiency of the EFG method is low, especially for solving three-dimensional (3D) problems. In addition, the MLS approximation maybe causes an ill-conditioned or singular system of equations. To improve the computational efficiency of the EFG method, the improved MLS approximation [11, 12] and complex variable moving least-squares (CVMLS) approximation [13,14,15] were presented. In the improved MLS approximation, the basis functions of the approximation are orthogonal, which can avoid the ill-conditioned or singular equations. The improved MLS approximation improves the calculation efficiency under similar calculation accuracy because it doesnot require computing the inversion of matrices. By using the improved MLS approximation Zhang et al. [16,17,18] proposed the improved EFG method for wave equations, transient heat conduction and elastodynamics problems, and Peng et al. [19] and Cheng et al. [20, 21] presented the improved EFG method for viscoelasticity, elastoplasticity, and diffusional drug release problems. In the CVMLS approximation, the complex variable basis functions are used, which results in the fewer number of the coefficients of the basis functions in the trial function, then the calculation efficiency is improved. Based on the CVMLS approximation, the complex variable EFG method has been presented for solving temperature field [22], elastoplasticity [23] and plate bending problems [24].

In the above EFG method and the corresponding improved methods, the essential boundary conditions are enforced indirectly, and the Lagrange multiplier method or the penalty function method is used. To enforce the essential boundary conditions directly, based on the interpolating moving least-squares (IMLS) method [6], Ren et al. presented the improved IMLS method [25], and then the interpolating EFG method was proposed for elasticity and potential problems [26, 27]. Cheng et al. presented the interpolating EFG method for solving elastoplasticity [28] and large deformation problems [29, 30]. And Liu et al. solved the 3D problems by using the interpolating EFG method [31,32,33]. Based on nonsingular weight functions, the improved IMLS method is studied further [34, 35], and then the corresponding interpolating EFG method was presented for solving potential [36, 37], elasticity [38], elastoplasticity [39], two-point boundary value problems [40]. Liu et al. proposed the formulae of the interpolating EFG method for solving inhomogeneous swelling of polymer gels [41] and large deformation problems [42, 43].

The dimensional splitting method was introduced into meshless methods to improve the calculation efficiency of the EFG method for 3D problems. Cheng et al. presented the hybrid improved complex variable element-free Galerkin method for 3D potential [44], wave propagation [45], transient heat conduction [46], advection–diffusion [47] and elasticity problems [48]. Meng et al. combined the dimensional splitting method with the IEFG method and proposed the hybrid element-free Galerkin method for the 3D potential [49], transient heat conduction [50] and wave equation [51]. And Peng et al. presented the hybrid reproducing kernel particle method for solving 3D potential [52], transient heat conduction [53] and wave equation [54]. These methods can greatly improve the calculation efficiency for 3D problems greatly while ensuring calculation accuracy. In these methods, the essential boundary conditions are enforced indirectly.

In this paper, based on the improved IMLS method and dimension splitting method, the interpolating dimension splitting element-free Galerkin (IDSEFG) method for the 3D potential problems, is proposed. The key of the IDSEFG method is to split a 3D problem domain into a series of related two-dimensional (2D) subdomains. The shape function is constructed with the improved IMLS method on the 2D subdomain, and the Galerkin weak form based on the dimension splitting method is used to obtain the discretized equations. The discretized equations are coupled by using the finite difference method on these 2D subdomains. The essential boundary conditions can be enforced directly to improve the calculation accuracy, and the calculation efficiency is greatly improved because of the dimension splitting method, they are the advantages of the IDSEFG method. The effects of the number of nodes, the direction of dimension splitting, and the parameters of the influence domain on the calculation accuracy are studied through four numerical examples. The numerical solutions of the IDSEFG method are compared with the numerical solutions of the IEFG method and the analytical solutions. It is verified that the numerical solutions of the IDSEFG method are highly consistent with the analytical solution, and the calculation efficiency of the IDSEFG method is significantly better than that of the IEFG method.

2 The improved IMLS method

The improved IMLS method [25] is proposed by Ren and Cheng. It is based on Lancaster’s IMLS method [6].

Defining inner product of any f(x) and g(x) as

$$ \left( {f, g} \right)_{\varvec x} = \mathop {\mathop \sum \limits^{n} }\limits_{I = 1} w({\varvec x} - {\varvec x}_{I} )f({\varvec x}_{I} )g({\varvec x}_{I} ),\quad \forall f({\varvec x}), g({\varvec x}) \in C^{0} (\overline{\Omega }), $$
(1)

where \(C^{0} (\overline{\Omega })\) is a set of continuous functions in problem domain \(\overline{\Omega }\) and \(\overline{\Omega } = \Omega \cup \partial \Omega\), there are \(I = 1,2, \ldots ,n\) nodes in domain of point x. Therefore,

$$ f _{\varvec x} = \left[ {\left( {f, f } \right)_{\varvec x} } \right]^{\frac{1}{2}} . $$
(2)

On the space span \((d_{1} ,d_{2} , \ldots ,d_{k} )\), \(d_{1} ({\varvec x}) = 1,d_{2} ({\varvec x}), \ldots ,d_{k} ({\varvec x})\) are used to express the basis functions, where a function with the subscript \({\varvec x}\) is related to the selected point \({{\varvec x}}\). Normalizing \(d_{1} ({\varvec x}) \) we have.

$$ \beta_{{\varvec x}}^{(1)} ({\varvec x}) = \frac{{d_{1} }}{{||d_{1} ||_{{\varvec x}} }} = \frac{1}{{\left[ {\mathop {\mathop \sum \limits^{n} }\limits_{I = 1} w({\varvec x} - {\varvec x}_{I} )} \right]^{\frac{1}{2}} }}. $$
(3)

As we know \(i = 2,3, \ldots ,k\), the following functions can be generated and they are orthogonal to \(\beta_{\varvec x}^{(1)}\),

$$ \begin{aligned} b_{\varvec x}^{(i)} (\varvec x) & = d_{i} (\varvec x) - (d_{i} ,\beta_{\varvec x}^{(1)} )_{\varvec x} \beta_{\varvec x}^{(1)} \\ & = d_{i} (\varvec x) - \frac{{\mathop {\mathop \sum \limits^{n} }\limits_{I = 1} d_{i} ({\varvec x}_{I} )w({\varvec x} - {\varvec x}_{I} )}}{{\mathop {\mathop \sum \limits^{n} }\limits_{I = 1} w({\varvec x} - {\varvec x}_{I} )}} = d_{i} ({\varvec x}) - \mathop {\mathop \sum \limits^{n} }\limits_{I = 1} d_{i} ({\varvec x}_{I} )v_{ } ({\varvec x} - {\varvec x}_{I} ), \\ \end{aligned} $$
(4)

where

$$ {\varvec v} ({\varvec x} - {\varvec x}_{I} ) = \frac{{w({\varvec x} - {\varvec x}_{I} )}}{{\mathop {\mathop \sum \limits^{n} }\limits_{I = 1} w({\varvec x} - {\varvec x}_{I} )}},\quad (I = 1,2, \ldots ,n). $$
(5)

When we make \(\beta_{\varvec x}^{(1)} ({\varvec x}),b_{\varvec x}^{(2)} ({\varvec x}), \ldots ,b_{\varvec x}^{(k)} ({\varvec x})\) as the new basis functions, the approximation function of the MLS approximation is

$$ u^{h} ({\varvec x}) = {\varvec v}^{T} ({\varvec x}){\varvec u} + {\varvec b}^{T} ({\varvec x}){\varvec a}({\varvec x}) $$
(6)

where

$$ {\varvec u}^{T} = (u_{1} ,u_{2} , \ldots ,u_{n} ), $$
(7)
$$ {\varvec v}^{T} = (v_{ } ({\varvec x} - {\varvec x}_{1} ),v_{ } ({\varvec x} - {\varvec x}_{2} ), \ldots ,v_{ } ({\varvec x} - {\varvec x}_{n} )), $$
(8)
$$ {\varvec b}^{T} ({\varvec x}) = (b_{\varvec x}^{(2)} ({\varvec x}),b_{\varvec x}^{(3)} ({\varvec x}), \ldots ,b_{\varvec x}^{(k)} ({\varvec x})), $$
(9)
$$ {\varvec a}({\varvec x}) = (a_{1} ({\varvec x}),a_{2} ({\varvec x}), \ldots ,a_{k - 1} ({\varvec x}))^{T} . $$
(10)

Then using the MLS approximation, we have

$$ {\varvec a}({\varvec x}) = {\varvec A}_{\varvec x}^{ - 1} ({\varvec x}){\varvec B}_{\varvec x}^{ } ({\varvec x}){\varvec u}, $$
(11)

where

$$ {\varvec A}_{\varvec x}({\varvec x}) = {\varvec P}_{\varvec x}^{T} {\varvec W}({\varvec x}){\varvec P}_{\varvec x}, $$
(12)
$$ {\varvec B}_{\varvec x}({\varvec x}) = {\varvec P}_{\varvec x}^{T} {\varvec W}({\varvec x}), $$
(13)
$$ {\varvec P}_{\varvec x} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {b_{\varvec x}^{(2)} ({\varvec x}_{1} )} & {b_{\varvec x}^{(3)} ({\varvec x}_{1} )} \\ {b_{\varvec x}^{(2)} ({\varvec x}_{2} )} & {b_{\varvec x}^{(3)} ({\varvec x}_{2} )} \\ \end{array} } & {\begin{array}{*{20}c} \cdots & {b_{\varvec x}^{(k)} ({\varvec x}_{1} )} \\ \cdots & {b_{\varvec x}^{(k)} ({\varvec x}_{2} )} \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots & \vdots \\ {b_{\varvec x}^{(2)} ({\varvec x}_{n} )} & {b_{\varvec x}^{(3)} ({\varvec x}_{n} )} \\ \end{array} } & {\begin{array}{*{20}c} \ddots & \vdots \\ \cdots & {b_{\varvec x}^{(k)} ({\varvec x}_{n} )} \\ \end{array} } \\ \end{array} } \right], $$
(14)
$$ {\varvec W}({\varvec x}) = \left[ {\begin{array}{*{20}c} {w({\varvec x} - {\varvec x}_{1} )} & 0 & \cdots & 0 \\ 0 & {w({\varvec x} - {\varvec x}_{2} )} & \vdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \vdots & {w({\varvec x} - {\varvec x}_{n} )} \\ \end{array} } \right]. $$
(15)

It can be obtained by substituting Eq. (10) into Eq. (6)

$$ u^{h} \left( {\varvec x} \right) = {\varvec v}^{T} ({\varvec x}){\varvec u} + {\varvec b}^{T} ({\varvec x}){\varvec A}_{{\varvec x}}^{ - 1} ({\varvec x}){\varvec B}_{\varvec x} ({\varvec x}){\varvec u}. $$
(16)

Equation (16) can also be written as

$$ u^{h} ({\varvec x}) = {\varvec \Phi} ({\varvec x}){\varvec u}, $$
(17)

where

$$ {\varvec \Phi} ({\varvec x}) = (\Phi_{1} ({\varvec x}),\Phi_{2} ({\varvec x}), \ldots ,\Phi_{n} ({\varvec x})) = {\varvec v}^{T} ({\varvec x}) + {\varvec b}^{T} ({\varvec x}){\varvec A}_{\varvec x}^{- 1} ({\varvec x}){\varvec B}_{\varvec x} ({\varvec x}). $$
(18)

For the improved IMLS method, the shape function which shown as Eq. (18) is simpler than MLS approximation, it will improve the calculation efficiency, and

$$ \begin{aligned} (\Phi_{I} ({\varvec x}))_{,j} & = (\nu ({\varvec x} - {\varvec x}_{I} ) + {\varvec b}^{T} (\varvec x){\varvec A}_{\varvec x}^{ - 1} ({\varvec x})({\varvec B}_{\varvec x} ({\varvec x}))_{I} )_{,j} \\ & = \nu ({\varvec x} - {\varvec x}_{I} )_{,j} + {\varvec b}^{T}_{,j} {\varvec A}_{\varvec x}^{ - 1} ({\varvec B}_{\varvec x} )_{I} + {\varvec b}^{T} ({\varvec A}_{\varvec x}^{ - 1} )_{,j} ({\varvec B}_{\varvec x} )_{I} + {\varvec b}^{T} {\varvec A}_{\varvec x}^{ - 1} ({\varvec B}_{\varvec x} )_{I,j} , \\ \end{aligned} $$
(19)

where

$$ ({\varvec B}_{\varvec x}^{ } )_{I,j} = w({\varvec x} - {\varvec x}_{I} )_{,j} b_{\varvec x}^{ } ({\varvec x}_{I} ), $$
(20)
$$ ({\varvec A}_{\varvec x}^{ - 1} )_{,j} = - {\varvec A}_{\varvec x}^{ - 1} ({\varvec A}_{\varvec x} )_{,j} {\varvec A}_{\varvec x}^{ - 1} , $$
(21)
$$ \begin{aligned} ({\varvec A}_{\varvec x} )_{,j} & = \mathop {\mathop \sum \limits^{n} }\limits_{I = 1} w({\varvec x} - {\varvec x}_{I} )_{,j} {\varvec b}_{\varvec x} ({\varvec x}_{I} ){\varvec b}_{\varvec x}^{ T} ({\varvec x}_{I} ) + \mathop {\mathop \sum \limits^{n} }\limits_{I = 1} w({\varvec x} - {\varvec x}_{I} ){\varvec b}_{\varvec x} ({\varvec x}_{I} )_{,j} {\varvec b}_{\varvec x}^{ T} ({\varvec x}_{I} ) \\ & + \mathop {\mathop \sum \limits^{n} }\limits_{I = 1} w({\varvec x} - {\varvec x}_{I} ){\varvec b}_{\varvec x} ({\varvec x}_{I} ){\varvec b}_{\varvec x}^{ T} ({\varvec x}_{I} )_{,j} . \\ \end{aligned} $$
(22)

Then we have

$$ {\varvec a}({\varvec x}) = {\varvec A}_{\varvec x}^{ - 1} ({\varvec x}){\varvec B}_{\varvec x}({\varvec x})({\varvec u} - ({\varvec v}^{T} ({\varvec x}){\varvec u})d_{1} ), $$
(23)

where \(d_{1} ({\varvec x}_{I} ) = 1\).

The weight function \(w({\varvec x} - {\varvec x}_{I} )\) in the improved IMLS method can be selected as

$$ w = w({\varvec x} - {\varvec x}_{I} ) = \left\{ {\begin{array}{*{20}c} {\frac{{\rho^{\sigma } }}{{\left| {\left. {{\varvec x} - {\varvec x}_{I} } \right|} \right. ^{\sigma } }}(1 - \frac{\rho }{{\left| {\left. {{\varvec x} - {\varvec x}_{I} } \right|} \right. }}) ^{2} ,\quad \left| {\left. {\varvec {x} - {\varvec x}_{I} } \right|} \right. \le \rho } \\ {0,\quad {\text{otherwise}}} \\ \end{array} } \right., $$
(24)

where \(\rho\) is the radius of the influence domain in the function and \(\sigma\) is an even positive integer, we take \(\sigma = 4\) in all examples in this paper.

At any points \(\left\{ {{\varvec x}_{I} } \right\}_{I = 1}^{n}\), \(u^{h} ({\varvec x})\) of Eq. (17) can interpolate, so we obtain

$$ u^{h} ({\varvec x}_{I} ) = u({\varvec x}_{I} ), $$
(25)

then we have

$$ \Phi_{I} ({\varvec x}_{J} ) = \left\{ {\begin{array}{*{20}c} {1,\quad I = J,} \\ {0,\quad I \ne J,} \\ \end{array} } \right.. $$
(26)

In the improved IMLS method, the essential boundary conditions can be enforced directly when establishing the discretized equations because this method satisfies the property of the Kronecker delta function, which will definitely improve the calculation accuracy.

3 The IDSEFG method for 3D potential problems

The governing equation of 3D potential problems is

$$ \frac{{\partial^{2} u}}{{\partial x_{1}^{2} }} + \frac{{\partial^{2} u}}{{\partial x_{2}^{2} }} + \frac{{\partial^{2} u}}{{\partial x_{3}^{2} }} = b({\varvec x}),\quad ({\varvec x} = (x_{1} ,x_{2} ,x_{3} ) \in \Omega ), $$
(27)

with essential boundary condition

$$ u({\varvec x}) = \overline{u}({\varvec x}),\quad ({\varvec x} \in \Gamma_{u} ), $$
(28)

and natural boundary condition

$$ q({\varvec x}) = \frac{\partial u({\varvec x})}{{\partial {\varvec n}({\varvec x})}} = \overline{q}({\varvec x}),\quad \left( {{\varvec x} \in \Gamma_{q} } \right), $$
(29)

where \(\Omega\) is the problem domain, \(u({\varvec x})\) is an unknown variable, \(b({\varvec x})\) is a known function, \(\overline{u}({\varvec x})\) is the known potential function on \(\Gamma_{u}\), \(\overline{q}({\varvec x})\) is the known normal derivative on \(\Gamma_{q}\). Notice that \(\Gamma = \Gamma_{u} \cup \Gamma_{q}\) and \(\Gamma_{u} \cap \Gamma_{q} = \emptyset\), \(\Gamma\) is the boundary of \(\Omega\), and \({\varvec n}({\varvec x})\) is the outward unit normal vector of the boundary \({\Gamma }\).

When using the IDSEFG method to solve 3D potential problems, the splitting direction should be selected reasonably according to the characteristics of the control equation and the boundary conditions, this will bring better computing efficiency and make programming easier.

When applying the dimension splitting method, \({\Omega }\) can be split into \(L\) layers along one direction, we choose \(x_{3}\) here. \(\Delta x_{3}\) is the distance between layer to layer, we get \(L + 1\) 2D subdomains \( \Omega^{(k)} (k = 0,1,2, \ldots ,L)\),

$$ \Omega = \mathop {\mathop \cup \limits^{L - 1} }\limits_{k = 0} \Omega^{(k)} \times [x_{3}^{(k)} ,x_{3}^{(k + 1)} ) \cup \Omega^{(L)} , $$
(30)

where

$$ a = x_{3}^{(0)} < x_{3}^{(1)} \cdots < x_{3}^{(L)} = c, \quad x_{3} \in [a,c], $$
(31)
$$ \Delta x_{3} = x_{3}^{(k + 1)} - x_{3}^{\left( k \right)} = (c - a)/L, $$
(32)

Because \(\Delta x_{3}\) is a fixed value, \(u\) and \(\frac{{\partial^{2} u}}{{\partial x_{3}^{2} }}\) can be considered as functions of \(x_{1}\) and \(x_{2}\), therefore, the 3D problem of Eq. (27) above can be written as the following series of related 2D boundary value problems,

$$ \frac{{\partial^{2} u^{(k)} }}{{\partial x_{1}^{2} }} + \frac{{\partial^{2} u^{(k)} }}{{\partial x_{2}^{2} }} = b^{(k)} - \frac{{\partial^{2} u^{(k)} }}{{\partial x_{3}^{2} }},\quad \left( {(x_{1} ,x_{2} ) \in \Omega^{(k)} ,x_{3} = x_{3}^{(k)} } \right), $$
(33)

with the boundary conditions

$$ u^{(k)} (x_{1} ,x_{2} ) = \overline{u}^{(k)} (x_{1} ,x_{2} ) = \overline{u}(x_{1} ,x_{2} ,x_{3}^{(k)} ),\quad \left( {(x_{1} ,x_{2} ) \in \Gamma_{u}^{(k)} } \right), $$
(34)
$$ q^{(k)} (x_{1} ,x_{2} ) = \overline{q}^{(k)} (x_{1} ,x_{2} ) = \overline{q}(x_{1} ,x_{2} ,x_{3}^{(k)} ),\quad \left( {(x_{1} ,x_{2} ) \in \Gamma_{q}^{(k)} } \right), $$
(35)

where

$$ u^{(k)} = u(x_{1} ,x_{2} ,x_{3}^{(k)} ), $$
(36)
$$ b^{(k)} = b(x_{1} ,x_{2} ,x_{3}^{(k)} ), $$
(37)

\( u^{(k)} (x_{1} ,x_{2} )\) is the potential on subdomain \(\Omega^{(k)}\), \(\overline{u}(x_{1} ,x_{2} ,x_{3}^{(k)} )\) is the known potential function on \(\Gamma_{u}^{(k)}\), \(\overline{q}(x_{1} ,x_{2} ,x_{3}^{(k)} )\) is the known gradient function on \({\Gamma }_{{\text{q}}}^{{(k)}}\), \(\Gamma^{(k)} = \Gamma_{u}^{(k)} \cup \Gamma_{q}^{(k)}\) and \(\Gamma_{u}^{(k)} \cap \Gamma_{q}^{(k)} = \emptyset\).

The key step of the IDSEFG method is to solve the 2D boundary value problem (33)–(35) with the interpolating EFG method, then the solution of the 3D potential problem (Eqs. (27)–(29)) can be obtained by using the finite difference method in direction \(x_{3}\).

The equivalent function of Eqs. (33)–(35) is

$$ \Pi = \mathop \smallint \limits_{{\Omega^{(k)} }}^{ } \left[ {u^{(k)} \left( {\frac{{\partial^{2} u^{(k)} }}{{\partial x_{3}^{2} }} - b^{(k)} } \right)} \right]d\Omega^{(k)} - \mathop \smallint \limits_{{\Omega^{(k)} }}^{ } \frac{1}{2}\left[ {\left( {\frac{{\partial u^{(k)} }}{{\partial x_{1} }}} \right)^{2} + \left( {\frac{{\partial u^{(k)} }}{{\partial x_{2} }}} \right)^{2} } \right]d\Omega^{(k)} - \mathop \smallint \limits_{{\Gamma_{q}^{(k)} }}^{ } u^{(k)} \overline{q}^{(k)} d\Gamma^{(k)} . $$
(38)

Because the improved IMLS method satisfies the property of the Kronecker delta function, thus, the essential boundary conditions can be enforced directly.

Let

$$ \delta \Pi = 0, $$
(39)

we obtain the equivalent integral weak form

$$ \mathop \smallint \limits_{{\Omega^{(k)} }} \delta u^{(k)} \cdot \frac{{\partial^{2} u^{(k)} }}{{\partial x_{3}^{2} }}d\Omega^{(k)} - \mathop \smallint \limits_{{\Omega^{(k)} }} \delta ({\varvec L}u^{(k)} )^{T} \cdot ({\varvec L}u^{(k)} )d\Omega^{(k)} - \smallint_{{\Omega^{(k)} }} \delta u^{(k)} \cdot b^{(k)} d\Omega^{(k)} - \mathop \smallint \limits_{{\Gamma_{q}^{(k)} }} \delta u^{(k)} \cdot \overline{q}^{(k)} d\Gamma^{(k)} = 0. $$
(40)

where

$$ {\varvec L}( \cdot ) = \left[ {\begin{array}{*{20}c} {\frac{\partial }{{\partial x_{1} }}} \\ {\frac{\partial }{{\partial x_{2} }}} \\ \end{array} } \right]( \cdot ). $$
(41)

We distribute \(M\) nodes \({\varvec x}_{I}^{(k)}\) in the 2D subdomain \(\Omega^{(k)}\) obtained after dimension splitting, \(u^{(k)} ({\varvec x})\) at \({\varvec x}_{I}^{(k)}\) can be represented as

$$ u^{(k)} ({\varvec x}_{I}^{(k)} ) = u({\varvec x}_{I}^{(k)} ,x_{3}^{(k)} ). $$
(42)

The trial function \(u^{h} ({\varvec x}^{\left( k \right)} ,x_{3}^{(k)} )\) at \({\varvec x}^{(k)} = (x_{1} ,x_{2} )\) is related to the function at the node \({\varvec x}_{I}^{(k)}\) where the influence domain covers it. Constructing the shape function with the improved IMLS method, the trial function is

$$ u^{h} ({\varvec x}^{(k)} ,x_{3}^{(k)} ) = \mathop {\mathop \sum \limits^{n} }\limits_{I = 1} \Phi_{I} ({\varvec x}^{(k)} )u_{I}^{(k)} = {\varvec \Phi} ({\varvec x}^{(k)} ){\varvec u}, $$
(43)

where \({\varvec \Phi} ({\varvec x}^{(k)} )\) is the shape function and \(\Phi_{I,j} ({\varvec x}^{(k)} )\) is its derivative, they can be expressed as

$$ {\varvec \Phi} ({\varvec x}^{(k)} ) = (\Phi_{1} ({\varvec x}^{(k)} ),\Phi_{2} ({\varvec x}^{(k)} ), \ldots ,\Phi_{n} ({\varvec x}^{(k)} )) = {\varvec v}^{T} ({\varvec x}^{(k)} ) + {\varvec b}^{T} ({\varvec x}^{(k)} ){\varvec A}_{\varvec x}^{ - 1} ({\varvec x}^{(k)} ){\varvec B}_{\varvec x}({\varvec x}^{(k)} ), $$
(44)
$$ \Phi_{I,j} ({\varvec x}^{(k)} ) = v({\varvec x}^{(k)} - {\varvec x}_{I}^{(k)} )_{,j} + {\varvec b}^{T}_{,j} {\varvec A}_{\varvec x}^{ - 1} ({\varvec B}_{\varvec x} )_{I} + {\varvec b}^{T} ({\varvec A}_{\varvec x}^{ - 1} )_{,j} ({\varvec B}_{\varvec x} )_{I} + {\varvec b}^{T} {\varvec A}_{\varvec x}^{ - 1} ({\varvec B}_{\varvec x} )_{I,j} . $$
(45)

The following equations can be obtained from Eqs. (41) and (43),

$$ \frac{{\partial^{2} u({\varvec x}^{(k)} ,x_{3}^{(k)} )}}{{\partial x_{3}^{2} }} = \frac{{\partial^{2} }}{{\partial x_{3}^{2} }}\mathop {\mathop \sum \limits^{n} }\limits_{I = 1} \Phi_{I} ({\varvec x}^{(k)} )u({\varvec x}_{I}^{(k)} ,x_{3}^{(k)} ) = \mathop {\mathop \sum \limits^{n} }\limits_{I = 1} \Phi_{I} ({\varvec x}^{(k)} )\frac{{\partial^{2} u({\varvec x}_{I}^{(k)} ,x_{3}^{(k)} )}}{{\partial x_{3}^{2} }} = {\varvec \Phi} ({\varvec x}^{(k)} ){\varvec u}^{\prime \prime} , $$
(46)
$$ {\varvec L}u({\varvec x}^{(k)} ,x_{3}^{(k)} ) = \mathop {\mathop \sum \limits^{n} }\limits_{I = 1} \left[ {\begin{array}{*{20}c} {\frac{\partial }{{\partial x_{1} }}} \\ {\frac{\partial }{{\partial x_{2} }}} \\ \end{array} } \right]\Phi_{I} ({\varvec x}^{(k)} )u({\varvec x}_{I}^{(k)} ,x_{3}^{(k)} ) = \mathop {\mathop \sum \limits^{n} }\limits_{I = 1} {\varvec B}_{I} ({\varvec x}^{(k)} )u({\varvec x}_{I}^{(k)} ,x_{3}^{(k)} ) = {\varvec B}({\varvec x}^{(k)} ){\varvec u}, $$
(47)

where

$$ {\varvec u}^{\prime \prime } = \left( {\frac{{\partial^{2} u({\varvec x}_{1}^{(k)} ,x_{3}^{(k)} )}}{{\partial x_{3}^{2} }},\frac{{\partial^{2} u({\varvec x}_{2}^{(k)} ,x_{3}^{(k)} )}}{{\partial x_{3}^{2} }}, \ldots ,\frac{{\partial^{2} u({\varvec x}_{n}^{(k)} ,x_{3}^{(k)} )}}{{\partial x_{3}^{2} }}} \right)^{T} , $$
(48)
$$ {\varvec B}({\varvec x}^{(k)} ) = ({\varvec B}_{1} ({\varvec x}^{(k)} ),{\varvec B}_{2} ({\varvec x}^{(k)} ), \ldots ,{\varvec B}_{n} ({\varvec x}^{(k)} )), $$
(49)
$$ {\varvec B}_{I} ({\varvec x}^{(k)} ) = \left[ {\begin{array}{*{20}c} {\Phi_{I,1} ({\varvec x}^{(k)} )} \\ {\Phi_{I,2} ({\varvec x}^{(k)} )} \\ \end{array} } \right]. $$
(50)

Substituting Eqs. (43), (46) and (47) into Eq. (40) yields

$$ \mathop \smallint \limits_{{\Omega^{(k)} }} \delta \left[ {{\varvec \Phi} ({\varvec x}^{(k)} ){\varvec u}} \right] \cdot \left[ {{\varvec \Phi} ({\varvec x}^{(k)} ){\varvec u}^{\prime \prime } } \right]d\Omega^{(k)} - \mathop \smallint \limits_{{\Omega^{(k)} }} \delta \left[ {{\varvec B}({\varvec x}^{(k)} ){\varvec u}} \right]^{T} \cdot \left[ {{\varvec B}({\varvec x}^{(k)} ){\varvec u}} \right]d\Omega^{(k)} - \mathop \smallint \limits_{{\Omega^{(k)} }} \delta \left[ {{\varvec \Phi} ({\varvec x}^{(k)} ){\varvec u}} \right] \cdot b^{(k)} d\Omega^{(k)} - \mathop \smallint \limits_{{\Gamma_{q}^{(k)} }} \delta \left[ {{\varvec \Phi} ({\varvec x}^{(k)} ){\varvec u}} \right] \cdot \overline{q}^{(k)} d\Gamma^{(k)} = 0. $$
(51)

In order to obtain the discretized equations, every term of Eq. (51) need to be discussed.

The first integration term in Eq. (51) is

$$ \mathop \smallint \limits_{{\Omega^{(k)} }} \delta \left[ {{\varvec \Phi} ({\varvec x}^{(k)} ){\varvec u}} \right] \cdot \left[ {{\varvec \Phi} ({\varvec x}^{(k)} ){\varvec u}^{\prime \prime } } \right]d\Omega^{(k)} = \delta {\varvec u}^{T} \cdot \left[ {\mathop \smallint \limits_{{\Omega^{(k)} }} {\varvec \Phi}^{T} ({\varvec x}^{(k)} ){\varvec \Phi} ({\varvec x}^{(k)} )d\Omega^{(k)} } \right] \cdot {\varvec u}^{\prime \prime } = \delta {\varvec u}^{T} \cdot {\varvec C} \cdot {\varvec u}^{\prime \prime } , $$
(52)

where

$$ {\varvec C} = \mathop \smallint \limits_{{\Omega^{(k)} }} {\varvec \Phi}^{T} ({\varvec x}^{(k)} ){\varvec \Phi} ({\varvec x}^{(k)} )d\Omega^{(k)} . $$
(53)

The second integration term in Eq. (51) is

$$ \mathop \smallint \limits_{{\Omega^{(k)} }} \delta \left[ {{\varvec B}({\varvec x}^{(k)} ){\varvec u}} \right]^{T} \cdot \left[ {{\varvec B}({\varvec x}^{(k)} ){\varvec u}} \right]d\Omega^{(k)} = \delta {\varvec u}^{T} \cdot \left[ {\mathop \smallint \limits_{{\Omega^{(k)} }} {\varvec B}^{T} ({\varvec x}^{(k)} ){\varvec B}({\varvec x}^{(k)} )d\Omega^{(k)} } \right] \cdot {\varvec u} = \delta {\varvec u}^{T} \cdot {\varvec K} \cdot {\varvec u}, $$
(54)

where

$$ {\varvec K} = \mathop \smallint \limits_{{\Omega^{(k)} }} {\varvec B}^{T} ({\varvec x}^{(k)} ){\varvec B}({\varvec x}^{(k)} )d\Omega^{(k)} . $$
(55)

The third integration term in Eq. (51) is

$$ \mathop \smallint \limits_{{\Omega^{(k)} }} \delta \left[ {{\varvec \Phi} ({\varvec x}^{(k)} ){\varvec u}} \right] \cdot b^{(k)} d\Omega^{(k)} = \delta {\varvec u}^{T} \cdot \mathop \smallint \limits_{{\Omega^{(k)} }} {\varvec \Phi}^{T} ({\varvec x}^{(k)} )b^{(k)} d\Omega^{(k)} = \delta {\varvec u}^{T} \cdot {\varvec F}_{1} , $$
(56)

where

$$ {\varvec F}_{1} = \mathop \smallint \limits_{{\Omega^{(k)} }} {\varvec \Phi}^{T} ({\varvec x}^{(k)} )b^{(k)} d\Omega^{(k)} . $$
(57)

The fourth integration term in Eq. (51) is

$$ \mathop \smallint \limits_{{\Gamma_{q}^{(k)} }} \delta \left[ {{\varvec \Phi} ({\varvec x}^{(k)} ){\varvec u}} \right] \cdot \overline{q}^{(k)} d\Gamma^{(k)} = \delta {\varvec u}^{T} \cdot \mathop \smallint \limits_{{\Gamma_{q}^{(k)} }} {\varvec \Phi}^{T} ({\varvec x}^{(k)} )\overline{q}^{(k)} d\Gamma^{(k)} = \delta {\varvec u}^{T} \cdot {\varvec F}_{2} , $$
(58)

where

$$ {\varvec F}_{2} = \mathop \smallint \limits_{{\Gamma_{q}^{(k)} }} {\varvec \Phi}^{T} ({\varvec x}^{(k)} )\overline{q}^{(k)} d\Gamma^{(k)} . $$
(59)

Substituting Eqs. (52), (54), (56) and (58) into Eq. (51) yields

$$ \delta {\varvec u}^{T} \cdot ({\varvec{Cu}}^{\prime \prime } - {\varvec{Ku}} - {\varvec F}_{1} - {\varvec F}_{2} ) = 0. $$
(60)

Because \(\delta {\varvec u}^{T}\) is arbitrary, Eq. (60) can be written as the following differential equation

$$ {\varvec{Cu}}^{\prime \prime } - {\varvec{Ku}} = \hat{\varvec F}, $$
(61)

where

$$ \hat{\varvec F} = {\varvec F}_{1} + {\varvec F}_{2} . $$
(62)

\(L - 1\) nodes are evenly distributed in \(\Omega\) along the splitting direction \(x_{3}\) for solving Eq. (61) (that is, \({\Omega }\) is split into \(L\) layers along this direction, a total of \(L + 1\) planes), except for the first and last plane, we can obtain the numerical solutions of all nodes on the middle planes \(x_{3} = x_{3}^{(k)} , (k = 1,2, \ldots ,L - 1)\).

We make \({\varvec u}(x_{3}^{(k)} ), (k = 1,2, \ldots ,L - 1)\) respectively represent the approximate values of potential on every middle plane \(x_{3} = x_{3}^{(k)} , (k = 1,2, \ldots ,L - 1)\), let

$$ {\varvec u}(x_{3}^{(1)} ) = {\varvec u}^{(1)} , $$
(63)
$$ {\varvec u}(x_{3}^{(2)} ) = {\varvec u}^{(2)} , $$
(64)
$$ \vdots $$
$$ {\varvec u}(x_{3}^{(L - 1)} ) = {\varvec u}^{(L - 1)} , $$
(65)

the first and last plane

$$ {\varvec u}(x_{3}^{(0)} ) = {\varvec u}^{(0)} = {\varvec u}(a), $$
(66)
$$ {\varvec u}(x_{3}^{(L)} ) = {\varvec u}^{(L)} = {\varvec u}(c). $$
(67)

The following formulas can be obtained by using the finite difference method

$$ {\varvec u}^{\prime \prime (k)} \approx \frac{{{\varvec u}^{(k - 1)} - 2{\varvec u}^{(k)} + {\varvec u}^{(k + 1)} }}{{(\Delta x_{3} )^{2} }},\quad \left( {k = 1,2, \ldots ,L - 1} \right). $$
(68)

Equation (61) can be written as

$$ {\varvec C} \cdot \frac{{{\varvec u}^{(0)} - 2{\varvec u}^{(1)} + {\varvec u}^{(2)} }}{{(\Delta x_{3} )^{2} }} + {\varvec {Ku}}^{(1)} = \hat{\varvec F}^{(1)} ,\quad \left( {x_{3} = x_{3}^{(1)} } \right), $$
(69)
$$ {\varvec C} \cdot \frac{{{\varvec u}^{(1)} - 2{\varvec u}^{(2)} + {\varvec u}^{(3)} }}{{(\Delta x_{3} )^{2} }} + {\varvec {Ku}}^{(2)} = \hat{\varvec F}^{(2)} ,\quad \left( {x_{3} = x_{3}^{(2)} } \right), $$
(70)
$$ {\varvec C} \cdot \frac{{{\varvec u}^{(2)} - 2{\varvec u}^{(3)} + {\varvec u}^{(4)} }}{{(\Delta x_{3} )^{2} }} + {\varvec {Ku}}^{(3)} = \hat{\varvec F}^{(3)} ,\quad \left( {x_{3} = x_{3}^{(3)} } \right), $$
(71)
$$ \vdots $$
$$ {\varvec C} \cdot \frac{{{\varvec u}^{(L - 2)} - 2{\varvec u}^{(L - 1)} + {\varvec u}^{(L)} }}{{(\Delta x_{3} )^{2} }} + {\varvec {Ku}}^{(L - 1)} = \hat{\varvec F}^{(L - 1)} ,\quad \left( {x_{3} = x_{3}^{(L - 1)} } \right). $$
(72)

Equations (69)–(72) can be transformed into matrix as

$$ \frac{1}{{(\Delta x_{3} )^{2} }}\left[ {\begin{array}{*{20}c} {\varvec H} & {\varvec C} & & & & \\ {\varvec C} & {\varvec H} & {\varvec C} & & & \\ & {\varvec C} & {\varvec H} & {\varvec C} & & \\ & & \ddots & \ddots & \ddots & \\ & & & {\varvec C} & {\varvec H} & {\varvec C} \\ & & & & {\varvec C} & {\varvec H} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\varvec u}^{(1)} } \\ {{\varvec u}^{(2)} } \\ {{\varvec u}^{(3)} } \\ \vdots \\ {{\varvec u}^{(L - 2)} } \\ {{\varvec u}^{(L - 1)} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\hat{\varvec F}^{(1)} - \frac{{{\varvec{Cu}}^{(0)} }}{{(\Delta x_{3} )^{2} }}} \\ { \hat{\varvec F}^{(2)} } \\ {\hat{\varvec F}^{(3)} } \\ \vdots \\ { \hat{\varvec F}^{(L - 2)} } \\ {\hat{\varvec F}^{(L - 1)} - \frac{{{\varvec{Cu}}^{(L)} }}{{(\Delta x_{3} )^{2} }}} \\ \end{array} } \right], $$
(73)

where

$$ {\varvec H} = - 2{\varvec C} - (\Delta x_{3} )^{2} {\varvec K}. $$
(74)

Let

$$ {\varvec E} = \frac{1}{{(\Delta x_{3} )^{2} }}\left[ {\begin{array}{*{20}c} {\varvec H} & {\varvec C} & & & & \\ {\varvec C} & {\varvec H} & {\varvec C} & & & \\ & {\varvec C} & {\varvec H} & {\varvec C} & & \\ & & \ddots & \ddots & \ddots & \\ & & & {\varvec C} & {\varvec H} & {\varvec C} \\ & & & & {\varvec C} & {\varvec H} \\ \end{array} } \right], $$
(75)
$$ {\varvec U} = ({\varvec u}^{(1)T} ,{\varvec u}^{(2)T} ,{\varvec u}^{(3)T} , \ldots ,{\varvec u}^{(L - 2)T} ,{\varvec u}^{(L - 1)T} )^{T} , $$
(76)
$$ {\varvec G} = \left( {\left( {\hat{{\varvec F}}^{(1)} - \frac{{{\varvec{Cu}}^{(0)} }}{{(\Delta x_{3} )^{2} }}} \right)^{T} ,\hat{\varvec F}^{(2)T} ,\hat{\varvec F}^{(3)T} , \ldots ,\hat{\varvec F}^{(L - 2)T} ,\left( {\hat{\varvec F}^{(L - 1)} - \frac{{{\varvec{Cu}}^{(L)} }}{{(\Delta x_{3} )^{2} }}} \right)^{T} } \right)^{T} , $$
(77)

Equation (73) can be written as

$$ {\varvec {EU}} = {\varvec G}. $$
(78)

The solutions of Eq. (77) are the potential values of nodes on the middle planes \(x_{3} = x_{3}^{(k)} , (k = 1,2, \ldots ,L - 1)\), then we can obtain the approximate value of the potential of any node with the linear interpolation method, let \(\Delta x_{3} = x_{3}^{(k + 1)} - x_{3}^{(k)}\), \({\varvec u}(x_{3} )\) can be expressed as

$$ {\varvec u}(x_{3} ) = \frac{{x_{3} - x_{3}^{(k)} }}{{\Delta x_{3} }}{\varvec u}(x_{3}^{(k)} ) + \frac{{x_{3}^{(k + 1)} - x_{3} }}{{\Delta x_{3} }}{\varvec u}(x_{3}^{(k + 1)} ). $$
(79)

It is the IDSEFG method for 3D potential problems.

4 Algorithm implementation process

The IDSEFG method proposed in this paper is used to solve 3D potential problems, it is necessary to select an appropriate dimension splitting direction. In the solution process, the interpolating EFG method requires nodes to be placed evenly in these related subdomains, and the influence domain of these nodes must contain the entire 2D subdomain, which is a necessary condition. In this paper, Gauss integration is used to calculate the numerical integration, and the layout of the integration grid is regular, which provides convenience for establishing Gauss integration points. The integration grid is rectangular.

The algorithm implementation process of the IDSEFG method for 3D potential problems is:

  1. 1.

    According to the different boundary conditions and the governing equation, an appropriate dimension splitting direction need to be selected, then enter the corresponding parameters;

  2. 2.

    Determining each variable and coordinate system of the corresponding 2D potential problem, \(M\) nodes \({\varvec x}_{I}^{(k)} , I = (1,2, \ldots ,M)\) are distributed on \({\Omega }^{{\text{(k)}}}\) and its boundary \(\Gamma^{(k)} = \Gamma_{u}^{(k)} \cup \Gamma_{q}^{(k)}\), then number these nodes according to certain rules, node coordinates can be generated through the program, so as to quickly select the required nodes later;

  3. 3.

    For numerical integration, a background integration grid needs to be set up;

  4. 4.

    Establishing the integral element and corresponding corner information on the \(\Gamma_{q}\) boundary;

  5. 5.

    Establishing Gauss integration points, using the background integration grid and boundary information in Steps 3 and 4 to calculate the coordinates, integration weights, and Jacobian of the integration points;

  6. 6.

    Establishing the Matrix \({\varvec C}\), Matrix \({\varvec K}\) and the first term \({\varvec F}_{1}\) of Array \({\varvec F}\);

    1. A.

      Looping through all background integration grids;

      1. a)

        In every integration grid, looping all Gauss points;

      2. b)

        If it is verified that the Gauss point is inside the 2D subdomains \({\Omega }^{{\text{(k)}}}\), then continue to Steps (c)–(f), if not, proceed directly to Step (f) to end the integration point loop;

      3. c)

        Finding these node numbers located in domain of the Gauss point \({\varvec x}_{Q}^{(k)}\);

      4. d)

        Calculating shape function \({\varvec \Phi} ({\varvec x}_{Q}^{(k)} )\) and its derivative \(\Phi_{I,j} ({\varvec x}_{Q}^{(k)} )\);

      5. e)

        Calculating the contribution values of Gauss points to the Matrix \({\varvec C}\), \({\varvec K}\) and the first term \({\varvec F}_{1}\) of Array \({\varvec F}\) with Eqs. (53), (55), (57);

      6. f)

        Finishing the Gauss integration points loop.

    2. B.

      Finishing the background grids loop.

  7. 7.

    The numerical integration calculation on the boundary of \(\Gamma_{q}^{(k)}\): the process is similar to Step 6, and finally obtain the second term \({\varvec F}_{2}\) of the load Array \(\hat{\varvec F}\) by Eq. (59);

  8. 8.

    Adding the \({\varvec {F}}_{{1}}\) obtained in Step 6 and the \({\varvec F}_{2}\) obtained in Step 7 to get \(\hat{\varvec F}\);

  9. 9.

    Substituting displacement boundary conditions directly into the Matrix \({\varvec K}\) and Array \(\hat{\varvec F}\);

  10. 10.

    Using Eqs. (74), (75), (77) and Matrix \({\varvec C}\), Matrix \({\varvec K}\), Array \(\hat{\varvec F}\) to obtain the Matrix \({\varvec E}\) and Matrix \({\varvec G}\);

  11. 11.

    Substituting the Matrix \({\varvec E}\) and Matrix \({\varvec G}\) into the system of Eq. (78), the numerical solution \({\varvec U}\) of the potential function at each node in the original 3D problem domain \(\Omega^{ }\) can be obtained;

  12. 12.

    According to the obtained numerical solution \({\varvec U}\) and Eq. (79), the numerical solution of the potential function at any point in \(\Omega^{ }\) can be obtained by fitting;

  13. 13.

    Outputting the potential values.

5 Numerical examples

It is necessary to verify the effectiveness and efficiency of the IDSEFG method for 3D potential problems, the influence domain of the weight function is rectangular, \(4 \times 4 \) Gaussian integration points are chosen in each integration cell. Four numerical examples are calculated using this method. By selecting different node distributions, the number of dimension splitting layers and the influence domain parameter \(d_{\max }\), its convergence is discussed and the calculation results are compared with the results of the IEFG method and the analytical solution.

The following relative error is defined to compare the accuracy of the results of the IEFG method and the IDSEFG method.

$$ u - u_{{L^{2} (\Omega )}}^{{{\text{hrel}}}} = \frac{{u - u^{h}_{{L^{2} (\Omega )}} }}{{u_{{L^{2} (\Omega )}} }}, $$
(80)

where

$$ u - u^{h}_{{L^{2} (\Omega )}} = \left[ {\mathop \smallint \limits_{\Omega } (u - u^{h} )^{2} d\Omega } \right]^{1/2} , $$
(81)

is the \(L^{2}\)-norm of the error.

5.1 A Laplace’s equation in a 3D cube

The governing equation is

$$ \nabla^{2} u = \frac{{\partial^{2} u({\varvec x})}}{{\partial {\varvec x}_{1}^{2} }} + \frac{{\partial^{2} u({\varvec x})}}{{\partial x_{2}^{2} }} + \frac{{\partial^{2} u({\varvec x})}}{{\partial x_{3}^{2} }} = 0, \quad ({\varvec x} \in \Omega ), $$
(82)

with boundary conditions

$$ u = \sin (\pi x_{2} )\sin (\pi x_{3} ),\quad \left( {x_{1} = 0} \right), $$
(83)
$$ u = 2\sin (\pi x_{2} )\sin (\pi x_{3} ),\quad \left( {x_{1} = 1} \right), $$
(84)
$$ u = 0,\quad \left( {x_{2} = 0,x_{2} = 1,x_{3} = 0,x_{3} = 1} \right). $$
(85)

The problem domain is \(\Omega = [0,1] \times [0,1] \times [0,1].\)

The analytical solution is

$$ u = \frac{{\sin (\pi x_{2} )\sin (\pi x_{3} )}}{\sinh (\pi \sqrt 2 )}\left[ {2\sinh (\pi \sqrt 2 x_{1} ) + \sinh (\pi \sqrt 2 (1 - x_{1} )} \right]. $$
(86)

According to the boundary conditions and the form of governing equation, direction \(x_{1}\) is chosen as splitting direction. Splitting the problem domain \({\Omega }\) into \(L_{ }\) subdomains uniformly along \(x_{1}\), then \(M_{ }\) nodes should be distributed in 2D subdomain on the plane \({\text{O}}^{(k)} x_{2} x_{3}\).

The following results are given to verify the effectiveness and convergence of the IDSEFG method.

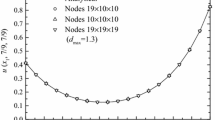
Figure 1 is the result of the IDSEFG method with different node distributions for this numerical example. It can be seen that in the case of different node distributions but \(d_{\max }\) is taken to be 1.15, the numerical solutions obtained by this method are very close to the analytical solution.

Fig. 1
figure 1

The numerical results of IDSEFG method for different number of nodes

Full size image

\(d_{\max }\) is a parameter of the size of the influence domain of a node, and it is directly related to the computational accuracy of the numerical results. The value of \(d_{\max }\) should ensure the problem domain covered by the influence domains of the weight functions of all nodes, and the inverse matrix in the improved IMLS method can be obtained. If the value of \(d_{\max }\) is too small, the singularity of the equation systems maybe exists. Therefore, we need to find an appropriate value of \(d_{\max }\) for different examples according to the numerical results.

Figure 2 shows the result that the IDSEFG method with different \(d_{\max }\). When the node distribution is \(15 \times 15 \times 15 \) but different \(d_{\max }\), it can be seen that the relative error of the numerical solutions is very small compared with the analytical solution.

Fig. 2
figure 2

The numerical results of IDSEFG method for different \(d_{\max }\)

Full size image

Figure 3 shows the results obtained by the IDSEFG method in this example when a different number of splitting layer is selected. \((L + 1) \times 15 \times 15 \) is chosen as the node distribution on \({\Omega }\). We can see that the relative error gradually decreases and tends to be stable as the number of splitting layer increases, indicating that the method is convergent.

Fig. 3
figure 3

The relative error for different number of splitting layers

Full size image

Figure 4 shows the relative error of the IDSEFG method with different \(d_{\max }\). We found that when \(d_{\max } = 1.15\) and \(15 \times 15 \times 15 \) node distribution is used, the relative error reaches the minimum.

Fig. 4
figure 4

The relative error for different \(d_{\max }\)

Full size image

Table 1 shows that when different node distributions are chosen, the CPU time and calculation accuracy of the IDSEFG method and the IEFG method. It can be concluded that the IDSEFG method is significantly better than the IEFG method in terms of calculation accuracy and efficiency when the same node distribution is chosen.

Table 1 The comparison of relative error and CPU time of the IDSEFG method and IEFG method with different node distributions
Full size table

Further analysis of the results, the IEFG method has a tendency to improve the calculation accuracy when the number of nodes continues to increase, but the results are not stable and the CPU time keeps extending. In contrast, the IDSEFG method will improve the calculation accuracy when the number of nodes gradually increases. We can select an appropriate number of nodes according to the accuracy requirements to save calculation time. In this example, \(15 \times 15 \times 15 \) node distribution is used, then we got a relatively high calculation accuracy while taking relatively little time to calculate.

If the smaller relative error 0.25% obtained by the IEFG method is compared with the relative error 0.26% obtained by the IDSEFG method, we found that the calculation efficiency of the IDSEFG method is about 13 times that of the IEFG method when the calculation accuracy is similar.

Figures 5, 6, 7 are the comparison results of the IDSEFG, IEFG method and analytical solution at \((x_{1} ,1/2,1/2)\), \((2/7,x_{2} ,9/14)\), \((1/2,4/7,x_{3} )\) respectively. The node distribution of the two methods is \(15 \times 15 \times 15\), the \(d_{\max }\) of the IDSEFG method is 1.15, and the \(d_{\max }\) of the IEFG method is 1.3, penalty factor \( \alpha = 1.0 \times 10^{3}\). It can be concluded that the accuracy of the results of the IDSEFG method is good enough, and there is still small error on individual nodes of the IEFG method.

Fig. 5
figure 5

The numerical results of IDSEFG method and IEFG method at \((x_{1} ,1/2,1/2)\)

Full size image
Fig. 6
figure 6

The numerical results of IDSEFG method and IEFG method at \((_{ } 2/7,x_{2} ,9/14)\)

Full size image
Fig. 7
figure 7

The numerical results of IDSEFG method and IEFG method at \((1/2,4/7,x_{3} )\)

Full size image

To sum up, the IDSEFG method is not only significantly higher in accuracy than the IEFG method, but its efficiency has increased several times or even more than ten times.

5.2 A Poisson’s equation in a cuboid

The governing equation is

$$ \nabla^{2} u({\varvec x}) = f({\varvec x}),\quad \left( {{\varvec x} \in \Omega } \right), $$
(87)
$$ f({\varvec x}) = - \left( {\frac{1}{{a^{2} }} + \frac{1}{{b^{2} }} + \frac{1}{{c^{2} }}} \right)\pi^{2} \sin \frac{{\pi x_{1} }}{a}\sin \frac{{\pi x_{2} }}{b}\sin \frac{{\pi x_{3} }}{c}, $$
(88)

with the boundary condition

$$ u({\varvec x}) = 0,\quad \left( {{\varvec x} \in \Gamma } \right). $$
(89)

In the example, the values of a, b and c are 1, 2, 3, \(\Omega = \left[ {0,1} \right] \times \left[ {0,2} \right] \times [0,3]\) is the problem domain. The analytical solution is

$$ u({\varvec x}) = \sin \pi x_{1} \sin \frac{{\pi x_{2} }}{2}\sin \frac{{\pi x_{3} }}{3}. $$
(90)

Because the solution domain is a cuboid with different lengths in three directions, it is necessary to consider that different splitting directions may affect the calculation accuracy and efficiency.

First, according to the length of the problem domain in the three directions of \(x_{1}\), \(x_{2}\), and \(x_{3}\) are 1, 2, and 3, respectively, using \(9 \times 17 \times 25\) node distribution.

5.2.1 \(x_{1}\) as the splitting direction

In 2D subdomain on the plane \(O^{(k)} x_{2} x_{3}\), the node distribution is \(17 \times 25\), and 9 nodes are distributed in the splitting direction \(x_{1}\), \(d_{\max } = 1.91\), running the program to get a relative error of 0.96% and a CPU time of 13.81 s.

5.2.2 \(x_{2}\) as the splitting direction

In 2D subdomain on the plane \(O^{(k)} x_{1} x_{3}\), the node distribution is \(9 \times 25\), and 17 nodes are distributed in the splitting direction \(x_{2}\), \(d_{\max } = 1.15\), running the program to get a relative error of 0.80% and a CPU time of 10.18 s.

5.2.3 \(x_{3}\) as the splitting direction

In 2D subdomain on the plane \(O^{(k)} x_{1} x_{2}\), the node distribution is \(9 \times 17\), and 25 nodes are distributed in the splitting direction \(x_{3}\), \(d_{\max } = 1.15\), running the program to get a relative error of 0.95% and a CPU time of 9.65 s.

It can be seen from the above results that when the node distribution is the same, selecting different splitting directions will get different calculation accuracy and efficiency, so it is necessary to select an appropriate splitting direction to obtain better calculation results. In this example, the results when the splitting direction is \(x_{2}\) or \(x_{3}\) are significantly better than the results obtained by choosing direction \(x_{1}\), but there are both advantages and disadvantages in accuracy and efficiency with choosing \(x_{2}\) and \(x_{3}\), we need to continue the discussion.

Table 2 shows the results of the IDSEFG method with different splitting layers in this example when \(x_{3}\) is chosen as the splitting direction, \(9 \times 17\) node distribution is used in 2D subdomain on the plane \(O^{(k)} x_{1} x_{2}\). From this table, we can see that with the continuous increase of the number of splitting layers, the calculation accuracy is slightly improved and then the relative error is stabilized at 0.95%, and the calculation time continues to increase. Therefore, the number of splitting layers has a relatively small impact on the calculation accuracy for this example, but it has a greater impact on the CPU time. In general, choosing a direction with long length as the splitting direction can save time and get a better result.

Table 2 The comparison of relative error and CPU time of the IDSEFG method at different splitting layers
Full size table

To sum up, we select \(x_{3}\) as the splitting direction finally, the node distribution in 2D subdomain on the plane \(O^{(k)} x_{1} x_{2}\) is \(14 \times 26\), and 8 nodes are distributed on the splitting direction, \(d_{\max } = 1.14\), then the relative error is 0.28% and CPU time is 8.51 s. The node distribution of the IEFG method is also \(14 \times 26 \times 8\), \(d_{\max } = 1.23\), penalty factor \(\alpha = 4.5 \times 10^{6}\), then the relative error we got is 0.68% and the CPU time is 29.89 s.

Figures 8, 9, 10 are the comparison results of IDSEFG, IEFG method and analytical solution at \((x_{1} ,14/25,6/7)\), \((9/13,x_{2} ,12/7)\), \((5/13,28/25,x_{3} )\) respectively. The node distribution of the two methods is \(14 \times 26 \times 8\), the \(d_{\max }\) of the IDSEFG method is 1.14 and the \(d_{\max }\) of the IEFG method is 1.22. It can be concluded that the results obtained by the two methods are very close to the analytical solution, but the calculation accuracy and calculation efficiency of the IDSEFG method are 2.43 times and 3.51 times that of the IEFG method, respectively, indicating that the IDSEFG method has significant advantages.

Fig. 8
figure 8

The numerical results of IDSEFG method and IEFG method at \((x_{1} ,14/25,6/7)\)

Full size image
Fig. 9
figure 9

The numerical results of IDSEFG method and IEFG method at \((_{ } 9/13,x_{2} ,12/7)\)

Full size image
Fig. 10
figure 10

The numerical results of IDSEFG method and IEFG method at \((_{ } 5/13,28/25,x_{3} )\)

Full size image

5.3 A Laplace’s equation in a 3D cube

The governing equation is

$$ \nabla^{2} u({\varvec x}) = 0,\quad \left( {{\varvec x} \in \Omega } \right), $$
(91)

with the boundary conditions

$$ \frac{{\partial u(0,x_{2} ,x_{3} )}}{{\partial x_{1} }} = \frac{{\partial u(1,x_{2} ,x_{3} )}}{{\partial x_{1} }} = 0, $$
(92)
$$ \frac{{\partial u(x_{1} ,0,x_{3} )}}{{\partial x_{2} }} = \frac{{\partial u(x_{1} ,1,x_{3} )}}{{\partial x_{2} }} = 0, $$
(93)
$$ \frac{{\partial u(x_{1} ,x_{2} ,0)}}{{\partial x_{3} }} = \cos (\pi x_{1} )\cos (\pi x_{2} ), $$
(94)
$$ \frac{{\partial u(x_{1} ,x_{2} ,1)}}{{\partial x_{3} }} = 0. $$
(95)

\(\Omega = \left[ {0,1} \right] \times \left[ {0,1} \right] \times [0,1]\) is the problem domain. The analytical solution is

$$ u({\varvec x}) = \left[ {\frac{{\sinh (\sqrt 2 \pi x_{3} )}}{\sqrt 2 \pi } - \frac{{\cosh (\sqrt 2 \pi x_{3} )}}{\sqrt 2 \pi \tanh (\sqrt 2 \pi )}} \right]\cos (\pi x_{1} )\cos (\pi x_{2} ). $$
(96)

The splitting direction is direction \(x_{3}\), \(6 \times 6 \times 7\) node distribution is chosen and \(d_{\max }\) is 1.0. Running the program to get a relative error 0.074% and a CPU time 0.43 s of the IDSEFG method. As a comparison, the node distribution of the IEFG method is \(11 \times 11 \times 13\), \(d_{\max }\) is taken as 1.49, then the relative error is 0.36% and the CPU time is 6.69 s.

Figures 11, 12, 13 are the comparison results of the IDSEFG, IEFG method and analytical solution at \((x_{1} ,1,0)\), \((0,x_{2} ,0)\), \((1/5,1/5,x_{3} )\) respectively. It can be concluded that the numerical results of two methods are close to the analytical solution, but the calculation efficiency of the IDSEFG method is 15.6 times that of the IEFG method, and even if the IDSEFG method has fewer nodes, the calculation accuracy is still improved by 386.5% that of the IEFG method.

Fig. 11
figure 11

The numerical results of IDSEFG method and IEFG method at \((x_{1} ,1,0)\)

Full size image
Fig. 12
figure 12

The numerical results of IDSEFG method and IEFG method at \((0,x_{2} ,0)\)

Full size image
Fig. 13
figure 13

The numerical results of IDSEFG ethod and IEFG method at \((1/5,1/5,x_{3} )\)

Full size image

5.4 A Laplace’s equation in a half circular cylinder

The governing equation is

$$ \nabla^{2} u({\varvec x}) = 0,\quad (r \in \left[ {1,2} \right],\theta \in \left[ {0,\pi } \right],x_{3} \in [0,1]), $$
(97)

with following boundary conditions

$$ u(1,\theta ,x_{3} ) = \sin \theta + x_{3} , $$
(98)
$$ u(2,\theta ,x_{3} ) = x_{3} , $$
(99)
$$ u(r,0,x_{3} ) = x_{3} , $$
(100)
$$ u(r,\pi ,x_{3} ) = x_{3} , $$
(101)
$$ u(r,\theta ,0) = \frac{4}{3}(\frac{1}{r} - \frac{r}{4})\sin \theta , $$
(102)
$$ u(r,\theta ,1) = \frac{4}{3}\left( {\frac{1}{r} - \frac{r}{4}} \right)\sin \theta + 1. $$
(103)

The analytical solution is

$$ u(r,\theta ,x_{3} ) = \frac{4}{3}\left( {\frac{1}{r} - \frac{r}{4}} \right)\sin \theta + x_{3} . $$
(104)

The splitting direction is direction \(x_{3}\), \(29 \times 7 \times 11\) is the node distribution, and \(d_{\max } = 1.0\). Splitting 11 subdomains uniformly in the direction \(x_{3}\), the node distribution on the 2D half-circle subdomain is \(29 \times 7\) as shown in Fig. 14.

Fig. 14
figure 14

The node distribution in the 2D subdomain of a harf-torus

Full size image

The relative error and the CPU time obtained by the IDSEFG method are 0.14% and 1.63 s. With the same node distribution and \(d_{\max } = 1.11\), penalty factor \(\alpha = 1.0 \times 10^{4}\), the relative error and the CPU time of the IEFG method are 0.21% and 53.73 s.

Figures 15, 16, 17 are the comparisons of the numerical solutions of the IDSEFG, IEFG method and the analytical solutions in three directions. The numerical results of the IEFG method and the IDSEFG method are very accurate, but we can see that the running time of the IDSEFG method is only 3.03% of the IEFG method. This result once illustrates the excellent computational efficiency of the IDSEFG method again.

Fig. 15
figure 15

The numerical results of IDSEFG method and IEFG method along direction \(r\)

Full size image
Fig. 16
figure 16

The numerical results of IDSEFG method and IEFG method along direction \(\theta\)

Full size image
Fig. 17
figure 17

The numerical results of IDSEFG method and IEFG method along direction \(x_{3}\)

Full size image

6 Conclusions

In this paper, the IDSEFG method for 3D potential problems is established. The key of the IDSEFG method is to split a 3D solution domain into many related 2D subdomains. The shape function is constructed by the improved IMLS method on the 2D subdomain, and the discretized equations are obtained by the Galerkin weak form based on dimension splitting method. The discrete equations on these 2D subdomains are coupled by the finite difference method. Finally, the numerical solution of the potential of any node can be obtained. The number of undetermined coefficients of the approximation function constructed by the improved IMLS method is less than that of the MLS approximation, which improves the computational efficiency. The essential boundary conditions can be enforced directly because the IDSEFG method satisfies the property of the Kronecker delta function. Comparing the results of IDSEFG method and IEFG method with analytical solution through four numerical examples, it is proved that both methods are effective and further shows that the IDSEFG method improves the calculation efficiency and calculation accuracy. At the same time, the last numerical example shows that the IDSEFG method is also applicable to the ring-like problem domain.

We have discussed how to choose the splitting direction in Eg. 2 because its problem domain is a cuboid with different lengths in three directions. In the Example, we finally found that if we choose a direction with a long length as the splitting direction can save CPU time and obtain better results. In other examples, we chose the direction with more complicated boundary conditions as the splitting direction. During the test of the examples, we found that if the boundary conditions of the two-dimensional problem after the dimension splitting are complicated, it will not only bring some difficulties to program code but also reduce the efficiency. Choosing the direction with more complicated boundary conditions as the dimension splitting direction is easier to program code, and better results can be obtained.