The dimension split element-free Galerkin method for three-dimensional potential problems

Abstract

This paper presents the dimension split element-free Galerkin (DSEFG) method for three-dimensional potential problems, and the corresponding formulae are obtained. The main idea of the DSEFG method is that a three-dimensional potential problem can be transformed into a series of two-dimensional problems. For these two-dimensional problems, the improved moving least-squares (IMLS) approximation is applied to construct the shape function, which uses an orthogonal function system with a weight function as the basis functions. The Galerkin weak form is applied to obtain a discretized system equation, and the penalty method is employed to impose the essential boundary condition. The finite difference method is selected in the splitting direction. For the purposes of demonstration, some selected numerical examples are solved using the DSEFG method. The convergence study and error analysis of the DSEFG method are presented. The numerical examples show that the DSEFG method has greater computational precision and computational efficiency than the IEFG method.

1 Introduction

The meshless method is an effective tool to solve boundary value problems of partial differential equations in addition to the finite difference method (FDM), finite element method (FEM), and boundary element method (BEM). The main difference between these conventional numerical methods and meshless method is the different approaches to obtain the shape functions. However, once the shape function has been formed, they use the same procedure to obtain the equation system to get the numerical solution of a problem. FDM, FEM, and BEM rely on meshes, then remeshing must be used to solve some complicated problems, such as extremely large deformations and crack growth problems. The meshless method only needs nodes or particles, and it can solve many complicated physical and engineering problems that cannot be solved well with conventional computational methods [1, 2].

The potential problem is an important physical and engineering problem, whose governing equations are commonly Laplace’s equations or Poisson’s equations. The popular numerical methods solving potential problems include FEM, FDM, BEM, and meshless methods [3,4,5,6,7]. The meshless method is actually a more effective numerical method to solve partial differential equations that govern various physical and engineering phenomena than traditional methods.

In recent years, several meshless methods, such as boundary node method [8,9,10], element-free Galerkin method [11,12,13,14,15,16,17,18], boundary element-free method [19, 20], and meshless local Petro-Galerkin method coupled with FEM [21], were developed to solve potential problems. The improved element-free Galerkin (IEFG) method is an effective meshless method to solve three-dimensional potential problems, because in the IEFG method, the improved moving least-squares (IMLS) approximation, in which the orthogonal function system is selected as the basis function, is used to obtain the shape function [12, 22]. The algebraic equations system in the IMLS approximation is well-conditioned, and it can be solved without deriving the inverse matrix. There are fewer coefficients in the IMLS approximation than the ones in the moving least-squares (MLS) approximation, which is the basis of the EFG method, then the computational efficiency of the IEFG method is greater than the EFG method. Using the IEFG method, the three-dimensional potential problem was effectively solved [12]. Furthermore, the IEFG method can also be successfully applied to other science and engineering problems. In their work, Zhang et al. [23] employed the IEFG method for two-dimensional elasticity problems, 2D fracture problems [24], three-dimensional wave equation [25], and two-dimensional elastodynamics problems [26].

The dimension split method (DSM) was proposed by Li and Huang [27]. The essential features of the DSM are that the three-dimensional domain is partitioned by several two-dimensional surfaces into several sub-domains. They used optimal control to deal with the stream-function equations of compressible turbomachinery flows and their finite element approximation [27]. They also applied the DSM for the 3D compressible Navier–Stokes equations in turbomachine [28], the three dimensional rotating Navier–Stokes equations [29], the incompressible Navier–Stokes equations in three dimensions [30], and the linearly elastic shell [31]. Additionally, Hansen and Ostermann [32] presented the DSM for evolution and quasilinear parabolic equations [33]. The dimension split method is actually an efficient and convenient numerical method to solve various problems [34,35,36,37]. The work of Cheng et al. [38, 39] introduced the DSM into the improved complex variable element-free Galerkin method for solving three-dimensional potential and wave propagation problems. It is obvious that the DSM is different from the traditional domain decomposition method because only two-dimensional problems are solved in each sub-domain without solving a three-dimensional problem, then the computational efficiency is improved greatly.

Three-dimensional potential problems are effectively solved with the dimension split element-free Galerkin method. For these two-dimensional problems, the IMLS approximation is applied to construct the shape function. The Galerkin weak form is applied to obtain a discretized system equation, and the penalty method is employed to impose the essential boundary condition. The finite difference method is selected in the splitting direction. Finally, several numerical examples are solved using the dimension split element-free Galerkin (DSEFG) method. These numerical examples test and verify DSEFG theoretical result. The convergence study and error analysis of the DSEFG method are presented. The numerical examples show that the DSEFG method has greater computational precision and computational efficiency than the IEFG method.

2 The basic equations of three-dimensional potential problems with dimension split scheme

Consider the following three-dimensional potential problem

$$\begin{aligned}&\frac{\partial ^{2}u}{\partial x_1^2 }+\frac{\partial ^{2}u}{\partial x_2^2 }+\frac{\partial ^{2}u}{\partial x_3^2 }=b({{\varvec{x}}}){,}\quad {{\varvec{x}}}=(x_1 ,x_2 ,x_3 )\in \varOmega , \end{aligned}$$

(1)

$$\begin{aligned}&u({{\varvec{x}}})=\bar{{u}}({{\varvec{x}}}), \quad {{\varvec{x}}}\in \varGamma _u , \end{aligned}$$

(2)

$$\begin{aligned}&q({{\varvec{x}}})=\frac{\partial u({{\varvec{x}}})}{\partial {{\varvec{n}}}}= \bar{{{{q}}}}({{\varvec{x}}}){,} \quad {{\varvec{x}}}\in \varGamma _q , \end{aligned}$$

(3)

where $u({{{\varvec{x}}}})$ is an unknown function, $b({{{\varvec{x}}}})$ is a known function. In the general case, there exist mixed boundary conditions on the boundary $\varGamma$ of the domain $\varOmega$. $\varGamma _u$ is one part of the boundary $\varGamma$ with known potential function $\bar{{u}}({{{\varvec{x}}}})$, and $\varGamma _q$ is the remaining boundary with known normal derivative $\bar{{q}}({{{\varvec{x}}}})$. Notice that $\varGamma =\varGamma _u \cup \varGamma _q$, $\varGamma _u \cap \varGamma _q =\varnothing$, and ${{\varvec{n}}}$ is the unit outward normal to the boundary $\varGamma$.

When using the DSEFG method to solve potential problems, we can choose the splitting direction according to the control equations and boundary conditions, which results in that the process of calculating and programming are easy to achieve.

In this paper, we assume that the problem domain $\varOmega$ is split into L layers along the direction $x_3$, and the distance between adjacent layers is $\Delta x_3$. Then we have $L+1$ two-dimensional sub-domains $\varOmega ^{(k)}, k=0,1,\ldots ,L$, and

$$\begin{aligned} \varOmega =\bigcup _{k=0}^{L\hbox {-}1} {\varOmega ^{(k)}\times \left[ x_3^{(k)} ,x_3^{(k+1)} \right] } \cup \varOmega ^{(L)}, \end{aligned}$$

(4)

where

$$\begin{aligned}&a=x_3^{(0)}<x_3^{(1)} \ldots <x_3^{(L)} =c, \quad x_3 \in [a,c], \end{aligned}$$

(5)

$$\begin{aligned}&\Delta x_3 =x_3^{(k+1)} -x_3^{(k)} ={(c-a)}/L. \end{aligned}$$

(6)

For a fixed $x_3^{(k)}$, u, and $\frac{\partial ^{2}u}{\partial x_3^2 }$ can be considered the function of $x_1$ and $x_2$. Three-dimensional potential problem is translated into a series of two-dimensional boundary value problems, i.e.

$$\begin{aligned} \frac{\partial ^{2}u^{(k)}}{\partial x_1^2 }+\frac{\partial ^{2}u^{(k)}}{\partial x_2^2 }=b^{(k)}-\frac{\partial ^{2}u^{(k)}}{\partial x_3^2 },\,(x_1 ,x_2 )\in \varOmega ^{(k)},\,x_3 =x_3^{(k)},\!\!\!\!\!\nonumber \\ \end{aligned}$$

(7)

The corresponding boundary conditions are

$$\begin{aligned}&u\left( x_1 ,x_2 \right) =\bar{{u}}\left( x_1 ,x_2 \right) =\bar{{u}}\left( x_1 ,x_2 \hbox {,}x_ 3 ^{\left( k\right) } \right) , \nonumber \\&\quad \left( x_1 ,x_2 \right) \in \varGamma _u^{\left( k\right) } , \end{aligned}$$

(8)

$$\begin{aligned}&q\left( x_1 ,x_2 \right) =\bar{{q}}\left( x_1 ,x_2 \right) =\bar{{q}}\left( x_1 ,x_2 ,x_ 3 ^{\left( k\right) } \right) , \nonumber \\&\quad \left( x_1 ,x_2 \right) \in \varGamma _q^{\left( k\right) }, \end{aligned}$$

(9)

where

$$\begin{aligned} u^{\left( k\right) }= & {} u\left( x_1 ,x_2 ,x_3^{\left( k\right) } \right) , \end{aligned}$$

(10)

$$\begin{aligned} b^{\left( k\right) }= & {} b\left( x_1 ,x_2 ,x_3^{\left( k\right) } \right) , \end{aligned}$$

(11)

$u(x_1 ,x_2 )$ is the field potential in the sub-domain $\varOmega ^{(k)}$, $\bar{{u}}(x_1 ,x_2 \hbox {,}x_ 3 ^{\hbox {(}k\hbox {)}} )$ is the given potential on essential boundary $\varGamma _u^{(k)}$, $\bar{{q}}(x_1 ,x_2 \hbox {,}x_ 3 ^{\hbox {(}k\hbox {)}} )$ is the given gradient on natural boundary $\varGamma _q^{(k)}$, $\varGamma ^{(k)}=\varGamma _u^{(k)} \cup \varGamma _q^{(k)}$, and $\varGamma _u^{(k)} \cap \varGamma _q^{(k)} =\varnothing$.

Then we can solve Eqs. (7)–(9) in the sub-domain $\varOmega ^{(k)}$ by using the IEFG method, and in the direction $x_3$ finite difference method is used to obtain the solution of the original problem, i.e. Eqs. (1)–(3). This is the idea of the DSEFG method for three-dimensional potential problems.

The equivalent functional of Eqs. (7)–(9) is

$$\begin{aligned}&\varPi =\int _{\varOmega ^{(k)}} {\left[ {u\left( {\frac{\partial ^{2}u}{\partial x_3^2 }-b} \right) } \right] {\hbox {d}}\varOmega ^{(k)}} \nonumber \\&\quad -\int _{\varOmega ^{(k)}} {\frac{1}{2}} \left[ {\left( {\frac{\partial u}{\partial x_1 }} \right) ^{2}+\left( {\frac{\partial u}{\partial x_2 }} \right) ^{2}} \right] {\hbox {d}}\varOmega ^{(k)}\nonumber \\&\quad -\int _{\varGamma _q^{(k)} } {u\bar{{q}}\hbox {d}\varGamma ^{(k)}} . \end{aligned}$$

(12)

The shape function of the IMLS approximation does not satisfy the property of the Kronecker delta function; therefore, the essential boundary cannot be directly imposed to Eq. (12). In this paper, the penalty method is used to impose the essential boundary conditions. The modified functional can then be expressed as

$$\begin{aligned} \varPi ^{{*}}=\varPi +\frac{\alpha }{2}\int _{\varGamma _u^{(k)} } {(u-\bar{{u}})(u-\bar{{u}})\hbox {d}\varGamma ^{(k)}}, \end{aligned}$$

(13)

where $\alpha$ is the penalty factor.

Let

$$\begin{aligned} \delta \varPi ^{{*}}=0, \end{aligned}$$

(14)

the equivalent integral weak form can be obtained as

$$\begin{aligned}&\int _{\varOmega ^{(k)}} {\delta u\cdot \frac{\partial ^{2}u}{\partial x_3^2 }\hbox {d}\varOmega ^{(k)}} -\int _{\varOmega ^{(k)}} \delta ({\varvec{L}}u)^{\text {T}}\cdot ({\varvec{L}}u)\hbox {d}\varOmega ^{(k)} \nonumber \\&\quad -\int _{\varOmega ^{(k)}} {\delta u} \cdot b\hbox {d}\varOmega ^{(k)}-\int _{\varGamma _q^{(k)} } {\delta u\cdot \bar{{q}}\hbox {d}\varGamma ^{(k)}} \nonumber \\&\quad +\,\alpha \int _{\varGamma _u^{(k)} } {\delta u\cdot u\hbox {d}\varGamma ^{(k)}}-\,\alpha \int _{\varGamma _u^{(k)} } {\delta u\cdot \bar{{u}}\hbox {d}\varGamma ^{(k)}} =0, \end{aligned}$$

(15)

where

$$\begin{aligned} {{\varvec{L}}}(\cdot )=\left[ {{\begin{array}{l} {\frac{\partial }{\partial x_1 }} \\ {\frac{\partial }{\partial x_2 }} \\ \end{array} }} \right] (\cdot ). \end{aligned}$$

(16)

3 The dimension split element-free Galerkin method for three-dimensional potential problems

3.1 Improved moving least-squares approximation

M nodes ${{\varvec{x}}}_I^{\left( k\right) }$, $I=1,2,\ldots ,M$ are distributed in a two-dimensional sub-domain $\varOmega ^{\left( k\right) }$. The $u\left( {{\varvec{x}}}\right)$ at node ${{\varvec{x}}}_I^{\left( k\right) }$ is represented as

$$\begin{aligned} u_I =u\left( {{\varvec{x}}}_I^{\left( k\right) } ,x_3^{\left( k\right) } \right) . \end{aligned}$$

(17)

$u\left( {{\varvec{x}}}^{\left( k\right) } ,x_{{3}}^{\left( k\right) } \right)$ at any ${{\varvec{x}}}^{\left( k\right) } =\left( x_1^{\left( k\right) } ,x_{2}^{\left( k\right) } \right)$ is approximated by nodes ${{\varvec{x}}}_I^{\left( k\right) }, I=1,2,\ldots ,n$ whose influence domains cover the point ${{\varvec{x}}}^{\left( k\right) }$.

The IMLS approximation is used to construct shape functions. The approximation of $u\left( {{\varvec{x}}}\right)$ at point ${{\varvec{x}}}^{\left( k\right) }$ in the two-dimensional sub-domain $\varOmega ^{\left( k\right) }$ is donated as $u^{h}\left( {{\varvec{x}}}^{\left( k\right) } ,x_3^{\left( k\right) } \right)$, and the trial function is

$$\begin{aligned} u^{h}\left( {{\varvec{x}}}^{\left( k\right) },x_3^{\left( k\right) } \right)= & {} \sum _{i=1}^m {p_i \left( {{\varvec{x}}}^{\left( k\right) }\right) } a_i \left( {{\varvec{x}}}^{\left( k\right) }\right) \nonumber \\= & {} {{\varvec{p}}}^{\text {T}}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{\varvec{a}}}\left( {{\varvec{x}}}^{\left( k\right) }\right) ,\quad \;{{\varvec{x}}}^{\left( k\right) }\in \varOmega ^{\left( k\right) },\nonumber \\ \end{aligned}$$

(18)

where $p_i \left( {{\varvec{x}}}^{\left( k\right) }\right)$ is the basis function, ${{\varvec{p}}}^{\text {T}}\left( {{\varvec{x}}}^{\left( k\right) }\right)$ is a vector of basis functions that consist mostly of monomials of the lowest order to ensure minimum completeness, m is the number of terms of the monomials, and ${{\varvec{{\varvec{a}}}}}\left( {{\varvec{x}}}^{\left( k\right) }\right)$ is a vector of coefficients. For the two-dimensional sub-domain $\varOmega ^{\left( k\right) }$, in this paper the basis function is chosen as the linear basis, i.e.

$$\begin{aligned} {{\varvec{p}}}^{\text {T}}=\left( 1 ,x_1 ,x_2 \right) ,\quad m=3. \end{aligned}$$

(19)

Define a functional

$$\begin{aligned} J=\sum _{I=1}^n {w\left( {{\varvec{x}}}^{\left( k\right) }-{{\varvec{x}}}_I^{\left( k\right) } \right) } \left[ {\sum _{i=1}^m {p_i \left( {{\varvec{x}}}^{\left( k\right) }\right) } a_i \left( {{\varvec{x}}}^{\left( k\right) }\right) -u_I } \right] ^{2},\nonumber \\ \end{aligned}$$

(20)

where ${\varvec{x}}_I^{\left( k\right) }$, $I=1,2,\ldots ,n$, are nodes with domains of influence that cover the point ${{\varvec{x}}}^{\left( k\right) }$, $w\left( {{\varvec{x}}}^{\left( k\right) }-{{\varvec{x}}}_I^{\left( k\right) } \right)$ is a weight function with a domain of influence, and $u_I =u\left( {{\varvec{x}}}_I^{\left( k\right) } ,x_3^{\left( k\right) } \right)$.

From

$$\begin{aligned} \frac{\partial J}{\partial {{\varvec{a}}}}=0, \end{aligned}$$

(21)

we obtain

$$\begin{aligned} {{\varvec{a}}}\left( {{\varvec{x}}}^{\left( k\right) }\right) ={{\varvec{A}}}^{-1}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{\varvec{B}}}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{\varvec{u}}}, \end{aligned}$$

(22)

where

$$\begin{aligned}&{{\varvec{A}}}\left( {{\varvec{x}}}^{\left( k\right) }\right) ={{\varvec{P}}}^{\hbox {T}}{{\varvec{W}}}{{\varvec{P}}},\end{aligned}$$

(23)

$$\begin{aligned}&{{\varvec{B}}}\left( {{\varvec{x}}}^{\left( k\right) }\right) ={{\varvec{P}}}^{\hbox {T}}{{\varvec{W}}},\end{aligned}$$

(24)

$$\begin{aligned}&{{\varvec{u}}}^{\hbox {T}}=\left( u_1 ,u_2 ,\ldots ,u_n \right) ,\end{aligned}$$

(25)

$$\begin{aligned}&{{\varvec{P}}}=\left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {p_1 \left( {{\varvec{x}}}_1^{\left( k\right) } \right) }&{} {p_2 \left( {{\varvec{x}}}_1^{\left( k\right) } \right) }&{} \cdots &{} {p_m \left( {{\varvec{x}}}_1^{\left( k\right) } \right) } \\ {p_1 \left( {{\varvec{x}}}_2^{\left( k\right) } \right) }&{} {p_2 \left( {{\varvec{x}}}_2^{\left( k\right) } \right) }&{} \cdots &{} {p_m \left( {{\varvec{x}}}_2^{\left( k\right) } \right) } \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {p_1 \left( {{\varvec{x}}}_n^{\left( k\right) } \right) }&{} {p_2 \left( {{\varvec{x}}}_n^{\left( k\right) } \right) }&{} \cdots &{} {p_m \left( {{\varvec{x}}}_n^{\left( k\right) } \right) } \\ \end{array} }} \right] ,\end{aligned}$$

(26)

$$\begin{aligned}&{{\varvec{W}}}=\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {w\left( {{\varvec{x}}}^{\left( k\right) }-{{\varvec{x}}}_1^{\left( k\right) } \right) }&{} 0&{} \cdots &{} 0 \\ 0&{} {w\left( {{\varvec{x}}}^{\left( k\right) }-{{\varvec{x}}}_2^{\left( k\right) } \right) }&{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0&{} 0&{} \cdots &{} {w\left( {{\varvec{x}}}^{\left( k\right) }-{{\varvec{x}}}_n^{\left( k\right) } \right) } \\ \end{array} }} \right] .\nonumber \\ \end{aligned}$$

(27)

In the IMLS approximation, a weighted orthogonal polynomial set $\left( p_1 ,p_2 ,\ldots ,p_m \right)$ is selected as the basis functions, which results in

$$\begin{aligned} a\left( {{\varvec{x}}}^{\left( k\right) }\right) ={{\varvec{A}}}^{*}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{\varvec{B}}}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{\varvec{u}}}, \end{aligned}$$

(28)

where

$$\begin{aligned} {{\varvec{A}}}^{*}\left( {{\varvec{x}}}^{\left( k\right) }\right) =\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {\frac{1}{\left( p_1 ,p_1 \right) }}&{} 0&{} \cdots &{} 0 \\ 0&{} {\frac{1}{\left( p_2 ,p_2 \right) }}&{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0&{} 0&{} \cdots &{} {\frac{1}{\left( p_m ,p_m \right) }} \\ \end{array} }} \right] . \end{aligned}$$

(29)

Substituting Eq. (28) into Eq. (18), we can obtain

$$\begin{aligned} u^{h}\left( {{\varvec{x}}}^{\left( k\right) },x_3^{\left( k\right) } \right)= & {} \sum _{I=1}^n {\varPhi _I^*} \left( {{\varvec{x}}}^{\left( k\right) }\right) u_I \left( {{\varvec{x}}}^{\left( k\right) }\right) \nonumber \\= & {} \varvec{\varPhi }^{*}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{\varvec{u}}}, \end{aligned}$$

(30)

where $\varvec{\varPhi }^{*}\left( {{\varvec{x}}}^{\left( k\right) }\right)$ is a shape function

$$\begin{aligned} \varvec{\varPhi }^{*}\left( {{\varvec{x}}}^{\left( k\right) }\right)= & {} \left( \varPhi _1^*\left( {{\varvec{x}}}^{\left( k\right) }\right) ,\varPhi _2^*\left( {{\varvec{x}}}^{\left( k\right) }\right) ,\ldots ,\varPhi _n^*\left( {{\varvec{x}}}^{\left( k\right) }\right) \right) \nonumber \\= & {} {{\varvec{P}}}^{\text {T}}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{\varvec{A}}}^{*}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{\varvec{B}}}\left( {{\varvec{x}}}^{\left( k\right) }\right) , \end{aligned}$$

(31)

$$\begin{aligned} \varPhi _I^*\left( {{\varvec{x}}}^{\left( k\right) }\right)= & {} \sum _{j=1}^m {p_j } \left( {{\varvec{x}}}^{\left( k\right) }\right) \left[ {{{\varvec{A}}}^{*}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{\varvec{B}}}\left( {{\varvec{x}}}^{\left( k\right) }\right) } \right] _{jI}. \end{aligned}$$

(32)

For the monomial basis function

$$\begin{aligned} {{\varvec{q}}}=\left( q_i \right) =\left( 1,x_1 ,x_2 ,x_1^2 ,x_1 x_2 ,x_2^2 ,\ldots \right) , \end{aligned}$$

(33)

the weighted orthogonal basis function set can be written as

$$\begin{aligned} p_i =q_i -\sum _{k=1}^{i-1} {\frac{\left( q_i ,p_k \right) }{\left( p_k ,p_k \right) }} p_k ,\quad i=1,2,3,\ldots . \end{aligned}$$

(34)

In this paper, we select cubic spline function

$$\begin{aligned} w\left( d \right) =\left\{ {{\begin{array}{l@{\quad }l} \frac{2}{3}-4d^{2}+4d^{3},&{}d\leqslant \frac{1}{2}, \\ \frac{4}{3}-4d+4d^{2}-\frac{4}{3}d^{3}, &{} \frac{1}{2}<d\leqslant 1, \\ 0,&{} d>1, \\ \end{array} }} \right. \end{aligned}$$

(35)

as the weight function. Here

$$\begin{aligned} d=\frac{d_I }{\hat{{d}}}=\frac{\left| {{{\varvec{x}}}-{{\varvec{x}}}_I } \right| }{\hat{{d}}}, \end{aligned}$$

(36)

$\hat{{d}}$ is the size of the domain of influence of the node ${{\varvec{x}}}_I$, $\hat{{d}}=d_{\max } \cdot c_I$, $d_{\max }$ is a scaling parameter, and $c_I$ is the distance between ${{\varvec{x}}}_I$ and the nearest node from it.

3.2 The dimension split element-free Galerkin method for three-dimensional potential problems

To obtain the solution of the original problem, i.e. Eqs. (1)–(3), the Galerkin weak form of the three-dimensional potential problem is used to get the final discretized equations.

From Eq. (30), we have

$$\begin{aligned} \frac{\partial ^{ 2 }u\left( {{\varvec{x}}}^{\left( k\right) },x_3^{\left( k\right) } \right) }{\partial x_3^2 }= & {} \frac{\partial }{\partial x_3^2 }\sum _{I=1}^n {\varPhi _I^*} \left( {{\varvec{x}}}^{\left( k\right) }\right) u_I \left( {{\varvec{x}}}^{\left( k\right) },x_3^{\left( k\right) } \right) \nonumber \\= & {} \sum _{I=1}^n {\varPhi _I^*\left( {{\varvec{x}}}^{\left( k\right) }\right) } \frac{\partial ^{2}u_I }{\partial x_3^2 }={\varvec{\varPhi }} ^{*}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{{\varvec{u}}}}'', \nonumber \\\end{aligned}$$

(37)

$$\begin{aligned} {{\varvec{L}}}u\left( {{\varvec{x}}}^{\left( k\right) },x_3^{\left( k\right) } \right)= & {} \sum _{I=1}^n {\left[ {{\begin{array}{l} {\frac{\partial }{\partial x_1 }} \\ {\frac{\partial }{\partial x_2 }} \\ \end{array} }} \right] } \varPhi _I^*\left( {{\varvec{x}}}^{\left( k\right) }\right) u_I \nonumber \\= & {} \sum _{I=1}^n {{{\varvec{B}}}_I \left( {{\varvec{x}}}^{\left( k\right) }\right) u_I ={{\varvec{B}}}\left( {{\varvec{x}}}^{\left( k\right) }\right) } {{\varvec{u}}}, \end{aligned}$$

(38)

where

$$\begin{aligned}&{{{\varvec{u}}}}''=\left( {\frac{\partial ^{2}u_1 }{\partial x_3^2 },\frac{\partial ^{2}u_2 }{\partial x_3^2 },\ldots ,\frac{\partial ^{2}u_n }{\partial x_3^2 }} \right) ^{\mathrm{T}}, \end{aligned}$$

(39)

$$\begin{aligned}&{{\varvec{B}}}\left( {{\varvec{x}}}^{\left( k\right) }\right) =\left( {{\varvec{B}}}_1 \left( {{\varvec{x}}}^{\left( k\right) }\right) ,{{\varvec{B}}}_2 \left( {{\varvec{x}}}^{\left( k\right) }\right) ,\ldots ,{{\varvec{B}}}_n \left( {{\varvec{x}}}^{\left( k\right) }\right) \right) ,\quad \end{aligned}$$

(40)

$$\begin{aligned} {{\varvec{B}}}_I \left( {{\varvec{x}}}^{\left( k\right) }\right)= & {} \left[ {{\begin{array}{l} {\varPhi _{I,1}^*\left( {{\varvec{x}}}^{\left( k\right) }\right) } \\ {\varPhi _{I,2}^*\left( {{\varvec{x}}}^{\left( k\right) }\right) } \\ \end{array} }} \right] . \end{aligned}$$

(41)

Substituting Eqs. (30), (37), and (38) into Eq. (15) yields

$$\begin{aligned}&\int _{\varOmega ^{\left( k\right) }} {\delta \left[ {\varvec{\varPhi }} ^{*}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{\varvec{u}}}\right] \cdot \left[ {\varvec{\varPhi }} ^{*}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{{\varvec{u}}}}''\right] \hbox {d} \varOmega ^{\left( k\right) }} \nonumber \\&\quad -\int _{\varOmega ^{\left( k\right) }} {\delta \left[ {{\varvec{B}}}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{\varvec{u}}}\right] ^\mathrm{T}\cdot \left[ {{\varvec{B}}}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{\varvec{u}}}\right] \hbox {d}\varOmega ^{\left( k\right) }} \nonumber \\&\quad -\int _{\varOmega ^{\left( k\right) }} {\delta \left[ {\varvec{\varPhi }} ^{*}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{\varvec{u}}}\right] \cdot b\hbox {d}\varOmega ^{\left( k\right) }} \nonumber \\&\quad -\int _{\varGamma _q^{\left( k\right) } } {\delta \left[ {\varvec{\varPhi }} ^{*}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{\varvec{u}}}\right] \cdot \bar{{q}}\hbox {d}\varGamma ^{\left( k\right) }} \nonumber \\&\quad + \int _{\varGamma _u^{\left( k\right) } } {\delta \left[ {\varvec{\varPhi }} ^{*}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{\varvec{u}}}\right] \cdot \alpha \cdot \left[ {\varvec{\varPhi }} ^{*}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{\varvec{u}}}\right] \hbox {d}\varGamma ^{\left( k\right) }} \nonumber \\&\quad -\int _{\varGamma _{{u}}^{\left( k\right) } } {\delta \left[ {\varvec{\varPhi }} ^{*}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{\varvec{u}}}\right] \cdot \alpha \bar{{u}}\hbox {d}\varGamma ^{\left( k\right) }} = 0 _{.} \end{aligned}$$

(42)

In order to obtain the discrete equations, we discuss each integration term of Eq. (42) as follows.

The first integration term of Eq. (42) is

$$\begin{aligned}&\int _{\varOmega ^{\left( k\right) }} {\delta \left[ {\varvec{\varPhi }} ^{{*}}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{\varvec{u}}}\right] \cdot \left[ {\varvec{\varPhi }} ^{*}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{{\varvec{u}}}}''\right] \hbox {d}\varOmega ^{\left( k\right) }} \nonumber \\&\quad =\delta {{\varvec{u}}}^{\mathrm{T}}\cdot \left[ \int _{\varOmega ^{\left( k\right) }} {{\varvec{\varPhi }} ^{{*}^{\mathrm{T}}}\left( {{\varvec{x}}}^{\left( k\right) }\right) } {\varvec{\varPhi }} ^{*}\left( {{\varvec{x}}}^{\left( k\right) }\right) \hbox {d}\varOmega ^{\left( k\right) }\right] \cdot {{{\varvec{u}}}}''\nonumber \\&\quad =\delta {{\varvec{u}}}^\mathrm{T}\cdot {{\varvec{C}}}\cdot {{{\varvec{u}}}}'', \end{aligned}$$

(43)

where

$$\begin{aligned} {{\varvec{C}}}=\int _{\varOmega ^{\left( k\right) }} {{\varvec{\varPhi }} ^{{*}^{\mathrm{T}}}\left( {{\varvec{x}}}^{\left( k\right) }\right) } {\varvec{\varPhi }} ^{*}\left( {{\varvec{x}}}^{\left( k\right) }\right) \hbox {d}\varOmega ^{\left( k\right) }. \end{aligned}$$

(44)

The second integration term of Eq. (42) is

$$\begin{aligned}&\int _{\varOmega ^{\left( k\right) }} {\delta \left[ {{\varvec{B}}}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{\varvec{u}}}\right] ^{\mathrm{T}}\cdot \left[ {{\varvec{B}}}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{\varvec{u}}}\right] \hbox {d}\varOmega ^{\left( k\right) }} \nonumber \\&\quad =\delta {{\varvec{u}}}^{\mathrm{T}}\cdot \left[ \int _{\varOmega ^{\left( k\right) }} {{{\varvec{B}}}^\mathrm{T}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{\varvec{B}}}\left( {{\varvec{x}}}^{\left( k\right) }\right) \hbox {d}\varOmega ^{\left( k\right) }} \right] \cdot {{\varvec{u}}}\nonumber \\&\quad =\delta {{\varvec{u}}}^{\mathrm{T}}\cdot {{\varvec{K}}}\cdot {{\varvec{u}}}, \end{aligned}$$

(45)

where

$$\begin{aligned} {{\varvec{K}}}=\int _{\varOmega ^{\left( k\right) }} {{{\varvec{B}}}^{\mathrm{T}}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{\varvec{B}}}\left( {{\varvec{x}}}^{\left( k\right) }\right) \hbox {d}\varOmega ^{\left( k\right) }} . \end{aligned}$$

(46)

The third integration term of Eq. (42) is

$$\begin{aligned}&\int _{\varOmega ^{\left( k\right) }} {\delta \left[ {\varvec{\varPhi }} ^{*}\left( {{\varvec{x}}}^{\left( {{k}}\right) }\right) {{\varvec{u}}}\right] \cdot b\hbox {d}\varOmega ^{\left( k\right) }}\nonumber \\&\quad =\delta {{\varvec{u}}}^\mathrm{T}\cdot \int _\varOmega {{\varvec{\varPhi }} ^{{*}^{\mathrm{T}}}\left( {{\varvec{x}}}^{\left( k\right) }\right) } b\hbox {d}\varOmega ^{\left( k\right) }\nonumber \\&\quad =\delta {{\varvec{u}}}^{\mathrm{T}}\cdot {{\varvec{F}}}_1 , \end{aligned}$$

(47)

where

$$\begin{aligned} {{\varvec{F}}}_1 =\int _{\varOmega ^{\left( k\right) }} {{\varvec{\varPhi }} ^{{*}^{\mathrm{T}}} \left( {{\varvec{x}}}^{\left( k\right) }\right) } b\hbox {d}\varOmega ^{\left( k\right) }. \end{aligned}$$

(48)

The fourth integration term of Eq. (42) is

$$\begin{aligned}&\int _{\varGamma _q^{\left( k\right) } } {\delta \left[ {\varvec{\varPhi }} ^{*}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{\varvec{u}}}\right] \cdot \bar{{q}}\hbox {d}\varGamma ^{\left( k\right) }} \nonumber \\&\quad =\delta {{\varvec{u}}}^{\mathrm{T}}\cdot \int _{\varGamma _q^{\left( k\right) } } {{\varvec{\varPhi }} ^{{*}^{\mathrm{T}}}\left( {{\varvec{x}}}^{\left( k\right) }\right) } \bar{{q}}\hbox {d}\varGamma ^{\left( k\right) }=\delta {{\varvec{u}}}^{\mathrm{T}}\cdot {{\varvec{F}}}_2 , \end{aligned}$$

(49)

where

$$\begin{aligned} {{\varvec{F}}}_2 =\int _{\varGamma _q^{\left( k\right) } } {{\varvec{\varPhi }} ^{{*}^{\mathrm{T}}}\left( {{\varvec{x}}}^{\left( k\right) }\right) } \bar{{q}}\hbox {d}\varGamma ^{\left( k\right) }. \end{aligned}$$

(50)

The fifth integration term of Eq. (42) is

$$\begin{aligned}&\int _{\varGamma _u^{\left( k\right) } } {\delta \left[ {{{\varvec{\varPhi }}}}^{*}\left( {{\varvec{x}}}^{\left( k\right) }\right) {{\varvec{u}}}\right] \cdot \alpha \cdot \left[ {\varvec{\varPhi }} ^{*} \left( {{\varvec{x}}}^{\left( k\right) }\right) {{\varvec{u}}}\right] \hbox {d}\varGamma ^{\left( k\right) }} \nonumber \\&\quad =\delta {{\varvec{u}}}^\mathrm{T}\cdot \left[ {\int _{\varGamma _u^{\left( k\right) } } {{\varvec{\varPhi }} ^{{*}^{\mathrm{T}}} \left( {{\varvec{x}}}^{\left( k\right) }\right) } \alpha {\varvec{\varPhi }} ^{*} \left( {{\varvec{x}}}^{\left( k\right) }\right) \hbox {d}\varGamma ^{\left( k\right) }} \right] \cdot \nonumber \\&{{\varvec{u}}}=\delta {{\varvec{u}}}^{\mathrm{T}}\cdot {{\varvec{K}}}_\alpha \cdot {{\varvec{u}}}, \end{aligned}$$

(51)

where

$$\begin{aligned} {{\varvec{K}}}_\alpha =\alpha \int _{\varGamma _u^{\left( k\right) } } {{\varvec{\varPhi }} ^{{*}^{\mathrm{T}}}\left( {{\varvec{x}}}^{\left( k\right) }\right) } {\varvec{\varPhi }} ^{*}\left( {{\varvec{x}}}^{\left( k\right) }\right) \hbox {d}\varGamma ^{\left( k\right) }. \end{aligned}$$

(52)

The sixth integration term of Eq. (42) is

$$\begin{aligned}&\int _{\varGamma _u^{(k)} } {\delta \left[ {\varvec{\varPhi }} ^{*}({{\varvec{x}}}^{(k)}){{\varvec{u}}}\right] \cdot \alpha \bar{{u}}\hbox {d}\varGamma ^{(k)}} =\delta {{\varvec{u}}}^\mathrm{T}\nonumber \\&\qquad \cdot \int _{\varGamma _u^{(k)} } {{\varvec{\varPhi }} ^{{*}^\mathrm{T}}({{\varvec{x}}}^{(k)})} \alpha \bar{{u}}\hbox {d}\varGamma ^{(k)}\nonumber \\&\quad =\delta {{\varvec{u}}}^\mathrm{T}\cdot {{\varvec{F}}}_\alpha , \end{aligned}$$

(53)

where

$$\begin{aligned} {{\varvec{F}}}_\alpha =\alpha \int _{\varGamma _u^{(k)} } {{{{\varvec{\varPhi }}}}^{{*}^\mathrm{T}}({{\varvec{x}}}^{(k)})} \bar{{u}}\hbox {d}\varGamma ^{(k)}. \end{aligned}$$

(54)

Substituting Eqs. (43), (45), (47), (49), (51), and (53) into Eq. (42), we obtain

$$\begin{aligned} \delta {\varvec{u}}^\mathrm{T}\cdot ({{\varvec{C{u}}}}''-{{\varvec{Ku}}}+{{\varvec{K}}}_\alpha {{\varvec{u}}}-{{\varvec{F}}}_1 -{{\varvec{F}}}_2 -{{\varvec{F}}}_\alpha )=\mathbf{0 }. \end{aligned}$$

(55)

As $\delta u^\mathrm{T}$ is arbitrary, we have

$$\begin{aligned} {{\varvec{C{u}}}}''+{\bar{{{\varvec{K}}}}}{{\varvec{u}}}={{\varvec{F}}}, \end{aligned}$$

(56)

where

$$\begin{aligned} {\bar{{{\varvec{K}}}}}= & {} {{\varvec{K}}}_\alpha -{{\varvec{K}}}, \end{aligned}$$

(57)

$$\begin{aligned} {{\varvec{F}}}= & {} {{\varvec{F}}}_1 +{{\varvec{F}}}_2 +{{\varvec{F}}}_\alpha . \end{aligned}$$

(58)

To solve Eq. (56), $L-1$ points are uniformly inserted to the domain [a, c], and [a, c] in direction $x_3$ is equally divided into L parts. That is, the domain $\varOmega$ is divided into $L-1$ planes in direction $x_3,$ then we consider the potential of the plane when $x_3 =x_3^{(1)} ,x_3^{(2)} ,\ldots ,x_3^{(L-1)}$.

Suppose ${{\varvec{u}}}(x_3^{(1)} ),{{\varvec{u}}}(x_3^{(2)} ),\ldots ,{{\varvec{u}}}(x_3^{(L-1)} )$ represent the approximation of the potential of the plane when $x_3 =x_3^{(1)} ,x_3^{(2)} ,\ldots ,x_3^{(L-1)}$. Let

$$\begin{aligned} {{\varvec{u}}}(x_3^{(1)} )= & {} {{\varvec{u}}}^{(1)} , \end{aligned}$$

(59)

$$\begin{aligned} {{\varvec{u}}}(x_3^{(2)} )= & {} {{\varvec{u}}}^{(2)}, \end{aligned}$$

(60)

$$\begin{aligned} \vdots \end{aligned}$$

$$\begin{aligned} {{\varvec{u}}}(x_3^{(L-1)} )= & {} {{\varvec{u}}}^{(L-1)}, \end{aligned}$$

(61)

and

$$\begin{aligned} {{\varvec{u}}}(x_3^{(0)} )= & {} {{\varvec{u}}}^{(0)}={{\varvec{u}}}(a), \end{aligned}$$

(62)

$$\begin{aligned} {{\varvec{u}}}(x_3^{(L)} )= & {} {{\varvec{u}}}^{(L)}={{\varvec{u}}}(c), \end{aligned}$$

(63)

by using the finite difference method, we have

$$\begin{aligned} {{{\varvec{u}}}}''^{(k)}\approx \frac{{{\varvec{u}}}^{(k-1)}-2{{\varvec{u}}}^{(k)}+{{\varvec{u}}}^{(k+1)}}{(\Delta x_3 )^{2}}, \quad k=1,2,\ldots ,L-1.\nonumber \\ \end{aligned}$$

(64)

Then, Eq. (56) can be written as

$$\begin{aligned}&{{\varvec{C}}}\cdot \frac{{{\varvec{u}}}^{(0)}-2{{\varvec{u}}}^{(1)}+{{\varvec{u}}}^{(2)}}{(\Delta x_3 )^{2}}+{\bar{{{\varvec{K}}}}}{{\varvec{u}}}^{(1)}={{\varvec{F}}}^{(1)}, \end{aligned}$$

(65)

$$\begin{aligned}&{{\varvec{C}}}\cdot \frac{{{\varvec{u}}}^{(1)}-2{{\varvec{u}}}^{(2)}+{{\varvec{u}}}^{(3)}}{(\Delta x_3 )^{2}}+{\bar{{{\varvec{K}}}}}{{\varvec{u}}}^{(2)}={{\varvec{F}}}^{(2)}, \end{aligned}$$

(66)

$$\begin{aligned}&{{\varvec{C}}}\cdot \frac{{{\varvec{u}}}^{(2)}-2{{\varvec{u}}}^{(3)}+{{\varvec{u}}}^{(4)}}{(\Delta x_3 )^{2}}+{\bar{{{\varvec{K}}}}}{{\varvec{u}}}^{(3)}={{\varvec{F}}}^{(3)}, \end{aligned}$$

(67)

$$\begin{aligned}&\qquad \qquad \qquad \quad \vdots \nonumber \\&{{\varvec{C}}}\cdot \frac{{{\varvec{u}}}^{(L-2)}-2{{\varvec{u}}}^{(L-1)}+{{\varvec{u}}}^{(L)}}{(\Delta x_3 )^{2}}+{\bar{{{\varvec{K}}}}}{{\varvec{u}}}^{(L-1)}={{\varvec{F}}}^{(L-1)}. \end{aligned}$$

(68)

The corresponding matrix form is

$$\begin{aligned}&\frac{1}{(\Delta x_3 )^{2}}\left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {{\varvec{H}}}&{} {{\varvec{C}}}&{} &{} &{} &{} \\ {{\varvec{C}}}&{} {{\varvec{H}}}&{} {{\varvec{C}}}&{} &{} &{} \\ &{} {{\varvec{C}}}&{} {{\varvec{H}}}&{} {{\varvec{C}}}&{} &{} \\ &{} &{} \ddots &{} \ddots &{} \ddots &{} \\ &{} &{} &{} {{\varvec{C}}}&{} {{\varvec{H}}}&{} {{\varvec{C}}} \\ &{} &{} &{} &{} {{\varvec{C}}}&{} {{\varvec{H}}} \\ \end{array} }} \right] \left[ {{\begin{array}{c} {{{\varvec{u}}}^{(1)}} \\ {{{\varvec{u}}}^{(2)}} \\ {{{\varvec{u}}}^{(3)}} \\ \vdots \\ {{{\varvec{u}}}^{(L-2)}} \\ {{{\varvec{u}}}^{(L-1)}} \\ \end{array} }} \right] \nonumber \\&\quad = \left[ {{\begin{array}{c} {{{\varvec{F}}}^{(1)}-\frac{{{\varvec{Cu}}}^{(0)}}{(\Delta x_3 )^{2}}} \\ {{{\varvec{F}}}^{(2)}} \\ {{{\varvec{F}}}^{(3)}} \\ \vdots \\ {{{\varvec{F}}}^{(L-2)}} \\ {{{\varvec{F}}}^{(L-1)}-\frac{{{\varvec{Cu}}}^{(L)}}{(\Delta x_3 )^{2}}} \\ \end{array} }} \right] , \end{aligned}$$

(69)

where

$$\begin{aligned} {{\varvec{H}}}=-\,2{{\varvec{C}}}+(\Delta x_3 )^{2}{\bar{{{\varvec{K}}}}}. \end{aligned}$$

(70)

Let

$$\begin{aligned}&{{\varvec{E}}}=\frac{1}{(\Delta x_3 )^{2}}\left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {{\varvec{H}}}&{} {{\varvec{C}}}&{} &{} &{} &{} \\ {{\varvec{C}}}&{} {{\varvec{H}}}&{} {{\varvec{C}}}&{} &{} &{} \\ &{} {{\varvec{C}}}&{} {{\varvec{H}}}&{} {{\varvec{C}}}&{} &{} \\ &{} &{} \ddots &{} \ddots &{} \ddots &{} \\ &{} &{} &{} {{\varvec{C}}}&{} {{\varvec{H}}}&{} {{\varvec{C}}} \\ &{} &{} &{} &{} {{\varvec{C}}}&{} {{\varvec{H}}} \\ \end{array} }} \right] , \end{aligned}$$

(71)

$$\begin{aligned}&{{\varvec{U}}}=\left[ {{{\varvec{u}}}^{{(1)}^\mathrm{T}},{{\varvec{u}}}^{{(2)}^\mathrm{T}}, {{\varvec{u}}}^{{(3)}^\mathrm{T}},\ldots ,{{\varvec{u}}}^{{(L-2)}^\mathrm{T}},{{\varvec{u}}}^{{(L-1)}^\mathrm{T}}} \right] ^\mathrm{T}, \end{aligned}$$

(72)

$$\begin{aligned}&{{\varvec{R}}}=\left[ {\left( {{\varvec{F}}}^{(1)}-\frac{{{\varvec{Cu}}}^{(0)}}{(\Delta x_3)^{2}} \right) ^\mathrm{T},}\quad {{{\varvec{F}}}^{{(2)}^\mathrm{T}},}\quad {{{\varvec{F}}}^{{(3)}^\mathrm{T}},}\quad {\ldots ,}\quad {{{\varvec{F}}}^{{(L-2)}^\mathrm{T}},}\quad \right. \nonumber \\&\quad \left. {\left( {{{\varvec{F}}}^{(L-1)}-\frac{{{\varvec{Cu}}}^{(L)}}{(\Delta x_3 )^{2}}} \right) ^\mathrm{T}} \right] ^\mathrm{T}. \end{aligned}$$

(73)

Equation (69) can be simplified as

$$\begin{aligned} {{\varvec{EU}}}={{\varvec{R}}}. \end{aligned}$$

(74)

By solving Eq. (74), we can obtain the potential of nodes on each layer ${{\varOmega }} ^{(k)}$, $k=1,2,\ldots ,L-1$. Then the potential of any nodes in the domain [a, c] can be obtained using linear interpolation method. Let $\Delta x_3 =x_3^{(k+1)} -x_3^{(k)}$, ${\varvec{u}}(x_3 )$ can be expressed as

$$\begin{aligned} {\varvec{u}}(x_3 )=\frac{x_3 -x_3^{(k)} }{\Delta x_3 }{\varvec{u}}(x_3^{(k)} )+\frac{x_3^{(k+1)} -x_3 }{\Delta x_3 }{\varvec{u}}(x_3^{(k+1)} ). \end{aligned}$$

(75)

4 Example problems

Four example problems are selected to demonstrate the effectiveness and advantages of the DSEFG method presented in this paper. The convergence of the DSEFG method is discussed by analyzing the final potential function values under different nodes distribution and different scaling factors. The numerical results of these examples are compared with analytical solutions and the ones of the IEFG method.

In this section, Gaussian quadrature scheme with $4\times 4$ points is used for numerical integrations on each cell of the background mesh. The cubic spline function is used as the weight function, and the linear basis function is selected.

4.1 Laplace’s equation with Dirichlet boundary conditions on a cube

As the first example, we consider Laplace’s equation

$$\begin{aligned} \nabla ^{2}u({{\varvec{x}}})=\frac{\partial ^{2}u({{\varvec{x}}})}{\partial x_1^2 }+\frac{\partial ^{2}u({{\varvec{x}}})}{\partial x_2^2 }+\frac{\partial ^{2}u({{\varvec{x}}})}{\partial x_3^2 }=0,\quad {{\varvec{x}}}\in \varOmega ,\nonumber \\ \end{aligned}$$

(76)

with boundary conditions

$$\begin{aligned} u= & {} \sin ({\uppi }x_2 )\sin ({\uppi }x_3 ),\quad x_1 =0, \end{aligned}$$

(77)

$$\begin{aligned} u= & {} 2\sin ({\uppi }x_2 )\sin ({\uppi }x_3 ),\quad x_1 = 1 , \end{aligned}$$

(78)

$$\begin{aligned} u= & {} 0,\quad x_2 =0,x_2 =1,x_3 =0,x_3 =1, \end{aligned}$$

(79)

The problem domain is $\varOmega =[0,1]\times [0,1]\times [0,1]$.

Fig. 1

Results obtained by the DSEFG method with different node distributions

Fig. 2

Results obtained by the DSEFG method with different $d_{\max }$

The analytical solution is

$$\begin{aligned}&u=\frac{\sin ({\uppi } x_2 )\sin ({\uppi }x_3 )}{\sinh ({\uppi }\sqrt{2})}[2\sinh (\uppi \sqrt{2}x_1 )\nonumber \\&\quad +\sinh ({\uppi }\sqrt{2}(1-x_1 ))]. \end{aligned}$$

(80)

Depending on the boundary conditions, the domain $\varOmega$ is divided into L equal parts along $x_1$ direction. Uniform node distribution is used in the plane $Ox_2 x_3$. That is, the domain $\varOmega$ can be represented as $\varOmega =\mathop \cup \limits _{k=0}^{L-1} \varOmega ^{(k)}\times [x_1 ^{(k)},x_1 ^{(k+1)}]\cup \varOmega ^{(L)}$.

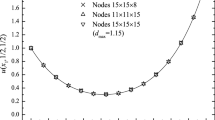
Results obtained with the DSEFG method with different node distributions and different $d_{\max }$ along the direction $x_1$ are shown in Figs. 1 and 2.

The convergence of the DSEFG method with different node distributions and different $d_{\max }$ along the direction $x_1$ are shown in Figs. 3 and 4. In Fig. 3, the domain $\varOmega$ is divided into L equal parts in direction $x_1$, and the node distribution in the plane $Ox_2 x_3$ is $10 \times 10$, that is, the node distribution in the problem domain $\varOmega$ is $(L+1)\times 10\times 10$.

Fig. 3

The convergence of the DSEFG method with different node distributions.

Fig. 4

The convergence of the DSEFG method with different $d_{\max }$

Table 1 The relative error norm and CPU time of the DSEFG and IEFG methods under different node distributions

Table 2 The relative error norm and CPU time of the DSEFG and IEFG methods under different $d_{\max }$

Fig. 5

The results of the DSEFG and IEFG methods along the direction $x_1$

From Figs. 1–4, we can observe that the DSEFG method has greater computational precision under the node distribution $1 9\times 10 \times 10$ when $d_{\max } =1.3$.

The relationship between the relative error norm and the CPU time of the DSEFG and IEFG methods under different node distributions and different $d_{\max }$ are shown in Tables 1 and 2.

From Tables 1 and 2, we can see that the DSEFG method has higher accuracy and computational efficiency than the IEFG method under the same node distribution and $d_{\max }$.

Figures 5–7 show the numerical solutions obtained by both the IEFG method and DSEFG method along the three axes with the node distribution $1 9\times 10 \times 10$ and $d_{\max } =1.3$. We can observe that the result of the DSEFG method and the IEFG method are in agreement with the analytical solution, and the DSEFG method has greater computational precision and efficiency than the IEFG method.

Fig. 6

The results of the DSEFG and IEFG methods along the direction $x_2$

Fig. 7

The results of the DSEFG and IEFG methods along the direction $x_3$

4.2 Poisson’s equation with Dirichlet boundary conditions

As a second example, we solve a three-dimensional Poisson’s equation

$$\begin{aligned}&\nabla ^{2}u({{\varvec{x}}})=f({{\varvec{x}}}),\quad {{\varvec{x}}}\in \varOmega , \end{aligned}$$

(81)

$$\begin{aligned}&f({{\varvec{x}}})=-\left( {1+\frac{1}{4}+\frac{1}{9}} \right) {\uppi }^{2}\sin ({\uppi }x_1) \sin \frac{{\uppi }{x_2}}{2}\sin \frac{{\uppi }{x_3}}{3},\nonumber \\ \end{aligned}$$

(82)

with Dirichlet boundary conditions

$$\begin{aligned} u({{\varvec{x}}})=0,\quad {{\varvec{x}}}\in \varGamma , \end{aligned}$$

(83)

where $\varOmega =[0,1]\times [0,2]\times [0,3]$.

The analytical solution of this problem is

$$\begin{aligned} u({{\varvec{x}}})=\sin ({\uppi }x_1) \sin \frac{{\uppi }x_2 }{2}\sin \frac{{\uppi }x_3 }{3}. \end{aligned}$$

(84)

Using the IEFG method to solve this problem, $9\times 21\times 17$ regular nodes are distributed in the problem domain $\varOmega$ and $d_{\max } =1.22$. The relative error is 0.0025 and CPU time is 68.3 s.

Then using the DSEFG method to solve this problem, and three cases in which different splitting direction is selected are discussed.

• (1) The splitting direction is $x_1$. For the first case, the problem domain $\varOmega$ is divided into 8 planes equally along the direction $x_1$. And on each plane $Ox_2 x_3$, $21\times 17$ nodes are regularly chosen. It means that the integral node distribution is $9\times 21\times 17$. And $d_{\max } =2.1$, $\alpha =3.0\times 10 ^{3}$. Then the relative error is 0.0091 and the CPU time is 7.06 s.

• (2) The splitting direction is $x_2$. For the second case, the problem domain $\varOmega$ is divided into 20 planes equally along the direction $x_2$. And on each plane $Ox_1 x_3$, $9\times 17$ nodes are regularly chosen. This means that the integral node distribution is also $9\times 21\times 17$ and $d_{\max } =1.7$, $\alpha =3.0\times 10 ^{3}$. Then the relative error is 0.0016 and the CPU time is 5.24 s.

• (3) The splitting direction is $x_3$. For the third case, the problem domain $\varOmega$ is divided into 16 planes equally along the direction $x_3$. On each plane $Ox_1 x_2$, $9\times 21$ nodes are regularly chosen. This means that the integral node distribution is also $9\times 21\times 17$. And $d_{\max } = 1 . 1 3$, $\alpha =3.0\times 10 ^{3}$. Then the relative error is 0.0013 and the CPU time is 4.55 s.

From the discussion above, we can see that splitting direction will influence the computational accuracy. Thus, we should select the apposite splitting direction according to the control equations and boundary conditions.

In this paper, we choose $x_3$ as the splitting direction and the better result can be obtained. Figures 8–10 show the numerical solutions obtained with the IEFG method and the DSEFG method along the three axes under the same node distribution $9\times 21\times 17$. From these figures, we can observe that the numerical results obtained with the IEFG method and the DSEFG method are in agreement with the analytical ones. The CPU time of the DSEFG is less than the one for the IEFG method.

Fig. 8

The results of the DSEFG and IEFG methods along the direction $x_1$

Fig. 9

The results of the DSEFG and IEFG methods along the direction $x_2$

Fig. 10

The results of the DSEFG and IEFG methods along the direction $x_3$

Fig. 11

The results of the DSEFG and IEFG methods along the direction $x_1$

4.3 Laplace’s equation with Neumann boundary conditions on a cube

As a third example, we study Laplace’s equation

$$\begin{aligned} \nabla ^{2}u({{\varvec{x}}})=0,\quad {{\varvec{x}}}\in \varOmega , \end{aligned}$$

(85)

with Neumann boundary conditions

$$\begin{aligned}&\frac{\partial u(0,x_2 ,x_3 )}{\partial x_1 }=\frac{\partial u(1,x_2 ,x_3 )}{\partial x_1 }=0, \end{aligned}$$

(86)

$$\begin{aligned}&\frac{\partial u(x_1 ,0,x_3 )}{\partial x_2 }=\frac{\partial u(x_1 ,1,x_3 )}{\partial x_2 }=0, \end{aligned}$$

(87)

$$\begin{aligned}&\frac{\partial u(x_1 ,x_2 ,0)}{\partial x_3 }=\cos ({\uppi }x_1 )\cos ({\uppi }x_2 ), \end{aligned}$$

(88)

$$\begin{aligned}&\frac{\partial u(x_1 ,x_2 ,1)}{\partial x_3 }=0, \end{aligned}$$

(89)

where $\varOmega =[0,1]\times [0,1]\times [0,1]$.

The analytical solution of this problem is

$$\begin{aligned} u(x)= & {} \left[ \frac{\sinh (\sqrt{2}{\uppi } x_3 )}{\sqrt{2}\uppi }-\frac{\cosh (\sqrt{2}{\uppi } x_3 )}{\sqrt{2}\uppi \tanh (\sqrt{2}\uppi )} \right] \nonumber \\&\times \cos (\uppi x_1 )\cos (\uppi x_2 ). \end{aligned}$$

(90)

For this example, we select $x_3$ as the splitting direction and the uniform node distribution is also adopted. Figures 11–13 show the numerical results obtained with the IEFG method and the DSEFG method along the three axes under the node distribution $11\times 11\times 11$ and $d_{\max } =1.19$. For the IEFG method, the error is 0.0072, and the CPU time is 9.56 s. For the DSEFG method, the error is 0.0043, and the CPU time is 0.613 s. Comparing both methods, the computation accuracy and computation speed of the DSEFG method is higher than IEFG method.

Fig. 12

The results of the DSEFG and IEFG methods along the direction $x_2$

Fig. 13

The results of the DSEFG and IEFG methods along the direction $x_3$

Fig. 14

Node distribution in two-dimensional sub-domain of a half-torus

Fig. 15

The results of the DSEFG and IEFG methods along the direction $x_3$

Fig. 16

The results of the DSEFG and IEFG methods along the radial direction r

4.4 Laplace’s equation with Dirichlet boundary conditions on a half-torus cylinder

As a fourth example, we study Laplace’s equation

$$\begin{aligned} \nabla ^{2}u({{\varvec{x}}})=0,\quad r\in [1,2],\;\theta \in [0,\uppi ],\;x_3 \in [0,1], \end{aligned}$$

(91)

with Dirichlet boundary conditions

$$\begin{aligned}&u(1,\theta ,x_3 )=\sin \theta +x_3 , \end{aligned}$$

(92)

$$\begin{aligned}&u(2,\theta ,x_3 )=x_3 , \end{aligned}$$

(93)

$$\begin{aligned}&u(r,0,x_3 )=x_3 , \end{aligned}$$

(94)

$$\begin{aligned}&u(r,\uppi ,x_3 )=x_3 , \end{aligned}$$

(95)

$$\begin{aligned}&u(r,\theta ,0)=\frac{4}{3}\left( {\frac{1}{r}-\frac{r}{4}} \right) \sin \theta , \end{aligned}$$

(96)

$$\begin{aligned}&u(r,\theta ,1)=\frac{4}{3}\left( {\frac{1}{r}-\frac{r}{4}} \right) \sin \theta +1. \end{aligned}$$

(97)

The analytical solution of this problem is

$$\begin{aligned} u(r,\theta ,x_3 )=\frac{4}{3}\left( {\frac{1}{r}-\frac{r}{4}} \right) \sin \theta +x_3 . \end{aligned}$$

(98)

For this example, the problem domain is divided into 20 equal parts along the $x_3$ direction. $9\times 31$ nodes are distributed on a half-torus domain of two-dimensional problem. Nine nodes are laid along the radial direction r in a 1.1 proportion and 31 nodes are uniformly laid along the angle axis $\theta$ as shown in Fig. 14. It means that the integral node distribution is $9\times 31\times 21$, and $d_{\max } =1.2$, $\alpha = 1 .0\times 10 ^{4}$.

Figures 15–17 show the results obtained using the IEFG method and the DSEFG method. It can be found that the results of two methods are in agreement with the analytical solution. Under similar precision, the CPU time of the IEFG method is 224.57 s, and the one for the DSEFG method is 3.74 s. Then the DSEFG method has greater computational efficiency than the IEFG method.

Fig. 17

The results of the DSEFG and IEFG methods along the angle axis $\theta$

5 Conclusions

This paper presents a new fast meshless method to solve the three-dimensional potential problems. The main idea of the DSEFG method is that a three-dimensional problem can be transformed into a series of two-dimensional problems. We only need to solve a two-dimensional problem in each sub-domain. For two-dimensional problems, the IEFG method is applied, which uses an orthogonal function system with a weight function as the basis functions. It is efficient to avoid an ill-conditioned system of equations. Then, the finite difference method is selected for the splitting direction. From numerical results obtained by the DSEFG method, together with comparisons with analytical solutions and the ones for the IEFG method, we can observe that DSEFG method is efficient to solve three-dimensional potential problems and generally has greater computational precision and higher computation speed than the IEFG method.