Meshless upwind local radial basis function-finite difference technique to simulate the time- fractional distributed-order advection–diffusion equation

Abstract

The main objective in this paper is to propose an efficient numerical formulation for solving the time-fractional distributed-order advection–diffusion equation. First, the distributed-order term has been approximated by the Gauss quadrature rule. In the next, a finite difference approach is applied to approximate the temporal variable with convergence order $\mathcal{O}(\tau ^{2-\alpha })$ as $0<\alpha <1$. Finally, to discrete the spacial dimension, an upwind local radial basis function-finite difference idea has been employed. In the numerical investigation, the effect of the advection coefficient has been studied in terms of accuracy and stability of the proposed difference scheme. At the end, two examples are studied to approve the impact and ability of the numerical procedure.

1 Introduction

The fractional PDEs with distributed-order derivative are solved by some approaches such as multi-fractal memory kernels [37], the matrix approach [35], a novel difference procedure [28], compact difference technique [43], two ADI difference schemes [25], second-order finite difference approximation [53], discontinuous spectral element methods [52], hybrid functions approximation [32], and discontinuous Galerkin method [41].

Recently, Atangana and Baleanu [6] developed a new fractional derivative to describe some questions in the field of fractional calculus. Authors of [7] convoluted Riemann–Liouville–Caputo derivative with the Mittag–Leffler function for the Atangana–Baleanu fractional differential operators. The model of transmission dynamics of vector-borne diseases is proposed in [3] to the concept of fractional differentiation and integration. Authors of [31] considered a new time distributed-order and two-sided space-fractional advection–dispersion equation.

The RBF-FD method has been introduced in [21, 23, 24]. Author of [38] developed a generalization of the RBF-FD method that computes RBF-FD weights in finite-sized neighborhoods around the centers of RBF-FD stencils. The local RBF method has been used for solving some models such as high-dimensional time-fractional convection–diffusion equation [36], the convection-dominated diffusion problems [39], and incompressible viscous Navier–Stokes equations [26].

The time-fractional distributed-order advection–diffusion equation is

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \int \limits _0^1 {w(\alpha )_0^CD_t^\alpha u({\mathbf{x}},t){\text {d}}\alpha } = \Delta u({\mathbf{x}},t) - \nu \cdot \nabla u({\mathbf{x}},t) + f({\mathbf{x}},t),\quad (x,y) = {\mathbf{x}} \in \Omega ,\quad 0 < t \le T,\\ \\ u({\mathbf{x}},0) = \psi ({\mathbf{x}}),\quad (x,y) = {\mathbf{x}} \in \Omega ,\\ \\ u({\mathbf{x}},t) = g({\mathbf{x}},t),\quad (x,y) = {\mathbf{x}} \in \partial \Omega . \end{array} \right. \end{aligned}$$

(1)

Also, for $w{:}[0,1] \rightarrow {\mathbb {R}}$, we have the following conditions:

$$\begin{aligned}&\forall \; \alpha \in [0,1],\quad w(\alpha )> 0,\quad {\mathrm{and}}\quad \nonumber \\&\quad \int \limits _0^1 {w(\alpha ){\text {d}}\alpha } = W > 0. \end{aligned}$$

Furthermore, $_0^CD_t^\alpha$ denotes

$$\begin{aligned} \frac{{{\partial ^\alpha }u(x,y,t)}}{{\partial {t^\alpha }}}= & {} \, _0^CD_t^\alpha u(x,y,t) \nonumber \\= & {} \, \frac{1}{\Gamma (1-\alpha )}\int _{0}^{t}\frac{\partial u(x,s)}{\partial s}\frac{{\text {d}}s}{(t-s)^{\alpha }},\quad \alpha \in (0,1). \end{aligned}$$

(2)

The Legendre wavelet approach has been proposed in [44] for the solution of the linear and nonlinear distributed fractional differential equations. A novel second-order numerical approximation for the Riemann–Liouville tempered fractional derivative is derived in [17] using the tempered Grünwald difference operator and its asymptotic expansion. The numerical solution of distributed-order time-fractional PDEs is studied in [33] based on the mid-point quadrature rule and linear B-spline interpolation. The main aim of [29] is to discuss the properties of the time-tempered fractional derivative, and studying the well-posedness and the Jacobi-predictor–corrector algorithm for the tempered fractional ordinary differential equation. The Keller Box method is used in [34] to spatially discretise the fractional subdiffusion equation. Author of [18] developed fourth-order fractional-compact difference operator to solve the time–space tempered fractional diffusion-wave equation. A new high-order numerical algorithm and its error analysis are developed in [19] for solving the Riesz tempered space-fractional diffusion equation. Authors of [20] developed a class of high-order numerical algorithms for Riesz derivatives based on constructing new generating functions.

The aim of [4, 5] is to prove the existence of the solution to the Cauchy problem for the time distributed-order diffusion equation as well as to calculate it. Authors of [10] proposed diffusion-like equations with time- and space-fractional derivatives of the distributed order for the kinetic description of anomalous diffusion and relaxation phenomena. Authors of [11] provided explicit strong solutions and stochastic analogs for distributed-order time-fractional diffusion equations on bounded domains with Dirichlet boundary conditions. The main aim of [30] is to study the uniqueness and existence solution of the boundary value problems for the generalized time-fractional diffusion equation of distributed order over an open bounded domain. Author of [45] developed efficient algorithms based on the Legendre-tau approximation for one- and two-dimensional fractional Rayleigh–Stokes problems for a generalized second-grade fluid.

The Jacobi–Gauss–Lobatto (J–G–L) collocation approach is used in [9] to solve the distributed-order time- and Riesz space-fractional Schrödinger equation (DOT–RSFSE). Authors of [47] constructed and analyzed a Legendre spectral-collocation method for the numerical solution of distributed-order fractional initial value problems. The main aim of [48] is applying a Legendre collocation method for solving distributed-order fractional optimal control problems. Two efficient spectral algorithms based on the Jacobi–Galerkin methods are proposed in [27] for solving unsteady advection–reaction–diffusion equations with constant and variable coefficients. Authors of [46] derived the generalized necessary conditions for optimal control problems with dynamics described by ordinary distributed-order fractional differential equations (DFDEs) and then they proposed an efficient numerical scheme for solving an unconstrained convex distributed optimal control problem governed by the DFDE. Existence and uniqueness of solutions of a nonlinear tempered fractional boundary value problems are studied in [49]. Author of [50] derived and analyzed an exponentially accurate Jacobi spectral-collocation method for the numerical solution of nonlinear terminal value problems involving the Caputo fractional derivative. Author of [50] proved that the convergence rate for non-smooth solutions can be enhanced using a suitable smoothing transformation, which allows us to adjust a parameter in the solution in view of a priori known regularity of the given data. A Legendre–Jacobi collocation approach is developed in [51] for solving a nonlinear system of two-point boundary value problems with derivative orders.

Author of [1] proposed an error estimate of second-order finite difference scheme for solving the Riesz space distributed-order diffusion equation. The main aim of [13] is to propose a new numerical scheme based on the spectral element procedure for simulating the neutral delay distributed-order fractional damped diffusion-wave equation. The main aim of [2] is to combine the alternating direction implicit approach with the interpolating element-free Galerkin method to solve two-dimensional distributed-order time-fractional diffusion-wave equation. A finite element method has been proposed in [14] for solving the Rayleigh–Stokes problem for a heated generalized second-grade fluid with fractional derivatives. An error estimate has been proposed in [15] to solve the two-dimensional weakly singular integro-partial differential equation with space and time-fractional derivatives based on the finite element/finite difference scheme. Authors of [16] applied the homotopy analysis method to solve nonlinear fractional partial differential equations such as the fractional KdV, K(2, 2), Burgers, BBM-Burgers, cubic Boussinesq, coupled KdV, and Boussinesq-like B(m, n) equations.

In the advection–diffusion equation, there are two important constants, e.g., advection and diffusion parameters [12]. The main difficulty of this equation is when the advection constant is larger than the diffusion parameter in which there are a few numerical procedures that solve the mentioned problems to find an acceptable result. In the current paper, we employ an upwind local RBF-FD technique to overcome the mentioned difficulty. Also, we could solve this equation on the non-rectangular domains.

2 Semi-discrete scheme

To discrete the time variable and integral term, we employ the following notations:

$$\begin{aligned} \begin{array}{l} {t_k} = k\tau ,\quad \tau = \displaystyle \frac{T}{N},\quad k = 0,1, \ldots ,N,\\ \\ {h_\alpha } = \displaystyle \frac{1}{{2J}},\quad {\alpha _l} = 1 + l{h_\alpha },\quad 0 \le l \le 2J. \end{array} \end{aligned}$$

At first, we want to discrete the integral term in the model (1)

Lemma 2.1

[8] The Gaussian–Legendre integration is

$$\begin{aligned} \int \limits _{ - 1}^1 {f(x){\text {d}}x} = \sum \limits _{j = 1}^n {{w_j}f({x_j})} +{E_n}(f),\quad \forall \,f(x)\in C^{\infty }[-1,1], \end{aligned}$$

(3)

where $x_j$ are roots of Legendre polynomial $P_n(x)$ and weights are defined as

$$\begin{aligned} {w_j} = \frac{{ - 2}}{{(n + 1){P_n}'({x_j}){P_{n + 1}}({x_j})}},\quad j = 1,2, \ldots ,n. \end{aligned}$$

(4)

We employ the following notations:

$$\begin{aligned} {u^{n - \frac{1}{2}}} = \displaystyle \frac{1}{2}\left( {{u^n} + {u^{n - 1}}} \right) , \quad {\delta _t}{u^{n - \frac{1}{2}}} = \displaystyle \frac{1}{\tau }\left( {{u^n} - {u^{n - 1}}} \right) , \end{aligned}$$

where $u^n=u(x,y,t_n)$.

Lemma 2.2

[40] Suppose $0<\alpha <1$ and $g(t) \in C^{2}[0,t_{k}]$, it holds that

$$\begin{aligned}&\left| {\frac{1}{{\Gamma (1 - \alpha )}}\int \limits _0^{{t_k}} {\frac{{v'(t)}}{{{{({t_k} - t)}^\alpha }}}} {\text {d}}t - {}^C{{\mathcal {P}}}_t^\alpha (v(t))} \right| \\&\quad \le {C_\alpha }\mathop {\max \mathop {|v''(t)|{\tau ^{2 - \alpha }}}\limits _{} }\limits _{0 \le t \le {t_k}} , \end{aligned}$$

in which $a_{m}=(m+1)^{1-\alpha }-m^{1-\alpha }$ and

$$\begin{aligned} {}^C{{\mathcal {P}}}_t^\alpha (v(t))= & {} \frac{{{\tau ^{ - 1 }}}}{{\Gamma (2 - \alpha )}}\left[ {a_0}v({t_k}) - \sum \limits _{m = 1}^{k - 1} ({a_{k - m - 1}} \right. \\&- \left. {a_{k - m}}) v({t_m}) - {a_{k - 1}}v({t_0}) \phantom {\sum \limits _{m = 1}^{k - 1}}\right] . \end{aligned}$$

Lemma 2.3

[40] For any ${{\mathcal {Q}}} = \left\{ {{{{\mathcal {Q}}}_1},{{{\mathcal {Q}}}_2}, \ldots {{{\mathcal {Q}}}_N}} \right\}$ and q, we obtain

$$\begin{aligned}&\sum \limits _{n = 1}^N \left[ {{a_0}{{{\mathcal {Q}}}_n} - \sum \limits _{k = 1}^{n - 1} {\left( {{a_{n - k - 1}} - {a_{n - k}}} \right) {{{\mathcal {Q}}}_k} - {a_{n - 1}}q} } \right] {{{\mathcal {Q}}}_n} \\&\quad \ge \frac{{t_N^{ - \alpha }}}{2} \tau \sum \limits _{n = 1}^N {{{\mathcal {Q}}}_n^2 - \frac{{t_N^{1 - \alpha }}}{{2(2 - \alpha )}}{q^2},} \quad N = 1,2,3, \ldots . \end{aligned}$$

Let

$$\begin{aligned}&\vartheta ^\alpha (x,y,t) = \frac{1}{{\Gamma (1 - \alpha )}}\int \limits _0^t {\frac{{\partial u(x,y,s)}}{{\partial s}}} \frac{{{\text {d}}s}}{{{{(t - s)}^{\alpha }}}}. \end{aligned}$$

(5)

Then Eq. (1) can be written as follows:

$$\begin{aligned}&\int \limits _0^1 {w(\alpha ){\vartheta ^\alpha }(x,y,t){\text {d}}\alpha } = \Delta u(x,y,t) - \nu \cdot \nabla u(x,y,t) \nonumber \\&\quad + f(x,y,t), \quad (x,y) \in \Omega ,\quad 0 < t \le T. \end{aligned}$$

(6)

If we set

$$\begin{aligned} {\mathcal {J}}(\alpha ,x,y,t) = w(\alpha ){\vartheta ^\alpha }(x,y,t), \end{aligned}$$

(7)

then

$$\begin{aligned} \int \limits _0^1 {{\mathcal {J}}(\alpha ,{\mathbf{x}},t){\text {d}}\alpha } = \Delta u({\mathbf{x}},t) - \nu \cdot \nabla u({\mathbf{x}},t) + f({\mathbf{x}},t). \end{aligned}$$

(8)

Applying Lemma 2.1, we get

$$\begin{aligned}&\displaystyle \int \limits _0^1 {{\mathcal {J}}(\alpha ,x,y,t)} {\text {d}}\alpha \nonumber \\&\quad = \sum \limits _{l = 0}^{{N_q}} {{\omega _l}{\mathcal {J}}({\alpha _l},x,y,t)} - {{\text {e}}_n}{\left. {\frac{{{{\mathcal {J}}^{(2n)}}(\alpha ,x,y,t)}}{{(2n)!}}} \right| _{\alpha = \eta }} \nonumber \\&\quad = \displaystyle \sum \limits _{l = 0}^{{N_q}} {{\omega _l}{\mathcal {J}}({\alpha _l},x,y,t)} + {\mathcal {R}_{{\mathrm{Gauss}}}} \nonumber \\&\quad = \sum \limits _{l = 0}^{{N_q}} {{\omega _l}w({\alpha _l}){\vartheta ^{{\alpha _l}}}(x,y,t)} + {\mathcal {R}}_\alpha ^{n-\frac{1}{2}}, \end{aligned}$$

(9)

in which

$$\begin{aligned} {\mathcal {R}}_{Gauss}= & {} - {{\text {e}}_n}{\left. {\frac{{{{\mathcal {J}}^{(2n)}}(\alpha ,x,y,t)}}{{(2n)!}}} \right| _{\alpha = \eta }},\nonumber \\ {\mathcal {R}}_\alpha ^{n-\frac{1}{2}}= & {} {\mathcal {R}}_{Gauss} + {h_\alpha }\displaystyle \sum \limits _{l = 0}^{N_q} {{\omega _l}w({\alpha _l})\mathcal{R}_1^{{\alpha _l}}}, \end{aligned}$$

(10)

and also

$$\begin{aligned} {\mathcal {R}}_1^{{\alpha _l}} = {C_{{\alpha _l}}}\mathop {\max \left| {\frac{{{\partial ^2}v(x,y,t)}}{{\partial {t^2}}}} \right| {\tau ^{3 - {\alpha _l}}}}\limits _{0 \le t \le {t_n}}. \end{aligned}$$

At this moment, we know

$$\begin{aligned} \left| {{\mathcal {R}_{Gauss}}} \right| \le {C_1}{e_n},\quad \left| {\mathcal {R}_1^{{\alpha _l}}} \right| \le {C_2}{\tau ^{3 - {\alpha _l}}}, \end{aligned}$$

(11)

then we have

$$\begin{aligned} \left| {\mathcal {R}_\alpha ^{n - {\textstyle {1 \over 2}}}} \right|= & {} \left| {{\mathcal {R}_{Gauss}} - \sum \limits _{l = 0}^{{N_q}} {{\omega _l}w({\alpha _l})\mathcal {R}_1^{{\alpha _l}}} } \right| \nonumber \\\le & {} \left| {{\mathcal {R}_{Gauss}}} \right| + \left| {\sum \limits _{l = 0}^{{N_q}} {{\omega _l}w({\alpha _l})\mathcal {R}_1^{{\alpha _l}}} } \right| \le C({{\text {e}}_n} + {\tau ^{1 + \frac{1}{{2{N_q}}}}}). \end{aligned}$$

(12)

Now, substituting (9) in (8), we obtain

$$\begin{aligned} \sum \limits _{l = 0}^{{N_q}} {{\omega _l}w({\alpha _l}){\vartheta ^{{\alpha _l}}}} + {\mathcal {R}_{{\mathrm{Gauss}}}} = \Delta u - \nu \cdot \nabla u + f + \mathcal {E}_\alpha ^{n - \frac{1}{2}}, \end{aligned}$$

(13)

as Lemma 2.2 gives

$$\begin{aligned}&\displaystyle \sum \limits _{l = 0}^{N_q} \left\{ {\omega _l}w({\alpha _l})\frac{1}{{\Gamma (2 - {\alpha _l})\tau }}\left\{ a_0^{{\alpha _l}}{u^{n - \frac{1}{2}}} - \sum \limits _{k = 1}^{n - 1} \left( a_{n - k - 1}^{{\alpha _l}} \right. \right. \right. \nonumber \\&\qquad \left. \left. \left. - a_{n - k}^{{\alpha _l}} \right) {u^{k - \frac{1}{2}}} - a_{n - 1}^{{\alpha _l}}\varphi \right\} \right\} \nonumber \\&\quad = \Delta u(x,y,{t_{n - \frac{1}{2}}}) - \nu \cdot \nabla u(x,y,{t_{n - \frac{1}{2}}})\nonumber \\&\qquad + f(x,y,{t_{n - \frac{1}{2}}})+ {{\mathcal {E}}}_\alpha ^{n-\frac{1}{2}}, \end{aligned}$$

(14)

in which there exists a positive constant C such that

$$\begin{aligned} {{\mathcal {E}}}_\alpha ^{n-\frac{1}{2}}<C\tau ^{3-\alpha _{max}}. \end{aligned}$$

(15)

Omitting the small term ${{\mathcal {E}}}_\alpha ^{n-\frac{1}{2}}$ in Eq. (14), we can get

$$\begin{aligned}&\displaystyle \sum \limits _{l = 0}^{{N_q}} \left\{ {\omega _l}w({\alpha _l})\frac{1}{{\Gamma (2 - {\alpha _l}){\tau }}}\left\{ a_0^{{\alpha _l}}{U^{n - \frac{1}{2}}} - \sum \limits _{k = 1}^{n - 1} \left( a_{n - k - 1}^{{\alpha _l}} \right. \right. \right. \nonumber \\&\quad \left. \left. \left. - a_{n - k}^{{\alpha _l}} \right) {U^{k - \frac{1}{2}}} - a_{n - 1}^{{\alpha _l}}\varphi \phantom {\sum \limits _{k = 1}^{n - 1}}\right\} \phantom {\sum \limits _{k = 1}^{n - 1}}\right\} \nonumber \\&\quad = \Delta U^{n - \frac{1}{2}} - \nu \cdot \nabla U^{n - \frac{1}{2}} + f(x,y,{t_{n - \frac{1}{2}}}). \end{aligned}$$

(16)

2.1 Stability and convergence of the semi-discrete scheme

In the current section, we study the stability and convergence of the time-discrete scheme.

Theorem 2.4

Let $U^n\in H^1_0(\Omega )$. Then difference scheme (16) is unconditionally stable.

Proof

Multiplying both sides of Eq. (16) by ${U^{n - \frac{1}{2}}}$ and integrating on $\Omega$ give

$$\begin{aligned}&\displaystyle \sum \limits _{l = 0}^{{N_q}} \left\{ {\omega _l}w({\alpha _l})\frac{1}{{\Gamma (2 - {\alpha _l}){\tau }}}\left\{ a_0^{{\alpha _l}}\left\| {{U^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2 - \sum \limits _{k = 1}^{n - 1} \left( a_{n - k - 1}^{{\alpha _l}}\right. \right. \right. \nonumber \\&\qquad \left. \left. \left. - a_{n - k}^{{\alpha _l}} \right) \left( {{U^{k - \frac{1}{2}}},{U^{n - \frac{1}{2}}}} \right) - a_{n - 1}^{{\alpha _l}}\left( {\varphi ,{U^{n - \frac{1}{2}}}} \right) \phantom {\sum \limits _{k = 1}^{n - 1}}\right\} \phantom {\sum \limits _{k = 1}^{n - 1}}\right\} \nonumber \\&\quad = \left( {\Delta {U^{n - \frac{1}{2}}},{U^{n - \frac{1}{2}}}} \right) - \left( {\nu \cdot \nabla {U^{n - \frac{1}{2}}},{U^{n - \frac{1}{2}}}} \right) \nonumber \\&\qquad + \left( {f(x,y,{t_{n - \frac{1}{2}}}),{U^{n - \frac{1}{2}}}} \right) . \end{aligned}$$

(17)

By simplification the above relation, we can get

$$\begin{aligned}&\displaystyle \sum \limits _{l = 0}^{{N_q}} \left\{ \frac{{\omega _l}w({\alpha _l})}{{\Gamma (2 - {\alpha _l}){\tau }}}\left\{ a_0^{{\alpha _l}}\left\| {{U^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^{} - \sum \limits _{k = 1}^{n - 1} \left( a_{n - k - 1}^{{\alpha _l}} \right. \right. \right. \nonumber \\&\qquad \left. \left. \left. - a_{n - k}^{{\alpha _l}} \right) \left\| {{U^{k - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^{} - a_{n - 1}^{{\alpha _l}}{{\left\| \varphi \right\| }_{{L^2}(\Omega )}} \right\} \right\} {\left\| {{U^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}}\nonumber \\&\quad + \left\| {\nabla {U^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2 \le - \left( {\nu \cdot \nabla {U^{n - \frac{1}{2}}},{U^{n - \frac{1}{2}}}} \right) \nonumber \\&\quad + \left( {f(x,y,{t_{n - \frac{1}{2}}}),{U^{n - \frac{1}{2}}}} \right) . \end{aligned}$$

(18)

Applying Lemma 2.3 for the left-hand side of Eq. (18), results

$$\begin{aligned}&\displaystyle \sum \limits _{l = 0}^{{N_q}} {\omega _l}w({\alpha _l})\left\{ \frac{{t_N^{ - {\alpha _l}}}}{{2\Gamma (2 - {\alpha _l})}}\sum \limits _{n = 1}^N {\left\| {{U^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} \right. \nonumber \\&\quad \left. - \frac{{t_N^{1 - {\alpha _l}}}}{{\Gamma (2 - {\alpha _l})(1 - {\alpha _l})}}\left\| \varphi \right\| _{{L^2}(\Omega )}^2 \right\} \nonumber \\&\quad + \displaystyle \sum \limits _{n = 1}^N {\left\| {\nabla {U^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} \le - \sum \limits _{n = 1}^N {\left( {\nu \cdot \nabla {U^{n - \frac{1}{2}}},{U^{n - \frac{1}{2}}}} \right) } \nonumber \\&\quad + \sum \limits _{n = 1}^N {\left( {f\left( x,y,{t_{n - \frac{1}{2}}}\right) ,{U^{n - \frac{1}{2}}}} \right) } . \end{aligned}$$

(19)

The Cauchy–Schwarz and Young’s inequalities, yield

$$\begin{aligned}&\sum \limits _{l = 0}^{{N_q}} {\sum \limits _{n = 1}^N {\frac{{{\omega _l}w({\alpha _l})t_N^{ - {\alpha _l}}}}{{2\Gamma (2 - {\alpha _l})}}\left\| {{U^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} }\nonumber \\&\quad - \sum \limits _{l = 0}^{{N_q}} {\frac{{{\omega _l}w({\alpha _l})t_N^{1 - {\alpha _l}}}}{{\Gamma (2 - {\alpha _l})(1 - {\alpha _l})}}\left\| \varphi \right\| _{{L^2}(\Omega )}^2} \nonumber \\&\quad + \sum \limits _{n = 1}^N {\left\| {\nabla {U^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} \le \sum \limits _{l = 0}^{{N_q}} {\sum \limits _{n = 1}^N {\frac{{\Gamma (2 - {\alpha _l})}}{{{\omega _l}w({\alpha _l})t_N^{ - {\alpha _l}}}}\left\| {\nu \cdot \nabla {U^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} } \nonumber \\&\quad + \sum \limits _{l = 0}^{{N_q}} {\sum \limits _{n = 1}^N {\frac{{{\omega _l}w({\alpha _l})t_N^{ - {\alpha _l}}}}{{4\Gamma (2 - {\alpha _l})}}\left\| {{U^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} } \nonumber \\&\quad + \sum \limits _{l = 0}^{{N_q}} {\sum \limits _{n = 1}^N {\frac{{\Gamma (2 - {\alpha _l})}}{{{\omega _l}w({\alpha _l})t_N^{ - {\alpha _l}}}}\left\| {{f^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} } \nonumber \\&\quad + \sum \limits _{l = 0}^{{N_q}} {\sum \limits _{n = 1}^N {\frac{{{\omega _l}w({\alpha _l})t_N^{ - {\alpha _l}}}}{{4\Gamma (2 - {\alpha _l})}}\left\| {{U^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} }. \end{aligned}$$

(20)

After simplification the above inequality, we can write

$$\begin{aligned}&\sum \limits _{n = 1}^N {\left\| {\nabla {U^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} \nonumber \\&\quad \le \sum \limits _{l = 0}^{{N_q}} {\sum \limits _{n = 1}^N {\frac{{\Gamma (2 - {\alpha _l})}}{{{\omega _l}w({\alpha _l})t_N^{ - {\alpha _l}}}}\left\| {\nu \cdot \nabla {U^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} } \nonumber \\&\qquad + \sum \limits _{l = 0}^{{N_q}} {\sum \limits _{n = 1}^N {\frac{{\Gamma (2 - {\alpha _l})}}{{{\omega _l}w({\alpha _l})t_N^{ - {\alpha _l}}}}\left\| {{f^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} } \nonumber \\&\qquad + \sum \limits _{l = 0}^{{N_q}} {\frac{{{\omega _l}w({\alpha _l})t_N^{1 - {\alpha _l}}}}{{\Gamma (2 - {\alpha _l})(1 - {\alpha _l})}}\left\| \varphi \right\| _{{L^2}(\Omega )}^2}, \end{aligned}$$

(21)

or equivalently

$$\begin{aligned} \left\| {\nabla {U^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2\le & {} \sum \limits _{l = 0}^{{N_q}} {\sum \limits _{j = 1}^n {\frac{{\Gamma (2 - {\alpha _l})}}{{{\omega _l}w({\alpha _l})t_n^{ - {\alpha _l}}}}\left\| {\nu \cdot \nabla {U^{j - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} } \nonumber \\&+ \sum \limits _{l = 0}^{{N_q}} {\sum \limits _{j = 1}^n {\frac{{\Gamma (2 - {\alpha _l})}}{{{\omega _l}w({\alpha _l})t_n^{ - {\alpha _l}}}}\left\| {{f^{j - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} } \nonumber \\&+ \sum \limits _{l = 0}^{{N_q}} {\frac{{{\omega _l}w({\alpha _l})t_n^{1 - {\alpha _l}}}}{{\Gamma (2 - {\alpha _l})(1 - {\alpha _l})}}\left\| \varphi \right\| _{{L^2}(\Omega )}^2} . \end{aligned}$$

(22)

The use of Grönwall’s inequality, gives

$$\begin{aligned}&\left\| {\nabla {U^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2\nonumber \\&\quad \le \left[ {\sum \limits _{l = 0}^{{N_q}} {\sum \limits _{j = 1}^n {\frac{{\Gamma (2 - {\alpha _l})}}{{{\omega _l}w({\alpha _l})t_n^{ - {\alpha _l}}}}\left\| {{f^{j - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} } } \right. \nonumber \\&\qquad +\left. { \sum \limits _{l = 0}^{{N_q}} {\frac{{{\omega _l}w({\alpha _l})t_n^{1 - {\alpha _l}}}}{{\Gamma (2 - {\alpha _l})(1 - {\alpha _l})}}\left\| \varphi \right\| _{{L^2}(\Omega )}^2} } \right] \exp \left( {\sum \limits _{l = 0}^{{N_q}} {\frac{{\nu \Gamma (2 - {\alpha _l})}}{{{\omega _l}w({\alpha _l})}}\sum \limits _{j = 1}^n {t_n^{{\alpha _l}}} } } \right) \nonumber \\&\quad \le \left[ {\sum \limits _{l = 0}^{{N_q}} {\sum \limits _{j = 1}^n {\frac{{\Gamma (2 - {\alpha _l})}}{{{\omega _l}w({\alpha _l})t_n^{ - {\alpha _l}}}}\left\| {{f^{j - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} } } \right. \nonumber \\&\qquad +\left. { \sum \limits _{l = 0}^{{N_q}} {\frac{{{\omega _l}w({\alpha _l})t_n^{1 - {\alpha _l}}}}{{\Gamma (2 - {\alpha _l})(1 - {\alpha _l})}}\left\| \varphi \right\| _{{L^2}(\Omega )}^2} } \right] \exp \left( {\sum \limits _{l = 0}^{{N_q}} {\frac{{\nu \Gamma (2 - {\alpha _l})}}{{{\omega _l}w({\alpha _l})}}\frac{{n\tau }}{{1 - n\tau }}} } \right) , \end{aligned}$$

(23)

also, using the Poincare inequality we can get the following relation:

$$\begin{aligned} \left\| {{U^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2\le & {} {C_\Omega }\left\| {\nabla {U^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2 \nonumber \\\le & {} C\left[ \sum \limits _{l = 0}^{{N_q}} {\sum \limits _{j = 1}^n {\frac{{\Gamma (2 - {\alpha _l})}}{{{\omega _l}w({\alpha _l})t_n^{ - {\alpha _l}}}}\left\| {{f^{j - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} } \right. \nonumber \\&\left. + \sum \limits _{l = 0}^{{N_q}} {\frac{{{\omega _l}w({\alpha _l})t_n^{1 - {\alpha _l}}}}{{\Gamma (2 - {\alpha _l})(1 - {\alpha _l})}}\left\| \varphi \right\| _{{L^2}(\Omega )}^2} \right] . \end{aligned}$$

(24)

Finally, we have the following inequality:

$$\begin{aligned} \left\| {{U^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^{}\le & {} {C_\Omega }\left[ \sum \limits _{l = 0}^{{N_q}} {\sum \limits _{j = 1}^n {\frac{{\Gamma (2 - {\alpha _l})}}{{{\omega _l}w({\alpha _l})t_n^{ - {\alpha _l}}}}\left\| {{f^{j - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^{}} } \right. \nonumber \\&\left. + \sum \limits _{l = 0}^{{N_q}} {\frac{{{\omega _l}w({\alpha _l})t_n^{1 - {\alpha _l}}}}{{\Gamma (2 - {\alpha _l})(1 - {\alpha _l})}}\left\| \varphi \right\| _{{L^2}(\Omega )}^{}} \right] , \end{aligned}$$

(25)

which completes the proof. $\square$

Theorem 2.5

Let $u^n$ and $U^n$ be solutions of Eqs. (14) and (16), respectively, and they belong to $H^1_0(\Omega )$. Then, difference scheme (16) is convergent with convergence order $O({\tau ^{\frac{3}{2}}})$.

Proof We define the following notation:

$$\begin{aligned} {\Phi ^n} = {u^n} - {U^n}. \end{aligned}$$

Subtracting Eq. (16) from Eq. (14), gives

$$\begin{aligned}&\sum \limits _{l = 0}^{{N_q}} \left\{ {\omega _l}w({\alpha _l})\frac{1}{{\Gamma (2 - {\alpha _l})\tau }}\left\{ a_0^{{\alpha _l}}{\Phi ^{n - \frac{1}{2}}} - \sum \limits _{k = 1}^{n - 1} \left( a_{n - k - 1}^{{\alpha _l}} \right. \right. \right. \nonumber \\&\quad \left. \left. \left. - a_{n - k}^{{\alpha _l}} \right) {\Phi ^{k - \frac{1}{2}}} \phantom {\sum \limits _{k = 1}^{n - 1}}\right\} \phantom {\sum \limits _{k = 1}^{n - 1}}\right\} = \Delta {\Phi ^{n - \frac{1}{2}}} - \nu \cdot \nabla {\Phi ^{n - \frac{1}{2}}} + {\mathcal {E}}_\alpha ^{n - \frac{1}{2}}. \end{aligned}$$

(26)

Multiplying both sides of Eq. (26) by ${\Phi ^{n - \frac{1}{2}}}$ and integrating on $\Omega$ result in

$$\begin{aligned}&\displaystyle \sum \limits _{l = 0}^{{N_q}} \left\{ {\omega _l}w({\alpha _l})\frac{1}{{\Gamma (2 - {\alpha _l})\tau }}\left\{ a_0^{{\alpha _l}}\left\| {{\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2 \right. \right. \nonumber \\&\qquad \left. \left. - \displaystyle \sum \limits _{k = 1}^{n - 1} {\left( {a_{n - k - 1}^{{\alpha _l}} - a_{n - k}^{{\alpha _l}}} \right) \left( {{\Phi ^{k - \frac{1}{2}}},{\Phi ^{n - \frac{1}{2}}}} \right) } \right\} \right\} \nonumber \\&\quad = - \left( {\nabla {\Phi ^{n - \frac{1}{2}}},\nabla {\Phi ^{n - \frac{1}{2}}}} \right) - \left( {\nu \cdot \nabla {\Phi ^{n - \frac{1}{2}}},{\Phi ^{n - \frac{1}{2}}}} \right) \nonumber \\&\qquad + \left( {{{\mathcal {E}}}_\alpha ^{n - \frac{1}{2}},{\Phi ^{n - \frac{1}{2}}}} \right) , \end{aligned}$$

(27)

and also, we can get

$$\begin{aligned}&\displaystyle \sum \limits _{l = 0}^{{N_q}} \left\{ {\omega _l}w({\alpha _l})\frac{1}{{\Gamma (2 - {\alpha _l})\tau }}\left\{ a_0^{{\alpha _l}}{{\left\| {{\Phi ^{n - \frac{1}{2}}}} \right\| }_{{L^2}(\Omega )}} \right. \right. \nonumber \\&\quad \left. \left. - \displaystyle \sum \limits _{k = 1}^{n - 1} \left( {a_{n - k - 1}^{{\alpha _l}} - a_{n - k}^{{\alpha _l}}} \right) {{\left\| {{\Phi ^{k - \frac{1}{2}}}} \right\| }_{{L^2}(\Omega )}} \right\} \right\} {\left\| {{\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}}\nonumber \\&\quad + \left\| {\nabla {\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2 \le \left\| {v \cdot \nabla {\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^{}\left\| {{\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^{} \nonumber \\&\quad + \left( {{{\mathcal {E}}}_\alpha ^{n - \frac{1}{2}},{\Phi ^{n - \frac{1}{2}}}} \right) . \end{aligned}$$

(28)

Summing the above relation for n from $n=1$ to $n=N$ results in

$$\begin{aligned}&\displaystyle \sum \limits _{l = 0}^{{N_q}} \phantom {\sum \limits _{k = 1}^{n - 1}}\left\{ {\omega _l}w({\alpha _l})\frac{1}{{\Gamma (2 - {\alpha _l})\tau }}\displaystyle \sum \limits _{n = 1}^N \phantom {\sum \limits _{k = 1}^{n - 1}}\left\{ a_0^{{\alpha _l}}{{\left\| {{\Phi ^{n - \frac{1}{2}}}} \right\| }_{{L^2}(\Omega )}} \right. \right. \nonumber \\&\quad \left. \left. - \sum \limits _{k = 1}^{n - 1} {\left( {a_{n - k - 1}^{{\alpha _l}} - a_{n - k}^{{\alpha _l}}} \right) {{\left\| {{\Phi ^{k - \frac{1}{2}}}} \right\| }_{{L^2}(\Omega )}}} \right\} \right\} {\left\| {{\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}}\nonumber \\&\quad +\displaystyle \sum \limits _{n = 1}^N {\left\| {\nabla {\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} \le \sum \limits _{n = 1}^N {\left\| {v \cdot \nabla {\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^{}\left\| {{\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^{}} \nonumber \\&\quad + \sum \limits _{n = 1}^N {\left( {{{\mathcal {E}}}_\alpha ^{n - \frac{1}{2}},{\Phi ^{n - \frac{1}{2}}}} \right) } . \end{aligned}$$

(29)

Employing Lemma 2.3 for the left-hand side of Eq. (29) gives

$$\begin{aligned}&\displaystyle \sum \limits _{l = 0}^{{N_q}} {\sum \limits _{n = 1}^N {\frac{{{\omega _l}w({\alpha _l})t_N^{ - {\alpha _l}}}}{{2\Gamma (2 - {\alpha _l})}}\left\| {{\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} } + \sum \limits _{n = 1}^N {\left\| {\nabla {\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} \nonumber \\&\quad \displaystyle \le \sum \limits _{l = 0}^{{N_q}} \left\{ {\omega _l}w({\alpha _l})\frac{1}{{\Gamma (2 - {\alpha _l})\tau }}\sum \limits _{n = 1}^N \left\{ a_0^{{\alpha _l}}{{\left\| {{\Phi ^{n - \frac{1}{2}}}} \right\| }_{{L^2}(\Omega )}} \right. \right. \nonumber \\&\qquad \left. \left. - \sum \limits _{k = 1}^{n - 1} {\left( {a_{n - k - 1}^{{\alpha _l}} - a_{n - k}^{{\alpha _l}}} \right) {{\left\| {{\Phi ^{k - \frac{1}{2}}}} \right\| }_{{L^2}(\Omega )}}} \right\} \right\} {\left\| {{\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}}\nonumber \\&\qquad + \displaystyle \sum \limits _{n = 1}^N {\left\| {\nabla {\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} \le \sum \limits _{n = 1}^N {\left\| {v \cdot \nabla {\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^{}\left\| {{\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^{}} \nonumber \\&\qquad + \sum \limits _{n = 1}^N {\left( {{{\mathcal {E}}}_\alpha ^{n - \frac{1}{2}},{\Phi ^{n - \frac{1}{2}}}} \right) } . \end{aligned}$$

(30)

Using the Cauchy–Schwarz and Young’s inequalities, the following relation can be constructed:

$$\begin{aligned}&\sum \limits _{l = 0}^{{N_q}} {\sum \limits _{n = 1}^N {\frac{{{\omega _l}w({\alpha _l})t_N^{ - {\alpha _l}}}}{{2\Gamma (2 - {\alpha _l})}}\left\| {{\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} } + \sum \limits _{n = 1}^N {\left\| {\nabla {\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} \nonumber \\&\quad \le \sum \limits _{n = 1}^N {\frac{{2\Gamma (2 - {\alpha _l})}}{{{\omega _l}w({\alpha _l})t_N^{ - {\alpha _l}}}}\left\| {v \cdot \nabla {\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2}\nonumber \\&\qquad + \sum \limits _{l = 0}^{{N_q}} {\sum \limits _{n = 1}^N {\frac{{{\omega _l}w({\alpha _l})t_N^{ - {\alpha _l}}}}{{4\Gamma (2 - {\alpha _l})}}\left\| {{\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} } \nonumber \\&\qquad + \sum \limits _{l = 0}^{{N_q}} {\sum \limits _{n = 1}^N {\frac{{2\Gamma (2 - {\alpha _l})}}{{{\omega _l}w({\alpha _l})t_N^{ - {\alpha _l}}}}\left\| {{{\mathcal {E}}}_\alpha ^{n - \frac{1}{2}}} \right\| _{{L^2}(\Omega )}^2} } \nonumber \\&\qquad + \sum \limits _{l = 0}^{{N_q}} {\sum \limits _{n = 1}^N {\frac{{{\omega _l}w({\alpha _l})t_N^{ - {\alpha _l}}}}{{4\Gamma (2 - {\alpha _l})}}\left\| {{\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} } . \end{aligned}$$

(31)

Simplifying the above relation yields

$$\begin{aligned}&\sum \limits _{n = 1}^N {\left\| {\nabla {\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} \le \sum \limits _{n = 1}^N {\frac{{2v\Gamma (2 - {\alpha _l})}}{{{\omega _l}w({\alpha _l})t_N^{ - {\alpha _l}}}}\left\| {\nabla {\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} \nonumber \\&\quad + \sum \limits _{l = 0}^{{N_q}} {\sum \limits _{n = 1}^N {\frac{{2\Gamma (2 - {\alpha _l})}}{{{\omega _l}w({\alpha _l})t_N^{ - {\alpha _l}}}}\left\| {{{\mathcal {E}}}_\alpha ^{n - \frac{1}{2}}} \right\| _{{L^2}(\Omega )}^2} }, \end{aligned}$$

(32)

or equivalently

$$\begin{aligned}&\left\| {\nabla {\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2 \le \sum \limits _{j = 1}^n {\left\| {\nabla {\Phi ^{j - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} \nonumber \\&\quad \le \sum \limits _{j = 1}^n {\frac{{2v\Gamma (2 - {\alpha _l})}}{{{\omega _l}w({\alpha _l})t_N^{ - {\alpha _l}}}}\left\| {\nabla {\Phi ^{j - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} \nonumber \\&\qquad + \sum \limits _{l = 0}^{{N_q}} {\sum \limits _{j = 1}^n {\frac{{2\Gamma (2 - {\alpha _l})}}{{{\omega _l}w({\alpha _l})t_n^{ - {\alpha _l}}}}\left\| {{{\mathcal {E}}}_\alpha ^{j - \frac{1}{2}}} \right\| _{{L^2}(\Omega )}^2} }. \end{aligned}$$

(33)

From relation (15), we can conclude the following estimates:

$$\begin{aligned} \left\| {\nabla {\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2\le & {} \sum \limits _{j = 1}^n {\left\| {\nabla {\Phi ^{j - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} \nonumber \\\le & {} \sum \limits _{j = 1}^n {\frac{{2v\Gamma (2 - {\alpha _l})}}{{{\omega _l}w({\alpha _l})t_N^{ - {\alpha _l}}}}\left\| {\nabla {\Phi ^{j - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} \nonumber \\&+ \sum \limits _{l = 0}^{{N_q}} {\sum \limits _{j = 1}^n {\frac{{2\Gamma (2 - {\alpha _l})}}{{{\omega _l}w({\alpha _l})t_n^{ - {\alpha _l}}}}\left\| {{{\mathcal {E}}}_\alpha ^{j - \frac{1}{2}}} \right\| _{{L^2}(\Omega )}^2} } \nonumber \\\le & {} \sum \limits _{j = 1}^n {\frac{{2v\Gamma (2 - {\alpha _l})}}{{{\omega _l}w({\alpha _l})t_N^{ - {\alpha _l}}}}\left\| {\nabla {\Phi ^{j - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} \nonumber \\&+ \sum \limits _{l = 0}^{{N_q}} {\frac{{2C{\left( {{\tau ^{3 - {\alpha _{max}}}}} \right) ^2} \Gamma (2 - {\alpha _l})}}{{{\omega _l}w({\alpha _l})t_n^{ - {\alpha _l}}}}} \nonumber \\\le & {} \sum \limits _{j = 1}^n {\frac{{2v\Gamma (2 - {\alpha _l})}}{{{\omega _l}w({\alpha _l})t_N^{ - {\alpha _l}}}}\left\| {\nabla {\Phi ^{j - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} \nonumber \\&+ C({\alpha _{\max }},\omega )n{\left( {{\tau ^{3 - {\alpha _{max}}}}} \right) ^2}.\end{aligned}$$

(34)

Multiplying $\tau$ on both sides of the above relation and applying the Grönwall’s inequality, we arrive at

$$\begin{aligned}&\tau \left\| {\nabla {\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2 \nonumber \\&\quad \le \tau \sum \limits _{j = 1}^n {\frac{{2v\Gamma (2 - {\alpha _l})}}{{{\omega _l}w({\alpha _l})t_n^{ - {\alpha _l}}}}\left\| {\nabla {\Phi ^{j - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^2} \nonumber \\&\qquad + C({\alpha _{\max }},\omega )T{\left( {{\tau ^{3 - {\alpha _{max}}}}} \right) ^2} \nonumber \\&\quad \le C({\alpha _{\max }},\omega )T{{\left( {{\tau ^{3 - {\alpha _{max}}}}} \right) ^2}}\exp \left( {\tau \sum \limits _{j = 1}^n {\frac{{2v\Gamma (2 - {\alpha _l})}}{{{\omega _l}w({\alpha _l})t_n^{ - {\alpha _l}}}}} } \right) \nonumber \\&\quad \le {C^*}({\alpha _{\max }},\omega )T{\left( {{\tau ^{3 - {\alpha _{max}}}}} \right) ^2}. \end{aligned}$$

(35)

Finally, we can obtain the following bound:

$$\begin{aligned} \tau \left\| {{\Phi ^{n - \frac{1}{2}}}} \right\| _{{L^2}(\Omega )}^{} \le \sqrt{{C^*}({\alpha _{\max }},\omega )T} {\tau ^{3-\alpha _{\max }}}. \end{aligned}$$

(36)

$\square$

3 Radial basis function approximation

The main advantage of the mesh-free methods is that they are not dependent on any mesh or element. The mesh-free methods are related to a set of scattered data points. Thus, we can consider any geometry as a computational domain. One of the mesh-free techniques is the RBF collocation procedure. Thus, we explain some basic concepts.

Definition 3.1

[42] A symmetric function $\phi \in {\mathbb {R}}^d\times {\mathbb {R}}^d\longrightarrow {\mathbb {R}}$ is so-called strictly conditionally positive definite of order m, if for all sets $X=\{x_1,\ldots ,x_N\}\subset {\mathbb {R}}^d$, and all vectors $c\in {\mathbb {R}}^d$ satisfying

$$\begin{aligned} \displaystyle \sum \limits _{i = 1}^N {{c _i}p({x_i})} = 0, \end{aligned}$$

as for $p\in {\mathbb {P}}_{m-1}^d$

$$\begin{aligned} {c ^T}Ac = \sum \limits _{i = 1}^N {\sum \limits _{j = 1}^N {{c _i}{\lambda _j}\phi ({x_i} - {x_j}),} } \end{aligned}$$

is positive, whenever $c \ne 0$.

Let $\phi$ be a strictly conditionally positive definite of order m, then the interpolation of a continuous function $f:{\mathbb {R}}^d\longrightarrow {\mathbb {R}}$ on a set $X=\{x_1,\ldots ,x_N\}$ is

$$\begin{aligned} {{\mathcal {P}}}f(x) = \sum \limits _{i = 1}^N {{c_i}\phi (x - {x_i})} + \sum \limits _{j = 1}^l {{\eta _j}{p_j}(x)} , \end{aligned}$$

such as $l = ( \begin{array}{l} d + m - 1\\ \,\,\,\,m - 1 \end{array} )$ and $\{p_1,p_2,\ldots ,p_l\}$ is a basis of ${\mathbb {P}}_{m-1}^d$ . We want to find $N+l$ unknown coefficients $c _i$ and $\eta _j$ as

$$\begin{aligned} \mathcal {P}f(x_i)=f_i,\quad i=1,\ldots ,N, \end{aligned}$$

and

$$\begin{aligned} \displaystyle \sum \limits _{i = 1}^N {{c _i}{p_j}({x_i})} = 0,\quad 1 \le j \le l. \end{aligned}$$

Definition 3.2

[42] The density of X in $\Omega$ is the number

$$\begin{aligned} h = h_{X, \Omega} = \mathop {\sup }\limits _{x \in \Omega } \mathop {\min }\limits _{{x_j} \in X} \left\| {x - {x_j}} \right\| . \end{aligned}$$

3.1 Preliminary for local meshless collocation method

The local interpolation concept is as follows: [23, 24]

$$\begin{aligned} {\mathcal {P}_m}f( x ) = \sum \limits _{j \in {\mathcal {I}_i}} {{{\vec {\lambda } }_j}\phi \left( {\left\| { x - {{ y }_j}} \right\| } \right) } , \end{aligned}$$

(37)

in which

• 1. y is a set of center points,

• 2. $\mathcal {I}_i$ is support domain of ith node,

• 3. $\vec {\lambda }$ is the unknown coefficient that must be calculated.

Employing the interpolation condition yields [23, 24]

$$\begin{aligned} {\mathcal {P}_m}f({ x _j}) = f({ x _j}). \end{aligned}$$

(38)

The vector-matrix form of Eq. (38) is

$$\begin{aligned} {\mathbf{M}}\vec {\lambda } = {\mathbf{F}}, \end{aligned}$$

(39)

in which

• ${\mathbf{F}} = {\left[ {f({x_1}),f({x_2}), \ldots ,f({x_{\left| {{{{\mathcal {I}}}_i}} \right| }})} \right] ^\mathrm{T}},$

• ${{\mathbf{M}}_{jk}} = \phi \left( {{{\left\| {{{x}_j} - {{x}_k}} \right\| }_2}} \right) ,\quad j,k \in {\mathcal {I}_i}.$

The local RBF operator can be introduced [23, 24]

$$\begin{aligned} \mathcal {L}f({x}) = \displaystyle \sum \limits _{j \in {\mathcal {I}_i}} {{{\lambda } _j}\mathcal {L}\psi \left( {{{\left\| {{x} - {{y}_j}} \right\| }_2}} \right) }. \end{aligned}$$

(40)

Also, we can write

$$\begin{aligned} \mathcal {L}f(x) = {\Lambda ^T}\vec {\lambda }, \end{aligned}$$

(41)

in which

$$\begin{aligned} {\left( \Lambda \right) _i} = \phi \left( {{{\left\| {x - {y_i}} \right\| }_2}} \right) ,\quad i \in {\mathcal {I}_i}. \end{aligned}$$

(42)

Thus, Eqs. (39) and (41) result [23, 24]

$$\begin{aligned} {\left. {\mathcal {L}f(\vec {x})} \right| _{{\mathcal {I}_i}}} = {\left. {\left( {{\Lambda ^T}{{\mathbf {B}}^{ - 1}}} \right) {\mathbf {f}}} \right| _{{\mathcal {I}_i}}} = \left( {{\vec {w}_i}} \right) {\mathbf {f}}, \end{aligned}$$

(43)

in which $\vec {w}_i$ is the stencil weights at RBFs center i.

3.2 The meshless local RBF-FD (LRBF-FD) technique

Let arbitrary points $(x_i,y_i)\in \Omega$ be scattered in the computational domain ${\bar{\Omega }}$. We can consider a support domain including $n_i$ nodes for each point $(x_i,y_i)\in \Omega$ as is depicted in Fig. 1. According to the previous section, the weight coefficients at each local domain can be calculated as

$$\begin{aligned}&{\left. {\frac{{{\partial ^m}v(x,y)}}{{\partial {x^m}}}} \right| _{(x,y) = ({x_i},{y_i})}} = \sum \limits _{j = 0}^{{n_i}} {\rho _{i,j}^{m,x}v(x_j^i,y_j^i)}, \nonumber \\&\quad i = 0,1,2, \ldots ,N. \end{aligned}$$

(44)

Fig. 1

Configuration in the local support

Also, the mth derivative of RBFs at center point $(x_i,y_i)$ is

$$\begin{aligned}&{\left. {\frac{{{\partial ^m}{\phi _j}(x,y)}}{{\partial {x^m}}}} \right| _{(x,y) = ({x_i},{y_i})}} = \sum \limits _{p = 0}^{{n_i}} {\rho _{i,p}^{m,x}{\phi _j}(x_p^i,y_p^i)} ,\nonumber \\&\quad i,j = \left\{ {0,1,2, \ldots ,{n_i}} \right\} , \quad i \ne j, \end{aligned}$$

(45)

$$\begin{aligned}&{\left. {\frac{{{\partial ^m}{\phi _j}(x,y)}}{{\partial {y^m}}}} \right| _{(x,y) = ({x_i},{y_i})}} = \sum \limits _{p = 0}^{{n_i}} {\rho _{i,p}^{m,y}{\phi _j}(x_p^i,y_p^i)} , \nonumber \\&\quad i,j = \left\{ {0,1,2, \ldots ,{n_i}} \right\} , \quad i \ne j, \end{aligned}$$

(46)

where $\phi _j$ is a RBF. By collocating all nodes in the local domain of center point $(x_i,y_i)$ in Eqs. (45) and (46), the following matrix equations have been resulted:

$$\begin{aligned} {[}{\rho ^{x,m}}]= & {} {[A]^{ - 1}}\left[ {\frac{{{\partial ^m}\phi ({x_i},{y_i})}}{{\partial {x^m}}}} \right] ,\nonumber \\ {[}{\rho ^{y,m}}]= & {} {[A]^{ - 1}}\left[ {\frac{{{\partial ^m}\phi ({x_i},{y_i})}}{{\partial {y^m}}}} \right] , \end{aligned}$$

(47)

in which A is the interpolation matrix.

3.3 The upwind LRBFs-DQ approach

Shu et al. [39] developed a new version of LRBFs-DQ technique based on the upwind approach. We consider model (6) as follows:

$$\begin{aligned} _0^CD_t^\alpha {\mathbf{U}} + \left[ {{\mathcal {M}}({\mathbf{U}}) - {\mathcal {H}}({\mathbf{U}})} \right] {{\mathbf{U}}_x} + \left[ {{\mathcal {N}}({\mathbf{U}}) - {\mathcal {J}}({\mathbf{U}})} \right] {{\mathbf{U}}_y} = {\mathbf{K}}. \end{aligned}$$

(48)

At first, we employ nodes between the center point and its support that are depicted in Fig. 2. Also, we call these points as the “mid-points”.

Fig. 2

Configuration in the local support

Applying the LRBFs-DQ technique to discrete the space variable gives

$$\begin{aligned} _0^CD_t^\alpha {\mathbf{U}}_i= & {} - \sum \limits _{k = 0}^{{n_i}} \left\{ \rho _{i,k}^{(x)}\left[ {{\mathcal {M}}({{\mathbf{U}}_{i,k}}) -{\mathcal {H}}({{\mathbf{U}}_{i,k}})} \right] \right. \nonumber \\&\left. + \rho _{i,k}^{(y)}\left[ {{\mathcal {N}}({{\mathbf{U}}_{i,k}}) - {\mathcal {J}}({{\mathbf{U}}_{i,k}})} \right] \right\} ^n + \left. {\mathbf{K}} \right| _i^n, \end{aligned}$$

(49)

where [39]

• ${{{\mathbf{U}}_{i,k}}}$ denotes the conservative variables at the mid-points,

• ${\rho _{i,k}^{(x)}}$ and ${\rho _{i,k}^{(y)}}$ are weight coefficients based on the first-order derivatives in the x- and y-directions, respectively,

• $n_i$ denotes the total number of supporting points for the reference point i.

From Eq. (49), we can derive a new flux according to the mid-point and a unit vector

$$\begin{aligned} {\overrightarrow{\alpha }_\rho } = \left( {{\mu _{i,k}},{\eta _{i,k}}} \right) . \end{aligned}$$

Thus, we have

$$\begin{aligned} {{\mathbf{S}}_{i,k}}= & {} {\mu _{i,k}}\left[ {{\mathcal {M}}({{\mathbf{U}}_{i,k}}) - {\mathcal {H}}({{\mathbf{U}}_{i,k}})} \right] \nonumber \\&+\, {\eta _{i,k}}\left[ {{\mathcal {N}}({{\mathbf{U}}_{i,k}}) - {\mathcal {J}}({{\mathbf{U}}_{i,k}})} \right] , \end{aligned}$$

(50)

in which [39]

$$\begin{aligned} {\mu _{i,k}}= & {} \frac{{\rho _{i,k}^{(x)}}}{{\sqrt{{{\left( {\rho _{i,k}^{(x)}} \right) }^2} + {{\left( {\rho _{i,k}^{(y)}} \right) }^2}} }}, \nonumber \\ {\eta _{i,k}}= & {} \frac{{\rho _{i,k}^{(y)}}}{{\sqrt{{{\left( {\rho _{i,k}^{(x)}} \right) }^2} + {{\left( {\rho _{i,k}^{(y)}} \right) }^2}} }}. \end{aligned}$$

(51)

By assuming

$$\begin{aligned} {\Theta _{i,k}} = \sqrt{{{\left( {\rho _{i,k}^{(x)}} \right) }^2} + {{\left( {\rho _{i,k}^{(y)}} \right) }^2}}. \end{aligned}$$

(52)

Equation (49) can be rewritten as follows:

$$\begin{aligned} _0^CD_t^\alpha {\mathbf{U}}_i = - \sum \limits _{k = 0}^{{N_1}} {{\Theta _{i,k}}{{\mathbf{S}}_{i,k}}} + \left. {\mathbf{K}} \right| _i. \end{aligned}$$

(53)

4 Numerical surveys

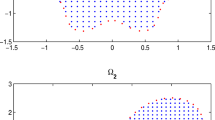
Here, we report the obtained results based on the developed technique on the non-rectangular domains that are depicted in Fig. 3.

Fig. 3

The used computational regions

4.1 Example 1

We will study the following model:

$$\begin{aligned} \int \limits _0^1 {w(\alpha )_0^CD_t^\alpha u{\text {d}}\alpha } = \frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{\partial ^2}u}}{{\partial {y^2}}} - \nu \frac{{\partial u}}{{\partial x}} - \nu \frac{{\partial u}}{{\partial y}} + f(x,y,t), \end{aligned}$$

(54)

with the homogeneous initial and boundary conditions. Also, $w(\alpha )=\Gamma (3-\alpha )$ and the analytical solution is

$$\begin{aligned} u(x,y,t) = {\exp (-\pi ^2 t)}\sin (\pi x)\sin (\pi y); \end{aligned}$$

thus, the source term can be obtained from the analytical solution. In this example, the effect of the advection coefficient has been studied. Figure 4 displays the error obtained based on the values of $\nu$ on rectangular domain for Example 1. In Fig. 5, the graphs of approximate and error have been depicted with $\nu =10$ on rectangular domain for Example 1. Tables 1 and 2 show the errors obtained based on the different values of advection coefficient $\nu$ with rectangular domain and domain $\Omega _2$ for Example 1. Figures 7, 9, 11 and 13 demonstrate the approximation solutions based on the different computational geometries. Figures 6, 8, 10 and 12 illustrate error obtained based on the different values of and $\nu$ for the computational domains $\Omega _1$, $\Omega _2$, $\Omega _3$ and $\Omega _4$, respectively.

Fig. 4

Error obtained based on the values of $\nu$ on rectangular domain for Example 1

Fig. 5

Graph of approximate and error with $\nu =10$ on rectangular domain for Example 1

Fig. 6

Error obtained based on the values of $\nu$ on domain $\Omega _2$ for Example 1

Fig. 7

Graph of approximate and error with $\nu =10$ on domain $\Omega _2$ for Example 1

Fig. 8

Error obtained based on the values of $\nu$ on domain $\Omega _3$ for Example 1

Fig. 9

Graph of approximate and error with $\nu =10$ on domain $\Omega _3$ for Example 1

Fig. 10

Error obtained based on the values of $\nu$ on domain $\Omega _4$ for Example 1

Fig. 11

Graph of approximate and error with $\nu =10$ on domain $\Omega _4$ for Example 1

Fig. 12

Error obtained based on the values of $\nu$ on domain $\Omega _4$ for Example 1

Fig. 13

Graph of approximate and error with $\nu =10$ on domain $\Omega _4$ for Example 1

Table 1 Errors obtained on rectangular domain for Example 1

Table 2 Errors obtained on domain $\Omega _2$ for Example 1

Fig. 14

Error obtained with $\sigma =7/4$ for Example 2

Fig. 15

Error obtained with $\nu =50$ for Example 2

Fig. 16

Approximate solution with $\nu =50$ for Example 2

4.2 Example 2

Consider the following model:

$$\begin{aligned} \int \limits _0^1 {w(\alpha )_0^CD_t^\alpha u(x,y,t){\text {d}}\alpha }= & {} \frac{{{\partial ^2}u(x,y,t)}}{{\partial {x^2}}} + \frac{{{\partial ^2}u(x,y,t)}}{{\partial {y^2}}}\nonumber \\&- \nu \frac{{\partial u(x,y,t)}}{{\partial x}} - \nu \frac{{\partial u(x,y,t)}}{{\partial y}} \nonumber \\&+ f(x,y,t), \end{aligned}$$

(55)

with the homogeneous initial and boundary conditions. The analytical solution is

$$\begin{aligned} u(x,y,t) = {t^2}{(1 - {x^2})^\sigma }{(1 - {y^2})^\sigma }, \end{aligned}$$

where $\sigma$ is a positive constant as this solution belongs to Sobolev space $H_0^{\sigma +\frac{1}{2}}$ and also $w(\alpha )=\Gamma (3-\alpha )$. Figure 14 demonstrates error obtained with $\sigma =7/4$ and different values of $\nu$ and also Fig. 15 illustrates error obtained with $\nu =50$ and different values of $\sigma$ for Example 2. Furthermore, Fig. 16 displays approximate solution with $\nu =50$ and different values of $\sigma$ for Example 2. Table 3 presents the error achieved based on the values of $\sigma =\frac{4}{3}$ and $\sigma =\frac{13}{3}$. According to these parameters, we choose different advection coefficients $\nu =10$ and $\nu =50$. In Table 3 the effect of the regularity solution and advection coefficient can be observed, clearly.

Table 3 Errors achieved with $\tau =10^{-5}$ for Example 2

5 Conclusion

In the current manuscript, the fractional distributed-order advection–diffusion equation has been investigated by a truly meshless method. In the developed technique, the time derivative has been approximated by a finite difference scheme. As well as, the spatial variable has been discretized by a meshless local procedure based on the upwind RBF-FD technique. The effect of the advection coefficient has been checked in the approximation results. Also, the used technique has been applied on some irregular domains. The stability and convergence of the proposed method are numerically studied.