A priori error estimates of a Jacobi spectral method for nonlinear systems of fractional boundary value problems and related Volterra-Fredholm integral equations with smooth solutions

Abstract

Our aim in this paper is to develop a Legendre-Jacobi collocation approach for a nonlinear system of two-point boundary value problems with derivative orders at most two on the interval (0,T). The scheme is constructed based on the reduction of the system considered to its equivalent system of Volterra-Fredholm integral equations. The spectral rate of convergence for the proposed method is established in both L²- and $L^{\infty }$- norms. The resulting spectral method is capable of achieving spectral accuracy for problems with smooth solutions and a reasonable order of convergence for non-smooth solutions. Moreover, the scheme is easy to implement numerically. The applicability of the method is demonstrated on a variety of problems of varying complexity. To the best of our knowledge, the spectral solution of such a nonlinear system of fractional differential equations and its associated nonlinear system of Volterra-Fredholm integral equations has not yet been studied in literature in detail. This gap in the literature is filled by the present paper.

1 Introduction

Fractional differential equations are the mathematical formulation of many physical and engineering phenomena. In particular, they have attracted much attention within the natural and social sciences, since they can properly model phenomena dominated by memory effects. The nonlocal nature of the fractional integral makes the numerical treatment of fractional differential equations expensive in terms of computational effort and memory requirements. Direct approaches for discretizing these equations require that the entire solution history is stored and used throughout the computation. Therefore, the design of efficient solvers for the numerical simulation of such problems is a difficult task [1,2,3,4,5].

The analytical solutions of many fractional differential equations have been hindered by the difficulties in the computation of the fractional operator. Though some fractional differential equations with a simple form, e.g., linear equations, can be solved by analytical methods, e.g., the Laplace transform method or the Fourier transform method [6], the analytical solutions of many nonlinear fractional differential equations are rather difficult to obtain. Therefore, the development of efficient methods to tackle the numerical approximation of such problems has been of great interest and has attracted the attention of many scientists over the past decades [7,8,9,10]. Due to the non-locality and singularity of the fractional operator, existing methods including finite difference and finite element methods mostly lead to low-order schemes. Spectral methods are capable of providing highly accurate solutions to smooth problems with significantly less unknowns than using finite difference or finite element methods [11,12,13,14,15].

A great deal of papers are devoted to the numerical solution of initial value problems for fractional differential equations (see, e.g., [16,17,18,19,20]). In contrast to this, only a few papers concern the numerical solution of boundary value problems for fractional differential equations. Kopteva and Stynes [21] proposed a piecewise polynomial collocation method for a two-point linear boundary value problem, where the leading term in the differential operator is a Caputo fractional-order derivative of order 2 − δ with 0 < δ < 1. Pedas and Tamme [22] discussed a piecewise polynomial collocation method for a class of linear boundary value problems which involve Caputo-type fractional derivatives. They derived some regularity properties of the exact solution using an integral equation reformulation of the boundary value problem. Sheng and Shen [23] proposed a hybrid spectral element method for fractional two-point boundary value problem involving both Caputo and Riemann-Liouville fractional derivatives, following a similar procedure in [21]. Wang et al. [24] developed Bernoulli wavelets operational matrix approach for solving coupled systems of nonlinear fractional integro-differential equations. Wang et al. [25] developed a Legendre spectral collocation method for fractional boundary value problems. Gu [26] provided an hp-version spectral collocation method to solve system of Volterra integral equations. Graef et al. [27] presented a Chebyshev spectral collocation method for solving Riemann-Liouville fractional boundary value problems. Li et al. [28] derived effective algorithms based on Legendre, Chebyshev, and Jacobi polynomials to solve fractional boundary value problems. Doha et al. [29] applied Chebyshev tau and collocation methods to solve linear and nonlinear fractional boundary value problems. Ezz-Eldien and Doha [30] presented and analyzed a spectral collocation method for solving systems of pantograph type Volterra integro-differential equations. Doha et al. [31] proposed Jacobi-Gauss–collocation approaches for solving Volterra, Fredholm and systems of Volterra-Fredholm integro-differential equations with initial and nonlocal boundary conditions. Mokhtary et al. [32] developed a well-conditioned Jacobi spectral Galerkin method for the analysis of Volterra-Hammerstein integral equations with weakly singular kernels and proportional delay. Zacky [33] developed and analyzed a singularity preserving spectral-collocation method for the numerical solution of nonlinear tempered fractional boundary value problems.

Recently, many researchers have devoted their attention to studying the existence of solutions of nonlinear fractional boundary value problems [34, 35]. We mention that the fractional order λ involved is generally in (1,2] with the exception that λ ∈ (2,3] in [36] and λ ∈ (3,4] in [37]. Though there have been extensive studies on the properties of the solutions of many kinds of fractional differential equations, relatively little progress has been made on systems of fractional differential equations [38,39,40].

Following the spirit of [1, 25], the purpose of the present work is to study the convergence behavior of the spectral collocation method for the system of fractional boundary value problems of the form:

$$ \left\{\begin{array}{llll} {~}_{0}^{C} D_{t}^{\lambda} u_{1}(t) = g_{1}(t,u_{1}(t),\ldots,u_{Q}(t)),\ 0< t< T, \\ {~}_{0}^{C} D_{t}^{\lambda} u_{2}(t) = g_{2}(t,u_{1}(t),\ldots,u_{Q}(t)),\ 0< t< T, \\ \vdots\\ {~}_{0}^{C} D_{t}^{\lambda} u_{Q}(t) = g_{Q}(t,u_{1}(t),\ldots,u_{Q}(t)),\ 0< t< T,\\ u_{i}(0) = u_{i}(T) = 0,\ i= 1,2, \ldots, Q,\quad {\lambda \in (1,2),} \end{array}\right. $$

(1.1)

where $g_{i}:[0,T] \times \mathbb {R}^{Q} \to \mathbb {R}$ are continuous and ${~}_{0}^{C} D_{t}^{\nu }$ is the Caputo fractional derivative of order ν ∈ (n,n − 1) defined by (see, e.g., [6]):

$$ {~}_{0}^{C} D_{t}^{\nu} \psi = {~}_{0}I_{t}^{n - \nu } \left( {\frac{{d^{n}\psi }}{{dt^{n}}}} \right),\quad n \in \mathbb{N}. $$

(1.2)

Here, ${~}_{0}I_{t}^{\nu }$ for ν > 0 is the Riemann-Liouville fractional integral of order ν defined by (see, e.g., [6]):

$$ {~}_{0}I_{t}^{\nu } \psi = \frac{1}{{{\Gamma} (\nu )}}{{\int}_{0}^{t}} {(t - s)^{\nu - 1} \psi (s)ds}. $$

(1.3)

In case of λ = 2, ${~}_{0}^{C} D_{t}^{\lambda }$ coincides with the usual second order derivative $u^{\prime \prime }(t)$, and the model (1.1) recovers the classical system of two-point boundary value problems. We will show that our methodology is an implicit technique which is spectrally convergent.

The outline of the paper is as follows. In Section 2, some properties of the Jacobi polynomial and its Gauss interpolation are presented to be used throughout the paper. In Section 3, the formulation of the spectral collocation method is introduced. In Section 4, abstract error bounds are initially proved as a key step in the analysis of the collocation method. In Section 5, the convergence analysis under the L²-norm is provided. In Section 6, the convergence analysis under the $L^{\infty }$-norm is established. In Section 6, two numerical examples are implemented to support our results and to illustrate the performance of the presented numerical method. Finally, Section 7 offers a summary of the main results and directions for future research.

2 Jacobi polynomials and Jacobi-Gauss interpolation

For λ,μ > − 1 and t ∈Λ := (− 1,1), the Jacobi polynomials can be expressed via the hypergeometric function [41]:

$$ \begin{array}{llll} \mathscr{P}^{\lambda ,\mu }_{i}(t)=\frac{{(\lambda + 1)_{i} }}{{i!}}{~}_{2}F_{1} \left( { - i,\lambda + \mu + i + 1;\lambda + 1;\frac{{1 - t}}{2}} \right),\ t \in {\Lambda} ,\ i \in \mathbb{N}. \end{array} $$

(2.1)

Here, (⋅)_i is the Pochhammer symbol. This yields the following equivalent three-term recurrence relation

$$ \begin{array}{llll} &\mathscr{P}^{\lambda ,\mu }_{0}(t)=1,\\ & \mathscr{P}^{\lambda ,\mu }_{1}(t)=\frac{1}{2}(\lambda+\mu+2)t+\frac{1}{2}(\lambda-\mu), \\ &\mathscr{P}^{\lambda ,\mu }_{i+1}(t)=\left( \hat{a}^{\lambda ,\mu }_{i} t-\hat{b}^{\lambda ,\mu }_{i}\right)\mathscr{P}^{\lambda ,\mu }_{i}(t)-\hat{c}^{\lambda ,\mu }_{i} \mathscr{P}^{\lambda ,\mu }_{i-1}(t),\quad\quad i\geq1, \end{array} $$

(2.2)

where

$$ \begin{array}{llll} \hat{a}^{\lambda ,\mu }_{i}=&\frac{(2i+\mu+\lambda+1)(2i+\mu+\lambda+2)}{2(i+1)(i+\mu+\lambda+1)},\\ \hat{b}^{\lambda ,\mu }_{i}=&\frac{(2i+\mu+\lambda+1)({\mu}^{2}-{\lambda}^{2})}{2(i+1)(i+\mu+\lambda+1)(2i+\mu+\lambda)},\\ \hat{c}^{\lambda ,\mu }_{i}=&\frac{(2i+\mu+\lambda+2)(i+\lambda)(i+\mu)}{(i+1)(i+\mu+\lambda+1)(2i+\mu+\lambda)}. \end{array} $$

(2.3)

It is worth recalling two important special cases of the Jacobi polynomials, e.g., the Legendre polynomials

$$ \begin{array}{llll} L_{i} (t) = \mathscr{P}^{0 ,0 }_{i}(t) = {~}_{2}F_{1} \left( { - i,i + 1;1;\frac{{1 - t}}{2}} \right), \end{array} $$

(2.4)

and the Chebyshev polynomials

$$ \begin{array}{llll} T_{i} (t) = \frac{{\sqrt \pi i!}}{{{\Gamma} \left( {i + \frac{1}{2}} \right)}}_{i} \mathscr{P}_{i}^{- \frac{1}{2}, - \frac{1}{2}} (t), \end{array} $$

(2.5)

where Γ(⋅) represents the Gamma function.

The Jacobi polynomials are orthogonal with respect to the weight function: ω^λ,μ(t) = (1 − t)^λ(1 + t)^μ, namely,

$$ {\int}_{{\Lambda} } {\mathscr{P}_{i}^{\lambda,\mu}(t)\mathscr{P}_{j}^{\lambda,\mu}(t)\omega^{\lambda,\mu}(t)dt} = \gamma_{i}^{\lambda ,\mu } \delta_{i,j}, $$

(2.6)

where δ_i,j is the Dirac Delta symbol, and

$$ \gamma_{i}^{\lambda ,\mu } = \frac{{2^{(\lambda + \mu+1)} {\Gamma} (i + \mu + 1){\Gamma} (i + \lambda + 1)}} {{i!(2i + \lambda + \mu + 1){\Gamma} (i + \lambda + \mu + 1)}}. $$

(2.7)

Let $\left \{ {t_{i}^{\lambda ,\mu },\ \varpi _{i}^{\lambda ,\mu } } \right \}_{i = 0}^{N}$ be the set of Jacobi-Gauss nodes and weights. The Jacobi-Gauss quadrature enjoys the exactness

$$ {\int}_{{\Lambda} } {\varphi (t)\omega^{\lambda ,\mu } (t)dt} = \sum\limits_{i = 0}^{N} {\varphi (t_{i} )\varpi_{i}^{\lambda ,\mu } },\ \forall \varphi(x) \in \mathcal{P}_{2N+1}({\Lambda} ), $$

(2.8)

where $\mathcal {P}_{N}({\Lambda } )$ is the set of all polynomials of degree not exceeding N. Hence,

$$ \sum\limits_{k=0}^{N} \mathscr{P}_{i}^{\lambda ,\mu }(t_{k}^{\lambda,\mu}) \mathscr{P}_{j}^{\lambda ,\mu }(t_{k}^{\lambda,\mu}) \varpi_{k}^{\lambda,\mu}=\gamma_{i}^{\lambda ,\mu } \delta_{i,j}, \forall \ 0 \leq i+j \leq 2N+1. $$

(2.9)

Let $\mathcal {I}_{t,N}^{\lambda ,\mu } u$ be the Jacobi-Gauss interpolation of u ∈ C(Λ) defined by

$$ \mathcal{I}_{t,N}^{\lambda,\mu} u (t) = \sum\limits_{i=0}^{N} \widehat{u}_{i}^{\lambda,\mu} \mathscr{P}_{i}^{\lambda ,\mu } (t) \!\in\! \mathcal{P}_{N}, \quad \text{where}\! \quad \widehat{u}_{i}^{\lambda,\mu} = \frac{1}{\gamma_{i}^{\lambda ,\mu }} \sum\limits_{j=0}^{N} u (t_{j}) \mathscr{P}_{i}^{\lambda ,\mu }(t_{j}) \varpi_{j}^{\lambda,\mu}. $$

(2.10)

To alleviate the burden of heavy notation, we drop the parameters λ, μ in the notation whenever λ = μ = 0.

3 Jacobi collocation discretization

The numerical approach for solving the system of fractional differential (1.1) is essentially based on recasting (1.1) in the form of the following nonlinear system of Fredholm integral equations, to which we will apply a collocation method.

Lemma 3.1 (see 42, Lemma 6.43)

Letλ ∈ (1,2).Assume thatu_i(t), i = 1,…,Qarefunctions with an absolutely continuous first derivative,and$g_{i}:[0,T] \times \mathbb {R}^{Q} \to \mathbb {R}$arecontinuous. Then, we have thatu ∈ C¹[0,T] isa solution of the boundary value problem (1.1) if and only if it is a solutionof the Fredholm integral equation:

$$ \begin{array}{llll} \mathbf{u}(t) &= \frac{1}{{\Gamma}(\lambda)} {{\int}_{0}^{t}} (t-\tau)^{\lambda-1} \mathbf{g}\left( \tau,\mathbf{u}(\tau)\right)d\tau - \frac{t}{T {\Gamma}(\lambda)} {{\int}_{0}^{T}} (T-\tau)^{\lambda-1} \mathbf{g}\left( \tau,\mathbf{u}(\tau)\right)d\tau, \end{array} $$

(3.1)

where $\mathbf {u}(t)=\left [u_{1}(t),u_{2}(t),\ldots ,u_{Q}(t)\right ]^{T}, \mathbf {g}=[g_{1},g_{2},\ldots ,g_{Q}]^{T}$.

For ease of analysis, we employ the transformation

$$ t(x)= \frac{T}{2} (x+1), \quad x \in {\Lambda} , $$

(3.2)

to describe the spectral method on the standard interval Λ. Then, (3.1) becomes

$$ \begin{array}{llll} \mathbf{u}\left( \frac{T}{2} (x+1)\right) =& \frac{1}{{\Gamma}(\lambda)} {\int}_{0}^{\frac{T}{2} (x+1)} \left( \frac{T}{2} (x+1)-\tau\right)^{\lambda-1} \mathbf{g}(\tau,\mathbf{u}(\tau)))d\tau\\ & - \frac{x+1}{2 {\Gamma}(\lambda)} {{\int}_{0}^{T}} (T-\hat{\tau})^{\lambda-1} \mathbf{g}(\hat{\tau},\mathbf{u}(\hat{\tau}))d\hat{\tau}. \end{array} $$

(3.3)

Furthermore, to change the interval $\left (0,\frac {T}{2} (x+1)\right )$ to (− 1,x) and the interval (0,T) to Λ, we use the variable transformations

$$ \begin{array}{llll} \tau(\sigma) &=\frac{T}{2} (\sigma+1), \quad \sigma \in (-1,x),\\ \hat{\tau}(\beta)&=\frac{T}{2} (\beta+1),\quad \beta \in {\Lambda} . \end{array} $$

(3.4)

Then, (3.3) can be written as

$$ \mathbf{U}(x) = \frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda)} {\int}_{-1}^{x} (x-\sigma)^{\lambda-1} \mathbf{G}\left( \sigma,\mathbf{U}(\sigma)\right)d \sigma- \frac{ T^{\lambda}(x+1)}{2^{\lambda+1} {\Gamma}(\lambda)} {\int}_{-1}^{1} (1-\beta)^{\lambda-1} \mathbf{G}\left( \beta,\mathbf{U}(\beta)\right)d\beta, $$

(3.5)

where

$$ \begin{array}{llll} &\mathbf{U}(x):=\left[U_{1}(x),\ldots,U_{Q}(x)\right]^{T}\equiv\mathbf{u}\left( \tau(x)\right),\\ &\mathbf{G}\left( \sigma,\mathbf{U}(\sigma)\right):=\left[G_{1}\left( \sigma,\mathbf{U}(\sigma)\right),\ldots,G_{Q}\left( \sigma,\mathbf{U}(\sigma)\right)\right]^{T} \equiv \mathbf{g}\left( \tau(\sigma),\mathbf{u}\left( \tau(\sigma)\right)\right). \end{array} $$

(3.6)

Finally, for ease of implementation and analysis, we use the variable transformation

$$ \sigma(x,\eta)=\frac{x+1}{2} \eta+\frac{x-1}{2}, \quad x, \eta \in {\Lambda} , $$

(3.7)

to convert the interval (− 1,x) to the unit interval Λ. Equation (3.5) becomes

$$ \begin{array}{llll} \mathbf{U}(x) =& \frac{T^{\lambda}(x+1)^{\lambda}}{4^{\lambda} {\Gamma}(\lambda)} {\int}_{-1}^{1} (1-\eta)^{\lambda-1} \mathbf{G}(\sigma(x,\eta),\mathbf{U}(\sigma(x,\eta)))d\eta\\ & - \frac{ T^{\lambda} (x+1) }{2^{\lambda+1} {\Gamma}(\lambda)} {\int}_{-1}^{1} (1-\beta)^{\lambda-1} \mathbf{G}\left( \beta,\mathbf{U}(\beta)\right)d\beta. \end{array} $$

(3.8)

The spectral collocation method to (3.8) is implemented in the frequency space by seeking approximate solution in the form

$$ \begin{array}{llll} U_{m,N}(x)=\sum\limits_{i=0}^{N} \hat{u}_{m,i} L_{i}(x) \in \mathcal{P}_{N}({\Lambda} ), \quad m=1,{\ldots} Q. \end{array} $$

(3.9)

Hence, inserting (3.9) into (3.8) leads to the following system

$$ \begin{array}{llll} \mathbf{U}_{N}(x) =& \frac{T^{\lambda}}{4^{\lambda} {\Gamma}(\lambda)} \mathcal{I}_{x,N} \left[(x+1)^{\lambda} {\int}_{-1}^{1} (1-\eta)^{\lambda-1} \mathcal{I}_{\eta,N}^{\lambda-1,0} \mathbf{G}(\sigma(x,\eta),\mathbf{U}_{N}(\sigma(x,\eta)))d\eta\right]\\ & - \frac{T^{\lambda} (x+1) }{2^{\lambda+1} {\Gamma}(\lambda)} \left[{\int}_{-1}^{1} (1-\beta)^{\lambda-1} \mathcal{I}_{\beta,N}^{\lambda-1,0} \mathbf{G}(\beta,\mathbf{U}_{N}(\beta))d\beta\right], \end{array} $$

(3.10)

where $\mathbf {U}_{N}(x)=\left [U_{1,N}(x),\ldots ,U_{Q,N}(x)\right ]^{T}$. To verify the existence of a solution of (3.10), see “Appendix” of this paper. We now provide a detailed implementation procedure for (3.10). Setting

$$ \begin{array}{llll} &\mathcal{I}_{x,N}\mathcal{I}_{\eta,N}^{\lambda-1,0}\left( (x+1)^{\lambda} G_{m}\left( \sigma(x,\eta),U_{1,N}(\sigma(x,\eta)),\ldots,U_{Q,N}(\sigma(x,\eta))\right)\right)\\ &\qquad\qquad =\sum\limits_{i=0}^{N} \sum\limits_{j=0}^{N} \hat{v}_{m,i,j} L_{i}(x) \mathscr{P}_{j}^{\lambda-1,0 } (\eta),\quad m=1,\ldots,Q, \end{array} $$

(3.11)

thanks to (2.6), we have

$$ \begin{array}{llll} \frac{T^{\lambda}}{4^{\lambda} {\Gamma}(\lambda)} &\mathcal{I}_{x,N} \left[(x+1)^{\lambda} {\int}_{-1}^{1} (1-\eta)^{\lambda-1} \mathcal{I}_{\eta,N}^{\lambda-1,0} G_{m}\left( \sigma(x,\eta),U_{1,N}(\sigma(x,\eta)),\ldots,U_{Q,N}(\sigma(x,\eta))\right)d\eta\right] \\ &=\frac{T^{\lambda}}{4^{\lambda} {\Gamma}(\lambda)} \sum\limits_{i=0}^{N}\sum\limits_{j=0}^{N} \hat{v}_{m,i,j} L_{i}(x) {\int}_{-1}^{1} (1-\eta)^{\lambda-1} \mathscr{P}_{j}^{\lambda-1,0}(\eta) d\eta\\ &= \frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda+1)} \sum\limits_{i=0}^{N } \hat{v}_{m,i,0} L_{i}(x), \quad m=1,\ldots,Q. \end{array} $$

(3.12)

Using (2.9) and (3.11) yields

$$ \begin{array}{@{}rcl@{}} &&\hat{v}_{m,i,0}=\frac{\lambda (2i+1)}{2^{1+\lambda}} \\ & &\times \sum\limits_{r=0}^{N} \sum\limits_{s=0}^{N}(x_{r}+1)^{\lambda} G_{m}\left( \sigma\left( x_{r},x_{s}^{\lambda-1,0}\right),U_{1,N}\left( \sigma(x_{r},x_{s}^{\lambda-1,0})\right),\ldots,\right.\\&&\left.U_{Q,N}\left( \sigma(x_{r},x_{s}^{\lambda-1,0})\right)\right) L_{i}(x_{r}) \varpi_{r} \varpi_{s}^{\lambda-1,0}. \end{array} $$

(3.13)

Moreover, by (2.8), we have

$$ \begin{array}{llll} &{\int}_{-1}^{1} (1-\beta)^{\lambda-1} \mathcal{I}_{\beta,N}^{\lambda-1,0} G_{m}(\beta,U_{1,N}(\beta),\ldots,U_{Q,N}(\beta))d\beta= \hat{w}_{m}=\\ &\qquad\qquad\qquad \sum\limits_{j=0}^{N} \varpi_{j}^{\lambda-1,0}G_{m} \left( x_{j}^{\lambda-1,0},U_{1,N}(x_{j}^{\lambda-1,0}),\ldots,U_{Q,N}(x_{j}^{\lambda-1,0}) \right). \end{array} $$

(3.14)

Hence, using (3.10)–(3.14), we deduce that

$$ \begin{array}{llll} \sum\limits_{i=0}^{N} \hat{u}_{m,i} L_{i}(x)=&\frac{T^{\lambda}}{ {\Gamma}(\lambda+1) 2^{\lambda}} \sum\limits_{i=0}^{N }\hat{v}_{m,i,0} L_{i}(x)-\frac{T^{\lambda}(x+1)}{2^{\lambda+1} {\Gamma}(\lambda)} \hat{w}_{m},\ m=1,\ldots,Q. \end{array} $$

(3.15)

Finally, using (2.6) yields

$$ \left\{\begin{array}{llll} \hat{u}_{m,0} =\frac{T^{\lambda}}{ {\Gamma}(\lambda+1) 2^{\lambda}} \hat{v}_{m,0,0} - \frac{T^{\lambda}}{2^{\lambda+1} {\Gamma}(\lambda)} \hat{w}_{m}, \ m=1,\ldots,Q, \\ \hat{u}_{m,1} =\frac{T^{\lambda}}{ {\Gamma}(\lambda+1) 2^{\lambda}} \hat{v}_{m,1,0} - \frac{T^{\lambda}}{2^{\lambda+1} {\Gamma}(\lambda)} \hat{w}_{m}, \ m=1,\ldots,Q, \\ \hat{u}_{m,i} =\frac{T^{\lambda}}{ {\Gamma}(\lambda+1) 2^{\lambda}} \hat{v}_{m,i,0}, \ i=2,\ldots,N,\ m=1,\ldots,Q{,} \vphantom{\frac{5_A}{4,10^3}} \end{array}\right. $$

(3.16)

which can be solved using a standard iterative method such as the Newton’s method.

Remark 3.1

If the Dirichlet boundary conditions become non-zero, that is,

$$u_{i} (0) = a_{i},\quad u_{i} (T) = b_{i}, \quad i = 1,2, {\ldots} Q,$$

where the boundary conditions a_i and b_i are not zero identically. Denote

$$w_{i} (t) = u_{i} (t) - \frac{{T - x}}{T}a_{i} - \frac{x}{T}b_{i}.$$

then, we can get

$$w_{i} (0) = w_{i} (T) = 0.$$

Based on the above process, we could solve the problem with homogeneous boundary conditions instead of the inhomogeneous conditions.

4 Abstract error bounds

In order to give the subsequent results conveniently, we consider the following family of spaces. For notational convenience, we denote by $\mathcal {I}$ the identity operator and ${\partial _{x}^{q}} u(x)$ the q-th derivative of u, i.e., ${\partial _{x}^{q}} u(x): = \frac {{d^{q} u}}{{dx^{q} }}(x)$.

We denote by $L^{2}_{\omega ^{\lambda ,\mu } }({\Lambda } )$ the space of the measurable functions on Λ such that ${\int }_{{\Lambda } } {\left | {u(x)} \right |^{2} \omega ^{\lambda ,\mu } dx} < + \infty$. It is a Hilbert space with the inner product and norm given by

$$ \left( {u,v} \right)_{\omega^{\lambda ,\mu } } : = {\int}_{{\Lambda} } {u(x)v(x)\omega^{\lambda ,\mu } dx} , $$

(4.1)

$$ \left\| u \right\|_{\omega^{\lambda ,\mu } } : = \left( {{\int}_{{\Lambda} } {\left| {u(x)} \right|^{2} \omega^{\lambda ,\mu } dx} } \right)^{1/2} . $$

(4.2)

Definition 4.1

Let s ≥ 1 be an integer. The Sobolev space $H_{\omega ^{\lambda ,\mu } }^{s} ({\Lambda } )$ is the space of functions $u \in L^{2}_{\omega ^{\lambda ,\mu } }({\Lambda } )$ such that all the distribution of u of order up to s can be represented by functions in $L^{2}_{\omega ^{\lambda ,\mu } }({\Lambda } )$. That is,

$$ \begin{array}{llll} H_{\omega^{\lambda ,\mu } }^{s} ({\Lambda} ) : = \left\{ {u \in L^{2}_{\omega^{\lambda ,\mu } }({\Lambda} ) : {\partial_{x}^{m}} u \in L_{\omega^{{\lambda ,\mu} } }^{2} ({\Lambda} ),\ 0 \le m \le s} \right\}, \end{array} $$

(4.3)

endowed with the inner product and norm

$$ \left( {u,v} \right)_{H_{\omega^{\lambda ,\mu } }^{s} } = \sum\limits_{m = 0}^{s} {\left( {{\partial_{x}^{m}} u,{\partial_{x}^{m}} v} \right)_{\omega^{{\lambda ,\mu} } } }, $$

(4.4)

$$ \left\| u \right\|_{H_{\omega^{\lambda ,\mu } }^{s} } = \left( {u,u} \right)_{H_{\omega^{\lambda ,\mu } }^{s} }^{1/2}. $$

(4.5)

Definition 4.2

For a non-negative integer s, the non-uniformly Jacobi-weighted Sobolev space:

$$ \begin{array}{llll} B_{\omega^{\lambda ,\mu } }^{s} ({\Lambda} ) : = \left\{ {u : {\partial_{x}^{m}} u \in L_{\omega^{{\lambda + m,\mu + m}} }^{2} ({\Lambda} ),\ 0 \le m \le s} \right\}, \end{array} $$

(4.6)

equipped with the inner product, norm, and semi-norm

$$ \begin{array}{llll} &\left( {u,v} \right)_{B_{\omega^{\lambda ,\mu } }^{s} } = \sum\limits_{m = 0}^{s} {\left( {{\partial_{x}^{m}} u,{\partial_{x}^{m}} v} \right)_{\omega^{{\lambda + m,\mu + m}} } },\\ &\left\| u \right\|_{B_{\omega^{\lambda ,\mu } }^{s} } = \left( {u,u} \right)_{B_{\omega^{\lambda ,\mu } }^{s} }^{1/2} ,\qquad \left| u \right|_{B_{\omega^{\lambda ,\mu } }^{s} } = \left\| {{\partial_{x}^{s}} u} \right\|_{\omega^{{\lambda + m,\mu + m}} }. \end{array} $$

(4.7)

In particular, $L^{2}({\Lambda } )=B_{\omega ^{0 ,0 } }^{0} ({\Lambda } )$ and $\left \| \cdot \right \|=\left \| \cdot \right \|_{\omega ^{0 ,0 } }$. The space $B_{\omega ^{\lambda ,\mu } }^{s} ({\Lambda } )$ distinguishes itself from the usual weighted Sobolev space $H_{\omega ^{\lambda ,\mu } }^{s} ({\Lambda } )$ by involving different weight functions for derivatives of different orders. It is obvious that $H_{\omega ^{\lambda ,\mu } }^{s} ({\Lambda } )$ is a subspace of $B_{\omega ^{\lambda ,\mu } }^{s} ({\Lambda } )$, that is

$$\left\| u \right\|_{B_{\omega^{\lambda ,\mu } }^{s}}\leq c \left\| u \right\|_{H_{\omega^{\lambda ,\mu } }^{s} }.$$

The space $L^{\infty } ({\Lambda } )$ is the Banach space of the measurable functions u that are bounded outside a set of measure zero, equipped the norm

$$ \left\| u \right\|_{\infty} = \mathop {\text{ess} \sup }\limits_{x \in {\Lambda} } \left| {u(x)} \right|. $$

(4.8)

Definition 4.3

Let $\mathbf {U}(t)=\left (u_{ij}(t)\right )_{m \times n}$ be a matrix function of t ∈Λ, we define the non-negative real function

$$ \left|\mathbf{U}(t) \right|= \sum\limits_{i=1}^{m}\sum\limits_{j=1}^{n} \left|{u}_{ij}(t)\right|, $$

(4.9)

and the norms

$$ \begin{array}{llll} &\left\|\mathbf{U} \right\|_{\omega^{\lambda,\mu}}:=\left( {\int}_{{\Lambda} }\left|\mathbf{U}(t) \right|^{2}\omega^{\lambda,\mu}dt\right)^{1/2},\\ &\left\|\mathbf{U} \right\|_{\infty}:=ess \sup_{t\in {\Lambda} } \left|\mathbf{U}(t)\right|. \end{array} $$

(4.10)

Lemma 4.1

Letλ, μ > − 1.For any$\mathbf {U} \in B^{s}_{\omega ^{\lambda ,\mu }} ({\Lambda } )$withs ≥ 1 and0 ≤ k ≤ s ≤ N + 1,

$$ \left\| {\partial^{k}_{x}}(\mathbf{U}-\mathcal{I}_{x,N}^{\lambda,\mu}\mathbf{U}) \right\|_{\omega^{\lambda+k,\mu+k}}\leq c N^{k-s} \left\| {\partial_{x}^{s}} \mathbf{U} \right\|_{\omega^{\lambda+s,\mu+s}}, $$

(4.11)

where $\mathcal {I}_{x,N}^{\lambda ,\mu }$ is the Jacobi-Gauss interpolation operator.

Proof

Using the Cauchy-Schwarz inequality, we obtain

$$ \begin{array}{llll} \left\| {\partial^{k}_{x}} (\mathbf{U}-\mathcal{I}_{x,N}^{\lambda,\mu}\mathbf{U}) \right\|_{\omega^{\lambda+k,\mu+k}}& = \left\| \sum\limits_{q=1}^{Q} \left| (I-\mathcal{I}_{x,N}^{\lambda,\mu})U_{q} \right| \right\|_{\omega^{\lambda+k,\mu+k}}\\ & = \left( {\int}_{{\Lambda} } \left( \sum\limits_{q=1}^{Q} \left| (I-\mathcal{I}_{x,N}^{\lambda,\mu})U_{q} \right| \right)^{2} \omega^{\lambda+k,\mu+k} dx \right)^{1/2}\\ & \!\leq\! \left( {\int}_{{\Lambda} } \left( \sum\limits_{q=1}^{Q} \left| (I - \mathcal{I}_{x,N}^{\lambda,\mu})U_{q} \right|^{2}\right) \left( \sum\limits_{q=0}^{Q} 1\right)\omega^{\lambda+k,\mu+k} dx \right)^{1/2}\\ & \!\leq\! c \left( \sum\limits_{q=1}^{Q} \left\|(I-\mathcal{I}_{x,N}^{\lambda,\mu})U_{q} \right\|^{2}_{\omega^{\lambda+k,\mu+k}}\right)^{1/2}. \end{array} $$

(4.12)

Using the Jacobi-Gauss interpolation error estimate (see [43] page 133)

$$ \left\| {\partial^{k}_{x}} (U_{q}-\mathcal{I}_{x,N}^{\lambda,\mu}U_{q}) \right\|_{\omega^{\lambda+k,\mu+k}}\leq c N^{k-s} \left\| {\partial_{x}^{s}} U_{q} \right\|_{\omega^{\lambda+s,\mu+s}}, $$

(4.13)

it follows that

$$ \begin{array}{llll} \left\| {\partial^{k}_{x}}(\mathbf{U}-\mathcal{I}_{x,N}^{\lambda,\mu}\mathbf{U}) \right\|_{\omega^{\lambda+k,\mu+k}}& \leq c N^{k-s} \left( \sum\limits_{q=1}^{Q} \left\| {\partial_{x}^{s}} U_{q} \right\|^{2}_{\omega^{\lambda+s,\mu+s}} \right)^{1/2}\\ & = c N^{k-s} \left( \sum\limits_{q=1}^{Q} {\int}_{{\Lambda} } \omega^{\lambda+s,\mu+s} \left( {\partial_{x}^{s}} U_{q}(x)\right)^{2} dx \right)^{1/2}\\ & = c N^{k-s} \left( {\int}_{{\Lambda} } \sum\limits_{q=1}^{Q} \omega^{\lambda+s,\mu+s} \left( {\partial_{x}^{s}} U_{q}(x)\right)^{2} dx \right)^{1/2}\\ & \leq c N^{k-s} \left( {\int}_{{\Lambda} } \omega^{\lambda+s,\mu+s} \left( \left|{\partial_{x}^{s}} \mathbf{U}(x)\right|\right)^{2} dx \right)^{1/2}\\ &=c N^{k-s} \left\| {\partial_{x}^{s}} \mathbf{U} \right\|_{\omega^{\lambda+s,\mu+s}}. \end{array} $$

(4.14)

□

Lemma 4.2

For anyu ∈ H^s(Λ) with0 ≤ s ≤ N + 1,

$$ \left\| \mathbf{U}-\mathcal{I}_{x,N}\mathbf{U} \right\|_{\infty}\leq c N^{\frac{3}{4}-s} \left\| {\partial_{x}^{s}} \mathbf{U} \right\|. $$

(4.15)

Proof

Using the Sobolev inequality, we obtain

$$ \begin{array}{llll} \left\| (I-\mathcal{I}_{x,N})\mathbf{U} \right\|_{\infty}&= \left\| \sum\limits_{q=1}^{Q} \left| (I-\mathcal{I}_{x,N})U_{q} \right| \right\|_{\infty}\\ & \leq \sum\limits_{q=1}^{Q} \left\| (I-\mathcal{I}_{x,N})U_{q} \right\|_{\infty}\\ & \leq c \sum\limits_{q=1}^{Q} \left\| (I-\mathcal{I}_{x,N})U_{q} \right\|^{\frac{1}{2}} \left\| (I-\mathcal{I}_{x,N})U_{q} \right\|^{\frac{1}{2}}_{H^{1}({\Lambda} )}. \end{array} $$

(4.16)

Using (4.13) gives

$$ \begin{array}{llll} \left\| (I-\mathcal{I}_{x,N})\mathbf{U} \right\|_{\infty} \leq c \sum\limits_{q=1}^{Q} N^{-\frac{s}{2}} \left\| {\partial_{x}^{s}} U_{q} \right\|^{\frac{1}{2}} \left\| (I-\mathcal{I}_{x,N})U_{q} \right\|^{\frac{1}{2}}_{H^{1}({\Lambda} )}. \end{array} $$

(4.17)

The Legendre-Gauss interpolation error measured in the usual Sobolev space is given by (cf. [44], pp. 289)

$$ \left\| (I-\mathcal{I}_{x,N})U_{q} \right\|_{H^{1}({\Lambda} )} \leq c N^{\frac{3}{2}-s} \left\| {\partial_{x}^{s}} U_{q} \right\|. $$

(4.18)

Therefore,

$$ \begin{array}{llll} \left\| (I-\mathcal{I}_{x,N})\mathbf{U} \right\|_{\infty}&\leq c N^{\frac{3}{4}-s} \sum\limits_{q=1}^{Q} \left\| {\partial_{x}^{s}} U_{q} \right\|\leq c N^{\frac{3}{4}-s} Q \left\| {\partial_{x}^{s}} \mathbf{U} \right\|\\ & \leq c N^{\frac{3}{4}-s} \left\| {\partial_{x}^{s}} \mathbf{U} \right\|. \end{array} $$

(4.19)

□

Lemma 4.3 (cf. 45, pp. 330)

Let$\left \{ {F_{i}(x) } \right \}_{i = 0}^{N}$bethe N-th Lagrange interpolation polynomials associated with theN + 1 Gausspoints of the Jacobi polynomials. Then,

$$ \left\| {\mathcal{I}_{N}^{\lambda ,\mu } } \right\|_{\infty} : = \mathop {\max }\limits_{x \in {\Lambda} } \sum\limits_{i = 0}^{N} {\left| {F_{i} (x)} \right| = }\left\{\begin{array}{llll} \mathcal{O} \left( {\log N} \right),\quad - 1 < \lambda ,\mu \le - \frac{1}{2}, \\ \mathcal{O} \left( {N^{\gamma + \frac{1}{2}} } \right),\quad \gamma = \max (\lambda ,\ \mu ),\quad \text{otherwise.} \vphantom{\frac{5_A}{4,10^3}} \end{array}\right. $$

(4.20)

Let $\eta _{i}^{\lambda -1}$ be the Jacobi-Gauss nodes in Λ and $\sigma _{i}^{\lambda -1,0} = \sigma \left ({x,\eta _{i}^{\lambda -1,0} } \right )$. The mapped Jacobi-Gauss interpolation operator ${~}_{x} \widetilde {\mathcal {I}}_{\sigma ,N}^{\lambda -1,0}: C(- 1,x) \longrightarrow \mathcal {P}_{N} (- 1,x)$ is defined by

$$ {~}_{x} \widetilde{\mathcal{I}}_{\sigma ,N}^{\lambda-1,0} U_{q}\left( {\sigma_{i}^{\lambda-1,0} } \right) = U_{q}\left( {\sigma_{i}^{\lambda-1,0} } \right), \quad 0 \le i \le N. $$

(4.21)

Hence,

$$ {~}_{x}\widetilde{\mathcal{I}}_{\sigma ,N}^{\lambda-1,0} U_{q}\left( {\sigma_{i}^{\lambda-1,0} } \right) = U_{q}\left( {\sigma_{i}^{\lambda-1,0} } \right) = U_{q}\left( {\sigma (x,\eta_{i}^{\lambda-1,0} )} \right) = \mathcal{I}_{\eta ,N}^{\lambda-1,0} U_{q}\left( {\sigma (x,\eta_{i}^{\lambda-1,0} )} \right), $$

(4.22)

and

$$ {~}_{x}\widetilde{\mathcal{I}}_{\sigma ,N}^{\lambda-1,0} U_{q}\left( \sigma \right) = \left. {\mathcal{I}_{\eta,N}^{\lambda-1,0} U_{q}\left( {\sigma (x,\eta)} \right)} \right|_{\eta = \frac{{2\sigma }}{{x + 1}} + \frac{{1 - x}}{{1 + x}}}. $$

(4.23)

Accordingly, we can easily derive the following results

$$ \begin{array}{llll} {\int}_{-1}^{x} (x-\sigma)^{\lambda-1} {~}_{x} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} U_{q}(\sigma)d\sigma &=\left( \frac{1+x}{2}\right)^{\lambda} {\int}_{-1}^{1} (1-\eta)^{\lambda-1} \mathcal{I}_{\eta,N}^{\lambda-1,0}U_{q}\left( \sigma\left( x,\eta\right)\right)d\eta\\ &= \left( \frac{1+x}{2}\right)^{\lambda} \sum\limits_{j=0}^{N} U_{q} \left( \sigma(x,\eta_{j}^{\lambda-1,0})\right) \varpi_{j}^{\lambda-1,0}\\ &= \left( \frac{1+x}{2}\right)^{\lambda} \sum\limits_{j=0}^{N} U_{q} \left( \sigma_{j}^{\lambda-1,0}\right) \varpi_{j}^{\lambda-1,0}. \end{array} $$

(4.24)

Similarly,

$$ {\int}_{-1}^{x} (x-\sigma)^{\lambda-1} \left( {~}_{x} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} U_{q}(\sigma)\right)^{2} d\sigma= \left( \frac{1+x}{2}\right)^{\lambda} \sum\limits_{j=0}^{N} {U_{q}^{2}} \left( \sigma_{j}^{\lambda-1,0}\right) \varpi_{j}^{\lambda-1,0}. $$

(4.25)

Moreover, we have that for integer 1 ≤ s ≤ N + 1,

$$ \begin{array}{llll} &{\int}_{- 1}^{x} {(x - \sigma )^{\lambda-1} \left| {\left( \mathcal{I}- {~}_{x} \widetilde{\mathcal{I}}_{\sigma ,N}^{\lambda-1,0 } \right) \mathbf{U}\left( \sigma \right)} \right|^{2} d\sigma }\\ &\qquad \leq Q \left( {\frac{{1 + x}}{2}} \right)^{\lambda} {\int}_{- 1}^{1} {(1 - \eta)^{\lambda-1}\sum\limits_{q = 1}^{Q} \left| { U_{q}\left( {\sigma (x,\eta)} \right) - \mathcal{I}_{\eta,N}^{\lambda -1,0}U_{q}\left( {\sigma (x,\eta)} \right) } \right|^{2} d\eta}\\ &\qquad \le cN^{- 2s} \left( {\frac{{1 + x}}{2}} \right)^{\lambda} \sum\limits_{q = 1}^{Q} {\int}_{- 1}^{1} {(1 - \eta)^{\lambda + s-1 } (1 + \eta)^{s} \left| {\partial_{\eta}^{s} U_{q}\left( {\sigma (x,\eta)} \right)} \right|^{2} d\eta}\\ & \qquad = cN^{- 2s} {\int}_{- 1}^{x} {(x - \sigma )^{\lambda + s-1 } (1 + \sigma )^{s} \left| {\partial_{\sigma}^{s} \mathbf{U}(\sigma )} \right|^{2} d\sigma } . \end{array} $$

(4.26)

5 Convergence analysis in L²(Λ)

In this section, we analyze and characterize the convergence of the scheme (3.10). Our results generalize and extend the excellent results obtained in [25]. For convenience, we denote E = U(x) −U_N(x). Clearly,

$$ \left\| \mathbf{E} \right\| \leq \left\| \mathbf{U}-\mathcal{I}_{x,N} \mathbf{U} \right\| + \left\| \mathcal{I}_{x,N} \mathbf{U}- \mathbf{U}_{N} \right\|. $$

(5.1)

Lemma 5.1

The following inequality holds

$$ \left\| \mathbf{E} \right\| \leq \sum\limits_{j=1}^{5} \left\| \boldsymbol{E}_{j} \right\|. $$

(5.2)

where

$$ \begin{array}{llll} \mathbf{E}_{1} &=\mathbf{U}(x)-\mathcal{I}_{x,N} \mathbf{U}(x) ,\\ \mathbf{E}_{2} &=\mathcal{I}_{x,N} {\int}_{-1}^{x} \mathbf{R}(x,\sigma) (\mathcal{I}-{~}_{x} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0}) \mathbf{G}(\sigma,\mathbf{U}(\sigma)) d\sigma,\\ \mathbf{E}_{3} &=\mathcal{I}_{x,N} {\int}_{-1}^{x} \mathbf{R}(x,\sigma) {~}_{x} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} \left( \mathbf{G}(\sigma,\mathbf{U}(\sigma))-\mathbf{G}(\sigma,\mathbf{U}_{N}(\sigma))\right) d\sigma,\\ \mathbf{E}_{4} &= \frac{x+1}{2} {\int}_{-1}^{1} \mathbf{R}(1,\beta) \mathcal{I}_{\beta,N}^{\lambda-1,0} \left( \mathbf{G}(\beta,\mathbf{U}_{N}(\lambda))-\mathbf{G}(\beta,\mathbf{U}(\beta))\right) d\beta,\\ \mathbf{E}_{5} & =\frac{x+1}{2} {\int}_{-1}^{1} \mathbf{R}(1,\beta) \left( \mathcal{I}_{\beta,N}^{\lambda-1,0}-\mathcal{I}\right) \mathbf{G}(\beta,\mathbf{U}(\beta))d\beta, \end{array} $$

(5.3)

and R = (R_ij) with $R_{ij} = \frac {T^{\lambda }(x-\sigma )^{\lambda -1}}{2^{\lambda } {\Gamma }(\lambda )} \delta _{ij},\ i,\ j=1,\ldots ,Q.$

Proof

By (3.5), we get

$$ \begin{array}{llll} \mathcal{I}_{x,N} \mathbf{U}(x) &= \frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda)} \mathcal{I}_{x,N} {\int}_{-1}^{x} (x-\sigma)^{\lambda-1} \mathbf{G}\left( \sigma,\mathbf{U}(\sigma)\right)d \sigma - \frac{ T^{\lambda}(x+1)}{2^{\lambda+1} {\Gamma}(\lambda)} {\int}_{-1}^{1} (1-\beta)^{\lambda-1} \mathbf{G}\left( \beta,\mathbf{U}(\beta)\right)d\beta, \end{array} $$

(5.4)

and

$$ \begin{array}{llll} \mathbf{U}_{N}(x) &= \frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda)} \mathcal{I}_{x,N} {\int}_{-1}^{x} (x-\sigma)^{\lambda-1} {~}_{x} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} \mathbf{G}(\sigma,\mathbf{U}_{N}(\sigma))d\sigma\\ & \quad - \frac{T^{\lambda}(x+1)}{2^{\lambda+1} {\Gamma}(\lambda)} {\int}_{-1}^{1} (1-\beta)^{\lambda-1} \mathcal{I}_{\beta,N}^{\lambda-1,0} \mathbf{G} \left( \beta,\mathbf{U}_{N}(\beta) \right) d\beta. \end{array} $$

(5.5)

Subtracting (5.5) from (5.4) yields

$$ \begin{array}{llll} \mathcal{I}_{x,N} \mathbf{U}-\mathbf{U}_{N}(x) &= \frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda)} \mathcal{I}_{x,N} {\int}_{-1}^{x} (x-\sigma)^{\lambda-1}\left( \mathbf{G}(\sigma,\mathbf{U}(\sigma)) -{~}_{x} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} \mathbf{G}(\sigma,\mathbf{U}_{N}(\sigma))\right)d\sigma\\ & + \frac{T^{\lambda}(x+1)}{2^{\lambda+1} {\Gamma}(\lambda)} {\int}_{-1}^{1} (1-\beta)^{\lambda-1} \left( \mathcal{I}_{\beta,N}^{\lambda-1,0} \mathbf{G} \left( \beta,\mathbf{U}_{N}(\beta) \right) - \mathbf{G} \left( \beta,\mathbf{U}_{i}(\beta) \right) \right) d\beta{,} \end{array} $$

(5.6)

which can be rewritten as

$$ \begin{array}{llll} \mathcal{I}_{x,N} \mathbf{U} -\mathbf{U}_{N}(x) &=\mathcal{I}_{x,N} {\int}_{-1}^{x} \boldsymbol{R}(x,\sigma) (\mathcal{I}-{~}_{x} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0}) \mathbf{G}(\sigma,\mathbf{U}(\sigma)) d\sigma,\\ &+\mathcal{I}_{x,N} {\int}_{-1}^{x} \boldsymbol{R}(x,\sigma) {~}_{x} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} \left( \mathbf{G}(\sigma,\mathbf{U}(\sigma))-\mathbf{G}(\sigma,\mathbf{U}_{N}(\sigma))\right) d\sigma,\\ &+ \frac{x+1}{2} {\int}_{-1}^{1} \boldsymbol{R}(1,\eta) \mathcal{I}_{\eta,N}^{\lambda-1,0} \left( \mathbf{G}(\beta,\mathbf{U}_{N}(\lambda))-\mathbf{G}(\beta,\mathbf{U}(\beta))\right) d\beta,\\ & +\frac{x+1}{2} {\int}_{-1}^{1} \boldsymbol{R}(1,\beta) \left( \mathcal{I}_{\beta,N}^{\lambda-1,0}-\mathcal{I}\right) \mathbf{G}(\beta,\mathbf{U}(\beta))d\beta. \end{array} $$

(5.7)

Hence, the desired result is a direct consequence of (5.7). □

Throughout this section, we denote by $\mathbb {G}_{q}$ the Nemytskii operator corresponding to G_q, which is defined by $\mathbb {G}_{q}(\mathbf {U})(x):=G_{q}(x,\mathbf {U}(x))$. Moreover, we suppose that G_q fulfill the Lipschitz conditions with the Lipschitz constants L_q,i and $\mathop {\max }\limits _{1 \le i \le Q} \sum \limits _{q = 1}^{Q} {L_{q,i} } \le \frac {{{\Gamma } (\lambda + 1)}}{{2T^{\lambda } }}$.

Theorem 5.1

LetU(x) andU_N(x) bethe solutions of the system of (3.8) and (3.10), respectively. Assumethat$\mathbf {U} \in B^{s}_{\omega ^{s,s}}({\Lambda } )$,$\mathbb {G}_{q}: B^{s}_{\omega ^{s,s}}({\Lambda } ) \longrightarrow B^{s}_{\omega ^{\lambda +s-1,s}}({\Lambda } )$withinteger 1 ≤ s ≤ N + 1 andN ≥ 1.Then, we have the following estimate:

$$ \left\| \mathbf{U}-\mathbf{U}_{N} \right\| \leq c N^{-s} \left( \left\| {\partial_{x}^{s}} \mathbf{U} \right\|_{\omega^{s,s}}+\left\| {\partial_{x}^{s}} \mathbf{G}(\cdot,\mathbf{U}(\cdot)) \right\|_{\omega^{\lambda+s-1,s}}\right). $$

(5.8)

Proof

By Lemma 4.1, we get

$$ \left\|\mathbf{E}_{1}\right\| =\left\|\mathbf{U}(x)-\mathcal{I}_{x,N} \mathbf{U}(x)\right\| \leq CN^{-s} \left\| {\partial_{x}^{s}} \mathbf{U} \right\|_{\omega^{s,s}}. $$

(5.9)

We next estimate the term $\left \|\mathbf {E}_{2} \right \|$. Using the Legendre-Gauss integration formula (2.8), we have

$$ \begin{array}{llll} \left\|\mathbf{E}_{2} \right\|^{2} &=\left\|\mathcal{I}_{x,N} {\int}_{-1}^{x} \mathbf{R}(x,\sigma) (\mathcal{I}-{~}_{x} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0}) \mathbf{G}\left( \sigma,\mathbf{U}(\sigma)\right) d\sigma\right\|^{2}\\ &= \left\| \sum\limits_{q=1}^{Q}\mathcal{I}_{x,N} {\int}_{-1}^{x} R_{qq}(x,\sigma) (\mathcal{I}-{~}_{x} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0}) G_{q}(\sigma,\mathbf{U}(\sigma)) d\sigma\right\|^{2}\\ &= {\int}_{-1}^{1} \left( \sum\limits_{q=1}^{Q}\mathcal{I}_{x,N} {\int}_{-1}^{x} R_{qq}(x,\sigma) (\mathcal{I}-{~}_{x} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0}) G_{q}(\sigma,\mathbf{U}(\sigma)) d\sigma\right)^{2} dx\\ &= \sum\limits_{j=0}^{N} w_{j} \left( \sum\limits_{q=1}^{Q} {\int}_{-1}^{x_{j}} R_{qq}(x_{j},\sigma) (\mathcal{I}-{~}_{x_{j}} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0}) G_{q}(\sigma,\mathbf{U}(\sigma)) d\sigma\right)^{2}. \end{array} $$

(5.10)

Then, by the Cauchy-Schwarz inequality, we deduce that

$$ \begin{array}{llll} \left\|\mathbf{E}_{2} \right\|^{2} &\leq \sum\limits_{j=0}^{N} w_{j} \sum\limits_{q=1}^{Q} \left( {\int}_{-1}^{x_{j}} R_{qq}(x_{j},\sigma) (\mathcal{I}-{~}_{x_{j}} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0}) G_{q}(\sigma,\mathbf{U}(\sigma)) d\sigma\right)^{2} \sum\limits_{q=1}^{Q}(1)^{2} \\ &\leq C \sum\limits_{j=0}^{N} \sum\limits_{q=1}^{Q} w_{j} {\int}_{-1}^{x_{j}} R_{qq}(x_{j},\sigma) d\sigma {\int}_{-1}^{x_{j}} R_{qq}(x_{j},\sigma) \left| (\mathcal{I}-{~}_{x_{j}} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0}) G_{q}(\sigma,\mathbf{U}(\sigma))\right|^{2} d\sigma \\ &= C \sum\limits_{j=0}^{N} \sum\limits_{q=1}^{Q} w_{j} (x_{j}+1)^{\lambda} {\int}_{-1}^{x_{j}} (x_{j}-\sigma)^{\lambda-1} \left| (\mathcal{I}-{~}_{x_{j}} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0}) G_{q}(\sigma,\mathbf{U}(\sigma))\right|^{2} d\sigma. \end{array} $$

(5.11)

By (4.26), we get that

$$ \begin{array}{llll} \left\|\mathbf{E}_{2} \right\|^{2} & \leq C N^{-2s} \sum\limits_{q=1}^{Q} {\int}_{-1}^{x} \left| \partial_{\sigma}^{s} G_{q}(\sigma,\mathbf{U}(\sigma)) \right|^{2} (x-\sigma)^{\lambda+s-1} (1+\sigma)^{s} d\sigma\\ & \leq C N^{-2s} {\int}_{-1}^{x} \sum\limits_{q=1}^{Q} \left| \partial_{\sigma}^{s} G_{q}(\sigma,\mathbf{U}(\sigma)) \right|^{2} (x-\sigma)^{\lambda+s-1} (1+\sigma)^{s} d\sigma\\ & \leq C N^{-2s} {\int}_{-1}^{x} \left| \partial_{\sigma}^{s} \mathbf{G}(\sigma,\mathbf{U}(\sigma)) \right|^{2} (x-\sigma)^{\lambda+s-1} (1+\sigma)^{s} d\sigma\\ &\leq C N^{-2s} \left\| \partial_{\sigma}^{s} \mathbf{G}(\sigma,\mathbf{U}(\sigma)) \right\|^{2}_{\omega^{\lambda+s-1,s}}. \end{array} $$

(5.12)

We now estimate the term $\left \|\mathbf {E}_{3} \right \|$. Using the Legendre-Gauss integration formula (2.8), we have

$$ \begin{array}{llll} &\left\|\mathbf{E}_{3} \right\| \\ &= \left\| \mathcal{I}_{x,N} {\int}_{-1}^{x} \mathbf{R}(x,\sigma) {~}_{x}\widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} \left( \mathbf{G}(\sigma,\mathbf{U}(\sigma))-\mathbf{G}(\sigma,\mathbf{U}_{N}(\sigma))\right) d\sigma \right\|\\ &=\left( {\int}_{-1}^{1} \left( \sum\limits_{q=1}^{Q} \mathcal{I}_{x,N} {\int}_{-1}^{x} \frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda)} (x-\sigma)^{\lambda-1} {~}_{x}\widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} \left( G_{q}\left( \sigma,\mathbf{U}(\sigma)\right)-G_{q}\left( \sigma,\mathbf{U}_{N}(\sigma)\right) \right)d\sigma \right)^{2} dx\right)^{\frac{1}{2}}\\ &=\frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda)}\left( \sum\limits_{j=0}^{N} \varpi_{j} \left( {\int}_{-1}^{x_{j}} (x_{j}-\sigma)^{\lambda-1}\sum\limits_{q=1}^{Q} {~}_{x_{j}}\widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} \left( G_{q}\left( \sigma,\mathbf{U}(\sigma)\right)-G_{q}\left( \sigma,\mathbf{U}_{N}(\sigma)\right) \right)d\sigma \right)^{2}\right)^{\frac{1}{2}} \\ & \leq \frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda)} \left( \sum\limits_{j=0}^{N} \varpi_{j} {\int}_{-1}^{x_{j}} (x_{j} - \sigma)^{\lambda-1} d\sigma {\int}_{-1}^{x_{j}}(x_{j} - \sigma)^{\lambda-1} \left( \left| \sum\limits_{q=1}^{Q} {~}_{x_{j}}\widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} \left( G_{q}(\sigma,\mathbf{U}(\sigma)) - G_{q}(\sigma,\mathbf{U}_{N}(\sigma))\right) \right| \right)^{2} d\sigma\right)^{\frac{1}{2}} \\ & \leq \frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda)} \left( \sum\limits_{j=0}^{N} \varpi_{j} \frac{(x_{j}+1)^{\lambda}}{\lambda} {\int}_{-1}^{x_{j}}(x_{j}-\sigma)^{\lambda-1} \left( \sum\limits_{q=1}^{Q} \left| {~}_{x_{j}}\widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} \left( G_{q}(\sigma,\mathbf{U}(\sigma))-G_{q}(\sigma,\mathbf{U}_{N}(\sigma))\right) \right| \right)^{2} d\sigma \right)^{\frac{1}{2}} \\ & \leq \frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda)} \left( \sum\limits_{j=0}^{N} \varpi_{j} \frac{(x_{j}+1)^{2\lambda}}{2^{\lambda}\lambda} \sum\limits_{k=0}^{N} \left( \sum\limits_{q=1}^{Q} \left|G_{q}(\sigma_{k}^{\lambda-1,0},\mathbf{U}(\sigma_{k}^{\lambda-1,0}))-G_{q}(\sigma_{k}^{\lambda-1,0},\mathbf{U}_{N}(\sigma_{k}^{\lambda-1,0})) \right|\right)^{2} \varpi_{k}^{\lambda-1,0}\right)^{\frac{1}{2}}. \end{array} $$

(5.13)

For x_j ∈ (− 1,1), we know that

$$ \sum\limits_{j=0}^{N} \varpi_{j} (x_{j}+1)^{\lambda}\leq \frac{8}{3}, \quad \forall \lambda \in [1,2]. $$

(5.14)

Therefore, by (4.25), (4.26), (5.14), the Lipschitz condition, and the triangle inequality, we obtain that

$$ \begin{array}{llll} & \left\|\mathbf{E}_{3} \right\|\\ & \leq \frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda)} \left( \sum\limits_{j=0}^{N} \varpi_{j} \frac{(x_{j}+1)^{2\lambda}}{2^{\lambda}\lambda} \sum\limits_{k=0}^{N} \left( \sum\limits_{q=1}^{Q} \sum\limits_{i=1}^{Q} L_{q,i} \left| U_{i}(\sigma_{k}^{\lambda-1,0})-U_{N,i}(\sigma_{k}^{\lambda-1,0}) \right|\right)^{2} \varpi_{k}^{\lambda-1,0} \right)^{\frac{1}{2}}\\ & = \frac{\lambda}{ 2^{\lambda+1}}\left( \sum\limits_{j=0}^{N} \varpi_{j} \frac{(x_{j}+1)^{2\lambda}}{2^{\lambda}\lambda} \sum\limits_{k=0}^{N} \left( \sum\limits_{i=1}^{Q} \left| U_{i}(\sigma_{k}^{\lambda-1,0})-U_{N,i}(\sigma_{k}^{\lambda-1,0}) \right|\right)^{2} \varpi_{k}^{\lambda-1,0} \right)^{\frac{1}{2}}\\ & \leq \frac{\lambda}{ 2^{\lambda+1}} \left( \sum\limits_{j=0}^{N} \varpi_{j} \frac{(x_{j}+1)^{\lambda}}{\lambda} {\int}_{-1}^{x_{j}} (x_{j}-\sigma)^{\lambda-1} \left( \sum\limits_{i=1}^{Q}\left| {~}_{x_{j}}\widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} \left( U_{i}(\sigma)-{U_{N,i}}(\sigma) \right) \right|\right)^{2} d\sigma\right)^{\frac{1}{2}}\\ & \leq \frac{\lambda}{ 2^{\lambda+1}} \left( \sum\limits_{j=0}^{N} \varpi_{j} \frac{(x_{j}+1)^{\lambda}}{\lambda}\right)^{\frac{1}{2}} \max\limits_{0\leq j \leq N} \left( {\int}_{-1}^{x_{j}} (x_{j}-\sigma)^{\lambda-1} \left( \sum\limits_{i=1}^{Q} \left| {~}_{x_{j}}\widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} \left( U_{i}(\sigma)-U_{N,i}(\sigma) \right) \right|\right)^{2} d\sigma\right)^{\frac{1}{2}}\\ & \leq \frac{\lambda}{ 2^{\lambda+1}} \sqrt{\frac{8}{3 \lambda}} \max\limits_{0\leq j \leq N} \left[ \left( {\int}_{-1}^{x_{j}} (x_{j}-\sigma)^{\lambda-1} \left( \sum\limits_{i=1}^{Q} \left|{~}_{x_{j}}\widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} U_{i}(\sigma)-U_{i}(\sigma) \right| \right)^{2} d\sigma \right)^{\frac{1}{2}} \right.\\ & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \left. + \left( {\int}_{-1}^{x_{j}} (x_{j}-\sigma)^{\lambda-1} \left( \sum\limits_{i=1}^{Q} \left| U_{i}(\sigma)-U_{N,i}(\sigma) \right| \right)^{2} d\sigma\right)^{\frac{1}{2}} \right]\\ &\leq cN^{-s} \max\limits_{0\leq j \leq N} \left( {\int}_{-1}^{x_{j}} (x_{j}-\sigma)^{\lambda+s-1} (1+\sigma)^{s} \left( \sum\limits_{i=1}^{Q}\left| \partial_{\sigma}^{s} U_{i}(\sigma) \right|\right)^{2}d\sigma\right)^{\frac{1}{2}}\\ & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + \frac{\lambda}{ 2^{\lambda+1}} { \sqrt{\frac{8 }{3 \lambda}}}\max\limits_{0\leq j \leq N} \left( {\int}_{-1}^{x_{j}} (x_{j}-\sigma)^{\lambda-1} \left( \sum\limits_{i=1}^{Q} \left| U_{i}(\sigma)-U_{N,i}(\sigma) \right| \right)^{2} d\sigma\right)^{\frac{1}{2}}\\ &\leq cN^{-s} \left\|\partial_{\sigma}^{s} \mathbf{U} \right\|_{\omega^{\lambda+s-1,s}}+ \frac{\lambda}{ 2^{\lambda+1}} \sqrt{\frac{2^{\lambda+2}}{3 \lambda}} \left( {\int}_{-1}^{1} \left( \sum\limits_{i=1}^{Q} \left| U_{i}(\sigma)-U_{N,i}(\sigma) \right| \right)^{2} d\sigma\right)^{\frac{1}{2}}\\ &\leq cN^{-s} \left\|\partial_{\sigma}^{s} \mathbf{U} \right\|_{\omega^{\lambda+s-1,s}}+ \sqrt{\frac{\lambda}{3 \times 2^{\lambda} }} \left\| \mathbf{E} \right\|. \end{array} $$

(5.15)

We now estimate the following term

$$ \begin{array}{llll} \left\|\boldsymbol{E}_{4} \right\| &= \frac{\left\|x+1\right\|}{2} \left|{\int}_{-1}^{1} \boldsymbol{R}(1,\beta) \mathcal{I}_{\beta,N}^{\lambda-1,0} \left( \mathbf{G}(\beta,\mathbf{U}_{N}(\beta))-\mathbf{G}(\beta,\mathbf{U}(\beta))\right) d\beta\right|\\ &= \frac{T^{\lambda} \left\|x+1\right\|}{2^{\lambda+1} {\Gamma}(\lambda)} \left|{\int}_{-1}^{1} \sum\limits_{q=1}^{Q} (1-\beta)^{\lambda-1} \mathcal{I}_{\beta,N}^{\lambda-1,0} \left( G_{q}(\beta,\mathbf{U}_{N}(\beta))-G_{q}(\beta,\mathbf{U}(\beta))\right) d\beta\right|\\ & \leq \frac{T^{\lambda}}{2^{\lambda+1} {\Gamma}(\lambda)} \sqrt{\frac{2^{\lambda+3}}{3 \lambda}} \left( {\int}_{-1}^{1} (1-\beta)^{\lambda-1} \left( \sum\limits_{q=1}^{Q} \left| \mathcal{I}_{\beta,N}^{\lambda-1,0} \left( G_{q}(\beta,\mathbf{U}_{N}(\beta))-G_{q}(\beta,\mathbf{U}(\beta))\right) d\beta\right| \right)^{2} \right)^{\frac{1}{2}}\\ & \leq \frac{T^{\lambda}}{2^{\lambda+1} {\Gamma}(\lambda)} \sqrt{\frac{2^{\lambda+3}}{3 \lambda}} \left( \sum\limits_{j=0}^{N} \varpi_{j}^{\lambda-1 ,0 } \left( \sum\limits_{q=1}^{Q} \left| \left( G_{q}(x_{j}^{\lambda-1,0},\mathbf{U}_{N}(x_{j}^{\lambda-1,0}))-G_{q}(x_{j}^{\lambda-1,0},\mathbf{U}(x_{j}^{\lambda-1,0}))\right) \right|\right)^{2}\right)^{\frac{1}{2}}\\ & \leq \frac{T^{\lambda}}{2^{\lambda+1} {\Gamma}(\lambda)} \sqrt{\frac{2^{\lambda+3}}{3 \lambda}} \left( \sum\limits_{j=0}^{N} \varpi_{j}^{\lambda-1 ,0 } \left( \sum\limits_{q=1}^{Q} \sum\limits_{i=1}^{Q} L_{q,i} \left| U_{N,i}(x_{j}^{\lambda-1,0}))-U_{i}(x_{j}^{\lambda-1,0})) \right|\right)^{2}\right)^{\frac{1}{2}}\\ & \leq \frac{ \lambda }{2^{\lambda+2}} \sqrt{\frac{2^{\lambda+3}}{3 \lambda}} \left( \sum\limits_{j=0}^{N} \varpi_{j}^{\lambda-1 ,0 } \left( \sum\limits_{i=1}^{Q} \left| U_{N,i}(x_{j}^{\lambda-1,0})-U_{i}(x_{j}^{\lambda-1,0}) \right|\right)^{2}\right)^{\frac{1}{2}}\\ & = \frac{ \lambda }{2^{\lambda+2}} \sqrt{\frac{2^{\lambda+3}}{3 \lambda}} \left( {\int}_{-1}^{1} (1-\beta)^{\lambda-1}\left( \sum\limits_{i=1}^{Q} \left| U_{N,i}(\beta)-\mathcal{I}_{\beta,N}^{\lambda-1,0}U_{i}(\beta)\right|\right)^{2} d\beta\right)^{\frac{1}{2}} \\ & \leq \sqrt{\frac{\lambda}{3 \times 2^{\lambda+1} }} \left( \left\| \boldsymbol{U_{N}}-\mathbf{U} \right\|_{\omega^{\lambda-1,0}} + \left\| \mathbf{U}-\mathcal{I}_{\beta,N}^{\lambda-1,0}\mathbf{U} \right\|_{\omega^{\lambda-1,0}} \right)\\ & \leq \sqrt{\frac{\lambda}{12}} \left\| \mathbf{E} \right\| + cN^{-s} {\left\|{\partial_{x}^{s}} \mathbf{U} \right\| }_{\omega^{\lambda+s-1,s}}. \end{array} $$

(5.16)

It remains to estimate the term $\left \| \boldsymbol {E}_{5} \right \|$. By Lemma 4.1 and (4.26), we have

$$ \begin{array}{llll} \left\| \boldsymbol{E}_{5} \right\| & =\frac{\left\| x+1 \right\|}{2} \left| {\int}_{-1}^{1} \boldsymbol{R}(1,\beta) \left( \mathcal{I}_{\beta,N}^{\lambda-1,0}-\mathcal{I}\right) \mathbf{G}(\beta,\mathbf{U}(\beta))\right| d\beta\\ & = \frac{T^{\lambda}}{2^{\lambda+1} {\Gamma}(\lambda)} \sqrt{\frac{8}{3}} {\int}_{-1}^{1} (1-\beta)^{\lambda-1} \left| \sum\limits_{q=1}^{Q}\left( \mathcal{I}_{\beta,N}^{\lambda-1,0}-\mathcal{I}\right) G_{q}(\beta,\mathbf{U}(\beta))\right| d\beta\\ & \leq c \left( {\int}_{-1}^{1} (1-\beta)^{\lambda-1} d\beta\right)^{\frac{1}{2}} \left( {\int}_{-1}^{1} (1-\beta)^{\lambda-1} \left( \sum\limits_{q=1}^{Q} \left|\left( \mathcal{I}_{\beta,N}^{\lambda-1,0}-\mathcal{I}\right) G_{q}(\beta,\mathbf{U}(\beta))\right|\right)^{2} d\beta\right)^{\frac{1}{2}}\\ & \leq cN^{-s} {\left\|{\partial_{x}^{s}} \mathbf{G} \left( \cdot ,\mathbf{U}(\cdot)\right) \right\| }_{\omega^{\lambda+s-1,s}}. \end{array} $$

(5.17)

□

Theorem 5.2

Let$\mathbf {u}_{N}(t):={\mathbf {U}}_{N}\left ({\frac {{2t}}{T} - 1} \right )$bethe numerical solution of the system of (1.1) witht ∈ (0,T) andχ^λ,μ(t) := (T − t)^λt^μ.Then, we have the following estimate:

$$ \left\| \mathbf{u}-\mathbf{u}_{N} \right\| \leq c N^{-s} \left( \left\| {\partial_{t}^{s}} \mathbf{u} \right\|_{\chi^{s,s}}+\left\| {\partial_{t}^{s}} \mathbf{g}(\cdot,\mathbf{u}(\cdot)) \right\|_{\chi^{\lambda+s-1,s}}\right). $$

(5.18)

6 Convergence analysis in $L^{\infty }({\Lambda } )$

In this section, we derive the error estimation in the function space $L^{\infty }({\Lambda } )$.

Theorem 6.1

LetU(x) andU_N(x) bethe solutions of the system of (3.8) and (3.10), respectively. Assumethat$\mathbf {U} \in L^{\infty } \cap B^{s}({\Lambda } )$,$\mathbb {G}_{q}: B^{s}({\Lambda } ) \longrightarrow B^{s}_{\omega ^{\lambda +s-1,s}}({\Lambda } )$with1 ≤ s ≤ N + 1 andN ≥ 1.Then, we have the following estimate:

$$ \left\| \mathbf{U}-\mathbf{U}_{N} \right\|_{\infty} \leq c N^{\frac{3}{4}-s} \left\| {\partial_{x}^{s}} \mathbf{U} \right\|+ c N^{\frac{1}{2}-s} \left\| {\partial_{x}^{s}} \mathbf{G}(\cdot,\mathbf{U}(\cdot)) \right\|_{\omega^{\lambda+s-1,s}}. $$

(6.1)

Proof

It follows from (5.1) that

$$ \left\| \mathbf{E} \right\|_{\infty} \leq \left\| \mathbf{U}- \mathcal{I}_{x,N}\mathbf{U} \right\|_{\infty} + \left\| \mathcal{I}_{x,N}\mathbf{U} - \mathbf{U}_{N} \right\|_{\infty} \leq \sum\limits_{i=1}^{5} \left\| \mathbf{E}_{i} \right\|_{\infty}. $$

(6.2)

Using Lemma 4.2 gives

$$ \begin{array}{llll} \left\| \mathbf{E}_{1} \right\|_{\infty} &= \left\| {\mathbf{U} - \mathcal{I}_{x,N} \mathbf{U}} \right\|_{\infty} \leq c N^{\frac{3}{4}-s} \left\| {\partial_{x}^{s}} \mathbf{U} \right\|. \end{array} $$

(6.3)

Next, by Lemma 4.3, we deduce that

$$ \begin{array}{llll} \left|\boldsymbol{E}_{2}\right| &=\left|\mathcal{I}_{x,N} {\int}_{-1}^{x} \boldsymbol{R}(x,\sigma) \left( \mathcal{I}-{~}_{x} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0}\right) \mathbf{G}(\sigma,\mathbf{U}(\sigma)) d\sigma\right|\\ &=\frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda)} \left| \mathcal{I}_{x,N} {\int}_{-1}^{x} \left( x-\sigma\right)^{\lambda-1} \sum\limits_{q=1}^{Q} \left( \mathcal{I}-{~}_{x} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0}\right) G_{q}(\sigma,\mathbf{U}(\sigma)) d\sigma \right|\\ & \leq \frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda)} \left\| \mathcal{I}_{x,N} \right\|_{\infty} \max\limits_{-1 \leq x \leq 1} \left| {\int}_{-1}^{x} \left( x-\sigma\right)^{\lambda-1} \sum\limits_{q=1}^{Q} \left( \mathcal{I}-{~}_{x} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0}\right) G_{q}(\sigma,\mathbf{U}(\sigma)) d\sigma \right|\\ & \leq c N^{\frac{1}{2}} \max\limits_{-1 \leq x \leq 1} {\int}_{-1}^{x} \left( x-\sigma\right)^{\lambda-1} \left| \sum\limits_{q=1}^{Q} \left( \mathcal{I}-{~}_{x} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0}\right) G_{q}(\sigma,\mathbf{U}(\sigma)) d\sigma \right|\\ & \leq c N^{\frac{1}{2}} \max\limits_{-1 \leq x \leq 1} {\int}_{-1}^{x} \left( x-\sigma\right)^{\lambda-1} \sum\limits_{q=1}^{Q} \left| \left( \mathcal{I}-{~}_{x} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0}\right) G_{q}(\sigma,\mathbf{U}(\sigma)) d\sigma \right|. \end{array} $$

(6.4)

By the Cauchy-Schwarz inequality and (4.26),

$$ \begin{array}{llll} \left|\boldsymbol{E}_{2}\right|& \leq c N^{\frac{1}{2}} \max\limits_{-1 \leq x \leq 1} \left[ {\int}_{-1}^{x} \left( x-\sigma\right)^{\lambda-1} d\sigma\right.\\ & \left.\quad \quad \quad \quad \quad \quad \quad \quad \times {\int}_{-1}^{x} \left( x-\sigma\right)^{\lambda-1} \left( \sum\limits_{q=1}^{Q} \left| \left( \mathcal{I}-{~}_{x} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0}\right) G_{q}(\sigma,\mathbf{U}(\sigma))\right|\right)^{2} d\sigma \right]^{\frac{1}{2}} \\ & \leq c N^{\frac{1}{2}} \max\limits_{-1 \leq x \leq 1} \left[ {\int}_{-1}^{x} \left( x-\sigma\right)^{\lambda-1} \left( \sum\limits_{q=1}^{Q} \left| \left( \mathcal{I}-{~}_{x} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0}\right) G_{q}(\sigma,\mathbf{U}(\sigma))\right|\right)^{2} d\sigma \right]^{\frac{1}{2}} \\ & \leq c N^{\frac{1}{2}-s} \max\limits_{-1 \leq x \leq 1} \left[ {\int}_{-1}^{x} \left( x-\sigma \right)^{\lambda+s-1} \left( 1+\sigma \right)^{s} \left| \sum\limits_{q=1}^{Q} \partial_{\sigma}^{s} G_{q}(\sigma,\mathbf{U}(\sigma)) \right|^{2} d\sigma \right]^{\frac{1}{2}}\\ & \leq cN^{\frac{1}{2}-s} {\left\|\partial_{\sigma}^{s} \mathbf{G} \left( \cdot,\mathbf{U}(\cdot)\right) \right\|^{2} }_{\omega^{\lambda+s-1,s}}. \end{array} $$

(6.5)

Similarly, using Lemma 4.3 leads to

$$ \begin{array}{llll} \left|\boldsymbol{E}_{3}\right|&= \left|\mathcal{I}_{x,N} {\int}_{-1}^{x} \boldsymbol{R}(x,\sigma) {~}_{x} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} \left( \mathbf{G}(\sigma,\mathbf{U}(\sigma))-\mathbf{G}(\sigma,\mathbf{U}_{N}(\sigma))\right) d\sigma\right|\\ &= \frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda)} \left|\mathcal{I}_{x,N} {\int}_{-1}^{x} (x-\sigma)^{\lambda-1} \sum\limits_{q=1}^{Q} {~}_{x} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} \left( G_{q}(\sigma,\mathbf{U}(\sigma))-\mathbf{G}(\sigma,\mathbf{U}_{N}(\sigma))\right) d\sigma\right|\\ & \leq c \left\| \mathcal{I}_{x,N} \right\|_{\infty} \max\limits_{-1 \leq x \leq 1} \left| {\int}_{-1}^{x} (x-\sigma)^{\lambda-1} \sum\limits_{q=1}^{Q} {~}_{x} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} \left( G_{q}(\sigma,\mathbf{U}(\sigma))-\mathbf{G}(\sigma,\mathbf{U}_{N}(\sigma))\right) d\sigma\right|\\ & \leq c N^{\frac{1}{2}} \max\limits_{-1 \leq x \leq 1} {\int}_{-1}^{x} (x-\sigma)^{\lambda-1} \left| \sum\limits_{q=1}^{Q} {~}_{x} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} \left( G_{q}(\sigma,\mathbf{U}(\sigma))-\mathbf{G}(\sigma,\mathbf{U}_{N}(\sigma))\right) d\sigma\right|\\ & \leq c N^{\frac{1}{2}} \max\limits_{-1 \leq x \leq 1} {\int}_{-1}^{x} (x-\sigma)^{\lambda-1} \sum\limits_{q=1}^{Q} \left| {~}_{x} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} \left( G_{q}(\sigma,\mathbf{U}(\sigma))-\mathbf{G}(\sigma,\mathbf{U}_{N}(\sigma))\right) d\sigma\right|\\ & \leq c N^{\frac{1}{2}} \max\limits_{-1 \leq x \leq 1} \left[{\int}_{-1}^{x} (x-\sigma)^{\lambda-1} d\sigma\right.\\ &\left.\quad \quad \quad \quad \times {\int}_{-1}^{x} (x-\sigma)^{\lambda-1} \left( \sum\limits_{q=1}^{Q} \left| {~}_{x} \widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} \left( G_{q}(\sigma,\mathbf{U}(\sigma))-\mathbf{G}(\sigma,\mathbf{U}_{N}(\sigma))\right) d\sigma\right|\right)^{2}\right]^{\frac{1}{2}}\\ & \leq c N^{\frac{1}{2}} \max\limits_{-1 \leq x \leq 1} \left[ \frac{(x+1)^{\lambda}}{2^{\lambda}} \sum\limits_{k=0}^{N} \left( \sum\limits_{q=1}^{Q} \left|G_{q}(\sigma_{k}^{\lambda-1,0},\mathbf{U}(\sigma_{k}^{\lambda-1,0}))-G_{q}(\sigma_{k}^{\lambda-1,0},\mathbf{U}_{N}(\sigma_{k}^{\lambda-1,0})) \right|\right)^{2} \omega_{k}^{\lambda-1,0} \right]^{\frac{1}{2}}. \end{array} $$

(6.6)

Further, by the triangle inequality, (4.25), and (4.26), we deduce that

$$ \begin{array}{llll} \left|\boldsymbol{E}_{3}\right| & \leq c N^{\frac{1}{2}} \max\limits_{-1 \leq x \leq 1} \left[\frac{(x+1)^{\lambda}}{2^{\lambda}} \sum\limits_{k=0}^{N} \left( \sum\limits_{i=1}^{Q} \left| U_{i}(\sigma_{k}^{\lambda-1,0})-U_{N,i}(\sigma_{k}^{\lambda-1,0}) \right|\right)^{2} \omega_{k}^{\lambda-1,0} \right]^{\frac{1}{2}}\\ & \leq c N^{\frac{1}{2}} \max\limits_{-1 \leq x \leq 1} \left[{\int}_{-1}^{x} (x-\sigma)^{\lambda-1} \left( \sum\limits_{i=1}^{Q} \left|{~}_{x}\widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} U_{i}(\sigma)-U_{N,i}(\sigma) \right|\right)^{2} d\sigma \right]^{\frac{1}{2}}\\ & \leq c N^{\frac{1}{2}} \max\limits_{-1 \leq x \leq 1} \left[{\int}_{-1}^{x} (x-\sigma)^{\lambda-1} \left( \sum\limits_{i=1}^{Q} \left|{~}_{x}\widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} U_{i}(\sigma)-U_{N,i}(\sigma) \right|\right)^{2} d\sigma\right.\\ &\left. \quad\quad\quad\quad\quad\quad\quad+ {\int}_{-1}^{x} (x-\sigma)^{\lambda-1} \left( \sum\limits_{i=1}^{Q} \left| U_{i}(\sigma)-U_{N,i}(\sigma) \right|\right)^{2} d\sigma \right]^{\frac{1}{2}}\\ & \leq cN^{\frac{1}{2}-s} {\left\|{\partial_{x}^{s}} \mathbf{U} \right\| }_{\omega^{\lambda+s-1,s}}+cN^{\frac{1}{2}} \left\| \mathbf{E} \right\|. \end{array} $$

(6.7)

We obtain from the Cauchy-Schwarz inequality that

$$ \begin{array}{llll} \left|\boldsymbol{E}_{4}\right| & = \left| \frac{x+1}{2} {\int}_{-1}^{1} \boldsymbol{R}(1,\beta) \mathcal{I}_{\beta,N}^{\lambda-1,0} \left( \mathbf{G}(\beta,\mathbf{U}_{N}(\lambda))-\mathbf{G}(\beta,\mathbf{U}(\beta))\right) d\beta\right|\\ & = \left| \frac{T^{\lambda} (x+1)}{2^{\lambda+1} {\Gamma}(\lambda)} {\int}_{-1}^{1} \sum\limits_{q=1}^{Q} (1-\beta)^{\lambda-1} \mathcal{I}_{\beta,N}^{\lambda-1,0} \left( G_{q}(\beta,\mathbf{U}_{N}(\lambda))-G_{q}(\beta,\mathbf{U}(\beta))\right) d\beta\right|\\ & \leq \frac{T^{\lambda} }{2^{\lambda} {\Gamma}(\lambda)} {\int}_{-1}^{1} (1-\beta)^{\lambda-1} \left| \sum\limits_{q=1}^{Q} \mathcal{I}_{\beta,N}^{\lambda-1,0} \left( G_{q}(\beta,\mathbf{U}_{N}(\lambda))-G_{q}(\beta,\mathbf{U}(\beta))\right) d\beta\right|\\ & \leq \frac{T^{\lambda} }{2^{\lambda} {\Gamma}(\lambda)} {\int}_{-1}^{1} (1-\beta)^{\lambda-1} \sum\limits_{q=1}^{Q} \left| \mathcal{I}_{\beta,N}^{\lambda-1,0} \left( G_{q}(\beta,\mathbf{U}_{N}(\lambda))-G_{q}(\beta,\mathbf{U}(\beta))\right) d\beta\right| \end{array} $$

$$ \begin{array}{llll} & \leq \frac{T^{\lambda} }{2^{\lambda} {\Gamma}(\lambda)} \left( {\int}_{-1}^{1} (1-\beta)^{\lambda-1} d\beta \right.\\ & \quad\quad\quad\quad\quad \left. \times {\int}_{-1}^{1} (1-\beta)^{\lambda-1} \left( \sum\limits_{q=1}^{Q} \left| \mathcal{I}_{\beta,N}^{\lambda-1,0} \left( G_{q}(\beta,\mathbf{U}_{N}(\lambda))-G_{q}(\beta,\mathbf{U}(\beta))\right) d\beta\right|\right)^{2} \right)^{\frac{1}{2}}\\ & \leq \frac{T^{\lambda} }{2^{\lambda} {\Gamma}(\lambda)} \left( \frac{2^{\lambda}}{\lambda}\right)^{\frac{1}{2}} \left( {\int}_{-1}^{1} (1-\beta)^{\lambda-1} \left( \sum\limits_{q=1}^{Q} \left| \mathcal{I}_{\beta,N}^{\lambda-1,0} \left( G_{q}(\beta,\mathbf{U}_{N}(\lambda))-G_{q}(\beta,\mathbf{U}(\beta))\right) d\beta\right|\right)^{2} \right)^{\frac{1}{2}}. \end{array} $$

(6.8)

Hence, a combination of the above result, (4.25), (4.26), Lemma 4.1, and the Lipschitz condition yields

$$ \begin{array}{llll} \left|\boldsymbol{E}_{4}\right| & \leq \frac{T^{\lambda} }{2^{\lambda} {\Gamma}(\lambda)} \left( \frac{2^{\lambda}}{\lambda}\right)^{\frac{1}{2}} \left( \sum\limits_{j=0}^{N} \varpi_{j}^{\lambda-1 ,0 }\left( \sum\limits_{q=1}^{Q}\left| \left( G_{q}(x_{j}^{\lambda-1,0},\mathbf{U}_{N}(x_{j}^{\lambda-1,0}))-G_{q}(x_{j}^{\lambda-1,0},\mathbf{U}(x_{j}^{\lambda-1,0}))\right) \right| \right)^{2} \right)^{\frac{1}{2}}\\ & \leq \frac{T^{\lambda} }{2^{\lambda} {\Gamma}(\lambda)} \left( \frac{2^{\lambda}}{\lambda}\right)^{\frac{1}{2}} \left( \sum\limits_{j=0}^{N} \varpi_{j}^{\lambda-1 ,0 }\left( \sum\limits_{q=1}^{Q}\sum\limits_{i=1}^{Q} L_{q,i} \left| \mathbf{U}_{N,i}(x_{j}^{\lambda-1,0})-\mathbf{U}_{i}(x_{j}^{\lambda-1,0}) \right| \right)^{2} \right)^{\frac{1}{2}}\\ & \leq \frac{\lambda}{2^{\lambda+1}} \left( \frac{2^{\lambda}}{\lambda}\right)^{\frac{1}{2}} \left( \sum\limits_{j=0}^{N} \varpi_{j}^{\lambda-1 ,0 }\left( \sum\limits_{i=1}^{Q} \left| \mathbf{U}_{N,i}(x_{j}^{\lambda-1,0})-\mathbf{U}_{i}(x_{j}^{\lambda-1,0}) \right| \right)^{2} \right)^{\frac{1}{2}}\\ & \leq \frac{\lambda}{2^{\lambda+1}} \left( \frac{2^{\lambda}}{\lambda}\right)^{\frac{1}{2}} \left( {\int}_{-1}^{1} (1-\beta)^{\lambda-1}\left( \sum\limits_{i=1}^{Q} \left| \mathbf{U}_{N,i}(\beta)-\mathcal{I}_{\beta,N}^{\lambda-1,0}\mathbf{U}_{i}(\beta) \right| \right)^{2} \right)^{\frac{1}{2}}\\ & \leq \frac{\lambda}{2^{\lambda+1}} \left( \frac{2^{\lambda}}{\lambda}\right)^{\frac{1}{2}} \left( {\int}_{-1}^{1} (1-\beta)^{\lambda-1}\left( \sum\limits_{i=1}^{Q} \left| \mathbf{U}_{N,i}(\beta)-\mathbf{U}_{i}(\beta) \right| \right)^{2} d\beta \right.\\ &\quad\quad\quad\quad\quad\quad\quad \left. + {\int}_{-1}^{1} (1-\beta)^{\lambda-1}\left( \sum\limits_{i=1}^{Q} \left| \mathbf{U}_{i}(\beta)-\mathcal{I}_{\beta,N}^{\lambda-1,0}\mathbf{U}_{i}(\beta) \right| \right)^{2} d\beta \right)^{\frac{1}{2}}\\ & \leq \frac{1}{2 } \left\| \mathbf{U}_{N} -\mathbf{U} \right\|_{\infty} + c N^{-s} \left\| {\partial_{x}^{s}} \mathbf{U} \right\|_{\omega^{\lambda+s-1,s}}. \end{array} $$

(6.9)

The last term is bounded by

$$ \begin{array}{llll} \left|\boldsymbol{E}_{5}\right| & =\left|\frac{x+1}{2} {\int}_{-1}^{1} \boldsymbol{R}(1,\beta) \left( \mathcal{I}_{\beta,N}^{\lambda-1,0}-\mathcal{I}\right) \mathbf{G}(\beta,\mathbf{U}(\beta))d\beta\right|\\ & =\left|\frac{T^{\lambda}(x+1)}{2^{\lambda+1} {\Gamma}(\lambda)} {\int}_{-1}^{1} \sum\limits_{q=1}^{Q} (1-\beta)^{\lambda-1} \left( \mathcal{I}_{\beta,N}^{\lambda-1,0}-\mathcal{I}\right) G_{q}(\beta,\mathbf{U}(\beta))d\beta\right|\\ & \leq \frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda)} {\int}_{-1}^{1} (1-\beta)^{\lambda-1} \left|\sum\limits_{q=1}^{Q} \left( \mathcal{I}_{\beta,N}^{\lambda-1,0}-\mathcal{I}\right) G_{q}(\beta,\mathbf{U}(\beta))d\beta\right|\\ & \leq \frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda)} {\int}_{-1}^{1} (1-\beta)^{\lambda-1} \sum\limits_{q=1}^{Q} \left| \left( \mathcal{I}_{\beta,N}^{\lambda-1,0}-\mathcal{I}\right) G_{q}(\beta,\mathbf{U}(\beta))d\beta\right|\\ & \leq \frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda)} \left( {\int}_{-1}^{1} (1-\beta)^{\lambda-1} d\beta {\int}_{-1}^{1} (1-\beta)^{\lambda-1} \left( \sum\limits_{q=1}^{Q} \left| \left( \mathcal{I}_{\beta,N}^{\lambda-1,0}-\mathcal{I}\right) G_{q}(\beta,\mathbf{U}(\beta))d\beta\right|\right)^{2} d\beta\right)^{\frac{1}{2}}\\ & \leq cN^{-s} \left\|{\partial_{x}^{s}} \mathbf{G} \left( \cdot,\mathbf{U}(\cdot)\right) \right\|_{\omega^{\lambda+s-1,s}}. \end{array} $$

(6.10)

Hence, a combination of (6.3), (6.5), (6.7), (6.8), (6.10), and Theorem 5.1 yields 6.1. □

Theorem 6.2

Let$\mathbf {u}_{N}(t):={\mathbf {U}}_{N}\left ({\frac {{2t}}{T} - 1} \right )$bethe numerical solution of the system of (1.1) witht ∈ (0,T) andχ^λ,μ(t) := (T − t)^λt^μ.Then, we have the following estimate:

$$ \left\| \mathbf{u}-\mathbf{u}_{N} \right\|_{\infty} \leq c N^{\frac{3}{4}-s} \left\| {\partial_{t}^{s}} \mathbf{u} \right\|+c N^{\frac{1}{2}-s} \left\| {\partial_{t}^{s}} \mathbf{g}(\cdot,\mathbf{u}(\cdot)) \right\|_{\chi^{\lambda+s-1,s}}. $$

(6.11)

7 Numerical results

In order to illustrate the performance of the Jacobi spectral collocation method, we perform various numerical examples for smooth and non-smooth solutions. The implementation of the method has been carried out in Mathematica 11.3. The functions Maximize and NIntegrate have been used to estimate the $L^{\infty }$- and L²- absolute errors.

Example 1

We consider the following linear system of fractional differential equations:

$$ \left\{\begin{array}{llll} {~}_{0}^{C} D_{t}^{\lambda} u_{1}(t) = a_{1}(t)u_{1}(t)+a_{2}(t)u_{2}(t)+g_{1}(t),\ 0 < t < 1, \\ {~}_{0}^{C} D_{t}^{{\lambda}} u_{2}(t) = a_{3}(t)u_{1}(t)+a_{4}(t)u_{2}(t)+g_{2}(t),\ 0 < t < 1, \\ u_{i}(0) = u_{i}(1) = 0,\ i=1,\ 2, \vphantom{\frac{5_A}{4,10^3}} \end{array}\right. $$

(7.1)

where a₁(t) = a₄(t) = 20t³(1 − t)e^−t and $a_{2}(t)=a_{3}(t)=\sin (t)$.

The exact solution is $u_{1}(t)=t - t^{\frac {111}{17}}$, which is a smooth solution on the interval [0,1], and u₂(t) = t − t^λ+ 1, which is a weakly singular solution at the endpoint t = 0. The functions g₁(t) and g₂(t) are obtained using the exact solution. The $L^{\infty }$- and L²- errors for the three fractional orders λ = {1.3, 1.5, 1.9} are listed in Table 1. We observe a much faster decay of the errors for the smooth solution for all employed values of λ, and a slower rate of convergence for the weakly singular solution. Hence, the proposed method is able to deal with problems with smooth solutions in a very effective manner.

Table 1 The $L^{\infty }$- and L²- errors for problem (7.1) versus N

Example 2

We consider the following nonlinear system of fractional differential equations:

$$ \left\{\begin{array}{llll} {~}_{0}^{C} D_{t}^{\lambda} u_{1}(t) = \cos \left( {u_{2} (t) + u_{3} (t)} \right) + g_{1} (t) , \\ {~}_{0}^{C} D_{t}^{\lambda} u_{2}(t) = u_{1} (t) + e^{u_{3} (t)} + g_{2} (t), \\ {~}_{0}^{C} D_{t}^{\lambda} u_{3}(t) =u_{3} (t) + \sin \left( {u_{1} (t) + u_{2} (t)} \right) + g_{3} (t), \\ u_{i}(0) = 0,\ u_{i}(1) = 1,\ i=1,\ 2,\ 3. \vphantom{\frac{5_A}{4,10^3}} \end{array}\right. $$

(7.2)

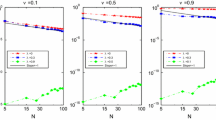
The corresponding exact solution is given by u₁(t) = t⁴, u₂(t) = t⁵, u₂(t) = t⁶. The functions g_i(t) are obtained using the exact solution. The numerical results are plotted for several fractional orders λ = 1.3, 1.5, 1.9 in Figs. 1, 2, and 3, respectively.

Fig. 1

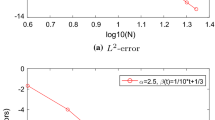
The L²- and $L^{\infty }$- errors versus the number of collocation points for problem (7.2) with λ = 1.3

Fig. 2

The L²- and $L^{\infty }$- errors versus the number of collocation points for problem (7.2) with λ = 1.5

Fig. 3

The L²- and $L^{\infty }$- errors versus the number of collocation points for problem (7.2) with λ = 1.9

Example 3

We consider the following nonlinear system of fractional differential equations:

$$ \left\{\begin{array}{llll} {~}_{0}^{C} D_{t}^{\lambda} u_{1}(t) = {u^{2}_{2}}(t)+g_{1}(t),\ 0 < t < 1, \\ {~}_{0}^{C} D_{t}^{{\lambda}} u_{2}(t) ={u^{2}_{1}}(t)+g_{2}(t),\ 0 < t < 1, \\ u_{i}(0) = u_{i}(1) = 0,\ i=1,\ 2. \vphantom{\frac{5_A}{4,10^3}} \end{array}\right. $$

(7.3)

The exact solution is u₁(t) = t^λ+ 1 − t², which is a weakly singular solution at the endpoint t = 0, and $u_{2}(t)=t^{3} - t^{\frac {113}{15}}$, which is smooth on the interval [0,1]. The functions g₁(t) and g₂(t) are obtained using the exact solution. The $L^{\infty }$- and L²- errors for the three fractional orders λ = {1.3, 1.5, 1.9} are presented in Table 2. We observe a much faster decay of the errors for the smooth solution for all employed values of λ, and a slower rate of convergence for the weakly singular solution. The results are in good agreement with what we expect.

Table 2 The $L^{\infty }$- and L²- errors for problem (7.3) versus N

8 Conclusion and future work

This paper developed a numerical approach for solving a nonlinear system of fractional differential equations based on the Legendre-Jacobi spectral collocation method. The strategy is derived using some variable transformations to reduce the problem into the equivalent system of Fredholm integral equations, so that the spectral theory can be applied conveniently. The most important contribution of this work is that we were able to demonstrate rigorously that the errors of smooth solutions decay exponentially in L²- and $L^{\infty }$-norms, which is a desired feature for a spectral method. Two numerical examples showed the results in agreement with the theoretical analysis. We believe that the ideas introduced in this paper will serve as a basis for future spectral methods for systems of nonlinear fractional differential equations and systems of integral equations with non-sooth solutions. An exciting generalization of this work will be to high dimensional problems and problems with non-smooth solutions.

Appendix: Existence of the approximate solution

We consider the following iteration process:

$$ \begin{array}{llll} \mathbf{U}_{N}^{m}(x) = & \frac{T^{\lambda}}{4^{\lambda} {\Gamma}(\lambda)} \mathcal{I}_{x,N} \left[(x + 1)^{\lambda} {\int}_{-1}^{1} (1 - \eta)^{\lambda-1} \mathcal{I}_{\eta,N}^{\lambda-1,0} \mathbf{G}(\sigma(x,\eta),\mathbf{U}_{N}^{m-1}(\sigma(x,\eta)))d\eta\right]\\ & - \frac{T^{\lambda} (x+1) }{2^{\lambda+1} {\Gamma}(\lambda)} \left[{\int}_{-1}^{1} (1-\beta)^{\lambda-1} \mathcal{I}_{\beta,N}^{\lambda-1,0} \mathbf{G}(\beta,\mathbf{U}_{N}^{m-1}(\beta))d\beta\right]. \end{array} $$

(A.1)

Let $\overrightarrow {\mathbf {U}}_{N}^{m}(x) = \mathbf {U}_{N}^{m}(x)-\mathbf {U}_{N}^{m-1}(x)$. Then, we have from (A.1) and (4.24) that

$$ \begin{array}{llll} \overrightarrow{\mathbf{U}}_{N}^{m}(x)=& \frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda)} \mathcal{I}_{x,N} \left[ {\int}_{-1}^{x} (x-\sigma)^{\lambda-1} {~}_{x}\widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} \left( \mathbf{G}\left( \sigma,\mathbf{U}_{N}^{m-1}(\sigma) \right) -\mathbf{G}\left( \sigma,\mathbf{U}_{N}^{m-2}(\sigma) \right) \right) d\sigma \right]\\ &- \frac{T^{\lambda}(x+1)}{2^{\lambda+1} {\Gamma}(\lambda)} {\int}_{-1}^{1} (1-\beta)^{\lambda-1} \mathcal{I}_{\beta,N}^{\lambda-1,0} \left( \mathbf{G}\left( \beta,\mathbf{U}_{N}^{m-1}(\beta) \right) -\mathbf{G}\left( \beta,\mathbf{U}_{N}^{m-2}(\beta) \right) \right) d\beta \\ &=:B_{1} +B_{2}, \end{array} $$

(A.2)

where

$$ \begin{array}{llll} & \mathbf{B}_{1}= \frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda)} \mathcal{I}_{x,N} \left[ {\int}_{-1}^{x} (x-\sigma)^{\lambda-1} {~}_{x}\widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} \left( \mathbf{G}\left( \sigma,\mathbf{U}_{N}^{m-1}(\sigma) \right) -\mathbf{G}\left( \sigma,\mathbf{U}_{N}^{m-2}(\sigma) \right) \right) d\sigma \right],\\ & \mathbf{B}_{2}=\frac{T^{\lambda}(x+1)}{2^{\lambda+1} {\Gamma}(\lambda)} {\int}_{-1}^{1} (1-\beta)^{\lambda-1} \mathcal{I}_{\beta,N}^{\lambda-1,0} \left( \mathbf{G}\left( \beta,\mathbf{U}_{N}^{m-1}(\beta) \right) -\mathbf{G}\left( \beta,\mathbf{U}_{N}^{m-2}(\beta) \right) \right) d\beta. \end{array} $$

We obtain from the Cauchy-Schwarz inequality that

$$ \begin{array}{llll} &\left\|\mathbf{B}_{1} \right\| \\ &=\frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda)} \left\| \mathcal{I}_{x,N} {\int}_{-1}^{x} (x-\sigma)^{\lambda-1} {~}_{x}\widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} \left( \mathbf{G}\left( \sigma,\mathbf{U}_{N}^{m-1}(\sigma) \right) -\mathbf{G}\left( \sigma,\mathbf{U}_{N}^{m-2}(\sigma) \right) \right) d\sigma \right\|\\ &= \frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda)} \left( {\int}_{-1}^{1} \left( \sum\limits_{q=1}^{Q} \mathcal{I}_{x,N} {\int}_{-1}^{x} (x-\sigma)^{\lambda-1} {~}_{x}\widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} \left( G_{q}\left( \sigma,\mathbf{U}_{N}^{m-1}(\sigma)\right)-G_{q}\left( \sigma,\mathbf{U}_{N}^{m-2}(\sigma)\right) \right)d\sigma \right)^{2} dx\right)^{\frac{1}{2}}\\ &=\frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda)}\left( \sum\limits_{j=0}^{N} \varpi_{j} \left( {\int}_{-1}^{x_{j}} (x_{j}-\sigma)^{\lambda-1}\sum\limits_{q=1}^{Q} {~}_{x_{j}}\widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} \left( G_{q}\left( \sigma, \mathbf{U}_{N}^{m-1}(\sigma) \right)-G_{q}\left( \sigma,\mathbf{U}_{N}^{m-2}(\sigma)\right) \right)d\sigma \right)^{2}\right)^{\frac{1}{2}} \\ & \leq \frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda)} \left( \sum\limits_{j=0}^{N} \varpi_{j} {\int}_{-1}^{x_{j}} (x_{j}-\sigma)^{\lambda-1} d\sigma {\int}_{-1}^{x_{j}}(x_{j}-\sigma)^{\lambda-1} \right.\\ & \left. \qquad \qquad \qquad \times \left( \left| \sum\limits_{q=1}^{Q} {~}_{x_{j}}\widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} \left( G_{q}(\sigma, \mathbf{U}_{N}^{m-1}(\sigma) )-G_{q}(\sigma,\mathbf{U}_{N}^{m-2}(\sigma))\right) \right| \right)^{2} d\sigma\right)^{\frac{1}{2}} \\ & \leq \frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda)} \left( \sum\limits_{j=0}^{N} \varpi_{j} \frac{(x_{j}+1)^{\lambda}}{\lambda} {\int}_{-1}^{x_{j}}(x_{j}-\sigma)^{\lambda-1}\right.\\ & \left. \qquad \qquad \qquad \times \left( \sum\limits_{q=1}^{Q} \left| {~}_{x_{j}}\widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} \left( G_{q}(\sigma, \mathbf{U}_{N}^{m-1}(\sigma) )-G_{q}(\sigma,\mathbf{U}_{N}^{m-2}(\sigma))\right) \right| \right)^{2} d\sigma \right)^{\frac{1}{2}} \\ & \leq \frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda)} \left( \sum\limits_{j=0}^{N} \varpi_{j} \frac{(x_{j}+1)^{2\lambda}}{2^{\lambda}\lambda} \right.\\ & \left. \qquad \qquad \qquad \times \sum\limits_{k=0}^{N} \left( \sum\limits_{q=1}^{Q} \left|G_{q}(\sigma_{k}^{\lambda-1,0},\mathbf{U}_{N}^{m-1}(\sigma_{k}^{\lambda-1,0}))-G_{q}(\sigma_{k}^{\lambda-1,0},\mathbf{U}_{N}^{m-2}(\sigma_{k}^{\lambda-1,0})) \right|\right)^{2} \varpi_{k}^{\lambda-1,0}\right)^{\frac{1}{2}}. \end{array} $$

Hence, by (4.25), (5.14) and the Lipschitz condition, we obtain that

$$ \begin{array}{llll} & \left\|\mathbf{B}_{1} \right\|\\ & \leq \frac{T^{\lambda}}{2^{\lambda} {\Gamma}(\lambda)} \left( \sum\limits_{j=0}^{N} \varpi_{j} \frac{(x_{j}+1)^{2\lambda}}{2^{\lambda}\lambda} \sum\limits_{k=0}^{N} \left( \sum\limits_{q=1}^{Q} \sum\limits_{i=1}^{Q} L_{q,i} \left| U_{N,i}^{m-1}(\sigma_{k}^{\lambda-1,0})-U_{N,i}{m-2}(\sigma_{k}^{\lambda-1,0}) \right|\right)^{2} \varpi_{k}^{\lambda-1,0} \right)^{\frac{1}{2}}\\ & = \frac{\lambda}{ 2^{\lambda+1}}\left( \sum\limits_{j=0}^{N} \varpi_{j} \frac{(x_{j}+1)^{2\lambda}}{2^{\lambda}\lambda} \sum\limits_{k=0}^{N} \left( \sum\limits_{i=1}^{Q} \left| U_{N,i}^{m-1}(\sigma_{k}^{\lambda-1,0})-U_{N,i}^{m-2}(\sigma_{k}^{\lambda-1,0}) \right|\right)^{2} \varpi_{k}^{\lambda-1,0} \right)^{\frac{1}{2}}\\ & \leq \frac{\lambda}{ 2^{\lambda+1}} \left( \sum\limits_{j=0}^{N} \varpi_{j} \frac{(x_{j}+1)^{\lambda}}{\lambda} {\int}_{-1}^{x_{j}} (x_{j}-\sigma)^{\lambda-1} \left( \sum\limits_{i=1}^{Q}\left| {~}_{x_{j}}\widetilde{\mathcal{I}}_{\sigma,N}^{\lambda-1,0} \overrightarrow{U}_{N,i}^{m-1}(\sigma) \right|\right)^{2} d\sigma\right)^{\frac{1}{2}}\\ & \leq \frac{\lambda}{ 2^{\lambda+1}} \left( \sum\limits_{j=0}^{N} \varpi_{j} \frac{(x_{j}+1)^{\lambda}}{\lambda}\right)^{\frac{1}{2}} \max\limits_{0\leq j \leq N} \left( {\int}_{-1}^{x_{j}} (x_{j}-\sigma)^{\lambda-1} \left( \sum\limits_{i=1}^{Q} \left| \overrightarrow{U}_{N,i}^{m-1}(\sigma) \right|\right)^{2} d\sigma\right)^{\frac{1}{2}}\\ & \leq \frac{\lambda}{ 2^{\lambda+1}} \sqrt{\frac{8}{3 \lambda}} \max\limits_{0\leq j \leq N} \left( {\int}_{-1}^{x_{j}} (x_{j}-\sigma)^{\lambda-1} \left( \sum\limits_{i=1}^{Q} \left| \overrightarrow{U}_{N,i}^{m-1}(\sigma) \right|\right)^{2} d\sigma\right)^{\frac{1}{2}}\\ &\leq \frac{\lambda}{ 2^{\lambda+1}} \sqrt{\frac{2^{\lambda+2}}{3 \lambda}} \left( {\int}_{-1}^{1} \left( \sum\limits_{i=1}^{Q} \left| \overrightarrow{U}_{N,i}^{m-1}(\sigma) \right| \right)^{2} d\sigma\right)^{\frac{1}{2}}\\ &\leq \sqrt{\frac{\lambda}{3 \times 2^{\lambda} }} \left\| \overrightarrow{\mathbf{U}}^{m-1} \right\|. \end{array} $$

(A.3)

It remains to estimate the term $\left \|\boldsymbol {B}_{2} \right \|$. By the Cauchy-Schwarz inequality, we have

$$ \begin{array}{llll} \left\|\boldsymbol{B}_{2} \right\| &= \frac{T^{\lambda} \left\|x+1\right\|}{2^{\lambda+1} {\Gamma}(\lambda)} \left|{\int}_{-1}^{1} (1-\beta)^{\lambda-1} \mathcal{I}_{\beta,N}^{\lambda-1,0} \left( \mathbf{G}\left( \beta,\mathbf{U}_{N}^{m-1}(\beta) \right) -\mathbf{G}\left( \beta,\mathbf{U}_{N}^{m-2}(\beta) \right) \right) d\beta\right|\\ &= \frac{T^{\lambda}}{2^{\lambda+1} {\Gamma}(\lambda)} \sqrt{\frac{2^{\lambda+3}}{3 \lambda}} \left|{\int}_{-1}^{1} \sum\limits_{q=1}^{Q} (1-\beta)^{\lambda-1} \mathcal{I}_{\beta,N}^{\lambda-1,0} \left( G_{q}(\beta,\mathbf{U}_{N}^{m-1}(\beta))-G_{q}(\beta,\mathbf{U}^{m-2}(\beta))\right) d\beta\right|\\ & \leq \frac{T^{\lambda}}{2^{\lambda+1} {\Gamma}(\lambda)} \sqrt{\frac{2^{\lambda+3}}{3 \lambda}} \left( {\int}_{-1}^{1} (1-\beta)^{\lambda-1} \left( \sum\limits_{q=1}^{Q} \left| \mathcal{I}_{\beta,N}^{\lambda-1,0} \left( G_{q}(\beta,\mathbf{U}^{m-1}_{N}(\beta))-G_{q}(\beta,\mathbf{U}^{m-2}(\beta))\right) d\beta\right| \right)^{2} \right)^{\frac{1}{2}} \end{array} $$

The previous result, along with (2.8) and Lipschitz condition, yields

$$ \begin{array}{llll} \left\|\boldsymbol{B}_{2} \right\| & \leq \frac{T^{\lambda}}{2^{\lambda+1} {\Gamma}(\lambda)} \sqrt{\frac{2^{\lambda+3}}{3 \lambda}} \left( \sum\limits_{j=0}^{N} \varpi_{j}^{\lambda-1 ,0 } \left( \sum\limits_{q=1}^{Q} \left| \left( G_{q}(x_{j}^{\lambda-1,0},\mathbf{U}_{N}^{m-1}(x_{j}^{\lambda-1,0}))-G_{q}(x_{j}^{\lambda-1,0},\mathbf{U}_{N}^{m-2}(x_{j}^{\lambda-1,0}))\right) \right|\right)^{2}\right)^{\frac{1}{2}}\\ & \leq \frac{T^{\lambda}}{2^{\lambda+1} {\Gamma}(\lambda)} \sqrt{\frac{2^{\lambda+3}}{3 \lambda}} \left( \sum\limits_{j=0}^{N} \varpi_{j}^{\lambda-1 ,0 } \left( \sum\limits_{q=1}^{Q} \sum\limits_{i=1}^{Q} L_{q,i} \left| U_{N,i}^{m-1}(x_{j}^{\lambda-1,0}))-U_{N,i}^{m-2}(x_{j}^{\lambda-1,0})) \right|\right)^{2}\right)^{\frac{1}{2}}\\ & \leq \frac{ \lambda }{2^{\lambda+2}} \sqrt{\frac{2^{\lambda+3}}{3 \lambda}} \left( \sum\limits_{j=0}^{N} \varpi_{j}^{\lambda-1 ,0 } \left( \sum\limits_{i=1}^{Q} \left| \overrightarrow{U}_{N,i}^{m-1}(x_{j}^{\lambda-1,0}) \right|\right)^{2}\right)^{\frac{1}{2}}\\ & = \frac{ \lambda }{2^{\lambda+2}} \sqrt{\frac{2^{\lambda+3}}{3 \lambda}} \left( {\int}_{-1}^{1} (1-\beta)^{\lambda-1}\left( \sum\limits_{i=1}^{Q} \left| \overrightarrow{U}_{N,i}^{m-1}(\beta)\right|\right)^{2} d\beta\right)^{\frac{1}{2}} \\ & \leq \sqrt{\frac{\lambda}{12}} \left\| \overrightarrow{\mathbf{U}}^{m-1} \right\|, \qquad \qquad \forall \lambda \in (1,2). \end{array} $$

(A.4)

Hence,

$$ \left\| \overrightarrow{\mathbf{U}}_{N}^{m} \right\|\le \left( \sqrt{\frac{\lambda}{3 \times 2^{\lambda} }}+\sqrt{\frac{\lambda}{12}} \right) \left\| \overrightarrow{\mathbf{U}}^{m-1} \right\|. $$

since

$$ \sqrt{\frac{\lambda}{3 \times 2^{\lambda} }}+\sqrt{\frac{\lambda}{12}} < 1, \qquad \qquad \forall \lambda \in (1,2), $$

we have $\left \| \overrightarrow {\mathbf {U}}_{N}^{m} \right \| \longrightarrow 0$ as $m\longrightarrow \infty .$ It implies the existence of solution of (3.10).