1 Introduction

Shell structures have found widespread applications in a variety of practical structures in civil, mechanical and aerospace engineering. For this reason, the study of shell theory and its conversion into numerical methods such as finite element method (FEM) has continuously received strong interests from many researchers [1–4]. Shell elements in FEM can be classified into three categories: degenerated shell elements derived from three-dimensional continuum elements, curved shell elements based on general shell theories, and flat shell elements based on combining membrane elements with plate bending elements. Among these three types, triangular flat shell elements have been widely employed in the analysis of shell structures because of their simple formulations and general applicability. However, flat shell elements would yield very erroneous results compared with other types of shell elements. Accordingly, the development of a simple and efficient flat shell element for the analysis of general shell structures is still required to improve the element performance.

It is well known that there are two fundamental theories for shell elements: thick and thin shell theories. Formulations in thin and thick shell elements are based on Kirchhoff–Love theory [5–8] and Reissner–Mindlin theory [9–11], respectively. In general, thin shell elements are limited to thin shell problems, but Reissner–Mindlin shell elements can be applied to both thin and thick shell problems. However, thick shell elements encounter the shear-locking phenomenon which induces overly stiff behavior as the shell structure becomes progressively thinner. To eliminate this difficulty, a lot of techniques have been proposed to avoid shear locking: the reduced integration method by Zienkiewicz et al. [2], the selective integration method by Hughes et al. [3], the mixed interpolation of tensorial components (MITC) element family by Bathe and Dvorkin [4], the three-node Mindlin plate element (MIN3) by Tessler and Hughes [12], the discrete shear triangular (DST) element family by Batoz and Lardeur [13], the discrete shear gap (DSG) technique [10] and others.

As a recent development of advanced finite element technologies, the smoothed finite element method(S-FEM) proposed by Liu and Nguyen [14] has achieved better performance than standard FEM. The S-FEM is formulated by incorporating a strain smoothing technique into conventional FEM. The difference in S-FEM series in the literature is that the weak form is evaluated by smoothing domains created from the entities associated with cells/elements [15], edges [16] and nodes [17]. Each of these S-FEMs delivers different desired properties for a wide range of benchmark and practical mechanics problems.

Among these S-FEMs, edge-based S-FEM (ES-FEM) and node-based S-FEM (NS-FEM) using triangular elements demonstrate good performances for two-dimensional problems [16, 17]. In ES-FEM, the system stiffness matrix is computed using strains smoothed over the smoothing domains associated with the edges of triangular elements. The numerical results [16] showed that ES-FEM has the following properties: (1) ES-FEM model possesses a close-to-exact stiffness: it is much softer than the ‘‘overly-stiff’’ FEM and is stiffer than the “soft” NS-FEM; (2) numerical results are often found super-convergent and much more accurate than those of the standard FEM with the same sets of nodes; and (3) there are no spurious non-zeros energy modes found and hence the method is also stable and works well. On the other hand, the system stiffness matrix for NS-FEM is computed using strains smoothed over the smoothing domains associated with the nodes of triangular elements, and has the following properties [17]: (1) NS-FEM provides an upper bound to the strain energy of the exact solution when a reasonably fine mesh is used; (2) numerical results showed that NS-FEM is immune from the volumetric locking; and (3) NS-FEM is relatively insensitive to element distortion.

Recently, Nguyen-Xuan et al. [19–22] presented Reissner–Mindlin plate elements using ES-FEM, NS-FEM, cell-based S-FEM (CS-FEM) and alpha S-FEM (αFEM) with DSG technique [10]. Cui et al. [18] proposed an ES-FEM for Reissner–Mindlin flat shell elements. Some other S-FEM methods have been also studied for plate and shell structures [23–31]. As a hybrid approach, αFEM [22, 32] was developed by introducing a scale factor \( \alpha \in [0,1] \) to establish a continuous function of strain energy that contains contributions from both conventional FEM and NS-FEM. Numerical results confirm that αFEM shows an excellent performance compared to both conventional FEM and NS-FEM. It has clearly opened a novel window of opportunity to obtain numerical solutions that are nearly exact solutions.

In this paper, we propose a combined scheme of ES-FEM and NS-FEM, named edge/node-based S-FEM (ENS-FEM), to improve the accuracy and effectiveness of triangular Reissner–Mindlin shell elements. In ENS-FEM, the membrane, the bending and the shear strain fields are smoothed by the means of a gradient smoothing technique over the smoothing domains constructed based on a combination of ES-FEM and NS-FEM. ES-FEM produces usually lower bound solutions in strain energy of the exact solution as presented in numerical results [14, 16, 32, 33], and NS-FEM possesses the upper bound property when a reasonably fine mesh is used [14, 17, 32, 33]. Hence, ENS-FEM model could be softer than ES-FEM model and stiffer than NS-FEM model. To avoid shear-locking phenomenon in thin shell elements, DSG technique [10] is used in ENS-FEM for Reissner–Mindlin shell elements. In this study, an average combination of ES-FEM and NS-FEM is proposed for all practical purpose to obtain better results for shell structural problems, compared with other methods such as DSG3 [10], MIN3 [12], MITC4 [4], ES-FEM [18, 19] and NS-FEM [17, 20]. Numerical results for some benchmark shell problems confirm that the present method has a good performance and is compatible to four-node quadrilateral shell elements MITC4.

2 Triangular Reissner–Mindlin flat shell elements

2.1 Weak form of Reissner–Mindlinflat shells

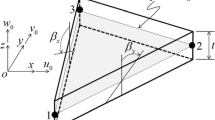
Consider a flat shell element deformed by in-plane forces and bending moments as shown in Fig. 1. In this figure, Oxyz and \( \hat{O}\hat{x}\hat{y}\hat{z} \) are the global and the local coordinate systems of a flat shell, respectively. The middle (neutral) surface of the shell is chosen as the reference plane that occupies a domain \( \Omega \subset \Re^{3} \). Let \( \hat{u},\hat{v} \) and \( \hat{w} \) be the displacements of the middle plane in the \( \hat{x},\hat{y} \) and \( \hat{z} \) directions, respectively; \( \hat{\beta }_{x} ,\hat{\beta }_{y} \) and \( \hat{\beta }_{z} \) be the rotations of the middle surface of the shell around the \( \hat{y} \), \( \hat{x} \) and \( \hat{z} \) axis, respectively, as indicated in Fig. 1. The unknown vector of a flat shell including six independent variables at any point in the problem domain can be written as:

$$ {\hat{\mathbf{u}}}^{T} = \left[ {\hat{u},\hat{v},\hat{w},\hat{\beta }_{x} ,\hat{\beta }_{y} ,\hat{\beta }_{z} } \right]. $$
(1)
Fig. 1
figure 1

A shell element with local coordinate system \( \hat{O}\hat{x}\hat{y}\hat{z} \) in global coordinate system Oxyz

Full size image

An application of membrane theory to the Reissner–Mindlin plate theory provides a mean to determine the Reissner–Mindlin flat shell behavior, wherein the membrane strain \( {\boldsymbol{\hat{{\varepsilon}}}} \), the bending strain \( {\boldsymbol{\hat{{\kappa }}}} \) and the shear strains \( {\boldsymbol{\hat{{\gamma }}}} \) in local coordinate system \( \hat{O}\hat{x}\hat{y}\hat{z} \) are defined, respectively, by

$$ {\hat{\boldsymbol{\varepsilon }}} = \left[ {\begin{array}{*{20}c} \tfrac{{\partial \hat{u}}}{\partial x} \\ \tfrac{{\partial \hat{v}}}{\partial y} \\ \tfrac{{\partial \hat{u}}}{\partial y} + \tfrac{{\partial \hat{v}}}{\partial x} \\ \end{array}} \right] = {\mathbf{L}}^{m} {\hat{\mathbf{u}}}\quad {\text{with}}\quad {\mathbf{L}}^{m} = \left[ {\begin{array}{*{20}c} {\tfrac{\partial }{\partial x}} & 0 & 0 & 0 & 0 & 0 \\ 0 & {\tfrac{\partial }{\partial y}} & 0 & 0 & 0 & 0 \\ {\tfrac{\partial }{\partial y}} & {\tfrac{\partial }{\partial x}} & 0 & 0 & 0 & 0 \\ \end{array} } \right] $$
(2)
$$ {\hat{\varvec{\kappa }}} = \left[ {\begin{array}{*{20}c} \tfrac{{\partial \hat{\beta }_{x} }}{\partial x} \\ \tfrac{{\partial \hat{\beta }_{y} }}{\partial y} \\ \tfrac{{\partial \hat{\beta }_{x} }}{\partial y} + \tfrac{{\partial \hat{\beta }_{y} }}{\partial x} \\ \end{array}} \right] = {\mathbf{L}}^{b} {\hat{\mathbf{u}}}\quad {\text{with}}\quad {\mathbf{L}}^{b} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & {\tfrac{\partial }{\partial x}} & 0 & 0 \\ 0 & 0 & 0 & 0 & {\tfrac{\partial }{\partial y}} & 0 \\ 0 & 0 & 0 & {\tfrac{\partial }{\partial y}} & {\tfrac{\partial }{\partial x}} & 0 \\ \end{array} } \right] $$
(3)
$$ {\boldsymbol{\hat{{\gamma }}}} = \left[ \begin{aligned} \tfrac{{\partial \hat{w}}}{\partial x} + \hat{\beta }_{x} \hfill \\ \tfrac{{\partial \hat{w}}}{\partial y} + \hat{\beta }_{y} \hfill \\ \end{aligned} \right] = {\mathbf{L}}^{s} {\hat{\mathbf{u}}}\quad {\text{with}}\quad {\mathbf{L}}^{s} = \left[ {\begin{array}{*{20}c} 0 & 0 & {\tfrac{\partial }{\partial x}} & 1 & 0 & 0 \\ 0 & 0 & {\tfrac{\partial }{\partial y}} & 0 & 1 & 0 \\ \end{array} } \right] $$
(4)

The elastic strain energy and the work done by external forces of Reissner–Mindlin flat shells are now expressed as:

$$ U_{\text{sh}} = \frac{1}{2}\left( {\int_{\Omega } {\left( {{\mathbf{L}}^{m} {\hat{\mathbf{u}}}} \right)^{T} {\mathbf{D}}^{m} {\mathbf{L}}^{m} {\hat{\mathbf{u}}}\text{d}\Omega } + \int_{\Omega } {\left( {{\mathbf{L}}^{b} {\hat{\mathbf{u}}}} \right)^{T} {\mathbf{D}}^{b} {\mathbf{L}}^{b} {\hat{\mathbf{u}}}\text{d}\Omega } + \int_{\Omega } {\left( {{\mathbf{L}}^{s} {\hat{\mathbf{u}}}} \right)^{T} {\mathbf{D}}^{s} {\mathbf{L}}^{s} {\hat{\mathbf{u}}}\text{d}\Omega } } \right),\,{\text{and}} $$
(5)
$$ W = \int_{\Omega } {{\hat{\mathbf{u}}\mathbf{b}}\text{d}\Omega } , $$
(6)

where b is the body force, and D m, D b, and D s are the material matrices related to the membrane, bending and shear deformations, respectively. The material matrices are given by

$$ {\mathbf{D}}_{{}}^{m} = \frac{Eh}{{1 - \nu^{2} }}\left[ {\begin{array}{*{20}c} 1 & \nu & 0 \\ \nu & 1 & 0 \\ 0 & 0 & {\tfrac{1 - \nu }{2}} \\ \end{array} } \right],\;{\mathbf{D}}_{{}}^{b} = \frac{{Eh^{3} }}{{12\left( {1 - \nu^{2} } \right)}}\left[ {\begin{array}{*{20}c} 1 & \nu & 0 \\ \nu & 1 & 0 \\ 0 & 0 & {\tfrac{1 - \nu }{2}} \\ \end{array} } \right],{\mathbf{D}}_{{}}^{s} = khG\left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right], $$
(7)

where G is the shear modulus, k = 5/6 is the shear correction factor, h is the thickness of shell, E is the Young’s modulus, and ν is the Poisson’s ratio. For static analysis of a Reissner–Mindlin flat shell model, the weak form can now be written as:

$$ \int_{\Omega } {\delta {\hat{\mathbf{u}}}^{T} \left( {{\mathbf{L}}^{mT} {\mathbf{D}}^{m} {\mathbf{L}}^{m} + {\mathbf{L}}^{mT} {\mathbf{D}}^{m} {\mathbf{L}}^{m} + {\mathbf{L}}^{mT} {\mathbf{D}}^{m} {\mathbf{L}}^{m} } \right){\hat{\mathbf{u}}}\text{d}\Omega } = \int_{\Omega } {\delta {\hat{\mathbf{u}}\mathbf{b}}\text{d}\Omega } . $$
(8)

2.2 Finite element formulation of triangular Reissner–Mindlin flat shell elements

In FEM, the problem domain is discretized using a mesh of n e three-node finite elements such that \( \Omega = \bigcup\nolimits_{e = 1}^{{n^{e} }} {\Omega^{e} } \) and \( \Omega^{i} \cap \Omega^{j} = \)∅ for \( i \ne j. \). The finite element approximation \( {\hat{\mathbf{u}}}_{h}^{e} = \sum\nolimits_{j = 1}^{{n^{ne} }} {\left[ {\hat{u}_{j}^{e} ,\hat{v}_{j}^{e} ,\hat{w}_{j}^{e} ,\hat{\beta }_{xj}^{e} ,\hat{\beta }_{yj}^{e} ,\hat{\beta }_{zj}^{e} } \right]}^{T} \) for triangular Reissner–Mindlin shell elements, as shown in Fig. 2, can be expressed as:

$$ {\hat{\mathbf{u}}}_{h}^{e} = \sum\nolimits_{j = 1}^{3} {N_{j}^{e} {\mathbf{I}}_{6} {\hat{\mathbf{d}}}_{j}^{e} } = \sum\nolimits_{j = 1}^{3} {{\mathbf{N}}_{j}^{e} {\hat{\mathbf{d}}}_{j}^{e} } $$
(9)

where I 6 is the unit matrix of 6th rank, \( {\hat{\mathbf{d}}}_{j}^{e} = \left[ {\hat{u}_{j}^{e} ,\hat{v}_{j}^{e} ,\hat{w}_{j}^{e} ,\hat{\beta }_{xj}^{e} ,\hat{\beta }_{yj}^{e} ,\hat{\beta }_{zj}^{e} } \right]^{T} \) is the vector containing nodal degrees of freedom of \( {\hat{\mathbf{u}}}_{h}^{e} \) associated with the jth node of the element, and \( N_{j}^{e} \) is the shape function at the jth node of the triangular element defined by

$$ N_{1} = 1 - \xi - \eta ,\quad N_{2} = \xi ,\quad N_{3} = \eta $$
(10)
Fig. 2
figure 2

Three-node triangular element and local coordinates

Full size image

According to Eqs. (2) and (3), the approximation of the membrane and the bending strains in the triangular element can then be expressed in matrix forms as:

$$ {\hat{\varvec{\varepsilon }}}^{e} = \left[ {\begin{array}{*{20}c} {{\mathbf{R}}_{1}^{e} } & {{\mathbf{R}}_{2}^{e} } & {{\mathbf{R}}_{3}^{e} } \\ \end{array} } \right]{\hat{\mathbf{d}}}^{e} = {\mathbf{R}}^{e} {\hat{\mathbf{d}}}^{e} $$
(11)
$$ {\hat{\varvec{\kappa }}}^{e} = \left[ {\begin{array}{*{20}c} {{\mathbf{B}}_{1}^{e} } & {{\mathbf{B}}_{2}^{e} } & {{\mathbf{B}}_{3}^{e} } \\ \end{array} } \right]{\hat{\mathbf{d}}}^{e} = {\mathbf{B}}^{e} {\hat{\mathbf{d}}}^{e} $$
(12)

with

$$ \begin{gathered} {\mathbf{R}}_{1}^{e} = \frac{1}{{2A^{e} }}\left[ {\begin{array}{llllll} {b - c} & 0 & 0 & 0 & 0 & 0 \\ 0 & {d - a} & 0 & 0 & 0 & 0 \\ {d - a} & {b - c} & 0 & 0 & 0 & 0 \\ \end{array} } \right],\,\,{\mathbf{R}}_{2}^{e} = \frac{1}{{2A^{e} }}\left[ {\begin{array}{llllll} c & 0 & 0 & 0 & 0 & 0 \\ 0 & { - d} & 0 & 0 & 0 & 0 \\ { - d} & c & 0 & 0 & 0 & 0 \\ \end{array} } \right] \hfill \\ {\mathbf{R}}_{3}^{e} = \frac{1}{{2A^{e} }}\left[ {\begin{array}{*{20}c} { - b} & 0 & 0 & 0 & 0 & 0 \\ 0 & a & 0 & 0 & 0 & 0 \\ a & { - b} & 0 & 0 & 0 & 0 \\ \end{array} } \right] \hfill \\ \end{gathered} $$
(13)
$$ \begin{gathered} {\mathbf{B}}_{1}^{e} = \frac{1}{{2A^{e} }}\left[ {\begin{array}{llllll} 0 & 0 & 0 & {b - c} & 0 & 0 \\ 0 & 0 & 0 & 0 & {d - a} & 0 \\ 0 & 0 & 0 & {d - a} & {b - c} & 0 \\ \end{array} } \right],\,\,{\mathbf{B}}_{2}^{e} = \frac{1}{{2A^{e} }}\left[ {\begin{array}{llllll} 0 & 0 & 0 & c & 0 & 0 \\ 0 & 0 & 0 & 0 & { - d} & 0 \\ 0 & 0 & 0 & { - d} & c & 0 \\ \end{array} } \right] \hfill \\ {\mathbf{B}}_{3}^{e} = \frac{1}{{2A^{e} }}\left[ {\begin{array}{llllll} 0 & 0 & 0 & { - b} & 0 & 0 \\ 0 & 0 & 0 & 0 & a & 0 \\ 0 & 0 & 0 & a & { - b} & 0 \\ \end{array} } \right] \hfill \\ \end{gathered} $$
(14)

where \( a = x_{2}^{{}} - x_{1}^{{}} ,b = y_{2}^{{}} - y_{1}^{{}} ,c = y_{3}^{{}} - y_{1}^{{}} ,d = x_{3}^{{}} - x_{1}^{{}} , \) as indicated in Fig. 2, and A e is the area of the triangular element.

In this study, discrete shear gap (DSG) method [10] is adopted here to avoid the shear-locking phenomenon. According to Eq. (4), the shear strain \( {\boldsymbol{\hat{{\gamma }}}}^{e} \) in each element can be defined by

$$ {\boldsymbol{\hat{{\gamma }}}}^{e} = \underbrace {{\left[ {\begin{array}{*{20}c} {{\mathbf{S}}_{1}^{e} } & {{\mathbf{S}}_{2}^{e} } & {{\mathbf{S}}_{3}^{e} } \\ \end{array} } \right]}}_{{{\hat{\mathbf{S}}}^{e} }}{\hat{\mathbf{d}}}^{e} = {\mathbf{S}}^{e} {\hat{\mathbf{d}}}^{e} $$
(15)

where

$$ \begin{gathered} {\mathbf{S}}_{1}^{e} = \frac{1}{{2A^{e} }}\left[ {\begin{array}{llllll} 0 & 0 & {b - c} & {A^{e} } & 0 & 0 \\ 0 & 0 & {d - a} & 0 & {A^{e} } & 0 \\ \end{array} } \right],\,\,{\mathbf{S}}_{2}^{e} = \frac{1}{{2A^{e} }}\left[ {\begin{array}{llllll} 0 & 0 & c & {\tfrac{ac}{2}} & {\tfrac{bc}{2}} & 0 \\ 0 & 0 & { - d} & { - \tfrac{ad}{2}} & { - \tfrac{bd}{2}} & 0 \\ \end{array} } \right] \hfill \\ {\mathbf{S}}_{3}^{e} = \frac{1}{{2A^{e} }}\left[ {\begin{array}{llllll} 0 & 0 & { - b} & { - \tfrac{bd}{2}} & { - \tfrac{bc}{2}} & 0 \\ 0 & 0 & a & {\tfrac{ad}{2}} & {\tfrac{ac}{2}} & 0 \\ \end{array} } \right]. \hfill \\ \end{gathered} $$
(16)

By substituting the discrete displacement field into Eq. (8), we can obtain a discretized equation for triangular Reissner–Mindlin flat shell elements such as

$$ {{\hat{\mathbf{K}}\hat{\mathbf{d}}}} = {\hat{\mathbf{F}}}, $$
(17)

where

$$ {\hat{\mathbf{K}}} = \sum\nolimits_{e = 1}^{{n^{e} }} {{\hat{\mathbf{K}}}^{e} } = \sum\nolimits_{e = 1}^{{n^{e} }} {\int_{{\Omega^{e} }} {\left( {{\mathbf{R}}^{eT} {\mathbf{D}}^{m} {\mathbf{R}}^{e} + {\mathbf{B}}^{eT} {\mathbf{D}}^{b} {\mathbf{B}}^{e} + {\mathbf{S}}^{eT} {\mathbf{D}}^{s} {\mathbf{S}}^{e} } \right){\text{d}}\Omega } } , $$
(18)
$$ {\hat{\mathbf{F}}} = \sum\nolimits_{e = 1}^{{n^{e} }} {{\hat{\mathbf{F}}}^{e} } = \sum\nolimits_{e = 1}^{{n^{e} }} {\int_{{\Omega^{e} }} {{\mathbf{N}}^{eT} {\mathbf{b}}{\text{d}}\Omega } } . $$
(19)

In the above formulas, each shell element occupies different local coordinates; the data need to be transferred to the global coordinates before conducting the assembling process of element stiffness matrices. The transformation of coordinates from a local coordinate system to a global coordinate system is performed by the transformation matrix \( {\varvec{\Lambda}}_{0}^{e} \):

$$ {\hat{\mathbf{d}}}_{j}^{e} = {\varvec{\Lambda}}_{0j}^{e} {\mathbf{d}}_{j}^{e} , $$
(20)

where \( {\hat{\mathbf{d}}}_{j}^{e} \left( {\hat{u}_{j}^{e} ,\hat{v}_{j}^{e} ,\hat{w}_{j}^{e} ,\hat{\beta }_{xj}^{e} ,\hat{\beta }_{yj}^{e} ,\hat{\beta }_{zj}^{e} } \right) \) and \( {\mathbf{d}}_{j}^{e} \left( {u_{j}^{e} ,v_{j}^{e} ,w_{j}^{e} ,\beta_{xj}^{e} ,\beta_{yj}^{e} ,\beta_{zj}^{e} } \right) \) are the displacement fields of jth node of the shell element in \( \hat{O}\hat{x}\hat{y}\hat{z} \) and Oxyz, respectively. In Eq. (20), \( {\varvec{\Lambda}}_{0j}^{e} \) is given by

$$ {\varvec{\Lambda}}_{0j}^{e} = \left[ {\begin{array}{*{20}c} {{\varvec{\uplambda}}^{T} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\varvec{\uplambda}}^{T} } \\ \end{array} } \right], $$
(21)

with

$$ {\varvec{\uplambda}} = \left[ {\begin{array}{*{20}c} {\cos \left( {i_{1} ,\hat{i}_{1} } \right)} & {\cos \left( {i_{1} ,\hat{i}_{2} } \right)} & {\cos \left( {i_{1} ,\hat{i}_{3} } \right)} \\ {\cos \left( {i_{2} ,\hat{i}_{1} } \right)} & {\cos \left( {i_{2} ,\hat{i}_{2} } \right)} & {\cos \left( {i_{2} ,\hat{i}_{3} } \right)} \\ {\cos \left( {i_{3} ,\hat{i}_{1} } \right)} & {\cos \left( {i_{3} ,\hat{i}_{2} } \right)} & {\cos \left( {i_{3} ,\hat{i}_{3} } \right)} \\ \end{array} } \right], $$
(22)

where \( \left( {\hat{i}_{1} ,\hat{i}_{2} ,\hat{i}_{3} } \right) \) and \( \left( {i_{1} ,i_{2} ,i_{3} } \right) \) are the unit vectors of the middle surface of the shell element in \( \hat{O}\hat{x}\hat{y}\hat{z} \) and Oxyz, respectively.

From Eqs. (17), (20) and (21), the global system equation in Oxyz for flat shell elements can be expressed as:

$$ {\mathbf{Kd}} = {\mathbf{F}}, $$
(23)

where

$$ {\mathbf{K}} = \sum\nolimits_{e = 1}^{{n^{e} }} {\underbrace {{{\varvec{\Lambda}}_{0}^{eT} {\hat{\mathbf{K}}}^{e} {\varvec{\Lambda}}_{0}^{e} }}_{{{\mathbf{K}}^{e} }}} = \sum\nolimits_{e = 1}^{{n^{e} }} {{\mathbf{K}}^{e} } , $$
(24)
$$ {\mathbf{F}} = \sum\nolimits_{e = 1}^{{n^{e} }} {\underbrace {{{\varvec{\Lambda}}_{0}^{eT} {\hat{\mathbf{F}}}^{e} }}_{{{\mathbf{K}}^{e} }}} = \sum\nolimits_{e = 1}^{{n^{e} }} {{\mathbf{F}}^{e} } , $$
(25)

3 An edge/node-based smoothed FEM for Reissner–Mindlin flat shells

3.1 ES-FEM and NS-FEM for Reissner–Mindlin flat shells

Computational cost of flat shell elements is directly affected by the order of approximation and the number of degrees of freedom associated with FE formulations. Therefore, using a low-order element such as three-node triangular elements, we can expect an efficient analysis in terms of computational time. Triangular elements, however, in general give poor solutions compared to high-order elements. In this study, smoothed finite element method (S-FEM) is employed to enhance the performance of triangular flat shell elements. The shape functions used in S-FEM are identical to those in conventional FEM, and hence the displacement field in S-FEM is also ensured to be continuous on the whole problem domain. However, being different from conventional FEM which computes the stiffness matrix based on the element domains, S-FEM uses a gradient smoothing technique to compute the stiffness matrix based on edges or nodes of elements.

In S-FEM, the finite element mesh is further divided into n k smoothing domains Ω(k) based on edges or nodes of elements such that \( \Omega = \bigcup\nolimits_{k = 1}^{{n^{k} }} {\Omega^{\left( k \right)} } \) and \( \Omega^{\left( i \right)} \cap \Omega^{\left( i \right)} = \)∅ for \( i \ne j \). In edge-based S-FEM (ES-FEM), the smoothing domain Ω(k) associated with the edge k is created by connecting two end nodes of the edge k to the centroids of adjacent elements, as shown in Fig. 3. The smoothing domain of an inner edge is formed by assembling two sub-domains of adjacent triangular elements while the smoothing domain of a boundary edge is a single sub-domain. On the other hand, the smoothing domain Ω(k) for node-based S-FEM (NS-FEM) associated with the node k is created by connecting sequentially the mid-edge-points to the centroids of the surrounding triangular elements (sub-domains) of the node k, as shown in Fig. 4.

Fig. 3
figure 3

A mesh of triangular elements and the smoothing domains Ω(k) associated with edges in ES-FEM

Full size image
Fig. 4
figure 4

A mesh of triangular elements and smoothing domains Ω(k) associated with the nodes in NS-FEM

Full size image

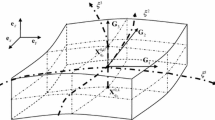
For flat shell elements, the local coordinate system \( \hat{O}\hat{x}\hat{y}\hat{z} \) is defined in each element, and the compatible strains are computed in the local coordinates. The smoothed strains in S-FEM are computed using the smoothing coordinate system \( \tilde{O}\tilde{x}\tilde{y}\tilde{z} \) defined on sub-domains of adjacent elements sharing an edge or a node. In ES-FEM, the smoothing domain Ω(k)associated with the inner edge k consists of two sub-domains with local coordinate systems \( \hat{O}_{1} \hat{x}_{1} \hat{y}_{1} \hat{z}_{1} \) and \( \hat{O}_{2} \hat{x}_{2} \hat{y}_{2} \hat{z}_{2} \), respectively, as shown in Fig. 5. The smoothing coordinate system \( \tilde{O}\tilde{x}\tilde{y}\tilde{z} \) for the smoothing domain Ω(k) is defined by the \( \tilde{x} \) axis coinciding with the edge k, the \( \tilde{z} \) axis with the average normal direction between the \( \hat{z}_{1} \) and \( \hat{z}_{2} \) axis, and the \( \tilde{y} \) axis is given by the cross product of the unit vectors in the \( \tilde{x} \) and \( \tilde{z} \) axis. In NS-FEM, the smoothing domain Ω(k) in NS-FEM associated with the inner node k consists of four sub-domains having local coordinate systems \( \hat{O}_{1} \hat{x}_{1} \hat{y}_{1} \hat{z}_{1} \) \( \hat{O}_{2} \hat{x}_{2} \hat{y}_{2} \hat{z}_{2} \) \( \hat{O}_{3} \hat{x}_{3} \hat{y}_{3} \hat{z}_{3} \) and \( \hat{O}_{4} \hat{x}_{4} \hat{y}_{4} \hat{z}_{4} \), respectively, as indicated in Fig. 6. The smoothing coordinate system \( \tilde{O}\tilde{x}\tilde{y}\tilde{z} \) for the smoothing domain Ω(k) is defined by the \( \tilde{x} \) axis that coincides with an edge connected between the node k and a node of arbitrary surrounding triangular elements; the \( \tilde{z} \) axis is the average normal direction of the \( \hat{z}_{1} \), \( \hat{z}_{2} \), \( \hat{z}_{3} \) and \( \hat{z}_{4} \) axis; the \( \tilde{y} \) axis is the cross product of the unit vectors in the \( \tilde{x} \) and \( \tilde{z} \) axis.

Fig. 5
figure 5

Local, global and smoothing coordinates of flat shell element for edge-based smoothing technique

Full size image
Fig. 6
figure 6

Local, global and smoothing coordinates of the flat shell element for node-based smoothing technique

Full size image

As a result, a smoothed membrane strain \( {\varvec{\upvarepsilon}}_{g}^{\left( k \right)} \), a smoothed bending strain \( {\varvec{\upkappa}}_{g}^{\left( k \right)} \) and a smoothed shear strain \( {\varvec{\upgamma}}_{g}^{\left( k \right)} \) in Oxyz can be derived as:

$$ {\varvec{\upvarepsilon}}_{g}^{\left( k \right)} = \int_{{\Omega^{\left( k \right)} }} {{\varvec{\Lambda}}_{m1} {\varvec{\Lambda}}_{m2} {\boldsymbol{\hat{{\varepsilon}}}}^{e} \varPhi^{\left( k \right)} \left( {\mathbf{x}} \right){\text{d}}\Omega } , $$
(26)
$$ {\varvec{\upkappa}}_{g}^{\left( k \right)} = \int_{{\Omega^{\left( k \right)} }} {{\varvec{\Lambda}}_{b1} {\varvec{\Lambda}}_{b2} {\boldsymbol{\hat{{\kappa }}}}^{e} \varPhi^{\left( k \right)} \left( {\mathbf{x}} \right){\text{d}}\Omega } , $$
(27)
$$ {\varvec{\upgamma}}_{g}^{\left( k \right)} = \int_{{\Omega^{\left( k \right)} }} {{\varvec{\Lambda}}_{s2} {\varvec{\Lambda}}_{s2} {\boldsymbol{\hat{{\gamma }}}}^{e} \varPhi^{\left( k \right)} \left( {\mathbf{x}} \right){\text{d}}\Omega } , $$
(28)

where \( {\boldsymbol{\hat{{\varepsilon}}}}^{e} \), \( {\boldsymbol{\hat{{\kappa }}}}^{e} \) and \( {\boldsymbol{\hat{{\gamma }}}}^{e} \) are the membrane, the bending and the shear strains in the local coordinate system of each sub-domain attached to edge k or node k, respectively, and \( \varPhi^{\left( k \right)} \left( {\mathbf{x}} \right) \) is a given smoothing function that satisfies \( \int_{{\Omega^{\left( k \right)} }} {\varPhi^{\left( k \right)} \left( {\mathbf{x}} \right){\text{d}}\Omega } = 1. \) The smoothing function can be defined by

$$ \varPhi^{\left( k \right)} \left( {\mathbf{x}} \right) = \left\{ {\begin{array}{*{20}c} {\frac{1}{{A^{\left( k \right)} }}} & {{\mathbf{x}} \in \Omega^{\left( k \right)} } \\ 0 & {{\mathbf{x}} \notin \Omega^{\left( k \right)} } \\ \end{array} } \right., $$
(29)

where A (k)is the area of the smoothing domain Ω(k)and is computed by

$$ A^{\left( k \right)} = \int_{{\Omega^{\left( k \right)} }} {\text{d}\Omega = } \frac{1}{3}\sum\nolimits_{i = 1}^{{n^{ek} }} {A^{i} } $$
(30)

In this equation, n ek is the number of the adjacent triangular elements in the smoothing domain Ω(k), and A i is the area of the ith sub-domain in a triangular element.

In Eqs. (26), (27) and (28), the strain transformation matrices Λ m1, Λ m2, Λ b1, Λ b2 , Λ s1 and Λ s2 can be expressed as:

$$ {\varvec{\Lambda}}_{m1} = {\varvec{\Lambda}}_{b1} = \left[ {\begin{array}{*{20}c} {c_{{x\tilde{x}}}^{2} } & {c_{{x\tilde{y}}}^{2} } & {c_{{x\tilde{z}}}^{2} } & {2c_{{x\tilde{x}}} c_{{x\tilde{y}}} } & {2c_{{x\tilde{y}}} c_{{x\tilde{z}}} } & {2c_{{x\tilde{x}}} c_{{x\tilde{z}}} } \\ {c_{{y\tilde{x}}}^{2} } & {c_{{y\tilde{y}}}^{2} } & {c_{{y\tilde{z}}}^{2} } & {2c_{{y\tilde{x}}} c_{{y\tilde{y}}} } & {2c_{{y\tilde{y}}} c_{{y\tilde{z}}} } & {2c_{{y\tilde{x}}} c_{{y\tilde{z}}} } \\ {c_{{x\tilde{x}}} c_{{y\tilde{x}}} } & {c_{{x\tilde{y}}} c_{{y\tilde{y}}} } & {c_{{x\tilde{z}}} c_{{y\tilde{z}}} } & {c_{{x\tilde{x}}} c_{{y\tilde{y}}} + c_{{y\tilde{x}}} c_{{x\tilde{y}}} } & {c_{{x\tilde{y}}} c_{{y\tilde{z}}} + c_{{y\tilde{y}}} c_{{x\tilde{z}}} } & {c_{{x\tilde{x}}} c_{{y\tilde{z}}} + c_{{y\tilde{x}}} c_{{x\tilde{z}}} } \\ \end{array} } \right] $$
(31)
$$ {\varvec{\Lambda}}_{s1} = \left[ {\begin{array}{*{20}c} {c_{{x\tilde{x}}} c_{{z\tilde{x}}} } & {c_{{x\tilde{y}}} c_{{z\tilde{y}}} } & {c_{{x\tilde{z}}} c_{{z\tilde{z}}} } & {c_{{x\tilde{x}}} c_{{z\tilde{y}}} + c_{{z\tilde{x}}} c_{{x\tilde{y}}} } & {c_{{x\tilde{y}}} c_{{z\tilde{z}}} + c_{{z\tilde{y}}} c_{{x\tilde{z}}} } & {c_{{x\tilde{x}}} c_{{z\tilde{z}}} + c_{{z\tilde{x}}} c_{{x\tilde{z}}} } \\ {c_{{y\tilde{x}}} c_{{z\tilde{x}}} } & {c_{{y\tilde{y}}} c_{{z\tilde{y}}} } & {c_{{y\tilde{z}}} c_{{z\tilde{z}}} } & {c_{{y\tilde{x}}} c_{{z\tilde{y}}} + c_{{z\tilde{x}}} c_{{y\tilde{y}}} } & {c_{{y\tilde{y}}} c_{{z\tilde{z}}} + c_{{z\tilde{y}}} c_{{y\tilde{z}}} } & {c_{{y\tilde{x}}} c_{{z\tilde{z}}} + c_{{z\tilde{x}}} c_{{y\tilde{z}}} } \\ \end{array} } \right] $$
(32)
$$ {\varvec{\Lambda}}_{m2}^{T} = {\varvec{\Lambda}}_{b2}^{T} = \left[ {\begin{array}{*{20}c} {c_{{\tilde{x}\hat{x}}}^{2} } & {c_{{\tilde{x}\hat{y}}}^{2} } & {c_{{\tilde{x}\hat{z}}}^{2} } & {2c_{{\tilde{x}\hat{x}}} c_{{\tilde{x}\hat{y}}} } & {2c_{{\tilde{x}\hat{y}}} c_{{\tilde{x}\hat{z}}} } & {2c_{{\tilde{x}\hat{x}}} c_{{\tilde{x}\hat{z}}} } \\ {c_{{\tilde{y}\hat{x}}}^{2} } & {c_{{\tilde{y}\hat{y}}}^{2} } & {c_{{\tilde{y}\hat{z}}}^{2} } & {2c_{{\tilde{y}\hat{x}}} c_{{\tilde{y}\hat{y}}} } & {2c_{{\tilde{y}\hat{y}}} c_{{\tilde{y}\hat{z}}} } & {2c_{{\tilde{y}\hat{x}}} c_{{\tilde{y}\hat{z}}} } \\ {c_{{\tilde{x}\hat{x}}} c_{{\tilde{y}\hat{x}}} } & {c_{{\tilde{x}\hat{y}}} c_{{\tilde{y}\hat{y}}} } & {c_{{\tilde{x}\hat{z}}} c_{{\tilde{y}\hat{z}}} } & {c_{{\tilde{x}\hat{x}}} c_{{\tilde{y}\hat{y}}} + c_{{\tilde{y}\hat{x}}} c_{{\tilde{x}\hat{y}}} } & {c_{{\tilde{x}\hat{y}}} c_{{\tilde{y}\hat{z}}} + c_{{\tilde{y}\hat{y}}} c_{{\tilde{x}\hat{z}}} } & {c_{{\tilde{x}\hat{x}}} c_{{\tilde{y}\hat{z}}} + c_{{\tilde{y}\hat{x}}} c_{{\tilde{x}\hat{z}}} } \\ \end{array} } \right] $$
(33)
$$ {\varvec{\Lambda}}_{s2}^{T} = \left[ {\begin{array}{*{20}c} {c_{{\tilde{x}\hat{x}}} c_{{\tilde{z}\hat{x}}} } & {c_{{\tilde{x}\hat{y}}} c_{{\tilde{z}\hat{y}}} } & {c_{{\tilde{x}\hat{z}}} c_{{\tilde{z}\hat{z}}} } & {c_{{\tilde{x}\hat{x}}} c_{{\tilde{z}\hat{y}}} + c_{{\tilde{z}\hat{x}}} c_{{\tilde{x}\hat{y}}} } & {c_{{\tilde{x}\hat{y}}} c_{{\tilde{z}\hat{z}}} + c_{{\tilde{z}\hat{y}}} c_{{\tilde{x}\hat{z}}} } & {c_{{\tilde{x}\hat{x}}} c_{{\tilde{z}\hat{z}}} + c_{{\tilde{z}\hat{x}}} c_{{\tilde{x}\hat{z}}} } \\ {c_{{\tilde{y}\hat{x}}} c_{{\tilde{z}\hat{x}}} } & {c_{{\tilde{y}\hat{y}}} c_{{\tilde{z}\hat{y}}} } & {c_{{\tilde{y}\hat{z}}} c_{{\tilde{z}\hat{z}}} } & {c_{{\tilde{y}\hat{x}}} c_{{\tilde{z}\hat{y}}} + c_{{\tilde{z}\hat{x}}} c_{{\tilde{y}\hat{y}}} } & {c_{{\tilde{y}\hat{y}}} c_{{\tilde{z}\hat{z}}} + c_{{\tilde{z}\hat{y}}} c_{{\tilde{y}\hat{z}}} } & {c_{{\tilde{y}\hat{x}}} c_{{\tilde{z}\hat{z}}} + c_{{\tilde{z}\hat{x}}} c_{{\tilde{y}\hat{z}}} } \\ \end{array} } \right] $$
(34)

where \( c_{{x\tilde{x}}} \) is the cosine of the angle between the x axis and the \( \tilde{x} \) axis, \( {\varvec{\Lambda}}_{m1} \), \( {\varvec{\Lambda}}_{b1} \), and \( {\varvec{\Lambda}}_{s1} \) are the strain transformation matrices between Oxyz and \( \tilde{O}\tilde{x}\tilde{y}\tilde{z} \), and \( {\varvec{\Lambda}}_{m2} \), \( {\varvec{\Lambda}}_{b2} \), and \( {\varvec{\Lambda}}_{s2} \) are the strain transformation matrices between \( \hat{O}\hat{x}\hat{y}\hat{z} \) of adjacent triangular elements and \( \tilde{O}\tilde{x}\tilde{y}\tilde{z} \).

Substituting Eqs. (11), (12), (15) and (29) into Eqs. (26)–(28), the approximation of the smoothed strains on the smoothing domain Ω(k)in Oxyz can be expressed as:

$$ {\varvec{\upvarepsilon}}_{g}^{\left( k \right)} = \sum\nolimits_{j = 1}^{{n^{nk} }} {{\mathbf{R}}_{gj}^{\left( k \right)} {\mathbf{d}}_{j}^{\left( k \right)} } ;\;{\varvec{\upkappa}}_{g}^{\left( k \right)} = \sum\nolimits_{j = 1}^{{n^{nk} }} {{\mathbf{B}}_{gj}^{\left( k \right)} {\mathbf{d}}_{j}^{\left( k \right)} } ;\;{\varvec{\upgamma}}_{g}^{\left( k \right)} = \sum\nolimits_{j = 1}^{{n^{nk} }} {{\mathbf{S}}_{gj}^{\left( k \right)} {\mathbf{d}}_{j}^{\left( k \right)} } $$
(35)

where n nk is the number of the neighboring nodes of edge k or node k, \( {\mathbf{d}}_{j}^{\left( k \right)} \) is the nodal degrees of freedom at the jth node of the smoothing domain Ω(k) in Oxyz, \( {\mathbf{R}}_{gj}^{\left( k \right)} \), \( {\mathbf{B}}_{gj}^{\left( k \right)} \) and \( {\mathbf{S}}_{gj}^{\left( k \right)} \) are the membrane, the bending and the shear smoothed gradient matrices at the jth node of the smoothing domain Ω(k)in Oxyz, respectively. \( {\mathbf{R}}_{gj}^{\left( k \right)} \), \( {\mathbf{B}}_{gj}^{\left( k \right)} \) and \( {\mathbf{S}}_{gj}^{\left( k \right)} \) can be computed by

$$ {\mathbf{R}}_{gj}^{\left( k \right)} = \frac{1}{{A^{\left( k \right)} }}\sum\nolimits_{i = 1}^{{n^{ek} }} {\frac{1}{3}A^{i} {\varvec{\Lambda}}_{m1}^{\left( k \right)} {\varvec{\Lambda}}_{m2}^{i} {\mathbf{R}}_{j}^{i} {\varvec{\Lambda}}_{0j}^{i} } $$
(36)
$$ {\mathbf{B}}_{gj}^{\left( k \right)} = \frac{1}{{A^{\left( k \right)} }}\sum\nolimits_{i = 1}^{{n^{ek} }} {\frac{1}{3}A^{i} {\varvec{\Lambda}}_{b1}^{\left( k \right)} {\varvec{\Lambda}}_{b2}^{i} {\mathbf{B}}_{j}^{i} {\varvec{\Lambda}}_{0j}^{i} } $$
(37)
$$ {\mathbf{S}}_{gj}^{\left( k \right)} = \frac{1}{{A^{\left( k \right)} }}\sum\nolimits_{i = 1}^{{n^{ek} }} {\frac{1}{3}A^{i} {\varvec{\Lambda}}_{s1}^{\left( k \right)} {\varvec{\Lambda}}_{s2}^{i} {\mathbf{S}}_{j}^{i} {\varvec{\Lambda}}_{0j}^{i} } $$
(38)

where \( {\varvec{\Lambda}}_{m1}^{\left( k \right)} \), \( {\varvec{\Lambda}}_{b1}^{\left( k \right)} \), and \( {\varvec{\Lambda}}_{s1}^{\left( k \right)} \) are given by Eqs. (31) and (32), \( {\varvec{\Lambda}}_{m2}^{i} \), \( {\varvec{\Lambda}}_{b2}^{i} \), and \( {\varvec{\Lambda}}_{s2}^{i} \) of the ith adjacent triangular element are given by Eqs. (33) and (34), \( {\varvec{\Lambda}}_{0j}^{i} \) is the transformation matrix between the local coordinate system \( \hat{O}\hat{x}\hat{y}\hat{z} \) at the jth node of the ith adjacent triangular element and the global coordinate system Oxyz.

The global stiffness matrix of the flat shell in Eq. (24) is replaced by the global stiffness matrix of ES-FEM or NS-FEM:

$$ {\mathbf{K}}_{ES} = \sum\nolimits_{k = 1}^{{n^{k} }} {{\mathbf{K}}_{ES}^{\left( k \right)} } \quad {\text{and}}\quad {\mathbf{K}}_{NS} = \sum\nolimits_{k = 1}^{{n^{k} }} {{\mathbf{K}}_{NS}^{\left( k \right)} } , $$
(39)

where \( {\mathbf{K}}_{ES}^{\left( k \right)} \) and \( {\mathbf{K}}_{NS}^{\left( k \right)} \) are the smoothed stiffness matrices given by

$$ \begin{aligned} {\mathbf{K}}_{I}^{\left( k \right)} & = \int_{{\Omega_{I}^{\left( k \right)} }} {\left( {{\mathbf{R}}_{gI}^{\left( k \right)T} {\mathbf{D}}^{m} {\mathbf{R}}_{gI}^{\left( k \right)} + {\mathbf{B}}_{gI}^{\left( k \right)T} {\mathbf{D}}^{b} {\mathbf{B}}_{gI}^{\left( k \right)} + {\mathbf{S}}_{gI}^{\left( k \right)T} {\mathbf{D}}^{s} {\mathbf{S}}_{gI}^{\left( k \right)} } \right){\text{d}}\Omega } \\ & = A_{I}^{\left( k \right)} \left( {{\mathbf{R}}_{gI}^{\left( k \right)T} {\mathbf{D}}^{m} {\mathbf{R}}_{gI}^{\left( k \right)} + {\mathbf{B}}_{gI}^{\left( k \right)T} {\mathbf{D}}^{b} {\mathbf{B}}_{gI}^{\left( k \right)} + {\mathbf{S}}_{gI}^{\left( k \right)T} {\mathbf{D}}^{s} {\mathbf{S}}_{gI}^{\left( k \right)} } \right),\quad I = {\text{ES}}\;{\text{or}}\;{\text{NS}} \\ \end{aligned} $$
(40)

In Eq. (40), \( A_{I}^{\left( k \right)} \), \( {\mathbf{R}}_{gI}^{\left( k \right)} \), \( {\mathbf{B}}_{gI}^{\left( k \right)} \) and \( {\mathbf{S}}_{gI}^{\left( k \right)} \) are the area, the membrane, the bending and the shear gradient matrices in ES-FEM or NS-FEM, respectively.

It is important to note that the in-plane actions do not affect the bending strains and vice versa, and the rotation about z axis (drilling rotation) does not raise the deformations of shell. Therefore, there is no stiffness associated with the local rotation degrees of freedom β z and if all elements are coplanar, the rank deficient phenomena appearing in the global stiffness matrix would increase. To deal with this issue, the null values of the stiffness corresponding to the drilling degree of freedom are then replaced by approximate values. These approximate values are taken to be equal to 10−3 times the maximum diagonal value in the element stiffness matrix [30].

3.2 A combination of ES-FEM and NS-FEM for Reissner–Mindlin flat shells

3.2.1 An edge/node-based smoothed FEM (ENS-FEM)

ES-FEM and NS-FEM can be combined to improve the accuracy of numerical results by introducing the scale factor \( \alpha \in [0,1] \) that controls the contributions from ES-FEM and NS-FEM, which was proposed similarly by Liu et al. [32]. Note that the αFEM in [32] uses FE formulations based on smoothing domains constructed based on conventional FEM and NS-FEM. In ENS-FEM, the area of each triangle is divided into three triangles for ES-FEM and three quadrilaterals for NS-FEM as depicted in Fig. 7. In the present edge/node-based S-FEM(ENS-FEM), the area A (e) of a triangular element is divided into four parts with a scale factor α: three quadrilaterals scaled down by \( (1 - \alpha^{2} ) \) at three corners with equal area of \( \tfrac{1}{3}\left( {1 - \alpha^{2} } \right)A^{\left( e \right)} \) and three pentagons in the middle of the element with equal area of \( \tfrac{1}{3}\alpha^{2} A^{\left( e \right)} . \) NS-FEM is used to calculate for three quadrilaterals at the three corners, while ES-FEM is used to calculate for three pentagons in the middle of the element.

Fig. 7
figure 7

Smoothing domains based on a combination of ES-FEM and NS-FEM for triangular elements: NS-FEM uses the three quadrilaterals, and ES-FEM uses the three pentagons

Full size image

The global smoothed stiffness K ENS is then assembled from the entries of those of both ES-FEM and NS-FEM as follows:

$$ {\mathbf{K}}_{\text{ENS}} = \sum\nolimits_{k = 1}^{{n^{k} }} {{\mathbf{K}}_{\text{ES}}^{{\left( {k,\alpha } \right)}} + \sum\nolimits_{k = 1}^{{n^{k} }} {{\mathbf{K}}_{\text{NS}}^{{\left( {k,\alpha } \right)}} } } , $$
(41)

where \( {\mathbf{K}}_{\text{ES}}^{{\left( {k,\alpha } \right)}} \) and \( {\mathbf{K}}_{\text{NS}}^{{\left( {k,\alpha } \right)}} \) are given by

$$ {\mathbf{K}}_{I}^{{\left( {k,\alpha } \right)}} = \int_{{\Omega_{I}^{{\left( {k,\alpha } \right)}} }} {\left( {{\mathbf{R}}_{gI}^{{\left( {k,\alpha } \right)T}} {\mathbf{D}}^{m} {\mathbf{R}}_{gI}^{{\left( {k,\alpha } \right)}} + {\mathbf{B}}_{gI}^{{\left( {k,\alpha } \right)T}} {\mathbf{D}}^{b} {\mathbf{B}}_{gI}^{{\left( {k,\alpha } \right)}} + {\mathbf{S}}_{gI}^{{\left( {k,\alpha } \right)T}} {\mathbf{D}}^{s} {\mathbf{S}}_{gI}^{{\left( {k,\alpha } \right)}} } \right){\text{d}}\Omega } ,\quad I = {\text{ES}}\,{\text{or}}\,{\text{NS}} $$
(42)

In the above, \( \Omega_{\text{ES}}^{{\left( {k,\alpha } \right)}} \) is the smoothing domain associated with the edge k and bounded by the boundaries \( \varGamma_{\text{ES}}^{\left( k \right)} \) and \( \varGamma_{\text{ES}}^{{\left( {k,\alpha } \right)}} \) as shown in Fig. 8a, and \( \Omega_{\text{NS}}^{{\left( {k,\alpha } \right)}} \) is the smoothing domain associated with the node k and bounded by the boundary \( \varGamma_{\text{NS}}^{{\left( {k,\alpha } \right)}} \) as shown in Fig. 8b. Note that the following relation between the area \( A^{{\left( {k,\alpha } \right)}} \) of the smoothing domain \( \Omega^{{\left( {k,\alpha } \right)}} \) and the area \( A^{\left( k \right)} \) of the smoothing domain Ω(k) is used:

$$ A_{\text{ES}}^{{\left( {k,\alpha } \right)}} = \int_{{\Omega_{\text{ES}}^{{\left( {k,\alpha } \right)}} }} {{\text{d}}\Omega } = \sum\nolimits_{i = 1}^{{n^{ek} }} {\frac{1}{3}\alpha^{2} A^{i} } = \alpha^{2} A_{\text{ES}}^{\left( k \right)} $$
(43)
$$ A_{\text{NS}}^{{\left( {k,\alpha } \right)}} = \int_{{\Omega_{\text{NS}}^{{\left( {k,\alpha } \right)}} }} {{\text{d}}\Omega } = \sum\nolimits_{i = 1}^{{n^{ek} }} {\frac{1}{3}\left( {1 - \alpha^{2} } \right)A^{i} } = \left( {1 - \alpha^{2} } \right)A_{\text{NS}}^{\left( k \right)} $$
(44)
Fig. 8
figure 8

Smoothing domains associated with a edge k in ES-FEM, and b node k in NS-FEM for triangular elements in ENS-FEM

Full size image

Therefore, the smoothed gradient matrices forthe smoothing domain \( \Omega_{\text{ES}}^{{\left( {k,\alpha } \right)}} \) can be calculated by

$$ {\mathbf{R}}_{\text{gES}}^{{\left( {k,\alpha } \right)}} = \frac{1}{{A_{\text{ES}}^{{\left( {k,\alpha } \right)}} }}\sum\nolimits_{i = 1}^{{n^{ek} }} {\frac{1}{3}\alpha^{2} A^{i} {\varvec{\Lambda}}_{m1}^{\left( k \right)} {\varvec{\Lambda}}_{m2}^{i} {\mathbf{R}}^{i} {\varvec{\Lambda}}_{0}^{i} } = \frac{1}{{A_{\text{ES}}^{\left( k \right)} }}\sum\nolimits_{i = 1}^{{n^{ek} }} {\frac{1}{3}A^{i} {\varvec{\Lambda}}_{m1}^{\left( k \right)} {\varvec{\Lambda}}_{m2}^{i} {\mathbf{R}}^{i} {\varvec{\Lambda}}_{0}^{i} } = {\mathbf{R}}_{\text{gES}}^{\left( k \right)} , $$
(45)
$$ {\mathbf{B}}_{\text{gES}}^{{\left( {k,\alpha } \right)}} = \frac{1}{{A_{\text{ES}}^{{\left( {k,\alpha } \right)}} }}\sum\nolimits_{i = 1}^{{n^{ek} }} {\frac{1}{3}\alpha^{2} A^{i} {\varvec{\Lambda}}_{b1}^{\left( k \right)} {\varvec{\Lambda}}_{b2}^{i} {\mathbf{B}}^{i} {\varvec{\Lambda}}_{0}^{i} } = \frac{1}{{A_{\text{ES}}^{\left( k \right)} }}\sum\nolimits_{i = 1}^{{n^{ek} }} {\frac{1}{3}A^{i} {\varvec{\Lambda}}_{b1}^{\left( k \right)} {\varvec{\Lambda}}_{b2}^{i} {\mathbf{B}}^{i} {\varvec{\Lambda}}_{0}^{i} } = {\mathbf{B}}_{\text{gES}}^{\left( k \right)} , $$
(46)
$$ {\mathbf{S}}_{\text{gES}}^{{\left( {k,\alpha } \right)}} = \frac{1}{{A_{\text{ES}}^{{\left( {k,\alpha } \right)}} }}\sum\nolimits_{i = 1}^{{n^{ek} }} {\frac{1}{3}\alpha^{2} A^{i} {\varvec{\Lambda}}_{s1}^{\left( k \right)} {\varvec{\Lambda}}_{s2}^{i} {\mathbf{S}}^{i} {\varvec{\Lambda}}_{0}^{i} } = \frac{1}{{A_{\text{ES}}^{\left( k \right)} }}\sum\nolimits_{i = 1}^{{n^{ek} }} {\frac{1}{3}A^{i} {\varvec{\Lambda}}_{s1}^{\left( k \right)} {\varvec{\Lambda}}_{s2}^{i} {\mathbf{S}}^{i} {\varvec{\Lambda}}_{0}^{i} } = {\mathbf{S}}_{\text{gES}}^{\left( k \right)} , $$
(47)

The smoothed gradient matrices for the smoothing domain \( \Omega_{NS}^{{\left( {k,\alpha } \right)}} \) can be calculated similarly. Consequently, we can express the global smoothed stiffness matrix K ENS using the original stiffness matrices in ES-FEM and NS-FEM such that

$$ {\mathbf{K}}_{\text{ENS}} = \sum\nolimits_{k = 1}^{{n^{k} }} {\alpha^{2} {\mathbf{K}}_{\text{ES}}^{\left( k \right)} } + \sum\nolimits_{k = 1}^{{n^{k} }} {\left( {1 - \alpha^{2} } \right){\mathbf{K}}_{\text{NS}}^{\left( k \right)} } $$
(48)

It should be noted that the scale factor α acts as a knob controlling the contributions from ES-FEM and NS-FEM. When the scale factor α varies from 0 to 1, a continuous solution function from the solution of ES-FEM to that of NS-FEM is obtained. Since ES-FEM produces usually lower bound solutions in strain energy of the exact solution [14, 16, 32, 33] and NS-FEM possesses the upper bound property [14, 17, 32, 33], ENS-FEM can be expected to give better solutions than ES-FEM and NS-FEM.

3.2.2 An average edge/node-based smoothed FEM (aENS-FEM)

Development of a generalized method for estimating the best scale factor \( \alpha_{\text{best}} \) is no easy task, because it is difficult to clarify mathematical aspects of ENS-FEM in terms of the scale factor, and the best scale factor depends on the mesh, geometry and boundary conditions. Liu et al. [32] proposed a method for αFEM to estimate the scale factor by taking the intersection point of strain energy versus scale factor curves for a sequence of meshes with different resolutions. They recommended the scale factor \( \alpha_{\text{best}} \in [0.5,0.7] \) through numerical experiments. However, these methods require a high computational cost for preparing and solving a series of analysis models.

As a simple approach, the scale factor α in ENS-FEM can be chosen as a constant if one can obtain better solutions by ENS-FEM with a constant scale factor than other methods such as FEM, ES-FEM and NS-FEM. We, therefore, propose immediately the average combination \( (\alpha = 0.5) \) of ES-FEM and NS-FEM for all practical purpose. Numerical experiments show that the present method gives better solutions of shell problems than other existing techniques including stabilized discrete shear gap method using three-node triangular elements (DSG3) [10], three-node Mindlin method (MIN3) [12], edge-based smoothed discrete shear gap triangular element method [18, 19], andnode-based smoothed discrete shear gap triangular element method [17, 20]. It should be noted that the accuracy of solutions is often much better than FEM solutions when the average combination of ES-FEM and NS-FEM is chosen. The ENS-FEM with \( \alpha = 0.5 \) is named by aENS-FEM, and the global smoothed stiffness \( {\mathbf{K}}_{{a{\text{ENS}}}} \) can be then expressed as:

$$ {\mathbf{K}}_{{a{\text{ENS}}}} = \frac{1}{4}\left( {{\mathbf{K}}_{\text{ES}} + 3{\mathbf{K}}_{\text{NS}} } \right) $$
(49)

In aENS-FEM, formulae of ES-FEM and NS-FEM are used directly to calculate the entries of the stiffness matrices, and then the stiffness matrix of aENS-FEM can be obtained by averaging the stiffness matrices of ES-FEM and NS-FEM. Therefore, aENS-FEM code is very similar to conventional FEM code, and the bandwidth of the stiffness matrix of aENS-FEM is exactly the same to that of the stiffness matrix of conventional FEM. The computational cost for solving the system equations will also be the same. All numerical examples in the next section use aENS-FEM, and numerical results are compared with those of other methods.

4 Numerical results

In this section, various numerical examples are solved to verify the accuracy and efficiency of the proposed aENS-FEM compared to the analytical solutions and reference solutions. To demonstrate the performance of numerical results, the relative deflection error is defined by

$$ {\text{er}} = \frac{{\left| {d^{\text{num}} - d^{\text{ref}} } \right|}}{{d^{\text{ref}} }} \times 100\;\% , $$
(50)

where \( d^{\text{ref}} \) and \( d^{\text{num}} \) are the reference and numerical deflections, respectively. For the convergence rate of the relatively deflection error in Eq. (50), we use the dimensionless length \( l_{h} \) [38] defined by

$$ l_{h} = \frac{1}{{\sqrt {n^{\text{dof}} } }}, $$
(51)

where \( n^{\text{dof}} \) is the total number of degrees of freedom of the whole domain.

4.1 Spherical shell panel subjected to a point load problem

In this example, a simply supported spherical shell panel in Fig. 9 is considered. The spherical shell has dimensions and elastic properties: a = b = 400 mm, r = 2400 mm, h = 2.54 mm, E = 7037 kgf/mm2 and ν = 0.3. The shell is subjected to a point central load P = 45.4 kgf. Due to its symmetry, only one quarter of the structure is modeled, as shown in Fig. 9. The spherical shell is uniformly discretized by 8 × 8, 12 × 12, 16 × 16, 20 × 20, 24 × 24 and 28 × 28 triangular and quadrilateral elements. The FE model with the 16 × 16 mesh is plotted in Fig. 10. The reference solution of the center deflection at the point load proposed by Mousa and Naggar [35] is 1 mm. We now use two scale factors estimated from strain energy curves of analysis models and from the average combination of ES-FEM and NS-FEM. As shown in Fig. 11, the strain energy at the intersection of strain energy versus scale factor curves for three fine meshes 20 × 20, 24 × 24 and 28 × 28 is 5.6749 at \( \alpha = 0.363 \). Figure 12 and Tables 1 and 2 show the convergence of deflection at the center of the spherical shell panel in terms of the relative errors and the strain energy of present method with \( \alpha = 0.363 \) and \( \alpha = 0.5 \). It can be seen that the results obtained using the scale value of \( \alpha = 0.363 \) are clearly the best competitor: the displacement and strain energy for the scale factor estimated from strain energy curves are much more accurate than those for the quadrilateral shell element MITC4. Since the selection of the scale factor depends on analysis models and problems, one can use the average combination of ES-FEM and NS-FEM as an alternative choice for all practical purpose. Although ENS-FEM with the \( \alpha = 0.5 \) (aENS-FEM) is not the best solution, it is still more accurate than DSG3, MIN3, ES-FEM and NS-FEM, and is a good competitor with quadrilateral shell elements (MITC4). Figure 13 shows the deformed configuration of the spherical shell panel.

Fig. 9
figure 9

Geometry of the spherical shell panel with simply supported on the boundaries

Full size image
Fig. 10
figure 10

Two discretizations of the spherical shell panel using a triangular elements, and b quadrilateral elements

Full size image
Fig. 11
figure 11

Strain energy of the spherical shell panel problem

Full size image
Fig. 12
figure 12

Results of the spherical shell panel problem: a convergence of vertical displacement at the center, b relative error under log–log scale, and c convergence of strain energy

Full size image
Table 1 Vertical displacement at the center of spherical shell panel obtained by different methods
Full size table
Table 2 The strain energy of the spherical shell panel obtained by different methods
Full size table
Fig. 13
figure 13

Deformed configuration of the spherical shell panel (displacements of the spherical shell panel are amplified by a factor 100)

Full size image

4.2 A cantilever cylinder shell stiffened by concentric beams

We now study a cantilever cylindrical shell stiffened by three concentric stiffeners at two curved edges and one straight edge. The dimensions, material parameters and boundary conditions are given in Fig. 14. The cantilever cylindrical shell is discretized into 8 × 8, 12 × 12, 16 × 16, 20 × 20 and 24 × 24 triangular and quadrilateral elements. The FE model with the 12 × 12 mesh is plotted in Fig. 15. The numerical results obtained by the aENS-FEM are compared with those by DSG3, MIN3, ES-FEM, NS-FEM and MITC4. Sinha et al. [40] presented a highly accurate solution to this problem using a higher-order shell theory. However, we use the numerical results obtained by MITC4 as a reference solution, because the solution given by Sinha et al. [40] is not close to the numerical solutions in this study. Figure 16 shows that the strain energy versus scale factor curves do not intersect each other for any meshes. Hence, we take the value of \( \alpha \) at the intersection point between the strain energies for MITC4 and ENS-FEM using the mesh 24 × 24. The strain energy at the intersection is 0.9372 at \( \alpha = 0.67 \), as shown in Fig. 16. Figure 17 shows the convergence of the radial displacement and strain energy for ENS-FEM with \( \alpha = 0.67 \) and \( \alpha = 0.5. \) This figure indicates that ENS-FEM with \( \alpha = 0.5 \) (aENS-FEM) has better performance than DSG3, MIN3, ES-FEM and NS-FEM, and can be a good competitor to the quadrilateral shell elements (MITC4). Tables 3 and 4 summarize the values of the radial displacement and strain energy at the loaded point of the concentric stiffened cylinders. The deformed configuration of the cantilever cylinder shell stiffened by concentric beams is plotted in Fig. 18.

Fig. 14
figure 14

Geometry, material parameters and loaded point of the cantilever cylinder shell stiffened by concentric stiffeners

Full size image
Fig. 15
figure 15

Two discretizations of the stiffened cantilever cylinder shell using a triangular elements and b quadrilateral elements

Full size image
Fig. 16
figure 16

Strain energy of the stiffened cantilever cylinder shell

Full size image
Fig. 17
figure 17

Results of the cantilever cylinder shell stiffened by concentric stiffeners: a convergence of radial displacement at the loaded point (cm), and b convergence of strain energy

Full size image
Table 3 Radial displacements at the loaded point of the cantilever cylinder shell stiffened by concentric stiffeners
Full size table
Table 4 The strain energy of the cantilever cylinder shell stiffened by concentric stiffeners
Full size table
Fig. 18
figure 18

Deformed configuration of the cantilever cylinder shell stiffened by concentric stiffeners (displacements of the stiffened cantilever cylinder shell are amplified by a factor 3 × 102)

Full size image

4.3 Spherical shell with cross stiffeners

Lastly, a simply supported spherical panel stiffened by two cross concentric stiffeners under a concentrated load 45 kN at the center is investigated. The dimensions and the material properties of the stiffened shell are listed in Fig. 19. Sinha et al. [37] and Prusty et al. [39] solved this problem for the spherical shell with cross stiffeners. The stiffened shell is uniformly discretized by 4 × 4, 8 × 8, 12 × 12, 16 × 16, and 20 × 20 triangular and quadrilateral elements, and only the 12 × 12 mesh is plotted in Fig. 20. The vertical displacement at the center load is monitored, and the results given by Prusty et al. [39] with 12 × 12 eight-noded isoparametric quadrilateral elements, w = 0.04327 m, are taken as a reference solution. In this problem, we found that the value of \( \alpha \) is 0.444 at the intersection of four strain energy versus scale factor curves for four meshes, as shown in Fig. 21. Figure 22 shows the comparison of the vertical displacement at the center of stiffened shell and strain energy, listed in Tables 5 and 6. It can be seen that with the same number of degrees of freedom, ENS-FEM with \( \alpha = 0.444 \) and \( \alpha = 0.5 \) outperforms all other elements in terms of accuracy and convergence. It should be noted that ENS-FEM with \( \alpha = 0.5 \) (aENS-FEM) is much more accurate than all other methods including ES-FEM, NS-FEM and FEM. The deformed configuration of the spherical shell with cross stiffeners is plotted in Fig. 23.

Fig. 19
figure 19

Geometry of the stiffened spherical shell panel with simply supported on the boundaries

Full size image
Fig. 20
figure 20

Two discretizations of the stiffened spherical shell panel using a triangular elements and b quadrilateral elements

Full size image
Fig. 21
figure 21

Strain energy of the stiffened spherical shell panel

Full size image
Fig. 22
figure 22

Results of the stiffened spherical shell panel problem: a convergence of vertical displacement at the center, b relative error under log–log scale, and c convergence of strain energy

Full size image
Table 5 The vertical displacement at the center load of stiffened spherical shell panel by different methods
Full size table
Table 6 The strain energy of stiffened spherical shell panel by different methods
Full size table
Fig. 23
figure 23

Deformed configuration of the stiffened spherical shell panel (displacements of the stiffened spherical shell panel are amplified by a factor 5)

Full size image

5 Conclusion

In this study, we propose a combined scheme (ENS-FEM) of node-based smoothed finite element method (NS-FEM) and edge-based smoothed finite element method (ES-FEM) for triangular Reissner–Mindlin flat shells. A discrete shear gap (DSG) technique is employed to avoid shear-locking phenomenon in Reissner–Mindlin flat shell elements. The smoothing domains based on a combination of ES-FEM and NS-FEM are defined to compute the stiffness matrix for Reissner–Mindlin flat shells. The present ENS-FEM uses three-node triangular elements that are much easily generated automatically even for complicated geometries. In this study, the average combination of ES-FEM and NS-FEM (aENS-FEM) with the scale factor α = 0.5 is proposed for all practical purpose and verified through numerical examples. The numerical results obtained by aENS-FEM show a good agreement with the reference solutions, and are more accurate than those obtained by other methods such as DSG3, MIN3, ES-FEM and NS-FEM. In addition, some benchmark shell problems confirm that the present method has a good performance and is compatible to four-node quadrilateral shell elements (MITC4).