Geometrically nonlinear analysis of functionally graded shells using an edge-based smoothed MITC3 (ES-MITC3) finite elements

Abstract

An edge-based smoothed finite element method (ES-FEM) combined with the mixed interpolation of tensorial components technique (MITC) for triangular elements, named as ES-MITC3, was recently proposed to enhance the accuracy of the original MITC3 for analysis of shells. In this study, the ES-MITC3 is extended to the geometrically nonlinear analysis of functionally graded shells. In the ES-MITC3, the stiffness matrices are obtained using the strain smoothing technique over the smoothing domains that formed by two adjacent MITC3 triangular shell elements sharing an edge. The material properties of functionally graded (FG) shells are assumed to vary through the thickness direction by a power rule distribution of volume fractions of the constituents. The nonlinear finite element formulation based on the first-order shear deformation theory with the von Kármán’s large deflection assumption is used to describe the large deformations of the FG shells. Several numerical examples are given to demonstrate the performance of the present approach in comparison with other existing methods.

1 Introduction

Functionally graded materials (FGM) are inhomogeneous composites formed by a mixture of distinct material phases, e.g., ceramic and metal, in which their volume fraction is gradually varying along a certain dimension of the structure. It is well known that the ceramic materials can survive in environments with high-temperature gradients, while the metal materials give structural strength and fracture toughness. Based on the great mixture of ceramic and metal materials, the FGM have been successfully applied to use in aircraft, space vehicle, and nuclear plants. In the FGM study, analysis and simulation behavior of the FGM plate/shell structures have been studied by many researchers.

For analysis of the FGM plate structures, Reddy [1] used finite element (FE) model based on the third-order shear deformation theory (TSDT) to solve nonlinear geometric problems under thermos-mechanical loadings. Praveen and Reddy [2] investigated the nonlinear static and transient responses of the FGM plates subjected to thermal and mechanical loadings. In this study, a combination between the first-order shear deformation theory (FSDT) and von Kármán assumptions is used to establish equations of motion. Ferreira et al. [3] proposed the meshless method relied on the radial basis functions and the TSDT to analyze a simply supported FGM plate. Mantari et al. [4] presented an exact solution to study the static response of simply supported FGM plates subjected to bi-sinusoidal and distributed loads using a new high-order shear deformation theory (HSDT). Nguyen-Xuan et al. [5, 6] developed a smoothed finite element method (SFEM) based on the FSDT to investigate static, free vibration and buckling of the FGM plates under thermal and mechanical loads. Tran et al. [7, 8] carried out isogeometric analysis (IGA) combining with the HSDT to study linear and nonlinear thermomechanical stability of the FGM plates. Phung-Van et al. [9] proposed a cell-based smoothed three-node Mindlin plate element based on the HSDT for geometrically nonlinear analysis of the FGM plates under thermal and mechanical loadings.

For analysis of the FGM shell structures, Arciniega and Reddy [10] presented a geometrically nonlinear analysis of the FGM shells using a tensor-based FE method with high-order Lagrange interpolation and the FSDT based on seven parameters. Tornabene and Viola [11, 12] developed the generalized differential quadrature (GDQ) method combined with the FSDT theory to investigate the dynamic behavior of the moderate and thick FGM parabolic and circular shells. An analytical solution for the nonlinear post-buckling behavior of the FGM cylindrical shells under external pressure in thermal environments is proposed by Shen [13, 14]. In this research, the classical shell theory with von Kármán–Donnell-type of kinematic nonlinearity is used to deal the governing equations of the FGM shell. Zhao and Liew [15] introduced a nonlinear analysis of the FGM shells subjected to thermomechanical loading based on the element-free kp-Ritz method with Sander’s nonlinear shell theory [16]. Pradyumna and Bandyopadhyay [17] obtained the FE method relied on the HSDT to investigate for free vibration of the FGM shells. Shell structures in this work are discretized using an eight-node element with nine degrees of freedom (df) and the strain displacement relations of the doubly curved shell using Sanders’ approximation [18]. In addition, some novel approaches for shell analysis can be found in Refs. [19,20,21,22,23,24,25].

It has long been known that the classical shell theories are limitary for thin shells thus the most of investigations in recent years have used Reissner–Mindlin theory to analyze for both thick and thin shells. However, the shear-locking phenomenon can arise in the case of a very small thickness of shells. To eliminate the shear-locking phenomenon, there were many improved techniques which have been proposed such as the reduced integration method [26], discrete shear gap (DSG) [27], assumed natural strains (ANS) [28], SFEM [29,30,31,32,33,34,35,36], mixed interpolation of tensorial components (MITC) [37,38,39,40,41,42,43,44,45] and so on.

Recently, to enhance the performance of the original MITC3 triangular element, a combination between the edge-based smoothed finite element method (ES-FEM) [31, 46,47,48,49,50] and the MITC3, named ES-MITC3, is proposed [51,52,53,54]. In the formulation of the ES-MITC3, the strain smoothing technique is used to smooth the strains on the adjacent MITC3 triangular elements, wherein a smoothing domain is formed by two adjacent MITC3 triangular elements sharing an edge. The numerical results showed that (1) the ES-MITC3 elements are often found fast convergent and much more accurate than an original MITC3 element with the same of df; (2) the shear-locking is eliminated even the ratio of thickness reaches $10^{ - 8}$. Motivated by the advantages of the ES-MITC3 elements, geometrically nonlinear analysis of functionally graded shell structures is solved in this study. The continuous and smooth material properties through the thickness of functionally graded shells are assumed in this study based on a simple power law of the volume fractions of the constituents. The nonlinear FE formulation is based on the FSDT of the shell with the von Kármán’s large deflection theory which considers a small strain and large deformations assumptions. The solution of the nonlinear equation system is accomplished using the cylindrical arc-length method combined with an automatic incremental algorithm [55] to obtain the full load–displacement path. Several numerical results show that the present method is a strong competitor to other existing methods.

2 Theoretical formulation

2.1 Functionally grade material

In the composite materials field, functionally grade material is made from a mixture of distinct material phases, e.g., ceramic and metal, as shown in Fig. 1. The material properties change continuously from a surface to the other surface according to a simple power law in terms of the volume fractions of the constituents as

$$V_{\text{c}} (z) = \left( {\frac{1}{2} + \frac{z}{h}} \right)^{n} ,\quad V_{\text{m}} (z) = 1 - V_{\text{c}} (z),$$

(1)

where $V_{\text{c}}$ and $V_{\text{m}}$ are the volume fractions of ceramic and metal constituents, respectively, $h$ is the thickness of structure; $n \ge 0$ is the volume fraction exponent; and $z \in [ - \,h/2,h/2]$ is the thickness coordinate of the structure. Thus, the effective material properties such as Young’s modulus $E$, Poisson’s ratio $v$ and mass density $\rho$, can be expressed as the following rule:

$$P(z) = P_{\text{m}} V_{\text{m}} (z) + P_{\text{c }} V_{\text{c}} (z),$$

(2)

where $P_{\text{c }}$ and $P_{\text{m}}$ are the properties of the ceramic and metal, respectively. Figure 2 illustrates the volume fraction of ceramic and metal varying through the non-dimensional thickness $(z/h)$ via the volume fraction exponents $n$. It is clear to see that the value of the power $n = 0$ when the structure is fully ceramic. In contrast, the homogeneous metal is retrieved at the power $n = \infty$.

Fig. 1

A functionally graded material

Fig. 2

Variation of the volume fraction versus the non-dimensional thickness

2.2 The FGM shell model

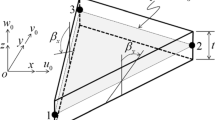
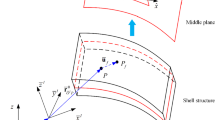
In the FSDT theory [56], the displacement field of a shell element in the local coordinate system $Oxyz$ can be defined as follows:

$$\begin{aligned} & u(x,y,z) = u_{0} (x,y) + z\beta_{x} (x,y), \\ & v(x,y,z) = v_{0} (x,y) + z\beta_{y} (x,y), \\ & w(x,y,z) = w_{0} (x,y), \\ \end{aligned}$$

(3)

where $u_{0}$, $v_{0}$ and $w_{0}$ are, respectively, the displacements of the middle surface in the $x$, $y$ and $z$ directions; $\beta_{x}$ and $\beta_{y}$ indicate the rotations in the $xz$ and $yz$ plane, respectively, see Fig. 3. A vector of in-plane Green–Lagrangian strain for large deformation analysis at any point in a shell element is formed as

$$\varvec{\varepsilon}= \left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\gamma_{xy} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {u_{,x} + \frac{1}{2}(u_{,x}^{2} + v_{,x}^{2} + w_{,x}^{2} )} \\ {v_{,y} + \frac{1}{2}(u_{,y}^{2} + v_{,y}^{2} + w_{,y}^{2} )} \\ {u_{,y} + v_{,x} + (u_{,x} u_{,y} + v_{,x} v_{,y} + w_{,x} w_{,y} )} \\ \end{array} } \right\} .$$

(4)

Fig. 3

The three-node triangular element

Using the von Kármán’s large deflection assumption [57], the nonlinear strain–displacement relationship can be rewritten as

$$\varvec{\varepsilon}= \left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\gamma_{xy} } \\ \end{array} } \right\} =\varvec{\varepsilon}_{m} + z\varvec{\kappa} \,{\text{and}}\,\varvec{\gamma}= \left\{ {\begin{array}{*{20}c} {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {w_{0,x} + \beta_{x} } \\ {w_{0,y} + \beta_{y} } \\ \end{array} } \right\},$$

(5)

where

$$\varvec{\varepsilon}_{m} =\varvec{\varepsilon}_{m}^{L} +\varvec{\varepsilon}_{m}^{NL} ,$$

(6)

$$\varvec{\kappa}= \left\{ {\begin{array}{*{20}c} {\beta_{x,x} } \\ {\beta_{y,y} } \\ {\beta_{x,y} + \beta_{y,x} } \\ \end{array} } \right\} ;\,\varvec{\varepsilon}_{m}^{L} { = }\left\{ {\begin{array}{*{20}c} {u_{0,x} } \\ {v_{0,y} } \\ {u_{0,y} + v_{0,x} } \\ \end{array} } \right\}\,{\text{and}}\,\varvec{\varepsilon}_{m}^{NL} { = }\frac{1}{2}\underbrace {{\left[ {\begin{array}{*{20}c} {w_{0,x} } & 0 \\ 0 & {w_{0,y} } \\ {w_{0,y} } & {w_{0,x} } \\ \end{array} } \right]}}_{\varvec{H}}\underbrace {{\left\{ {\begin{array}{*{20}c} {w_{0,x} } \\ {w_{0,y} } \\ \end{array} } \right\}}}_{\varvec{\theta}} = \frac{1}{2}\varvec{H\theta }.$$

(7)

The constitutive relationship of FGM shells can be expressed as

$$\underbrace {{\left\{ {\begin{array}{*{20}c} \varvec{N} \\ \varvec{M} \\ \varvec{Q} \\ \end{array} } \right\}}}_{{\overline{\varvec{\sigma}} }} = \underbrace {{\left[ {\begin{array}{*{20}c} \varvec{A} & \varvec{B} & 0 \\ \varvec{B} & \varvec{D} & 0 \\ 0 & 0 & {\varvec{C}^{\varvec{*}} } \\ \end{array} } \right]}}_{{\overline{\varvec{D}} }}\underbrace {{\left\{ {\begin{array}{*{20}c} {\varvec{\varepsilon}_{m} } \\\varvec{\kappa}\\\varvec{\gamma}\\ \end{array} } \right\}}}_{{\overline{\varvec{\varepsilon}} }};\quad \overline{\varvec{\sigma}} = \overline{\varvec{D}} \overline{\varvec{\varepsilon}} ,$$

(8)

where $\varvec{N}$, $\varvec{M}$ and $\varvec{Q}$ denote for the in-plane force resultants, moment resultants and shear force resultants, respectively, and are given by

$$\varvec{N} = \left\{ {\begin{array}{*{20}c} {N_{x} } \\ {N_{y} } \\ {N_{xy} } \\ \end{array} } \right\},\quad \varvec{M} = \left\{ {\begin{array}{*{20}c} {M_{x} } \\ {M_{y} } \\ {M_{xy} } \\ \end{array} } \right\},\quad \varvec{Q} = \left\{ {\begin{array}{*{20}c} {Q_{x} } \\ {Q_{y} } \\ \end{array} } \right\}.$$

(9)

In Eq. (8), $\varvec{A}$, $\varvec{D}$, $\varvec{B}$ and $\varvec{C}^{\varvec{*}}$ represent for the matrices of extensional, bending, bending–extensional coupling, and transverse shear stiffness matrices, respectively, which are defined as

$$\begin{aligned} & \varvec{A} = \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & {A_{16} } \\ {A_{21} } & {A_{22} } & {A_{26} } \\ {A_{61} } & {A_{62} } & {A_{66} } \\ \end{array} } \right],\quad \varvec{B} = \left[ {\begin{array}{*{20}c} {B_{11} } & {B_{12} } & {B_{16} } \\ {B_{21} } & {B_{22} } & {B_{26} } \\ {B_{61} } & {B_{62} } & {B_{66} } \\ \end{array} } \right], \\ & \varvec{D} = \left[ {\begin{array}{*{20}c} {D_{11} } & {D_{12} } & {D_{16} } \\ {D_{21} } & {D_{22} } & {D_{26} } \\ {D_{61} } & {D_{62} } & {D_{66} } \\ \end{array} } \right],\quad \varvec{C}^{\varvec{*}} = \left[ {\begin{array}{*{20}c} {C_{55} } & {C_{45} } \\ {C_{45} } & {C_{44} } \\ \end{array} } \right], \\ \end{aligned}$$

(10)

where $A_{ij}$, $B_{ij}$, $D_{ij}$ and $C_{ij}$ are given by

$$(A_{ij} ,B_{ij} ,D_{ij} ) = \mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} Q_{ij} (1,z,z^{2} ){\text{d}}z,\quad i,j = 1,2,6,$$

(11)

$$C_{ij} = \kappa \mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} Q_{ij} {\text{d}}z,\quad i,j = 4,5,$$

(12)

where $\kappa = 5/6$ is the transverse shear correction coefficient and

$$\begin{aligned} & Q_{11} (z) = Q_{22} (z) = \frac{E(z)}{{1 - v(z)^{2} }}, \\ & Q_{12} (z) = Q_{21} (z) = v(z)Q_{11} (z), \\ & Q_{16} (z) = Q_{61} (z) = Q_{26} (z) = Q_{62} (z) = 0 \\ & Q_{44} (z) = Q_{55} (z) = Q_{66} (z) = \frac{E(z)}{2(1 + v(z))} \\ & Q_{45} (z) = Q_{54} (z) = 0, \\ \end{aligned}$$

(13)

in which $E$ and $v$ are the elastic moduli and the Poisson’s ratios, respectively.

2.3 Finite element formulation for geometrically nonlinear shell analysis

2.3.1 Finite element analysis

The bounded domain is discretized into $n^{e}$ finite three-node triangular elements with $n^{n}$ nodes such that $\varOmega \approx \sum\nolimits_{e = 1}^{{n^{e} }} {\varOmega_{e} }$ and $\varOmega_{i} \cap \varOmega_{j} = \emptyset ,\,i \ne j$. Then the FE approximation $\varvec{u}_{{}}^{e} = \left[ {u_{j}^{e} , v_{j}^{e} , w_{j}^{e} , \beta_{xj}^{e} , \beta_{yj}^{e} } \right]^{T}$ for elements of the shell can be expressed as

$$\varvec{u}^{e} = \mathop \sum \limits_{j = 1}^{{n_{{}}^{ne} }} \varphi_{j}^{e} ({\mathbf{x}})\varvec{I}_{5} \varvec{d}_{j}^{e} = \mathop \sum \limits_{j = 1}^{{n_{{}}^{ne} }} \varvec{\varphi }_{j}^{e} ({\mathbf{x}})\varvec{d}_{j}^{e} ,$$

(14)

where $\varvec{I}_{5}$ is the unit matrix of fifth rank; $n_{{}}^{ne}$ is the number of nodes of the shell element; $\varphi_{j}^{e} ({\mathbf{x}})$ is the shape function at the jth node of the element and $\varvec{d}_{j}^{e} = [u_{j}^{e} , v_{j}^{e} , w_{j}^{e} , \beta_{xj}^{e} , \beta_{yj}^{e} ]^{T}$ is the nodal degrees of freedom of $\varvec{u}_{{}}^{e} \varvec{ }$ associated with the jth node of the element.

The approximation of the linear membrane, the nonlinear membrane and the bending strains of a triangular element can be written in matrix forms as follows:

$$\varvec{\varepsilon}_{m}^{eL} = \left[ {\begin{array}{*{20}c} {\varvec{B}_{m1}^{eL} } & {\varvec{B}_{m2}^{eL} } & {\varvec{B}_{m3}^{eL} } \\ \end{array} } \right]\varvec{d}^{e} = \varvec{B}_{m }^{eL} \varvec{d}^{e} ,$$

(15)

$$\varvec{\varepsilon}_{m}^{eNL} = \frac{1}{2}\varvec{B}_{m}^{eNL} \varvec{d}^{e} ,$$

(16)

$$\varvec{\kappa}_{{}}^{e} = \left[ {\begin{array}{*{20}c} {\varvec{B}_{b1}^{e} } & {\varvec{B}_{b2}^{e} } & {\varvec{B}_{b3}^{e} } \\ \end{array} } \right]\varvec{d}^{e} = \varvec{B}_{b }^{e} \varvec{d}^{e} ,$$

(17)

where

$$\varvec{B}_{m1}^{eL} = \frac{1}{{2A_{e} }}\left[ {\begin{array}{*{20}c} {b - c} & 0 & 0 & 0 & 0 \\ 0 & {d - a} & 0 & 0 & 0 \\ {d - a} & {b - c} & 0 & 0 & 0 \\ \end{array} } \right],$$

(18)

$$\varvec{B}_{m2}^{eL} = \frac{1}{{2A_{e} }}\left[ {\begin{array}{*{20}c} c & 0 & 0 & 0 & 0 \\ 0 & { - d} & 0 & 0 & 0 \\ { - d} & c & 0 & 0 & 0 \\ \end{array} } \right],$$

(19)

$$\varvec{B}_{m3}^{eL} = \frac{1}{{2A_{e} }}\left[ {\begin{array}{*{20}c} { - b} & 0 & 0 & 0 & 0 \\ 0 & a & 0 & 0 & 0 \\ a & { - b} & 0 & 0 & 0 \\ \end{array} } \right],$$

(20)

$$\varvec{B}_{b1}^{e} = \frac{1}{{2A_{e} }}\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & {b - c} & 0 \\ 0 & 0 & 0 & 0 & {d - a} \\ 0 & 0 & 0 & {d - a} & {b - c} \\ \end{array} } \right],$$

(21)

$$\varvec{B}_{b2}^{e} = \frac{1}{{2A_{e} }}\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & c & 0 \\ 0 & 0 & 0 & 0 & { - d} \\ 0 & 0 & 0 & { - d} & c \\ \end{array} } \right],$$

(22)

$$\varvec{B}_{b3}^{e} = \frac{1}{{2A_{e} }}\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & { - b} & 0 \\ 0 & 0 & 0 & 0 & a \\ 0 & 0 & 0 & a & { - b} \\ \end{array} } \right],$$

(23)

$$\varvec{B}_{m}^{eNL} = \varvec{HG}\,{\text{with}}\,\varvec{G} = \left[ {\begin{array}{*{20}c} {\varvec{G}_{1}^{{}} } & {\varvec{G}_{2}^{{}} } & {\varvec{G}_{3}^{{}} } \\ \end{array} } \right],$$

(24)

$$\varvec{G}_{1}^{{}} = \frac{1}{{2A_{e} }}\left[ {\begin{array}{*{20}c} 0 & 0 & {b - c} & 0 & 0 \\ 0 & 0 & {d - a} & 0 & 0 \\ \end{array} } \right],$$

(25)

$$\varvec{G}_{2}^{{}} = \frac{1}{{2A_{e} }}\left[ {\begin{array}{*{20}c} 0 & 0 & c & 0 & 0 \\ 0 & 0 & { - d} & 0 & 0 \\ \end{array} } \right],$$

(26)

$$\varvec{G}_{3}^{{}} = \frac{1}{{2A_{e} }}\left[ {\begin{array}{*{20}c} 0 & 0 & { - b} & 0 & 0 \\ 0 & 0 & a & 0 & 0 \\ \end{array} } \right],$$

(27)

in which $a = x_{2} - x_{1}$, $b = y_{2} - y_{1}$,$c = y_{3} - y_{1}$ and $d = x_{3} - x_{1}$ are pointed out in Fig. 4 and $A_{e}$ is the area of the three-node triangular element.

Fig. 4

Three-node triangular element in the local coordinates

For the shear strains field, the MITC3 triangular element [38] is used to eliminate the shear-locking phenomenon in this study. The explicitly transverse shear strain field [51, 53] can be expressed as

$$\varvec{\gamma}_{{}}^{e} = \left[ {\begin{array}{*{20}c} {\varvec{B}_{s1}^{e} } & {\varvec{B}_{s2}^{e} } & {\varvec{B}_{s3}^{e} } \\ \end{array} } \right]\varvec{d}^{e} = \varvec{B}_{s }^{e} \varvec{d}^{e} ,$$

(28)

where

$$\varvec{B}_{s1}^{e} = \varvec{J}^{ - 1} \left[ {\begin{array}{*{20}c} 0 & 0 & { - 1} & {\frac{a}{3} + \frac{d}{6}} & {\frac{b}{3} + \frac{c}{6}} \\ 0 & 0 & { - 1} & {\frac{d}{3} + \frac{a}{6}} & {\frac{c}{3} + \frac{b}{6}} \\ \end{array} } \right],$$

(29)

$$\varvec{B}_{s2}^{e} = \varvec{J}^{ - 1} \left[ {\begin{array}{*{20}c} 0 & 0 & 1 & {\frac{a}{2} - \frac{d}{6}} & {\frac{b}{2} - \frac{c}{6}} \\ 0 & 0 & 0 & {\frac{d}{6}} & {\frac{c}{6}} \\ \end{array} } \right],$$

(30)

$$\varvec{B}_{s3}^{e} = \varvec{J}^{ - 1} \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & {\frac{a}{6}} & {\frac{b}{6}} \\ 0 & 0 & 1 & {\frac{d}{2} - \frac{a}{6}} & {\frac{c}{2} - \frac{b}{6}} \\ \end{array} } \right],$$

(31)

with

$$\varvec{J}^{ - 1} = \frac{1}{{2A_{e} }}\left[ {\begin{array}{*{20}c} c & { - b} \\ { - d} & a \\ \end{array} } \right].$$

(32)

Applying the principle of virtual work, the variation of the total energy of shell can be given by

$$\delta \varPi = \mathop \sum \limits_{e = 1}^{{n^{e} }} \left( {\int\limits_{{\varOmega_{e} }} {\delta \bar{\varvec{\varepsilon }}^{{\varvec{e}T}} \bar{\varvec{\sigma }}^{e} {\text{d}}\varOmega - \int\limits_{{\varOmega_{e} }} {\delta \varvec{u}^{eT} \varvec{b}{\text{d}}\varOmega } } } \right) = 0,$$

(33)

where $\varPi$ is the total potential energy in the domain $\varOmega$ and $\varvec{b}$ is the external load vector. In Eq. (33), $\bar{\varvec{\varepsilon }}^{e}$ and $\bar{\varvec{\sigma }}^{e}$ are derived based on Eq. (8) as follows:

$$\bar{\varvec{\varepsilon }}^{e} = \left\{ {\begin{array}{*{20}c} {\varvec{\varepsilon}_{m}^{eL} +\varvec{\varepsilon}_{m}^{eNL} } \\ {\varvec{\kappa}^{e} } \\ {\varvec{\gamma}^{e} } \\ \end{array} } \right\},\quad \bar{\varvec{\sigma }}^{e} = \varvec{\bar{D}\bar{\varepsilon }}^{e} .$$

(34)

By substituting the discrete displacement field into Eq. (33) lead to the discrete system equations for shell now becomes

$$\mathop \sum \limits_{e = 1}^{{n^{e} }} \varvec{K}^{e} \varvec{d}^{e} = \mathop \sum \limits_{e = 1}^{{n^{e} }} \varvec{F}^{\varvec{e}} ,$$

(35)

where

$$\varvec{K}^{e} = \varvec{K}^{eL} + \varvec{K}^{eNL} .$$

(36)

The transformation of the displacement fields of $j$th node of shell element between the local coordinate system $Oxyz$ and the global coordinate system $\hat{O}\hat{x}\hat{y}\hat{z}$ defined by

$$\varvec{d}_{j}^{e} =\varvec{\varLambda}_{0j}^{e} \hat{\varvec{d}}_{j}^{e} ,$$

(37)

where $\varvec{d}_{j}^{e}$ and $\hat{\varvec{d}}_{j}^{e}$ are the displacement fields of $j{\text{th}}$ node of the shell element in local and global coordinates, respectively, and $\varvec{\varLambda}_{0j}^{e}$ is the transformation matrix [58, 59].

Substituting Eq. (37) into Eq. (35), the global system equation in $\hat{O}\hat{x}\hat{y}\hat{z}$ for shell can be expressed as

$$\varvec{K\hat{d}} = \varvec{F},$$

(38)

where

$$\varvec{K} = \mathop \sum \limits_{e = 1}^{{n^{e} }}\varvec{\varLambda}_{0}^{eT} \varvec{K}^{e}\varvec{\varLambda}_{0}^{e} ,\,\varvec{F } = \mathop \sum \limits_{e = 1}^{{n^{e} }}\varvec{\varLambda}_{0}^{eT} \varvec{F}^{\varvec{e}} .$$

(39)

2.3.2 Linearization of the nonlinear equations

Substituting Eqs. (14)–(17), (28) and (34) into Eq. (33) the principle of virtual work can be rewritten as

$$\delta \varPi = \mathop \sum \limits_{e = 1}^{{n^{e} }} \delta \varvec{d}^{eT} \left( {\int\limits_{{\varOmega_{e} }} {\bar{\varvec{B}}^{T} \bar{\varvec{\sigma }}^{e} {\text{d}}\varOmega - \int\limits_{{\varOmega_{e} }} {\varvec{\varphi }_{{}}^{eT} \varvec{b}{\text{d}}\varOmega } } } \right) = 0,$$

(40)

where

$$\bar{\varvec{B}} = \varvec{B}^{eL} + \varvec{B}^{eNL} \,{\text{with}}\,\varvec{B}^{eL} = \left[ {\begin{array}{*{20}c} {\varvec{B}_{m}^{eL} } \\ {\varvec{B}_{b}^{e} } \\ {\varvec{B}_{s}^{e} } \\ \end{array} } \right],\quad \varvec{B}^{eNL} = \left[ {\begin{array}{*{20}c} {\varvec{B}_{m }^{eNL} } \\ \varvec{0} \\ \varvec {0} \\ \end{array} } \right].$$

(41)

Linearization of the principal of the virtual work to determine a tangent matrix for using a Newton–Raphson is iteration procedure to solve the geometric nonlinearity and assume for simplicity that loading is conservative so that ${\text{d}}\left( {\int\limits_{{\varOmega_{e} }} {\varvec{\varphi }^{eT} \varvec{b}{\text{d}}\varOmega } } \right) = 0$, then Eq. (40) can be rewritten as [60]

$${\text{d}}(\delta \varPi ) = \mathop \sum \limits_{e = 1}^{{n^{e} }} \delta \varvec{d}^{eT} \int\limits_{{\varOmega_{e} }} {[{\text{d}}(\bar{\varvec{B}}^{T} )\bar{\varvec{\sigma }}^{e} + \bar{\varvec{B}}^{T} {\text{d}}(\bar{\varvec{\sigma }}^{e} )]} {\text{d}}\varOmega .$$

(42)

The one to be linearized is the nonlinear part of the strain–displacement matrix, $\varvec{B}_{m }^{eNL}$, the term $\int\limits_{{\varOmega_{e} }} {{\text{d}}(\bar{\varvec{B}}^{T} )\bar{\varvec{\sigma }}^{e} {\text{d}}\varOmega }$ in Eq. (42) can be derived as follows:

$$\int\limits_{{\varOmega_{e} }} {{\text{d}}(\varvec{B}_{m }^{eNL} )^{T} \varvec{N}{\text{d}}\varOmega } .$$

(43)

Substituting Eq. (9) and Eq. (24) into Eq. (43), we can obtain

$$\begin{aligned} \int\limits_{{\varOmega_{e} }} {{\text{d}}(\varvec{B}_{m }^{eNL} )^{T} \varvec{N}{\text{d}}\varOmega } & = \int\limits_{{\varOmega_{e} }} {\varvec{G}^{T} \underbrace {{\left[ {\begin{array}{*{20}c} {{\text{d}}(w_{,x} )} & 0 & {{\text{d}}(w_{,y} )} \\ 0 & {{\text{d}}(w_{,y} )} & {{\text{d}}(w_{,x} )} \\ \end{array} } \right]}}_{{{\text{d}}(\varvec{H}^{T} )}}\left\{ {\begin{array}{*{20}c} {N_{x} } \\ {N_{y} } \\ {N_{xy} } \\ \end{array} } \right\}\,} {\text{d}}\varOmega \\ & = \int\limits_{{\varOmega_{e} }} {\varvec{G}^{T} \underbrace {{\left[ {\begin{array}{*{20}c} {N_{x} } & {N_{xy} } \\ {N_{xy} } & {N_{y} } \\ \end{array} } \right]}}_{{\varvec{N}_{\varvec{m}} }}\left\{ {\begin{array}{*{20}c} {{\text{d}}(w_{,x} )} \\ {{\text{d}}(w_{,y} )} \\ \end{array} } \right\}{\text{d}}\varOmega\,} = \left( {\int\limits_{{\varOmega_{e} }} {\varvec{G}^{T} \varvec{N}_{\varvec{m}} \varvec{G}{\text{d}}\varOmega } } \right)\,{\text{d}}(\varvec{d}^{e} ). \\ \end{aligned}$$

(44)

The term $\int\limits_{{\varOmega_{e} }} {\bar{\varvec{B}}^{T} {\text{d}}(\bar{\varvec{\sigma }}^{e} ) {\text{d}}\varOmega }$ in Eq. (42) can be derived as

$$\int\limits_{{\varOmega_{e} }} {\bar{\varvec{B}}^{T} {\text{d}}(\bar{\varvec{\sigma }}^{e} )d\varOmega } = \int\limits_{{\varOmega_{e} }} {[\varvec{B}^{eL} + \varvec{B}^{eNL} ]^{T} } \bar{\varvec{D}}[\varvec{B}^{eL} + \varvec{B}^{eNL} ]{\text{d}}(\varvec{d}^{e} ){\text{d}}\varOmega .$$

(45)

Substituting Eq. (44) and Eq. (45) into Eq. (42) the variation of the principle of virtual work can be rewritten as

$${\text{d}}(\delta \varPi ) = \mathop \sum \limits_{e = 1}^{{n^{e} }} \delta \varvec{d}^{eT} \varvec{K}_{t}^{e} {\text{d}}(\varvec{d}^{e} ),$$

(46)

in which $\varvec{K}_{t}^{e}$ is the element tangent stiffness matrix defined as

$$\varvec{K}_{t}^{e} = \varvec{K}^{eL} + \varvec{K}^{eNL} + \varvec{K}_{g}^{e} ,$$

(47)

where $\varvec{K}^{eL}$ represents for the linear stiffness matrix, $\varvec{K}^{eNL}$ denotes the nonlinear stiffness matrix which is a function of displacement and $\varvec{K}_{g}^{e}$ is the geometric stiffness matrix. These matrices can be expressed as

$$\varvec{K}^{eL} = \int\limits_{{\varOmega_{e} }} {(\varvec{B}^{eL} )^{T} \bar{\varvec{D}}\varvec{B}^{eL} {\text{d}}\varOmega } ,$$

(48)

$$\varvec{K}^{eNL} = \int\limits_{{\varOmega_{e} }} {(\varvec{B}^{eL} )^{T} \bar{\varvec{D}}\varvec{B}^{eNL} {\text{d}}\varOmega } + \int\limits_{{\varOmega_{e} }} {(\varvec{B}^{eNL} )^{T} \bar{\varvec{D}}\varvec{B}^{eL} {\text{d}}\varOmega } + \int\limits_{{\varOmega_{e} }} {(\varvec{B}^{eNL} )^{T} \bar{\varvec{D}}\varvec{B}^{eNL} {\text{d}}\varOmega } ,$$

(49)

$$\varvec{ K}_{g}^{e} = \int\limits_{{\varOmega_{e} }} {\varvec{G}^{T} \varvec{N}_{m} \varvec{G}{\text{d}}\varOmega } .$$

(50)

2.3.3 Solution of the nonlinear equations using the arc-length iterative algorithm and modified Newton–Raphson method

To solve the nonlinear equation system Eq. (38), a combination of the arc-length iterative algorithm and modified Newton–Raphson method are used to track the full load–displacement path. The governing Eq. (38) is rewritten as

$$\varvec{r}(\hat{\varvec{d}}) = \varvec{K\hat{d}} - \varvec{F} = 0.$$

(51)

The external load is assumed to be proportional to a fixed load $\varvec{F}_{0}$:

$$\varvec{F} = \lambda \varvec{F}_{0} ,$$

(52)

in which $\lambda$ is the load scale factor. Substituting Eq. (52) into Eq. (51), the nonlinear equilibrium equation can be re-expressed as

$$\varvec{r}(\hat{\varvec{d}},\lambda ) = \varvec{K\hat{d}} - \lambda \varvec{F}_{0} = 0.$$

(53)

By updating increments both the scale factor $\lambda$ and the displacement vector $\hat{\varvec{d}}$, a new equilibrium state is obtained

$$\varvec{r}(\hat{\varvec{d}} + \Delta \hat{\varvec{d}},\lambda + \Delta \lambda ) = 0.$$

(54)

Applying the Taylor series expansion to Eq. (54):

$$\varvec{r}(\hat{\varvec{d}} + \Delta \hat{\varvec{d}},\lambda + \Delta \lambda ) = \varvec{r}(\hat{\varvec{d}},\lambda ) + \varvec{K}_{t} \Delta \hat{\varvec{d}} - \Delta \lambda \varvec{F}_{0} = 0,$$

(55)

where $\Delta \lambda$ and $\Delta \hat{\varvec{d}}$ represent the increment load factor and the increment displacement, respectively, $\varvec{K}_{t}$ is the tangent stiffness matrix as given in Eq. (47). In the incremental-iterative method, the Eq. (55) can be expressed as

$$[\varvec{K}_{t} ]_{n} \Delta \hat{\varvec{d}}_{n}^{m} = \Delta \lambda_{n}^{m} \varvec{F}_{0} - \varvec{r}_{n}^{m - 1} = \Delta \lambda_{n}^{m} \varvec{F}_{0} - \left[ {\varvec{K}\left( {\hat{\varvec{d}}_{n}^{m - 1} } \right)\hat{\varvec{d}}_{n} - \lambda_{n}^{m - 1} \varvec{F}_{0} } \right],$$

(56)

in which the subscript $n$ and $m$ are the load step number and the iteration cycle, respectively. The incremental displacement vector $\Delta \hat{\varvec{d}}_{n}^{m}$ consists a part of the external increment and the other one from the residual force which is given by

$$\Delta \hat{\varvec{d}}_{n}^{m} = \left[ {(\varvec{K}_{t} )_{\varvec{n}} } \right]_{{}}^{ - 1} \left\{ {\Delta \lambda_{n}^{m} \varvec{F}_{0} - \left[ {\varvec{K}\left( {\hat{\varvec{d}}_{n}^{m - 1} } \right)\hat{\varvec{d}}_{n} - \lambda_{n}^{m - 1} \varvec{F}_{0} } \right]} \right\}.$$

(57)

In this paper, the increment of the external load $\Delta \lambda_{n}^{m}$ can be determined by arc-length method [55] and the convergence is used the following criterion:

$$\frac{|{\varvec{g}(\hat{\varvec{d}}, \lambda )}|}{{|\varvec{F}(\hat{\varvec{d}}, \lambda )}|} < \zeta .$$

(58)

The tolerance for convergence constant $\zeta$ is taken to be 0.001 in this study.

2.4 Formulation of an ES-MITC3 method for FGM shells

To enhance the performance of the MITC3 triangular shell elements for static responses and free vibration of laminated composite shells, Pham et al. [53] recently proposed a combination of the MITC3 and the edge-based smoothed method (ES-FEM), named ES-MITC3. In this method, the edge-based smoothed strain is calculated in the domain that constructed by two adjacent MITC3 triangular elements sharing an edge. On a curved geometry of shell models, the edge-based smoothed strain can be performed on the virtual plane based on strain transformation matrices between the global coordinate of two adjacent MITC3 triangular elements and this virtual coordinate. The ES-MITC3 shell elements not only produce stable and accurate results for all tested problems but also are the best performance compared to the DSG3, ES-DSG3, MITC3, and MITC4 elements. Because of the above advantages, the ES-MITC3 is applied in this study for geometrically nonlinear analysis of the functionally graded shells. Readers can find more detailed information about the ES-MITC3 method in Ref. [53].

In the ES-FEM, a domain $\varOmega$ is divided into $n^{k}$ smoothing domains $\varOmega^{k}$ based on edges of elements, such as $\varOmega = \bigcup\nolimits_{k = 1}^{{n^{k} }} {\varOmega^{k} }$ and $\varOmega_{i}^{k} \cap \varOmega_{j}^{k} = \emptyset \,{\text{for}}\,i \ne j$. An edge-based smoothing domain $\varOmega^{k}$ associated with the inner edge $k$ is formed by two sub-domains of two non-planar adjacent MITC3 triangular elements as shown in Fig. 5. These triangular elements are defined by two local coordinate systems $O_{1} x_{1} y_{1} z_{1}$ and $O_{2} x_{2} y_{2} z_{2}$. To compute edge-based smoothing strain the $\varOmega^{k}$ for two non-planar adjacent elements, the virtual coordinate system $\tilde{O}\tilde{x}\tilde{y}\tilde{z}$ is proposed as shown in Fig. 6, whereas the $\tilde{x}$-axis coinciding with the edge $k$, the $\tilde{z}$-axis with the average direction between the $z_{1}$-axis and $z_{2}$-axis, and the $\tilde{y}$-axis is given by the cross-product of the unit vectors in the $\tilde{x}$-axis and $\tilde{z}$-axis.

Fig. 5

The smoothing domain $\varOmega^{k}$ is formed by triangular elements

Fig. 6

Global, local and virtual coordinates

Now, applying the edge-based smoothed FE [61], the membrane strain $\varvec{\varepsilon}_{m}^{L}$, the bending strain $\varvec{\kappa}$, the shear strain $\varvec{\gamma}$ and the nonlinear strain $\varvec{\varepsilon}_{m}^{NL}$ in Eqs. (5) and (6) are, respectively, used to create a smoothed membrane strain $\tilde{\varvec{\varepsilon }}^{kL}$, a smoothed bending strain $\tilde{\varvec{\kappa }}^{k}$, a smoothed shear strain $\tilde{\varvec{\gamma }}_{{}}^{k}$ and a smoothed nonlinear strain $\tilde{\varvec{\varepsilon }}_{{}}^{kNL}$ of the smoothing domain $\varOmega^{k}$ in the global coordinate system $\hat{O}\hat{x}\hat{y}\hat{z}$ can be derived as

$$\tilde{\varvec{\varepsilon }}^{kL} = \int\limits_{{\varOmega^{k} }} {\varvec{\varepsilon}_{m}^{L} \varPhi^{k} ({\mathbf{x}}){\text{d}}\varOmega } ,$$

(59)

$$\tilde{\varvec{\kappa }}^{k} = \int\limits_{{\varOmega^{k} }} {\varvec{\kappa}\varPhi^{k} ({\mathbf{x}}){\text{d}}\varOmega } ,$$

(60)

$$\tilde{\varvec{\gamma }}^{k} = \int\limits_{{\varOmega^{k} }} {\varvec{\gamma}\varPhi^{k} ({\mathbf{x}}){\text{d}}\varOmega } ,$$

(61)

$$\tilde{\varvec{\varepsilon }}^{kNL} = \int\limits_{{\varOmega^{k} }} {\varvec{\varepsilon}_{m}^{NL} \varPhi^{k} ({\mathbf{x}}){\text{d}}\varOmega } ,$$

(62)

where $\varPhi^{k} ({\mathbf{x}})$ is a given smoothing function that satisfies at least unity property $\int\limits_{{\varOmega^{k} }} {\varPhi^{k} ({\mathbf{x}}){\text{d}}\varOmega = 1}$. In this work, we use the constant smoothing function:

$$\varPhi^{k} ({\mathbf{x}}) = \left\{ {\begin{array}{*{20}c} {\frac{1}{{A^{k} }}} & {x \in \varOmega^{k} } \\ 0 & {x \notin \varOmega^{k} } \\ \end{array} } \right.,$$

(63)

in which $A^{k}$ is the area of the smoothing domain $\varOmega^{k}$ and is given by

$$A^{k} = \int\limits_{{\varOmega^{k} }} {{\text{d}}\varOmega } = \frac{1}{3}\mathop \sum \limits_{i = 1}^{{n^{ek} }} A^{i} ,$$

(64)

where $n^{ek}$ is the number of the adjacent triangular elements in the smoothing domain $\varOmega^{k}$; and $A^{i}$ is the area of the $i{\text{th}}$ triangular element attached to the edge $k.$

Substituting Eqs. (15)–(17) and (28) into Eqs. (59)–(62), the smoothed membrane strain $\tilde{\varvec{\varepsilon }}^{kL}$, the smoothed bending strain $\tilde{\varvec{\kappa }}^{k}$, the smoothed shear strain $\tilde{\varvec{\gamma }}^{k}$ and the smoothed nonlinear strain $\tilde{\varvec{\varepsilon }}^{kNL}$ of the smoothing domain $\varOmega^{k}$ in the global coordinate system $\hat{O}\hat{x}\hat{y}\hat{z}$ can be derived as

$$\tilde{\varvec{\varepsilon }}^{kL} = \mathop \sum \limits_{j = 1}^{{n^{nk} }} \tilde{\varvec{B}}_{mj}^{kL} \varvec{d}_{j}^{k} ,\quad \tilde{\varvec{\kappa }}^{k} = \mathop \sum \limits_{j = 1}^{{n^{nk} }} \tilde{\varvec{B}}_{bj}^{k} \varvec{d}_{j}^{k} ,\quad \tilde{\varvec{\gamma }}^{k} = \mathop \sum \limits_{j = 1}^{{n^{nk} }} \tilde{\varvec{B}}_{sj}^{k} \varvec{d}_{j}^{k} ,\quad \tilde{\varvec{\varepsilon }}^{kNL} = \mathop \sum \limits_{j = 1}^{{n^{nk} }} \tilde{\varvec{B}}_{mj}^{kNL} \varvec{d}_{j}^{k} ,$$

(65)

where $n^{nk}$ is the number of the neighboring nodes of edge $k$, $\varvec{d}_{j}^{k}$ is the nodal degrees of freedom at the jth node of the smoothing domain $\varOmega^{k}$ in $\hat{O}\hat{x}\hat{y}\hat{z}$; $\tilde{\varvec{B}}_{mj}^{kL}$, $\tilde{\varvec{B}}_{mj}^{kNL}$, $\tilde{\varvec{B}}_{bj}^{k}$ and $\tilde{\varvec{B}}_{sj}^{k}$ are the membrane, the nonlinear, the bending and the MITC3 shear matrices at the jth node of the smoothing domain $\varOmega^{k}$ in the global coordinate system $\hat{O}\hat{x}\hat{y}\hat{z}$, respectively. The $\tilde{\varvec{B}}_{mj}^{kL}$, $\tilde{\varvec{B}}_{bj}^{k}$, $\tilde{\varvec{B}}_{sj}^{k}$ and $\tilde{\varvec{B}}_{mj}^{kNL}$ can be computed by

$$\tilde{\varvec{B}}_{mj}^{kL} = \frac{1}{{A^{k} }}\mathop \sum \limits_{i = 1}^{{n^{ek} }} \frac{1}{3}A^{i}\varvec{\varLambda}_{m1}^{k}\varvec{\varLambda}_{m2}^{i} \varvec{B}_{mj}^{iL}\varvec{\varLambda}_{0j}^{i} ,$$

(66)

$$\tilde{\varvec{B}}_{bj}^{k} = \frac{1}{{A^{k} }}\mathop \sum \limits_{i = 1}^{{n^{ek} }} \frac{1}{3}A^{i}\varvec{\varLambda}_{b1}^{k}\varvec{\varLambda}_{b2}^{i} \varvec{B}_{bj}^{i}\varvec{\varLambda}_{0j}^{i} ,$$

(67)

$$\tilde{\varvec{B}}_{sj}^{k} = \frac{1}{{A^{k} }}\mathop \sum \limits_{i = 1}^{{n^{ek} }} \frac{1}{3}A^{i}\varvec{\varLambda}_{s1}^{k}\varvec{\varLambda}_{s2}^{i} \varvec{B}_{sj}^{i}\varvec{\varLambda}_{0j}^{i} ,$$

(68)

$$\tilde{\varvec{B}}_{mj}^{kNL} = \frac{1}{{A^{k} }}\mathop \sum \limits_{i = 1}^{{n^{ek} }} \frac{1}{3}A^{i}\varvec{\varLambda}_{m1}^{k}\varvec{\varLambda}_{m2}^{i} \varvec{B}_{mj}^{iNL}\varvec{\varLambda}_{0j}^{i} ,$$

(69)

in which $\varvec{\varLambda}_{0j}^{i}$ is the transformation matrix between the local coordinate system $Oxyz$ at the $j{\text{th}}$ node of the $i{\text{th}}$ adjacent triangular element and the global coordinate system $\hat{O}\hat{x}\hat{y}\hat{z}$; $\varvec{\varLambda}_{m1}^{k}$, $\varvec{\varLambda}_{b1}^{k}$, and $\varvec{\varLambda}_{s1}^{k}$ are strain transformation matrices between the global coordinate system $\hat{O}\hat{x}\hat{y}\hat{z}$ and the virtual coordinate system $\tilde{O}\tilde{x}\tilde{y}\tilde{z}$, respectively; $\varvec{\varLambda}_{m2}^{i}$, $\varvec{\varLambda}_{b2}^{i}$, and $\varvec{\varLambda}_{s2}^{i}$ are the strain transformation matrices between the local coordinate system $Oxyz$ and the virtual coordinate system $\tilde{O}\tilde{x}\tilde{y}\tilde{z}$, respectively. More detailed information about these quantities can be found in [59].

As a result, Eq. (55) is rewritten as

$$\varvec{r}(\hat{\varvec{d}} + \Delta \hat{\varvec{d}},\lambda + \Delta \lambda ) = \varvec{r}(\hat{\varvec{d}},\lambda ) + \tilde{\varvec{K}}_{t} \Delta \hat{\varvec{d}} - \Delta \lambda \varvec{F}_{0} = 0,$$

(70)

where

$$\tilde{\varvec{K}}_{t}^{{}} = \tilde{\varvec{K}}^{L} + \tilde{\varvec{K}}^{NL} + \tilde{\varvec{K}}_{g}^{{}} = \mathop \sum \limits_{k = 1}^{{n^{k} }} \tilde{\varvec{K}}^{kL} + \mathop \sum \limits_{k = 1}^{{n^{k} }} \tilde{\varvec{K}}^{kNL} + \mathop \sum \limits_{k = 1}^{{n^{k} }} \tilde{\varvec{K}}_{g}^{k} .$$

(71)

In Eq. (71), the smoothed stiffness matrices $\tilde{\varvec{K}}^{kL} ,\tilde{\varvec{K}}^{kNL}$ and $\tilde{\varvec{K}}_{g}^{k}$ in the smoothing domain $\varOmega^{k}$ are expressed as

$$\tilde{\varvec{K}}^{kL} = \int\limits_{{\varOmega^{k} }} {(\tilde{\varvec{B}}^{kL} )^{T} \varvec{\bar{D}\tilde{B}}^{kL} {\text{d}}\varOmega^{k} } ,$$

(72)

$$\tilde{\varvec{K}}^{kNL} = \int\limits_{{\varOmega^{k} }} {(\tilde{\varvec{B}}^{kL} )^{T} \varvec{\bar{D}\tilde{B}}^{kNL} {\text{d}}\varOmega^{k} } + \int\limits_{{\varOmega^{k} }} {(\tilde{\varvec{B}}^{kNL} )^{T} \varvec{\bar{D}\tilde{B}}^{kL} {\text{d}}\varOmega^{k} } + \int\limits_{{\varOmega^{k} }} {(\tilde{\varvec{B}}^{kNL} )^{T} \varvec{\bar{D}\tilde{B}}^{kNL} {\text{d}}\varOmega^{k} } ,$$

(73)

$$\tilde{\varvec{K}}_{g}^{k} = \int\limits_{{\varOmega^{k} }} {(\tilde{\varvec{G}}^{k} )^{T} \varvec{N}_{m} \tilde{\varvec{G}}^{k} {\text{d}}\varOmega^{k} } ,\quad \tilde{\varvec{G}}^{k} = \frac{1}{{A^{k} }}\mathop \sum \limits_{i = 1}^{{n^{ek} }} \frac{1}{3}A^{i} \varvec{G\varLambda }_{0j}^{i} ,$$

(74)

where

$$\tilde{\varvec{B}}_{{}}^{kL} = \left[ {\begin{array}{*{20}c} {\tilde{\varvec{B}}_{m}^{kL} } & {\tilde{\varvec{B}}_{b}^{k} } & {\tilde{\varvec{B}}_{s}^{k} } \\ \end{array} } \right]^{T} ,\quad \tilde{\varvec{B}}^{kNL} = \left[ {\begin{array}{*{20}c} {\tilde{\varvec{B}}_{m}^{kNL} } & \varvec{0} & \varvec{0} \\ \end{array} } \right]^{T} .$$

(75)

3 Numerical results

Several numerical examples are investigated in the section to show the performance of the proposed element where obtained results are compared to several other elements in the literature. For convenience, the non-dimensional central deflection $\bar{w}$, load parameter $\bar{P}$ and normal stress $\bar{\sigma }_{xx}$ are expressed as the following equations:

$$\bar{w} = \frac{w}{h};\quad \bar{P} = \frac{{q_{0} a^{4} }}{{E_{2} h^{4} }};\quad \bar{\sigma }_{xx} = \frac{{\sigma_{xx} h^{2} }}{{Pa^{2} }}.$$

(76)

3.1 Geometrically nonlinear analysis of isotropic square plate (planar shell)

Let us consider that the models of the isotropic square plate are subjected to a uniform load $q_{0}$ as shown in Fig. 7. The geometry data: length $a = 300\,{\text{in}}.$, thickness $h = 3$ in. An elastic material with Young’s modulus $E = 3 \times 10^{7} \,{\text{psi}}$ and Poisson’s ratio $\upsilon = 0.3$ is used for this example. A fully clamped (CCCC) boundary condition is considered for this example. The plate is discretized used into a mesh of $10 \times 10$ triangular and quadrilateral elements. The results of the present method are compared with several other elements such as MITC3 [38], DSG3 [27], MXFEM [62] and FEM-Q9 [63]. In this example, the results of MXFEM [62] are used as the reference solutions. To demonstrate the performance of the numerical results, the relative non-dimensional central deflection error is defined by

$$e = \frac{{\left| {\bar{w} - \bar{w}^{\text{ref}} } \right|}}{{\bar{w}^{\text{ref}} }} \times 100\% ,$$

(77)

where $\bar{w}^{\text{ref}}$ is the reference solution. The relative non-dimensional central deflection errors with different elements are plotted in Fig. 8. The results obtained using present method (ES-MITC3) are closer to the results of the reference solution (MXFEM) than those obtained using MITC3, DSG3 triangular elements and a good competitor with the nine-node quadrilateral element (FEM-Q9) [63]. The non-dimensional central deflections with different incremental load parameters are also plotted in Fig. 9. Table 1 shows detailed results of non-dimensional central deflection of the isotropic square plate that is subjected to a uniform load using different methods.

Fig. 7

Square plate model

Fig. 8

Relative errors of central deflections of the clamped isotropic plate with different incremental load parameters

Fig. 9

Non-dimensional central deflection of the clamped isotropic plate with different incremental load parameters using ES-MITC3 element

Table 1 The central deflection of the clamped isotropic plate

3.2 Geometrically nonlinear analysis of functionally graded square plate (planar shell)

The nonlinear response of simply supported FGM plate under uniform loading $q_{0 } = 1 \times 10^{4} \,{\text{N/m}}^{2}$ is investigated as the second example. The FGM square plate has a side length $a = 0.2\,{\text{m}}$, thickness $h = 0.01\,{\text{m}}$ as shown in Fig. 7. The FGM plate in this example is a combination between aluminum (Al) and zirconia (ZnO₂) with the material properties: $E_{\text{m}} = 70 \times 10^{9} \,{\text{N/m}}^{2}$; $v_{\text{m}} = 0.3$; $E_{\text{c}} = 151 \times 10^{9} \,{\text{N/m}}^{2}$; $v_{\text{c}} = 0.3$. The plate is modeled with a mesh of $8 \times 8$ three-node triangular elements. The non-dimensional central deflection $\bar{w}$ and the normal central axial stress $\bar{\sigma }_{xx}$ distribution with different volume fraction exponents of the FGM plate Al–ZnO₂ are shown in Figs. 10 and 11, respectively. To demonstrate the performance of the present approach in comparison with other existing methods, the solutions of the element-free kp-Ritz method proposed by Zhao and Liew [57] are used as the reference solutions. Figure 12 shows the non-dimensional central deflection $\bar{w}$ with the volume fraction exponent $n = 2$ of the present element (ES-MITC3) and DSG3 and MITC3 triangular elements. As shown in this figure, the results of the present method are more accurate than those obtained using MITC3, DSG3 triangular elements. In addition, the results of ES-MITC3 element show a good agreement with the results of the element-free kp-Ritz method [57]. Table 2 presents non-dimensional central deflection results with the load parameter for simply supported FGM plate Al–ZnO₂ with volume fraction exponents $n = 2$.

Fig. 10

Non-dimensional central deflection with the load parameter for simply supported FGM plate Al–ZnO₂ with different volume fraction exponents

Fig. 11

Non-dimensional central axial stresses for simply supported FGM plate Al–ZnO₂ with different volume fraction exponents

Fig. 12

The central deflection with the load parameter for simply supported Al–ZnO₂ FGM plate with n = 2

Table 2 The central deflection of simply supported Al–ZnO₂ FGM plate with the load parameter

3.3 Nonlinear analysis of hinged cylindrical shell under point load

Consider a cylindrical roof subjected to a point load at the center as shown in Fig. 13, wherein the longitudinal edges are hinged and the curved edges are free. In Fig. 13, the length of the cylindrical shell is $L = 508\,{\text{mm}}$, the radius is $R = 2540\,{\text{mm}}$ and open angle $2\varphi = 0.2\,{\text{rad}}$. The material properties are $E = 3.10275\,{\text{kN/mm}}^{2}$, $v = 0.3$. Owing to symmetry, a quarter of the cylindrical shell is modeled and uniformly discretized by $6 \times 6$ triangular elements as shown in Fig. 13. Figure 14 plots the load–deflection curves at the center of the cylindrical shell with two different thicknesses: $h = 12.7\,{\text{mm}}$ and $h = 6.35\,{\text{mm}}$. As shown in this figure, the present ES-MITC3 solutions capture and close to the solutions obtained by Sze et al. [64]. It can be concluded that the present element is successfully applied to the geometrically nonlinear analysis of shell structures.

Fig. 13

A hinged cylindrical shell panel under a point load

Fig. 14

Comparison of the load–deflection for a hinged-free isotropic shell panel under a point load

3.4 Nonlinear analysis of hinged functionally graded cylindrical shell under point load

Finally, the nonlinear response of functionally graded cylindrical shell subjected to point load is investigated. The geometry and the boundary conditions of the cylindrical shell in this example are the same as example 3.3. A quarter of the cylindrical shell is also discretized using a $6 \times 6$ mesh. The material properties of the functionally graded shell are aluminum-zirconia. Figures 15 and 16 plot the load–displacement response of the ES-MITC3 solutions with several different values of the exponent $n$ for two different thicknesses: $h = 12.7\,{\text{mm}}$ and $h = 6.35\,{\text{mm}}$. It can be seen that the limit points of the load–deflection curves of the volume faction exponent $n = 0$ (Zirconia) for both cases of thickness ($h = 12.7\,{\text{mm}}$ and $h = 6.35\,{\text{mm}}$) are higher than others. A snap-through and snap-back phenomenon are observed in this problem with respect to $h = 12.7\,{\text{mm}}$ and $h = 6.35\,{\text{mm}}$. In addition, the magnitude of the load decreases when the volume fraction exponent increases. As expected, due to a larger volume exponent of FGM shell, i.e., the smaller ratio of the ceramic component, the stiffness of the FGM shell becomes weaker. To demonstrate the performance of the present ES-MITC3 element, the solution proposed by Arciniega and Reddy [65] is used as the reference solution in this example. Figure 17 illustrates the load–displacement response of the volume fraction exponent $n = 2$. It is observed from Fig. 17 that the result of the present method is in good agreement with the result that is given by Arciniega and Reddy [65]. It is pointed again that the present ES-MITC3 element is able to offer good predictions in geometrically nonlinear analysis of the FGM shells.

Fig. 15

Variation in the central deflection for a hinged-free FGM (aluminum/zirconia) shell panel under a point load with the thickness $h = 12.7\,{\text{mm}}$

Fig. 16

Variation in the central deflection for a hinged-free FGM (aluminum/zirconia) shell panel under a point load with the thickness $h = 6.35\,{\text{mm}}$

Fig. 17

The central deflection for a hinged-free FGM (aluminum/zirconia, $n = 2$) shell panel under a point load with the thickness $h = 12.7\,{\text{mm}}$

4 Conclusion

In this paper, the geometrically nonlinear analysis of FGM shells is studied using a combination between the ES-FEM and the MITCs technique, named as ES-MITC3. Herein, the stiffness matrices obtained based on the strain smoothing technique over the smoothing domains associated with edges of MITC3 triangular elements. In this study, the FSDT with the von Kármán large deflection theory is applied for the nonlinear formulation of the shells. To obtain the full load–displacement path, the cylindrical arc-length method combined with an automatic incremental algorithm is used. Through the numerical results, we can withdraw the following points:

• The present ES-MITC3 element is a simple and efficient element based on a combination between the ES-FEM technique and the MITC3 element.

• The results obtained by ES-MITC3 element are more accurate than those obtained using the MITC3, DSG3 elements.

• The accuracy and reliability of the proposed ES-MITC3 element for geometrically nonlinear analysis of FGM shells are also good agreement with most of the case which is compared to the reference and analytical solutions.