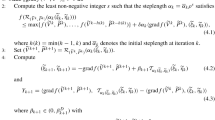Greedy Algorithms for High-Dimensional Eigenvalue Problems

Abstract

In this article, we present two new greedy algorithms for the computation of the lowest eigenvalue (and an associated eigenvector) of a high-dimensional eigenvalue problem and prove some convergence results for these algorithms and their orthogonalized versions. The performance of our algorithms is illustrated on numerical test cases (including the computation of the buckling modes of a microstructured plate) and compared with that of another greedy algorithm for eigenvalue problems introduced by Ammar and Chinesta.

1 Introduction

High-dimensional problems are encountered in many application fields, including electronic structure calculation, molecular dynamics, uncertainty quantification, multiscale homogenization, and mathematical finance. The numerical simulation of these problems, which requires specific approaches due to the so-called curse of dimensionality [5], has fostered the development of a wide variety of new numerical methods and algorithms, such as sparse grids [10, 34, 37], reduced bases [9], sparse tensor products [20], and adaptive polynomial approximations [15, 16].

In this article, we focus on an approach introduced by Ladevèze [24], Chinesta [2], Nouy [29], and coauthors in different contexts, relying on the use of greedy algorithms [35, 36]. This class of methods is also called progressive generalized decomposition [14] in the literature.

Let $V$ be a Hilbert space of functions depending on $d$ variables $x_1 \in {\mathcal {X}}_1, \ldots , x_d \in {\mathcal {X}}_d$, where, typically, ${\mathcal {X}}_j \subset {\mathbb {R}}^{m_j}$. For all $1\le j \le d$, let $V_j$ be a Hilbert space of functions depending only on the variable $x_j$ such that for all $d$-tuple $\left( \phi ^{(1)}, \ldots , \phi ^{(d)} \right) \in V_1\times \cdots \times V_d$, the tensor-product function $\phi ^{(1)} \otimes \cdots \otimes \phi ^{(d)}$ defined by

$$\begin{aligned} \phi ^{(1)} \otimes \cdots \otimes \phi ^{(d)}{:}\, \left\{ \, \begin{array}{lll} {\mathcal {X}}_1 \times \cdots \times {\mathcal {X}}_d &{} \rightarrow &{} {\mathbb {R}}, \\ (x_1, \ldots , x_d) &{} \mapsto &{} \phi ^{(1)}(x_1) \cdots \phi ^{(d)}(x_d),\\ \end{array}\right. \end{aligned}$$

belongs to $V$. Let $u$ be a specific function of $V$, for instance the solution of a partial differential equation (PDE). Standard linear approximation approaches such as Galerkin methods consist in approximating the function $u(x_1, \ldots , x_d)$ as

$$\begin{aligned} u(x_1, \ldots , x_d) \approx \sum _{1\le i_1, \ldots , i_d \le N} \lambda _{i_1, \ldots , i_d} \phi _{i_1}^{(1)}\otimes \cdots \otimes \phi _{i_d}^{(d)}(x_1, \ldots , x_d), \end{aligned}$$

(1)

where $N$ is the number of degrees of freedom per variate (chosen to be the same for each variate to simplify the notation), and where for all $1\le j \le d$, $\left( \phi _i^{(j)} \right) _{1\le i \le N}$ is an a priori chosen discretization basis of functions belonging to $V_j$. To approximate the function $u$, the set of $N^d$ real numbers $\left( \lambda _{i_1, \ldots , i_d} \right) _{1\le i_1, \ldots , i_d \le N}$ must be computed. Thus, the size of the discretized problem to solve scales exponentially with $d$, the number of variables. Because of this difficulty, classical methods cannot be used in practice to solve high-dimensional PDEs. Greedy algorithms also consist in approximating the function $u(x_1, \ldots , x_d)$ as a sum of tensor-product functions

$$\begin{aligned} u(x_1, \ldots , x_d) \approx u_n(x_1, \ldots , x_d) = \sum _{k=1}^n r_k^{(1)}\otimes \cdots \otimes r_k^{(d)}(x_1,\ldots , x_d), \end{aligned}$$

where for all $1\le k \le n$ and all $1\le j \le d$, $r_k^{(j)} \in V_j$. But in contrast with standard linear approximation methods, the sequence of tensor-product functions $\left( r_k^{(1)}\otimes \cdots \otimes r_k^{(d)} \right) _{1\le k \le n}$ is not chosen a priori; it is constructed iteratively using a greedy procedure. Let us illustrate this on the simple case when the function $u$ to be computed is the unique solution of a minimization problem of the form

$$\begin{aligned} u=\mathop {\text{ argmin }}_{v\in V} {\mathcal {E}}(v), \end{aligned}$$

(2)

where ${\mathcal {E}}: V\rightarrow {\mathbb {R}}$ is a strongly convex functional. Denoting by

$$\begin{aligned} \varSigma ^\otimes := \left\{ r^{(1)} \otimes \cdots \otimes r^{(d)}\; | \; r^{(1)} \in V_1, \; \ldots , \; r^{(d)} \in V_d\right\} \end{aligned}$$

the set of rank-1 tensor-product functions, the pure greedy algorithm (PGA) [35, 36] for solving (2) reads

Pure Greedy Algorithm (PGA):

• Initialization: set $u_0 := 0$;

• Iterate on $n\ge 1$: find $z_n:= r_n^{(1)} \otimes \cdots \otimes r_n^{(d)} \in \varSigma ^\otimes$ such that

  $$\begin{aligned} z_n \in \mathop {\text{ argmin }}_{z \in \varSigma ^\otimes } {\mathcal {E}}\left( u_{n-1} + z \right) , \end{aligned}$$

  and set $u_n := u_{n-1} + z_n$.

The advantage of such an approach is that if, as above, a discretization basis $\left( \phi ^{(j)}_i \right) _{1\le i \le N}$ is used for the approximation of the function $r_n^{(j)}$, each iteration of the algorithm requires the resolution of a discretized problem of size $dN$. The size of the problem to solve at iteration $n$ therefore scales linearly with the number of variables. Thus, using the above PGA enables one to approximate the function $u(x_1, \ldots , x_d)$ through the resolution of a sequence of low-dimensional problems instead of one high-dimensional problem.

Greedy algorithms have been extensively studied in the framework of problem (2). The PGA has been analyzed from a mathematical point of view, first in [26] in the case when ${\mathcal {E}}(v) := \Vert v-u\Vert _V^2$, then in [11] in the case of a more general nonquadratic strongly convex energy functional ${\mathcal {E}}$. In the latter article, it is proved that the sequence $(u_n)_{n\in {\mathbb {N}}^*}$ strongly converges in $V$ to $u$ and provided that: (i) $\varSigma ^\otimes$ is weakly closed in $V$ and $\text{ Span }\left( \varSigma ^\otimes \right)$ is dense in $V$; (ii) the functional ${\mathcal {E}}$ is strongly convex, differentiable on $V$, and its derivative is Lipschitz on bounded domains. An exponential convergence rate is also proved in the case when $V$ is finite dimensional. In [30], these results have been extended to the case when general tensor subsets $\varSigma$ are considered instead of the set of rank-1 tensor products $\varSigma ^{\otimes }$, and under weaker assumptions on the functional ${\mathcal {E}}$. The authors also generalized the convergence results to other variants of greedy algorithms, such as the Orthogonal Greedy Algorithm (OGA), and to the case when the space $V$ is a Banach space.

The analysis of greedy algorithms for other kinds of problems is less advanced [14]. We refer to Cancès et al. [12] for a review of the mathematical issues arising in the application of greedy algorithms to nonsymmetric linear problems for example. To our knowledge, the literature on greedy algorithms for eigenvalue problems is very limited. Penalized formulations of constrained minimization problems enable one to recover the structure of unconstrained minimization problems and to use the existing theoretical framework for the PGA and the OGA [11, 17]. The only reference we are aware of about greedy algorithms for eigenvalue problems without the use of a penalized formulation is an article by Ammar and Chinesta [1], in which the authors propose a greedy algorithm to compute the lowest eigenstate of a bounded from below self-adjoint operator and apply it to electronic structure calculation. No analysis of this algorithm is given though. Let us also mention that the use of tensor formats for eigenvalue problems has been recently investigated [6, 7, 20, 23, 33], still in the context of electronic structure calculation.

In this article, we propose two new greedy algorithms for the computation of the lowest eigenstate of high-dimensional eigenvalue problems and prove some convergence results for these algorithms and their orthogonalized versions. We would like to point out that these algorithms are not based on a penalized formulation of the eigenvalue problem.

The outline of the article is as follows. In Sect. 2, we introduce some notation and give some prototypical examples of problems and tensor subsets for which our analysis is valid. In Sect. 3, the two new approaches are presented along with our main convergence results. The first algorithm is based on the minimization of the Rayleigh quotient associated with the problem under consideration. The second algorithm is inspired from the well-known inverse power method and relies on the minimization of a residual associated with the eigenvalue problem. Orthogonal and weak versions of these algorithms are also introduced. In Sect. 4, we detail how these algorithms can be implemented in practice in the case of rank-1 tensor-product functions. The numerical behaviors of our algorithms and of the one proposed in [1] are illustrated in Sect. 5, first on a toy example, then on the computation of the buckling modes of a microstructured plate. For the sake of brevity, we only give here the proof of the results related to our first greedy strategy (see Sect. 7). We refer the reader to Section 6.5 of [13] for a detailed analysis of our second strategy and for further implementation details. Let us mention that we do not cover here the case of parametric eigenvalue problems, which will make the subject of a forthcoming article.

2 Preliminaries

2.1 Notation and Main Assumptions

Let us consider two Hilbert spaces $V$ and $H$, endowed, respectively, with the scalar products $\langle \cdot , \cdot \rangle _V$ and $\langle \cdot , \cdot \rangle$, such that, unless otherwise stated,

• (HV) the embedding $V \hookrightarrow H$ is dense and compact.

The norms of $V$ and $H$ are denoted, respectively, by $\Vert \cdot \Vert _V$ and $\Vert \cdot \Vert$. Let us recall that it follows from (HV) that weak convergence in $V$ implies strong convergence in $H$.

Let $a:V\times V \rightarrow {\mathbb {R}}$ be a symmetric continuous bilinear form on $V\times V$ such that

• (HA) $\exists \gamma , \nu >0, \; \text{ such } \text{ that } \; \forall v\in V, \; a(v,v) \ge \gamma \Vert v\Vert _V^2 - \nu \Vert v\Vert ^2.$

The bilinear form $\langle \cdot , \cdot \rangle _a$, defined by

$$\begin{aligned} \forall v,w\in V, \quad \langle v, w\rangle _a := a(v,w) + \nu \langle v, w\rangle , \end{aligned}$$

(3)

is a scalar product on $V$, whose associated norm, denoted by $\Vert \cdot \Vert _a$, is equivalent to the norm $\Vert \cdot \Vert _V$. In addition, we can also assume without loss of generality that the constant $\nu$ is chosen so that for all $v\in V$, $\Vert v\Vert _a \ge \Vert v\Vert$.

It is well known (see, e.g., [31]) that, under the above assumptions (namely (HA) and (HV)), there exists a sequence $(\psi _p, \mu _p)_{p\in {\mathbb {N}}^*}$ of solutions to the elliptic eigenvalue problem

$$\begin{aligned} \left\{ \begin{array}{l} \text{ find } (\psi ,\mu )\in V\times {\mathbb {R}} \text{ such } \text{ that } \Vert \psi \Vert =1 \text{ and } \\ \forall v\in V, \; a(\psi ,v) = \mu \langle \psi ,v \rangle \\ \end{array}\right. \end{aligned}$$

(4)

such that $(\mu _p)_{p\in {\mathbb {N}}^*}$ forms a nondecreasing sequence of real numbers going to infinity and $(\psi _p)_{p\in {\mathbb {N}}^*}$ is an orthonormal basis of $H$. We focus here on the computation of $\mu _1$, the lowest eigenvalue of $a(\cdot , \cdot )$, and of an associated $H$-normalized eigenvector. Let us note that, from (HA), for all $p\in {\mathbb {N}}^*$, $\mu _p + \nu >0$.

Definition 2.1

A set $\varSigma \subset V$ is called a dictionary of $V$ if $\varSigma$ satisfies the following three conditions:

$(\hbox {H}\varSigma 1)$ :

$\varSigma$ is a nonempty cone, i.e., $0\in \varSigma$ and for all $(z,t)\in \varSigma \times {\mathbb {R}}$, $tz\in \varSigma$;

$(\hbox {H}\varSigma 2)$ :

$\varSigma$ is weakly closed in $V$;

$(\hbox {H}\varSigma 3)$ :

$\text{ Span }(\varSigma )$ is dense in $V$.

In practical applications for high-dimensional eigenvalue problems, the set $\varSigma$ is typically an appropriate set of tensor formats used to perform the greedy algorithms presented in Sect. 3.2. We also define

$$\begin{aligned} \varSigma ^*:= \varSigma \setminus \{ 0\}. \end{aligned}$$

(5)

2.2 Prototypical Example

Let us present a prototypical example of the high-dimensional eigenvalue problems we have in mind, along with possible dictionaries.

Let ${\mathcal {X}}_1,\; \ldots , \;{\mathcal {X}}_d$ be bounded regular domains of ${\mathbb {R}}^{m_1}, \;\ldots ,\; {\mathbb {R}}^{m_d}$, respectively. Let $V = H^1_0({\mathcal {X}}_1 \times \cdots \times {\mathcal {X}}_d)$ and $H= L^2({\mathcal {X}}_1\times \cdots \times {\mathcal {X}}_d)$. It follows from the Rellich–Kondrachov theorem that these spaces satisfy assumption (HV). Let $b:{\mathcal {X}}_1 \times \cdots \times {\mathcal {X}}_d \rightarrow {\mathbb {R}}$ be a measurable real-valued function such that

$$\begin{aligned} \exists \beta , B>0, \!\; \text{ such } \text{ that } \!\; \beta \!\le \! b(x_1, \ldots , x_d) \!\le \! B, \; \text{ for } \text{ a.a. } (x_1, \ldots , x_d)\!\in \! {\mathcal {X}}_1\times \cdots \times {\mathcal {X}}_d. \end{aligned}$$

In addition, let $W\in L^q({\mathcal {X}}_1\times \cdots \times {\mathcal {X}}_d)$ with $q = 2$ if $m\le 3$, and $q > m/2$ for $m\ge 4$, where $m := m_1 + \cdots + m_d$. A prototypical example of a continuous symmetric bilinear form $a: V\times V \rightarrow {\mathbb {R}}$ satisfying (HA) is

$$\begin{aligned} \forall v,w\in V, \quad a(v,w) := \int _{{\mathcal {X}}_1\times \cdots \times {\mathcal {X}}_d} \left( b \nabla v \cdot \nabla w + W vw\right) . \end{aligned}$$

(6)

In this particular case, the eigenvalue problem (4) also reads

$$\begin{aligned} \left\{ \begin{array}{l} \text{ find } (\psi ,\mu )\in H^1_0({\mathcal {X}}_1\times \cdots \times {\mathcal {X}}_d)\times {\mathbb {R}} \text{ such } \text{ that } \Vert \psi \Vert _{L^2({\mathcal {X}}_1 \times \cdots \times {\mathcal {X}}_d)} = 1 \text{ and } \\ -\text{ div }\left( b \nabla \psi \right) + W\psi = \mu \psi \text{ in } \mathcal {D}'({\mathcal {X}}_1\times \cdots \times {\mathcal {X}}_d).\\ \end{array}\right. \end{aligned}$$

For all $1\le j \le d$, we define $V_j:= H^1_0({\mathcal {X}}_j)$. Some examples of dictionaries $\varSigma$ based on tensor formats satisfying (H$\varSigma 1$), (H$\varSigma 2$), and (H$\varSigma 3$) are the set of rank-$1$ tensor-product functions

$$\begin{aligned} \varSigma ^\otimes := \left\{ r^{(1)} \otimes \cdots \otimes r^{(d)}\;| \; \forall 1\le j \le d, \; r^{(j)} \in V_j\right\} , \end{aligned}$$

(7)

as well as other tensor formats [20, 23], for instance the sets of rank-$R$ Tucker or rank-$R$ tensor train functions, with $R\in {\mathbb {N}}^*$.

3 Greedy Algorithms for Eigenvalue Problems

In the rest of the article, we define and study two different greedy algorithms to compute an eigenpair associated with the lowest eigenvalue of the elliptic eigenvalue problem (4).

The first one relies on the minimization of the Rayleigh quotient of $a(\cdot , \cdot )$ and is introduced in Sect. 3.2.1. The second one, presented in Sect. 3.2.2, shares common features with the inverse power method and is based on the use of a residual for problem (4). We recall the algorithm introduced in [1] in Sect. 3.2.3. Orthogonal and weak versions of these algorithms are defined, respectively, in Sects. 3.2.4 and 3.2.5. Section 3.3 contains our main convergence results. The choice of a good initial guess for all these algorithms is discussed in Sect. 3.4.

Let us first start with a few preliminary results.

3.1 Two Useful Lemmas

For all $v\in V$, we denote by

$$\begin{aligned} {\mathcal {J}}(v):= \left\{ \begin{array}{l@{\quad }l} \frac{a(v,v)}{\Vert v\Vert ^2} \;&{} \text{ if } v\ne 0,\\ +\infty \; &{} \text{ if } v=0,\\ \end{array}\right. \end{aligned}$$

the Rayleigh quotient associated with (4), and define

$$\begin{aligned} \lambda _\varSigma := \mathop {\inf }_{z\in \varSigma } {\mathcal {J}}(z) = \mathop {\inf }_{z \in \varSigma ^*} \frac{a(z, z)}{\Vert z\Vert ^2}. \end{aligned}$$

Note that, since $\varSigma \subset V$, $\displaystyle \lambda _\varSigma \ge \mu _1= \mathop {\inf }\nolimits _{v\in V} {\mathcal {J}}(v)$.

Lemma 3.1

Let $w\in V$ such that $\Vert w\Vert =1$. The following two assertions are equivalent:

• (i) $\forall z\in \varSigma , \quad {\mathcal {J}}(w+z) \ge {\mathcal {J}}(w)$;

• (ii) $w$ is an eigenvector of the bilinear form $a(\cdot , \cdot )$ associated with an eigenvalue less than or equal to $\lambda _\varSigma$; i.e., there exists $\lambda _w \in {\mathbb {R}}$ such that $\lambda _w \le \lambda _\varSigma$ and

  $$\begin{aligned} \forall v\in V, \; a(w,v) = \lambda _w \langle w, v \rangle . \end{aligned}$$

Proof of Lemma 3.1

Proof that $(i) \Rightarrow (ii)$

Let $z\in \varSigma$. For all $\varepsilon \in {\mathbb {R}}$ such that $|\varepsilon | \Vert z\Vert < \Vert w\Vert$, $w + \varepsilon z \ne 0$. Then, since $\Vert w\Vert =1$, $(i)$ implies that

$$\begin{aligned} {\mathcal {J}}(w+\varepsilon z)-{\mathcal {J}}(w)&= \frac{\left( 2\varepsilon a(w,z) + \varepsilon ^2 a(z, z)\right) - \left( 2\varepsilon \langle w, z\rangle + \varepsilon ^2 \Vert z\Vert ^2\right) a(w,w)}{ \Vert w+ \varepsilon z\Vert ^2}\\&= \frac{2\varepsilon \left( a(w,z) - a(w,w)\langle w,z\rangle \right) + \varepsilon ^2 \left( a(z, z) - a(w,w) \Vert z\Vert ^2 \right) }{ \Vert w+ \varepsilon z\Vert ^2}\\&\ge 0. \end{aligned}$$

Considering $\varepsilon \in {\mathbb {R}}$ with $|\varepsilon |$ arbitrarily small, the above inequality yields

$$\begin{aligned} a(w,z) - a(w,w) \langle w, z\rangle = 0 \quad \text{ and } \quad a(z, z) - \Vert z\Vert ^2 a(w,w) \ge 0. \end{aligned}$$

These relationships are valid for any vector $z\in \varSigma$. Together with assumption (H$\varSigma 3$), and denoting by $\lambda _w:= a(w,w)$, the first equality implies that

$$\begin{aligned} \forall v \in V, \; a(w,v) = \lambda _w \langle w , v \rangle , \end{aligned}$$

and the second inequality yields

$$\begin{aligned} \lambda _w \le \mathop {\inf }_{z\in \varSigma ^*} \frac{a(z, z)}{\Vert z\Vert ^2} = \lambda _\varSigma , \end{aligned}$$

where $\varSigma ^*$ is defined by (5). Hence (ii).

Proof that (ii) $\Rightarrow$ (i)

Using (ii), similar calculations yield that for all $z\in \varSigma$ such that $w+z \ne 0$,

$$\begin{aligned} {\mathcal {J}}(w+z) - {\mathcal {J}}(w)&= \frac{a(w+ z, w + z)}{\Vert w + z\Vert ^2} - a(w,w)\\&= \frac{ 2 a(w,z) + a(z,z) - \left( 2 \langle w, z\rangle + \Vert z\Vert ^2\right) a(w,w)}{ \Vert w+ z\Vert ^2}\\&= \frac{a(z,z) - \lambda _w \Vert z\Vert ^2}{\Vert w+z\Vert ^2}. \end{aligned}$$

This implies that ${\mathcal {J}}(w+z) - {\mathcal {J}}(w) \ge 0$. Hence (i), since the inequality is trivial in the case when $w + z = 0$. $\square$

Lemma 3.2

Let $w\in V \setminus \varSigma ^*$. Then, the minimization problem

$$\begin{aligned} \text{ find } z_0\in \varSigma \text{ such } \text{ that } z_0 \in \mathop {\text{ argmin }}_{z\in \varSigma } {\mathcal {J}}(w + z) \end{aligned}$$

(8)

has at least one solution.

When $w\in \varSigma ^*$, problem (8) may have no solution (see Example 7.1 of [13] for an example).

Proof of Lemma 3.2

Let us first prove that (8) has at least one solution in the case when $w=0$. Let $(z_m)_{m\in {\mathbb {N}}^*}$ be a minimizing sequence: $\forall m\in {\mathbb {N}}^*$, $z_m\in \varSigma$, $\Vert z_m\Vert = 1$, and $\displaystyle a(z_m , z_m) \mathop {\longrightarrow }_{m\rightarrow \infty } \lambda _\varSigma$. The sequence $\left( \Vert z_m\Vert _a \right) _{m\in {\mathbb {N}}^*}$ being bounded, there exists $z_* \in V$ such that $(z_m)_{m\in {\mathbb {N}}^*}$ weakly converges, up to extraction, to some $z_*$ in $V$. By (H$\varSigma 2$), $z_*$ belongs to $\varSigma$. In addition, using (HV), the sequence $(z_m)_{m\in {\mathbb {N}}^*}$ strongly converges to $z_*$ in $H$, so that $\Vert z_*\Vert = 1$. Lastly,

$$\begin{aligned} \Vert z_*\Vert _a \le \mathop {\lim }_{m \rightarrow \infty } \Vert z_m\Vert _a, \end{aligned}$$

which implies that $\displaystyle a(z_*, z_*) = {\mathcal {J}}(z_*) \le \lambda _\varSigma = \mathop {\lim }_{m\rightarrow \infty } a(z_m, z_m)$. Hence, $z_*$ is a minimizer of problem (8) when $w=0$.

Let us now consider $w\in V\setminus \varSigma$ and $(z_m)_{m\in {\mathbb {N}}^*}$ a minimizing sequence for problem (8). There exists $m_0\in {\mathbb {N}}^*$ large enough such that for all $m\ge m_0$, $w+z_m \ne 0$. Let us define $\alpha _m:= \frac{1}{\Vert w + z_m\Vert }$ and $\widetilde{z}_m:= \alpha _m z_m$. It holds that $\Vert \alpha _m w + \widetilde{z}_m \Vert = 1$ and $\displaystyle a(\alpha _m w + \widetilde{z}_m, \alpha _m w + \widetilde{z}_m) \mathop {\longrightarrow }_{m\rightarrow \infty } \mathop {\inf }\nolimits _{z\in \varSigma } {\mathcal {J}}(w + z)$.

If the sequence $(\alpha _m)_{m\in {\mathbb {N}}^*}$ is bounded, then so is the sequence $(\Vert \widetilde{z}_m\Vert _a)_{m\in {\mathbb {N}}^*}$, and reasoning as above, we can prove that there exists a minimizer to problem (8).

To complete the proof, let us now argue by contradiction and assume that, up to the extraction of a subsequence, $\displaystyle \alpha _m \mathop {\longrightarrow }_{m\rightarrow \infty } + \infty$. Since the sequence $\left( \Vert \alpha _m w + \widetilde{z}_m\Vert _a \right) _{m\in {\mathbb {N}}^*}$ is bounded and for all $m\in {\mathbb {N}}^*$,

$$\begin{aligned} \Vert \alpha _m w + \widetilde{z}_m\Vert _a = \alpha _m \Vert w + z_m\Vert _a, \end{aligned}$$

the sequence $(z_m)_{m\in {\mathbb {N}}^*}$ strongly converges to $-w$ in $V$. Using assumption (H$\varSigma 2$), this implies that $w \in \varSigma$, which leads to a contradiction. $\square$

3.2 Description of the Algorithms

3.2.1 Pure Rayleigh Greedy Algorithm

The following algorithm, called hereafter the pure Rayleigh greedy algorithm (PRaGA), is inspired by the PGA for convex minimization problems (see [11, 13, 30] for further details).

Pure Rayleigh Greedy Algorithm (PRaGA):

• Initialization: choose an initial guess $u_0\in V$ such that $\Vert u_0\Vert = 1$ and

  $$\begin{aligned} \lambda _0:= a(u_0,u_0) < \lambda _\varSigma ; \end{aligned}$$

• Iterate on $n\ge 1$: find $z_n\in \varSigma$ such that

  $$\begin{aligned} z_n \in \mathop {\text{ argmin }}_{z\in \varSigma } {\mathcal {J}}(u_{n-1} + z), \end{aligned}$$

  (9)

  and set $u_n := \frac{u_{n-1} + z_n}{\Vert u_{n-1} + z_n\Vert }$ and $\lambda _n:=a(u_n, u_n)$.

Let us point out that in our context, the functional ${\mathcal {J}}$ is not convex, so that the analysis existing in the literature for the PGA in the context of minimization of convex functionals does not apply to the PRaGA.

The choice of an initial guess $u_0\in V$ satisfying $\Vert u_0\Vert = 1$ and $a(u_0, u_0) < \lambda _\varSigma$ is discussed in Sect. 3.4.2. Let us mention that the two other algorithms (PReGA and PEGA, presented in the following sections) only require $a(u_0, u_0) \le \lambda _\varSigma$. This is discussed in Sect. 3.4.1.

Lemma 3.3

Let $V$ and $H$ be separable Hilbert spaces satisfying (HV), $\varSigma$ a dictionary of $V$, and $a: V\times V\rightarrow {\mathbb {R}}$ a symmetric continuous bilinear form satisfying (HA). Then, all the iterations of the PRaGA are well defined in the sense that for all $n\in {\mathbb {N}}^*$, and there exists at least one solution to the minimization problem (9). In addition, the sequence $(\lambda _n)_{n\in {\mathbb {N}}^*}$ is nonincreasing.

Proof

Lemma 3.3 can be easily proved by induction using Lemma 3.2, the fact that the initial guess $u_0$ is chosen such that $\lambda _0 = {\mathcal {J}}(u_0) < \lambda _\varSigma$, and the fact that a vector $w\in V$ which satisfies ${\mathcal {J}}(w) < \lambda _\varSigma$ is necessarily such that $w\notin \varSigma ^*$. $\square$

3.2.2 Pure Residual Greedy Algorithm

The pure residual greedy algorithm (PReGA) we propose is based on the use of a residual for problem (4).

Pure Residual Greedy Algorithm (PReGA):

• Initialization: choose an initial guess $u_0\in V$ such that $\Vert u_0\Vert = 1$ and

  $$\begin{aligned} \lambda _0:= a(u_0,u_0)\le \lambda _\varSigma ; \end{aligned}$$

• Iterate on $n\ge 1$: find $z_n\in \varSigma$ such that

  $$\begin{aligned} z_n \in \mathop {\text{ argmin }}_{z\in \varSigma } \frac{1}{2}\Vert u_{n-1} + z\Vert _a^2 - (\lambda _{n-1} + \nu )\langle u_{n-1}, z\rangle , \end{aligned}$$

  (10)

  and set $u_n := \frac{u_{n-1} + z_n}{\Vert u_{n-1} + z_n\Vert }$ and $\lambda _n := a(u_n, u_n)$.

The term residual can be justified as follows: It is easy to check that for all $n\in {\mathbb {N}}^*$, problem (10) is equivalent to the minimization problem

$$\begin{aligned} \text{ find } z_n\in \varSigma \text{ such } \text{ that } z_n\in \mathop {\text{ argmin }}_{z\in \varSigma } \frac{1}{2}\Vert R_{n-1} -z \Vert _a^2, \end{aligned}$$

(11)

where $R_{n-1}\in V$ is the Riesz representative in $V$ for the scalar product $\langle \cdot , \cdot \rangle _a$ of the linear form $l_{n-1}: v\in V \mapsto \lambda _{n-1}\langle u_{n-1}, v \rangle - a(u_{n-1}, v)$. In other words, $R_{n-1}$ is the unique element of $V$ such that

$$\begin{aligned} \forall v\in V, \quad \langle R_{n-1} , v \rangle _a = \lambda _{n-1}\langle u_{n-1}, v \rangle - a(u_{n-1}, v). \end{aligned}$$

The linear form $l_{n-1}$ can indeed be seen as a residual for (4) since $l_{n-1} = 0$ if and only if $\lambda _{n-1}$ is an eigenvalue of $a(\cdot , \cdot )$ and $u_{n-1}$ an associated $H$-normalized eigenvector.

Let us point out that in order to carry out the PReGA in practice, one needs to know the value of a constant $\nu$ ensuring (HA), whereas this is not needed for the PRaGA or for the algorithm PEGA introduced in [1] and considered in the next section.

Lemma 3.4

Let $V$ and $H$ be separable Hilbert spaces such that the embedding $V\hookrightarrow H$ is dense, $\varSigma$ a dictionary of $V$, and $a: V\times V\rightarrow {\mathbb {R}}$ a symmetric continuous bilinear form satisfying (HA). Then, all the iterations of the PReGA are well defined in the sense that for all $n\in {\mathbb {N}}^*$, there exists at least one solution to the minimization problem (10).

Proof

The existence of a solution to (10) for all $n\in {\mathbb {N}}^*$ follows from standard results on the PGA for the minimization of quadratic functionals. We refer the reader to Section 2.3 and Lemma 3.4 of [13], for instance, for more details. $\square$

Remark 3.1

Actually, the PReGA can be seen as a greedy version of the inverse power method, defined as follows:

Inverse Power Method:

• Initialization: let $\widetilde{u}_0\in V$ such that $\Vert \widetilde{u}_0\Vert = 1$ and let $\widetilde{\lambda }_0 := a\left( \widetilde{u}_0, \widetilde{u}_0\right)$;

• Iterate on $n\ge 1$: find $\widetilde{z}_n\in V$ such that

  $$\begin{aligned} \widetilde{z}_n \in \mathop {\text{ argmin }}_{\widetilde{z} \in V} \frac{1}{2}\left\| \widetilde{u}_{n-1} + \widetilde{z} \right\| _a^2 - (\lambda _{n-1} + \nu ) \langle \widetilde{u}_{n-1}, \widetilde{z} \rangle , \end{aligned}$$

  (12)

  and set $\widetilde{u}_n:= \frac{\widetilde{u}_{n-1} + \widetilde{w}_n}{\Vert \widetilde{u}_{n-1} + \widetilde{w}_n\Vert }$.

Let us point out that for all $n\in {\mathbb {N}}^*$, there exists a unique solution $\widetilde{z}_n\in V$ to (12) which is equivalently the unique solution of the following problem: find $\widetilde{\zeta }_n\in V$ such that

$$\begin{aligned} \forall v \in V, \quad \langle \widetilde{u}_{n-1} + \widetilde{z}_n, v\rangle _a = (\widetilde{\lambda }_{n-1} + \nu )\langle \widetilde{u}_{n-1}, v \rangle . \end{aligned}$$

The inverse power method is a classical approach for computing the smallest eigenvalue and an associated eigenvector of the bilinear form $a(\cdot , \cdot )$. In particular, if the smallest eigenvalue $\mu _1$ of the bilinear form $a(\cdot , \cdot )$ is simple, the sequence $(\widetilde{u}_n)_{n\in {\mathbb {N}}}$ converges exponentially fast to an $H$-normalized eigenvector of $a(\cdot , \cdot )$ associated with $\mu _1$. In the PReGA, for all $n\in {\mathbb {N}}^*$, a vector $z_n\in \varSigma$ solution of (10) can be seen as the vector given by the first iteration of a standard PGA for the resolution of (12) with $\widetilde{u}_{n-1} = u_{n-1}$ and $\widetilde{\lambda }_{n-1} = \lambda _{n-1}$, and using the energy functional $\mathcal {E}_{n-1}: V \rightarrow {\mathbb {R}}$ such that for all $v\in V$, $\mathcal {E}_{n-1}(v):= \frac{1}{2} \Vert v\Vert _a^2 + \langle u_{n-1},v\rangle _a - (\lambda _{n-1} + \nu )\langle u_{n-1}, v \rangle$.

3.2.3 Pure Explicit Greedy Algorithm

The above two algorithms are new, at least to our knowledge. In this section, we describe an algorithm very closely related to the one which has already been proposed in [1], which we call in the rest of the article the pure explicit greedy algorithm (PEGA).

Unlike the above two algorithms, the PEGA is not defined for general dictionaries $\varSigma$ satisfying (H$\varSigma$1), (H$\varSigma$2), and (H$\varSigma$3). We need to assume in addition that $\varSigma$ is a differentiable manifold [25] in $V$. In this case, for all $z\in \varSigma$, we denote by $T_\varSigma (z)$ the tangent subspace to $\varSigma$ at point $z$ in $V$.

Let us point out that if $\varSigma$ is a differentiable manifold in $V$, for all $n\in {\mathbb {N}}^*$, the Euler equations associated with the minimization problems (9) and (10), respectively, read:

$$\begin{aligned} \forall \delta z\in T_\varSigma (z_n), \quad a\left( u_{n-1} + z_n, \delta z\right) = \lambda _n \langle u_{n-1} + z_n, \delta z\rangle , \end{aligned}$$

(13)

and

$$\begin{aligned} \forall \delta z \in T_\varSigma (z_n), \quad a\left( u_{n-1} + z_n, \delta z\right) + \nu \langle z_n, \delta z\rangle = \lambda _{n-1} \langle u_{n-1} , \delta z\rangle . \end{aligned}$$

(14)

The PEGA consists in solving at each iteration $n\in {\mathbb {N}}^*$ of the greedy algorithm the following equation, which is of a similar form as the Euler equations (13) and (14) above:

$$\begin{aligned} \forall \delta z \in T_\varSigma (z_n), \quad a\left( u_{n-1} + z_n , \delta z\right) = \lambda _{n-1} \langle u_{n-1} + z_n, \delta z \rangle . \end{aligned}$$

(15)

More precisely, the PEGA algorithm reads:

Pure Explicit Greedy Algorithm (PEGA):

• Initialization: choose an initial guess $u_0\in V$ such that $\Vert u_0\Vert = 1$ and

  $$\begin{aligned} \lambda _0:= a(u_0,u_0) \le \lambda _\varSigma ; \end{aligned}$$

• Iterate for $n\ge 1$: find $z_n\in \varSigma$ such that

  $$\begin{aligned} \forall \delta z \in T_\varSigma (z_n), \quad a\left( u_{n-1} + z_n , \delta z\right) - \lambda _{n-1} \langle u_{n-1} + z_n, \delta z \rangle = 0, \end{aligned}$$

  (16)

  and set $u_n := \frac{u_{n-1} + z_n}{\Vert u_{n-1} + z_n\Vert }$ and $\lambda _n := a(u_n, u_n)$.

Notice that (16) is very similar to (13) except that $\lambda _{n-1}$ is used instead of $\lambda _n$. The PEGA can be seen as an explicit version of the PRaGA, hence the name pure explicit greedy algorithm.

It is not clear whether there always exists a solution $z_n$ to (16), since (16) does not derive from a minimization problem, unlike the other two algorithms. We have not been able so far to prove convergence results for the PEGA.

In Sect. 4, we will discuss in more detail how these three algorithms (PRaGA, PReGA, and PEGA) are implemented in practice in the case when $\varSigma$ is the set of rank-1 tensor-product functions.

3.2.4 Orthogonal Algorithms

We introduce here slightly modified versions of the PRaGA, PReGA, and PEGA, inspired from the OGA for convex minimization problems (see [13, 30]).

Orthogonal (Rayleigh, Residual, or Explicit) Greedy Algorithm (ORaGA, OReGA, and OEGA):

• Initialization: choose an initial guess $u_0\in V$ such that $\Vert u_0\Vert = 1$ and $\lambda _0:= a(u_0,u_0) \le \lambda _\varSigma$. For the ORaGA, we assume in addition that $\lambda _0:= a(u_0,u_0) < \lambda _\varSigma$.

• Iterate on $n\ge 1$:

  • – for the ORaGA: find $z_n\in \varSigma$ satisfying (9);

  • – for the OReGA: find $z_n\in \varSigma$ satisfying (10);

  • – for the OEGA: find $z_n\in \varSigma$ satisfying (16);

  find $\left( c_0^{(n)}, \ldots , c_n^{(n)} \right) \in {\mathbb {R}}^{n+1}$ such that

  $$\begin{aligned} \left( c_0^{(n)}, \ldots , c_n^{(n)}\right) \in {\mathop {\hbox {argmin}}\limits _{(c_0, \ldots , c_n) \in {\mathbb {R}}^{n+1}}} {\mathcal {J}}\left( c_0 u_0 + c_1 z_1+ \cdots + c_nz_n\right) , \end{aligned}$$

  (17)

  and set $u_n:= \frac{c_0^{(n)} u_0 + c_1^{(n)} z_1 + \cdots + c_n^{(n)} z_n}{\Vert c_0^{(n)} u_0 + c_1^{(n)} z_1 + \cdots + c_n^{(n)} z_n\Vert }$; if $\left\langle u_{n-1}, u_n \right\rangle \le 0$, set $u_n:=-u_n$; set $\lambda _n:= a(u_n, u_n)$.

Let us point out that the original algorithm proposed in [1] is the OEGA. In addition, for the three algorithms and all $n\in {\mathbb {N}}^*$, there always exists at least one solution to the minimization problem (17).

The orthogonal versions of the greedy algorithms can be easily implemented from the pure versions: At any iteration $n\in {\mathbb {N}}^*$, only one additional step is performed, which consists in choosing an approximate eigenvector $u_n$ as a linear combination of the elements $u_0, z_1, \ldots , z_n$ minimizing the Rayleigh quotient associated with the bilinear form $a(\cdot , \cdot )$. Since $u_n$ is meant to be an approximation of an eigenvector associated with the lowest eigenvalue of $a(\cdot , \cdot )$, which is a minimizer of the Rayleigh quotient on the Hilbert space $V$, this additional step is very natural.

3.2.5 Weak Versions of the Algorithms

Several weak versions of the greedy algorithms have been proposed (see [35] for a review) and analyzed for quadratic minimization problems, to take into account the fact that the minimization problems defining the iterations of a greedy algorithm are rarely solved exactly. Similarly, weak versions of the PRaGA and the PRega could read as follows:

Weak (Rayleigh or Residual) Greedy Algorithm (WRaGA and WReGA): let $(t_n)_{n\in {\mathbb {N}}^*}$ be a sequence of positive real numbers.

• Initialization: choose an initial guess $u_0\in V$ such that $\Vert u_0\Vert = 1$ and

  $$\begin{aligned} \lambda _0:= a(u_0,u_0)\le \lambda _\varSigma . \end{aligned}$$

  For the WRaGA, we assume in addition that $\lambda _0:= a(u_0,u_0) < \lambda _\varSigma$.

• Iterate on $n\ge 1$:

  • – for the WRaGA: find $z_n\in \varSigma$ satisfying

    $$\begin{aligned} {\mathcal {J}}(u_{n-1} +z_n) \le (1+t_n) \mathop {\inf }_{z\in \varSigma } {\mathcal {J}}(u_{n-1} + z); \end{aligned}$$

    (18)

  • – for the WReGA: find $z_n\in \varSigma$ satisfying

    $$\begin{aligned}&\frac{1}{2}\Vert u_{n-1} + z_n\Vert _a^2 - (\lambda _{n-1} + \nu )\langle u_{n-1}, z_n\rangle \le (1+t_n)\mathop {\inf }_{z\in \varSigma } \frac{1}{2}\Vert u_{n-1} + z\Vert _a^2\nonumber \\&\quad - (\lambda _{n-1} + \nu )\langle u_{n-1}, z\rangle , \end{aligned}$$

    (19)

  and set $u_n:= \frac{u_{n-1} +z_n}{\Vert u_{n-1} + z_n\Vert }$ and $\lambda _n:= a(u_n, u_n)$.

Since the sequence of vectors $(z_n)_{n\in {\mathbb {N}}^*}$ produced by the PEGA cannot be defined as solutions of minimization problems, it is not clear what a weak version of the PEGA could be. In this article, we do not analyze the convergence properties of such relaxed versions of the greedy strategies we propose, but mention their existence for the sake of completeness.

3.3 Convergence Results

3.3.1 The Infinite-Dimensional Case

Theorem 3.1

Let $V$ and $H$ be separable Hilbert spaces satisfying (HV), $\varSigma$ a dictionary of $V$ and $a: V\times V\rightarrow {\mathbb {R}}$ a symmetric continuous bilinear form satisfying (HA). The following properties hold for the PRaGA, ORaGA, PReGA, and OReGA:

• 1. All the iterations of the algorithms are well defined.

• 2. The sequence $(\lambda _n)_{n\in {\mathbb {N}}}$ is nonincreasing and converges to a limit $\lambda$ which is an eigenvalue of $a(\cdot ,\cdot )$ for the scalar product $\langle \cdot , \cdot \rangle$.

• 3. The sequence $(u_n)_{n\in {\mathbb {N}}}$ is bounded in $V$ and any subsequence of $(u_n)_{n\in {\mathbb {N}}}$ which weakly converges in $V$ also strongly converges in $V$ toward an $H$-normalized eigenvector associated with $\lambda$. This implies in particular that

  $$\begin{aligned} d_a(u_n, F_\lambda ):= \mathop {\inf }_{w\in F_\lambda } \Vert w-u_n\Vert _a \mathop {\longrightarrow }_{n\rightarrow \infty } 0, \end{aligned}$$

  where $F_\lambda$ denotes the set of the $H$-normalized eigenvectors of $a(\cdot , \cdot )$ associated with $\lambda$.

• 4. If $\lambda$ is a simple eigenvalue, and if $w_\lambda$ is an $H$-normalized eigenvector associated with $\lambda$, then the whole sequence $(u_n)_{n\in {\mathbb {N}}}$ converges either to $w_\lambda$ or to $-w_\lambda$ strongly in $V$.

It may happen that $\lambda > \mu _1$, if the initial guess $u_0$ is not properly chosen. An example where such a situation occurs is given in Example 7.2 of [13]. If $\lambda$ is degenerate, it is not clear whether the whole sequence $(u_n)_{n\in {\mathbb {N}}}$ converges. We will see, however, in Sect. 3.3.2 that it is always the case in finite dimension, at least for the pure versions of these algorithms.

The proof of Theorem 3.1 is given in Sect. 7.1 for the PRaGA and in Sect. 7.2 for its orthogonal version ORaGA. We refer the reader to Section 6.4 of [13] for the detailed proof of this result for the PReGA and OReGA (which follows the same lines as for the PRaGA and ORaGA).

Remark 3.2

For the PReGA and the OReGA, we can prove similar convergence results without assuming that the Hilbert space $V$ is compactly embedded in $H$, provided that the self-adjoint operator $A$ defined as the Friedrichs extension associated with the quadratic form $a(\cdot , \cdot )$ has at least one eigenvalue below the minimum of its essential spectrum $\sigma _\mathrm{ess}(A)$, and that the initial guess $u_0$ satisfies $\min \sigma (A) \le \lambda _0:=a(u_0,u_0) < \min \sigma _\mathrm{ess}(A)$. This extension shows that the PReGA or OReGA can be used to solve electronic structure calculation problems (at least in principle) for molecular systems, which are eigenvalue problems associated with Schrödinger operators defined over functions of the whole space ${\mathbb {R}}^{3N}$, where $N$ is the number of electrons in the molecule under consideration. How to implement efficiently such an algorithm in practice will be the object of a forthcoming article. The exact statement of this result and its proof are also given in Proposition 3.1 of [13].

3.3.2 The Finite-Dimensional Case

From now on, for any differentiable function $f: V \rightarrow {\mathbb {R}}$, and all $v_0\in V$, we denote by $f'(v_0)$ the derivative of $f$ at $v_0$, that is $f'(v_0)\in V'$ is the unique continuous linear form on $V$ such that for all $v\in V$,

$$\begin{aligned} f(v) = f(v_0) + \langle f'(v_0), v \rangle _{V', V} + r(v), \text{ with } \mathop {\lim }_{\Vert v\Vert _a \rightarrow 0} \frac{r(v)}{\Vert v\Vert _a} = 0. \end{aligned}$$

In addition, we define the injective norm on $V'$ associated with $\varSigma$ as follows:

$$\begin{aligned} \forall l\in V', \; \Vert l\Vert _* = \mathop {\sup }_{z\in \varSigma ^*} \frac{\langle l, z\rangle _{V',V}}{\Vert z\Vert _a}. \end{aligned}$$

(20)

In the rest of this section, we assume that $V$, hence $H$ (since the embedding $V\hookrightarrow H$ is dense), are finite-dimensional vector spaces. The convergence results below rely heavily on the Łojasiewicz inequality [28] and the ideas presented in [3, 8, 27].

The Łojasiewicz inequality [28] reads as follows:

Lemma 3.5

Let $\varOmega$ be an open subset of the finite-dimensional Euclidean space $V$ and $f$ a real-analytic function defined on $\varOmega$. Then, for each $v_0 \in \varOmega$, there is a neighborhood $U\subset \varOmega$ of $v_0$ and two constants $K \in {\mathbb {R}}_+$ and $\theta \in (0,1/2]$ such that for all $v\in U$, it holds that:

$$\begin{aligned} |f(v) - f(v_0)|^{1-\theta } \le K \Vert f'(v)\Vert _*. \end{aligned}$$

(21)

Before stating our main result in finite dimension, we prove a useful lemma.

Lemma 3.6

Let $V$ and $H$ be finite-dimensional Euclidean spaces, $\varOmega := \{ v\in V, \; 1/2 < \Vert v\Vert < 3/2 \}$, $\lambda$ be an eigenvalue of the bilinear form $a(\cdot , \cdot )$, and $F_\lambda$ the set of the $H$-normalized eigenvectors of $a(\cdot , \cdot )$ associated with $\lambda$. Then, ${\mathcal {J}}: \varOmega \rightarrow {\mathbb {R}}$ is real-analytic, and there exists $K \in {\mathbb {R}}_+$, $\theta \in (0,1/2]$ and $\varepsilon >0$ such that

$$\begin{aligned} \text{ for } \text{ all }\,v\in \varOmega \text{ such } \text{ that } d(v,F_\lambda )&:= \mathop {\inf }_{w\in F_\lambda } \Vert v-w\Vert \le \varepsilon , \text{ it } \text{ holds } \text{ that } \left| {\mathcal {J}}(v) - \lambda \right| ^{1-\theta }\nonumber \\&\le K \Vert {\mathcal {J}}'(v)\Vert _*. \end{aligned}$$

(22)

Proof

The functional ${\mathcal {J}}:\varOmega \rightarrow {\mathbb {R}}$ is real-analytic as a composition of real-analytic functions. Thus, from (21), for all $w\in F_\lambda$, there exists $\varepsilon _w>0$, $K_w \in {\mathbb {R}}_+$, and $\theta _w\in (0,1/2]$ such that

$$\begin{aligned} \forall v\in B(w,\varepsilon _w), \quad |{\mathcal {J}}(v) - \lambda |^{1-\theta _w} \le K_w \Vert {\mathcal {J}}'(v)\Vert _*, \end{aligned}$$

(23)

where $B(w, \varepsilon _w):= \left\{ v\in V, \; \Vert v-w\Vert \le \varepsilon _w\right\}$. In addition, for all $w\in F_\lambda$, we can choose $\varepsilon _w$ small enough so that $B(w, \varepsilon _w) \subset \varOmega$. The family $(B(w, \varepsilon _w))_{w\in F_\lambda }$ forms a cover of open sets of $F_\lambda$. Since $F_\lambda$ is a compact subset of $V$ (it is a closed bounded subset of a finite-dimensional space), we can extract a finite subcover from the family $(B(w, \varepsilon _w))_{w\in F_\lambda }$, from which we deduce the existence of constants $\varepsilon >0$, $K >0$, and $\theta \in (0,1/2]$ such that

$$\begin{aligned} \text{ for } \text{ all } v\in \varOmega \text{ such } \text{ that } d(v, F_\lambda ) \le \varepsilon , \text{ it } \text{ holds } \text{ that } \left| {\mathcal {J}}(v) - \lambda \right| ^{1-\theta } \le K \Vert {\mathcal {J}}'(v)\Vert _*, \end{aligned}$$

hence the result. $\square$

The proof of the following theorem is given in Sect. 7.3 for the PRaGA and in Section 6.4 of [13] for the PReGA.

Theorem 3.2

Let $V$ and $H$ be finite-dimensional Euclidian spaces and $a:V\times V\rightarrow {\mathbb {R}}$ be a symmetric bilinear form. The following properties hold for both PRaGA and PReGA:

• 1. the whole sequence $(u_n)_{n\in {\mathbb {N}}}$ strongly converges in $V$ to some $w_\lambda \in F_\lambda$;

• 2. the convergence rates are as follows, depending on the value of the parameter $\theta$ in (22):

  • if $\theta = 1/2$, there exists $C\in {\mathbb {R}}_+$ and $0 < \sigma < 1$ such that for all $n\in {\mathbb {N}}$,

    $$\begin{aligned} \Vert u_n -w_\lambda \Vert _a \le C\sigma ^n; \end{aligned}$$

    (24)

  • if $\theta \in (0, 1/2)$, there exists $C \in {\mathbb {R}}_+$ such that for all $n\in {\mathbb {N}}^*$,

    $$\begin{aligned} \Vert u_n -w_\lambda \Vert _a \le C n^{-\frac{\theta }{1-2\theta }}. \end{aligned}$$

    (25)

3.4 Discussion About the Initial Guess

3.4.1 Possible Choice of Initial Guess

We present here a generic procedure to choose an initial guess $u_0\in V$ satisfying $\Vert u_0\Vert = 1$ and $a(u_0,u_0) \le \lambda _\varSigma$ (actually such that $a(u_0,u_0) = \lambda _\varSigma$), which is required by the two algorithms PReGA and PEGA:

Choice of an initial guess:

• Initialization: find $z_0\in \varSigma$ such that

  $$\begin{aligned} z_0 \in \mathop {\text{ argmin }}_{z\in \varSigma } {\mathcal {J}}(z), \end{aligned}$$

  (26)

  and set $u_0 := \frac{z_0}{\Vert z_0\Vert }$.

From Lemma 3.2, (26) always has at least one solution, and it is straightforward to see that $\Vert u_0\Vert = 1$ and $a(u_0,u_0) = \lambda _\varSigma$.

3.4.2 Special Case of the PRaGA

Let us recall that in the case of the PRaGA, we required that the initial guess $u_0$ of the algorithm satisfies $a(u_0, u_0) < \lambda _\varSigma$, whereas the above procedure generates an initial guess $u_0$ with $a(u_0,u_0) = \lambda _\varSigma$. Let us comment on this condition. We distinguish here two different cases:

• If the element $u_0$ computed with the procedure presented in Sect. 3.4.1 is an eigenvector of $a(\cdot , \cdot )$ associated with the eigenvalue $\lambda _0$, then from Lemma 3.1, ${\mathcal {J}}(u_0 + z) \ge {\mathcal {J}}(u_0)$ for all $z\in \varSigma$. We exclude this case from now on in all the rest of the article. Let us point out though that this case happens only in very particular situations. Indeed, it can be proved that if we consider the prototypical example presented in Sect. 2.2 with $b = 1$, $W$ a Hölder-continuous function (this assumption can be weakened) and $\varSigma = \varSigma ^\otimes$ defined by (7), then a vector $z\in \varSigma$ is an eigenvector associated with the bilinear form $a(\cdot , \cdot )$ defined by (6) if and only if the potential $W$ can be written as a sum of one-body potentials, that is, if

  $$\begin{aligned} W(x_1, \ldots , x_d) = W_1(x_1) + \cdots + W_d(x_d). \end{aligned}$$

  A proof of this result is given in Lemma 7.1 of [13].

• If $u_0$ is not an eigenvector of $a(\cdot , \cdot )$ associated with the eigenvalue $\lambda _0$, since $u_0\in \varSigma$, it may happen that the minimization problem: find $z_1\in \varSigma$ such that

  $$\begin{aligned} z_1 \in \mathop {\text{ argmin }}_{z\in \varSigma } {\mathcal {J}}(u_0 + z), \end{aligned}$$

  does not have a solution (see Example 7.1 for an example where such a situation occurs). However, from Lemma 3.1, there exists some $\widetilde{z}_0 \in \varSigma$ such that ${\mathcal {J}}(u_0 + \widetilde{z}_0) < {\mathcal {J}}(u_0)$. Thus, up to taking $\widetilde{u}_0:= u_0 +\widetilde{z}_0$ as the new initial guess, we have that $\widetilde{\lambda }_0:= a(\widetilde{u}_0, \widetilde{u}_0) < \lambda _\varSigma$. In practice, we compute a vector $\widetilde{z_0}$ satisfying this property by running the alternating direction method procedure described in Sect. 4.2 for a fixed number of iterations from the initial guess $u_0$ computed with the strategy described in Sect. 3.4.1. In all the numerical cases we tested, this was enough to ensure that ${\mathcal {J}}(u_0 + \widetilde{z}_0) < {\mathcal {J}}(u_0)$.

3.4.3 Convergence Toward the Lowest Eigenstate

As mentioned above, the greedy algorithms may not converge toward the lowest eigenvalue of the bilinear form $a(\cdot , \cdot )$. Of course, if $u_0$ is chosen so that $\lambda _0 = a(u_0,u_0) < \mu ^*_2:= \mathop {\inf }\nolimits _{j\in {\mathbb {N}}^*}\left\{ \mu _j\; | \; \mu _j > \mu _1\right\}$, then the sequences $(\lambda _n)_{n\in {\mathbb {N}}}$ generated by the greedy algorithms automatically converge to $\mu _1$. However, the construction of such an initial guess $u_0$ in the general case is not obvious.

One might hope that using the procedure to choose the initial guess $u_0$ presented in Sect. 3.4.1 would be sufficient to ensure that the greedy algorithms converge to $\mu _1$. Unfortunately, this is not the case, as shown in Example 7.2 of [13]. However, we believe that this only happens in pathological situations, and that, in most practical cases, the eigenvalue approximated by a greedy algorithm choosing the initial guess as in Sect. 3.4.1 is indeed $\mu _1$.

4 Numerical Implementation

In this section, we present how the above algorithms, and the one proposed in [1] can be implemented in practice in the case when $\varSigma$ is the set of rank-1 tensor-product functions of the form (7): $\varSigma := \varSigma ^{\otimes }$.

Let us note that the numerical methods which are used in practice for the implementation of the greedy algorithms do not guarantee that the elements $z_n\in \varSigma$ computed at each iteration of the iterative procedure are indeed solutions of the optimization problems (9) and (10). Usually, in the case when the set $\varSigma$ is a differentiable manifold, the obtained functions are solutions of the associated Euler equations, but it is not even clear in general if the obtained functions are local minima of the optimization problems used to define the iterations of the PRaGA or PReGA. From this point of view, there is a gap between the theoretical results we presented above and the way these greedy algorithms are implemented in practice, even if the way these numerical methods are implemented in practice seem sufficient for the whole procedure to converge toward the desired solution in general.

We consider here the case when $V$ and $H$ are Hilbert spaces of functions depending on $d$ variables $x_1, \;\ldots , \; x_d$, for some $d\in {\mathbb {N}}^*$, such that (HV) is satisfied. For all $1\le j \le d$, let $V_j$ be a Hilbert space of functions depending only on the variable $x_j$ such that the subset

$$\begin{aligned} \varSigma := \left\{ r^{(1)} \otimes \cdots \otimes r^{(d)}\; | \; r^{(1)} \in V_1, \ldots , r^{(d)} \in V_d \right\} \end{aligned}$$

(27)

is a dictionary of $V$, according to Definition 2.1. For all $z_n\in \varSigma$ such that $z_n = r_n^{(1)}\otimes \cdots \otimes r_n^{(d)}$ with $\left( r_n^{(1)} , \ldots , r_n^{(d)} \right) \in V_1 \times \cdots \times V_d$, the tangent space to $\varSigma$ at $z_n$ is denoted by

$$\begin{aligned} T_\varSigma (z_n)&:= \left\{ \delta r^{(1)} \otimes r_n^{(2)} \otimes \cdots \otimes r_n^{(d)} + r_n^{(1)}\otimes \delta r^{(2)} \otimes \cdots \otimes r_n^{(d)} + \cdots \right. \\&\quad \;\left. + \,r_n^{(1)} \otimes r_n^{(2)} \otimes \cdots \otimes \delta r^{(d)}, \delta r^{(1)} \in V_1, \ldots , \delta r^{(d)} \in V_d\right\} . \end{aligned}$$

4.1 Computation of the Initial Guess

Using the method described in Sect. 3.4.1, the initial guess $u_0\in V$ of all the greedy algorithms mentioned in this article is computed as follows: choose

$$\begin{aligned} u_0:= z_0 = r_0^{(1)} \otimes \cdots \otimes r_0^{(d)} \in \text{ argmin }_{\left( r^{(1)}, \ldots , r^{(d)}\right) \in V_1 \times \cdots \times V_d} {\mathcal {J}}\left( r^{(1)} \otimes \cdots \otimes r^{(d)}\right) \end{aligned}$$

such that $\Vert u_0\Vert = \Vert z_0\Vert = 1$. To compute this initial guess in practice, we use the well-known alternating direction method (ADM) (also called alternating least square method in [20, 22, 33], or fixed-point procedure in [1, 26]):

ADM for the computation of the initial guess

• Initialization: choose $\left( s_0^{(1)}, \ldots , s_0^{(d)} \right) \in V_1 \times \cdots \times V_d$ such that $\left\| s_0^{(1)} \otimes \cdots \otimes s_0^{(d)} \right\| = 1$;

• Iterate on $m=1, \ldots , m_{max}$:

  • – Iterate on $j=1, \ldots , d$: find $s_m^{(j)} \in V_j$ such that

    $$\begin{aligned} s_m^{(j)} \in \mathop {\text{ argmin }}_{s^{(j)}\in V_j} {\mathcal {J}}\left( s_m^{(1)}\otimes \cdots \otimes s_m^{(j-1)} \otimes s^{(j)} \otimes s_{m-1}^{(j+1)} \otimes \cdots \otimes s_{m-1}^{(d)}\right) ; \end{aligned}$$

    (28)

• set $r_0^{(1)} \otimes \cdots \otimes r_0^{(d)} = s_m^{(1)} \otimes \cdots \otimes s_m^{(d)}$.

It is observed that the ADM converges quite fast in practice. Actually, solving (28) amounts to computing the smallest eigenvalue and an associated eigenvector of a low-dimensional eigenvalue problem, since $s_m^{(j)}$ is an eigenvector associated with the smallest eigenvalue of the bilinear form $a_{m,j}: V_j \times V_j \rightarrow {\mathbb {R}}$ with respect to the scalar product $\langle \cdot , \cdot \rangle _{m,j}: V_j \times V_j \rightarrow {\mathbb {R}}$, such that for all $v_1^{(j)}, v_2^{(j)} \in V_j$,

$$\begin{aligned} a_{m,j}\left( v_1^{(j)}, v_2^{(j)}\right)&= a\left( s_m^{(1)}\otimes \cdots \otimes s_m^{(j-1)} \otimes v_1^{(j)} \otimes s_{m-1}^{(j+1)}\right. \\&\left. \otimes \cdots \otimes s_{m-1}^{(d)}, s_m^{(1)}\otimes \cdots \otimes s_m^{(j-1)} \otimes v_2^{(j)} \otimes s_{m-1}^{(j+1)} \otimes \cdots \otimes s_{m-1}^{(d)}\right) \end{aligned}$$

and

$$\begin{aligned} \left\langle v_1^{(j)}, v_2^{(j)}\right\rangle _{m,j}&= \left\langle s_m^{(1)}\otimes \cdots \otimes s_m^{(j-1)} \otimes v_1^{(j)} \otimes s_{m-1}^{(j+1)}\right. \\&\left. \otimes \cdots \otimes s_{m-1}^{(d)}, s_m^{(1)}\otimes \cdots \otimes s_m^{(j-1)} \otimes v_2^{(j)} \otimes s_{m-1}^{(j+1)} \otimes \cdots \otimes s_{m-1}^{(d)}\right\rangle . \end{aligned}$$

4.2 Implementation of the Pure Rayleigh Greedy Algorithm

We also use an ADM to compute the tensor product $z_n=r_n^{(1)} \otimes \cdots \otimes r_n^{(d)}$, which reads as follows:

ADM for the PRaGA:

• Initialization: choose $\left( s_0^{(1)}, \ldots , s_0^{(d)}\right) \in V_1 \times \cdots \times V_d$;

• Iterate on $m = 1, \ldots , m_{max}$:

  • – Iterate on $j = 1, \ldots , d$: find $s_m^{(j)}\in V_j$ such that

    $$\begin{aligned} s_m^{(j)} \in \mathop {\text{ argmin }}_{s^{(j)} \in V_j} {\mathcal {J}}\left( u_{n-1} \!+\! s_m^{(1)} \otimes \cdots \otimes s_m^{(j-1)} \otimes s^{(j)} \otimes s_{m-1}^{(j+1)} \otimes \cdots \otimes s_{m-1}^{(d)} \right) ; \end{aligned}$$

    (29)

• set $\left( r_n^{(1)}, \ldots , r_n^{(d)} \right) = \left( s_m^{(1)}, \ldots , s_m^{(d)} \right)$.

For $n\ge 1$, the minimization problems (29) are well defined. Let us now detail an efficient method for solving (29) in the discrete case. For all $1\le j \le d$, let $N_j\in {\mathbb {N}}^*$ and let $\left( \phi _i^{(j)} \right) _{1\le i \le {N_j}}$ be a Galerkin basis of some finite-dimensional subspace $V_{j, N_j}$ of $V_j$.

In the discretized setting, problem (29) reads: find $s_m^{(j)}\in V_{j,N_j}$ such that

$$\begin{aligned} s_m^{(j)} \in \mathop {\text{ argmin }}_{s^{(j)} \in V_{j,N_j}} {\mathcal {J}}\left( u_{n-1} + s_m^{(1)} \otimes \cdots \otimes s_m^{(j-1)} \otimes s^{(j)} \otimes s_{m-1}^{(j+1)} \otimes \cdots \otimes s_{m-1}^{(d)} \right) . \end{aligned}$$

(30)

We present below how (30) is solved for a fixed value of $j\in \{1, \cdots , d\}$. To simplify the notation and without loss of generality, we assume that all the $N_j$’s are equal and are denoted by $N$ their common value. Denoting by $S = \left( S_i\right) _{1\le i \le N}\in {\mathbb {R}}^N$ the vector of the coordinates of the function $s^{(j)}$ in the basis $\left( \phi _i^{(j)} \right) _{1\le i \le N}$, so that

$$\begin{aligned} s^{(j)} = \sum _{i=1}^N S_i \phi _i^{(j)}, \end{aligned}$$

it holds that

$$\begin{aligned} {\mathcal {J}}\left( u_{n-1} + s_m^{(1)} \otimes \cdots \otimes s_m^{(j-1)} \otimes s^{(j)} \otimes s_{m-1}^{(j+1)} \otimes \cdots \otimes s_{m-1}^{(d)} \right) = \frac{S^T \mathcal {A}S + 2 A^TS + \alpha }{S^T\mathcal {B}S + 2 B^TS + 1}, \end{aligned}$$

where the symmetric matrix $\mathcal {A}\in {\mathbb {R}}^{N\times N}$, the positive definite symmetric matrix $\mathcal {B}\in {\mathbb {R}}^{N\times N}$, the vectors $A,B \in {\mathbb {R}}^N$ and the real number $\alpha := a(u_{n-1}, u_{n-1})$ are independent of $S$. Making the change of variable $T = \mathcal {B}^{1/2}S + \mathcal {B}^{-1/2}B$, we obtain

$$\begin{aligned}&{\mathcal {J}}\left( u_{n-1} + s_m^{(1)} \otimes \cdots \otimes s_m^{(j-1)} \otimes s^{(j)} \otimes s_{m-1}^{(j+1)} \otimes \cdots \otimes s_{m-1}^{(d)} \right) \\&\quad = {\mathcal {L}}(T):= \frac{T^T{\mathcal {C}}T +2 C^T T + \gamma }{T^T T + \delta }, \end{aligned}$$

where the symmetric matrix ${\mathcal {C}}\!\in \! {\mathbb {R}}^{N\times N}$, the vector $C \!\in \! {\mathbb {R}}^N$, and the real numbers $\gamma \!\in \! {\mathbb {R}}$ and $\delta >0$ are independent of $T$. Solving problem (30) is therefore equivalent to solving

$$\begin{aligned} \text{ find } T_m \in {\mathbb {R}}^N \text{ such } \text{ that } T_m \in \mathop {\text{ argmin }}_{T\in {\mathbb {R}}^N} {\mathcal {L}}(T). \end{aligned}$$

(31)

An efficient method to solve (31) is the following. Let us denote by $(\kappa _i)_{1\le i \le N}$ the eigenvalues of the matrix ${\mathcal {C}}$ (counted with multiplicity), and let $(K_i)_{1\le i \le N }$ be an orthonormal family (for the Euclidean scalar product of ${\mathbb {R}}^N$) of associated eigenvectors. Let $(c_i)_{1\le i\le N}$ (resp. $(t_i)_{1\le i\le N}$) be the coordinates of the vector $C$ (resp. of the trial vector $T$) in the basis $(K_i)_{1\le i \le N }$:

$$\begin{aligned} C = \sum _{i=1}^N c_i K_i, \quad T = \sum _{i=1}^N t_i K_i. \end{aligned}$$

We aim at finding $(t_{i,m})_{1\le i \le N}$ the coordinates of a vector $T_m$ solution of (31) in the basis $(K_i)_{1\le i \le N }$. For any $T\in {\mathbb {R}}^N$, we have

$$\begin{aligned} {\mathcal {L}}(T) = \frac{\sum _{i=1}^N \kappa _i t_i^2 + 2 \sum _{i=1}^N c_i t_i +\gamma }{\sum _{i=1}^N t_i^2 + \delta }. \end{aligned}$$

Setting $\rho _m := {\mathcal {L}}(T_m)\ge \mu _1$, the Euler equation associated with (31) reads:

$$\begin{aligned} \forall 1\le i \le N, \quad \kappa _i t_{i,m} + c_i = \rho _m t_{i,m}, \end{aligned}$$

so that

$$\begin{aligned} \forall 1\le i \le N, \quad t_{i,m} = \frac{c_i}{\rho _m - \kappa _i}. \end{aligned}$$

(32)

This implies that

$$\begin{aligned} {\mathcal {L}}(T_m) = \frac{\sum _{i=1}^N \kappa _i \frac{c_i^2}{(\rho _m - \kappa _i)^2} + 2 \sum _{i=1}^N \frac{c_i^2}{\rho _m - \kappa _i} + \gamma }{\sum _{i=1}^N \frac{c_i^2}{(\rho _m - \kappa _i)^2} + \delta }. \end{aligned}$$

Setting for all $\rho \in {\mathbb {R}}\setminus \{\kappa _i\}_{1\le i \le N}$,

$$\begin{aligned} {\mathcal {M}}(\rho ) = \frac{\sum _{i=1}^N \kappa _i \frac{c_i^2}{(\rho - \kappa _i)^2} + 2 \sum _{i=1}^N \frac{c_i^2}{\rho - \kappa _i} + \gamma }{\sum _{i=1}^N \frac{c_i^2}{(\rho - \kappa _i)^2} + \delta }, \end{aligned}$$

(33)

it holds that

$$\begin{aligned} \rho _m = {\mathcal {L}}(T_m) = {\mathcal {M}}(\rho _m) \le \mathop {\inf }_{\rho \in {\mathbb {R}}\setminus \{\kappa _i\}_{1\le i \le N}} {\mathcal {M}}(\rho ) = \mathop {\inf }_{\rho \in {\mathbb {R}}\setminus \{\kappa _i\}_{1\le i \le N}} {\mathcal {L}}(T(\rho )), \end{aligned}$$

where $T(\rho ) = \sum _{i=1}^N t_i(\rho ) K_i$ with $t_i(\rho ) = \frac{c_i}{\rho - \kappa _i}$ for all $1\le i \le N$. Thus,

$$\begin{aligned} \rho _m = \mathop {\text{ argmin }}_{\rho \in {\mathbb {R}}\setminus \{\kappa _i\}_{1\le i \le N}} {\mathcal {M}}(\rho ). \end{aligned}$$

(34)

The Euler equation associated with the one-dimensional minimization problem (34) reads, after some algebraic manipulations,

$$\begin{aligned} \rho _m \delta = \sum _{i=1}^N \frac{ c_i^2 }{\rho _m - \kappa _i} + \gamma . \end{aligned}$$

Setting $f:\rho \in {\mathbb {R}}\setminus \{\kappa _i\}_{1\le i \le N} \mapsto \sum _{i=1}^N \frac{c_i^2}{\rho - \kappa _i} + \gamma$, we have the following lemma:

Lemma 4.1

Let $T_m$ be a solution to (31). The real number $\rho _m := {\mathcal {L}}(T_m)$ is the smallest solution to the equation

$$\begin{aligned} \text{ find } \rho \in {\mathbb {R}}\setminus \{\kappa _i\}_{1\le i \le N} \text{ such } \text{ that } \rho \delta = f(\rho ). \end{aligned}$$

(35)

Proof

The calculations detailed above show that $\rho _m$ is a solution of (35). On the other hand, for all $\rho \in {\mathbb {R}}$ satisfying (35), it can be easily seen after some algebraic manipulations that $\rho = {\mathcal {M}}(\rho ) = {\mathcal {L}}(T(\rho ))$. Hence, since $\rho _m$ is a solution to (34), in particular, for all $\rho \in {\mathbb {R}}$ solutions of (35), we have

$$\begin{aligned} \rho _m = {\mathcal {L}}(T(\rho _m)) = {\mathcal {M}}(\rho _m)\le {\mathcal {M}}(\rho ) = \rho = {\mathcal {L}}(T(\rho )). \end{aligned}$$

$\square$

For all $1\le i \le N$, $f(\kappa _i^-) = -\infty$, $f(\kappa _i^+) = +\infty$, $f(-\infty )= f(+\infty ) = \gamma$, and the function $f$ is decreasing on each interval $(\kappa _i, \kappa _{i+1})$ (with the convention $\kappa _0 = -\infty$ and $\kappa _{N+1} = +\infty$). Thus, Eq. (35) has exactly one solution in each interval $(\kappa _i, \kappa _{i+1})$. Thus, $\rho _m$ is the unique solution of (35) lying in the interval $(-\infty , \kappa _1)$ (see Figure 1).

Fig. 1

Solutions of equation (35)

To compute $\rho _m$ numerically, we first find a real $\kappa _0^{num} < \kappa _1$ such that $f(\kappa _0^{num}) - \delta \kappa _0^{num}<0$. We then know that $\rho _m\in (\kappa _0^{num}, \kappa _1)$. We first perform a few (typically two or three) iterations of a dichotomy method to solve equation (35) and use the obtained approximation as a starting guess to run a standard Newton algorithm to compute $\rho _m$. We observe numerically that this procedure converges very quickly toward the desired solution. The coordinates of a vector $T_m$ solution of (31) are then determined using (32). Thus, solving (30) amounts to fully diagonalizing the low-dimensional $N\times N$ matrix $\mathcal {C}$.

Let us point out that problems (28) and (29) are different in nature: in particular, (28) is an eigenvalue problem whereas (29) is not. In the discrete setting, the strategy presented in this section for solving (29) could also be applied to solve (28); however, since it requires the full diagonalization of matrices of sizes $N\times N$, it is more expensive from a computational point of view than standard algorithms dedicated to the computation of the smallest eigenvalue of a matrix, which can be used for the resolution of (28).

4.3 Implementation of the Pure Residual Greedy Algorithm

The Euler equation associated with the minimization problem (10) reads:

$$\begin{aligned} \forall \delta z \in T_\varSigma (z_n), \quad \langle u_{n-1} + z_n , \delta z\rangle _a - (\lambda _{n-1} +\nu ) \langle u_{n-1}, \delta z \rangle = 0. \end{aligned}$$

This equation is solved using again an ADM, which reads as follows:

ADM for the PReGA:

• Initialization: choose $\left( s_0^{(1)} , \ldots , s_0^{(d)} \right) \in V_1 \times \cdots \times V_d$;

• Iterate on $m=1, \ldots , m_{max}$:

  • – Iterate on $j = 1, \ldots , d$: find $s_m^{(j)} \in V_j$ such that for all $\delta s^{(j)} \in V_j$,

    $$\begin{aligned} \left\langle u_{n-1} + z_m^{(j)}, \delta z_m^{(j)} \right\rangle _a -( \lambda _{n-1} + \nu )\left\langle u_{n-1}, \delta z_m^{(j)} \right\rangle =0, \end{aligned}$$

    (36)

    where

    $$\begin{aligned} z_m^{(j)} = s_m^{(1)} \otimes \cdots \otimes s_m^{(j-1)} \otimes s_m^{(j)} \otimes s_{m-1}^{(j+1)} \otimes \cdots \otimes s_{m-1}^{(d)} \end{aligned}$$

    and

    $$\begin{aligned} \delta z_m^{(j)} = s_m^{(1)} \otimes \cdots \otimes s_m^{(j-1)} \otimes \delta s^{(j)} \otimes s_{m-1}^{(j+1)} \otimes \cdots \otimes s_{m-1}^{(d)}; \end{aligned}$$

• set $\left( r_n^{(1)}, \ldots , r_n^{(d)} \right) = \left( s_m^{(1)}, \ldots , s_m^{(d)} \right)$.

In our numerical experiments, we observed that this algorithm rapidly converges to a fixed point. Let us point out that using the same discretization space as in Sect. 4.2, namely a Galerkin basis of $N$ functions for all $1\le j \le d$, solving (36) only requires the inversion (and not the diagonalization) of low-dimensional $N\times N$ matrices.

4.4 Implementation of the Pure Explicit Greedy Algorithm

At each iteration of this algorithm, Eq. (16) is also solved using a very similar ADM as the one detailed in the previous section. The only difference is that (36) is replaced with

$$\begin{aligned} a\left( u_{n-1} + z_m^{(j)}, \delta z_m^{(j)} \right) - \lambda _{n-1}\langle u_{n-1} + z_m^{(j)}, \delta z_m^{(j)}\rangle = 0. \end{aligned}$$

We observe numerically that this algorithm usually converges quite fast. However, we have noticed cases when this ADM does not converge, which leads us to think that there may not always exist solutions $z_n\ne 0$ to (16), even when $u_{n-1}$ is not an eigenvector associated with $a(\cdot , \cdot )$.

4.5 Implementation of the Orthogonal Versions of the Greedy Algorithms

An equivalent formulation of (17) is the following: find $\left( c_0^{(n)}, \ldots , c_n^{(n)} \right) \in {\mathbb {R}}^{n+1}$ such that

$$\begin{aligned}&\left( c_0^{(n)}, \ldots , c_n^{(n)}\right) \in {\mathop {\hbox {argmin}}\limits _{(c_0, \ldots , c_n) \in {\mathbb {R}}^{n+1},\,\Vert c_0 u_0 + c_1 z_1+\cdots + c_nz_n\Vert ^2 = 1}} a\left( c_0 u_0 + c_1 z_1+ \cdots \right. \nonumber \\&\quad \left. + c_nz_n, c_0 u_0 + c_1 z_1+ \cdots + c_nz_n\right) . \end{aligned}$$

(37)

Actually, for all $0\le k,l\le n+1$, defining (using the abuse of notation $z_0 = u_0$):

$$\begin{aligned} \mathcal {B}_{kl}&:= \langle z_k, z_l\rangle ,\\ \mathcal {A}_{kl}&:= a(z_k, z_l),\\ \end{aligned}$$

and $\mathcal {A}:=\left( \mathcal {A}_{kl}\right) \in {\mathbb {R}}^{(n+1)\times (n+1)}$ and $\mathcal {B}:=\left( \mathcal {B}_{kl} \right) \in {\mathbb {R}}^{(n+1)\times (n+1)}$, the vector $C^{(n)} = (c_0^{(n)}, \ldots , c_n^{(n)})\in {\mathbb {R}}^{n+1}$ is a solution of (37) if and only if $C$ is an eigenvector associated with the smallest eigenvalue of the following generalized eigenvalue problem:

$$\begin{aligned} \left\{ \begin{array}{l} \text{ find } (\tau , C)\in {\mathbb {R}}\times {\mathbb {R}}^{n+1} \text{ such } \text{ that } C^T\mathcal {B}C = 1 \text{ and } \\ \mathcal {A}C =\tau \mathcal {B}C, \\ \end{array}\right. \end{aligned}$$

which is easy to solve in practice provided that $n$ remains small enough.

4.6 About the Convergence of the ADM

Let us comment about the convergence properties of the different ADMs presented in the preceding sections. A priori, it is not obvious that such algorithms, in which the functions composing the pure tensor product $z_n:=r_n^1\otimes \cdots \otimes r_n^d$ are optimized dimension-by-dimension, converge toward solutions of (26), (9), (10), and (16), respectively, or even only to local minima of these minimization problems.

In the literature, the analysis of ADM is well documented for the resolution of minimization problems such as those arising for the minimization of the Rayleigh quotient associated with a symmetric bilinear form (arising in the computation of the initial guess) and for the minimization of a convex energy functional (arising in the PReGA) [21, 32]) for advanced tensor formats such as tensor train functions for instance. It can be proved that these methods converge toward a local (but not necessarily global) minimizer of the minimization problems (26) and (10).

However, there is no analysis of the ADM applied to the minimization problems defining the PRaGA. We observe numerically that the algorithm is very good in practice, in the sense that it seems to quickly converge toward a local minimizer of the minimization problem (9) which ensures the decrease of the sequence $\left( {\mathcal {J}}(u_n)\right) _{n\in {\mathbb {N}}}$. In addition, in Sect. 4.2, we provide a way to efficiently solve in practice the problems that arise at each iteration of the ADM in the case when we use a dictionary composed of pure tensor-product functions. However, it is not clear to us yet how we could generalize such a numerical strategy to deal with dictionaries using different formats such as Tucker or tensor train functions. Both the theoretical analyses of the convergence properties of this ADM and its practical implementation in the case of more advanced tensor formats are interesting questions, but we will not address them in this paper.

In the case of the PEGA, it is not clear whether there exists in general a solution to (16) such that $z_n\ne 0$ if $u_{n-1}$ is not an eigenvector of $a(\cdot , \cdot )$ associated with $\lambda _{n-1}$. It is therefore difficult to analyze the ADM in this framework, even if it seems to be quite efficient in practice.

It is to be noted though that even in the case of the PReGA, the convergence results we prove rely heavily on the fact that the sequences of vectors $(z_n)_{n\in {\mathbb {N}}}$ produced by the greedy algorithms are global minimizers of problems (9) and (10), as is usually the case in the analysis of such greedy methods. There is indeed a gap between the theoretical analysis of these algorithms and the way they are implemented in practice, since the ADM procedures described in this section cannot guarantee in general that the sequence of tensor products obtained are indeed global minimizers of the optimization problems defining each version of the greedy algorithms presented above. However, from our numerical observations, it seems that these procedures are sufficiently efficient to ensure the convergence of the global procedures, and we refer the reader to the numerical tests we performed in Sect. 5.

5 Numerical Results

We present here some numerical results obtained with the greedy algorithms studied in this article (PRaGA, PReGA, PEGA, and their orthogonal versions) on toy examples involving only two Hilbert spaces ($d=2$). We refer the reader to [1] for numerical examples involving a larger number of variables. Section 5.1 presents basic numerical tests performed with small-dimensional matrices, which lead us to think that the greedy algorithms presented above converge in general toward the lowest eigenvalue of the bilinear form under consideration, except in pathological situations which are not likely to be encountered in practice. In Sect. 5.2, we consider the problem of computing the first buckling mode of a microstructured plate with defects.

5.1 A Toy Problem with Matrices

In this simple example, we take $V = H = {\mathbb {R}}^{N_x\times N_y}$, $V_x = {\mathbb {R}}^{N_x}$, and $V_y = {\mathbb {R}}^{N_y}$ for some $N_x, N_y\in {\mathbb {N}}^*$ (here typically $N_x = N_y = 51$). Let $D^{1x}, D^{2x} \in {\mathbb {R}}^{N_x\times N_x}$ and $D^{1y}, D^{2y} \in {\mathbb {R}}^{N_y\times N_y}$ be (randomly chosen) symmetric definite positive matrices. We aim at computing the lowest eigenstate of the symmetric bilinear form

$$\begin{aligned} a(U,V) = \text{ Tr }\left( U^T \left( D^{1x} V D^{1y} + D^{2x} V D^{2y}\right) \right) , \end{aligned}$$

or, in other words, of the symmetric fourth-order tensor $A$ defined by

$$\begin{aligned} \forall 1\le i,k\le N_x, \; 1\le j,l \le N_y, \quad A_{ij,kl} = D^{1x}_{ik}D^{1y}_{jl} + D^{2x}_{ik}D^{2y}_{jl}. \end{aligned}$$

Let us denote by $\mu _1$ the lowest eigenvalue of the tensor $A$, by $I$ the identity operator, and by $P_{\mu _1} \in {\mathcal {L}}({\mathbb {R}}^{N_x\times N_y})$ the orthogonal projector onto the eigenspace of $A$ associated with $\mu _1$. Figure 2 shows the decay of the error on the eigenvalues $\log _{10}(|\mu _1 - \lambda _n|)$ and of the error on the eigenvectors $\log _{10}(\Vert (I-P_{\mu _1})U_n\Vert _F)$, where $\Vert \cdot \Vert _F$ denotes the Frobenius norm of ${\mathbb {R}}^{N_x\times N_y}$, as a function of $n$ for the three algorithms and their orthogonal versions.

Fig. 2

Decay of the error of the three algorithms and their orthogonal versions: eigenvalues (left) and eigenvectors (right)

These tests were performed with several matrices $D^{1x}, D^{1y}, D^{2x}, D^{2y}$, either drawn randomly or chosen such that the eigenspace associated with the lowest eigenvalue is of dimension greater than $1$. In any case, the three greedy algorithms converge toward a particular eigenstate associated with the lowest eigenvalue of the tensor $A$. In addition, the rate of convergence always seems to be exponential with respect to $n$. The error on the eigenvalues decays twice as fast as the error on the eigenvectors, as usual when dealing with variational approximations of linear eigenvalue problems.

We observe that the PRaGA and PEGA have similar convergence properties with respect to the number of iterations $n$. The behavior of the PReGA strongly depends on the value $\nu$ chosen in (HA): The larger the $\nu$, the slower the convergence of the PReGA. To ensure the efficiency of this method, it is important to choose the numerical parameter $\nu \in {\mathbb {R}}$ appearing in (3) as small as possible so that (HA) remains true. If the value of $\nu$ is well chosen, the PReGA may converge as fast as the PRaGA or the PEGA, as illustrated in Sect. 5.2. In the example presented in Fig. 2 where $\nu$ is chosen to be $0$ and $\mu _1 \approx 116$, we can clearly see that the rate of convergence of the PReGA is lower than those of the PRaGA and PEGA.

We also observe that the use of the ORaGA, OReGA, and OEGA, instead of the pure versions of the algorithms, improves the convergence rate with respect to the number of iterations $n\in {\mathbb {N}}^*$. However, as $n$ increases, the cost of the $n$-dimensional optimization problems (17) becomes more and more significant.

5.2 First Buckling Mode of a Microstructured Plate with Defects

We now consider the more difficult example of the computation of the first buckling mode of a plate [4].

The plate is composed of two linear elastic materials, with different Young’s moduli $E_1 = 1$ and $E_2 = 20$, respectively, and the same Poisson’s ratio $\nu _\mathrm{P} = 0.3$. The rectangular reference configuration of the thin plate is $\varOmega = \varOmega _x\times \varOmega _y$ with $\varOmega _x = (0,1)$ and $\varOmega _y = (0,2)$. The composition of the plate in the $(x,y)$ plane is displayed in Figure 3: The white parts represent regions occupied by the first material and the black parts indicate the location of the second material. The measurable function $E: (x,y)\in \varOmega _x \times \varOmega _y \mapsto E(x,y)$ is defined such that $E(x,y) = E_1$ if $(x,y)$ belongs to the subset of $\varOmega _x\times \varOmega _y$ occupied by the first material, and $E(x,y) = E_2$ otherwise. The thickness of the plate is denoted by $h$.

Fig. 3

Composition of the plate

The bottom part $\varGamma _b := [0,1]\times \{0\}$ of the plate is fixed, and a constant force $F = -0.05$ is applied in the $y$ direction on its top part $\varGamma _t:= [0,1]\times \{2\}$. The sides of the plate $\varGamma _s:= \left( \{0\}\times \varOmega _y\right) \cup \left( \{1\}\times \varOmega _y \right)$ are free, and the outerplane displacement fields of the plate (and their derivatives) are imposed to be zero on the boundaries $\varGamma _b \cup \varGamma _t$.

The precise model (von Karman model) and discretization we consider are detailed in Section 5.2 of [13]. For the sake of brevity, we do not give the details here, but determining if the plate buckles or not amounts to determining the sign of the smallest eigenvalue of a symmetric continuous bilinear form $a(\cdot , \cdot )$ on $V\times V$ where

$$\begin{aligned} V&:= \Bigg \{ v \in H^2(\varOmega _x\times \varOmega _y), \; v(x,0) = v(x,2) = \frac{\partial v}{\partial y}(x,0) = \frac{ \partial v}{\partial y}(x,2)\\&\quad = 0 \text{ for } \text{ almost } \text{ all } x\in \varOmega _x\Bigg \}, \end{aligned}$$

and for all $v,w\in V$,

$$\begin{aligned}&a(v,w) := 2\int _{\varOmega _x\times \varOmega _y} \frac{E(x,y)h^3}{12(1-\nu _\mathrm{P}^2)} \left[ \nu _\mathrm{P} \text{ Tr } \chi (v)\text{ Tr }\chi (w) + (1-\nu _\mathrm{P})\chi (v) : \chi (w) \right] \,{\text {d}}x\,{\text {d}}y\\&\quad +\,2 \int _{\varOmega _x\times \varOmega _y} \frac{E(x,y)h}{(1\!-\!\nu _\mathrm{P}^2)} \left[ \nu _\mathrm{P} \phi _0(x,y) \text{ Tr } e(v,w) \!+\! (1\!-\!\nu _\mathrm{P}) \varPhi _0(x,y) : e(v,w) \right] \,{\text {d}}x\,{\text {d}}y \end{aligned}$$

for some $\phi _0\in L^2(\varOmega _x\times \varOmega _y)$ and $\varPhi _0\in \left( L^2(\varOmega _x\times \varOmega _y)\right) ^4$ whose expressions we do not detail here, and where for all $v,w\in V$,

$$\begin{aligned} e(v,w) := \left[ \begin{array}{l@{\quad }l} \frac{\partial v}{\partial x}\frac{\partial w}{\partial x} &{} \frac{1}{2}\left( \frac{\partial v}{\partial x}\frac{\partial w}{\partial y} + \frac{\partial v}{\partial y}\frac{\partial w}{\partial x} \right) \\ \frac{1}{2}\left( \frac{\partial v}{\partial x}\frac{\partial w}{\partial y} + \frac{\partial v}{\partial y}\frac{\partial w}{\partial x} \right) &{} \frac{\partial v}{\partial y}\frac{\partial w}{\partial y}\\ \end{array}\right] \end{aligned}$$

and

$$\begin{aligned} \chi (v):= \left[ \begin{array}{l@{\quad }l} \frac{\partial ^2 v}{\partial x^2} &{} \frac{\partial ^2 v}{\partial x\partial y}\\ \frac{\partial ^2 v}{\partial x\partial y} &{} \frac{\partial ^2 v}{\partial y^2}\\ \end{array}\right] . \end{aligned}$$

To compute this eigenvalue, the following particular dictionary is used:

$$\begin{aligned} \varSigma := \left\{ r\otimes s, \; r\in V_x, \; s\in V_y \right\} , \end{aligned}$$

where

$$\begin{aligned} V_x:= H^2(\varOmega _x) \quad \text{ and } V_y:= \left\{ s\in H^2(\varOmega _y), \; s(0) = s'(0) = s(2) = s'(2) = 0\right\} . \end{aligned}$$

It can be easily checked that assumptions (HV), (HA), (H$\varSigma 1$), (H$\varSigma 2$), and (H$\varSigma 3$) are satisfied in the continuous and discretized setting we consider so that the above greedy algorithms can be carried out. We have performed the PRaGA, PReGA, and PEGA on this problem. The approximate eigenvalue is found to be $\lambda \approx 1.53$. At each iteration $n\in {\mathbb {N}}^*$, each algorithm produces an approximation $\lambda _n$ of the eigenvalue and an approximation $u_n\in {\widetilde{V}}^v$ of the associated eigenvector.

The smallest eigenvalue $\mu _1$ of $a(\cdot , \cdot )$, and an associated eigenvector $\psi _1$, are computed using an inverse power method and used as reference solutions in the error plots shown below. Figure 4 shows the decay of the error on the eigenvalue, and on the eigenvector in the $H^2(\varOmega _x\times \varOmega _y)$ norm as functions of $n\in {\mathbb {N}}^*$, for the PRaGA, PReGA, and PEGA. More precisely, the quantities $\log _{10}\left( \frac{|\lambda _n - \mu _1|}{|\mu _1|}\right)$ and $\log _{10}\left( \frac{\Vert u_n - \psi _1\Vert _{H^2(\varOmega _x\times \varOmega _y)}}{\Vert \psi _1\Vert _{H^2(\varOmega _x\times \varOmega _y)}}\right)$ are plotted as a function of $n\in {\mathbb {N}}^*$. As for the toy problem dealt with in the previous section, the numerical behaviors of the PEGA and PRaGA are similar. In addition, we observe that the rate of convergence of the PReGA is comparable with those of the other two algorithms. Let us note that we have chosen here $\nu = 0$.

Fig. 4

Decay of the error as a function of $n$ for the PRaGA, PReGA, and PEGA: on the eigenvalue (left) and on the eigenvector in the $H^2(\varOmega _x\times \varOmega _y)$ norm (right)

Fig. 5

Isolines of the approximation of the first buckling mode of the plate given by the Rayleigh quotient algorithm for $n=1$ (left), $n=5$ (center), and $n=50$ (right)

The level sets of the approximation $u_n$ given by the PRaGA are drawn in Fig. 5 for different values of $n$ (the approximations given by the other two algorithms are similar). We can observe that the influence of the different defects of the plate appears gradually when $n$ grows.

Let us mention that in this article, for the sake of simplicity, we restricted ourselves to toy numerical tests where the number of Hilbert spaces $d$ introduced to decompose the solution using rank-1 tensors as described in Sect. 4 was equal to $2$. One could ask if the ADM procedures presented in this section are robust as the number of Hilbert spaces $d$ arising in the decomposition of the solution becomes large. Actually, these numerical strategies seem to work fine also in cases of rank-1 tensors where $d$ is larger than $2$. We refer the reader to a forthcoming work of the second author and L. Giraldi where these strategies were tested in combination with the use of hierarchical tensor formats in numerical tests with $d=20$.

6 Conclusion

In this paper, we have proposed two new greedy algorithms for the computation of the smallest eigenvalue of a symmetric continuous bilinear form, proved some convergence results along with convergence rates in finite dimensions for them, and compared their numerical behavior with the strategy proposed in [1].

A lot of theoretical and numerical questions remain open though. A first theoretical question concerns the state which is attained in the limit by these greedy strategies. Indeed, as it is usually the case for iterative algorithms for eigenvalue problems, the sequence $(\lambda _n)_{n\in {\mathbb {N}}}$ of approximate eigenvalues produced by these methods converges toward a limit $\lambda$ which is an eigenvalue of the bilinear form $a(\cdot , \cdot )$ under consideration, but this limit may not be the smallest eigenvalue of $a(\cdot , \cdot )$.

Another theoretical issue is the convergence of the ADM for the PRaGA, which seems to be very efficient on the numerical tests we have performed, but for which we have no theoretical proof of convergence. In addition, it would be interesting to generalize our numerical procedure to implement the iterations of this ADM for pure tensor-product functions to the case of more advanced tensor formats.

Lastly, it would be interesting to compare these greedy approaches with other numerical methods using more advanced tensor formats than pure tensor-product functions as dictionaries. Our guess is that the most efficient methods would combine both mathematical tools, in a spirit similar to the one proposed in [18, 19], where the greedy strategy was used in combination to hierarchical tensor formats in order to enrich the discretization subspaces. Some numerical tests using these combined approaches will be the object of a forthcoming article of the second author and L. Giraldi.

We will address the case of electronic structure calculations (and in particular the numerical issues arising from the antisymmetry of the wavefunctions) and parametric eigenvalue problems in forthcoming works.

7 Proofs

7.1 Proof of Theorem 3.1 for the PRaGA

Throughout this section, we use the notation of Sect. 3.2.1.

Lemma 7.1

For all $n \ge 1$, it holds that

$$\begin{aligned} a(u_n, z_n) - \lambda _n \langle u_n, z_n\rangle = 0. \end{aligned}$$

(38)

Proof

Let us define $\mathcal {S}: {\mathbb {R}}\ni t\mapsto {\mathcal {J}}(u_{n-1} + tz_n)$. From Lemma 3.3, since $\lambda _0 < \lambda _\varSigma$, all the iterations of the PRaGA are well defined, the sequence $(\lambda _n)_{n\in {\mathbb {N}}}$ is nonincreasing, and for all $n\in {\mathbb {N}}^*$, we have $u_{n-1}\notin \varSigma$. Hence, $u_{n-1} + z_n \ne 0$, and since $\varSigma$ satisfies (H$\varSigma 1$), the function $\mathcal {S}$ is differentiable in the neighborhood of $t=1$ and admits a minimum at this point. The first-order Euler equation at $t=1$ reads

$$\begin{aligned} \frac{1}{\Vert u_{n-1} + z_n\Vert ^2}\left( a(u_{n-1} + z_n, z_n) - \lambda _n \langle u_{n-1}+z_n, z_n\rangle \right) = 0, \end{aligned}$$

which immediately leads to (38). $\square$

In the rest of this section, we will define $\alpha _n = \frac{1}{\Vert u_{n-1} + z_n\Vert }$ and $\widetilde{z}_n = \frac{z_n}{\Vert u_{n-1} + z_n\Vert }$, so that for all $n\in {\mathbb {N}}^*$, $u_n = \alpha _n u_{n-1} + \widetilde{z}_n$. We first prove the following intermediate lemma.

Lemma 7.2

The series $\sum _{n=1}^{+\infty } \Vert \widetilde{z}_n\Vert ^2$ and $\sum _{n=1}^{+\infty } \Vert \widetilde{z}_n\Vert _a^2$ are convergent, and there exists $\tau >0$ such that for all $n\ge 1$,

$$\begin{aligned} \lambda _{n-1} - \lambda _n \ge \tau \Vert \widetilde{z}_n\Vert _a^2. \end{aligned}$$

(39)

Proof

Let us first prove that the series $\sum _{n=1}^{+\infty } \Vert \widetilde{z}_n\Vert ^2$ is convergent. For all $n\in {\mathbb {N}}^*$, we have

$$\begin{aligned} a(u_n, u_n) = \frac{a(u_{n-1} + z_n, u_{n-1} + z_n)}{\Vert u_{n-1} + z_n\Vert ^2}. \end{aligned}$$

Thus, using (38) at the fifth equality,

$$\begin{aligned} \lambda _{n-1} - \lambda _n&= a(u_{n-1}, u_{n-1}) - a(u_n, u_n) \nonumber \\&= \frac{a(u_{n-1}, u_{n-1})\left( 2 \langle u_{n-1}, z_n\rangle + \Vert z_n\Vert ^2\right) -2a(u_{n-1}, z_n) - a(z_n, z_n)}{\Vert u_{n-1} + z_n\Vert ^2} \nonumber \\&= \frac{2\left( \lambda _{n-1} \langle u_{n-1} + z_n, z_n \rangle -a(u_{n-1} + z_n, z_n)\right) -\lambda _{n-1}\Vert z_n\Vert ^2 + a(z_n, z_n) }{\Vert u_{n-1} + z_n\Vert ^2} \nonumber \\&= 2\left( \lambda _{n-1}\langle u_n, \widetilde{z}_n\rangle -a(u_n, \widetilde{z}_n)\right) + a(\widetilde{z}_n, \widetilde{z}_n) - \lambda _{n-1} \Vert \widetilde{z}_n\Vert ^2 \nonumber \\&= 2(\lambda _{n-1} - \lambda _n)\langle u_n, \widetilde{z}_n\rangle + a(\widetilde{z}_n , \widetilde{z}_n) - \lambda _{n-1} \Vert \widetilde{z}_n\Vert ^2 \nonumber \\&\ge (\lambda _{\varSigma } - \lambda _{n-1}) \Vert \widetilde{z}_n\Vert ^2 - 2(\lambda _{n-1} - \lambda _n)|\langle u_n, \widetilde{z}_n\rangle | \nonumber \\&\ge (\lambda _{\varSigma } - \lambda _{n-1}) \Vert \widetilde{z}_n\Vert ^2 - 2(\lambda _{n-1} - \lambda _n)\Vert u_n\Vert \Vert \widetilde{z}_n\Vert \nonumber \\&\ge (\lambda _{\varSigma } - \lambda _{n-1}) \Vert \widetilde{z}_n \Vert ^2 - (\lambda _{n-1} - \lambda _n)\Vert \widetilde{z}_n\Vert ^2 - (\lambda _{n-1} - \lambda _n). \end{aligned}$$

(40)

This implies that

$$\begin{aligned} 2(\lambda _{n-1} - \lambda _n) \ge \left[ (\lambda _\varSigma - \lambda _{n-1}) - (\lambda _{n-1} - \lambda _n) \right] \Vert \widetilde{z}_n\Vert ^2. \end{aligned}$$

(41)

From Lemma 3.3, $(\lambda _n)_{n\in {\mathbb {N}}}$ is a nonincreasing sequence. In addition, since it is bounded from below by $\mu _1 = {\mathop {\min }}_{v\in V} {\mathcal {J}}(v)$, it converges toward a real number $\displaystyle \lambda = \mathop {\lim }_{n\rightarrow +\infty } \lambda _n$ which satisfies $\lambda \le \lambda _0 < \lambda _\varSigma$. Estimate (41) implies that there exists $\delta >0$ and $n_0\in {\mathbb {N}}^*$ such that for all $n\ge n_0$,

$$\begin{aligned} \lambda _{n-1} - \lambda _n \ge \delta \Vert \widetilde{z}_n\Vert ^2. \end{aligned}$$

(42)

Hence, the series $\sum _{n=1}^{+\infty } \Vert \widetilde{z}_n\Vert ^2$ is convergent, since the series $\sum _{n=1}^{+\infty }( \lambda _{n-1} - \lambda _n)$ is obviously convergent.

Let us now prove that the series $\sum _{n=1}^{+\infty } \Vert \widetilde{z}_n\Vert _a^2$ is convergent. Using (40), it holds that

$$\begin{aligned} \lambda _{n-1} - \lambda _n&= 2(\lambda _{n-1} - \lambda _n)\langle u_n, \widetilde{z}_n\rangle + a(\widetilde{z}_n, \widetilde{z}_n) - \lambda _{n-1} \Vert \widetilde{z}_n\Vert ^2\\&\ge -2(\lambda _{n-1} - \lambda _n)\Vert u_n\Vert \Vert \widetilde{z}_n\Vert + a(\widetilde{z}_n, \widetilde{z}_n) - \lambda _{n-1} \Vert \widetilde{z}_n\Vert ^2\\&\ge - (\lambda _{n-1} - \lambda _n) \Vert \widetilde{z}_n\Vert ^2 - (\lambda _{n-1} - \lambda _n) + a(\widetilde{z}_n, \widetilde{z}_n) - \lambda _{n-1} \Vert \widetilde{z}_n\Vert ^2. \end{aligned}$$

Thus,

$$\begin{aligned} 2 (\lambda _{n-1} - \lambda _n) + (\nu +\lambda _{n-1} + (\lambda _{n-1} - \lambda _n)) \Vert \widetilde{z}_n\Vert ^2 \ge \Vert \widetilde{z}_n\Vert _a^2. \end{aligned}$$

(43)

This last inequality implies that the series $\sum _{n=1}^{+\infty } \Vert \widetilde{z}_n\Vert _a^2$ is convergent since $\nu + \lambda \ge \nu + \mu _1 >0$, and that there exists $\tau >0$ such that for all $n\in {\mathbb {N}}^*$, $\lambda _{n-1} - \lambda _n \ge \tau \Vert \widetilde{z}_n\Vert _a^2$.

$\square$

Proof of Theorem 3.1

We know that $(\lambda _n)_{n \in {\mathbb {N}}}$ converges to $\lambda$, which implies that $(\Vert u_n\Vert _a)_{n\in {\mathbb {N}}}$ is bounded. Thus, $(u_n)_{n\in {\mathbb {N}}}$ converges, up to the extraction of a subsequence, to some $w\in V$, weakly in $V$, and strongly in $H$ from (HV). Let us denote by $(u_{n_k})_{k\in {\mathbb {N}}}$ such a subsequence. In particular, $\displaystyle \Vert w\Vert = \mathop {\lim }_{k\rightarrow +\infty } \Vert u_{n_k}\Vert = 1$. Let us prove that $w$ is an eigenvector of the bilinear form $a(\cdot , \cdot )$ associated with $\lambda$ and that $(u_{n_k})_{k\in {\mathbb {N}}}$ strongly converges in $V$ to $w$.

Lemma 7.2 implies that $\displaystyle \widetilde{z}_n \mathop {\longrightarrow }_{n\rightarrow \infty } 0$ strongly in $V$, and since $\Vert u_n\Vert = \Vert \alpha _n u_{n-1} + \widetilde{z}_n\Vert = \Vert u_{n-1} \Vert = 1$ for all $n\in {\mathbb {N}}^*$, necessarily $\displaystyle \alpha _n\mathop {\longrightarrow }_{n\rightarrow \infty } 1$. Thus, $z_n = \frac{1}{\alpha _n}\widetilde{z}_n$ also converges to $0$ strongly in $V$.

In addition, for all $n\ge 1$ and all $z\in \varSigma$, it holds that

$$\begin{aligned} {\mathcal {J}}(u_{n-1} + z) \ge {\mathcal {J}}(u_{n-1} + z_n). \end{aligned}$$

Using the fact that $\Vert u_{n-1}\Vert = 1$ and $a(u_{n-1}, u_{n-1})=\lambda _{n-1}$, this inequality also reads

$$\begin{aligned}&\lambda _{n-1} \left[ 2 \langle u_{n-1}, z_n\rangle + \Vert z_n\Vert ^2 -2 \langle u_{n-1} , z\rangle - \Vert z\Vert ^2\right] \nonumber \\&\quad + \left[ 2a(z, u_{n-1}) + a(z,z) \right] \left[ 1 + 2\langle u_{n-1}, z_n\rangle + \Vert z_n\Vert ^2\right] \nonumber \\&\quad - \left[ 2a(u_{n-1}, z_n) + a(z_n, z_n)\right] \left[ 1 + 2\langle u_{n-1} , z \rangle + \Vert z\Vert ^2\right] \ge 0. \end{aligned}$$

(44)

In addition, $(z_n)_{n\in {\mathbb {N}}^*}$ strongly converges to $0$ in $V$ and $(\lambda _n)_{n\in {\mathbb {N}}}$ converges toward $\lambda$. As a consequence, taking $n = n_k+1$ in (44) and letting $k$ go to infinity, it holds that for all $z\in \varSigma$,

$$\begin{aligned} - 2\lambda \langle w, z\rangle - \lambda \Vert z\Vert ^2 + 2a(w,z)+ a(z,z) \ge 0. \end{aligned}$$

From (H$\varSigma 1$), for all $\varepsilon >0$ and $z\in \varSigma$, $\varepsilon z\in \varSigma$. Thus, taking $\varepsilon z$ instead of $z$ in the above inequality yields

$$\begin{aligned} - 2\lambda \varepsilon \langle w, z\rangle - \lambda \varepsilon ^2 \Vert z\Vert ^2 + 2\varepsilon a(w,z)+ \varepsilon ^2 a(z,z) \ge 0. \end{aligned}$$

(45)

Letting $\varepsilon$ go to $0$ in (45), we obtain that for all $z\in \varSigma$,

$$\begin{aligned} a(w,z) = \lambda \langle w, z\rangle \quad \text{ and } \quad a(z,z) \ge \lambda \Vert z\Vert ^2. \end{aligned}$$

Thus, using (H$\varSigma 3$), this implies that for all $v\in V$, $a(w,v) = \lambda \langle w, v\rangle$ and $w$ is an $H$-normalized eigenvector of $a(\cdot , \cdot )$ associated with the eigenvalue $\lambda$. Since $\displaystyle a(w,w) = \mathop {\lim }_{k\rightarrow \infty } a(u_{n_k}, u_{n_k})$ and $\displaystyle \Vert w\Vert = \mathop {\lim }_{k\rightarrow \infty } \Vert u_{n_k}\Vert$, it holds that $\displaystyle \Vert w\Vert _a = \mathop {\lim }_{k\rightarrow \infty } \Vert u_{n_k}\Vert _a$, and the convergence of the subsequence $(u_{n_k})_{k\in {\mathbb {N}}}$ toward $w$ also holds strongly in $V$.

Let us prove now that $\displaystyle d_a(u_n, F_\lambda ) \mathop {\longrightarrow }_{n\rightarrow \infty } 0$. Let us argue by contradiction and assume that there exists $\varepsilon >0$ and a subsequence $(u_{n_k})_{k\in {\mathbb {N}}}$ such that $d_a(u_{n_k}, F_\lambda ) \ge \varepsilon$. Up to the extraction of another subsequence, from the results proved above, there exists $w\in F_\lambda$ such that $u_{n_k} \rightarrow w$ strongly in $V$. Thus, along this subsequence,

$$\begin{aligned} d_a(u_{n_k}, F_\lambda ) \le \Vert u_{n_k} - w\Vert _a \mathop {\longrightarrow }_{n\rightarrow \infty } 0, \end{aligned}$$

yielding a contradiction.

Lastly, if $\lambda$ is a simple eigenvalue, the only possible limits of subsequences of $(u_n)_{n\in {\mathbb {N}}}$ are $w_\lambda$ and $-w_\lambda$ where $w_\lambda$ is an $H$-normalized eigenvector associated with $\lambda$. As $(z_n)_{n\in {\mathbb {N}}^*}$ strongly converges to $0$ in $V$, the whole sequence $(u_n)_{n\in {\mathbb {N}}}$ converges, either to $w_\lambda$ or to $-w_\lambda$, and the convergence holds strongly in $V$. $\square$

7.2 Proof of Theorem 3.1 for the ORaGA

It is clear that there always exists at least one solution to the minimization problems (17).

For all $n\in {\mathbb {N}}^*$, let us define $\alpha _n:= \frac{1}{\Vert u_{n-1} + z_n\Vert }$, $\widetilde{z}_n = \alpha _n z_n$, $\widetilde{u}_n:= \alpha _n u_{n-1} + \widetilde{z}_n$, and $\widetilde{\lambda }_n =a(\widetilde{u}_n, \widetilde{u}_n)$.

For all $n\in {\mathbb {N}}^*$, $\lambda _n = a(u_n, u_n) \le \widetilde{\lambda }_n = a(\widetilde{u}_n, \widetilde{u}_n)$. In addition, the same calculations as the ones presented in Sect. 7.1 can be carried out, replacing $u_n$ by $\widetilde{u}_n$. This implies that for all $n\in {\mathbb {N}}^*$, $\widetilde{\lambda }_n \le \lambda _{n-1}$ (and thus the sequence $(\lambda _n)_{n\in {\mathbb {N}}}$ is nonincreasing). In addition, the series of general term $\left( \Vert \widetilde{z}_n\Vert _a^2 \right) _{n\in {\mathbb {N}}}$ is convergent.

Thus, Eq. (44) is still valid for the orthogonalized version of the algorithm. Following exactly the same lines as in Sect. 7.1, we obtain the desired results. The fact that for all $n\in {\mathbb {N}}^*$, $\langle u_n, u_{n-1} \rangle \ge 0$ ensures the uniqueness of the limit of the sequence in the case when the eigenvalue $\lambda$ is simple.

7.3 Proof of Theorem 3.2 for the PRaGA

Lemma 7.3

Consider the PRaGA in finite dimension. Then, there exists $C \in {\mathbb {R}}_+$ such that for all $n\in {\mathbb {N}}$,

$$\begin{aligned} \Vert {\mathcal {J}}'(u_n)\Vert _* \le C \Vert z_{n+1}\Vert _a. \end{aligned}$$

(46)

Let us recall that the norm $\Vert \cdot \Vert _*$ is the injective norm on $V'$ defined by (20) and that for all $v\in \varOmega = \{ u\in V, \; 1/2 < \Vert u\Vert < 3/2 \}$, the derivative of ${\mathcal {J}}$ at $v$ is given by

$$\begin{aligned} \forall w\in V, \quad \langle {\mathcal {J}}'(v), w \rangle _{V',V} = \frac{1}{\Vert v\Vert ^2}\left( a(v,w) - a(v,v) \langle v, w \rangle \right) . \end{aligned}$$

Proof

Since ${\mathcal {J}}$ is analytic on the compact set $\overline{\varOmega }$, the Hessian of ${\mathcal {J}}$ at any $v\in \varOmega$ is uniformly bounded in the sense of the continuous bilinear forms on $V\times V$; i.e., there exists $C>0$ such that

$$\begin{aligned} \forall v\in \varOmega , \; \forall w,w'\in V, \quad |{\mathcal {J}}''(v)(w,w')| \le \frac{C}{2} \Vert w\Vert _V\Vert w'\Vert _V. \end{aligned}$$

Thus, since $\Vert u_n\Vert = 1$ for all $n\in {\mathbb {N}}$ and $\displaystyle z_n \mathop {\longrightarrow }_{n\rightarrow +\infty } 0$ strongly in $H$, there exists $n_0\in {\mathbb {N}}$ and $\varepsilon _0 >0$ such that for all $n\ge n_0$, all $\varepsilon \le \varepsilon _0$, and all $z\in \varSigma$ such that $\Vert z\Vert _a \le 1$,

$$\begin{aligned} {\mathcal {J}}(u_{n} + z_{n+1})&\le {\mathcal {J}}(u_n + \varepsilon z) \le {\mathcal {J}}(u_n+z_{n+1}) + \langle {\mathcal {J}}'(u_n+z_{n+1}), \varepsilon z - z_{n+1} \rangle _{V',V}\\&+\, C \Vert \varepsilon z - z_{n+1}\Vert _a^2. \end{aligned}$$

Since $\langle {\mathcal {J}}'(u_n + z_{n+1}), z_{n+1} \rangle _{V',V} = 0$ from Lemma 7.1, the above inequality implies that

$$\begin{aligned} \varepsilon \left| \langle {\mathcal {J}}'(u_n+z_{n+1}), z \rangle _{V',V}\right| \le C \Vert \varepsilon z - z_{n+1}\Vert _a^2 \le 2C \left( \varepsilon ^2 \Vert z\Vert _a^2 + \Vert z_{n+1}\Vert _a^2\right) . \end{aligned}$$

Taking $\varepsilon = \frac{\Vert z_{n+1}\Vert _a}{\Vert z\Vert _a}$ in the above expression yields

$$\begin{aligned} \forall z\in \varSigma , \quad \left| \langle {\mathcal {J}}'(u_n+z_{n+1}), z \rangle _{V',V}\right| \le 4C \Vert z\Vert _a\Vert z_{n+1}\Vert _a. \end{aligned}$$

Using again the fact that the Hessian of ${\mathcal {J}}$ is uniformly bounded in $\varOmega$, and that $\displaystyle \mathop {\lim }_{n\rightarrow \infty } \Vert z_{n+1}\Vert _a=0$, there exists $n_0\in {\mathbb {N}}$ such that for all $n\ge n_0$,

$$\begin{aligned} \forall z\in \varSigma , \quad \left| \langle {\mathcal {J}}'(u_n+z_{n+1}), z \rangle _{V',V} -\langle {\mathcal {J}}'(u_n), z \rangle _{V',V} \right| \le C \Vert z\Vert _a \Vert z_{n+1}\Vert _a, \end{aligned}$$

and finally

$$\begin{aligned} \forall z\in \varSigma , \quad \left| \langle {\mathcal {J}}'(u_n), z \rangle _{V',V}\right| \le 5C \Vert z\Vert _a\Vert z_{n+1}\Vert _a, \end{aligned}$$

which yields the desired result. $\square$

Proof of Theorem 3.2

Since $\displaystyle d_a(u_n, F_\lambda ) \mathop {\longrightarrow }_{n\rightarrow \infty } 0$, using (22), there exists $n_0\in {\mathbb {N}}$ such that for $n\ge n_0$,

$$\begin{aligned} \left| {\mathcal {J}}(u_n) - \lambda \right| ^{1-\theta } = \left( \lambda _n - \lambda \right) ^{1-\theta } \le K \Vert {\mathcal {J}}'(u_n)\Vert _*. \end{aligned}$$

Thus, using the concavity of the function ${\mathbb {R}}_+ \ni t \mapsto t^{\theta }$, we have

$$\begin{aligned} (\lambda _n -\lambda )^\theta - (\lambda _{n+1}\! -\! \lambda )^{\theta } \ge \frac{\theta }{(\lambda _n - \lambda )^{1-\theta }}\left( \lambda _n - \lambda _{n+1}\right) \ge \frac{\theta }{K \Vert {\mathcal {J}}'(u_n)\Vert _* } \left( \lambda _n - \lambda _{n+1}\right) . \end{aligned}$$

Equations (42) and (43) imply that there exists a constant $\tau >0$ such that for all $n\in {\mathbb {N}}$, $\lambda _n - \lambda _{n+1} \ge \tau \Vert \widetilde{z}_{n+1}\Vert _a^2$. In addition, since $\Vert u_n\Vert ^2 = 1$, it holds that for all $v\in V$,

$$\begin{aligned} \langle {\mathcal {J}}'(u_n), v \rangle _{V',V} = a(u_n, v) - \lambda _n \langle u_n, v \rangle . \end{aligned}$$

Consequently, for $n$ large enough, using (39), (46), and the fact that $\displaystyle \alpha _n \mathop {\longrightarrow }_{n\rightarrow \infty } 1$, we obtain

$$\begin{aligned} (\lambda _n -\lambda )^\theta - (\lambda _{n+1} - \lambda )^{\theta }&\ge \frac{\theta }{K \Vert {\mathcal {J}}'(u_n)\Vert _* } \left( \lambda _n - \lambda _{n+1}\right) \ge \frac{\theta \tau }{K C \Vert z_{n+1}\Vert _a } \Vert \widetilde{z}_{n+1}\Vert _a^2\\&\ge \frac{\theta \tau \alpha _{n+1}}{KC } \Vert \widetilde{z}_{n+1}\Vert _a \ge \frac{\theta \tau }{2KC} \Vert \widetilde{z}_{n+1}\Vert _a. \end{aligned}$$

Since $\displaystyle \mathop {\lim }_{n\rightarrow \infty } \alpha _n = 1$ and the series of general term $\left( (\lambda _n -\lambda )^\theta - (\lambda _{n+1} - \lambda )^{\theta }\right) _{n\in {\mathbb {N}}}$ is convergent, the series of general terms $(\Vert \widetilde{z}_n\Vert _a)_{n\in {\mathbb {N}}^*}$ and $(\Vert z_n\Vert _a)_{n\in {\mathbb {N}}^*}$ are convergent as well. In addition, since $\alpha _n = \frac{1}{\Vert u_{n-1} + z_n\Vert }$, it can be easily seen that $|1-\alpha _n| = \mathcal {O}(\Vert z_n\Vert )$ is also the general term of a convergent series. Thus, since $\Vert u_n - u_{n-1}\Vert _a \le |1-\alpha _n| (\lambda _\varSigma + \nu ) + \Vert \widetilde{z}_n\Vert _a$, the sequence $(u_n)_{n\in {\mathbb {N}}}$ strongly converges in $V$ to some $w\in F_\lambda$. This also implies that there exists $c>0$ and $n_0\in {\mathbb {N}}^*$ such that for all $n\ge n_0$, $\Vert u_n - u_{n-1}\Vert _a \le c \Vert \widetilde{z}_{n}\Vert _a$. Defining $e_n:= \sum _{k=n}^{+\infty } \Vert \widetilde{z}_k\Vert _a$, we therefore have

$$\begin{aligned} \Vert u_n -w\Vert _a \le \sum _{k=n}^{+\infty } \Vert u_{k+1} -u_k\Vert _a \le c e_n. \end{aligned}$$

(47)

Let us now prove the rates (24) and (25). The strategy of proof is identical to the one used in [3, 8, 27].

The above calculations imply that for $k$ large enough,

$$\begin{aligned} |\lambda _k -\lambda |^\theta - |\lambda _{k+1} - \lambda |^{\theta } \ge \frac{\tau \theta }{ACK} \Vert \widetilde{z}_{k+1}\Vert _a \end{aligned}$$

(48)

for any constant $A >2$. We choose $A$ large enough to ensure that $M = \frac{1}{CK}\left( \frac{\tau \theta }{ACK} \right) ^{\frac{1-\theta }{\theta }} <1$. Let us first prove that for all $n\in {\mathbb {N}}^*$,

$$\begin{aligned} e_{n+1} \le e_n - M e_n^{\frac{1-\theta }{\theta }}. \end{aligned}$$

(49)

By summing inequalities (48) for $k$ ranging from $n-1$ to infinity, we obtain

$$\begin{aligned} \frac{\tau \theta }{ACK} e_n \le |\lambda _{n-1} -\lambda |^\theta , \end{aligned}$$

which yields

$$\begin{aligned} \left( \frac{\tau \theta }{ACK} e_n \right) ^{\frac{1-\theta }{\theta }} \le |\lambda _{n-1} \!-\!\lambda |^{1-\theta } \le K \Vert {\mathcal {J}}'(u_{n-1})\Vert _* \le CK\Vert \widetilde{z}_n\Vert _a = CK (e_n - e_{n+1}). \end{aligned}$$

Hence, (49). If $\theta = \frac{1}{2}$, (49) reduces to $e_{n+1} \le (1-M)e_n$. Thus, there exists $c_0>0$ such that for all $n\in {\mathbb {N}}^*$, $e_n \le c_0 (1-M)^n$. Since we have chosen $A$ large enough so that $0 < 1-M <1$, (47) immediately yields (24).

If $\theta \in (0, 1/2)$, we set $t := \frac{\theta }{1 - 2\theta }$ and, for $n$ large enough, $y_n = Bn^{-t}$ for some constant $B>0$ which will be chosen later. Then,

$$\begin{aligned} y_{n+1} = B (n+1)^{-t} = Bn^{-t}\left( 1 + \frac{1}{n}\right) ^{-t} \ge B n^{-t} \left( 1 \!-\! \frac{t}{n}\right) = y_n \left( 1 -t B^{-1/t}y_n^{1/t}\right) \!. \end{aligned}$$

Choosing $B$ large enough so that $B> \left( \frac{M}{t}\right) ^{-t}$ with $M = \frac{1}{CK}\left( \frac{\tau \theta }{2CK} \right) ^{\frac{1-\theta }{\theta }}$, and using (49), we finally prove by induction that $e_n \le y_n$, which yields (25). $\square$