1 Introduction

When studying a set of time series observations, the first step is to find “whether the data exhibit significant serial dependence or not”, Jung and Tremayne (2003) and Jung and Tremayne (2006). If no serial dependence is observed, the standard methods for analyzing independent observations should be applied. Otherwise, if existence of significant serial correlation is confirmed, the researcher can go for identifying the type of correlation structure and specifying the appropriate time series model for the data. Based on the Box-Jenkins methodology, model identification, parameter estimation, diagnostic checking and forecasting are steps that must be taken through analyzing any time series observations.

Goodness-of-fit tests is one of the most important tools for checking the adequacy of the fitted model to a set of data. In the analysis of time series data, these tests are commonly defined based on the characteristics of the residuals, Li (2003) and Box et al. (2015). For example, in linear time series, the fitted model is considered to be adequate if the plot of the autocorrelations of the residuals resembles the plot of the autocorrelations of a noise sequence and, for this purpose, several test statistics have been suggested by various researchers. For instance, Ljung-Box and McLeod-Li test statistics were introduced based on sums of autocorrelations of residuals and squared residuals, respectively, and have the asymptotic chi-square distribution; see (Ljung and Box 1978) and McLeod and Li (1983) for more details. Peña and Rodríguez (2002) proposed a portmanteau test based on the K-th root of the determinant of the autocorrelation matrix of order K. Besides, in 2006, they presented a modification of the test statistic using the logarithm of the determinant. They demonstrated that this test is more powerful than the ones proposed by Ljung and Box (1978) and McLeod and Li (1983).

Although the focus of proposed test statistics for goodness-of-fit tests in time series analysis was mainly on i.i.d noise sequence, in 2005, Francq et al. considered tests for lack of fit in ARMA models with dependent innovations. In their research, which is one of the cornerstones of the present study, they derived the test statistic based on the autocorrelations for residuals of ARMA models, when the underlying noise process is assumed to be uncorrelated rather than independent or a martingale difference. Additionally, Katayama (2016) studied the portmanteau tests and the Lagrange multiplier test for goodness of fit in ARMA models with uncorrelated errors.

In recent years, time series of counts become increasingly important in research and applications. These time series, which are arising from counting certain objects or events at specified times, can be studied from two aspects. In one aspect, if an integer-valued time series has a big enough range, it can be approximated by a standard continuous model and, in the other aspect, it is necessary to use integer-valued model to fit and forecast the appropriate model for the series. Although different features of integer-valued time series, such as model building and estimation of the parameters, are studied by various researchers, the third step in Box-Jenkins methodology for these kind of processes is still less developed. Based on the literature review, although there are some publications attempting to address the goodness-of-fit and portmanteau tests for count time series, they are mainly limited to specific models. In the following, a brief literature review concerning the third step in Box-Jenkins methodology is presented to clarify this gap.

In (2008), Bu and McCabe considered INAR(p) model with Poisson innovations. Although the focus of this research was on the model selection, estimation and forecasting, they tested the adequacy of the fitted model to the real dataset using the estimated Pearson residuals and Ljung-Box portmanteau tests. Their suggested method was to propose \(p+1\) sets of residuals and check “the existence of any dependence structure” in these sets. Zhu and Wang (2010) proposed five portmanteau test statistics, which can be applied in checking the adequacy of a fitted integer-valued ARCH model. Park and Kim (2012) proposed diagnostic checks for the same model as the one studied in Bu and McCabe (2008) using two forms of expected residuals. In (2013), Fokianos and Neumann studied non-parametric goodness-of-fit tests for the Poisson INGARCH\((p,\;q)\) models. Meintanis and Karlis (2014) proposed a goodness-of-fit test based on the joint probability generating function for the distribution of innovations, when they are from a general family of distributions called Poisson stopped-sum distributions. They applied their method to INAR(1) model and suggested that their approach can be applied to low order models and, as the order of the model increases, the test statistic would become considerably complicated. Kim and Weiß (2015) presented some diagnostic tests for the binomial AR(1) model and Schweer (2016) proposed the empirical joint probability generating function in order to test the adequacy of the fit of the model for a class of Markovian models. Finally, Weiß et al. (2019) tried to find solutions to some concerns about the adequacy of the fit of the model using Pearson residuals. For this purpose, they considered different types of “count time series models and inadequacy scenarios” and tried to answer to raised questions using a “comprehensive simulation study”.

Along with these studies, some searchers proposed goodness-of-fit tests for the marginal distribution of the integer-valued time series. For example, Hudecová et al. (2015) focused on goodness-of-fit tests for distributional assumptions on count time-series models. Schweer and Weiß (2016) suggested a test to identify a Poisson INAR(1) model from models with a different distribution of the innovations. As one of the last studies in this area, Weiß (2018) discussed the use of the Pearson test statistic to check the marginal distribution of count time series, such as CLAR(1), INAR(p), discrete ARMA and Hidden-Markov models. Although the focus of this paper was on the tests for the marginal distribution, but it also accounted for the selection of the order of the model. Based on the simulation studies, it was suggested that in practice, if the researcher is in doubt about the order of the mode, it is better to choose a model with higher order.

This paper tries to present some portmanteau test statistics for the class of generalized integer-valued autoregressive processes. These processes, which are introduced by Latour (1998), are formed by extending the idea of binomial thinning operator and include Binomial, Geometric, Poisson, new geometric (Ristić et al. 2009), dependent Bernoulli (Ristić et al. 2013) and \(\rho \)-binomial (Borges et al. 2016) integer-valued autoregressive processes. The portmanteau test statistics, which are studied in this paper, possess two advantages compared to their competitor. First, as pointed out in the previous paragraphs, most of the previous studies in this area concentrated on some specific models for count time series, mainly with binomial thinning operators. However, the proposed test statistics in this study can be applied to a wide class of integer-valued processes as GINAR(p) models covering a wide range of thinning operators and marginal distributions. In fact, these two components of integer-valued time series, which are of great importance in the studies that have been done so far, do not affect the performance of presented test statistics. Secondly, as mentioned in Park and Kim (2012), the thinning operators make residuals unobservable, and it is the main difficulty in developing diagnostic tools for integer-valued time series. Some researchers tried to overcome this challenge by substituting residuals by other forms, such as expected residuals, Park and Kim (2012) or Pearson residuals (Weiß 2018). The portmanteau tests presented in this paper are based on residuals, which are obtained by transforming integer-valued processes to real-valued time series with uncorrelated error terms and are easily feasible. Although these test statistics resemble the classic ones mentioned above, their asymptotic distributions are different because of the uncorrelatedness of the error terms.

This paper is in two parts. In the first part, which is consisted of Sects. 2 and 3, the theoretical structure of generalized integer-valued autoregressive models are introduced and their relation with real-valued autoregressive models are presented. Besides, the empirical autocovariance and autocorrelation functions of autoregressive models with uncorrelated error terms and their properties are studied. Moreover, different forms of portmanteau tests for generalized integer-valued autoregressive models and their asymptotic distributions are derived. In the second part, Sects. 4 and 5, the finite sample properties of the test statistics are compared through Monte Carlo simulations and a real-data example is illustrated.

2 Generalized integer-valued autoregressive models of order p

In the study of integer-valued time series, various models have been presented by different researchers in this field, which are mainly based on thinning operators. Binomial thinning operator or the Steutel and van Harn operator, Steutel and Van Harn (1979), is one of the first operators of this kind. This operator is applied by Al-Osh and Alzaid (1987) and Du and Li (1991), and, in a slightly more general form by Dion et al. (1995) in defining integer-valued time series models.

Definition 1

Let \(\left\{ Y_j\right\} _{j\in {\mathbb {N}}}\) be a sequence of independent and identically distributed (i.i.d.) Bernoulli random variables with mean \(\theta \) and independent of X,  which is a non-negative integer-valued random variable. The binomial thinning operator in the analysis of integer-valued time series, is denoted by \(\theta \circ \) and is defined as

$$\begin{aligned} \theta \circ X=\left\{ \begin{array}{ll}\sum _{j=1}^X Y_j&{} X>0\\ 0&{}X=0\end{array}\right. . \end{aligned}$$
(1)

The sequence \(\left\{ Y_j\right\} _{j\in {\mathbb {N}}}\) is a counting series and, obviously, \(\theta \circ X\sim B\left( X,\theta \right) .\)

Based on the binomial thinning operator, Du and Li (1991) defined the integer-valued autoregressive model of order p,  INAR(p) in abbreviation, as

$$\begin{aligned} X_t=\sum _{j=1}^p \theta _j\circ X_{t-j}+\varepsilon _t,\qquad t \in {\mathbb {Z}}, \end{aligned}$$
(2)

where \(\left\{ \varepsilon _t\right\} _{t\in {\mathbb {Z}}}\) is an i.i.d. sequence of non-negative integer-valued random variables with mean \(\mu _\varepsilon \) and variance \(\sigma _{\varepsilon }^2\) and \(\left( \theta _1,\ldots , \theta _p,\mu _\varepsilon , \sigma _{\varepsilon }^2\right) ^T\) is the vector of parameters, where T stands for the transpose.

In 1998, Latour tried to modify the idea of binomial thinning operator by substituting any non-negative integer-valued random variable with finite mean \(\theta _j\) and variance \(\beta _j\) for the counting series involved in the operator \(\theta _j\circ .\) The new thinning operator, that he called it ”generalized thinning operator”, is defined as:

$$\begin{aligned} \theta \bullet X:=\sum _{j=1}^X Y_j, \qquad \theta \in \left( 0,1\right) ,\qquad \beta >0, \end{aligned}$$
(3)

where the counting series \(Y_j\) is allowed to have the range \(\left\{ 0,1,2,\ldots \right\} \) instead of \(\left\{ 0,1\right\} .\) Consequently, the generalized INAR(p), GINAR(p) in abbreviation, is defined as:

$$\begin{aligned} X_t=\sum _{j=1}^p \theta _j\bullet X_{t-j}+\varepsilon _t,\qquad t \in {\mathbb {Z}}, \end{aligned}$$
(4)

and \(\left\{ \varepsilon _t\right\} _{t\in {\mathbb {Z}}}\) is defined similarly as in Eq. (2) and it is independent of the counting series involved in the thinning operators. Let us assume that \(\left\{ X_t\right\} _{t\in {\mathbb {Z}}}\) has a constant mean. Consequently, taking expectations on both sides of (4) leads to

$$\begin{aligned} E\left( X_t\right) =\mu _{\varepsilon }\left( 1-\sum _{j=1}^p\theta _j\right) ^{-1}. \end{aligned}$$

Since \(\theta _j\ge 0,\) \(j= 1,\ldots , p-1,\) \(\theta _p>0,\) \(\mu _\varepsilon >0\) and \(E\left( X_t\right) >0,\) we must have \(\sum _{j=1}^p\theta _j<1.\)

Assumption 1. \(\sum _{j=1}^p\theta _j<1.\)

To show the importance of Assumption 1, set \(\theta \left( Z\right) =1-{\theta }_1Z-\dots -{\theta }_pZ^p.\) Using Rouche’s theorem, Assumption 1 implies that \(\theta \left( Z\right) \) has all its 0’s inside the unit circle. Besides, Du and Li (1991) proved that if the roots of \(\theta \left( Z\right) \) are inside the unit circle, the process is second-order stationary. Therefore, Assumption 1 guarantees the stationarity of \(\left\{ X_t\right\} _{t\in {\mathbb {Z}}}.\)

Moreover, by considering the innovation process \(\left\{ \varepsilon _t\right\} _{t\in {\mathbb {Z}}}\) to be a sequence of i.i.d. non-negative integer-valued random variables, it can be proved that the process \(\left\{ X_t\right\} _{t\in {\mathbb {Z}}}\) is not only second-order stationary but also it is strictly stationary, Latour (1997). Ergodicity is another characteristic of \(\left\{ X_t\right\} _{t\in {\mathbb {Z}}}.\) To demonstrate this property, note that sigma-field generated by \(\left\{ X_j\right\} _{j\le t},\) denoted as \({\mathcal {F}}\left( X_t,X_{t-1},\ldots \right) ,\) is a subset of the sigma-field generated by \(\left\{ \varepsilon _j\right\} _{j\le t}\) and the related counting series. On the other hand, by independence of \(\left\{ \varepsilon _j\right\} \) and the counting series and Kolmogorove’s 0-1 law, the tail sigma-field of the latter contains only the measurable sets with probability 0 or 1, and consequently, the same is true for any event in \(\bigcap _{t=0}^{-\infty }{\mathcal {F}}\left( X_t,X_{t-1},\ldots \right) ,\) which results in the ergodicity of \(\left\{ X_t\right\} _{t\in {\mathbb {Z}}},\) (Du and Li 1991).

The mixing notion is useful for derivation of the asymptotic distribution of estimators and holds for a wild class of processes, Pham (1986). The strong mixing coefficient of a stationary process \(\left\{ X_t;\;t\in {\mathbb {Z}}\right\} \) is the number \(\alpha _X\left( k\right) \) introduced as \(\alpha _X\left( k\right) :=\sup _{A\in {\mathcal {F}}_{-\infty }^0,\;B\in {\mathcal {F}}_k^\infty }\left| P\left( A\cap B\right) -P\left( A\right) P\left( B\right) \right| ,\) \(k=1,2,\ldots ,\) where the sub-\(\sigma \)-fields \({\mathcal {F}}_{-\infty }^0\) and \({\mathcal {F}}_k^\infty \) are defined as \({\mathcal {F}}_{-\infty }^0=\sigma \left\{ X_t;\;t\le 0 \right\} \) and \( {\mathcal {F}}_k^\infty =\sigma \left\{ X_t;\;t\ge k \right\} ,\) \( k\ge 1,\) respectively. The stationary process \(\left\{ X_t;\;t\in {\mathbb {Z}}\right\} \) is called strong mixing if \(\alpha _X\left( k\right) \rightarrow 0,\) as k goes to infinity.

In the following, we will make some assumptions on the moments and the strong mixing coefficients of \( \left\{ X_t\right\} ,\) which will be applied in the subsequent sections.

Assumption 2. For the GINAR\(\left( p\right) \) process \( \left\{ X_t\right\} ,\) \(E{\left| X_t\right| }^{4+2\nu }<\infty \) and, for some \(\nu >0,\) \(\sum ^{\infty }_{k=0}{{\alpha }_X\left( k\right) }^{{v}/{v+2}}<\infty .\)

Consider a sequence of GINAR(p) process, \(\left\{ X_t\right\} _{t\in {\mathbb {Z}}},\) following Eq. (4). As can obviously be seen, this equation resembles the standard equation of the AR model. By setting \(\epsilon _t=X_t-E\left( X_t|{\mathcal {F}}_{t-1}\right) ,\) which is a martingale difference, a GINAR(p) process can be transformed to a common AR(p) process, Latour (1998). This transformation is stated in the following corollary and relaxes restrictive assumptions on the type of the thinning operator and the marginal distributions in GINAR(p) models. This approach will be beneficial when dealing with order selection and diagnostic checking for a model. However, moving to the forecasting step in the Box-Jenkins methodology and based on the structure of the data, it will be required to clarify the type of these two elements.

Corollary 1

(Latour 1998) Let \(\left\{ X_t\right\} _{t\in {\mathbb {Z}}}\) be a GINAR(p) process satisfying Eq. (4). Then, \(\left\{ X_t\right\} _{t\in {\mathbb {Z}}}\) can be written as an AR(p) process,

$$\begin{aligned} X_t-E\left( X_t\right) =\sum _{j=1}^p\theta _j \left( X_{t-j}-E\left( X_t\right) \right) +\epsilon _t, \end{aligned}$$
(5)

where \(\epsilon _t\) is a white noise process with \(\sigma ^2_{\epsilon }:=var\left( \epsilon _t\right) =\sigma ^2_ \varepsilon +E\left( X_t\right) \sum _{i=1}^p\sigma ^2_i,\) where \(\sigma ^2_i\) is the variance of the counting variables, \(Y_{i,j},\) \(i=1,\ldots ,p,\) \(j=1,\ldots , X_{t-i},\) which are involved in the i th thinning operator, \(i=1,\ldots ,p.\)

By substituting \(X_t-E\left( X_t\right) \) with \(W_t,\) Eq. (5) can be rewritten as:

$$\begin{aligned} W_t= & {} \sum _{j=1}^p\theta _j W_{t-j}+\epsilon _t. \end{aligned}$$
(6)

Consider \({\pmb {\theta }}_0=\left( {{\theta }}_{01},\ldots ,{{\theta }}_{0p} \right) ^T\) be the true values of \({\pmb {\theta }}=\left( {{\theta }}_1,\ldots ,{{\theta }}_p \right) ^T\) in model (6). Throughout the paper, the random variable \(\hat{\pmb {\theta }}=\left( \hat{{\theta }}_1,\ldots ,\hat{{\theta }}_p \right) ^T\) denotes the least-square estimator (LSE) of \({\pmb {\theta }},\) where \(\hat{\pmb {\theta }}\) is the minimizing value of \(Q_n\left( \pmb {\theta } \right) =\frac{1}{n}\sum ^n_{t=1}{{e_t}^2\left( \pmb {\theta }\right) }\) and \({e_t}\left( \pmb {\theta }\right) \) is the estimation of the error term based on a sequence of observations of length n. Based on Francq et al. (2005), it can be proved that, under Assumptions 1 and 2 , \(\hat{\pmb {\theta }}\) is a strongly consistent and asymptotically normal estimator of \({\pmb {\theta }};\) i.e.,

$$\begin{aligned} {\hat{\pmb {\theta }}}&\xrightarrow []{{a.s.}}&{\pmb {\theta }_0}, \end{aligned}$$
(7)

and

$$\begin{aligned} \sqrt{n}\left( \hat{\pmb {\theta }}-{\pmb {\theta }_0}\right)&\xrightarrow [] {{\;\;d\;\;}}&N_p\left( {\mathbf {0}},{\mathbf {J}}^{-1}{\mathbf {I}}{\mathbf {J}}^{-1}\right) , \end{aligned}$$
(8)

where \({\mathbf {J}}:={\mathbf {J}} \left( \pmb {\theta }_0\right) \) and \({\mathbf {I}}:={\mathbf {I}}\left( \pmb {\theta }_0\right) \) are defined as \({\mathbf {J}}= \left. \lim _{n\rightarrow \infty }\frac{\partial ^2}{\partial {\pmb {\theta }}\partial {\pmb {\theta }}^T}Q_n \left( {\pmb {\theta }}\right) \right| _{\pmb {\theta }=\pmb {\theta }_0}\) and \({\mathbf {I}}=\left. \lim _{n\rightarrow \infty }Var \left( \sqrt{n}\frac{\partial }{\partial {\pmb {\theta }}}Q_n\left( {\pmb {\theta }}\right) \right) \right| _{\pmb {\theta }=\pmb {\theta }_0},\) respectively.

Generally, portmanteau test statistics are designed based on the empirical autocovariance function (ACVF) or empirical autocorrelation function (ACF). So, to construct the portmanteau test statistic for GINAR(p) models, it seems desirable to survey the properties of the empirical ACVFs of the uncorrelated error terms, \(\epsilon _t,\) in model (6).

2.1 Empirical ACVF and ACF of the uncorrelated error terms: properties and asymptotic distributions

Let \({\pmb {\gamma }}_m=\left( \gamma \left( 1\right) ,\gamma \left( 2\right) ,\ldots ,\gamma \left( m\right) \right) ^T\) be the vector of white noise ACVFs and , for \(\epsilon _t\) in (6), \(\gamma \left( l\right) \) is defined as:

$$\begin{aligned}\gamma \left( l\right) =\frac{1}{n}\sum ^{n-l}_{t=1}\epsilon _t\epsilon _{t+l},\qquad l\ge 0 . \end{aligned}$$

It can be proved that \(\sum ^{\infty }_{h=-\infty }{\left| E\left( \epsilon _{t}\epsilon _{t+l}{\epsilon }_ {t+h}{\epsilon _{t+h+l'}}\right) \right| }<\infty \) and

$$\begin{aligned} cov\left( \sqrt{n}\gamma \left( l\right) ,\sqrt{n}\gamma \left( l'\right) \right)= & {} \frac{1}{n}\sum ^{n-l}_{t=1} {\sum ^{n-l'}_{t'=1}E\left( \epsilon _{t}\epsilon _{t+l}{\epsilon }_{t'}{\epsilon _{t'+l'}}\right) }\\\rightarrow & {} \sum ^{\infty }_{h=-\infty }E\left( \epsilon _{t}\epsilon _{t+l}{\epsilon }_{t+h}{\epsilon _{t+h+l'}}\right) :=\Gamma \left( l,l'\right) , \end{aligned}$$

as n goes to infinity, see (Francq et al. 2005) for the detailed proofs.

Let \({\pmb {\Gamma }}_{m,m'}=\left( \Gamma \left( l,l'\right) \right) _{1\le l\le m,\; 1\le l'\le m'}.\) Additionally, let \({\pmb {\Lambda }}_m=\left( {\pmb {\lambda }}_1,\ldots ,{\pmb {\lambda }}_m\right) ,\) where \({\pmb {\lambda }}_i=\left( -\theta ^*_{i-1},\ldots ,-\theta _{i-p}^*\right) ^T\) and

$$\begin{aligned} \theta ^*_{i}=\left\{ \begin{array}{ll}0,&{}\;\;{ \text{ if } }i<0\\ 1,&{}\;\;{ \text{ if } }i=0\\ \sum _{0<k\le i}\theta _{0k}\theta _{i-k}^*,&{}\;\;{ \text{ if } }0< i<\max \left\{ p,1\right\} \\ \sum _{0<k\le p}\theta _{0k}\theta _{i-k}^*,&{}\;\;{ \text{ if } } i\ge \max \left\{ p,1\right\} \end{array}\right. . \end{aligned}$$
(9)

The next theorem, which is a restatement of Theorem 1 in Francq et al. (2005) for GINAR(p) processes, specifies the asymptotic joint distribution of \(\hat{\pmb {\theta }}-{\pmb {\theta }}_0\) and \({\pmb {\gamma }}_m.\)

Theorem 1

Assume that \(p> 0.\) Under Assumptions 1 and 2, \(\sqrt{n}\left( \hat{\pmb {\theta }}-{\pmb {\theta }}_0,{\pmb {\gamma }}_m\right) ^T\) is asymptotically distributed as \(N_{p+m}\left( {\mathbf {0}},\Sigma _{\hat{\pmb {\theta }},{\pmb {\gamma }}_m}\right) ,\) where

$$\begin{aligned} \Sigma _{\hat{\pmb {\theta }},{\pmb {\gamma }}_m}=\left( \begin{array}{cc} \Sigma _{11}&{}\Sigma _{12}\\ \Sigma _{21}&{}\Sigma _{22} \end{array}\right) , \end{aligned}$$

and

$$\begin{aligned}&\Sigma _{11}=\left\{ \sigma _{\epsilon }^2\pmb {\Lambda }_\infty \pmb {\Lambda }^T_\infty \right\} ^{-1}\pmb {\Lambda }_\infty \pmb {\Gamma }_{\infty ,\infty }\pmb {\Lambda }^T_\infty \left\{ \sigma _{\epsilon }^2\pmb {\Lambda }_\infty \pmb {\Lambda }^T_\infty \right\} ^{-1},\\&\Sigma _{12}= -\left\{ \sigma _{\epsilon }^2\pmb {\Lambda }_\infty \pmb {\Lambda }^T_\infty \right\} ^{-1}\pmb {\Lambda }_\infty \pmb {\Gamma }_{\infty ,m},\\&\Sigma _{21} =-\pmb {\Gamma }_{m,\infty }\pmb {\Lambda }_\infty \left\{ \sigma _{\epsilon }^2\pmb {\Lambda }_\infty \pmb {\Lambda }^T_\infty \right\} ^{-1},\\&\Sigma _{22}=\pmb {\Gamma }_{m,m}. \end{aligned}$$

Proof

Assumption 1, which is stated for GINAR(p) processes, can be transformed to equivalent assumption for AR(p) processes. In this case, the proof is a straightforward consequence of Francq et al. (2005). \(\square \)

Remark 1

Based on (8), \(\Sigma _{11}\) is equal to \({\mathbf {J}}^{-1}{\mathbf {I}}{\mathbf {J}}^{-1}.\) Besides, it can be shown that \(\pmb {\Lambda }_\infty \pmb {\Lambda }^T_\infty =\sum _{i=1}^\infty {\pmb {\lambda }}_i{\pmb {\lambda }}^T_i,\) \(\pmb {\Lambda }_\infty \pmb {\Gamma }_{\infty ,\infty }\pmb {\Lambda }^T_\infty =\sum _{l,l'}^\infty {\pmb {\lambda }}_l\Gamma \left( l,l'\right) \pmb {\lambda }_{l'}\) and \(\pmb {\Gamma }_{m,\infty }\pmb {\Lambda }_\infty =\sum _{l'=1}^\infty \sum _{l=1}^m\Gamma \left( l,l'\right) {\pmb {\lambda }}^T_{l'}.\)

Let \(W_1,W_2,\dots ,W_n\) be a realization of length n of the process \(\left\{ W_t\right\} _{t\in {\mathbb {Z}}}\) in model (6). The value of \(\epsilon _t, \) \(0<t\le n,\) can be approximated by \({\widehat{\epsilon }}_t\left( \pmb {\theta }\right) ,\) defined as \({\widehat{\epsilon }}_t\left( \pmb {\theta }\right) =W_t-\sum ^p_{i=1}{{\theta }_iW_{t-i}},\) \(t=1,\ldots ,n.\) We don’t consider the past of the process and set the unknown starting values equal to zero, i.e.,

$$\begin{aligned}W_t=0,\; \; t\le 0.\end{aligned}$$

To study the adequacy of the model, a suitable statistic based on the noise empirical ACVFs and ACFs is required. Therefore, as the first step towards introducing this test statistic, the estimation of the noise empirical ACVFs are presented.

Consider \({\hat{\pmb {\gamma }}}_m=\left( {\hat{\gamma }}\left( 1\right) ,{\hat{\gamma }}\left( 2\right) ,\ldots ,{\hat{\gamma }}\left( m\right) \right) ^T\) to be the estimation of the noise empirical ACVFs \({\pmb {\gamma }}_m,\) where

$$\begin{aligned}{\hat{\gamma }}\left( l\right) =\frac{1}{n}\sum ^{n-l}_{t=1}{{\widehat{\epsilon }}_t(\hat{\varvec{\theta }}) {\widehat{\epsilon }}_{t+l}(\hat{\varvec{\theta }})},\end{aligned}$$

and \(\hat{\varvec{\theta }}\) is the LS estimator of \(\varvec{\theta }.\) The estimation of \({\gamma }\left( l\right) \) can be rewritten as \({\hat{\gamma }}\left( l\right) =\gamma \left( l\right) + E\left( \epsilon _{t}\left( \frac{\partial }{\partial \varvec{\theta }^T}\epsilon _{t+l}\right) \right) _{{\varvec{\theta }} ={\varvec{\theta }}_0}\left( \hat{\varvec{\theta }}-{\varvec{\theta }}_0\right) +R_n,\) where \(\frac{\partial }{\partial \varvec{\theta }^T}\epsilon _{t+l}\) stands for the vector \(\frac{\partial }{\partial \varvec{\theta }^T}\epsilon _{t+l}=\left( \frac{\partial }{\partial \theta _1}\epsilon _{t+l},\ldots ,\frac{\partial }{\partial \theta _p }\epsilon _{t+l}\right) \) and \(R_n=O_p(\frac{1}{n}),\) (Francq et al. 2005). Following the same steps as in the proof of Theorem 1 of Francq et al. (2005), it can be demonstrated that, \( \frac{\partial }{\partial \varvec{\theta }^T}\epsilon _{t+l}=\sum _{i\ge 1} \epsilon _{t+l-i}{\pmb {\lambda }}^T_{i} .\) Therefore, \({\hat{\gamma }}\left( l\right) \) can be restated as \({\hat{\gamma }}\left( l\right) =\gamma \left( l\right) + \sigma ^2_{\epsilon }{\pmb {\lambda }}^T_{l}\left( \hat{\varvec{\theta }}-{\varvec{\theta }}_0\right) +R_n\) and, equivalently,

$$\begin{aligned} {\hat{\pmb {\gamma }}}_m={\pmb {\gamma }}_m+ \sigma ^2_{\epsilon }\pmb {\Lambda }_m^T\left( \hat{\varvec{\theta }}-\varvec{\theta }_0\right) + O_p(\frac{1}{n}). \end{aligned}$$
(10)

Let \(p>0.\) Under Assumption 1 and using Theorem 1, Slutsky’s Theorem and Eq. (10), it can be shown that \(\sqrt{n}{\hat{\pmb {\gamma }}}_m\) is asymptotically distributed as \({N}_{m}\left( \varvec{0},\Sigma _{{\hat{\pmb {\gamma }}}_m}\right) ,\) where

$$\begin{aligned} \Sigma _{{\hat{\pmb {\gamma }}}_m}&=\sigma ^4_{\epsilon }\pmb {\Lambda }^T_m \Sigma _{11}\pmb {\Lambda }_m+\sigma ^2_{\epsilon } \pmb {\Lambda }^T_m \Sigma _{12} +\sigma ^2_{\epsilon }\Sigma _{21} \pmb {\Lambda }_m+\Sigma _{22}, \end{aligned}$$
(11)

and \(\Sigma _{11},\) \( \Sigma _{12},\) \( \Sigma _{21} \) and \( \Sigma _{22}\) are defined in Theorem 1.

Let us defined the noise empirical autocorrelation and its estimation as \({\rho }\left( l\right) ={\gamma }\left( l\right) /{\gamma }\left( 0\right) \) and \({\hat{\rho }}\left( l\right) ={\hat{\gamma }}\left( l\right) /{\hat{\gamma }}\left( 0\right) ,\) respectively, and let \(\hat{\pmb {\rho }}_m\) stands for \(\big ({\hat{\rho }}\left( 1\right) ,{\hat{\rho }}\left( 2\right) ,\ldots ,{\hat{\rho }}\left( m\right) \big )^T.\) As mentioned in Francq et al. (2005), it can be demonstrated that

$$\begin{aligned} {\hat{\pmb {\rho }}}_m=\hat{\pmb {\gamma }}_m/ \sigma _{\epsilon }^2+O_p(\frac{1}{n}). \end{aligned}$$
(12)

Consequently, for \(p>0\) and under Assumption 1, it can be proved that the asymptotic distribution of \(\sqrt{n}{\hat{\pmb {\rho }}}_m\) is \({N}_{m}\left( \varvec{0},\Sigma _{\hat{{\pmb {\rho }}}_m}\right) ,\) where

$$\begin{aligned} \Sigma _{{\hat{\pmb {\rho }}}_m}&=\pmb {\Lambda }^T_m \Sigma _{11}\pmb {\Lambda }_m+\pmb {\Lambda }^T_m \Sigma _{12}+\Sigma _{21} \pmb {\Lambda }_m+\frac{1}{\sigma ^4_{\epsilon }}\Sigma _{22}.\end{aligned}$$
(13)

3 The portmanteau test statistics

Although various forms of portmanteau test statistics are introduced for real-valued time series, these test statitics are not studied sufficiently in the analysis of integer-valued time series. Here, we will bring two areas in the analysis of time series together to bridge this gap. More precisely, in one hand, there are GINAR processes, which covers a large class of INAR processes, and can be transformed to AR processes by subtracting the mean and, on the other hand, we have portmanteau tests for AR processes with uncorrelated error terms.

In the following, we will present four portmanteau test statistics for GINAR processes to test if the data follows an assumed model. In other words, we are going to test the null hypothesis that \(X_t\) satisfies a GINAR\(\left( p\right) \) model versus the alternative hypothesis that \(X_t\) does not admit a GINAR representation, or admits a GINAR\(\left( p'\right) \) with \(p'>p.\)

Although, we apply \(\hat{\pmb {\rho }}_m\) to formulate the portmanteau test statistics, by (12), it can be concluded that the test statistics can either be presented based on the empirical autocovariance or autocorrelation functions. The following test statistics are adopted from the analysis of real-valued time series with independent errors and we use the authors’ initials to discriminate them. For example, the statistic \(Q_{L}:=n{\hat{\pmb {\rho }}_{m}}^T {\hat{\Sigma }}^{-1}_{\hat{{\pmb {\rho }}}_m}{\hat{\pmb {\rho }}_{m}}\) is defined by Li (2003, 1992) for the analysis of non-linear time series with independent errors. Besides, \(Q_{BP}:=n{\hat{\pmb {\rho }}_{m}}^T{\hat{\pmb {\rho }}_{m}},\) \(Q_{LB}:=n\left( n+2\right) \sum _{l=1}^m\frac{\rho ^2\left( l\right) }{n-l}\) and \(Q_{LM}:=n{\hat{\pmb {\rho }}_{m}}^T{\hat{\pmb {\rho }}_{m}}+\frac{m\left( m+1\right) }{2n},\) are introduced, respectively, by Box and Pierce (1970); Ljung and Box (1978) and Li and McLeod (1981), in real-valued time series. In the following, the asymptotic distribution of these test statistics are presented for GINAR(p) processes.

  • Li test statistic: If \({\hat{\Sigma }}_{\hat{{\pmb {\rho }}}_m}\) is an invertible matrix and Assumption 1 holds, then, \(Q_{L}:=n{\hat{\pmb {\rho }}_{m}}^T {\hat{\Sigma }}^{-1}_{\hat{{\pmb {\rho }}}_m}{\hat{\pmb {\rho }}_{m}}\) converges in distribution to \(\chi ^2_m.\)

The portmanteau test statistic \(Q_{L}\) is designed directly using the results mentioned in previous sections and its asymptotic distribution is chi-square. The assumption of the invertibility of \({\hat{\Sigma }}_{\hat{{\pmb {\rho }}}_m}\) may be restrictive. Therefore, if \({\hat{\Sigma }}_{\hat{{\pmb {\rho }}}_m}\) is singular or, equivalently, not invertible, the generalized inverse or {2}-inverse can be applied, which results in a test statistic with asymptotic chi-square distribution as well. However, the range of application of these test statistics is limited, Duchesne and Francq (2008), and consequently, this test statistic is not considered in the simulation studies.

The constraint imposed by the invertability assumption leads to defining a test statistic which can be applied if \({\hat{\Sigma }}_{\hat{{\pmb {\rho }}}_m}\) is invertible or non-invertible. The suggested test statistic resembles the one defined by Box and Pierce (1970) and it can be proved that its asymptotic distribution is a weighted sum of chi-square variables and , consequently, the critical values are found using Imhof’s algorithm (1961). In this case, the weights are eigenvalues of \(\Sigma _{{\hat{\pmb {\rho }}}_m}.\) This case is studied by Francq et al. (2005) and is stated as follows:

  • Box and Pierce test statistic: If Assumption 1 holds, then, \(Q_{BP}:=n{\hat{\pmb {\rho }}_{m}}^T{\hat{\pmb {\rho }}_{m}}\) converges in distribution to \(\sum _{i=1}^m \eta _{i,m}Z_i^2,\) where \(\left( \eta _{1,m},\ldots ,\eta _{mm}\right) ^T\) is the vector of eigenvalues of \(\Sigma _{{\hat{\pmb {\rho }}}_m}\) and \(Z_1,\ldots ,Z_m\) are independent standard normal variables.

This test statistic can be modified following the same approach as Ljung and Box (1978) and Li and McLeod (1981).

  • Ljung and Box test statistic: Under Assumption 1, \(Q_{LB}:=n\left( n+2\right) \sum _{l=1}^m\frac{\rho ^2\left( l\right) }{n-l}\) converges in distribution to \(\sum _{i=1}^m \eta _{i,m}Z_i^2,\) where \(\left( \eta _{1,m},\ldots ,\eta _{mm}\right) ^T\) is the vector of eigenvalues of \(\Sigma _{{\hat{\pmb {\rho }}}_m}\) and \(Z_1,\ldots ,Z_m\) are independent standard normal variables.

  • Li and McLeod test statistic: If Assumption 1 holds, \(Q_{LM}:=n{\hat{\pmb {\rho }}_{m}}^T{\hat{\pmb {\rho }}_{m}}+\frac{m\left( m+1\right) }{2n}\) converges in distribution to \(\sum _{i=1}^m \eta _{i,m}Z_i^2,\) where \(\left( \eta _{1,m},\ldots ,\eta _{mm}\right) ^T\) is the vector of eigenvalues of \(\Sigma _{{\hat{\pmb {\rho }}}_m}\) and \(Z_1,\ldots ,Z_m\) are independent standard normal variables.

As can be expected, the last three statistics have the same performance for large sample. However, as will be seen in the simulation studies, the significance level of \(Q_{BP}\) is lower than \(Q_{LB}\) and \(Q_{LM}\) even for moderate sample sizes.

4 Simulation study

In this section, we conduct a comparative study of the empirical size and power of the portmanteau test statistics \(Q_{BP},\) \(Q_{LB}\) and \(Q_{LM}.\) The size and power of the statistics have been obtained by using the weighted sum of chi-square distributions and the critical values are found using Imhof’s (1961) algorithm. As mentioned in Sect. 3, because of its limited applications, the test statistic \(Q_L\) is not studied here.

For the statistics, we consider different values of m,  \(m=2,3,4,8,12,\) and the sample size \(n=200, 500, 1000\) and each entry for the tables is based on \(N=1000\) independent replications.

4.1 Empirical size

To analyze the size of the test in finite samples, we present the results for some different versions of model (4). We consider GINAR(1) and GINAR(2), with binomial and negative-binomial thinning operators and Poisson and geometric error terms, with different parameter values. These models are labeled as in Table 6. The results of empirical sizes of the portmanteau tests at the nominal level \(\alpha _0= 5\%\) are summarized in Tables 2, 3, 4 and 5.

Table 1 Labels of the considered hypotheses in empirical size simulation studies
Full size table

Considering each replication in the simulation study as a Bernoulli trial, we can apply the test statistic \(Q=\left( {\hat{\alpha }}-\alpha _0\right) /\sqrt{\alpha _0\left( 1-\alpha _0\right) /N}\) with asymptotic normal distribution to decide if the actual level coincides with nominal one or not. If the actual level agrees with the nominal level, the empirical size over the N = 1000 independent replications should belong to the interval \(\left[ 3.65\%, 6.35\%\right] \) with probability 95%, and to the interval \(\left[ 3.23\%, 6.77\%\right] \) with probability 99%, Carbon and Francq (2011) and Mainassara et al. (2021).

For GINAR(1) processes, we consider three parameter values, \(\theta =0.1,\;0.5\) and 0.8. As can be seen, for models M1–M4, the performance of the test statistics improve by increasing the number of samples and the value of parameter \(\theta .\) Besides, the empirical size of \(Q_{LB}\) is closer to the nominal value \(5\%\) and, by increasing n,  all the three statistics perform almost the same. Moreover, If we consider the empirical size to be a function of m,  the decreasing nature of this function can be observed from Tables 2 and 3. Although this behavior is obvious for small values of n,  the difference between the empirical size for \(m=2\) and \(m=12\) decreases as n increases.

For GINAR(2) processes, models M5–M8, are defined using three sets of parameter values, \((\theta _1,\theta _2)=(0.1,0.5),\;(0.4,\;0.4)\) and (0.5, 0.1). As can be seen from Tables 4 and 5, increasing number of observations, improve the performance of the test. Besides for small values of n,  the test statistic Q\(_{LB}\) has a better performance compared to the other two statistics and they have almost similar performance for large values of n.

Remark 2

Concerning the value of m,  the simulation studies of the empirical size demonstrate that, for small sample sizes, the value of m should preferably be taken as 3 or 4, to keep the nominal level, but for large sample sizes, this range can be extended up to 12.

Table 2 Empirical size (in %) under models M1 and M2 with \(\alpha =5\%\)
Full size table
Table 3 Empirical size (in %) under models M3 and M4 with \(\alpha =5\%\)
Full size table
Table 4 Empirical size (in %) under models M5 and M6 with \(\alpha =5\%\)
Full size table
Table 5 Empirical size (in %) under models M7 and M8 with \(\alpha =5\%\)
Full size table

4.2 Empirical power

As mentioned in Sect. 3, in the portmanteau test, which is studied in this paper, the null hypothesis is that \(X_t\) satisfies a GINAR\(\left( p\right) \) model and the alternative hypothesis is that \(X_t\) does not admit a GINAR representation, or admits a GINAR\(\left( p'\right) \) with \(p'>p.\) To investigate the power of the tests we simplify the testing procedure as follows:

$$\begin{aligned} \left\{ \begin{array}{l}H_0:\; X_t{ \text{ follows } \text{ a } \text{ GINAR(p) } \text{ process }} \\ H_1:\; X_t{ \text{ follows } \text{ a } \text{ GINAR( }p+1\text{) } \text{ process }}\end{array}\right. , \end{aligned}$$
(14)

for \(p=1,2.\) In other words, we will generate processes from GINAR(\(p+1\)) and fit a GINAR(p) model and conducted the tests to a 5% significance level. The considered testing procedures are labeled as in Table 6.

Table 6 Labels of the considered models in empirical power simulation studies
Full size table

The results of the simulation studies are summarized in Tables 7, 8, 9 and 10. For testing T1–T4, three sets of parameters are considered, \((\theta _1,\theta _2)=(0.1,0.5),\;(0.4,\;0.4)\) and (0.5, 0.1). As expected, the models with \((\theta _1,\theta _2)=(0.5,0.1),\) have the smallest values of empirical power. For all cases, by increasing n,  the power improves. The test statistic \(Q_{LB}\) has the highest empirical power among the test statistics studied in this paper. Besides, the empirical power is a decreasing function of m and, increasing the sample size, results in the same performance for all test statistics.

For testing T5–T8, the parameters are defined as \((\theta _1,\theta _2,\theta _3)=(0.1,0.1,0.5),\) (0.1, 0.5, 0.1) and (0.5, 0.1, 0.1). The models with parameters (0.1, 0.1, 0.5) have the highest powers and it generally reaches 100% as the sample size increases.

Remark 3

As mentioned previously, the advantage of transformation (5) is to counteract the effect of thinning operator and the marginal distributions. Therefore, the value of empirical size and power do not depend on these features and just rely on the sample sizes and parameter values.

Remark 4

An important point in performing portmanteau tests is determining the optimal value of m. This issue has been studied by different researchers for real-valued time series. For example, considering Ljung-Box statistics, this value ranges between 3 and 50, depending on different factors such as the sample size and nominal size of the test, Ljung (1986); Tsay (2005); Shumway and Stoffer (2000), Hyndman and Athanasopoulos (2018) and Hassani and Yeganegi (2020). For integer-valued time series, although this issue has not been comprehensively studied yet, it has been partially explored by Kim and Weiß (2015). Their findings indicated that, for their considered model, the empirical size and the power of Box-Pierce and Ljung-Box test statistics decrease as m increases, consequently, smaller values of m were reported to be preferable. In the present study, as pointed out in Remark 2, the suggested value for m ranges between 3 and 12, depending on the sample size. Putting all together, it seems that determining the optimal value of m such “the actual size of the test does not exceed the nominal size” and the power of the test is at an acceptable level, Hassani and Yeganegi (2020), needs some different simulation process and it will be the focus of future studies.

Table 7 Empirical power (in %) under models T1 and T2 with \(\alpha =5\%\)
Full size table
Table 8 Empirical power (in %) under models T3 and T4 with \(\alpha =5\%\)
Full size table
Table 9 Empirical power (in %) under models T5 and T6 with \(\alpha =5\%\)
Full size table
Table 10 Empirical power (in %) under models T7 and T8 with \(\alpha =5\%\)
Full size table

5 Illustrative example

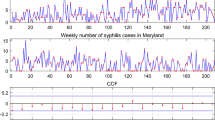
In the following, we investigate a real example to illustrate the application of the test statistics given in Sect. 3. The example is concerned with the daily download count of the program CW TeXpert from June 1, 2006, to February 28, 2007 (267 observations). This data has already been analyzed by Weiß (2008); Zhu and Wang (2010) and Li et al. (2016).

This dataset is analyzed in two steps. In the first step, the order of the model is determined using visual inspection of the data and the associated sample autocorrelation function (ACF) and partial autocorrelation function (PACF). Afterwards, the suggested order is confirmed using the test statistics presented in Sect. 3. In the second step, since the performed test specifies the order of the model not the associated thinning operator and the distribution of the error term, we examine some different integer-valued time series models to find the model with the best fit. This stage is required since the final step in time series analysis is forecasting and, without a clear picture about the structure of the model, this stage will remain obscure.

Figure 1 presents the data, its sample autocorrelation and partial autocorrelation functions. As can be seen, the observations exhibit serial dependencies and, at the first glance, because GINAR models are just AR models (from a second-order point of view), it seems reasonable to model this series using a GINAR process of order 1.

Fig. 1
figure 1

Top: The daily download count of the program CW TeXpert from June 1, 2006, to February 28, 2007, Bottom-Left: The sample autocorrelation function, Bottom-Right: The partial autocorrelation function

Full size image

To check the adequacy of a GINAR(1) model for this data set, the test statistics \(Q_{BP},\) \(Q_{LB}\) and \(Q_{LM},\) are calculated with \(m=2,3,4,8,12.\) The P-values of these test statistics are reported in Table 11, which indicate the appropriateness of the GINAR(1) model.

Finally, to decide which GINAR(1) model has a better fit to the data, the Akaike’s information criterion (AIC), corrected version of the AIC (AICc), Bayesian information criterion (BIC) and root mean squares of differences of observations and predicted values (RMS) for POISINAR(1), NBINAR(1) and GEINAR(1) are compared. These models, which are presented in brief in Table 12, are among the most popular models based on the distribution of the error term, Aghababaei Jazi et al. (2012); Al-Osh and Alzaid (1987) and Bisaglia and Gerolimetto (2019). The maximum likelihood estimation of parameters, along with AIC, AICc, BIC and RMS are presented in Table 13. As can be seen, since the ML estimation for r in the NBINAR(1) model is 0.83, the values of AIC, AICc, BIC and RMS for GEINAR(1) and NBINAR(1) models are very close. Besides, the difference between the AIC, AICc and BIC of these two models and POISINAR(1) is not negligible. On the other hand, the values of RMS for three models are almost similar. Based on the value of the criteria considered for comparing these models, the GEINAR(1) model, which is the model with the lowest AIC, AICc and BIC is suggested as the model with the best fit to this data.

Table 11 =P-value for the test statistics for the download counts series when \(m=2,3,4,8,12.\)
Full size table
Table 12 The thinning operators and the distribution of the error terms of the considered models
Full size table
Table 13 The maximum likelihood estimation of the parameters, AIC, AICc, BIC and RMS for the fitted GINAR(1) models to the download counts series
Full size table

6 Conclusions

The aim of this paper is to introduce some portmanteau test statistics for a wide group of INAR processes, which are one of the most widely applied integer-valued time series models. To present the test statistics for this class of INAR processes, which is abbreviated as GINAR, the process is transformed to its associated AR process with uncorrelated error terms. The asymptotic distribution of some classical test statistics, such as Box-Pierce, Ljung-Box and Li-McLeod, are obtained and their performance is tested using some simulation studies. It is worth mentioning that , as can be seen in the simulation studies, the performance of the test statistics depends on the value of the lag order m. Here, we consider a predefined set of values for m. However, it is valuable to find an optimal value for m such that the actual size of the test does not exceed the nominal size and the power of the test is higher than a threshold. Furthermore, there exists other forms of portmanteau test statistics, which are defined for real-valued time series with independent error terms. Extending these forms to uncorrelated error terms and, afterwards, applying them in the study of GINAR processes opens up a a new line of research in the diagnostic checkings of integer-valued time series.