1 Introduction

Linear mixed models (LMMs) are regression-type models with an extra random term which represents the individual/subject effects on repeated measures. LMMs include both fixed and random effects; fixed-effect parameters represent the relations of the covariates to the dependent variable for the population; while random-effect parameters represent the clusters or individuals within a population (West et al. 2007), named individual (subject) specific parameters.

Linear mixed models were first used for animal breeding studies by Eisenhart (1947) and by Henderson (1950). As a theoretical point of view, Harville (1977) reviewed the maximum likelihood (ML) approach to variance component estimation related to LMMs. Based on Harville’s work (1977), Laird and Ware (1982) introduced a two-staged model for repeated measurements and Lindstrom and Bates (1988) further studied on the same issue includes both Newton-Raphson and EM-algorithms. Laird and Ware (1982) introduced population parameters, individual effects and within-person variation at the first stage, and between-person variation at the second stage in their model. Their work included EM algorithm for ML estimates, following parameter estimations.

LMMs include more parameters, such as random effect coefficients to be estimated than classical regression-based models. Depending on that fact, integrating process includes more computational burden and the parameter estimations includes other unknown-parameters in the final equations. Therefore, some iterative algorithms such as EM-type (Dempster et al. 1977) are used in LMM to find ML estimators. EM is used for a wide variety of situations such as random effects, mixtures, log linear models, latent class and latent variable situations (Healy and Westmacott 1956; Kleinbaum 1973; McLachlan and Krishnan 1997) in addition to incomplete data structures.

Classical LMMs include the normality assumption for both random and error terms, but it may be too restrictive especially for repeated measures and clustered data. The existence of missing data or e- and b-outliers makes normality assumption being doubtful for the model. Even normality assumption allows applying the model easily, it is too restrictive for the data with heavy tails and/or skewed. So, it is critical for LMMs to choose a robust distribution for random effects/error terms rather than normal distribution.

There has been wide ranges of studies robustfying linear mixed models (Lin and Lee 2008; Lin 2008; Pinheiro et al. 2001; Verbeke and Lesaffre 1996) following studies robustfying linear regression models (Hampel et al. 1986; Huber 1973, 1981; Lange et al. 1989; Zellner 1976). Verbeke and Lesaffre (1996) used finite mixtures of normal distribution for random effects to detect the subgroups in the population. Pinheiro et al. (2001) proposed a linear mixed model with both random effects and residuals which were assumed to be multivariate t-distributed with the same degrees of freedom and they used an EM-type algorithm for the estimation of parameters. Lin (2008) proposed a t-linear mixed effects model with AR(p) dependence structure for repeated measures with thick tails and serial correlations. Likelihood inference is then required degrees-of-freedom parameter which is not required for classical LMM and the proposed model of us. In the study of Osorio et al. (2007), both light and heavy-tailed distributions were covered for elliptical linear models under different perturbation schemes. They conducted the study for the different types of elliptical distributions with error terms, not for the random terms.

In this study, we use multivariate Laplace distribution which is a special case of multivariate exponential power (EP) distribution (Arslan 2010; Gómez-Sánchez-Manzano et al. 2006, 2008) to handle with the situations being doubtful to assume a normal distribution. It has heavier tails than normal distribution and the number of parameters of Laplace distribution is less than t-distribution that makes the estimation procedures simpler than the estimations based on t-distribution. Additionally, EM algorithm can be implemented easily to estimate the parameters of interest, since Laplace distribution is written as a scale mixture of normal distribution.

The paper is structured as follows: Sect. 2 describes LMMs briefly. Section 3 includes multivariate EP distribution, the mixture form of it, and also the integration of this distribution into LMMs. Section 4 includes the general scheme of EM algorithm, and EM for Laplace LMM. The application part of the study is composed of a simulation study and a real life data example at the 5th and the 6th sections, respectively. Our conclusions are presented in Sect. 7. The originality of this study comes from using Laplace distribution with LMMs and also describes ECM with this new form.

2 Linear mixed models

The LMM has the following form (Laird and Ware 1982)

$$\begin{aligned} \varvec{y}_{\varvec{i}} = \varvec{X}_{\varvec{i}} \varvec{\beta } + \varvec{Z}_{\varvec{i}} \varvec{u}_{\varvec{i}} + \varvec{e}_{\varvec{i}} , \quad i=1,2\ldots n, \end{aligned}$$
(1)

where,

$$\begin{aligned} \varvec{e}_{\varvec{i}} \sim N_{n_i } ( {0,\varvec{R}_{\varvec{i}} }),\\ \varvec{u}_{\varvec{i}} \sim N_r ( {0,\varvec{D}}), \end{aligned}$$

\(\varvec{y}_{\varvec{i}}\) denotes a (\(n_i \times 1)\) vector of continuous responses for the i-th subject, \(\varvec{\beta }\) denotes a (p x 1) vector of unknown population parameters, \(\varvec{X}_{\varvec{i}} \) is a known (\(n_i \times p)\) design matrix, \(\varvec{u}_{\varvec{i}} \) denotes a \((r \times 1)\) vector of unknown individual effects, \(\varvec{Z}_{\varvec{i}} \) is a known (\(n_i \times r)\) design matrix, and \(\varvec{e}_{\varvec{i}} \) denotes a (\(n_i \times 1)\) vector of residual errors assumed to be independent of \(\varvec{u}_{\varvec{i}} \). The marginal distribution of \(\varvec{y}_{\varvec{i}} \) can be obtained as normal with mean \(\varvec{X}_{\varvec{i}} \varvec{\beta } \) and the covariance \(\varvec{Z}_{\varvec{i}} \varvec{DZ}_{\varvec{i}}^{\prime } +\varvec{R}_{\varvec{i}} \) \((\varvec{y}_{\varvec{i}} \sim N(\varvec{X}_{\varvec{i}} \varvec{\beta } , \varvec{{Z}}_{\varvec{i}} \varvec{DZ}_{\varvec{i}}^{\prime } +\varvec{R}_{\varvec{i}}))\).

The general form of the LMM is defined as in model (1) for a given subject i. This model definition is not the only way to define the model, there is an alternative specification of the LMM which is “stacking” the vectors of the model such as \(\varvec{y}_{\varvec{i}} \) or \(\varvec{u}_{\varvec{i}} \) for all subjects vertically. This specification is used in SAS, R, SPSS, S documentations; while HLM uses the hierarchical approach of Raudenbush and Bryk (2002) (West et al. 2007).

Comprehensive work on LMMs is found in Searle et al. (1992), Verbeke and Molenberghs (2000), McCulloch and Searle (2001) and Demidenko (2004), among others. Parameter estimations are described in these studies under the assumptions above.

3 Linear mixed models with multivariate Laplace distribution

3.1 Multivariate exponential power distribution to Laplace distribution and the mixture form

The exponential power family was introduced by Box and Tiao (1973) and it has been found a place in the Bayesian modelling for robustness context. The normal scale mixture property of EP distributions and its relationship with the class of stable distributions were discussed by West (1987). The multivariate EP distribution is defined as the generalization of multivariate normal distribution with an extra parameter \({\mathrm{K}} \) which governs the kurtosis, and this parameter indicates the difference between EP distribution and the normal distribution (Gómez-Villegas et al. 2011).

An n-dimensional random vector \(\varvec{X}=(\varvec{X}_{\varvec{1}} ,\ldots ,\varvec{X}_{\varvec{n}} )^{\prime }\) is said to have EP distribution (\(EP_n ( {\varvec{\mu },{\varvec{\Sigma }}, {\mathrm{K}}}))\) with parameters, \(\varvec{\mu } \in {\mathbb {R}}, {\varvec{\Sigma }}\) is a positive definite symmetric matrix and \({\mathrm{K}}\in (0, \infty )\), if its density function is as follow

$$\begin{aligned} f( {\varvec{x}; \varvec{\mu } , \varvec{\varSigma } , {\mathrm{K}}})= & {} d\left| \varvec{ \varSigma } \right| ^{-\frac{1}{2}}exp\left( {-\frac{1}{2}\big ((\varvec{x}-\varvec{\mu } )^{\prime }{\varvec{\Sigma }}^{-1}(\varvec{x}-\varvec{\mu } )\big )^{\mathrm{K}}}\right) ,\\ d= & {} \frac{n{\Gamma }(\frac{n}{2})}{\pi ^{\frac{n}{2}}{\Gamma }\big (1+\frac{n}{2{\mathrm{K}}}\big )2^{1+\frac{n}{2{\mathrm{K}}}}},\nonumber \end{aligned}$$
(2)

\(\mathrm{K}\) is the kurtosis parameter [i.e., see (Arslan 2010; Fang et al. 1990; Gómez-Sánchez-Manzano et al. 2008; Gómez et al. 1998)]. It is obvious that if \({\mathrm{K}}\)=1, it turns into the normal distribution.

EP distribution is written as a scale mixture of normal distributions if and only if \({\mathrm{K} }\in (0,1]\), and it is denoted as \({{\mathbf{X}}}\sim \text{ SMN }_\mathrm{n} ({\varvec{\upmu }},{\varvec{\Sigma }}, \text{ h }_{\mathrm{K}} )\) where the mixing distribution function \(\text{ h }_{\mathrm{K}} \) is the absolutely continuous distribution function with (Gómez-Sánchez-Manzano et al. 2008)

$$\begin{aligned} h_{K} ( \upsilon )=\frac{2^{1+\frac{n}{2}-\frac{n}{2{K}}}\varGamma \left( {1+\frac{n}{2}}\right) }{\varGamma \left( {1+\frac{n}{2{K}}}\right) }\upsilon ^{n-3}S_{K} \left( {\upsilon ^{-2};2^{1-\frac{1}{{K}}}}\right) , \quad \upsilon >0. \end{aligned}$$

\(\text{ S }_{\mathrm{K}} \) is referred to stable distribution which has the characteristic function for \(K\in (0,1)\) as (Samorodnitsky and Taqqu 1994)

$$\begin{aligned} \varphi ( t)=exp\left\{ {-\sigma ^K\left| t \right| ^Ke^{-i\frac{\pi }{2}Ksign(t)}} \right\} . \end{aligned}$$

Gómez-Sánchez-Manzano et al. (2008) use \(\sigma =2^{-\frac{1}{K}}\) and the Laplace transform of its distribution function becomes \(\mathcal{L}_F ( t)=exp\left\{ {-\frac{1}{2}t^K} \right\} =g_K (t)\).

As a special case of multivariate EP distribution; if \({\mathrm{K}}=\frac{1}{2}\), it is considered as the multivariate Laplace distribution (double exponential distribution) and the mixture form is denoted as \(\text{ SMN }_\mathrm{n} ({\varvec{\upmu }},{\varvec{\Sigma }},\text{ h }_{1/2} )\) with the following density of mixing function

$$\begin{aligned} h_{1/2} ( \upsilon )=\frac{{\Gamma }( {\frac{n}{2}})}{2^{\frac{n}{2}}{\Gamma }( n)}\upsilon ^{n-3}S_{\frac{1}{2}} \left( {\upsilon ^{-2};\frac{1}{2}}\right) , \end{aligned}$$

for y \(>\) 0, \(S_{\frac{1}{2}} ( {y;\sigma })=\frac{1}{2}\pi ^{-\frac{1}{2}}\sigma ^{\frac{1}{2}}y^{-\frac{3}{2}}\text{ exp }(-\frac{1}{4}\sigma y^{-1})\) is an inverted-gamma distribution \(IG(\frac{1}{2},\frac{\sigma }{4})\); so the mixing distribution becomes as (Gómez-Sánchez-Manzano et al. 2008)

$$\begin{aligned} h_{1/2} ( \upsilon )=\frac{1}{2^{\frac{3n+1}{2}}{\Gamma }( {\frac{n+1}{2}})}\upsilon ^n\exp \big ( {-\frac{1}{8}\upsilon ^2}\big )I_{( {0,\infty })} ( \upsilon ). \end{aligned}$$
(3)

Further, if \(\varvec{X}\) is a random vector with \(Laplace_n ( {\varvec{\mu } ,{\varvec{\Sigma }}})\), the expectation and the variance of \(\varvec{X}\) are \(E(\varvec{X})=\varvec{\mu } \) and \(Var(\varvec{X})=\frac{4{\Gamma }( {n+2})}{n{\Gamma }(n)}{\varvec{\Sigma }}\). Scale mixture of normal distribution property of Laplace distribution provides more modeling alternatives, since it creates longer tails than normal distribution (Arslan 2010).

3.2 Linear mixed models with multivariate Laplace distribution

The joint distribution of \(\varvec{y}_{\varvec{i}} \) and \(\varvec{u}_{\varvec{i}} \) in classical LMM is defined as follow

$$\begin{aligned} \left[ {{ \begin{array}{*{20}c} {\varvec{y}_{\varvec{i}} } \\ {\varvec{u}_{\varvec{i}} } \\ \end{array} }} \right] \sim N_{n_i +r} \left( {\left[ {{ \begin{array}{*{20}c} {\varvec{X}_{\varvec{i}} \varvec{\beta } } \\ 0 \\ \end{array} }} \right] ,\left[ {{ \begin{array}{*{20}c} {\varvec{Z}_{\varvec{i}} \varvec{DZ}_{\varvec{i}}^{\prime } +\varvec{R}_{\varvec{i}}} &{} {\varvec{Z}_{\varvec{i}} \varvec{D}} \\ {\varvec{DZ}_{\varvec{i}}^{\prime } } &{} \varvec{D} \\ \end{array} }} \right] }\right) , \quad i=1,\ldots ,n. \end{aligned}$$
(4)

We replace multivariate normal distribution in model (4) with multivariate Laplace distribution for both random effects and subject-specific errors (LLMM or l-LMM) by proceeding as in Lange et al. (1989) and Pinheiro et al. (2001) as follow

$$\begin{aligned} \left[ {{ \begin{array}{*{20}c} {\varvec{y}_{\varvec{i}} } \\ {\varvec{u}_{\varvec{i}} } \\ \end{array} }} \right] \sim Laplace_{{n_{i}} +r} \left( {\left[ {{\begin{array}{*{20}c} {\varvec{X}_{\varvec{i}} \varvec{\beta } } \\ 0 \\ \end{array} }} \right] ,\left[ {{ \begin{array}{*{20}c} {\varvec{Z}_{\varvec{i}} \varvec{DZ}_{\varvec{i}}^{\prime } +\varvec{R}_{\varvec{i}}} &{} {\varvec{Z}_{\varvec{i}} \varvec{D}} \\ {\varvec{DZ}_{\varvec{i}} ^{\prime }} &{} \varvec{D} \\ \end{array} }} \right] }\right) , \quad i=1,\ldots ,n. \end{aligned}$$
(5)

From this distribution, the marginal distribution of \(\varvec{y}_{\varvec{i}} \) is obtained as

$$\begin{aligned} \varvec{y}_{\varvec{i}} \sim Laplace_{n_{i}} ( {\varvec{X}_{\varvec{i}} \varvec{\beta } ,\varvec{Z}_{\varvec{i}} \varvec{DZ}_{\varvec{i}}^{\prime } +\varvec{R}_{\varvec{i}} }), \end{aligned}$$

(Arslan 2010; Gómez et al. 1998). According to the scale mixture property of Laplace distribution and Theorem 3.1 in Gómez-Sánchez-Manzano et al. (2008), the corresponding conditional distributions of \(\left[ {\varvec{y}_{\varvec{i}}^{\prime } ,\varvec{u}_{\varvec{i}}^{\prime } } \right] ^{\prime }\) are as follow (\(\varvec{V}_{\varvec{i}} =\varvec{Z}_{\varvec{i}} \varvec{DZ}_{\varvec{i}}^{\prime } +\varvec{R}_{\varvec{i}} )\)

$$\begin{aligned}&\left. {\left[ {{ \begin{array}{*{20}c} {\varvec{y}_{\varvec{i}} } \\ {\varvec{u}_{\varvec{i}} } \\ \end{array} }} \right] } \right| \tau _i \sim N_{n_i +r} \left( {\left[ {{\begin{array}{*{20}c} {\varvec{X}_{\varvec{i}} \varvec{\beta } } \\ 0 \\ \end{array} }} \right] ,\tau _i^2 \left[ {{ \begin{array}{*{20}c} {\varvec{V}_{\varvec{i}} } &{} {\varvec{Z}_{\varvec{i}} \varvec{D}} \\ {\varvec{DZ}_{\varvec{i}} ^{\prime }} &{} \varvec{D} \\ \end{array} }} \right] }\right) ,\nonumber \\&\tau _i \sim h_{1/2} ({\tau _i }). \end{aligned}$$
(6)

It follows from (6) that the hierarchical representations of the conditional distributions of \(\varvec{y}_{\varvec{i}} \) and \(\varvec{u}_{\varvec{i}} \) vectors are as follow

$$\begin{aligned}&\varvec{y}_{\varvec{i}} \vert \varvec{u}_{\varvec{i}} ,\tau _i \sim N( {\varvec{X}_{\varvec{i}} \varvec{\beta } +\varvec{Z}_{\varvec{i}} \varvec{u}_{\varvec{i}} ,\tau _i^2 \varvec{R}_i }), \quad i=1,\ldots ,n,\nonumber \\&\varvec{u}_{\varvec{i}} \vert \tau _i \sim N( {0, \tau _i^2 \varvec{D}}),\nonumber \\&\tau _i \sim h_{1/2} ( {\tau _i}). \end{aligned}$$
(7)

The maximum likelihood estimation of unknown parameters in this hierarchical representation of Laplace LMM leads to EM implementations. Different than classical LMM, there is an extra unknown term, \(\tau _i \) needs to be estimated from the data. The next section includes both parameter estimations and EM algorithm of (7).

4 EM algorithm

EM algorithm takes its name from the study of Dempster et al. (1977) and it is composed of two steps; the expectation step (E-step) and the maximization step (M-step). The conditional expectation of the complete data log likelihood is calculated for given parameter estimates and observed data is computed in E-step. M-step updates the parameter estimates by maximizing conditional expectation in the E-step. These two steps are iterated until the convergence and the final parameter is taken as MLE or a local maximizer. EM is used for a wide variety of situations such as incomplete data, random effects, mixtures, log linear models, latent class and latent variable situations (McLachlan and Krishnan 1997).

We illustrate a general scheme for EM for classical/Gaussian LMM and it has similar approach for Laplace LMM with extra CM-steps explained in the next section.

Consider model (7) and take \(\varvec{u}_{\varvec{i}} \) as “missing data” and the complete data is \(\left\{ {({\varvec{y}_{\varvec{i}} ,\varvec{u}_{\varvec{i}} }), \, i=1,\ldots ,n} \right\} \), where \(\left\{ {\varvec{y}_{\varvec{i}} ,i=1,\ldots ,n} \right\} \) is observed data. Let \(\varvec{\theta } =( {\varvec{\beta } ,\varvec{R},\varvec{D}})\) denote all parameters. The complete data likelihood for subject i is given by

$$\begin{aligned} {l_i}^{(c)} ( {\varvec{\theta } \vert \varvec{y}_{\varvec{i}} ,\varvec{u}_{\varvec{i}} })=ln f( {\varvec{y}_{\varvec{i}} \vert \varvec{u}_{\varvec{i}} ,\varvec{\beta },\varvec{R}})+ln f( {\varvec{u}_{\varvec{i}} \vert \varvec{D}}). \end{aligned}$$

Begin with a starting value \(\varvec{\theta } ^0\). At the k-th iteration, the conditional expectation is computed as following:

$$\begin{aligned} \mathrm{E}{\text{- }} \mathrm{Step}:\mathcal{Q}( {\varvec{\theta } \vert \varvec{\theta } ^k})= & {} E\left[ {\mathop \sum \limits _{i=1}^n l_i^{( c)} ( {\varvec{\theta } \vert \varvec{y}_{\varvec{i}} ,\varvec{u}_{\varvec{i}} })\vert \varvec{y}_{\varvec{i}} ,\varvec{\theta } ^{( k)}} \right] \\= & {} E\left[ {\mathop \sum \limits _{i=1}^n ln f( {\varvec{y}_{\varvec{i}} \vert \varvec{u}_{\varvec{i}} ,\varvec{\beta } ,\varvec{R}})+ln f( {\varvec{u}_{\varvec{i}} \vert \varvec{D}})\vert \varvec{y}_{\varvec{i}} ,\varvec{\theta } ^{(k)}} \right] . \end{aligned}$$

M-Step requires to maximize \(\mathcal{Q}( {\varvec{\theta } \vert \varvec{\theta } ^{\varvec{k}}})\) with respect to \({\varvec{\uptheta } }\) to acquire an updated estimate \(\varvec{\theta } ^{(\varvec{k}+\varvec{1})}\). At the k-th iteration of the EM algorithm, since \(\varvec{\theta } ^{(\varvec{k}+\varvec{1})}\) maximizes \(\mathcal{Q}( {\varvec{\theta } \vert \varvec{\theta } ^{\varvec{k}}})\):

$$\begin{aligned} \mathcal{Q}( {\varvec{\theta } ^{({\varvec{k}+\varvec{1}})}\vert \varvec{\theta } ^{\varvec{k}}}) \ge \mathcal{Q}( {\varvec{\theta } \vert \varvec{\theta } ^{\varvec{k}}}), \quad k=0,1,2,\ldots \end{aligned}$$

This property shows that EM is guaranteed to converge to a maximum (Wu 1983).

4.1 EM for Laplace LMM

This section includes the maximum likelihood estimation of unknown parameters of Laplace linear mixed model (5) with EM-type algorithm. The maximization process for log-likelihood of LMM leads to some non-linear equations; consequently, solutions could be too complex to be solved. Solving these equations are not solely enough for implementations; since we need to count for acquiring our parameters to be in parameters space (Searle et al. 1992). For the maximum likelihood estimations (MLE) of the parameters, we utilize the EM algorithm by using hierarchical model with both \(\tau _i \) and \(\varvec{u}_{\varvec{i}} \) are threated as missing. Since maximization (M) step of EM is computationally unattractive for LMM, expectation-conditional maximization (ECM) (Meng and Rubin 1993) is used in this study.The ECM algorithm, which is the extension of EM algorithm, implemented by conditioning on some function of the parameters under estimation and replaced M-steps with computationally easier CM-step. ECM has the same stable monotone convergence property of EM (McLachlan and Krishnan 1997).

Let \(\varvec{\theta } =\left[ {\varvec{\beta } ^{\prime },\varvec{D}^{\prime },\varvec{R}^{\prime }} \right] ^{\prime }\) denotes all parameters, \(\varvec{y}=\left[ {\varvec{y}_1^{\prime } ,\ldots ,\varvec{y}_n^{\prime } } \right] ^{\prime }\) is observed data \(\varvec{u}=\left[ {\varvec{u}_1^{\prime } ,\ldots ,\varvec{u}_n^{\prime } } \right] ^{\prime }\) and \(\varvec{\tau } =\left[ {\tau _1 ,\ldots ,\tau _n } \right] \) are treated as “missing data”, so the “complete data” are \(\left\{ {\varvec{y},\varvec{u},\varvec{\tau } } \right\} \). Because of the conditional structure of model (7), the joint density of complete data can be factored into the product of the conditional densities, so the complete data likelihood based on model (7) is given by

$$\begin{aligned} lnL(\varvec{\beta } ,\varvec{D},\varvec{R} {\vert }\varvec{y},\varvec{u},\varvec{\tau } )=lnL_1 ( {\varvec{\beta } ,\varvec{R}\vert \varvec{y},\varvec{u},\varvec{\tau } })+lnL_2 ( {\varvec{D}\vert \varvec{u},\varvec{\tau } })+constant. \end{aligned}$$

‘Constant’ represents the terms without any parameters to be estimated. E-step of EM algorithm requires conditional expectations of log-likelihood function acquired as below

$$\begin{aligned} \begin{array}{l} E\left[ {lnL(\varvec{\beta } ,\varvec{D},\varvec{R}{\vert }\varvec{y},\varvec{u},\varvec{\tau } )\vert \varvec{y},{\widehat{{\varvec{\theta }}}} } \right] = \\ E\left[ {lnL_1 ( {\varvec{\beta } ,\varvec{R}\vert \varvec{y},\varvec{u},\varvec{\tau } })\vert \varvec{y},{\widehat{{\varvec{\theta }}}} } \right] +E\left[ {lnL_2 ( {\varvec{D}\vert \varvec{u},\varvec{\tau } })\vert \varvec{y},{\widehat{{\varvec{\theta }}}} } \right] +constant \\ =-\frac{1}{2}\mathop \sum \limits _{i=1}^n \left\{ {( {\varvec{y}_{\varvec{i}} -\varvec{X}_{\varvec{i}} \varvec{\beta } -\varvec{Z}_{\varvec{i}} {\widehat{{\varvec{u}}}} _{\varvec{i}} })^{\prime }( {{\hat{{{\tau }}}} _i^2 \varvec{R}_{\varvec{i}} })^{-1}( {\varvec{y}_{\varvec{i}} -\varvec{X}_{\varvec{i}} \varvec{\beta } -\varvec{Z}_{\varvec{i}} {\widehat{{\varvec{u}}}} _{\varvec{i}} })+ln\left| {\varvec{R}_{\varvec{i}} } \right| } \right\} \\ \quad -\frac{1}{2}\left\{ {nln\left| \varvec{D} \right| +\mathop \sum \limits _{i=1}^n \varvec{\tau } _{\varvec{i}}^{-2} \varvec{u}_{\varvec{i}}^{\prime } \varvec{D}^{-1}\varvec{u}_{\varvec{i}} } \right\} +constant. \\ \end{array} \end{aligned}$$

Letting

$$\begin{aligned} {\widehat{\mathbf{u}}} _i= & {} E(\varvec{u}_{\varvec{i}} {\vert }\varvec{\theta } ={\widehat{{\varvec{\theta }}}} ,\varvec{y}),\\ {\widehat{{\varvec{\Omega }}}} _{\varvec{i}}= & {} cov(\varvec{u}_{\varvec{i}} {\vert }\varvec{\theta } ={\widehat{{\varvec{\theta }}}} ,\varvec{y}),\\ {\hat{{{\tau }}}} _i^2= & {} E( {\tau _i^2 \vert \varvec{\theta } ={\widehat{{\varvec{\theta }}}} ,\varvec{y}}),\\ {\hat{{{\tau }}}} _i^{-2}= & {} E( {\tau _i^{-2} \vert \varvec{\theta } ={\widehat{{\varvec{\theta }}}} ,\varvec{y}}), \end{aligned}$$
$$\begin{aligned} E(\varvec{u}_{{i}} \varvec{u}_{\varvec{i}}^{\prime } )=cov( {\varvec{u}_{\varvec{i}} \varvec{u}_{\varvec{i}}^{\prime } })+E( {\varvec{u}_{\varvec{i}} })E( {\varvec{u}_{\varvec{i}}^{\prime } })={\hat{{\varvec{\Omega }}}} _{\varvec{i}} +{\hat{{\varvec{u}}}}_{\varvec{i}} {\hat{{\varvec{u}}}} _{\varvec{i}}^{\prime }, \end{aligned}$$

we find following estimations

$$\begin{aligned}&{\hat{\mathbf{u}}} _{\varvec{i}} ={\hat{{\varvec{D}}}} \varvec{Z}_{\varvec{i}}^{\prime } {\hat{{\varvec{V}}}} ^{\varvec{-1}}( {\varvec{y}_{\varvec{i}} -\varvec{X}_{\varvec{i}} {\hat{{\varvec{\beta }}}} })={\hat{{\varvec{D}}}} \varvec{Z}_{\varvec{i}}^{\prime } (\varvec{Z}_{\varvec{i}} {\hat{{\varvec{D}}}} \varvec{Z}_{\varvec{i}}^{\prime } +{\hat{{\varvec{R}}}} _{\varvec{i}} )^{\varvec{-1}}( {\varvec{y}_{\varvec{i}} -\varvec{X}_{\varvec{i}} {\hat{{\varvec{\beta }}}} }) \\&\,\,\,\quad =( {{\hat{{\varvec{D}}}} ^{\varvec{-1}}+\varvec{Z}_{\varvec{i}}^{\prime } {\hat{{\varvec{R}}}} _{\varvec{I}}^{-1} \varvec{Z}_{\varvec{i}} })^{-1}\varvec{Z}_{\varvec{i}}^{\prime } {\hat{{\varvec{R}}}} _{\varvec{i}}^{\varvec{-1}} ( {\varvec{y}_{\varvec{i}} -\varvec{X}_{\varvec{i}} {\hat{{\varvec{\beta }}}} }), \\&{\hat{{\varvec{\Omega }}}} _{\varvec{i}} ={\hat{{{\tau }}}} _{\varvec{i}}^{2} {\hat{{\varvec{D}}}} -{\hat{{{\tau }}}} _{\varvec{i}}^{2} {\hat{{\varvec{D}}}} \varvec{Z}_{\varvec{i}} ^{\prime }( {{\hat{{{\tau }}}} _{\varvec{i}}^{2} {\hat{{\varvec{V}}}} _{\varvec{i}} })^{\varvec{-1}}\varvec{Z}_{\varvec{i}} {\hat{{\varvec{D}}}} {\hat{{\varvec{\tau }}}} _{\varvec{i}}^2 ={\hat{{\varvec{\tau }}}} _{\varvec{i}}^2 ( {{\hat{{\varvec{D}}}} -{\hat{{\varvec{D}}}} \varvec{Z}_{{\varvec{i}}} ^{\prime }{\hat{{\varvec{V}}}} _{\varvec{i}} ^{\varvec{-1}}\varvec{Z}_{\varvec{i}} {\hat{{\varvec{D}}}} }) \\&\qquad ={\hat{{{\tau }}}} _{\varvec{i}}^2 ( {{\hat{{\varvec{D}}}} -{\hat{{\varvec{D}}}} \varvec{Z}_{\varvec{i}} ^{\prime }( {\varvec{Z}_{\varvec{i}} {\hat{{\varvec{D}}}} \varvec{Z}_{\varvec{i}}^{\prime } +{\hat{{\varvec{R}}}} _{\varvec{i}} })^{-1}\varvec{Z}_{\varvec{i}} {\hat{{\varvec{D}}}} })={\hat{{{\tau }}}} _{\varvec{i}}^2 ( {{\hat{{\varvec{D}}}} ^{-1}+\varvec{Z}_{\varvec{i}}^{\prime } {\hat{{\varvec{R}}}} _{\varvec{i}}^{-1} \varvec{Z}_{\varvec{i}} })^{-1}. \end{aligned}$$

\({\hat{{\varvec{\beta }}}} , \quad {\hat{{\varvec{D}}}} \) and \({\hat{{\varvec{R}}}} _{\varvec{i}} \) are found by differentiating expected values of conditional log-likelihood functions with respect to parameters. Different from the Gaussian LMM (1), the Laplace LMM (7) requires \(\tau _i \) that is unobserved but imputed from the data for each subject. To find \({\hat{{{\tau }}}} _i^2 \) and \({\hat{{{\tau }}}} _i^{-2} \), the conditional distribution of \(\tau _i \) is required. We find it with the Bayesian approach, \(f( {\tau _i \vert \varvec{y}_{\varvec{i}} })=\frac{f( {\varvec{y}_{\varvec{i}} \vert \varvec{\tau } _{\varvec{i}} })f(\varvec{\tau } _{\varvec{i}} )}{f( {\varvec{y}_{\varvec{i}}})}\). After some algebra, the final equation is found as below

$$\begin{aligned} f( {\tau _i \vert \varvec{y}_{\varvec{i}} })= & {} \frac{{\Gamma }( {n+1})2^{\frac{n}{2}+1}}{n{\Gamma }( {\frac{n}{2}})}\tau _i^{-1} exp\left\{ -\frac{1}{2}( {\varvec{y}_{\varvec{i}} -\varvec{X}_{\varvec{i}} \varvec{\beta } })^{\prime }( {\tau _i^2 \varvec{V}_{\varvec{i}} })^{-1}( {\varvec{y}_{\varvec{i}} -\varvec{X}_{\varvec{i}} \varvec{\beta } }) \right. \\&\left. +\frac{1}{2}\big ( {( {\varvec{y}_{\varvec{i}} -\varvec{X}_{\varvec{i}} \varvec{\beta } })^{\prime }( {\varvec{V}_{\varvec{i}} })^{-1}( {\varvec{y}_{\varvec{i}} -\varvec{X}_{\varvec{i}} \varvec{\beta } })}\big )^{\frac{1}{2}} \right\} \times h_{1/2} ({\tau _i }), \end{aligned}$$

where \(h_{1/2} ( {\tau _i })\) is described in (3). Adapting this mixing function into the conditional distribution above leads to

$$\begin{aligned} f( {\tau _i \vert \varvec{y}_{\varvec{i}} })\!=\!\frac{{\Gamma }(n)}{{\Gamma }( {\frac{n}{2}}){\Gamma }( {\frac{n+1}{2}})}2^{\frac{1}{2}-n}\exp \Big ( {\frac{1}{2}C_i^{\frac{1}{2}} }\Big )\tau _i ^{n-1}exp\left\{ {-\frac{1}{2}\big ( {\tau _i^{-2} C_i +\frac{1}{4}\tau _i ^2}\big )} \right\} I_{( {0,\infty })} ( \upsilon ), \end{aligned}$$

where,

$$\begin{aligned}&C_i =( {\varvec{y}_{\varvec{i}} -\varvec{X}_{\varvec{i}} \varvec{\beta } })^{\prime }( {\varvec{V}_{\varvec{i}} })^{-1}( {\varvec{y}_{\varvec{i}} -{\varvec{X}}_{\varvec{i}} \varvec{\beta } }),\\&f( {\tau _i \vert \varvec{y}_{\varvec{i}} })\propto \tau _i ^{n-1}exp\left[ {-\frac{1}{2}\big ( {\tau _i^{-2} C_i +\frac{1}{4}\tau _i ^2}\big )} \right] . \end{aligned}$$

Redefining the function by letting \(\xi _i =\tau _i ^2\), \(\tau _i =\xi _i^{1/2} \), \(\frac{\partial \tau _i }{\partial \xi _i }=\frac{1}{2\xi _i^{1/2} }\) gives

$$\begin{aligned} f( {\xi _i \vert \varvec{y}_{\varvec{i}} })\propto \xi _i ^{\frac{n-1}{2}}exp\left[ {-\frac{1}{2}\big ( {\xi _i ^{-1}C_i +\frac{1}{4}\xi _i }\big )} \right] \frac{1}{2\xi _i ^{\frac{1}{2}}}=\frac{1}{2}\xi _i ^{\frac{n}{2}-1}exp\left[ {-\frac{1}{2}\big ( {\xi _i ^{-1}C_i \!+\!\frac{1}{4}\xi _i }\big )} \right] . \end{aligned}$$

The final distribution takes the form of generalized inverse Gaussian distribution. The moment of this distribution is as follow (Barndorff-Nielsen 1978; Barndorff-Nielsen and Halgreen 1977)

$$\begin{aligned} E( {\xi _i ^\alpha })=\Big ( {\frac{C_i }{1/4}}\Big )^{\alpha /2}\frac{M_{\frac{n}{2}+\alpha } \Big ( {\sqrt{C_i \frac{1}{4}} }\Big )}{M_{\frac{n}{2}} \Big ( {\sqrt{C_i \frac{1}{4}} }\Big )}, \end{aligned}$$

\(M_{(.)} \) is modified Bessel function of the third kind (Jorgensen 1982; Watson 1966). By using this property, the moments are as followings for \(\alpha =1 \text{ and } \alpha =-1\), respectively

$$\begin{aligned} E( {\xi _i })=\Big ( {\frac{C_i }{1/4}}\Big )^{1/2}\frac{M_{\frac{n}{2}+1} \Big ( {\sqrt{C_i \frac{1}{4}} }\Big )}{M_{\frac{n}{2}} \Big ( {\sqrt{C_i \frac{1}{4}} }\Big )},E( {\xi _i ^{-1}})=\Big ({\frac{C_i }{1/4}}\Big )^{-1/2}\frac{M_{\frac{n}{2}-1} \Big ( {\sqrt{C_i \frac{1}{4}} }\Big )}{M_{\frac{n}{2}} \Big ( {\sqrt{C_i \frac{1}{4}} }\Big )}. \end{aligned}$$

Having starting values of the parameters \(\varvec{\theta } ^{\varvec{0}}=( {\varvec{\beta } ^{\varvec{0}},\varvec{D}^{\varvec{0}},\varvec{R}^{\varvec{0}}})\); an iterative algorithm in which current values of the unknown parameters are updated in the following steps:

E-Step For a given \(={\hat{{\varvec{\theta }}}} \), calculate \({\hat{{\varvec{u}}}}_{\varvec{i}} ,{\hat{{{\tau }}}}_i^{-2} ,{\hat{{{\tau }}}} _i^2 ,and\, {\hat{{\varvec{\Omega }}}}_i \quad i=1,\ldots ,n\).

$$\begin{aligned} {\hat{\mathbf{u}}} _{\varvec{i}} ^{({\varvec{m}})}= & {} \Big ( {{\hat{{\varvec{D}}}} ^{-\varvec{1}(\varvec{m})}+\varvec{Z}_{\varvec{i}}^{\prime } {\hat{{\varvec{R}}}}_{\varvec{\dot{I}}}^{\varvec{-1}}{\varvec{(m)}} \varvec{Z}_{\varvec{i}} }\Big )^{\varvec{-1}}\varvec{Z}_{\varvec{i}}^{\prime } {\hat{{\varvec{R}}}} _{\varvec{i}}^{\varvec{-1}}{(\varvec{m})} \Big ( {\varvec{y}_{\varvec{i}} -\varvec{X}_{\varvec{i}} {\hat{{\varvec{\beta }}}} ^{(\varvec{m})}}\Big ),\\ {\hat{{\varvec{\Omega }}}} _{\varvec{i}} ^{(\varvec{m})}= & {} {\hat{{{\tau }}}} _i^{2(m)} \Big ({\hat{{\varvec{D}}}} ^{-1(\varvec{m})}+\varvec{Z}_{\varvec{i}}^{\prime } {\hat{{\varvec{R}}}} _{\varvec{i}}^{(\varvec{-1m})} \varvec{Z}_{\varvec{i}} \Big )^{\varvec{-1}},\\ {\hat{{\varvec{\tau }}}} _i^{2(m)}= & {} \Big ( {\frac{{\hat{{{C}}}} _i }{1/4}}\Big )^{1/2}\frac{M_{\frac{n}{2}+1} \Big ( {\sqrt{{\hat{{\varvec{C}}}} _i \frac{1}{4}} }\Big )}{M_{\frac{n}{2}} \Big ( {\sqrt{{\hat{{{C}}}} _i \frac{1}{4}} }\Big )},\\ {\hat{{\varvec{\tau }}}} _i^{-2(m)}= & {} \Big ( {\frac{{\hat{{\varvec{C}}}} _i }{1/4}}\Big )^{-1/2}\frac{M_{\frac{n}{2}-1} \Big ( {\sqrt{{\hat{{\varvec{C}}}} _i \frac{1}{4}} }\Big )}{M_{\frac{n}{2}} \Big ( {\sqrt{{\hat{{\varvec{C}}}} _i \frac{1}{4}} }\Big )}. \end{aligned}$$

CM-Step 1 Fix \(\varvec{R}_{\varvec{i}} ={\hat{{\varvec{R}}}} _{\varvec{i}} \) and update \({\hat{{\varvec{\beta }}}} \) for \(i=1,\ldots ,n\) by maximizing \(E\left[ {L_1 ( {\varvec{\beta } ,{\hat{{\varvec{R}}}} \vert \varvec{y},\varvec{u},\varvec{\tau } }){\vert }\varvec{y},{\hat{{\varvec{\theta }}}} } \right] \) over \(\varvec{\upbeta } \).

$$\begin{aligned} {\hat{{\varvec{\beta }}}} ^{({\varvec{m+1}})}=\left( {\mathop \sum \limits _{i=1}^n {\hat{{{\tau }}}} _i^{-2(m)} \varvec{X}_i^{\prime } {\hat{{\varvec{R}}}} _{\varvec{i}}^{\varvec{-1}(\varvec{m})} \varvec{X}_{\varvec{i}} }\right) ^{-1}\mathop \sum \limits _{i=1}^n {\hat{{{\tau }}}} _i^{-2(m)} \varvec{X}_{\varvec{i}}^{\prime } {\hat{{\varvec{R}}}} _{\varvec{i}}^{\varvec{-1}(\varvec{m})} ( {\varvec{y}_{\varvec{i}} -\varvec{Z}_{\varvec{i}} {\hat{{\varvec{u}}}} _{\varvec{i}} ^{(\varvec{m})}}). \end{aligned}$$

CM-Step 2 Fix \(\varvec{\beta } ={\hat{{\varvec{\beta }}}} \) and update \({\hat{{\varvec{R}}}} _{\varvec{i}} \) for \(i=1,\ldots ,n\) by maximizing \(E\left[ {L_1 ( {\varvec{R},{\hat{{\varvec{\beta }}}} \vert \varvec{y},\varvec{u},\varvec{\tau } }){\vert }\varvec{y},{\hat{{\varvec{\theta }}}} } \right] \) over \(\varvec{R}_{\varvec{i}} \).

CM-Step 3 Update \({\hat{{\varvec{D}}}} \) by maximizing \(E\left[ {L_2 ( {\varvec{D}\vert \varvec{u},{\tau } }){\vert }\varvec{y},{\hat{{\varvec{u}}}}} \right] \) over \(\varvec{D}\).

$$\begin{aligned} {\hat{{\varvec{D}}}} ^{(\varvec{m+1})}=\frac{1}{n}\mathop \sum \limits _{i=1}^n {\hat{{\varvec{\tau }}}} _i^{-2(m)} \big ( {{\hat{{\varvec{\Omega }}}} _{\varvec{i}} ^{(\varvec{m})}+{\hat{{\varvec{u}}}} _{\varvec{i}} ^{(\varvec{m})}{\hat{{\varvec{u}}}} _{\varvec{i}}^{'(\varvec{m})} }\big ). \end{aligned}$$

Repeating the cycles creates sequences of related parameters.

5 Simulation studies

We conducted a simulation study similar to Pinheiro et al. (2001) and generated the data from the mixture of normals. The “rmnorm” function in mvtnorm library in R is used to generate the data after the model definition. In addition to their study, we added an extra scenario (2nd one) with Laplace distribution (8).

Let us define a model as below:

$$\begin{aligned} \varvec{y}_{i} =\varvec{X}( {\varvec{\beta } +\varvec{u}_{\varvec{i}} })+\varvec{e}_{\varvec{ij}} , \quad i=1,\ldots ,27, \quad j=1,\ldots ,4,\varvec{X}=\left[ {{ \begin{array}{*{20}c} 1 &{}\quad 8 \\ 1 &{}\quad {10} \\ 1 &{}\quad {12} \\ 1 &{}\quad {14} \\ \end{array} }} \right] . \end{aligned}$$

First scenario

$$\begin{aligned}&\varvec{u}_{\varvec{i}} \sim ind( {1-p_b })\mathcal{N}_2 ( {0,\varvec{D}})+p_b f\mathcal{N}_2 ( {0,\varvec{D}}),\\&\varvec{e}_{\varvec{ij}} \sim ind( {1-p_e })\mathcal{N}_4 ( {\varvec{0},\varvec{R}})+p_e f\mathcal{N}_4 ( {0,\varvec{R}}),\qquad \qquad i=1,\ldots ,27, \quad j\!=\!1,\ldots ,4. \end{aligned}$$

Second scenario

$$\begin{aligned}&\varvec{u}_{\varvec{i}} \sim ind( {1-p_b })Laplace_2 ( {0,\varvec{D}})+p_b fLaplace_2 ( {0,\varvec{D}}),\nonumber \\&\varvec{e}_{\varvec{ij}} \sim ind( {1-p_e })Laplace_4 ( {\varvec{0,\varvec{R}}})+p_e fLaplace_4 ( {0,\varvec{R}}),\nonumber \\&i=1,\ldots ,27,\quad j=1,\ldots ,4. \end{aligned}$$
(8)

\(p_b \) and \(p_e \) denotes the expected percentage of b- and e-outliers. f denotes contamination factor. \(p_b \) and \(p_e \) are taken 0, 0.05, 0.10 values and f is taken 0, 1, 2 values for each replicates. \(Var( {\varvec{u}_{\varvec{i}} })\) and \(Var( {\varvec{e}_{\varvec{ij}} })\) is the natural extension of (8)

$$\begin{aligned} E( {\varvec{y}_{\varvec{i}} })= & {} \varvec{X}\varvec{\beta } ,\\ Var(\varvec{y}_{{i}} )= & {} \varvec{X}Var( {\varvec{u}_{\varvec{i}} })\varvec{X}^{\prime }+Var( {\varvec{e}_{\varvec{ij}} }),\\ Var( {\varvec{u}_{\varvec{i}} })= & {} ( {1-p_b })\varvec{D}+p_b f^{2}\varvec{D}=\left[ {1+(f^2-1)p_b } \right] \varvec{D},\\ Var( {\varvec{e}_{\varvec{ij}} })= & {} ( {1-p_e })\varvec{R}+p_e f^{2}\varvec{R}=\left[ {1+(f^2-1)p_e } \right] \varvec{R}. \end{aligned}$$

As a first step, we generated \(\varvec{y}_{\varvec{i}} \)s depending on the parameters above. Four replicates for 27 subjects with 100 Monte Carlo replicates for each scenario are generated. Then, we obtain parameter estimations of our proposed model (7) and also parameter estimations of classical LMM (1). The proposed model is implemented by generating new functions in R. For classical LMM, the lmer function in ‘nlme’ package is used in R. See the target values (starting values) below

$$\begin{aligned} \left[ {{\begin{array}{*{20}c} {\beta _0 } \\ {\beta _1 } \\ \end{array} }} \right] =\left[ {{\begin{array}{*{20}c} {17} \\ {0.8} \\ \end{array} }} \right] , \quad \varvec{D}=\left[ {{\begin{array}{*{20}c} 4 &{}\quad 0 \\ 0 &{}\quad {0.0225} \\ \end{array} }} \right] , \quad \varvec{R}=\left[ {{\begin{array}{*{20}c} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ \end{array} }} \right] . \end{aligned}$$

The parameter comparisons are directly implemented for \(\beta _0 \) and \(\beta _1 \). On the other hand, we need to do the transformation for \(\varvec{D}\) comparisons defined as

$$\begin{aligned} \varvec{D}_{Laplace} =\frac{2^2{\Gamma }( 4)}{2{\Gamma }( 2)}\varvec{\varSigma } =( {12})\varvec{D}. \end{aligned}$$

The graphs below (Table 1) show the distributions of \(\left| {{\hat{{\varvec{\theta }}}} -\theta _0 } \right| \) for each parameter. Black lines show the differences between our proposed model estimations and starting values, purple dashed lines show the differences between lmer function estimations and starting values in all graphs.

Table 1 The figures of first scenario (on the left) and second scenario (on the right) simulations
Full size table

Because of the space limitations, we preferred to display two extreme combinations of f, \(p_b \) and \(p_e \). The first one is for \(f = p_b = p_e = 0\) which indicates the non-contamination factor without b- and e-outliers. The second one is \(f = 2, p_b = 0.10, p_e = 0.10 \) located on the second part of the Table 1. We acquired similar results for Laplace LMM and classical LMM approaches, especially for the first scenario, as it is seen on the left side of the Table 1. The differences of parameter estimations from the target values (starting values) are getting higher for the second scenario which are seen on the right side of the Table 1. We observe more gaps in the differences for the second combination with 10 % expected b- and e-outliers and also contamination factor, than the first one, especially for variance components of D and R. For the data sampled from a distribution shaped more like Laplace distribution, our model outperforms the classical LMM. AIC values comparisons of two models for both scenarios are located at the final section.

6 Orthodont data

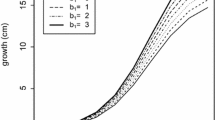
Orthodont data is firstly reported by Potthoff and Roy (1964) and named as Orthodont Study/Data found in nlme library in R. The data represents the distance (in millimeters) between the pituitary and the pterygomaxillary (we call it ‘distance’ for the rest of the study) measured at 8, 10, 12 and 14 years of each girl and boy. The graph below shows age versus distance for each subject. We mainly observe a linear trend over time in addition to some within and between variations (Fig. 1).

Fig. 1
figure 1

Age versus distance for each subject

Full size image
Fig. 2
figure 2

Fitted parameters with confidence intervals for each subject on the left. Fitted regression lines for each subject with age versus distance on the right

Full size image

To better understand these variations, we conduct a single linear regression for each subject and acquire intercept and slope with centered age variable versus distance with lmList function in R. The following graphs (Fig. 2) are related to these regression models.

The figure on the left depicts the confidence intervals of intercepts and slopes with standardized data obtained with a single regression for each subject (Fig. 2). The regressions lines for each subject with age versus distance values are located on the right figure (Fig. 2). Both graphs give us a clue to fit the model on behalf of the one with random effects. The variations among confidence intervals and also regression lines are observed in both graphs. They also reveal the potential outliers of the data. For example, the slope for M13 is larger than others which may be indicator of being a b-outlier. Two observations of M09 may be an e-outlier because of the more variations around the regression line. We observe the linear trend on the distance with different ratios. It is also obvious that the first measurements for distances are different for each subject. These findings indicate random intercept and potentially random slope for the data. Using random terms in addition to fixed parameters most probably makes the model more consistent and persistent. Detailed investigations and related R codes for Orthodont data can be found in Pinheiro and Bates (2000).

Both classical LMM and our proposed model with Laplace distributed error and random terms are applied for this data. The related parameter estimations are located at Table 2 (the gender effect is omitted for the ease of the computation):

We observe similar behavior from both models. This is actually expected since the behavior of ‘Orthodont’ data is close to normality. However, we observe the superiority of Laplace LMM over the normal LMM when we have atypical observations in the data in simulation study. Additionally, there is a gap between \(\sigma ^2\) obtained from lmer and our base-code. It is because of the fact that lmer function takes \(\varvec{R}\) matrix as \(\sigma ^2I_{n_i } \), as a consequence, the output includes single value. Our base code gives an estimated \(\varvec{R}\) matrix, which has the same dimensional with target value. We use the mode of the single value decomposition of \(\varvec{R}\) matrix as \(\sigma ^2\). The figure below shows the fitted values from our model versus classical LMM for each subject (Fig. 3).

Table 2 Parameter estimation results from LMM versus Laplace LMM
Full size table
Fig. 3
figure 3

Fitted values from proposed method versus classical LMM

Full size image

7 Conclusion and discussion

In this study, we aimed to enhance LMMs with different distributions than normal distribution. As a first step, we used Laplace-normal hierarchical structure and implemented corresponding mathematical inferences. To the extend of our knowledge, it is the first attempt in literature using Laplace distribution in LMMs with both random effects and error terms are assumed to follow Laplace distributions. It gives us the opportunity to use a robust distribution with less parameter than t-distribution (e.g., Pinheiro et al. 2001; Lin 2008) as an alternative to normal distribution.

Laplace LMM allows to use hierarchical structure and to define the conditional distributions of response and error/random terms. After defining these conditional distributions given the scalar with a mixing distribution (7), the conditional distribution of that scalar is found for estimation process of parameters. The originality of this paper also comes from the definition of this conditional distribution of the scalar (\(\tau _i )\), since we come up with the generalized inverse Gaussian (GIG) distribution after some algebra and defined the conditional distribution of this scalar. Estimation process and EM algorithm is finalized using the properties of GIG distribution.

Simulation studies are implemented with two different scenarios; the first one is generated from mixtures of normal distributions, while the second scenario is generated from mixtures of Laplace distributions with/without contamination factor. We apply these inferences with orthodont data and acquired similar predictions with classical LMM. The parameter estimations from the proposed method are close to classical LMM estimations, since the behavior of this data is very likely normal.

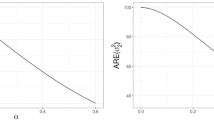
See the AIC values of LMM (purple-dashed line) and Laplace LMM (black straight line) for the second scenario (samples are generated from mixtures of Laplace distribution) at Fig. 4. The one on the left is for \(f=0, p_b =0, p_e =0\); while the one on the right is for \(f=2, p_b =0.10, p_e =0.10. \)For each model, AICs for Laplace LMM is smaller than AICs for LMM. And also, the gap between AIC values is getting bigger for the case with contamination factor and higher expected values for b- and e- outliers (Fig. 4).

Fig. 4
figure 4

AIC values for LMM (purple-dashed line) and for Laplace LMM (black straight line)

Full size image

For the future work, we plan to use skew Laplace distribution for LMM as an alternative to skew-normal (Arellano-Valle et al. 2005) and skew-t distributions (Choudhary et al. 2014; Lachos et al. 2009). We also, want to enhance and redefine our base R-code in R-package format and add additional properties such as hypothesis tests for parameters.