Effort comparisons for a class of four-player tournaments

Abstract

We propose a novel tournament design that incorporates some properties of a round-robin tournament, a Swiss tournament, and a race. The new design includes an all-play-all structure with endogenous scheduling and a winning threshold. Considering a standard round-robin tournament as a baseline model, we first characterize the equilibrium strategies in round-robin tournaments with exogenous and endogenous schedules. Afterward, following an equilibrium analysis of the new tournament design, we compare thirty-six tournament structures inherent in our model with round-robin tournaments on the basis of expected equilibrium effort per battle. We show that a round-robin tournament with an endogenous schedule outperforms all the other tournament structures considered here. We further note that if expected total equilibrium effort is used as a comparison criterion instead, then the new tournament design has a potential to improve upon round-robin tournaments.

1 Introduction

A tournament is a type of multi-battle contest game, which is commonly used in sports, labor markets, politics, and so on (see Lazear and Rosen 1981; Rosen 1986; Prendergast 1999; Szymanski 2003; Harbaugh and Klumpp 2005). Two well-known examples are round-robin tournaments and Swiss tournaments. In a round-robin tournament, players are pairwise matched in each round to compete in two-player component battles. It is an all-play-all tournament in that each player competes with all other players in turn. The schedule (i.e., who is matched with whom in which round) is exogenously given and common knowledge among all players. In a Swiss tournament, as in a round-robin tournament, players are pairwise matched in each round to compete in two-player component battles. However, a player does not necessarily compete with all other players, but competes with a selection of them, which is determined based on their performances in previous rounds. The latter property can be referred to as endogenous scheduling. Finally, although its structure is quite different from the tournament types mentioned above, a property of another well-known multi-battle contest is worth noting here. In a race, multiple players compete in a component battle in each round and a player who reaches a certain number of battle victories wins the race (i.e., victory threshold) (see Klumpp and Polborn 2006; Konrad and Kovenock 2009; Doğan et al. 2018).

In this paper we propose a novel tournament design with four symmetric players, which incorporates some properties of a round-robin tournament, a Swiss tournament, and a race. In each round, players are pairwise matched to compete in two-player component battles. The two battles in the same round take place at the same time. The winner of each battle is determined by a Tullock contest success function. A battle cannot end in a draw. A player competes against each of the other players, and in the first-three rounds, no player competes against the same opponent twice (similar to a round-robin tournament). Each player aims to win a total of three component battles, before another player achieves the same (similar to a race). Moreover, we implement endogenous scheduling, which means that the order of games depends on the outcomes of the earlier component battles (similar to a Swiss tournament). With this assumption, considering all possibilities for second round and fourth round match-ups, we obtain 36 different tournament structures.¹

Our tournament model is inspired by the following observations. In round-robin tournaments, the tournament champions are relatively more successful than the losing players. However, this does not necessarily mean that the champions are sufficiently successful in absolute terms. For instance, in a four-player tournament, three players can share the trophy by collecting two battle victories each. The contest designer may not be satisfied with such a result, believing that a player who could not win a certain number of battles does not deserve to be a champion. In order to make sure that a champion is also successful in absolute terms, the designer may choose to introduce a threshold number of battle victories, as in a model of race.

Our model can be thought of as an alternative to a round-robin tournament in the sense that it implements modifications to a standard round-robin tournament in two dimensions: (i) endogenous scheduling and (ii) additional tie-braking games.² We structure our paper around this observation. We start with the equilibrium analyses of round-robin tournaments with exogenously-given and endogenously-determined schedules. Afterward, we formally introduce the alternative tournament model, analyze its equilibria for all possible versions, and compare all these tournament structures on the basis of expected equilibrium effort per battle.

The comparison analysis requires the calculation of expected total equilibrium effort and expected number of battles.³ Refraining from going into the technical details, here we provide a brief intuition for the versions with the maximum expected total equilibrium effort. In the second round, a winner of the first round competes against the non-played loser of the first round. Normally, this would have resulted in a discouragement effect for the latter side, but then the fourth round match-ups are optimally selected such that if the player who lost in the first round wins in the second round, she will be incentivized to exert even more effort in the third round. Furthermore, independent of the outcomes of the second round battles, there will always be at least two players who are very motivated to exert high efforts in the third round, and all players would do that in case each player collects one battle victory in the first two rounds. Due to similar incentives, it turns out that many versions of our alternative tournament model yield relatively higher expected total equilibrium efforts compared to round-robin tournaments. However, this comes with a cost. Unlike any version of a round-robin tournament with four players that always ends in three rounds, any version of the alternative tournament model has a potential to proceed to the fourth round. Accordingly, expected number of battles turns out to be above six for each version of the alternative tournament model, and the comparison results depend on whether the increase in expected total equilibrium effort is enough to compensate for the increase in expected number of battles. Our main result shows that when expected equilibrium effort per battle is used as a comparison criterion, a round-robin tournament with an endogenous schedule outperforms all the other tournament structures considered in this paper.

Now, we relate the research carried out in this paper to the existing literature. Round-robin tournaments are extensively studied in the operations research literature (see Fleurent and Ferland 1993; Russel and Leung 1994; Nemhauser and Trick 1998; Henz et al. 2004; Rasmussen and Trick 2008 among others). Yet, those studies mostly assume non-strategic players, and thus they ignore the effects of players’ strategic effort choices on the tournament outcome. On the other hand, possibly due to the complexity of the respective equilibrium analysis (see Krumer et al. 2017b, pg. 634), there are only a few papers in the game theory literature that contribute a new perspective to the discussion by considering strategic players.

Among those papers, Krumer et al. (2017b) analyze a three-player round-robin tournament with one strong player and two equally-weak players. They report that in order to maximize expected total equilibrium effort, the designer should use a round-robin tournament rather than a one-shot contest if the asymmetry between the strong player and the weak players is sufficiently high. Krumer et al. (2017a) examine round-robin tournaments with three or four symmetric players. In case of four players, they assume that two battles in a round are scheduled one after the other. Using an all-pay contest success function, they show that a player who competes in the first game of each of the first two rounds ends up with a higher equilibrium winning probability. Later, utilizing a similar model, Sahm (2019) investigates fairness when the winner of each battle is determined by a Tullock contest success function and shows that the discrimination is weaker in Tullock contests compared to all-pay contests. Following this result, the author also analyzes endogenous scheduling in a three-player round-robin tournament. Krumer et al. (2020) study an optimal tournament design problem for a round-robin tournament with three symmetric players and either one prize or two prizes. They find that the designer should allocate only one prize if she aims to maximize expected total equilibrium effort. Finally, Laica et al. (2021) examine round-robin tournaments with three or more players and under a more generalized contest success function, showing that multiple prizes can maximize expected total equilibrium effort in three-player tournaments if the discriminatory power of the success function is sufficiently high.⁴

The paper is organized as follows. In Sect. 2, we provide equilibrium analyses of four-player round-robin tournaments with exogenous and endogenous schedules. In Sect. 3, we formulate a new tournament design. Section 4 presents our results that compare all these tournament structures. Sect. 5 concludes.

2 A round-robin tournament

Following Dagaev and Zubanov (2017), we define a round-robin tournament by $\Gamma ^{RR} = \left( N, \left( M_t \right) , P(\cdot ), V\right)$, where $N = \{1, \ldots , n\}$ is the set of players, $\left( M_t \right)$ consists of all pairwise matching of players representing a total of $\frac{n (n-1)}{2}$ component battles, $P(\cdot )$ denotes the contest success function, and V is the prize collected by the tournament champion.

To elaborate, consider four symmetric players in $N = \{1,2,3,4\}$ competing in a round-robin tournament. The procedure is as follows. In each round, players are pairwise matched. For each pair of players, there is a component battle in which the players choose how much effort to exert, a Tullock contest success function determines who wins the battle, and the winning player collects one point from this round. For example, assuming that players $i, j \in N$ are matched in a given round, player i wins the battle with a probability of

$$\begin{aligned} \frac{e_i}{e_i + e_j}, \end{aligned}$$

where $e_{i}, e_j \in [0, \infty )$ denote the respective efforts exerted. If both players exert zero effort, then a tie-breaker rule applies: the player with more battle victories wins with a probability of 1,⁵ but if both players have the same number of battle victories, then each player would have a winning probability of 1/2. The two battles in the same round take place at the same time. We also assume that the marginal cost of effort is one for every player and in each round.

A player competes against each of the other players and no player competes against the same opponent twice. The tournament always ends in three rounds. At the end, whichever player has more battle victories becomes the tournament champion and collects a winning prize of $V > 0$. If there are multiple such players, they become co-champions and share the winning prize equally.⁶

To illustrate, in a component battle between players 1 and 2 in any given round, player 1 aims to maximize

$$\begin{aligned} \frac{e_3}{e_3 + e_4} \left( \frac{e_1}{e_1 + e_2} W_{1}^3 + \frac{e_2}{e_1 + e_2} L_{1}^3 \right) + \frac{e_4}{e_3 + e_4} \left( \frac{e_1}{e_1 + e_2} W_{1}^4 + \frac{e_2}{e_1 + e_2} L_{1}^4\right) - e_1 , \end{aligned}$$

where $W_1^j$ is the continuation payoff for player 1 in case players 1 and $j \in \{3,4\}$ win their battles this round, and $L_1^j$ is the same in case players 2 and $j \in \{3,4\}$ win their battles this round.

The standard round-robin tournament as studied in the literature considers an exogenously-given schedule. This means that who will be matched with whom in each round is known before the tournament starts. A different specification may consider a tournament with an endogenously-determined schedule: depending on the results of the first round battles, it is possible for player $i \in N$ to compete against either of the other two players in the second round. Notice that once the second round battles are set, there is only one possible match-up for the third round battles. In this specification, there are two versions to be considered: (a) winners of the first round compete against each other, or (b) a winner of the first round competes with the non-played loser of the first round.⁷

Fig. 1

Round-robin tournaments with an endogenous schedule

Before proceeding further, we introduce the following notation. A node is denoted by a quadruple (a, b, c, d) where each entry represents the total number of battle victories achieved by the respective player before the start of the given round. Though, when we refer to a specific node (a, b, c, d), it does not necessarily mean that player 1 has a battle victories, player 2 has b battle victories, and so on. Instead, such a node represents all cases in which one player has a battle victories, another player has b battle victories, and so on. That is to say, we consider anonymity among players when reporting our results.

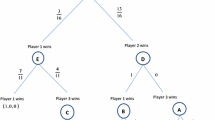
Figure 1 illustrates which nodes are followed in either version of a round-robin tournament with an endogenous schedule. It is worth noting that the game starts on the left, ends on the right, and each movement from one node to another is due to the outcomes of two component battles that simultaneously take place in the respective round. Furthermore, a round-robin tournament with an exogenous schedule can take either of the two forms, i.e., Fig. 1a or b, depending on the outcomes of the first round battles.

Below we report the unique subgame perfect Nash equilibrium (SPNE) in each version with an endogenously-determined schedule. As it will be revealed later, this result makes it easier to analyze the unique SPNE in the standard round-robin tournament with an exogenously-given schedule.

Proposition 1

There exists a unique SPNE in either version of a round-robin tournament with an endogenously-determined schedule. The expected total effort that will be exerted in equilibrium is 0.7407 V if the winners of the first round compete against each other in the second round and 0.7585 V if each winner of the first round competes with the non-played loser of the first round in the second round.

Proof

We analyze SPNE via backward induction.⁸

$\blacklozenge$ First, we consider the version in which the winners of the first round compete against each other in the second round, which is illustrated in Fig. 1.

Round 3: Consider node (2, 1, 1, 0). Without loss of generality, assume that player 1 has two battle victories, players 2 and 3 have one battle victory each, so that player 4 could not win any battle in the first two rounds.

For a subcase, assume that player 1 competes against player 4 in the third round. The result is trivial: since player 4 is totally discouraged, she exerts zero effort. Thus, player 1 wins this battle for sure even when she exerts zero effort herself (due to the tie-breaking assumption). As a result, player 1 becomes a champion with an expected payoff of V. Anticipating the outcome of that battle, and knowing that there is no possibility that they will become a champion, players 2 and 3 exert zero effort in their own component battle.

For another subcase, assume that player 3 competes against player 4 in the third round. The result is again trivial: since player 4 is totally discouraged, she exerts zero effort. Thus, player 3 wins this battle for sure even when she exerts zero effort herself (due to the tie-breaking assumption). As a result, player 3 becomes one of the three co-champions in case player 2 wins against player 1 in their own battle. Anticipating this outcome, player 1 maximizes

$$\begin{aligned} \frac{e_1}{e_1 + e_2} V + \frac{e_2}{e_1 + e_2} \frac{V}{3} - e_1, \end{aligned}$$

whereas player 2 maximizes

$$\begin{aligned} \frac{e_2}{e_1 + e_2} \frac{V}{3} - e_2. \end{aligned}$$

We find that $e_1 = 4V/27$ and $e_2 = 2V/27$, which yields an expected payoff of 17V/27 to player 1 and an expected payoff of V/27 to player 2. Furthermore, player 3 has an expected payoff of 3V/27.

Round 2: Consider node (1, 1, 0, 0). Without loss of generality, assume that players 1 and 2 have one battle victory each, so that players 3 and 4 could not win in the first round. In the current version, players 1 and 2 compete in a component battle.

Assuming that player 1 played against player 3 in the first round, player 1 maximizes

$$\begin{aligned} \frac{e_3}{e_3 + e_4} \left( \frac{e_1}{e_1 + e_2} V + \frac{e_2}{e_1 + e_2} \frac{3V}{27} \right) + \frac{e_4}{e_3 + e_4} \frac{e_1}{e_1 + e_2} \frac{17V}{27} - e_1, \end{aligned}$$

in this round. Player 2’s maximization problem can be written symmetrically. Furthermore, player 3 maximizes

$$\begin{aligned} \frac{e_2}{e_1 + e_2} \frac{e_3}{e_3 + e_4} \frac{V}{27} - e_3, \end{aligned}$$

in this round. Player 4’s maximization problem can be written symmetrically. Taking the first-order conditions and solving the respective system of equations, we find $e_1 = e_2 = 41V/216 \approx 0.1898V$ and $e_3 = e_4 = V/216 \approx 0.0046V$. This yields an expected payoff of $53V/216 \approx 0.2454V$ to players 1 and 2 and an expected payoff of $V/216 \approx 0.0046V$ to players 3 and 4.

Round 1: Consider node (0, 0, 0, 0). Each player can anticipate that her continuation payoff would be 0.2454V if she wins now and 0.0046V if she loses now. One can find that $e_i \approx 0.0602V$ for each player $i \in N$ in the first round. This completes the equilibrium analysis for the current version.

Given these results, the expected total effort that will be exerted in equilibrium is

$$\begin{aligned} (4 \times 0.0602V) + (2 \times 0.1898V)+ (2 \times 0.0046V) + \frac{1}{4} \left( 2 \times \frac{6V}{27}\right) = 0.7407V . \end{aligned}$$

$\blacklozenge$ Second, we consider the version in which each winner of the first round competes with the non-played loser of the first round in the second round, which is illustrated in Fig. 1a.

Round 3: There are three possible nodes to analyze.

Consider node (2, 2, 0, 0). Without loss of generality, assume that players 1 and 2 have two battle victories each, so that players 3 and 4 could not win any battle in the first two rounds. Now, the laggards compete against each other. Since there is no possibility that they will become a champion, both players exert zero effort in equilibrium.

In the battle between players 1 and 2, player $i \in \{1,2\}$ maximizes

$$\begin{aligned} \frac{e_i}{e_1 + e_2} V - e_i. \end{aligned}$$

In the equilibrium, we find $e_1 = e_2 = V/4$. This yields an expected payoff of V/4 to each player $i \in \{1,2\}$.

Consider node (1, 1, 1, 1). In this symmetric node, a player $i \in N$ maximizes

$$\begin{aligned} \frac{e_i}{e_1 + e_2} \frac{V}{2} - e_i, \end{aligned}$$

in her respective battle. Then, we find $e_i = V/8$ for each $i \in N$ in the equilibrium. This yields an expected payoff of V/8 to each player $i \in N$.

Finally, consider node (2, 1, 1, 0). The equilibrium analysis follows the same as in the version in which the winners of the first round compete against each other in the second round.

Round 2: Consider node (1, 1, 0, 0). Without loss of generality, assume that players 1 and 2 have one battle victory each, so that players 3 and 4 could not win in the first round. Further assume that player 1 played against player 3 in the first round. Then, in the current version, players 1 and 4 compete in a component battle now.

Then, player 1 maximizes

$$\begin{aligned} \frac{e_2}{e_2 + e_3} \left( \frac{e_1}{e_1 + e_4} \frac{V}{4} + \frac{e_4}{e_1 + e_4} \frac{V}{27} \right) + \frac{e_3}{e_2 + e_3} \left( \frac{e_1}{e_1 + e_4} \frac{17V}{27} + \frac{e_4}{e_1 + e_4} \frac{V}{8} \right) - e_1, \end{aligned}$$

in this round. Furthermore, player 3 maximizes

$$\begin{aligned} \frac{e_1}{e_1 + e_4} \frac{e_3}{e_2 + e_3} \frac{3V}{27} + \frac{e_4}{e_1 + e_4} \frac{e_3}{e_2 + e_3} \frac{V}{8} - e_3, \end{aligned}$$

in this round. The maximization problems for players 2 and 4 can be written symmetrically. Taking the first-order conditions and solving the respective system of equations, we find $e_1 = e_2 \approx 0.0595V$ and $e_3 = e_4 \approx 0.0232V$. This yields an expected payoff of 0.2143V to players 1 and 2 and an expected payoff of 0.0091V to players 3 and 4.

Round 1: Consider node (0, 0, 0, 0). Each player can anticipate that her continuation payoff would be 0.2143V if she wins now and 0.0091V if she loses now. One can find that $e_i \approx 0.0513V$ for each player $i \in N$ in the first round. This completes the equilibrium analysis for the current version.

Given these results, the expected total effort that will be exerted in equilibrium is

$$\begin{aligned} &4 \times 0.0513V) + (2 \times 0.0595V)+ (2 \times 0.0232V) \\ &\quad +p^2 \left( 2 \times \frac{V}{4}\right) + p (1-p) \left( 2 \times \frac{6V}{27}\right) + (1-p)^2 \left( 4 \times \frac{V}{8}\right) = 0.7585V, \end{aligned}$$

where $p \approx 0.0595/(0.0595 + 0.0232) = 0.7195$. This completes the proof. $\square$

To analyze the standard round-robin tournament with an exogenous schedule, we start with the following observation. The equilibrium analysis for the last two rounds follow similarly as in the proof of Proposition 1 above. As for the first round battles, the equilibrium analysis would be different because of the changes in the continuation payoffs. To be more precise, those payoffs would be written as convex combinations of the continuation payoffs from the two versions of the model with an endogenous schedule. Then, the next result follows.

Proposition 2

There exists a unique SPNE in a round-robin tournament with an exogenously-given schedule. The expected total effort that will be exerted in this equilibrium is 0.7496 V.

Proof

Utilizing our observation above, we focus on the analysis of the first round battles. Without loss of generality, assuming that player 1 competes with player 2 in the first round and that player 1 will compete with player 3 in the second round, we know that player 1 maximizes

$$\begin{aligned} &\frac{e_3}{e_3 + e_4} \left( \frac{e_1}{e_1 + e_2} 0.2454 V + \frac{e_2}{e_1 + e_2} 0.0091 V \right) \\ &\quad + \frac{e_4}{e_3 + e_4} \left( \frac{e_1}{e_1 + e_2} 0.2143 V + \frac{e_2}{e_1 + e_2} 0.0046 V \right) - e_1 . \end{aligned}$$

The maximization problems for the other players can be written symmetrically. Taking the first-order conditions and solving the respective system of equations, we find $e_i \approx 0.0557V$ for each player $i \in N$.

Given these results, the expected total effort that will be exerted in equilibrium is

$$\begin{aligned} (4 \times 0.0557V) + \frac{1}{2} \mathbf {TE}_{W} + \frac{1}{2} \mathbf {TE}_{L} = 0.7496V, \end{aligned}$$

where

$$\begin{aligned} \mathbf {TE}_{W} \approx (2 \times 0.1898V)+ (2 \times 0.0046V) + \frac{1}{4} \left( 2 \times \frac{6V}{27}\right) , \end{aligned}$$

is the expected total equilibrium effort (after the first round) in case winners of the first round compete against each other and

$$\begin{aligned} &\mathbf {TE}_{L} \approx (2 \times 0.0595V)+ (2 \times 0.0232V) \\ &\quad +p^2 \left( 2 \times \frac{V}{4}\right) + p (1-p) \left( 2 \times \frac{6V}{27}\right) + (1-p)^2 \left( 4 \times \frac{V}{8}\right) , \end{aligned}$$

is the expected total equilibrium effort (after the first round) in case each winner of the first round competes with the non-played loser of the first round, where $p \approx 0.7195$ as calculated earlier. $\square$

Krumer et al. (2017a) and Sahm (2019) report that a sequential round-robin tournament (in which no pair of component battles take place at the same time) is discriminatory in the sense that symmetric players end up with different winning probabilities in the equilibrium. However, it is left as a conjecture that a round-robin tournament would be fair if the battles in the same round were scheduled to take place at the same time. This conjecture is proven by our Propositions 1 and 2: the unique SPNE is symmetric, so that each player has the same winning probability in the equilibrium.⁹

Another related observation is that the expected total equilibrium effort in a sequential round-robin tournament is 0.7299V (see Sahm 2019). Given the expected total equilibrium effort reported in our Proposition 2 above, it can be seen that a round-robin tournament with simultaneous battles is more intense than a round-robin tournament with sequential battles.

In the following two sections, we formally introduce various versions of our alternative tournament model and identify the optimal one(s) after reporting their expected total equilibrium efforts and expected equilibrium efforts per battle.¹⁰

3 An alternative tournament model

Consider four symmetric players in the player set $N = \{1,2,3,4\}$. In a similar manner, we define an alternative tournament model by $\Gamma ^{AT} = \left( N, \left( M^*_t \right) , P(\cdot ), V\right)$, where $\left( M^*_t \right)$ now represents a potentially longer sequence of component battles. The tournament procedure is as follows. In each round, players are pairwise matched. For each pair of players, there is a component battle in which the players choose how much effort to exert, a Tullock contest success function determines who wins the battle, and the winning player collects one point from this round. Similar to a round-robin tournament, assuming that players $i, j \in N$ are matched in a given round, player i wins the battle with a probability of

$$\begin{aligned} \frac{e_i}{e_i + e_j}, \end{aligned}$$

where $e_{i}, e_j \in [0, \infty )$ denote the respective efforts exerted. If both players exert zero effort, then a tie-breaker rule applies: the player with more battle victories wins with a probability of 1, but if both players have the same number of battle victories, then each player would have a winning probability of 1/2. The two battles in the same round take place at the same time. We also assume that the marginal cost of effort is one for every player and in each round.

Each player’s objective is to collect a total of three battle victories before any of the other players succeeds the same. If a player achieves this on her own, then the tournament ends, that player is declared to be the tournament champion, and she collects a winning prize of $V > 0$. Given the tournament design, there may be two players who achieve this at the same time, and for that, we consider two specifications of the model: (i) both three-victory players win the tournament and equally share a total prize of V;¹¹ and (ii) there is an additional round where the three-victory players compete in a final game to determine the tournament champion who will then collect a prize of V.

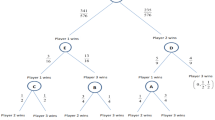
This tournament design displays some similarities with a round-robin tournament, a Swiss tournament, and a race. The first three rounds are played as in a round-robin tournament with a Swiss-type endogenous schedule. Notice that if one player wins three component battles in three rounds, the tournament ends exactly in three rounds with that player becoming the champion. However, it is also possible that such a player does not exist, in which case we either have two or three players with two battle victories.¹² In this latter case, our alternative model allows for tie-braking games to be played in additional rounds. This is a direct consequence of defining a victory threshold, which is an apparent similarity to a race model.

Before proceeding further, it is essential to recall the anonymity assumption on notation: a node is denoted by a quadruple (a, b, c, d), which represents all cases in which one player has a battle victories, another player has b battle victories, and so on. As such, the players’ identities do not matter when reporting our results.

As it was the case earlier, we consider two versions for the second round match-ups: (a) winners of the first round compete against each other, or (b) each winner of the first round competes with the non-played loser of the first round. But now, if the tournament is not finalized in three rounds, there are two possible nodes in the fourth round: (2, 2, 1, 1) or (2, 2, 2, 0). For the former node, there are three versions: (a) the leaders compete against each other, (b) the leader who defeated the other leader competes with the laggard who defeated the other laggard, or (c) the leader who defeated the other leader competes with the laggard who was defeated by the other laggard. For the latter node, there are three versions: (a) the leader who lost in the first round competes with the laggard, (b) the leader who lost in the second round competes with the laggard, or (c) the leader who lost in the third round competes with the laggard. Furthermore, in case the tournament is not finalized in four rounds, (2, 2, 2, 2) would be the only possible node in the fifth round. Given that it is a symmetric node, we do not make any specific assumption here. This leads to $2 \times 3 \times 3 = 18$ tournament structures. And considering the two specifications mentioned earlier, we have a total of 36 alternative tournament structures.

Fig. 2

Two versions of the alternative tournament model

Finally, Fig. 2 illustrates which nodes are followed in this alternative tournament model, with versions differing in the second round battles. Similarly as in the previous figure, the game starts on the left, ends on the right, and each movement from one node to another is due to the outcomes of two component battles that simultaneously take place in the respective round. It is worth noting that the figure does not distinguish between the fourth round match-ups, and as such, not all nodes are possible in all 36 alternative tournament structures.

4 The results

In this section, we compare different tournament structures mentioned above on the basis of expected equilibrium effort per battle. This comparison criterion is defined as the expected total equilibrium effort divided by the expected number of battles. Thus, the comparison analysis requires the calculation of expected total equilibrium effort and expected number of battles for each tournament structure. The following two lemmas are concerned with the tournament structures that yield the highest expected total equilibrium effort under each specification of our tournament model: (i) two three-victory players equally share V and (ii) those three-victory players compete in a final game after which the winner collects V. In that regard, the complete characterization of equilibrium strategies in each version of our model is necessary. Considering the length of the equilibrium analyses for all 36 tournament structures, we do not report them in the main body of the paper. The equilibrium efforts and winning probabilities are reported in a supplementary file.¹³

Lemma 1

In the alternative tournament model, consider the first specification with co-champions. Among the 18 possible versions, expected total equilibrium effort is maximized when (i) in the second round, a winner of the first round competes with the non-played loser of the first round; (ii) on node (2, 2, 1, 1) of the fourth round, a leader competes with either laggard; and (iii) on node (2, 2, 2, 0) of the fourth round, the leader who lost in the second round competes with the laggard. The respective expected total equilibrium effort is 0.7929 V.

Proof

The equilibrium analysis follows as in the proof of Proposition 1. For each version of the tournament, by performing backward induction, starting from the furthest decision node (2,2,2,2) and ending at the first decision node (0,0,0,0), we characterize the unique stationary subgame perfect Nash equilibrium of the model.

Table 1 The expected total equilibrium efforts under specification C

The interested reader is referred to the supplementary material for the respective equilibrium efforts and equilibrium winning probabilities on each possible node. Here we summarize the expected total equilibrium efforts in Table 1. $\square$

The intuition is that if in the second round, a winner of the first round competes with the non-played loser of the first round (as specified in (i)), then a possible third round battle is between a player with two battle victories and a player who won the first round battle but lost the second round battle. The latter player knows that if she wins in the third round, she will be playing against a totally discouraged player in the fourth round (as specified in (iii)). This creates an additional incentive for that player to exert a higher effort in the third round against her opponent who already has a strong incentive to exert high effort due to her two battle victories.

As for (ii), on node (2,2,1,1), if the leaders compete against each other, then they would exert V/4 and end up with an expected payoff of V/4 each; but if a leader competes with a laggard, then the laggards would be totally discouraged, so that even the leaders would have no reason to exert any effort, but then they would end up with an expected payoff of V/2 each. Since the latter expected payoff is much higher, it creates an additional incentive to exert higher efforts in the earlier rounds. Note also that although some positive amount of total effort would be exerted in the former case, as it turns out, its overall effect is not dominant due to the fact that node (2,2,1,1) will not be visited with a high probability.

Lemma 2

In the alternative tournament model, consider the second specification with a final game. Among the 18 possible versions, expected total equilibrium effort is maximized when (i) in the second round, winners of the first round compete against each other; and (ii) on node (2, 2, 2, 0) of the fourth round, the leader who lost in the first round competes with the laggard. The respective expected total equilibrium effort is 0.7851 V.

Proof

The equilibrium analysis follows as in the proof of Proposition 1. For each version of the tournament, by performing backward induction, starting from the final game and ending at the first decision node (0,0,0,0), we characterize the unique stationary subgame perfect Nash equilibrium of the model.

Table 2 The expected total equilibrium efforts under specification F

The interested reader is referred to the supplementary material for the respective equilibrium efforts and equilibrium winning probabilities on each possible node. Here we summarize the expected total equilibrium efforts in Table 2. $\square$

The intuition is quite similar to the one we provided for Lemma 1. The match-ups specified in (i) and (ii) aim to motivate the player who will be competing against an opponent with two victories in the third round. There are two differences. First, given the current second round battles, we see that node (2,2,1,1) is not reached in equilibrium.¹⁴ Accordingly, the match-ups on node (2,2,1,1) will not have any effect on the expected total equilibrium effort. Second, there is now an important final game in which players would exert a total contest effort of V/2. Thus, the version where the probability of reaching node (3,3,2,0)¹⁵ is the highest turns out to be the total-effort-maximizing one.

This brings us to the calculation of expected number of battles. Notice that although there are always six component battles in a round-robin tournament with four players (as analyzed in Sect. 2), the expected number of battles varies in each version of our alternative tournament model. The following proposition considers all those expected values and reports the tournament structures that yield the highest expected equilibrium efforts per battle under each specification.

Proposition 3

Considering all versions of the alternative tournament model, CL5 and CL8 maximize the expected equilibrium effort per battle in the co-champion specification, while FL5 and FL8 maximize the expected equilibrium effort per battle in the final game specification. The respective maximum values are 0.1249V for the former pair and 0.1251V for the latter pair.

Proof

See Tables 3 and 4 for all calculated values.

Table 3 The expected number of battles

Table 4 The expected equilibrium efforts per battle

The interested reader is referred to the supplementary material for details. $\square$

Given the expected total equilibrium efforts presented in Propositions 1 and 2 for three versions of a round-robin tournament and the expected equilibrium efforts per battle reported in Proposition 3 for all versions of the alternative tournament model, we are now ready to state our main result in the following proposition. In short, we show that a version of the round-robin tournament with an endogenous schedule outperforms the other tournament structures considered here.

Proposition 4

Among all the tournament structures considered in this paper, the round-robin tournament with an endogenous schedule in which each winner of the first round competes with the non-played loser of the first round in the second round maximizes the expected equilibrium effort per battle.

Proof

There are six component battles in any version of a round-robin tournament with four players. Given the expected total equilibrium efforts reported in Propositions 1 and 2, we can find that the maximum expected equilibrium effort per battle is reached in the version in which each winner of the first round competes with the non-played loser of the first round in the second round. The maximum value is 0.1264V. This completes the proof since this value is greater than any expected equilibrium effort per battle reported in Table 4. $\square$

As observed in Tables 1 and 2, there is no big difference between the expected total equilibrium efforts in our alternative model and in round-robin tournaments. And as observed in Table 3, the versions of the alternative model that yield higher total efforts mostly have higher expected number of battles. Accordingly, when our comparison criterion normalizes the total effort by dividing it by the expected number of battles, a round-robin tournament with an endogenous schedule comes out as the best performer. However, it is worth noting that the second-best performer is FL5 or FL8, which yields a higher expected equilibrium effort per battle compared to a standard round-robin tournament with an exogenous schedule (also to the other tournament structures considered here). This indicates that switching to an endogenous schedule improves the model’s performance, whereas adding a winning threshold and as such creating a potentially longer tournament structure decreases the performance, when the objective is to maximize expected equilibrium effort per battle.

We conclude our comparison results by returning back to expected total equilibrium effort and using it as another comparison criterion. Since all necessary calculations are already made above, we can directly state that among all the tournament structures considered in this paper, CL5 and CL8 maximize the expected total equilibrium effort. At this point, noting that which comparison criterion is more appealing is a matter of debate, we provide a brief discussion on the pros and cons of the two criteria. While expected total equilibrium effort would be useful as a comparison criterion especially when the contest designer is concerned with the total revenue generated, expected equilibrium effort per battle is arguably more useful in case the designer is mostly concerned with the competitiveness of the tournament. Another important issue is that expected total equilibrium effort may be considered undesirable, since it favors longer (but, possibly less exciting) tournaments. On the other hand, it can also be argued that expected equilibrium effort per battle is undesirable, as it favors very short tournaments with one or two battles, which may be difficult to implement due to fairness concerns.

Finally, while conducting our analysis we made some further observations on the equilibrium path, which we think are worthy of presenting here.

• If node (2, 2, 1, 1) is reached and if the leaders do not compete against each other in the current round, then the laggards are totally discouraged in their respective contests. The game moves to node (3, 3, 1, 1) for sure. That is, the game never reaches node (2, 2, 2, 2) in equilibrium: a maximum of four rounds will be played (neglecting the final game).

• A player who won at most once in the first three rounds is totally discouraged. In particular, a player who lost the first two rounds is totally discouraged.

• If node (2, 1, 1, 0) is reached and (a) if the leader competes with the laggard, then the game moves to node (3, 2, 1, 0) for sure; but (b) if the leader competes with a one-victory player, then the game moves either to node (3, 2, 1, 0) or to node (2, 2, 2, 0). The game never reaches node (3, 1, 1, 1) in equilibrium.

5 Conclusion

In this paper we propose a novel tournament design that incorporates some properties of a round-robin tournament, a Swiss tournament, and a race. We conduct equilibrium analyses for various versions of our alternative model as well as three versions of a round-robin tournament. Afterward, we compare all those tournament structures on the basis of expected equilibrium effort per battle. We find that many versions of the alternative tournament model yield higher expected total equilibrium efforts compared to round-robin tournaments. However, due to the fact that the alternative model has relatively higher expected number of battles than round-robin tournaments, it turns out that a round-robin tournament with an endogenous schedule yields the highest expected equilibrium effort per battle. At the very end, some further observations on the equilibrium behavior in our tournament design are presented. Future work may study fairness properties of our tournament, conduct comparisons using different objective criteria, and develop computational methods to extend it to more than four players and/or three battle victories.