1 Introduction

Sequential all-pay auctions have been intensively studied as they have many real-life applications. These include political lobbying (Becker 1983), patent races (Wright 1983), R&D races (Dasgupta 1986) and job promotion (Rosen 1986), among many others. Most studies dealing with these contests considered a two-stage contest under complete information. For example, Konrad and Leininger (2007) characterized the equilibrium of the all-pay auction in which a group of players choose their effort early and the other group of players choose it late. Kovenock and Roberson (2009) studied a two-stage all-pay auction in which the difference in the players’ expenditures in the first stage serves as a head start advantage to one of the contestants in the second stage. In this paper we study a more complicated form of a multi-stage contest in which every player plays against each other player once. This form of a multi-stage contest is known as the round-robin tournament.Footnote 1 In this tournament there are \(\frac{n}{2 }(n-1)\) pair-wise games when \(n>2\) is the number of players. If n is even, there are \((n-1)\) rounds, each of which includes \(\frac{n}{2}\) pair-wise games. The \(\frac{n}{2}\) games in each round could be either simultaneous or sequential. All the players compete in every round such that in each of the \(n-1\) rounds a player competes once against a different opponent. If n is odd, there will be n rounds, each of which includes \( \frac{n-1}{2}\) pair-wise games. The \(\frac{n-1}{2}\) games in each round could also be either simultaneous or sequential. In each round only \(n-1\) players compete such that every player does not have a game in one round only, and in all the other \(n-1\) rounds he competes once against a different opponent.

Sportive events are commonly organized as round-robin tournaments, two well known examples being professional football and basketball. Sometimes sportive events can be organized as a combination of a round-robin tournament in the first part of the season and then as an elimination tournament in the second part where in the elimination tournament, players play pair-wise games and the winner advances to the next round while the loser is eliminated from the competition (see Gradstein and Konrad 1999; Groh et al. 2012). Examples include US-Basketball, NCAA College Basketball, the FIFA (soccer) World Cup Playoffs and the UEFA Champions’ League. However, the round-robin structure has also been used in non-sport related settings. In the 2015 elections for Israel’s Knesset, for example, a representative of each party was invited for a TV debate which was organized as a round-robin tournament where in each stage the parties’ representatives were divided into different pairs, with each pair confronting each other for several minutes.

The literature on round-robin tournaments seems to be quite sparse, the reason being the complexity of its analysis. This paper attempts to fill this gap by studying three-player and four-player round-robin tournaments in which each player competes against each of the other players in the all-pay auction. Three-player round-robin tournaments are often found in real-life situations like the Olympic badminton games of 2008 and 2012 as well as the Olympic wrestling events of 2000 and 2004, soccer, rugby and even debate competitions. Four-player round-robin tournaments are very common in soccer and basketball, among other sports.

It would seem that the round-robin tournament is the fairest way to determine the winner among a set of players since each player plays against all the others in pair-wise games and hence has an equal chance to win. However, this is not exactly the case since their outcomes could be affected by the timing of the play, namely, the order of the players in the contest. In other words, the allocation of players may affect their probabilities of winning as well as their expected payoffs. Indeed, in the round-robin tournaments we study here, we will show that the first mover indeed has a meaningful advantage.

In the round-robin tournament with three players every player competes against all the other players and in each round two players compete against each other in an all-pay auction. Thus, there are three rounds where in each round only one game takes place and one player does not have a game in that round. The allocation of players in the different rounds is decided before the beginning of the tournament and not decided contingently on the outcomes. Because of the symmetry of players, namely, each player has the same value of winning the tournament, all the possible allocations of players are equivalent in the round-robin tournament with three players. We characterize the subgame perfect equilibrium when the players are symmetric and prove that the expected payoff of each player is maximized when he competes in the first and last rounds. We then examine the robustness of our results by considering three asymmetric players: two players with a high value of winning and one player with a low value of winning. We find that even when the asymmetry between the players’ values is relatively strong, the players prefer to compete in the first and last rounds.

We also consider round-robin tournaments with four players in which every player competes against all the others, and in every round a player plays a pair-wise game against a different opponent in an all-pay auction. There are three rounds where in each round two games take place. We assume that the two games in each round are scheduled one after the other.Footnote 2 Accordingly, we have six different games that take place one after another in three rounds such that in every round there are two sequential games in which all the players participate. Again, the allocation of the players in all the rounds is decided before the beginning of the tournament. Because of the symmetry of players, all the possible allocations of players are divided into two different sets of equivalent allocations in each of which one of the players plays in the first game of the first two rounds. We characterize the subgame perfect equilibrium for the two possible allocations of players and prove that the player who plays in the first game in each of the first two rounds, namely, games 1 and 3, has a significantly higher probability of winning the tournament as well as a significantly higher expected payoff than his opponents. Although all four players are ex-ante symmetric, the player who plays in the first game of each of the first two rounds has a winning probability that is more than twice higher than the player with the second highest probability of winning and he also has an expected payoff that is more than seven (!) times higher than the player with the second highest expected payoff.

The intuition behind the above results is as follows: the player who wins the first game has an advantage in the next games since such a win has an effect on all the opponents, whether or not they compete against the winner in the next game. The reason is that the win in the first game changes the other players’ continuation values of winning such that the winner of the first game has on average a higher continuation value of winning than his opponents. Moreover, in the round-robin tournament with four players when each player plays in every round the other players who do not play in the first game of the second round could find that the tournament has practically been decided before playing their second game, i.e., the players already have no chance to have a positive expected payoff. In the round-robin tournament with three players, a player prefers to play in the first round similarly to the round-robin with four players because of the first-mover advantage, but he also prefers to play his second game in the third round and not in the second one. The reason is that the continuation value of his opponent in the last round on average will be lower than that of his opponent in the second round, since if he wins in the first round and plays in the third round, his opponent in the third round will have a low incentive to compete in the third round since similarly to the four players’ case he has no chance to have a positive expected payoff. On the other hand, if he wins in the first round and plays in the second round, his opponent in the second round knows that if he wins in that round he will have a high chance to be the winner of the tournament and therefore he will have a relatively high incentive to compete in the second round. As such, a player prefers a competition in the third round over the second one.

One surprising result of this study is that the order of games in the last round of the round-robin tournament with four players has no effect on the players’ winning probabilities and their expected payoffs. The intuition for this result derives from the first-mover advantage. Since the first-mover advantage is so strong the tournament is over before the last round for at least one of the players who does not have a positive expected payoff at that point of time. Therefore, in the last round there will actually be only one game between the players who have a chance to win the tournament and make a positive expected payoff. Since the two possible orders of the games are different only in the last round, the only game in which there is a real competition in this round is the same independent of the order of the games.

Our paper is related to the statistical literature on the design of various forms of tournaments. The pioneering paper of which is David (1959) who considered the winning probability of the top player in a four player tournament with a random seeding.Footnote 3 This literature assumes that, for each game among players i and j, there is a fixed, exogenously given probability that i beats j. In particular, this probability does not depend on the stage of the tournament where the particular game takes place nor on the identity of the expected opponent at the next stage. In contrast, in our round-robin model each game among two players is an all-pay auction. As a result, the winning probabilities in each game become endogenous in that they result from mixed equilibrium strategies and are dependent on continuation values of winning. Moreover, the win probabilities depend on the stage of the tournament in which the game takes place as well as on the identity of the future expected opponents.

The paper is organized as follows: Section 2 presents the equilibrium analysis of the round-robin tournament with three symmetric and asymmetric players. Section 3 presents the equilibrium analysis of the round-robin tournament with four symmetric players. Section 4 concludes. All the possible paths in the tournaments are presented by game trees in Appendix A and some of the calculations appear in Appendix B.

2 The round-robin tournament with three symmetric players

In this section we consider a round-robin all-pay tournament with three symmetric players (or teams) \(i\in \{1,2,3\}\). In each round t,  \(t\in \{1,2,3\}\) there is a different pair-wise game such that each player competes in two different rounds. The player who wins two games wins the tournament, but if each player wins only once, each of them wins the tournament with the same probability. If one of the players wins in the first two rounds, the winner of the tournament is then decided and the players in the last round do not exert any efforts (zero effort). We model each game among two players as an all-pay auction in which both players exert efforts and the one exerting the higher effort wins. Without loss of generality, we assume that player i’s value of winning the tournament is \(v=1\) and his cost function is \(c(x_{i})=x_{i}\), where \(x_{i}\) is his effort. It is important to note that when a player has no incentive to exert a positive effort we actually do not have an equilibrium. However, to overcome this problem we can assume, similarly to Groh et al. (2012), that in every game each player obtains a payment \(m>0\), independent from his performance, and then we consider the limit behavior as \( m\rightarrow 0\). This assumption does not affect the players’ behavior but ensures the existence of an equilibrium.

Fig. 1
figure 1

The game tree of the round-robin tournament with three symmetric players

Full size image

We begin the analysis by explaining how the players’ strategies are calculated in each game of the tournament. Suppose that players i and j compete in game \(g,g\in \{1,2,3\}.\) We denote by \(p_{ij}\) the probability that player i wins the game against player j and by \(E_{i},E_{j}\) the expected payoffs of players i and j, respectively. The mixed strategies of the players in game g will be denoted by \(F_{kg}(x),k\in \{i,j\}.\) Assume now that if player i wins this game, his conditional expected payoff is \(w_{ig}\) given the previous outcomes and the possible future outcomes. Similarly, if player i loses this game, his conditional expected payoff is \(l_{ig}\). Without loss of generality, we assume that \( w_{ig}-l_{ig}\ge w_{jg}-l_{jg}\). Then, according to Baye et al. (1996), there is always a unique mixed-strategy equilibrium in which players i and j randomize on the interval \([0,w_{jg}-l_{jg}]\) according to their effort cumulative distribution functions, which are given by

$$\begin{aligned} E_{i}= & {} w_{ig}F_{jg}(x)+l_{ig}(1-F_{jg}(x))-x=l_{jg}+w_{ig}-w_{jg} \\ E_{j}= & {} w_{jg}F_{ig}(x)+l_{jg}(1-F_{ig}(x))-x=l_{jg} \end{aligned}$$

Thus, player i’s equilibrium effort in game g is uniformly distributed; that is

$$\begin{aligned} F_{ig}(x)=\frac{x}{w_{jg}-l_{jg}} \end{aligned}$$

while player j’s equilibrium effort is distributed according to the cumulative distribution function

$$\begin{aligned} F_{jg}(x)=\frac{l_{jg}-l_{ig}+w_{ig}-w_{jg}+x}{w_{ig}-l_{ig}} \end{aligned}$$

Player j’s probability of winning against player i is then

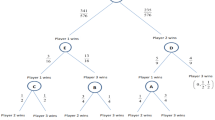
$$\begin{aligned} p_{ji}=\frac{w_{jg}-l_{jg}}{2(w_{ig}-l_{ig})} \end{aligned}$$

In order to analyze the subgame perfect equilibrium of this tournament we begin with the last round and go backwards to the previous rounds. Figure 1 presents the symmetric round-robin tournament as a game tree. We denote by \(p_{ij}^{*}\) the probability that player i wins against player j in vertex \(*\) of the game tree, and by \( F_{i}^{(*)}\) player i’s mixed strategy in vertex \(*\) of the game tree. In the decision node F, players 1 and 2 compete in the first round. In the decision nodes E and D,  players 1 and 3 compete in the second round, and in the decisions nodes A, B and C, players 2 and 3 compete in the third round. For each decision node (\(A-E\)) there is a different path from the initial node F, namely, a different history of the games in the previous rounds. The players’ payoffs are indicated in the terminal nodes. The formulas on the sides of the branches in Fig. 1 denote the winning probabilities of the players who compete in the appropriate decision nodes.

2.1 Round 3—player 2 vs. player 3

Players 2 and 3 compete in the last round only if at least one of them won in the previous rounds. Thus, we have the following three scenarios:

  1. 1.

    Assume first that player 2 won the game in the first round and player 3 won in the second round (vertex A in Fig. 1). Then if each of the players wins in round 3, he also wins the tournament. Thus, following Hillman and Riley (1989) and Baye et al. (1996), there is always a unique mixed strategy equilibrium in which both players randomize on the interval [0, 1] according to their cumulative distribution functions \( F_{i}^{(A)},i=2,3\) which are given by

    $$\begin{aligned} 1\cdot F_{i}^{(A)}(x)-x=0 \quad i=2,3 \end{aligned}$$
    (1)

    Then, player 2’s probability of winning in the third round is

    $$\begin{aligned} p_{23}^{A}=0.5 \end{aligned}$$
  2. 2.

    Assume now that player 2 won the game in the first round and player 3 lost in the second round (vertex B in Fig. 1). Then, if player 2 wins in the third round, he wins the tournament and his payoff is 1,  whereas player 3’s payoff is zero. But, if player 3 wins in this round, then each of the players has exactly one win and an expected payoff of 1 / 3. Thus, we obtain that players 2 and 3 randomize on the interval [0, 1 / 3] according to their effort cumulative distribution functions \( F_{i}^{(B)}, i=2,3\) which are given by

    $$\begin{aligned}&1\cdot F_{3}^{(B)}(x)+\frac{1}{3}\cdot (1-F_{3}^{(B)}(x))-x =\frac{2}{3} \nonumber \\&\frac{1}{3}\cdot F_{2}^{(B)}(x)-x =0 \end{aligned}$$
    (2)

    Then, player 2’s probability of winning in the third round is

    $$\begin{aligned} p_{23}^{B}=1-\frac{1}{4}=0.75 \end{aligned}$$
  3. 3.

    Finally, assume that player 2 lost the game in the first round and player 3 won in the second round (vertex C in Fig. 1). Then, similarly to the previous case, we obtain that players 2 and 3 randomize on the interval [0, 1 / 3] according to their effort cumulative distribution functions \( F_{i}^{(C)},i=2,3\) which are now given by

    $$\begin{aligned}&1\cdot F_{2}^{(C)}(x)+\frac{1}{3}\cdot (1-F_{2}^{(C)}(x))-x =\frac{2}{3} \nonumber \\&\frac{1}{3}\cdot F_{3}^{(C)}(x)-x =0 \end{aligned}$$
    (3)

    Then, player 2’s probability of winning in the third round is

    $$\begin{aligned} p_{23}^{C}=0.25 \end{aligned}$$

2.2 Round 2—player 1 vs. player 3

Based on the results of the game in the first round, we have two possible scenarios:

  1. 1.

    Assume first that player 1 lost the game in the first round (vertex D in Fig. 1). Then, if player 3 wins in this round, by (1), his expected payoff in the next round is zero. If player 3 loses in this round, by (2) his expected payoff is zero as well. Thus, in such a case, player 3 has no incentive to exert a positive effort and player 1 wins with a probability of one.

  2. 2.

    Assume now that player 1 won the game in the first round (vertex E in Fig. 1). Then, if he wins again in this round he also wins the tournament and therefore his payoff is 1 while the other players’ payoffs are then zero. However, if player 1 loses in this round, then by (3) player 3’s expected payoff is 2 / 3 and player 1’s expected payoff depends on the result of the game between players 2 and 3 in the last round. If player 3 wins which happens with a probability of 0.75, player 1’s expected payoff is zero. On the other hand, if player 2 wins, which happens with a probability of 0.25, each of the players has one win and therefore an expected payoff of 1 / 3. In sum, if player 1 loses, his expected payoff is 1 / 12. Thus, we obtain that players 1 and 3 randomize on the interval [0, 2 / 3] according to their effort cumulative distribution functions \(F_{i}^{(E)},i=1,3\) which are given by

    $$\begin{aligned}&1\cdot F_{3}^{(E)}(x)+\frac{1}{12}\cdot (1-F_{3}^{(E)}(x))-x =\frac{1}{3} \nonumber \\&\frac{2}{3}\cdot F_{1}^{(E)}(x)-x =0 \end{aligned}$$
    (4)

    Then, player 1’s probability of winning in the second round is

    $$\begin{aligned} p_{13}^{E}=1-\frac{8}{22}=\frac{7}{11} \end{aligned}$$

2.3 Round 1—player 1 vs. player 2

If player 1 wins the game in the first round (vertex F in Fig. 1), by (4) his expected payoff in the next round is 1 / 3. But if player 1 loses the game, he has an expected payoff of 1 / 3 only if he wins in the second round which happens with a probability of one, and player 2 loses against player 3 in the last round which happens with a probability of 0.25. Thus, if player 1 loses in the first round his expected payoff in the next round is 1 / 12.

Now, if player 2 wins the game in the first round (vertex F in Fig. 1), player 1 wins for sure in the second round and then by (2 ) player 2’s expected payoff is 2 / 3. However, if player 2 loses the game in the first round, and player 1 wins also in the second round, player 2 has an expected payoff of zero. Furthermore, even if player 1 loses in the second round, by (3) player 2 has an expected payoff of zero. Thus, we obtain that players 1 and 2 randomize on the interval [0, 1 / 4] according to their effort cumulative distribution functions \( F_{i}^{(F)},i=1,2\) which are given by

(5)

Then, player 1’s probability of winning in the first round is

$$\begin{aligned} p_{12}^{F}=\frac{3}{16} \end{aligned}$$

The above analysis yields the following result.

Theorem 1

In the unique subgame perfect equilibrium of the round-robin tournament with three symmetric players, the player who competes in the first and last rounds has the highest probability of winning as well as the highest expected payoff, whereas a player who competes in the two last games has the lowest probability of winning as well as the lowest expected payoff.Footnote 4

Proof

By the above analysis we obtain that the players’ expected payoffs are as follows: player 1’s expected payoff is 1 / 12,  player 2’s is 5 / 12,  and player 3’s is zero. In addition, the players’ probabilities to win the tournament are:

Player 1’s probability of winning is

$$\begin{aligned} P_{1}=p_{12}^{F}\cdot p_{13}^{E}+\frac{p_{12}^{F}\cdot p_{31}^{E}\cdot p_{23}^{C}}{3}+\frac{p_{21}^{F}\cdot p_{13}^{D}\cdot p_{32}^{B}}{3}=0.193; \end{aligned}$$

Player 2’s probability of winning is

$$\begin{aligned} P_{2}=p_{21}^{F}\cdot p_{13}^{D}\cdot p_{23}^{B}+p_{21}^{F}\cdot p_{31}^{D}\cdot p_{23}^{A}+\frac{p_{12}^{F}\cdot p_{31}^{E}\cdot p_{23}^{C}}{ 3}+\frac{p_{21}^{F}\cdot p_{13}^{D}\cdot p_{32}^{B}}{3}=0.682; \end{aligned}$$

and player 3’s probability of winning is

$$\begin{aligned} P_{3}=p_{12}^{F}\cdot p_{31}^{E}\cdot p_{32}^{C}+p_{21}^{F}\cdot p_{31}^{D}\cdot p_{32}^{A}+\frac{p_{12}^{F}\cdot p_{31}^{E}\cdot p_{23}^{C}}{ 3}+\frac{p_{21}^{F}\cdot p_{13}^{D}\cdot p_{32}^{B}}{3}=0.125 \end{aligned}$$

Thus, player 2, who competes in the first and the last rounds, has the highest probability of winning as well as the highest expected payoff. \(\square \)

The intuitive explanation to Theorem 1 is as follows: If a player loses in any round he no longer has any chance to be the single winner and then his expected payoff is relatively low. On the other hand, if a player wins in the first round, by (1), (2) and (4) he will have a continuation value of winning higher than or equal to his opponent in each of the next rounds and then his chance to win is much higher. In addition, a player prefers to compete in the third round over the second round, since in the second round the opponent (player 3) has on average a higher continuation value of winning than in the third round. To illustrate, if player 2 wins in the first round, by (2) player 3’s continuation value is equal to \(\frac{1}{3}\) in the third round. On the other hand, if player 1 wins in the first round, by (4) player 3’s continuation value is equal to \(\frac{2}{3}\) in the second round. Hence, each of the players who competes in the first round (players 1 and 2) and wins in that stage prefers to compete against player 3 in the third round since then he has a lower incentive to compete than in the second round.

Theorem 1 demonstrates the first-mover advantage in the round-robin tournament with three symmetric players where the player who does not play in the first round (player 3) has the lowest probability of winning as well as the lowest expected payoff. This result is obtained under our tie-breaking rule according to which if each player wins only once, each of them wins the tournament with the same probability. In order to ensure that the assumption of the tie-breaking rule does not have a significant effect on the result in Theorem 1, we also considered a completely different tie-breaking rule according to which if each player wins only once, none of the players wins the tournament, namely the prize worth 1 is not allocated to each of the players. In this case, the players’ expected payoffs are as follows: player 1’s expected payoff is 0,  player 2’s is 0.5,  and player 3’s is zero. Likewise, the players’ probabilities to win the tournament are then as follows: player 1’s probability of winning is 0,  player 2’s is 0.75,  and player 3’s is 0.25 (the mathematical analysis is available upon request). Hence, also when we drastically change the tie breaking rule such that no one wins in the case of a tie, the player who competes in the first and last rounds has the highest probability of winning as well as the highest expected payoff.

We also examined if the above results hold in the asymmetric round-robin tournament with three players. For this purpose, we assumed that the players’ values of winning are \(v_{1}=v_{2}=v>v_{3}=1,\) namely we have one weak player (player 3) and two strong players (players 1 and 2). We say that the symmetry is weak if v is sufficiently close to 1 and that the asymmetry is strong if v is sufficiently larger than 1. We find that, independent of whether the asymmetry is weak or strong, the strong player who plays in the first and last rounds has a higher (or equal) expected payoff than the other players. Moreover, if the weak player plays in the first and last rounds he might have a higher expected payoff than one of the strong players (the mathematical analysis is available upon request). In sum, independent of whether the asymmetry is weak or strong, the players prefer to be allocated in the first and last rounds of the round-robin all-pay tournament. In the next section we show that the first-mover advantage is even stronger in the round-robin tournament with four symmetric players.

3 The round-robin tournament with four symmetric players

Without loss of generality, we assume that the players’ value of winning the tournament is \(v=1\) and that this value is commonly known. The players play pair-wise games and each game between two players is modelled as an all-pay auction where both players simultaneously exert efforts, and the player with the higher effort wins the game. The players compete one time against each of their opponents in sequential games, such that every player plays three games. There are three rounds which are denoted by \(r\in \{1,2,3\}\) and each player plays one game in each of them. In each round there are two sequential games such that we have six different games which are denoted by \( g\in \{1,2,3,4,5,6\}\). Player i’s cost in game g is \(c(x_{ig})=x_{ig}\), where \(x_{ig}\) is his effort. A player that wins the highest number of games wins the tournament. If two or more players have the same highest number of wins, a draw takes place to determine the winner. If one of the players has three wins before the last game, the winner of the tournament is decided and the players do not exert any effort (zero effort) in the subsequent game. Now, suppose that players i and j compete in game \(g,g\in \{1,2,3,4,5,6\}.\) As in Sect. 2, we denote by \(p_{ij}^{*}\) the probability that player i wins against player j in vertex \(*\) of the game trees in Figs. 2, 3, 4 and 5 and by \(F_{i}^{(*)}\) player i’s mixed strategy in vertex \(*\) of these game trees. We also denote by \( E_{i},E_{j}\) the expected payoffs of players i and j, respectively.

While in a round-robin tournament with four asymmetric players, there are many possible allocations of the players in the six games, in our model with four symmetric players there are only two different allocations. The first allocation is for one of the players to always play in the first game of each round, namely, to play in games 1, 3 and 5. In the second, one of the players always plays in the second game of each round, namely, he plays in games 2, 4 and 6. Any other allocation is equivalent to one of these two possible allocations because of the symmetry among the players. In the following we analyze the subgame equilibrium for each possible allocation of players and calculate for every possible game the players’ strategies, their expected payoffs and their probabilities of winning.

3.1 Case A

Here we assume that one player (player 1) always plays in the first game of each round. Then, without loss of generality, the order of the games is

Round 1

Game 1: player 1–player 2

Game 2: player 3–player 4

Round 2

Game 3: player 1–player 3

Game 4: player 2–player 4

Round 3

Game 5: player 1–player 4

Game 6: player 2–player 3

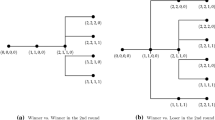
Figs. 2 and 3 in Appendix A present all the possible paths of this tournament and Table 1 in Appendix B provides the calculations of the players’ expected payoffs and their winning probabilities. In each decision node \(j,j=1,\ldots ,55\) two players compete against each other in one of the rounds. The players’ payoffs are indicated in the terminal nodes. In order to analyze the subgame perfect equilibrium for this tournament we begin with the last game and go backwards to the previous games. Because of the complexity of the analysis, we provide only the final results (see Table 1, Appendix B). These results include the players’ mixed strategies, their expected payoffs as well as their winning probabilities in each vertex (game) of the game tree given by Figs. 2 and 3 (Appendix A). Similarly to the previous sections, we can assume that each player obtains a payment of \(m>0\) when he wins a single game, in which case we can consider the limit behavior as \(m\rightarrow 0\). The following result provides the ranking of the players’ winning probabilities and their expected payoffs and highlights the first-mover advantage.

Proposition 1

In the subgame perfect equilibrium of the round-robin tournament with four symmetric players, if player 1 plays in the first game of each of the rounds he has the highest expected payoff as well as the highest probability of winning.

Proof

By the analysis given in Table 1 (Appendix B), the players’ expected payoffs and their winning probabilities are

Player

Expected payoff

Winning probability

1

0.3

0.621

2

0.039

0.051

3

0.009

0.252

4

0.001

0.076

\(\square \) The intuition behind Proposition 1 can be explained by the first-mover advantage. A player who does not play in the first games of the first two rounds could find that the tournament is almost decided before he completed his games such that his chance to be the winner of the tournament as well as his expected payoff will be relatively low. To see that, we compare between player 1 and 2 who compete against each other in the first round but in the second round player 1 plays (game 3) before player 2 (game 4). Player 1 competes against player 3 in the next round and his continuation value as well his chance to win in that round depend only on his and player 3’s result in the first round. If both players won or lost in the first round (vertexes 49 and 52 in Table 1) then they have the same chance to win in the second round, and if one of them won and the other lost in the first round then the one who won has a higher continuation value of winning as well as a higher chance to win in that round (vertexes 50 and 51 in Table 1). However, the continuation value of player 2 who competes against player 4 in the second round depends not only on his and player 4’s result in the first round, but also on the results of players 1 and 3 in the first two rounds. For example, even if player 2 wins in the first round, if player 3 wins in the first two rounds, then player 2’s continuation value of winning in the second round will be quite low (vertex 46 in Table 1). The reason is that since player 3 already has two wins, player 2 has a low chance to win the tournament. Thus, the continuation value of player 2 at the beginning of the second round is low and is different than the continuation value of player 1 at the beginning of the second round. Similar arguments can explain why player 1 has an advantage over players 3 and 4.

As we did for the round-robin tournament with three players, we examine the effect of our tie-breaking rule on the above results. In order to ensure that the assumption of this tie-breaking rule does not have a significant effect on the results in this section we assume another tie-breaking rule according to which if none of the players wins the tournament, namely, the prize worth 1 is not allocated to any of the players. The players’ expected payoffs and winning probabilities are (the analysis is available upon request)

Player

Expected payoff

Winning probability

1

0.25

0.625

2

0

0

3

0

0.25

4

0

0.125

As can be seen, the differences between the players’ expected payoffs and their winning probabilities under our tie-breaking rule and the alternative one are significantly small. In particular, under the alternative tie-breaking rule, player 1 has the highest expected payoff as well as the highest probability of winning.

3.2 Case B

We assume now that one player (player 4) always plays in the second game of each round. Then, without loss of generality, the order of the games is

Round 1

Game 1: player 1–player 2

Game 2: player 3–player 4

Round 2

Game 3: player 1–player 3

Game 4: player 2–player 4

Round 3

Game 5: player 2–player 3

Game 6: player 1–player 4

Figs. 4 and 5 in Appendix A present all the possible paths of this tournament, and Table 2 in Appendix B provides the calculations of the players’ expected payoffs and their winning probabilities. A comparison of the results given in Tables 1 and 2 reveals that the players’ expected payoffs and their probabilities of winning in Case B are the same as in Case A. Therefore we obtain the following main result.

Theorem 2

In the subgame perfect equilibrium of the round-robin all-pay tournament with four symmetric players, the player who plays in the first games of each of the first two rounds has the highest expected payoff as well as the highest probability of winning.

It is important to emphasize that according to Theorem 2 the player who plays in the first games of the first two rounds has a winning probability that is 2.5 (!) times higher than the player with the second highest probability of winning and an expected payoff that is 7.7 (!) times higher than the player with the second highest expected payoff. Hence, the first-mover advantage in the round-robin tournament with four symmetric players is quite dramatic and affects the players’ ex-ante probabilities to win.

If we compare the order of the games in cases A and B we can see that the difference between them is only in the last round. Thus, given that the players’ expected payoffs and their probabilities of winning in Case B are the same as in Case A we obtain the following result.

Proposition 2

In the subgame perfect equilibrium of the round-robin tournament with four symmetric players, the order of the games in the last round of the tournament (games 5 and 6) has no effect on the players’ expected payoffs as well as on their winning probabilities.

The intuition behind Proposition 2 is that for cases A and B the games and their order in the first two rounds are identical but the order in the third round is different. However, the latter has no effect on the players’ strategies since, independent of the outcomes in the previous rounds, at least one of the players (the same one in both cases) exerts zero effort in the third round. Thus, there is only one real competition that occurs in both cases in the last round. As such, the order of the games in that round has no effect on the players’ strategies as well as on their expected payoffs.

4 Concluding remarks

We began this paper by analyzing the subgame perfect equilibrium of the round-robin tournaments with three symmetric players who compete for a single prize and showed that a player’s expected payoff is maximized when he plays in the first and the last rounds. We then analyzed the subgame perfect equilibrium of the round-robin tournament with four symmetric players and one prize. We found that a player who plays in the first game of each of the first two rounds has a significantly higher probability of winning as well as a significantly higher expected payoff than his opponents. These results emphasize the first-mover advantage in the round-robin tournaments and thus raises the issue of fairness in real-life tournaments. A possible solution to this problem could be to make the order of the games endogenous. In other words, the pair-wise game in each round should be decided contingently on the outcomes in the previous rounds. For this reason, we also analyzed the round-robin tournament with three players where the winner in the first round has to play in the second round which is in contrast to the players’ preference to play in the first and last rounds. Indeed, we found that in such a case, all the players’ expected payoffs are the same and equal to zero, and the players’ probabilities of winning are close to each other.Footnote 5 In order for the round-robin tournament with four players to be more balanced we also recommend that all the games be scheduled in the same round at the same time. Then, when the players play simultaneously in each round, because of the symmetry, all the players will have the same ex-ante expected payoff as well as the same ex-ante probability to win.

We also found that the order of the games in the last round of the tournament with four players has no effect on the players’ winning probabilities and their expected payoffs. The reason is that there is a high probability that the tournament will be decided before the last round and then at least one of the players will have no incentive to compete in that round. In that case, there is only one real competition in the last round and it is not important whether it occurs at the beginning or at the end of the last round.

Our results are obtained under the assumption that when more than one player has the highest number of wins, each of them wins the tournament with the same probability. We demonstrated the robustness of our results by showing that under a tie-breaking rule that is completely different than the one we use according to which no one wins in the case of a tie, the players’ expected utilities and their probabilities of winning are quite similar. Since the probabilities of a tie in our round-robin tournament are relatively small (about 0.2) and are even smaller when the number of players is larger, it is likely that a tie-breaking rule when more than one player has the highest number of wins will not have a significant effect on our results.

We focused on a round-robin tournament in which the players compete in the all-pay auction. The question of whether our results hold when players compete in other contest forms such as the Tullock contest is not at all clear and is worth investigating. The study of a round-robin tournament with more than four players is not tractable. However, from our results on the round-robin tournament with three and four players we can conjecture that, independent of the number of players, each player will prefer to play in the first game of the first round(s). Further research could be extended to include several prizes in order to investigate whether the first-mover advantage exists also in multi-prize round-robin tournaments. In addition it might be interesting to examine our results in a laboratory setting or using real-world data.