1 Introduction

In recent years, thanks to its important properties and numerous advantages, quantum entanglement has been widely exploited in quantum systems. It is well-known that entanglement is a purely quantum property which has no equivalent in classical physics [1], manifests itself more particularly in microscopic systems [13,14,15,16,17,18,19,20,21,22,23]. In this respect, it represents a non-local form of quantum correlations between spatially separated systems.Besides entanglement, quantum correlations manifest in many other forms [2], such as Bell non-locality [3] quantum steering [4, 5] and quantum discord [6, 7]. In this respect, they are the main pillar of quantum information processing and computational tasks [8], quantum cryptography [9], quantum teleportation [10], telecloning [11] and quantum metrology [12]. Moreover, entanglement has been widely studied in Fabry–Pérot cavity-based optomechanical systems [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45], which are useful and efficient to study the interaction between light and mechanical oscillators [46, 47], and, therefore, allow to share the entanglement between cavity modes and mechanical resonators.

Cavity quantum optomechanics is a recently developed field of research that promises many applications in quantum information; It can be used to perform precision measurements [48, 49] and also generate quantum superpositions [50]. The optomechanical cavity of Fabry–Pérot type consists of two spatially separated mirrors, one of the two mirrors is fixed and semi-transparent, while the other is mobile and perfectly reflective [51]. The device made it possible to highlight the quantum effects of the mutual interaction by radiation pressure, also called optomechanical coupling, between electromagnetic radiation and the mechanical vibrations of the mobile mirror [52]. The optical modes of the cavity are controlled by a laser beam, the part of which transmitted inside the cavity will act on the mobile mirror by the force of the radiation pressure, which causes its movement (mechanical mode). On the other hand, the movement of the mirror causes a modification of the length of the cavity and, therefore, involves the modulation of the phase of the laser light in the cavity. It is the combination of these two processes (movement of the mirror and modification of the phase of the cavity field) which can generate various optomechanical phenomena (entanglement, cooling, transparency, etc.). Some works have used two Fabry–Pérot cavities coupled via photon hopping process and by two-mode squeezed light [53], while others have considered two Fabry–Pérot cavities coupled by photon hopping process and phonon tunneling process [54].

Unlike classical correlations, the sharing of correlations in multipartite quantum systems is governed by monogamy law [55, 56], i.e., quantum correlations cannot be freely shared between different parts of the system. Therefore, for example, in a tripartite quantum system, if two parts are maximally entangled, there is no shared quantum correlation with the remaining third part [57,58,59,60,61,62]. Monogamy plays an important role in quantum information protocols such as quantum cryptography [63] and entanglement distillation [64] as well as in the characterization of multipartite quantum systems [65,66,67,68,69,70,71,72,73]. In particular, tripartite entanglement has great importance in the area of quantum information, so it seems reasonable to recall tripartite entanglement quantifiers in multimode Gaussian states like tripartite negativity [74], Residual contangle and CKW–monogamy inequality [75].

In the present work, we consider a double-cavity optomechanical system where we explore intracavity quantum correlations in terms of phonon tunneling strength and photon hopping strength to find an appropriate choice of these two coupling strengths to enhance quantum correlations. The two cavities are also coupled by squeezed light; therefore, the generated quantum correlations will also be affected by the squeezed light.

This paper is organized as follows. In Sect. 2, we present the optomechanical model of the system under consideration, we give the effective Hamiltonian for this system, then, we derive the non linear quantum Langevin equations. In Sect. 3, we linearize the quantum Langevin equations describing the dynamics of the quadrature fluctuations, then, we develop the dynamics in the rotating wave approximation. In Sect. 4, we derive the explicit formula for the covariance matrix of the two–three-mode states. We present in Sect. 5 three different quantum measures to explore quantum correlations. In Sect. 6, we discuss the numerical results of different quantum measures. Finally, our concluding remarks are given in Sect. 7.

2 Model

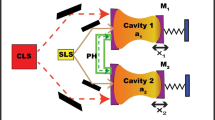
We present in Fig. 1 an illustration of the considered hybrid optomechanical system consisting of two Fabry–Pérot cavities \(k \; (k=1, 2)\) coupled to a two mode squeezed light (SL). Each of both cavities have movable end mirror \(M_{k}\) and pumped by coherent laser source (CLS). Inside each cavity, the mechanical mode \(b_{k}\) characterized by a frequency \(\omega _{b_{k}}\) is coupled to the corresponding optical mode \(a_{k}\) by the optomechanical coupling strength, i.e., radiation pressure, at a rate \(g_{k} = \frac{ \omega _{a_{k}}}{L_{k}} \sqrt{\frac{ \hbar }{m_{k}\omega _{b_{k}}}}\) [46], where \(L_{k}\) and \(\omega _{a_{k}}\) are, respectively, the length and the frequency of kth cavity \(M_{k}\); \((k=1,2)\) and \(m_{k}\) is the mass of the movable mirror. Moreover, we consider two other coupling strengths between the two cavities, namely, the coupling between the optical modes \(a_{k}\; (k= 1, 2)\) by a photon hopping process at rate \(\tau\), and the coupling strength between the mechanical modes \(b_{k} (k= 1, 2)\) via a phonon tunneling process at rate \(\eta\) [76] assuming that phonon and photon tunneling can be achieved between two neighboring Fabry–Pérot cavities due to the finite overlap between their modes. Thereafter, we denote the operators of annihilation (creation) of the kth optical and mechanical modes, respectively, \({a_{k}}\)(\(a^{+}_{k}\)) and \({b_{k}}\)(\(b^{+}_{k}\)) which satisfy the usual commutation relations: [\({a_{k}}\), \(a^{+}_{k}\)]=1 and [\({b_{k}}\), \(b^{+}_{k}\)]=1.

Fig. 1
figure 1

Schematic of two cavities 1(2). Both cavities are pumped by coherent light source (CLS) and coupled to a two-mode squeezed light (SL). The different couplings strength between photons (\(\tau\)) and phonons (\(\eta\))

Full size image

The Hamiltonian governing the system at hand, in a rotating frame at the lasers frequency \(\omega _{L_{k}}\), reads \((\hbar =1)\):

$$\begin{aligned} H={} & {} \Sigma _{k=1}^{2} \left[ \omega _{b_{k}} \left( b^{+}_{k}b_{k} + \frac{1}{2} \right) - \Delta _{k} a^{+}_{k}a_{k}-g_{k}a^{+}_{k}a_{k}(b^{+}_{k}+ b_{k}) \right. \nonumber \\{} & {} \left. + (a^{+}_{k}E_{k}e^{i\varphi _{k}} + a_{k}E_{k}e^{-i\varphi _{k}})\right] -\tau (a^{+}_{1}a_{2}+a^{+}_{2}a_{1} )\nonumber \\{} & {} -\eta (b^{+}_{1}b_{2}+b^{+}_{2}b_{1} ) \end{aligned}$$
(1)

where \(E_{k}= \sqrt{\frac{2 \mu _{k}\varrho _{k}}{\hbar \omega _{L_{k}}}}\) and \(\varphi _{k}\); \((k=1,2)\) are, respectively, the amplitude and the phase of the input coherent laser field, \(\mu _{k}\) is the damping rate of kth cavity and \(\varrho _{k}\) is the drive pump power of kth input field.

The terms \(\Sigma _{k=1}^{2}\omega _{b_{k}}\left( b^{+}_{k}b_{k} + \frac{1}{2}\right)\) and \(-\Sigma _{k=1}^{2}\Delta _{k} a^{+}_{k}a_{k}\) represent the free Hamiltonians describing, respectively, the mechanical modes and the optical modes, the term \(-g_{k}a^{+}_{k}a_{k}(b^{+}_{k}+b_{k})\) denotes the optomechanical interaction via radiation pressure, the optical driving of the system is described by the term \(\Sigma _{k=1}^{2}(a^{+}_{k}E_{k}e^{i\varphi _{k}}+a_{k}E_{k}e^{-i\varphi _{k}})\) and the coupling between the two mechanical modes (two optical modes) through a phonon tunneling (photon hopping) reads as \(\eta (b^{+}_{1}b_{2}+b^{+}_{2}b_{1} )\)(\(\tau (a^{+}_{1}a_{2}+a^{+}_{2}a_{1})\)).

The non-linear quantum Langevin equations of the mechanical and optical modes can be written as

$$\begin{aligned} \frac{\partial b_{1}}{\partial t}{} & {} =- \left( i\omega _{b_{1}} + \frac{\lambda _{1}}{2} \right) b_{1} + ig_{1}a^{+}_{1}a_{1} \nonumber \\{} & {} \quad + i\eta b_{2} + \sqrt{\lambda _{1}}b_{1}^{in} \end{aligned}$$
(2)
$$\begin{aligned} \frac{\partial b_{2}}{\partial t}{} & {} =- \left( i\omega _{b_{2}} + \frac{\lambda _{2}}{2} \right) b_{1} + ig_{2}a^{+}_{2}a_{2}\nonumber \\{} & {} \quad +i\eta b_{1} + \sqrt{\lambda _{2}}b_{2}^{in} \end{aligned}$$
(3)
$$\begin{aligned} \frac{\partial a_{1}}{\partial t}{} & {} = \left( i\Delta _{1} - \frac{\mu _{1}}{2}\right) a_{1} + ig_{1}a_{1}(b^{+}_{1} + b_{1}) \nonumber \\{} & {} \quad + i\tau a_{2} - iE_{1}e^{i \varphi _{1}} + \sqrt{\mu _{1}}a_{1}^{in} \end{aligned}$$
(4)
$$\begin{aligned} \frac{\partial a_{2}}{\partial t}{} & {} =\left( i\Delta _{2} - \frac{\mu _{2}}{2} \right) a_{2} + ig_{2}a_{2}(b^{+}_{2} \nonumber \\{} & {} \quad + b_{2}) + i\tau a_{1} - iE_{2}e^{i \varphi _{2}} + \sqrt{\mu _{2}}a_{2}^{in} \end{aligned}$$
(5)

with \(b_{k}^{in}\) being the kth noise operator representing the coupling between the mechanical mode and its own environment and \(a_{k}^{in}\) is the kth squeezed vacuum operator. \(\lambda _{k}\) and \(\Delta _{k} = \omega _{L_{k}} - \omega _{a_{k}}\) are, respectively, the kth mechanical damping rate and the kth laser detuning. Assuming that \(\omega _{b_{k}}\gg \lambda _{k}\) and \(\Delta _{k}\gg \mu _{k}\), we can apply the rotating wave approximation. In the Markovian approximation, the operator \(b_{k}^{in}\) is characterized by the following correlation functions [77, 78]:

$$\begin{aligned}{} & {} \langle b_{k}^{in}(t)b_{k}^{in+}(t')\rangle =({\hat{n}}_{k}+1)\delta (t-t') \end{aligned}$$
(6)
$$\begin{aligned}{} & {} \langle b_{k}^{in+}(t)b_{k}^{in}(t')\rangle ={\hat{n}}_{k}\delta (t-t') \end{aligned}$$
(7)

where \({\hat{n}}_{k}= \left[ \exp \left( \frac{\hbar \omega _{b_{k}}}{K_{\text {B}}T_{k}}\right) -1\right] ^{-1}\) is the mean number of thermal phonons at frequency \(\omega _{b_{k}}\) of the kth mechanical mode, \(K_{\text {B}}\) and \(T_{k}\) are, respectively, the Boltzmann constant and the the kth thermal bath temperature.

The squeezed vacuum operators \(a_{k}^{in}\) and \(a_{k}^{in+}\) satisfy the following correlation functions [79]:

$$\begin{aligned}{} & {} \langle a_{k}^{in}(t)a_{k}^{in+}(t')\rangle = (N+1)\delta (t-t') \end{aligned}$$
(8)
$$\begin{aligned}{} & {} \langle a_{k}^{in+}(t)a_{k}^{in}(t')\rangle = N\delta (t-t') \end{aligned}$$
(9)
$$\begin{aligned}{} & {} \langle a_{k}^{in}(t)a_{k'}^{in}(t')\rangle = Me^{-i \omega _{b}(t+t')} \nonumber \\{} & {} \delta (t-t') \ \ \ \ k \ne k' \end{aligned}$$
(10)
$$\begin{aligned}{} & {} \langle a_{k}^{in+}(t)a_{k'}^{in+}(t') \rangle = Me^{i \omega _{b}(t+t')} \nonumber \\{} & {} \delta (t-t') \ \ \ \ k \ne k' \end{aligned}$$
(11)

we have assumed that \(\omega _{b_{1}}\) = \(\omega _{b_{2}}\) = \(\omega _{b}\), N and M depend on the squeezing parameter characterizing the squeezed light r, with \(N = \sinh ^{2}r\) and \(M=\sinh r \cosh r\).

3 Linearization of quantum Langevin equations

Since the non-linearity of the Langevin quantum equations (2)–(5) makes their analytical resolution very difficult, we proceed to the linearization scheme consisting in decomposing each operator as follows [75]:

$$\begin{aligned} b_{k}= \langle b_{k}\rangle + \delta b_{k} \;\; a_{k}= \langle a_{k}\rangle + \delta a_{k} \quad (k=1,2) \end{aligned}$$

where \(\delta b_{k}\) and \(\delta a_{k}\) are the fluctuations operators. The steady-state mean values denoted \(\langle b_{k} \rangle\) and \(\langle a_{k} \rangle\) can be read as

$$\begin{aligned}{} & {} \langle b_{1}\rangle = \frac{ig_{1}(i\omega _{b_{2}}+\frac{\lambda _{2}}{2})\vert \langle a_{1}\rangle \vert ^{2}-\eta g_{2}\vert \langle a_{2}\rangle \vert ^{2}}{(i\omega _{b_{1}}+\frac{\lambda _{1}}{2})(i\omega _{b_{2}}+\frac{\lambda _{2}}{2})+\eta ^{2}} \end{aligned}$$
(12)
$$\begin{aligned}{} & {} \langle b_{2}\rangle =\frac{ig_{2}(i\omega _{b_{1}}+\frac{\lambda _{1}}{2})\vert \langle a_{2}\rangle \vert ^{2}-\eta g_{1}\vert \langle a_{1}\rangle \vert ^{2}}{(i\omega _{b_{2}}+\frac{\lambda _{2}}{2})(i\omega _{b_{1}}+\frac{\lambda _{1}}{2})+\eta ^{2}} \end{aligned}$$
(13)
$$\begin{aligned}{} & {} \langle a_{1}\rangle =\frac{i\beta _{2}E_{1}e^{i \varphi _{1}}+\tau E_{2}e^{i \varphi _{2}} }{\beta _{1}\beta _{2} + \tau ^{2}} \end{aligned}$$
(14)
$$\begin{aligned}{} & {} \langle a_{2}\rangle =\frac{i\beta _{1}E_{2}e^{i \varphi _{2}}+\tau E_{1}e^{i \varphi _{1}} }{\beta _{2}\beta _{1} + \tau ^{2} }; \end{aligned}$$
(15)

with \(\beta _{k}= -\frac{\mu }{2} + i\Delta '_{k}\) and \(\Delta '_{k}\) is the effective cavity detuning \(\lbrace \Delta '_{k}= \Delta _{k} + g_{k}(\langle b_{k}\rangle ^{*} + \langle b_{k}\rangle )\rbrace\). Now, we deal with identical cavities (\(m_{1} = m_{2} = m; g_{1} = g_{2 }= g; \omega _{b_{1}} =\omega _{b_{2}} = \omega _{b}; \omega _{a_{1}} = \omega _{a_{2}} = \omega _{a}; \omega _{L_{1}} = \omega _{L_{2}} = \omega _{L}; \lambda _{1} = \lambda _{2} = \lambda ; \mu _{1} = \mu _{2} = \mu\)), equal temperature (\(T_{1} = T_{2} = T\)); for \(E_{1} = E_{2} =E\), \(\beta _{1} = \beta _{2} = \beta\), \(\varphi _{1} = \varphi _{2} = \varphi\), one has \(\langle a \rangle\) = \(-i\frac{Ee^{i \varphi }}{\frac{\mu }{2}-i(\Delta '+\tau )}\). We take \(\varphi = -\arctan [2(\Delta '+\tau )/\mu ]\) and \(\langle a \rangle = - i\vert \langle a\rangle \vert\). In this case, the many-photon optomechanical coupling inside each cavity is [46]:

$$\begin{aligned}{} & {} \Lambda = g \vert \langle a\rangle \vert =\frac{\omega _{a}}{L}\nonumber \\{} & {} \sqrt{\frac{2\mu \varrho }{m\omega _{b}\omega _{L}[(\Delta '+ \tau )^{2}+ \mu ^{2}/4]}} \end{aligned}$$
(16)

The linearized QLES describing the dynamics of the quadrature fluctuations are given by

$$\begin{aligned}{} & {} \delta {\dot{b}}_{1}=- \left( i\omega _{b}+\frac{\lambda }{2} \right) \delta b_{1}\nonumber \\{} & {} \quad +\Lambda ( \delta a^{+}_{1}-\delta a_{1} )+i\eta \delta b_{2}+\sqrt{\lambda } b^{in}_{1} \end{aligned}$$
(17)
$$\begin{aligned}{} & {} \delta {\dot{b}}_{2} = -\left( i\omega _{b}+\frac{\lambda }{2} \right) \delta b_{2}\nonumber \\{} & {} \quad +\Lambda ( \delta a^{+}_{2}-\delta a_{2})+i\eta \delta b_{1}+\sqrt{\lambda }b^{in}_{2} \end{aligned}$$
(18)
$$\begin{aligned}{} & {} \delta {\dot{a}}_{1} = \beta \delta a_{1}+\Lambda (\delta b^{+}_{1} +\delta b_{1})\nonumber \\{} & {} \quad + i\tau \delta a_{2}+ \sqrt{\mu }a^{in}_{1} \end{aligned}$$
(19)
$$\begin{aligned}{} & {} \delta {\dot{a}}_{2} = \beta \delta a_{2}+\Lambda (\delta b^{+}_{2} +\delta b_{2}) + i\tau \delta a_{1}\nonumber \\{} & {} \quad + \sqrt{\mu }a^{in}_{2} \end{aligned}$$
(20)

We introduce the operators: \(\delta b_{k}(t)= \delta {\tilde{b}}_{k}(t)e^{-i\omega _{b_{k}}t}\), \(\delta a_{k}(t)= \delta {\tilde{b}}_{k}(t)e^{i\Delta 't}\), \({\tilde{a}}^{in}_{k}= e^{-i\Delta 't} {a}^{in}_{k}\), \({\tilde{b}}^{in}_{k}= e^{i\omega _{b_{k}}t} {b}^{in}_{k} (k=1,2)\) and by assuming that \(\omega _{b}\gg \mu\), and \(\Delta '=-\omega _{b}\), we can neglect the rotating terms at \(\pm \omega _{b}\). This allows us rewrite Eqs. (17)–(20) in a frame rotating wave approximation (RWA) [46, 80] as

$$\begin{aligned}{} & {} \delta \dot{{\tilde{b}}}_{1}(t) =-\frac{\lambda }{2}\delta {\tilde{b}}_{1}(t) - \Lambda \delta {\tilde{a}}_{1}(t)\nonumber \\{} & {} \quad + i\eta \delta {\tilde{b}}_{2}(t) + \sqrt{\lambda } \delta {\tilde{b}}^{in}_{1} \end{aligned}$$
(21)
$$\begin{aligned}{} & {} \delta \dot{{\tilde{b}}}_{2}(t) =-\frac{\lambda }{2}\delta {\tilde{b}}_{2}(t) - \Lambda \delta {\tilde{a}}_{2}(t)\nonumber \\{} & {} \quad + i\eta \delta {\tilde{b}}_{1}(t) + \sqrt{\lambda } \delta {\tilde{b}}^{in}_{2} \end{aligned}$$
(22)
$$\begin{aligned}{} & {} \delta \dot{{\tilde{a}}}_{1}(t) =-\frac{\mu }{2}\delta {\tilde{a}}_{1}(t) + \Lambda \delta {\tilde{b}}_{1}(t) \nonumber \\{} & {} \quad + i\tau \delta {\tilde{a}}_{2}(t) + \sqrt{\mu } \delta {\tilde{a}}^{in}_{1} \end{aligned}$$
(23)
$$\begin{aligned}{} & {} \delta \dot{{\tilde{a}}}_{2}(t) =-\frac{\mu }{2}\delta {\tilde{a}}_{2}(t) + \Lambda \delta {\tilde{b}}_{2}(t)\nonumber \\{} & {} \quad + i\tau \delta {\tilde{a}}_{1}(t) + \sqrt{\mu } \delta {\tilde{a}}^{in}_{2} \end{aligned}$$
(24)

4 Covariance matrix

To study the quantum entanglement between different tripartite subsystems in the suggested scheme, we consider the following steps to get the steady state of the correlation matrix of quantum fluctuations.

We define the quadrature operators for the two mechanical and optical modes as

$$\begin{aligned}{} & {} \delta {\tilde{q}}_{b_{k}}=\frac{\delta {\tilde{b}}^{+}_{k}+\delta {\tilde{b}}_{k}}{\sqrt{2}};\nonumber \\{} & {} \delta {\tilde{Y}}_{b_{k}}=\frac{\delta {\tilde{b}}_{k}-\delta {\tilde{b}}^{+}_{k}}{i\sqrt{2}};\nonumber \\{} & {} \delta {\tilde{q}}_{a_{k}} = \frac{\delta {\tilde{a}}^{+}_{k}+\delta {\tilde{a}}_{k}}{\sqrt{2}};\nonumber \\{} & {} \delta {\tilde{Y}}_{a_{k}}= \frac{\delta {\tilde{a}}_{k}-\delta {\tilde{a}}^{+}_{k}}{i\sqrt{2}};(k=1,2) \end{aligned}$$
(25)

Therefore, we get:

$$\begin{aligned}{} & {} \delta \dot{{\tilde{q}}}_{b_{1}} =\frac{-\lambda }{2} \delta {\tilde{q}}_{b_{1}} - \Lambda \delta {\tilde{q}}_{a_{1}} - \eta \delta {\tilde{Y}}_{b_{2}} + \sqrt{\lambda }{\tilde{q}}_{b^{in}_{1}} \end{aligned}$$
(26)
$$\begin{aligned}{} & {} \delta \dot{{\tilde{q}}}_{b_{2}}= \frac{-\lambda }{2} \delta {\tilde{q}}_{b_{2}} - \Lambda \delta {\tilde{q}}_{a_{2}} - \eta \delta {\tilde{Y}}_{b_{1}}+\sqrt{\lambda } {\tilde{q}}_{b^{in}_{2}} \end{aligned}$$
(27)
$$\begin{aligned}{} & {} \delta \dot{{\tilde{Y}}}_{b_{1}} = \frac{-\lambda }{2} \delta {\tilde{Y}}_{b_{1}} - \Lambda \delta {\tilde{Y}}_{a_{1}} + \eta \delta {\tilde{q}}_{b_{2}} + \sqrt{\lambda } {\tilde{Y}}_{b^{in}_{1}} \end{aligned}$$
(28)
$$\begin{aligned}{} & {} \delta \dot{{\tilde{Y}}}_{b_{2}} = \frac{-\lambda }{2} \delta {\tilde{Y}}_{b_{2}} - \Lambda \delta {\tilde{Y}}_{a_{2}} + \eta \delta {\tilde{q}}_{b_{1}}+\sqrt{\lambda } {\tilde{Y}}_{b^{in}_{2}} \end{aligned}$$
(29)
$$\begin{aligned}{} & {} \delta \dot{{\tilde{q}}}_{a_{1}} =\frac{-\mu }{2} \delta {\tilde{q}}_{a_{1}}+\Lambda \delta {\tilde{q}}_{b_{1}}-\tau \delta {\tilde{Y}}_{a_{2}}+\sqrt{\mu }{\tilde{q}}_{a^{in}_{1}} \end{aligned}$$
(30)
$$\begin{aligned}{} & {} \delta \dot{{\tilde{q}}}_{a_{2}}=\frac{-\mu }{2} \delta {\tilde{q}}_{a_{2}}+\Lambda \delta {\tilde{q}}_{b_{2}} - \tau \delta {\tilde{Y}}_{a_{1}} +\sqrt{\mu }{\tilde{q}}_{a^{in}_{2}} \end{aligned}$$
(31)
$$\begin{aligned}{} & {} \delta \dot{{\tilde{Y}}}_{a_{1}} =\frac{-\mu }{2} \delta {\tilde{Y}}_{a_{1}} +\Lambda \delta {\tilde{Y}}_{b_{1}} + \tau \delta {\tilde{q}}_{a_{2}}+\sqrt{\mu }{\tilde{Y}}_{a^{in}_{1} } \end{aligned}$$
(32)
$$\begin{aligned}{} & {} \delta \dot{{\tilde{Y}}}_{a_{2}}=\frac{-\mu }{2} \delta {\tilde{Y}}_{a_{2}}+\Lambda \delta {\tilde{Y}}_{b_{2}}+ \tau \delta {\tilde{q}}_{a_{1}}+\sqrt{\mu }{\tilde{Y}}_{a^{in}_{2}} \end{aligned}$$
(33)

We can rewrite Eqs. (26)–(34) in the following compact matrix form [81]:

$$\begin{aligned} {\dot{\theta }}(t)=\sigma \theta (t) + \nu (t) \end{aligned}$$
(34)

where \(\theta ^{T}(t)= (\delta {\tilde{q}}_{b_{1}}, \delta {\tilde{Y}}_{b_{1}}, \delta {\tilde{q}}_{b_{2}}, \delta {\tilde{Y}}_{b_{2}}, \delta {\tilde{q}}_{a_{1}}, \delta {\tilde{Y}}_{a_{1}}, \delta {\tilde{q}}_{a_{2}}, \delta {\tilde{Y}}_{a_{2}})\) is the quadrature vector,

\(\nu ^{T}(t)= ({\tilde{q}}^{in}_{b_{1}}, {\tilde{Y}}^{in}_{b_{1}},{\tilde{q}}^{in}_{b_{2}},{\tilde{Y}}^{in}_{b_{2}},{\tilde{q}}^{in}_{a_{1}},{\tilde{Y}}^{in}_{a_{1}},{\tilde{q}}^{in}_{a_{2}}, {\tilde{Y}}^{in}_{a_{2}})\). The matrix \(\sigma\) takes the form:

$$\begin{aligned} \sigma = \begin{bmatrix} -\frac{\lambda }{2} &{} 0 &{} 0 &{} -\eta &{} -\Lambda &{} 0 &{} 0 &{} 0\\ 0 &{} -\frac{\lambda }{2} &{} \eta &{} 0 &{} 0 &{} -\Lambda &{} 0 &{} 0 \\ 0 &{} -\eta &{} -\frac{\lambda }{2} &{} 0 &{} 0 &{} 0 &{} -\Lambda &{} 0\\ \eta &{} 0 &{} 0 &{} -\frac{\lambda }{2} &{} 0 &{} 0 &{} 0 &{} -\Lambda \\ \Lambda &{} 0 &{} 0 &{} 0 &{} -\frac{\mu }{2} &{} 0 &{} 0 &{} -\tau \\ 0 &{}\Lambda &{} 0 &{} 0 &{} 0 &{}-\frac{\mu }{2} &{} \tau &{} 0 \\ 0 &{} 0 &{} \Lambda &{} 0 &{} 0 &{} -\tau &{} -\frac{\mu }{2} &{} 0\\ 0 &{} 0 &{} 0 &{} \Lambda &{} \tau &{} 0 &{} 0 &{} -\frac{\mu }{2} \\ \end{bmatrix} \end{aligned}$$
(35)

The steady state covariance matrix can be derived directly by solving the Lyapunov equation [82, 83]:

$$\begin{aligned} \sigma \sqcap +\sqcap \sigma ^{T}+\curlywedge =0 \end{aligned}$$
(36)

where \(\curlywedge\) is the stationary noise matrix defined by: \(\curlywedge _{pq}\delta (t-t')=\frac{1}{2}(\langle \nu _{p}(t)\nu _{q}(t')+\nu _{q}(t')\nu _{p}(t)\rangle )\), which is written as

$$\begin{aligned} \curlywedge = \begin{bmatrix} \lambda ' &{} 0 &{} 0&{} 0 &{} 0 &{} 0&{} 0 &{} 0\\ 0&{}\lambda ' &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{}0 \\ 0 &{}0&{}\lambda '&{} 0 &{} 0&{} 0 &{} 0&{} 0\\ 0 &{} 0 &{} 0 &{} \lambda ' &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{}0 &{}\mu '&{}0&{} M\mu &{} 0 \\ 0 &{} 0&{} 0 &{} 0 &{} 0 &{} \mu ' &{} 0&{}-M\mu \\ 0 &{} 0&{} 0 &{} 0 &{} M\mu &{} 0 &{} \mu '&{} 0 \\ 0 &{}0 &{}0 &{} 0 &{} 0 &{} -M\mu &{} 0 &{}\mu ' \\ \end{bmatrix} \end{aligned}$$
(37)

where \(\lambda '=\lambda (n+\frac{1}{2})\) and \(\mu '=\mu (N+\frac{1}{2})\). The covariance matrix describing the two mechanical modes and the two optical modes can be written in (\(\delta {\tilde{q}}_{b_{1}}, \delta {\tilde{Y}}_{b_{1}}, \delta {\tilde{q}}_{b_{2}}, \delta {\tilde{Y}}_{b_{2}}, \delta {\tilde{q}}_{a_{1}}, \delta {\tilde{Y}}_{a_{1}}, \delta {\tilde{q}}_{a_{2}}, \delta {\tilde{Y}}_{a_{2}}\)) basis as

$$\begin{aligned} \sqcap = \begin{bmatrix} \sqcap _{1} &{} \sqcap _{2} &{} \sqcap _{3} &{} 0 &{} \sqcap _{4} &{} \sqcap _{5}&{} \sqcap _{6} &{} \sqcap _{7}\\ \sqcap _{2} &{} \sqcap _{1} &{} 0 &{}-\sqcap _{3} &{} \sqcap _{5} &{}\sqcap _{4} &{} -\sqcap _{7} &{} -\sqcap _{6} \\ \sqcap _{3} &{} 0 &{}\sqcap _{1} &{} \sqcap _{2} &{} \sqcap _{6} &{} \sqcap _{7} &{} \sqcap _{4} &{} \sqcap _{5}\\ 0 &{}-\sqcap _{3} &{} \sqcap _{2} &{} \sqcap _{1} &{} -\sqcap _{7} &{}-\sqcap _{6} &{} \sqcap _{5} &{} \sqcap _{4} \\ \sqcap _{4} &{} \sqcap _{5} &{}\sqcap _{6} &{} -\sqcap _{7} &{} \sqcap _{10} &{} \sqcap _{8} &{} \sqcap _{9} &{} 0\\ \sqcap _{5} &{} \sqcap _{4} &{} \sqcap _{7} &{} -\sqcap _{6} &{} \sqcap _{8} &{}\sqcap _{10} &{} 0 &{} -\sqcap _{9} \\ \sqcap _{6} &{} -\sqcap _{7} &{} \sqcap _{4} &{} \sqcap _{5} &{} \sqcap _{9} &{} 0 &{} \sqcap _{10} &{} \sqcap _{8}\\ \sqcap _{7} &{}-\sqcap _{6} &{} \sqcap _{5} &{} \sqcap _{4}&{} 0 &{}-\sqcap _{9} &{} \sqcap _{8} &{} \sqcap _{10} \\ \end{bmatrix} \end{aligned}$$
(38)

where the different elements of this matrix are

$$\begin{aligned}{} & {} \sqcap _{1}=\frac{(1+2n)(\mu ^{2}+\mu (2+C)\lambda +(1+C)\lambda ^{2}+4( \Gamma \mu -\chi \mu )^{2})+\mu C(\mu +\lambda )\cosh (2r)}{2(\mu ^{2}(1+C)+2\mu (1+C)\lambda +(1+C)\lambda ^{2}+4(\Gamma \mu - \chi \mu )^{2})} \end{aligned}$$
(39)
$$\begin{aligned}{} & {} \sqcap _{2}= \frac{\mu ^{2}C\lambda (\mu ^{3}\Gamma +\mu (2+C)\lambda (\Gamma \mu + \chi \mu )+\chi \mu (\lambda ^{2}-4\Gamma \mu (\Gamma \mu + \chi \mu )))\sinh (2r)}{(\mu ^{2}((1+C)^{2}\lambda ^{2}+4(\Gamma \mu )^{2}) - 8C\lambda \Gamma \chi \mu ^{3} + 4( \lambda ^{2} + 4(\Gamma \mu )^{2})(\chi \mu )^{2})(\mu ^{2}+2\mu \lambda + \lambda ^{2} + 4(\Gamma \mu + \chi \mu )^{2})} \end{aligned}$$
(40)
$$\begin{aligned}{} & {} \sqcap _{3}=\frac{\mu ^{2}C\lambda (\mu ^{2}(1+C)\lambda +\mu (1+C)\lambda ^{2}-4\lambda \chi \mu (2\Gamma \mu + \chi \mu ) - 4\Gamma \mu ^{2}(\Gamma \mu +2\chi \mu ))\sinh (2r) }{2(\mu ^{2}((1 + C)^{2}\lambda ^{2}+4(\Gamma \mu )^{2}) - 8C\lambda \Gamma \chi \mu ^{3}+4(\lambda ^{2}+4(\Gamma \mu )^{2})(\chi \mu )^{2})(\mu ^{2}+2\mu \lambda +\lambda ^{2}+4(\Gamma \mu +\chi \mu )^{2}) } \end{aligned}$$
(41)
$$\begin{aligned}{} & {} \sqcap _{4}= -\frac{\sqrt{\mu C\lambda }(\mu +\lambda )(-1-2n+\cosh (2r))}{2(\mu ^{2}(1+C)+ 2\mu (1+C)\lambda +(1+C)\lambda ^{2}+ 4(\Gamma \mu -\chi \mu )^{2})} \end{aligned}$$
(42)
$$\begin{aligned}{} & {} \sqcap _{5}=\frac{\mu \sqrt{\mu C\lambda }(C \lambda (\Gamma \mu ^{3} -\lambda \chi \mu ^{2})-(\lambda ^{2} + 4 (\Gamma \mu )^{2})(\lambda \chi \mu + \mu ^{2}(\Gamma + 2\chi )))\sinh (2r)}{(\mu ^{2}((1+C)^{2}\lambda ^{2}+ 4(\Gamma \mu )^{2})-8C\lambda \Gamma \chi \mu ^{3}+ 4(\lambda ^{2}+4(\Gamma \mu )^{2})(\chi \mu )^{2})(\mu ^{2}+2\mu \lambda + \lambda ^{2} +4(\Gamma \mu + \chi \mu )^{2})} \end{aligned}$$
(43)
$$\begin{aligned}{} & {} \sqcap _{6}= -\frac{\mu \sqrt{\mu C\lambda }(\mu C\lambda (\mu \lambda +\lambda ^{2}+ 4\Gamma \mu ^{2}(\Gamma + \chi )) + (\lambda ^{2} + 4(\Gamma \mu )^{2})(\mu ^{2} + \mu \lambda - 4 \chi \mu ^{2}(\Gamma + \chi )))\sinh (2r)}{2(\mu ^{2}((1+C)^{2}\lambda ^{2} + 4(\Gamma \mu )^{2}) - 8C\lambda \Gamma \chi \mu ^{3}+4(\lambda ^{2} + 4(\Gamma \mu )^{2})(\chi \mu )^{2})(\mu ^{2}+2\mu \lambda +\lambda ^{2}+4(\Gamma \mu + \chi \mu )^{2})} \end{aligned}$$
(44)
$$\begin{aligned}{} & {} \sqcap _{7}= \frac{\sqrt{\mu C\lambda }(\Gamma \mu -\chi \mu )(1+2n-\cosh (2r))}{(\mu ^{2} +2\mu \lambda + \lambda ^{2})(1 + C) + 4(\Gamma \mu - \chi \mu )^{2}} \end{aligned}$$
(45)
$$\begin{aligned}{} & {} \sqcap _{8}=\frac{\mu (\mu ^{2}C^{2}\lambda ^{2}(\Gamma \mu + \chi \mu )+(\lambda ^{2}+4(\Gamma \mu )^{2})\chi \mu (\mu ^{2}+2\mu \lambda +\lambda ^{2}+4(\Gamma \mu +\chi \mu )^{2}))\sinh (2r)}{(\mu ^{2}((1+C)^{2}\lambda ^{2}+4(\Gamma \mu )^{2})-8C\lambda \Gamma \chi \mu ^{3}+4(\lambda ^{2} +4(\Gamma \mu )^{2})(\chi \mu )^{2})(\mu ^{2}+2\mu \lambda +\lambda ^{2}+4 (\Gamma \mu +\chi \mu )^{2})}\nonumber \\{} & {} -\frac{\mu (\mu C \lambda (\lambda ^{2} (\Gamma \mu -\chi \mu )-2\lambda \chi \mu ^{2}+4\Gamma \mu ((\Gamma \mu )^{2}+3\Gamma \chi \mu ^{2}+2(\chi \mu )^{2})))\sinh (2r)}{(\mu ^{2}((1+C)^{2}\lambda ^{2}+4(\Gamma \mu )^{2})-8C\lambda \Gamma \chi \mu ^{3}+4(\lambda ^{2} +4(\Gamma \mu )^{2})(\chi \mu )^{2})(\mu ^{2}+2\mu \lambda +\lambda ^{2}+4 (\Gamma \mu +\chi \mu )^{2})} \end{aligned}$$
(46)
$$\begin{aligned}{} & {} \sqcap _{9}=\frac{\mu ^{2}(\mu ^{2}((1+C)^{2}\lambda ^{2}+4(\Gamma \mu )^{2}) +(\lambda ^{2}+4(\Gamma \mu )^{2})((1+C) \lambda ^{2}+4(\Gamma \mu +\chi \mu )^{2}))\cosh (r) \sinh (r)}{(\mu ^{2}((1+C)^{2}\lambda ^{2}+4(\Gamma \mu )^{2})-8 C\lambda \Gamma \chi \mu ^{3}+4(\lambda ^{2}+4(\Gamma \mu )^{2}) (\chi \mu )^{2})(\mu ^{2}+2\mu \lambda +\lambda ^{2}+4(\Gamma \mu +\chi \mu )^{2}) } \nonumber \\{} & {} +\frac{\mu ^{2}(\mu ((2+3C+C^{2})\lambda ^{3}-4\lambda \Gamma \mu ((-2+C)\Gamma \mu +2C\chi \mu )))\cosh (r)\sinh (r)}{(\mu ^{2}((1+C)^{2}\lambda ^{2}+4(\Gamma \mu )^{2})-8C\lambda \Gamma \chi \mu ^{3}+4(\lambda ^{2}+4(\Gamma \mu )^{2})(\chi \mu )^{2})(\mu ^{2}+2\mu \lambda +\lambda ^{2}+4(\Gamma \mu +\chi \mu )^{2})} \end{aligned}$$
(47)
$$\begin{aligned}{} & {} \sqcap _{10}=\frac{(1+2n)C\lambda (\mu +\lambda )+(\mu ^{2}(1+C)+\mu (2+C)\lambda +\lambda ^{2}+4(\Gamma \mu - \chi \mu )^{2})\cosh (2r)}{2((\mu ^{2}+2\mu \lambda +\lambda ^{2})(1+C)+4(\Gamma \mu -\chi \mu )^{2})} \end{aligned}$$
(48)

The optomechanical cooperativity C is defined as [46, 53]:

$$\begin{aligned} C= \frac{4\Lambda ^{2}}{\lambda \mu }= \frac{8\omega ^{2}_{a}}{m\lambda \omega _{b}\omega _{L}L^{2}}\frac{\varrho }{\mu ^{2}[\frac{1}{4}+(\chi - \omega _{b}/\mu )^{2}]} \end{aligned}$$
(49)

we have set \(\chi = \frac{\tau }{\mu }\) and \(\Gamma =\frac{\eta }{\mu }\), where \(\chi\) is the photon hopping strength and \(\Gamma\) the phonon tunneling strength.

5 Bipartite and tripartite entanglement

In this paragraph, we examine bipartite and tripartite entanglement in two–three-mode blocks (\(b_{1}, b_{2}, a_{1}\)) and (\(b_{2}, a_{1 }, a_{2}\)) whose corresponding reduced covariance matrices are, respectively, \(\sqcap _{(b_{1}, b_{2}, a_{1})}\) and \(\sqcap _{(b_{2}, a_{1}, a_{2})}\):

$$\begin{aligned}{} & {} \sqcap _{(b_{1}, b_{2}, a_{1})}= \begin{bmatrix} \sqcap _{1} &{} \sqcap _{2} &{} \sqcap _{3} &{} 0 &{} \sqcap _{4} &{} \sqcap _{5}\\ \sqcap _{2} &{} \sqcap _{1} &{} 0 &{}-\sqcap _{3} &{} \sqcap _{5} &{}\sqcap _{4}\\ \sqcap _{3} &{} 0 &{}\sqcap _{1} &{} \sqcap _{2} &{} \sqcap _{6} &{} \sqcap _{7} \\ 0 &{}-\sqcap _{3} &{} \sqcap _{2} &{} \sqcap _{1} &{} -\sqcap _{7} &{}-\sqcap _{6}\\ \sqcap _{4} &{} \sqcap _{5} &{} \sqcap _{6} &{} -\sqcap _{7} &{} \sqcap _{10} &{} \sqcap _{8}\\ \sqcap _{5} &{} \sqcap _{4} &{} \sqcap _{7} &{} -\sqcap _{6} &{} \sqcap _{8} &{}\sqcap _{10}\\ \end{bmatrix};\nonumber \\{} & {} \sqcap _{(b_{2}, a_{1}, a_{2})} = \begin{bmatrix} \sqcap _{1} &{} \sqcap _{2} &{} \sqcap _{6} &{} \sqcap _{7} &{} \sqcap _{4} &{} \sqcap _{5}\\ \sqcap _{2} &{} \sqcap _{1} &{} -\sqcap _{7} &{}-\sqcap _{6} &{} \sqcap _{5} &{} \sqcap _{4} \\ \sqcap _{6} &{} -\sqcap _{7} &{} \sqcap _{10} &{} \sqcap _{8} &{} \sqcap _{9} &{} 0\\ \sqcap _{7} &{} -\sqcap _{6} &{} \sqcap _{8} &{}\sqcap _{10} &{} 0 &{} -\sqcap _{9} \\ \sqcap _{4} &{} \sqcap _{5} &{} \sqcap _{9} &{} 0 &{} \sqcap _{10} &{} \sqcap _{8}\\ \sqcap _{5} &{} \sqcap _{4}&{} 0 &{}-\sqcap _{9} &{} \sqcap _{8} &{} \sqcap _{10} \\ \end{bmatrix} \end{aligned}$$
(50)

Two-mode bipartite entanglement can be quantified by means of one-mode (l) versus one-mode (s) logarithmic negativity \(\epsilon _{l\vert s}\). For a two-mode Gaussian state, the logarithmic negativity is given by [84, 85]

$$\begin{aligned} \epsilon _{l\vert s} = max[0, -ln(2 \alpha ^{-}_{l \vert s})] \end{aligned}$$
(51)

\(\alpha ^{-}_{l \vert s}\) is the smallest symplectic eigenvalue of partial transposed covariance matrix \(\sqcap _{(l,s)}\)

where \(\sqcap _{(l,s)} = \begin{bmatrix} X(t) &{} Z(t)\\ Z^{T}(t) &{} Y(t)\\ \end{bmatrix}\)\(\Delta _{l\vert s} = det X(t) + det Y(t)- 2det Z(t)\)

$$\begin{aligned} \alpha ^{-}_{l \mid s} =\sqrt{\frac{\Delta -\sqrt{ \Delta ^{2}-4 det \sqcap _{(l,s)}}}{2}};(l\ne s) \end{aligned}$$

To quantify three-mode bipartite entanglement, we use the one-mode (l) versus two-mode (sp) logarithmic negativity \(\epsilon _{l \vert sp}\), defined as [74, 87]

$$\begin{aligned} \epsilon _{l \vert sp}= max[0,-ln(2 \alpha ^{-}_{l \vert sp})] \end{aligned}$$
(52)

where, \(\alpha ^{-}_{l \vert sp}= min\ \ eig\vert i \Omega _{3} (\Sigma _{l \vert sp} \sqcap _{(l,s,p)}\Sigma _{l \vert sp})\vert\), with, \(\Omega _{3}=\bigoplus ^{3}_{k=1}i\sigma _{y}\) (\(\sigma _{y}\) is the y-Pauli matrix), \(\Sigma _{l\vert sp}\) is the matrix that inverts the sign of momentum of mode l (\(l\ne s \ne p\)).

To study the genuine tripartite entanglement, we introduce the tripartite negativity defined as [74, 87]

$$\begin{aligned} \epsilon _{(l,s,p)}=(\epsilon _{l \vert sp}\epsilon _{s\vert pl}\epsilon _{p \vert ls})^{\frac{1}{3}} \end{aligned}$$
(53)

6 Analyse and discussion

Fig. 2
figure 2

Plots of logarithmic negativity (\(\epsilon _{l\vert s}\),\(\epsilon _{l\vert sp}\)) as a function of squeezing parameter r, with \(\chi =0.05\); \(\Gamma =0.05\); \(T=0.1\)mk; \(C=32.35\) in the three-mode block (\(b_{1}, b_{2}, a_{1}\))

Full size image
Fig. 3
figure 3

Plots of logarithmic negativity (\(\epsilon _{l\vert s}\),\(\epsilon _{l\vert sp}\)) as a function of squeezing parameter r, with \(\chi =0.05\); \(\Gamma =0.05\); \(T=0.1\)mk; \(C=32.35\) in the three-mode block (\(b_{2}, a_{1}, a_{2}\))

Full size image

By exploiting experimental values reported in Ref [86] \(\lbrace \frac{\omega _{b}}{2\pi }= 947\times 10^{3}\)Hz, the mechanical damping rate \(\frac{\lambda }{2\pi }=140\)Hz and the mass of the movable mirror \(m= 145\)ng, the cavity length and frequency are, respectively, \(L=25\)mm and \(\frac{\omega _{a}}{2\pi }= 5.26\times 10^{14}\)Hz, the laser frequency \(\frac{\omega _{L}}{2\pi }=2.82\times 10^{14}\)Hz and the drive laser power \(\varrho =11\) mW \(\rbrace\), we plot one-mode versus one-mode logarithmic negativity \(\epsilon _{l \vert s}\); (\(l\ne s\)) and one-mode versus two-mode logarithmic negativity \(\epsilon _{l\vert sp}\); (\(l\ne s\ne p\)) as a function of the squeezing parameter r for fixed values of the photon hopping strength (\(\chi =\frac{\tau }{\mu }\)) and the phonon tunneling strength (\(\Gamma =\frac{\eta }{\mu }\)). The numerical results are shown in Figs. 2 and 3. In Fig. 2a which presents the behavior of the entanglement in the block with three modes (\(b_{1}, b_{2}, a_{1}\)), i.e., the entanglement shared by the mode \(b_{1}\) is either individually with mode \(b_{2}\) and mode \(a_{1}\) (\(\epsilon _{b_{1}\vert b_{2}}, \epsilon _{b_{1}\vert a_{1}}\)), or jointly with the two-mode (\(b_{2} - a_{1}\)) ( \(\epsilon _{b_{1}\vert b_{2}a_{1}}\)). Note that for small values of r, \(\epsilon _{b_{1}\vert a_{1}}\) rapidly vanishes, while \(\epsilon _{b_{1}\vert b_{2}}\) and \(\epsilon _{b_{1}\vert b_{2}a_{1}}\) remain non-zero. This means that mode \(b_{1}\) can simultaneously share entanglement with the two-mode (\(b_{2} - a_{1}\)) and also individually with mode \(b_{2}\) but it cannot share entanglement with single mode \(a_{1}\). \(\epsilon _{b_{1}\vert b_{2}}\) remains robust against the rise of r, but eventually vanishes for \(r \ge 1.96\). For \(1.96 \le r \le 2.2\), there is no entanglement sharing individually between the mode \(b_{1}\) and each single remaining modes (\(b_{2}\), \(a_{1}\)), while, there is entanglement sharing by mode \(b_{1}\) to the two-mode (\(b_{2} - a_{1}\)), i.e., \(\lbrace \epsilon _{b_{1}\vert b_{2}}=0, \epsilon _{b_{1} \vert a_{1}}=0, \epsilon _{b_{1} \vert b_{2}a_{1}} \ne 0 \rbrace\). Now, we investigate the behavior of entanglement in the configurations \(\epsilon _{b_{2} \vert a_{1}}, \epsilon _{b_{2} \vert b_{1}}\) and \(\epsilon _{b_{2} \vert a_{1}b_{1}}\) (Fig. 2b). We remark that all terms \(\epsilon _{b_{2}\vert a_{1}}, \epsilon _{b_{2}\vert b_{1}}\) and \(\epsilon _{b_{2} \vert a_{1}b_{1}}\) are non-zero, meaning that the mode \(b_{2}\) is correlated with single modes \(b_{1}\) and \(a_{1}\) and with the two-mode (\(b_{1} - a_{1}\)) in a small range of very lower values of r (\(0.00 \le r \lneq 0.11\)). Obviously, we observe that with an increase of the squeezing parameter, \(\epsilon _{b_{2}\vert a_{1}}\) becomes zero, while the quantities \(\epsilon _{b_{2}\vert b_{1}}\) and \(\epsilon _{b_{2}\vert a_{1}b_{1}}\) are non-zero. This means that the mode \(b_{2}\) is not able to share entanglement individually with mode \(a_{1}\) but it can remarkably share it individually with mode \(b_{1}\) as well as with two modes (\(a_{1} - b_{1}\)). Unlike \(\epsilon _{b_{2}\vert b_{1}}\) and \(\epsilon _{b_{2}\vert a_{1}}\), when r becomes larger (\(1.96 \le r \le 2.2\)), \(\epsilon _{b_{2}\vert a_{1}b_{1}}\) remains non-zero. Thus, although \(b_{2}\) is unable to share the entanglement with the individual modes \(a_{1}\) and \(b_{1}\), it can nevertheless share it simultaneously with the two-mode (\(a_{1} - b_{1}\)). In the configurations \(\epsilon _{a_{1}\vert b_{1}}, \epsilon _{a_{1}\vert b_{2}}\) and \(\epsilon _{a_{1}\vert b_{1}b_{2}}\) (Fig. 2c), the entanglement shared by \(a_{1}\) conjointly with \(b_{1}\) and \(b_{2}\) is the most dominated especially for a higher values of r (\(0.16 \le r \lneq 0.62\)), where \(\epsilon _{a_{1}\vert b_{1}}\) and \(\epsilon _{a_{1}\vert b_{2}}\) are totally vanished. In this case \(a_{1}\) can share entanglement with modes \(b_{1}\) and \(b_{2}\) only in a collective way. We notice also that for the smallest values of r (\(r \le 0.11\)), \(a_{1}\) can share entanglement individually and collectively with \(b_{1}\) and \(b_{2}\), i.e., \(\lbrace \epsilon _{a_{1}\vert b_{1}} \ne 0, \epsilon _{a_{1}\vert b_{2}}\ne 0, \epsilon _{a_{1}\vert b_{1}b_{2}} \ne 0 \rbrace\). In addition we remark that for a small range of r (\(0.11 \le r \le 0.16\)), \(\epsilon _{a_{1}\vert b_{2}}\) is zero, while \(\epsilon _{a_{1}\vert b_{1}}\) and \(\epsilon _{a_{1}\vert b_{1}b_{2}}\) are non-zero, which means that \(a_{1}\) is correlated individually only to mode \(b_{1}\), and that entanglement sharing occurs with the two-mode (\(b_{1} - b_{2}\)). From this part of our study, we can conclude that sharing entanglement between modes \(b_{1}\), \(b_{2}\) and \(a_{1}\) is monogamous.

Subsequently, we will inspect the property of monogamy in a three-mode block (\(b_{2}\), \(a_{1}\), \(a_{2}\)). Figure 3a shows that entanglement cannot be shared freely between modes. Indeed, in the configurations \(\epsilon _{b_{2}\vert a_{2}}, \epsilon _{b_{2}\vert a_{1}}\) and \(\epsilon _{b_{2}\vert a_{1}a_{2}}\), the simultaneous emergence of individual and collective sharing of entanglement between mode \(b_{2}\) and modes \(a_{1}\) and \(a_{2}\) (\(\epsilon _{b_{2}\vert a_{2}} \ne 0, \epsilon _{b_{2}\vert a_{1}} \ne 0, \epsilon _{b_{2}\vert a_{1}a_{2}} \ne 0\)) occurs just in a very restricted range of small values of r (\(0.00 \le r \le 0.11\)). By increasing the values of r, we find that \(\epsilon _{b_{2}\vert a_{1}}=0\), while \(\epsilon _{b_{2}\vert a_{2}}\) and \(\epsilon _{b_{2}\vert a_{1}a_{2}}\) are non-zero, which means that the mode \(b_{2}\) can share the entanglement with the mode \(a_{2}\) and with the two-mode (\(a_{1} - a_{2}\)), but cannot be individually entangled with mode \(a_{1}\). If we further increase the values of r, then \(\epsilon _{b_{2}\vert a_{2}}\) vanishes, while \(\epsilon _{b_{2}\vert a_{1}a_{2}}\) is non-zero. In this range of large values of r (\(0.16 \le r \lneq 0.64\)), the mode \(b_{2}\) can share entanglement with the two-mode (\(a_{1} - a_{2}\)), but it is unable to share entanglement individually with each of them.

In the following, we will examine the sharing of entanglement in the three-mode block (\(a_{1}, a_{2}, b_{2}\)), discussing in more detail the bipartite and tripartite logarithmic negativities \(\epsilon _{a_{1}\vert b_{2}}, \epsilon _{a_{1}\vert a_{2}}\) and \(\epsilon _{a_{1}\vert a_{2}b_{2}}\) (Fig. 3b). For a wide range of values of r (\(0.11 \lneq r \lneq 1.9\)), we remark that \(\epsilon _{a_{1}\vert b_{2}}=0\), \(\epsilon _{a_{1}\vert a_{2}}\) and \(\epsilon _{a_{1}\vert a_{2}b_{2}}\) are non-zero, meaning that the mode \(a_{1}\) cannot be entangled individually with \(b_{2}\) but it is able to share entanglement individually with mode \(a_{2}\) in addition to sharing it with the two-mode (\(a_{2} - b_{2}\)). For very small values of r (\(0.00 \le r \lneq 0.11\)), the mode \(a_{1}\) can share entanglement individually with \(b_{2}\) and \(a_{2}\) in addition to sharing it with the two-mode (\(a_{2} - b_{2}\)), i.e., \(\epsilon _{a_{1}\vert b_{2}} \ne 0\), \(\epsilon _{a_{1}\vert a_{2}} \ne 0\) and \(\epsilon _{a_{1}\vert a_{2}b_{2}} \ne 0\). When \(1.89 \le r \le 2.0\), we find that \(\epsilon _{a_{1}\vert b_{2}}=0\), \(\epsilon _{a_{1}\vert a_{2}} = 0\) and \(\epsilon _{a_{1}\vert a_{2}b_{2}} \ne 0\), meaning that mode \(a_{1}\) cannot be entangled individually neither with \(b_{2}\) nor with \(a_{2}\), but it is able to share entanglement with the two-mode (\(a_{2} - b_{2}\)).

Finally, we investigate entanglement behavior in the three-mode block (\(a_{2}, a_{1}, b_{2}\)), i.e., \(\epsilon _{a_{2}\vert b_{2}}, \epsilon _{a_{2}\vert a_{1}}\) and \(\epsilon _{a_{2}\vert b_{2}a_{1}}\) (Fig. 3c). We notice as Fig. 3 shows that during the evolution of quantities \(\epsilon _{a_{2}\vert b_{2}}, \epsilon _{a_{2} \vert a_{1}}\) and \(\epsilon _{a_{2} \vert b_{2}a_{1}}\) versus r, three intervals of r can be distinguished. In the first one (\(0.00 \le r \le 0.16\)) we remark that \(\lbrace \epsilon _{a_{2} \vert b_{2}}\ne 0, \epsilon _{a_{2}\vert a_{1}}\ne 0, \epsilon _{a_{2}\vert b_{2}a_{1}} \ne 0 \rbrace\), which shows that mode \(a_{2}\) is able to share entanglement individually with mode \(b_{2}\) and mode \(a_{1}\) and also collectively with the two-mode (\(b_{2} - a_{1}\)). In the second range (\(0.16 \le r \le 1.88\)) which is the largest one, the mode \(a_{2}\) is individually entangled only with mode \(a_{1}\) and with the two-mode (\(b_{2} - a_{1}\)). Regarding the third range (\(1.88 \le r \le 2.03\)), there is no individual entanglement shared between mode \(a_{2}\) and the other remaining modes , i.e., \(\lbrace \epsilon _{a_{2}\vert b_{2}}= 0, \epsilon _{a_{2}\vert a_{1}}=0\rbrace\), whereas there exist collective entanglement sharing between mode \(a_{2}\) and the two-mode (\(b_{2} - a_{1}\)), i.e., \(\epsilon _{a_{2} \vert b_{2}a_{1}} \ne 0\).

In general, we notice that all the quantities (\(\epsilon _{l\vert s}\);(\(l\ne s\)) and (\(\epsilon _{l \vert sp}\); (\(l\ne s\ne p\)) in the two three-mode blocks (\(b_{1}, b_{2}, a_{1}\)) and (\(b_{2}, a_{1}, a_{2}\)) have the same evolution with r: the entanglement begins by increasing, reaches a maximum then it decreases and ends up canceling out. As shown in Fig. 2(3), the degree of entanglement shared by \(a_{1}(b_{2})\) jointly or individually with modes \(b_{1}\) and \(b_{2}\) (\(a_{1}\) and \(a_{2}\)) remains very low compared to that of modes \(b_{1}(a_{1})\) and that of mode \(b_{2}(a_{2})\). In addition, we find that one-mode versus two-mode entanglement is robust against increasing of r values than one-mode versus one-mode entanglement. Moreover, the former has a very large degree compared to the degree of the latter one, as expected by CKW-monogamy [75].

Fig. 4
figure 4

Effect of phonon tunneling strength \(\Gamma\) and photon hopping strength \(\chi\) on tripartite entanglement with \(r=0.1\) and \(T=0.1\)mK

Full size image

In Fig. 4, we plot the tripartite negativity as a function of the phonon tunneling strength \(\Gamma\) and the photon jumping strength \(\chi\) in the two three-mode blocks (\(b_{1}, b_{2}, a_{1}\))Fig. 4a and (\(b_{2}, a_{1}, a_{2}\)) (Fig. 4b). Based on the results shown in Fig. 4a, it is clearly indicated that for a fixed value of \(\Gamma\), the tripartite entanglement degrades with increasing \(\chi\) and eventually vanishes for: \(0.9 \le \chi \le 2.0\) and \(0.0 \le \Gamma \le 0.2\), signifying the disappearance of tripartite entanglement when \(\chi\) has reached 0.9. The emergence of tripartite entanglement requires a minimum value of \(\Gamma\)(\(\Gamma = 0.01\)), then it increases with the increasing of \(\Gamma\) values. Remarkably, the area for which the entanglement exists widens with the rise of both \(\Gamma\) and \(\chi\). For instance, for \(\Gamma = 0.05\), tripartite entanglement is observed when \(0.0 \le \chi \le 0.3\), while for \(\Gamma = 0.20\) it is observed when \(0.0 \le \chi \le 0.9\). As an example of the optimal situation for strong entanglement, the area selected is one in which the value of \(\Gamma\) can be chosen between 0.18 and 0.20, while \(\chi\) can be taken between 0.0 and 0.1. In Fig. 4b, we examine the effects of the parameters \(\chi\) and \(\Gamma\) on tripartite entanglement strength in the three-mode block (\(b_{2}, a_{1}, a_{2}\)). Note that, in the range of values of \(\Gamma\) between 0.0 and 0.8, the maximum of shared entanglement is obtained for \(\Gamma\) = 0.3 whatever the value of \(\chi\). For a fixed value of \(\chi\), the tripartite entanglement increases with \(\Gamma\), then it decreases when \(\Gamma\) = 0.3. For a fixed value of \(\Gamma\), varying the values of \(\chi\) has a negligible effect on the amount of entanglement. Besides, Fig. 4b shows a strong decrease in the range of entanglement with increasing values of \(\chi\). For example, for \(\chi =0.00\), tripartite entanglement is strong when \(0.2 \le \Gamma \le 0.4\), whereas for \(\chi =0.03\), tripartite entanglement is strong when \(0.2 5\le \Gamma \le 0.35\). Contrary to the first region, the tripartite entanglement degrades and remains low for higher values of \(\Gamma\) compared to values of \(\chi\), i.e., \(0.00 \le \chi \le 0.2\) and \(0.9 \le \Gamma \le 2.0\).

7 Conclusion

This work focused on the study of entanglement monogamy as well as the behavior of tripartite entanglement, in two blocks with three modes \((b_{1}, b_{2}, a_{1})\) and \((b_{2}, a_{1}, a_{2})\), depending on the phonon tunneling force \(\Gamma\) and photon jump force \(\chi\). It follows that, in the case of the two blocks, the sharing of the entanglement obeys the law of monogamy, this means that each mode cannot freely share the entanglement with the other modes. We also analyzed the effects of the combined actions of squeezing light, photon hopping process and phonon tunneling process on entanglement sharing.

For our purpose, we have fixed the value of r and we have varied both the values of \(\chi\) and the values of \(\Gamma\). Combining the effects of \(\chi\) and \(\Gamma\) can produce strong tripartite entanglement. Moreover, the tripartite entanglement degrades and sometimes vanishes due to a very large difference between the values of \(\chi\) and the values of \(\Gamma\). Finally, the main result of this article is that quantum entanglement cannot be freely shared between the three modes constituting each of the two blocks studied \((b_{1}, b_{2}, a_{1})\) and \((b_{2}, a_{1}, a_{2})\). The analysis of the combined action of the parameters governing the system on the emergence and the degree of entanglement are of great importance to use the considered system with a greater precision to bring a great performance.