1 Introduction

The main difference between quantum physics and classical physics is the nonclassical correlations in microscopic systems called quantum correlation [1]. Researchers have spent many years trying to understand such quantum correlation. At first, entanglement was regarded as the sole quantum correlation in a quantum system [2]. But things have changed when researchers realize that certain separable states possess quantum correlation that entanglement can’t characterize it. Such kind of quantum correlation can be quantified by some new measures, e.g., quantum discord [3, 4]. Quantum discord is the difference between two expressions of the mutual information extended from classical to quantum condition. It has gained comprehensive attentions after being presented by Zurek et al. Inspired by the meaningful results [5–7] about quantum discord, people have proposed different kinds of quantum correlation measures, such as geometric discord [8], measurement-induced disturbance [9] and measurement-induced nonlocality [10]. These measures of quantum correlation have shed new light on many fields, e.g., quantum phase transition (QPT).

QPT [11] is a qualitative change in the ground state by varying a physical parameter in the quantum many-body system. Unlike classical phase transition, which occurs at a nonzero temperature, the QPT occurs at absolute zero temperature [12]. There is a critical point which separates the two different ground states. So, the critical phenomenon is meaningful and definite to the quantum many-body systems. The main method used to investigate the quantum critical phenomenon is the renormalization group theory. During the past years, much effort had been made to investigate the QPT in solid-state system using this theory; especially, the entanglement in the Heisenberg and Ising systems has been extensively studied by the approach of quantum renormalization group (QRG) [13–17]. It is found that a nonanalytic behavior will be exhibited by the first derivative of the entanglement at the critical point [18]. The minimum value of the first derivative for entanglement and its positions scales with an exponent of the system size [19]. All these results enrich our knowledge about the QPT and quantum information theory. But there is still some work needed to be investigated. First of all, most previous studies mainly concentrate on the two-block state entanglement in the model. But we also have to know the global entanglement in the system and to get the effects of every block on the entanglement. Secondly, as is mentioned above, entanglement cannot account for all the aspects of quantum correlation. These motivate us to investigate the global quantum correlation and QPT by using QRG theory. In addition, monogamy relation for entanglement [20] has been a subject in the quantum information theory over the years. It is worthwhile to investigate whether the monogamy relation of entanglement and quantum correlation exhibits QPT after enough steps of the renormalization.

In this paper, we investigate the renormalization of global quantum correlation and monogamy relation in the Heisenberg XXZ model. Our paper is organized as follows. In Sect. 2, we review the analytical solution of the Heisenberg XXZ model. In Sect. 3, we analyze the global entanglement and obtain the exact expressions of the negativities \(N_{1\text {--}23}\), \(N_{2\text {--}13}\) and \(N_{3\text {--}12}\). We give the nonanalytic and the scaling behaviors of those quantities. The property of renormalized monogamy relation for entanglement is also given in this part. In Sect. 4, we investigate the anisotropy parameter-dependence behavior, the scaling behavior, and the monogamy relation of global measurement-induced disturbance through QRG theory. Finally, in Sect. 5, we give a conclusion of this paper.

2 Analytical solution of the anisotropic Heisenberg XXZ model

The main purpose of QRG method is to eliminate the degrees of freedom of the model followed by a repeated operation. The number of variables gradually reduces until a more manageable condition is reached [21, 22]. In this way, we can get the effective Hamiltonian \(H_\mathrm{eff}\), which has structural similarities to the original Hamiltonian H. The original Hilbert space is also replaced by a reduced Hilbert space that acts on the renormalized subspace [18].

The Hamiltonian of the anisotropic Heisenberg XXZ model on a periodic chain of N sites is [19]

$$\begin{aligned} H = \frac{J}{4}\left( {\sum _{i=1}^N {\sigma _i^x \sigma _{i+1}^x +\sigma _i^y \sigma _{i+1}^y +\Delta \sigma _i^z \sigma _{i+1}^z}} \right) , \end{aligned}$$
(1)

where J is the exchange interaction, \(\Delta \) is the anisotropy parameter and \(\sigma _i^\tau ({\tau =x,y,z})\) are Pauli operators at site i.

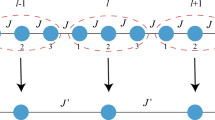
To get a self-similar Hamiltonian after each QRG step, it is essential to divide the spin chain into three-site blocks. The corresponding block Hamiltonian has two degenerate ground states as follows [16, 19]

$$\begin{aligned} \left| {\psi _0 } \right\rangle= & {} \frac{1}{\sqrt{2+q^{2}}}\left( {\left| {110} \right\rangle +q\left| {101} \right\rangle +\left| {011} \right\rangle } \right) , \nonumber \\ \left| {\psi _0^{\prime } } \right\rangle= & {} \frac{1}{\sqrt{2+q^{2}}}\left( {\left| {100} \right\rangle +q\left| {010} \right\rangle +\left| {001} \right\rangle } \right) , \end{aligned}$$
(2)

where

$$\begin{aligned} q=-\frac{\Delta +\sqrt{\Delta ^{2}+8}}{2}. \end{aligned}$$
(3)

The density matrix of the ground state is defined by

$$\begin{aligned} \rho =\left| {\psi _0 } \right\rangle \left\langle {\psi _0 } \right| \hbox { or } \rho =\left| {\psi _0^{\prime }} \right\rangle \left\langle {\psi _0^{\prime } } \right| . \end{aligned}$$
(4)

The effective Hamiltonian of the renormalized system is again a XXZ model with the scaled couplings \(J^{\prime }\) and \(\Delta ^{\prime }\)

$$\begin{aligned} H_\mathrm{eff} =\frac{J^{{\prime }}}{4}\left( {\sum _{i=1}^{N/3} {\left( {\sigma _i^x \sigma _{i+1}^x +\sigma _i^y \sigma _{i+1}^y } \right) +\Delta ^{\prime }\left( {\sigma _i^z \sigma _{i+1}^z } \right) }} \right) , \end{aligned}$$
(5)

where the renormalized couplings are

$$\begin{aligned} J^{{\prime }} = J\left( {\frac{2q}{2+q^{2}}} \right) ^{2}, \quad \Delta ^{{\prime }} = \frac{\Delta q^{2}}{4}. \end{aligned}$$
(6)

3 Renormalization of global negativity

Using negativity, Canosa and Rossignoli [23] have discussed the global bipartite entanglement in the XXZ chain. For a given quantum state with density matrix \(\rho \), the negativity is defined by [24]

$$\begin{aligned} Ne\left( \rho \right) =\frac{||\rho ^{T_i }||-1}{2}, \end{aligned}$$
(7)

where \(||\rho ^{T_i }||\) is the sum of the absolute values of the eigenvalues of \(\rho ^{T_i}\) and \(\rho ^{T_i}\) denotes the partial transpose of density matrix \(\rho \) with respect to party i. As is known, the partial transpose of a density matrix does not change the trace of a density matrix, so we can easily find that the negativity of \(\rho \) equals the sum of the absolute values of the negative eigenvalues of \(\rho ^{T_i}\). It has verified to be an entanglement monotone and hence a proper measure of entanglement [25].

After the nth step renormalization group, the size of the system will be a three-site block model. The density matrix of the ground state is

$$\begin{aligned} \rho = \left| {\psi _0 } \right\rangle \left\langle {\psi _0 } \right| = \frac{1}{k^{2}}\left[ {{\begin{array}{cccccccc} 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 1&{}\quad q&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad q&{}\quad {q^{2}}&{}\quad 0&{}\quad q&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 1&{}\quad q&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ \end{array} }} \right] , \end{aligned}$$
(8)

where \(k=\sqrt{2+q^{2}}\).

Fig. 1
figure 1

Diagrams of the partial transpose a the corner side of the block and b the middle side of the block

Full size image

In Fig. 1, we plot the two kinds of partial transpose diagrams. According to the methods mentioned before, the partial transpose of density matrix \(\rho \) with respect to block 1 or 3 is

$$\begin{aligned} \rho _{1\text {--}23}^T =\rho _{3\text {--}12}^T =\frac{1}{k^{2}}\left[ {{\begin{array}{cccccccc} 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad q&{}\quad 0 \\ 0&{}\quad 1&{}\quad q&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad q&{}\quad {q^{2}}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ q&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ \end{array} }} \right] . \end{aligned}$$
(9)

The partial transpose of density matrix \(\rho \) with respect to block 2 is

$$\begin{aligned} \rho _{_{2\text {--}13} }^T =\frac{1}{k^{2}}\left[ {{\begin{array}{cccccccc} 0&{}\quad 0&{}\quad 0&{}\quad q&{}\quad 0&{}\quad 0&{}\quad q&{}\quad 0 \\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad {q^{2}}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ q&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ q&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ \end{array} }} \right] . \end{aligned}$$
(10)

The global negativity between the subsystems of 1–23, 3–12 and 2–13 is obtained, respectively

$$\begin{aligned} Ne_{1\text {--}23}= & {} Ne_{3\text {--}12} =\frac{\sqrt{q^{2}+1}}{k^{2}}, \nonumber \\ Ne_{2\text {--}13}= & {} -\frac{\sqrt{2}q}{k^{2}}. \end{aligned}$$
(11)

3.1 The \(\triangle \)-dependence of global negativity

In Fig. 2, we have plotted \(Ne_{1\text {--}23}\) (left) and \(Ne_{2\text {--}13}\) (right) versus \(\Delta \) at different QRG steps. There is a cross- point for every plot. The intersection point coordinates for \(Ne_{1\text {--}23}\) and \(Ne_{2\text {--}13}\) are different. The coordinates are(1, 0.3727) and(1, 0.4714), respectively. So the critical point of global entanglement is at \(\Delta _\mathrm{c} =1\). The global negativity will develop two different saturated values: \(Ne_{1\text {--}23} =0.433\) for \(0 \le \Delta <1\) and 0 for \(\Delta >1\), while \(Ne_{2\text {--}13} =0.5\) for \(0 \le \Delta <1\) and 0 for \(\Delta >1\). The saturated value of \(Ne_{2\text {--}13}\) is larger than that of \(Ne_{1\text {--}23}\). This implies that for a three-site block system, the partial transpose of an asymmetric particle can get stronger entanglement than that of the symmetric one.

Fig. 2
figure 2

\(Ne_{1\text {--}23}\) and \(Ne_{2\text {--}13}\) as a function of \(\Delta \) at different QRG steps

Full size image

The first derivative of the negativity for the 0-th step of QRG is

$$\begin{aligned} Ne_{1\text {--}23}^1= & {} Ne_{3\text {--}12}^1 =\frac{q^{3}\eta }{k^{4}\sqrt{q^{2}+1}}, \nonumber \\ Ne_{2\text {--}13}^1= & {} -\frac{\sqrt{2}\Delta }{\left( {\Delta ^{2}+8} \right) ^{3/2}}, \end{aligned}$$
(12)

where \(\eta =\left( {\frac{\Delta }{2\sqrt{\Delta ^{2}+8}} + \frac{1}{2}} \right) \).

Because of the tedious expressions of the first derivative of negativity for the nth step QRG, we will not write out them here. We present the numerical results of the quantities below.

Fig. 3
figure 3

First derivative of \(Ne_{1\text {--}23}\) and \(Ne_{2\text {--}13}\) as a function of \(\Delta \) at different QRG steps

Full size image

We have plotted the first derivative of \(Ne_{1\text {--}23}\) and \(Ne_{2\text {--}13}\) versus \(\Delta \) in Fig. 3. From the figures, we find that the derivative of global negativity tends to diverge at the critical point \(\Delta _\mathrm{c} =1\) [15]. Every plot in the figure exhibits as an asymmetrical function about \(\Delta _\mathrm{c}\). There is a minimum value for each curve, and the minimum value becomes more pronounced close to the critical point \(\Delta _\mathrm{c} =1\). This means that the system presents a second-order QPT. Comparing the two figures, we find that the absolute minimum value of \({dNe_{1\text {--}23} }/{d\Delta }\) is smaller than that of \({dNe_{2\text {--}13} }/{d\Delta }\).

Fig. 4
figure 4

a The logarithm of the absolute value of the minimum \(\ln \left| {{dNe_{1\text {--}23} }/{d\Delta }} \right| _\mathrm{m}\) and \(\ln \left| {{dNe_{2\text {--}13}}/{d\Delta }} \right| _\mathrm{m}\) versus the logarithm of the chain size \(\ln \left( N \right) \). b The scaling behavior of \(\Delta _\mathrm{m}\) in terms of system size \(\ln \left( N \right) \)

Full size image

3.2 Nonanalytic and scaling behavior

Figure 4 gives the behavior about the \({dNe}/{d\Delta }\) and the position of the minimum (\(\Delta _\mathrm{m}\)) of \({dNe}/{d\Delta }\) versus the increasing size of the model. The global negativity against the chain size shows linear behavior and the two quantities \(Ne_{1\text {--}23}\) and \(Ne_{2\text {--}13}\) are parallel to each other. The results demonstrate that the QRG implementation of global negativity also genuinely gains the critical property of the model. The exponent for the plot is \({|dNe}/{d \Delta }|_{\mathrm{m}} \sim N^{0.47}\). For a more particular analysis of the scaling behavior of the system, we have also plotted \(\ln |\Delta _\mathrm{m} -1|\) versus the system size. It can be seen that the positions of the minimum \(\Delta _\mathrm{m}\) of \({dNe_{1\text {--}23}} /{d\Delta }\) and \({dNe_{2\text {--}13}} /{d\Delta }\) gradually tend to the critical point \(\Delta _\mathrm{c} =1\). The scaling behaviors are found in the figure. The positions of the minimum \(\Delta _\mathrm{m}\) of \({dNe_{1\text {--}23}} /{d\Delta }\) and \({dNe_{2\text {--}13}}/{d\Delta }\) nearly overlap.

3.3 The behavior of the monogamy relation for negativity

Now, we analyze the monogamy relation for negativity. In multi-party quantum states, there is a strict constraint on distributing pairwise entanglement in a three-qubit pure state, the so-called monogamy. For a three-site block state, the inequality in terms of negativity is [26]

$$\begin{aligned} {Ne}_{12}^{\prime 2} + {Ne}_{13}^{\prime 2} \le {Ne}_{1(23)}^{\prime 2} , \end{aligned}$$
(13)

where \({Ne}_{12}^{\prime }\) and \({Ne}_{13}^{\prime }\) are the negativities of the mixed states \(\rho _{12} =Tr_3 \left( \rho \right) \) and \(\rho _{13} =Tr_2 \left( \rho \right) \), respectively. In order to keep consistent with Ref. [26], we take \({Ne}^{\prime } = ||\rho ^{T_i}||-1\) here. \({Ne}_{1(23)}^{\prime }\) is the entanglement between 1 and the object 23. From the Ref. [26], we know \({Ne}_{1(23)}^{\prime } =\sqrt{2\left( {1-Tr\rho _1^2 } \right) }\). The analytical expressions for \({Ne}_{12}^{\prime }\) and \({Ne}_{13}^{\prime }\) can be easily computed through the above formula. The result is \({Ne}_{12}^{\prime } =2{\left( {\sqrt{4q^{2}+1}-1} \right) }/{\left( {q^{2}+2} \right) }\) and \({Ne}_{13}^{\prime } ={\left( {\sqrt{q^{4}+4}-q^{2}} \right) }/{\left( {q^{2}+2} \right) }\), respectively. In a similar way, we can get the monogamy inequalities for blocks 2 and 3. The expressions will be \({Ne}_{21}^{\prime 2} + {Ne}_{23}^{\prime 2} \le {Ne}_{2(13)}^{\prime 2} \) and \({Ne}_{31}^{\prime 2} + {Ne}_{32}^{\prime 2} \le {Ne}_{3(12)}^{\prime 2}\). Notice that \({Ne}_{21}^{\prime } ={Ne}_{23}^{\prime } = {Ne}_{32}^{\prime } = {Ne}_{12}^{\prime }\), \({Ne}_{31}^{\prime } ={Ne}_{13}^{\prime }\). The difference between the two sides of inequality relation can be set as the residual entanglement \(\tau _{1(23)} =\tau _{3(12)} ={Ne}_{1(23)}^{\prime 2} -{Ne}_{12}^{\prime 2} -{Ne}_{13}^{\prime 2} \) and \(\tau _{2(13)} = {Ne}_{2(13)}^{\prime 2} - {Ne}_{21}^{\prime 2} - {Ne}_{23}^{\prime 2}\). The \({Ne}_{2(13)}^{\prime }\) is \(\sqrt{2 \left( {1-Tr\rho _2^2 } \right) }\). Now, we begin to investigate the behavior of the residual entanglement.

Fig. 5
figure 5

\(\tau _{1(23)}\) and \(\tau _{2(13)}\) as a function of \(\Delta \) at different QRG steps

Full size image

We plot \(\tau _{1(23)}\) (left) and \(\tau _{2(13)}\) (right) versus \(\Delta \) in Fig. 5 for different QRG steps. The curves of \(\tau _{1(23)}\) and \(\tau _{2(13)}\) also cross each other at \(\Delta _\mathrm{c} =1\). This means that the residual entanglement also can be used to indicate the QPT. It is shown that both quantities obey the monogamy relation. This suggests that the entanglement between any two blocks in a three-site block system is limited by the entanglement between these two blocks and the third block [27]. Ref. [28] proposed that the negativity of a state can never exceed its concurrence, this means \({Ne}_{12}^{\prime } \le C_{12}, {Ne}_{13}^{\prime } \le C_{13}\). As the existence of \(C_{12} +C_{13} \le C_{1(23)}\) [20], the monogamy relation of negativity is identical with it.

Fig. 6
figure 6

a The logarithm of the absolute value of the minimum \(\ln \left| {{d\tau _{1(23)} }/{d\Delta }} \right| _\mathrm{m}\) and \(\ln \left| {{d\tau _{2(13)} }/{d\Delta }} \right| _\mathrm{m}\) versus the logarithm of the chain size \(\ln \left( N \right) \). b The scaling behavior of \(\Delta _\mathrm{m}\) in terms of system size \(\ln \left( N \right) \)

Full size image

Figure 6 gives the scaling behavior of the residual entanglement versus the increasing size of the model. Clearly, the residual entanglement catches the critical behavior of the XXZ model too. The critical exponent \(\theta \) of the residual entanglement has no change because the critical exponent directly associates with the correlation length exponent, i.e., \(\theta =1/\upsilon =0.47\).

4 Renormalization of global measurement-induced disturbance

Measurement-induced disturbance (MID) is defined as the difference of two quantum mutual information, respectively, of a given state \(\rho \) shared by two parties A and B and the corresponding post-measurement state \(\varPi \left( \rho \right) \) [9]

$$\begin{aligned} \hbox {MID}(\rho )=I(\rho )-I\left( {\varPi \left( \rho \right) } \right) , \end{aligned}$$
(14)

where the mutual information, \(I(\rho )=S(\rho _A )+S(\rho _B) - S(\rho )\). Here \(S(\rho )=-tr\left( {\rho \log _2 \rho } \right) \) denotes the von Neumann entropy, with \(\rho _A\) and \(\rho _B\) being the reduced density matrix of \(\rho \) by tracing out A and B, respectively. \(I\left( {\varPi \left( \rho \right) } \right) \) quantifies the classical correlation in \(\rho \), with \(\varPi \rho = \sum \limits _{i,j} {\left( {\varPi _i^A \otimes \varPi _i^B} \right) \rho \left( {\varPi _i^A \otimes \varPi _i^B } \right) }\), where the measurement is induced by the spectral resolutions of the reduced states \(\rho _A =\sum _i {p_i^A \varPi }_i^A\) and \(\rho _B =\sum _i {p_i^B \varPi }_i^B\). \(\varPi \left( \rho \right) \) is a classical state for any complete set of projective measurements \(\left\{ {\varPi _i^A } \right\} \) and \(\left\{ {\varPi _i^B} \right\} \) [9, 29, 30].

4.1 The \(\triangle \)-dependence of global MID

For a three-site block system, \(\varPi \rho = \sum \limits _{i,j,k} {\left( {\varPi _i^{1} \otimes \varPi _i^{2} \otimes \varPi _i^{3} } \right) \rho \left( {\varPi _i^{1} \otimes \varPi _i^{2} \otimes \varPi _i^{3} } \right) }\). By taking \(\varPi _i =\left| i \right\rangle \left\langle i \right| \), \(\varPi _j =\left| j \right\rangle \left\langle j \right| \) and \(\varPi _k =\left| k \right\rangle \left\langle k \right| \left( {i,j,k=1,0} \right) \), we have

$$\begin{aligned} \varPi \left( \rho \right) =\frac{1}{k^{2}}\left[ {{\begin{array}{cccccccc} 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad {q^{2}}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ \end{array} }} \right] . \end{aligned}$$
(15)

According to Eq. (14), the global MID for this model is given by

$$\begin{aligned} \hbox {MID} = \frac{q^{2}}{k^{2}}\log _2 \left( {1+2/{q^{2}}} \right) +\frac{2}{k^{2}}\log _2 \left( {2+q^{2}} \right) . \end{aligned}$$
(16)
Fig. 7
figure 7

MID a and the first derivative of MID b of the model as a function of \(\Delta \) at different QRG steps

Full size image

The renormalization results for the MID and the first derivative of the MID are given in Fig. 7. We find that the MID curves will cross each other at the critical point \(\Delta _\mathrm{c} =1\). The cross-point coordinate is (1, 1.252). After enough QRG steps, there are two saturated values: for \(0\le \Delta <1\), MID =1.5, while for \(\Delta >1\), MID =0, which are associated with the two different phases, the spin-liquid and Néel phases [31]. Just like global negativity, the global MID also precisely indicates the QPT by reaching its minimums.

Fig. 8
figure 8

The scaling behavior of \(\ln |{d\hbox {MID}}/{d\Delta }|_\mathrm{m}\) and the \(\Delta _\mathrm{m}\) in terms of system size \(\ln \left( N \right) \)

Full size image

4.2 Scaling behavior

Figure 8 gives the scaling behaviors of \(\ln \left| {{d\hbox {MID}} /{d\Delta }} \right| _\mathrm{m}\) and the positions of \(\Delta _\mathrm{m}\) with the size of the model adding. MID also shows a linear behavior about the size of the system. Numerical results demonstrate that the exponent for this behavior is \(\left| {{d\hbox {MID}}/{d\Delta }} \right| \sim N^{0.47}\). The positions of the minimum \(\Delta _\mathrm{m}\) will gradually tend to the critical point \(\Delta _\mathrm{c} =1\). The typical exponent function relation is \(\Delta _\mathrm{m} =\Delta _\mathrm{c} +N^{-0.47}\). Compare the Fig. 8b with Fig. 4b, we find that every \(\Delta _\mathrm{m}\) of \({d\hbox {MID}}/{d\Delta }\) is smaller than that of \({dN\hbox {e}}/{d\Delta }\). This result indicates that the MID is quicker than the negativity in detecting the critical point \(\Delta _\mathrm{c}\) if we take the same iterations.

4.3 The property of the monogamy relation for MID

In the previous sections, we have shown that in a tripartite system, sharing entanglement between several parties is restricted by the monogamy relation. Researchers [32–35] have investigated such type of monogamy properties of quantum correlation

$$\begin{aligned} \xi _{12} +\xi _{13} \le \xi _{1(23)} \end{aligned}$$
(17)

Here, we want to know whether the global MID also obeys the monogamy relation?

$$\begin{aligned} \hbox {MID}_{12} +\hbox {MID}_{13} \le \hbox {MID}_{1(23)} \hbox { or } \hbox {MID}_{21} +\hbox {MID}_{23} \le \hbox {MID}_{2(13)} \end{aligned}$$
(18)

After some straightforward computation, we get the analytical expressions for the equation (18) as \(\hbox {MID}_{12} ={q^{2}\log _2 \left( {1+1/{q^{2}}} \right) }/{k^{2}}+{\log _2 \left( {1+q^{2}} \right) }/{k^{2}}\), \(\hbox {MID}_{13} =2/{k^{2}}\), \(\hbox {MID}_{1(23)} =S(\rho _1 )={-\log _2 (1/{k^{2}})}/{k^{2}}{-(1+q^{2})\log _2 ({(1+q^{2})}/{k^{2}})}/{k^{2}}\), \(\hbox {MID}_{2(13)} =S(\rho _2 ){=-2\log _2 (2/{k^{2}})}/{k^{2}}{-q^{2}\log _2 ({q^{2}}/{k^{2}})}/{k^{2}}\). In our model, we know \(\hbox {MID}_{12} =\hbox {MID}_{21} =\hbox {MID}_{23}\). We define the difference between the two sides of inequality relation \(Q_{\hbox {MID}} =\hbox {MID}_{12} +\hbox {MID}_{13} -\hbox {MID}_{1(23)} =\hbox {MID}_{21} +\hbox {MID}_{23} -\hbox {MID}_{2(13)}\). It is coincident that the two expressions are identical in this model.

Fig. 9
figure 9

a \(Q_\mathrm{MID}\) as a function of \(\Delta \) at different QRG steps. b The logarithm of the absolute value of minimum \(\ln \left| {{dQ_\mathrm{MID}} /{d\Delta }} \right| _\mathrm{m}\) versus the logarithm of the chain size \(\ln \left( N \right) \)

Full size image

Numerical simulations are performed for \(Q_\mathrm{MID}\) in Fig. 9, and the violation of monogamy is obtained for the model. Clearly, monogamy is an important aspect of entanglement which means the valuable resource is not freely sharable. But monogamy is not an intrinsic characteristic of other quantum correlation methods. We have known that the quantum discord will violate monogamy relation. MID is similar to QD. So, it is understandable that this measure demonstrates polygamy behavior. Particular for the state of Eq. (2) is a W state which does not follow the monogamy [35]. Figure 9b exhibits the linear behavior of \({dQ_\mathrm{MID} }/{d\Delta }\) versus \(\ln \left( N \right) \). Like previous quantities, the exponent relation for this behavior is \(\left| {{dQ_\mathrm{MID} }/{d\Delta }} \right| \sim N^{0.47}\) for it also comes from the property of the correlation length near the critical point.

5 Conclusion

In this work, we investigate the global quantum correlation and QPT in the anisotropic Heisenberg XXZ model using the QRG method. The negativity and the MID are adopted as the measures of the quantum correlation. The quantum critical phenomenon of the system is obtained through the QRG theory. The divergent behavior of the first derivative of the negativity and MID is accompanied by the scaling behavior in the vicinity of the critical point. The result shows that the MID is quicker than the negativity in detecting the critical point. In addition, the monogamy relation for every block is given and it can be used to exhibit QPT after enough steps of renormalization. The entanglement measured by negativity obeys the monogamy relation, while nonclassical correlation quantified by MID violates it, which means MID is polygamy in this model. These results convince us that the global negativity, measurement-induced disturbance, and the difference between monogamy relations also signify the criticality of the system.